Efficient Estimation of Semiparametric Transformation Models for the Cumulative Incidence of Competing Risks

Summary

The cumulative incidence is the probability of failure from the cause of interest over a certain time period in the presence of other risks. A semiparametric regression model proposed by Fine and Gray (1999) has become the method of choice for formulating the effects of covariates on the cumulative incidence. Its estimation, however, requires modeling of the censoring distribution and is not statistically efficient. In this paper, we present a broad class of semiparametric transformation models which extends the Fine and Gray model, and we allow for unknown causes of failure. We derive the nonparametric maximum likelihood estimators (NPMLEs) and develop simple and fast numerical algorithms using the profile likelihood. We establish the consistency, asymptotic normality, and semiparametric efficiency of the NPMLEs. In addition, we construct graphical and numerical procedures to evaluate and select models. Finally, we demonstrate the advantages of the proposed methods over the existing ones through extensive simulation studies and an application to a major study on bone marrow transplantation.

1. Introduction

Competing risks data arise when each study subject can experience one and only one of several distinct types of events or failures. A classical example of competing risks is death from different causes. In addition, patients who undergo an invasive surgical procedure to treat a particular disease, such as bone marrow transplantation for the treatment of leukemia (Kalbfleisch and Prentice (2002), chapter 8), may experience relapse of that disease or death related to the surgical procedure itself. Another example of competing risks is infection with a pathogen such as HIV-1 (Hudgens et al., 2001), whereby infection with one viral subtype precludes infection with other subtypes.

Competing risks data may be analyzed through the cause-specific hazard or cumulative incidence function. The cause-specific hazard function is the instantaneous rate of failure from a specific cause at a particular time given that the subject has not experienced a failure of any cause up until that point, and the cumulative incidence function measures the probability of occurrence of a specific failure type over a certain time period (Kalbfleisch and Prentice (2002), chapter 8). These two approaches are complementary: the cause-specific hazard is an instantaneous risk function whereas the cumulative incidence characterizes the subject's ultimate clinical experience. Standard survival analysis methods, such as the log-rank test and proportional hazards regression, can be applied to the cause-specific hazard function. The way in which covariates affect the cause-specific hazards may not coincide with the way in which they affect the cumulative incidence (Andersen et al., 2012).

Statistical methods have been developed to make inference about the cumulative incidence. Gray (1988) proposed a nonparametric log-rank-type test for comparing the cumulative incidence functions of a particular failure type among different groups. In the regression setting, Fine and Gray (1999) proposed a semiparametric proportional hazards model for the subdistribution of a competing risk. This model has become the method of choice with 2,000 citations and been incorporated into the statistical guidelines of the European Group for Blood and Marrow Transplantation (Iacobelli, 2013).

The Fine and Gray methodology has important limitations, however. First, it requires the modelling of the censoring distribution and may yield invalid inference if the censoring distribution is mis-modeled. Second, the estimation is based on the inverse probability of censoring weighting, such that the estimators are statistically inefficient and numerically unstable. Third, the model is restricted to the proportional subdistribution hazards structure, which may not hold in practice, and there are no model-checking tools. Fourth, the cause of failure needs to be known for every subject. Finally, joint inference on multiple risks is not provided.

Jeong and Fine (2006, 2007) proposed parametric regression models for the cumulative incidence function and derived maximum likelihood estimators. Their approach does not model the censoring distribution. However, it is difficult to parametrize failure time distributions, especially when there are multiple failure types. Incorrect parametrization can lead to erroneous inference.

In this paper, we develop semiparametric regression methods that avoid the aforementioned limitations of the existing methods. Specifically, we formulate the effects of covariates on the cumulative incidence function using a flexible class of semiparametric transformation models, which encompasses both proportional and non-proportional subdistribution hazards structures. We allow the cause of failure information to be partially missing. We derive efficient estimators for the proposed models through the NPMLE approach, which does not involve modelling the censoring distribution. We construct simple and fast numerical algorithms based on the profile likelihood (Murphy and van der Vaart, 2000) to obtain the estimators. We establish the asymptotic properties of the estimators through modern empirical process theory (van der Vaart and Wellner, 1996) and semiparametric efficiency theory (Bickel et al., 1993). Our approach allows for joint inference on multiple risks, which is desirable because an increase in the incidence of one risk decreases the incidence of other risks. We also develop numerical and graphical procedures to evaluate and select models.

There is some literature on the NPMLEs for semiparametric models with censored data (e.g., Murphy et al., 1997; Kosorok et al., 2004; Scheike and Martinussen, 2004; Zeng and Lin, 2006, 2007). Our setting is unique in that the regression parameters and infinite-dimensional cumulative hazard functions are all intertwined due to the the constraint that the sum of the cumulative incidence functions must not exceed one. Because of this constraint, existing asymptotic arguments, such as the general theory of Zeng and Lin (2007), do not directly apply. A further complication arises from the missing information on the cause of failure. To tackle these challenges, we use novel techniques to prove the asymptotic properties, especially the consistency. In addition, we develop novel numerical algorithms through the profile likelihood so as to avoid direct maximization over high-dimensional parameters. Finally, we extend the martingale residuals for traditional survival data to competing risks data and study the theoretical properties of the cumulative sums of residuals so as to provide objective model-checking procedures.

The rest of this paper is organized as follows. In Section 2, we introduce the models, describe the estimation approach, and present the asymptotic results. We also define appropriate residuals and use the cumulative sums of residuals to develop model-checking techniques. In Section 3, we conduct simulation studies to assess the performance of the proposed methods in finite samples and to make comparisons with existing methods. We provide an application to a major bone marrow transplantation study in Section 4. We make some concluding remarks in Section 5.

2. Methods

2.1. Model Specification

We are interested in estimating the effects of a set of covariates Z on a failure time T with K competing causes. We characterize the regression effects through the conditional cumulative incidence functions

$$F_k(t;\mathit{Z})=\mathrm{Pr}(T\le t,D=k\mid \mathit{Z}),k=1,\dots ,K,$$

where D indicates the cause of failure. We formulate each F_k through a class of linear transformation models:

$$g_k\left\{F_k\right(t;\mathit{Z}\left)\right\}=Q_k\left(t\right)+{\beta }_k^{\mathrm{T}}\mathit{Z},$$ (1)

where g_k is a known increasing function, Q_k(·) is an arbitrary increasing function, and β_k is a set of regression parameters.

To allow time-dependent covariates, we consider the conditional subdistribution hazard function

$${\lambda }_k(t;\mathit{Z})=\underset{\Delta t\to 0}{\lim }\frac{1}{\Delta t}\mathrm{Pr}\{t\le T<t+\Delta t,D=k\mid T\ge t\cup (T\le t\cap D\ne k),\mathit{Z}\},$$

which pertains to the hazard function of the improper random variable $T_k^{\ast }\equiv I(D=k)T+I(D\ne k)\infty$, where I(·) is the indicator function, and Z consists of time-dependent external covariates (Kalbfleisch and Prentice (2002), chapter 6). Clearly, F_k(t; Z) = 1−exp{−Λ_k(t; Z)}, where ${\Lambda }_k(t;\mathit{Z})={\int }_0^t{\lambda }_k(s;\mathit{Z})ds$. We specify that

$${\Lambda }_k(t;\mathit{Z})=G_k\left\{{\int }_0^t{e}^{{\beta }_k^{\mathrm{T}}\mathit{Z}\left(s\right)}d{\Lambda }_k\left(s\right)\right\},$$ (2)

where G_k is a known increasing function, and Λ_k(·) is an arbitrary increasing function. The choices of G_k(x) = x and G_k(x) = log(1 + x) yield the proportional subdistribution hazards model (Cox, 1972) and the proportional (subdistribution) odds model (Bennett, 1983), respectively. If the covariates are all time-independent, then equation (2) can be expressed in the form of (1). Transformation models without competing risks have been studied by Cheng et al. (1995), Chen et al. (2002), Lu and Ying (2004), Yin and Zeng (2006), and Zeng and Lin (2006, 2007), among others.

2.2. Parameter Estimation

Suppose that T is subject to right censoring by C. Then we observe $\tilde{T}$ and $\tilde{D}$ instead of T and D, where $\tilde{T}=\min (T,C)$, and $\tilde{D}=I(T\le C)D$. Let ξ indicate, by the values 1 versus 0, whether or not the cause of failure is observed. We set ξ to 1 if $\tilde{D}=0$. For a random sample of size n, the data consist of (${\tilde{T}}_i$, ξ_i, ${\xi }_i{\tilde{D}}_i$, Z_i) (i = 1, …, n). Under the missing at random (MAR) assumption, the likelihood function for $\beta \equiv {({\beta }_1^{\mathrm{T}},\cdots ,{\beta }_K^{\mathrm{T}})}^{\mathrm{T}}$ and Λ ≡ (Λ₁, ⋯, Λ_K) takes the form

$$L_n(\beta ,\Lambda )=\prod _{i=1}^n\left[\prod _{k=1}^K{F}_k^{\prime }{({\tilde{T}}_i;{\mathit{Z}}_i,\beta ,\Lambda )}^{I({\xi }_i{\tilde{D}}_i=k)}{\left\{\sum _{k=1}^K{F}_k^{\prime }({\tilde{T}}_i;{\mathit{Z}}_i,\beta ,\Lambda )\right\}}^{I({\xi }_i=0)}\times {\left\{1-\sum _{k=1}^K{F}_k({\tilde{T}}_i;{\mathit{Z}}_i,\beta ,\Lambda )\right\}}^{I({\tilde{D}}_i=0)}\right],$$ (3)

where F_k(t; Z, β, Λ) denotes the conditional cumulative incidence function under model (2). Here and in the sequel, f′(t) = df(t)/dt for any function f.

To obtain the NPMLEs, we treat Λ_k as a right-continuous step function with jump size Λ_k{t} at time t. Then the calculation of the NPMLEs is tantamount to maximizing (3) with respect to β and ${\Lambda }_k\left\{{\tilde{T}}_i\right\}$ for ${\tilde{D}}_i=k(k=1,\dots ,K)$. The maximization can be implemented through optimization algorithms, as described by Zeng and Lin (2007).

We propose an explicit algorithm to compute the NPMLEs for time-independent covariates with fully observed causes of failure. Let t_k1 < ⋯ < t_kmk be the distinct failure times of cause k. Denote d_kj = Λ_k{t_kj} for j = 1, ⋯ m_k and k = 1, ⋯, K. Let t₁ < ⋯ < t_m be the distinct failure times regardless of cause with t_m+1 = ∞, and let δ₁, ⋯, δ_m and d₁, ⋯, d_m be the corresponding causes and jump sizes, respectively. Write ${\Lambda }_{kj}={\sum }_{l=1}^{j}I({\delta }_l=k)d_l$ and ${\Lambda }_{\left(kj\right)}={\sum }_{l=1}^j{d}_{kl}$, which pertain to Λ_k at times t_j and t_kj, respectively. Then the log-likelihood can be written as

$$\begin{array}{cc}\hfill l_n(\beta ,\Lambda )& =\sum _{k=1}^K\sum _{j=1}^{m_k}\log d_{kj}+\sum _{k=1}^K\sum _{j=1}^{m_k}{H}_k\left(e^{{\beta }_k^{\mathrm{T}}{\mathit{Z}}_{\left(kj\right)}}{\Lambda }_{\left(kj\right)}\right)\hfill \\ \hfill & +\sum _{j=1}^m\sum _{t_j\le {\tilde{T}}_i<t_{j+1}}I({\tilde{D}}_i=0)\log \left[\sum _{k=1}^K\exp \{-G_k(e^{{\beta }_k^{\mathrm{T}}{\mathit{Z}}_i}{\Lambda }_{kj}\left)\right\}-K+1\right]\hfill \\ \hfill & +\sum _{i=1}^n\sum _{k=1}^{K}I({\tilde{D}}_i=k){\beta }_k^{\mathrm{T}}{\mathit{Z}}_i,\hfill \end{array}$$ (4)

where $H_k=\log G_k^{\prime }-G_k$, and Z_(kj) denotes the covariate vector for the subject having the kth cause of failure at time t_kj.

We construct the profile likelihood (Murphy and van der Vaart, 2000) of β by “profiling out” Λ. This task is complicated by the fact that ∂l_n(β, Λ)/∂d = 0 is a system of nonlinear equations of d ≡ (d₁, ⋯, d_m)^T. From those equations, however, we can express d_kj as a function of the d_l's corresponding to the failure times preceding t_kj. That is, we can write

$$d_{kj}=q\left(\right\{d_l:t_l<t_{kj}\left\}\right),j=2,\dots ,m_k,k=1,\dots ,K,$$ (5)

where q is some data-dependent function. This equation defines a recursive formula to compute d_kj (j = 2, ⋯, m_k) given β and d_k1 (k = 1, ⋯, K); see Section S.1 in the Supplementary Materials.

Write α_k = d_k1, α = (α₁, ⋯, α_K)^T, and θ = (β^T, α^T)^T. Then $\widehat{\Lambda }\left(\theta \right)\equiv \arg {\max }_{\Lambda }{l}_n(\theta ,\Lambda )$ can be calculated by the recursive formula given in (S.2) of the Supplementary Materials. The profile log-likelihood $p{l}_n\left(\theta \right)\equiv l_n(\theta ,\widehat{\Lambda }(\theta \left)\right)$ can be computed as well. The first and second derivatives of pl_n(θ) involve the derivatives of Λ with respect to θ; they can be obtained through the recursive formula by differentiating both sides of (5) with respect to θ. We can then use the Newton-Raphson algorithm to obtain the NPMLE of θ, denoted by $\widehat{\theta }$. We set the initial value of β to 0 and the initial value of α_k to 1/m_k.

To accommodate unknown causes of failure, we construct an EM algorithm by treating the ${\tilde{D}}_i$ associated with ξ_i = 0 as missing data. The complete-data log-likelihood is precisely (4). In the E-step, we compute $E\left\{I\right({\tilde{D}}_i=k)\mid {\tilde{T}}_i,{\mathit{Z}}_i,{\xi }_i=0;\beta ,\Lambda \}$, which can be expressed as

$$w_{ik}(\beta ,\Lambda )=\frac{F_k^{\prime }({\tilde{T}}_i;{\mathit{Z}}_i,\beta ,\Lambda )}{\sum _{l=1}^K{F}_l^{\prime }({\tilde{T}}_i;{\mathit{Z}}_i,\beta ,\Lambda )}.$$

In the M-step, we maximize the weighted version of (4) with the weights w_ik and 1 for ξ_i = 0 and ξ_i = 1, respectively.

Remark 1. In the iterations of the algorithm, the overall survival function $1-{\sum }_{k=1}^K{F}_k({\tilde{T}}_i;{\mathit{Z}}_i,\beta ,\Lambda )$ may become zero or negative. To improve the convergence of the algorithm, one may impose a small positive number on the survival function as a “buffer” to force it to be strictly positive, along the lines of Groeneboom and Wellner (1992, page 70). We have not encountered non-positive survival function estimates in our numerical experiences, so we have not actually used any buffer. If one directly maximizes the likelihood, the constraint would automatically be satisfied. Another way to incorporate the constraint is to decompose the cumulative incidence function using the mixture cure model representation of Lu and Peng (2008).

2.3. Asymptotic Properties

We assume the following regularity conditions:

• (C1)The true value of β, denoted by β₀, lies in the interior of a compact subset of the Euclidean space ${\mathbb{R}}^p$, where p is the dimension of β; the true value of Λ_k, denoted by Λ_k0, is continuously differentiable with ${\Lambda }_{k0}^{\prime }\left(t\right)>0$ on [0, τ] for some constant τ > 0.
• (C2)The components of Z(·) are uniformly bounded and have bounded total variation with probability one, and if β^TZ(t) = d(t) almost surely for some constant function d for all t ∈ [0, τ], then β = 0 and d(t) = 0.
• (C3)With probability one, there exists a constant δ₀ such that Pr(T ≥ τ|Z) ≥ δ₀ > 0 and Pr(C ≥ τ|Z) = Pr(C = τ|Z) ≥ δ₀ > 0.
• (C4)
  The function G_k is four-times differentiable with G_k(0) = 0 and $G_k^{\prime }\left(x\right)>0$, and for any c₀ > 0,

  $$\underset{x\to \infty }{\text{lim sup}}\left[{\left\{G_k\right(c_{0}x\left)\right\}}^{-1}\log \right\{x\underset{y\le x}{\sup }{G}_k^{\prime }\left(y\right)\left\}\right]=0.$$ (6)
• (C5)With probability one, $\mathrm{Pr}(\xi =1\mid \tilde{D},\tilde{T},T\le C,\mathit{Z})=\mathrm{Pr}(\xi =1\mid \tilde{T},T\le C,\mathit{Z})>{\zeta }_0$ for some ξ₀ > 0.

Remark 2. Conditions (C1)–(C3) are standard regularity conditions in survival analysis. (C4) is satisfied by the Box-Cox transformations G_k(x) = {(1 + x)^γ − 1}/γ (γ ≥ 0). Equation (6) is not satisfied by the logarithmic transformations G_k(x) = r⁻¹ log(1 + rx) (r ≥ 0). However, this equation, which ensures that ${\widehat{\Lambda }}_k\left(\tau \right)$ stays bounded, is used only in proving the consistency of the NPMLEs, and the proof actually goes through for the logarithmic transformations by the partitioning device described in the technical report of Zeng and Lin (2006). Condition (C5) ensures that the MAR assumption holds.

The following theorem on the consistency of the NPMLEs is proved in Section S.2 of the Supple-mentary Materials.

Theorem 1. Under Conditions (C1)–(C4), $\widehat{\beta }$ and ${\widehat{\Lambda }}_k(k=1,\dots ,K)$ are strongly consistent, i.e.,

$$\Vert \widehat{\beta }-{\beta }_0\Vert +\underset{t\in [0,\tau ]}{\overset{\text{sup}}{}}\sum _{k=1}^K\mid {\widehat{\Lambda }}_k\left(t\right)-{\Lambda }_{k0}\left(t\right)\mid \to 0$$

almost surely, where ∥ · ∥ denotes the Euclidean norm.

Remark 3. A major challenge in proving this theorem is that the Λ_k's are defective (i.e., Λ_k(τ) cannot be arbitrarily large) and constrained by the condition that $1-{\sum }_{k=1}^K{F}_k(\tau ;\mathit{Z},\beta ,\Lambda )>0$. To overcome this technical difficulty, we show that lim inf_n $\{1-{\sum }_{k=1}^K{F}_k(\tau ;\mathit{Z},\widehat{\beta },\widehat{\Lambda }\}>0$.

Let BV₁ denote the space off unctions on [0,τ] that are uniformly bounded by 1 and with total variation bounded by 1. Write $\mathcal{V}=\{\mathit{v}\in {\mathbb{R}}^p:\Vert \mathit{v}\Vert \le 1\}$ and $\mathcal{W}=B{V}_1^{\otimes K}$, which is the K-product space of BV₁. Let $\mathit{v}\in \mathcal{V}$ and $\mathit{w}=(h_1,\cdots ,h_K)\in \mathcal{W}$. Then we can identify (β, Λ) as elements in $l^{\infty }(\mathcal{V}\times \mathcal{W})$, which is the space of bounded functions on $\mathcal{V}\times \mathcal{W}$, by ${\mathit{v}}^{\mathrm{T}}\beta +{\sum }_{k=1}^K{\int }_0^{\tau }{h}_{k}d{\Lambda }_k$. Likewise, we identify $\sqrt{n}(\widehat{\beta }-{\beta }_0,\widehat{\Lambda }-{\Lambda }_0)$ as random elements in $l^{\infty }(\mathcal{V}\times \mathcal{W})$ such that

$$\sqrt{n}(\widehat{\beta }-{\beta }_0,\widehat{\Lambda }-{\Lambda }_0)\left[v,w\right]=\sqrt{n}{\mathit{v}}^{\mathrm{T}}(\widehat{\beta }-{\beta }_0)+\sqrt{n}\sum _{k=1}^K\int h_{k}d({\widehat{\Lambda }}_k-{\Lambda }_{k0}).$$

The following theorem on the distribution of the NPMLEs is proved in Section S.3 of the Supplementary Materials.

Theorem 2. Under Conditions (C1)–(C4), $\sqrt{n}(\widehat{\beta }-{\beta }_0,\widehat{\Lambda }-{\Lambda }_0)$ converges weakly to a zero-mean Gaussian process in $l^{\infty }(\mathcal{V}\times \mathcal{W})$. In addition, $\widehat{\beta }$ is semiparametric efficient in the sense of Bickel et al. (1993).

This theorem implies that $\sqrt{n}(\widehat{\beta }-{\beta }_0)$ is asymptotically multivariate zero-mean normal and $\sqrt{n}({\widehat{\Lambda }}_1-{\Lambda }_{10},\cdots ,{\widehat{\Lambda }}_K-{\Lambda }_{K0})$ converges to a multivariate zero-mean Gaussian process on [0, τ]^⊗K, the K-product space of [0, τ]. In the special case of no missing cause of failure, the covariance matrix of $\widehat{\beta }$ can be estimated by the upper left block of ${-\left\{{\partial }^{2}p{l}_n\right(\widehat{\theta })∕\partial \theta \partial {\theta }^{\mathrm{T}}\}}^{-1}$, which is a natural by-product of the algorithm. In the general case, we estimate the covariance matrix by inverting the information matrix for β and the nonzero d_kj's. This approach also provides variance estimation for the ${\widehat{\Lambda }}_k’s$; see Section S.4 in the Supplementary Materials for justifications.

Since Λ_k(t) is positive, we construct its confidence interval by using the log transformation: ${\widehat{\Lambda }}_k\left(t\right)\exp \{\pm z_{1-\alpha ∕2}{\widehat{\sigma }}_k(t)∕{\widehat{\Lambda }}_k(t\left)\right\}$, where ${\widehat{\sigma }}_k\left(t\right)$ is the estimated standard error of ${\widehat{\Lambda }}_k\left(t\right)$, and z_1−α/2 is the upper (1 − α/2)100th percentile of the standard normal distribution. To estimate Λ_k(t; z) for covariate value z, we subtract z from Z; then Λ_k(t) corresponds to Λ_k(t; z). Inference on F_k(t; z) follows from the simple relationship F_k(t; z) = 1 − e^−Λ_k(t;z).

2.4. Model Checking

The class of models given in (2) requires specification of the following components: the functional form of each covariate; the link function, i.e., the exponential regression function; the proportionality structure, i.e., the multiplicative effect of the regression function within the transformation; and the transformation function G_k. To check these components, we define appropriate residuals and consider cumulative sums of residuals. We assume for now that the causes of failure are fully observed. We define $N_k\left(t\right)=I(\tilde{T}\le t,\tilde{D}=k)$ and $Y\left(t\right)=I(\tilde{T}\ge t)$. Then the following process is centered at zero

$$\begin{array}{cc}\hfill M_k(t;\beta ,\Lambda )& =N_k\left(t\right)-{\int }_0^{t}Y\left(u\right)S^{-1}(u;\mathit{Z},\beta ,\Lambda )d{F}_k(u;\mathit{Z},\beta ,\Lambda )\hfill \\ \hfill & =N_k\left(t\right)-{\int }_0^{t}Y\left(u\right){\Psi }_k(u;\mathit{Z},\beta ,\Lambda )d{\Lambda }_k\left(u\right),\hfill \end{array}$$ (7)

where $S(t;\mathit{Z},\beta ,\Lambda )=1-{\sum }_{k=1}^K{F}_k(t;\mathit{Z},\beta ,\Lambda )$, and

$${\Psi }_k(t;\mathit{Z},\beta ,\Lambda )=S^{-1}(t;\mathit{Z},\beta ,\Lambda )\exp \left[H_k\left\{{\int }_0^t{e}^{{\beta }_k^{\mathrm{T}}\mathit{Z}\left(u\right)}d{\Lambda }_k\left(u\right)\right\}+{\beta }_k^{\mathrm{T}}\mathit{Z}\left(t\right)\right].$$

We obtain the residual process $M_k(t;\widehat{\beta },\widehat{\Lambda })$ by replacing (β, Λ) in (7) with the NPMLEs.

Let M_ki denote the value of M_k for the ith subject, and let Z_ji denote the jth component of Z_i. To check the functional form of the jth covariate, we consider the cumulative sum of residuals over this covariate:

$$W_{kc}^{\left(j\right)}(z,t)=n^{-1∕2}\sum _{i=1}^n{\int }_0^{t}I\left\{Z_{ji}\right(s)\le z\}d{M}_{ki}(s;\widehat{\beta },\widehat{\Lambda }).$$

To check the link function, we consider the cumulative sum over the linear predictor:

$$W_{kl}(x,t)=n^{-1∕2}\sum _{i=1}^n{\int }_0^{t}I\left\{{\widehat{\beta }}_k^{\mathrm{T}}{\mathit{Z}}_i\left(s\right)\le x\right\}d{M}_{ki}(s;\widehat{\beta },\widehat{\Lambda }).$$

To check the transformation function G_k, we take the cumulative sum over its argument:

$$W_{\mathit{ktr}}(x,t)=n^{-1∕2}\sum _{i=1}^n{\int }_0^{t}I\left\{{\int }_0^s{e}^{{\widehat{\beta }}_k^T{\mathit{Z}}_i\left(u\right)}d{\widehat{\Lambda }}_k\left(u\right)\le x\right\}d{M}_{ki}(s;\widehat{\beta },\widehat{\Lambda }).$$

To check the proportionality for the jth covariate, we consider the “score” process

$$W_{kp}^{\left(j\right)}\left(t\right)=n^{-1∕2}\sum _{i=1}^n{\int }_0^t{\tilde{Z}}_{\mathit{kji}}(s;\widehat{\beta },\widehat{\Lambda })d{M}_{ki}(s;\widehat{\beta },\widehat{\Lambda }),$$

where ${\tilde{Z}}_{\mathit{kji}}(t;\beta ,\Lambda )$ is the jth component of

$$\frac{\partial }{\partial {\beta }_k}\log {\Psi }_k(t;{\mathit{Z}}_i,\beta ,\Lambda )={\mathit{Z}}_i\left(t\right)+\left[H_k^{\prime }\left\{{\int }_0^t{e}^{{\beta }_k^T{\mathit{Z}}_i\left(u\right)}d{\Lambda }_k\left(u\right)\right\}+S^{-1}(t;{\mathit{Z}}_i,\beta ,\Lambda )\times \exp \left\{H_k\left({\int }_0^t{e}^{{\beta }_k^T{\mathit{Z}}_i\left(u\right)}d{\Lambda }_k\left(u\right)\right)\right\}\right]{\int }_0^t{\mathit{Z}}_i\left(u\right)e^{{\beta }_k^T{\mathit{Z}}_i\left(u\right)}d{\Lambda }_k\left(u\right),$$

which pertains to the score function of β_k based on the data available up to time t. Finally, to assess the overall fit of the model, we consider the process

$$W_{ko}(\mathit{z},t)=n^{-1∕2}\sum _{i=1}^n{\int }_0^{t}I\left\{{\mathit{Z}}_i\right(s)\le \mathit{z}\}d{M}_{ki}(s;\widehat{\beta },\widehat{\Lambda }).$$

All above processes are special cases of the multi-parameter process

$$W_{kn}(\mathit{x},t)=n^{-1∕2}\sum _{i=1}^n{\int }_0^{t}f(\mathit{x},u;{\mathit{Z}}_i,\widehat{\beta },\widehat{\Lambda })d{M}_{ki}(u;\widehat{\beta },\widehat{\Lambda }),$$

where f is some function. We use Monte Carlo simulation to evaluate its null distribution. Specifically, we define

$${\widehat{W}}_{kn}(\mathit{x},t)=n^{-1∕2}\sum _{i=1}^n\left\{{\int }_0^{t}f(\mathit{x},u;{\mathit{Z}}_i,\widehat{\beta },\widehat{\Lambda })d{M}_{ki}(u;\widehat{\beta },\widehat{\Lambda })+{\widehat{S}}_i(\mathit{x},t)\right\}{Q}_i,$$

where (Q₁, ⋯, Q_n) are independent standard normal variables, and ${\widehat{S}}_1(\mathit{x},t),\cdots ,{\widehat{S}}_n(\mathit{x},t)$ are described in Section S.5 of the Supplementary Materials. We show in that section that the conditional distribution of ${\widehat{W}}_{kn}$ given the observed data $({\tilde{T}}_i,{\tilde{D}}_i,{\mathit{Z}}_i)$ (i = 1,…, n) is asymptotically the same as the distribution of W_kn.

To approximate the null distribution of W_kn, we simulate the distribution of ${\widehat{W}}_{kn}$ by repeatedly generating the normal random sample (Q₁, ⋯, Q_n) while holding the observed data fixed. To visually inspect model mis-specification, we compare the observed residual process with a few, say 20, realizations from the simulated process. We can also perform formal goodness-of-fit tests by calculating the p-values for the suprema of the residual processes based on a large number, say 1000, realizations. We establish the consistency of the supremum tests in Section S.5 of the Supplementary Materials.

To accommodate missing causes of failure, we re-define the mean-zero process M_k(t; β, Λ). Specifically, we replace N_k(t) in (7) by ${\tilde{N}}_k(t;\beta ,\Lambda )\equiv \xi N_k\left(t\right)+(1-\xi )w_k(\beta ,\Lambda )I(\tilde{T}\le t)$, where $w_k(\beta ,\Lambda )=F_k^{\prime }(\tilde{T};\mathit{Z},\beta ,\Lambda )∕{\sum }_{i=1}^K{F}_l^{\prime }(\tilde{T};\mathit{Z},\beta ,\Lambda )$. The rest of the development follows from the arguments in Section S.5 of the Supplementary Materials.

3. Simulation Studies

We conducted extensive simulation studies to evaluate the proposed and existing methods. We set K = 2 and Z = (Z₁, Z₂)^T, where Z₁ is binary with Pr(Z₁ = −1) = Pr(Z₁ = 1) = 0.5, and Z₂ is Un(−1, 1). We let Λ_k(t) = ρ_k (1 − e^−t), where ρ_k > 0. We assumed fully observed causes of failure except for the simulation studies described in the last paragraph of this section.

First, we compared the NPMLE with the Fine and Gray (1999) (FG) method under proportional subdistribution hazards models. We let the censoring time be the minimum of a Un(5, 6) variable and an Exp(0.1) variable. We set β₁ = 0, β₂ = (0.5, 0.5)^T, ρ₁ = 0.1, and ρ₂ = 0.75, 1.1, and 1.5, corresponding to 50%, 40%, and 25% censoring, respectively. The algorithm was deemed convergent when the Euclidean distance between the β values of the current and previous iterations was less than 10⁻⁴ and the number of iterations did not exceed 100. Convergence rates for the NPMLE with sample sizes 100, 200, and 500 were approximately 99.5%, 99.8%, and 99.9%, respectively. For most (> 98.6%) of the simulated datasets, convergence criteria were met with 3 to 10 iterations. It took about 1 second and 0.5 second on a Dell Inspiron 2000 machine to analyze one dataset with n = 200 for the NPMLE and FG methods, respectively.

The results for the estimation of β₁₁ are summarized in Table 1. For both methods, the estimators are virtually unbiased and the standard error estimators reflect the true variations well. Thus, the confidence intervals have accurate coverage probabilities. However, the standard error of the FG estimator is always larger than that of the NPMLE. The difference is more pronounced when there are more events of the second type and lower censoring rate because FG models the censoring distribution while discarding the information in the second type of event.

Table 1.

Comparison of the NPMLE and Fine and Gray methods in the estimation of β₁₁ under proportional subdistribution hazards models^†

		NPMLE				FG
Censoring	n	Bias	SE	SEE	CP	Bias	SE	SEE	CP	RE
50%	100	−0.004	0.396	0.388	0.948	−0.002	0.401	0.394	0.954	1.03
	200	0.000	0.270	0.267	0.951	−0.008	0.272	0.276	0.946	1.01
	500	−0.001	0.162	0.153	0.945	−0.003	0.162	0.164	0.953	1.00
40%	100	−0.006	0.389	0.397	0.944	−0.001	0.409	0.412	0.965	1.11
	200	−0.003	0.263	0.267	0.942	−0.008	0.278	0.273	0.954	1.12
	500	−0.008	0.161	0.163	0.942	0.001	0.169	0.167	0.958	1.10
25%	100	−0.001	0.385	0.385	0.949	−0.001	0.413	0.408	0.956	1.15
	200	0.001	0.257	0.264	0.957	0.006	0.270	0.272	0.949	1.10
	500	0.006	0.161	0.158	0.958	0.005	0.174	0.176	0.948	1.17

^†Bias and SE are the bias and standard error of the parameter estimator; SEE is the mean of the standard error estimator; CP is the coverage probability of the 95% confidence interval; RE is the variance of FG over that of the NPMLE. Each entry is based on 10,000 replicates.

We evaluated the NPMLE further under different transformation models. We considered the family of logarithmic transformations G_r(x) = r⁻¹ log(1 + rx), in which r = 0 and 1 correspond to the proportional subdistribution hazards and odds models, respectively. We set ρ₂ = 0.75 and varied the value of β₁ while fixing β₂ at (0.5, 0.5)^T. The results for the estimation of β₁ are shown in Table S.1 of the Supplementary Materials. The NPMLE performs very well under all transformation models.

We also considered estimation of the cumulative hazard functions Λ_k under β₁ = β₂ = 0. The results for Λ₁(t) are summarized in Table S.2 of the Supplementary Materials. The parameter estimators are virtually unbiased, the standard error estimators are accurate, and the confidence intervals have correct coverages.

We evaluated the FG method further under mis-specified censoring distributions. We used the set-up for Table 1 with ρ₂ = 0.75 but let the censoring time be the minimum of a Un(3, 6) variable and an Exp(exp(ηZ₁)) variable, where η = 1 or 2. Thus, the censoring distribution depends on the first covariate in a non-proportional hazards manner. In the FG method, the censoring distribution is estimated by the Kaplan-Meier estimator. Fine and Gray (1999) suggested to use the proportional hazards model for the censoring distribution but did not derive the corresponding variance estimators. Table 2 compares the NPMLE, the original FG estimator, and the modification based on the proportional hazards modelling of the censoring distribution, denoted by FG*. FG has considerable bias and the bias becomes greater as the censoring distributions become more uneven. For FG*, the bias is smaller but still appreciable relative to the standard error, especially when the sample size is large. For both FG and FG*, the mean square error is considerably larger than that of the NPMLE.

Table 2.

Simulation results for the Fine and Gray methods in the estimation of β₁₁ under mis-specified censoring distributions^†

		NPMLE			FG			FG*
		Bias	SE	MSE	Bias	SE	MSE	Bias	SE	MSE
1	100	0.002	0.396	0.157	−0.119	0.404	0.177	−0.054	0.414	0.174
	200	0.003	0.270	0.073	−0.116	0.275	0.089	−0.049	0.275	0.078
	500	−0.003	0.161	0.026	−0.114	0.161	0.039	−0.053	0.165	0.030
2	100	0.002	0.395	0.156	−0.231	0.401	0.214	−0.031	0.418	0.176
	200	0.002	0.266	0.071	−0.223	0.282	0.129	−0.028	0.281	0.080
	500	−0.001	0.155	0.024	−0.227	0.163	0.078	−0.027	0.173	0.032

^†FG and FG* are based on the Kaplan-Meier estimator and proportional hazards model for the censoring distribution, respectively. Bias and SE are the bias and standard error of the parameter estimator; MSE is the mean square error. Each entry is based on 10,000 replicates.

Next, we compared our NPMLE to the parametric MLE of Jeong and Fine (2007). We used the set-up of Table 1 with ρ₂ = 0.75 but set β₁ = β₂ = 0. In this setting, Λ₁ and Λ₂ are correctly modeled by the parametric method. As shown in Table S.3 of the Supplementary Materials, the parametric MLE tends to be more efficient than the NPMLE; however, the efficiency gain is rather moderate.

We conducted additional studies to assess the bias of the parametric method under mis-specified failure distributions. We used the proportional subdistribution hazards models and set β₁ = (0.5, 0)^T and β₂ = 0. We let λ_k(t) = 0.5t exp(−t²/2) and used the same censoring distributions as in Table 1. As shown in Table S.4 of the Supplementary Materials, the estimation for the cumulative hazard function is severely biased.

To show that the estimation of β can also be biased, we considered a more wiggly hazard function, i.e., λ_k(t) = 0.15{1 + cos(πt)}. We set β₁ = (0.5, 0)^T and β₂ = 0 and focused on the estimation of β₁₁. As shown in Table S.5 of the Supplementary Materials, the parametric method underestimates β₁₁. The bias is considerable relative to the standard error, especially when the sample size is large.

Then, we assessed the robustness of the NPMLE for the risk of interest to model mis-specification on other risks. We used the set-up of Table 1 with ρ₂ = 0.75. We generated data under the proportional subdistribution hazards and odds models for the first and second risks, respectively, but fit the proportional subdistribution hazards models to both risks. As shown in Table S.6 of the Supplementary Materials, mis-specification of the second risk has little impact on the inference on the first risk.

We also evaluated the performance of the goodness-of-fit tests in the set-up of Table 1 with ρ₂ = 0.75, β₁ = (0.5, 0)^T, and β₂ = (0, 0)^T. We evaluated the type I error of the supremum tests for the first risk at the nominal significance level of 0.05. We simulated 10,000 datasets with n = 100 and used 1,000 normal samples to calculate the p-value. For checking the functional form of Z₁, the exponential link function, the transformation function, the proportionality on Z₁, and the overall fit, the empirical type I error rates were found to be 0.051, 0.059, 0.062, 0.042, and 0.048, respectively. Thus, the asymptotic approximations for the supremum tests are accurate enough for practical use.

Finally, we considered missing causes of failure. We generated the missing indicators for non-censored subjects from the logistic model

$$\mathrm{Pr}(\xi =0\mid \tilde{D},\tilde{T},T\le C,\mathit{Z})=\frac{\exp (-0.5+\gamma Z_1)}{1+\exp (-0.5+\gamma Z_1)}.$$

We set γ = 0 and −0.2, which correspond to missing completely at random (MCAR) and MAR, respectively. We used the set-up of Table 1 with ρ₂ = 0.75, β₁ = (−0.5, 0)^T, and β₂ = (0, 0)^T. We compared the NPMLE with the FG complete-case analysis (i.e., excluding subjects with missing causes of failure). The complete-case analysis is expected to be biased even under MCAR because only non-censored subjects may be excluded due to missing causes of failure. (The causes of failure are naturally unknown for censored subjects, such that censored subjects are always included in the analysis. Since shorter failure times are more likely to be censored than longer failure times, the subjects with non-missing causes of failure are not representative of all subjects.) The results for the estimation of β₁₁ are summarized in Table 3. The NPMLE remains unbiased. The FG estimator is biased, especially under MAR. In addition, the FG estimator is substantially less efficient than the NPMLE.

Table 3.

Comparison of the NPMLE and Fine and Gray methods in the estimation of β₁₁ with missing causes of failure^†

		NPMLE				FG
	n	Bias	SE	SEE	CP	Bias	SE	SEE	CP	RE
MCAR	100	0.003	0.479	0.482	0.953	0.038	0.523	0.524	0.941	1.190
	200	−0.001	0.291	0.295	0.955	0.050	0.319	0.321	0.929	1.197
	500	0.002	0.189	0.192	0.952	0.036	0.217	0.220	0.920	1.313
MAR	100	0.006	0.426	0.429	0.953	0.189	0.473	0.474	0.881	1.235
	200	−0.006	0.306	0.305	0.949	0.203	0.336	0.337	0.825	1.202
	500	−0.002	0.223	0.223	0.949	0.213	0.243	0.246	0.722	1.186

^†See the note to Table 1.

4. A Real Example

We present a major study on bone marrow transplantation in patients with multiple myeloma (MM) (Kumar et al., 2011). The standard treatment for MM is autologous hematopoietic stem cell transplantation (auto-HCT). An alternative treatment, allogeneic hematopoietic cell transplantation (allo-HCT), is less commonly used because of its high treatment-related mortality (TRM). However, recent advances in medical care have lowered TRM rates of allo-HCT (Kumar et al., 2011). To evaluate the effects of various risk factors on clinical outcomes after allo-HCT for MM, we consider data collected from years 1995–2005 by the Center for International Blood and Marrow Transplantation Research (CIBMTR). The CIBMTR is comprised of clinical and basic scientists who confidentially share data on their blood and bone marrow transplant patients with the Data Collection Center located at the Medical College of Wisconsin; it provides a repository of information about results of transplants from more than 450 transplant centers worldwide.

The database contains 864 patients, among whom 376 received transplantation in 1995–2000 and 488 received transplantation in 2001–2005. The two competing risks are TRM and relapse of MM. A total of 297 patients experienced TRM, and 348 experienced relapse. Risk factors include cohort indicator (transplantation years 1995–2000 or 2001–2005), type of donor (unrelated or HLA-identical sibling donor), history of a prior auto-HCT (yes or no), and time from diagnosis to transplantation (≤ 24 months or > 24 months).

We first fit the proportional subdistribution hazards models for both risks and compare our method with the FG method. As shown in Table 4, the two methods produce considerably different results. The differences are largely attributed to uneven censoring distributions. By fitting a proportional hazards model to the censoring distribution with the same set of covariates, we find that cohort indicator, prior auto-HCT, and waiting time increase the censoring rate. Thus, the FG estimates of their effects are biased downward for both risks. By contrast, donor type decreases the censoring rate, such that the FG estimates of its effects on the two risks are biased upward. At the significance level of 0.05, waiting time is associated with both risks under the NPMLE method but is not associated with either risk under the FG method. The more recent cohort (years 2001–2005) has a significantly lower incidence of TRM but higher incidence of relapse. Transplantation involving an unrelated donor significantly increases the risk of both TRM and relapse. Prior auto-HCT reduces the risk of TRM but increases the risk of relapse. We test the global null hypothesis that waiting time does not affect TRM or relapse. The p-value of the ${\chi }_2^2$ test is <0.001, so that the null hypothesis is strongly rejected.

Table 4.

Proportional subdistribution hazards analysis of the bone marrow transplantation data

		NPMLE			FG
		Est	SE	p-value	Est	SE	p-value
TRM
	Years 2001–2005	−0.543	0.132	<0.001	−0.578	0.139	<0.001
	Unrelated donor	0.476	0.126	<0.001	0.521	0.128	<0.001
	Prior auto-HCT	−0.451	0.162	0.005	−0.463	0.153	0.003
	TX > 24 months	0.296	0.123	0.017	0.248	0.135	0.065
Relapse
	Years 2001–2005	0.518	0.129	<0.001	0.401	0.122	0.001
	Unrelated donor	0.293	0.101	0.004	0.330	0.122	0.007
	Prior auto-HCT	0.399	0.116	0.001	0.351	0.125	0.005
	TX > 24 months	0.310	0.121	0.018	0.216	0.123	0.078

We also fit the proportional cause-specific hazards models, and the results are shown in Table S.7 of the Supplementary Materials. The parameter estimates are quite different from their counterparts in Table 4, but the signs are the same. Thus, the covariate effects on the cause-specific and subdistribution hazards are in the same directions, but with different magnitudes.

Next, we consider the family of transformation functions G_k(x) = r⁻¹ log(1 + rx) (k = 1, 2). We fit 4 pairs of models with r = 0 or 1 for the two competing risks. We label the choices of r = i (i = 0, 1) for TRM and r = j (j = 0, 1) for relapse as Model 2j + i + 1. To evaluate these transformations, we use the sup_x,t |W_ktr(x, t)| test for k = 1, 2. The p-values, based on 1000 realizations, for testing the transformation functions for TRM under Models 1–4 are 0.035, 0.543, 0.029, and 0.382, respectively, and the corresponding p-values for testing the transformation functions for relapse are 0.056, 0.045, 0.282, and 0.307. These results suggest that the proportional subdistribution hazards assumption is not appropriate for TRM and relapse. We also fit the models with r ranging from 0 to 2. As shown in Figure S.1 of the Supplementary Materials, the log-likelihood is maximized at r = 0.8 for TRM and r = 1.3 for relapse, which would be the combination selected by the Akaike information criterion. The selected combination is close to Model 4 (i.e., proportional odds models for both risks), which we adopt for ease of interpretation.

The results from Model 4 are summarized in Table 5. These results differ markedly from the NPMLE results in Table 4, and the interpretations of the regression effects are quite different. We assess the proportionality assumption using the sup |W_kp| test. The p-values are 0.297, 0.123, 0.687, and 0.673, respectively, for the effects of cohort indicator, donor type, history and waiting time on TRM; the corresponding p-values for relapse are 0.818, 0.361, 0.352, and 0.940. Thus, the proportionality assumption holds on all covariates. The p-value for the omnibus test is 0.412, indicating overall goodness of fit.

Table 5.

Proportional odds analysis of the bone marrow transplant data

		Est	SE	p-value
TRM
	Years 2001–2005	−0.582	0.123	<0.001
	Unrelated donor	0.504	0.108	<0.001
	Prior auto-HCT	−0.420	0.143	0.003
	TX > 24 months	0.217	0.126	0.084
Relapse
	Years 2001–2005	0.353	0.116	<0.001
	Unrelated donor	0.337	0.088	<0.001
	Prior auto-HCT	0.314	0.123	0.002
	TX > 24 months	0.343	0.138	0.013

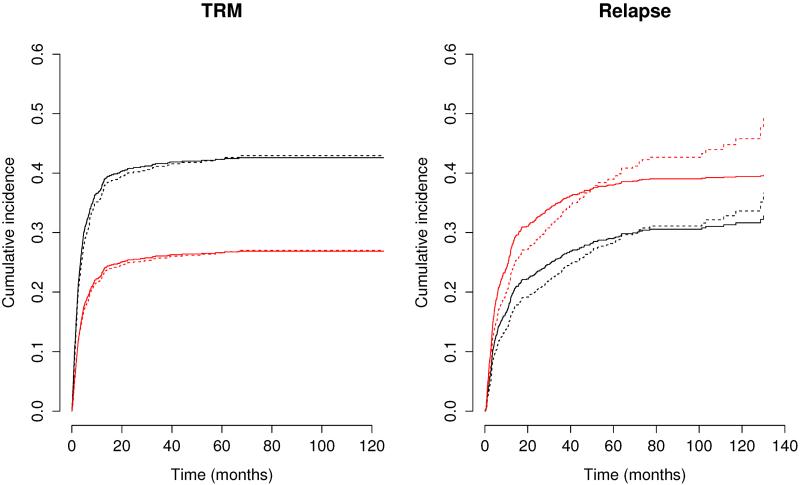
To compare the predictions from the initial proportional subdistribution hazards models and the chosen proportional odds models, we show in Figure 1 the estimated cumulative incidence functions for the two cohorts with HLA-identical sibling donor, no history of prior auto-HCT treatment, and waiting time ≤ 24 months. The two pairs of models yield rather different estimates, especially for relapse. Thus, proper choice of the transformation function is crucial to accurate prediction of the incidence of competing risks.

Fig. 1.

Estimated cumulative incidence of TRM and relapse for a subject with HLA-identical sibling donor, no prior auto-HCT treatment, and waiting time ≤ 24 months. The black and red curves indicate years 1995–2000 and 2001–2005, respectively; the dashed and solid curves pertain to the proportional subdistribution hazards and odds models, respectively.

5. Discussion

Our work represents the first likelihood-based approach to semiparametric regression analysis of cumulative incidence functions with competing risks data. It offers major improvements over the pioneer work of Fine and Gray (1999). First, it does not require modelling of the censoring distribution, such that the inference is valid regardless of the censoring patterns. Second, it provides flexible choices of models for covariate effects, accommodating both proportional and non-proportional subdistribution hazards structures. Third, it provides efficient parameter estimators. Fourth, it allows for missing information on the cause of failure. Fifth, it performs simultaneous inference on multiple risks. Finally, it provides graphical and numerical techniques to evaluate and select models. These improvements have important implications in actual data analysis, as demonstrated in the simulation studies and real example.

Because an increase in the incidence of one risk reduces the incidence of other risks, it is necessary to take into account all other risks when interpreting the results on one particular risk. Thus, it is desirable to model all risks even when one is interested in only one of them. Our simulation results show that the inference on one risk is robust to model mis-specification on other risks. The FG method only models the risk of interest and thus seems to involve fewer model assumptions. However, it requires modelling the censoring distribution, which is of no scientific interest at all. As shown in our simulation studies, mis-specification of the censoring distribution may bias the inference. In addition, the estimated inverse weights can be quite unstable under heavy censoring.

For maximizing the nonparametric likelihood, many authors have resorted to optimization algorithms. Due to the high dimensionality of the argument, such algorithms are slow and their convergence is not guaranteed. We have developed a recursive formula to compute the profile likelihood and its derivatives. Our strategy greatly reduces the dimension of the problem and is fast and stable.

For notational simplicity, we have assumed that the covariates are the same for all risks. All theoretical results hold when covariates are risk-specific, i.e., dependent on k. Our formulation accommodates time-dependent covariates, but only external time-dependent covariates (Kalbfleisch and Prentice (2002), chapter 6) are allowed. A common example of such covariates is time×covariate interaction; other examples include temperature, particulate levels, and precipitation. For internal time-dependent covariates, the relationship between the cumulative incidence function and the subdistribution hazard function does not hold, and the likelihood does not conform to (3). The FG method is also restricted to external covariates (Latouche et al., 2005).

In our analysis of the CIBMTR data, deaths after relapse were excluded from the definition of TRM. This practice differentiates treatment-related mortality unequivocally from disease-related mortality and has been commonly adopted in the analysis of transplantation data (e.g., Scheike and Zhang, 2008; Kumar et al., 2011). For analysis of all-cause mortality and relapse, however, semicompeting risks models (e.g., Peng and Fine, 2007; Lin et al., 2014), in which death is not censored by relapse, are more appropriate and make fuller use of data.

In some applications, the events are asymptomatic, such that the event times are only known to lie between monitoring times. For example, in the HIV clinical trial cited in Section 1, blood tests were performed periodically on study subjects for evidence of HIV-1 sero-conversion (Hudgens et al., 2001). We plan to extend our work to handle such interval-censored competing risks data.