Modelling of Successive Cancer Risks in Lynch Syndrome Families in the presence of competing risks using Copulas

Summary

In this paper, we propose an association model to estimate the penetrance (risk) of successive cancers in the presence of competing risks. The association between the successive events is modelled via a copula and a proportional hazards model is specified for each competing event. This work is motivated by the analysis of successive cancers for people with Lynch Syndrome in the presence of competing risks. The proposed inference procedure is adapted to handle missing genetic covariates and selection bias, induced by the data collection protocol of the data at hand. The performance of the proposed estimation procedure is evaluated by simulations and its use is illustrated with data from the Colon Cancer Family Registry (Colon CFR).

1. Introduction

Lynch Syndrome (LS) is the most common hereditary colorectal cancer (CRC) syndrome and accounts for 2-5% of all colorectal cancers (CRCs) (Hampel et al., 2005; Lynch et al., 2008). LS is an autosomal dominant disorder (with variable penetrance) caused by mutations in DNA mismatch repair (MMR) genes (de la Chapelle, 2004). As a clinical disorder, LS is defined by the clustering of related cancers across generations of kindreds, characterized by early onset CRC (mean age 45), right-sided predominance, and the increased incidence of synchronous and metachronous CRCs. Additionally, people with LS are at increased risk for other malignancies (e.g. endometrium, ovaries, stomach, etc.) (Lynch et al., 2009). It is now defined by having a germline mutation in a MMR gene, irrespective of personal or family cancer history, and these people have a high risk of developing cancer (de la Chapelle, 2004; Dowty et al., 2013). The risk of developing CRC by age 70 years for MLH1 and MSH2 mutation carriers was estimated to be 34% and 47% respectively for male carriers and 36% and 37% for female carriers (Dowty et al., 2013). In addition, several studies have shown that people with LS have an increased risk of developing a second cancer after a first cancer, including a second CRC (Parry et al., 2011; Win et al., 2013; Choi et al., 2014) and extra-colonic cancers (Win et al., 2012). In this paper, we are mainly concerned with the estimation of the penetrance (risk) of the second CRC. An important issue when estimating the risk associated with a single or multiple cancer events is the presence of competing events.

Competing risks concern the situation where more than one cause of failure are possible (Putter et al., 2007). A classical example relates to several causes of death (e.g. from cancer) where the occurrence of any cause of death prevents the event of interest from occurring. Treating the events of the competing causes as censored observations will lead to biased estimates of the penetrance function of the event of interest when we are in the presence of correlated competing risks (Putter et al., 2007). In genetic studies, the estimation of the probability for an individual affected with a specific cancer (e.g. breast/ovarian cancer) to carry a specific gene mutation can be affected by competing risks if for example mutation carriers have different probabilities of surviving all causes of cancers compared to non-carriers (Katki et al., 2008). Another application of competing risks is when one is interested in modelling the risk of observing a first type of cancer, e.g. for people with LS, a CRC vs. any other LS-related cancer. In this example, multiple cancer events “compete” to be the first event where each event has a different probability to occur among mutation carriers. Competing risks models have a particular interest in many cancer applications because they allow us to estimate cause-specific hazards, which are hazard functions related to a specific cancer event while accounting for the probability of surviving all other events. This is particularly suitable whenever one is interested to assess a treatment/intervention effect for a particular type of cancer, e.g. colonoscopy for colorectal cancer for people with LS.

Competing events can also occur from successive events, e.g., a first primary CRC and a second primary CRC. In our situation, individuals are initially at risk of observing either a first primary CRC or death before the first primary CRC. Individuals who observe the first CRC are afterwards at risk of observing either a second primary CRC or death before second primary CRC. Therefore, we are in the presence of successive competing risks.

Several statistical methods have been developed for correlated cause-specific event times in the context of competing risks; see Scheike et al. (2010) and the references therein for a review. However, all these approaches concern parallel competing risks and to our knowledge, no methods are available for successive competing risks.

In this paper, we propose a general methodology to estimate the risks of observing a first cancer and a second cancer given the age at onset of the first cancer in people with LS while accounting for the presence of competing risk events. The dependence between the successive competing risks is modelled via a copula whose parameter measures the degree of association between the ages at onset of the first and second cancers. The proposed inference procedure is adapted to handle missing genotype information and ascertainment bias caused by the data collection design of the LS families. We investigate the performance of the developed method by simulations and illustrate its use with a large collection of LS families from the Colon Cancer Family Registry (Colon CFR).

2. Model specifications and quantities of interest

Consider the following progressive multistate model with competing risks. The model includes 5 states, healthy and events 1 to 4, where events 1 and 2 are successive events of interest and events 3 and 4 represent competing events for events 1 and 2, respectively.

2.1 Marginal distributions

Let T₁ and T₃ be the times from the healthy state to events 1 and 3, respectively and Y₁ = min{T₁, T₃}. Define ε₁ by ε₁ = 1 if T₁ < T₃ and ε₁ = 3, otherwise. Note that events 1 and 3 are competing risks so it is of interest to define the following cause-specific hazard functions

$${\lambda }_k(y|G,X)=\underset{\mathit{\text{dy}}\to 0}{lim}\frac{1}{\mathit{\text{dy}}}P(y<Y_1\le y+\mathit{\text{dy}},{\epsilon }_1=k|G,X,Y_1>y),k=1,3,$$

where G is the individual genotype information corresponding to the mutation carrier status (carrier=1, non-carrier=0) and X a set of measured covariates. By standard theory of competing risks,

$$h_1(y|G,X)={\lambda }_1(y|G,X)+{\lambda }_3(y|G,X)\text{and}{S}_1(y|G,X)=exp\{-{\int }_0^y{h}_1(u|G,X)\mathit{\text{du}}\}$$

are the hazard and survival functions associated with Y₁, respectively and

$$F_{11}(y|G,X)=P(Y_1\le y,{\epsilon }_1=1|G,X)={\int }_0^y{S}_1(u|G,X){\lambda }_1(u|G,X)\mathit{\text{du}}$$

is the cause-specific cumulative incidence function of event 1.

Individuals satisfying ε₁ = 1 are afterwards at risk of observing either event 2 or event 4. Let T₂ and T₄ be the times from event 1 to events 2 and 4, respectively and Y₂ = min(T₂, T₄). Define ε₂ by ε₂ = 2 if T₂ < T₄ and ε₂ = 4, otherwise. Similarly, define the conditional cause-specific hazard functions given ε₁ = 1 by

$${\lambda }_k(y|G,X)=\underset{\mathit{\text{dy}}\to 0}{lim}\frac{1}{\mathit{\text{dy}}}P(y<Y_2\le y+\mathit{\text{dy}},{\epsilon }_2=k|G,X,Y_2>y,{\epsilon }_1=1),k=2,4.$$

The conditional hazard and survival functions associated with Y₂ given ε₁ = 1 are then, respectively,

$$h_2(y|G,X)={\lambda }_2(y|G,X)+{\lambda }_4(y|G,X)\text{and}{S}_2(y|G,X)=exp\{-{\int }_0^y{h}_2(u|G,X)\mathit{\text{du}}\}.$$

We assume that the cause-specific hazard for event k, k = 1, 2, 3, 4, follows a proportional hazards regression model

$${\lambda }_k(y|G,X)={\lambda }_{k0}(y)e^{{\beta }_k^{\top }X+{\beta }_{g_k}G},$$

where λ_k0 is the baseline hazard function and β_k and β_gk are the regression coefficients related to event k. Two approaches are considered in this paper: (i) a parametric approach where a parametric distribution is specified for each λ_k0, and (ii) a piecewise constant hazard approach where λ_k0 is assumed to be constant within each interval of a partition of [0, ∞). In both cases, we denote by θ_k the set of baseline distribution parameters and regression coefficients related to event k.

2.2 Association model

For individuals satisfying ε₁ = 1, we model the dependence in the pair (Y₁, Y₂) through a semi-survival copula, 𝒞_γ, (Lakhal-Chaieb et al., 2006; Zhao & Zhou, 2010; Ding, 2012) defined as follows:

$$P(Y_1\le y_1,Y_2>y_2|{\epsilon }_1=1,G,X)={\mathcal{C}}_{\gamma }\{P(Y_1\le y_1|{\epsilon }_1=1,G,X),P(Y_2>y_2|{\epsilon }_1=1,G,X)\}={\mathcal{C}}_{\gamma }\{F_{11}(y_1|G,X)/p(G,X),S_2(y_2|G,X)\},$$

where the parameter γ measures the conditional dependency in the pair (Y₁, Y₂) given ε₁ = 1 and $p(G,X)=P({\epsilon }_1=1|G,X)=\underset{t\to \infty }{lim}{F}_{11}(t|G,X)$.

The model is completed by specifying P(ε₂ = 2|G, X, Y₁ = y₁, Y₂ = y₂, ε₁ = 1). This probability has to satisfy

$$P({\epsilon }_2=2|G,X,Y_2=y_2,{\epsilon }_1=1)=E_{Y_1}\{P({\epsilon }_2=2|G,X,Y_1,Y_2=y_2,{\epsilon }_1=1)\}=\frac{{\lambda }_2(y_2|G,X)}{{\lambda }_2(y_2|G,X)+{\lambda }_4(y_2|G,X)},$$ (1)

where the expectation is taken with respect to Y₁. A natural and mathematically convenient strategy to ensure that (1) holds is to assume

$$P({\epsilon }_2=2|G,X,Y_1=y_1,Y_2=y_2,{\epsilon }_1=1)=P({\epsilon }_2=2|G,X,Y_2=y_2,{\epsilon }_1=1).$$ (2)

When this condition is not met, we are in the presence of an additional aspect of the dependency between the successive competing risks. In Web Appendix A, we present a procedure to test equation (2). Applying this test to the LS families cancer data suggests that it is plausible to assume (2) in our case. Therefore, the developments presented throughout the rest of this paper are relying on this assumption.

2.3 Penetrance functions

The penetrance functions are defined as cause-specific cumulative incidence functions. The penetrance for event 1 is 𝒫₁(y₁; G, X) = F₁₁(y₁|G, X), which is the cumulative risk of developing event 1 by age y₁ in the presence of the competing event 3. The penetrance function for event 2 is the cause-specific cumulative incidence function conditional on the age at onset of event 1. When the assumption (2) is satisfied, we show in Web Appendix B that this penetrance function equals

$${\mathcal{P}}_2(y_2;y_1,G,X)=P(Y_2\le y_2,{\epsilon }_2=2|Y_1=y_1,{\epsilon }_1=1,G,X)={\int }_0^{y_2}{C}_{\gamma }^{11}\{F_{11}(y_1|G,X)/p(G,X),S_2(u|G,X)\}{S}_2(u|G,X){\lambda }_2(u|G,X)\mathit{\text{du}},$$ (3)

where $C_{\gamma }^{ij}(u,\upsilon )={\partial }^{i+j}{\mathcal{C}}_{\gamma }(u,\upsilon )/{\partial }^{i}u{\partial }^j\upsilon$. It is the probability of developing event 2 within y₂ since event 1 which has occurred at y₁. One is often interested in a 5-year or 10-year penetrance for second event.

3. Observed data and inference procedures

3.1 Maximum likelihood estimation

In this section, we describe the observed data and derive an estimation procedure for the parameters {θ₁, θ₂, θ₃, θ₄, γ}. In the LS families, Y₁ is right-censored by the age of last follow-up a. The observed data related to the events 1 and 3 is then {a, Ỹ₁, ε̃₁}, where Ỹ₁ = min(Y₁, a) and ε̃₁ = ε₁ × I(Y₁ < a) ∈ {0,1, 3}. For those satisfying ε̃₁ = 1, we also observe Ỹ₂ = min(Y₂, a − Y₁) and ε̃₂ = ε₂ × I(Y₂ < a − Y₁) ∈ {0, 2, 4}.

The observations are clustered into I families. The data is then

$$\mathrm{\Delta }=\{(a_{ij},{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},{\stackrel{\sim }{Y}}_{2ij},{\stackrel{\sim }{\epsilon }}_{2ij},G_{ij},X_{ij}),i=1,\cdots ,I,j=1,\cdots ,n_i\},$$

where n_i is the size of the i^th family.

A family is included into the study if and only if the first examined person or proband has observed either event 1 or event 3 by age a. We assume a unique proband per family, whom we index by the subscript j = 1. Close relatives of this proband for whom some genotype and cancer history information are available from the corresponding family unit. As this data collection protocol induces a selection bias, an ascertainment correction is required. To this end, we employ a conditional likelihood approach where the contribution of each family is corrected for its probability of being ascertained. For parameter estimation, we consider a two-stage estimation procedure. In the first stage, we estimate the parameters related to events 1 and 3 by maximizing the conditional log-likelihood function

$$\sum _{i=1}^I\sum _{j=1}^{n_i}{l}_1({\theta }_1,{\theta }_3|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},G_{ij},X_{ij})-\sum _{i=1}^I{l}_c({\theta }_1,{\theta }_3|a_{i1},G_{i1},X_{i1}),$$ (4)

where

$$l_1({\theta }_1,{\theta }_3|{\stackrel{\sim }{Y}}_1,{\stackrel{\sim }{\epsilon }}_1,G,X)=\sum _{k\in \{1,3\}}I({\stackrel{\sim }{\epsilon }}_1=k)\times log\{{\lambda }_k({\stackrel{\sim }{Y}}_1|G,X)\}-{\int }_0^{{\stackrel{\sim }{Y}}_1}{h}_1(u|G,X)\mathit{\text{du}}$$

is the standard contribution of an individual to the log-likelihood function and

$$l_c({\theta }_1,{\theta }_3|a,G,X)=log\{P(Y_1<a|G,X)\}=log\{1-S_1(a|G,X)\}$$ (5)

is the familial ascertainment correction term. This log-likelihood function is derived under the assumption of conditional independence of ages at onset of cancer of family members given their mutation carrier statuses. This assumption is plausible in our case given the strong association between the genotype and the risk of developing cancer.

At the second stage, we estimate the parameters related to events 2 and 4 as well as the copula parameter γ by maximizing the log-likelihood function

$$\sum _{i=1}^I\sum _{j=1}^{n_i}I({\stackrel{\sim }{\epsilon }}_{1ij}=1)l_2({\theta }_2,{\theta }_4,\gamma |{\widehat{\theta }}_1,{\widehat{\theta }}_3,{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{Y}}_{2ij},{\stackrel{\sim }{\epsilon }}_{2ij},G_{ij},X_{ij}),$$

where

$$l_2({\theta }_2,{\theta }_4,\gamma |{\widehat{\theta }}_1,{\widehat{\theta }}_3,{\stackrel{\sim }{Y}}_1,{\stackrel{\sim }{Y}}_2,{\stackrel{\sim }{\epsilon }}_2,G,X)=I({\stackrel{\sim }{\epsilon }}_2=0)log[{\mathcal{C}}_{\gamma }^{10}\{{\widehat{F}}_{11}({\stackrel{\sim }{Y}}_1|G,X)/\widehat{p}(G,X),S_2({\stackrel{\sim }{Y}}_2|G,X)\}]+\sum _{k\in \{2,4\}}I({\stackrel{\sim }{\epsilon }}_2=k)log[{\mathcal{C}}_{\gamma }^{11}\{{\widehat{F}}_{11}({\stackrel{\sim }{Y}}_1|G,X)/\widehat{p}(G,X),S_2({\stackrel{\sim }{Y}}_2|G,X)\}{S}_2({\stackrel{\sim }{Y}}_2|G,X){\lambda }_k({\stackrel{\sim }{Y}}_2|G,X)]$$ (6)

and θ̂₁ and θ̂₃ are obtained from the first stage.

3.2 Missing genotypes

In this section, we modify the estimation procedure derived above in order to include the individuals whose genotype information is missing in the analysis. In what follows, we assume that the genotypes are missing at random and that the probands' genotypes are known. Let G̃_ij = G_ij if G_ij is observed and − 1 otherwise.

We consider the following two-stage procedure. At the first stage, we estimate the parameters related to events 1 and 3 via an Expectation-Maximization (EM) algorithm. After m iterations, the E-step and the M-step of this algorithm are

E-step: For i = 1, ⋯, I, j = 1, ⋯, n_i, if G̃_ij = − 1, compute

$$\begin{gathered} w_{ij}^{(m+1)}=P(G_{ij}=1|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\delta }}_{ij1},G_{i1},X_{ij}) \\ =\frac{p_{ij}{e}^{l_1({\widehat{\theta }}_1^{(m)},{\widehat{\theta }}_3^{(m)}|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},1,X_{ij})}}{p_{ij}{e}^{l_1({\widehat{\theta }}_1^{(m)},{\widehat{\theta }}_3^{(m)}|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},1,X_{ij})}+(1-p_{ij})e^{l_1({\widehat{\theta }}_1^{(m)},{\widehat{\theta }}_3^{(m)}|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},0,X_{ij})}}, \end{gathered}$$

where p_ij = P(G_ij = 1|G_i1) depends only on the relationship between the individual j and the proband in family i. In this paper, these probabilities are estimated empirically from the subset of data with observed genotypes.

M-step: Compute ${\widehat{\theta }}_1^{(m+1)}$ and ${\widehat{\theta }}_3^{(m+1)}$ by maximizing

$$\sum _{i=1}^I\sum _{j=1}^{n_i}I({\stackrel{\sim }{G}}_{ij}=-1)[w_{ij}^{(m+1)}{l}_1({\theta }_1,{\theta }_3|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},1,X_{ij})+(1-w_{ij}^{(m+1)})l_1({\theta }_1,{\theta }_3|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},1,X_{ij})]+\sum _{i=1}^I\sum _{j=1}^{n_i}I({\stackrel{\sim }{G}}_{ij}\ne -1)l_1({\theta }_1,{\theta }_3|{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{\epsilon }}_{1ij},G_{ij},X_{ij})-\sum _{i=1}^I{l}_c({\theta }_1,{\theta }_3|a_{i1},G_{i1},X_{i1}).$$

We iterate between these steps until convergence to obtain θ̂₁ and θ̂₃.

At the second stage, we estimate θ₂, θ₄ and γ by maximizing the weighted loglikelihood function

$$\sum _{i=1}^I\sum _{j=1}^{n_i}I({\stackrel{\sim }{\epsilon }}_{ij}=1,{\stackrel{\sim }{G}}_{ij}=-1)w_{ij}^{(\infty )}{l}_2({\theta }_2,{\theta }_4,\gamma |{\widehat{\theta }}_1,{\widehat{\theta }}_3,{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{Y}}_{2ij},{\stackrel{\sim }{\epsilon }}_{2ij},1,X_{ij})+\sum _{i=1}^I\sum _{j=1}^{n_i}I({\stackrel{\sim }{\epsilon }}_{ij}=1,{\stackrel{\sim }{G}}_{ij}=-1)(1-w_{ij}^{(\infty )})l_2({\theta }_2,{\theta }_4,\gamma |{\widehat{\theta }}_1,{\widehat{\theta }}_3,{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{Y}}_{2ij},{\stackrel{\sim }{\epsilon }}_{2ij},0,X_{ij})+\sum _{i=1}^I\sum _{j=1}^{n_i}I({\stackrel{\sim }{\epsilon }}_{ij}=1,{\stackrel{\sim }{G}}_{ij}\ne -1)l_2({\theta }_2,{\theta }_4,\gamma |{\widehat{\theta }}_1,{\widehat{\theta }}_3,{\stackrel{\sim }{Y}}_{1ij},{\stackrel{\sim }{Y}}_{2ij},{\stackrel{\sim }{\epsilon }}_{2ij},G_{ij},X_{ij}),$$

where $w_{ij}^{(\infty )}$ are the conditional probabilities computed at the E-step of the EM-algorithm evaluated at convergence.

3.3 Variance estimation

The estimation procedure derived in this paper simultaneously involves several inference techniques including a two-stage estimation setting and an EM-algorithm to handle missing genotypes. Therefore, it may not be straightforward to derive explicit formulae for the variances of the obtained estimators. In this work, we propose to estimate the variances using a nonparametric bootstrap procedure. At each bootstrap iteration, we resample I families with replacement from the original data in order to obtain a bootstrapped sample. Afterwards, we apply the iterative estimation procedure described above to each bootstrapped sample. Finally, the variances are computed empirically from B bootstrapped samples. Applying the complete estimation procedure to each bootstrapped sample insures the validity of this variance estimation procedure.

4. Simulation Study

4.1 Simulation study design

We conducted a simulation study to evaluate the performance of our proposed successive competing risks model by examining the accuracy and precision of the estimates of the model parameters and penetrance functions. We simulated samples of 781 families with family structures and inclusion criteria similar to those of the Lynch Syndrome families from the Colon CFR. For each family member, the times to the first and second events of interest were generated in the presence of competing events based on the proposed model assuming Weibull baseline hazard functions and a Clayton copula, with parameters estimated from the Colon CFR's data in order to mimic realistic disease risks. We considered 0% (no missing), 50% and 80% of missing genotypes among family members of the probands for studying the impact of missing genotypes. For each genotype missing rate, we generated 1000 samples and for each generated sample, we estimated the parameters of the model and deduced plug-in estimators for the penetrance functions for the first and second cancers. We fitted the simulated data assuming various forms for the baseline hazard functions: parametric Weibull, log-logistic, and gamma distributions and piecewise constant hazards, where λ₀₁ and λ₀₃ were assumed to be constant within the intervals (0, 5], (5,10], ⋯, (60, ∞) and λ₀₂ and λ₀₄ within (0, 5], ⋯, (30, ∞).

The EM-algorithm derived in Section 3.2 takes a very long time to converge with the piecewise constant hazards approach. Therefore, we consider this approach only when no genotypes are missing.

4.2 Simulation results

Our interest lies on the log cause-specific relative risks for gender and mutation status β_1sex, β_1gene for the first cancer, β_2sex, β_2gene for the second cancer, the copula parameter log(γ), the gender-specific penetrance among mutation carriers by age 70 for the first cancer 𝒫₁(70; G = 1, X) and the 10-year penetrance for the second event given the first cancer occurred at ages 40 and 50, 𝒫₂(10; 40, G = 1, X) and 𝒫₂(10;50, G = 1, X), respectively. For each of these quantities of interest, we computed the average bias, the empirical standard deviation (SE) and the root mean square error (RMSE). The results are summarized in Tables 1 (first cancer) and 2 (second cancer). From Table 1, the bias values for β_1sex estimates are small across the different baseline distributions even when data involves high proportion of missing genotypes. On the other hand, β_1gene estimates are almost unbiased when 0% and 50% of the genotypes are missing; however, they are slightly underestimated when 80% of the genotypes are missing. This Table also suggests that the biases of the penetrance estimates for the first cancer are generally small regardless the proportions of missing genotypes and the choice of the baseline distributions, although penetrance estimates for female carriers are slightly more biased and more variable compared to those for male carriers. For most of the estimates, as we expected, the SEs and RMSEs increase slightly when the proportion of missing genotypes increases.

Table 1.

Accuracy and precision of estimates of log relative risks and penetrance for mutation carriers by age 70 for the first cancer, 𝒫_i (70; X), given gender X, male (M) and female (F) based on 1000 simulations of sample size of 781 families. For each simulation, data were generated assuming Weibull baselines, and different baseline distributions assumptions were applied for fitting the data.

Baseline distribution		True value	No missing genotypes			50% Missing genotypes			80% Missing genotypes
			Bias	SE	RMSE	Bias	SE	RMSE	Bias	SE	RMSE
Weibull	βlsex	0.3706	0.0073	0.1399	0.1401	0.0187	0.1606	0.1617	0.0574	0.1947	0.2030
	βlgene	3.5206	0.0182	0.2256	0.2264	-0.0028	0.2801	0.2802	-0.1273	0.4026	0.4223
Log-logistic	βlsex	0.3706	0.0100	0.1488	0.1491	0.0123	0.1587	0.1591	0.0503	0.1998	0.2061
	βlgene	3.5206	0.0109	0.2394	0.2396	-0.0037	0.2891	0.2891	-0.1253	0.4411	0.4585
Gamma	βlsex	0.3706	0.0841	0.6589	0.6642	0.0294	0.1610	0.1637	0.0664	0.2000	0.2107
	βlgene	3.5206	0.0221	0.5245	0.5250	0.0134	0.2871	0.2874	-0.1259	0.4365	0.4543
Piecewise	βlsex	0.3706	0.0228	0.1412	0.1431
	βlgene	3.5206	0.0084	0.2017	0.2019
Penetrance for the first cancer by age 70
Weibull	𝒫1(70; M)	0.6250	0.0001	0.0177	0.0177	0.0010	0.0175	0.0176	-0.0017	0.0179	0.0179
	𝒫1(70; F)	0.4922	-0.0015	0.0460	0.0460	-0.0044	0.0533	0.0535	-0.0188	0.0628	0.0655
Log-logistic	𝒫1(70; M)	0.6250	0.0007	0.0239	0.0239	0.0000	0.0172	0.0172	-0.0020	0.0177	0.0178
	𝒫1(70; F)	0.4922	-0.0019	0.0502	0.0502	-0.0037	0.0526	0.0527	-0.0171	0.0648	0.0670
Gamma	𝒫1(70; M)	0.6250	-0.0010	0.0267	0.0267	-0.0275	0.1168	0.1200	-0.0354	0.1307	0.1354
	𝒫1(70; F)	0.4922	-0.0182	0.0621	0.0648	-0.0299	0.1026	0.1069	-0.0459	0.1159	0.1247
Piecewise	𝒫1(70; M)	0.6250	-0.0021	0.0279	0.0279
	𝒫1(70; F)	0.4922	-0.0087	0.0497	0.0505

SE is empirical standard error; RMSE is root mean square error.

Table 2.

Accuracy and precision of estimates of log relative risks, copula parameter, and 10-year penetrances, 𝒫₂(10; T₁, X), for the second cancer given T₁, the first cancer occurred at ages 40 and 50, and gender X, male (M) and female (F), based on 1000 simulations of sample size of 781 families. For each simulation, data were generated assuming Weibull baselines with θ = 0.15, and different baseline distributions assumptions were applied for fitting the data.

Baseline distribution		True value	No missing genotypes			50% Missing genotypes			80% Missing genotypes
			Bias	SE	RMSE	Bias	SE	RMSE	Bias	SE	RMSE
Weibull	β2sex	-0.0205	0.0005	0.1843	0.1843	-0.0056	0.1740	0.1741	-0.0064	0.1777	0.1778
	β2gene	-0.4174	0.0909	0.7302	0.7358	0.0106	0.3273	0.3275	0.0359	0.2362	0.2389
	log (γ)	-1.8877	-0.0619	0.5002	0.5040	-0.0437	0.4468	0.4490	-0.0256	0.3931	0.3939
Log-logistic	β2sex	-0.0205	0.0407	0.1861	0.1905	0.0563	0.1794	0.1881	0.0477	0.1750	0.1814
	β2gene	-0.4174	0.4625	0.7590	0.8889	0.3359	0.3686	0.4987	0.3221	0.2856	0.4305
	log (γ)	-1.8877	-0.1998	0.5920	0.6248	-0.1972	0.4898	0.5280	-0.1671	0.5635	0.5877
Gamma	β2sex	-0.0205	-0.0157	0.1929	0.1936	0.0046	0.1756	0.1757	-0.0055	0.1903	0.1904
	β2gene	-0.4174	0.1431	0.7074	0.7217	0.1021	0.4550	0.4663	0.0620	0.3324	0.3382
	log (γ)	-1.8877	-0.0864	0.6637	0.6693	-0.0836	0.6775	0.6826	-0.0184	0.4990	0.4993
Piecewise	β2sex	-0.0205	-0.0206	0.1829	0.1841
	β2gene	-0.4174	-0.1151	0.3467	0.3653
	log (γ)	-1.8877	0.0627	0.3350	0.3408
10- year penetrance for the second cancer conditioning on T1 and gender
Weibull	𝒫2(10; 40, M)	0.1243	0.0000	0.0113	0.0113	-0.0006	0.0111	0.0111	0.0001	0.0113	0.0113
	𝒫2(10; 40, F)	0.1246	0.0007	0.0192	0.0192	0.0004	0.0176	0.0176	0.0010	0.0179	0.0179
	𝒫2(10; 50, M)	0.1350	-0.0107	0.0113	0.0156	-0.0113	0.0111	0.0158	-0.0106	0.0113	0.0155
	𝒫2(10; 50, F)	0.1361	-0.0109	0.0192	0.0220	-0.0111	0.0176	0.0208	-0.0105	0.0179	0.0207
Log-logistic	𝒫2(10; 40, M)	0.1243	0.0046	0.0115	0.0124	0.0044	0.0116	0.0124	0.0049	0.0114	0.0124
	𝒫2(10; 40, F)	0.1246	0.0015	0.0197	0.0198	-0.0008	0.0187	0.0187	0.0003	0.0182	0.0182
	𝒫2(10; 50, M)	0.1350	-0.0061	0.0115	0.0130	-0.0063	0.0116	0.0132	-0.0058	0.0114	0.0128
	𝒫2(10; 50, F)	0.1361	-0.0100	0.0197	0.0221	-0.0123	0.0187	0.0224	-0.0112	0.0182	0.0214
Gamma	𝒫2(10; 40, M)	0.1243	-0.0712	0.0171	0.0732	-0.0729	0.0185	0.0752	-0.0748	0.0175	0.0768
	𝒫2(10; 40, F)	0.1246	-0.0696	0.0169	0.0716	-0.0724	0.0179	0.0746	-0.0739	0.0169	0.0758
	𝒫2(10; 50, M)	0.1350	-0.0819	0.0171	0.0837	-0.0836	0.0185	0.0856	-0.0855	0.0175	0.0873
	𝒫2(10; 50, F)	0.1361	-0.0811	0.0169	0.0828	-0.0839	0.0179	0.0858	-0.0854	0.0169	0.0871
Piecewise	𝒫2(10; 40, M)	0.1243	-0.0017	0.0136	0.0137
	𝒫2(10; 40, F)	0.1246	0.0004	0.0203	0.0203
	𝒫2(10; 50, M)	0.1350	-0.0007	0.0154	0.0154
	𝒫2(10; 50, F)	0.1361	0.0018	0.0233	0.0234

SE is empirical standard error; RMSE is root mean square error.

From Table 2, the biases in β_2sex and β_2gene estimates are small when the true baseline distribution, Weibull, is assumed; however, larger biases are observed when the baseline hazard functions are misspecified. Considering the true values of β_2sex and β_2gene are set close to zero, the model misspecification provides relatively large bias in those estimates. Despite of the biased parameter estimates, the penetrance estimates for the second cancer are generally unbiased, even in the presence of missing genotypes. We found that the misspecification of the baseline distribution can lead to biased penetrance estimates; gamma baseline distribution underestimes the penetrance while the log-logistic baselines provide almost unbiased penetrance estimates. Finally, the piecewise constant hazards provide penetrance estimates as accurate as using the true parametric baseline distribution. However, it only applies to the situation with no missing genotypes.

5. Application to Lynch Syndrome Families from the Colon CFR

5.1 Data

The Colon CFR is an international consortium regrouping six institutes in North America and Australia and formed as a resource to support studies on the etiology, prevention, and clinical management of CRC. Details of recruitment methods for each centre of the Colon CFR have been published previously (Newcomb et al., 2007) and can be found at http://coloncfr.org/. The Colon CFR includes lifestyle, medical history, and family history data collected from more than 41,000 men and women from 14,500 families with and without CRC. The Colon CFR recruited families between 1997 to 2012 and all participants were followed-up approximately every 5 years to update personal and family histories and expand recruitment if new cases have occurred since baseline. A total of 781 Lynch Syndrome (LS) families, defined as families in which at least one member is affected by CRC and carrying a mutation in one of the following genes: MLH1, MSH2, MSH6, MSP2 and EPCAM, has been identified through the Colon CFR. The risk of developing a first CRC in LS people has been well evaluated (Dowty et al., 2013), however the risk of developing a second CRC following a first CRC is not well known.

In this study, our goal is based on LS families from the Colon CFR, to estimate the cumulative risks (penetrances) of developing a first CRC and developing a second CRC following a first CRC for people who carry germline mutations in the five genes listed above, in males and females separately. Here, competing risks refer to death related to LS cancer and only families whose probands have observed the first CRC cancer are included in the sample.

The number of CRCs and competing events observed by mutation status and gender are given in Web Figure 1 and Web Table 1. For each family, we considered three generations including the probands, their children, spouses, parents, siblings, nephews and nieces. The sample considered consists of 781 LS families including a total of 7703 individuals. We observed 1501 individuals who developed a first primary CRC and 89 who died from other LS related cancers. Among the 1501 individuals who developed a first CRC, 276 developed a second primary CRC following the first one and 163 died from other LS related cancers. Deaths from other LS cancers were considered as competing events for both the first and second CRCs. Unknown mutation status was inferred as outlined in section 3.2.

5.2 Analysis assumptions

We analysed the LS families data using the methodology presented in Sections 2 and 3. We considered different survival models for λ_k, k = 1, ⋯,4: parametric Weibull and log-logistic models and piecewise constant baseline hazards model. Proportional hazards are assumed in the Weibull and piecewise constant baseline hazards models, whereas hazards ratios are not constant over time in the log-logistic model, which in fact assumes proportional odds. The same model was used for all four events (i.e. the first and second CRC and the two competing events). We also specified a Clayton copula to model the dependence between the first and second CRC times. We tested the proportional hazards assumption under the Weibull specification using the goodness-of-fit test described in Web Appendix C and obtained p-values equal to 0.24 and 0.59 for events 1 and 3, respectively. Therefore, the proportional hazards assumption seems plausible for our data. Furthermore, we tested the partial independence assumption given by equation (2), as outlined in Web Appendix A, and obtained a p-value equal to 0.92, which leads us to conduct the analysis under this assumption.

In our application, families whose proband was dead before observing the first CRC cancer were not identified by the data collection protocol. Therefore, we replaced the familial ascertainment term given by equation (5) by

$$l_c({\theta }_1,{\theta }_3|a,G,X)=log\{P(Y_1<a;{\epsilon }_1=1|G,X)\}=log\{F_{11}(a|G,X)\}$$

in the estimation process.

In addition, we analysed the data using a naive approach that ignores competing risks and treats LS related deaths as right-censored observations. This approach, whose details are given in Web Appendix D, is referred to as “No competing risks model” henceforth.

5.3 Risk of first CRC

The log-likelihood for the first step analysis (i.e. parameter estimates related to events 1 and 3) was –7533.21 for the log-logistic model, –7648.97 for the Weibull model and –7758.97 for the piecewise constant hazard model. Table 3 summarizes the estimates of model parameters and penetrance for the first and second CRCs from the three models with and without competing risks taken into account.

Table 3.

Log-relative risks and penetrance estimates for the first and second CRCs with and without competing risks obtained from different models using 781 Lynch Syndrome families; SE^bs are bootstrap standard errors obtained from 1000 bootstrapped samples of 781 families; 𝒫₁(70; X) represents the penetrance estimate for the first CRC by age 70 for mutation carriers; X represents gender, M for male and F for female; 𝒫₂(10; T₁, X) represents the 10-year penetrance estimates for the second CRC given the age at first CRC, T₁ and gender, X, for mutation carriers.

	Competing risks models			No competing risks models
	Weibull	Log-logistic	Piecewise	Weibull	Log-logistic	Piecewise
Parameters of interest
β1sex	0.406	0.452	0.319	0.419	0.457	0.333
SEb	0.084	0.095	–	0.086	0.098	–
β1gene	3.220	3.653	2.728	3.156	3.475	2.805
SEb	0.212	0.222	–	0.226	0.227	–
β2sex	-0.117	0.030	-0.089	-0.053	-0.013	-0.049
SEb	0.132	0.159	–	0.125	0.138	–
β2gene	-0.558	-0.445	-0.432	0.553	0.612	-0.459
SEb	0.465	0.430	–	0.191	0.228	–
γ	0.177	0.178	0.132	0.068	0.076	0.114
SEb	0.053	0.051	–	0.057	0.056	–
Penetrances
𝒫1(70; M)	55.93%	54.61%	50.16%	55.02%	54.23%	50.73%
SEb	2.88%	2.28%	–	3.04%	2.37%	–
𝒫1(70; F)	42.09%	43.32%	39.66%	40.88%	42.85%	39.80%
SEb	2.09%	1.89%	–	2.12%	2.06%	–
𝒫2(10; 40, M)	11.93%	13.80%	11.88%	12.77%	13.48%	14.02%
SEb	1.11%	1.27%	–	1.10 %	1.16%	–
𝒫2(10; 50, M)	13.32%	15.44%	13.02%	13.36%	14.20%	15.31%
SEb	1.20%	1.44%	–	1.29%	1.88%	–
𝒫2(10; 40, F)	12.87%	12.85%	12.91%	13.09%	13.25%	14.20%
SEb	1.11%	1.26%	–	1.13%	1.97%	–
𝒫2(10; 50, F)	14.45%	14.52%	14.22%	13.71%	14.01%	15.55%
SEb	1.21%	1.37%	–	1.24%	1.53%	–

Our results showed that mutation carriers of any of the five MMR genes had a very high risk of developing a first CRC with a corresponding log hazard ratio (HR), β_1gene, of 3.22 for the Weibull model and 2.73 for the piecewise constant hazard model. For the log-logistic model, the log HR varied with age, being in males 3.62 at 30 years, 3.53 at 40 years, 3.36 at 50 years and in females 3.63 at 30 years, 3.57 at 40 years and 3.46 at 50 years. The gender effect was highly significant in all the three models with substantial increased risks in males than in females. The cumulative probability of developing a first CRC (i.e. penetrance) by age 70 was among male carriers 55.9% with the Weibull model, 50.2% with the piecewise constant hazard model and 54.6% with the log-logistic model, and among female carriers 42.1%, 39.7% and 43.3%, respectively (see Web Figure 2). When no competing risks were considered, the Weibull and log-logistic models provided estimates of the genetic effect, β_1gene, of the mutation, equal to 3.48 and 3.16 respectively, which corresponds to cumulative penetrances of 54.2% and 42.9% in male and female carriers for the log-logistic model and 55.0% and 40.9%, respectively, for the Weibull model.

We also examined the risk of first CRCs for different types of MMR gene mutations (see Table 4). In 278 MLH1 carrier families, we observed 592 first CRCs (345 carriers, 6 non-carriers). The penetrance of the first cancer by age 70 was 72.2% in males and 52.3% in females. For 342 MSH2 carrier families, we observed 690 first CRCs (381 carriers, 11 non-carriers). The first cancer penetrance was 57.7% in males and 52.8% in females. Finally, for 101 MSH6 carrier families, we observed 135 first CRCs (76 carriers, 2 non-carriers). The penetrance for the first cancer was 30.5% in males and 15.8% in females.

Table 4.

Kendall's tau estimates for the dependence between the times to first and second CRCs, penetrance estimates of the first CRC by age 70, 𝒫₁(70), and 10-year risk estimates of the second CRC given the age at first CRC T₁, 𝒫₂(10; T₁), for different types of MMR gene mutation based on the log-logistic regression model; SE^bs are bootstrap standard errors obtained from 1000 bootstrapped family samples

Gene Mutation	no. of families	Kendall's τ	Male carriers			Female carriers
			𝒫1(70)	𝒫2(10; 40)	𝒫2(10; 50)	𝒫1(70)	𝒫2(10; 40)	𝒫2(10; 50)
MLH1	278	0.1092	72.23%	16.68%	19.13%	52.25%	12.46%	14.87%
SEb		0.0328	3.26%	2.71%	3.01%	3.25%	2.23%	2.68%
MSH2	342	0.0372	57.66%	13.10%	13.78%	52.79%	15.10%	15.91%
SEb		0.0217	2.96%	1.78%	1.90%	3.12%	2.08%	2.22%
MSH6	101	0.0084	30.46%	4.91%	4.99%	15.81%	9.34%	9.50%
SEb		0.0705	5.32%	2.40%	2.60%	3.12%	3.55%	3.91%
ALL*	781	0.0713	54.61%	12.00%	13.25%	43.32%	13.08%	14.56%
SEb		0.0192	2.22%	1.31%	1.43%	1.96%	1.28%	1.41%

^*ALL includes MLH1, MSH2, MSH6, MSP2 and EPCAM

5.4 Risk of second CRC following a first CRC

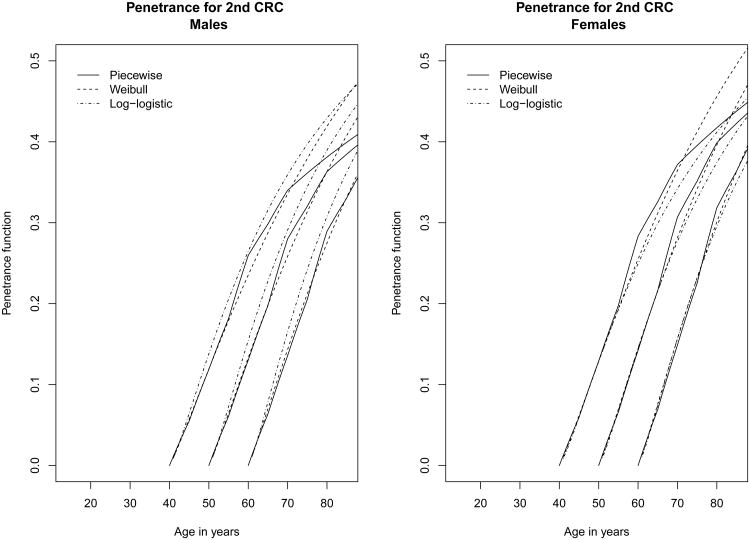
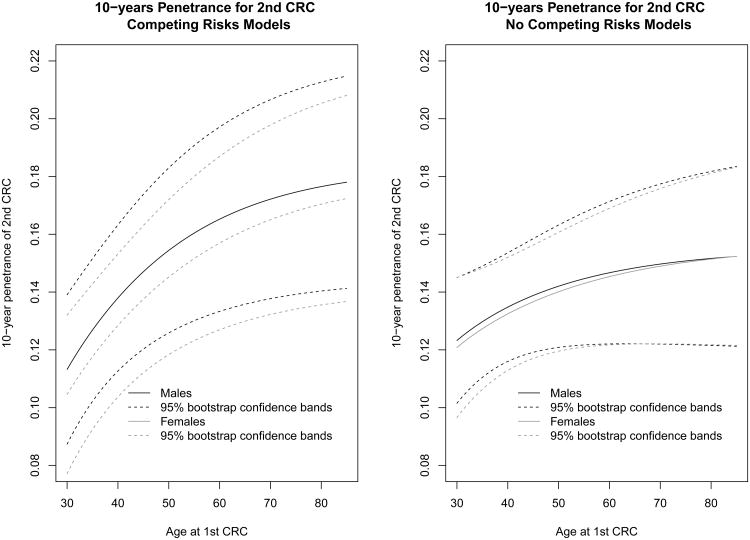
For the second step analysis (i.e. parameter estimates related to events 2 and 4), the log-likelihood of the model was –2246.78 for the log-logistic model, –2249.35 for the Weibull PH model and –2336.60 for the piecewise constant hazard model. Table 3 shows significant correlations between the two CRC events measured by the copula parameter. They correspond to a Kendall's tau of 0.082 (p<0.001) for the log-logistic and Weibull model and 0.062 (p=0.002) for the piecewise constant hazard model. These correlations are relatively small but highly significant, indicating that the gap time between the two CRCs depends significantly on the age at the first CRC. Among gene carriers, the 10-year risk of developing a second CRC after a first CRC under the log-logistic model was about 13.8% in males and 12.8% in females when the first CRC occurred at 40 years and it was close to 15.4% in males and 14.5% in females when the first CRC occurred at 50 years (Figure 1). Interestingly, the effect of the gene mutation on the second CRC was not significant for any of three models considered, nor the gender effect. When competing risks were ignored, the 10-year risk of developing a second CRC among gene carriers was slightly smaller with the log-logistic model.

Figure 1.

Penetrance estimates for second successive CRC after a first CRC occurred at age 40, 50, and 60 among male and female mutation carriers, assuming different baseline hazard functions

We also assessed the effect of the type of surgery after a first CRC on the risk of a second CRC using the log-logistic regression models. Among 788 individuals who had a first CRC and have had surgery recorded between the first and second CRCs, 6 had complete bowel removal and 170 partial removal. The rate of second CRCs (after exclusion of competing events) was 0/6 among individuals with complete bowel removal and 38/170 among those with partial removal (all of them being mutation carriers). Among mutation carriers, the 10-year risk of developing a second CRC after having partial surgery was close to 16.9% in males and 14.5% in females when a first CRC occurred at 40 years. Those rates were about 22.1% and 19.1% when the first CRC occurred at 50 years. The correlation between the times of first and second CRC corresponds to a Kendall's tau of 0.096 (SE^b=0.077), where SE^b is a bootstrap SE obtained from 1000 bootstrapped samples of the families.

Finally, we examined the risk of second CRCs for different types of MMR gene mutations and the dependence between the times to first and second CRCs. The results are summarized in Table 4. In 278 MLH1 carrier families, we observed 122 second CRCs (80 carriers, 42 unknown genotypes) among 592 first CRCs. The 10-year risk of developing a second CRC among carriers was 16.7% in males and 12.5% in females when a first CRC occurred at 40 years and 19.1% and 14.9% when the first CRC occurred at 50 years. For 342 MSH2 carrier families, we observed 139 second CRCs (94 carriers, 45 unknown genotypes) among 690 first CRCs. The 10-year risk of developing a second CRC among carriers was 13.1% in males and 15.1% in females when a first CRC occurred at 40 years and 13.8% and 15.9% when the first CRC occurred at 50 years. Finally, for 101 MSH6 carrier families, we observed 13 second CRCs (7 carriers, 6 unknown genotypes) among 135 first CRCs. The 10-year risk of developing a second CRC among carriers was 4.9% in males and 9.3% in females when a first CRC occurred at 40 years and 5.0% and 9.5% when the first CRC occurred at 50 years. Interestingly, the dependence between the times to first and second CRCs varied according to the mutation type, with a Kendall's tau of 0.109 (SE^b=0.033), 0.037 (SE^b=0.022), and 0.008 (SE^b=0.071) for MLH1, MSH2 and MSH6 mutations, respectively.

6. Discussion

Members of Lynch Syndrome families are exposed to a very high risk of developing multiple successive primary tumours. In this context, the estimation of the penetrance of a second cancer after a first cancer is complicated by the possible dependence between the two cancers (e.g. two successive CRCs) and by the presence of competing risks (e.g. deaths due to other LS-related cancers). In this paper, we developed a flexible approach based on Copula for modelling successive time-to-event data, where each event occurs in presence of a competing event. In addition, our approach can handle other problems typical to familial data analysis, in particular the presence of missing genotypes in high proportion and the complex ascertainment of families. To our knowledge, such an approach has not yet been developed for analyzing familial cancer syndromes.

Our simulation studies demonstrated the good performances of our approach in terms of bias and precision of the estimates of interest. For the first event, the estimation of covariate effects (gender, mutation status) and penetrance function was quite robust to the presence of missing genotypes, misspecification of the baseline and familial ascertainment. For the second event, although we noted larger biases of the covariate effects when the baseline hazard function was misspecified, the estimation of the penetrance function was generally unbiased even in the presence of missing genotypes. This is an important result since our main interest is in this penetrance function for the second event.

Our application to LS families from the Colon CFR illustrated the interest of our approach. Our analyses confirmed that mutation carriers of any MMR gene mutation have a high risk of developing a first primary CRC associated with an HR varying between 37.3 (age 30) and 28.8 (age 50) in males and between 37.7 (age 30) and 31.8 (age 50) in females. These risks were slightly attenuated compared to two recent reports (Dowty et al., 2013; Jenkins et al., 2015) but the latter only focused on MSH2/MLH1 mutations and did not account for competing risks due to LS-associated deaths. The penetrance function for the first CRC by age 70 was estimated at 54.6% in males and 43.3% in females which is in the range of previous estimates (Dowty et al., 2013). The advantage of our approach is that it also accounts for the dependence between the two successive CRCs. Interestingly, we found this dependence to vary by the type of mutation segregating within families, being stronger for MLH1 mutations (Kendall's tau of 0.106) and weaker for MSH2 and MSH6 mutations (Kendall's tau close to 0.04). Among MMR gene carriers, the 10-year risk of developing a second CRC after a first CRC under the log-logistic model was about 13.8% in males and 12.8% in females when the first CRC occurred at 40 years but was close to 15.4% in males and 14.5% in females when the first CRC occurred at 50 years. These estimates are also slightly attenuated compared to Parry et al. (2011) and Win et al. (2013), which could be due to the fact that some individuals had a complete bowel removal after the first CRC. When we just considered those individuals with partial surgery after the first CRC, the 10-year risk of developing a second CRC was close to 16.9% in males and 14.5% in females when a first CRC occurs at 40 years. Those rates are about 22.1% and 19.1% when the first CRC occurs at 50 years. Our model therefore provides compelling results about the risks of first and second CRCs but also on the dependence that links the occurrence of the two events for specific MMR mutation types.

Our approach also raises a few limitations. We modelled the risk of successive CRCs in people with LS regardless of their specific CRC site. We also ignored the risk of synchronous CRC tumours. Such events would lead to a more complex model where both sequential and parallel time-to-event processes could occur. Individuals with LS are also known to develop extra-colonic cancers either as first or second cancers, that might induce more complex dependences than those considered here. Finally, confounding factors such as CRC screening behaviours could have altered our cancer risk estimates. Future extensions of our approach will try to address some of these limitations.

Supplementary Material

Supp Appendix

Web appendices referenced in Sections 2 and 5 are available with this paper at the Biometrics website on Wiley Online Library.

Figure 2.

10-year risk of developing a second CRC conditional on the age of first CRC from log-logistic models; the black solid lines refer to estimates for males, whereas the grey solid lines represent estimates for females; the dotted lines are the corresponding 95% confidence bands obtained from 1000 bootstrapped samples of 781 families