Abstract
We have developed a color barcode labeling strategy for use with fluorescence in situ hybridization that enables the discrimination of multiple, identically labeled loci. Barcode labeling of chromosomes provides long-range path information and allows structural analysis at a scale and resolution beyond what was previously possible. Here, we demonstrate the use of a three-color, 13-probe barcode for the structural analysis of Drosophila chromosome 2L in blastoderm stage embryos. We observe the chromosome to be strongly polarized in the Rabl orientation and for some loci to assume defined positions relative to the nuclear envelope. Our analysis indicates packing ∼15- to 28-fold above the 30-nm fiber, which varies along the chromosome in a pattern conserved across embryos. Using a clustering implementation based on rigid body alignment, our analysis suggests that structures within each embryo represent a single population and are effectively modeled as oriented random coils confined within nuclear boundaries. We also found an increased similarity between homologous chromosomes that have begun to pair. Chromosomes in embryos at equivalent developmental stages were found to share structural features and nuclear localization, although size-related differences that correlate with the cell cycle also were observed. The methodology and tools we describe provide a direct means for identifying developmental and cell type-specific features of higher order chromosome and nuclear organization.
INTRODUCTION
Although the structure of DNA and nucleosomes are both relatively well understood (Wolffe, 1992; Alberts et al., 2002), higher levels or chromosome organization are not. Numerous studies indicate various degrees of coiling, looping, and random coil like variability. These features need not be exclusive, and most structural models suppose a hierarchy of organizational scales (Sedat and Manuelidis, 1978; Manuelidis and Chen, 1990; Belmont and Bruce, 1994). Analysis of the polytene chromosomes of Drosophila salivary glands, the only high-resolution interphase chromosome structures determined in their entirety, indicates significant variability but a well defined underlying helicity (Hochstrasser et al., 1986; Mathog and Sedat, 1989). In contrast, polymer statistical analysis based on the relationship between genomic separation and average spatial separation in mammalian interphase cells indicate a biphasic organization of large one to two mega base pairs (Mbp) loops, which themselves show largely random coil-like structure (Sachs et al., 1995; Yokota et al., 1995). Additionally, live imaging of yeast (Heun et al., 2001) and Drosophila (Marshall et al., 1997; Vazquez et al., 2001) chromosomes have revealed short time-scale Brownian movements confined within variably sized domains. These motions are consistent with the structural variability indicated by fluorescence in situ hybridization (FISH) studies.
Constrained motion and chromosome loops may be related. One study in Drosophila found specific FISH loci occupy distinct positions within the nucleus and relative to the nuclear envelope (Marshall et al., 1996). From these data, Marshall et al. (1996) extrapolated envelope attachment sites every one to two Mbp that would define loops of roughly the same size as those predicted from polymer statistics studies. As proposed by Vazquez et al. (2001), changes in the number of envelope attachment sites could provide a mechanism for controlling confinement domain size and hence chromosomal interactions. A looping structure also has been observed in connection with functionally defined insulator elements (Byrd and Corces, 2003), and mutations in these elements can induce major nuclear reorganization (Gerasimova and Corces, 1998; Gerasimova et al., 2000). Because insulator elements are related to the larger class of polycomb and trithorax genes that function to maintain chromatin states, this suggests that the organization of chromosomes into looped domains provides a mechanism for modulating gene expression (Gerasimova et al., 2000).
Beyond questions about intrinsic structure, it is important to understand how chromosomes are arranged relative to one another and within the nucleus. The polarized orientation of the chromosomes with centromeres at one nuclear pole and telomeres at the other (the Rabl configuration) is a dominant feature in Drosophila nuclei (Hochstrasser et al., 1986; Marshall et al., 1996, and it has been observed in many but not all species (Comings, 1980; Manuelidis and Borden, 1988; Dong and Jiang, 1998; Jin et al., 2000). Universally, it appears, individual chromosomes occupy distinct, largely nonoverlapping territories (Manuelidis, 1985; Schardin et al., 1985; Hochstrasser et al., 1986). Reports have been mixed as to whether the relative positions of chromosomes are fixed (Parada and Misteli, 2002), but the specificity of particular disease-causing DNA rearrangements indicates a nonrandom association between at least some loci (Kozubek et al., 1999; Nikiforova et al., 2000). One aspect of relative positioning with particular importance is the relationship of homologs in diploid nuclei. In Drosophila (Fung et al., 1998) and budding yeast (Burgess et al., 1999), nonmeiotic pairing of homologs is widespread, whereas in mammals it is not generally observed (Manuelidis and Borden, 1988; Vourc'h et al., 1993). Homologous interactions are implicated in imprinting (LaSalle and Lalande, 1996), transvection (Wu and Morris, 1999), and heterochromatin-mediated position effect variegation (Dernburg et al., 1996).
Understanding the biological importance of chromosome structure and nuclear organization will require high-resolution, sequence-specific structural information on a genomic scale. As recent advances in gene expression profiling have shown, state information on the full set of loci is invaluable for identifying correlated elements and dissecting systems level control circuits. However, beyond the original determination of interphase polytene structure, studies of chromosome structure have considered only a few loci together or have surrendered specificity to label very large domains. Primarily, this is due to the technical difficulty of resolving multiple chromosomal loci in interphase nuclei.
Leveraging the specificity and precision of single copy FISH, one could imagine an ordered set of probes mapped along a target chromosome with a unique color label for each probe. After hybridization and imaging, the 1:1 mapping of probes to labels would unambiguously define the chromosome path. Considered as such, the problem can be recast in terms of generating the necessary distinguishable labels. Only a handful of spectrally distinguishable fluorophores are currently available (∼5–8 with state-of-the-art imaging systems). Combinatorial (Schrock et al., 1996; Speicher et al., 1996) and ratiometric (Wiegant et al., 2000) labeling strategies can increase the effective number of labels, but ultimately these approaches provide only limited improvement.
In this article, we introduce barcode labeling as an adjunct strategy. The color barcode relies on a mathematically defined spatial relationship between probes ordered along a chromosome. The color code and the intrinsic geometric constraints of the chromatin fiber serve to differentiate the local environment of identically labeled probes and greatly reduce the possible global solutions. By increasing the effective number of distinguishable probes, this labeling strategy increases the long-range structural information obtained from FISH experiments.
We have used a barcode to investigate interphase chromosome structure in diploid Drosophila embryonic nuclei. We report here the results of that study and present new analysis methods for interpreting the wealth of data obtained from barcode FISH experiments.
MATERIALS AND METHODS
Barcode Design and Probe Preparation
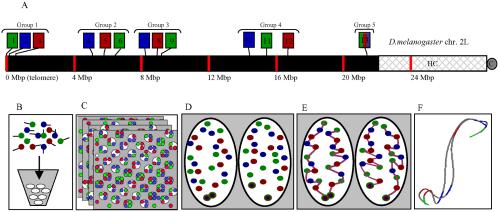
A three-color, 13-probe barcode was designed that maps to Drosophila melanogaster chromosome 2L as shown in Figure 1A. All probes (except 13 labeled histone) are P1s derived from the Drosophila Genome Project and average 80 kilobase pairs (Hartl et al., 1994). Probe 13 (histone) is a cosmid of the two main histone repeats and was originally provided by Gary Karpen (University of California, Berkeley, Berkeley, CA). Probes were grown in Escherichia coli cultures and purified using Midi-Prep kits (QIAGEN, Valencia, CA). Purified DNA was cut with a mix of four-base cutting restriction enzymes to an average size of 125 bp. Direct labeling of fluorophores was done using terminal transferase and either fluorescein isothiocyanate (FITC)-dUTP (PerkineElmer Life and Analytical Sciences, Boston, MA), FluorRed-dUTP, or Cy5-dUTP (Amersham Biosciences, Piscataway, NJ.). Unincorporated dUTPs and fragments <30 bp were removed using Bio-Rad P30 spin columns (Bio-Rad, Hercules, CA). The probes were then ethanol precipitated and resuspended in buffer. Approximately 0.5 μg of each labeled probe was used per reaction. Before the barcode hybridizations, the P1 probes were hybridized to polytene squashes and cycle 14 embryos to ensure proper chromosomal localization and minimal secondary signals.
Figure 1.
Experimental design. (A) A three-color, 13-probe barcode was designed which maps to D. melanogaster chromosome 2L. Probe localizations are based on release 3 of the Drosophila Genome Project Map. Euchromatin is shown in black (22.2 Mbp), heterochromatin is shown in gray mesh (6.2 Mbp), and the gray circle labeled C indicates the centromere. The probe labeled 13 maps to the histone locus and was labeled in all colors. The remaining probes were labeled with one color each. (B) The cut and labeled barcode probes were hybridized to cycle 14 Drosophila embryos. (C) Embryos were imaged using 3D wide-field fluorescence microscopy, and the data sets were deconvolved. (D) Nuclei and probe signals were segmented. (E) Chromosome paths were deduced using criteria described in the text. (F) The set of traces was subject to structural analysis.
Embryo Collection and FISH
Cycle 14 D. melanogaster (OregonR) embryos were obtained by collecting from population cages for 1 h and ageing for 1.75 h at room temperature. These were bleach dechorionated, fixed with fresh 3.7% formaldehyde in a 1:1 mixture of heptane/buffer A (15 mM PIPES, pH 7.0, 80 mM KCl, 20 mM NaCl, 0.5 mM EGTA, 2 mM EDTA, 0.5 mM spermidine, 0.2 mM spermine, 1 mM dithiothreitol) for 15 min, and then devitellinized. The full protocol has been described in detail previously (Hiraoka et al., 1993). Embryos were prepared for FISH with a series of washes moving from buffer A through 2× SSCT (0.3 M NaCl, 0.03 M Na3 citrate, 0.1% Tween 20) and finally into 50% formamide/2× SSCT. Approximately 50 μl of embryos and the probe containing hybridization solution (50% formamide, 10% dextran sulfate, 2× SSCT, 0.5 μg/P1 probe, 0.1 μg/histone probe) were mixed together in thin-walled polymerase chain reaction (pcr) tubes. Embryos and probes were denatured at 91°C for 2 min using a pcr heat block and left to hybridize overnight at 37°C in a humid chamber, on a slowly rotating rocker plate. The next day, embryos were washed in 50% formamide/2× SSCT, 25% formamide/2× SSCT, and three times in 2× SSCT (30 min/wash at room temperature except the first formamide wash at 37°C). Finally, embryos were rinsed twice with phosphate-buffered saline, stained with 2 μg/ml 4,6-diamidino-2-phenylindole (DAPI) for 10 min, and mounted on slides between no. 1 coverslip spacers. VectaShield mounting media (Vector Laboratories, Burlingame, CA) was applied, a coverslip overlaid, and the slides sealed using valap (1:1:1, petroleum jelly:lanolin:paraffin).
Microscopy, Image Processing, and Structure Modeling
Three-dimensional (3D) multiwavelength data sets were imaged using wide-field fluorescence microscopy coupled to a scientific grade cooled 12-bit charge-coupled device (Hiraoka et al., 1991). Image data sets were normalized for fading and lamp flicker and then processed using constrained iterative deconvolution with the enhanced ratio method (Agard et al., 1989). Initial segmentation was done within the Priism image visualization environment (Chen et al., 1996). Nuclei within the embryo field were manually defined using the signal of the DNA staining dye DAPI and then smoothed using a surface harmonic expansion algorithm (Marshall et al., 1996). The precise position and intensity of each FISH signal was determined using a Gaussian fitting algorithm.
Cross-wavelength offsets of the triple labeled histone probe (as a function of position within image relative to the optical axis) were used to calculate least-squares equations correcting cross-wavelength misalignment. The X, Y, and Z components of each wavelength correction were calculated separately The equations took the following form:
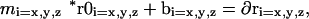 |
where m is the magnification correction factor, r0 is the original probe position relative to the optical axis, b is the off-axis translational offset, and ∂r is the correction factor (applied to r0). FITC was used as the reference wavelength. The center of each XY plane defined the optical axis, whereas the top of the datastack was set as the 0 position for the z-axis. (Offset data and specific correction factors are provided in online supplemental Figure S1.) As a result of these corrections, the total 3D cross-wavelength offsets (as measured by the histone positions) were reduced from 0.152 ± 0.061 to 0.049 ± 0.031 μm for the probe wavelengths. To calculate correction factors for the DAPI wavelength (which lacked the histone marker), we evaluated separate data sets, generated using an identical imaging setup, in which embryos had been stained with both DAPI and FITC-nuclear lamin antibodies. The nuclei were segmented in both wavelengths and the offset in nuclear volume centers between the two was used to calculate least squares correction factors as described above. This resulted in a reduction of the DAPI-FITC offsets from 1.010 ± 0.177 to 0.303 ± 0.150 μm. After checking the stability of the correction factors in three different data sets, they were applied to the DAPI wavelength in our original data.
Volume-rendered data and 3D models were manipulated using the VolumeViewer and ChromosomeViewer extensions to the Chimera molecular modeling software package (Pettersen et al., 2004). In the model view, connectivity between labels was displayed as spline curves generated with Catmull-Rom local path interpolation (Catmull and Rom, 1974).
Path Tracing
Chromosome paths were hand traced based on data visualization in both Priism and Chimera. Tracing began from the histone probes, which were easily identifiable since their signals colocalized in all three probe wavelengths. The remaining four groups of three probes with one color each were far enough separated in most nuclei to be unambiguously recognized. Once these groups were defined, they were linked to minimize path length while retaining the overall Rabl orientation. Before barcode hybridization, neighboring probes had been hybridized in sets containing one probe per color together with the histone probe that was triple labeled. From these tests, in which probe identity was unambiguous, we had calculated the average distance between nearest neighbor probes and between each probe and histone. This provided independent confirmation of the overall Rabl orientation of the chromosomes. (See online supplemental Figure S2 for a comparison of average pairwise distances in the probe test and barcode data.) By constraining solutions to match these expected distributions, we removed a major degree of tracing uncertainty. We assumed homologs did not intertwine, which required both arms to be traced concurrently. Variability among the probes in signal intensity was considered to a lesser degree. In a small number of cases where nuclei had two very similar solutions, preference was given to those that maximized homolog symmetry.
Structural Alignment and Clustering
A rigid body least-squares structural alignment algorithm was used (Horn, 1987). This routine takes two traces with coordinates for a corresponding set of labels and outputs the rotated and translated coordinates of the comparison trace relative to the reference trace. The transformed coordinates minimize the root mean square (rms) distance between corresponding labels. Pairwise rms between structures was then used as a basis for agglomerative clustering. The clustering algorithm is a variant of the weighted pair-group method using arithmetic averages (WPGMA) where at each iteration, clusters are merged to maximize the difference between average intercluster rms and intracluster rms (∂rmsavg). Details of the algorithm are given in the Appendix. This method has been shown to work well with both tightly clumped and elongated clusters (Sneath and Sokal, 1973).
Applied to our data, the WPGMA method generated multiple small clusters right up to the final clustering iteration when all clusters collapsed to a single cluster. Neither visual inspection nor plotting ∂rmsavg as clustering progressed provided a clear indication of when to stop merging clusters. Likewise, we had no external data on structurally or functionally defined clusters that might have been used to calibrate the algorithm. Instead, we developed mixture analysis to evaluate clustering.
Mixture Analysis
Mixture analysis combines two data sets and applies clustering to test whether they can be separated. We used mixture analysis to compare experimental data sets and simulated data sets generated with different models of chromosome structure (the models were random coil, Rabl-random, and confined-Rabl; details for each are given in the Appendix). To begin, traces from two data sets are merged into one (the source of each trace is saved). Next, clustering is run until completion on the merged data set. For each cluster at each clustering iteration, the number of traces from each of the original data sets is tabulated. If the original two populations are similar, traces from each should distribute across the set of clusters in proportional to their relative proportion in the merged data set. A X2 metric was used to calculate the deviation from equal proportion at each cycle of clustering:
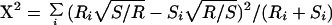 |
where Ri is the number of experimental traces in cluster i, Si is the number of simulated traces in cluster i, R ≡ ∑ Ri and S ≡ ∑ Si. Because many of these clusters have only a few traces, a gamma distribution cannot be used to determine the probability of the X2 value as is normally done. Instead, we used a resampling technique whereby 10,000 random distributions are generated for each iteration of clustering. Each distribution maintains the same number of clusters and traces in each cluster but randomizes the fraction of traces from each source within each cluster. A X2 for each distribution is calculated as described above and the cumulative probability equals the fraction of simulated distributions that have a X2 equal to or greater than the actual X2. Probabilities close to 1 indicate experimental and simulated traces are equally distributed across clusters, whereas probabilities close to 0 indicate data sets cluster separately and are statistically different. Plotting probability over the full course of clustering allows easy identification of iterations where the data sets are statistically separable. This approach thus sidesteps the problem of deciding at which iteration clustering should be stopped.
Nuclear Localization of Probes
In addition to measuring the average distance of each probe to the nuclear envelope, probe nuclear localization was analyzed using a methodology developed by Marshall et al. (1996). For each data point, a set of 1000 random points was generated within the same z-plane of the volume and the distance to the nuclear envelope for each of these was calculated. Those FISH points where <50% of the random points were closer to the envelope than the real point were defined as outer, whereas those that were not were defined as inner. This process was repeated for all traced arms to determine the total fraction of each label with inner or outer localization. The ratio of inner to outer points for each label was then tested for statistical significance by comparison with a normal distribution. Those labels with statistically insignificant bias toward inner or outer localization were defined as having random nuclear localization. [Note that although the test is identical, we have replaced the terminology of close/far (relative to the envelope) used by Marshall et al. (1996) with outer/inner (within the nuclear volume). We feel this better describes the test results.]
Additionally note that although Marshall et al. (1996) used lamin antibody staining to define the nuclear envelope, we have used the DAPI signal. In tests on separate data sets containing both types of signals, we have found that these give an almost identical boundary for the middle two-thirds of each nucleus. At the top and bottom of each nucleus, DAPI segmentation gave a slightly larger radius than lamin. It is not clear which is more accurate (our unpublished data).
We also tested whether equivalent points on homologous chromosomes or pairs of points on the same chromosome within the same nucleus were correlated in their nuclear envelope localization. For each label pair, the expected frequency of cooccurrence (inner or outer) equals the product of the frequency of independent events (as determined above). The expected frequencies for cooccurrence of label localization could then be compared with their actual frequency and statistically evaluated using the X2 test.
RESULTS
Representative Data
We wished to better understand long-range chromosome organization. Toward this end, the experimental strategy outlined in Figure 1 was implemented. Briefly, color barcode FISH and imaging provided us with the 3D coordinates for multiple points along chromosomal arms. The connectivity between points was deduced from the barcode and distance constraints (as described in Materials and Methods). After tracing multiple chromosome arms, the structures were characterized using a variety of analyses, including clustering based on the residual rms of rigid body alignment.
The barcode design used three colors and 13 probes. The histone root probe was labeled with all colors, whereas the others were labeled with one color each. The code was designed such that save the root probe, there were four semidistinct groups of three probes, each having one probe labeled with one of the three colors (Figure 1A). Within groups, probes were on average 0.5 Mbp apart, whereas the average group separation was 4.5 Mbp.
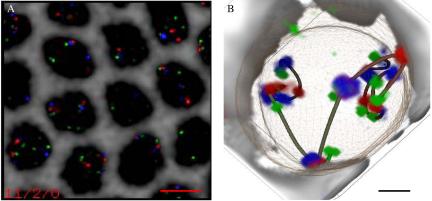
The barcode probe set was hybridized to cycle 14 blastoderm stage Drosophila embryos. We collected 3D multichannel images of the embryos and processed them as described in Materials and Methods. One example of a processed data set is shown in Figure 2A. The nuclear boundary and 3D coordinates for probes were segmented from the images. Chromosome arms were traced interactively with the Chimera molecular modeling package. An example of a traced nuclei is shown in Figure 2B. Note that spline curves were only used to indicate connectivity and the exact path between points is unknown. The splines were not used in the analysis, which is based only on the coordinates of the 13 barcode labels. In total, data are presented for two cycle 14 embryos (DS1 and DS5). For each, ∼100 arms were traced.
Figure 2.
Barcode FISH data set and volume-rendered, traced view. (A) Deconvolved and wavelength-aligned 1-μm projection through a region of the embryo hybridized using the barcode shown in Figure 1A. The four channels were imaged sequentially and are false colored as follows: FITC, green; Rhod, red; Cy5, blue; and DAPI, gray. The DAPI channel has been inverted to provide a clearer view of the probe hybridization. Bar, 5 μm. (B) One traced nucleus from the data set shown in A. Volume rendering and model overlay displayed using ChromosomeViewer and VolumeViewer extensions to Chimera. Deduced path connectivity is shown as an interpolated spline curve, and the nuclear envelope is shown as a mesh. Bar, 1 μm.
Structural Alignment and Clustering
Pairwise alignment and clustering was used to group structurally similar chromosomes and to characterize each set of traced chromosomes as either a single structural distribution or multiple subpopulations. Because clustering based on rigid body alignment might miss locally defined structures separated by flexible joints, we aligned and clustered subintervals in addition to the full-length chromosome (labels 1–13). We first discuss interval 1–6 to demonstrate the method of analysis. Then we present a summary of results for multiple intervals. Note that in the following discussion, clusters are sets of chromosomes with similar structures, whereas intervals are groups of adjacent probes in the barcode.
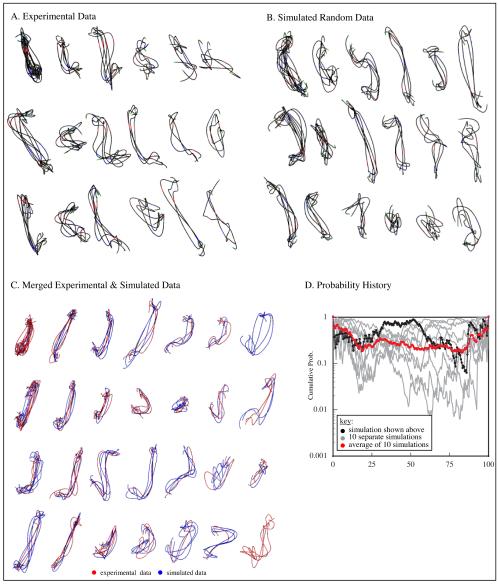
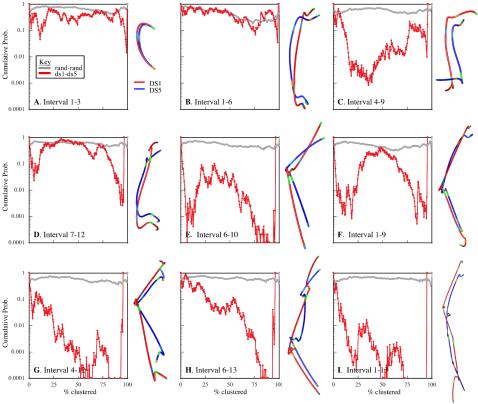
Figure 3A shows clusters of interval 1–6 with three or more traces when clustering is 80% complete. Whereas the 80% iteration is not unique, a general grouping should be established by this point if the data have clearly defined subgroups. Instead, we observed many sparsely populated clusters that seem to represent a continuum of structures. For comparison, we clustered chains generated according to a random coil model (see Appendix for details on this and other models). At 80% clustered (Figure 3B), the number of clusters and the distribution of traces within clusters is very similar to that observed in the experimental data. Because the simulated data are a single population distribution (i.e., all chains were generated with the same set of parameters), it suggested that the experimental data is also a single structural population.
Figure 3.
Clustering and mixture analysis. Analysis of interval 1–6 is used to demonstrate the method. In A–C, clusters with three or more traces at 80% completion are shown. (A) Experimental data. (B) Simulated random coil data. (C) Merged experimental and simulated data. (D) Probability of observed segregation of traces into clusters over the course of clustering (black line). Values near 1 indicate traces from the two data sets distribute randomly among clusters and thus the data sets were statistically inseparable. We also generated nine more simulated data sets with the same parameters, merged each in turn with the experimental data set and clustered as described above. Probability histories for these nine simulations are shown in gray. The log average for all 10 simulations is shown in red. Multiple simulations were run to reduce the influence of particular structures generated in any one simulation. Using mixture analysis, the experimental and simulated data were statistically inseparable. The results indicate that the experimental data represent one structural population that is effectively modeled as a Gaussian coil.
Moreover, the simulated and experimental data look very similar. In the random coil model, distance between adjacent labels matched the experimental distributions, but no other geometric constraints were imposed. To determine whether this random coil model contained sufficient information to characterize the experimental data, we applied mixture analysis (see Materials and Methods for details). The experimental and random coil simulated data were merged together and clustered. Figure 3C shows clusters with clustering 80% complete. The segregation of experimental and simulated data sets had a calculated probability of 0.17. Plotting the cumulative probability history (Figure 3D, black line) reveals no points during the clustering process when the partitioning of data into clusters was significantly nonrandom. To ensure that this result was not simply an artifact of the particular set of simulated structures, a total of 10 simulated data sets of 100 traces each were generated using the same step parameters. Each in turn, was merged with the experimental data, clustered and subject to mixture analysis (Figure 3D, gray lines). The log average of all 10 (Figure 3D, red line) provides a robust measure of the how well the experimental and simulated chains can be separated (note the log average is used in all plots that follow). The analysis indicates that for the 1–6 interval, the random coil model generates structures indistinguishable from our experimental data.
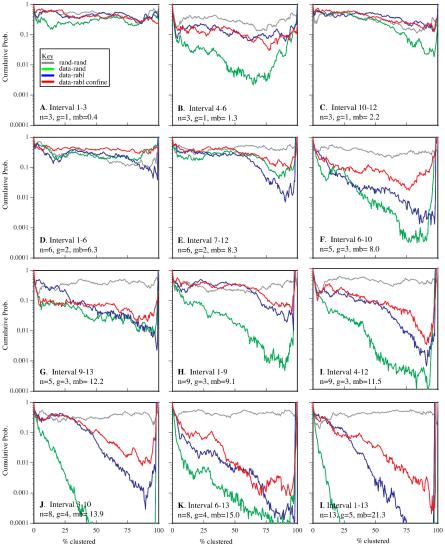
We used mixture analysis to compare experimental and simulated random coil data for several intervals. We found that the shorter intervals (labels 1–3, 10–12, 1–6, and 7–12) were statistically inseparable at the 0.05 probability threshold, whereas the remaining intervals were separable at a probability threshold of 0.01 or lower (Figure 4, green lines). With the exception of the 4–6 interval, the goodness of fit generally decreased as the interval size increased. In these cases, the clusters with predominantly experimental data had traces that were elongated relative to the simulated traces. To capture this polarized (Rabl) orientation of the chromosomes, a second chain model was developed.
Figure 4.
Summary of mixture analysis for several intervals with simulation models. Each line in each graph is the log average probability from 10 sets of simulated data merged with the experimental data and subject to mixture analysis. The results are shown for a set of intervals varying in the number of labels (n), the groups spanned by the labels (g), and the overall base pair separation between the first and last label (mb). For each interval, results from four analyses are shown. Two sets of simulated data generated with the same parameters as a control (gray), experimental data merged with random chains (green), experimental data merged with Rabl chains (blue), and experimental data merged with confined-Rabl chains (red). The control data sets were inseparable for all intervals. With the exception of the 4–6 interval, all models were essentially equal at the shorter intervals. As the intervals increased in size, the probability values drop, indicating that the experimental data and the random coil traces have separated into distinct clusters. Although the Rabl and confined-Rabl data also showed decreased goodness of fit, it was to a lesser degree. Overall, the confine-Rabl was clearly the best for modeling the data. Only for the very longest intervals (3–10, 4–12, 6–13, and 1–13) was it unable to generate data that could be separated from the experimental data over the course of clustering.
The Rabl-random model generates chains randomly oriented along two axes with a bias elongating them along the third axis. These Rabl-random chains were merged with the experimental data, clustered,and subject to mixture analysis. For every interval except 7–12, the Rabl model was as good as, or better than the random coil model and some (4–6, 1–9, 3–10, and 1–13) showed dramatic improvement (Figure 4, blue lines). However, with the exception of interval 4–6, the intervals that were statistically separable at the 0.05 probability threshold with the random coil model remain so with the Rabl model (just barely so for interval 1–9).
Confinement of chromosomes within boundaries defined by the nucleus also constrains structure. We hypothesized that this effect would be increasingly apparent at large size scales, and as such, would be important for modeling the longer intervals. We tested this possibility by modifying the Rabl model so that chains were restricted to lie within defined nuclear boundaries. For every interval, the confined-Rabl model was as good as or better than the random coil and Rabl-random models (Figure 4, red lines). For all but the largest intervals (3–10, 4–12, 6–13, and 1–13), the confined-Rabl model generated structures that were statistically inseparable from the experimental data. At the largest intervals, the confined-Rabl model came close, but it did not fully capture the structural features observed in the experimental data.
Comparison of Structure from Two Different Embryos
We traced the paths of 100 chromosomes in each of two embryos (defined as DS1 and DS5) labeled with the same 13 probe barcode. Based on the number and size of nuclei within the image field, both were determined to be mitotic cycle 14 pregastrulation embryos. It has previously been reported that nuclear height increases monotonically during cycle 14 (Fung et al., 1998). The average height of nuclei in DS1 was 13.62 ± 0.58 μm and in DS5 it was 11.95 ± 0.67 μm. Using the equation given by Fung et al. (1998), this puts DS1 33 min and DS5 24 min into cycle 14. Additionally, the average pairwise distances between adjacent chromosome arm points were 14 ± 10% longer in DS1 than in DS5. Together, these facts suggest neither embryo's nuclei have begun to condense for the next division.
Mixture analysis of DS5 produced results very similar to the DS1 mixture analysis discussed in the previous section (our unpublished data). Mixture analysis also was used to compare chromosome structure in DS1 against DS5. At the 0.01 probability threshold, DS1 was separable from DS5 for all intervals examined except 1–3 and 1–6 (Figure 5, plots). The separability of DS1 and DS5 increased with the number of probes and the number of triplet groups contained in the interval. Although the final composite average structures of DS5 were uniformly smaller than DS1, the shapes were remarkably similar. This can be seen particularly clearly for the intervals 1–6, 7–12, 1–9, and 4–12 (Figure 5, structures).
Figure 5.
Mixture Analysis of DS1 and DS5. For each interval, the probability history is shown on the left, and the final cluster average structures for each data set clustered independently are shown on the right, aligned, and overlaid. Except for intervals 1–3 and 1–6, the data sets are separable. Separability increases with interval size in parallel with size differences in the average structures. Despite this, the final cluster average shapes are themselves very similar. This is particularly obvious with the intervals 1–6 (B), 7–12 (D), 1–9 (F), and 4–12 (G). Comparison of the final cluster average structures, particularly for intervals 6–10 (E) and 4–12 (G), shows not only size differences, but also a wider, more open conformation of DS1 relative to DS5. Together with the nuclear height analysis that indicates DS1 has progress farther into interphase, this suggests Rabl polarization increases through the cell cycle.
Comparison of the final composite average structures for the larger intervals suggests a more pronounced Rabl orientation in DS1 relative to DS5. In intervals 6–10 (Figure 5E), not only was the contour length of the DS1 structure longer (4.25 μm for DS1 vs. 3.43 μm for DS5) but also the central angle was wider (138° for DS1 vs. 99° for DS5), creating a more pronounced Rabl polarization. A similar effect can be seen with interval 4–12, and to a lesser extent, intervals 6–13 and 1–13. Given the nuclear height analysis placing DS1 farther into cycle 14, this indicates that Rabl orientation increases through the cell cycle as chromosomes decondense, contradicting the usual assumption that Rabl orientation is strongest after telophase and relaxes through interphase.
Analysis of Distance Statistics
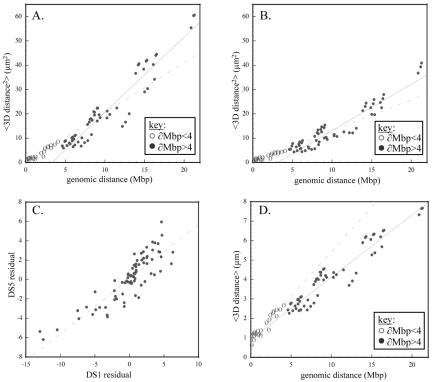
Analysis of distance statistics provides another way to characterize structure. For example, Gaussian random coil behavior of chromosomes will result in a linear correlation between the 3D average distance squared (<∂2>) and the genomic separation (∂bp) of probes (van den Engh et al., 1992). Additional structural features will modify this relationship. Plots of <∂2> versus ∂bp for DS1 and DS5 are roughly linear (Figure 6, A and B). However, upon closer inspection these plots seem to have multiple plateaus, which suggest a hierarchy of organizational scales. A large transition is apparent around 4 Mbp, so separate lines were fit to probes separated by <4 Mbp (dashed line) and greater than 4 Mbp (solid line). If confinement were the dominant effect at this size scale, we would expect the slope above 4 Mbp to decrease. Instead, it increases, reflecting the dominant effect of the Rabl orientation. Both above and below the 4-Mbp transition, the slopes from line-fitting the DS5 data are smaller than the equivalent DS1 line-fitting slopes. This reflects the more condensed state of DS5 relative to DS1, which also was seen during clustering. Strikingly, deviations from the line-fits are correlated between DS1 and DS5. This can be seen in Figure 6C, which plots the residuals of equivalent probe-pairs from the line-fits shown in Figure 6, A and B. This suggests there is an underlying structural basis for the deviations. Nonuniform compaction along the chromosome or domain confinement are possible causes.
Figure 6.
Analysis of pairwise distance statistics. Genomic distance (∂bp) versus average spatial distance squared (<d2>) for all probe pairs in the barcode are plotted for DS1 (A) and DS5 (B). The two lines in each graph correspond to the line-fit for probes separated by <4 Mbp (dotted line) or >4 Mbp (solid line). The steeper line-fit for probes >4 Mbp reflects the Rabl orientation, which extends the chromosome. Both above and below 4 Mbp, the DS1 line-fit slopes are steeper than those for DS5 because the DS1 structures are larger. Interestingly, both data sets display similar deviations from the line-fit, which implies an underlying structural cause. This can be seen clearly in C, which plots the residuals from the line-fits of DS1 versus DS5. To estimate compaction, we plot genomic distance (∂bp) versus average spatial distance (<d>) for all probe pairs in the DS1 data (D). From the points <4 Mbp, we estimate compaction at 1066× and from the points >4 Mbp we estimate compaction at 740×.
To derive a quantitative estimate of overall compaction, we looked at the relationship between ∂bp and <∂> (as opposed to ∂bp and <∂2> for the polymer model). In Figure 6D, we plot this line-fit for DS1 above and below the 4-Mbp transition as in the previous plots. The line-fit below and above 4 Mbp gives slopes of 0.459 μm/bp and 0.320 μm/bp, respectively. Based on a value of 0.34 nm/bp for DNA, this corresponds to packing ratios of 740× and 1066×. Equivalent calculations on DS5 (our unpublished data) give packing ratios of 1066× and 1386×. Assuming the nucleosomal and 30-nm fiber each give sevenfold compaction (Wolffe, 1992), these values indicate another 15- to 28-fold packing for interphase chromosomes.
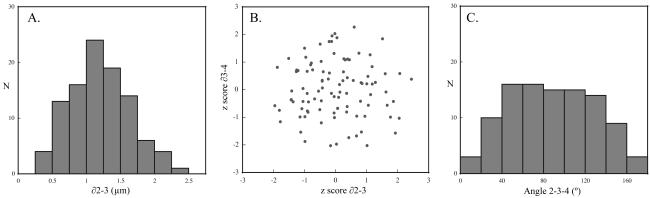
To investigate whether rigid-body alignment and clustering may have missed underlying structural subpopulations, we looked at histogram plots of individual probe pair distance distributions. The histogram for probe pair 2–3 (Figure 7A) showed a unimodal distribution, as did the others. We also considered whether the lengths of adjacent segments on the same arm were correlated, as might be expected if some traces in the data set were uniformly more or less condensed than others. A z-score was calculated for each segment of each trace, and the z-scores of adjacent segments (on the same arm) were plotted against each other. The results for the ∂2–3 versus ∂3–4 segments are shown in Figure 7B, and it can be seen that there is no correlation. The remaining intervals produced similar results. Finally, we considered the distribution of angles formed by groups of three consecutive probes, which should be sin(ø) for uncorrelated segment orientations. A histogram of angles formed by probes 2–3-4 (Figure 7C) closely matched the expected distribution, as did others. These tests confirm the conclusion from cluster analysis that each data set was a single structural population.
Figure 7.
Pairwise distributions. The pairwise distance histograms for adjacent probe pairs were evaluated. As expected for a single structural population, these distributions were unimodal (one example is shown in A). We next tested whether there was a correlation in compaction between adjacent segments. After determining the population average distance for each probe pair, a z score was calculated for each trace. In B, the z score for the 2–3 segment is plotted against the z score for the 3–4 segment (from the same trace). There is no correlation between the measures. Other probe pairs behaved similarly. One example angle distribution (probes 2–3-4) is shown in C. The roughly sin(ø) distribution is as expected based on a random coil model.
Homolog Similarity during Interphase
We questioned whether homologous chromosomes within the same nucleus were more similar to one another than to chromosomes in different nuclei. For about half the intervals tested in DS1, aligned homologs had a statistically lower rms than nonhomolog, as measured by a two-tailed t test (H vs. NH in Table 1). In contrast, only one interval in DS5 had homologs that were statistically more similar. Homologs pair early in Drosophila development, and we checked for pairing differences between data sets that might explain this difference. At cycle 14, only histone (label 13) is significantly paired, and the two data sets were paired at roughly similar degrees (70% for DS1 and 60% for DS5). Despite this, we separately compared the paired (pH) and unpaired (uH) homolog rms averages to the nonhomolog population averages (NH). In DS1, the results were striking. For all but two of the intervals, the homologs paired at histone were statistically more similar than nonhomologs, whereas none of the unpaired homologs were. In contrast, although the paired at histone homologs in DS5 were more similar than nonhomologs for many of the intervals, the difference was only statistically significant for one. None of the unpaired homologs were statistically different from the nonhomologs. Thus, pairing does not explain the differences in homolog similarity between DS1 and DS5, but it clearly increases overall similarity.
Table 1.
Analysis of homolog RMS
| Nonhomolog (NH) RMS Avg (μm) | Homolog (H) RMS Avg (μm) | UnPaired homolog (uH) RMS Avg (μm) | Paired homolog (pH) RMS Avg (μm) | H vs. NH RMS Avg pval | NH vs. uH RMS Avg pval | NH vs. pH RMS Avg pval | |
|---|---|---|---|---|---|---|---|
| ds1.1-3 | 0.37 | 0.39 | 0.40 | 0.38 | - | - | - |
| ds1.3-7 | 1.11 | 0.98 | 1.02 | 0.96 | ++ | - | ++ |
| ds1.6-10 | 1.12 | 1.07 | 1.12 | 1.04 | - | - | + |
| ds1.9-13 | 1.13 | 1.10 | 1.27 | 1.03 | - | - | + |
| ds1.1-6 | 1.03 | 0.95 | 1.00 | 0.93 | + | - | + |
| ds1.4-9 | 1.10 | 1.03 | 1.11 | 0.99 | - | - | + |
| ds1.7-12 | 1.14 | 1.14 | 1.31 | 1.07 | - | - | - |
| ds1.3-10 | 1.40 | 1.27 | 1.35 | 1.23 | ++ | - | ++ |
| ds1.6-13 | 1.39 | 1.30 | 1.42 | 1.25 | + | - | ++ |
| ds1.1-9 | 1.35 | 1.24 | 1.31 | 1.21 | ++ | - | ++ |
| ds1.4-12 | 1.37 | 1.29 | 1.45 | 1.22 | - | - | ++ |
| ds1.1-13 | 1.60 | 1.47 | 1.58 | 1.43 | ++ | - | ++ |
| ds5.1-3 | 0.33 | 0.32 | 0.33 | 0.32 | - | - | - |
| ds5.3-7 | 0.92 | 0.86 | 0.95 | 0.81 | - | - | - |
| ds5.6-10 | 0.94 | 0.91 | 0.99 | 0.86 | - | - | - |
| ds5.9-13 | 0.94 | 0.94 | 0.97 | 0.92 | - | - | - |
| ds5.1-6 | 0.91 | 0.91 | 0.97 | 0.87 | - | - | - |
| ds5.4-9 | 0.91 | 0.87 | 0.94 | 0.83 | - | - | - |
| ds5.7-12 | 0.93 | 0.93 | 1.01 | 0.87 | - | - | - |
| ds5.3-10 | 1.17 | 1.12 | 1.24 | 1.04 | - | - | + |
| ds5.6-13 | 1.17 | 1.16 | 1.22 | 1.12 | - | - | - |
| ds5.1-9 | 1.13 | 1.11 | 1.18 | 1.07 | - | - | - |
| ds5.4-12 | 1.14 | 1.12 | 1.20 | 1.07 | - | - | - |
| ds5.1-13 | 1.36 | 1.34 | 1.43 | 1.28 | - | - | - |
Table 1 shows the average alignment rms of nonhomologs (NH), all (paired and unpaired at histone) homologs (H), paired at histone homologs (pH), or unpaired at histone homologs (uH). The results of 2 tailed t-tests comparing these groups are also shown. In DS1 a few intervals showed a significant bias when comparing all homologs to nonhomologs. When the homologs were separated into paired or unpaired, it was clear that the increased similarity results from those homologs unpaired at histone homologs (uH). None of the unpaired homologs were statistically different from the nonhomologs. In DS5, the effect was much weaker. Only the 3-10 interval was statistically different at the 0.05 threshold between nonhomologs. In DS5, the effect was much weaker. Only the 3-10 interval was statistically different at the 0.05 threshold between nonhomologs and paired homologues. Qualitatively however, the effect was similar. For every interval but two (1-6, 7-12), the paired homologs were more statistically different than the paired homologs. +, pval < 0.05; ++, pval < 0.01.
Within the embryo, the cell cycles of nearby nuclei are quasi-synchronous at this developmental stage (Foe, 1989). Nevertheless, we considered the possibility that bias toward homolog similarity, where it was observed, might reflect differences in condensation related to the cell cycle (assuming homologs within the same nucleus are similarly condensed). We used overall path (contour) length as a measure of condensation and compared the difference between homolog and nonhomologs by using a two-tailed t test. The differences in average path length between homologs (paired and unpaired together) were not statistically significant different for any intervals in either data set. When the paired-at-histone homologs were separated from the unpaired homologs, only one interval in each data set (4–12 for DS1 and 1–3 for DS5) had a statistically significant similarity, whereas none of the unpaired homologs did (our unpublished data). Overall, these results indicate that the increased similarity of paired homologs is unrelated to condensation. More generally, the contour length analysis supports the assumption of cell cycle synchrony for nearby nuclei within the embryo.
Nuclear Localization of Chromosomes
We investigated the organization of chromosomes within the nucleus. To define the nuclear positions of labels, we approximated each nucleus as an oriented ellipsoid and used the ellipsoid axes to define a coordinate system. The label coordinates were then transformed such that nuclear height was coincident with the z-axis (see Appendix for details). Using the transformed coordinates, we determined the average xyz position of each label. The polarized (Rabl) orientation of the chromosomes was reflected in the increasing z coordinates of labels (Table 2). In contrast, the average xy components were all close to zero, consistent with an unbiased orientation.
Table 2.
Quantitative analysis of probe nuclear localization
| Code ID | DS1 axial pos (μm) | NE Dist Avg (μm) | fclose | Result (p < 0.001) | DS5 axial pos (μm) | NE Dist Avg (μm) | fclose | Result (p < 0.001) |
|---|---|---|---|---|---|---|---|---|
| 1 | -3.42 | 0.86 | 0.46 | RAND | -2.78 | 0.87 | 0.47 | RAND |
| 2 | -3.41 | 0.75 | 0.65 | OUTER (p < 0.01) | -2.63 | 0.77 | 0.62 | OUTER (p = 0.01) |
| 3 | -3.12 | 0.97 | 0.38 | INNER (p = 0.01) | -2.46 | 0.89 | 0.44 | RAND |
| 4 | -1.38 | 1.03 | 0.44 | RAND | -0.95 | 0.89 | 0.49 | RAND |
| 5 | -1.08 | 1.12 | 0.31 | INNER | -0.71 | 1.11 | 0.27 | INNER |
| 6 | -0.97 | 1.13 | 0.31 | RAND | -0.67 | 0.97 | 0.38 | INNER (p < 0.01) |
| 7 | 0.09 | 1.02 | 0.38 | INNER | 0.12 | 0.93 | 0.44 | RAND |
| 8 | 0.51 | 1.03 | 0.34 | INNER | 0.39 | 0.91 | 0.40 | RAND |
| 9 | 0.75 | 1.00 | 0.39 | RAND | 0.46 | 0.98 | 0.40 | RAND |
| 10 | 2.40 | 0.90 | 0.47 | RAND | 1.64 | 0.98 | 0.36 | INNER (p < 0.01) |
| 11 | 2.54 | 0.88 | 0.43 | RAND | 1.80 | 0.98 | 0.35 | INNER (p < 0.01) |
| 12 | 2.78 | 0.89 | 0.42 | RAND | 2.00 | 0.91 | 0.39 | RAND |
| 13 | 3.97 | 1.26 | 0.17 | INNER | 3.32 | 1.30 | 0.16 | INNER |
Table 2 gives the average Rabl position and the average distance to the nuclear envelope for each of the 13 labels in DS1 and DS5. Additionally, for each labeled point, the statistically defined nuclear envelope localization is shown. For both datasets, the z averages increase along the chromosome, reflecting their polarized orientation (the average x and y Rabl coordinates are close to zero and not shown). In DS1 and DS5, the analysis shows one point (label 2) consistently closer to the nuclear envelope than the randomly generated points.
Chromosome positions also were defined relative to the nuclear envelope. First, we calculated the average distance of each label to the envelope. Second, following the methodology of Marshall et al. (1996), the distribution of each label was statistically categorized as inner, outer, or random within the nuclear volume (Table 2). We found one probe (label 2 near the telomeric end of the chromosome) nonrandomly localized to the outer half of the nucleus in both DS1 and DS5. Five probes were found nonrandomly localized to the inner half of the nucleus in both DS1 and DS5, although not the same subset. In all, seven of the 13 labels had the same statistical localization (inner, outer, or random) in both data sets. Labels with similar localization in both data sets were predominately at the centromeric and telomeric ends of the chromosome. Even for the labels with statistically significant localization relative to the nuclear envelope, a large amount of variability across nuclei was observed.
We also tested for correlations in the statistically defined envelope localization of identical labels on homologous arms. Based on X2 analysis, the localization of all labels was uncorrelated between arms (our unpublished data). Using the same approach, we tested for correlations between the nuclear envelope localization of different labels on the same arms, as might be expected if cooccurring envelope attachment sites defined structural domains. The few correlations we did find were between the most closely spaced (by base pairs) probes and of little interest. The one exception to this was the label pair 7 and 12, whose localization was strongly correlated (p = 0.0064) despite a base pair separation of >8 Mbp.
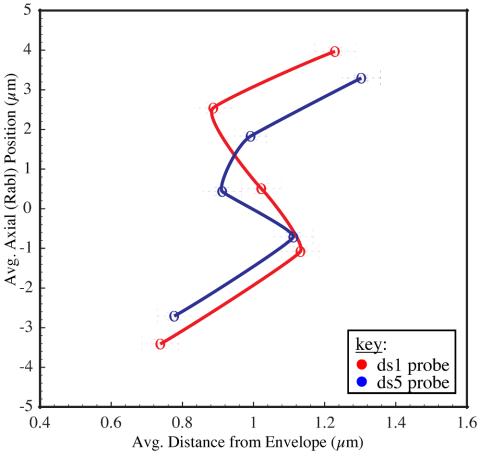
To visualize nuclear localization, we plotted the average axial (Rabl) position against the average distance to the envelope for each of the labels. The plots in Figure 8 show a high degree of similarity between DS1 and DS5. Both the stronger Rabl polarization of DS1 relative to DS5 and the greater condensation of DS5 relative to DS1 are apparent. Although the two data sets showed only partial similarity in nuclear envelope localization using the statistical test, the average distance to the envelope for the labels follow almost identical patterns. Overall, the correlation coefficient of axial (Rabl) positions in DS1 versus DS5 was 0.997, whereas for nuclear envelope distance it was 0.801.
Figure 8.
Visual plot of nuclear localization. We have plotted the average distance to the nuclear envelope against the average Rabl position for a few labels. Only 1 label from each group is shown for clarity (from the bottom, labels 2, 5, 8, 11, and 13). The results for DS1 and DS5 are overlaid. Although the envelope localizations were not statistically identical in both data sets, the average positions are qualitatively similar. The slight differences in Rabl positions between the two data sets reflect differences in overall size and the greater Rabl polarization of DS1 relative to DS5.
DISCUSSION
Due to the limited number of spectrally distinguishable fluorophores, previous studies of chromosome structure in diploid, interphase nuclei have been limited to the concurrent positional determination of at most a few loci. In this article, we introduce a color barcode labeling strategy whereby multiple, identically labeled loci can be distinguished. We used a barcode comprising three colors and 13 probes to roughly define the path of chromosome 2L in Drosophila embryonic nuclei at the cycle 14 pregastrulation stage. Analysis of these traced structures allowed us to characterize long-range chromosome organization in this system.
Distribution of Chromosome Structures
Structures were compared using mixture analysis of clustering based on rigid body alignment. For all but the largest intervals, a confine-Rabl model generated structures that were inseparable from the experimental data. Because the simulated data were one structural population and the experimental data were largely inseparable from it, this implies that the experimental data were also a single structural population. The pairwise probe distance distributions and angle distributions were all unimodal, which also support this interpretation.
It is not surprising to find that chromosomes within the embryo at this stage of Drosophila development are a single structural population. The blastoderm stage embryos we studied have just begun to express genes at a significant level (Anderson and Lengyel, 1981). Except for the pole cells, embryonic nuclei do not begin to show signs of differentiation until the onset of cellularization later in cycle 14 (Foe, 1989; Lawrence, 1992). As such, the largely undifferentiated chromosome organization we have observed may represent a ground state providing the necessary flexibility for the range of differentiated cell types that arise later in development. If this is true, chromosomes from nuclei at later stages should display more distinct structural features and these features should vary among cell types. This hypothesis can be tested by applying the barcode method to postgastrulation embryos, imaginal discs, and other cell in various stages of differentiation.
Parameters Defining Chromosome Structure
Beyond the conclusion that each embryo has a single structural distribution, the inability of mixture analysis to separate the experimental and confined-Rabl structures for all but the largest intervals suggests that the parameters defined in this model are largely sufficient to account for the observed structural features. How probable is it that this model of polarized random coils confined within nuclear boundaries is an accurate reflection of organization in living nuclei? Evidence of random coil organization has been reported previously (Trask et al., 1993) and is consistent with Brownian diffusive motion seen in studies of chromosome dynamics (Heun et al., 2001; Vazquez et al., 2001).
However, such a model is most likely an oversimplification. It is important to understand that all our models generate chains with step parameters defined by the experimental data. Because we are using cluster analysis to identify long-range structure this is reasonable, but it means features such as local compaction are built into the simulations. Our estimate of global compaction levels 15× to 28× higher than the 30-nm fiber suggests additional levels of folding, consistent with previous structural studies using electron microscopy (Belmont and Bruce, 1994). Even more significant was the observation of correlated variations in the distance statistics between DS1 and DS5 (Figure 6C), which suggests local variations in compaction are conserved across data sets. While variability in compaction along the chromosome has been built into the models, the factors defining the local relationship between genomic and spatial separation have not been explained.
Furthermore, the separability at the largest size scales of experimental and confined-Rabl model chains indicates there are unidentified parameters affecting structure. One important feature that has not been incorporated into our models is the spatial relationship between chromosome arms. The separation of chromosome arms into largely nonoverlapping territories has been observed in many systems. Whereas we relied on this constraint during path tracing, the simulated chains were free to intertwine. Although arms do not intertwine, they do interact. Chromosomal interactions such as those that occur during heterochromatic silencing (Csink and Henikoff, 1996; Dernburg et al., 1996; Brown et al., 1997; Grogan et al., 2001) and pairing of homologous arms (Fung et al., 1998) are likely to have a significant effect on chromosome structure. Indeed, we observed an increased similarity between homologs paired at just one locus (histone). In contrast, the chains in our confined-Rabl simulations were noninteracting and displayed no increased similarity between paired homologs (because these chains were initialized from the observed histone positions they had equivalent levels of histone pairing as the experimental data). Models that fully capture the range of observed structural behavior will have to address these aspects.
Nuclear Organization
The 13 probes in this study all showed nonrandom radial and axial positions within the nucleus, as did >40 probes shown to have equally well defined nuclear positions in a previous study by Marshall et al. (1996). The dominant factor in this positioning is Rabl polarization, which results in chromosome extension coincident with the longest nuclear axis. We found that DS1, which had progressed farther into interphase relative to DS5, was both more decondensed and more Rabl polarized (Figures 5I and 8). This was inconsistent with a previous model describing Rabl as a consequence of anaphase movement during mitotic division, which then relaxes during interphase (Dernburg et al., 1996). Instead, our results suggest that chromosome ends attach to opposing ends of nuclei, whereas they elongate through cycle 14. Possibly these attachments are transitory. There must be a mechanism enabling interactions between distant chromosomal loci as occurs during heterochromatic silencing (Dernburg et al., 1996).
Our analysis of probe proximity relative to the nuclear envelope was slightly ambiguous. Both data sets in our study did show very similar organization based on the average distance to the envelope for each label (Figure 8). In contrast, the statistically defined categories (inner, outer, or random) only partially agreed. The localizations of label 2 to the outer half of the nucleus and label 13 (histone) to the inner half of the nucleus were consistent across data sets, but the localization of other probes varied. Marshall et al. (1996) have identified cell cycle differences in envelope localization, which might account for the differences observed in our data. Although those changes were between telophase and interphase, changes between different interphase stages also might exist.
Based on their results, Marshall et al. (1996) predicted nuclear envelope attachment sites every 1–2 Mbp along the chromosome. If so, attachment sites would probably define chromosome organization just as strongly as Rabl polarization. The statistical localization of probes in our DS1 data set is entirely consistent with the published reports of Marshall et al. (1996). Although both ours and their probe sets map to chromosome 2L, there is only partial overlap. We had no coverage in one chromosomal span where Marshall et al. (1996) found many probes close to the envelope (outer in our terminology), whereas many of the probes we found localized to the nuclear interior were in a region where Marshall et al. (1996) had no coverage. [See online supplemental Figure S3 for a comparison of nuclear localization for our barcode probes and those localized by Marshall et al. (1996)]. Although our data do not explicitly contradict a model with attachment sites every 1–2 Mbp, neither does it provide very convincing support. Our results indicating Rabl orientation increases with time into interphase suggest a force extending chromosomes as they decondense. Multiple attachment sites along an elongating nuclear envelope might produce such an effect, although a simpler model consistent with the data only requires attachments at the centromeric and telomeric ends. A more closely spaced probe set covering a larger contiguous region would be useful for resolving this issue.
Caveats
Although we have tried at every step to use protocols that are minimally perturbing, chromosomes are exposed to potential damage during the heat denaturization step required for hybridization. Comparison of DAPI-stained nuclei imaged before and after FISH by using optimized buffers and hybridization conditions indicate no discernable structural changes (Manuelidis and Borden, 1988; Hiraoka et al., 1993). One published report based on detailed analysis indicates ultrastructural changes in chromatin structure do accompany FISH but that detectable changes at the optical level are limited to small shifts in relative position for widely spaced loci (Solovei et al., 2002). Thus, although it remains a formal possibility, the FISH protocol is unlikely to dramatically affect our conclusions.
There is also the issue of correct probe identification and path connectivity. We have carefully evaluated label assignments and ultimately excluded approximately one-third of nuclei as untraceable. Some nuclei were probably untraceable due to failed hybridizations and unresolved probe overlaps. Among those we did trace, uncertainties remain. Assuming (as we did) that the chromosome arms do not intertwine, the most common errors probably involve the switching of identically labeled probes that are spatially very close (particularly between the most closely spaced barcode groups 2 and 3; see Figure 1A). In these cases, the structural differences between the correct and incorrect mapping are actually very small, particularly in relation to the overall resolution of our data. Unless errors are systematic it is unlikely that these would qualitatively alter the course of clustering, especially where conserved structural features are present. Ultimately, data acquired using barcodes with a larger set of color labels will reduce ambiguities and strengthen confidence in path determination. Because some ambiguities will always be present, a more robust clustering implementation would allow multiple solutions for a given trace, each weighted by a likelihood of being correct. Such an approach might more effectively identify conserved structural features.
The variable spacing of our barcode probes also can produce misleading results with rigid body alignment. The barcode is organized in four groups of three relatively closely spaced probes, with the groups spaced widely from one another. This design, wherein each group has one probe labeled in each available wavelength, was chosen to minimize ambiguity during tracing. Although it is effective for this purpose, rigid body alignment places greater emphasis on large steps. For example, the interval 1–6 consists of two groups (1–3 and 4–6). The average intragroup distance is 0.96 μm, but the 3–4 step between groups averages 2.37 μm. As a result, alignment and clustering of the interval 1–6 is dominated by the 3–4 step. One alternative is to cluster the subintervals separately. While we have done this, it makes the identification of higher order structure more difficult. In general, the variable spacing of barcode probes is a confounding factor in the analysis. Ideally, barcode probes would be uniformly spaced. In addition to removing alignment bias, uniform probe spacing facilitates comparison of similarly sized intervals localized to different genomic regions and simplifies analysis of local changes in compaction.
Finally, it is possible there are higher order structural features that we failed to identify with clustering and mixture analysis based on rigid body alignment. For example, analysis of DS1 with DS5 showed final average structures with similar shapes which nevertheless aligned poorly because of differences in size. The separation of data sets as revealed by clustering is meaningful. However, a more sophisticated approach might use scaling to make the structural comparison size invariant or allow flexible alignments with hinge-bending and rotations (Verbitsky et al., 1999; Shatsky et al., 2002).
CONCLUSION
By virtue of its capacity to determine the position of multiple loci concurrently, barcode FISH provides a unique tool for understanding interphase chromosome architecture. We have used a three color 13 probe barcode to characterize the long-range interphase structure of Drosophila chromosome 2L in embryonic cycle 14 nuclei. Beyond demonstrating the feasibility of barcode FISH, the primary result from this work is that chromosomes within each embryo are a single structural distribution that can be largely modeled as oriented random coils confined within nuclear boundaries. We also observed packing ∼15- to 28-fold above the 30-nm fiber that varies along the chromosome in a pattern conserved across embryos. Additional experiments will be needed to determine the efficacy of our models with higher resolution data and to characterize how chromosome organization varies across cell types and through development.
Supplementary Material
Acknowledgments
Eric Branlund and Diana Hughes have provided invaluable support with Priism and FindPoints. Bettina Keszthelyi and Sebastian Haase have provided the cross-wavelength image alignment module. We are grateful to Brian Harmon for data used to evaluate DAPI and lamin cross-wavelength offsets. Many thanks to Thea Tlsty, Donna Albertson, Hao Li, Tziki Kam, and Wallace Marshall for critical readings of the manuscript. We also thank the members of the Sedat laboratory for advice and support. M.G.L. was supported in part with National Science Foundation and Program in Mathematics and Molecular Biology fellowships. T.D.G. is supported by National Institutes of Health grant P41-RR01081. J.W.S. is supported by National Institutes of Health grant GM-25101-25.
Appendix
Clustering
Clustering was done using pairwise alignment of chains allowing only rigid motions (translation and rotation). A chain C = {ci}, (i = 1,2,...,13) is just a sequence of points. The root mean square (RMS) deviation between two chains A = {ai} and B = {bi} was calculated as follows:
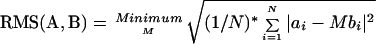 |
where M is any proper rigid motion defined by
Mv = Rv + t, for all vectors v,
where R is a proper rotation matrix and t is a translation vector.
The clustering of a set of chains proceeds in steps (iterations). Initially each chain belongs to a separate cluster. At each step two clusters are merged to form a single cluster. The two clusters that are merged are the ones that maximize the resulting difference between the average intercluster RMS and the average intracluster RMS (∂rmsavg). The average intercluster RMS is obtained by averaging the RMS values of all pairs of chains where the two chains belong to different clusters:
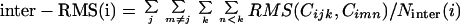 |
where Ninter(i) equals the number of intercluster chain pairs, Cijk denotes chain k in cluster j after i cluster mergings. Likewise, the intracluster RMS is the average RMS value for all pairs of different chains where the two chains belong to the same cluster:
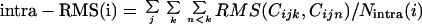 |
where Nintra(i) equals the number of intracluster chain pairs. The average intracluster RMS is a measure of the size of the clusters, whereas the average intercluster RMS is a measure of the distance between clusters. The clustering steps keep the distance between clusters large, and the size of clusters small.
Starting with M chains, the clustering algorithm produces a single cluster containing all chains after M-1 merging steps. To obtain useful cluster information, it is necessary to analyze the clusters at some point before M-1 mergings have been done. We looked at clusters after a fixed percentage (e.g., 80%) of the M-1 merging steps were completed.
The clustering can be performed using all 13 points in the traced chromosome arms, or it can be done using just a subset (subinterval) of the 13 probes. In the latter case, only the subset of chain points is used in the RMS calculations.
Each cluster has associated with it a spatial alignment of the chains in that cluster. From the alignment an average chain (cluster centroid structure) can be calculated. The position of point i in the average chain is the average of the positions of point i in all the aligned chains. Each chain is weighted equally. The alignment and average chain are not needed to perform the clustering but are used in visualizing the clusters. When two clusters A and B are merged the alignment of chains in the new cluster is obtained by aligning the average chain of cluster A to the average chain of cluster B by using the rigid motion that produces the minimum RMS. The aligned chains of the new cluster consist of the aligned cluster A chains together with the aligned cluster B chains transformed by this rigid motion. Note that the alignment depends on what mergings occurred to build the cluster and is not simply a function of the chains which compose the cluster.
Chain Simulations
We created simulated chromosome chains by using three models called random coil, Rabl-random, and confined-Rabl. Each chain consists of 13 points corresponding to the probes in the experimental data. All chains are generated by starting at a given point. A step vector is generated according to a probability distribution and added to the current position to get the next position. Twelve steps are generated to produce a chain of 13 points.
In the random coil model, the steps are chosen with isotropic direction, and with Gaussian distributed lengths. The Gaussian distribution can produce a step length less than zero in which case the step is set to zero. Each of the 12 steps that connect the 13 probe positions has its own mean length and SD, equal to the mean and SD of the step lengths observed in the chromosome arms traced using experimental data.
The Rabl-random model step vector has Gaussian distributed x, y, and z components. The z-axis is the Rabl axis. The x and y mean steps are close to zero, and the z mean step has a positive value that causes the chain to extend along the z-axis. Each x, y, and z coordinate of each step vector has its own mean value and SD calculated from the chains traced in the experimental data.
When calculating the means and standard deviations, the point positions of the experimental traced chains are expressed in a Rabl coordinate frame. The Rabl coordinate frame is different for each nucleus and is defined in terms of the shape of the nuclear envelope determined from the experimental data. Conceptually, the nuclear envelope is treated as a shell of constant mass per unit area, and an ellipsoid is found that matches the inertia tensor of this shell (Goldstein, 1980). This is simply a way to define an ellipsoid that approximates the shape of the nuclear envelope. The long axis of the ellipsoid corresponds to the Rabl axis.
The inertia tensor is calculated using the areas of the triangles in the triangulation of the nuclear envelope. Each vertex of a triangle receives a weight equal to one-third of the area of the triangle. The 3 by 3 inertia matrix is defined as follows:
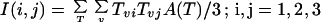 |
where T denotes a triangle in the nuclear envelope, Tv (v = 1,2,3) are the vertex positions of the triangle, and A(T) is the area of the triangle. The principal inertia axes are the three eigenvectors of this matrix. The Rabl z-axis is defined as the principal axis with largest eigenvalue (this corresponds to the long axis of the nuclear envelope). The Rabl y-axis is the principal inertia axis with second largest eigenvalue, and the Rabl x-axis is the principal inertia axis with smallest eigenvalue. The sign of the z-axis vector is chosen so that it makes an angle of <90 degrees with the z microscope axis. The coordinate system is right handed. There is an ambiguity where the sign of the x- and y-axes can both be flipped. That sign is chosen arbitrarily.
The confined-Rabl model uses the same step definition as the Rabl model, but steps that place the new point outside a specified nuclear envelope surface are rejected. When a step is rejected a new step is computed and it, too, is rejected if it lies outside the nuclear envelope. If a total of three or more steps are rejected while building a chain, then the whole chain is rejected and a new chain is generated. Nuclear envelopes from the experimental data were used for each simulated pair of chains and the starting point positions within the envelopes were chosen as the observed histone positions for the traced chromosome arms in that nucleus.
Article published online ahead of print. Mol. Biol. Cell 10.1091/mbc.E04–04–0289. Article and publication date are available at www.molbiolcell.org/cgi/doi/10.1091/mbc.E04–04–0289.
The online version of this article contains supplemental material at MBC Online (http://www.molbiolcell.org).
References
- Agard, D.A., Hiraoka, Y., Shaw, P., and Sedat, J.W. (1989). Fluorescence microscopy in three dimensions. Methods Cell Biol. 30, 353-377. [DOI] [PubMed] [Google Scholar]
- Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K., and Walter, P. (2002). Molecular Biology of the Cell, New York, NY: Garland Publishing.
- Anderson, K.V., and Lengyel, J.A. (1981). Changing rates of DNA and RNA synthesis in Drosophila embryos. Dev Biol. 82, 127-138. [DOI] [PubMed] [Google Scholar]
- Belmont, A.S., and Bruce, K. (1994). Visualization of G1 chromosomes: a folded, twisted, supercoiled chromonema model of interphase chromatid structure. J. Cell Biol. 127, 287-302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, K.E., Guest, S.S., Smale, S.T., Hahm, K., Merkenschlager, M., and Fisher, A.G. (1997). Association of transcriptionally silent genes with Ikaros complexes at centromeric heterochromatin. Cell 91, 845-854. [DOI] [PubMed] [Google Scholar]
- Burgess, S.M., Kleckner, N., and Weiner, B.M. (1999). Somatic pairing of homologs in budding yeast: existence and modulation. Genes Dev. 13, 1627-1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrd, K., and Corces, V.G. (2003). Visualization of chromatin domains created by the gypsy insulator of Drosophila. J. Cell Biol. 162, 565-574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catmull, E., and Rom, R. (1974). A class of local interpolation splines. In: Computer Aided Geometric Design, ed. R.E. Barnhill and R.F. Risenfeld, New York: Academic Press.
- Chen, H., Hughes, D.D., Chan, T.A., Sedat, J.W., and Agard, D.A. (1996). IVE (image visualization environment): a software platform for all three-dimensional microscopy applications. J. Struct. Biol. 116, 56-60. [DOI] [PubMed] [Google Scholar]
- Comings, D.E. (1980). Arrangement of chromatin in the nucleus. Hum. Genet. 53, 131-143. [DOI] [PubMed] [Google Scholar]
- Csink, A.K., and Henikoff, S. (1996). Genetic modification of heterochromatic association and nuclear organization in Drosophila. Nature 381, 529-531. [DOI] [PubMed] [Google Scholar]
- Dernburg, A.F., Broman, K.W., Fung, J.C., Marshall, W.F., Philips, J., Agard, D.A., and Sedat, J.W. (1996). Perturbation of nuclear architecture by long-distance chromosome interactions. Cell 85, 745-759. [DOI] [PubMed] [Google Scholar]
- Dong, F., and Jiang, J. (1998). Non-Rabl patterns of centromere and telomere distribution in the interphase nuclei of plant cells. Chromosome Res. 6, 551-558. [DOI] [PubMed] [Google Scholar]
- Foe, V.E. (1989). Mitotic domains reveal early commitment of cells in Drosophila embryos. Development 107, 1-22. [PubMed] [Google Scholar]
- Fung, J.C., Marshall, W.F., Dernburg, A., Agard, D.A., and Sedat, J.W. (1998). Homologous chromosome pairing in Drosophila melanogaster proceeds through multiple independent initiations. J. Cell Biol. 141, 5-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerasimova, T.I., Byrd, K., and Corces, V.G. (2000). A chromatin insulator determines the nuclear localization of DNA. Mol. Cell 6, 1025-1035. [DOI] [PubMed] [Google Scholar]
- Gerasimova, T.I., and Corces, V.G. (1998). Polycomb and trithorax group proteins mediate the function of a chromatin insulator. Cell 92, 511-521. [DOI] [PubMed] [Google Scholar]
- Goldstein, H. (1980). Classical Mechanics, Reading, MA: Addison-Wesley Publishing.
- Grogan, J.L., Mohrs, M., Harmon, B., Lacy, D.A., Sedat, J.W., and Locksley, R.M. (2001). Early transcription and silencing of cytokine genes underlie polarization of T helper cell subsets. Immunity 14, 205-215. [DOI] [PubMed] [Google Scholar]
- Hartl, D.L., Nurminsky, D.I., Jones, R.W., and Lozovskaya, E.R. (1994). Genome structure and evolution in Drosophila: applications of the framework P1 map. Proc. Natl. Acad. Sci. USA 91, 6824-6829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heun, P., Laroche, T., Shimada, K., Furrer, P., and Gasser, S.M. (2001). Chromosome dynamics in the yeast interphase nucleus. Science. 294, 2181-2186. [DOI] [PubMed] [Google Scholar]
- Hiraoka, Y., Dernburg, A.F., Parmelee, S.J., Rykowski, M.C., Agard, D.A., and Sedat, J.W. (1993). The onset of homologous chromosome pairing during Drosophila melanogaster embryogenesis. J. Cell Biol. 120, 591-600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiraoka, Y., Swedlow, J.R., Paddy, M.R., Agard, D.A., and Sedat, J.W. (1991). Three-dimensional multiple-wavelength fluorescence microscopy for the structural analysis of biological phenomena. Semin. Cell Biol. 2, 153-165. [PubMed] [Google Scholar]
- Hochstrasser, M., Mathog, D., Gruenbaum, Y., Saumweber, H., and Sedat, J.W. (1986). Spatial organization of chromosomes in the salivary gland nuclei of Drosophila melanogaster. J. Cell Biol. 102, 112-123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn, B.K.P. (1987). Closed-form solution of absolute orientation using unit quaternions. J. Optical Soc. Am. Ser. A. 4, 629-642. [Google Scholar]
- Jin, Q.W., Fuchs, J., and Loidl, J. (2000). Centromere clustering is a major determinant of yeast interphase nuclear organization. J. Cell Sci. 113, 1903-1912. [DOI] [PubMed] [Google Scholar]
- Kozubek, S., Lukasova, E., Mareckova, A., Skalnikova, M., Kozubek, M., Bartova, E., Kroha, V., Krahulcova, E., and Slotova, J. (1999). The topological organization of chromosomes 9 and 22 in cell nuclei has a determinative role in the induction of t(9,22) translocations and in the pathogenesis of t(9,22) leukemias. Chromosoma 108, 426-435. [DOI] [PubMed] [Google Scholar]
- LaSalle, J.M., and Lalande, M. (1996). Homologous association of oppositely imprinted chromosomal domains. Science 272, 725-728. [DOI] [PubMed] [Google Scholar]
- Lawrence, P.A. (1992). The Making of a Fly: The Genetics of Animal Design, Cambridge, MA: Blackwell Science.
- Manuelidis, L. (1985). Individual interphase chromosome domains revealed by in situ hybridization. Hum. Genet. 71, 288-293. [DOI] [PubMed] [Google Scholar]
- Manuelidis, L., and Borden, J. (1988). Reproducible compartmentalization of individual chromosome domains in human CNS cells revealed by in situ hybridization and three-dimensional reconstruction. Chromosoma 96, 397-410. [DOI] [PubMed] [Google Scholar]
- Manuelidis, L., and Chen, T.L. (1990). A unified model of eukaryotic chromosomes. Cytometry 11, 8-25. [DOI] [PubMed] [Google Scholar]
- Marshall, W.F., Dernburg, A.F., Harmon, B., Agard, D.A., and Sedat, J.W. (1996). Specific interactions of chromatin with the nuclear envelope: positional determination within the nucleus in Drosophila melanogaster. Mol. Biol. Cell 7, 825-842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall, W.F., Straight, A., Marko, J.F., Swedlow, J., Dernburg, A., Belmont, A., Murray, A.W., Agard, D.A., and Sedat, J.W. (1997). Interphase chromosomes undergo constrained diffusional motion in living cells. Curr. Biol. 7, 930-939. [DOI] [PubMed] [Google Scholar]
- Mathog, D., and Sedat, J.W. (1989). The three-dimensional organization of polytene nuclei in male Drosophila melanogaster with compound XY or ring X chromosomes. Genetics 121, 293-311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikiforova, M.N., Stringer, J.R., Blough, R., Medvedovic, M., Fagin, J.A., and Nikiforov, Y.E. (2000). Proximity of chromosomal loci that participate in radiation-induced rearrangements in human cells. Science 290, 138-141. [DOI] [PubMed] [Google Scholar]
- Parada, L., and Misteli, T. (2002). Chromosome positioning in the interphase nucleus. Trends Cell Biol. 12, 425-432. [DOI] [PubMed] [Google Scholar]
- Pettersen, E.F., Goddard, T.D., Huang, C.C., Couch, G.S., Greenblatt, D.M., Meng, E.C., and Ferrin, T.E. (2004). UCSF chimera—a visualization system for exploratory research and analysis. J. Comput. Chem.. 13, 1605-1612. [DOI] [PubMed] [Google Scholar]
- Sachs, R.K., van den Engh, G., Trask, B., Yokota, H., and Hearst, J.E. (1995). A random-walk/giant-loop model for interphase chromosomes. Proc. Natl. Acad. Sci. USA 92, 2710-2714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schardin, M., Cremer, T., Hager, H.D., and Lang, M. (1985). Specific staining of human chromosomes in Chinese hamster x man hybrid cell lines demonstrates interphase chromosome territories. Hum. Genet. 71, 281-287. [DOI] [PubMed] [Google Scholar]
- Schrock, E., et al. (1996). Multicolor spectral karyotyping of human chromosomes. Science 273, 494-497. [DOI] [PubMed] [Google Scholar]
- Sedat, J., and Manuelidis, L. (1978). A direct approach to the structure of eukaryotic chromosomes. Cold Spring Harb. Symp. Quant. Biol. 42, 331-350. [DOI] [PubMed] [Google Scholar]
- Shatsky, M., Nussinov, R., and Wolfson, H.J. (2002). Flexible protein alignment and hinge detection. Proteins 48, 242-256. [DOI] [PubMed] [Google Scholar]
- Sneath, P.H.A., and Sokal, R.R. (1973). Numerical Taxonomy: The Principles and Practice of Numerical Classification, San Francisco, CA: W.H. Freeman.
- Solovei, I., Cavallo, A., Schermelleh, L., Jaunin, F., Scasselati, C., Cmarko, D., Cremer, C., Fakan, S., and Cremer, T. (2002). Spatial preservation of nuclear chromatin architecture during three-dimensional fluorescence in situ hybridization (3D-FISH). Exp. Cell Res. 276, 10-23. [DOI] [PubMed] [Google Scholar]
- Speicher, M.R., Gwyn, B.S., and Ward, D.C. (1996). Karyotyping human chromosomes by combinatorial multi-fluor FISH. Nat. Genet. 12, 368-375. [DOI] [PubMed] [Google Scholar]
- Trask, B.J., Allen, S., Massa, H., Fertitta, A., Sachs, R., van den Engh, G., and Wu, M. (1993). Studies of metaphase and interphase chromosomes using fluorescence in situ hybridization. Cold Spring Harb. Symp. Quant. Biol. 58, 767-775. [DOI] [PubMed] [Google Scholar]
- van den Engh, G., Sachs, R., and Trask, B.J. (1992). Estimating genomic distance from DNA sequence location in cell nuclei by a random walk model. Science 257, 1410-1412. [DOI] [PubMed] [Google Scholar]
- Vazquez, J., Belmont, A.S., and Sedat, J.W. (2001). Multiple regimes of constrained chromosome motion are regulated in the interphase Drosophila nucleus. Curr. Biol. 11, 1227-1239. [DOI] [PubMed] [Google Scholar]
- Verbitsky, G., Nussinov, R., and Wolfson, H. (1999). Flexible structural comparison allowing hinge-bending, swiveling motions. Proteins 34, 232-254. [DOI] [PubMed] [Google Scholar]
- Vourc'h, C., D. Taruscio, A. L. Boyle, and D. C. Ward. (1993). Cell cycle-dependent distribution of telomeres, centromeres, and chromosome-specific subsatellite domains in the interphase nucleus of mouse lymphocytes. Exp. Cell Res. 205, 142-151. [DOI] [PubMed] [Google Scholar]
- Wiegant, J., Bezrookove, V., Rosenberg, C., Tanke, H.J., Raap, A.K., Zhang, H., Bittner, M., Trent, J.M., and Meltzer, P. (2000). Differentially painting human chromosome arms with combined binary ratio-labeling fluorescence in situ hybridization. Genome Res. 10, 861-865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolffe, A.P. (1992). Chromatin: Structure and Function, San Diego, CA: Academic Press.
- Wu, C.T., and Morris, J.R. (1999). Transvection and other homology effects. Curr. Opin. Genet. Dev. 9, 237-246. [DOI] [PubMed] [Google Scholar]
- Yokota, H., van den Engh, G., Hearst, J.E., Sachs, R.K., and Trask, B.J. (1995). Evidence for the organization of chromatin in megabase pair-sized loops arranged along a random walk path in the human G0/G1 interphase nucleus. J. Cell Biol. 130, 1239-1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.