Importance of Hydrophilic Hydration and Intramolecular Interactions in the Thermodynamics of Helix–Coil Transition and Helix–Helix Assembly in a Deca-Alanine Peptide

Abstract

For a model deca-alanine peptide the cavity (ideal hydrophobic) contribution to hydration favors the helix state over extended states and the paired helix bundle in the assembly of two helices. The energetic contributions of attractive protein–solvent interactions are separated into quasi-chemical components consisting of a short-range part arising from interactions with solvent in the first hydration shell and the remaining long-range part that is well described by a Gaussian. In the helix–coil transition, short-range attractive protein–solvent interactions outweigh hydrophobic hydration and favor the extended coil states. Analysis of enthalpic effects shows that it is the favorable hydration of the peptide backbone that favors the unfolded state. Protein intramolecular interactions favor the helix state and are decisive in favoring folding. In the pairing of two helices, the cavity contribution outweighs the short-range attractive protein–water interactions. However, long-range, protein–solvent attractive interactions can either enhance or reverse this trend depending on the mutual orientation of the helices. In helix–helix assembly, change in enthalpy arising from change in attractive protein–solvent interactions favors disassembly. In helix pairing as well, favorable protein intramolecular interactions are found to be as important as hydration effects. Overall, hydrophilic protein–solvent interactions and protein intramolecular interactions are found to play a significant role in the thermodynamics of folding and assembly in the system studied.

Graphical Abstract

INTRODUCTION

Helices have been termed the “ ‘hydrogen’ atoms of biomolecular complexity”.¹ In proteins the α-helix is a common secondary structural motif and understanding the formation of α-helices occupies a pre-eminent place in efforts to understand protein folding. Using computer simulations and a new approach to free energy calculations,^2,3 we re-examine this classic problem and study two transitions in a model decaalanine peptide. Mirroring the primary-to-secondary and secondary-to-tertiary transitions in protein folding, we study the extended coil-to-helix transition and the pairing of two helices to form a helix dimer, respectively. Our principal focus is to explicate the cavity (ideal hydrophobic) and hydrophilic hydration contributions in these transitions.

There are several reasons for re-examining the fundamental premises about hydration thermodynamics of proteins and the forces driving protein folding. Recent experiments and simulations challenge the conventional view that hydrophobic interactions drive protein folding. These studies show that the all-backbone polyglycine, and analogous archetypes of intrinsically disordered peptides, can undergo a collapse transition in water.^4–8 Recent computer simulations^9–12 also reveal important fundamental limitations in the group-additive approach that has been a convenient approximate approach to understand protein hydration thermodynamics in experiments (for example, see refs 13, 14). Many of the prevailing views of protein hydration thermodynamics^15–17 trace back to this group-additive reasoning. Force field dependencies¹⁸ notwithstanding, simulations can in principle provide a detailed molecular thermodynamics understanding of hydration,^19,20 but such studies are not as yet common for realistic proteins and polypeptides.²¹ The availability of a complementary approach³ that enables, for the first time, detailed free energy calculations on proteins thus presents an opportunity to re-examine a classic problem in protein folding.

Earlier studies based on continuum solvent or lattice models have come to differing conclusions about solvent effects in the coil-to-helix transition. Some have suggested that hydrophobicity drives the transition,^22,23 while others have emphasized the role of favorable electrostatics.²⁴ Experiments suggest that helix extension is enthalpically driven,²⁵ as has also been found in computer simulations interpreted within the Zimm–Bragg or Lifson–Roig formalisms (for example, see refs 26–28.). Interestingly, both experiments²⁹ and computer simulations^26–28 show a negative heat capacity upon unfolding, the opposite of what is observed in unfolding of globular proteins.³⁰ The negative heat capacity has been interpreted as arising due to the favorable hydration of the backbone upon unfolding,²⁹ but a molecular scale description of this signature remains to be found.

The approach we have developed is based on a quasichemical organization^31–33 of the potential distribution theorem.³⁴ Using this approach, we are able to interrogate the hydration thermodynamics of proteins^2,3 comparable to that for small molecular solutes. Our studies on the protein cytochrome c helped reveal limitations of continuum models of hydration,³ as was also later observed in studies on several protein interfaces using standard thermodynamic integration approaches.²¹ Our subsequent studies have helped illuminate conceptual limitations of the group-additive description of the hydration thermodynamics of the peptide backbone¹¹ and of a hydrophobic side-chain in the context of model peptides.¹² Extending these studies, here we study the hydration thermodynamics in the coil-to-helix transition and helix–helix assembly in a decaalanine peptide.

We find that hydrophobic hydration is not decisive in the formation of the helix, but it does play an important stabilizing role in helix-dimerization. Hydrophilic hydration is found to play a nontrivial role in the coil-to-helix transition and helix–helix assembly. Indeed, hydrophilic hydration can drive unfolding of a helix and disassembly of a helix dimer; backbone hydration is found to be the most important component of the overall hydrophilic hydration. For the systems studied here, hydrophilic hydration and the intramolecular interactions are as important as, if not more important than, hydrophobic effects.

THEORY

The excess chemical potential, μ^ex, is that part of the Gibbs free energy that arises from intermolecular interactions and is of principal interest in understanding the solubility of a solute in a solvent. Here μ^ex is defined relative to the ideal gas at the same density and temperature. To calculate μ^ex, we regularize the statistical problem of calculating it from the potential distribution theorem βμ^ex = ln〈e^βε〉,^32,34 where the averaging 〈…〉 is over the solute–solvent binding energy (ε) distribution P(ε). As usual, β = 1/k_BT, with T the temperature and k_B the Boltzmann constant.

We introduce an auxiliary field ϕ(λ; r) that moves the solvent away from the solute. The distance between the center of the field and the solvent molecule is r. For r > λ, ϕ = 0. Since the solvent interface is pushed away from the solute, the solute–solvent interaction is tempered and the conditional distribution P(ε|ϕ) is better behaved than P(ε).^2,3,11 In practice, we adjust the range λ such that P(ε|ϕ) is Gaussian. With the introduction of the field, we have^2,3,11

$$\beta {\mu }^{\text{ex}}=\underset{\text{local chemistry}}{\underbrace{\text{ln }{x}_0[\varphi ]}}+\underset{\text{long}-\text{range}}{\underbrace{\beta {\mu }^{\text{ex}}[P(\epsilon |\varphi )]}}-\underset{\text{G packing}}{\underbrace{\text{ln }{p}_0[\varphi ]}}$$ (1)

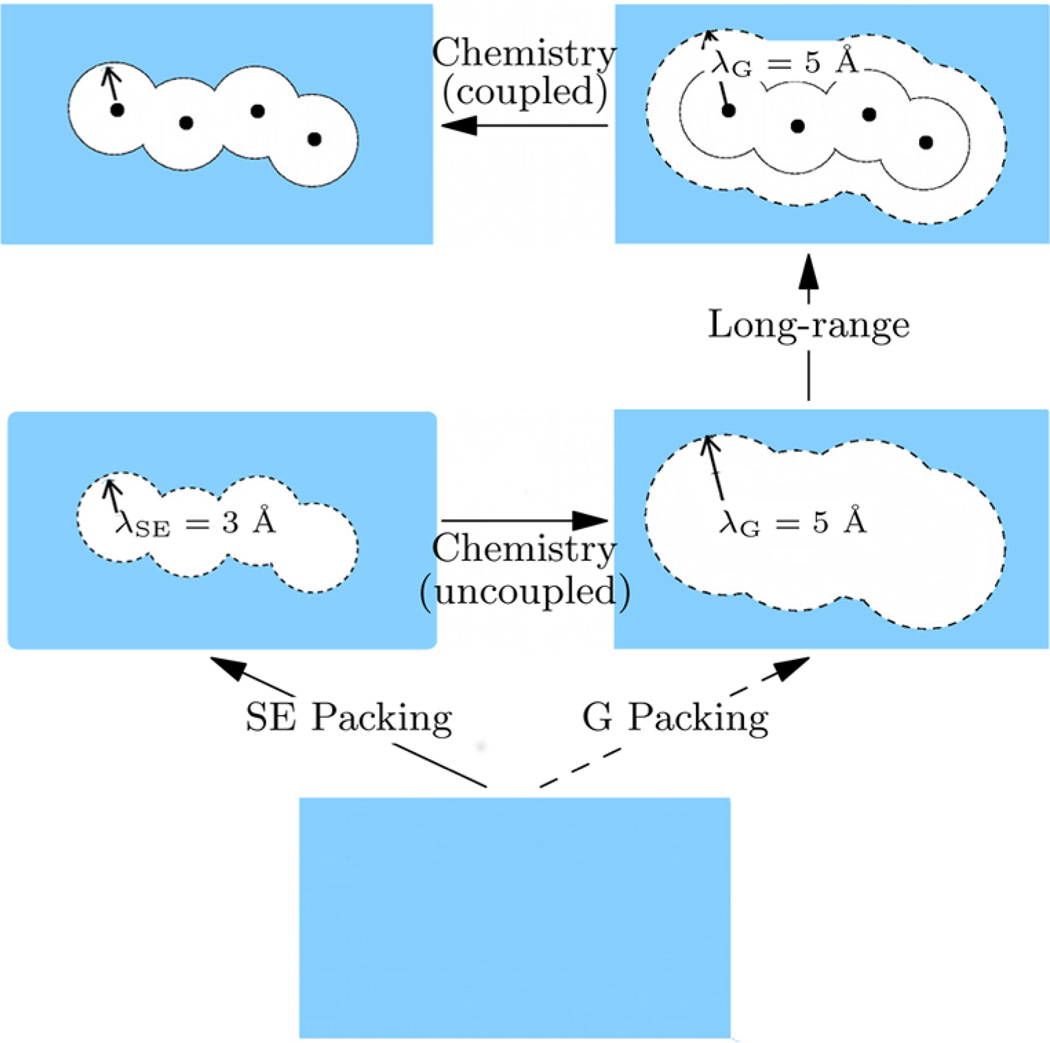
where −k_BT ln x₀[ϕ(λ)] is the work done to apply the field in the presence of the solute, −k_BT ln p₀[ϕ(λ)] is the corresponding quantity in the absence of the solute, and βμ^ex[P(ε|ϕ)] is the contribution to the interaction free energy in the presence of the field. Figure 1 provides a schematic description of eq 1.

Figure 1.

Quasichemical organization of the excess chemical potential. The λ_SE = 3 Å envelope defines the solvent excluded (SE) volume and λ_G = 5 Å defines the envelope for which the conditional solute–solvent binding energy P(ε|ϕ) is Gaussian. For chemistry coupled (uncoupled), the solute–solvent interaction is present (absent). In eq 1 we follow G-packing to the hydrated solute; in eq 2 we follow SE-packing. Figure adapted from ref 11 with permission from Elsevier.

We apply the field about each heavy atom to carve out the molecular shape in the liquid (Figure 1). For convenience we use the same value of λ for all the heavy atoms. Our analysis shows that ln x₀ ≈ 0 for λ ≤ 3.0 Å, irrespective of the conformation of the peptide. This suggests that the space enclosed by λ_SE = 3.0 Å is excluded for the solvent and thereby provides a natural definition of molecular extent of the cavity to be used in discussions of hydrophobic hydration.

For λ ≥ 5 Å, P(ε|ϕ) is well-described by a Gaussian; this suggests that for λ ≥ 5 Å, the net solute–solvent interaction arises from a large collection of small, nonspecific contributions. We define this surface by λ_G = 5 Å. Interestingly, the range between 3 and 5 Å corresponds to the first hydration shell for a methyl carbon³⁵ and is a conservative description of the first hydration shell of groups containing nitrogen and oxygen heavy atoms.

On the basis of domains defined by λ_SE and λ_G, we rearrange eq 1 as

$$\beta {\mu }^{\text{ex}}=\underset{\text{revised chemistry}}{\underbrace{\text{ln}\frac{x_0[\varphi ({\lambda }_{\mathrm{G}})]}{p_0[\varphi ({\lambda }_{\mathrm{G}})]/p_0[\varphi ({\lambda }_{\mathrm{S}\mathrm{E}})]}}}+\underset{\text{long}-\text{range}}{\underbrace{\beta {\mu }^{\text{ex}}[P(\epsilon |\varphi ({\lambda }_{\mathrm{G}}))]}}-\underset{\mathrm{S}\mathrm{E}\text{ packing}}{\underbrace{\text{ln }{p}_0[\varphi ({\lambda }_{\mathrm{S}\mathrm{E}})]}}$$ (2)

Note that SE packing and the revised chemistry plus long-range contribution is precisely defined for the given force field. Physically, the revised chemistry contribution measures the free energy contribution from solute interaction with solvent in the first shell relative to a noninteracting (uncoupled) solute (Figure 1).

The revised chemistry and long-range contributions describe the role of short-range and long-range attractive protein–solvent interactions in the thermodynamics of hydration. These two components of the hydrophilic contribution occur at different energy (and length) scales. Usually within common continuum models of electrostatic interactions this distinction is lost, and often aspects of both the short-range and long-range interactions are treated as part of long-ranged interactions (e.g., see ref 17). From the perspective of such continuum models, our definition of long-range interaction is more conservative.

The SE packing contribution is a measure of the hydrophobic hydration of an ideal hydrophobe.^36,37 In theoretical discussions of hydrophobic effects, a cavity with a hard-wall interaction in water is often considered. The packing contribution in our calculation uses a soft repulsive cavity. This soft-cavity packing estimate is always a lower-bound to the hard-cavity estimate and can be easily corrected to give the latter.² We do not pursue those corrections here and instead use the soft-cavity packing result as a measure of model hydrophobic effects. (Importantly, distinction between a hard-and soft-repulsive cavity is minimized in the relative balance of chemistry and packing contributions (eqs 1 and 2).) We refer the reader to published papers^2,3,11 for more extensive details about the approach.

Helix–Helix PMF

We employ the development above in the calculation of W(r), the potential of mean force (PMF) to bring two helices a distance r apart, where r is the separation between the helix axes with the axes parallel to each other. The PMF

$$W(r)=W_{\text{solv}}(r)+\mathrm{\Delta }U(r)$$ (3)

where W_solv is the solvent (or indirect) contribution³⁵ and ΔU is the contribution from direct protein–protein interactions. $W_{\text{solv}}(r)={\mu }_{\text{dimer}}^{\text{ex}}(r)-2{\mu }^{\text{ex}}$, where ${\mu }_{\text{dimer}}^{\text{ex}}(r)$ is the excess hydration free energy of the pair of helices (for a given separation and orientation) and μ^ex is the excess hydration free energy of a monomer helix.

Entropic and Enthalpic Contributions

Ignoring the pressure–volume correction and contribution due to a finite isothermal compressibility of water, the enthalpy of hydration, h^ex, may be decomposed as

$$h^{\text{ex}}=E_{\text{sw}}+E_{\text{reorg}}$$ (4)

where E_sw is the average peptide–solvent interaction energy and E_reorg is the (average) water reorganization energy. Additionally, if the contribution due to a finite thermal expansivity of water is ignored, the entropy of hydration is then similarly given by

$$T{s}^{\text{ex}}=h^{\text{ex}}-{\mu }^{\text{ex}}$$ (5)

For calculating E_reorg, we adapted the hydration-shell-wise calculation described earlier^12,35 (Sec. S.III).

METHODS

The simulation approach closely followed previous work,¹¹ and for completeness the details of the implementation of the regularization approach are summarized in the Supporting Information (Sec. S.I). The deca-alanine peptide was modeled with an acetylated (ACE) N-terminus and n-methyl-amide (NME) capped C-terminus. The extended β-conformation (ϕ, ψ = −154 ± 12, 149 ± 9) was aligned such that the end-to-end vector lay along the diagonal of the simulation cell. We label this coil state C₀. The helix was aligned with the helix axis along the x-axis of the cell. The initial structures were energy minimized with weak restraints on the heavy atoms to relieve any strain in the structure. The peptides were solvated in 3500 TIP3P^38,39 water molecules. Version C31 of the CHARMM⁴⁰ force field with correction (cmap) terms for dihedral angles⁴¹ was used for the peptides.

We sampled unfolded states using the adaptive-bias force (ABF^42,43) approach which also additionally provided the free energy of unfolding the polypeptide in a vacuum (Sec. S.II). From the ABF trajectory, we sampled nine structures with end-to-end distances between terminal carbon atoms ranging between 28 Å and 36 Å in increments of 1 Å. We label these extended coil states from this unfolding simulation {C₁,…,C₉}. The ϕ, ψ for these unfolded states predominantly populate β and PPII regions of the Ramachandran plot. In the subsequent hydration free energy calculations, the structures were held rigid.

The same framework was used to investigate helix pairing. Additionally, we consider two relative orientations of the helix dipoles, parallel and antiparallel. (Note that the helix dipoles will be antiparallel in the simplest helix-turn-helix motif.) These arrangements help illuminate the role of long-range protein–solvent interactions in helix–helix complexation. We note that in nature helices almost never align perfectly parallel or antiparallel,⁴⁴ but the hydration effects that are of principal interest here are expected to be insensitive to minor distortions in the relative orientation.

RESULTS AND DISCUSSION

Coil-to-Helix Transition

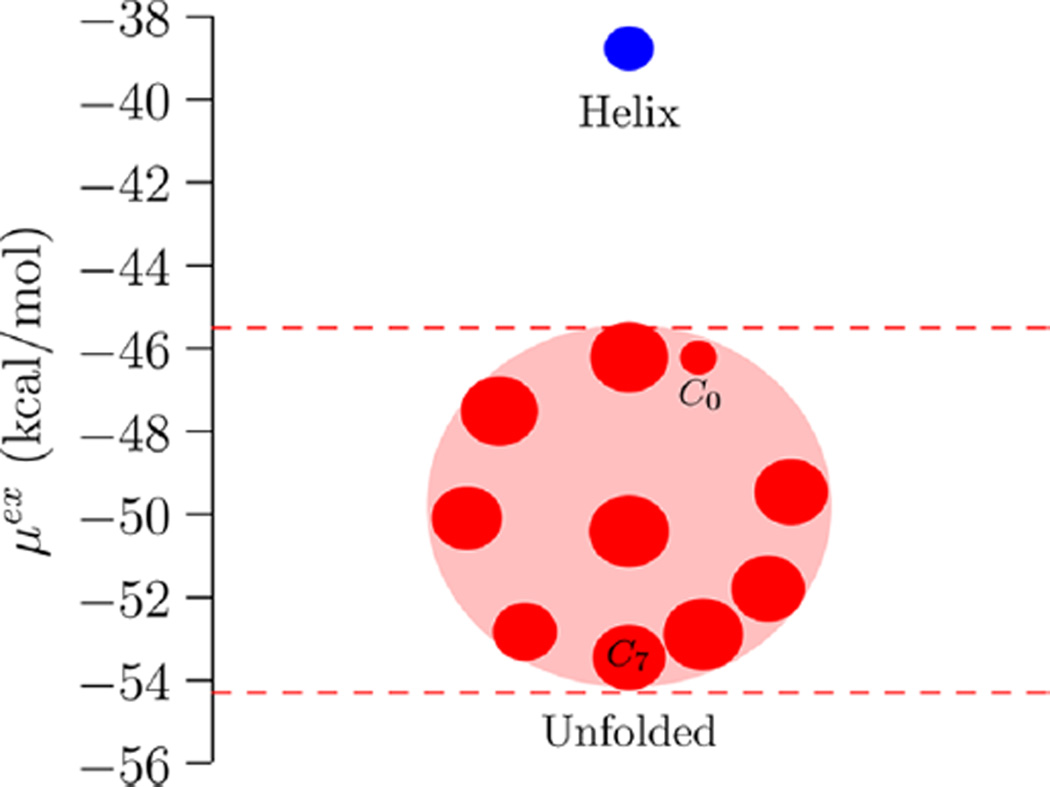
At the outset we must emphasize that the coil states considered here represent only a subset of the unfolded and partially unfolded states along the helix-to-coil transition. This undoubtedly limits a direct comparison with previous experimental studies (for example, refs 25, 29) and computational efforts that interpret ensemble properties within standard helix–coil theories (for example, refs 26–28). Nevertheless, the helix and coil states considered here bracket the helix–coil transition and help provide important insights into the overall role of hydration and intramolecular effects in the transition. In particular, if hydration drives helix formation, then we should expect to find that the hydration free energy of the coil states is more positive than that of the helix state. Figure 2 makes it clear that this is not the case; hydration in fact favors unfolding. In Table 1 we present the free energy components of the helix state, the least favorably hydrated coil state (C₀), and the most favorably hydrated coil state (C₇).

Figure 2.

Hydration free energies of the helix and {C₀,…,C₉} coil states. The horizontal axis has no meaning and is used solely to differentiate multiple coil states with similar μ^ex values. (One could plot the data versus R_g or R_c, but the physical picture that the less compact structure has a more negative free energy is independent of these considerations.) The radius of the symbol is equal to twice the standard error of the mean (2σ). The C₀ state is the smallest circle in the collection of unfolded states; the standard error is about half compared to the other estimates because we had 4 times more data for C₀ (Sec. S.I).

Table 1.

Components of the Hydration Free Energy for the Helix and the Least Favorably (C₀) and Most Favorably (C₇) Hydrated Coil States^a

conformation	SE packing	revised chemistry	long-range	μex	Ereorg	Esw	Tsex
Helix	44.4(0.4)	−51.6(0.2)	−31.6(0.2)	−38.8(0.5)	75(6)	−150.9(0.6)	−37.1
Helix (Q = 0)		−22.4(0.3)	−18.1(0.0)	3.9(0.5)	42(4)	−59.7(0.6)	−21.6
Coil (C0)	58.4(0.3)	−77.1(0.3)	−27.6(0.1)	−46.3(0.4)	92(6)	−186.8(0.6)	−48.9
Coil (Q = 0)		−30.9(0.4)	−24.7(0.0)	2.8(0.5)	50(8)	−80.8(0.6)	−33.6
Coil (C7)	58.3(0.5)	−83.4(0.3)	−28.3(0.4)	−53.4(0.8)	98(4)	−201.4(0.6)	−57.4

^aFor the helix and C₀ states, results with partial charges turned off (indicated by Q = 0) are also noted. The radius of gyration (relative to the center of mass) R_g (Å), the end-to-end distance between terminal carbon atoms R_c (Å), and solvent accessible surface area SASA (Ų) for the structures are as follows: helix (R_c = 16.3, R_g = 5.3, SASA = 876), C₀ (R_c = 36.8, R_g = 11.1, SASA = 1260), and C₇ (R_c = 34.0, R_g = 10.6, SASA = 1249). All energy values are in kcal/mol. Standard error of the mean is given in parentheses at the 2σ level.

Before we discuss our results, we first compare our calculations with existing hydration free energy data. As already noted above, until recently very few all-atom calculations of the hydration free energy of polypeptides with around 10 residues appear to have been reported. Helms and co-workers¹⁹ have studied blocked-(Ala)_n helix hydration with n up to 9. Extrapolating their results suggests a value of about −40 kcal/mol for the deca-alanine helix, consistent with the quasichemical results (Table 1). Kokubo et al.²⁰ computed the van der Waals and electrostatic contribution to the hydration of a deca-alanine helix and for several coil states. Our hydration free energies based on their structures are in fair agreement (data not shown), and the agreement becomes excellent with more extensive sampling in the calculation of the van der Waals contribution.⁴⁵ Besides these, the regularization approach has been tested in studies on water,² ions,⁴⁶ short peptides,^11,12 and the protein cytochrome c.³ Further, the quasichemical framework has also been thoroughly documented.^31–33

In the results of this study, Table 1 indicates that, at least for the coil states considered here, the packing is somewhat insensitive to the peptide structure. At the scale of the cavities, we expect the packing contributions to scale with surface area,^47–49 and the data in the table conforms to this expectation. The free energy per unit SASA is similar to values reported for hard-spheres using scaled-particle theory^49,50 and explicit all-atom simulations,⁵¹ where we equate the hard-sphere radius to the radius of gyration to provide approximately equivalent measures of particle size. The cavity free energy per unit SASA is about a factor of 10 larger than the surface energy parameter often used in a continuum surface-area based model of hydrophobic hydration.⁵² (Consistent with recent studies,^53,54 the Q = 0 case shows that adding the effects of van der Waals attractions to the cavity contribution leads to a free energy per unit SASA that is of similar magnitude to values used in continuum models.) Since the solvent-accessible surface areas of C₀ and C₇ are not very different, despite overall differences in the structure, we expect the packing contribution to be similar for these states, as found in simulations. The packing contribution favors the helix state by about −14 kcal/mol: as expected, hydrophobic hydration favors the compact state of the protein.

The revised chemistry contribution, however, favors the coil states by between −31.8 kcal/mol for the C₇ state and −25.5 kcal/mol for the C0 state. Thus, the local protein–solvent interaction outweighs the packing contribution by between 11 and 18 kcal/mol favoring the coil state. Comparing the chemistry contribution for the peptide and its Q = 0 analog (Table 1) suggests that the favorable local protein–solvent interactions arise primarily from favorable peptide backbone–water interactions, the role of the methyl groups in electrostatic interactions being comparatively negligible. This suggestion is directly confirmed by the analysis of the solute–solvent interaction contribution to the enthalpy: for example, for the helix, of the −91.2 (= −150.9 + 59.7) kcal/mol change in solute–solvent binding that results upon turning-on of partial charges (Table 1), − 86.6 kcal/mol is contributed by the backbone partial charges and the remaining −4.6 kcal/mol is contributed by the methyl group partial charges. (Similar trends hold for the coil states.)

Table 1 also shows that the entropy of hydration is negative, but here it arises due to attractive solute–solvent interactions. Anticipating a forthcoming study on temperature effects, we note that the entropy calculated using eq 5 is in agreement within statistical uncertainties with s^ex calculated from the temperature derivative of μ^ex, as expected from thermodynamic consistency.

Results for the Q = 0 analog suggest that attractive solute–water dispersion interactions alone can inhibit chain collapse brought about by packing effects (Table 1). The enthalpy of hydration is large negative, despite the positive contribution from solvent reorganization (Table 1), emphasizing the role of attractive dispersion interactions between the Q = 0 peptide and solvent. These observations emphasize that care is needed in assuming the relevance of the poor solubility of nonpolar solutes in rationalizing the collapse of a polypeptide. Our observation that hydration does not explain the collapse of a nonpolar chain is consistent with the observation of similar behavior in alkanes (see ref 55 and the reanalysis of data in ref 56 presented therein). Interestingly, attractive solute–water interactions also oppose the pairing of the prototypical hydrophobe methane,³⁵ and this effect is more pronounced for larger alkanes.⁵⁷

Solute–solvent long-range interactions (Figure 1) contribute a substantial fraction—between 50% and 82%—of the net hydration free energy of the peptide. About 90% of the (favorable) long-range contribution for the C₀ and C₇ states arises from van der Waals interactions, while for the helix it is about 60%. The long-range electrostatic and van der Waals contributions balance in the coil-to-helix transition resulting in a free energy change of about −4.0 kcal/mol in favor of the helix (Table 1).

The above analysis shows that the hydrophilic contributions to hydration outweigh the hydrophobic driving force and favor the unfolded state of the peptide. Experiments show that a coil-to-helix transition in a predominantly alanine-based peptide can occur for a polypeptide chain comprising as few as 13 residues.⁵⁸ We expect the role of hydration in disfavoring the coil-to-helix transition to hold for this slightly larger chain, provided the coil states are such that the backbone remains accessible to solvent. This then suggests that the experimentally observed coil-to-helix transition must be driven by changes in peptide intramolecular interactions, an inference that is in consonance with the suggestion that enthalpy changes drive helix formation,²⁵ albeit in longer chains. Results in Table 2 support this expectation.

Table 2.

Components of the Enthalpy Change in the Coil-to-Helix Transition for the Coil States Noted Below^a

coil	ΔEreorg	ΔEbb–w	ΔEsc–w	ΔEint	Δhtotal
C0	−17.0(8.0)	34.0(0.4)	1.9(0.2)	−43.3	−24.0(8.0)
C7	−23.0(6.0)	51.1(0.2)	−0.6(0.2)	−55.0	−28.0(6.0)

^aThe change in excess enthalpy (Δh^ex) reveals the role of hydration and the change in internal energy (ΔE_int) the role of intramolecular interactions. Δh^ex is further divided into ΔE_reorg, the change in the water reorganization contribution, and ΔE_sw, the peptide–water interaction contribution. The latter is subdivided into contributions from the backbone water, ΔE_bb–w, and side chain water, ΔE_sc–w, interactions. Standard error of the mean is given in parentheses at the 2σ level. All values are in kcal/mol.

Table 2 shows that the favorable hydration of the backbone is lost in the coil-to-helix transition (ΔE_bb–w > 0) and this is larger than the change in enthalpy of solvent reorganization (ΔE_reorg < 0) which favors the more compact helical state. It is clear that a favorable change in the internal energy (ΔE_int < 0) is necessary to obtain a favorable change in the net enthalpy Δh_total < 0. Rationalizing heat-capacity changes require temperature dependent studies that are outside the scope of the present work, but the observed importance of the backbone appears to accord well with the suggested importance of backbone hydration in rationalizing the heat capacity signatures in the helix-to-coil transition.²⁹

On a per-residue basis, the net change in enthalpy in the coil-to-helix transition is estimated to be between −2.4 ± 0.8 kcal/mol/residue (C₀) and −2.8 ± 0.6 kcal/mol/residue (C₇), with statistical uncertainty reported at the 2σ level. A direct comparison of our estimated enthalpy change per residue with experiments (interpreted within helix–coil theory) is hampered by (a) the lack of a rigorous conformational averaging of the denatured or coil states in our calculations, (b) the length of our polypeptide, and (c) the fact that in experiments there are residues besides alanine to aid in solubilizing the peptide, thus changing the chemical potential and the folding surface. Experiments on predominantly alanine peptides (with about 50 residues)²⁵ suggest a value of −1.0 kcal/mol/residue. A multistate generalization of the inverse potential distribution theorem suggests that coil states that are less well hydrated, similar to the C₀ state, will dominate the net hydration thermodynamics (for example, see refs 59, 60 for a corresponding result for ions). These are also the states that appear to have an enthalpy change closer to the experimental result (within statistical uncertainties of the calculation). Force field bias can be an issue,^18,61 but using the recently reoptimized variant (C36⁶²) of the force field changes our results by only an additional 5%.

Helix–Helix Complexation

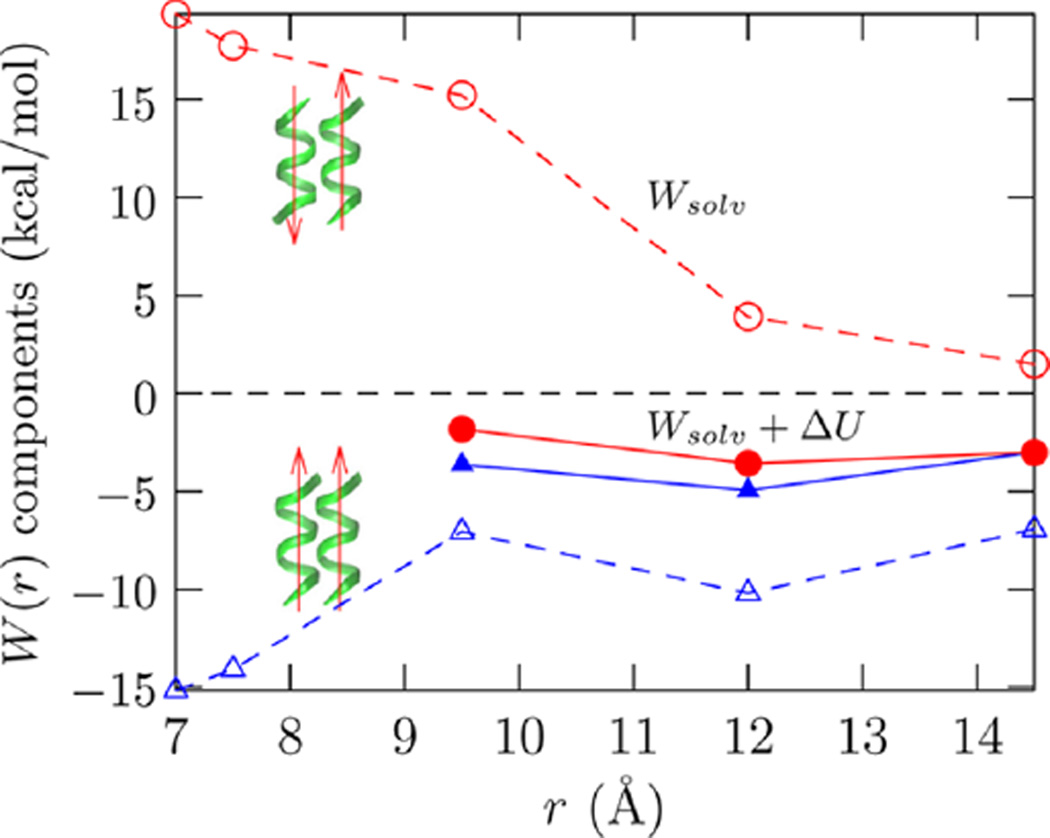
We next consider the free energy of helix association or the potential of mean force between two helices. Figure 3 shows that the net free energy of association for the helices in parallel or antiparallel orientation is nearly the same. Reminiscent of protein folding free energies, the net free energy of complexation is roughly −2 kcal/mol, but this small net result emerges from a balance of large competing hydration and intermolecular interaction effects that are sensitively dependent on the relative orientation of the helices.

Figure 3.

Components of the potential of mean force in bringing two helices together. The helices are shown in green and the parallel (blue △) and antiparallel (red ○) arrangements are indicated by the arrows. W_solv is the solvent contribution (open symbols), and W_solv + ΔU (eq 3) is the net PMF (filled symbols). For r ≲ 8 Å, there is steric overlap between the helices and ΔU rises rather sharply. Data including these values of ΔU are thus not shown.

Figure 3 shows that hydration opposes the complexation of helices in the antiparallel orientation. Given that the repulsion starts at a considerable interhelical distance, our choice of helical registration is probably a minor effect. Our results suggest that hydration will oppose formation of the helix-turn-helix motif. Interestingly, the direct intramolecular contributions (ΔU) can outweigh the hydration effects to drive complexation. For the parallel arrangement hydration favors complexation, but the unfavorable ΔU of interaction between parallel helices tempers the favorable hydration effects.

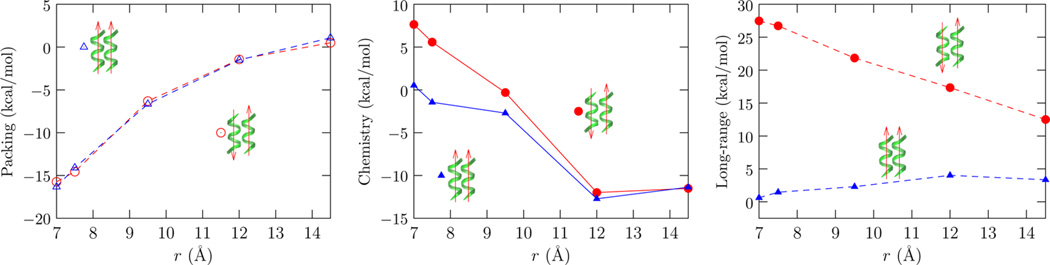
The quasichemical decomposition of the hydration contribution in helix association reveals important insights into the origins of the orientational dependence of the hydration free energy noted above. Figure 4 shows that the short-range hydrophilic contributions favor the helices being close (r ≈ 12 Å) relative to the helices infinitely apart (Figure 4, middle panel), but below this distance they oppose the helices being driven into contact, as might be expected from the loss of favorable hydration. Primitive hydrophobic effects (Figure 4, left panel) do drive helix–helix complexation and, in contrast to the coil-to-helix transition, they outweigh the local chemistry contributions at contact (r ≲ 8 Å). In helix–helix dimerization, the long-range hydration interactions play an entirely nontrivial role, despite the peptides being net neutral. Indeed, for the antiparallel arrangement, these long-range contributions can easily outweigh the hydrophobic contribution.

Figure 4.

SE packing, revised chemistry, and long-range (eq 2) contributions to the free energy of helix–helix complexation. The data is presented relative to two helices infinitely apart. At contact (r ≈ 9.5 Å) the packing effects outweigh the local chemistry effects, but this trend can be easily reversed by long-range interactions.

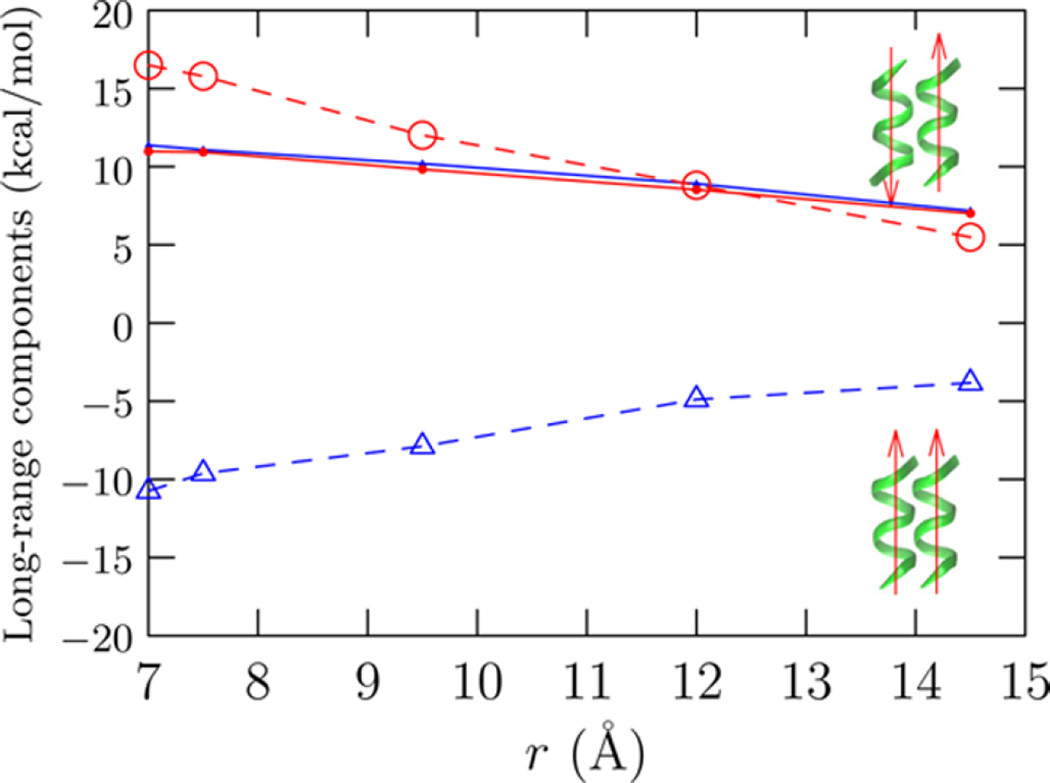
Figure 5 shows that the orientation dependence of the long-range contribution arises solely due to electrostatic interactions. While van der Waals interactions between the solute and solvent (outside the first hydration shell) do not discriminate between the two orientations, its magnitude is non-negligible on the scale of the helix complexation free energy. The electrostatic basis is readily appreciated by approximating the helices as macro-dipoles. For the antiparallel arrangement of the helices, the two helix macro-dipoles are individually well hydrated when the helices are far apart, but because of the approximate cancellation of the dipoles near contact, there is a considerable loss in long-range helix dimer–solvent interactions. For the parallel arrangement of helices, the combined effect of helix macro-dipoles is enhanced near contact, enhancing the hydration effects. Overall, the loss of hydration of the helix dipole explains the unfavorable hydration free energy contribution for the antiparallel arrangement, while the enhanced hydration of the helix pair explains the favorable solvation free energy contribution for the parallel arrangement.

Figure 5.

Van der Waals (solid line) and electrostatic (open symbols, dashed lines) contributions to the free energy. The long-range contribution to free energy is uniquely decomposable^11,63 into electrostatic and van der Waals contributions because P(ε|ϕ) = P(ε_vdw|ϕ) × P(ε_elec|ϕ), where ε = ε_vdw + ε_elec, i.e., the individual binding energy distributions are uncorrelated.

Analysis of enthalpic and entropic effects in pairing shows that for both parallel and antiparallel configurations entropic effects favor complexation (Table 3), but enthalpic effects do not. However, the characteristics of the change in reorganization and interaction components emphasize the need for caution in interpreting the entropic driving force in terms of changes in water structure. This cautionary note is best appreciated by noting that for the antiparallel configuration, the change in the water reorganization energy favors helix pairing, but its effect is negligible for pairing of parallel helices, although for both cases entropic driving forces favor helix pairing. For both orientations, the loss of hydrophilic backbone–solvent and side chain–solvent interactions inhibits helix association. Emphasizing the importance of electrostatic interactions between the backbone and the solvent, the backbone–solvent contributions are sensitive to the orientation of the helices, but the side chain–solvent contributions are essentially of similar magnitude.

Table 3.

Enthalpic (h^ex) and Entropic Contributions (TΔs^ex) to the Change in the Hydration Contribution to the Potential of Mean Force, W_solv, as the Helices Are Brought from 14.5 to 9.5 Å^a

conformation	ΔEbb–w	ΔEsc–w	ΔEreorg	Δhex	ΔWsolv	TΔsex	TΔsex (r = 14.5 Å)
Antiparallel	24.7(0.5)	6.2(0.1)	−7.5(5.0)	23.4(5.0)	13.8(1.2)	9.6	−70.2
Parallel	4.3(0.4)	4.1(0.1)	0.8(5.0)	9.2(5.0)	−0.1(1.2)	9.2	−69.3

^aThe change in hydration enthalpy, Δh^ex, is further divided into ΔE_reorg, the change in the water reorganization contribution, and ΔE_sw, the peptide–water interaction contribution. The latter is subdivided into contributions from the backbone–water interactions, ΔE_bb–w, and side chain–water interactions, ΔE_sc–w. ΔX = X(9.5 Å) – X(14.5 Å), for all X. Standard error of the mean is given in parentheses at the 1σ level. The value of Ts^ex (r = 14.5 Å) is explicitly noted to contrast with the sign of ΔE_reorg. All values are in kcal/mol.

CONCLUDING DISCUSSION

We have considered the hydration contributions to aspects of both secondary and tertiary protein structure formation by considering the change of a solvent-exposed extended coil to helix and the association of two such helices in a model decaalanine peptide. The latter idealized model ignores the role that loops connecting the helices play in the pairing, but it is a reasonable starting point to understand solvent effects in tertiary structure formation.

The association of the cavities, the prototypical hydrophobic interaction, tends to favor the compact state of the polypetide and favor both the coil-to-helix transition and helix–helix complexation. However, in the coil-to-helix transition, hydrophilic effects (protein–water attractive interactions) overwhelm the hydrophobic contribution and favor unfolding of the peptide. Even for a peptide with no partial charges, essentially a nonpolar chain, attractive solute–solvent dispersion interactions suffice to favor the unfolded state.

In the pairing of helices, cavity (ideal hydrophobic) interactions outweigh the short-range peptide–water interactions in favoring helix complexation. This occurs at a larger length-scale than the coil-to-helix transition of a single peptide. However, long-range protein–solvent attractive interactions, especially for the antiparallel arrangement of helices, outweighs the net effect of the packing plus short-range attraction contributions to favor the disassembly of the helices.

In both coil-to-helix transition and helix-pairing, the predominant hydrophilic effects (in our model system) arise from the interaction of the backbone with water. This observed importance of the backbone appears to be consistent with recent studies that encourage a reappreciation of the role of the backbone in protein folding (for example, see refs 4–8, 64, 65).

We find in both the coil-to-helix transition and the pairing of the helices in the antiparallel orientation that changes in the intramolecular energy of the protein are essential in shifting the balance to the folded or collapsed state. The limitations of the models and force field notwithstanding, our study suggests that in protein folding hydrophilic effects and protein intramolecular interactions are as important as, if not more important than, hydrophobic (cavity) effects.