Integral Projection Models for host-parasite systems with an application to amphibian chytrid fungus

Abstract

1. Host parasite models are typically constructed under either a microparasite or macroparasite paradigm. However, this has long been recognized as a false dichotomy because many infectious disease agents, including most fungal pathogens, have attributes of both microparasites and macroparasites.

2. We illustrate how Integral Projection Models (IPM)s provide a novel, elegant modeling framework to represent both types of pathogens. We build a simple host-parasite IPM that tracks both the number of susceptible and infected hosts and the distribution of parasite burdens in infected hosts.

3. The vital rate functions necessary to build IPMs for disease dynamics share many commonalities with classic micro and macroparasite models and we discuss how these functions can be parameterized to build a host-parasite IPM. We illustrate the utility of this IPM approach by modeling the temperature-dependent epizootic dynamics of amphibian chytrid fungus in Mountain yellow-legged frogs (Rana muscosa).

4. The host-parasite IPM can be applied to other diseases such as facial tumor disease in Tasmanian devils and white-nose syndrome in bats. Moreover, the host-parasite IPM can be easily extended to capture more complex disease dynamics and provides an exciting new frontier in modeling wildlife disease.

Introduction

Following the influential papers by Anderson and May (Anderson & May 1979; May & Anderson 1979), host parasite models have usually been constructed within one of two model structures. In their simplest form, microparasite models classify individuals as susceptible, infected or recovered (SIR), with the implicit assumption that all infected hosts can be considered similar because once a host is infected microparasites can rapidly multiply within the host. Under this simple structure, prevalence, the proportion of infected individuals, is therefore adequate to characterize the level of infection within a host population. In contrast, macroparasite models generally assume that parasites cannot complete their entire life cycle within an individual host. Therefore, infection levels within a host are strongly influenced by the number of infective stages the host has encountered, and parasite burden influences host survival, reproduction and the transmission of infective stages. As a result, in macroparasite models, the proportion of individuals infected is not adequate to characterize the level of infection within a host population, and therefore it is necessary to model the frequency distributions of parasites among individuals.

In some pathogens traditionally categorized as microparasites, pathogen within-host reproduction occurs at a slow enough rate that it can be tracked from one time point to the next (e.g. Briggs et al. 2010; Langwig et al. 2015a). In these instances, it is useful to take a macroparasite approach and model the distribution of loads across hosts as this measure is both more consistent with the type of data collected on these diseases and allows for the prediction of additional epidemiological patterns such as the dynamics of parasite aggregation (Scott 1987). Fungal pathogens are increasingly recognized as important threats to biodiversity, agricultural production and human health (Fisher et al. 2012) and may exhibit this relatively slow, measurable on-host reproduction. A modeling framework that accounts for both their microparasite and macroparasite characteristics is critical for understanding their dynamics.

To this end, Briggs et al. (2010) developed an individual based model for the fungal pathogen Batrachochytrium dendrobatidis in frog populations and were able to predict the biological criteria necessary for population persistence as well as the efficacy of different treatment strategies during epizootics (Drawert et al. 2015). However, this model required a separate equation for the fungal load on each individual and was difficult to parameterize from field or experimental data. In general, there is a need for an intermediate modeling framework for “slow” microparasites that accounts for the information in the distribution of parasites across hosts, while allowing for straightforward parameterization from laboratory or field data.

In this paper, we illustrate the potential for integral projection models (IPM)s to address this need. Several recent papers have provided excellent overviews of the construction and use of IPMs (Rees & Ellner 2009; Coulson 2012; Metcalf et al. 2013; Merow et al. 2014a; Rees et al. 2014; Metcalf et al. 2015). In very general terms, IPMs assume that demographic parameters of individuals are affected by one or more continuous variables that describe some property of those individuals. The models then iterate population dynamics in discrete time with state variables of the form N(x, t), representing the frequency of individuals with continuous property x at the time t.

The models can be readily parameterized from data using linear or non-linear regression based approaches. For population models, the continuous variable x is often the size, such as body mass (e.g. Coulson 2012), or age of an organism, but in principle any continuous variable or variables could be used. Here we illustrate their use, using a measure of parasite load. It has been pointed out that this approach may well be suitable for modeling host parasite interactions (Cooch et al. 2012; Metcalf et al. 2015), but we know of only one application of these models for wildlife pathogens: a model of the fungal infection aspergillosis in sea fans (Bruno et al. 2011). The model in that study categorized sea fans into either infected or uninfected categories, and the continuous variable modeled by the integral projection approach was the size of the sea fan, and not the parasite load itself. Recently, Metcalf et al. (2015) have proposed a general framework for using IPM models for disease in which they highlight some of the benefits and challenges of fitting disease data to these models. Here we build on the ideas proposed by Metcalf et al. by providing a detailed case study and other examples of how these methods could be used to address key questions in disease ecology and evolution. Where possible, we try to use similar notation as Metcalf et al..

Materials and Methods

The basic model we examine is a modification of a susceptible-infected-susceptible (SIS) model. In our model, individuals that clear the infection immediately re-enter the susceptible class, with no immunity. Including a recovered class simply requires adding an additional discrete stage to the IPM (Metcalf et al. 2015). The model has the following state variables:

• S(t): Number of susceptible/uninfected hosts at time t

• I(x, t): Frequency of infected hosts with load x at time t (where x ≠ 0). i.e. The number of hosts at time t with a load between lower bound (L) and upper bound (U) is ${\int }_L^{U}I(x,t)dx$

In a traditional macroparasite model x is an integer, so the integral could be replaced with a summation. However, an advantage of the IPM approach is that regression techniques can be used to parameterize the model, rather than needing to estimate a large number of individual matrix parameters. For most fungal infections and many other parasites, data on infection intensity are generally measured using quantitative PCR (Boyle et al. 2004), and continuous measures of infection load are more appropriate than discrete counts.

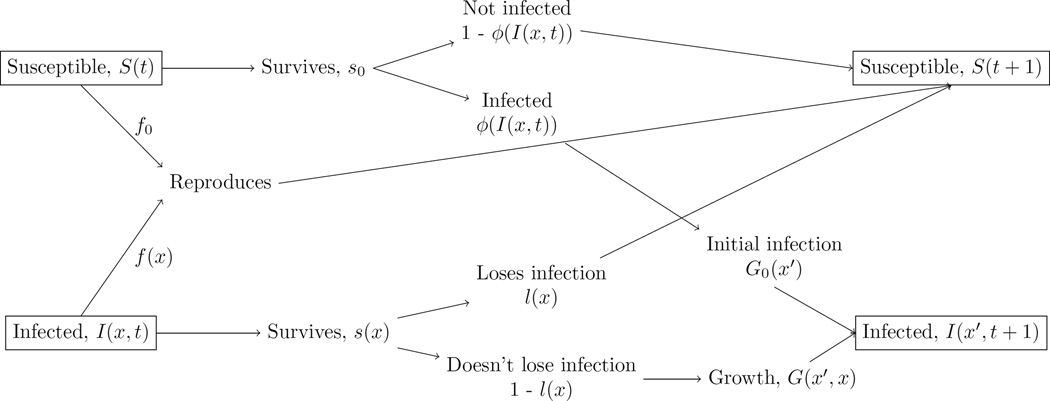
Following Rees et al. (2014), the system can be represented by the life history flow chart in Figure 1. This can be written as the following equation for susceptible/uninfected hosts at time t + 1

$$S(t+1)=S(t)s_0(1-\varphi (I(x,t))+{\int }_L^{U}I(x,t)s(x)l(x)dx+(f_{0}S(t)+{\int }_L^{U}f(x)I(x,t)dx)$$ (1)

Figure 1.

Life history flow chart for the host-parasite Integral Projection Model. The chart shows how an infected host with a parasite load of x at time t can transition to an infected host or susceptible/uninfected host with a parasite load of x′ or 0, respectively, at time t + 1. The chart also shows how an susceptible/uninfected host at time t can transition to an infected host or susceptible/uninfected host with a parasite load of x′ or 0, respectively, at time t + 1.

The first term in this equation gives the number of hosts who remain uninfected in a time step. The second term gives the number of infected hosts who lose an infection and enter the uninfected class in a time step. The third term gives the number of uninfected hosts who are born from uninfected hosts in a time step. The fourth terms give the number of uninfected hosts that are born from infected hosts in a time step.

The equation for infected hosts with load x′ at time t + 1 is given by

$$I(x\prime ,t+1)={\int }_L^{U}I(x,t)s(x)(1-l(x))G(x\prime ,x)dx+S(t)s_0\varphi (I(x,t))G_0(x\prime )$$ (2)

The first term in this equation gives the number of infected individuals with load x that transition to load x′ in a time step. The second term gives the number of uninfected individuals that transition to an infected individual with load x′ in a time step. Below we more thoroughly discuss the terms in equations 1 and 2, how they relate to classic macroparasite and microparasite models, and how they can be parameterized. When parameterizing the functions below, we assume that each process obeys the Markov property such that only the load at time t predicts the event at time t+1 (e.g. growth of the parasite, host survival, loss of infection, etc.) (Easterling et al. 2000).

The growth function: G(x′, x)

For continuous measures of parasite load, the growth function G(x′, x) specifies the probability density of transitioning to load x′ at time t + 1, dependent on having a load of x at time t. In comparison to standard macroparasite and microparasite models, this function allows for pathogen growth on a host to be driven by both within host pathogen birth/rapid self-reinfection (e.g. microparasites and some macroparasites) and from acquiring additional parasites from the environment or other infected hosts. The dependence of G(x′, x) on the free-living stages of the parasites can be made explicit by writing G(x′, x) as dependent on the number of free-living parasites at time t.

This function can be estimated with data on the parasite load of individual hosts at time t and time t + 1. Using standard regression techniques, load at time t, the number of free-living parasites at time t, and/or the density and abundance of other infected hosts can be regressed against load at time t+1 and the resulting model can be used to parametrize the growth function G(x′, x) (Easterling et al. 2000). For continuous parasite loads, the load at time t + 1 could be described by a lognormal or gamma distribution, while discrete disease loads could be fit by a negative binomial distribution (Anderson & May 1978; Shaw et al. 1998). The growth of a parasite on a host will often depend on other abiotic variables that can be accounted for as additional fixed or random effects in the regression model (Rees & Ellner 2009).

The survival function: s₀ and s(x)

s₀ specifies the survival probability of uninfected hosts. 1 − s₀ gives the probability of a host dying without any infection, which parallels the death rate of uninfected hosts in classic micro and macroparasite models. s₀ can be estimated by the proportion of uninfected hosts that survive from t to t + 1.

The survival function s(x) specifies the probability of a host with a parasite load x surviving from time t to time t + 1. In classic macroparasite models, it is assumed that parasite-induced host mortality increases linearly with load at rate α, where α specifies the pathogenicity of the parasite (Anderson & May 1978). In the IPM framework, a commonly used function to measure survival probability is the logistic function given by

$$s(x)=\frac{\text{exp}(b_0-b_{1}x)}{1+\text{exp}(b_0-b_{1}x)}$$ (3)

where b₁ is similar to the pathogenicity parameter α (Anderson & May 1978; Wilber et al. 2015). When b₁ is held constant, b₀ dictates the parasite load at which substantial parasite-induced host mortality begins to occur (Wilber et al. 2015). The logistic function could be replaced by other functions, as dictated by the data (Dahlgren et al. 2011).

The survival function s(x) can be estimated with logistic regression using host survival and load data from laboratory or mark-recapture studies conducted at the appropriate time scale. If other biotic or abiotic factors are also thought to contribute to the survival probability of a host from t to t + 1, they can be included as additional predictor variables in the survival function.

The loss of infection function: l(x)

The loss of infection function l(x) specifies the probability of a host having a parasite load of x at time t and losing the infection by time t + 1. In comparison with classic microparasite susceptible-infected models, this function is analogous to the rate at which infected individuals recover from infection and reenter the susceptible/uninfected class. We similarly assume that individuals that lose an infection immediately reenter the susceptible/uninfected class, though a resistant class could easily be included in this modeling framework (Metcalf et al. 2015).

A logistic function (equation 3) could also be used for the loss of infection function and could be parameterized using parasite load data at time t and t + 1 and fitting a logistic regression where the response variable is whether or not a host lost an infection by time t + 1 and the predictor variable is the infection intensity x at time t. As with the survival function, if other biotic or abiotic factors also contributed to l(x) they could be included as additional predictor variables in the logistic regression.

The transmission function: ϕ(I(x, t))

The transmission function ϕ(I(x, t)) specifies the probability of transitioning from the uninfected class to the infected class. The transmission function is critically important for the dynamics of a disease and can take a variety of different functional forms. Some common examples include the density-dependent or mass action transmission function βIS and the frequency-dependent transmission function βSI/N (McCallum et al. 2001).

Over a unit time interval, a density-dependent, mass action transmission function results in the following probability of an individual host not being infected: $\text{exp }(-\beta {\int }_L^{U}I(x,t)dx)$, where ${\int }_L^{U}I(x,t)dx$ gives the total number of infected individuals. Allowing β to be a function of parasite load, ϕ(I(x, t)) can be written as

$$\varphi (I(x,t))=1-\text{exp }(-{\int }_L^U\beta (x)I(x,t)dx)$$ (4)

where ${\int }_L^U\beta (x)I(x,t)dx$ is the force of infection and β(x) specifies the effect of an individual with an infection load of x on the infection probability of an uninfected individual. This formulation assumes that new infections occur following a Poisson process with rate ${\int }_L^U\beta (x)I(x,t)dx$.

While this functional form may be appropriate for many microparasites in which direct transmission among hosts is the primary mode of acquiring infection, the transmission of some pathogens depends on the number of free-living parasites in a system as well as the number of infected hosts (Briggs et al. 2010). If we assume that number of free-living parasites is proportional to the total number of parasites in all infected hosts in the system at time t, then we can modify β(x)I(x, t) to β(x)xI(x, t) to capture this biology.

Finally, some pathogens have an environmental reservoir such that the probability of infection is non-zero even when no infected hosts are present. This could be captured by rewriting equation 4 as

$$\varphi (I(x,t))=1-\text{exp }(-(a+{\int }_L^U\beta (x)I(x,t)dx))$$ (5)

where 1 − exp(−a) defines the probability of infection when no infected hosts are present (e.g. from an environmental reservoir). This environmental reservoir could be more explicitly accounted for by including an additional state variable in the IPM that tracks how the number of parasites in the environment grows and decays in a time step (Rohani et al. 2009).

Methods for estimating the transmission function and/or its corresponding parameters are well-described in the host-pathogen literature (e.g. McCallum 2000; Smith et al. 2009), though choosing between transmission functions is typically a data-intensive procedure (Rachowicz & Briggs 2007; Smith et al. 2009).

The initial infection burden function: G₀(x′)

The function G₀(x′) specifies the probability density of the infection intensity of a host when it first becomes infected and can be a function of the total number of infected hosts in the population, the total number of infectious agents in the population and/or various other host or abiotic covariates. This function can be estimated by fitting a regression model where the response variable is the pathogen load of infected hosts at time t+1 that were uninfected at time t. For continuous disease loads, a variety of different distributions such as gamma, lognormal, and normal could be explored.

In comparison with standard stochastic macroparasite models, this function is analogous to clumped infection distributions in which a host can acquire a random number of free-living parasites in a small time step (Isham 1995; Pugliese et al. 1998). However, depending on the time step used to parameterize the IPM, G₀(x′) will also be influenced by the growth of the parasite on the host as a “clump” of parasites can infect a host and then grow in the time interval t to t + 1.

Moreover, the above host-parasite IPM assumes that after acquiring an initial infection burden the growth of the parasite on a host is then driven by G(x′, x) and is independent of the density of infected hosts. If one has reason to believe that transmission and the function G₀(x′) are important drivers of disease dynamics on hosts after the initial infection, the growth function may be redefined as

$$G\prime (x\prime ,x,I(x,t))=(1-\varphi (I(x,t))G(x\prime ,x)+\varphi (I(x,t)[G_0(x\prime -x)+\text{higher order terms}]$$ (6)

where an increase in load from x to x′ in a time step could be because of 1) no transmission occurring and parasite load increasing due to within host growth (first term) or 2) transmission occurring and a host acquiring a “clump” of infections of size y such that y = x′ − x (second term) or 3) some combination of both within host growth and transmission occurring such that parasite load increases from x to x′ in a time step. This is given by higher order terms and will depend on the length of the time step t to t + 1 relative to the dynamics of the pathogen.

The fecundity function: f₀ and f(x)

The fecundity function f(x) specifies the mean number of offspring produced by individuals with a parasite load of x (or by susceptible/uninfected individuals f₀) and the host-parasite IPM assumes that all offspring enter the uninfected class. It is easy to relax this assumption and include vertical transmission into the host-parasite IPM by allowing newly born hosts to enter the infected class with a parasite load specified by some probability density function. Standard macroparasite models assume that host reproduction decreases linearly with increasing parasite load (May & Anderson 1978). However, as pointed out by May & Anderson, this is an over simplification as the response of host reproductive effort to parasitism is often non-linear (e.g. Weatherly 1971) and reproduction itself can never take on a negative value (Roberts et al. 1995). Alternative formulations of parasite-induced reduction in host fertility that account for this non-linear relationship have been discussed (Roberts et al. 1995).

In the IPM framework, the fecundity function can be fit using Poisson or negative binomial regression where the predictor variable is parasite load and the response variable is the number of offspring produced by a host with that parasite load (Easterling et al. 2000). If the response variable is a non-integer value, a continuous distribution such as gamma or lognormal could be used. Depending on the link function, these regressions can produce non-linear fecundity functions that are always positive. Similar to the other vital functions discussed above, other factors that affect mean reproductive output can be included in the regression.

For many host-parasite systems, host reproduction occurs on a much longer time scale than the dynamics of the parasite and it may not be biologically realistic to include host reproduction at each time step in the IPM model as is done in equation 1. For example, if host reproduction occurs at a particular time during the year it may be useful to break the year into separate IPMs (e.g. an IPM for summer, fall, winter and spring; Caswell 2001) such that load-dependent host reproduction only occurs in a particular season or as a discrete pulse at the beginning of a particular season (e.g. host reproduction is only non-zero in the spring and fall). One may also want to include host age as an additional discrete or continuous host attribute (Childs et al. 2003) to account for reproductive differences among hosts of different ages. On the other hand, if one is particularly interested in the fate of a host population over a single seasonal epizootic where host reproduction does not occur, the fecundity function may be excluded from the host-parasite IPM as it will not affect host population persistence during the epizootic. In this case, appropriately modeling vital rates such as the survival function s(x) and the growth function G(x′, x) will be critically important for understanding host-parasite dynamics. In general, how to include host reproduction into the host-parasite IPM will depend on the questions that are being addressed.

Application of model to amphibian chytrid fungus: Laboratory experiment

We use the above IPM framework to examine the population dynamics of amphibian hosts infected with the fungal pathogen Batrachochytrium dendrobatidis (Bd). Bd is a devastating amphibian pathogen that has led to declines in many amphibian populations around the globe (Skerratt et al. 2007; Kilpatrick et al. 2010). Bd is a cutaneous fungus that disrupts the osmoregulatory ability of amphibian skin, eventually leading to chytridiomycosis and amphibian mortality (Voyles et al. 2007, 2009). In contrast to traditional macroparasities, Bd rapidly reinfects an infected host in a process analogous to within host birth (Rollins-Smith 2009). The generation time of Bd is between four to ten days depending on temperature (Woodhams et al. 2008), such that the on-host Bd growth dynamics can be captured via repeated swabbing of an animal every few days, with the fungal load on the frog estimated as the number of copies of Bd DNA detected on the skin swabs via quantitative PCR (Boyle et al. 2004). Quantitative PCR provides a continuous measure of infection intensity between 0 (uninfected) and an arbitrarily large Bd infection. These characteristics of Bd make it an ideal candidate for applying the host-parasite IPM described above.

We use the IPM framework to gain insight into how temperature affects the epizootic dynamics of Bd in populations of the Mountain yellow-legged frog complex (Rana muscosa and Rana sierrae, henceforth R. muscosa). Rana muscosa are native to the California Sierra Nevada mountains and have suffered severe Bd-induced population declines (Vredenburg et al. 2010; Briggs et al. 2010). The severity of Bd infection is highly temperature dependent (Berger et al. 2004; Andre et al. 2008), with optimal Bd growth occurring between 17 – 25 °C in laboratory conditions (Piotrowski et al. 2004), but depending on host-Bd interactions (Piotrowski et al. 2004; Raffel et al. 2012). While these are the temperatures at which amphibians often suffer more severe chytridiomycosis and mortality, this pathology is species-dependent (Kilpatrick et al. 2010).

We use data from a laboratory experiment in which 20 adult R. muscosa were housed separately at 4 different temperatures (4 °C, 12 °C, 20 °C, 26 °C; 5 frogs per temperature), exposed to approximately 10⁶ zoospores of Bd and then monitored for 119 days. Every three days starting eight days after exposing the frogs to Bd, the frogs were swabbed and Bd zoospore load was estimated using quantitative PCR. Mortality that occurred between swabbing events was recorded at the next swabbing event. Frogs housed at 26 °C were visibly distressed and suffered much higher Bd-independent mortality than those housed at lower temperatures. For this reason, and because we wished to examine how temperature affected R. muscosa-Bd dynamics at the much cooler temperatures typically observed in the field (4–20 °C, Knapp et al. 2011), we excluded individuals at 26 °C.

Model description

To fit the IPM to Bd load data from laboratory experiments, we made two simplifying assumptions. First, we excluded reproduction/recruitment because we lack data on the effect of infection on reproduction. As a result, we used this model to address questions regarding epizootic dynamics of Bd and R. muscosa over the course of a single summer season, rather than to examine long-term population persistence with disease.

Second, we assumed the probability of infection ϕ(T) was temperature (T)-dependent, but independent of the density of infected hosts (i.e. I(x, t) does not affect the probability of infection). In our experiments individual animals were housed in separate containers and initial infection was solely due to an amphibian acquiring Bd zoospores from the environment. We subsequently explore different transmission functions that do include I(x, t) to understand their implications on Bd epizootic dynamics. With these assumptions, the modified IPM is given by

$$S(t+1)=S(t)s_0(T)(1-\varphi (T))+{\int }_L^{U}I(x,t)s(x,T)l(x,T)dx$$ (7)

$$I(x\prime ,t+1)={\int }_L^{U}I(x,t)s(x,T)(1-l(x,T))G(x\prime ,x,T)dx+S(t)s_0(T)\varphi (T)G_0(x\prime ,T)$$ (8)

where the various vital functions are now dependent on temperature T. Note that x refers to ln(x) (log zoospore load) when x ≠ 0 and 0 (uninfected) when a frog was uninfected. In this case, 0/uninfected represents a discrete state of the frog and is not equivalent to ln(x) = 0. In this model, a single time step represents three days, which was the time between swabbing events in the laboratory experiment.

Vital rate functions

We modeled the survival function s(x) of a frog with a log zoospore load of x as a logistic regression with the link function given by

$$\text{logit}(s(x))=b_{0,0}+b_{1,0}x$$ (9)

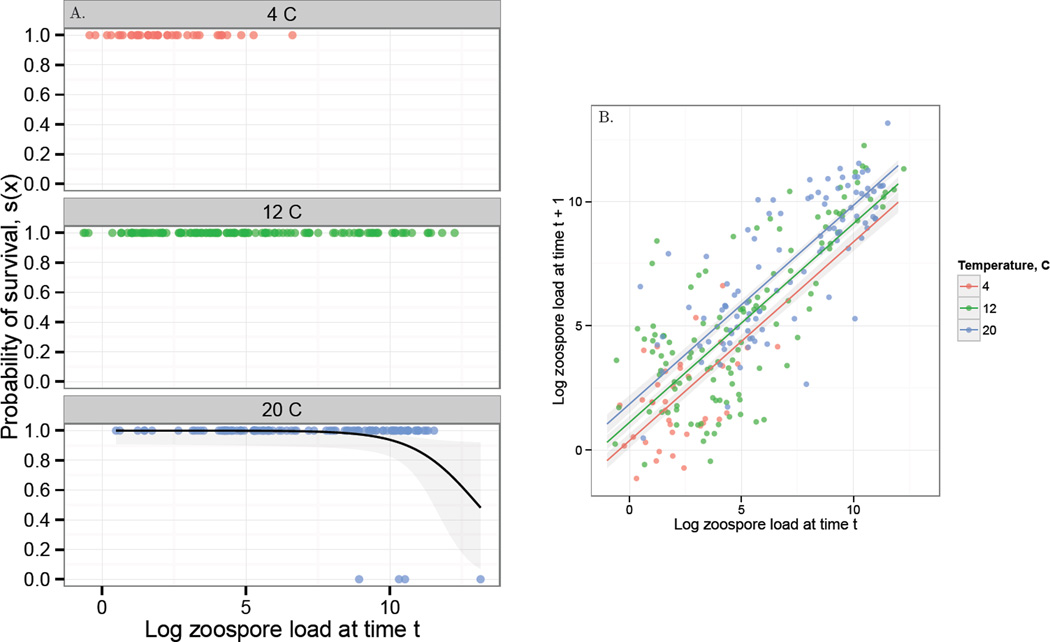
where b_0,0 is the intercept of the link function on the logit scale, and b_1,0 is the effect of log zoospore load on the logit-transformed probability of survival. We could not estimate the effect of temperature on this vital rate function because no individuals died at 4 °C or 12 °C (Fig. 2A). This result was surprising because individuals at 12 °C had loads as high or higher than individuals at 20 °C and did not experience mortality. Based on previous results in the field which show that R. muscosa suffer a roughly consistent Bd-induced mortality across a variable lake temperatures in the field (i.e. the ≈ 10,000 zoospore threshold, Vredenburg et al. 2010), additional results in the laboratory that show that frogs experience significant Bd-induced mortality at temperatures below 20 °C (17 °C, Andre et al. 2008), and extensive field observations that decreased temperature does not have a large protective effect on R. muscosa in the field (Knapp et al. 2011), we think there is very little evidence that the survival curve of R. muscosa and Bd-load interacts with temperature. Therefore, we assumed that Bd-induced mortality is dependent only on load and not on temperature directly. We therefore parameterized the survival function using only individuals at 20 °C (Fig. 2A, see SI 1 for a comparison with a survival function fitted with all of the temperature data), but assumed a temperature-independent survival function. However, temperature influenced fungal growth, as detailed next.

Figure 2.

A. The laboratory data used to estimate the survival function s(x). Each panel gives a different temperature and each point gives the load of an individual frog at time t and whether it survived to time t+1. A value of 1 indicates that a frog survived and a value of 0 indicates that it died. No frogs died in temperature treatments 4 and 12 °C. The black line in the 20 °C plot gives the fit of the temperature-independent survival function used in the analysis, plus or minus the standard error about the prediction. B. The laboratory Bd growth data and corresponding temperature-dependent growth function G(x′, x) from the Bd-Rana muscosa laboratory experiment. Each point gives the log zoospore load on an individual at time t and time t + 1. The different colors show different temperatures. The corresponding lines give the predicted growth function for a given temperature along with the standard error about the predicted mean. Growth of Bd on an individual frog increases with both temperature and the number of zoospores at time t. Alternative models for this growth function are discussed in SI 1.

We modeled the growth function G(x′, x) as a normal distribution X ~ N(μ(x, T), σ²(x)) where T is temperature. Mean fungal loads were modeled as

$$\mu (x,T)=b_{0,1}+b_{1,1}x+b_{2,1}T$$ (10)

where b_0,1 is the intercept and b_1,1 and b_2,1 give the effect of a unit change in log zoospore load and temperature on the log zoospore load at time t + 1, respectively. We also allowed the variance of G(x′, x) to be an exponential function of log zoospore load at time t

$${\sigma }^2(x)={\nu }_{0,1}\text{exp}(2c_{0,1}x)$$ (11)

where ν_0,1 is a constant and c_0,1 dictates the effect of log zoospore load on the variance.

We modeled the loss of infection function l(x) as a logistic regression with the link function

$$\text{logit}(l(x,T))=b_{0,2}+b_{1,2}x+b_{2,2}T$$ (12)

where b_0,2 is the intercept and b_1,2 and b_2,2 are the coefficients giving the effect of a unit change in log zoopsore load and temperature on the logit-transformed probability of losing an infection in a single time step, respectively.

We modeled the initial infection burden function G₀(x′) as a normal distribution X ~ N(μ(T), σ²(T)). We defined the mean of the distribution as μ(T) = b_0,3 + b_1,3T where b_0,3 and b_1,3 are defined similarly to the growth function. We modeled the variance as σ²(T) = ν_0,3 exp(2c_0,3T) where ν_0,3 and c_0,3 are defined similarly as in the growth function.

Finally, we modeled the probability of an individual becoming infected ϕ(T) in a time step as a function of temperature T using a logistic model logit[ϕ (T)] = b_0,4 + b_1,4T where b_0,4 and b_1,4 are defined similar to the recovery function. We performed model selection and validation various for each vital rate functions described above and these results are given in SI 1. We fit the vital rate functions in R version 3.1.2 using the functions gls, lme, and glm and all code used for this analysis can be found at https://github.com/mqwilber/ipm_for_parasites.

Analyzing the IPM

After fitting the parameters of the vital rate functions, we analyzed the resulting IPM (equation 7) by discretizing the continuous variable Bd load and using the midpoint rule to evaluate the IPM at each time step (Rees et al. 2014). For the infected portion of the host-parasite IPM, we used 100 discretized bins (i.e. a mesh size of 100) and lower and upper bounds of −5 and 18 log zoospore load, which we chose to minimize the effects of eviction on the IPM predictions (loss of individuals from the model because their predicted future loads are outside the model range, SI 2; Williams et al. 2012). To put these bounds in context, the log zoospore range from our experiment was (−1.14, 13.15) and the approximate log zoospore load at which R. muscosa begin experiencing substantial die-off in the field is at or above a log zoospore load of 9.21 (Vredenburg et al. 2010). To incorporate the discrete, uninfected stage into the IPM, we appended an extra row giving transitions of various infected individuals to an uninfected state (top-most row) and an extra column specifying the transition of uninfected individuals into various infected states (left-most column) to the 100 × 100 parasite load transition matrix described above (Merow et al. 2014a).

We calculated the local elasticity of the population growth rate (λ) to the lower-level regression parameters b_i,j of the vital functions defined above by perturbing each regression parameter by δ = 0.001 and calculating the elasticity as e_i,j = [(λ_perturbed − λ_fitted)/δ × b_i,j] × (b_i,j/λ_fitted) (Merow et al. 2014b). To propagate the uncertainty in our estimates of the lower-level vital rate parameters through to our estimates of the population growth rate and lower-level parameter elasticity, we took the following parametric bootstrap approach. Using standard asymptotic likelihood results (McCullagh & Nelder 1989), we assumed that each parameter set from a vital rate function followed a multivariate normal distribution with a mean and variance-covariance matrix equal to the values given by the regression procedure used to fit the vital rate function. Next, we ran 1000 simulations in which we randomly drew the lower-level regression parameters from their respective multivariate normal distributions and parameterized the IPM using these parameters. We then calculated either the population growth rate or the elasticity of a given lower-level parameter with these randomly drawn values and stored the result. This provided us with estimates of the population growth rate and lower-level parameter elasticity while accounting for the uncertainty in the lower-level parameters used to build the IPM. We note that this approach likely underestimates the uncertainty as it does not account for the uncertainty in the variance estimates, does not account for covariance of parameters between vital rate functions, and assumes multivariate normality. A fully Bayesian approach can capture this uncertainty more completely (Merow et al. 2014b; Elderd & Miller 2015).

Exploring density-dependent transmission dynamics

In equation 7, we assumed density and frequency independent transmission of Bd. We also explored how a mass action, density-dependent transmission function affected the epizootic dynamics of Bd. In particular we assumed the following transmission function

$$\varphi (I(x,t))=1-\text{exp }(-(a+\beta {\int }_L^{U}xI(x,t)dx))$$ (13)

which specifies that the probability of infection at time t is dependent on the total number of zoospores present in the host population $({\int }_L^{U}xI(x,t)dx)$ at time t as well as a constant probability of infection from an environmental reservoir ω = 1 − exp(−a). We followed the example of previous Bd modeling work and assumed that the Bd epizootic dynamics depend on the number zoospores in the aquatic environment rather than just the number of infected amphibians in a population (Briggs et al. 2010). The term ${\int }_L^{U}xI(x,t)dx$ reflects this assumption, albeit ignoring potential dynamics of free-living zoospores. Moreover, we assumed that density dependence affects only the probability of transitioning from uninfected to infected, such that once an amphibian is infected the increase in Bd is independent of infected host density. This assumption is realistic if the parasite reproduction on the host swamps out the effects of reinfection from other individuals or the environment.

To explore the effects of this transmission function on epizootic dynamics, we first parameterized the density-independent portion of the IPM model using the maximum likelihood estimates of the vital rate function parameters discussed above. Because we could not estimate the density-dependent transmission function from the data we collected, we explored the effect of this function on population dynamics by choosing (ω, β) pairs on a grid and using these values to parameterize the density-dependent transmission function. The estimated values of ω used in the density-independent model suggested that ω was between 0.22 and 0.6 depending on the temperature, so we explored values of ω between 0.01 and 0.6. We did not have a good a priori estimate of β, so we explored β within the range 0 to 1.17 × 10⁻³, where this upper bound was chosen arbitrarily after preliminary simulations showed that larger values of β had little effect on the population dynamics. For every (ω, β) pair, we iterated the density-dependent IPM for 120 days, which is the approximate length of the summer in the Sierra Nevada during which Bd epizootics tend to occur (Briggs et al. 2005, 2010). We initialized each population with 100 uninfected individuals and for each combination of (ω, β) we calculated the proportion of surviving amphibians and the prevalence of Bd infection at the end of the epizootic.

Results

Vital rate functions

Increasing log zoospore load x significantly decreased survival probability of amphibians (Fig. 2A; ${\chi }_{df=1}^2=12.197$, p = 0.0005; Table 1).

Table 1.

Vital rate parameters used to parameterize the density-independent integral projection model. logit specifies a logistic link, x is log zoospore load, and T is temperature.

Description	Functional Form	Parameters	Details of Parameterizatio
Infected survival function, s(x)	logit[s(x)] = b0,0 + b1,0x	b0,0 = 11.824 b1,0 = −0.8605	Logistic Regression
Uninfected survival prob- ability, s0	Constant	s0 = 1	Briggs et al. 2005
Growth function, G (x′, x)	μ(x, T) = b0,1 + b1,1x + b2,1T σ2 (x) = ν0,1 exp (2c0,1x)	b0,1 = 0.012 b1,1 = 0.799 b2,1 = 0.092 ν0,1 = 5.92 c0,1 = −0.049	Generalized Least Squares
Loss of infection function, l(x)	logit[l(x, T)] = b0,2 + b1,2x + b2,2T	b0,2 = 1.213 b1,2 = −0.472 b2,2 = −0.151	Logistic Regression
Initial infection burden function, G0(x′)	μ(T) = b0,3 + b1,3T σ2(T) = ν0,3 exp(2c0,3T)	b0,3 = 0.642 b1,3 = 0.137 ν0,3 = 0.59 c0,3 = 0.063	Generalized Least Squares
Transmission function, ϕ	logit[ϕ(T)] = b0,4 + b1,4T	b0,4 = −1.66 b1,4 = 0.102	Logistic Regression

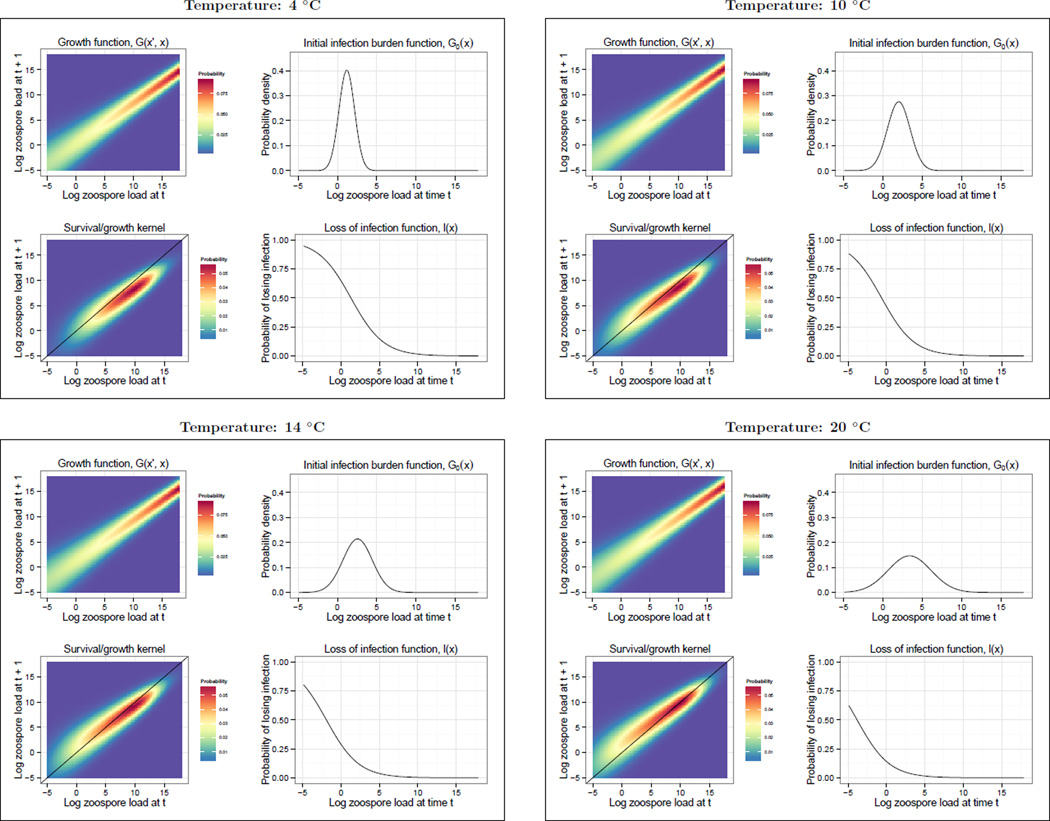
Both temperature and log zoospore load at time t significantly increased log zoospore load at time t + 1 (Likelihood Ratio Test (LRT) for load at time t: ${\chi }_{df=1}^2=196.36$, p < 0.0001; LRT for temperature: ${\chi }_{df=1}^2=13.56$, p = 0.0002). Moreover, log zoospore load at time t was important for describing the variance structure of the growth function, as compared to a model with constant variance structure (LRT comparing full model to model with constant variance: ${\chi }_{df=1}^2=9.8$, p = 0.0017; Table 1; Fig. 2B, Fig. 3).

Figure 3.

The growth function G(x′, x), loss of infection function l(x), initial infection burden function G₀(x′) and the survival/growth kernel (G(x′, x)s(x)) used to parameterize the Bd-Rana muscosa Integral Projection Model for temperatures between 4 and 20 °C. The four temperatures shown were chosen to illustrate how the various vital rate functions change with temperature. Because each vital rate function shown is a linear function of temperature (see Vital rate functions) we were not restricted to choosing the 3 temperatures used to fit the vital rate functions (4, 12, and 20 °C) and could chose any temperature between 4 and 20 °C. The black line on the survival/growth kernel plots is a one to one line representing stasis: above this line the Bd load on a host gets larger in a time step and below this line the Bd load on a host gets smaller in a time step.

Temperature and log zoospore load were both highly significant predictors of whether an amphibian would clear Bd infection in a given time step (temperature: ${\chi }_{df=1}^2=14.555$, p = 0.0001; log zoospore load: ${\chi }_{df=1}^2=23.701$, p < 0.0001; Fig. 3). Amphibians were more likely to clear infection at lower temperatures and when the load at time t was smaller.

Increasing temperature significantly increased the mean and variance of the initial infection load distribution G₀(x′) (temperature effect on mean: t_df=41 = 2.53, p = 0.015; temperature effect on variance: LRT comparing model with variance structure to without: ${\chi }_{df=1}^2=6.00$, p = 0.0143; Fig. 3).

Finally, increasing temperature significantly increased the probability of infection ϕ (${\chi }_{df=1}^2=6.0361$, p = 0.014; Table 1).

Laboratory dynamics of amphibians and Bd

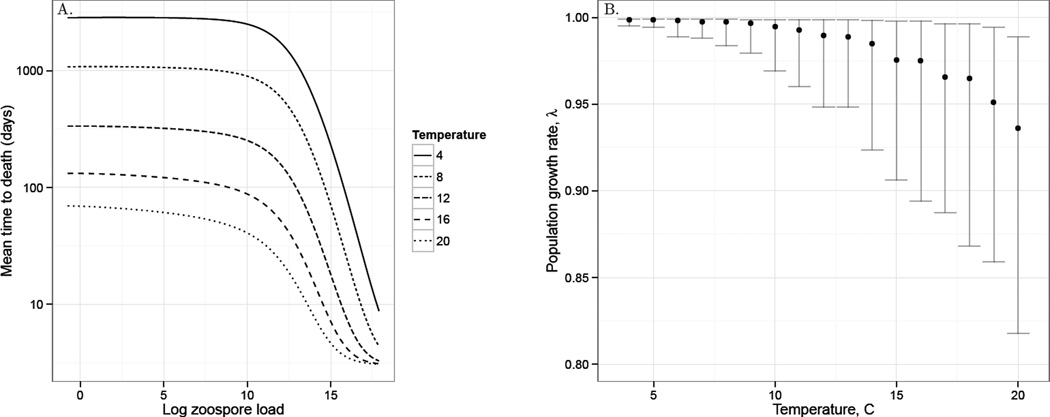
The parameterized IPM model predicted that individual amphibians at low temperatures would survive significantly longer than amphibians at high temperatures, with the largest difference being when log zoospore loads were low (Fig. 4A). Over a summer epizootic, amphibian populations at low temperatures experienced a minimal effect of Bd-induced population declines (λ ≈ 1), while amphibians at higher temperatures experience substantially more rapid declines, with large uncertainty around these estimates (Fig. 4B). Elasticity analysis on the lower-level parameters used in the vital rate functions showed that overall population growth rate was most sensitive to proportional changes in the growth rate of Bd (the parameters of the growth function; Fig. S5) as well as the pathogenicity of Bd and the threshold at which Bd-induced mortality began to occur (the parameters of the survival function; Fig. S5).

Figure 4.

The host-parasite Integral Projection Model predictions for A. how the expected time to Bd-induced Rana muscosa death varies with log zoospore load and temperature and B. how the population growth rate (λ) of R. muscosa varies with temperature. The black points are the median population growth rate for 1000 simulations that account for the uncertainty in the vital rate function parameters. The error bars give the first and third quartiles of λ from these simulations.

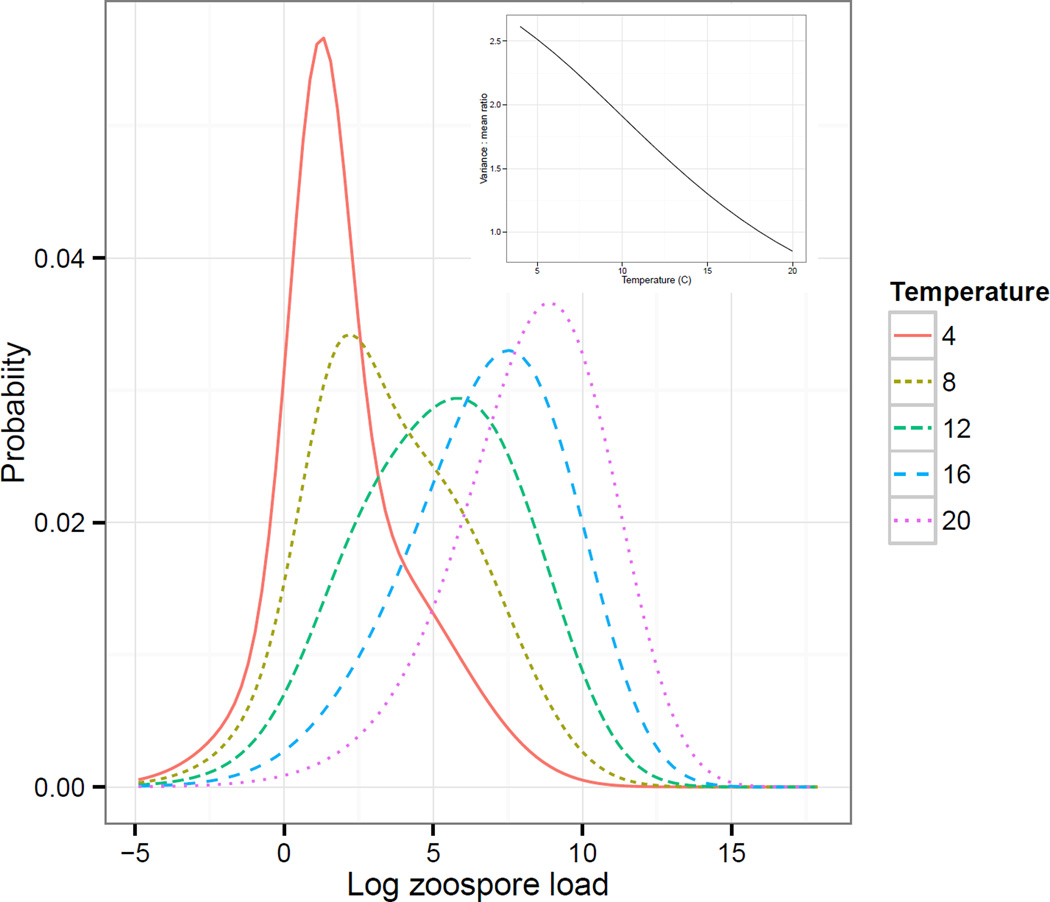
The IPM model also allowed us to examine how the stable log zoospore distribution of Bd on surviving hosts changed with temperature (Fig. 5). For surviving, infected amphibians, the mean infection intensity increased with temperature, but the variance to mean ratio decreased with temperature (Fig. 5), consistent with experimental and model results showing that hosts experienced greater Bd-induced mortality at higher temperatures. This is also consistent with previous theoretical results from macroparasite models which predict that increased parasite-induced host mortality generally decreases the variance to mean ratio (Barbour & Pugliese 2000).

Figure 5.

The stable Bd load distribution for infected Rana muscosa as predicted by the parameterized host-parasite Integral Projection Model for various different temperatures. The inset plot shows that the variance to mean ratio of this distribution decreases with temperature.

Effects of density-dependent transmission on epizootic dynamics

The effect of density-dependent transmission on Bd-R. muscosa population dynamics varied with temperature, the probability of infection from the environmental reservoir (ω) and the transmission coefficient (β). In general, over the range of density-dependent transmission values we examined, density-dependent transmission had little effect on prevalence and the proportion of population decline over the course of a summer epizootic (Fig. S7–S8). In contrast, the probability of infection from the environment had a large effect on both prevalence patterns and population decline (Fig. S7–S8). Given a probability of infection from the environment above approximately 0.15, increasing density-dependent transmission had very little effect on Bd prevalence or R. muscosa population decline. Over the parameter space we examined, the density-dependent transmission model predicted that populations at 12 °C will experience a maximum of a 20% population decline over the course of an epizootic with 70% prevalence, while populations at 20 °C will experience a greater than 80% population decline with close to 100% prevalence (Fig. S7–S8).

Discussion

Integral projection models provide an ideal framework to model diseases that do not fall neatly into the microparasite/macroparasite dichotomy. By taking an intermediate approach between individual-based disease models which explicitly track the parasite load on every individual in a population (Briggs et al. 2010) and classic macroparasite/microparasite models which only track the total number of hosts and parasites in a population (Anderson & May 1978), IPMs can elegantly investigate population outcomes of infectious diseases while still incorporating critical information about disease dynamics at the individual-level (Metcalf et al. 2015). While the IPM approach can theoretically be used to explore the dynamics in any macroparasite or microparasite system, we believe it will be practically most useful in host-parasite systems where the growth rate of a parasite is slow enough that measurements of parasite load at time t and t+1 are on the same time scale as the growth rate of the parasite. This allows for empirical estimation of the vital rate functions and an investigation regarding how these vital rate functions vary with environmental factors such as temperature and/or differ between host populations in which a disease is established or invading.

We used the host-parasite IPM model to explore the consequences of different temperatures on R. muscosa-Bd dynamics over the course of an epizootic. The effect of temperature on Bd growth is well-known both in culture and on amphibian hosts (Longcore et al. 1999; Piotrowski et al. 2004; Berger et al. 2004; Andre et al. 2008; Raffel et al. 2012) and previous work has estimated the expected time to death of amphibians infected with Bd over various different temperatures (Berger et al. 2004; Andre et al. 2008). However, the effect of temperature-Bd interactions on amphibians at the population level is much less clear (Rohr & Raffel 2010; Knapp et al. 2011). Using an IPM model, we were able to make specific, quantitative predictions about how temperature and transmission dynamics affected population growth rates of Rana muscosa.

The density-independent IPM model predicted that population-level growth rate decreased with increasing temperature and naive populations at or above about 18 degrees had a 50% chance of experiencing an 80% decline or greater over the course of a summer epizootic. This result likely represents a best case scenario for Rana muscosa as this density-independent model does not account for Bd transmission dynamics (Rachowicz & Briggs 2007) or additional factors leading to increased frog mortality or Bd-susceptibility in the field. Our elasticity analysis showed that the population-level growth rate was most sensitive to proportional changes in parameters relating to the Bd growth function and the survival function. If in situ factors slightly reduced the Bd-load at which frogs began experiencing disease-induced mortality, for example, R. muscosa populations could experience extirpation during a summer epizootic for a wide range of temperatures, which would be consistent with the patterns observed in the field (Knapp et al. 2011). In particular, we assumed a temperature-independent survival function in the IPM model (described in Vital rate functions) and including temperature-dependence into this function would have significant impacts the ability of R. muscosa populations to persist through an epizootic.

We extended this density-independent IPM to explore how density-dependent transmission and transmission from an environmental reservoir affected population dynamics. Our results suggest that density-dependent transmission had a small effect on the population dynamics of Bd epizootics, particularly when an environmental reservoir was present. While this result is largely due to our assumption that density-dependent transmission does not effect the the growth of Bd on an already infected frog, it is consistent with predictions from a fully individual-based model that predicts that density manipulations (i.e. culling infected frogs) will likely have little effect on mitigating population outcomes during Bd epizootics in this system (Drawert et al. 2015). A natural next step will be to use this IPM to investigate how varying temperature regimes and R. muscosa demography affect the persistence of R. muscosa populations infected with Bd over longer time scales. In general, the question of how temperature interacts with Bd and in turn affects amphibian host persistence is a critical question in amphibian conservation (Rohr & Raffel 2010) and IPMs provide a novel means by which this question can be quantitatively addressed.

In addition to these population-level predictions, host-parasite IPMs also allow for explicit predictions about how the distribution of parasites loads over hosts changes with different vital parameters and/or over the course of an epizootic or enzootic. Macroparasite models have long recognized the importance of the distribution of parasite loads over hosts for determining the dynamics of host-parasite interactions (Anderson & May 1978; Tompkins et al. 2002), and classic macroparasite models addressed this by using a statistical distribution (often negative binomial, Shaw et al. 1998) and then looking at how different levels of parasite aggregation affected host-parasite dynamics (Anderson & May 1978; Kretzschmar & Alder 1993). These approaches have been extended to include fluctuating aggregation (Rosà & Pugliese 2002; Rosà et al. 2003), but still rely on explicitly defining the shape of the host-parasite distribution. In contrast, IPMs do not assume a host-parasite distribution, rather one emerges as a result of the vital functions specified when parameterizing the model. Therefore, one can explore how sensitive the aggregation of the host-parasite distribution is to different vital function parameters, providing an intriguing way to parse the contribution of different processes to parasite aggregation. Moreover, as it is straightforward to include seasonal fluctuations and/or environmental stochasticity into the IPM framework (Rees & Ellner 2009; Eager et al. 2013), more complex predictions of aggregation patterns, such as the fluctuation of parasite aggregation over time (Scott 1987; Rosà & Pugliese 2002), could be explored.

Using the parameterized IPM for Bd-R. muscosa we examined how the distribution of Bd-loads changed with temperature. The IPM showed that fundamental insight from macroparasite distributions also applies to Bd. For example, as predicted by macroparasite models (Barbour & Pugliese 2000), increasing Bd-induced host mortality with increasing temperature decreased the aggregation of Bd across hosts and reduced positive skew as individuals with high Bd loads were removed from the population through mortality. In fact, a sensitivity analysis of the variance to mean ratio of the Bd-load distributions showed that this measure of aggregation became progressively more sensitive to the survival function as temperature increased and more frogs experienced Bd load-dependent mortality (Fig. S6). In addition, the variance to mean ratio was more sensitive to the variance in the growth function (ν_0,1 and c_0,1) than the variance in the initial infection burden function (ν_0,3 and c_0,3, Fig. S6), suggesting that explaining the individual-level heterogeneity in Bd growth rate may be more important for understanding the shape of the Bd-load distribution than explaining the individual-level heterogeneity in the load of Bd at initial infection. The IPM approach highlights the importance of this unexplained variance in the Bd growth function and future studies could identify whether this heterogeneity is due to biological factors such as differences in immune responses among hosts or methodological factors such as quantitative PCR error when measuring Bd load.

In addition to allowing for a more rigorous analysis of parasite aggregation, an IPM approach can be used to examine a variety of different classic patterns in host-parasite systems. For example, host age can easily be included as an additional host attribute (Childs et al. 2003, 2004), such that IPMs could then be used to examine observed patterns between parasite intensity and host age (i.e. age-intensity profiles, Duerr et al. 2003). Similarly, host-heterogeneity in susceptibility could be included as an additional host attribute such that IPMs could be used to explore non-linear dose-response relationships (Dwyer et al. 1997; Gomes et al. 2014). We also discuss in SI 3 how R₀, a canonical epidemiological measure of the ability of a parasite to invade a fully susceptible host population (Diekmann et al. 1990), can be calculated from the host-parasite IPM. While these are just a few examples, the theoretical application of IPMs for exploring observed host-parasite patterns is extensive.

While this study focused on using IPMs to describe epizootic dynamics of amphibian chytrid fungus, there are a variety of other wildlife diseases in which host-parasite IPMs could be applicable to explore the population and evolutionary outcomes of infection. For example, Tasmanian devils Sarcophilus harrisii are threatened with extinction by an infectious cancer, Tasmanian devil facial tumor disease (McCallum et al. 2009). A critical question for management is to predict the impact of the disease as it enters currently uninfected populations and to investigate evidence of selection for increased resistance to infection or reduced tumor growth rates. Intensive mark-recapture data are available, enabling the estimation of survival rates of infected and uninfected animals, together with transition rates from uninfected to infected states (Hamede et al. 2012). In addition, measurements of tumor size are taken from all infected animals at every capture opportunity and repeated tumor measurements are available for a substantial number of individuals, which could be used to estimate the tumor growth function. One could examine whether the death rate of infected devils is related to the size of the tumor, and then use the IPMs to examine how differences in tumor growth among populations or over time might alter the dynamics of devil populations. It is highly likely that the death rate of infected devils is related to the size of the tumor. This problem may therefore be well-suited for an IPM approach, permitting more accurate modeling of the impact of the tumor on devil population dynamics.

Similarly, an IPM approach could also be taken to explore various aspects of the ecology and evolution of bats affected by white-nose syndrome, an emerging fungal disease of North American bats (Blehert et al. 2008). White-nose syndrome is characterized by intense transmission, such that nearly 100% of bats of multiple species may become infected during the first winter after the fungus reaches a site (Langwig et al. 2015b). Mortality, which occurs 70–100 days after initial infection in lab studies (Warnecke et al. 2012), usually occurs in mid to late winter when fungal loads are highest (Langwig et al. 2015a). IPMs could be fit to pathogen loads and population dynamics of bats to explore how temperature and humidity influence pathogen growth and disease impacts (Langwig et al. 2012). Through modification of the growth function and survival function, IPMs could be used to determine whether persistence of some stabilizing populations could be explained by resistance or tolerance, or other factors affecting host-parasite interactions.

In conclusion, the use of IPMs can answer important questions regarding host-pathogen interactions in wildlife and plant disease. Moreover, IPMs can provide new insight into many classic micro and macroparasite patterns such as the distribution of parasites across hosts, age-intensity profiles, and the dynamics of infection prevalence. By bridging the gap between micro and macroparasites, IPMs provide an exciting new frontier in modeling wildlife disease.