Abstract
There is extensive controversy over whether the adult visual cortex is able to reorganize following visual field loss (scotoma) as a result of retinal or cortical lesions. Functional magnetic resonance imaging (fMRI) methods provide a useful tool to study the aggregate receptive field properties and assess the capacity of the human visual cortex to reorganize following injury. However, these methods are prone to biases near the boundaries of the scotoma. Retinotopic changes resembling reorganization have been observed in the early visual cortex of normal subjects when the visual stimulus is masked to simulate retinal or cortical scotomas. It is not known how the receptive fields of higher visual areas, like hV5/MT+, are affected by partial stimulus deprivation. We measured population receptive field (pRF) responses in human area V5/MT+ of 5 healthy participants under full stimulation and compared them with responses obtained from the same area while masking the left superior quadrant of the visual field (“artificial scotoma” or AS). We found that pRF estimations in area hV5/MT+ are nonlinearly affected by the AS. Specifically, pRF centers shift towards the AS, while the pRF amplitude increases and the pRF size decreases near the AS border. The observed pRF changes do not reflect reorganization but reveal important properties of normal visual processing under different test-stimulus conditions.
Keywords: fMRI, hV5/MT+, Reorganization, Artificial scotoma
Introduction
An important question is whether the adult visual cortex is able to reorganize in subjects with visual field defects (scotomas) as a result of retinal or cortical lesions. Studies in subjects suffering from macular degeneration or retinal lesions produced controversial results (Kaas et al., 1990; Heinen and Skavenski, 1991; Chino et al., 1992, 1995; Gilbert and Wiesel, 1992; DeAngelis et al., 1995; Schmid et al., 1996; Murakami et al., 1997; Horton and Hocking, 1998; Calford et al., 1999; Sunness et al., 2004; Baker et al., 2005, 2008; Smirnakis et al., 2005; Giannikopoulos and Eysel, 2006; Masuda et al., 2008; Schumacher et al., 2008; Dilks et al., 2009; Wandell and Smirnakis, 2009; Baseler et al., 2011). Similarly, studies on subjects with lesions of the primary visual cortex or the optic radiation remain inconclusive (Eysel and Schmidt-Kastner, 1991; Eysel and Schweigart, 1999; Eysel et al., 1999; Rumpel et al., 2000; Mittmann and Eysel, 2001; Barmashenko et al., 2003; Zepeda et al., 2003; Dilks et al., 2007; Yan et al., 2012; Imbrosci et al., 2013; Papanikolaou et al., 2014).
Interestingly, changes in the retinotopic maps of the early visual cortex have been observed even in normal subjects after masking the visual stimulus to simulate retinal or cortical scotomas. In particular, when the stimulus was masked to simulate a foveal scotoma, population receptive fields (pRFs) representing the scotoma shifted in locations outside the scotoma border and increased in size (Baseler et al., 2011; Haak et al., 2012a). It was suggested that these pRF changes were due to a combination of the position and size scatter of individual receptive fields within a voxel influenced by modulatory feedback signals from extrastriate visual areas (Haak et al., 2012a). However, a recent study suggests that the observed pRF changes are an artifact of the analysis method and that pRF biases can be eliminated if the masked stimulus is incorporated in the model when estimating the pRF (Binda et al., 2013). It is important to characterize these biases in order to ensure that changes in the retinotopic organization observed in patients are not simply an artifact of model estimation in the context of incomplete stimulus presentation (artificial scotoma).
In addition, presenting a truncated visual stimulus, as is typically done in the artificial scotoma, can have nonlinear effects that can modify receptive field location and size estimates in individual neurons. This is expected to be especially prominent for receptive fields in higher areas, which cover a large portion of the visual field. Area V5/MT+ is of particular interest as it has been shown to be modulated by visual stimuli presented inside the scotoma following lesions of the primary visual cortex (V1) (Bruce et al., 1986; Rodman et al., 1989, 1990; Maunsell et al., 1990; Girard et al., 1992; Barbur et al., 1993; ffytche et al., 1996; Rosa et al., 2000; Schoenfeld et al., 2002; Morland et al., 2004; Bridge et al., 2010; Schmid et al., 2010) and has been associated with the phenomenon of subconscious visual perception, called “blindsight” (Poppel et al., 1973; Weiskrantz et al., 1974). Visual field maps and population receptive field sizes have been recently characterized for the human hV5/MT+ complex in normals (Amano et al., 2009). However, it is not known how these are affected by partial stimulus presentation.
Here we used a new method, which estimates the population receptive field (pRF) topography in the visual cortex with minimal bias (Lee et al., 2013) to measure pRF changes that occur in area hV5/MT+ of five healthy subjects after masking the stimulus in the left upper quadrant of the visual field (“artificial scotoma” or AS). This simulates a homonymous quadrantanopic scotoma that occurs often as result of partial V1 or optic radiation lesions. We compared responses obtained under the AS condition with simulations obtained from a linear AS model (or LAS model). The LAS model simulates the pRFs under the AS condition based on the actual pRFs derived under the full stimulus condition (pRFFF) assuming that the only effect of the AS is that it does not stimulate the corresponding part of the pRF. This provides a prediction of the expected position and shape of the residual pRFs under the AS. In other words, the LAS model provides an estimation of the pRF changes expected to occur as a result of the truncated stimulus assuming that the pRF linearly integrates the AS (pRFLAS). We found pRF changes in hV5/MT+ under the AS condition (pRFAS) that are significantly different than those obtained with the LAS model suggesting that the pRFs are nonlinearly affected by the truncated stimulus presented. In particular, pRFAS centers shift towards the border of the AS, the pRFAS amplitude increases and the pRFAS size decreases near the border of the AS. In addition, we found significant errors in pRF estimation which extend inside the AS when estimating the pRF topography using the full stimulus instead of the masked stimulus. These erroneous estimates are not due simply to a methodological artifact, but are the result a significant BOLD spread that occurs inside the AS during the presentation of the truncated stimulus. It is important to understand the changes that occur in order to be able to separate them from true reorganization. We undertake this task below.
Materials and methods
Subjects
Five healthy subjects (S1–S5, 22–65 years old, 1 female) were recruited. All subjects had normal or corrected-to-normal visual acuity. The experiments were approved by the Ethical Committee of the Medical Faculty of the University of Tuebingen.
Data acquisition and preprocessing
Functional and structural MRI experiments were performed at the Max Planck Institute for Biological Cybernetics, Tuebingen, Germany using a 3.0 Tesla high-speed echo-planar imaging device (Trio, Siemens Ltd., Erlargen, Germany) with a quadrature head coil. At least two T1-weighted anatomical volumes were acquired for each subject with a three-dimensional magnetization prepared rapid acquisition gradient echo (T1 MPRAGE scan) and averaged following alignment to increase signal to noise ratio (matrix size = 256 × 256, voxel size = 1 × 1 × 1 mm3, 176 partitions, flip angle = 9°, repetition time [TR] = 1900 ms, echo time [TE] = 2.26 ms, TI = 900 ms). Blood oxygen level dependent (BOLD) image volumes were acquired using gradient echo sequences of 28 contiguous 3 mm-thick slices covering the entire brain (repetition time [TR] = 2000 ms, echo time [TE] = 40 ms, matrix size = 64 × 64, voxel size = 3 × 3 × 3 mm3, flip angle = 90°).
At least 5 functional scans were acquired for each subject, consisting of 195 image volumes, the first 3 of which were discarded. The functional images were corrected for motion in between and within scans (Nestares and Heeger, 2000). The functional images were aligned to the high-resolution anatomical volume using a mutual information method (Maes et al., 1997) where the resampled time series values in the volume are spatially interpolated relative to the nearest functional voxels. All subsequent analysis was performed in the interpolated data. However, we took care that this does not affect the retinotopic maps obtained and the statistical comparisons that are performed, because the interpolation method we used does not distort the generated time series and the comparisons we made were between different groups of subjects rather than between different numbers of voxels. Preprocessing steps were performed in MATLAB using the mrVista toolbox (http://white.stanford.edu/software/).
Stimuli
Full field stimulus
Subjects were presented with moving square-checkerboard bars (100% contrast) through MRI compatible digital goggles (VisuaStim, Resonance Technology Company, Inc., Northridge, CA, USA; 30° horizontal and 22.5° vertical field of view, 800×600 resolution, min luminance = 0.3 cd/m2 and max luminance = 12.2 cd/m2). The stimulus was presented within a circular aperture with a radius of 11.25° around the fixation point. The bar width was 1.875° and travelled sequentially in 8 different directions, moving by a step half of its size (0.9375°) every image volume acquisition (TR = 2 seconds). Stimuli were generated using Psychtoolbox (Brainard, 1997) and an open toolbox (VISTADISP) in MATLAB (The Mathworks, Inc.). The subjects’ task was to fixate a small dot in the center of the screen (radius: 0.0375°; 2 pixels) and respond to the color change by pressing a button. The color was changing randomly with a frequency of one every 6.25 seconds. An infrared eye tracker was used to record eye movements inside the scanner (iView XTM, SensoMotoric Instruments GmbH) (Fig. S4). For two of the subjects (S4–S5) the eye movements under the full field stimulus presentation were not recorded due to technical problems. However, they performed a challenging detection task at fixation and their performance was always >95% correct.
AS-stimulus
Subjects were asked to participate for a second session during which an isoluminant mask was placed in the left superior quadrant of the visual field, simulating a left upper quadrantanopia (“artificial scotoma” or AS). All other stimulus’ parameters stayed the same. Eye movements were recorded for all subjects under the AS stimulus presentation (Fig. S4B).
Population receptive field topography
We used a recent method developed by Lee and colleagues which estimates the population receptive field (pRF) topography in the visual cortex (Lee et al., 2013). The pRF structure pi at voxel i is represented by a set of weights which predicts the BOLD signal di(t) at voxel i and time t, using the stimulus protocol s(t) and the hemodynamic response function h(t) as . The weight vector p is estimated by solving a linear model based on ridge regression with a bias: where , α is a constant value to account for the bias and λ1 is a free parameter to control the extent to which the least-square function is regularized. The regularization parameter λ1 is selected after cross validation between different scans for each subject.
PRF topography estimates when subjects were scanned under the AS stimulation were derived in two ways. First, we used the actual AS stimulus as stimulus protocol to predict the BOLD signal. In this case, the lack of stimulus forces the topography weights to be ~0 within the AS area. Using the AS stimulus in the model is a good way to represent complete deprivation of input and allows to make more accurate predictions of the pRFs outside of the AS. Second, we examined the effects of using the full field stimulus as stimulus protocol to model pRFs under the AS condition. A summary of the different methodologies used to derive the pRF topography under different stimulation paradigms is presented in Fig. 1.
Fig. 1.
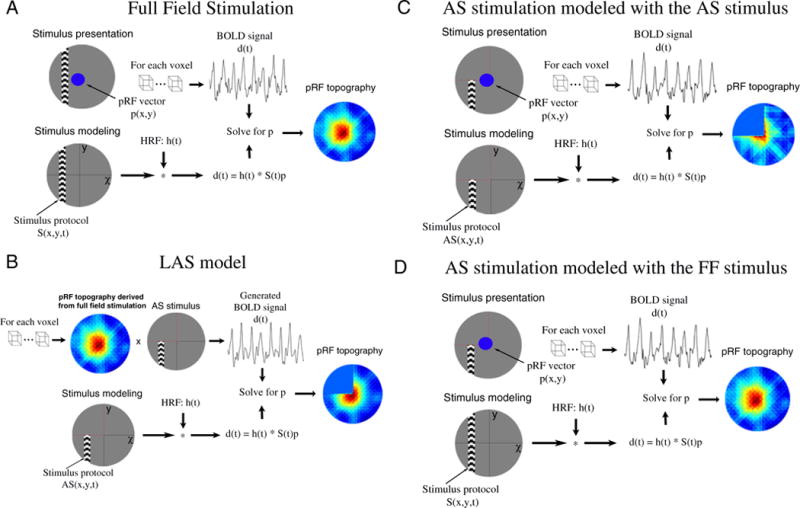
PRF topography derived under different stimulation and modeling conditions. (A) A schematic illustration of the process followed to estimate the pRF topography under full field stimulation (pRFFF). Subjects are presented with moving bars covering the full visual field. The BOLD signal of each voxel is predicted using the full field stimulus protocol and the hrf to derive the pRF topography as described in the methods section. (B) The pRF topography derived under the full field stimulation (A) is convolved with the AS stimulus to generate BOLD time series that simulate the expected BOLD signal under the AS condition assuming that the pRF linearly integrates the AS stimulus. The generated BOLD signal is then used to re-estimated the pRF topography using the AS stimulus protocol in the model (pRFLAS). The border of the AS is indicated by red dashed lines. (C) The process followed to derive the pRF topography under AS stimulation using the AS stimulus in the model (pRFAS). (D) The process followed to derive the pRF topography under AS stimulation using the full field stimulus in the model.
In contrast to direct-fit methods (Dumoulin and Wandell, 2008), the method we use does not assume a priori the pRF shape and thus is useful for studies of reorganization where the actual pRF shape cannot be anticipated. We retained only those voxels in the visual area, for which the topography explained more than 12% of the variance. This threshold was set after measuring the mean explained variance in a non-visually responsive area (6% ± 2%) and setting the value of the threshold at 3 standard deviations above the mean.
LAS model
We compared actual pRF topography estimates derived when the AS is applied to linear expectations arising by the lack of stimulation inside the AS region. To do this, we developed a model that predicts the pRF topography under the AS condition based on the pRF topography estimated under the full stimulus condition (Fig. 1B). Briefly, the pRF topography of each voxel with variance explained above 12%, as estimated under full stimulation, is convolved with the AS stimulus. In this way the part of the pRF overlapping with the AS area is omitted. The product of the convolution is used to re-estimate the topography. The regularization parameter used to estimate the AS-prediction topography was set to be ¾ of the regularization parameter under the full stimulus condition because the stimulus space under the AS is ¾ of the stimulus space under full stimulation (Poppel et al., 1973). Using a regularization parameter same as in the full field stimulus condition did not affect the results presented here.
PRF center, size and amplitude estimates
Because pRFs near the border of the AS may not have a circular shape we could not fit a Gaussian model to get an estimate of the pRF center and size. Instead we used the topography directly to get eccentricity and polar angle values corresponding to the center of the pRF as well as an estimate of the pRF size.
To do so, the pRF topography of each visually responsive voxel is normalized to range between 0 and 1. A lower threshold of 0.4 is applied to the pRF topography in order to keep only the central region of the pRF. This threshold was selected after calculating the average amplitude (0.3 ± 0.1) in non-visually responsive areas (i.e. areas of the far ipsilateral visual field) and setting the value of the threshold at 1 standard deviation above the mean. This was calculated by averaging the pRF topography amplitude in visual field locations with eccentricity greater than 7° in the ipsilateral visual field of V1, where the stimulus can produce no response. If there are more than one disconnected peaks of activity in the topography, then we keep only the one that covers the largest area in the topography. This way small peaks of activity that may be the result of noise are discarded. The thresholded topography is then converted to a binary image by replacing all values above threshold to value 1 and all other pixels with value 0. The pRF center is estimated by finding the center of mass of the binary image (centroid of all pixels with value 1). This gives us the corresponding elevation and azimuth coordinates which can also be translated to the respective eccentricity and polar angle. We also calculated the center of mass of the original image and confirmed that binarizing does not affect the results.
The pRF size is estimated as the area of the topography that lies above the 0.4 threshold. That is the number of pixels with value 1 in the binary image calculated as described above. This gives us an estimate of the area of the visual field that activates the corresponding voxel. Using different thresholds to estimate the pRF does not change the main results presented in this paper.
The pRF amplitude of each voxel is estimated as the peak amplitude of the pRF topography before normalization.
Visual field coverage maps
The visual field coverage maps define the locations within the visual field that evoke a significant response from voxels within a region of interest (ROI) in the cortex. To estimate this we plot at each visual field location the maximum value between all pRF topographies that cover this location (color map). The pRF topography of each voxel is normalized, thresholded and all peaks of noise are discarded as described above. Using different thresholds for the pRF does not change the conclusions presented in the paper (Fig. S1). The pRF centers (estimated from the pRF topography as described above) across all voxels within the ROI are overlaid as grey dots.
Deconvolution of the BOLD signal
A deconvolution method was applied to the BOLD time series of each voxel in order to estimate the actual response of the voxel as the stimulus is presented at each visual field location. To do so, the BOLD time series of each voxel was averaged across scans to reduce the signal to noise ratio. The averaged signal was further smoothed using locally weighted linear regression (lowess method in MATLAB) in order to avoid outliers that can be amplified after deconvolution. Then a Fast Fourier transform deconvolution is applied to extract the hemodynamic response function from the data.
The baseline was calculated for each voxel as the average BOLD signal change over 5 steps of the bar when the horizontal bar was located between 7–10° in the hemifield ipsilateral to our ROI. After deconvolution and removal of the baseline, the BOLD time series is averaged over all voxels in the ROI and plotted as a function of the bar location.
Significance tests
A two-sample Kolmogorov-Smirnov test was performed in order to compare the pRF center location and size distributions between the AS condition and the LAS model. The significance level selected to reject the NULL hypothesis (same distributions) was estimated by comparing the distribution of each subject with the average distribution for each condition. The minimum p-value of these comparisons was then used to test for significance between the mean distribution of the AS condition and the LAS model. We note that this is a conservative choice, and may suppress the identification of small differences.
Direct-fit pRF method
To compare with prior literature, we also derived pRF estimates using a direct-fit pRF method (Dumoulin and Wandell, 2008). In this case, the implementation of the pRF model is a circularly symmetric Gaussian receptive field in visual space, whose center and radius are estimated by fitting the BOLD signal responses to estimated responses elicited by convolving the model with the moving bar stimuli. We estimated visual field coverage maps by plotting the pRF centers across all voxels within each area (grey dots, Fig. 8a) and the relative pRF size by fitting a 2D Gaussian with peak amplitude normalized to one. The color map is estimated by plotting at each visual field location the maximum normalized pRF amplitude between all Gaussian shaped pRFs that cover this location.
Fig. 8.
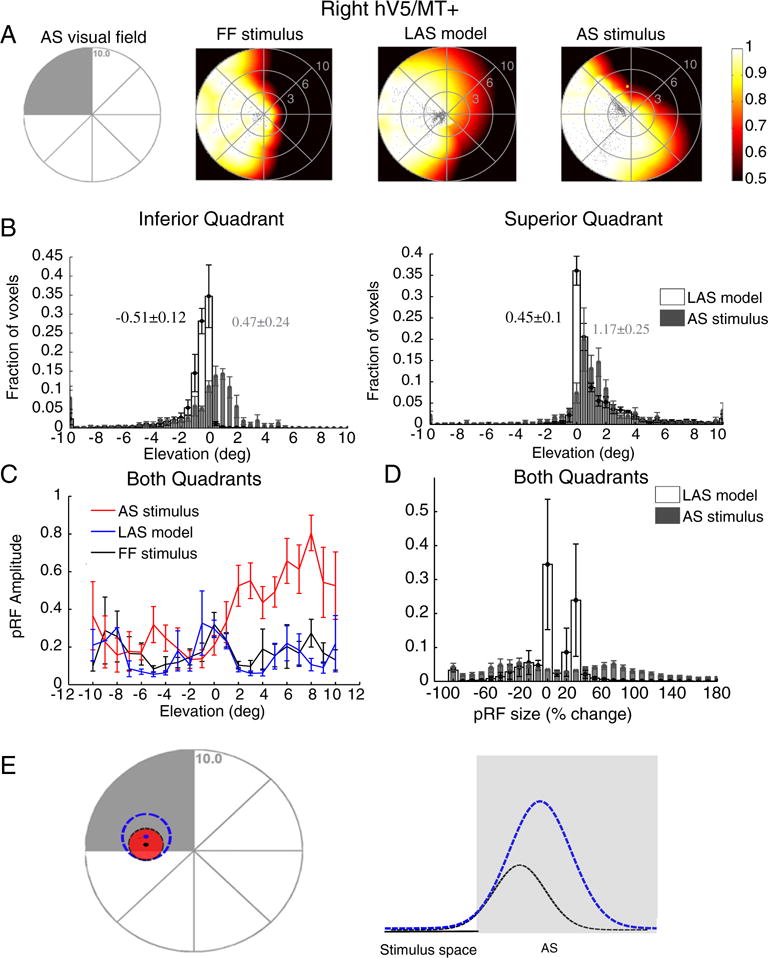
PRF changes in contralateral hV5/MT+ under the AS condition using a direct-fit method. (A) Visual field coverage maps of area hV5/MT+ contralateral to the AS (right hemisphere) for a subject under the full field (FF) stimulus condition (2nd column), under the LAS model (3rd column) and under the AS condition (4th column). On the left, a sketch of the visual field indicates the location of the AS (shaded gray area). The visual field coverage maps extend significantly within the area of the AS at the upper left quadrant of the visual field both under the LAS model and under the AS condition. (B) Average pRF center elevation distribution from voxels in right hV5/MT+ of 5 subjects under the AS condition (gray bars) and under the LAS model (white bars). As in Fig. 4A, the voxels are divided into two groups according to their pRF center location as estimated from the full field stimulus condition, one for pRFs in the inferior quadrant (left panel) and the other for pRFs at the superior quadrant (right panel). The mean and standard error of the mean of each distribution is indicated on top of the graphs with gray color for the AS stimulus and black color for the LAS model. The pRF center elevation distributions are significantly shifted within the AS under the AS condition for both voxels in the inferior (left) and superior quadrants (right) compared with the distributions of the LAS model. (C) Average pRF amplitude of the pRFs in right hV5/MT+ of 5 subjects under the full stimulus condition (black), under the LAS model (blue) and under the AS condition (red) as a function of pRF elevation. The pRF amplitude is larger under the AS condition for pRFs located in the superior quadrant (elevation >0). (d) Average percent change of the pRF size (as described in Fig. 4B) for 5 subjects under the LAS model (white bars) and the AS stimulus condition (gray bars) plotted for all voxels in right hV5/MT+. For all graphs, the error bars indicate the standard error of the mean across subjects (N = 5). (E) Schematic illustration of a pRF located at the edge of the AS. The light gray represents the area of the AS. The red circle represents the true pRF. The black and the blue dashed lines represent different model fits. The black and blue dots denote the corresponding pRF centers. The direct-fit model extrapolates estimates of the pRF that fall outside the stimulus space (inside the AS) by applying a Gaussian fit to the tail of the pRF that lies inside the stimulus space. This approach however may potentially result in erroneous model fits. For example, see the black versus the blue curves in the right panel, which both fit the part of the stimulus space outside the AS very well, but result in markedly different pRFs. These methods are therefore prone to errors in capturing the actual pRF shape near stimulus presentation borders (such as the border of the AS) (Lee et al., 2013), potentially resulting, for example, in an enlarged and mislocalized pRF (blue dashed line).
Results
pRF changes in the hemisphere contralateral to the artificial scotoma
We measured pRF responses in right area hV5/MT+ of 5 subjects under full stimulation and after masking the left superior quadrant of the visual field (“artificial scotoma” or AS), thereby simulating a left upper quadrantanopia (methods).
Changes in the size and phase maps of activated area hV5/MT+
We measured visual responsiveness in area hV5/MT+ by the number of voxels whose pRF topography explains above 12% of the variance in the BOLD data. This threshold was set after calculating the mean explained variance in regions of interest that correspond to non-visually responsive voxels (6%, standard deviation 2%) and setting it at 3 standard deviations above the mean. Using this criterion, we found that only ~12% of voxels become unresponsive when the AS is applied. The mean size of area hV5/MT+ under the full stimulus condition is 1379 ± 156 mm2 (mean ± standard error of the mean, N = 5 subjects) and decreases slightly under the AS condition to 1202 ± 144 mm2. This is in contrast to area V1, whose visually responsive area is reduced by approximately 36% in the presence of the AS (2250 ± 356 mm2 under the full stimulus condition versus 1420 ± 88 mm2 under the AS condition). Since voxels in area hV5/MT+ have considerably larger pRF size than voxels in area V1 (Smith et al., 2001), more hV5/MT+ voxels can be activated by parts of the stimulus that fall outside the AS area, partially explaining this disparity. A signature of this is a shift of hV5/MT+ voxel pRF centers to reflect locations outside the AS. Accordingly, the angular map shows that a relatively small number of voxels (16%) with centers inside the superior visual field quadrant (e.g. inside the AS) become unresponsive after the AS stimulus is applied (Fig. 3A.b; magenta). The remaining voxels (84%) shift their pRF centers towards the blue color that corresponds to the lower visual field quadrant (Fig. 3A.b). PRF location shifts outside of the AS are expected if we assume we are mapping the residual part of the pRFs that falls outside of the AS.
Fig. 3.
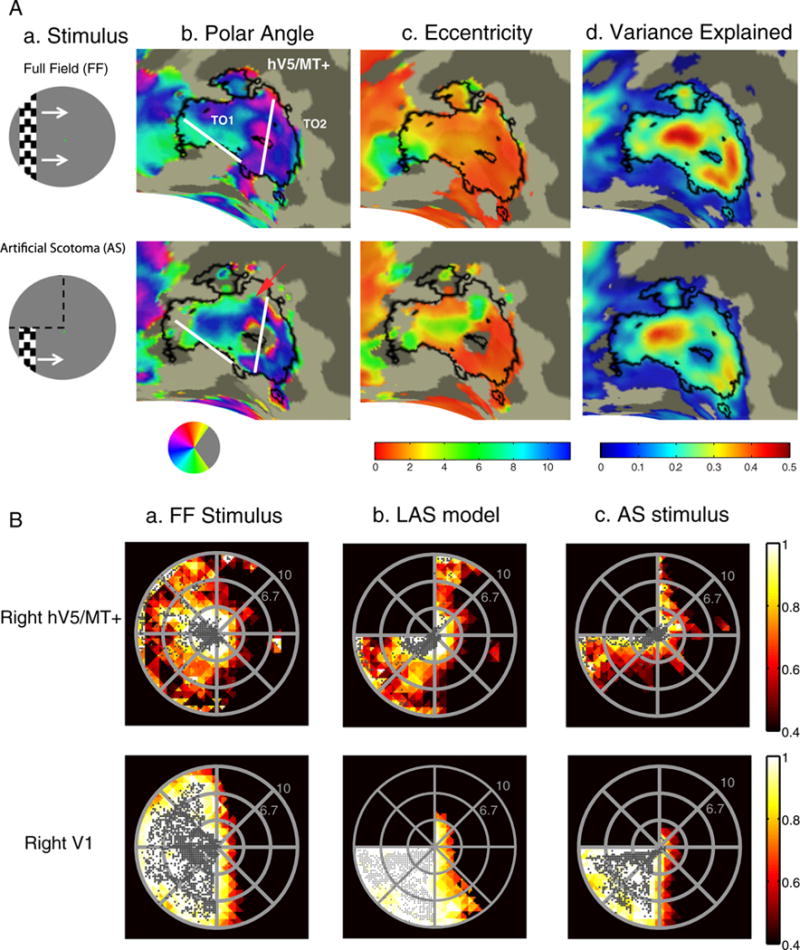
Retinotopy and visual field coverage maps of area hV5/MT+. (A.a) A snapshot of the stimulus for the vertical bar excursion under the full field (FF) stimulation (top) and when and artificial scotoma (AS) is placed on the upper left quadrant (bottom). White arrows (top) indicate the bar direction of motion and black dotted lines (bottom) the location of the AS. (A.b–d) Polar angle (b), eccentricity (c) and variance explained (d) maps overlaid on the inflated right occipito-temporal region of a subject under the full stimulus condition (top) versus the AS condition (bottom). Angular and eccentricity color maps indicate the visual field angle and eccentricity of the center of the pRF topography respectively, at each cortical location. Significantly activated voxels (explained variance >12%) of area hV5/MT+ under the full stimulus condition are selected and overlaid on the maps as a black-bordered ROI. Areas TO1 and TO2 could be identified as described in (Amano et al., 2009) and are shown here on the angular maps. We use the whole area hV5/MT+ for the subsequent analysis. A small part of area hV5/MT+ with voxels devoted to the superior visual field quadrant (magenta color on the angular map; A.b top) become unresponsive under the AS stimulation condition (A.b bottom). A larger fraction of pRFs with blue/cyan color, corresponding to the lower visual field quadrant, are observed on the angular map under the AS condition compared to the full stimulus condition (red arrow). This suggests that, as expected, under the AS condition some pRFs shift their locations to the lower quadrant where stimulus is present. (B) Top: Visual field (VF) coverage maps of area hV5/MT+ (top) from a subject (S1) under the full stimulus condition (a) under the LAS model (b) and under the actual AS condition (c). The color map indicates the maximum pRF amplitude of the topography (after appropriately thresholding and normalizing, see methods) at each visual field location of all the pRFs that cover this location. The pRF centers across all voxels within the area of interest are overlaid as gray dots. The visual field coverage of right hV5/MT+ under the full stimulus condition (top left) largely covers the contralateral hemifield. The visual field coverage of hV5/MT+ under the AS stimulus condition (c) shows a clustering of pRF centers near the border of the AS. Note that it differs from the coverage expected based on the LAS model (b) or the visual field coverage of V1 (c bottom). This suggests that the truncated stimulus has a nonlinear effect in modulating the response of hV5/MT+ voxels, leading to pRF profiles that concentrate near the AS border. Visual field coverage maps of the remaining subjects are shown in Fig. S2. Bottom: the visual field coverage of area V1 under the full stimulus condition (a) under the LAS model (b) and under the AS condition (c) is shown for comparison. We found no significant difference between the pRFs derived under the AS stimulus condition and after applying the LAS model in area V1 (Fig. S3a). Nonlinear effects of the truncated stimulus are less prominent (not seen) here, likely because of the smaller V1 receptive field size.
To differentiate between pRF changes that are expected as a result of stimulating only a part of the receptive field versus unexpected pRF changes under the AS condition, we compared pRF responses obtained under the AS condition with estimates obtained from a model which simulates the pRF topography expected under the AS condition based on the actual pRF topography derived under the full stimulus condition. To do so, the topography of each voxel in hV5/MT+ as estimated under the full stimulus condition is convolved with the AS stimulus. This way, the part of the pRFFF which overlaps with the AS is omitted and does not contribute in the estimation. The output of the convolution is then used as data set to re-estimate the pRF topography (Fig. 1B). The new topography estimate is derived by using the AS stimulus in the model. This results in a prediction of the expected position and shape of the residual pRFs under the assumption that the only effect of the AS is that it does not stimulate the corresponding part of the pRF topography (as derived by the full field stimulus). This pRF estimate is referred to as the Linear Artificial Scotoma model or “LAS” (Fig. 1B; see methods), and is denoted pRFLAS. We used the AS stimulus paradigm to estimate the pRF topography for both data derived from the LAS model (Fig. 1B; pRFLAS) and from the actual AS stimulation condition (Fig. 1C; pRFAS). We reasoned that using the AS stimulus in the model is a good way to represent complete deprivation of input as in the normal subjects with AS stimulus we use here or patients with retinal lesions. The effects of using the full-field stimulus in the model are presented in a later section.
As expected, the LAS model properly captures the residual part of a pRFFF which lies outside the AS (Fig. 2B). The part of the pRF which overlaps with the AS is omitted resulting in a decrease of the pRFLAS size and a shift of the pRFLAS center away from the AS (red dashed circle; Fig. 2B bottom). We would expect to see the same pRF changes under the AS condition assuming that the pRF linearly integrates the AS. However, pRFs estimated under the AS condition (pRFAS) appear to be smaller in size and shift closer to the border of the AS (light purple dashed circle; Fig. 2C bottom) compared with the predictions of the LAS model (pRFLAS), suggesting that the truncated stimulus exerts a nonlinear effect.
Fig. 2.
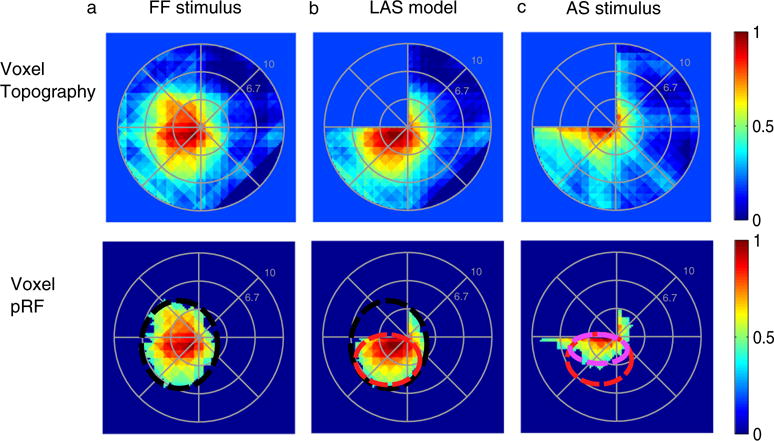
pRF topographies of a voxel in right hV5/MT+ partly covered by the AS. Top row: (A) pRF topography of one voxel in hV5/MT+ under the full field stimulus condition (pRFFF). The pRF covers locations both in the left upper and lower quadrants. (B) pRF topography of the same voxel under the LAS model (pRFLAS). In brief, from the topography of the full field stimulus pRFFF, the part of the pRF falling within the AS area is omitted by convolving the pRFFF with the AS stimulus. The result of the convolution is then used to re-estimate the topography using the AS stimulus at this case, deriving the pRFLAS. In this case only of the part of the pRF which falls outside of the AS area is mapped. This gives us an estimate of the expected pRF topography under the AS condition, assuming linearity. (C) pRF topography of the same voxel under the AS condition (pRFAS). The pRFAS looks different than it would be expected based on the LAS model (pRFLAS). The pRFAS topography seems to have shifted towards the AS-border. Bottom row: The pRF topographies of the same voxel are presented under the different stimulation conditions after thresholding at 0.4 of the maximum value. By thresholding we derive only the central area of the pRF, useful for estimating the pRF center location and pRF size. The black, red, and light purple circles indicate the visual field area covered by the pRF under the full field stimulus condition, under the LAS model and under the AS condition respectively. These do not represent model fits but they are manually drawn for illustration purposes.
Topography and coverage maps
We examined how all pRFs in hV5/MT+ cover the visual field under the different stimulation conditions by plotting the visual field coverage maps from all hV5/MT+ voxels (Amano et al., 2009). These maps are estimated by deriving appropriately normalized pRFs from the topography of each voxel (Fig. S1B) and plotting the maximum pRF amplitude at each visual field location of all the pRFs that cover this location (methods). No activity is predicted in the upper visual field quadrant where the AS is placed for both the LAS model and the AS stimulation condition, since the lack of stimulus forces the topography weights to be ~0 in that area (Fig. 3B.b,c top). Area hV5/MT+ under the LAS model covers the lower visual field quadrant as expected (Fig. 3B.b). The visual field coverage of hV5/MT+ under the AS-stimulus condition, however, shows a clustering of pRF centers near the border of the AS (Fig. 3B.c). This results from the fact that pRF centers under the AS condition appear to be smaller in size and shift closer to the border of the AS as shown by the topography of individual voxels (Fig. 2 and Fig. S1A–B). In addition, visual field locations in the inferior quadrant, away of the AS border, appear to be less well covered by the contralateral hV5/MT+ (Fig. 3B.c top, Fig. S1.C–D) relative to the prediction of the LAS model (Fig. 3B.b top, Fig. S1.C–D) as a result of the pRF location shift and the reduction in the pRF size. This also contrasts with the complete visual field coverage of the inferior quadrant seen in the contralateral area V1 (Fig. 3B.c_bottom) suggesting that the observed effect is the result of post-V1 processing. The shift in pRF center location under the AS condition is mainly observed for pRFs in hV5/MT+ that are partly covered by the AS and suggests a nonlinear effect of the truncated stimulus in modulating the pRF of these voxels. PRFs in area V1 are generally smaller than pRFs in area hV5/MT+ and thus less affected by the truncated stimulus.
PRF center location and size shifts
To summarize the findings for all subjects we compared the distribution of pRFAS center elevation (distance from the horizontal meridian) for subjects under the AS condition with the expected pRFLAS center elevation distribution based on the LAS model, in the hV5/MT+ contralateral to AS hemisphere. As expected pRF centers that belong to the superior visual field quadrant (elevation >0) under full stimulation, shift their location towards the lower visual field quadrant both in the case of the AS condition and the LAS model (elevation >0, Fig. 4A right). This shift, however, is significantly different for the AS condition with pRFAS centers clustering near the AS border (elevation = 0, gray bars) compared to the expected distribution based on the LAS model (white bars, Fig. 4A right; p = 10−87 < 10−51, Kolmogorov-Smirnov test, significance is reported as p = a < b, where b is the value selected to reject the NULL hypothesis; see methods). PRF centers that belong in the inferior visual field quadrant (elevation <0) under full stimulation also shift their location towards the AS-border when the AS is applied (Fig. 4A left). Note the greater clustering of pRFAS centers near the AS-border (elevation = 0) for the AS condition (gray bars, Fig. 4A left) compared to the LAS model (white bars). The distributions are significantly different (p ≈ 0 < 10−27). For both quadrants, the differences were significant not only for the aggregate distributions but also for each individual subject (Table S1). Note that there is no significant difference in the pRF center elevation distribution of the inferior quadrant between the pRFs derived under the full bar stimulation and after applying the LAS model (Fig. S3b, p = 10−19 > 10−32) suggesting that the observed differences under the AS condition are not the result of a methodological error.
Fig. 4.
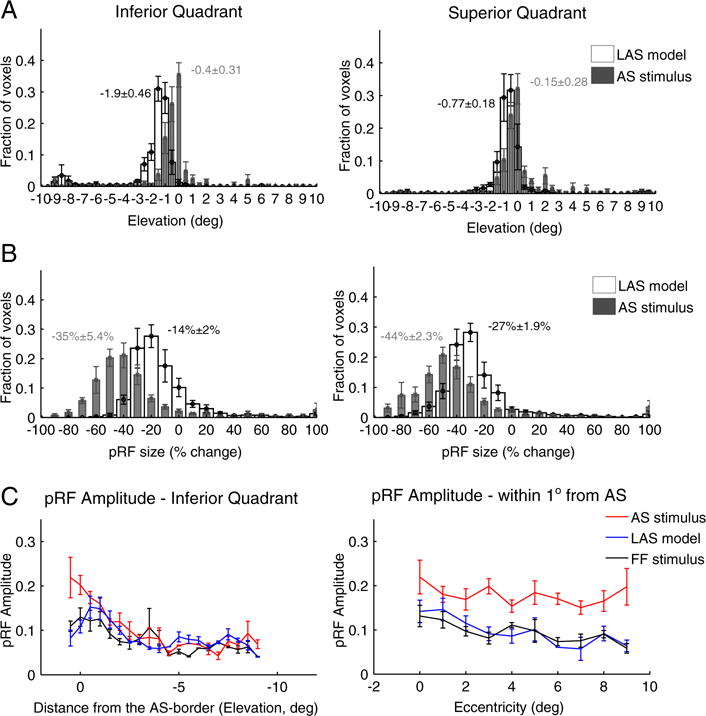
PRF location, size and amplitude changes in contralateral hV5/MT+ under the AS stimulus condition. (A) Average distributions of the pRF center elevation from voxels in hV5/MT+ of 5 subjects under the AS condition (gray bars) and under the LAS model (white bars). The voxels are divided into two groups according to their pRF center location as estimated from the full field stimulus condition, one for pRFs in the inferior quadrant (left) and one for pRFs at the superior quadrant (right). PRFs originally located in the left superior quadrant (where the AS is applied; see right panel) shift towards the lower quadrant (negative values) in both the LAS model and the AS stimulus condition. The shift observed for the pRF centers under the AS condition however is smaller than expected based on the LAS model and seems to cluster more near the AS-border (elevation = 0). PRFs with centers in the inferior quadrant also shift their location towards the AS-border in the presence of the AS, in contrast to the LAS model (left panel). The mean distributions are significantly different for pRFs both in the superior (p = 10−50 < 10−44) and inferior (p = 0 < 10−31) quadrants. The mean and standard error of the mean of each distribution is indicated on top of the graphs with gray color for the AS stimulus and black color for the LAS model. (B) Average distributions of the percent change in pRF size for the LAS model (white bars) versus the AS stimulus condition (gray bars). The change in pRF size is calculated as the difference between the pRF size under the AS condition (or under the LAS model) and the pRF size of the same voxels under the full stimulus condition, normalized by the pRF size under the full stimulus condition (see methods). When the AS is applied we have a significantly larger decrease in pRF size than expected based on the LAS model. This is true for voxels with pRF centers in either the superior (AS; right panel) or inferior (left panel) quadrants. (C) Left: Average pRF topography amplitude in the right (contralateral to the scotoma) hV5/MT+ of 5 subjects under the full stimulus (FF) condition (black), the LAS model (blue) and the AS condition (red) as a function of distance from the AS-border (pRF elevation, left panel). The pRF amplitude is larger within one degree from the AS-border when the AS is applied compared with the LAS model and the full stimulus condition. Right: Average pRF topography amplitude of voxels in the right hV5/MT+ with pRF centers located within 1 degree from the AS-border (−1–0° elevation), as a function of eccentricity. The pRF amplitude is larger across the whole range of eccentricities in the AS-condition (red) compared with the LAS model (blue) and the full stimulus condition (black). For all graphs, the error bars indicate the standard error of the mean across subjects (N = 5).
In addition, we observed a large decrease in pRF size in the presence of the AS. PRFs in the superior quadrant had a mean pRF size decrease of 44 ± 2.3% (mean ± standard error of the mean, N = 5 subjects), significantly larger than the expected pRF size decrease based on the LAS model (27 ± 1.9%, Fig. 4B right; p = 10−4, two sample t-test). PRFs in the inferior quadrant also had a decrease in pRF size of 35 ± 5.4% significantly larger than the smaller decrease expected from the LAS model (14 ± 2%, Fig. 4B left; p = 10−3, two sample t-test). A significant difference was observed between the mean of the pRF size distribution under the AS condition versus the LAS model, both for pRFs in the superior (p = 10−135 b 10−8, Kolmogorov-Smirnov test) and inferior (p ≈ 0 b 10−32) quadrants (Fig. S3c).
The change in location and size of the pRFs under the AS condition was also associated with an increase of pRF amplitude near the AS-border. We measured the peak amplitude of the pRF topography as a function of distance from the AS-border averaged over all 5 subjects. We found that the pRF amplitude is significantly increased under the AS condition near the AS-border and within 1° from it compared with both the LAS model and the full stimulus condition (p = 10−3 < 10−2 at 1° elevation while p = 0.32 > 10−2 at 3° elevation, two sample t-test; Fig. 4C left). The increase occurs across the whole range of eccentricities for the pRFs that are within 1° from AS-border (Fig. 4C right).
The differences between the LAS model and the AS condition cannot be explained by eye movements. Subjects were able to maintain fixation within 1.5° radius from the center of fixation for scans both under the full field stimulus condition and under the AS stimulus condition except for very occasional excursions beyond this range (Fig. 5A). The results remain unchanged after removing from the analysis the epochs where the subjects had eye deviations (>1.5°) from the fixation point. In addition, a pRF shift towards a specific direction in the visual field (AS border), would require systematic eye movements towards the opposite direction. However, the distributions of eye position with respect to the azimuth and elevation of the visual field are similar for both sessions under the full stimulus condition (LAS model) and under the AS condition (Fig. 5B) suggesting that even small deviations from the fixation point cannot explain the observed findings (Kolmogorov-Smirnov test, p = 0.55 for the azimuth distributions and p = 0.77 for the elevation distributions).
Fig. 5.
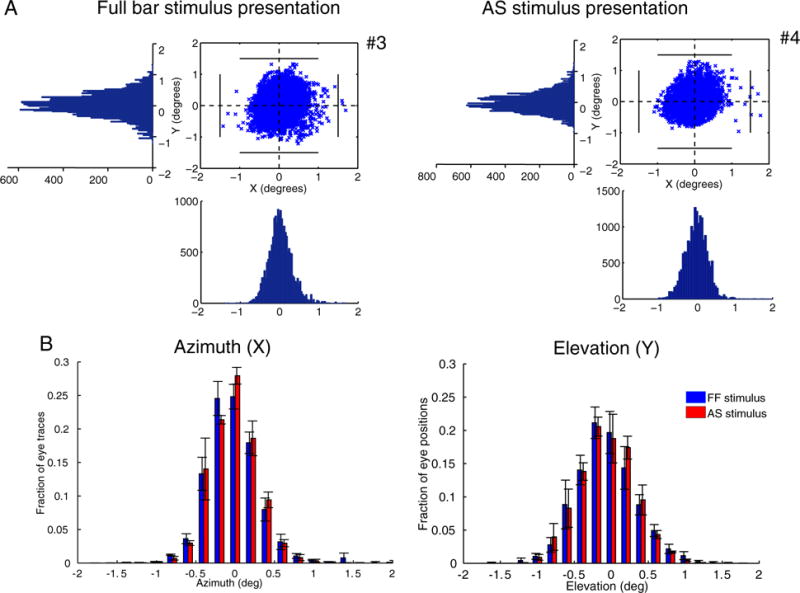
Eye positions for different stimulus presentations. (A) Eye movements of one control subject (S1) under the full field stimulus presentation (left) and under the AS stimulus presentation (right). Eye positions plotted at 60Hz for one whole session (6.4 min). The number of eye deviations, defined as excursions >1.5° from the fixation point is indicated next to the graphs with the number sign (#). The eye movements for all subjects are shown in Fig. S4. (B) Average fraction of eye traces with respect to the azimuth (left) and elevation (right) for the full field stimulus presentation (blue bars) and the AS stimulus presentation (red bars) for 3/5 control subjects. Two of the subjects (S4 and S5) were excluded as their eye movements under the full field stimulus presentation were not recorded. However, their eye movements were recorded under the AS assuring that the subjects were able to maintain fixation (Fig. S4B). The error bars indicate the standard error of the mean across subjects (N = 3). The distributions are not significantly different between conditions (p = 0.55 for the azimuth distributions and p = 0.77 for the elevation distributions) suggesting that the pRF changes seen in Fig. 4 are not the result of eye movements.
In summary, we observed a shift of the pRF centers towards the AS-border when the stimulus is excluded from the upper left quadrant of the visual field (AS-condition). The shift was associated with a relative increase in pRF amplitude near the AS-border and a decrease in pRF size. This suggests that using a truncated stimulus can reveal nonlinear aspects of receptive field summation that could be mistaken for reorganization in the appropriate context.
pRF changes in the hemisphere ipsilateral to the artificial scotoma
Visual deprivation of one quadrant in the visual field may potentially induce changes in the location, shape and amplitude of pRFs in the ipsilateral hV5/MT+ that have ipsilateral or bilateral responses. We found that 12 ± 7% (mean ± standard error of the mean, N = 5) of voxels become unresponsive in the ipsilateral (left) hemisphere under the AS condition (stimulus exclusion from the left upper visual field quadrant). The mean size of area hV5/MT+ in the left hemisphere was found to be 1360 ± 236 mm2 (mean ± standard error of the mean, N = 5 subjects), falling to 1151 ± 159 mm2 under the AS condition. As expected, the visual field coverage maps of area hV5/MT+ of the left hemisphere, both under full field stimulation or under the LAS model, span the contralateral hemifield (Fig. 6A). Surprisingly, the visual field coverage under the AS condition showed a displacement of the pRF centers towards the superior quadrant (dots in Fig. 6A right). The displacement occurred mainly for pRF centers originally located in the inferior quadrant (Fig. 6B left). The average distribution of pRF center elevation shows a significant shift of the pRF centers towards the superior quadrant (elevation N 0) under the AS condition (Fig. 6B; p ≈ 0 < 10−20). The effect was also significant for each individual subject (Table S1). No significant shift was observed for the average elevation distribution of pRFs originally located in the superior quadrant (Fig. 6B right; p = 10−20 > 10−21). However, there was a significant shift in the pRF center azimuth (distance from the vertical meridian) distributions towards the vertical meridian (azimuth = 0) for both the inferior (p = 10−244 < 10−56) and superior quadrants (p = 10−199 < 10−32; Fig. 6C) suggesting that the pRF centers of both the superior and inferior quadrants in ipsilateral hV5/MT+ shift their location towards the vertical border of the scotoma.
Fig. 6.
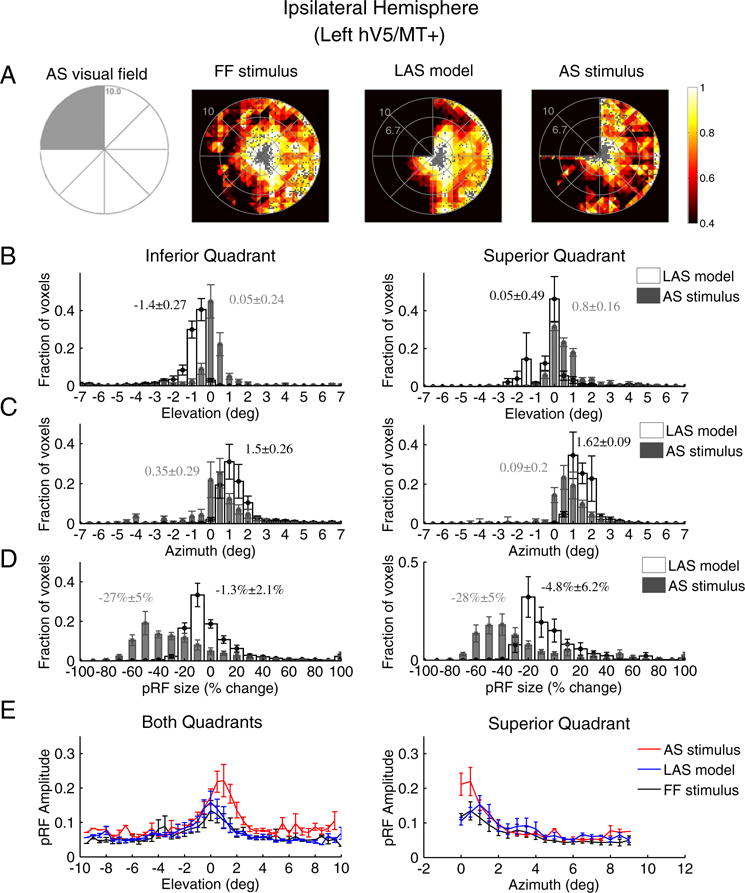
PRF location, size and amplitude changes in ipsilateral hV5/MT+ under the AS condition. (A) Visual field coverage maps of area hV5/MT+ ipsilateral to the AS (left hemisphere) for a subject under the full field (FF) stimulus condition (2nd column), under the LAS model (3rd column) and under the AS condition (4th column). On the left, a sketch of the visual field indicates the location of the AS (shaded gray area). The visual field coverage maps under full field stimulation or under the LAS model, span the contralateral hemifield. The visual field coverage under the AS condition on the other hand shows a relative displacement of the pRFs towards the superior quadrant, which is the quadrant opposite from the AS. (B) Average pRF center elevation distribution from voxels in ipsilateral hV5/MT+ of 5 subjects under the AS condition (gray bars) and under the LAS model (white bars). As in Fig. 4A, the voxels are divided into two groups according to their pRF center location as estimated from the full field stimulus condition, one for pRFs in the inferior quadrant (left panel) and the other for pRFs at the superior quadrant (right panel). The mean and standard error of the mean of each distribution is indicated on top of the graphs with gray color for the AS stimulus and black color for the LAS model. The pRF center elevation distribution does not change significantly in the presence of the AS for voxels in the superior quadrant (right). PRFs of the inferior quadrant, however, shift their location towards the superior quadrant in the case of the AS condition (gray bars, left) compared with the distribution of the LAS model. (C) Same as in b for the pRF center azimuth. The pRF center azimuth distributions significantly shift towards the vertical meridian under the AS condition for both the inferior and superior quadrants. (D) Average percent change of the pRF size (as described in Fig. 4B) for 5 subjects under the LAS model (white bars) and the AS stimulus condition (gray bars) separately plotted for voxels located in the inferior quadrant (left panel) and the superior quadrant (right panel). The pRF size of left (ipsilateral) hV5/MT+ under the AS condition is decreased more than expected based on the LAS model (white bars). (E) Left: average pRF amplitude of the pRF topographies in left hV5/MT+ of 5 subjects under the full stimulus condition (black), under the LAS-prediction condition (blue) and under the AS condition (red) as a function of pRF elevation. The pRF amplitude is larger under the AS condition for pRFs located in the superior quadrant (elevation >0). Right, average pRF amplitude of voxels in left hV5/MT+ with pRF center locations in the superior quadrant as a function of pRF azimuth. The pRF amplitude is larger within 1° from the vertical border of the AS (azimuth = 0) in the AS stimulus case (red) compared with the LAS-prediction (blue) and the full stimulus condition (black). For all graphs, the error bars indicate the standard error of the mean across subjects (N = 5).
There was a significant decrease in pRFAS size of ~28% in both quadrants (28 ± 5% for the superior quadrant and 27 ± 5% for the inferior quadrant, p = 10−5, two sample t-test; Fig. 6D) compared to the relatively small decrease expected from the LAS model (4.8 ± 6% for the superior quadrant and 1.3 ± 2% for the inferior quadrant).
Furthermore, we observed a significantly increased pRF amplitude under the AS condition for pRFs in the superior quadrant (p = 10−3 < 10−2 at 1° elevation, two sample t-test; Fig. 6E left). PRFs under the AS scotoma in the inferior quadrant had a pRF amplitude similar to the full stimulus condition (p = 0.3 > 10−2 at −2° elevation; Fig. 6E left). The increase in the superior quadrant occurred mainly for pRFs near the vertical meridian which is the vertical border of the AS and within 1° from AS (Fig. 6E right) similar to the increase observed in the horizontal border of the AS in the contralateral hV5/MT+ (Fig. 4C left). The mean amplitude of AS pRFs at 1° azimuth was significantly larger compared with the full field stimulus pRFs (p = 10−3 < 10−2; Fig. 6E right). PRFs away from the AS vertical border did not have a significant increase in the pRF amplitude (p = 0.48 > 10−2 at −4° azimuth; Fig. 6E right). This suggests that pRFs in ipsilateral hV5/MT+ are also subject to nonlinear influences from the truncated stimulus even though it is presented in the ipsilateral hemifield.
In summary, the results so far demonstrate a displacement of pRF center location of voxels in area hV5/MT+ when an AS is used in the upper left quadrant of the visual field. The observed displacement is towards the AS border compared to LAS model prediction, suggesting that significant nonlinearities influence the pRF estimation when using the truncated stimulus. A further signature of these nonlinearities is an increase in pRF amplitude observed near the horizontal border of the AS (Fig. 4C left). PRF center shifts are not restricted to the hemisphere contralateral to the AS, but are also observed in the hemisphere ipsilateral to the AS. In this case, pRFs shift towards the quadrant contralateral to the AS (right superior quadrant), and the pRF amplitude increases particularly near the vertical meridian (vertical border of the AS). The more striking finding is a significant decrease in average pRF size observed in area hV5/MT+ of both hemispheres. Notably pRF size under the AS condition is significantly smaller than the pRF size expected from the LAS model, further supporting the influence of nonlinear interactions in pRF estimation when using the truncated stimulus.
Biases in pRF estimation depend on the stimulus condition used for modeling
For all aforementioned results, our method uses the AS stimulus to estimate the pRF topography under the AS condition (Fig. 1C). As a result, pRF weights outside the stimulus space, i.e. inside the AS area, cannot be estimated. This is appropriate for studies of normal subjects with AS stimuli like here as well as in studies of patients with dense retinal lesions since the input never reaches the brain. However, a question in studies of patients with visual cortical lesions is whether activity arises from the interior of the visual field scotoma. Typically, retinotopic mapping in patients is performed using a full stimulus (bar, wedge or ring), which overlaps the area of the scotoma (Dilks et al., 2007; Baseler et al., 2011; Papanikolaou et al., 2014). In this case, modeling both sets of responses using the full stimulus condition might be more appropriate for comparing patients and AS subjects. Thus we also examined whether pRF biases occur in subjects stimulated with the AS stimulus when their pRF topographies are modeled using the full stimulus (Fig. 1D).
As expected, we found no pRF centers within the AS area when we used the full stimulus to estimate the pRFs from the data generated by the LAS model (Fig. 7A, left). However, the visual field coverage maps of the right hV5/MT+ under the AS condition cover most of the area of the AS itself (Fig. 7A, right). PRFs lie well within the area of the AS, well beyond the eye movements’ range (Fig. 5). In patients, such pRFs could be erroneously interpreted as arising from stimuli presented in the interior of the scotoma. However, in the case of normal subjects stimulated with the AS stimulus there is in fact no stimulus presented inside the AS, and thus the observed pRF topographies are the result of an artifact, in the sense that they do not represent the weights by which the voxel would integrate a stimulus that falls in the AS. Our method fits well the fMRI BOLD signal (Fig. 7B) suggesting they do not simply represent a mistake in fitting. To understand how this signal arises, we computed the average neural responses (estimated by the deconvolved BOLD signal change) of all significantly activated voxels in hV5/MT+ separately for different bar directions of motion (see Fig. 7C, methods). The BOLD signal response of each voxel was calculated as a difference from the baseline, defined as the signal elicited when the vertical bar is in the furthest part of the visual field contralateral to the scotoma (ipsilateral to the hV5/MT+ considered). This location is expected to produce little if any activity to area hV5/MT+ contralateral to the scotoma. This procedure sets the baseline of each voxel to zero.
Fig. 7.
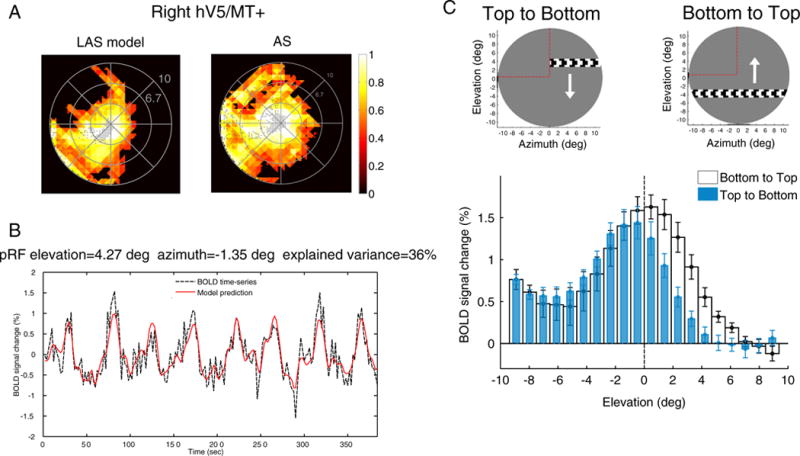
PRF biases under the AS condition. (A) Visual field coverage of the right hV5/MT+ in one subject under the LAS model (left) and under the AS condition (right) assuming the full bar stimulus for modeling the pRFs (Fig. 1D). The map covers significantly the area of the AS at the upper left quadrant of the visual field under the AS condition in contrast to the LAS model. (B) The BOLD time series of a voxel with pRF center located well within the area of the AS (elevation = 4.27°, azimuth = −1.35°). The model predicts 36% of the variance in the data suggesting that the pRF prediction is not a fitting artifact. (C) The average BOLD signal change from all voxels in the right hV5/MT+ as a horizontal bar is moving from the top (elevation >0; AS) to the bottom of the visual field (elevation <0; seeing quadrant; blue bars) and vice versa (white bars). On top, a snapshot of the orientation of the bar, the direction of motion (white arrow) and the AS location (marked with red dashed lines, for illustration purposes). Before averaging, the BOLD time series of each voxel is deconvolved to adjust for the hemodynamic response function and the baseline is subtracted. The baseline is defined as the signal value when the vertical bar is located in the far ipsilesional part of the visual field, which should produce little or no visual modulation in the region examined (see methods). This procedure sets the baseline of each voxel to zero. When the bar is moving from the top to the bottom of the visual field (blue bars), the average BOLD signal change when the bar is in the superior quadrant (location of the AS; elevation >0) drops to baseline values compared with the average signal under the full field stimulus condition. Activity starts when the bar is near 2° from the horizontal meridian (AS border), commensurate with the subject’s fixation eye movements. On the other hand, when the bar moves from the bottom to the top of the visual field (white bars), activity spreads beyond the horizontal border of the AS (elevation = 0) well within the superior quadrant corresponding to the AS. The error bars indicate the standard error of the mean across subjects (N = 5).
When a horizontal bar is moving from the top (AS location) to the bottom (stimulated) visual field quadrant, the average BOLD signal in the right hemisphere is initially at baseline (zero) as there is no stimulus presented within the AS (blue bars, Fig. 7C). Activity greater than baseline starts to be elicited when the bar is near 2° from the horizontal meridian (AS border), commensurate with the size of the subject’s fixation eye movements. In contrast, when the horizontal bar is moving in the opposite direction, from the bottom (stimulated) to the top (AS) visual field quadrant, the BOLD signal spreads further into the superior quadrant (positive elevations) where no stimulus was presented (white bars, Fig. 7C). The BOLD signal seen within the AS in this case is likely to be the result of increased hemodynamic spread resulting from the fact that the bar comes from the inferior (seeing) to the superior (blind) quadrant. This activates hV5/MT+ likely eliciting a hemodynamic wave that persists beyond the entry of the bar to the region of the scotoma. Similar spread occurs for other bar directions as long as the part of the stimulus moves from lower (seeing) to higher (non-seeing) visual field locations. It is also possible that this effect may be in part due to neural activity related to stimulus anticipation. However, what argues against this is that there is minimal to no shift in the BOLD signal profile elicited in the right hV5/MT+ when the bar moves from left to right versus right to left (Fig. S5a). In this case the bar is moving from the contralateral (left) to the ipsilateral (right) visual field or vice versa, crossing different hemispheres and vascular territories, so vascular spread should not occur. In accordance to this the BOLD signal shift should essentially disappear for the left to right bar transitions, as is shown to happen in Fig. S5a. It is difficult to imagine why this would happen if the dominant underlying mechanism for the shift were to be neural anticipation. The discrepancy in the BOLD time series within the AS area for the different bar directions is in part the cause of the pRF coverage observed within the AS when fitting the data using the full stimulus model. Note that although BOLD differences between bar directions occur also in early visual areas with small receptive fields (such as area V1, Fig. S5b), the effect is smaller (~2°) and affect visual field coverage estimates less (Fig. S5b).
Therefore, a different approach is needed for comparing responses between patients and AS subjects when using the drifting bar stimulus. One solution would be if one fits the BOLD time series of each voxel separately for each bar direction and model the boundaries of the pRF by marking the visual field locations where the BOLD signal rises above baseline for each direction. This would allow us to observe directly the spread of BOLD activity in each direction, taking into account asymmetries that may arise.
Comparison to direct-fit methods
We compared results obtained with our method with a method that fits directly a 2-dimensional Gaussian pRF model to predict the fMRI time-series (Dumoulin and Wandell, 2008). This method has been previously applied to characterize pRF changes in the early visual cortex of healthy participants with artificial scotomas (Baseler et al., 2011; Haak et al., 2012a; Binda et al., 2013). The direct-fit model can extrapolate estimates of the pRF that fall outside the stimulus space (i.e. inside the AS) by applying a Gaussian fit to the tail of the pRF that lies inside the stimulus space (Binda et al., 2013). As a result, when the direct-fit method is used to estimate the pRFs, the visual field coverage maps of the right hV5/MT+ cover the area of the AS both under the LAS model and under the AS condition (Fig. 8A). The visual field coverage maps cover the area of the AS whether we incorporate the AS stimulus in the model or we use the full field stimulus (Fig. S6A). Whether this extrapolation is justified is an open question. Nevertheless, even with this method we did observe differences between the AS condition and the LAS model. In particular, pRF centers originally located in the inferior quadrant (under the full field stimulus condition) shift within the AS (superior quadrant, elevation > 0) under the AS condition compared to pRFs estimated using the LAS model which retain their location within the inferior quadrant as expected (Fig. 8B, left). The distributions are significantly different (p = 10−215 < 10−19). PRFs originally located in the superior quadrant retain their location within the AS (elevation > 0) for both the LAS model and the AS condition (Fig. 8B, right). In this case, the pRF elevation distribution under the AS condition appears to be significantly shifted, with more voxels lying within the AS compared to the LAS model (p = 10−51 < 10−30). In addition, the pRF centers found within the AS have increased amplitude compared to both the LAS model and the full field stimulus condition (Fig. 8C). These findings are comparable with those observed using our method confirming that the pRFs are nonlinearly affected by the truncated stimulus. Contrary to our method though, we did not observe a clear pattern for the pRF size when using the direct-fit method. Most pRFs under the LAS model had no change in the pRF size compared with the full field stimulus condition, while some pRFs had increased size (Fig. 8D). PRFs under the AS condition on the other hand have large variability, many voxels showing markedly decreased or increased pRF size (Fig. 8D), sometimes almost triple the size of the original pRF under the full field stimulus condition (pRF change of 180%). We have previously shown that direct-fit methods are subject to potentially large errors in extrapolating the pRF structure and center when it lies outside the stimulus presentation space (Lee et al., 2013). For example, for a pRF located near the edge of the AS, the direct-fit method could potentially fail to capture the actual pRF center and size (Fig. 8E). This is because direct-fit methods use the visible (residual) portion of the pRF that falls outside of the AS to extrapolate how the pRF should look like inside the AS. This might result in a correct prediction where the pRFs under the AS condition match with those under the full field stimulus condition, as in (Binda et al., 2013). However, in other cases the extrapolated pRFs within the AS may differ from the pRFs under the full field stimulus condition as a result of a fitting error (Fig. 8E), nonlinearity or both (Fig. S6B). Our method only captures the portion of the pRF topography that lies within the stimulus presentation space and thus results in more veridical estimates in this case.
Discussion
Nonlinear pRF changes in hV5/MT+ under an “Artificial Scotoma” condition
Population receptive field (pRF) measurements provide a way to gauge the degree of reorganization after injury in human visual areas (Baseler et al., 2011; Papanikolaou et al., 2014). Because fMRI voxels contain more than 106 neurons (Leuba and Garey, 1989), pRF estimates depend both on the size of individual neuron receptive fields and on their scatter within each voxel. When different subsets of neurons within a voxel get activated, pRF estimates may change. For example, if only a subset of the neuronal population is activated in the case of the artificial scotoma, the pRF estimate will change (Baseler et al., 2011; Haak et al., 2012a,b; Binda et al., 2013) without reflecting cortical reorganization. In addition, presenting a truncated visual stimulus can have nonlinear effects that can modify receptive field location and size estimates in individual neurons. It is important to understand how such changes manifest in pRF estimation to be able to separate them from true reorganization. Here, we measured pRF changes that occur in area hV5/MT+ of five normal subjects after masking the stimulus in the upper left quadrant of the visual field (“artificial scotoma” or AS), thereby simulating a quadrantanopic scotoma.
The results show that most of the pRFs in the superior quadrant (AS) remain responsive and shift their location outside the boundaries of the AS (inferior quadrant). One possible reason for this might be that we can only map the part of the pRF that extends outside of the AS area, where stimulus is presented (Wandell and Smirnakis, 2009). However, this does not appear to be the whole story. Interestingly, pRF centers cluster at the AS border under the AS condition whereas they are expected to lie further within the inferior quadrant based on the prediction of the LAS model (Fig. 4A). In addition, pRFs located in the inferior quadrant (outside the AS), which are expected to have minimal change, also shift towards the AS border (Fig. 4A). This is accompanied by a significant reduction in the pRF size of hV5/MT+ voxels (Fig. 4B) as well as an increase in the amplitude of pRFs that occurs within 1° of the horizontal AS border (Fig. 4C). Notably, similar pRF changes were observed in the hV5/MT+ complex of the hemisphere ipsilateral to the AS (Fig. 6), except in this case pRF centers shift towards the vertical border of the AS. These changes suggest that nonlinear processes contribute to the BOLD response elicited by the truncated stimulus presented in the case of the artificial scotoma (AS). They may for example be the result of decreased inhibition close to the AS border resulting in disproportional increase of the pRF amplitude compared to the amplitude expected when using the full bar stimulus. Importantly, these deviations from linearity occurring in hV5/MT+ pRF estimation under the AS condition do not reflect true reorganization, but rather properties of normal visual processing under different test-stimulus conditions.
Comparison with prior studies
Previous studies have found ectopic pRFs in locations of the early visual cortex (areas V1–V3) that correspond to the AS (Baseler et al., 2011; Haak et al., 2012a,b). In particular, Haak et al. found that, in the presence of a foveal artificial scotoma, pRFs at the center of the visual field shifted to more peripheral locations and increased in size (Haak et al., 2012a). Here we show that a shift of pRFs originally located inside the AS to locations outside of the AS, but not an increase in pRF size, can be partially explained by the LAS model, which models what is expected when stimulating only the part of the pRFFF that does not fall inside the artificial scotoma. However, we also show that pRF shifts under the AS condition differ from shifts predicted by the LAS model suggesting that nonlinear processes contribute to the BOLD response elicited by the AS stimulus. In particular, pRFs cluster more at the border of the AS and the pRF size is decreased compared to the LAS model. In addition, we show a shift of the pRF centers originally located outside of the AS towards the AS border and an increase in the pRF amplitude near the AS border, which have not been previously reported.
Although these findings differ from those of Haak et al. (Haak et al., 2012a), we note that the pRF shifts reported by Haak et al. are found in the early visual cortex (area V1), while our results reflect pRF changes in hV5/MT+. However, we have not observed pRF shifts in area V1 under the AS condition in the magnitude reported by Haak et al. (Haak et al., 2012a). It is important to note that Haak et al. used a direct-fit method for pRF estimation, and this may be the source of a bias near a stimulus presentation border, such as the border of AS (Lee et al., 2013). This bias can potentially lead to significant mislocalization of the pRF center as well as erroneous estimation of the pRF size (see Fig. 8 for an illustration). It is therefore possible that the pRF changes observed in (Haak et al., 2012a) may reflect a bias as a result the pRF method used. The method we used here (Lee et al., 2013) is considerably more robust to such a bias. Another possibility is that the differences between the study of Haak et al. and ours originate from the fact that a different AS stimulus is used. Haak et al. used a large foveal scotoma while we used a scotoma covering one quadrant. It is possible that stimulating only the periphery may affect pRF responses in the central visual field, an effect that might be hidden in our case since we stimulate both peripheral and central locations in the seeing quadrant.
Another study (Binda et al., 2013) adopted an approach more similar to ours, and compared responses obtained under the AS condition with simulated responses computed using pRFs estimated from the full-field stimulus condition (similar to the LAS model). They found that when a multifocal stimulus presentation is used, pRF shifts in the AS condition can be largely predicted by the simulations. This agrees with our estimations in early visual cortex (area V1; Fig. 3B) but not in area hV5/MT+, where we show that pRFs under the AS condition differ from pRFs obtained using the LAS model. Binda et al. did not study responses in higher visual cortex where receptive fields cover a large portion of the visual field and thus they are likely to be more susceptible to the presence of a truncated stimulus.
Interestingly, when using a moving bar stimulus presentation, Binda et al. found pRF shifts under the AS condition that are different than those obtained from the model predictions (i.e. LAS model) suggesting that the pattern of visual stimulation (multifocal versus moving bar stimulation) may play a critical role in the conclusions that can be drawn. However, we do not believe that the effects we observed here represent simply an artifact of the stimulus presentation paradigm. First, we did not observe this effect in early visual areas. Specifically, we saw no significant difference between pRF estimates obtained by LAS versus the true AS condition in area V1 under our moving bar stimulation paradigm (Fig. S3a). Second, the main question is whether some of the nonlinearities we observe may be the result of differences in hemodynamic effects induced by the moving bar stimulus presentation in the AS versus the LAS stimulus condition (Fig. 7). Although there is a differential spread of the BOLD signal depending on bar stimulus direction (see next section), this does not fully explain the findings presented here. For example, it cannot explain the shift of the pRFs that are located outside of the AS towards the scotoma border, nor the increase in the pRF amplitude near the AS border. Note also that artifacts related to potential hemodynamic spread inside the area of the AS are minimized by our use of the AS-stimulus model for pRF estimation, which effectively restricts pRF weight estimation outside the AS, in the part of the visual field that was actually visually stimulated.
PRF estimates in hV5/MT+ depend strongly on whether the full bar or the truncated (AS) bar stimulus model is used for estimation
PRF estimation in the presence of an artificial scotoma represents an important control in most studies of patients suffering from visual field defects (Dilks et al., 2007; Baseler et al., 2011; Papanikolaou et al., 2014). However, it is an open question whether the appropriate stimulus model to use for pRF estimation is a truncated bar versus a full bar stimulus. We found significant differences in hV5/MT+ pRFs estimated when using the truncated bar (AS stimulus) versus the full bar stimulus model. Note that in both cases the actual stimulus presentation is done with the AS stimulus. Specifically, visual field coverage maps of the contralateral area hV5/MT+ covered most of the AS area when pRFs were estimated using the full bar model compared to the truncated bar model, which showed minimal coverage (Fig. 7A versus Fig. 3B). This has important implications regarding the interpretation of pRF topographies. In general, nonzero pRF weights that correspond to the region of the AS should not be straightforwardly interpreted as direct pRF measurements, since no visual stimulus was actually presented there. Rather they represent a form of extrapolation from responses arising outside the AS, which are subject to the assumptions underlying the pRF model. To avoid the interpretation difficulties this entails, our analysis primarily focused on comparing pRF weights estimated outside the AS region, derived under the truncated bar stimulus model (Figs. 3–6). This ensures that conclusions drawn are not subject to potential extrapolation errors.
We derived pRF estimates under the full bar stimulus model to make a link with existing literature (Fig. 7). Differences in the pRF estimation when applying two different stimulus models (full bar versus truncated bar) to the same actual stimulation condition (AS) have been reported before in the early visual cortex of subjects with artificial scotomas (Binda et al., 2013). However, the reported effect was largely opposite to what we observe here. Binda et al. report that when the full bar stimulus model is used to estimate pRF location, pRFs originally inside the artificial scotoma (AS) region shift outside the AS boundaries. On the other hand, when the AS stimulus model is used, pRFs are found within the AS area. The difference between Binda et al. and our study can be partially explained by the different approach we used to estimate pRFs. Our method, uses a linear topography estimation approach to estimate the pRF structure (Lee et al., 2013) and, when the AS-model is applied, it appropriately cannot cover areas outside the stimulus presentation space. Binda et al. use a direct-fit method, which can extrapolate pRF weights that fall outside the stimulus space, i.e. inside the AS, by fitting the tail of the pRF that lies inside the stimulus space (Fig. 8). This extrapolation is easier to perform when the AS-model (truncated bar) is applied, resulting in significant pRF coverage inside the scotoma in this case. Our method instead yields significant pRF coverage inside the scotoma, when we apply the full bar stimulus condition (Fig. 7). The lesson here is that the particular type of extrapolation accomplished depends strongly on the pRF model used, and resulting pRF estimates should be considered with caution, pending empirical validation.
Comparison with the direct method of pRF estimation
To ensure that the effects we report are not the result of the method of pRF estimation we used, we repeated our analysis using the direct method of pRF estimation (Dumoulin and Wandell, 2008) to estimate responses in hV5/MT+. We found that our main conclusions remain valid (Fig. 8) confirming that the pRFs are nonlinearly affected by the truncated stimulus.
We note that direct estimation methods can lead to biased estimates for pRFs that lie close to a stimulus presentation boundary (Lee et al., 2013) (Fig. 8E) and should be used with caution in subjects with sharp visual field scotoma boundaries. For example, when we used the direct-fit method to estimate pRFs in area hV5/MT+ we found that visual field coverage maps covered the area of the AS, whether we use the truncated bar (AS-model) or the full bar stimulus model (Fig. 8A, Fig. S6A). One interpretation of these extrapolated pRF topographies that extend inside the AS is that they represent the actual pRF profiles that would have been obtained had the artificial scotoma not been there (Binda et al., 2013). However, this does not occur in our case as both the pRF center elevation and size distributions obtained under the AS condition differ from those obtained under the full field stimulus condition (Fig. S6B). Since errors in parameter estimation can arise easily by extrapolating partial data fitting of this nature (see Fig. 8E), careful validation of results obtained is required. Here we concentrated on modeling the part of the receptive field that lies outside the artificial scotoma, in order to minimize potential for error.
Directional asymmetry of the BOLD response elicited by the bar stimulus at the border of AS
In our case, activity observed within the AS area appears to be in part the result of asymmetric BOLD responses occurring when the bar stimulus moves from seeing to non-seeing locations of the visual field (Fig. 7C). One possibility is that BOLD signal responses differ within the AS because the brain generates an expectation of the upcoming stimulus (Kastner et al., 1999; Ghose and Bearl, 2010) or because of filling-in phenomena (Meng et al., 2005). Anticipation of the upcoming stimulus may in part explain the BOLD spread within the AS area, however, it is unlikely to be the whole explanation here. Effects of stimulus expectation should be apparent also when the bar is moving from the contralateral to the ipsilateral visual hemifield. Although there is a small BOLD spread when the vertical bar moves from the contralateral to the ipsilateral visual hemifield that could be the result of anticipation (Fig. S5a), the effect does not occur in the same magnitude as when the horizontal bar enters the scotoma (Fig. 7C), suggesting that the BOLD spread within the AS area is likely the result of persistent hemodynamic activity which cannot occur across hemispheres. Moreover, the type of stimulus we use (moving bar truncated in the area of the AS) is not conducive to filling-in phenomena (De Weerd et al., 1998) effectively ruling out this possibility.
Such asymmetric differences in the BOLD signal may potentially be avoided by changing stimulus design, for example by having the bar stimulus positions interleaved randomly rather than presented sequentially, as Binda et al. suggest (Binda et al., 2013). However, the ability of such stimuli to activate hV5/MT+ and yield reliable pRF estimates in higher areas warrants further investigation (Binda et al., 2013). An alternative approach is to calculate directly the boundaries of the pRF from the BOLD time series of each voxel separately for each direction of motion of the visual stimulus (bar). For example, one could identify the visual field location where the BOLD activity starts to rise above baseline separately for each bar direction. In this way, hysteresis phenomena also become apparent and can be taken into account or investigated as needed. This approach has some similarity to classical receptive field mapping methods (Hubel and Wiesel, 1962)), although the time scales involved are of course much different.
Conclusions
We have shown that pRF estimates in area hV5/MT+ are non-linearly affected by a truncated stimulus presented (AS) in order to simulate a quadrantanopic visual field scotoma. This was signified by a shift of the pRF centers towards the border of the AS, a decrease in pRF size and an increase in pRF amplitude near the AS border. In addition, we found erroneous pRF estimates inside the area corresponding to the AS, when we used the full bar stimulus model for predicting the pRF topography when the actual stimulus presented included the AS. These biases are not the result of a trivial methodological artifact but appear to originate from asymmetric BOLD responses occurring when the stimulus moves from seeing to non-seeing locations of the visual field. We argue that these responses are not simply neural anticipatory responses but likely contain a significant hemodynamic component. Distinguishing pRF changes that occur as the result of true reorganization versus different test-stimulus presentation conditions is an important task that needs to be undertaken when studying the organization of visual cortex in patients with visual field deficits. The purpose of this work was to point out some of the issues involved.
Supplementary Material
Acknowledgments
This work was supported by National Eye Institute R01 (EY024019) to SMS, the Deutsche Forschungsgemeinschaft, the Plasticise Consortium (Project HEALTH-F2-2009-223524) and the Max Planck Society.
Footnotes
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2015.06.085.
References
- Amano K, Wandell BA, Dumoulin SO. Visual field maps, population receptive field sizes, and visual field coverage in the human MT+ complex. J Neurophysiol. 2009;102:2704–2718. doi: 10.1152/jn.00102.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker CI, Peli E, Knouf N, Kanwisher NG. Reorganization of visual processing in macular degeneration. J Neurosci. 2005;25:614–618. doi: 10.1523/JNEUROSCI.3476-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker CI, Dilks DD, Peli E, Kanwisher N. Reorganization of visual processing in macular degeneration: replication and clues about the role of foveal loss. Vis Res. 2008;48:1910–1919. doi: 10.1016/j.visres.2008.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbur JL, Watson JD, Frackowiak RS, Zeki S. Conscious visual perception without V1. Brain. 1993;116(Pt 6):1293–1302. doi: 10.1093/brain/116.6.1293. [DOI] [PubMed] [Google Scholar]
- Barmashenko G, Eysel UT, Mittmann T. Changes in intracellular calcium transients and LTP in the surround of visual cortex lesions in rats. Brain Res. 2003;990:120–128. doi: 10.1016/s0006-8993(03)03447-4. [DOI] [PubMed] [Google Scholar]
- Baseler HA, Gouws A, Haak KV, Racey C, Crossland MD, Tufail A, Rubin GS, Cornelissen FW, Morland AB. Large-scale remapping of visual cortex is absent in adult humans with macular degeneration. Nat Neurosci. 2011;14:649–655. doi: 10.1038/nn.2793. [DOI] [PubMed] [Google Scholar]
- Binda P, Thomas JM, Boynton GM, Fine I. Minimizing biases in estimating the reorganization of human visual areas with BOLD retinotopic mapping. J Vis. 2013;13:13. doi: 10.1167/13.7.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
- Bridge H, Hicks SL, Xie J, Okell TW, Mannan S, Alexander I, Cowey A, Kennard C. Visual activation of extra-striate cortex in the absence of V1 activation. Neuropsychologia. 2010;48:4148–4154. doi: 10.1016/j.neuropsychologia.2010.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce CJ, Desimone R, Gross CG. Both striate cortex and superior colliculus contribute to visual properties of neurons in superior temporal polysensory area of macaque monkey. J Neurophysiol. 1986;55:1057–1075. doi: 10.1152/jn.1986.55.5.1057. [DOI] [PubMed] [Google Scholar]
- Calford MB, Schmid LM, Rosa MG. Monocular focal retinal lesions induce short-term topographic plasticity in adult cat visual cortex. Proc Biol Sci. 1999;266:499–507. doi: 10.1098/rspb.1999.0665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chino YM, Kaas JH, Smith EL, 3rd, Langston AL, Cheng H. Rapid reorganization of cortical maps in adult cats following restricted deafferentation in retina. Vis Res. 1992;32:789–796. doi: 10.1016/0042-6989(92)90021-a. [DOI] [PubMed] [Google Scholar]
- Chino YM, Smith EL, 3rd, Kaas JH, Sasaki Y, Cheng H. Receptive-field properties of deafferentated visual cortical neurons after topographic map reorganization in adult cats. J Neurosci. 1995;15:2417–2433. doi: 10.1523/JNEUROSCI.15-03-02417.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Weerd P, Desimone R, Ungerleider LG. Perceptual filling-in: a parametric study. Vis Res. 1998;38:2721–2734. doi: 10.1016/s0042-6989(97)00432-x. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Anzai A, Ohzawa I, Freeman RD. Receptive field structure in the visual cortex: does selective stimulation induce plasticity? Proc Natl Acad Sci U S A. 1995;92:9682–9686. doi: 10.1073/pnas.92.21.9682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dilks DD, Serences JT, Rosenau BJ, Yantis S, McCloskey M. Human adult cortical reorganization and consequent visual distortion. J Neurosci. 2007;27:9585–9594. doi: 10.1523/JNEUROSCI.2650-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dilks DD, Baker CI, Peli E, Kanwisher N. Reorganization of visual processing in macular degeneration is not specific to the “preferred retinal locus”. J Neurosci. 2009;29:2768–2773. doi: 10.1523/JNEUROSCI.5258-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin SO, Wandell BA. Population receptive field estimates in human visual cortex. NeuroImage. 2008;39:647–660. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eysel UT, Schmidt-Kastner R. Neuronal dysfunction at the border of focal lesions in cat visual cortex. Neurosci Lett. 1991;131:45–48. doi: 10.1016/0304-3940(91)90333-o. [DOI] [PubMed] [Google Scholar]
- Eysel UT, Schweigart G. Increased receptive field size in the surround of chronic lesions in the adult cat visual cortex. Cereb Cortex. 1999;9:101–109. doi: 10.1093/cercor/9.2.101. [DOI] [PubMed] [Google Scholar]
- Eysel UT, Schweigart G, Mittmann T, Eyding D, Qu Y, Vandesande F, Orban G, Arckens L. Reorganization in the visual cortex after retinal and cortical damage. Restor Neurol Neurosci. 1999;15:153–164. [PubMed] [Google Scholar]
- ffytche DH, Guy CN, Zeki S. Motion specific responses from a blind hemifield. Brain. 1996;119(Pt 6):1971–1982. doi: 10.1093/brain/119.6.1971. [DOI] [PubMed] [Google Scholar]
- Ghose GM, Bearl DW. Attention directed by expectations enhances receptive fields in cortical area MT. Vis Res. 2010;50:441–451. doi: 10.1016/j.visres.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannikopoulos DV, Eysel UT. Dynamics and specificity of cortical map reorganization after retinal lesions. Proc Natl Acad Sci U S A. 2006;103:10805–10810. doi: 10.1073/pnas.0604539103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert CD, Wiesel TN. Receptive field dynamics in adult primary visual cortex. Nature. 1992;356:150–152. doi: 10.1038/356150a0. [DOI] [PubMed] [Google Scholar]
- Girard P, Salin PA, Bullier J. Response selectivity of neurons in area MT of the macaque monkey during reversible inactivation of area V1. J Neurophysiol. 1992;67:1437–1446. doi: 10.1152/jn.1992.67.6.1437. [DOI] [PubMed] [Google Scholar]
- Haak KV, Cornelissen FW, Morland AB. Population receptive field dynamics in human visual cortex. PLoS One. 2012a;7:e37686. doi: 10.1371/journal.pone.0037686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haak KV, Langers DR, Renken R, van Dijk P, Borgstein J, Cornelissen FW. Abnormal visual field maps in human cortex: A mini-review and a case report. Cortex. 2012b;56:14–25. doi: 10.1016/j.cortex.2012.12.005. [DOI] [PubMed] [Google Scholar]
- Heinen SJ, Skavenski AA. Recovery of visual responses in foveal V1 neurons following bilateral foveal lesions in adult monkey. Exp Brain Res. 1991;83:670–674. doi: 10.1007/BF00229845. [DOI] [PubMed] [Google Scholar]
- Horton JC, Hocking DR. Monocular core zones and binocular border strips in primate striate cortex revealed by the contrasting effects of enucleation, eyelid suture, and retinal laser lesions on cytochrome oxidase activity. J Neurosci. 1998;18:5433–5455. doi: 10.1523/JNEUROSCI.18-14-05433.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imbrosci B, Neubacher U, White R, Eysel UT, Mittmann T. Shift from phasic to tonic GABAergic transmission following laser-lesions in the rat visual cortex. Pflugers Arch. 2013;465:879–893. doi: 10.1007/s00424-012-1191-y. [DOI] [PubMed] [Google Scholar]
- Kaas JH, Krubitzer LA, Chino YM, Langston AL, Polley EH, Blair N. Reorganization of retinotopic cortical maps in adult mammals after lesions of the retina. Science. 1990;248:229–231. doi: 10.1126/science.2326637. [DOI] [PubMed] [Google Scholar]
- Kastner S, Pinsk MA, De Weerd P, Desimone R, Ungerleider LG. Increased activity in human visual cortex during directed attention in the absence of visual stimulation. Neuron. 1999;22:751–761. doi: 10.1016/s0896-6273(00)80734-5. [DOI] [PubMed] [Google Scholar]
- Lee S, Papanikolaou A, Logothetis NK, Smirnakis SM, Keliris GA. A new method for estimating population receptive field topography in visual cortex. NeuroImage. 2013;81C:144–157. doi: 10.1016/j.neuroimage.2013.05.026. [DOI] [PubMed] [Google Scholar]
- Leuba G, Garey LJ. Comparison of neuronal and glial numerical density in primary and secondary visual cortex of man. Exp Brain Res. 1989;77:31–38. doi: 10.1007/BF00250564. [DOI] [PubMed] [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;16:187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- Masuda Y, Dumoulin SO, Nakadomari S, Wandell BA. V1 projection zone signals in human macular degeneration depend on task, not stimulus. Cereb Cortex. 2008;18:2483–2493. doi: 10.1093/cercor/bhm256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maunsell JH, Nealey TA, DePriest DD. Magnocellular and parvocellular contributions to responses in the middle temporal visual area (MT) of the macaque monkey. J Neurosci Off J Soc Neurosci. 1990;10:3323–3334. doi: 10.1523/JNEUROSCI.10-10-03323.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng M, Remus DA, Tong F. Filling-in of visual phantoms in the human brain. Nat Neurosci. 2005;8:1248–1254. doi: 10.1038/nn1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittmann T, Eysel UT. Increased synaptic plasticity in the surround of visual cortex lesions in rats. Neuroreport. 2001;12:3341–3347. doi: 10.1097/00001756-200110290-00039. [DOI] [PubMed] [Google Scholar]
- Morland AB, Le S, Carroll E, Hoffmann MB, Pambakian A. The role of spared calcarine cortex and lateral occipital cortex in the responses of human hemianopes to visual motion. J Cogn Neurosci. 2004;16:204–218. doi: 10.1162/089892904322984517. [DOI] [PubMed] [Google Scholar]
- Murakami I, Komatsu H, Kinoshita M. Perceptual filling-in at the scotoma following a monocular retinal lesion in the monkey. Vis Neurosci. 1997;14:89–101. doi: 10.1017/s0952523800008798. [DOI] [PubMed] [Google Scholar]
- Nestares O, Heeger DJ. Robust multiresolution alignment of MRI brain volumes. Magn Reson Med. 2000;43:705–715. doi: 10.1002/(sici)1522-2594(200005)43:5<705::aid-mrm13>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- Papanikolaou A, Keliris GA, Papageorgiou TD, Shao Y, Krapp E, Papageorgiou E, Stingl K, Bruckmann A, Schiefer U, Logothetis NK, Smirnakis SM. Population receptive field analysis of the primary visual cortex complements perimetry in patients with homonymous visual field defects. Proc Natl Acad Sci U S A. 2014;111:E1656–E1665. doi: 10.1073/pnas.1317074111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poppel E, Held R, Frost D. Leter: Residual visual function after brain wounds involving the central visual pathways in man. Nature. 1973;243:295–296. doi: 10.1038/243295a0. [DOI] [PubMed] [Google Scholar]
- Rodman HR, Gross CG, Albright TD. Afferent basis of visual response properties in area MT of the macaque. I. Effects of striate cortex removal. J Neurosci Off J Soc Neurosci. 1989;9:2033–2050. doi: 10.1523/JNEUROSCI.09-06-02033.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodman HR, Gross CG, Albright TD. Afferent basis of visual response properties in area MT of the macaque. II. Effects of superior colliculus removal. J Neurosci Off J Soc Neurosci. 1990;10:1154–1164. doi: 10.1523/JNEUROSCI.10-04-01154.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosa MG, Tweedale R, Elston GN. Visual responses of neurons in the middle temporal area of new world monkeys after lesions of striate cortex. J Neurosci Off J Soc Neurosci. 2000;20:5552–5563. doi: 10.1523/JNEUROSCI.20-14-05552.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumpel S, Hoffmann H, Hatt H, Gottmann K, Mittmann T, Eysel UT. Lesion-induced changes in NMDA receptor subunit mRNA expression in rat visual cortex. Neuroreport. 2000;11:4021–4025. doi: 10.1097/00001756-200012180-00024. [DOI] [PubMed] [Google Scholar]
- Schmid LM, Rosa MG, Calford MB, Ambler JS. Visuotopic reorganization in the primary visual cortex of adult cats following monocular and binocular retinal lesions. Cereb Cortex. 1996;6:388–405. doi: 10.1093/cercor/6.3.388. [DOI] [PubMed] [Google Scholar]
- Schmid MC, Mrowka SW, Turchi J, Saunders RC, Wilke M, Peters AJ, Ye FQ, Leopold DA. Blindsight depends on the lateral geniculate nucleus. Nature. 2010;466:373–377. doi: 10.1038/nature09179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoenfeld MA, Noesselt T, Poggel D, Tempelmann C, Hopf JM, Woldorff MG, Heinze HJ, Hillyard SA. Analysis of pathways mediating preserved vision after striate cortex lesions. Ann Neurol. 2002;52:814–824. doi: 10.1002/ana.10394. [DOI] [PubMed] [Google Scholar]
- Schumacher EH, Jacko JA, Primo SA, Main KL, Moloney KP, Kinzel EN, Ginn J. Reorganization of visual processing is related to eccentric viewing in patients with macular degeneration. Restor Neurol Neurosci. 2008;26:391–402. [PubMed] [Google Scholar]
- Smirnakis SM, Brewer AA, Schmid MC, Tolias AS, Schuz A, Augath M, Inhoffen W, Wandell BA, Logothetis NK. Lack of long-term cortical reorganization after macaque retinal lesions. Nature. 2005;435:300–307. doi: 10.1038/nature03495. [DOI] [PubMed] [Google Scholar]
- Smith AT, Singh KD, Williams AL, Greenlee MW. Estimating receptive field size from fMRI data in human striate and extrastriate visual cortex. Cereb Cortex. 2001;11:1182–1190. doi: 10.1093/cercor/11.12.1182. [DOI] [PubMed] [Google Scholar]
- Sunness JS, Liu T, Yantis S. Retinotopic mapping of the visual cortex using functional magnetic resonance imaging in a patient with central scotomas from atrophic macular degeneration. Ophthalmology. 2004;111:1595–1598. doi: 10.1016/j.ophtha.2003.12.050. [DOI] [PubMed] [Google Scholar]
- Wandell BA, Smirnakis SM. Plasticity and stability of visual field maps in adult primary visual cortex. Nat Rev Neurosci. 2009;10:873–884. doi: 10.1038/nrn2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiskrantz L, Warrington EK, Sanders MD, Marshall J. Visual capacity in the hemianopic field following a restricted occipital ablation. Brain. 1974;97:709–728. doi: 10.1093/brain/97.1.709. [DOI] [PubMed] [Google Scholar]
- Yan L, Imbrosci B, Zhang W, Neubacher U, Hatt H, Eysel UT, Mittmann T. Changes in NMDA-receptor function in the first week following laser-induced lesions in rat visual cortex. Cereb Cortex. 2012;22:2392–2403. doi: 10.1093/cercor/bhr318. [DOI] [PubMed] [Google Scholar]
- Zepeda A, Vaca L, Arias C, Sengpiel F. Reorganization of visual cortical maps after focal ischemic lesions. J Cereb Blood Flow Metab. 2003;23:811–820. doi: 10.1097/01.WCB.0000075010.31477.1E. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


