A typology of four notions of confounding in epidemiology

Abstract

Confounding is a major concern in epidemiology. Despite its significance, the different notions of confounding have not been fully appreciated in the literature, leading to confusion of causal concepts in epidemiology. In this article, we aim to highlight the importance of differentiating between the subtly different notions of confounding from the perspective of counterfactual reasoning. By using a simple example, we illustrate the significance of considering the distribution of response types to distinguish causation from association, highlighting that confounding depends not only on the population chosen as the target of inference, but also on the notions of confounding in distribution and confounding in measure. This point has been relatively underappreciated, partly because some literature on the concept of confounding has only used the exposed and unexposed groups as the target populations, while it would be helpful to use the total population as the target population. Moreover, to clarify a further distinction between confounding “in expectation” and “realized” confounding, we illustrate the usefulness of examining the distribution of exposure status in the target population. To grasp the explicit distinction between confounding in expectation and realized confounding, we need to understand the mechanism that generates exposure events, not the product of that mechanism. Finally, we graphically illustrate this point, highlighting the usefulness of directed acyclic graphs in examining the presence of confounding in distribution, in the notion of confounding in expectation.

1. Introduction

Confounding is a major concern in epidemiology. Since the publication of the seminal paper by Greenland and Robins,¹ many epidemiologists have explained the concept of confounding by examining risk measures under a simple potential-outcome (or counterfactual) model for a cohort of individuals.^2–8 Exchangeability of potential outcomes between the exposed and unexposed groups is one of the most fundamental assumptions in making causal inference, and confounding is a common source of lack of exchangeability.⁹ Despite its significance, the different notions of confounding have not been fully appreciated in the literature, leading to confusion of causal concepts in epidemiology.

This article aims to highlight the importance of differentiating between the subtly different notions of confounding from the perspective of counterfactual reasoning. We also show that directed acyclic graphs (DAGs) provide a simple algorithm to identify a sufficient set of confounders if the underlying causal structure is properly reflected. To achieve these goals, we use the concept of response types in a simple example. The concept of response type is an essential foundation of causal inference because the causal effect of exposure on disease frequency in a population depends on the distribution of the response types of individuals in that population, not necessarily on the population distribution of the covariates.¹ This point, however, has been relatively underappreciated because, despite its sophistication and usefulness, the response type of each individual is unobservable.

2. Overview of a simple example

To consider the effect of smoking cessation on lung cancer during a defined time period, we use an example of four subjects (Table 1). In an epidemiologic study of these subjects, let us suppose that subjects #1 (male) and #3 (female) were actually exposed (i.e., quit smoking) and subjects #2 (male) and #4 (female) were actually unexposed (i.e., did not quit smoking). During the follow-up, one of the exposed and both of the unexposed subjects suffered from lung cancer. Consequently, the observed risk difference (RD) estimate for the effect of smoking cessation on lung cancer can be calculated as: 1/2 −2/2 = −1/2. Likewise, the observed risk ratio (RR) estimate can be calculated as: (1/2)/(2/2) = 1/2. These results suggest that smoking cessation can prevent lung cancer.

Table 1. Characteristics of the four smoking subjects during the target time period.^a.

Subject ID	Sex	History of asbestos exposure	Smoking	Lung cancer	Lung cancer if male/femaleb		Response type
					Quit smoking (i.e., exposure)	Did not quit (i.e., non-exposure)
Subject #1	Male	Yes	Quit	Diseased	Diseased	(Diseased)	Doomed
Subject #2	Male	No	Did not quit	Diseased	(Non-diseased)	Diseased	Preventive
Subject #3	Female	No	Quit	Non-diseased	Non-diseased	(Non-diseased)	Immune
Subject #4	Female	No	Did not quit	Diseased	(Non-diseased)	Diseased	Preventive

^aEffect of smoking cessation on lung cancer.

^bParentheses indicate that these particular outcomes are counterfactual.

When we consider a binary exposure and a binary outcome, individuals can be classified into the following four different response types.¹

• •Type 1 or “doomed” persons: Exposure is irrelevant because outcome occurs with or without exposure
• •Type 2 or “causal” persons: Outcome occurs if and only if they are exposed
• •Type 3 or “preventive” persons: Outcome occurs if and only if they are unexposed
• •Type 4 or “immune” persons: Exposure is irrelevant because outcome does not occur with or without exposure

Response types of the four subjects are shown in Table 1. No subjects are classified as a “causal” response type, implying that the effect of smoking cessation is in the same direction for all four subjects. This assumption has been referred to as negative monotonicity.^10,11 Although monotonicity assumptions may be biologically plausible in some situations, they can never be empirically verified with data because they make reference to all individuals in the population. Here, we use such an assumption to simplify the discussion. The conditions presented in our paper can be used even when the monotonicity assumption is violated.

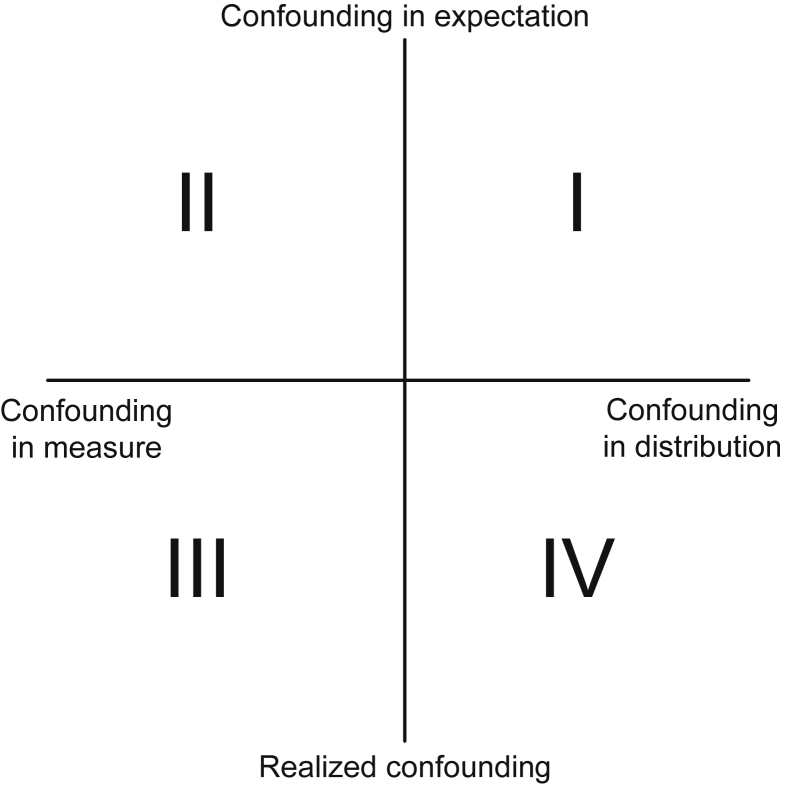
In the following sections, we illustrate a typology of four notions of confounding by exploring and extending this simple example (Box 1 and Fig. 1). For simplicity, we use deterministic counterfactuals for each subject and assume that no random error attributable to sampling variability exists.⁶

Box 1. Four notions of confounding.

• •Confounding in distribution: We say that there is no confounding in distribution of the effect of exposure on outcome if the group that actually had a particular exposure is representative of what would have occurred had the entire target population been exposed to the same level of exposure.
• •Confounding in measure: We say that there is no confounding in measure of the effect of exposure on outcome if a particular measure of interest is equivalent to the corresponding causal measure in the target population.
• •Confounding in expectation: We say that there is no confounding in expectation of the effect of exposure on outcome if the exposure assignment mechanism results in balance.
• •Realized confounding: We say that there is no realized confounding of the effect of exposure on outcome if a particular exposure assignment results in balance, irrespective of the exposure assignment mechanism.

Fig. 1. Typology of four notions of confounding. DAGs are primarily useful to examine the presence of confounding in the first quadrant. DAG, directed acyclic graph.

3. Significance of differentiating between the notions of confounding in distribution and confounding in measure

The causal effect of exposure on disease frequency in a population depends on the distribution of response types of individuals in that population. Table 2 shows the distribution of response types in the exposed and unexposed groups of the abovementioned example. We also show the distribution in the total population; let p_i, q_i, and r_i, i = 1–4, be proportions of response type i in the exposed group, the unexposed group, and the total population, respectively. Note that r_i can be calculated as p_i/2 + q_i/2 because the numbers of the exposed and unexposed groups are balanced (Table 1). Among the exposed group, only type 1 and type 2 persons will develop the outcome, and the risk, or incidence proportion, of lung cancer in the exposed group is p₁ + p₂. Among the unexposed group, only type 1 and type 3 persons will develop the outcome, and the corresponding risk is q₁ + q₃. Therefore, the associational RD can be obtained using the proportions of response types as: (p₁ + p₂) − (q₁ + q₃) = 1/2 − 2/2 = −1/2, which is equivalent to the abovementioned observed RD estimate under the assumption of no sampling variability.

Table 2. Response types and their distribution in Table 1.

Response type	Response under		Description	Proportion of response types in
	Exposure	Non-exposure		Exposeda	Unexposedb	Total populationc
1	1	1	Doomed	p1 = 1/2	q1 = 0	r1 = 1/4
2	1	0	Causal	p2 = 0	q2 = 0	r2 = 0
3	0	1	Preventive	p3 = 0	q3 = 2/2	r3 = 2/4
4	0	0	Immune	p4 = 1/2	q4 = 0	r4 = 1/4

Effect of smoking cessation on lung cancer (1 = diseased, 0 = non-diseased). The associational risk difference is calculated as: (p₁ + p₂) − (q₁ + q₃) = 1/2 − 2/2 = −1/2. Note that the distribution in this table applies to scenario #2 in Table 3.

^aCausal risk difference in the exposed group is defined as: (p₁ + p₂) − (p₁ + p₃) = p₂ − p₃ = 0 − 0 = 0 .

^bCausal risk difference in the unexposed group is defined as: (q₁ + q₂) − (q₁ + q₃) = q₂ − q₃ = 0 − 2/2 = −2/2 .

^cAs shown in Table 1, numbers of the exposed and unexposed groups are balanced, so a proportion of response type i in the total population, r_i, can be calculated as: p_i/2 + q_i/2. The causal risk difference in the total population is defined as: (r₁ + r₂) − (r₁ + r₃) = r₂ − r₃ = 0 − 2/4 = −2/4 .

It has been well established that the target population concept plays a key role in discussions of causal inference in epidemiology.^4,5 Based on the distribution of these response types, we can define the true value of the causal parameters of interest in the corresponding target populations. For example, if exposure had been absent in the exposed group, only type 1 and type 3 persons would have developed the outcome, and the counterfactual risk of lung cancer would have been p₁ + p₃. Therefore, the causal RD in the exposed group (i.e., subjects #1 and #3) can be calculated as: (p₁ + p₂) − (p₁ + p₃) = p₂ − p₃ = 0 − 0 = 0. Likewise, the causal RDs in the unexposed group (i.e., subjects #2 and #4) and the total population can be calculated as: (q₁ + q₂) − (q₁ + q₃) = q₂ − q₃ = 0 − 2/2 = −2/2 and (r₁ + r₂) − (r₁ + r₃) = r₂ − r₃ = 0 − 2/4 = −2/4, respectively.

These descriptions in terms of response types are valuable in highlighting the significance that the notion of confounding can be defined with respect to both the distribution of potential outcomes (i.e., confounding in distribution) and a specific effect measure (i.e., confounding in measure).^2,12,13 If we use RD as a measure of interest, when the exposed group is the target population, we say that there is confounding in measure if the causal RD in the exposed group (i.e., (p₁ + p₂) − (p₁ + p₃)) is not equivalent to the associational RD (i.e., (p₁ + p₂) − (q₁ + q₃)). Therefore, a sufficient and necessary condition for no confounding in measure is given by¹:

$$\left(p_1+p_2\right)-\left(p_1+p_3\right)=\left(p_1+p_2\right)-\left(q_1+q_3\right)\iff \left(p_1+p_3\right)=\left(q_1+q_3\right)\text{,}$$ (1)

which is violated in Table 2. Conversely, when the unexposed group is the target population, a sufficient and necessary condition for no confounding in measure is given by:

$$\left(q_1+q_2\right)-\left(q_1+q_3\right)=\left(p_1+p_2\right)-\left(q_1+q_3\right)\iff \left(p_1+p_2\right)=\left(q_1+q_2\right)\text{,}$$ (2)

which is also violated in Table 2. Note that these conditions can be also derived when the notion of confounding is defined with respect to the distribution of potential outcomes, rather than with respect to a specific effect measure.^12,13 For example, when the exposed group is the target population, we say that there is confounding in distribution if the actual unexposed group is not representative of what would have occurred in the actual exposed group had they been unexposed. Therefore, a sufficient and necessary condition for no confounding in distribution is identical to Equation (1). When the exposed and unexposed groups are used as target populations, distinguishing between the notions of confounding in distribution and confounding in measure becomes a subtle issue, and there is confounding in distribution and confounding in measure in Table 2. When the target is the total population, however, it is crucial to distinguish between these because conditions for no confounding vary according to the two notions of confounding. If we use the notion of confounding in distribution, a sufficient and necessary condition for no confounding is given by:

$$\left\{\left(r_1+r_2\right)=\left(p_1+p_2\right)\right\}\wedge \left\{\left(r_1+r_3\right)=\left(q_1+q_3\right)\right\}\iff \left\{\left(p_1+p_2\right)=\left(q_1+q_2\right)\right\}\wedge \left\{\left(p_1+p_3\right)=\left(q_1+q_3\right)\right\}\text{,}$$ (3)

which is obviously violated in Table 2. If Equation (3) holds, the groups that are actually exposed and unexposed are representative of what would have occurred had the total population been exposed and unexposed, respectively. Note that confounding in distribution is scale-independent. Meanwhile, if we use RD as a measure of interest, a sufficient and necessary condition for no confounding in measure is given by:

$$\left(r_1+r_2\right)-\left(r_1+r_3\right)=\left(p_1+p_2\right)-\left(q_1+q_3\right)\iff \left(p_2+q_2\right)/2-\left(p_3+q_3\right)/2=\left(p_1+p_2\right)-\left(q_1+q_3\right)\iff \left(p_1+p_3\right)+\left(p_1+p_2\right)=\left(q_1+q_3\right)+\left(q_1+q_2\right)\text{,}$$ (4)

which is weaker than Equation (3) and is met in Table 2. Note that confounding in measure is scale-dependent. For example, if we use RR as a measure of interest, a sufficient and necessary condition for no confounding in measure is given by:

$$\left(r_1+r_2\right)/\left(r_1+r_3\right)=\left(p_1+p_2\right)/\left(q_1+q_3\right)\iff \left[\left\{\left(p_1+q_1\right)+\left(p_2+q_2\right)\right\}/2\right]/\left[\left\{\left(p_1+q_1\right)+\left(p_3+q_3\right)\right\}/2\right]=\left(p_1+p_2\right)/\left(q_1+q_3\right)\iff \left(p_1+p_2\right)\left(p_1+p_3\right)=\left(q_1+q_3\right)\left(q_1+q_2\right),$$ (5)

which is, though weaker than Equation (3), violated in Table 2.

Consequently, even if the distribution of response types in the exposed and unexposed groups are not comparable (i.e., (p₁,p₂,p₃,p₄) ≠ (q₁,q₂,q₃,q₄)), as in Table 2, we may obtain an unconfounded estimate for the target population. Complete comparability of response types between the exposed and unexposed groups (i.e., (p₁,p₂,p₃,p₄) = (q₁,q₂,q₃,q₄)) is a sufficient, but not a necessary, condition for no confounding in the three target populations, irrespective of whether one uses the notion of confounding in distribution or confounding in measure.

In conclusion, confounding depends not only on the population chosen as the target of inference, but also on the notion of confounding itself, when the target is the total population.^2,12,13 This point has been relatively underappreciated, partly because some books (including Modern Epidemiology⁷ and Encyclopedia of Epidemiology¹⁴) discuss the concept of confounding using only the exposed and unexposed groups as the target populations. As examples of the confusion surrounding the concept of confounding, a recent review article by Gatto et al.¹⁵ explains the conditions for no confounding that are implicitly derived from the notion of confounding in distribution, whereas Maldonado¹⁶ implicitly used the notion of confounding in measure when discussing the concept of confounding. To clarify the significance of differentiating the two notions of confounding, it would be helpful to use not only the exposed and unexposed groups, but also the total population as the target populations.

4. Extension of a simple example to clarify a further distinction between confounding “in expectation” and “realized” confounding

As discussed in an update of the classic methodology paper by Greenland and Robins,¹⁷ a further distinction can be drawn between confounding “in expectation” and “realized” confounding.¹² Epidemiologic literature has typically addressed the issue of “no confounding” in the notion of realized confounding; however, the notion of confounding in expectation is also valuable. The concept of bias is defined by comparing the expected value of an estimator and the true value of the parameter,^18–20 and confounding is a common source of bias.

In an ideal randomized controlled trial, the randomized groups will be comparable in their potential outcomes on average, over repeated experiments. For any given experiment, however, the particular randomization may result in imbalances by chance, because of the particular allocation or exposure assignment.²¹ Such a scenario would result in no confounding in expectation but there would be realized confounding for that particular trial.¹² Confounding in expectation and realized confounding have been also referred to as confounded mechanisms and confounded assignments, respectively.¹⁴ To grasp the explicit distinction between these notions of confounding, we need to understand the mechanism that generates exposure events, not the product of that mechanism. In the example of four smokers, the mechanism that generates the exposure events remains unknown. The lack of comparability of response types between the exposed and unexposed groups in the example could be because the configuration was observed randomly, with the estimator being unconfounded in expectation, or there could be a reason for the lack of comparability that is not revealed in the above explanation.

To obtain the expected value of an estimator in the target population, we need to consider the distribution of exposure status in that population. To illustrate this, the following discussion focuses on the situation in which the target population is the total population. Note that Table 1 shows only one pattern of exposure status of the four subjects. Given a total of four subjects, we can consider a maximum of six patterns of exposure status, when the numbers of the exposed and unexposed groups are balanced (Table 3) (The exposure status shown in Table 1 corresponds to scenario #2 in Table 3.). In each scenario, we can calculate an RD estimate for the four subjects.

Table 3. Six possible scenarios when the numbers of the exposed and unexposed groups are balanced.^a.

	Actually exposed	Actually unexposed
Scenario #1
Subject ID	#1, #2	#3, #4
Response type	doomed, preventive	immune, preventive
Scenario #2b
Subject ID	#1, #3	#2, #4
Response type	doomed, immune	preventive, preventive
Scenario #3
Subject ID	#1, #4	#2, #3
Response type	doomed, preventive	preventive, immune
Scenario #4
Subject ID	#2, #3	#1, #4
Response type	preventive, immune	doomed, preventive
Scenario #5
Subject ID	#2, #4	#1, #3
Response type	preventive, preventive	doomed, immune
Scenario #6
Subject ID	#3, #4	#1, #2
Response type	immune, preventive	doomed, preventive

^aScenarios #1 and #3 are identical from the perspective of counterfactual reasoning, because the distributions of response types are the same in these scenarios. Similarly, scenarios #4 and #6 are identical from the perspective of counterfactual reasoning. Consequently, these six scenarios are grouped into a total of four patterns in terms of the distributions of response types.

^bExposure status shown in Table 1 corresponds to scenario #2.

From the perspective of counterfactual reasoning, scenarios #1 and #3 in Table 3 are essentially identical; the distributions of response types in the exposed and unexposed groups are the same. Therefore, the observed RD estimates are identical in these scenarios (i.e., 0). Similarly, scenarios #4 and #6 are essentially identical, because the distributions of response types in these scenarios are the same. As a result, the six scenarios can be grouped into a total of four patterns in terms of the distributions of response types. To highlight the distinction between confounding in expectation and realized confounding, we discuss two situations below, according to different mechanisms that generate the exposure events. In Situation 1, the treatment assignment is randomly determined, whereas, in Situation 2, the treatment assignment is causally influenced by the subject's sex. See eAppendix 1 and eTable 1, eTable 2, eTable 3, and eTable 4 for a technical discussion of these situations.

4.1. Situation 1 (with random assignment of the treatment)

When the treatment assignment of each subject is randomly determined, we assume the probability of the two males quitting smoking is equal to the probability of the two females quitting smoking (i.e., P[quitting | male] = P[quitting | female] = 1/2). In this situation, the six scenarios are induced randomly, with a probability of 1/6 (Table 4).

Table 4. Expected values of the estimators for risk and their difference in Situations 1 and 2.

	Observed values			Situation 1				Situation 2
	Risk estimates in		RD estimates	Weightsa	Observed risk × weight		RD estimator	Weightsb	Observed risk × weight		RD estimator
	Exposed	Unexposed			Exposed	Unexposed			Exposed	Unexposed
Scenario #1	1/2	1/2	0	1/6	1/12	1/12		16/33	8/33	8/33
Scenario #2	1/2	2/2	−1/2	1/6	1/12	2/12		4/33	2/33	4/33
Scenario #3	1/2	1/2	0	1/6	1/12	1/12		4/33	2/33	2/33
Scenario #4	0/2	2/2	−2/2	1/6	0	2/12		4/33	0	4/33
Scenario #5	0/2	1/2	−1/2	1/6	0	1/12		4/33	0	2/33
Scenario #6	0/2	2/2	−2/2	1/6	0	2/12		1/33	0	1/33
Expected value					1/4	3/4	−1/2		4/11	7/11	−3/11

RD, risk difference.

^aProbability of the four subjects quitting smoking is 1/2, so the six scenarios are induced randomly. See Table 3 and eAppendix 1 for details.

^bProbabilities of the two males and the two females quitting smoking are 2/3 and 1/3, respectively, so scenario #1 is expected to occur 16 times (i.e., 2⁴) as often as scenario #6. Likewise, each of the scenarios #2–5 is expected to occur four times (i.e., 2²) as often as scenario #6. See Table 3 and eAppendix 1 for details.

The expected values of the estimators for risk in the exposed and unexposed groups are calculated as: 3 × (1/6 × 1/2) + 3 × (1/6 × 0/2) = 1/4 and 3 × (1/6 × 1/2) + 3 × (1/6 × 2/2) = 3/4, respectively (Table 4). Consequently, the expected value of the estimator for RD in the four subjects is calculated as: 1/4 − 3/4 = −1/2, which is equivalent to the causal RD in the four subjects. In the notion of confounding in expectation, we say that there is no confounding in measure of the effect of smoking cessation on lung cancer in the four subjects (i.e., the second quadrant in Fig. 1). In this case, we describe the estimator as being an unbiased estimator and the realized value is referred to as an unbiased estimate.^18,20 Using the notion of confounding in expectation, each of the observed RD estimates in the six scenarios is referred to as an unbiased estimate for the four subjects, even if it is not equivalent to the causal RD in the four subjects. Conversely, if the notion of realized confounding is used, we simply compare the observed RD estimate in each scenario with the causal RD in the four subjects. Although there is no realized confounding in measure in scenarios #2 and #5, there is realized confounding in measure in scenarios #1, #3, #4, and #6 (i.e., the third quadrant in Fig. 1). This clearly demonstrates that realized confounding can be present even if the exposure assignment mechanism is completely random, especially if the study size is small.

A similar discussion applies when examining the presence of confounding in distribution. Note that the expected values of the estimators for risk in the exposed and unexposed groups (i.e., 1/4 and 3/4, respectively) are equivalent to the risk if all four subjects had been exposed and unexposed, respectively (Table 4). In the notion of confounding in expectation, there is no confounding in distribution of the effect of smoking cessation on lung cancer in the four subjects (i.e., the first quadrant in Fig. 1). Conversely, if the notion of realized confounding is used in Table 1, the observed risk in the exposed group (i.e., 1/2) is not equivalent to the risk if all four subjects had been exposed (i.e., 1/4). The observed risk of the unexposed group (i.e., 2/2) is not equivalent to the risk if all four subjects had been unexposed (i.e., 3/4). In the notion of realized confounding, there is confounding in distribution (i.e., the fourth quadrant in Fig. 1).

4.2. Situation 2 (with non-random assignment of the treatment)

Here, we consider a situation in which the treatment assignment of each subject is influenced by his or her sex. For example, the probability of the two males quitting smoking is twice as high as the probability of the two females quitting smoking (i.e., P[quitting | male] = 2/3 and P[quitting | female] = 1/3). Consequently, scenario #1 is expected to occur 16 times (i.e., 2⁴) as often as scenario #6. Likewise, each of the scenarios #2–5 is expected to occur four times (i.e., 2²) as often as scenario #6. In other words, scenario #1 is expected to occur with a probability of 16/33; each of the scenarios #2–5 is expected to occur with a probability of 4/33; and scenario #6 is expected to occur with a probability of 1/33 (Table 4).

The expected values of the estimators for risk in the exposed and unexposed groups are calculated as: (16/33 × 1/2) + 2 × (4/33 × 1/2) + 2 × (4/33 × 0/2) + (1/33 × 0/2) = 4/11 and (16/33 × 1/2) + 2 × (4/33 × 2/2) + 2 × (4/33 ×1/2) + (1/33 × 2/2) = 7/11, respectively (Table 4). Consequently, the expected value of the estimator for RD in the four subjects are calculated as: 4/11 − 7/11 = −3/11, which is not equivalent to the causal RD in the four subjects (i.e., −1/2). In this case, the estimator is a biased estimator, and the differential between the two values (i.e., −3/11 − (−1/2) = 5/22) is called bias.²⁰ In Situation 2, the observed RD estimate in Table 1 (i.e., −1/2) is confounded in the notion of confounding in expectation (i.e., the second quadrant in Fig. 1), although it is equivalent to the causal RD in the four subjects. In contrast, in the notion of realized confounding, there is no confounding in measure of the effect of smoking cessation on lung cancer in the four subjects (i.e., the third quadrant in Fig. 1).

When examining the presence of confounding in distribution, the expected values of the estimators for risk in the exposed and unexposed groups (i.e., 4/11 and 7/11, respectively) are not equivalent to the risk had all four subjects been exposed and unexposed, respectively (Table 4). In the notion of confounding in expectation, there is confounding in distribution of the effect of smoking cessation on lung cancer in the four subjects (i.e., the first quadrant in Fig. 1). Using the notion of realized confounding in Table 1, there is also confounding in distribution of the effect of smoking cessation on lung cancer in the four subjects (i.e., the fourth quadrant in Fig. 1).

4.3. Further implications from the extended simple example

A simple example to clarify the distinction between confounding in expectation and realized confounding is a useful educational tool to explain the concept of confounding more clearly. However, it is important to note that the exposed and unexposed groups are, by definition, determined by the specific pattern of exposure status. If these subpopulations are used as target populations, the discussion is logically restricted to the notion of realized confounding for the two target populations in that particular pattern. Therefore, to teach a generalized concept of bias, it is important to use the total population as the target population, as this facilitates the differentiation between notions of confounding in expectation and realized confounding.

As pointed out in a recent review by Schwartz et al.,²² there are discrepancies in the literature regarding whether random error should be included as a bias. Part of the confusion stems from lack of appreciation of the distinction between the notions of confounding in expectation and realized confounding. Similarly, the notion of confounding in expectation is essential to understand the relationship between accuracy, validity, and precision. See eAppendix 2 for further discussion, including a numerical description of the relationships in Situations 1 and 2. We also show mathematical definitions of the four notions of confounding in eAppendix 3.

5. Notions of confounding and directed acyclic graphs

In epidemiologic research, DAGs have been used extensively to determine the variables for which it is sufficient to control for confounding to estimate causal effects.^23–28 In this section, we graphically illustrate this point, highlighting the usefulness of DAGs in examining the presence of confounding in distribution in the notion of confounding in expectation (i.e., the first quadrant in Fig. 1).^12,14

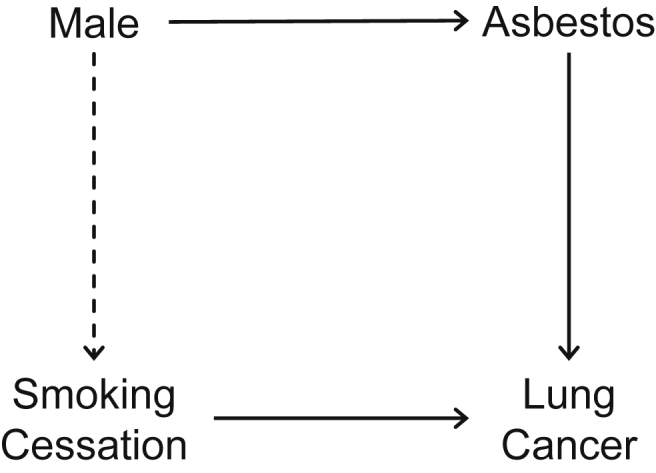
Fig. 2 shows a DAG for the total population in the example. The presence of a dashed arrow from “Male” to “Smoking Cessation” is determined by comparing the probability of the two males quitting smoking (i.e., P[quitting | male]) and the probability of the two females quitting smoking (i.e., P[quitting | female]). This is explained simply, using the two previously discussed situations.

Fig. 2. DAG for a study of the effect of smoking cessation on lung cancer. The presence of a dashed arrow from “Male” to “Smoking Cessation” is determined by comparing the probabilities of the two males and two females quitting smoking. If we use a DAG with signed edges in Situation 2, all the edges including the dashed arrow are positive. By applying the signed DAG approach, the sign of a backdoor path from “Smoking Cessation” to “Lung Cancer” is the product of the signs of the edges that constitute that path, and we can conclude that the sign of the bias is positive. This is consistent with the fact that, when the target population is the total population, there is positive bias in Situation 2 in the notion of confounding in expectation. DAG, directed acyclic graph.

5.1. Situation 1 (with random assignment of the treatment)

When the treatment assignment of the four subjects is randomly determined (i.e., P[quitting | male] = P[quitting | female] = 1/2), “Male” and “Smoking Cessation” are independent; there is no association between these two events. The dashed arrow from “Male” to “Smoking Cessation” in Fig. 2 is absent, and there is no backdoor path (i.e., a non-causal path that has an arrow pointing into the exposure) from “Smoking Cessation” to “Lung Cancer”. Consistent with our explanation in the previous section, in the notion of confounding in expectation, when the target population is the total population, bias does not occur in Situation 1; there is no confounding in distribution.

5.2. Situation 2 (with non-random assignment of the treatment)

When the treatment assignment of the four subjects are influenced by their sex (i.e., P[quitting | male] ≠ P[quitting | female]), “Male” and “Smoking Cessation” are not independent; there is a causal association between these two events. The dashed arrow from “Male” to “Smoking Cessation” in Fig. 2 is present, resulting in a backdoor path from “Smoking Cessation” to “Lung Cancer”. Consistent with our explanation in the previous section, in the notion of confounding in expectation, when the target population is the total population, bias occurs in Situation 2; there is confounding in distribution.

5.3. What are the implications from the directed acyclic graph?

DAGs are primarily useful to examine the presence of confounding in distribution in the notion of confounding in expectation (i.e., the first quadrant in Fig. 1). They are also practical tools to identify realized confounding, if the size of population is large enough. Furthermore, it has been shown that DAGs with signed edges, or signed DAGs, are useful in drawing conclusions about the direction of bias because of unmeasured confounders (Fig. 2).²⁷

Finally, although the causal effect of exposure on disease frequency in a population depends on the distribution of response types of individuals in that population, and DAGs have been used to provide visual summaries of hypothetical relationships among variables, they do not describe the relationships between underlying response types. To overcome this, Suzuki et al.²⁹ discussed how DAGs can be extended by integrating response types and observed variables, showing the conceptual link between unobservable response types and observed (or observable) data frequencies in the population. As an example of their usefulness, the principal stratification approach can be illustrated using extended DAGs.³⁰

6. Discussion

In this paper, we provide a typology of the four notions of confounding in epidemiology from the perspective of counterfactual reasoning. In eTable 5, we summarize sufficient and necessary conditions for no confounding in terms of response types, when the target population is the total population. Confounding in expectation is dependent on each mechanism that generates exposure events, whereas realized confounding is dependent on each product of that mechanism (or scenario). In both the notions of confounding in expectation and realized confounding, no confounding in distribution is a sufficient condition for no confounding in measure, irrespective of whether RD or RR are used as a measure of interest. Both confounding and selection bias result in a lack of exchangeability,²⁹ and comparable conditions apply to selection bias.

The different notions of confounding have not been fully appreciated in the literature, which has led to confusion of causal concepts in epidemiology. This lack of clear understanding could lead to inappropriate use of and underappreciation of DAGs,^16,31 which provide a simple algorithm for examining the presence of confounding in distribution in the notion of confounding in expectation.

For simplicity, throughout this paper we have ignored that causal effects estimated in one population are often intended for use in making decisions in another population.^32–35 This has been referred to as “transportability” of the causal effect,^32,33 and this is a question of external validity. When transporting the causal effect estimates to external targets, we need to consider the distributions of effect modifiers, interference patterns, and versions of treatment across populations.³² Although we have focused on the three usual internal target populations (i.e., the exposed group, the unexposed group, and the total population), our discussion about the notions of confounding analogously applies when using external targets. The potential outcomes and causal graph frameworks are also relevant, as they are for internal targets.

Simple examples can be powerful tools for understanding complex causal concepts; the power of simplicity, however, should be carefully exercised to achieve this goal.³¹ Recent developments in epidemiologic methods have demonstrated that substantial insight can be obtained from simplified representations of complex biological reality. None of us would deny the value of an old dictum (often referred to as Occam's razor) that one should not introduce needless complexity for purposes of prediction or explanation. Undeniably, however, all of us should also keep in mind Einstein's razor, the warning against being too simplistic: “Everything should be made as simple as possible, but not simpler”.³⁶ We hope that our simple example can serve as an effective tool to illustrate a typology of notions of confounding.

Conflicts of interest

None declared.

Acknowledgments

The authors are grateful to Jay S. Kaufman (McGill University) and M. Maria Glymour (University of California, San Francisco) for their helpful comments on earlier versions of this manuscript. This work was supported by The Okayama Medical Foundation and Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP26870383 and JP15K08776. The funding source had no role in the study design; data collection, analysis, or interpretation; writing of the manuscript; or the decision to submit the manuscript for publication.

Appendix A. Supplementary data

Supplementary data related to this article can be found at http://dx.doi.org/10.1016/j.je.2016.09.003.