Distributed representation of context by intrinsic subnetworks in prefrontal cortex

Significance

Information is represented in the brain by distributed patterns of cortical activity. In sensory cortex, these patterns are expressed across circuits with an intrinsic functional architecture that is organized along relevant stimulus dimensions. However, it is unknown whether similar organizational principles underlie distributed representations of more abstract information, such as rules or goals. We analyzed correlations in spontaneous activity to identify fine-scaled subnetworks in human prefrontal cortex. These subnetworks were differentially engaged when subjects followed rules in a complex decision-making task. Our results show how the abstract representations that support goal-directed cognition are constrained by an intrinsic functional architecture and prompt new models of information representation in association cortex.

Abstract

Human prefrontal cortex supports goal-directed behavior by representing abstract information about task context. The organizational basis of these context representations, and of representations underlying other higher-order processes, is unknown. Here, we use multivariate decoding and analyses of spontaneous correlations to show that context representations are distributed across subnetworks within prefrontal cortex. Examining targeted prefrontal regions, we found that pairs of voxels with similar context preferences exhibited spontaneous correlations that were approximately twice as large as those between pairs with opposite context preferences. This subnetwork organization was stable across task-engaged and resting states, suggesting that abstract context representations are constrained by an intrinsic functional architecture. These results reveal a principle of fine-scaled functional organization in association cortex.

The cerebral cortex exhibits functional organization at multiple spatial scales. At a coarse scale, the cortex is parcellated into functional areas (1, 2) that coordinate as networks through long-range connections (3–5). These areas represent and compute information with functional circuitry that is organized more finely. Some fine-scaled, intrinsic principles have been described in detail, particularly for sensory cortex (6, 7). In contrast, the subregional organization of prefrontal cortex (PFC), which gives rise to higher-order processes, including attention, decision-making, and goal-directed action (8, 9), remains largely uncharacterized. Whether PFC representations are encoded within an equipotential system or constrained by an intrinsic functional architecture is currently unknown.

Sensory cortex can be mapped by parametrically varying stimulus attributes and measuring changes in the neural response, but complex and dynamic response properties limit the effectiveness of this approach for mapping PFC and other association regions. An alternate strategy is to leverage spontaneous variability in neural activity. Neural responses to repeated presentations of sensory stimuli, or in the absence of stimulation and explicit task demands, exhibit variability that is attributed to ongoing spontaneous activity (10–13). Traditional analyses consider spontaneous activity to be noise, but there is increasing evidence that shared spontaneous variability is a signature of functional organization (14). Analyses of spontaneous correlations have been used to identify multiple large-scale functional networks (4, 5, 15) and boundaries between functional areas (2, 16–18) in human and nonhuman primate association cortex. The spontaneous correlation structure also mirrors established fine-scaled principles of functional organization in visual cortex, such as preferences for retinotopic position (19) and stimulus orientation (20). We therefore leveraged spontaneous activity to examine the fine-scaled functional organization of human PFC.

We focused our investigation on prefrontal computations that enable goal-directed behavior. Across two experiments, we scanned subjects with high-resolution fMRI while they performed tasks that demanded selective integration of noisy sensory evidence according to a shifting decision rule, or context. During rule-based decision-making, distributed patterns of activation in lateral PFC encode a representation of task context (21–23). We have previously reported that these context representations are strongly expressed in the inferior frontal sulcus (IFS), a prefrontal region defined through large-scale analyses of spontaneous correlations (24, 25). Here, we use multivariate decoding and analyses of subregional spontaneous correlations to show that context representations are organized across subnetworks within the IFS. Our results demonstrate that abstract cognitive representations emerge from an intrinsic functional organization in human PFC.

Results

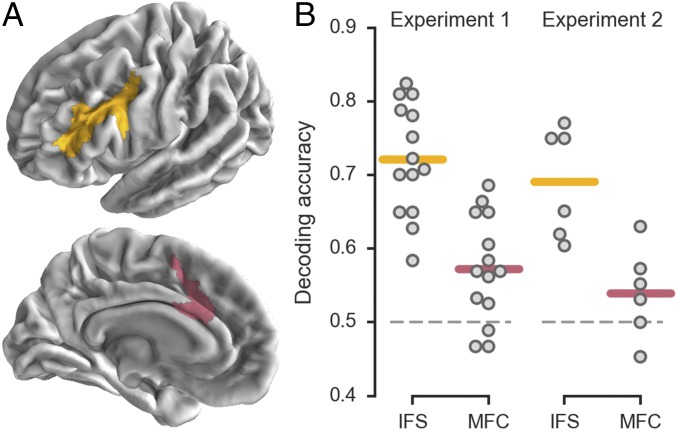
In experiment 1, subjects viewed a bivalent random dot stimulus and were cued to discriminate either the direction of coherent motion or the more prevalent color (Fig. S1A). We first sought to identify distributed patterns representing the task context (i.e., the motion vs. color rule). Guided by our previous findings (24), we applied linear classifiers to patterns of activation within the bilateral IFS (Fig. 1A). Cross-validated decoding accuracy exceeded chance at both the group (mean = 72.2%, t₁₃ = 11.22, P < 0.001; Fig. 1B) and subject (13/14 subjects P < 0.05, permutation test) levels. We also evaluated a region in medial frontal cortex (MFC) (Fig. 1A) that is widely implicated in cognitive control processes (26). Decoding performance in MFC exceeded chance at the group level (mean = 57.3%, t₁₃ = 3.89, P = 0.001) and in some individual subjects (6/14 subjects P < 0.05, permutation test) but was significantly weaker than in the IFS (paired t₁₃ = 7.09, P < 0.001; Fig. 1B). Because we could reliably decode task context representations from the IFS in nearly all subjects, we focus on this region in subsequent analyses.

Fig. S1.

Task design and behavior. (A and B) Experimental designs for experiments (A) 1 and (B) 2. (C) Mean RT and choice accuracy shown separately for each subject in experiment 1. (D) Mean RT and choice accuracy shown separately for each subject In experiment 2. Dark and light colors indicate behavior on trials with high and low stimulus strength, respectively.

Fig. 1.

Decoding task context in targeted PFC regions. (A) Region labels as defined on the group surface. Labels were reverse-normalized to individual subject brains before analysis. (B) Cross-validated accuracy for decoding task context (motion vs. color rule in experiment 1; orientation vs. color rule in experiment 2). Each point corresponds to the accuracy for an individual subject; horizontal lines indicate group means.

To examine the functional organization of these representations, we inverted the decoding models and obtained voxelwise estimates of context preference (Methods). When plotted on the cortical surface, voxel context preferences appeared organized into relatively fine-scaled, but not random, clusters (Fig. 2A and Fig. S2). To quantify the spatial organization, we asked whether it was possible to reliably predict a voxel’s preference from those of its neighbors at different distances (Fig. 2B and Fig. S3). This analysis suggested that voxel context preferences were both clustered and interdigitated relative to a simulated random organization, with an estimated upper bound for the local neighborhood size of 13.9 $\pm$ 1.7 mm (mean $\pm$ SD).

Fig. 2.

Spatial organization of voxel context preferences in the IFS. (A) Preferences shown on the cortical surface for two example subjects (for all subjects, Figs. S2 and S5). Left and Right correspond to left and right hemispheres, respectively. Colored histogram bars indicate voxels selected, using a permutation test, for analysis of spontaneous correlations. (B) Analysis of spatial clustering with mean-squared error of predictions about the context preference of each voxel using the average preferences of its neighbors at different distances on the cortical surface. Errors are normalized with respect to a simulated random distribution. Traces show mean across subjects for each experiment; error bands show SEM. Fig. S3 for individual subject plots.

Fig. S2.

Voxelwise context preferences for all subjects in experiment 1. Conventions are as in Fig. 2. Subjects are ordered (left to right and top to bottom) by decoding accuracy.

Fig. S3.

Voxelwise context preferences exhibit relatively fine-scaled spatial interdigitation. Black lines show the mean-squared error predicting the preference in ROI voxels by the average of the preferences at the specified radius. Gray bands show the 95% prediction interval from a permutation test where we randomly shuffled voxel preferences. Plots are scaled relative to the mean of the null distribution for ease of visual comparison. The vertical line shows the first point at which the observed error is larger than the error in the null distribution. Significantly lower error before this point provides evidence of spatial clustering, whereas significantly higher error after this point provides evidence of spatial interdigitation. Each plot shows data from one subject, and subjects are ordered by decoding accuracy.

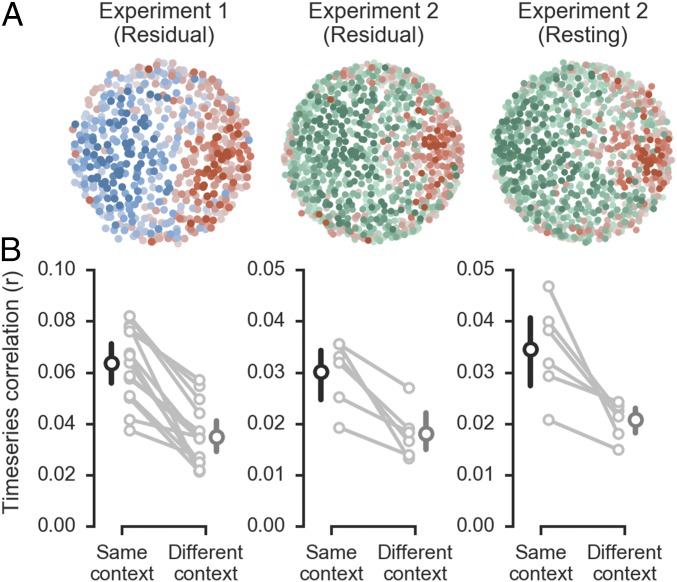
Our main question was whether the functional organization of distributed context representations corresponds to patterns of spontaneous activity within IFS. To answer this question, we first used a permutation test to identify voxels with relatively strong preferences for color or motion trials (Fig. 2 and Fig. S2). For each selected voxel, we then regressed out a model of task variables to produce an estimate of spontaneous activity and computed all pairwise time series correlations (12, 27). We next used multidimensional scaling (MDS) to reduce the dimensionality of the spontaneous correlation structure and visualize its relationship to context preferences (Fig. 3A and Fig. S4). We found that the first two dimensions accounted for 26.3% $\pm$ 4.9% (mean $\pm$ SD) of the variance in the spontaneous correlation structure. Within this low-dimensional space, voxels with similar context preferences were spatially clustered. This clustering implies that voxels with similar context preferences exhibit elevated spontaneous correlations.

Fig. 3.

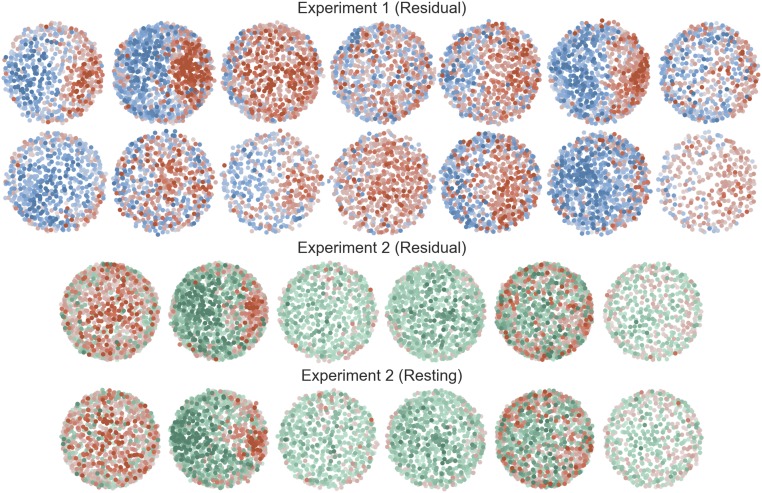
Spontaneous correlations reveal subnetworks that represent task context. (A) The relationship between spontaneous correlation structure and voxel-wise context preferences is shown for two example subjects. The positions of voxels were determined using an MDS of the spontaneous correlation matrix; the voxel context preferences are shown with the colormaps from Fig. 2. The same subject is shown for both experiment 2 analyses. Fig. S4 for all individual subjects. (B) Mean same-context and different-context spontaneous correlations. Large points and error bars show the group means and 95% confidence intervals; correlation values for individual subjects are connected with a line.

Fig. S4.

The relationship between spontaneous correlation structure and context preference for all subjects. Conventions are as in Fig. 3. Each plot shows data from one subject, and subjects are ordered by decoding accuracy.

To formally test the relationship between spontaneous correlations and context preferences, we computed the mean time series correlations between all pairs of voxels with the same binary context preference and all pairs with different context preferences. Same-context spontaneous correlations were approximately twice as large as different-context spontaneous correlations (paired t₁₃ = 8.05, P < 0.001; 14/14 subjects P < 0.05, permutation test; Fig. 3B). Stronger spontaneous correlations between voxels with similar context preferences indicate that they are organized into functionally specific subnetworks.

In experiment 2, we sought to identify subnetworks from spontaneous activity in the absence of sensory stimulation or explicit task demands. We therefore scanned an additional set of subjects both in the resting state and during performance of a context-dependent perceptual discrimination task. In this task, subjects were cued to determine either the more prevalent orientation or color of a field of small “sticks” (Fig. S1B). As in experiment 1, we applied linear classifiers to identify a distributed representation of task context in the IFS (mean = 69.1%, t₅ = 6.46, P < 0.001; 6/6 subjects P < 0.05, permutation test; Fig. 1B), which was, at best, weakly observed in the MFC (mean = 54.0%, t₅ = 1.58, P = 0.08; 2/6 subjects P < 0.05, permutation test; IFS vs. MFC paired t₅ = 3.11, P = 0.027; Fig. 1B). The spatial organization of context preferences in experiment 2 also provided evidence for fine-scaled clustering and interdigitation (Fig. 2 and Figs. S3 and S5).

Fig. S5.

Voxelwise context preferences for all subjects in experiment 2. Conventions are as in Fig. 2. Subjects are ordered (left to right and top to bottom) by decoding accuracy.

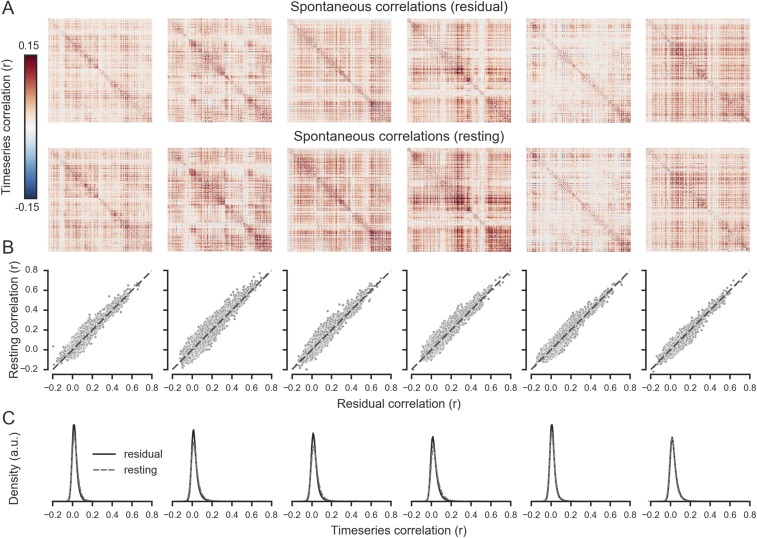
To determine whether the overall within-IFS spontaneous correlation structure was stable between rest and task performance, we evaluated the similarity of the voxelwise correlation matrices corresponding to each state (Fig. S6A). This test confirmed that the correlation structure was highly stable (mean r = 0.83, t₅ = 73.6, P < 0.001; 6/6 subjects P < 0.05, Mantel test; Fig. S6B). Moreover, we did not observe any general trends for elevated correlations in either of the two states (Fig. S6C). We conclude that task-engaged and resting-state measurements provide convergent information about the structure of fine-scaled spontaneous correlations in IFS.

Fig. S6.

The relationship between spontaneous correlations estimated using residuals in task-engaged state or during rest. (A) Spontaneous correlation matrices for IFS voxels estimated from task-engaged or resting-state data. (B) Scatterplots showing the similarity between the upper triangles of the two matrices in A. (C) Density plots showing the distribution of correlations across all pairs of voxels in the IFS. Each column shows data from one subject, and subjects are ordered by decoding accuracy.

The results of experiment 2 replicated the finding that distributed representations of context are expressed across fine-scaled subnetworks in IFS and extended this observation to subnetworks identified in the resting state (Fig. 3). As in experiment 1, spontaneous correlations identified from the residual signal in a task-engaged state were approximately twice as large for voxel pairs with the same context preference relative to voxel pairs with different context preferences (paired t₅ = 4.58, P = 0.006; 6/6 subjects P < 0.05, permutation test; Fig. 3B). Importantly, this was also the case when spontaneous correlations were identified in resting-state scans (paired t₅ = 3.67, P = 0.014; 6/6 subjects P < 0.05, permutation test; Fig. 3B). Qualitative features of the subnetwork organization, as apparent in the MDS plots (Fig. 3A and Fig. S4), were also similar between task-engaged and resting states. However, the low-dimensional embedding explained less variance than in experiment 1 across both measurements (task: 10.3% $\pm$ 1.8%; rest: 12.1% $\pm$ 2.6%), likely reflecting the lower signal-to-noise ratio of the high-resolution image acquisition in experiment 2.

The identification of fine-scaled subnetworks in the resting state suggests that they are an intrinsic feature of prefrontal organization. Because the resting-state acquisitions alternated with task scans, however, it is possible that subnetworks dynamically emerge during task performance and persist for several minutes following the offset of a task. This alternative account would predict that subnetworks should not be identifiable in the first resting-state scan of each session, which was acquired before task performance, and, potentially, that subnetwork strength should increase over time. To evaluate these predictions, we recomputed the difference in same-context and different-context correlations for each of the four resting-state acquisition times (Fig. S7). This analysis confirmed that subnetworks were identifiable before task performance (6/6 subjects P < 0.05, permutation test) and provided no consistent evidence for change in subnetwork strength over time.

Fig. S7.

Subnetworks are stable in resting-state scans across the duration of the scanning sessions in Experiment 2. Spontaneous correlations were computed separately for each of the four resting scans in each session and then averaged over sessions. Asterisks indicate significant differences at P < 0.05 as determined using a permutation test. Each plot shows data from one subject, and subjects are ordered by decoding accuracy.

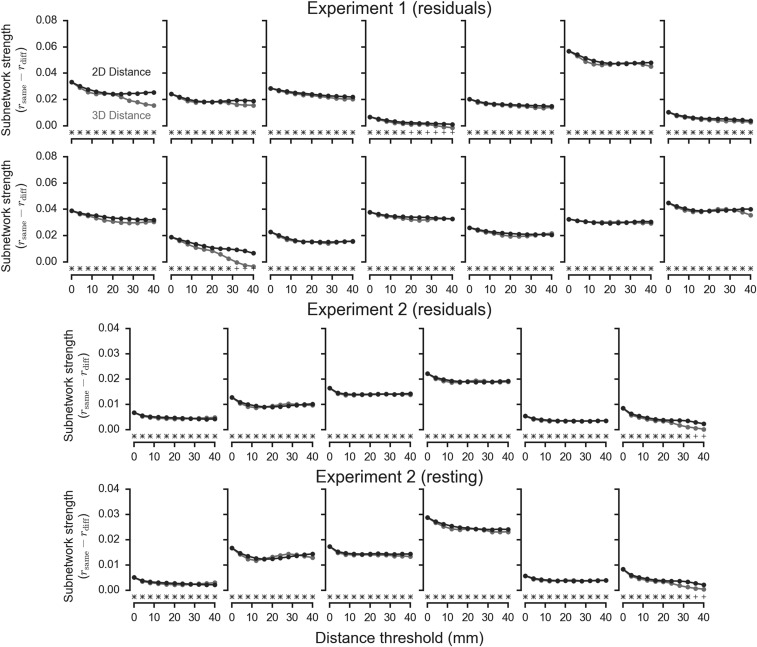
We also evaluated whether the relationship between context preference and spontaneous correlation could be fully attributed to short-range correlations between spatially clustered voxels with similar preferences. Specifically, we recomputed the mean same-context and different-context correlations while excluding voxel pairs below different distance thresholds (Fig. S8). The results indicated that subnetworks extend over relatively long distances, as the relationship remained significant even when excluding voxel pairs situated closer than 40 mm when measured either along the cortical surface (14/14 and 6/6 subjects P < 0.05, permutation test) or in the imaging volume (12/14 and 5/6 subjects). This analysis implies that our findings cannot be accounted for by spatial autocorrelation in the images.

Fig. S8.

Subnetworks extend over relatively long distances. Lines show the difference between mean same context and different context time series correlations computed while excluding pairs of voxels that are more proximal than the specified distance threshold. Distances were computed in two dimensions (along the cortical surface) and in three dimensions (in the imaging volume). Significant differences at P < 0.05, as determined using a permutation test, are shown for 2D analyses using a + and for 3D analyses using a ×. Each plot shows data from one subject, and subjects are ordered by decoding accuracy.

Discussion

Our results reveal an intrinsic organizational basis for the distributed representation of task context, a higher-order process that enables goal-directed behavior (8, 9). Our main result is that voxels with similar context preferences exhibited spontaneous correlations that were approximately twice as strong as those between voxels with opposite preferences. This finding provides evidence for the existence of functional subnetworks within the prefrontal components of the frontoparietal control network. Like large-scale functional networks, subnetworks were identified based on the spontaneous correlation structure in both resting-state activity and residual activity during task performance; this demonstrates that they are an intrinsic feature of prefrontal organization.

Spontaneous correlations are increasingly found to reflect functional organization (14), yet their role in and consequences for neural computations remain poorly understood. One proposal is that spontaneous correlations are tuned by Hebbian mechanisms to reflect the natural statistics of the environment (28) such that correlated spontaneous activity has the effect of regularizing task-evoked activity (11). This perspective relates to a computational model of abstract rule representations in PFC that suggests rule representations emerge from the learned statistical regularities of contextual elements that lead to goals (29). The subnetwork organization observed here may be a signature of these computations.

The presence and structure of spontaneous correlations in a network can also limit its representational capacity (30, 31). Indeed, humans exhibit striking capacity limits in attention and working memory (32), and these constraints are related to general cognitive abilities (33), including the active representation and evaluation of rules in dynamic environments (34). Our experiments lacked the statistical power to examine relationships between subnetwork organization and behavioral measurements of capacity, but our findings suggest a neural mechanism that underlies capacity constraints and prompt a novel approach for their future investigation.

We found that the fine-scaled spontaneous correlation structure in human PFC was highly stable during both rest and performance of a demanding cognitive task. This result is consistent with previous work examining large-scale networks in humans (12) and populations of neurons in macaque PFC (17). Therefore, both residual and resting-state spontaneous correlations largely reflect the intrinsic organization of PFC. Although task-evoked changes in large-scale spontaneous correlations are relatively small, they are statistically reliable (12, 35) and influence behavior (27, 36). Moreover, context-dependent information processing is also supported by dynamic changes in large-scale task-evoked correlations (37–39). Future work should examine changes in subnetwork correlation strength across a variety of cognitive tasks to determine how task performance shapes fine-scaled task-evoked and spontaneous correlations in PFC and whether temporal variability in subnetwork strength influences behavior.

The observed subnetwork organization qualitatively resembles densely interconnected “stripes” of neurons that have been characterized using anatomical tracers in nonhuman primate PFC (40). Computational models of working memory and cognitive control suggest that these stripes organize prefrontal representations (41), but their functional relevance has not been empirically determined. In line with model predictions, our results suggest that these design principles are relevant for structuring abstract representations in human PFC. Despite this qualitative agreement, our spatial clustering analyses indicate that context preferences are shared across larger spatial extents than can be accounted for by the stripe sizes previously observed in nonhuman primates (40). This may represent a difference between species or the effect of blurring within voxels. Quantitative between-species comparisons will require functional imaging data with a higher spatial resolution.

Multivariate decoding approaches are increasingly used to test theories about higher-order representations (42), but the organizational principles that underlie successful decoding in association cortex have remained unclear. Our data indicate that, for context decoding in lateral PFC, information is expressed across patches on the order of tens of millimeters and that multiple patches comprise functional subnetworks. It remains to be determined whether subnetwork organization is specific to the representation of context in lateral PFC or if it is a general principle in association cortex. We note that large-scale networks exhibit consistent organization across the brain (4, 5) and suggest that fine-scaled subnetworks in other regions may also provide structure for high-level cognitive representations.

Analyses of spontaneous correlations identify highly reproducible large-scale networks (4, 5) that are recruited in the performance of functional tasks (43–45). Despite this, the relevance of spontaneous correlations to the finer scales of organization that underlie cognitive representations has not been determined. Some aspects of fine-scaled organization in sensory cortex are reflected in spontaneous correlation structure, including retinotopic eccentricity biases (19) and orientation maps (20). Analyses that identify discontinuities in spontaneous correlation structure have also been applied in PFC to characterize areal boundaries (16, 18). Our results extend these previous findings in two important ways. First, they show that the fine-scale spontaneous correlation structure in PFC underlies task-evoked representations of abstract context information. Second, they indicate that subregional organization is characterized not just by discrete areas but by distributed subnetworks. These findings demonstrate the utility of spontaneous correlation analyses as a tool for studying the fine-scaled functional organization of association cortex and clarify the importance of functionally specific network organization in the human brain at multiple spatial scales.

Methods

Subjects.

Subjects were healthy right-handed members of the Stanford community and gave written informed consent before participating. The study was approved by the Stanford University Institutional Review Board. All subjects had normal or corrected-to-normal visual acuity and normal color vision. Subjects received $10/h for behavioral sessions and $20/h for scanning, and they additionally received a monetary bonus based on their performance during the imaging sessions.

In experiment 1, 20 subjects were recruited. Of this group, one was excluded early in the training session for poor color vision, one was excluded after the training session for performing at chance, and three ended the scanning session early due to fatigue or illness. One additional subject was excluded after initial data analysis suggested experimenter error during data acquisition; the decision to exclude this subject was made before performing the present analyses. The analyses reported here reflect data from the 14 remaining subjects (19 y to 29 y old; seven females). Each subject participated in one behavioral training session and one imaging session, for ∼3.5 total hours participation.

In experiment 2, eight subjects were recruited; all had extensive experience being scanned, one subject was author M.L.W., and one subject had participated in experiment 1. Of this group, one subject was excluded for early exit from the scanning session, and one subject was excluded due to data loss during image reconstruction. The analyses reported here reflect data from the remaining six subjects (24 y to 29 y old; three females). Each subject participated in two behavioral training sessions and two imaging sessions for ∼5 total hours participation.

Stimuli and Experimental Design.

Experiment 1.

The stimuli and experimental design for experiment 1 have been previously reported in detail (25). Briefly, subjects viewed a bivalent random dot stimulus and were cued to make either a motion or a color discrimination on each trial (Fig. S1A). Motion information was controlled by displacing a selected proportion of the dots coherently either up or down on each screen refresh, whereas the remainder of the dots were redrawn at a random location. Color information was controlled by drawing a selected proportion of the dots in either red or green on each screen refresh. The difficulties of the color and motion discriminations were set independently for each subject using a staircase procedure in a separate training session before scanning. On each trial, the relevant dimension (the context) was cued by the pattern of the frame surrounding the stimulus. Two distinct patterns cued a motion trial, and two distinct patterns cued a color trial. The cue appeared 1 s before the stimulus on one third of trials, it appeared concurrent with stimulus onset on one third of trials, and one third of trials were “cue-only” trials where the frame was presented for 1 s but was not followed by a stimulus. On trials with a stimulus, it was shown for 2 s. Subjects were instructed to respond as soon as they had made a decision, and they indicated their response with a button box held in the right hand. No feedback was presented during scanning. The experiment was structured into epochs with different proportions of motion and color trials (see ref. 25 for details). In total, each subject performed 900 trials (600 with a stimulus), evenly divided between motion and color contexts, across 12 scanner runs. Each run had a duration of 460 s (230 volumes).

Experiment 2.

The stimuli and experimental design for experiment 2 are reported in detail in the SI Methods. Briefly, subjects performed a context-dependent perceptual decision-making task that was similar to the task in experiment 1. Subjects viewed a bivalent stimulus that comprised a field of small sticks and were cued to make either an orientation or a color discrimination on each trial (Fig. S1B). Orientation and color information was manipulated by controlling the proportion of sticks drawn at either 45° or 135° and in either red or green. The difficulties of the orientation and color discriminations were set independently for each subject, using performance in two separate training sessions before scanning. In contrast to experiment 1, two different difficulty levels were used for each dimension during scanning. On each trial, the relevant dimension (the context) was cued by the shape of a polygon drawn at fixation. Two distinct polygons cued an orientation trial, and two distinct polygons cued a color trial. In contrast to experiment 1, the cue appeared concurrently with stimulus onset on every trial, the stimulus disappeared when subjects made their first button press response, and feedback was provided by blinking the fixation point after error trials. The relevant dimension on each trial was chosen randomly from a balanced distribution. In total, each subject performed 768 trials, evenly divided between orientation and color contexts, across 12 scanner runs in two separate scanning sessions. Each run had a duration of 370.8 s (515 volumes).

Resting-state scans.

During resting-state scans, a black fixation cross was displayed on a gray background drawn at 30% luminance. Subjects were instructed to fixate on the cross and to let their minds wander. Fixation and wakefulness were monitored with an eye-tracking camera. We collected eight separate resting-state scans from each subject in experiment 2. Each resting-state scan had a duration of 367.2 s (510 volumes). We aimed to collect an amount of data that has been previously shown to produce reliable estimates of spontaneous correlations at the individual subject level (46). Both scanning sessions began with a resting-state scan, and the remainder were interleaved with the task runs.

MRI Acquisition and Preprocessing.

Imaging data acquisition and preprocessing methods are described in detail in the SI Methods. Briefly, functional data were acquired with high spatial resolution in experiment 1 using a partial brain acquisition [2 × 2 × 2.3-mm voxels; 2,000-ms temporal resolution (TR)]) and high spatiotemporal resolution in experiment 2 using a whole-brain multiband acquisition (47) (2 × 2 × 2 mm; 720-ms TR). Functional data were distortion corrected (48) (only in experiment 2), spatially realigned, temporally interpolated (only in experiment 1), and high-pass temporally filtered. No spatial filtering or low-pass temporal filtering was applied. All analyses were performed in subject-specific space; no spatial normalization was applied. Functional time series data were denoised using estimates of head movements, nuisance signals derived from the white matter (49), and indicator vectors to remove frames with signal artifacts. Anatomical data were processed to construct a tessellated mesh model of the cortical surface (50), and functional data were placed in register by aligning each run’s mean volume with the anatomy (51).

Region of Interest Definition.

Data were analyzed within a priori regions of interest (ROIs) derived from a population atlas of large-scale resting-state networks (4). These regions are defined on the Freesurfer average cortical surface mesh. To obtain ROI masks in native functional space, we first reverse-normalized the ROI labels using the spherical registration parameters (52) and then transformed the vertex coordinates into the space of the first run using the inverse of the functional-to-anatomical registration. Voxels intersecting the midpoint between the gray–white and gray–pial boundaries were included in the analyses. This produced ROIs that respected the underlying 2D topology of the cortical surface and minimized the contributions of voxels lying outside of gray matter. To estimate distances between voxels along the cortical surface, we established a one-to-one mapping between voxels and surface vertices. A small number of vertices were originally mapped to multiple voxels; in these cases, we used the voxel whose center was closest to the vertex coordinate. We then constructed a distance matrix between each voxel center, where distances were measured with Djikstra’s algorithm on the midthickness cortex mesh (53).

Decoding Analyses and Context Preference Estimation.

We used linear classifiers to decode information about task context and estimate each voxel’s context preference. Decoding was implemented in three steps. We first used voxelwise general linear models to deconvolve the amplitude of the evoked response in different experimental conditions. The estimated response amplitudes were then used as samples in the multivariate analyses. Finally, we inverted the resulting decoding models to obtain estimates of each voxel’s context preference.

For experiment 1, the deconvolution model included 12 regressors reflecting a crossing between context (color or motion), trial type (early cue, concurrent cue, or cue only), and cue pattern. For experiment 2, the deconvolution model included 16 regressors reflecting a crossing between context (color or orientation), cue shape, color stimulus strength, and orientation stimulus strength. These regressors were dummy-coded such that, for each trial, there was only one regressor event. Regressors were defined as boxcars onsetting at the time of the cue and lasting for a duration equal to the sum of the cue duration and mean reaction time (RT), where applicable. To control for potentially confounding RT differences between contexts (54), we also included parametric regressors where the amplitude of the boxcar was determined by the z-scored RT on each trial. RT effects were modeled separately for each context and, in experiment 2, each stimulus strength. Condition regressors were convolved with a canonical difference-of-gammas model of the hemodynamic response function (HRF). We additionally included a set of identical regressors that were convolved with the temporal derivative of the HRF. After assembling and high-pass filtering the design matrix, the confound model that had been used to denoise the data was regressed out. The final deconvolution model was fit to the preprocessed time series from each voxel using ordinary least squares, separately for each run, producing a matrix of parameter estimates across conditions and voxels.

Multivariate analyses were performed using L2 penalized logistic regression models (55, 56) trained in a binary classification problem to predict task context (motion vs. color trials in experiment 1 and orientation vs. color trials in experiment 2). Specifically, this involved minimizing the following cost function:

$$\underset{\mathbf{w},c}{\text{min}}\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C{\displaystyle \sum _{i=1}^n}\text{log}\left\{\text{exp}\left[-y_i({\mathbf{X}}_i^T\mathbf{w}+c)\right]+1\right\},$$

where $y_i$ is the binary label for condition $i$, ${\mathbf{X}}_i$ is the sample vector of signal amplitude across the $n$ voxels in the ROI, and $C$ is a penalty parameter, which we set to the default value of 1.

We evaluated the accuracy of the decoding models using leave-one-run-out cross-validation. The cross-validation procedure was as follows: On each fold, we z-scored the training and test sets, regressed out any residual relationship with RT, fit the classifier to the training set, and evaluated its performance on the test set. We used the mean and SD of each feature in the training set to z-score the features in both the training and testing sets. RT effects were removed by averaging the RT across trials corresponding to each classifier sample. These vectors were then z-scored using the mean and SD in the training set. We regressed each feature in the training set onto the training set RT vector and used the resulting parameter estimates to residualize both the training and test set data with respect to RT.

We assessed the significance of the classification accuracy scores in a permutation framework where we randomly shuffled the context labels, within run, and then retrained and tested the classifier on each of 100 iterations to establish a distribution of accuracy scores under the null hypothesis (57). For group inferences, we subtracted the mean of each subject’s null distribution from the observed accuracy value and then performed a one-sample $t$ test against 0. For subject inferences, we used the percentile of the observed value in the null distribution to obtain a P value.

The weights that are estimated when training the decoding model are not directly interpretable, but they can be made interpretable by multiplying the weight vector $\mathbf{w}$ with the data covariance matrix, ${\mathrm{\Sigma }}_X$, to produce a vector of context preferences (58), $\mathbf{a}={\mathrm{\Sigma }}_X\mathbf{w}.$ The resulting vector, a, is a distributed pattern corresponding to each voxel’s relative preference for the two contexts. To identify voxels with strong context preferences, we compared each voxel’s preference value, $a_j$, to the vector of preferences assigned to voxel $j$ in the permutation test. Voxels where the observed value fell below the 10th percentile or above the 90th percentile in the null distribution were used in subsequent analyses. Note that this procedure uses a liberal threshold, as our goal was not to reject a null hypothesis in any individual voxel but rather to identify a suitably large population of voxels that expressed relatively strong preferences for each of the contexts. Our results did not depend on the specific threshold chosen.

To evaluate the spatial organization of the context representations, we determined how well we could predict the preference of a given voxel from the preferences of its neighbors at a given radius. Specifically, we quantified the error at radius $i$ as the mean-squared difference between the preference in each of the $n$ ROI voxels and the mean of the $m$ voxels that were separated from it by a distance within 2 mm of the specified radius,

$$e_i=\frac{1}{n}{\displaystyle \sum _{j=1}^n}{(a_j-\frac{1}{m}{\displaystyle \sum _{k=1}^m}{a}_k)}^2.$$

We then compared the observed error value to a null distribution of errors obtained by randomly shuffling the voxel preferences. To quantify the clustering, we estimated an upper bound for the neighborhood size as the first point at which the observed error values were greater than the mean of the null distribution at that distance.

Estimation of Spontaneous Correlation Strength.

We estimated the magnitude of spontaneous correlations in both task-engaged and resting states. Spontaneous activity in a task-engaged state was estimated using residual data after regressing out a model of task-evoked effects (12, 27). Specifically, the task models were structured identically to the models used during the deconvolution step of the decoding analyses, with the difference that, rather than convolving regressors with a canonical HRF model, we used a finite-impulse-response (FIR) basis to more flexibly fit and remove task-evoked responses. In experiment 1, where the design was oversampled relative to the data acquisition, we first upsampled the time series data to 1-s resolution using cubic spline interpolation. The sampling rate of the design of experiment 2 was matched to that of the data acquisition and so no resampling was applied. In each case, we used 24 FIR regressors per condition, onsetting two TRs before the cue. These models were fit using ordinary least squares to denoised time series data that had been concatenated across runs. Analyses of spontaneous correlations in the resting state were performed on the entire time series of denoised data. Spontaneous correlation matrices were created for both datasets by estimating the Pearson correlation between the time series from each voxel, separately within each run, and then averaging correlation values over runs.

We used the data from experiment 2, where we collected both task-based and resting-state data from the same subjects, to evaluate the similarity of the spontaneous correlation structure under these two conditions. Specifically, we vectorized the upper triangles of the two correlation matrices and then computed a Pearson correlation between the two vectors. We tested the significance of this value with the Mantel test, where, on each of 100 iterations, we applied the same permutation to the rows and columns of the resting-state correlation matrix and then recomputed the similarity to the task-engaged correlation matrix to generate a null distribution of similarity values.

Relating Context Preferences to Spontaneous Correlations.

To visualize the relationship between context preference and spontaneous correlation, we submitted the spontaneous correlation matrix to metric MDS, which embeds the similarity matrix in a 2D space. We then created scatterplots where each point corresponded to a voxel. The position of the points was determined by the MDS embedding coordinates, and the color of the points was determined by their context preferences. Because the axes returned by MDS are arbitrary, we computed the matrix−vector product between the MDS coordinates and the voxel preferences and then applied a rotation so that the resulting coordinate fell on the positive side of the x axis. We determined the amount of variance explained by the low-dimensional projection by computing the squared Pearson correlation between the pairwise correlation distance measurements submitted to the MDS algorithm and the pairwise euclidean distance of points in the resulting embedding space.

To quantify the relationship between spontaneous correlations and context preferences, we computed the mean correlation between voxels with the same context preference and the mean correlation between voxels with different context preferences. We then evaluated the significance of this value with a permutation test. On each of 100 iterations, we randomly shuffled the context preference labels and recomputed the two measures. We then compared the observed difference in correlations to the distribution of differences under the null hypothesis.

To determine the spatial extent of the functionally selective spontaneous correlations, we recomputed the above measures while systematically excluding correlations between voxels that were separated by less than a specified distance threshold. Note that this process is similar to how we evaluated the spatial clustering of the voxel preferences, but here we used all voxels separated by a distance larger than the threshold rather than voxels situated at that specific distance.

Code Availability.

Data were analyzed using published open-source software and custom code written in Python. Imaging data were processed with a workflow of FSL 5.0.8 (59) and FreeSurfer 5.3.0 (60) tools implemented in Nipype 0.11.0 (61). The Python code used a number of libraries including numpy, scipy, matplotlib, seaborn, pandas, and jupyter. Cortical surface visualizations were created using pysurfer. All custom code will be made available at https://github.com/WagnerLabPapers/Waskom_PNAS_2017.

SI Methods

Stimuli and Experimental Design: Experiment 2.

Subjects in experiment 2 performed a context-dependent perceptual discrimination task (Fig. S1B). The stimulus was a 5.5° radius circular array of 0.3° × 0.1° sticks centered on a 0.2° fixation point. No sticks were drawn within 1° of fixation. The stick centers were chosen using a Poisson disk sampling algorithm to ensure that sticks were densely positioned without overlapping (minimum distance between stick centers: 0.35°) or conforming to a rigid grid. Each stick was oriented 45° left or right of vertical and colored either red or green. Colors were chosen using the Commission Internationale de l'Eclairage (CIE) L_CH system to obtain distinct hues (red, 60; green, 140) with equal chroma (30) and luminance (80). The specific luminance values were calibrated before each session with a separate color discrimination task that used a staircase to match the perceived brightness of the colors. The screen background was drawn in gray at 30% luminance. During the scanning session, the stimulus was presented on a 1,920 $\times$ 1,080-pixel LCD display with a 60-Hz refresh rate, which was placed at the back of the scanner bore and viewed through a mirror attached to the head coil. Behavioral sessions were performed on MacBook Pro laptop computers. Stimulus presentation and response collection were controlled using PsychoPy.

The subject’s task was to make either a color or an orientation discrimination on each trial. On color trials, they had to determine whether more sticks were drawn in either red or green; on orientation trials, they had to determine whether more sticks were oriented left or right. The trial type (the context) was cued with a three- to six-sided 1°-wide polygon drawn at 40% luminance around the fixation point. Two distinct shapes cued a color trial, and two shapes cued an orientation trial. These assignments were counterbalanced across participants, and task demands did not otherwise vary between the two cues used for each context. Subjects were instructed to maintain fixation, and eye movements were monitored with a camera inside the scanner bore. Each trial began when the fixation point turned from black to white for 720 ms to signal the imminent trial. The cue and stimulus then appeared simultaneously. Subjects were instructed to respond as soon as they had reached a decision, balancing speed and accuracy. Responses were made using button boxes held in the left and right hands. The same buttons were used for both contexts. The mapping between color responses and hands was counterbalanced across participants, but left and right buttons always mapped to left and right orientation decisions. The stimulus disappeared when the subject made a response. Feedback was provided by blinking the fixation point at 10 Hz for 500 ms after errors. Following the trial, the fixation point turned black to signal the intertrial interval (ITI). The ITI duration was drawn from a truncated geometric distribution over TRs with p = 1/3 and a maximum of 10 TRs (mean ITI: 1.86 TRs). Each task run had a total duration of 370.8 s.

The stimulus changed dynamically over the course of each trial. This method was intended to decrease reliance on a strategy of searching for clusters of sticks with the same feature and, instead, to encourage integration of evidence over time. Specifically, individual sticks were replaced, possibly in a different color or orientation, with a probability of 0.05 on each screen refresh. During replacement, the stick disappeared for nine frames and then had a 0.5 probability of being redrawn on each subsequent frame. Stimulus strength was manipulated by controlling the proportion of sticks drawn with each color and orientation. We defined stimulus strength as p_feature − 0.5; that is, a trial where 60% of the sticks were red had a color strength of 0.1.

Subjects were trained on the task in a pair of 1-h behavioral sessions that occurred 1 d to 3 d before scanning. Subjects first performed the task with high stimulus strength to learn the meanings of the cues and the correct response mappings. This session began with blocked trials that shared a context, but the block length was decreased over the course of the introductory session so that subjects were gradually acclimated to context switching. Subjects then continued the high-stimulus strength practice until they reported comfort with the basic elements of the task and had reached near-perfect accuracy (subjects performed 650 trials of the practice task). They next performed two blocks of a calibration task (400 trials per block) where the stimulus strength was randomly varied between 0.02 and 0.18 in steps of 0.04 to find values to use during scanning. We fit cumulative Weibull functions to the resulting choice accuracy data, separately for color and motion trials, and chose stimulus strengths for hard and easy trials that would be expected to produce 65% and 95% accuracy, respectively.

Each task run consisted of 64 trials, representing a full crossing of context (color or orientation), context cue, color strength, orientation strength, dominant color, and dominant orientation. Event schedules for each run were optimized in two steps. First, a large space (n = 50,000) of possible event orders was searched, and the 16 schedules that best minimized the average deviation from the ideal first-order transition matrix within each of the six trial features were selected. Second, “null” events were inserted into each schedule to create a jittered distribution of ITIs that optimized the efficiency of estimating the HRF. For each subject, we used 12 of these schedules, in a random order, over the course of the experiment.

MRI Acquisition.

Brain imaging was performed on a 3T GE Discovery MR750 system (GE Medical Systems) using a 32-channel transmit-receive head coil (Nova Medical). In experiment 1, partial-brain functional images were obtained using a T2*-weighted 2D echo planar imaging sequence with a relatively high spatial resolution [TR = 2 s, echo time (TE) = 30 ms, flip angle = 77°, 33 slices, 96 $\times$ 96 matrix, 2 $\times$ 2 $\times$ 2.3-mm voxels, axial oblique interleaved acquisition]. Slices were acquired aligned with and dorsal to the superior temporal sulcus to provide coverage of frontal and parietal cortex. In experiment 2, whole-brain functional images were obtained with high spatial and temporal resolution using a T2*-weighted multiband 2D echo planar imaging sequence (47) (TR = 720 ms, TE = 30 ms, flip angle = 53°, 64 slices, 110 $\times$ 110 matrix, 2-mm isotropic voxels, multiband factor = 8, axial oblique interleaved acquisition). Aside from scan duration, acquisition parameters were identical for task and resting runs. In both experiments, whole-brain high-resolution (0.9-mm isotropic voxels) T₁-weighted SPGR volumes were acquired for cortical surface modeling and across-run alignment.

MRI Preprocessing.

Unless otherwise specified, data from experiments 1 and 2 were processed with the same workflow. After image reconstruction, images from experiment 2 underwent susceptibility distortion correction using two single-band images with reversed phase-encode blips (48). This step was omitted for experiment 1 because we did not collect fieldmap images. Next, each time series was realigned to its middle volume using a normalized correlation cost function and cubic spline interpolation. The time series data for experiment 1 were then temporally resampled using sinc interpolation to correct for slice timing differences. This step was not performed for experiment 2 data because of the high temporal resolution and multiband acquisition. Each time series was then scaled with a single multiplicative factor so that the median value across time and space (within a brain mask derived from the anatomical volume) equaled 10,000. Finally, the time series data were temporally high-pass filtered by fitting and removing Gaussian-weighted running lines with an effective cycle cutoff of 128 s. Functional data were not spatially smoothed.

Separately, the T₁-weighted anatomical volume (or average volume in the case of multiple acquisitions) was processed using Freesurfer to segment the gray–white matter boundary and construct tessellated meshes representing the cortical surface (50). A linear transformation (six degrees of freedom) between the native functional space and the native anatomical space was estimated for each run using the mean functional image from each time series. This registration was estimated by optimizing a boundary-based cost function, which aligns the data with the model of gray-white boundary (51).

Time series data were then denoised by fitting and removing models with head motion and anatomically derived nuisance variable information. Specifically, this model included six motion regressors (three rotations and three translations), six regressors representing principal components of signals extracted from the deep white matter (49), and indicator vectors identifying scans with signal artifacts. Nuisance variable extraction was performed by transforming the Freesurfer-segmented white matter mask into the functional space, eroding it by three voxels, and submitting the resulting time × voxel matrix to principal components analysis. Signal artifacts were automatically determined using the following criteria: any frame in which the motion parameters indicated a displacement relative to the previous frame larger than a threshold (0.5 mm in experiment 1 and 0.25 mm in experiment 2); any frame in which the median signal across the whole-brain mask deviated from the run median by more than five median absolute deviations (MAD); and any frame in which any median slice intensity, after subtracting the whole-brain median, deviated from the run median by greater than 10 MAD. All voxels were denoised using the same set of nuisance variables. These models were fit using linear regression, and the residual data were used in subsequent analyses.

The middle volume of the first functional task run served as the common space for each subject. Other frames from the first run were realigned to this space during motion correction. Frames from other runs were first realigned to that run’s middle volume and then transformed into the common space by concatenating the transformations from that run to the anatomy and the inverse of the transformation from the first run to the anatomy. Images were resampled with cubic spline interpolation. All analyses were performed in a subject-specific, voxel-based space; data were not normalized into a common group space.