The Sites of Evaporation within Leaves

Thomas N Buckley; Grace P John; Christine Scoffoni; Lawren Sack

doi:10.1104/pp.16.01605

. 2017 Feb 2;173(3):1763–1782. doi: 10.1104/pp.16.01605

The Sites of Evaporation within Leaves^¹^,^{^[OPEN]}

Thomas N Buckley ^1,^2,^*, Grace P John ^1,², Christine Scoffoni ^1,², Lawren Sack ^1,²

PMCID: PMC5338672 PMID: 28153921

Vapor transport within leaves influences tissue water potentials, requiring the reassessment of hypotheses related to the sites of evaporation, including that measured hydraulic and stomatal conductances are directly influenced by where evaporation occurs.

Abstract

The sites of evaporation within leaves are unknown, but they have drawn attention for decades due to their perceived implications for many factors, including patterns of leaf isotopic enrichment, the maintenance of mesophyll water status, stomatal regulation, and the interpretation of measured stomatal and leaf hydraulic conductances. We used a spatially explicit model of coupled water and heat transport outside the xylem, MOFLO 2.0, to map the distribution of net evaporation across leaf tissues in relation to anatomy and environmental parameters. Our results corroborate earlier predictions that most evaporation occurs from the epidermis at low light and moderate humidity but that the mesophyll contributes substantially when the leaf center is warmed by light absorption, and more so under high humidity. We also found that the bundle sheath provides a significant minority of evaporation (15% in darkness and 18% in high light), that the vertical center of amphistomatous leaves supports net condensation, and that vertical temperature gradients caused by light absorption vary over 10-fold across species, reaching 0.3°C. We show that several hypotheses that depend on the evaporating sites require revision in light of our findings, including that experimental measurements of stomatal and hydraulic conductances should be affected directly by changes in the location of the evaporating sites. We propose a new conceptual model that accounts for mixed-phase water transport outside the xylem. These conclusions have far-reaching implications for inferences in leaf hydraulics, gas exchange, water use, and isotope physiology.

The pathways for water transport through a plant are often perceived to end at the sites of evaporation outside the xylem within leaves (Holmgren et al., 1965; Meidner, 1975; Farquhar and Raschke, 1978; Blizzard and Boyer, 1980; Tyree and Yianoulis, 1980; Sheriff, 1984; Boyer, 1985; Yang and Tyree, 1994; Brodribb et al., 2002; Sperry et al., 2002; Buckley, 2005; Sack and Holbrook, 2006; Mott, 2007; Beerling and Franks, 2010; Berry et al., 2010; Pieruschka et al., 2010). This perception gave rise to a number hypotheses (summarized in Table I) that depend on the locations of the evaporating sites, with important implications for understanding and measurement of key processes across hydraulics and gas-exchange physiology. (1) The location of the evaporating sites determines the path length for water transport outside the xylem and, therefore, should strongly influence outside-xylem, leaf, and plant hydraulic conductances (K_ox, K_leaf, and K_plant, respectively; for a list of symbols, see Table II). (2) If the water potential (ψ) at the evaporating sites does not coincide with bulk leaf water potential (ψ_eq; the ψ of an equilibrated, excised, nontranspiring leaf, as typically measured in a Scholander-type pressure chamber), then estimates of K_leaf would be in error (Tyree and Zimmermann, 2013; Brodribb et al., 2016), because K_leaf is typically operationally defined for practical measurements as the ratio of the transpiratory flow rate to ψ_eq (Brodribb and Feild, 2000; Sack et al., 2002). (3) The rate of evaporation from a given tissue determines the rate of water flow through liquid phase pathways proximal to that tissue and, therefore, also determines the tissue’s ψ (Meidner, 1975; Cowan, 1977; Tyree and Yianoulis, 1980; Maier-Maercker, 1983; Sheriff, 1984). (4) Chemical species with low vapor pressure will become more concentrated at the sites of evaporation (Canny, 1990, 1993). (5) Because isotopologues of water that are heavier than H₂¹⁶O are enriched at the sites of evaporation (Craig and Gordon, 1965; Yakir et al., 1989; Barbour et al., 2000), the location of those sites affects the mixing of isotopically enriched water with xylem water and, thus, bulk leaf enrichment (Yakir et al., 1990; Roden and Ehleringer, 1999; Farquhar and Gan, 2003). (6) The location of the evaporating sites determines the extent to which the diffusion pathways for CO₂ and water vapor overlap, which, in turn, affects the interpretation of correlations between K_leaf and mesophyll conductance to CO₂ (g_m; Flexas et al., 2013; Tomás et al., 2013), as well as (7) the opportunity for diffusive interference between water vapor and CO₂ (reflected in the ternary corrections for gas-exchange calculations; Farquhar and Cernusak, 2012). (8) Given that stomatal conductance to water (g_s) is estimated as transpiration rate divided by the difference between the saturation vapor pressure of pure water at the measured leaf temperature (T) and the vapor pressure of air outside the stomata, and given that the vapor pressure in the intercellular airspaces is perceived to be closest to saturation at the sites of evaporation, the distance of the evaporating sites from stomatal pores should influence the calculated value of g_s as well as (9) the calculated value of intercellular CO₂ concentration (c_i), which is generally estimated using g_s (Meidner, 1975; Farquhar and Sharkey, 1982). (10) The humidity in the intercellular airspaces adjacent to the transpiring epidermis will be further from saturation (calculated at the T of the lower leaf surface) if evaporation occurs farther from the stomatal pores and closer to saturation if evaporation occurs closer to stomatal pores.

Table I. List of hypotheses that involve the location of the evaporating sites, with corrections based on insights presented in this article.

Hypotheses That Depend on the Location of Evaporating Sites	Suggested Modification Based on Model Findings
(1) The path length for water transport outside the xylem, and therefore the values of K_ox, K_leaf, and K_plant, are defined by where evaporation occurs; for example, if evaporation occurs close to the epidermis, then K will be smaller, all else being equal, because water will have to travel farther before evaporating	ψ at any given point in the leaf is influenced by both liquid and vapor phase transport, so the driving force for water transport and K_leaf are not causally related to the location of the evaporating sites; whether the term hydraulic conductance should be restricted to include only liquid phase pathways is a subjective matter; we argue that it is simpler to refine our interpretation of hydraulic to include vapor transport pathways, because they influence ψ values just as liquid pathways do and because operational measurements of hydraulic conductances often include contributions from vapor transport
(2) If the pressure chamber estimate of leaf ψ (ψ_eq) does not coincide with the ψ at the sites of evaporation, then ψ_eq will underestimate or overestimate the true driving force for water transport and, thus, overestimate or underestimate, respectively, the true values of K_ox, K_leaf, and K_plant
(3) The drawdown in ψ from the xylem to any given tissue will increase if the evaporation rate from that tissue increases, even if the overall transpiration rate does not change, because increased evaporation from a tissue implies increased flow through the hydraulic resistances proximal to that tissue	The ψ drawdowns to different tissues are largely unaffected by shifts in the location of the evaporating sites for a given total evaporation rate from the whole leaf (see Fig. 13), because such shifts are driven primarily by changes in the magnitude of anisothermal vapor transport (AVT), which is not affected directly by ψ
(4) Solutes dissolved in liquid water will tend to accumulate near the sites of evaporation (but will disperse by diffusion), because such solutes typically have negligible vapor pressures and, thus, remain in solution when a portion of their solvent (i.e. water) evaporates	No modification
(5) The effective diffusion length for water enriched in heavier isotopologs will be greater if the evaporating sites are farther from the xylem (i.e. closer to the stomatal pores), because enrichment occurs primarily at the evaporating sites	No modification
(6) If evaporation occurs closer to the stomatal pores, then the pathways for (liquid) water transport and for inward CO₂ diffusion will overlap to a greater extent, possibly helping to explain the observed correlations between measured K_leaf and mesophyll conductance to CO₂ (g_m)	A correlation between K_leaf and g_m could arise due to any overlap between the pathways for CO₂ diffusion and water transport, whether liquid, vapor, or both; however, K_leaf-g_m correlations would not imply the mutual involvement of aquaporins if CO₂ pathways overlapped primarily with vapor phase water pathways
(7) The opportunity for diffusive interference between water vapor efflux and CO₂ influx will be greater if the evaporating sites are farther from the stomatal pores, because this will increase the overlap between the diffusion pathways for water vapor and CO₂	This is correct if shifts in the location of the evaporating sites are accompanied by differences in vapor flux (flow per unit of area in the intercellular airspaces), as may occur when mesophyll evaporation is favored by increased photosynthetic photon flux density (PPFD), but incorrect when differences in the location of the evaporating sites result solely from differences in the airspace fraction (as may apply to comparisons between species)
(8) The gas-exchange estimate of g_s is lower than the true conductance through stomatal pores to the degree that the evaporating sites are located farther from the stomatal pores, because g_s measures diffusion from the sites of evaporation to the outside of the pores	The g_s value inferred by gas exchange describes diffusive pathways that begin at some location within the intercellular airspaces (specifically, where relative humidity is 100% as calculated based on the measured leaf T) and end just outside the stomatal pores; the origin of those pathways within the leaf can vary independently from, and even in opposite directions to, the location of the evaporating sites (see Figs. 8 and 12), so measured g_s and c_i are not related directly to the sites of evaporation; despite these shifts, the intercellular airspaces remain close to saturation, and inferred g_s only slightly underestimates the conductance of the (shorter) diffusive pathways that extend only across the stomatal pores themselves
(9) The gas-exchange estimate of c_i is larger than the true value of c_i prevailing in the mesophyll if the evaporating sites are closer to the stomatal pores, because c_i is estimated using g_s
(10) The intercellular airspaces in tissues closer to the transpiring epidermis will be farther below 100% relative humidity (calculated at the T of the lower leaf surface) to the extent that evaporation occurs farther from the transpiring epidermis

Open in a new tab

Table II. List of symbols.

Symbol	Description	Unit
AVT	Anisothermal vapor transport	–
c_i	Intercellular CO₂ concentration	μmol mol⁻¹
D_wa	Diffusivity of water vapor in air	m² s⁻¹
ΔT	Vertical temperature gradient within leaf	°C
E	Leaf transpiration rate	mmol m⁻² s⁻¹
E_i	Stomatal transpiration from node i	mol s⁻¹
F_aniso,ij	AVT from node i to node j	mol s⁻¹
F_i	Net AVT out of node i	mol s⁻¹
f_TK	Thermal conductivity of cells divided by that of pure water	Unitless
g_bh	Boundary layer conductance to heat	mol m⁻² s⁻¹
G_i	Net IVT and AVT out of node i	mol s⁻¹
g_bw	Boundary layer conductance to water	mol m⁻² s⁻¹
g_m	Mesophyll conductance to CO₂	mol m⁻² s⁻¹
g_s	g_s to water	mol m⁻² s⁻¹
g_tw	Total conductance to water	mol m⁻² s⁻¹
H_i	Net sensible heat loss from node i	J s⁻¹
IVT	Isothermal vapor transport	–
K_f,ij	Conductance for AVT from node i to node j	mol s⁻¹ K⁻¹
K_g,ij	Conductance for IVT from node i to node j	mol s⁻¹ Pa⁻¹
K_h,ij	Conductance for sensible heat transfer from node i to node j	mol s⁻¹ K⁻¹
K_leaf	Leaf hydraulic conductance	mmol m⁻² s⁻¹ Pa⁻¹
K_l,ij	Conductance for liquid water transport from node i to node j	mol s⁻¹ Pa⁻¹
K_ox	Outside-xylem hydraulic conductance	mmol m⁻² s⁻¹ MPa⁻¹
K_plant	Whole-plant hydraulic conductance	mmol m⁻² s⁻¹ MPa⁻¹
λ	Latent heat of vaporization	J mol⁻¹
L_i	Net liquid water loss from node i	mol s⁻¹
P_m	Cell membrane osmotic water permeability	μm s⁻¹
PPFD	Photosynthetic photon flux density at adaxial surface	μmol m⁻² s⁻¹
p_sat	Saturation vapor pressure	Pa
R_a	Effective Poiseuille radius of apoplastic nanopathways	nm
Q_i	Net radiative energy loss from node i	J s⁻¹
T	Temperature	°C or K
T_air	Air temperature	°C
t	Leaf thickness	m
T_i	Temperature at node i	°C
T_m	Measured leaf temperature (T at lower surface)	°C
V_i	Evaporation from node i	mol s⁻¹
VLA	Vein length per unit of leaf area	mm⁻¹
V_w	Molar volume of water	m³ mol⁻¹
w_air	Water vapor mole fraction of ambient air	mol mol⁻¹
w_avg	Average of w_air and w_leaf	mol mol⁻¹
w_leaf	Water vapor mole fraction in leaf intercellular airspaces	mol mol⁻¹
w_sat	Saturation vapor pressure divided by atmospheric pressure	mol mol⁻¹
w′_s	w_sat evaluated at T_m	mol mol⁻¹
ψ	Water potential	Pa or MPa
ψ_i	Water potential of node i	Pa
ψ_eq	Water potential of an excised, nontranspiring, equilibrated leaf	Pa or MPa

Open in a new tab

In addition to the hypotheses described above for processes within the leaf, stomatal biologists also have long been interested in the evaporating sites because of the perception that the ψ of epidermal and guard cells will be more negative if they support a large fraction of evaporation (a corollary of hypothesis 3 above), thus influencing stomatal function (Meidner, 1976; Cowan, 1977; Tyree and Yianoulis, 1980; Sheriff, 1984; Buckley, 2005; Mott, 2007). Stomatal aperture depends on the turgor of guard cells relative to that of adjacent epidermal cells, and preferential reduction of ψ and turgor pressure in the epidermis due to localized evaporation could signal guard cells to release osmolytes, closing stomata (Darwin, 1898; Stalfelt, 1929; Meidner, 1986; Buckley, 2005, McAdam et al., 2016). Similarly, preferential evaporation from guard cells in dry air could explain the stomatal response to humidity by causing a larger turgor decline in guard cells than in epidermal cells, overcoming the epidermal mechanical advantage (Maier-Maercker, 1983; Sheriff, 1984; Dewar, 1995, 2002).

Several previous authors have attempted to identify the sites of evaporation using experimental and/or modeling approaches. Some have inferred the sites of evaporation from the accumulation of dissolved tracer substances. For example, Tanton and Crowdy (1972) noted that lead chelate in the transpiration stream accumulated in guard cell walls, and they concluded that most evaporation occurred from very near the guard cells. However, Canny (1990, 1993) noted some essential weaknesses of tracer studies: namely, that tracers may be segregated from water flow by membranes and also may diffuse to locations outside the water flow pathway. Later authors used physical and mathematical models to explore evaporation from uniformly wet surfaces lining substomatal cavities (Meidner, 1976; Cowan, 1977; Tyree and Yianoulis, 1980). Although each of these studies concluded that a large percentage of evaporation would occur from surfaces very close to each stomatal pore, they also assumed that the epidermis and mesophyll surfaces were uniformly wetted, so they could not account for resistances within or proximal to those surfaces. Other indirect evidence suggested that the evaporating sites extend deeper into the leaf. Farquhar and Raschke (1978) estimated that the resistance for diffusion from the evaporating sites to stomata was approximately half that for diffusion across amphistomatous leaves, which Boyer (1985) interpreted as evidence that evaporation occurs near the vertical center of the leaf and, thus, in the mesophyll and perhaps near the vasculature. Barbour and Farquhar (2004) used an anatomical model of liquid water flow pathways in leaves of wheat (Triticum aestivum) to assess hypotheses about the location of the evaporating sites and found that the available isotopic data could not distinguish those hypotheses.

Environmental conditions also may affect the distribution of evaporation within the leaf. Cowan (1977) predicted that vertical T gradients between the illuminated upper mesophyll and the cooler lower epidermis could drive evaporation and vapor transport toward the lower epidermis, which Sheriff (1979) corroborated by observing condensation on the lower epidermis in transpiring leaves when the epidermis was cooler than the leaf center. More recent simulations by Rockwell et al. (2014), Buckley (2015), and Buckley et al. (2015) supported the notion that even small vertical T gradients (on the order of 0.1°C) between illuminated palisade mesophyll and transpiring epidermis could drive substantial vapor transport toward the lower epidermis. Together, these studies suggested that the mesophyll may, in fact, support a great deal of evaporation in illuminated leaves.

In summary, the available evidence suggests that the location of the sites of evaporation is important for many questions across plant physiology and that models must extend beyond the substomatal cavity to include realistic depictions of tissues and conditions deeper in the leaf to resolve these questions. However, most previous studies of the evaporating sites have been confined to single species or have used generic models that are not suitable for exploring the effects of species variation in leaf internal anatomy. To overcome these limitations, we used an anatomically and biophysically explicit model of coupled heat and water transport outside the xylem, MOFLO 2.0 (an extension of the MOFLO model; Buckley et al., 2015), parameterized for 14 diverse angiosperm species (Table III), to analyze the sites of evaporation within leaves in relation to anatomy and environmental conditions. Our objectives were to map the distribution of net evaporation across tissues within a single leaf areole, to determine how that distribution is affected by leaf anatomy and environmental conditions, and to explore the implications of the evaporating sites for measurements and inferences across plant physiology.

Table III. Summary data for species used in this study.

LHS, Leaf habit and structure (E, evergreen; D, deciduous; h, hypostomatous; a, amphistomatous; HE, heterobaric; HO, homobaric); LF, life form (t, tree; s, shrub; ah, annual herb; ph, perennial herb); LT, leaf thickness (μm); SP, spongy mesophyll airspace fraction (%).

Species	Family	Origin	LHS	LF	LT	SP
Bauhinia galpinii	Fabaceae	Africa	E, h, HE	t	90.6	0.10
Camellia sasanqua	Theaceae	Japan	E, h, HO	s	408.0	0.42
Cercocarpus betuloides	Rosaceae	California, Mexico	E, h, HE	s	248.0	0.63
Comarostaphylis diversifolia	Ericaceae	California, Mexico	E, h, HE	s	284.6	0.40
Helianthus annuus	Asteraceae	North America	D, a, HE	ah	182.3	0.43
Heteromeles arbutifolia	Rosaceae	California, Mexico	E, h, HO	s	268.0	0.60
Hedera canariensis	Araliaceae	Canary Islands	E, h, HO	s	301.8	0.52
Lantana camara	Verbenaceae	Pantropical	D, h, HO	s	207.7	0.33
Magnolia grandiflora	Magnoliaceae	Southern United States	E, h, HE	t	521.1	0.32
Platanus racemosa	Platanaceae	California, Mexico	D, h, HE	t	194.9	0.45
Quercus agrifolia	Fagaceae	California, Mexico	E, h, HE	t	278.0	0.27
Raphiolepis indica	Rosaceae	Southern China, India	E, h, HO	s	462.4	0.40
Romneya coulteri	Papaveraceae	California, Mexico	D, a, HE	ph	368.8	0.35^a
Salvia canariensis	Lamiaceae	Canary Islands	D, h, HO	ph	178.2	0.27

Open in a new tab

As R. coulteri does not contain spongy mesophyll, the airspace fraction value given is for the palisade mesophyll.

RESULTS

The MOFLO 2.0 model calculates heat and water transport outside the xylem in broad leaves by representing leaf tissues as a grid of interconnected nodes. Resistances for heat, liquid, and vapor transport between each node are calculated from anatomical and biophysical parameters (Buckley et al., 2015), and distributions of T and ψ are determined by solving a system of equations that arise from conservation laws (for details, see “Materials and Methods”). Net evaporation occurs from a given node if the vapor flow out of the node exceeds the vapor flow into the node. This requires at least one of two conditions to be satisfied: either (1) the ratio of vapor to liquid phase transport conductance is greater for the downstream (distal) pathways out of a node than for the proximal pathways into the node (where proximal and distal are defined by the direction of ψ gradients) and/or (2) anisothermal vapor transport (AVT) out of a node exceeds AVT into the node (AVT is vapor diffusion driven by T gradients independent of ψ gradients). Evaporation also consumes thermal energy and condensation releases it, which causes cooling or warming that act as a slight brake or negative feedback on local evaporation and condensation and tend to favor net evaporation in regions where excess heat is available from the absorption of light.

To provide a simple quantitative basis for understanding how evaporation is partitioned spatially within the leaf, we expressed the evaporation rate from each tissue as a fraction of the leaf transpiration rate (E). It is helpful to distinguish evaporation (a phase change experienced by water moving within the leaf) from transpiration (net water loss from the leaf as a whole via stomatal pores and through the cuticle). The net internal evaporation rate must equal the transpiration rate at steady state, but the processes are distinct: evaporation is a component of water transport within the leaf, and water that has evaporated from one region within the leaf may recondense elsewhere before finally evaporating at a third location. As our results will illustrate, the evaporation rate from a given tissue can change greatly without any change either in the rate of water flow to that tissue from proximal locations or in the net evaporation rate from the leaf as a whole.

For the simulations described below, environmental and gas-exchange parameters were set at default values, and all simulations were repeated for the 14 species listed in Table III, with results averaged across species, unless noted otherwise. The default environmental parameters were as follows: PPFD = 1,500 μmol m⁻² s⁻¹ incident on the adaxial surface, PPFD = 0 at the lower surface, air temperature (T_air) = 25°C, ambient water vapor mole fraction (w_air) = 15 mmol mol⁻¹ (0.015 mol mol⁻¹), g_s = 0.4 mol m⁻² s⁻¹, and boundary layer conductance to water (g_bw) = 3 mol m⁻² s⁻¹.

Effects of Leaf Anatomy on the Distribution of Evaporation

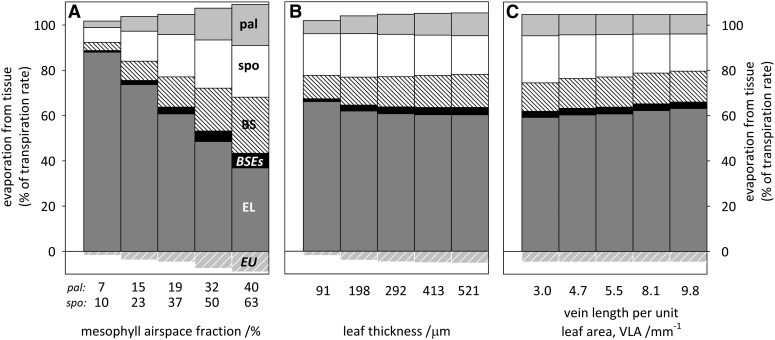
Our model predicted that evaporation is highly concentrated at the lower epidermis and the bundle sheath (BS), with some evaporation occurring from across the mesophyll but especially in the upper spongy mesophyll, just below the palisade/spongy transition. This is illustrated by contour plots of evaporation rate (Fig. 1, A and D) for two contrasting hypostomatous species: Bauhinia galpinii, which has thin leaves with relatively little airspace, and Heteromeles arbutifolia, which has much thicker leaves and greater airspace fraction (Table III lists leaf thickness, airspace fraction, and leaf habit for all 14 species). A much greater share of evaporation occurred from the mesophyll in H. arbutifolia (37.2%, versus 8.4% in B. galpinii) due to its greater airspace fraction and leaf thickness. In both species, ψ declined steeply with increasing distance from the nearest minor vein (located at the left edge of Fig. 1, B and E) and T peaked in the upper palisade mesophyll, declining toward the lower leaf surface (Fig. 1, C and F). Because B. galpinii and H. arbutifolia have similar vein spacing and, thus, similar areole radius but H. arbutifolia is much thicker, the ψ gradient was oriented more horizontally and the vertical T gradient was much smaller in B. galpinii than in H. arbutifolia (∼0.03°C versus 0.25°C, respectively). To verify that the difference in ψ gradient orientation was not caused by the larger T gradient in H. arbutifolia, we repeated the comparison in darkness (Supplemental Fig. S1) and found a similar difference in orientation.

Figure 1. — Spatial distribution of evaporation (A and D), ψ (MPa; B and E), and T (°C; C and F) across outside-xylem leaf tissues for *B. galpinii* (A–C) and *H. arbutifolia* (D–F). In A and D, the contours represent evaporation rate from each node in the grid (which represents a finite volume of tissue within the areole) as a percentage of the transpiration rate of the leaf area subtended by that node; dashed lines indicate net evaporation of zero. The diagram at top left shows the approximate location of each tissue type. Transdermal micrographs are shown with scale bars for each species to illustrate the large differences in leaf anatomy and dimensions between the two species. Dashed white lines in A and D indicate the boundary between regions with net evaporation and regions with net condensation. Tissue-specific percentage contributions to total evaporation rate were as follows (in the order lower epidermis, spongy mesophyll, palisade mesophyll, BS, and upper epidermis): for *B. galpinii*, 88.4, 6.4, 2.4, 3.4, and −0.9; for *H. arbutifolia*, 36.6, 26.5, 9.9, 32.3, and −6.7.

We explored how anatomy affects where evaporation occurs by changing individual anatomical parameters in the model while holding all others constant. As airspace fraction was increased from the smallest to the largest values observed across the 14 species listed in Table III (from 7% to 40% for palisade mesophyll and from 10% to 63% for spongy mesophyll), the fraction of evaporation contributed by the lower epidermis declined from 86% to 28%, while the mesophyll fraction increased from 9% to 41% and the BS fraction increased from 4% to 25% (Fig. 2A). Increasing leaf thickness across its all-species range (from 91 to 521 μm, holding relative tissue thicknesses and absolute cell dimensions constant) had a much smaller impact, reducing lower epidermis evaporation from 64% to 55% and increasing the mesophyll fraction from 24% to 27% and the BS fraction from 10% to 15% (Fig. 2B). A 3.3-fold increase in vein density (VLA) from the all-species minimum to maximum values (3 and 9.8 mm⁻¹, respectively) had very little effect on evaporation, increasing lower epidermis evaporation from 54% to 58%, decreasing mesophyll evaporation from 30% to 25%, and increasing BS evaporation from 13% to 14% (Fig. 2C).

Figure 2. — Effects of variations in tissue-scale parameters on evaporation among tissues: mesophyll airspace fraction (A), leaf thickness (B), and minor VLA (C). Each parameter was varied from the minimum to the maximum value observed across the 14 species listed in Table III while holding all other anatomical parameters constant at their all-species averages. pal, Palisade mesophyll; spo, spongy mesophyll; BSEs, BS extensions, or in homobaric species, mesophyll directly above and below the BS; EL, lower epidermis; EU, upper epidermis.

Cell dimensions also had very small impacts on the distribution of evaporation: varying individual cell sizes between the minimum and maximum values observed across species (which corresponded to 2.5- to 4.6-fold changes in each cell dimension) led to changes of no more than 6% in evaporation from any given tissue, with most effects much smaller (Table IV). Spongy cell radius had the largest effect, with a 4.6-fold (360%) increase in this parameter resulting in a 5.9% decrease in lower epidermis evaporation and a 4.7% increase in BS evaporation.

Table IV. Effects of cell dimensions on the distribution of evaporation.

Values show the percentage of total evaporation that occurs from a tissue when various cell dimensions were varied from the minimum value to the maximum value observed across the 14 species listed in Table III while all other anatomical parameters were held at their all-species averages. The second column gives the range of values across species for each cell dimension, expressed as percentage of the all-species mean and as fold change (e.g. 4-fold range for palisade cell radius). Epidermis refers to the lower epidermis.

Dimension	Cross-Species Range of Dimension	Change of Percentage Evaporation between All-Species Minimum and Maximum Values of Dimension
Dimension	Cross-Species Range of Dimension	BS	Epidermis	Mesophyll
Palisade cell radius	49–195; 4.0	+0.7	+0.3	−1.4
Palisade cell height	63–158; 2.5	+0.6	−0.1	−0.8
Spongy cell radius	35–161; 4.6	+4.7	−5.9	−0.9
Epidermis cell size	53–235; 4.0	+0.04	−4.5	+3.8
BS cell size	51–144; 2.8	−0.7	−0.2	+1.9
BS extension cell size	41–173; 4.2	+4.3	−1.7	−0.5

Open in a new tab

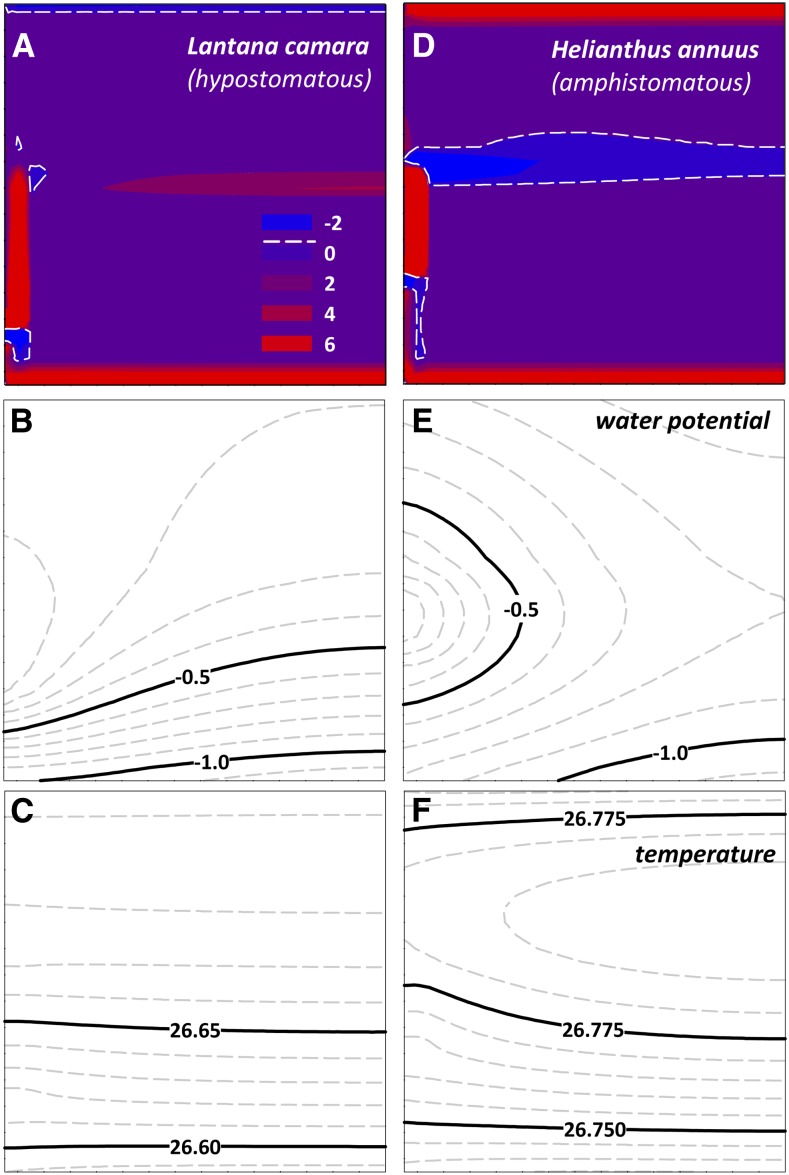
Two of our 14 study species (Helianthus annuus and Romneya coulteri) are amphistomatous, which had two important effects on the predicted location of the evaporating sites. First, and unsurprisingly, whereas evaporation occurred only from the lower epidermis in hypostomatous species (e.g. Lantana camara; Fig. 3A), it occurred from both epidermes in amphistomatous species (e.g. H. annuus; Fig. 3B). Second, whereas the palisade-spongy mesophyll transition was a site of enhanced evaporation in hypostomatous species (Figs. 1 and 3A), condensation occurred in the vertical center of the mesophyll in H. annuus (Fig. 3B); the total amount of condensation was equivalent to 3.4% of the transpiration rate in that simulation. Artificially varying the distribution of g_s between the two surfaces led to an approximately linear change in the magnitude of this condensation flux as a percentage of transpiration, reaching 15% for a totally epistomatous leaf of H. annuus (Supplemental Fig. S2). By contrast, the vertical center of the leaf did not support either enhanced evaporation or condensation in R. coulteri (data not shown), because this species lacks any differentiation between spongy and palisade mesophyll. This suggests that the enhanced condensation in H. annuus occurs because the net vertical direction of water transport at the spongy/palisade transition is upward (toward the adaxial surface) in this species, and enhanced evaporation in the same region in hypostomatous species occurs because water movement is toward the abaxial surface in those species. In both cases, the same mechanism explains the observations: namely, the shift in vapor phase conductance caused by a change in airspace fraction at the palisade/spongy transition.

Figure 3. — Simulated spatial distributions of evaporation (A and D), ψ (B and E), and T (C and F) in a hypostomatous species, *L. camara* (A–C), and an amphistomatous species, *H. annuus* (D–F). Colors, lines, and tissue orientations are as in Figures 1 and 8. In A and D, the contours represent evaporation rate from each node in the grid as a percentage of the transpiration rate of the leaf area subtended by that node. Dashed white lines indicate the boundary between regions with net evaporation and regions with net condensation; thus, the zone in the approximate vertical center of the *H. annuus* leaf experiences net condensation rather than evaporation. Default values were used for all parameters and conditions. Tissue-specific percentage contributions to total evaporation rate were as follows (in the order lower epidermis, spongy mesophyll, palisade mesophyll, BS, and upper epidermis): for *L. camara*, 62.7, 15, 7.1, 18.8, and −3.8; for *H. annuus*, 25.8, 11.1, 9.4, 20.9, and 26.7. In *H. annuus*, 58.2% of transpiration was assumed to occur from the lower (abaxial) surface.

The simulations shown in this study assumed that transpiration (vapor diffusion to the external atmosphere, as distinct from vapor diffusion among regions within the leaf) is distributed uniformly among nodes in the transpiring epidermes. In real leaves, the great majority of leaf water loss occurs only via stomatal pores, leaving some regions of epidermis with no direct water loss to the air except the typically minor evaporation that occurs through the cuticle. To test whether more realistic clustering of leaf water loss would affect our overall results, we compared a typical simulation with another in which the same total transpiration rate was distributed across just three nodes in the grid (spaced 69 μm apart to represent a stomatal density of approximately 244 mm⁻² and using anatomical parameters for Magnolia grandiflora). This clustered simulation predicted epidermal evaporation only very close to stomatal pores, with condensation occurring on intervening, nontranspiring regions of epidermis (Supplemental Fig. S3B), but the distribution of evaporation across other leaf tissues was nearly identical to that predicted in the uniform transpiration simulation (Supplemental Fig. S3A). We found qualitatively similar results for other species (data not shown). Because much greater spatial resolution than that provided by MOFLO 2.0 is needed to accurately simulate vapor flow in the vicinity of stomatal pores (Roth-Nebelsick, 2007), the simulation shown in Supplemental Figure S3 should be interpreted only heuristically; nevertheless, it does suggest that stomatal density has little impact on the distribution of evaporation at the larger scale of the whole areole.

Effects of Anatomical Changes during Dehydration

Cell and tissue dimensions may change during dehydration, which may, in turn, affect the distribution of evaporation. To assess such effects, we performed three pairs of simulations using anatomical parameters measured at full turgor and turgor loss point for three of our study species: Comarostaphylis diversifolia, Hedera canariensis, and L. camara. Individual cell dimensions and total leaf area shrank, and thus VLA increased, during dehydration in all three species, but whereas the airspace fraction increased in C. diversifolia and H. canariensis, it decreased in L. camara (Supplemental Table S1). As one would predict based on the results presented earlier, this led to increased mesophyll evaporation and decreased epidermal evaporation in the first two species but the opposite trend, as well as a large decline in BS evaporation, in the third species (Fig. 4).

Figure 4. — Effects of changes in anatomical parameters during dehydration, from full turgor (FT) to turgor loss point (TLP), for three species, with abbreviations as in Figure 2. Anatomical parameter changes are described in Supplemental Table S1.

Effects of Variation in Liquid Transport Properties

Several biophysical parameters that influence liquid phase water transport in MOFLO 2.0 lack reliable measurements, including the effective Poiseuille radius of apoplastic nanopathways (R_a), cell membrane osmotic water permeability (P_m; which includes the effect of aquaporins), and the percentage by which apoplastic flow across the BS is reduced by suberization and/or lignification in anticlinal BS cell walls. As we recently found that these parameters can strongly influence the partitioning of water flow among transport modes (apoplastic, transmembrane and transcellular, and gas phase; Buckley et al., 2015), we tested whether variation in these parameters also affected where evaporation is predicted to occur within the leaf. The model predicted that any change in these parameters that enhanced liquid phase transport relative to vapor transport (i.e., increases in P_m or R_a) increased the percentage of total evaporation that occurs from the epidermis and reduced evaporation from locations closer to the xylem (Fig. 5). However, the suppression of BS apoplastic transport had a negligible effect on the distribution of evaporation (Fig. 5C).

Figure 5. — Effects of liquid transport parameters on the distribution of evaporation across leaf tissues, with abbreviations as in Figure 2. A, P_m. B, R_a. C, Percentage by which apoplastic transport across the BS is assumed to be suppressed by suberization and/or lignification of cell walls. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

Effects of Variation in Environmental Parameters

The absorption of photosynthetically active radiation strongly affected the distribution of evaporation across leaf tissues: as PPFD increased from 0 to 1,500 μmol m⁻² s⁻¹, evaporation from the mesophyll (palisade and spongy combined) increased from 5% to 26% of the total, while lower epidermis evaporation decreased from 78% to 55% (averages across species; Fig. 6A). This shift was driven by an increase in the transdermal temperature gradient (ΔT), which drives AVT through the intercellular airspaces: species-average ΔT increased from 0.041°C in darkness to 0.145°C at the highest PPFD, with ΔT exceeding 0.2°C in five species and 0.3°C in one (Fig. 7A). Most of this variation in ΔT was driven by differences in leaf thickness (Supplemental Fig. S4). In darkness, slight condensation was predicted to occur across most of the palisade mesophyll, while evaporation occurred strongly from the lower epidermis, BS, and palisade/spongy boundary (as shown in Fig. 8A for C. diversifolia), whereas at PPFD = 1,500 μmol m⁻² s⁻¹, evaporation occurred from across the entire mesophyll, with a layer of slight condensation at the upper epidermis (Fig. 8C). The T gradient in darkness was small and peaked at the upper leaf surface (Fig. 8B), but in high light, it was larger and peaked in the palisade mesophyll due to cooling of the upper surface by sensible heat loss to the air (Fig. 8D). Absorption of PPFD also increased the T of all layers in the leaf (Fig. 7B; compare with Fig. 8, B and D).

Figure 6. — Effects of variation in environmental parameters on the distribution of evaporation across outside-xylem leaf tissues. A, PPFD. B, w_air. C, T_air. Abbreviations are as in Figure 2. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

Figure 7. — Effects of increasing PPFD incident on the adaxial leaf surface on the difference between maximum and minimum T in the leaf, for each of 14 species (colored lines are named at right; solid lines = hypostomatous species and dashed lines = amphistomatous species), and the median across species (dotted gray line; A) and T at the abaxial leaf surface (median across species; B).

Figure 8. — Effects of PPFD on the distribution of evaporation (percentage of transpiration rate for the subtended leaf area; A and C) and T (°C) across outside-xylem leaf tissues (B and D) for *C. diversifolia*. In A and B, PPFD = 0, and in C and D, PPFD = 1,500 μmol m⁻² s⁻¹. In A and C, the contours represent evaporation rate from each node in the grid as a percentage of the transpiration rate of the leaf area subtended by that node. Dashed lines in A and C indicate net evaporation of zero (the jagged lines at top left in A indicate a region where net evaporation is nearly uniform at equal to zero, such that the graphing program could not identify a single discrete boundary). The top and bottom of each image represent the adaxial and abaxial leaf surface, respectively, and the left and right sides represent the outer margin and the center of the areole, respectively. See the diagram in Figure 1 for tissue orientation. Tissue-specific percentage contributions to total evaporation rate were as follows (in the order lower epidermis, spongy mesophyll, palisade mesophyll, BS, upper epidermis): at PPFD = 0, 74.3, 6.7, 0, 12.9, and 1.1; at PPFD = 1,500 μmol m⁻² s⁻¹, 55.8, 22, 5.3, 15.3, and −3.1.

A similar shift in the location of the evaporating sites was predicted to occur in response to increasing humidity (Fig. 6B), with more evaporation occurring from the mesophyll and less from the epidermis as humidity increased. Increasing ambient T_air had smaller effects, with both epidermal and mesophyll evaporation decreasing slightly as T_air increased but BS evaporation increasing (Fig. 6C).

Effects of Thermal Transport Properties

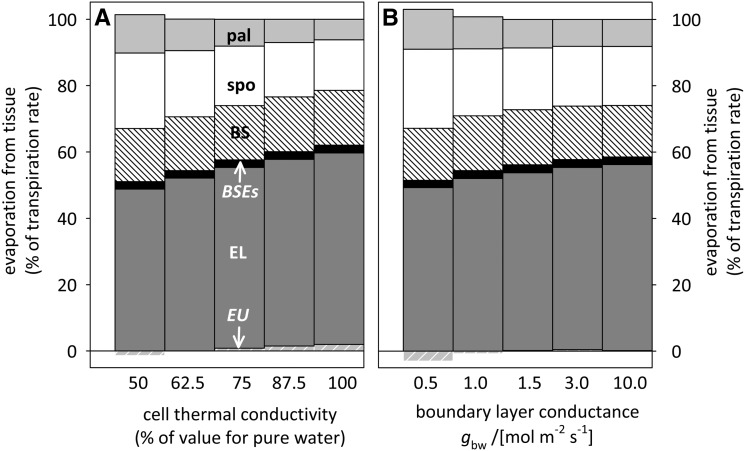
Thermal properties of the leaf and the leaf-air interface had relatively little effect on the distribution of evaporation across tissues. The thermal conductivity of leaf cells is unknown, so we assumed it was a fraction, f_TK, of the thermal conductivity of pure water, with a default value of 0.75; that value gives a species average of 0.34 J m⁻¹ s⁻¹ K⁻¹ for bulk leaf horizontal thermal conductivity, which compares well with the average (0.35) for 12 woody species reported by Vogel (1984). Increasing f_TK from 0.5 to 1 reduced mesophyll evaporation from 34% to 21% (average across species) and increased epidermal evaporation from 47% to 60%, with minor changes for other tissues (Fig. 9A). The leaf boundary layer conductance for heat (g_bh; g_bh = g_bw/1.08) influences the rate at which heat can be transferred from either leaf surface to the atmosphere, so it might influence ΔT and, hence, the distribution of evaporation. Increasing g_bw from 0.75 to 10 mol m⁻² s⁻¹ reduced mesophyll evaporation from 36% to 26% of the total and increased epidermal evaporation from 46% to 56% (Fig. 9B).

Figure 9. — Effects of thermal transport properties on the distribution of evaporation across leaf tissues, with abbreviations as in Figure 2. A, Thermal conductivity of cells as a percentage of the value for pure water. B, Leaf-to-air boundary layer conductance to water vapor. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

Latent cooling at the sites of evaporation reduces the saturation vapor pressure at those sites, which may influence where evaporation occurs. To determine the importance of evaporative cooling for the distribution of evaporation, we performed an additional simulation in which we reduced the latent heat of vaporization (λ) by 99% to exclude most evaporative cooling (Supplemental Fig. S5). Although this led to substantial warming of the leaf, increasing the lower surface T by 1.6°C, it also reduced the maximum T gradient, leaving the distribution of evaporation virtually unchanged (62.2% versus 60.7% for the lower epidermis [reduced λ versus true λ] and 27.1% versus 27.6% for the mesophyll). Thus, although evaporative cooling strongly affects overall leaf T, it does not appear to be a major determinant of where evaporation occurs within the leaf.

Effect of Stomatal Conductance

Variation in g_s had an effect similar to that of ambient humidity on the distribution of evaporation within the leaf: as g_s decreased, less evaporation occurred from the lower epidermis and more evaporation occurred from both the spongy and palisade mesophyll (Fig. 10). At g_s = 0.05 mol m⁻² s⁻¹, the net evaporation rate from the mesophyll was actually larger than the total transpiration rate, so mass balance required net condensation to occur at the lower epidermis, at a rate equal to 13.5% of E (average across species), or 0.15 mmol m⁻² s⁻¹.

Figure 10. — Changes in the distribution of evaporation across tissues resulting from changes in g_s to water vapor. PPFD = 1,500 μmol m⁻² s⁻¹, T_air = 25°C, and w_air = 15 mmol mol⁻¹. Abbreviations are as in Figure 2. Negative values for evaporation mean that net condensation occurred at the tissue in question. At very low g_s, AVT toward the lower epidermis driven by the T gradient between warmer palisade mesophyll and cooler lower epidermis exceeds the net transpirational flow of water out of the lower leaf surface; mass balance requires condensation of the excess water at the lower epidermis and liquid phase flow back up to the mesophyll. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

Effects of the Location of Evaporation on Inferred Hydraulic and Stomatal Conductance Values

We used the predicted distributions of T and ψ to estimate the values of K_ox and g_s that one would calculate using standard experimental methods under various environmental conditions, assuming no change in the anatomical or biophysical determinants of g_s and K_ox. K_ox increased by 10% as PPFD increased from darkness to 1,500 μmol m⁻² s⁻¹ (average across species), by 91% as T_air increased from 5°C to 45°C (at a constant relative humidity of 50%), and by 19% as ambient w_air increased from 0 to 31 mmol mol⁻¹ (Fig. 11).

Figure 11. — Changes in K_ox associated with changes in the distribution of evaporation resulting from variation in environmental parameters. Solid line, Effect of PPFD incident at the adaxial surface; short-dashed line, effect of T_air; dashed-dotted line, effect of w_air. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

We identified the origin of the pathways represented by the standard experimental measurement of g_s (i.e., the location where the water vapor mole fraction in the intercellular airspaces is equal to the saturated value calculated at the T of the lower leaf surface) in a simulation using anatomical parameters averaged across species and assuming default values for all other parameters. In darkness, the g_s origin was located mostly in the upper palisade mesophyll (Fig. 12A), but at high PPFD, the g_s origin was positioned below the vertical center of the mesophyll (Fig. 12B). When we reduced all ψ values outside the xylem by 1 MPa to simulate a leaf minor vein xylem ψ of −1 MPa, the origin of the g_s pathways at high PPFD occurred in a narrow region just above the BS, near the outer margin of the areole (Fig. 12D), and did not occur at all within the outside-xylem compartment in darkness (Fig. 12C). However, despite this variation in the origin of the g_s pathways, relative humidity in the intercellular airspaces (calculated at the temperature at the lower leaf surface) was quite close to saturation under all conditions, reaching only slightly below 98% adjacent to the lower epidermis in the center of the areole even at high PPFD and low xylem ψ (Fig. 12D). Even under arguably unrealistic conditions chosen to maximize the drying of the intercellular airspaces (PPFD = 1,500 μmol m⁻² s⁻¹, zero ambient humidity, T_air of 40°C, and g_s of 0.4 mol m⁻² s⁻¹, producing a transpiration rate of 21 mmol m⁻² s⁻¹, and assuming a leaf minor vein xylem ψ of −2 MPa), relative humidity was still above 95% even at the driest location in the intercellular airspaces and averaged 97.7% in the palisade mesophyll (data not shown). These results suggest that the gas-exchange estimate of g_s is close to the true value that it is meant to estimate (i.e., the conductance of diffusion pathways through the stomatal pores alone, not including any pathways extending farther into the leaf) and that this remains true despite large shifts in the location within the leaf of the origin of the pathways represented by g_s.

Figure 12. — Simulated spatial distribution of relative humidity in the intercellular airspaces, calculated at the T of the lower leaf surface (contours), at PPFD = 0 (A and C) and PPFD = 1,500 μmol m⁻² s⁻¹ (B and D) and assuming ψ in the leaf minor veins (ψ_xylem) of zero (A and B) or −1 MPa (C and D). The contours at which relative humidity = 100%, shown with thick solid lines, represent the origin of the vapor diffusion pathways described by gas-exchange estimates of g_s. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

Relationship between Tissue Evaporation Rate and Tissue Water Potential

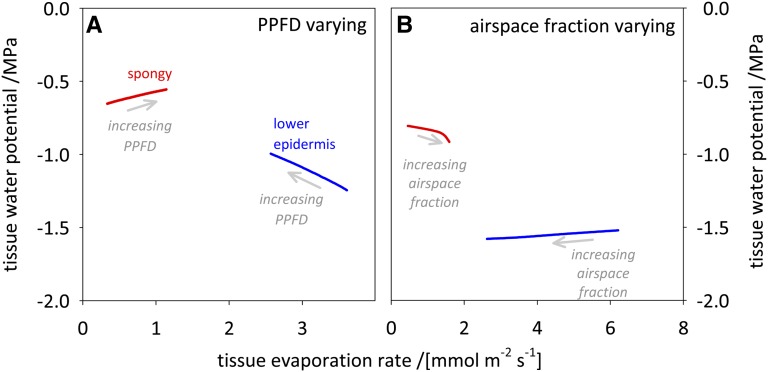
Hypothesis 3 in Table I predicts a negative relationship between tissue ψ and tissue evaporation rate, if liquid phase hydraulic conductivities proximal to that tissue are unchanged. To test this hypothesis, we conducted two additional sets of simulations in which we modified either PPFD or leaf airspace fraction in order to change the evaporation rates from the spongy mesophyll and lower epidermis in opposite directions while holding the whole-leaf evaporation rate constant by adjusting g_s. When PPFD was increased while holding the transpiration rate constant, spongy mesophyll evaporation increased 3.4-fold while lower epidermis evaporation decreased by 29%. However, this increase in spongy mesophyll evaporation was accompanied by a 15% increase in spongy mesophyll ψ (Fig. 13A). Similarly, when the mesophyll airspace fraction was increased 6-fold (from 10% to 63.3% for spongy and from 6.7% to 40% for palisade) while holding E constant, lower epidermis evaporation decreased by 58% but lower epidermis ψ decreased by 4%. These simulations demonstrate that hypothesis 3 is incorrect and that changes in tissue evaporation rate and ψ can occur independently of one another and often in opposite directions.

Figure 13. — The ψ of a tissue varies independently of the evaporation rate from that tissue. When the evaporation rates from the spongy mesophyll (red lines) and lower epidermis (blue lines) were modified by varying PPFD (A) or leaf airspace fraction (B) in the directions indicated by the gray arrows, while holding total evaporation rate constant by adjusting g_s, the ψ values of these tissues did not vary in the manner predicted by the hypothesis that an increase in evaporation rate from a tissue should cause its ψ to decline. In A, PPFD was varied between 0 and 1,500 μmol m⁻² s⁻¹ while holding all other parameters except g_s constant; g_s was adjusted between 0.4 and 0.24 mol m⁻² s⁻¹ in order to maintain a constant whole-leaf evaporation rate of 4.73 mmol m⁻² s⁻¹. In B, the mesophyll airspace fraction was adjusted between 10% and 63% (for spongy mesophyll) and between 6.7% and 40% (for palisade mesophyll) while holding all other parameters except g_s constant; g_s was adjusted between 0.4 and 0.409 mol m⁻² s⁻¹ to maintain whole-leaf evaporation rate constant at 7.07 mmol m⁻² s⁻¹. All anatomical parameters were set at their all-species average values (Supplemental Table S2).

DISCUSSION

We simulated coupled heat and water transport in an anatomically explicit model of the outside-xylem compartment in 14 diverse broadleaf angiosperm species to elucidate how anatomy and environmental conditions affect the distribution of evaporation across leaf tissues and what these results mean for the interpretation of key processes and measurements in leaf and plant physiology. Our results amount to a new understanding of where water evaporates in leaves, and they lead to a revised conceptual interpretation of what constitutes the end point of water transport within leaves. Our simulations suggested that most water evaporates from the transpiring epidermis under most conditions but that a large minority of evaporation also occurs from the mesophyll and BS, particularly under high light, and that the partitioning of evaporation across tissues is strongly affected by anatomy and environmental conditions. We confirmed the standard view that the intercellular airspaces are typically within 2% of the saturating value and found that, contrary to common assumptions and published hypotheses, the value of g_s that one would calculate by standard methods is not directly affected by shifts in the location of the evaporating sites caused by changes in environmental parameters.

How Does Anatomy Affect Where Evaporation Occurs?

Our simulations revealed a hierarchy of importance among anatomical and physiological parameters in controlling where water evaporates within leaves. The five most important factors, in order of descending importance (and with the direction of each effect on the epidermal share of evaporation shown in parentheses) were mesophyll airspace fraction (−) > cell wall hydraulic conductivity (+) > cell membrane hydraulic conductivity (+) > leaf thickness (−) > minor vein density (+). The effect of airspace fraction was by far the strongest: on average across species, the epidermal share of evaporation changed about 20 times more in response to a simulated doubling of airspace fraction than a simulated doubling of minor vein density (VLA). Cell size had very small impacts on the distribution of evaporation. The reason for each of these results is that anatomical features that make it easier for water to reach the transpiring epidermis in the liquid phase (e.g. greater cell wall or membrane conductivity) will favor water remaining as liquid through the mesophyll, whereas features that enhance the conductance for vapor transport (e.g. greater airspace fraction) will have the opposite effect. For example, suberization of the BS had little effect on where evaporation occurs because it does not affect the partitioning of flow between liquid and vapor phases distal to the BS, and VLA had little effect because it influences outside-xylem liquid and vapor phase transport similarly (via the total path length for water transport from the xylem to the transpiring epidermis). The minor roles of VLA and BS suberization in the distribution of evaporation contrast with their large impact on K_ox, predicted by MOFLO (Buckley et al., 2015) and also by MOFLO 2.0 (data not shown), which suggests that the location of the evaporating sites may not be an important causal determinant of K_ox (see “The Evaporating Sites Are Not the End Point of Water Transport” below).

Our findings about the role of anatomy are consistent with, but greatly expand upon and clarify, those of Rockwell et al. (2014). That study used a one-dimensional model in which the vertical center of the leaf is a fixed source of liquid water representing a vascular bundle, and described evaporation from the vertical center of the leaf as “perivascular”. That simple model structure allowed the derivation of an analytical solution, which can be very useful in gaining an understanding of the behavior of processes such as evaporation within leaves. However, analytical solutions, while elegant, limit the breadth of understanding that can be gained and its relevance to real systems. Our anatomically explicit numerical approach complements the approach of Rockwell et al. (2014) and allows evaluation of the impact of more realistic assumptions. For example, the vertical center of a leaf is predominantly mesophyll in real leaves, with vascular bundles only at the horizontal edges of a given areole space and continuous airspace connecting the palisade and spongy mesophyll across most of the horizontal domain. Our two-dimensional model allowed us to estimate how the total evaporation from this region is partitioned among the BS and spongy and palisade mesophyll. We found that evaporation from the BS is generally similar to or smaller than total evaporation from the mesophyll and is much less sensitive to changes in environmental conditions (as discussed in the next section). This does not contradict Rockwell et al.’s (2014) prediction that perivascular evaporation should increase strongly with illumination, because the perivascular region in their model included not only the BS but also the palisade/spongy mesophyll transition. Our findings also corroborate Rockwell et al.’s (2014) prediction that mesophyll evaporation increases in importance as leaf airspace fraction increases and showed that this effect was strong across 14 species varying in spongy mesophyll airspace fraction from 10% to 63%. Our findings also supported Rockwell et al.’s (2014) and Buckley’s (2015) prediction that the spongy/palisade transition should be a site of greater evaporation than throughout the rest of the mesophyll (Figs. 1 and 8). However, for the amphistomatous species H. annuus, we found the opposite (condensation rather than evaporation at the spongy/palisade transition), because the net vertical direction of water movement at the transition was toward the adaxial rather than the abaxial surface, so the airspace fraction decreased along flow pathways in that species, driving condensation. Our anatomy-driven model also allowed us to ask how the distribution of evaporation changes during dehydration due to changes in cell and tissue dimensions for three of our study species. We found that the dominant factor was again airspace fraction: when airspace increased, so did mesophyll evaporation, and vice versa. It should be noted that dehydration may have many other effects omitted from our model at present, such as changes in aquaporin expression and other transport properties (Scoffoni et al., in press).

How Do Environmental Conditions Affect Where Evaporation Occurs?

Changes in PPFD, ambient humidity, and ambient T each affected the distribution of evaporation in our model. For example, our model predicted that increases in ambient T should enhance BS evaporation at the expense of evaporation from the lower epidermis, with little impact on mesophyll evaporation (Fig. 6), which may have implications for patterns of isotopic discrimination (see “Other Implications of the Location of the Evaporating Sites” below). Our anatomically explicit model also was able to predict, to our knowledge for the first time, how the vertical T gradient in saturating light should vary across species. We predicted more than 10-fold variation in this parameter across species, from 0.03°C to 0.3°C, largely due to differences in leaf thickness (Supplemental Fig. S4). This variation greatly influences the impact of T-driven vapor transport within leaves. Our simulations corroborated modeling by Rockwell et al. (2014) and earlier predictions by Cowan (1977) and Sheriff (1979) that high illumination causes evaporation to shift from the epidermis into the mesophyll, particularly when the transpiration rate is low, such as under high ambient humidity or low g_s. To understand this phenomenon and its implications for the relationship between water flux and ψ within leaves, it is helpful to distinguish two components of vapor transport within leaves: a component that is driven by gradients in ψ and is essentially insensitive to variations in T and a component driven by gradients in T that is essentially insensitive to ψ. (Gradients in T directly influence ψ itself, but that effect is negligible, on the order of 0.1% or less for the small T gradients believed to occur within leaves.) We call these two components isothermal and anisothermal vapor transport, or IVT and AVT, respectively. The mechanism of the light-induced shift in evaporation from the epidermis into the mesophyll involves AVT: light absorption in the mesophyll generates vertical T gradients that drive AVT, requiring evaporation from mesophyll surfaces to satisfy mass balance. At a given PPFD, smaller transpiration rates cause the AVT flux to become a larger fraction of the total water movement toward the transpiring epidermis. In the extreme case where the AVT flux exceeds transpiration, mass balance requires a backward liquid water flux toward the mesophyll. Since liquid flux follows ψ gradients, it is possible for the net flow of water (AVT minus liquid back flow) to occur despite zero ψ gradient, or even against the ψ gradient. Therefore, the apparent hydraulic resistance from the mesophyll to the transpiring epidermis can approach zero and even become negative when AVT is large and E is small. This is reminiscent of electrical superconductivity, in which current flows against zero resistance, and we suggest the term hydraulic superconductivity to describe the apparent elimination of hydraulic resistance by AVT. A full exploration of these phenomena is beyond the scope of this study; we merely note here that the possibility of condensation at the transpiring epidermis, combined with highly localized evaporation from near the stomatal pores, is supported by the observations of Sheriff (1979) and earlier modeling by Cowan (1977), Pieruschka et al. (2010), and Rockwell et al. (2014).

The Evaporating Sites Are Not the End Point of Water Transport

Many published hypotheses depend on the location of the evaporating sites (Table I). Some of these hypotheses involve processes that are coupled directly to evaporation or vapor transport per se (hypotheses 4–10 in Table I), and we discuss these further below (see “Other Implications of the Location of the Evaporating Sites”). Other hypotheses (1–3 in Table I) arise from the notion that leaf and plant hydraulic conductances are strictly liquid-phase phenomena and the pathways that they represent thus end at the sites of evaporation (Holmgren et al., 1965; Farquhar and Raschke, 1978; Blizzard and Boyer, 1980; Tyree and Yianoulis, 1980; Sheriff, 1984; Boyer, 1985; Yang and Tyree, 1994; Brodribb et al., 2002; Sperry et al., 2002; Buckley, 2005; Sack and Holbrook, 2006; Mott, 2007; Beerling and Franks, 2010; Berry et al., 2010; Pieruschka et al., 2010; Rockwell et al., 2014). This seemingly obvious and unobjectionable notion imbues the evaporating sites with central significance for water transport, gas exchange, and associated measurements. For example, it predicts that any change in the location of the evaporating sites should directly cause a change in the path length for water flow, and thus in K_leaf: that is, K_leaf should be larger if evaporation occurs closer to the xylem, because water would not have to travel as far to reach the sites of evaporation, and conversely, K_leaf should be smaller if most evaporation occurs farther from the xylem, such as from the epidermis (hypothesis 1 in Table I). It also implies that the true K_leaf (which must describe strictly liquid-phase pathways if one believes that water transport ends at the evaporating sites) will be underestimated or overestimated if the ψ used for experimental measurements of K_leaf, which is typically an equilibrated, bulk-leaf value (ψ_eq), does not happen to correspond to the value of ψ at the evaporating sites (Sack et al., 2002; Mott, 2007; Tyree and Zimmermann, 2013; Brodribb et al., 2016; hypothesis 2). Another hypothesis holds that the rate of evaporation from a given tissue must equal the rate of water flow to that tissue through proximal liquid-phase pathways; therefore, the rate of evaporation determines the tissue’s ψ (because ψ = [water potential at proximal location] – [flow from proximal location]/[conductance of proximal pathways]). Consequently, an increase in the evaporation rate from a particular tissue should be accompanied by a decline in the tissue’s ψ (Cowan, 1977; Sheriff, 1984; Buckley et al., 2003; hypothesis 4).

Our simulations using MOFLO 2.0 directly contradict these hypotheses. First, K_ox (calculated from the volume-weighted average of ψ across all outside-xylem tissues), and hence K_leaf for a given xylem conductance, was only weakly affected by changes in environmental parameters that caused very large shifts in the location of the evaporating sites, and hence the path length for liquid-phase transport (Fig. 11). Although K_ox did tend to increase slightly when evaporation occurred closer to the xylem, the underlying mechanism did not involve changes in the path length for liquid water flow but rather changes in the importance of AVT, which delivers water to the transpiring epidermis without increasing the ψ drawdown to the epidermis. Hypothesis 1, therefore, is incorrect: the distance from the xylem to the evaporating site does not determine ψ drawdowns, nor, therefore, K_ox. Second, the ψ of tissues distal to the xylem was very clearly influenced by vapor transport, especially AVT. This demonstrates that vapor transport plays a role in moving water from the xylem to those tissues, which, in turn, obviates hypothesis 2: if vapor transport contributes substantially to water transport, then the driving force for water transport is not related directly to the sites of evaporation. Third, we found that an increase in tissue evaporation rate (while holding whole-leaf transpiration rate constant) can be accompanied by an increase, a decrease, or little change in that tissue’s ψ (Fig. 13), which contradicts hypothesis 3. For example, as PPFD increased while holding E constant, the ψ and evaporation rate of the spongy mesophyll both increased (Fig. 13A).

Our rejection of hypothesis 3 may appear at first glance to contradict mass conservation, so it deserves explanation. This hypothesis has two premises: that net evaporation from a tissue (e) must equal liquid flow to that tissue from the xylem (L_in), and that tissue ψ is determined by L_in, the resistance from the xylem to the tissue (R), and the xylem water potential (ψ_x): that is, e = L_in and L_in = (ψ_x – ψ)/R, which together imply ψ = ψ_x – e⋅R, and, hence, ψ should decline if e increases. Both of these premises are subtly incorrect, however. First, e must equal not L_in per se, but rather L_in minus any liquid flow to distal locations (L_out), and second, ψ is also affected by isothermal vapor flow arriving from proximal locations (V_in). These corrections change the equation for ψ to ψ = ψ_x – (e + V_in + L_out)⋅R', where R' is the proximal resistance accounting for the contribution of vapor pathways. Thus, if an increase in net evaporation is caused by something that also alters V_in and/or L_out, then ψ will not necessarily decline, even if ψ_x and R' are unchanged. For example, in Figure 13A, light absorption drives AVT distal to the spongy mesophyll at the expense of liquid flow, so L_out decreases.

This analysis assumes homogenous local ψ equilibrium between adjacent liquid and vapor phases, which implies that a tissue’s ψ will be affected by vapor transport to its vicinity even if that vapor does not condense at the tissue. It is possible that this assumption is inadequate, such that lateral movement of vapor normal to the predominant direction of transport (e.g. from the lateral face of a palisade cell to the center of the adjacent intercellular airspace) poses an additional resistance to vapor transport that our model does not account for. If so, this would lengthen the effective path lengths for vapor transport by a degree that would depend on the geometry of airspaces adjacent to the important sites of evaporation. It is not apparent that this would change our results qualitatively, except by reducing the relative importance of vapor transport.

Reconceiving Leaf Hydraulics as a Mixed-Phase Phenomenon: What Does Hydraulic Conductance Mean?

The central insight from the preceding discussion is that water transport does not end at the sites of evaporation within the leaf. Vapor pathways help to move water within the leaf just as liquid pathways do (they are part of the water transport system), and they influence the ψ values of all tissues distal to the xylem. The only fundamental distinctions between vapor and liquid pathways within the leaf are that vapor flow is driven not only by ψ gradients but also by T gradients and that latent cooling or heating occurs when water moves from one pathway to the other. We found that T-driven AVT was the main factor driving changes in the distribution of evaporation for a given leaf, whereas latent heat exchange had very small impacts on the spatial distribution of evaporation within the leaf (albeit large impacts on overall energy balance; Supplemental Fig. S5). Given that vapor transport beyond the sites of evaporation is a component of outside-xylem water transport, analogous in most respects to liquid phase transport, we suggest that the evaporating sites should not be considered to be the end point for water transport. Where do the pathways for water transport end within the leaf, and how do these pathways relate to operational and conceptual definitions of hydraulic conductance? The first part of this question has a simple answer: during active transpiration, water transport continues all the way to the stomatal pores, and during leaf rehydration, it ends at the rehydrating cells. The second part of the question is somewhat more difficult, because it requires an understanding of the pathways represented by operational measurements of K_leaf and K_plant. All such measurements combine an estimate of the rate of water flow through the leaf with an estimate of the ψ gradient that drives that flow, and all use bulk leaf water potential, the ψ of an equilibrated, excised, nontranspiring leaf (ψ_eq), as an estimate of the end point of that gradient. The question then becomes, at what location within the leaf does ψ_eq equal the actual value of ψ during active transpiration? By definition, ψ of the most distal tissues (near stomata) during transpiration will be more negative than that of the rest of the leaf, so those tissues will gain water during equilibration and thus experience an increase in ψ. Therefore, ψ_eq must be larger (closer to zero) than the transpiring ψ at the stomatal pores, which means that ψ_eq corresponds to transpiring ψ at some location proximal to the stomata. What matters here is that there is no reason to suppose that that location corresponds to the sites of evaporation; if it does, it is purely by coincidence, because the sites of evaporation can vary widely and independently of tissue ψ (and thus ψ_eq), as illustrated by Figure 13. Therefore, we suggest that when interpreting operational measurements of K_plant, K_leaf, and K_ox, one should recognize that they are unrelated to the evaporating sites, that they include a contribution from vapor phase transport in the intercellular airspaces, and that they represent pathways that end somewhere proximal to the stomata, probably in the mesophyll. Future work should aim to resolve precisely where those pathways end (i.e. where transpiring ψ equals ψ_eq).

Our suggested operational interpretation of hydraulic conductance conflicts with the historical interpretation of the term hydraulic in plant biology as referring strictly to liquid phase phenomena. Therefore, one might object that an ideal measure of K_ox, K_leaf, or K_plant would include only liquid pathways, but in our view, such a measure would be less informative. Hydraulic conductances are important to physiologists and ecologists because they predict the relationship between ψ and transpiration rate, variables that are intrinsically important because of their direct impacts on cell turgor, volume, and osmotic pressure and a range of metabolic processes including stomatal responses, photosynthesis, and growth, and since vapor transport influences ψ values, we suggest that the most useful and broadly applicable definition of hydraulic conductance should include vapor transport. Alternatively, one could define a total water transport conductance and reserve the term hydraulic for the liquid component; however, most published measurements of plant and leaf hydraulic conductance to date include a vapor contribution. We suggest that the simplest way forward is to recognize that what we have always called hydraulic in fact includes vapor transport. This is consistent with the etymology of hydraulic, which refers only to water (the Greek hydor) and pipes (aulos) and, thus, implicitly includes both liquid and vapor (pipes, after all, can carry both steam and liquid water). Indeed, the concept of hydraulic movement in soil has included both liquid and vapor phases at least since the early work of Penman (1940).

Other Implications of the Location of the Evaporating Sites

Several other hypotheses also depend on where evaporation occurs within leaves (hypotheses 4–10 in Table I). Two of these hypotheses involve changes in the composition of the liquid phase that occur at the sites of evaporation. First, dissolved solutes with a low vapor pressure will tend to increase in concentration wherever evaporation occurs (hypothesis 4). This may be important for stomatal sensing of hormonal signals such as abscisic acid (ABA) delivered in the transpiration stream from sites proximal to the epidermis; for example, if enhancement of mesophyll evaporation by light increases apoplastic ABA concentration in the mesophyll, this should increase the rate of ABA uptake into mesophyll cells by mass action (Kaiser and Hartung, 1981), in turn accelerating the metabolism of ABA by mesophyll cells (Hartung et al., 1998) and possibly reducing the amount of ABA that reaches stomatal guard cells. Second, leaf water oxygen and hydrogen isotope enrichment occurs at the evaporating sites because vapor pressure is smaller for heavier isotopologs of water than for lighter ones (Farquhar et al., 1989; Farquhar and Lloyd, 1993). Bulk leaf isotopic enrichment is affected by the degree of mixing of enriched water with unenriched xylem water and, thus, by the balance between advection and back diffusion of enriched water; this, in turn, depends on the proximity of the evaporating sites to key pools of leaf water (Farquhar and Lloyd, 1993; this is hypothesis 5). Our model predicts a strong shift in the location of evaporation from the transpiring epidermis into the mesophyll as PPFD increases and more so at high air humidity, which should reduce the effective path length for the diffusion of enriched water back to the xylem, consistent with data showing that the effect of back diffusion on steady-state bulk leaf water enrichment (the Peclet effect) is stronger when E is smaller (Farquhar and Lloyd, 1993).

Two other hypotheses involve the interaction between CO₂ and water transport. First, K_leaf is sometimes reported to correlate with g_m, which may reflect the overlap of the gas phase diffusion pathways for CO₂ and water vapor (Flexas et al., 2013; hypothesis 6). Our results suggest that these pathways overlap to a greater extent at high PPFD, which happens to coincide with most typical measurement conditions for K_leaf and g_m. One way to test this hypothesis might be to compare the correlation of K_leaf and g_m at high versus low PPFD. Second, the location of the evaporating sites also may affect interference between inward CO₂ diffusion and outward vapor diffusion, and the degree of such interference should depend on the extent to which the vapor and CO₂ diffusion paths overlap (Farquhar and Cernusak, 2012; hypothesis 7). For example, an increase in mesophyll evaporation driven by the absorption of PPFD may enhance CO₂/water vapor interference by increasing the flux (vapor flow per unit of area) in the airspaces between mesophyll cells. However, at a given PPFD, the vapor flux would be similar whether those airspaces were large (implying a large proportion of evaporation from the mesophyll) or small (implying that most evaporation occurs from the epidermis), even though the flow would be smaller in the latter case; that is, the pathways always overlap, because vapor flux will occur wherever there is airspace available. Thus, we suggest that hypothesis 7 should be revised to refer not to the degree of overlap between the CO₂ and vapor diffusion pathways but rather to the magnitude of the vapor flux in the airspaces.

The final three hypotheses involving the sites of evaporation are related to the vapor pressure or mole fraction in the intercellular airspaces. First, g_s is typically calculated as [(w_leaf – w_air)/(E⋅(1 – w_avg)) – 1/g_bw]⁻¹, where E is the transpiration rate, w_leaf is the estimated intercellular water vapor mole fraction, w_avg is 0.5⋅(w_leaf + w_air), and g_bw is the boundary layer conductance to water vapor (von Caemmerer and Farquhar, 1981). The value of w_leaf is normally estimated by assuming that the airspaces are saturated with water vapor at the measured leaf temperature, T_m: that is, w_leaf ≈ w_sat(T_m), where w_sat is the ratio of saturation vapor pressure to atmospheric pressure. Based on the perception that the airspaces are closest to saturation at the sites of evaporation, it is common to interpret g_s as a measurement of the diffusive conductance from the sites of evaporation to the leaf surface, which implies that g_s will be larger if the sites of evaporation are closer to the pore, and vice versa (hypothesis 8; Jarvis and Slatyer, 1970; Farquhar and Raschke, 1978; Farquhar and Sharkey, 1982). There are two corollaries of this hypothesis. First, if evaporation occurs close to the epidermis, the value of c_i inferred from g_s will overestimate the value of c_i deeper within the mesophyll (hypothesis 9; Sharkey et al., 1982). Second, if the sites of evaporation are deeper within the leaf, the intercellular airspaces adjacent to stomata will be farther below saturation because vapor concentration must decline from those sites to the epidermis in order to drive vapor flux (hypothesis 10).

Our analysis suggests that these three hypotheses are incorrect, because the diffusive pathways described by g_s begin not at the sites of evaporation but, instead, at a hypothetical surface where w = w_sat(T_m), and these two locations can vary quite independently of one another. For example, the location of the g_s origin surface varies widely in relation to environmental conditions, and in some cases, this surface does not exist within the intercellular airspaces at all: that is, w < w_sat(T_m) everywhere outside the xylem (Fig. 12C). More importantly, the location of this surface is not related to the sites of evaporation; in fact, whereas increasing PPFD causes the sites of evaporation to recede into the mesophyll, away from the transpiring epidermis (Figs. 6 and 8), increasing PPFD causes the g_s origin surface to move in the opposite direction, toward the epidermis (Fig. 12). However, these shifts in the g_s origin surface are not accompanied by a large depression of intercellular humidity below saturation: relative humidity (calculated at T_m) was approximately 98% adjacent to the transpiring lower epidermis even in high light and at low xylem ψ (Fig. 12D). This is partly because high light drives AVT, which delivers water to the epidermis without contributing to the ψ drawdown at the epidermis. Thus, our results suggest that the conventional interpretation of g_s as being related to the evaporating sites is not justified, and that gas-exchange estimates of g_s and c_i are robust to changes in the location of the evaporating sites. These findings also imply that the pathways for K_leaf and g_s often overlap: the origin of the g_s pathways shifts greatly with anatomy and environment, whereas the pathways implied by the common operational definition of K_leaf end wherever ψ = ψ_eq, and since these two locations are not related to one another, the pathways that they define may overlap quite variably.

CONCLUSION

We explored the implications of measured variation in leaf anatomy for the spatial distribution of evaporation outside the xylem in diverse broad-leafed angiosperms using a spatially and biophysically explicit model of outside-xylem heat and water transport. We concluded that most water evaporates from the transpiring epidermis in darkness but that, under high light or high humidity, the mesophyll also can provide a large share of total evaporation. These findings have important implications for a number of critical issues, including patterns of leaf isotopic enrichment, interference of CO₂, and vapor diffusion and distribution of hormonal signals carried in the transpiration stream. Notably, the distribution of evaporation is not related consistently to the distribution of ψ or T outside the xylem, so shifts in the location of the evaporating sites do not directly affect measured values of leaf hydraulic conductance or g_s, nor of other variables such as c_i that depend on them.

MATERIALS AND METHODS

The Model

The model used here, MOFLO 2.0 (code is available upon request from the authors), was derived from an earlier model, MOFLO (Buckley et al., 2015), which quantified water transport between positions (nodes) in a grid representing the outside-xylem tissues within a single circular areole (a leaf region bounded by minor veins) of a broad leaf. Areole dimensions are estimated from minor vein density (VLA); in this framework, the presence of free-ending veinlets within areoles simply modifies the average distance of tissues from the nearest minor vein, so uncertainty in that effective distance due to free-ending veinlets is accounted for by assessing the effect of variations in VLA, which were very small (Fig. 2). In MOFLO, the areole is represented as a network of interconnected nodes, and conductances for water transport between adjacent nodes are calculated based on measured anatomy and known or assumed biophysical parameters. Mass conservation at steady-state water flow leads to a system of linear equations, one for each node, in which the independent variables are ψ values at each node and the coefficients are internodal conductances. MOFLO 2.0 extends this system to include heat transport. Our model is similar to that of Rockwell et al. (2014) in being based on the conservation of heat and mass flux through the leaf. The system is based on two conservation laws. The first describes mass (water) conservation:

(1)

where L_i and V_i are net rates of water loss from node i in the liquid and vapor phase, respectively. The second conservation law describes energy conservation:

(2)

where Q_i is net loss of energy from node i by radiation exchange with the environment surrounding the leaf, H_i describes net sensible heat loss, and the product λV_i represents the net latent heat loss (evaporative cooling), where λ is the latent heat of vaporization. The terms in Equations 1 and 2 can be expanded further: for example, V_i is the sum of net isothermal (G_i) and anisothermal (F_i) losses from node i to other locations within the leaf as well as losses to the surrounding atmosphere (E_i). Thus,

(3)

Most of the terms describing heat and mass transport can be expressed as linear functions of the state variables (temperature T_i and water potential ψ_i) whose gradients drive heat and mass transport, with coefficients representing heat and water transport conductances between nodes. For example, net liquid phase water loss from node i, L_i, can be expressed as

graphic file with name PP_PP201601605DR2_equ4.jpg

(4)

where j denotes all nodes directly connected to node i, K_l,ij is the liquid phase hydraulic conductance between nodes i and j, and ψ_i and ψ_j are the ψ values at nodes i and j, respectively. Thus, L_i is a linear equation in the ψ values across nodes (L_i = k₁⋅ψ₁ + ... + k_i⋅ψ_i + ... + k_n⋅ψ_n, where n is the number of nodes). Vapor phase transport includes two components: isothermal and anisothermal (IVT and AVT, respectively), which are driven by gradients in ψ and T, respectively (for details about IVT and AVT, see Supplemental File S1). This leads to systems of linear equations analogous to Equation 4. Thus, for IVT (net isothermal vapor loss G_i from node i),

graphic file with name PP_PP201601605DR2_equ5.jpg

(5)

where K_g,ij is the isothermal conductance for vapor water transport between nodes i and j. Similarly, for AVT (net anisothermal vapor loss F_i from node i),

(6)

where K_f,ij is the anisothermal conductance for heat-coupled vapor transport between nodes i and j. Sensible heat loss from node i (H_i) also can be represented in the same fashion:

(7)

where K_h,ij is the conductance for sensible heat transport between nodes i and j.

Several fluxes occur across the system boundary (i.e. between the outside-xylem compartment of the leaf [the system] and the surrounding environment). These were calculated by imposing assumed values for stomatal and boundary layer conductances for water vapor (g_sw and g_bw, respectively), boundary layer conductance for heat (g_bh = g_bw/1.08), and external conditions (w_air, T_air, incident PPFD, and near-infrared radiation). We modeled the transdermal gradient of absorbed visible light by estimating the absorption by each transdermal layer based on its estimated chlorophyll content and assuming that near-infrared radiation absorption was equal in all layers due to high scattering of near-infrared radiation. Mass and infrared transfer between the leaf and its surroundings depended on values of ψ and/or T at nodes on the leaf surface, so we solved the system iteratively. A full description of how we calculated these boundary exchanges, including the transdermal gradient of light absorption, as well as an explanation of how we solved the system of equations for the distributions of ψ and T, is provided in Supplemental File S1.

Simulations

We ran the MOFLO 2.0 model, computing net evaporation for all nodes as described above, for a range of conditions. For several biophysical and anatomical parameters whose values are not well characterized, we assumed similar default values to those used for the simulations presented by Buckley et al. (2015); that is, we reduced cell wall thicknesses measured by light microscopy by 80%, assumed that BS apoplastic transport was not at all suppressed by suberization or lignification, assumed that horizontal connectivity among palisade mesophyll cells was limited to the thickness of cell walls, assumed that the R_a was 3 nm, and assumed that the P_m was 40 μm s⁻¹. We tested the impact of these assumptions by repeating simulations using different assumed degrees of suppression of BS apoplastic transport by cell wall suberization or lignification (from 0% to 100% suppression), different values for R_a (1.5–4.5 nm), and different values of P_m (8–200 μm s⁻¹), which accounts for differences in the role of aquaporins. Background, justification, and discussion of these parameter defaults and ranges can be found in the report of Buckley et al. (2015). Unless noted otherwise, all simulations were repeated for the 14 species listed in Table III, with results averaged across species, and environmental and gas-exchange parameters were set at the following default values: PPFD = 1,500 μmol m⁻² s⁻¹ incident on the adaxial surface (we assumed PPFD = 0 at the abaxial surface), T_air = 25°C, w_air = 15 mmol mol⁻¹ (0.015 mol mol⁻¹), g_s = 0.4 mol m⁻² s⁻¹, and g_bw = 3 mol m⁻² s⁻¹. In additional simulations, we tested the effect of variation in PPFD (from 0 to 1,500 μmol m⁻² s⁻¹), ambient T_air (from 5°C to 45°C), ambient w_air (from 0 to 30.8 mmol mol⁻¹, which is 99% relative humidity at the default T_air of 25°C), g_bw (from 0.75 to 10 mol m⁻² s⁻¹), and g_s (from 0.05 to 0.8 mol m⁻² s⁻¹). We assessed the impact of anatomical parameters by repeating simulations for a range of values between the all-species minimum and maximum observed values for each of the following parameters: VLA, airspace fraction, leaf thickness, palisade cell radius and height, spongy cell radius, upper and lower epidermis cell size, BS extension cell size, and BS cell size. All other anatomical parameters were held at their all-species averages in each case.

MOFLO 2.0 assumes that stomatal transpiration is distributed evenly across epidermal nodes in proportion to the leaf area subtended by each node. We originally adopted that assumption in order to keep the model output as general as possible, after noting that the simulated values of K_ox were negligibly affected by assuming various patterns of clustering of transpiration in just a few epidermal nodes, representing finite stomatal density. However, concentrated water loss from epidermal regions near stomatal pores may influence the distribution of evaporation (e.g. causing greater evaporation near stomatal pores, combined with net condensation on intervening regions of epidermal tissue), so we assessed this possibility by comparing one simulation that assumed uniform transpiration with another in which the same total transpiration rate was distributed across just three nodes in the grid. The latter assumption corresponds to a stomatal density of approximately 244 mm⁻² or a stomatal spacing of 69 μm. Both simulations used anatomical parameters for Magnolia grandiflora. This simulation is presented in Supplemental Figure S3.

Estimation of Operational Measurements of g_s and K_ox

We used MOFLO 2.0 to estimate the values of K_ox and g_s that one would estimate for a leaf given the distributions of T and ψ predicted by the model under various environmental conditions. Using the evaporative flux method, K_ox is conceptually defined as E/δψ, where E is the transpiration rate and δψ is the difference between the ψ of the xylem and of the equilibrated bulk leaf. Using traditional gas-exchange methods, g_s is defined as [(w_leaf – w_air)/(E⋅(1 – w_avg)) – 1/g_bw]⁻¹, where g_bw is boundary layer conductance to water vapor, w_leaf and w_air are intercellular and ambient w_air, and w_avg = 0.5⋅(w_leaf + w_air). To estimate g_s and K_ox from MOFLO 2.0, we estimated the equilibrated bulk leaf ψ as the volume-weighted average ψ across outside-xylem tissues during transpiration [δψ ≈ ∑(v_j⋅ψ_j)/∑(v_j), where v_j represents the volume of liquid water present at node j and ψ_j is the ψ at node j], and we estimated w_leaf as the saturated value that one would calculate based on the T of the lower leaf surface. The other quantities required to estimate g_s and K_ox are either inputs into MOFLO 2.0 (w_air, g_bw, and ψ_xylem) or are calculated from the distributions of ψ and T output by the model (E and w_leaf).

Supplemental Data

The following supplemental materials are available.

Supplemental Figure S1. Effect of light and leaf thickness on spatial distributions of ψ.
Supplemental Figure S2. Effect of stomatal distribution on midleaf condensation flux.
Supplemental Figure S3. Effect of clustering of stomatal transpiration on evaporation distribution.
Supplemental Figure S4. Relationship of vertical T gradient to leaf thickness.
Supplemental Figure S5. Effect of simulated 99% reduction in the latent heat of evaporation.
Supplemental Table S1. Anatomical changes during dehydration in three species.
Supplemental Table S2. Anatomical parameters for the 14 species used in this study.
Supplemental File S1. Boundary conditions, solution, vapor phase, and BS apoplastic transport in MOFLO 2.0.

Supplementary Material

Supplemental Data

supp_173_3_1763__index.html^{(938B, html)}

Acknowledgments

We thank Graham Farquhar and Margaret Barbour for helpful discussions as well as three reviewers and Tim Brodribb for constructive comments on earlier drafts.

Glossary

AVT: anisothermal vapor transport
PPFD: photosynthetic photon flux density
BS: bundle sheath
VLA: vein length per unit of leaf area
IVT: isothermal vapor transport
ABA: abscisic acid

Footnotes

This work was supported by the Australian Research Council (grant nos. DP150103863 and LP130100183 to T.N.B.), by the Grains Research and Development Corporation (US00089), and by the U.S. National Science Foundation (grant nos. 1557906 to T.N.B. and 1146514 to L.S. and T.N.B.).

^[OPEN]

Articles can be viewed without a subscription.

References

Barbour MM, Farquhar GD (2004) Do pathways of water movement and leaf anatomical dimensions allow development of gradients in H₂¹⁸O between veins and the sites of evaporation within leaves? Plant Cell Environ 27: 107–121 [Google Scholar]
Barbour MM, Schurr U, Henry BK, Wong SC, Farquhar GD (2000) Variation in the oxygen isotope ratio of phloem sap sucrose from castor bean: evidence in support of the Péclet effect. Plant Physiol 123: 671–680 [DOI] [PMC free article] [PubMed] [Google Scholar]
Beerling DJ, Franks PJ (2010) The hidden cost of transpiration. Nature 464: 495–496 [DOI] [PubMed] [Google Scholar]
Berry JA, Beerling DJ, Franks PJ (2010) Stomata: key players in the earth system, past and present. Curr Opin Plant Biol 13: 233–240 [DOI] [PubMed] [Google Scholar]
Blizzard WE, Boyer JS (1980) Comparative resistance of the soil and the plant to water transport. Plant Physiol 66: 809–814 [DOI] [PMC free article] [PubMed] [Google Scholar]
Boyer JS. (1985) Water transport. Annu Rev Plant Physiol 36: 473–516 [Google Scholar]
Brodribb TJ, Feild TS (2000) Stem hydraulic supply is linked to leaf photosynthetic capacity: evidence from New Caledonian and Tasmanian rainforests. Plant Cell Environ 23: 1381–1388 [Google Scholar]
Brodribb TJ, Holbrook NM, Gutierrez MV (2002) Hydraulic and photosynthetic coordination in seasonally dry tropical forest trees. Plant Cell Environ 25: 1435–1444 [Google Scholar]
Brodribb TJ, Skelton RP, McAdam SA, Bienaimé D, Lucani CJ, Marmottant P (2016) Visual quantification of embolism reveals leaf vulnerability to hydraulic failure. New Phytol 209: 1403–1409 [DOI] [PubMed] [Google Scholar]
Buckley TN. (2005) The control of stomata by water balance. New Phytol 168: 275–292 [DOI] [PubMed] [Google Scholar]
Buckley TN. (2015) The contributions of apoplastic, symplastic and gas phase pathways for water transport outside the bundle sheath in leaves. Plant Cell Environ 38: 7–22 [DOI] [PubMed] [Google Scholar]
Buckley TN, John GP, Scoffoni C, Sack L (2015) How does leaf anatomy influence water transport outside the xylem? Plant Physiol 168: 1616–1635 [DOI] [PMC free article] [PubMed] [Google Scholar]
Buckley TN, Mott KA, Farquhar GD (2003) A hydromechanical and biochemical model of stomatal conductance. Plant Cell Environ 26: 1767–1785 [Google Scholar]
Canny MJ. (1990) Tansley Review No. 22. What becomes of the transpiration stream? New Phytol 114: 341–368 [DOI] [PubMed] [Google Scholar]
Canny MJ. (1993) The transpiration stream in the leaf apoplast: water and solutes. Philos Trans R Soc Lond B Biol Sci 341: 87–100 [Google Scholar]
Cowan IR. (1977) Stomatal behaviour and environment. Adv Bot Res 4: 117–228 [Google Scholar]
Craig H, Gordon LI (1965) Deuterium and oxygen 18 variations in the ocean and the marine atmosphere. In Tongiorgi E, ed, Proceedings of a Conference on Stable Isotopes in Oceanographic Studies and Palaeotemperatures. Lischi and Figli, Spoleto, Italy, pp 9–130 [Google Scholar]
Darwin F. (1898) Observations on stomata. Philosophical Transactions of the Royal Society of London, Series B 190: 531–621 [Google Scholar]
Dewar RC. (1995) Interpretation of an empirical model for stomatal conductance in terms of guard cell function. Plant Cell Environ 18: 365–372 [Google Scholar]
Dewar RC. (2002) The Ball-Berry-Leuning and Tardieu-Davies stomatal models: synthesis and extension within a spatially aggregated picture of guard cell function. Plant Cell Environ 25: 1383–1398 [Google Scholar]
Farquhar G, Lloyd J (1993) Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere. In JR Ehleringer, AE Hall, GD Farquhar, eds, Stable Isotopes and Plant Carbon-Water Relations. Academic Press, San Diego, CA, pp 47–70 [Google Scholar]
Farquhar GD, Cernusak LA (2012) Ternary effects on the gas exchange of isotopologues of carbon dioxide. Plant Cell Environ 35: 1221–1231 [DOI] [PubMed] [Google Scholar]
Farquhar GD, Ehleringer JR, Hubick KT (1989) Carbon isotope discrimination and photosynthesis. Annu Rev Plant Biol 40: 503–537 [Google Scholar]
Farquhar GD, Gan KS (2003) On the progressive enrichment of the oxygen isotopic composition of water along a leaf. Plant Cell Environ 26: 801–819 [PubMed] [Google Scholar]
Farquhar GD, Raschke K (1978) On the resistance to transpiration of the sites of evaporation within the leaf. Plant Physiol 61: 1000–1005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Farquhar GD, Sharkey TD (1982) Stomatal conductance and photosynthesis. Annu Rev Plant Physiol 33: 317–345 [Google Scholar]
Flexas J, Scoffoni C, Gago J, Sack L (2013) Leaf mesophyll conductance and leaf hydraulic conductance: an introduction to their measurement and coordination. J Exp Bot 64: 3965–3981 [DOI] [PubMed] [Google Scholar]
Hartung W, Wilkinson S, Davies W (1998) Factors that regulate abscisic acid concentrations at the primary site of action at the guard cell. J Exp Bot 49: 361–367 [Google Scholar]
Holmgren P, Jarvis PG, Jarvis MS (1965) Resistances to carbon dioxide and water vapour transfer in leaves of different plant species. Physiol Plant 18: 557–573 [Google Scholar]
Jarvis PG, Slatyer RO (1970) The role of the mesophyll cell wall in leaf transpiration. Planta 90: 303–322 [DOI] [PubMed] [Google Scholar]
Kaiser WM, Hartung W (1981) Uptake and release of abscisic acid by isolated photoautotrophic mesophyll cells, depending on pH gradients. Plant Physiol 68: 202–206 [DOI] [PMC free article] [PubMed] [Google Scholar]
Maier-Maercker U. (1983) The role of peristomatal transpiration in the mechanism of stomatal movement. Plant Cell Environ 6: 369–380 [Google Scholar]
McAdam SAM, Sussmilch FC, Brodribb TJ (2016) Stomatal responses to vapour pressure deficit are regulated by high speed gene expression in angiosperms. Plant Cell Environ 39: 485–491 [DOI] [PubMed] [Google Scholar]
Meidner H. (1975) Water supply, evaporation, and vapour diffusion in leaves. J Exp Bot 26: 666–672 [Google Scholar]
Meidner H. (1976) Water vapour loss from a physical model of a substomatal cavity. J Exp Bot 27: 691–694 [Google Scholar]
Meidner H. (1986) Cuticular conductance and the humidity response of stomata. J Exp Bot 177: 517–525 [Google Scholar]
Mott KA. (2007) Leaf hydraulic conductivity and stomatal responses to humidity in amphistomatous leaves. Plant Cell Environ 30: 1444–1449 [DOI] [PubMed] [Google Scholar]
Penman H. (1940) Gas and vapour movements in the soil. I. The diffusion of vapours through porous solids. J Agric Sci 30: 437–462 [Google Scholar]
Pieruschka R, Huber G, Berry JA (2010) Control of transpiration by radiation. Proc Natl Acad Sci USA 107: 13372–13377 [DOI] [PMC free article] [PubMed] [Google Scholar]
Rockwell FE, Holbrook NM, Stroock AD (2014) The competition between liquid and vapor transport in transpiring leaves. Plant Physiol 164: 1741–1758 [DOI] [PMC free article] [PubMed] [Google Scholar]
Roden JS, Ehleringer JR (1999) Observations of hydrogen and oxygen isotopes in leaf water confirm the Craig-Gordon model under wide-ranging environmental conditions. Plant Physiol 120: 1165–1174 [DOI] [PMC free article] [PubMed] [Google Scholar]
Roth-Nebelsick A. (2007) Computer-based studies of diffusion through stomata of different architecture. Ann Bot (Lond) 100: 23–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
Sack L, Holbrook NM (2006) Leaf hydraulics. Annu Rev Plant Biol 57: 361–381 [DOI] [PubMed] [Google Scholar]
Sack L, Melcher PJ, Zwieniecki MA, Holbrook NM (2002) The hydraulic conductance of the angiosperm leaf lamina: a comparison of three measurement methods. J Exp Bot 53: 2177–2184 [DOI] [PubMed] [Google Scholar]
Scoffoni C, Albuquerque C, Brodersen C, Townes SV, John GP, Bartlett MK, Buckley TN, McElrone AJ, Sack L (2017) Outside-xylem vulnerability, not xylem embolism, controls leaf hydraulic decline during dehydration. Plant Phys 173: 1197–1210 [DOI] [PMC free article] [PubMed] [Google Scholar]
Sharkey TD, Imai K, Farquhar GD, Cowan IR (1982) A direct confirmation of the standard method of estimating intercellular partial pressure of CO₂. Plant Physiol 69: 657–659 [DOI] [PMC free article] [PubMed] [Google Scholar]
Sheriff D. (1979) Water vapour and heat transfer in leaves. Ann Bot (Lond) 43: 157–171 [Google Scholar]
Sheriff D. (1984) Epidermal transpiration and stomatal responses to humidity: some hypotheses explored. Plant Cell Environ 7: 669–677 [Google Scholar]
Sperry JS, Hacke UG, Oren R, Comstock JP (2002) Water deficits and hydraulic limits to leaf water supply. Plant Cell Environ 25: 251–263 [DOI] [PubMed] [Google Scholar]
Stalfelt MG. (1929) Die Abhngigkeit der Spaltoffnungsreaktionen von der Wasserbilanz. Planta 8: 287–329 [Google Scholar]
Tomás M, Flexas J, Copolovici L, Galmés J, Hallik L, Medrano H, Ribas-Carbó M, Tosens T, Vislap V, Niinemets Ü (2013) Importance of leaf anatomy in determining mesophyll diffusion conductance to CO₂ across species: quantitative limitations and scaling up by models. J Exp Bot 64: 2269–2281 [DOI] [PMC free article] [PubMed] [Google Scholar]
Tyree MT, Yianoulis P (1980) The site of water evaporation from sub-stomatal cavities, liquid path resistances and hydroactive stomatal closure. Ann Bot (Lond) 45: 175–193 [Google Scholar]
Tyree MT, Zimmermann MH (2013) Xylem Structure and the Ascent of Sap. Springer Science & Business Media, Berlin [Google Scholar]
Vogel S. (1984) The lateral thermal conductivity of leaves. Can J Bot 62: 741–744 [Google Scholar]
von Caemmerer S, Farquhar GD (1981) Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves. Planta 153: 376–387 [DOI] [PubMed] [Google Scholar]
Yakir D, DeNiro M, Gat J (1990) Natural deuterium and oxygen‐18 enrichment in leaf water of cotton plants grown under wet and dry conditions: evidence for water compartmentation and its dynamics. Plant Cell Environ 13: 49–56 [Google Scholar]
Yakir D, DeNiro MJ, Rundel PW (1989) Isotopic inhomogeneity of leaf water: evidence and implications for the use of isotopic signals transduced by plants. Geochim Cosmochim Acta 53: 2769–2773 [Google Scholar]
Yang S, Tyree MT (1994) Hydraulic architecture of Acer saccharum and A. rubrum: comparison of branches to whole trees and the contribution of leaves to hydraulic resistance. J Exp Bot 45: 179–186 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Data

supp_173_3_1763__index.html^{(938B, html)}

supp_pp.16.01605_PP2016-01605DR2_Related_Manuscript_Filesuppdata.pdf^{(428.5KB, pdf)}

[bib1] Barbour MM, Farquhar GD (2004) Do pathways of water movement and leaf anatomical dimensions allow development of gradients in H₂¹⁸O between veins and the sites of evaporation within leaves? Plant Cell Environ 27: 107–121 [Google Scholar]

[bib2] Barbour MM, Schurr U, Henry BK, Wong SC, Farquhar GD (2000) Variation in the oxygen isotope ratio of phloem sap sucrose from castor bean: evidence in support of the Péclet effect. Plant Physiol 123: 671–680 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib3] Beerling DJ, Franks PJ (2010) The hidden cost of transpiration. Nature 464: 495–496 [DOI] [PubMed] [Google Scholar]

[bib4] Berry JA, Beerling DJ, Franks PJ (2010) Stomata: key players in the earth system, past and present. Curr Opin Plant Biol 13: 233–240 [DOI] [PubMed] [Google Scholar]

[bib5] Blizzard WE, Boyer JS (1980) Comparative resistance of the soil and the plant to water transport. Plant Physiol 66: 809–814 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] Boyer JS. (1985) Water transport. Annu Rev Plant Physiol 36: 473–516 [Google Scholar]

[bib7] Brodribb TJ, Feild TS (2000) Stem hydraulic supply is linked to leaf photosynthetic capacity: evidence from New Caledonian and Tasmanian rainforests. Plant Cell Environ 23: 1381–1388 [Google Scholar]

[bib8] Brodribb TJ, Holbrook NM, Gutierrez MV (2002) Hydraulic and photosynthetic coordination in seasonally dry tropical forest trees. Plant Cell Environ 25: 1435–1444 [Google Scholar]

[bib9] Brodribb TJ, Skelton RP, McAdam SA, Bienaimé D, Lucani CJ, Marmottant P (2016) Visual quantification of embolism reveals leaf vulnerability to hydraulic failure. New Phytol 209: 1403–1409 [DOI] [PubMed] [Google Scholar]

[bib10] Buckley TN. (2005) The control of stomata by water balance. New Phytol 168: 275–292 [DOI] [PubMed] [Google Scholar]

[bib11] Buckley TN. (2015) The contributions of apoplastic, symplastic and gas phase pathways for water transport outside the bundle sheath in leaves. Plant Cell Environ 38: 7–22 [DOI] [PubMed] [Google Scholar]

[bib12] Buckley TN, John GP, Scoffoni C, Sack L (2015) How does leaf anatomy influence water transport outside the xylem? Plant Physiol 168: 1616–1635 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib13] Buckley TN, Mott KA, Farquhar GD (2003) A hydromechanical and biochemical model of stomatal conductance. Plant Cell Environ 26: 1767–1785 [Google Scholar]

[bib14] Canny MJ. (1990) Tansley Review No. 22. What becomes of the transpiration stream? New Phytol 114: 341–368 [DOI] [PubMed] [Google Scholar]

[bib15] Canny MJ. (1993) The transpiration stream in the leaf apoplast: water and solutes. Philos Trans R Soc Lond B Biol Sci 341: 87–100 [Google Scholar]

[bib16] Cowan IR. (1977) Stomatal behaviour and environment. Adv Bot Res 4: 117–228 [Google Scholar]

[bib17] Craig H, Gordon LI (1965) Deuterium and oxygen 18 variations in the ocean and the marine atmosphere. In Tongiorgi E, ed, Proceedings of a Conference on Stable Isotopes in Oceanographic Studies and Palaeotemperatures. Lischi and Figli, Spoleto, Italy, pp 9–130 [Google Scholar]

[bib65] Darwin F. (1898) Observations on stomata. Philosophical Transactions of the Royal Society of London, Series B 190: 531–621 [Google Scholar]

[bib18] Dewar RC. (1995) Interpretation of an empirical model for stomatal conductance in terms of guard cell function. Plant Cell Environ 18: 365–372 [Google Scholar]

[bib19] Dewar RC. (2002) The Ball-Berry-Leuning and Tardieu-Davies stomatal models: synthesis and extension within a spatially aggregated picture of guard cell function. Plant Cell Environ 25: 1383–1398 [Google Scholar]

[bib20] Farquhar G, Lloyd J (1993) Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere. In JR Ehleringer, AE Hall, GD Farquhar, eds, Stable Isotopes and Plant Carbon-Water Relations. Academic Press, San Diego, CA, pp 47–70 [Google Scholar]

[bib21] Farquhar GD, Cernusak LA (2012) Ternary effects on the gas exchange of isotopologues of carbon dioxide. Plant Cell Environ 35: 1221–1231 [DOI] [PubMed] [Google Scholar]

[bib66] Farquhar GD, Ehleringer JR, Hubick KT (1989) Carbon isotope discrimination and photosynthesis. Annu Rev Plant Biol 40: 503–537 [Google Scholar]

[bib22] Farquhar GD, Gan KS (2003) On the progressive enrichment of the oxygen isotopic composition of water along a leaf. Plant Cell Environ 26: 801–819 [PubMed] [Google Scholar]

[bib23] Farquhar GD, Raschke K (1978) On the resistance to transpiration of the sites of evaporation within the leaf. Plant Physiol 61: 1000–1005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] Farquhar GD, Sharkey TD (1982) Stomatal conductance and photosynthesis. Annu Rev Plant Physiol 33: 317–345 [Google Scholar]

[bib25] Flexas J, Scoffoni C, Gago J, Sack L (2013) Leaf mesophyll conductance and leaf hydraulic conductance: an introduction to their measurement and coordination. J Exp Bot 64: 3965–3981 [DOI] [PubMed] [Google Scholar]

[bib26] Hartung W, Wilkinson S, Davies W (1998) Factors that regulate abscisic acid concentrations at the primary site of action at the guard cell. J Exp Bot 49: 361–367 [Google Scholar]

[bib27] Holmgren P, Jarvis PG, Jarvis MS (1965) Resistances to carbon dioxide and water vapour transfer in leaves of different plant species. Physiol Plant 18: 557–573 [Google Scholar]

[bib28] Jarvis PG, Slatyer RO (1970) The role of the mesophyll cell wall in leaf transpiration. Planta 90: 303–322 [DOI] [PubMed] [Google Scholar]

[bib29] Kaiser WM, Hartung W (1981) Uptake and release of abscisic acid by isolated photoautotrophic mesophyll cells, depending on pH gradients. Plant Physiol 68: 202–206 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] Maier-Maercker U. (1983) The role of peristomatal transpiration in the mechanism of stomatal movement. Plant Cell Environ 6: 369–380 [Google Scholar]

[bib57] McAdam SAM, Sussmilch FC, Brodribb TJ (2016) Stomatal responses to vapour pressure deficit are regulated by high speed gene expression in angiosperms. Plant Cell Environ 39: 485–491 [DOI] [PubMed] [Google Scholar]

[bib31] Meidner H. (1975) Water supply, evaporation, and vapour diffusion in leaves. J Exp Bot 26: 666–672 [Google Scholar]

[bib32] Meidner H. (1976) Water vapour loss from a physical model of a substomatal cavity. J Exp Bot 27: 691–694 [Google Scholar]

[bib58] Meidner H. (1986) Cuticular conductance and the humidity response of stomata. J Exp Bot 177: 517–525 [Google Scholar]

[bib33] Mott KA. (2007) Leaf hydraulic conductivity and stomatal responses to humidity in amphistomatous leaves. Plant Cell Environ 30: 1444–1449 [DOI] [PubMed] [Google Scholar]

[bib34] Penman H. (1940) Gas and vapour movements in the soil. I. The diffusion of vapours through porous solids. J Agric Sci 30: 437–462 [Google Scholar]

[bib35] Pieruschka R, Huber G, Berry JA (2010) Control of transpiration by radiation. Proc Natl Acad Sci USA 107: 13372–13377 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib36] Rockwell FE, Holbrook NM, Stroock AD (2014) The competition between liquid and vapor transport in transpiring leaves. Plant Physiol 164: 1741–1758 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib37] Roden JS, Ehleringer JR (1999) Observations of hydrogen and oxygen isotopes in leaf water confirm the Craig-Gordon model under wide-ranging environmental conditions. Plant Physiol 120: 1165–1174 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib38] Roth-Nebelsick A. (2007) Computer-based studies of diffusion through stomata of different architecture. Ann Bot (Lond) 100: 23–32 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib39] Sack L, Holbrook NM (2006) Leaf hydraulics. Annu Rev Plant Biol 57: 361–381 [DOI] [PubMed] [Google Scholar]

[bib40] Sack L, Melcher PJ, Zwieniecki MA, Holbrook NM (2002) The hydraulic conductance of the angiosperm leaf lamina: a comparison of three measurement methods. J Exp Bot 53: 2177–2184 [DOI] [PubMed] [Google Scholar]

[bib60] Scoffoni C, Albuquerque C, Brodersen C, Townes SV, John GP, Bartlett MK, Buckley TN, McElrone AJ, Sack L (2017) Outside-xylem vulnerability, not xylem embolism, controls leaf hydraulic decline during dehydration. Plant Phys 173: 1197–1210 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib41] Sharkey TD, Imai K, Farquhar GD, Cowan IR (1982) A direct confirmation of the standard method of estimating intercellular partial pressure of CO₂. Plant Physiol 69: 657–659 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib42] Sheriff D. (1979) Water vapour and heat transfer in leaves. Ann Bot (Lond) 43: 157–171 [Google Scholar]

[bib43] Sheriff D. (1984) Epidermal transpiration and stomatal responses to humidity: some hypotheses explored. Plant Cell Environ 7: 669–677 [Google Scholar]

[bib44] Sperry JS, Hacke UG, Oren R, Comstock JP (2002) Water deficits and hydraulic limits to leaf water supply. Plant Cell Environ 25: 251–263 [DOI] [PubMed] [Google Scholar]

[bib61] Stalfelt MG. (1929) Die Abhngigkeit der Spaltoffnungsreaktionen von der Wasserbilanz. Planta 8: 287–329 [Google Scholar]

[bib45] Tomás M, Flexas J, Copolovici L, Galmés J, Hallik L, Medrano H, Ribas-Carbó M, Tosens T, Vislap V, Niinemets Ü (2013) Importance of leaf anatomy in determining mesophyll diffusion conductance to CO₂ across species: quantitative limitations and scaling up by models. J Exp Bot 64: 2269–2281 [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib46] Tyree MT, Yianoulis P (1980) The site of water evaporation from sub-stomatal cavities, liquid path resistances and hydroactive stomatal closure. Ann Bot (Lond) 45: 175–193 [Google Scholar]

[bib47] Tyree MT, Zimmermann MH (2013) Xylem Structure and the Ascent of Sap. Springer Science & Business Media, Berlin [Google Scholar]

[bib48] Vogel S. (1984) The lateral thermal conductivity of leaves. Can J Bot 62: 741–744 [Google Scholar]

[bib49] von Caemmerer S, Farquhar GD (1981) Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves. Planta 153: 376–387 [DOI] [PubMed] [Google Scholar]

[bib50] Yakir D, DeNiro M, Gat J (1990) Natural deuterium and oxygen‐18 enrichment in leaf water of cotton plants grown under wet and dry conditions: evidence for water compartmentation and its dynamics. Plant Cell Environ 13: 49–56 [Google Scholar]

[bib51] Yakir D, DeNiro MJ, Rundel PW (1989) Isotopic inhomogeneity of leaf water: evidence and implications for the use of isotopic signals transduced by plants. Geochim Cosmochim Acta 53: 2769–2773 [Google Scholar]

[bib52] Yang S, Tyree MT (1994) Hydraulic architecture of Acer saccharum and A. rubrum: comparison of branches to whole trees and the contribution of leaves to hydraulic resistance. J Exp Bot 45: 179–186 [Google Scholar]

PERMALINK

The Sites of Evaporation within Leaves1,[OPEN]

Thomas N Buckley

Grace P John

Christine Scoffoni

Lawren Sack

Abstract

Table I. List of hypotheses that involve the location of the evaporating sites, with corrections based on insights presented in this article.

Table II. List of symbols.

Table III. Summary data for species used in this study.

RESULTS

Effects of Leaf Anatomy on the Distribution of Evaporation

Figure 1.

Figure 2.

Table IV. Effects of cell dimensions on the distribution of evaporation.

Figure 3.

Effects of Anatomical Changes during Dehydration

Figure 4.

Effects of Variation in Liquid Transport Properties

Figure 5.

Effects of Variation in Environmental Parameters

Figure 6.

Figure 7.

Figure 8.

Effects of Thermal Transport Properties

Figure 9.

Effect of Stomatal Conductance

Figure 10.

Effects of the Location of Evaporation on Inferred Hydraulic and Stomatal Conductance Values

Figure 11.

Figure 12.

Relationship between Tissue Evaporation Rate and Tissue Water Potential

Figure 13.

DISCUSSION

How Does Anatomy Affect Where Evaporation Occurs?

How Do Environmental Conditions Affect Where Evaporation Occurs?

The Evaporating Sites Are Not the End Point of Water Transport

Reconceiving Leaf Hydraulics as a Mixed-Phase Phenomenon: What Does Hydraulic Conductance Mean?

Other Implications of the Location of the Evaporating Sites

CONCLUSION

MATERIALS AND METHODS

The Model

Simulations

Estimation of Operational Measurements of gs and Kox

Supplemental Data

Supplementary Material

Acknowledgments

Glossary

Footnotes

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

The Sites of Evaporation within Leaves^¹^,^{^[OPEN]}

Estimation of Operational Measurements of g_s and K_ox