Sequential Multiple Assignment Randomization Trials with Enrichment Design

Summary

Sequential multiple assignment randomization trial (SMART) is a powerful design to study Dynamic Treatment Regimes (DTRs) and allows causal comparisons of DTRs. To handle practical challenges of SMART, we propose a SMART with Enrichment (SMARTer) design, which performs stage-wise enrichment for SMART. SMARTer can improve design efficiency, shorten the recruitment period, and partially reduce trial duration to make SMART more practical with limited time and resource. Specifically, at each subsequent stage of a SMART, we enrich the study sample with new patients who have received previous stages’ treatments in a naturalistic fashion without randomization, and only randomize them among the current stage treatment options. One extreme case of the SMARTer is to synthesize separate independent single-stage randomized trials with patients who have received previous stage treatments. We show data from SMARTer allows for unbiased estimation of DTRs as SMART does under certain assumptions. Furthermore, we show analytically that the efficiency gain of the new design over SMART can be significant especially when the dropout rate is high. Lastly, extensive simulation studies are performed to demonstrate performance of SMARTer design, and sample size estimation in a scenario informed by real data from a SMART study is presented.

1. Introduction

Dynamic Treatment Regimes (DTRs), also referred to as adaptive treatment regimes or tailored treatment regimens, are sequential treatment rules tailored at each stage by patients’ time-varying characteristics and intermediate treatment responses (Thall et al., 2000; Lavori et al., 2000; Murphy et al., 2007; Dawson and Lavori, 2004). For example, an oncologist aiming to prolong survival for a cancer patient might use intermediate outcomes such as patient’s tumor response to induction therapy to guide the use of second-line therapy. Sequential multiple assignment randomization trials (SMARTs) (Lavori and Dawson, 2000, 2004; Murphy, 2005) generalize conventional randomized clinical trials to make causal comparisons of such DTRs. In SMARTs, patients are randomized to different treatments at each critical decision stage, where randomization probabilities may depend on patients’ time-varying response (e.g., changes in symptom severity, drug-resistance, treatment adherence) up to that stage. These trials also provide rich information to infer optimal treatment regimens tailored to individual patients. Murphy (2005) provides inferences and sample size formula to compare two DTRs in SMARTs, Almirall et al. (2012) proposed to use SMART design as a pilot study for building effective DTRs, and Nahum-Shani et al. (2012) illustrated several important design issues and primary analyses for SMART studies. Cheung et al. (2015) introduced an adaptive randomization scheme for a sequential multiple assignment randomized trial of DTRs. Lastly, Shortreed et al. (2014) discussed handling missing data for SMART through multiple imputation with applications to the CATIE study (Stroup et al., 2003).

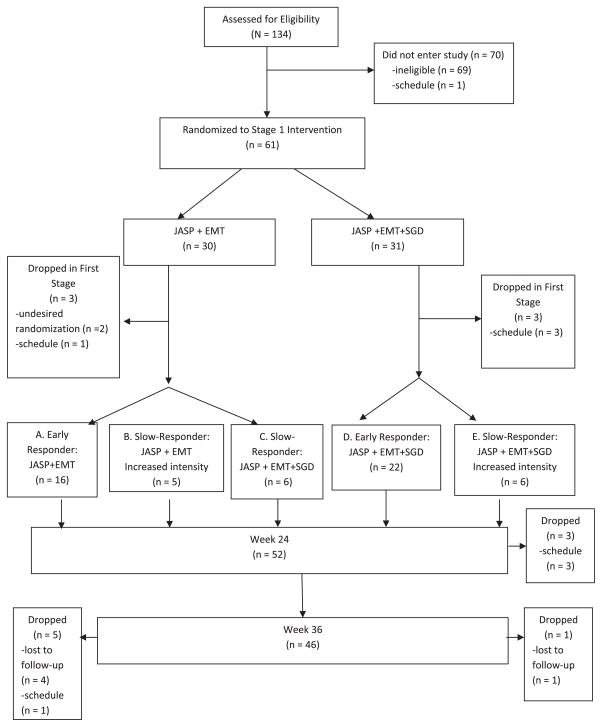
We use a real study (Kasari et al., 2014) to illustrate DTR and concepts in SMART. Kasari et al. (2014) conducted a SMART on communication intervention for minimally verbal children with autism. The study is a two-stage SMART targeted on testing the effect of a speech-generating device (SGD). We present the original diagram of the study in Figure 1. In the first stage, 61 children were randomized to a blended developmental/behavioral intervention (JASP + EMT) with or without augmentation of a SGD for 12 weeks with equal probability. At the end of the 12th week, children were assessed for early response versus slow response to stage 1 treatment. In the second stage, the early-responders continued with the first stage treatments. The slow-responders to (JASP + EMT) were randomized to (JASP + EMT + SGD) or intensified (JASP + EMT + SGD) with equal probability. The slow responders to JASP+EMT+SGD were not re-randomized. The second stage lasted 12 weeks and followed by a follow-up stage of 12 weeks. In this article, the primary aim was to compare the first stage treatment options SGD (JASP + EMT + SGD) versus spoken words alone (JASP + EMT). Secondary aim was to compare the dynamic treatment regimes (DTRs), namely: 1) beginning with JASP + EMT + SGD and intensifying JASP + EMT + SGD for slow responders; 2) beginning with JASP + EMT and to increase the intensity for slow responders; 3) beginning with JASP + EMT and to switch JASP + EMT + SGD for slow responders.

Figure 1.

Diagram for the autism example.

The cost of multistage and multitreatment studies such as SMARTs is high and the length of trial period is long (March et al., 2010). The implementation for administering multiple stages of multiple treatment is likely to be complex and operational cost can be high. Furthermore, study dropout is a common phenomenon in randomized clinical trials (RCTs) regardless of investigator’s best efforts to keep patients in the study. For example, meta analyses of study dropout rate for RCTs of antipsychotic drugs treating schizophrenia reported an average attrition rate of greater than 30% (Martin et al., 2006; Kemmler et al., 2005). In the Clinical Antipsychotic Trials of Intervention and Effectiveness (CATIE) study (Schneider et al., 2003), the attrition was 48% with 705 of 1460 patients staying for the entire 18 months. In some other SMARTs, the dropout rate was lower but still persists as in regular RCTs. In ExTENd for example (Lei et al., 2012), there was a drop-out rate of 17% during the first-stage treatment (52 out of 302), and an additional 13% during the second stage (41 out of 302).

In this article, we propose a stage-wise enrichment design to improve efficiency of SMART estimations. The key component is to include an enrichment sample who have received first stage treatments in a naturalistic fashion but will undergo randomization for the second stage treatments. This new design can be considered as a meta-analytic approach to enrich SMART sample and to synthesize single-stage trials without sacrificing the central feature of SMART to make causal conclusions. We show that the proposed SMART with Enrichment design (SMARTer) and its appropriate analysis method will boost the efficiency of SMART, improve practicability of SMART, address the attrition issue from the design and analysis perspective, and avoid pitfalls of incorrect inference on long-term DTR effect when combining single-stage randomized trials. Specifically, the proposed methodology can potentially 1) synthesize single-stage trials to integrate information to make causal inference on DTRs as is possible in a multi-stage SMART, while substantially shortening the trial time frame; 2) extract information from patients dropping out from the first stage; 3) recruit and randomize additional patients to the second-stage treatments without requiring randomization of the first-stage treatments, and thus achieve the same or superior efficiency as if there were no dropouts, which reduces the sample size of the initial stage and the overall sample size.

It is of interest to note that SMARTer design differs from an intuitive approach that pieces together results from separate randomized trials conducted at separate stages, as criticized in previous literature (Murphy et al., 2007; Collins et al., 2014). For the latter, an investigator may determine the best first-line treatment based on a conventional randomized trial comparing several first-line treatments and then next, compare second-line treatments for a new group of subjects already treated by the “best” first-stage treatment. Essentially, this intuitive approach compares available intervention options at each stage separately to infer the best DTR. It has several disadvantages (Murphy et al., 2007): first, it does not capture the delayed effect when the long-term effect begins to appear in latter stages; second, it fails to take into account the prescriptive effect of an early stage treatment which may not yield a larger intermediate outcome; third, single-stage trials tend to enroll more homogeneous patients to increase power for detection of treatment differences whereas SMART would not. In terms of design, SMARTer does not recommend enriching the sample with only the subjects who have received the “best” first-line treatment inferred from a single-stage trial. Instead, we recruit enrichment samples from subjects who have received any of the first-line treatments so that the enrichment population includes patients with all possible combinations of both lines of treatments to properly account for delayed effect and prescriptive effect. The main focus of SMARTer design is to improve efficiency through enrichment samples who only receive randomization in the latter stages. In terms of the analysis, instead of inferring the best treatment from each single stage separately, SMARTer can be used to infer optimal DTRs with backward induction algorithms such as Q-learning (Murphy and Collins, 2007), which uses the randomized samples for each stage including the enrichment participants.

2. SMARTer Design

2.1. Rationales of SMARTer Design

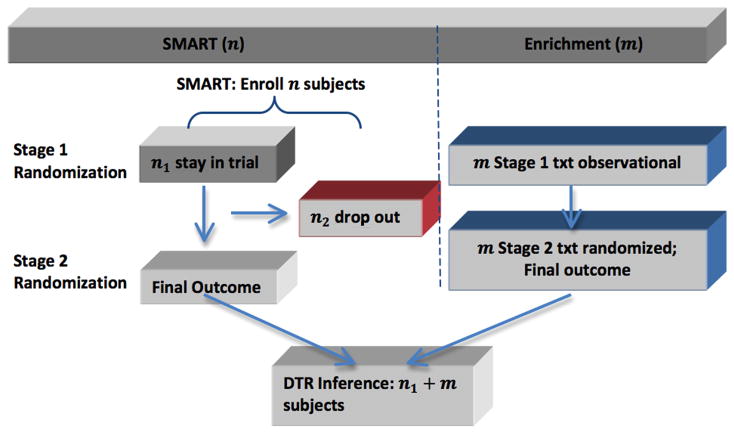
The essential idea of a SMARTer design is to consider stage-wise enrichment: at the kth stage (k > 1), augment the original SMART with new patients randomized among the kth stage treatment options without requiring randomization of previous stage treatments. Figure 2 illustrated the enrichment for a two-stage SMART with no intermediate outcomes. Generalizations to more than two stages and including intermediate outcomes are similar. Assume that n patients are randomized at the first stage in a SMART. Some patients complete the first stage treatment and undergo the second stage randomization (group 1), while some patients drop out before the second stage randomization (group 2). To improve efficiency and mitigate the problem of attrition after the first stage treatment, while the original SMART is progressing, we concurrently recruit m new patients as the enrichment sample (group 3). One key eligibility criterion for the enrichment group is that they have received one of the first stage treatments without randomization prior to the enrollment. For the enrichment subjects in group 3, their second-stage treatments will be randomized as in the original SMART.

Figure 2.

Diagram of SMARTer design.

Taking the autism study (Kasari et al., 2014) as an example, the primary outcome for this study was the total number of spontaneous communicative utterances (TSCU). The response status to the first stage treatment was the intermediate outcome that the second stage treatment choice and randomization probability depended on. For example, for a DTR starting with JASP + EMT, whether a patient participates in the second randomization to add SGD or intensify depends on whether he/she is a slow responder or not. Group 1 patients would be those who were randomized in the first stage and stayed through the trial until the end of the second stage. Group 2 patients include the six patients who dropped out after randomization in the first stage, and the additional three patients who dropped out after finishing first stage and on whom the intermediate response variables were recorded. In the next few sections, we will provide analysis of efficiency and sample size computation for the enrichment group three patients in the new SMARTer design to estimate the mean outcome of a given DTR and compare DTRs.

The final analysis sample of SMARTer consists of three groups of patients (also shown in Figure 2). Specifically, group 1 is the n₁ SMART subjects who stay through two stages of randomization and treatments; group 2 is the n₂ SMART subjects who drop out before the second randomization; and group 3 is the m enrichment subjects who only receive the second-stage randomization with known first-stage treatment history. Let Z_i denote the indicator of stage 2 completion status for subject i, S_i denote pre-treatment information at stage 1, A_ki denote treatment at stage k (k = 1, 2), and Y_i denote the observed outcome from the study. Then SMARTer data consists of the data from the original SMART subjects, (S_i, A_1i, Z_iA_2i, Z_iY_i, i = 1, …, n), and the data from the m enrichment subjects, (S_j, A_1j, A_2j, Y_j, j = 1, …, m). In the subsequent presentation, we assume S_i to take a finite number of discrete values for convenience.

To understand why SMARTer enables valid evaluation of DTRs under certain assumptions, we first focus on a two-stage trial and assume that there is no intermediate information after stage 1. For any DTR (d₁, d₂), a sequence of decision rules with d_k representing a function mapping historical information to the domain of A_k for k = 1, 2, our goal is to estimate the value function of (d₁, d₂) defined as E[Y (d₁, d₂)]. Here, Y (a₁, a₂) is the potential outcome associated with the treatment assignment (a₁, a₂). We assume the following conditions hold:

(C.1) Y = Σ_a1,a2 Y (a₁, a₂)I (A₁ = a₁, A₂ = a₂); (C.2) sequential ignorability or non-informative dropout: the dropout is independent of {Y (a₁, a₂)} given (S, A₁); (C.3) no selection bias: the conditional mean of Y given (S, A₁) in the enrichment group is the same as that in the original SMART population; (C.4) the first stage domain of A₁ (treatment options) for the enrichment group is identical to the treatment A₁ in the SMART population.

Condition (C.1) is the standard stable unit treatment value assumption (SUTVA) in causal inference. Condition (C.2) is the sequential ignorability, non-informative dropout, or missing at random (MAR) assumption also required in any analysis of an RCT. The key condition (C.3) requires no selection bias in the sense that the conditional treatment effect given S is the same between the original SMART samples and the enrichment samples. This assumption is required to use the enrichment sample to estimate E(Y (a₁, a₂)|S, A₁ = a₁, A₂ = a₂) and ensure the DTR estimands are the same in the enrichment population and the original SMART population. (C.4) ensures the first stage treatments are comparable in the SMART and enrichment samples. We further discuss these assumptions in Section 6.

Under conditions (C.1)–(C.4), we show SMARTer can provide an unbiased estimation of the average potential outcome under the DTR (d₁, d₂), that is, E[Y (d₁, d₂)]. Due to sequential ignorability, potential outcomes {Y (a₁, a₂)} are conditionally independent of A₂ given (S, A₁) in the enrichment sample, even if their first stage treatments is received in a naturalistic fashion without randomization. When comparing first stage treatment options, we only use the non-dropouts from the original SMART and estimate outcomes for n₂ dropouts whose first stage treatments are randomized. Thus potential outcomes {Y (a₁, a₂)} for these subjects are also independent of A₁. Let p_k (a_k |s_k ) denote the randomization probability of A_k given a patient’s covariates collected up to stage k, that is, s_k. Note that for simplicity, here we assume the second stage randomization probabilities depend on baseline covariates and first stage treatments. In Section 2.3, we generalize to allow them to depend on intermediate outcomes. Our key result is to show

$$\begin{array}{ll}\hfill E[Y(d_1,d_2)]& ={\mu }_1={\mu }_2,\hfill \\ \hfill \text{where}{\mu }_1& =E_1\left[\frac{I(A_1=d_1(S),A_2=d_2(S,A_1))}{p_1(A_1\mid S)p_2(A_2\mid S,A_1)}Y\right],\hfill \\ \hfill {\mu }_2& =E_2\left[\frac{I(A_1=d_1(S))}{p_1(A_1\mid S)}{Y}^{\ast }\right],\hfill \end{array}$$

E_g[·] denotes the expectation for subjects in group g, and Y^* denotes the conditional mean of Y given (S, A₁, A₂ = d₂(S, A₁)) for subjects in group 1 and 3. The rationale is that if this equality holds, then the average causal outcome, E[Y (d₁, d₂)], can be estimated unbiasedly using the data from SMARTer since Y^*, E₁[·], and E₂[·] can be estimated unbiasedly using their corresponding empirical averages. There are three observations of this result: 1) since group 1 subjects’ final outcomes Y are observed, we estimate their average causal mean using their observed outcomes; 2) group 2 subjects drop out after first-stage and have missing Y, but their outcomes can be estimated as Y^* from subjects in group 1 and 3; 3) group 3 subjects contribute to the estimation through estimating missing outcomes for subjects in group 2.

To see why the above equalities hold, first note that under condition (C.1), we obtain

$${\mu }_1=E_1\left[\frac{I(A_1=d_1(S),A_2=d_2(S,A_1))}{p_1(A_1\mid S)p_2(A_2\mid S,A_1)}Y(d_1,d_2)\right].$$

By randomization, A₂ is independent of potential outcome Y (d₁, d₂) given (S, A₁). Thus, since E₁[·] is equivalent to E[·] under the non-informative dropout condition (C.2), the above expression becomes

$${\mu }_1=E\left[\frac{I(A_1=d_1(S))}{p_1(A_1\mid S)}Y(d_1,d_2)\right].$$

Furthermore, by randomization of A₁ in the first stage for group 1 subjects, we obtain the above equation to also equal the average causal outcome, that is,

$$\begin{array}{l}{\mu }_1=E\left[E\left\{\frac{I(A_1=d_1(S))}{p_1(d_1\mid S)}\mid S\right\}E\{Y(d_1,d_2)\mid S\}\right]\\ =E[Y(d_1,d_2)].\end{array}$$

Next, due to randomization of A₂ for subjects in group 1 and group 3, under condition (C.3), we obtain

$$\begin{array}{l}{Y}^{\ast }=E[Y(A_1,d_2(S,A_1))\mid S,A_1,A_2=d_2(S,A_1)]\\ =E[Y(A_1,d_2(S,A_1))\mid S,A_1].\end{array}$$

Consequently,

$$\begin{array}{l}{\mu }_2=E\left[\frac{I(A_1=d_1(S))}{p_1(A_1\mid S)}E[Y(A_1,d_2(S,A_1))\mid S,A_1]\right]\\ =E\left[\frac{I(A_1=d_1(S))}{p_1(A_1\mid S)}E[Y(d_1,d_2)\mid S,A_1]\right].\end{array}$$

Again, by the randomization of A₁ for subjects in group 2, we conclude μ₂ = E[Y (d₁, d₂)].

2.2. Value Estimation and Inference in SMARTer

Given a DTR (d₁, d₂), for a patient with S = s and treatment assignment a₁ = d₁(s) and a₂ = d₂(s, a₁), an estimator of the expected outcome value associated with this DTR is

$$\begin{array}{l}\widehat{\mu }(d_1,d_2)={\left\{\sum _{i=1}^n\left(Z_i\frac{I(A_{1i}=d_1(S_i),A_{2i}=d_2(S_i,A_{1i}))}{p(A_{1i}\mid S_i)p(A_{2i}\mid S_i,A_{1i})}+(1-Z_i)\frac{I(A_{1i}=d_1(S_i))}{p(A_{1i}\mid S_i)}\right)\right\}}^{-1}\\ \times \left\{\sum _{i=1}^n\left(Z_i\frac{I(A_{1i}=d_1(S_i),A_{2i}=d_2(S_i,A_{1i}))}{p(A_{1i}\mid S_i)p(A_{2i}\mid S_i,A_{1i})}{Y}_i+(1-Z_i)\frac{I(A_{1i}=d_1(S_i))}{p(A_{1i}\mid S_i)}\widehat{Y}(S_i,A_{1i},d_2(S_i,A_{1i}))\right)\right\},\end{array}$$ (1)

where Ŷ(s, a₁, a₂) is the predicted outcomes for group 2 subjects using group 1 and group 3 data:

$$\widehat{Y}(s,a_1,a_2)=\frac{{\sum }_{i=1}^n{Z}_i{Y}_{i}I(S_i=s,A_{1i}=a_1,A_{2i}=a_2)+{\sum }_{j=1}^m{Y}_{j}I(S_j=s,A_{1j}=a_1,A_{2j}=a_2)}{{\sum }_{i=1}^n{Z}_{i}I(S_i=s,A_{1i}=a_1,A_{2i}=a_2)+{\sum }_{j=1}^{m}I(S_j=s,A_{1j}=a_1,A_{2j}=a_2)}.$$

The essential idea is to estimate the group 2 outcomes from the outcomes of group 1 and 3. The enrichment sample improves estimation efficiency by adding more samples for the nonparametric estimation. Note that from (1), even without an enrichment sample (i.e., m = 0), we can still estimate group 2 subjects’ outcomes using group 1 subjects’ to improve efficiency with no bias. It is clear that the estimator in (1) adheres to the intention-to-treat principal (Fisher et al., 1989) such that all subjects randomized are analyzed according to their original treatment assignments.

Next, we derive the asymptotic variance formula for estimator (1) under the conditions (C.1) through (C.4) assuming m = O(n). Specifically, we wish to obtain the asymptotic expansion of μ̂(d₁, d₂) − μ(d₁, d₂). To this end, we let p(s) be the probability of S = s and p(a₁|s) be the randomization probability of A₁ = a₁ given S = s in the SMART population in the first stage and let p(a₂|s, a₁) be the randomization probability of A₂ = a₂ given S = s and A₁ = a₁ in the second stage. These two conditional probabilities are known by design. Furthermore, we let q(s) and q(a₁|s) be the probability of enrichment sample with S = s and receiving first-stage treatment A = a₁ given S = s. Note that we allow the baseline covariates to have different distribution in the enrichment sample (q(s)) and SMART sample (p(s)), and the observed conditional probability q(a₁|s) can be different from the randomization probability p(a₁|s). We denote π₁(s, a₁, a₂) = p(a₂|s, a₁)p(a₁|s)p(s), π₂(s, a₁, a₂) = p(a₁|s)p(s)I (d₂(s, a₁) = a₂), and π₃(s, a₁, a₂) = p(a₂|s, a₁)q(a₁|s)q(s). Finally, denote α(s, a₁) = P (Z = 1|S = s, A₁ = a₁), β = m/n, and r(s, a₁) = q(a₁|s)q(s)/[p(a₁|s)p(s)].

We show in Web Appendix A the asymptotic variance of μ̂(d₁, d₂) is V/n, where

$$\begin{array}{l}V\equiv {\mathit{Var}}_s(Z\frac{I(A_1=d_1(S),A_2=d_2(S,A_1))}{p(A_1\mid S)p(A_2\mid S,A_1)}\\ \times \left\{(Y-\mu (d_1,d_2))+\frac{1-\alpha (S,A_1)}{\alpha (S,A_1)+\beta r(S,A_1)}(Y-E[Y\mid S,A_1,A_2])\right\}\\ +(1-Z)\frac{I(A_1=d_1(S))}{p(A_1\mid S)}E[Y-\mu (d_1,d_2)\mid S,A_1,A_2=d_2(S,A_2)])\\ +\beta {\mathit{Var}}_e\left(\frac{(1-\alpha (S,A_1))(Y-E[Y\mid S,A_1,A_2])}{\alpha (S,A_1)+\beta r(S,A_1)}\times \frac{I(A_1=d_1(S),A_2=d_2(S,A_1))}{p(A_1\mid S)p(A_2\mid S,A_1)}\right).\end{array}$$

The first term is the variability from subjects in group 1 and imputing outcomes for group 2, and the second term is the variability from enrichment subjects in group 3. The variance can be estimated by its empirical form.

Finally, to compare two DTRs, we can use the difference of SMARTer estimators for two DTRs (d₁, d₂) and ( $d_1^{\prime },d_2^{\prime }$), that is, $\widehat{\mu }(d_1,d_2)-\widehat{\mu }(d_1^{\prime },d_2^{\prime })$. Then its asymptotic variance is $V({\overline{d}}_2,{\overline{d}}_2^{\prime })/n$, where

$$\begin{array}{l}V({\overline{d}}_2,{\overline{d}}_2^{\prime })\equiv {\mathit{Var}}_s\{Z\frac{I(A_1=d_1(S),A_2=d_2(S,A_1))}{p(A_1\mid S)p(A_2\mid S,A_1)}\\ \times \left((Y-\mu (d_1,d_2))+\frac{1-\alpha (S,A_1)}{\alpha (S,A_1)+\beta r(S,A_1)}(Y-E[Y\mid S,A_1,A_2])\right)\\ -Z\frac{I(A_1=d_1^{\prime }(S),A_2=d_2^{\prime }(S,A_1))}{p(A_1\mid S)p(A_2\mid S,A_1)}\\ \times \left((Y-\mu (d_1^{\prime },d_2^{\prime }))+\frac{1-\alpha (S,A_1)}{\alpha (S,A_1)+\beta r(S,A_1)}(Y-E[Y\mid S,A_1,A_2])\right)\\ +(1-Z)\frac{I(A_1=d_1(S))}{p(A_1\mid S)}E[Y-\mu (d_1,d_2)\mid S,A_1,A_2=d_2(S,A_2)]\\ -(1-Z)\frac{I(A_1=d_1^{\prime }(S))}{p(A_1\mid S)}E[Y-\mu (d_1^{\prime },d_2^{\prime })\mid S,A_1,A_2=d_2^{\prime }(S,A_2)]\}\\ +\beta {\mathit{Var}}_e\left[\frac{(1-\alpha (S,A_1))(Y-E[Y\mid S,A_1,A_2])}{\alpha (S,A_1)+\beta r(S,A_1)}\times \frac{I(A_1=d_1,A_2=d_2)-I(A_1=d_1^{\prime },A_2=d_2^{\prime })}{p(A_1\mid S)p(A_2\mid S,A_1)}\right].\end{array}$$

This variance can also be estimated by its empirical form.

2.3. Incorporating Intermediate Outcomes

The previous section assumes no intermediate outcome is available especially for subjects who drop out from the SMART. When intermediate outcomes are available, the treatment rule d₂ may depend on the intermediate outcome. In this case, the observed data from a SMARTer consist of (S_1i, A_1i, S_2i, Z_iA_2i, Z_iY_i), i = 1, …, n, for i in the original SMART group, and the enrichment group observations (S_1j, A_1j, S_2j, A_2j, Y_j), j = 1, …, m. Here, we use S₁ to denote pre-treatment covariates at stage 1 and S₂ to denote intermediate outcomes and other covariates collected prior to stage 2. For simplicity of derivation, we assume S_1i and S_2j to be discrete. Similar to (1), a consistent estimator of the associated value using both the SMART and enrichment observations is

$$\begin{array}{l}\widehat{\mu }(d_1,d_2)={\left\{\sum _{i=1}^n\left(Z_i\frac{I(A_{1i}=d_1(S_{1i}),A_{2i}=d_2(S_{1i},A_{1i},S_{2i}))}{p(A_{1i}\mid S_{1i})p(A_{2i}\mid S_{1i},A_{1i},S_{2i})}+(1-Z_i)\frac{I(A_{1i}=d_1(S_{1i}))}{p(A_{1i}\mid S_{1i})}\right)\right\}}^{-1}\\ \times \left\{\sum _{i=1}^n\left(Z_i\frac{I(A_{1i}=d_1(S_{1i}),A_{2i}=d_2))}{p(A_{1i}\mid S_{1i})p(A_{2i}\mid S_{1i},A_{1i},S_{2i})}{Y}_i+(1-Z_i)\frac{I(A_{1i}=d_1(S_{1i}))}{p(A_{1i}\mid S_{1i})}\widehat{Y}(S_{1i},A_{1i},d_2(S_{1i},A_{1i}{S}_{2i}),S_{2i})\right)\right\},\end{array}$$

where Ŷ(s₁, a₁, s₂, a₂) is the imputed outcome from the second-stage data given as

$$\frac{{\displaystyle \sum _{i=1}^n}{Z}_i{Y}_{i}I(S_{1i}=s_1,A_{1i}=a_1,S_{2i}=s_2,A_{2i}=a_2,)+{\displaystyle \sum _{j=1}^m}{Y}_{j}I(S_{1j}=s_1,A_{1j}=a_1,S_{2j}=s_2,A_{2j}=a_2)}{{\displaystyle \sum _{i=1}^n}{Z}_{i}I(S_{1i}=s_1,A_{1i}=a_1,S_{2i}=s_2,A_{2i}=a_2)+{\displaystyle \sum _{j=1}^m}I(S_{1j}=s_1,A_{1j}=a_1,S_{2j}=s_2,A_{2j}=a_2)}.$$

The asymptotic variance is similar to before by re-defining π_k (s, a₁, a₂) as π_k (s₁, a₁, s₂, a₂) through conditioning on both the baseline covariates S₁ and intermediate outcome S₂. That is,

$$\begin{array}{l}V\equiv {\mathit{Var}}_s(Z\frac{I(A_1=d_1(S_1),A_2=d_2(S_1,A_1,S_2))}{p(A_1\mid S_1)p(A_2\mid S_1,A_1,S_2)}\{(Y-\mu (d_1,d_2))\\ +\frac{1-\alpha (S_1,A_1,S_2)}{\alpha (S_1,A_1,S_2)+\beta r(S_1,A_1,S_2)}(Y-E[Y\mid S_1,A_1,S_2,A_2])\}\\ +(1-Z)\frac{I(A_1=d_1(S_1))}{p(A_1\mid S_1)}E[Y-\mu (d_1,d_2)\mid S_1,A_1,A_2=d_2(S_1,A_2,S_2)])\\ +\beta {\mathit{Var}}_e\left(\frac{(1-\alpha (S_1,A_1,S_2))(Y-E[Y\mid S_1,A_1,S_2,A_2])}{\alpha (S,A_1)+\beta r(S_1,A_1,S_2)}\times \frac{I(A_1=d_1(S_1),A_2=d_2(S_1,A_1,S_2))}{p(A_1\mid S_1)p(A_2\mid S_1,A_1,S_2)}\right).\end{array}$$

3. Design Efficiency of SMARTer

In this section, we study the efficiency gain or loss of the proposed design as compared to a SMART with no dropout. For simplicity of illustration, we assume P(Z = 1|A₁, S) to be a constant α and let ω(s) = r(d₁(s), s). Furthermore, we denote p(d₁(s)|s) = p₁(s) and p(d₂(s, d₁(s))|d₁(s), s) = p₂(s), so the variance of μ̂(d₁, d₂) is V/n with

$$V=E_s\left[\left(\frac{\alpha }{p_1(S)p_2(S)}+\frac{1-\alpha }{p_1(S)}\right){(v(S)-\mu (d_1,d_2))}^2\right]+E_s\left[\frac{\sigma {(S)}^2}{p_1(S)p_2(S)}\frac{\alpha {(1+\beta \omega (S))}^2+\beta {(1-\alpha )}^2\omega (S)}{{(\alpha +\beta \omega (S))}^2}\right],$$

where E_s[·] is the expectation with respect to S in the SMART population,

$$\begin{array}{l}v(s)=E_s(Y\mid A_1=d_1(s),A_2=d_2(d_1(s),s),S=s)\\ =E_e(Y\mid A_1=d_1(s),A_2=d_2(d_1(s),s),S=s),\\ \text{and}\sigma {(s)}^2={\mathit{Var}}_s(Y\mid A_1=d_1(s),A_2=d_2(d_1(s),s),S=s)\\ ={\mathit{Var}}_e(Y\mid A_1=d_1(s),A_2=d_2(d_1(s),s),S=s).\end{array}$$

When α = 1, that is, no participant drops out from SMART, V reduces to

$$V_0=E_s\left[\frac{{(v(S)-\mu (d_1,d_2))}^2+\sigma {(S)}^2}{p_1(S)p_2(S)}\right],$$

which is the variance formula given in Murphy (2005) for SMART. Therefore, to measure the efficiency gain of the proposed design over SMART design without dropouts, we define relative efficiency ρ = V₀/V, where ρ > 1 implies the proposed enrichment design is more efficient than the original SMART without dropout.

To further gain insights on efficiency comparison, we consider a special situation when treatment randomization does not depend on tailoring variables, that is, p₁(S) = p₁, p₂(S) = p₂. We assume that the enrichment population is close to the SMART population so ω(s) ≈ 1, and let the ratio of within- and between-strata variance to be γ ≈ Eσ(s)²/E(ν(s) − μ(d₁, d₂))². Let α denote the completion (non drop-out) rate, and β = m/n denote the enrichment rate. We can show (2) holds and details are included in Web Appendix B.

$$\rho \approx \frac{1+\gamma }{1-(1-\alpha )(1-p_2)+\gamma \frac{\alpha {(1+\beta )}^2+\beta {(1-\alpha )}^2}{{(\alpha +\beta )}^2}}.$$ (2)

From (2), the relative efficiency depends on randomization probabilities, within- and between-strata (S) variability and distribution ratios between the enrichment and SMART populations. Note that ρ > 1 implies the proposed SMARTer is more efficient than a SMART without enrichment and no dropout. From the expression of ρ, we thus conclude:

1. When α = 1, there is no dropout after the first stage in SMARTer, our estimator reduces to be the same as the estimator in Murphy (2005), and thus ρ = 1.

2. When α = 0, that is, all subjects drop out after the first stage, ρ ≈ (1 + γ)/(p₂ + γ/β). There is efficiency gain if β >γ /(1 + γ − p₂). More specifically, there is always efficiency gain if β > 1. Note that this is the extreme case in the sense that all subjects drop out and we synthesize two independent randomized trials on the two stages.

3. For any 0 < α < 1, if α(1 + β)² + β(1 − α)² ≤ (α + β)², ρ > 1 implies efficiency gain. Particularly, the latter condition holds if we choose β ≥ 1.

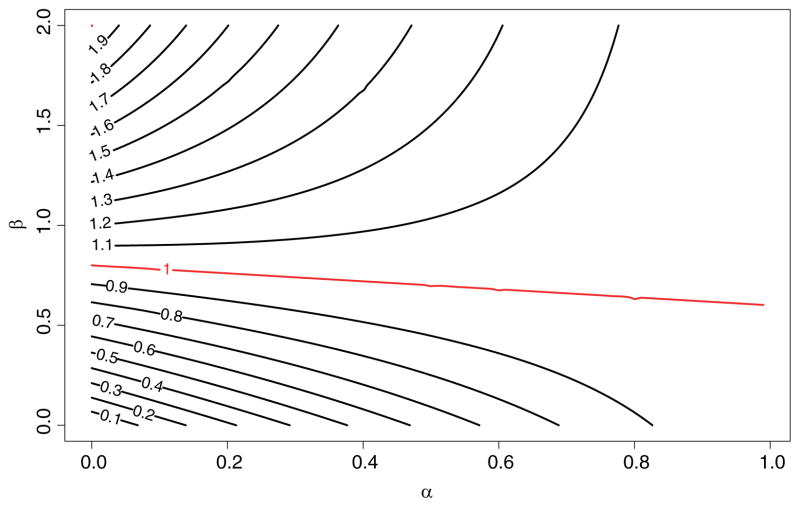
Figure 3 is the contour plot of ρ as a function of completion rate α and the enrichment rate β = m/n under γ = 0.5, 2, where each line represents the contour line of the marked relative efficiency ρ as defined above. For example, for the ρ = 0.9 line, α = 0.6 corresponds to β = 0.5. That is, at 60% completion rate, a study needs to enrich 50% sample to obtain a SMARTer estimator with variance 1/0.9 ≈ 1.11 times the variance of SMART estimator with the same initial sample size but no dropout. Similarly, at the same completion rate, to achieve the same efficiency, β needs to be above 0.75; and to achieve a relative efficiency of ρ = 1.1, β needs to be above 1.05. Note that the line with equal efficiency has a slow change rate indicating the increase of enrichment sample size is not sensitive to completion rate. The contour lines above the equal efficiency line (ρ = 1) are convex and increasing, indicating with lower dropout rate after the first stage, SMARTer requires more enrichment patients at the second stage to achieve higher efficiency than a SMART with no dropout. The opposite can be seen from the contour lines below the equal efficiency line which are concave and decreasing: with lower dropout rate, SMARTer requires less enrichment patients or no enrichment to achieve efficiency slightly lower than a SMART with no dropout.

Figure 3.

Contour Plot of Comparative Efficiency of SMARTer and SMART. α is the completion rate, β is the sample size ratio between enrichment group and original SMART group.

Another way to understand the design efficiency of SMARTer is through sample size calculation for comparing two DTRs in a SMARTer study. We denote the difference in the mean outcome value as Δμ and assume the type I error rate of a two-sided test is 0.05 and 80% power to detect a difference. In the above simplified setting, the total sample size of SMARTer is $8{(z_{0.05/2}+z_{0.2})}^2\frac{{\sigma }^2({\overline{d}}_2)}{{(\mathrm{\Delta }\mu )}^2}$, where σ²(d̄₂) = var(Y |Ā₂ = d̄₂), and z_q represents the q-th upper quantile of a standard normal distribution. With a completion rate of α, the sample size of SMART inflates to $8{(z_{0.05/2}+z_{\beta })}^2\frac{{\sigma }^2({\overline{d}}_2)}{\alpha {(\mathrm{\Delta }\mu )}^2}$ to ensure sufficient power at the end of the second stage. For two DTRs with different first stage treatments, that is, $d_1(S)\ne d_1^{\prime }(S)$ for any S, one can compute the variance of the difference as $V({\overline{d}}_2,{\overline{d}}_2^{\prime })=V({\overline{d}}_2)+V({\overline{d}}_2^{\prime })$. Assuming ${\sigma }^2({\overline{d}}_2)={\sigma }^2({\overline{d}}_2^{\prime })$, then ρ is also the ratio of variance of SMART and SMARTer estimator for comparing two DTRs. Thus the sample size of initial recruitment (n) for a SMARTer is $8{(z_{0.05/2}+z_{\beta })}^2\frac{{\sigma }^2}{{(\mathrm{\Delta }\mu )}^2\rho }$ to achieve the same efficiency. Table 1 provides the sample sizes for a SMARTer with an initial sample of n subjects and an enrichment sample of m subjects to achieve the same efficiency as a SMART recruiting 100 subjects and in an ideal case of no dropout. For example, if 40% patients drop out after the first stage randomization of SMARTer and the within- and between-stratum variance ratio γ = 1, Table 1 provides three combinations of initial stage and enrichment sample sizes for SMARTer to achieve the same efficiency: (109, 54), (80, 80), and (62, 124). In contrast, when accounting for dropouts at the design stage for a SMART without enrichment, one needs 100/0.6=250 subjects.

Table 1.

Sample sizes of SMARTer to achieve the same efficiency as SMART with 100 subjects for comparing two DTRs with different first stage treatments

α	0		0.2		0.4		0.5		0.6		0.8
SMARTera			β = 0.5
	n	m	n	m	n	m	n	m	n	m	n	m
γ = 0.5	100	50	92	46	91	46	92	46	93	46	96	48
γ = 1	125	62	109	54	102	51	100	50	99	50	99	49
γ = 2	150	75	125	62	112	56	108	54	105	53	102	51
			β = 1
γ = 0.5	67	67	73	73	80	80	83	83	87	87	93	93
γ = 1	75	75	80	80	85	85	88	88	90	90	95	95
γ = 2	83	83	87	87	90	90	92	92	93	93	97	97
			β = 2
γ = 0.5	50	100	61	122	72	143	77	153	82	163	91	182
γ = 1	50	100	62	124	73	145	78	155	82	165	91	183
γ = 2	50	100	62	125	73	147	78	157	83	166	92	184
SMART-misb	NA		500		250		200		167		125

^aSample sizes for SMARTer are to achieve same efficiency as a SMART trial with 100 patients and in an ideal case of no dropout. n is the sample size for the SMART group, m is the sample size for the enrichment group; β = m/n is the ratio of sample size between enrichment and SMART group; α is the completion rate; γ is ratio of within- and between-stratum variance.

^bSMART-mis is the sample size for a SMART accounting for the dropout rate of 1 − α in the second stage in the design, that is, 100/α.

4. Simulation Studies

Simulations results are based on 1000 replications of samples with initial enrollment of n = 800 patients. They demonstrate the consistency and comparative efficiency of SMARTer compared with SMART under various scenarios with or without intermediate outcomes.

4.1. Simulation Results without Intermediate Outcomes

Here, we assume there are two stages each with 2 candidate treatments, A₁ and A₂, and a randomization probability of 1/2. The baseline covariate S₁ takes random integer values (0, 1, 2) with probabilities (1/3, 1/3, 1/3). Let S₂ = A₁(1 − S₁), and the final outcome after the second stage is Y = S₂ + A₂(1 − S₁) + I (S₁ = 1, A₁ = 1, A₂ = −1) + e, where e ~ 𝒩(0, 1). The optimal dynamic rules for this setting are d₁(S₁) = 2I (S₁ < 2) − 1 and d₂(S₁, A₁) = 2I (S₁ < 1) − 1. Under this rule ν(S₁ = 0) = 2, ν(S₁ = 1) = 1, ν(S₁ = 2) = 2, thus the optimal rule has a value of μ(d₁, d₂) = 1.667. We consider two levels of completion rates α = 0, 0.5, three levels of enrichment proportions β = 0.5, 1, 2 and two scenarios for the m enrichment patients: scenario 1 simulates the distribution of A₁ for the enrichment patients the same as initially recruited patients, that is, q(A₁|S₁) = p(A₁|S₁) = 1/2, the baseline covariate has the same distribution in the enrichment sample and the SMART sample; and scenario 2 simulates different observed A₁ distribution q(A₁ = 1|S₁) = 1/(1 + exp(−0.5(2I(S₁ < 2) − 1))), that is, the enrichment patients are more likely to receive the optimal first-stage treatment, and the baseline covariate S₁ takes random integer values (0, 1, 2) with probabilities (1/2, 1/4, 1/4) for the enrichment sample.

Table 2 presents SMARTer estimators of a single DTR and comparison of two DTRs, as well as their efficiency gain (ρ) compared with SMART without dropout. We provide the estimates for the optimal treatment regime d₁(S₁) = 2I(S₁ < 2) − 1 and d₂(S₁, A₁) = 2I (S₁ < 1) − 1, and its comparison with an one-size-fits-all regime, $d_1^{\prime }(S_1,A_1)=-1$ and $d_2^{\prime }(S_1,A_1)=1$, for which the mean outcome is μ′ = 0

Table 2.

Results from the simulation study without intermediate outcomes

α	β	Scenario	Estimate	Estimated SE	Empirical SD	95% CI coverage	ρ̂
Value estimation of one DTR (true value 1.667)
0.0	0.5	1	1.665	0.102	0.104	0.940	0.599
0.0	0.5	2	1.668	0.100	0.100	0.943	0.647
0.0	1.0	1	1.666	0.074	0.078	0.941	1.073
0.0	1.0	2	1.663	0.073	0.072	0.955	1.230
0.0	2.0	1	1.667	0.055	0.055	0.951	2.142
0.0	2.0	2	1.669	0.054	0.053	0.957	2.316
0.5	0.5	1	1.663	0.084	0.085	0.948	0.875
0.5	0.5	2	1.663	0.082	0.082	0.944	0.946
0.5	1.0	1	1.665	0.076	0.076	0.949	1.075
0.5	1.0	2	1.664	0.075	0.074	0.948	1.141
0.5	2.0	1	1.666	0.069	0.070	0.950	1.295
0.5	2.0	2	1.665	0.069	0.068	0.948	1.353
Comparing two different DTRsa (true difference of values 1.667)
0.0	0	1	1.669	0.142	0.144	0.946	0.579
0.0	0	2	1.672	0.147	0.147	0.946	0.557
0.0	1	1	1.665	0.102	0.106	0.942	1.066
0.0	1	2	1.665	0.106	0.108	0.946	1.040
0.0	2	1	1.667	0.074	0.074	0.951	2.211
0.0	2	2	1.667	0.077	0.075	0.953	2.157
0.5	0	1	1.668	0.115	0.119	0.942	0.799
0.5	0	2	1.667	0.115	0.116	0.946	0.845
0.5	1	1	1.669	0.104	0.104	0.947	1.033
0.5	1	2	1.668	0.104	0.104	0.954	1.040
0.5	2	1	1.669	0.094	0.095	0.947	1.259
0.5	2	2	1.667	0.095	0.094	0.944	1.269

Note: α represents probability of non-dropout; β = m/n; ρ is the relative efficiency using the formula in Section 4, and ρ̂ is the empirical efficiency; scenario 1: the enrichment population has distribution q = (1/3, 1/3, 1/3) for (0, 1, 2), and q(A₁|S₁) = 1/2; scenario 2: q = (1/2, 1/4, 1/4) and observed treatment A₁ distribution q(A₁ = 1|S₁) = 1/(1 + exp(−0.5(2I(S₁ < 2) − 1))).

^aEfficiency ρ is the same for estimating one DTR and comparing two DTRs with different first stage treatments.

The results show the accuracy of the variance estimation and the simplified formula (2) of comparative efficiency. When all patients drop out (α = 0), the relative efficiency ρ increases from about 0.5 to 2 when the enrichment size m increases from 0.5 to 2 times the original sample size n; when half of patients drop out (α = 0.5), the relative efficiency ρ increases from about 0.9 to 1.3. As β increases, SMARTer is more efficient compared to SMART design even when all patients drop out after the initial randomization (α = 0) and SMARTer combines two single-stage randomized trials. We also observe that the relative efficiency ρ for comparing two DTRs is greater (more efficient) than estimating a single DTR.

4.2. Simulation Results with Intermediate Outcomes

The general settings are the same with Section 5.1. The intermediate outcome before the second stage treatment S₂ is simulated from a logistic model, where logit{P(S₂ = 1|S₁, A₁)} = A₁(1 − S₁), and the outcome after the second stage treatment is Y = S₂ + A₂(1 − X) + I (X = 1)A₂(2S₂ − 1) + e, where e ~ 𝒩(0, 1). The dynamic rules we are considering is the optimal rule under this scenario, which also depends on the intermediate outcome S₂: d₁(S₁, A₁) = 2I (S₁ = 1) − 1 and d₂(S₁) = I (S₁ ≠ 1)(2I(S₁ = 0) − 1) + I (S₁ = 1)sign(2S₂ − 1). Under this rule $v(S_1=0)=1+\frac{e}{1+e}$, ν(S₁ = 1) = 1.5, $v(S_1=2)=1+\frac{e}{1+e}$. Thus the mean outcome for the optimal rule is μ(d₁, d₂) = 1.654 with equal baseline distribution for S₁.

Table 3 presents SMARTer estimators of both a single DTR and comparison of two DTRs, as well as their efficiency gain (ρ) compared with SMART estimator with no dropout. We present the estimates for the optimal DTR and its comparison with an one-size-fits-all rule: $d_1^{\prime }(S_1,A_1)=-1$ and $d_2^{\prime }(S_1,A_1,S_2)=1$, for which the mean outcome is μ′ = 0.5. The true mean difference is 1.154. The results are similar to the case without intermediate outcome. When β = 1, ρ̂ is approximately equal or larger than 1, and it is higher for the difference comparison in Table 3. We observe that SMARTer estimator has efficiency gain even with β = 1 and it may boost efficiency especially when comparing two DTRs.

Table 3.

Results from the simulation study with intermediate outcomes

α	β	Scenario	Estimate	Estimated SE	Empirical SD	95% CI coverage	ρ̂
Value estimation of one DTR (true value 1.654)
0.0	0.5	1	1.655	0.101	0.106	0.929	0.581
0.0	0.5	2	1.653	0.105	0.114	0.924	0.504
0.0	1.0	1	1.653	0.074	0.076	0.939	1.085
0.0	1.0	2	1.650	0.078	0.079	0.941	1.011
0.0	2.0	1	1.658	0.055	0.055	0.951	2.086
0.0	2.0	2	1.658	0.058	0.059	0.948	1.812
0.5	0.5	1	1.654	0.084	0.083	0.949	0.908
0.5	0.5	2	1.653	0.084	0.084	0.942	0.901
0.5	1.0	1	1.655	0.076	0.074	0.952	1.130
0.5	1.0	2	1.656	0.077	0.074	0.955	1.150
0.5	2.0	1	1.653	0.070	0.071	0.944	1.244
0.5	2.0	2	1.653	0.070	0.071	0.939	1.243
Comparing two different DTRs (true difference of values 1.154)
0.0	0	1	1.157	0.163	0.165	0.937	0.583
0.0	0	2	1.160	0.174	0.191	0.921	0.435
0.0	1	1	1.153	0.119	0.121	0.943	1.016
0.0	1	2	1.147	0.127	0.138	0.929	0.778
0.0	2	1	1.157	0.089	0.091	0.949	1.906
0.0	2	2	1.157	0.095	0.096	0.950	1.719
0.5	0	1	1.161	0.133	0.135	0.942	0.868
0.5	0	2	1.159	0.135	0.134	0.953	0.876
0.5	1	1	1.156	0.120	0.120	0.948	1.038
0.5	1	2	1.156	0.123	0.121	0.956	1.016
0.5	2	1	1.154	0.110	0.110	0.941	1.241
0.5	2	2	1.153	0.112	0.112	0.950	1.206

Note: The general settings are the same with Table 2. The intermediate outcome before the second stage treatment S₂ is simulated from a logistic model, where logit{P(S₂ = 1|S₁, A₁)} = A₁(1 − S₁), and the outcome after the second stage treatment is Y = S₂ + A₂(1 − X) + I(X = 1)A₂(2S₂ − 1) + e, where e ~ 𝒩(0, 1).

5. Sample Size Calculation for an Autism SMART Study

We illustrate the sample size calculation and potential efficiency gain using results from the autism study (Kasari et al., 2014) introduced in Section 2.1. For the primary aim, the study found that SGD(JASP + EMT + SGD) has a better treatment effect compared with spoken words alone (JASP + EMT). Secondary aim results suggest that the adaptive intervention beginning with JASP + EMT + SGD and intensifying JASP + EMT + SGD for children who were slow responders led to better post-treatment outcomes.

Suppose we stratify by baseline variables and responding status (early or slow) after the first stage. Here, we provide the sample size calculation for comparing two adaptive treatment regimes as in the secondary study aim: one is starting with JASP + EMT + SGD and intensifying JASP + EMT + SGD for children who are slow responders (d̄₂); the other is starting with JASP + EMT, and the slow-responders to JASP + EMT receive $\text{JASP}+\text{EMT}+\text{SGD}({\overline{d}}_2^{\prime })$.

The original planned sample size was based on the primary aim to compare TSCU for two treatments in stage 1. The study assumed an attrition rate of 10% by week 24, and the planned total sample size was n = 97 to detect a moderate effect size of 0.6 in TSCU with 80% power using a two-sided two-sample t-test with a type I error rate of 5%. The actual study recruited 61 patients. The effect size for the primary aim comparison was 0.62 and it was significant at 0.05 level despite the insufficient power. As a secondary aim of the study, the effect size of the embedded DTRs d̄₂ and ${\overline{d}}_2^{\prime }$ for TSCU at week 24 was 0.55. There were approximately 15% patients dropped out after the first stage at week 12. The comparison of two DTRs in the secondary aim had approximately a power of 37% to detect a moderate effect size of 0.5.

We examine whether one can design a SMARTer to enrich the trial in the second stage so that the power for comparing two DTRs can be improved. To this end, note that $Z_{\beta }\le \frac{\mathrm{\Delta }\mu }{\eta /n}$, where Δμ is the effect size, and $\eta =(V({\overline{d}}_2)+V({\overline{d}}_2^{\prime }))/{\sigma }^2=\frac{4+0.8\alpha }{\gamma +1}+\frac{4.8\gamma }{1+\gamma }\frac{1+\alpha \beta }{\alpha +\beta }$. When γ = 0.5, we have Z_β ≤ −0.115 and we can achieve at most 55% in power by enrichment in the second stage. To achieve 80% power, at least 151 patients need to be recruited in the first stage.

Table 4 provides sample sizes for SMARTer and SMART that achieve the same power of 90, 85, or 80% for two-sided tests with a type I error rate of 5%. The sample size for the initial stage of SMARTer is computed by $n=\frac{(2+2\times 0.6+4\times 0.4){(Z_{\alpha /2}+Z_{\beta })}^2}{\mathrm{\Delta }{\mu }^2}$, where we take into account d̄₂ was randomized only in the first stage and for ${\overline{d}}_2^{\prime }$, only the 40% slow responders received two-stages of randomization. The enrichment ratio β is computed by solving $V({\overline{d}}_2)+V({\overline{d}}_2^{\prime })=V_0({\overline{d}}_2)+V({\overline{d}}_2^{\prime })$ (by independence of subjects following d̄₂ and $d_2^{\prime }$), that is, to solve the following equation $\frac{1}{1+\gamma }(2+2(1-\alpha )+(2\times 0.6+4\times 0.4)\alpha )+\frac{\gamma }{1+\gamma }(2+2.8)\frac{1+\alpha \beta }{\alpha +\beta }=2+2.8$. The solution is $\beta =\frac{6\gamma -\alpha }{6\gamma +1}$.

Table 4.

Sample sizes of SMARTer to achieve the same efficiency as SMART for the autism study

	Dropout Rate	Power 90%			Power 85%			Power 80%
		SMART	SMARTer		SMART	SMARTer		SMART	SMARTer
			n	m		n	m		n	m
	0%	202	202	0	173	173	0	151	151	0
γ = 0.2	15%	238	202	27	203	173	15	178	151	18
	40%	337	202	54	288	173	43	252	151	40
	0%	202	202	0	173	173	0	151	151	0
γ = 0.5	15%	238	202	104	203	173	81	178	151	76
	40%	337	202	120	288	173	100	252	151	89
	0%	202	202	0	173	173	0	151	151	0
γ = 1	15%	238	202	144	203	173	117	178	151	106
	40%	337	202	155	288	173	130	252	151	115

Sample sizes for SMARTer are to achieve same power as a SMART trial with the same initial recruitment as n and in an ideal case of no dropout. n is the sample size for the SMART group, m is the sample size for the enrichment group; γ is ratio of within- and between-stratum variance.

Since we do not have information on the ratio of within and between stratum variances γ, we provide results for three ratios γ = 0.2, 0.5, 1 and also two rates of attrition 15 and 40% after the first stage. According to Table 4, for this specific example, SMARTer would have smaller total sample size for initial recruitment and enrichment when γ is small (γ = 0.2) with attrition rate 15% and for γ = 0.5 with attrition rate 40%. SMARTer requires a smaller total number of patients than SMART if the within stratum variance is small, where one can estimate Ŷ_i for dropouts using enrichment sample with more accuracy due to using a more homogeneous enrichment group. When the dropout rate is high, recruiting an enrichment sample to recover the missing information is more beneficial and SMARTer demonstrates greater advantages in terms of a smaller total sample size.

6. Discussion

We propose a SMARTer design to improve efficiency of SMART by stage-wise enrichment in a multi-stage trial. We have shown that the new design retains the validity of making causal inference for DTRs and the efficiency gain is significant if the enrichment sample size is substantial and drop out rate is considerable. In all numerical results, we compared efficiency of SMARTer to SMART with no dropout. When comparing with SMART accounting for dropouts, the efficiency gain is expected to be greater than that shown here. One interesting application of SMARTer design is the extreme case when α = 0, the proposed design is equivalent to synthesizing different independent trials from each stage. One important implication is that if the conditions (C.1)–(C.4) hold, that is, the treatment response profiles given covariates are the same for the participants from each stage, and the treatment history in previous stages can be obtained from the enrichment sample, then it may be possible to not conduct a full SMART study but to synthesize existing trials conducted at separate stages to evaluate and compare DTRs, at least for the purpose of discovering optimal DTRs. At the other extreme, when there is no attrition (i.e., α = 1) SMARTer can still be used to gain efficiency by replacing Y_i in μ̂ (d₁, d₂) by the corresponding stratum mean estimated from the combined SMART and enrichment sample, which is less variable.

Although enrichment can improve the power for comparing DTRs, the maximal power that can be achieved still depends on the sample size in the first stage recruitment. Recruiting an enrichment sample can decrease the within-stratum variation of estimated DTRs but cannot decrease the between-stratum variation. Therefore, in a SMART with high dropout rate in the first stage of treatment, SMARTer may act as a salvage design to mitigate high drop out rate and improve power. In addition, one reason for the low participation rate in clinical trials and high attrition is the need for frequent in-person visits and the resulting time and travel costs (Ross et al., 1999), which can be reduced for the enrichment samples in SMARTer since these participants have already received first stage treatments. For the enrichment sample, the cost of monitoring first stage treatment is saved, and the duration of trial for this group can be less than recruiting patients to undergo multiple randomizations.

Here, the enrichment sample is only used to estimate outcomes for those who drop out from the original SMART randomized for the first stage treatments, and thus the enrichment samples are not directly included in the comparisons of the first-stage treatments. The second stage treatments are randomized in the enrichment samples and health information collected right before second stage randomization (including intermediate outcomes) is matched with the SMART group. Thus under the assumption (C.2) and (C.3) of the same conditional distribution given health information up to stage 2, valid inference can be drawn by estimating outcomes using enrichment sample for dropouts from the SMART. When no unmeasured confounding assumption is likely to hold, one can consider including enrichment sample for the first-stage treatment comparisons through propensity score adjustment. Data collected from the SMARTer can also be used to find optimal DTR (details in Web Appendix E). When two DTRs of interest start with the same first stage treatment, there are shared data used in the estimation of DTRs. Our method can be extended to allow for shared path between DTRs being compared by properly handling correlation between observations on the shared path using the asymptotic linear expansion of the variance given in the Web appendix A. More discussion of this issue is given in Kidwell and Wahed (Kidwell and Wahed). In practice, when continuous pre-treatment covariates S may be encountered, the proposed method can be directly applied by discretizing S. An alternative is to estimate Ŷ(s, a₁, a₂) by regression model. The former may lead to a less tailored DTR, that is, DTR only depends on discretized S; while the latter leads to a more tailored DTR but can be biased if the model is misspecified.

When the dropout patterns are complicated and depend on many intermediate outcomes, our simple estimation by stratification and matching may need to be improved. A straightforward modification is to match by cumulative summaries of main variables (e.g., number of interim outcome measures). Other model based methods or doubly robust estimation may be considered for more complex situations especially when auxiliary variables are available for estimating missingness. When exact measures of treatment history or health history are not available in the enrichment sample, one may consider collecting proxies such as summary statistics or cumulative information of treatment history (e.g., treatment history within past few months) to replace exact measures. In the recent literature (March et al., 2010), extended follow-up is implemented using survey methodology or through extracting clinical data from electronic health records. New research methods may be considered in designing a SMARTer. From a design point of view, although we allow the distribution of first-stage treatment history and covariates on the enrichment participants to be different from the SMART population, the more similar they are, the more efficiency we will gain by using the enrichment participants. This implies that when recruiting enrichment patients for the second stage treatments, similar inclusion/exclusion criteria as SMART may be used and appropriate sampling design may be implemented to improve matching.

Four assumptions are required for a valid inference using SMARTer. Assumptions (C.1) is required for regular RCTs and SMARTs to ensure causal interpretation. In practice, assumptions (C.2) and (C.3) might be violated when there is informative dropout or selection bias between SMART and enrichment sample, that is, when the conditional mean response is different due to different distribution of some unmeasured baseline covariates associated with the outcome. Sensitivity analyses in Web Appendix C and D show that results are robust to small or moderate deviation from the assumptions.

One complication regarding assumption (C.4) is that the quality and delivery of A₁ in the SMART and enrichment samples may be different. In the enrichment sample, A₁ is delivered in a naturalistic fashion, which may be subject to less monitoring as in a SMART. However, the purpose of conducting SMART/SMARTer is to inform clinical decision-making in practical settings. It may not be very useful to test a highly-standardized treatment that is not likely to be correctly implemented in practice. In SMARTs designed as pragmatic trials (March et al., 2010), both academic centers and community centers were recruited, which may represent a wide range of quality of treatment and assessment fidelity. For SMARTer, the interpretation of the effects of DTRs involving A₁ is necessarily a pragmatic one and potential differences of treatment delivery in each specific application needs to be discussed.

When the initial intervention is a novel treatment not immediately available in communities, it may be challenging to recruit patients who have naturally received this treatment. However, enrichment sample can still be recruited to improve efficiency of the estimation of DTRs containing a conventional first-stage treatment. In addition, for SMARTs such as CATIE (Stroup et al., 2003) and STAR*D (Rush et al., 2004), most first-line pharmacotherapies for treating depression and schizopherenia are commonly prescribed in practice. SMARTer design is useful in these settings where the first-line treatments are readily available but considerable uncertainty is encountered for second-line treatments when individuals do not achieve adequate response after a first-line treatment.

7. Supplementary Materials

Web Appendices contain the derivation of the asymptotic variance for μ̂(d₁, d₂) in Section 2.2, the derivation of simplified comparative efficiency in (2) from Section 3, sensitivity analysis for assumption C.2 and C.3 mentioned in Section 6, simulation results for learning the optimal DTR from SMARTer in Section 6, and description for the code and software provided with the paper. Web Appendices, Tables, Figures referenced in Sections 1,2,3,4,5,6 and the code are available with this paper at the Biometrics website on Wiley Online Library.