Assessing Hospital Performance Following Percutaneous Coronary Intervention Using Big Data

Abstract

Background

While risk adjustment remains a cornerstone for comparing outcomes across hospitals, optimal strategies continue to evolve in the presence of many confounders. We compared conventional regression-based model to approaches particularly suited to leveraging big data.

Methods and Results

We assessed hospital all-cause 30-day excess mortality risk among 8952 adults undergoing percutaneous coronary intervention (PCI) between October 1, 2011 and September 30, 2012 in 24 Massachusetts hospitals using clinical registry data linked with billing data. We compared conventional logistic regression models with augmented inverse probability weighted estimators and targeted maximum likelihood estimators to generate more efficient and unbiased estimates of hospital effects. We also compared a clinically informed and a machine learning approach to confounder selection, using elastic net penalized regression in the latter case. Hospital excess risk estimates range from −1.4% to 2.0% across methods and confounder sets. Some hospitals were consistently classified as low or as high excess mortality outliers; others changed classification depending on the method and confounder set used. Switching from the clinically selected list of 11 confounders to a full set of 225 confounders increased the estimation uncertainty by an average of 62% across methods as measured by confidence interval length. Agreement among methods ranged from fair, with a kappa statistic of 0.39 (SE: 0.16), to perfect, with a kappa of 1 (SE: 0.0).

Conclusions

Modern causal inference techniques should be more frequently adopted to leverage big data while minimizing bias in hospital performance assessments.

Numerous governmental and professional organizations rely on quality-based performance measures for public reporting and quality improvement.^1-9 Since June 2008, the Centers for Medicare and Medicaid Services (CMS) has reported hospital-specific risk-adjusted 30-day mortality for acute myocardial infarction, heart failure, and pneumonia,⁹ and since 2012, for 30-day all-cause readmission. The most common and persistent criticism of hospital assessments is the inadequacy of risk-adjustment – a concern that the statistical model does not capture true patient sickness (case-mix) and thus patient presentations confound differences in hospital outcomes.^10-12 In the presence of case-mix confounding, a hospital treating especially sick patients would have a higher rate of adverse outcomes regardless of the true hospital quality. Clinical registries, databases that contain hundreds and sometimes thousands of variables, have been increasingly used to mitigate inadequate risk-adjustment for hospital assessments.^1-3,5 Despite these efforts, unadjusted case-mix differences remain a concern. The unease is, in part, due to the inclusion of relatively few confounders in the risk-adjustment model because of the simultaneous problems of small numbers of patients per institution and low event rates. Modern approaches that exploit many case-mix confounders while imposing a causal framework are likely to improve the accuracy and enrich the interpretation of hospital comparisons.

The adequacy of risk-adjustment is not the only concern with hospital assessments. The virtues of 30-day versus in-hospital outcome assessments have been discussed^13-16 with most recommending the 30-day outcome. The choice of fixed versus random effects to represent hospitals has also received considerable attention.^17-21 Regardless of timing of the endpoint or how hospital effects are accounted for, parametric regression models are typically implemented to adjust either directly or indirectly for hospital case-mix differences.

With increased emphasis on ensuring that patient differences do not confound estimates of hospital effects, it is surprising that so few hospital assessments have adopted a causal inference framework, wherein researchers focus on estimating population level differences that would have occurred had all subjects been exposed to a certain intervention – in our setting, to a particular hospital. In causal inference researchers attempt to adjust for all confounders in order to meet the eponymous ‘no unmeasured confounding’ assumption, though this assumption is typically not met in practice because important confounding variables do not exist in the data. A few papers have explicitly framed profiling as a causal inference problem and used propensity scores to balance populations across hospitals.^10,19,22 Modern statistical techniques optimized for causal inference have been introduced in methodology papers but have rarely been implemented for profiling. Big datasets contain many potential confounders but important predictive variables may be hidden among many noisy variables. Machine learning for big data has been used frequently in genetics research, but these tools require tuning and may be unfamiliar to outcomes researchers. Exploiting big datasets to optimize risk adjustment, and gain new insights into risk factors and hospital quality has thus become both a promising opportunity and an important statistical challenge.

In this paper, we characterize the advantages of utilizing modern machine learning algorithms within a causal inference framework to assess hospital performance, contrasting findings to current, common approaches. The new approaches are specifically designed for causal inference and capitalize on the potential of big datasets to provide new insights. We utilize a state-mandated clinical registry cohort of patients undergoing percutaneous coronary intervention (PCI) linked to routinely collected billing, giving us access to hundreds of variables measured on thousands of patients treated at Massachusetts hospitals with 30-day all-cause mortality following PCI as an outcome.

Methods

Data Sources

We make use of four separate data sources. The first is a state-mandated clinical registry coordinated by the Massachusetts Data Analysis Center (Mass-DAC).⁵ The data are collected prospectively by trained hospital personnel who use the American College of Cardiology's (ACC) National Cardiovascular Data Registry's (NCDR) instrument²³ supplemented with detailed patient and physician identifying information for quality assessment. Data are harvested quarterly and adjudicated annually through medical record review using a panel of clinicians and data managers. Mass-DAC links the registry data to The Massachusetts Acute Hospital Case-Mix billing data comprised of the Inpatient Discharge Database from the Massachusetts Center for Health Information and Analysis (CHIA). Information is linked using criteria based on combinations of treatment hospital, medical record number, admission or discharge date, and date of birth.²⁴ The Inpatient Discharge Database includes up to 15 present on admission (POA) diagnoses, 15 discharge diagnoses, and a further 15 procedure codes based on the International Classification of Diseases, 9^th Version, Clinical Modification (ICD-9-CM) system. Because some PCIs can be performed in outpatient clinics located in hospitals, our third data source is the Outpatient Observation Database, also part of the Massachusetts Acute Hospital Case-Mix database maintained by CHIA. The outpatient data contains one principal diagnosis and up to five additional diagnoses. Henceforth these two data sources are collectively referred to as billing data. To ensure completeness of mortality information, the Mass-DAC cohort is linked to the Massachusetts Registry of Vital Records and Statistics (MRVRS). MRVRS personnel return merged results files to Mass-DAC based on three criteria sets: 1) Social Security number only, 2) date of birth and first three letters of last and first name, or 3) first three letters of first name and full last name.²⁵

Patients, Hospitals, and Confounders

We included adults aged 18 years or older undergoing PCI in all non-federal Massachusetts’ hospitals between October 1, 2011 and September 30th, 2012. We excluded patients who resided outside Massachusetts (to ensure completeness of 30-day follow-up) and those who were deemed to be of exceptional risk, defined as patients having high risk features not captured by any variable in the data or cases where PCI offered the ‘best’ or only option for improving the chance of survival. Cases submitted as exceptional risk were reviewed for exclusion by an independent committee.

Patients were assigned to the hospital in which they had their first PCI procedure within a 30-day window. Because patients can undergo more than one PCI during the hospitalization, we analyzed only the first or “index” PCI during the hospitalization. Patients could contribute more than one PCI admission to our study; however, their second PCI hospitalization had to be more than 30-days after their index PCI.

The Mass-DAC registry holds 329 variables per patient that are captured by hospital personnel using the ACC-NCDR data collection tool. Because we should only adjust for confounders, i.e. variables that influence both the outcomes and hospital selection, variables not fitting this criterion such as those recorded during or after the index PCI were excluded from our analysis. This resulted in 75 clinical variables from the registry. We gathered more confounders when we linked with billing data by including the 150 most frequently recorded present on admission diagnoses, thus bringing our final count of confounders to 225. Variables in the Mass-DAC data associated with missingness were identified and filled in using regression chained imputation implemented in the SAS callable program IVEware.²⁶

Primary Outcome Measure

The patient endpoint was all-cause mortality 30 days from the index PCI. The primary hospital outcome was excess mortality defined as the difference between the directly standardized mortality at a hospital and the average of the directly standardized mortality across all hospitals. Positive excess mortality rates suggest the hospital is performing poorly compared to other hospitals in the state, while negative rates indicate that the hospital is performing well.

Approaches

We adopted a total of six different approaches for assessing hospital performance. The approaches differed along two factors: how the confounders were selected for inclusion and how the casual effect of the hospital was estimated. For confounder selection, we used either a small, clinically determined subset of 11 variables²⁷ or a full set of 225 available confounders. Logistic regression with an elastic net penalty was used to adjust for the larger set of confounders. This approach begins by assuming that the association of each variable on mortality or hospital selection is zero or near zerobefore making the data prove the worth of each variable. The strength of this assumption is encoded as a “tuning parameter” which we set to maximize performance using cross-validation. Typically, many variables receive coefficients of 0, effectively eliminating them from the regression.

For these two confounder sets, we implemented three methods to estimate hospital effects on mortality adjusting for patient risk: regression “only”, augmented inverse probability weighting (A-IPW), and targeted maximum likelihood estimation (TMLE) approaches. For ease of exposition, we used hospital fixed effects rather than random effects to characterize hospital quality. Hospitals were included as a set of indicator variables identifying the hospital where the PCI was performed. In the regression only approach, we estimated a logistic regression model of mortality on hospital specific intercepts and the confounders. This is a commonly used method and served as our standard of comparison. A-IPW seeks to improve on the regression only approach by combining regression with propensity scores – in our setting estimates of the probability of undergoing PCI at a particular hospital. It has a “double-robust” property, yielding unbiased estimates if either the mortality regression or propensity scores are properly specified.^19,28,29 We estimated multinomial regressions using generalized logits to produce 24 propensity scores (one for each hospital) for every patient in the Mass-DAC database. The inverses of the propensity scores were used as weights in the A-IPW estimator, augmenting the outcome regression with information from the hospital regression. The TMLE approach also produces a doubly-robust estimator that combines a mortality and hospital regression using a more flexible algorithm that guarantees additional desirable statistical properties.^30,31 TMLE updates the initial mortality regression using the predicted propensity scores in a statistically optimal way to reduce bias in the estimate of hospital quality. For comparison purposes, we used the same fixed-effects mortality egression for all three methods and the same multinomial propensity score regression in the A-IPW and TMLE estimators. The Supplementary Appendix provides further details of the A-IPW and TMLE algorithms as well as our use of penalized regression.

Excess Hospital Mortality

Our mortality regressions yielded estimates of adjusted confounder and hospital effects, both on the log-odds (logit) scale. We multiplied each patient's baseline variables by the estimated confounder coefficients, summed them, and then added the estimated intercept associated with a given hospital. This yielded an estimate of the log-odds of mortality for each patient in the state had they been treated at the hospital. We then inverted the log-odds to get probability of mortality for each patient and averaged to get the overall risk-adjusted mortality at that hospital. This was repeated for each hospital before subtracting the mean of these 24 hospital estimates from each to get the “excess mortality” at each hospital. To quantify the uncertainty in our estimates, we used bias corrected bootstrap resampling to generate confidence intervals,³² resampling hospitals with replacement and using all admissions from the sampled hospital. These confidence intervals were Bonferonni adjusted to account for multiple comparisons so that the set of confidence intervals for the 24 hospitals had 95% confidence. All estimators were implemented using R software including the packages tmle and glmnet.^33,34

Comparing Approaches

We compared findings using 4 different summaries. First, for each hospital we graphically compared the propensity scores generated for all patients by the clinically informed confounders with those generated by the elastic net. Regressions producing a wider range of propensity scores are generally preferred. Second, we classified hospitals into 3 categories using each method and set of confounders: high mortality (if the lower limit of the confidence interval for excess mortality was above 0), expected mortality (if the interval included 0), and low mortality (if the upper limit of the interval was below 0) hospitals. We then compared the similarity of the approaches using kappa statistics, with a kappa statistic greater than 0.8 generally indicating very high agreement between two classifiers. ³⁵ We concluded that pairs of modeling approaches classified hospitals differently if their pairwise kappa statistic was 2 standard errors less than 0.8. We used the R package psych to calculate kappa statistics and standard errors.³⁶ Lastly, we computed the total lengths of the confidence intervals noting that shorter intervals are generally preferred.

Results

Exclusions and Missing Data

A total of 12554 PCI admissions were observed in Massachusetts between October 1, 2011 and September 30, 2012 of which 11114 remained after removing exceptional risk cases, non-Massachusetts residents, and multiple admissions within a 30 day period. Of these, 9389 (75%) admissions merged with the CHIA billing data. The 30-day mortality rates of hospitalizations retained and those excluded did not differ. Across hospitals, missingness due to unmerged data ranged from less than 1% of PCI admissions to 31% of PCI admissions. Finally, one hospital with no mortalities was eliminated because estimation was not possible with fixed-effects regression. Thus, the final cohort included 9325 PCI hospitalizations for 8952 unique patients across 24 hospitals.

We also dealt with a small amount of missing data in the Mass-DAC registry using imputation. In particular the stenosis percentage fields had significant amounts of missingness (2.4% to 3.7% missing). A few other fields had trace amounts of missing cells (<0.1%). Missing data, imputation, and the sensitivity of our results to inclusion of multiple patient admissions are discussed further in the Supplementary Appendix.

Unadjusted Mortality and Case-Mix

The unadjusted all-cause 30-day mortality rate across 24 hospitals is 2.0% for patients undergoing PCI, corresponding to 188 deaths out of 9325 admissions. Hospital unadjusted mortality ranged from 0.6% to 5.6%. Substantial case-mix heterogeneity among hospitals for the clinical confounders exists (Figure 1). In some cases the differences are large. For example, emergent or salvage PCI admissions ranged from 15% to 100% with a mean of 35%. Likewise, prior cardiac arrest ranged from 0% to 15%. The hospital differences become more apparent when examining the hospital-specific distributions of the full list of confounders from the Mass-DAC registry (Table 1).

Figure 1.

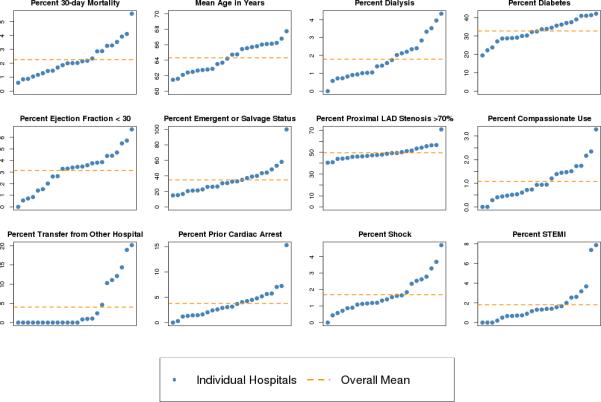
Distribution of clinically selected (parsimonious) confounders and unadjusted 30-day all-cause mortality at hospitals, sorted by prevalence or mean of condition. The y-axis is prevalence or mean; hospitals are represented by blue dots and change position from plot to plot according to rank; the orange dotted line is the overall mean across hospitals.

Table 1.

Prevalence or mean (standard deviation) of Mass-DAC registry confounders. Some variables are grouped to adhere to privacy regulations.

Registry Confounder	% or Mean (SD)
	All Admissions (N = 9325)	Survivors (N = 9137)	Non-Survivors (N = 188)
Male	70.7	70.9	62.2
Mean Age in Years (SD)	64.6 (12.4)	64.5 (12.4)	70.8 (13.1)
Mean Height in Centimeters (SD)	170.8 (10.3)	170.8 (10.3)	168.9 (11.3)
Mean Weight in Kilograms (SD)	86.4 (19.9)	86.6 (19.7)	77.4 (21.5)
Caucasian	92.7	92.7	93.1
Payor†
Government	52.4	52.0	70.1
Private Commercial or HMO	45.1	45.5	<30%
Other	2.5	2.5	<6%
Smoker†	25.8	25.8	26.6
Hypertension	80.3	80.3	81.4
Dyslipidemia	82.0	82.1	75.5
Family History CAD†	28.9	29.2	13.3
Dialysis	2.1	2.0	9.0
Chronic Lung Disease†	14.1	13.9	22.9
Diabetes	33.5	33.5	34.0
Cardiomyopathy or LV Systolic Dysfunction	11.0	10.8	24.5
Compassionate Use*	1.0	0.5	23.9
Mechanical Ventricular Support	0.6	0.4	8.0
Ejection Fraction <30%	3.2	3.0	14.4
Cardiac Transplant Evaluation	<0.1%	<0.1%	<6%
Left Main Disease	6.1	5.8	19.1
>70% LAD Stenosis	59.7	59.4	72.9
Right Dominant Coronary Anatomy	86.6	86.7	85.1
% Dominance Missing	0.1	0.1	0.0
Prior Myocardial Infarction	30.9	30.9	31.9
Prior Heart Failure	11.4	11.1	22.3
Prior Valve Surgery†	1.6	1.6	<6%
Prior PCI	31.9	32.0	27.1
Prior CABG	13.5	13.5	13.8
Prior Cerebrovascular Disease*	11.1	11.0	15.4
Prior Cardiogenic Shock	2.1	1.5	31.4
Prior Cardiac Arrest	3.1	2.6	25.0
Prior Peripheral Artery Disease†	12.5	12.3	19.7
Prior Thrombolytic Therapy	0.7	0.7	<6%
Prior 2 Weeks Anti-Anginal Medication
Beta Blockers	64.2	64.5	51.6
Calcium Channel Blockers	15.1	15.1	14.9
Long Acting Nitrates	14.5	14.5	12.2
Ranolazine	1.2	1.2	<6%
Other Agent	1.1	1.1	<6%
CAD Presentation
No symptom or mild angina	13.2	13.4	<6%
Unstable Angina	32.4	32.9	<10%
Non-STEMI	28.5	28.5	27.1
STEMI or Equivalent	25.9	25.2	60.6
Anginal Canadian Classification
< III	18.8	18.9	13.8
III	26.9	27.3	6.9
IV	54.3	53.8	79.3
Prior 2 Weeks HF	11.8	11.2	38.8
Prior 2 Weeks NYHA Class
No HF or <III	91.6	92.1	61.1
III	3.6	3.6	6.4
IV	4.8	4.3	27.1
Mean Left Main Stenosis % (SD)	8.16 (20.2)	7.97 (19.9)	17.22 (30.9)
% Left Main Stenosis Missing	3.5	3.5	4.3
Mean Proximal LAD Stenosis % (SD)	34.4 (39.5)	34.1 (39.4)	46.48 (43.1)
% Proximal LAD Stenosis Missing	3.2	3.2	2.7
Mean Mid Distal LAD Stensosis % (SD)	49.4 (39.7)	49.3 (39.6)	54.5 (42.4)
% Mid Distal LAD Stenosis Missing	3.7	3.7	5.9
Mean CIRC Stenosis % (SD)	49.8 (40.7)	49.5 (40.7)	60.37 (40.1)
% CIRC Stenosis Missing	2.5	2.5	0.5
Mean RCA Stenosis % (SD)	61.3 (39.7)	61.2 (39.7)	64.80 (41.8)
% RCA Stenosis Missing	3.0	2.9	4.7
PCI Status
Elective or Urgent	71.2	72.1	17.1
Emergent or Salvage	28.8	27.9	72.9
PCI Indication
STEMI PCI	26.3	25.6	61.7
Non-STEMI PCI	73.7	74.4	38.3
Cardiogenic Shock	1.6	1.1	28.2
Transfer in from Another PCI Hospital	5.9	5.9	<6%

^*Compassionate Use cases are those that meet Mass-DAC criteria involving extreme anatomic risk, ongoing CPR, and/or coma on presentation

^†<0.1% missing

Percentages suppressed when frequency corresponds to 10 or fewer patients as required by the Massachusetts Department of Public Health data privacy guidelines

The present on admission (POA) diagnosis codes (Table 2) indicate substantial chronic and acute coronary disease at admission, with 30-day mortality correlating with the more severe conditions. While we retained the 150 most frequent diagnoses, fewer than ten patients had no POA diagnosis, with a median diagnosis count of 6 per patient and a maximum of 15.

Table 2.

Prevalence of present on admission diagnosis codes overall and stratified by 30-day survival status. Codes have been grouped and truncated at 3 digits. Models utilize 150 full 5-digit codes.

Diagnosis Codes	Prevalence
	All Admissions (N = 9325)	Survivors (N = 9137)	Non-Survivors (N = 188)
414: Other chronic ischemic heart disease	93.8	94.3	71.3
272: Disorders of lipoid metabolism	69.3	69.9	37.8
401: Essential hypertension	61.3	61.7	41.0
410: Acute myocardial infarction	55.8	55.3	81.4
250: Diabetes mellitus	29.5	29.6	23.4
305: Nondependent abuse of drugs	21.9	22.1	13.3
411: Other acute/subacute ischemic heart disease	20.3	20.7	<6%
427: Cardiac dysrhythmias	17.6	17.1	43.1
530: Diseases of esophagus	16.9	17.1	7.4
428: Heart failure	15.2	14.7	38.3
278: Obesity and other hyperalimentation	12.7	12.9	<6%
403: Hypertensive renal disease	10.1	10.0	16.5
585: Chronic renal failure	10.1	10.0	12.8
300: Neurotic disorders	7.6	7.7	<6%
496: Chronic airways obstruction, not classified	7.2	7.1	10.6
244: Acquired hypothyroidism	7.0	7.1	<6%
996: Complications peculiar to specified procs	6.9	6.9	6.9
413: Angina pectoris	6.2	6.3	<6%
311: Depressive disorder, not classified	6.0	6.1	<6%
424: Other diseases of endocardium	5.6	5.5	12.2
327: Organic sleep disorders	5.3	5.3	<6%
276: Disorders of fluid/acid-base balance	5.1	4.9	18.6
443: Other peripheral vascular disease	5.1	5.0	<6%
285: Other and unspecified anemias	4.8	4.9	<6%
493: Asthma	4.8	4.8	<6%
600: Hyperplasia of prostate	4.2	4.2	<6%
426: Conduction disorders	4.0	4.0	<6%
274: Gout	3.6	3.6	<6%
584: Acute renal failure	3.5	3.4	6.4
724: Other and unspecified disorders of back	3.4	3.4	<6%
715: Osteoarthrosis and allied disorders	3.3	3.3	<6%
785: Symptoms involving cardiovascular system	2.9	2.3	34.0
425: Cardiomyopathy	2.7	2.7	<6%
338: Pain, not elsewhere classified	2.4	2.4	<6%
518: Other diseases of lung	2.4	2.0	21.3
357: Inflammatory and toxic neuropathy	2.3	2.3	<6%
780: General symptoms	2.3	2.3	<6%
416: Chronic pulmonary heart disease	2.0	2.0	<6%
599: Other disorders of urethra and urinary tract	1.7	1.7	<6%
433: Occlusion/stenosis of precerebral arteries	1.6	1.7	<6%
365: Glaucoma	1.5	1.5	<6%
440: Atherosclerosis	1.5	1.5	<6%
458: Hypotension	1.5	1.5	<6%
790: Nonspecific findings on blood exam	1.5	1.5	<6%
280: Iron deficiency anemias	1.4	1.4	<6%
733: Other disorders of bone and cartilage	1.4	1.4	<6%
287: Purpura and other hemorrhagic conditions	1.3	1.3	<6%
362: Other retinal disorders	1.3	1.3	<6%
714: Arthritis/inflammatory polyarthropathies	1.3	1.2	<6%
397: Diseases of other endocardial structures	1.2	1.2	<6%
486: Pneumonia, organism unspecified	1.2	1.2	<6%
288: Diseases of white blood cells	1.1	1.1	<6%
553: Hernia of abdominal cavity w/o obstruction	1.1	1.1	<6%
562: Diverticula of intestine	1.1	1.1	<6%
356: Hereditary/idiopathic peripheral neuropathy	1.0	1.0	<6%
294: Chronic organic psychotic conditions	0.9	0.8	<6%
345: Epilepsy	0.9	0.9	<6%
346: Migraine	0.9	0.9	<6%
429: Ill-defined complications of heart disease	0.9	0.9	<6%
441: Aortic aneurysm and dissection	0.9	0.9	<6%
716: Other/unspecified arthropathies	0.9	0.9	<6%
729: Other disorders of soft tissues	0.9	1.0	<6%
V49: Other conditions influencing health status	0.9	0.8	<6%
268: Vitamin D deficiency	0.8	0.8	<6%
296: Affective psychoses	0.8	0.8	<6%
696: Psoriasis and similar disorders	0.8	0.8	<6%
794: Abnormal results of function studies	0.8	0.9	<6%
491: Chronic bronchitis	0.7	0.6	<6%
583: Nephritis/nephropathy	0.7	0.7	<6%
070: Viral hepatitis	0.6	0.6	<6%
332: Parkinson's disease	0.6	0.6	<6%
564: Functional digestive disorders, not classified	0.6	0.6	<6%
593: Other disorders of kidney and ureter	0.6	0.6	<6%
786: Respiratory/chest symptoms	0.6	0.6	<6%
277: Unspecified disorders of metabolism	0.5	0.5	<6%
459: Other disorders of circulatory system	0.5	0.5	<6%
507: Pneumonitis due to solids and liquids	0.5	0.4	<6%
515: Postinflammatory pulmonary fibrosis	0.5	0.5	<6%

Percentages suppressed when frequency corresponds to 10 or fewer patients as required by the Massachusetts Department of Public Health data privacy guidelines

Probability of PCI Admission at Each Massachusetts Hospital

Figure 2 shows the distribution of propensity scores for each hospital across the entire patient population, stratified by confounder set. Patients with negative log-odds propensity scores are unlikely to be treated at a given hospital, while those with scores closer to or greater than zero are more likely to be treated at the hospital. The propensity scores estimated from clinical variables displayed in blue are quite narrow and centered near −3 corresponding to the baseline probability of ~1/24 for treatment at a given hospital. The propensity scores (orange dashed line) estimated using the full 225 variables discriminate better, placing the bulk of patients to the left of the clinically estimated scores (lower probability of treatment) and a few to the right (higher probability). The richer confounder set leads to more extreme propensity scores and consequently weights up to 1600000 (corresponding to a propensity score much less than 0.001). High weights can indicate a problem, as patients with low propensity scores for a given hospital cannot be compared to a similar patient who underwent PCI there.

Figure 2.

Propensity score distributions for all patients, by hospital. The x-axis is on the log-odds scale with larger values corresponding to a higher likelihood of care at the hospital; the y-axis reflects the relative frequency of PCI admissions at the hospital. Solid blue lines represent relative frequencies of propensity scores generated from clinically selected confounders; dashed orange lines represent relative frequency under full confounders.

Excess Hospital Risk

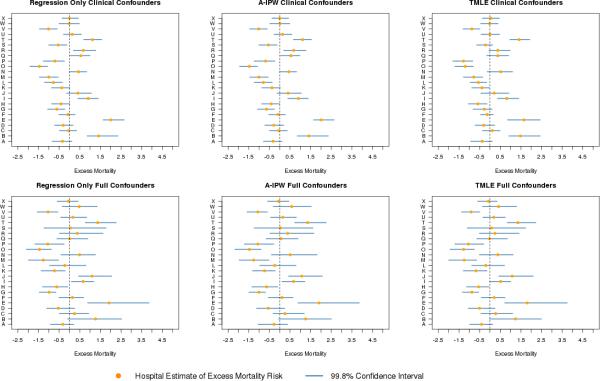
Analyses of hospital-specific excess mortality risk indicate differences related both to approach and to choice of confounders (Figure 3). Comparing the top to the bottom panels, all methods classify hospital B as an outlier under the clinical confounder set, but not under the full set. The full set of confounders accounts for the extra risk in hospital B's patient population not captured by the clinically selected set, a discrepancy also visible in the propensity score densities for hospital B (Figure 2). Hospital R's classification also benefits from the inclusion of more confounders. On the other hand, hospital J is not an outlier under any method with clinical confounders but is a high mortality outlier under all methods when the full confounders are used. Hospitals E and T are classified as having higher than expected mortality outliers across methods and confounder sets.

Figure 3.

Hospital level excess 30-day mortality risk (reported in percent) with 99.8% confidence intervals, by method and confounder set. Upper panels display estimates using the clinical confounders; lower panels displays estimates based on the full confounder models. The regression only, A-IPW, and TMLE estimates are displayed from left to right. Solid circles are point estimates; horizontal lines are confidence intervals; and dashed vertical line is zero excess risk.

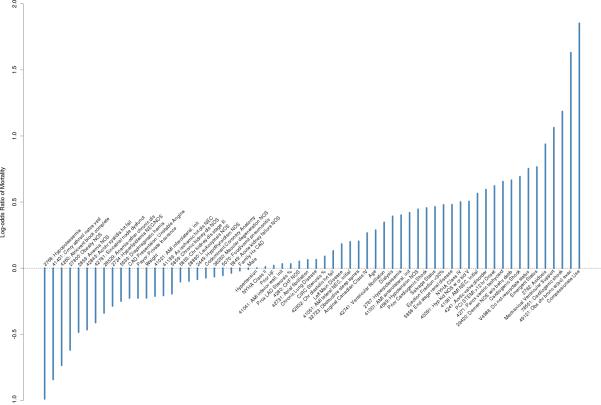
Figure 4 presents the estimated regression coefficients for the full set of confounders. Though all confounders are considered, the elastic net penalty selected 64 non-zero confounders, providing a much richer set of variables for risk-adjustment than the 11 preselected for the clinical confounder set. A similar coefficient plot for the clinical confounders appears in the appendix. In addition to the impact of the confounder set, some differences in conclusions arise when changing the approach used to estimate excess hospital mortality (Table 3). In the clinical set, TMLE classifies hospitals Q, R, S, and G as “as expected” hospitals while regression only and A-IPW classify all four as outliers. Both TMLE and A-IPW classify hospital H as having lower than expected mortality, while regression only does not. In the full confounder set, TMLE is the only method that does not classify hospital I as an outlier.

Figure 4.

Estimated coefficients selected for full confounder mortality outcome model. The y-axis displays the risk of 30-day mortality on the log odds (logits) scale. A higher risk indicates a higher chance of mortality with that confounder present. Negative risk indicates confounders that lower the risk of mortality in the studied population. 161 of the 225 confounders considered received estimates of zero and are not shown.

Table 3.

Hospital classification into low, as expected, or high 30-day mortality hospitals, based on 99.8% confidence intervals for each method and confounder set. Entries represent number of hospitals.

Method and Confounder Set	Low Mortality Hospitals	As Expected Hospitals	High Mortality Hospitals
Regression Only Clinical Confounders	7	11	6
A-IPW Clinical Confounders	8	10	6
TMLE Clinical Confounders	7	13	4
Regression Only Full Confounders	7	13	4
A-IPW Full Confounders	7	13	4
TMLE Full Confounders	7	14	3

Fewer hospitals are selected as outliers when utilizing the full set of confounders compared to the clinically selected set. This is due, at least in part, to increased uncertainty in the hospital estimates as reflected in the wider confidence intervals of the full confounder set. On average, the regression only, A-IPW, and TMLE interval estimates using the full confounder set are respectively 65%, 70%, and 51% longer compared to estimates using the clinically selected confounders.

Agreement Among Approaches

The least agreement and hence the largest hospital classification differences occur between the regression only approach with clinical confounders and the approaches that used the full confounder set, particularly TMLE with full confounders (Table 4). In contrast, the more sophisticated methods vary less when used across confounder sets. Hospital classifications obtained from A-IPW with clinical confounders did not agree with TMLE using full confounders. When the full confounder set was utilized, no significant differences in hospital classification were observed across methods.

Table 4.

Kappa statistics (asymptotic standard error) measuring agreement between methods after adjusting for chance agreement.

	Method and Confounder Set
	Reg Only Clinical Confounders	A-IPW Clinical Confounders	TMLE Clinical Confounders	Reg Only Full Confounders	A-IPW Full Confounders	TMLE Full Confounders
Reg Only Clinical	-	-	-	-	-	-
A-IPW Clinical	0.94 (.06)	-	-	-	-	-
TMLE Clinical	0.60 (.14)	0.67 (.13)	-	-	-	-
Reg Only Full	0.47 (.16)	0.54 (.15)	0.72 (.13)	-	-	-
A-IPW Full	0.47 (.16)	0.54 (.15)	0.72 (.13)	1.00 (0.0)	-	-
TMLE Full	0.39 (.16)	0.47 (.15)	0.64 (.14)	0.93 (.07)	0.93 (.07)	-

Discussion

Increased access to registry data linked with other data sources presents a number of opportunities to outcomes researchers, including the ability to better risk-adjust case-mix when assessing hospital performance. We introduced methods for direct standardization, which answers the question, “what is the mortality that would be observed if every patient in the state were treated at this hospital?” In contrast, indirect standardization seeks to determine the expected mortality for each hospitals’ patient population that would be observed if they were treated at a hypothetical average hospital.^10,19 Often, indirect standardization answers the more pertinent policy question, as hospitals will by necessity treat certain subsets of the population. Directly standardized outcomes may be of more interest to consumers, who can potentially choose where to receive care and would like to compare different hospitals.

We used a penalized regression approach to include more confounders, which led to wider confidence intervals. Wider intervals do not imply that the parsimonious subset is giving better estimates. In fact, when using a smaller set of confounders, the researcher implicitly assumes that the excluded variables are not true confounders and this prior knowledge is not based on the observed data. On the other hand, using a penalized regression method, such as the elastic net, explicitly considers each potential confounder and allows the data to determine which confounders contain important information. Wider confidence intervals reflect the fact that our estimates are truly more uncertain than a parsimonious confounder subset would have us believe. Penalized regression leverages large data sets to account for residual confounding in a way that is simply not possible with standard logistic models. Of course, data-driven variable selection doesn't negate the importance of subject-matter knowledge, and penalized regression should be used in conjunction with a generous set of clinically relevant variables to determine key variables from a large set of candidates.

We introduced A-IPW and TMLE as alternative approaches to the standard regression only approach for risk-adjustment. Both are double-robust estimators and involve estimation of a propensity score regression in addition to a mortality outcome regression, and are unbiased if either regression is consistently estimated. Despite this theoretical nicety, A-IPW yielded wider confidence intervals than our other methods. This finding is supported by theoretical and empirical studies.^19,30 Despite using the same hospital multinomial regression model, TMLE gave more stable results compared with A-IPW and is theoretically formulated to minimize bias compared with the standard regression only model.³⁰

An alternative approach to causal inference is the use of instrumental variables (IVs), variables associated with “treatment” and only with outcome by way of treatment. A canonical IV example in profiling is a patient's distance to a hospital.³⁷ Ultimately the choice of approach comes down to data availability – good IVs may avoid the problem of unmeasured confounding but require strong assumptions about the underlying causal mechanism. Our approaches instead mitigate confounding by explicitly considering many variables for risk-adjustment and are particularly useful when many confounders are available, as with registry and billing data.

Kappa statistics also support the use of the approaches we proposed in the sense that the larger confounder set gave more consistent results across methods, and the more advanced methods gave more consistent results across confounder sets. Our estimates of risk-adjusted hospital mortality became more similar when we dialed up the sophistication of our approach, theoretically converging on the true values as we took steps to minimize bias in our confounder selection and parameter estimation.

No approach is without limitations. We implemented a fixed effects framework for hospital effects to simplify our exposition and isolate the performance of the methods we introduced with respect to standard practice. A limitation of fixed effects models is the inability to estimate adjusted mortality for hospitals with no mortalities and even sometimes with few mortalities. As a result of this, we were forced to drop one of the hospitals in our original data set. A random effects framework would assert that hospital effects are related by a common distribution such as a normal (bell curve), allowing information to be shared between hospitals, stabilizing estimates, and often reducing the number of classified outliers.¹⁸ Moreover, we utilized single-based imputation - multiple imputation strategies would fully account for the additional uncertainty in the imputation itself. For our goals of comparative assessments between and among approaches, conclusions would be unlikely to change if we used multiple imputation. Additionally, we eliminated patients from study who did not link with the CHIA billing data from which to draw diagnosis codes. Although we found no difference in mortality, we did find that the success of linkages across hospitals differed, perhaps based on systematic features of the hospitals. These discrepancies are likely the result of inconsistent data collection and reporting procedures at the hospital level, and can present obstacles to good statistical inference if they become severe.

Finally, as in all causal inference, the possibility of residual confounding is a concern and could arise from uncollected patient measures. However, considering all 225 potential confounders for adjustment strengthens our confidence that residual confounding is minimized compared to our parsimonious approach that adjusts for only 11 risk factors.

Conclusion

Working in a causal inference framework with modern statistical techniques and including substantially more confounders can yield improvements over standard risk adjustment strategies. Better estimates of underlying hospital quality were obtained by including these additional confounders and adjusting estimates based on the propensity score. We support the use of TMLE in conjunction with penalized regression to leverage many confounders in large data sets when possible. If investigators are committed to working with small pre-chosen variable sets, TMLE can still be used to improve estimates. Such modifications have the potential to make substantive differences in hospital outlier classification.. In the future, researchers can expand upon this work by incorporating machine learning ensembles, adopting random effects models, or implementing fully Bayesian approaches for direct standardization.

What is known:

• Good estimates of hospital quality require adjustment for the baseline sickness of treated patients (case-mix).

• Because hospital profiling seeks to estimate the effect of treatment at a given hospital on outcomes it is best formulated as a causal inference problem, requiring consideration of underlying causal assumptions and methods designed for causal inference.

• Clinical registries and billing data can provide rich case-mix information, but most variables are often ignored in favor of a small subset deemed to be clinically relevant a priori.

What the paper adds:

• Leveraging the case-mix information in both clinical registries and billing data using penalized regression methods may alleviate unmeasured confounding and provide better estimates of hospital quality.

• Modern causal inference approaches like targeted maximum likelihood combine models of mortality with estimates of treatment hospital (propensity scores) to provide more accurate and efficient estimates of hospital quality.