Quantitative Frequency-Domain Passive Cavitation Imaging

Abstract

Passive cavitation detection has been an instrumental technique for measuring cavitation dynamics, elucidating concomitant bioeffects, and guiding ultrasound therapies. Recently, techniques have been developed to create images of cavitation activity to provide investigators with a more complete set of information. These techniques use arrays to record and subsequently beamform received cavitation emissions, rather than processing emissions received on a single-element transducer. In this paper, the methods for performing frequency-domain delay, sum, and integrate passive imaging are outlined. The method can be applied to any passively acquired acoustic scattering or emissions, including cavitation emissions. In order to compare data across different systems, techniques for normalizing Fourier transformed data and converting the data to the acoustic energy received by the array are described. A discussion of hardware requirements and alternative imaging approaches are additionally outlined. Examples are provided in MATLAB.

I. Introduction

RECEIVING and processing acoustic emissions has been a bedrock of diagnostic and therapeutic ultrasound for decades. Scattered emissions, especially cavitation emissions, can contain critical information about the interaction of ultrasound and the insonified medium. Passive detection of cavitation emissions has been pursued as early as 1954 [1] and has been used for medical applications in the following decades [2], [3]. In the past twenty years, hundreds of papers have used passive acoustic techniques for both basic and applied investigations in areas such as cavitation dynamics [4]–[7], thermal ablation [8]–[10], sonothrombolysis [11]–[16], blood-brain barrier disruption [17]–[19], and drug and gene delivery [20], [21]. The importance of passive acoustic monitoring is further highlighted in the Acoustical Society of America’s technical report on bubble detection and cavitation monitoring [22].

The vast majority of studies employing passive cavitation detection have used single-element transducers to record cavitation emissions. Although this approach continues to yield critical information, it has shortcomings. Most notably, the fixed receive sensitivity pattern of a single-element transducer inhibits spatially-resolved cavitation detection over an extended area. As a simple demonstration of this problem, consider two transducers with the same aperture and frequency characteristics, except that one transducer is focused and the other is unfocused. The unfocused transducer has a larger beamwidth and thus will record emissions over a larger area than the focused transducer. Although the unfocused transducer may detect emissions over a broader area, it cannot be used to spatially localize cavitation emissions as specifically as a focused transducer. Furthermore, unfocused passive cavitation detectors have a lower sensitivity. Because cavitation emissions are stochastic and often transient, mechanically steering a focused transducer is not a viable approach to obtaining broad spatial sensitivity with good localization.

One solution to the problem of mapping sound emissions from an unknown location is to beamform emissions received with an array [23], [24]. In seismology, Norton and Won [25] and Norton et al. [26] extended prior beamforming algorithms applied to passively received signals in ocean acoustics [27]–[29] to form images using a back-projection technique. Shortly after the work of Norton et al., Gyöngy et al. [30], Salgaonkar et al. [31], and Farny et al. [32] beamformed passively received cavitation emissions using a delay, sum, and integrate algorithm. The details of the implementation of the algorithm varied based on the ultrasound system used to collect the data: Salgaonkar et al. [31] and Farny et al. [32] did not have access to pre-beamformed data but Gyöngy et al. [30] did. Nonetheless, all three groups demonstrated that array-based passive cavitation detection could map cavitation.

Passive cavitation imaging has been used to study high-intensity focused ultrasound thermal ablation [30], [33]–[37], ultrasound-mediated delivery of drugs, drug substitutes, and therapeutic biologics [38]–[42], histotripsy [43], and cavitation dynamics [41], [44]–[50]. The imaging algorithm has also been modified to account for aberration [51]–[54] and to improve the image resolution [40], [55], [56]. These studies have all relied on relative time-of-flight information, which allows the image resolution to be independent of the therapy pulse shape. Synchronized passive imaging has also been achieved using absolute time-of-flight information, which can yield good axial resolution when the excitation ultrasound is a short pulse [57].

The present article will focus on the implementation of frequency-domain passive cavitation imaging using an algorithm based on the delay, sum, and integrate approach. Frequency-domain analysis has several potential advantages over time-domain processing. First, the frequency content of cavitation emissions is often analyzed as a method for determining the type of cavitation, such as stable cavitation or inertial cavitation [22], [58]. Operating in the frequency domain makes frequency selection simpler and more direct than using time-domain finite impulse response filters. It is also easier to select and analyze multiple discrete frequency bands for analysis simultaneously. Additionally, only the frequencies of interest need to be beamformed, which can dramatically reduce the computational time compared to beamforming the entire bandwidth (akin to the time-domain approach) [59]. If all frequencies satisfying the Nyquist criterion are beamformed, the time-domain approach can be less computationally intensive than the Fourier transforms required for the delay, sum, and integrate method. Finally, time-domain shifting results in temporal quantization error due to the discrete temporal sampling. The temporal quantization error can produce grating lobe artifacts [60] unless the received signals are sampled temporally at a very high sampling rate (often ten-fold or higher than the highest frequency of interest) or the received samples are interpolated to approximate a high sampling rate. In the frequency domain, the time delays become phase shifts where the quantization error is reduced to the floating-point precision.

To provide a pedagogical explanation of passive cavitation imaging, a conceptual and mathematical explanation of the beamforming is provided in the next section. The section also describes how to convert the measured emissions to received acoustic energy. Section III describes how to implement quantitatively the passive cavitation imaging algorithm with discrete-time samples that may include windowing and zero padding. For increased clarity, examples are provided. Section IV describes the image resolution and how it can be modified using both data-independent and data-dependent apodization. Section V describes experimental considerations when acquiring passive data, including hardware requirements, array orientation, and software implementation. Section VI discusses alternate frequency-domain passive beamforming algorithms that have been described in the literature. This text is followed by sections providing concluding remarks and examples are provided in MATLAB.

II. Passive Cavitation Imaging of Continuous-Time Signals

A. Algorithm

Passive cavitation imaging in the frequency domain using a delay, sum, and integrate algorithm to beamform the acoustic emissions received on a passive array has been previously described [61]. The delay, sum, and integrate algorithm is rooted in the assumption that signals originating from a single source and arriving at different elements of an array will be coherent, though arriving at different times based on the time of flight from the source to each individual element (Fig. 1A). To form an image, the received signals are individually temporally delayed based on the propagation times between the receiving elements and the spatial location that the pixel represents. The waveforms are summed across the elements and, due to their coherent nature, add constructively if the location of the pixel represents the source location (Fig. 1B). If the received signals are time delayed using propagation times to a location that is far from the source, the waveforms will not add constructively (Fig. 1C). The pixel amplitude is determined from the energy (or sometimes power) in the summed waveform. To form a complete image, the energy at each desired pixel location is computed. The algorithm for computing the pixel amplitude, $B(\overrightarrow{r})$, at location $\overrightarrow{r}$ is mathematically written as:

$$B(\overrightarrow{r})={{\displaystyle {\int }_{t_o}^{t_f}\left|{\displaystyle \sum _{l=1}^L{x}_l\left(t+\frac{\left|{\overrightarrow{r}}_l-\overrightarrow{r}\right|}{c}\right)}\right|}}^{2}dt,$$ (1)

where l indexes over the L elements of the array, t represents time, x_l(t) is the real signal recorded on the l^th element between times t_o and t_f, ${\overrightarrow{r}}_l$ is the location of the l^th element, and c is the speed of sound in the medium. The key difference between passive and B-mode imaging is that the passive algorithm does not use the absolute time of flight to determine the depth of the acoustic emission.

Fig. 1.

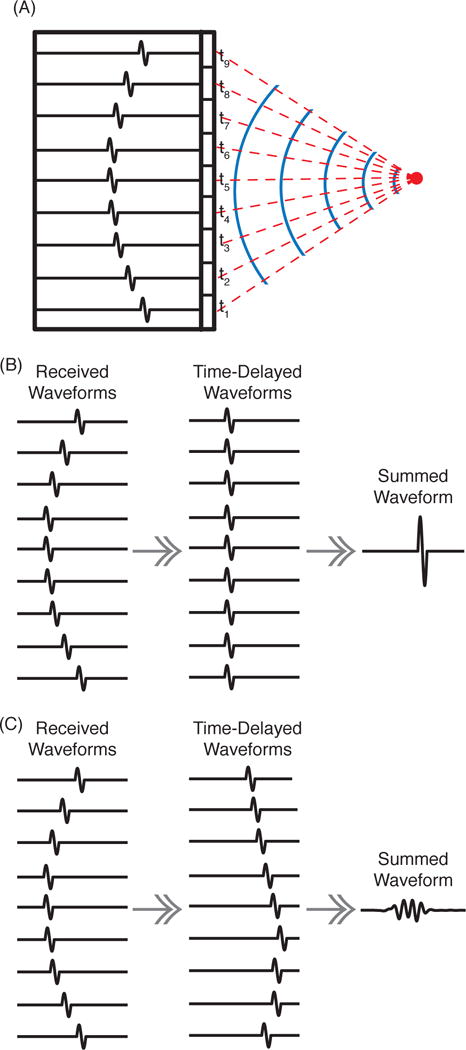
(A) An acoustic pulse is emitted from a point source (red circle). The solid blue lines represent wavefronts. The red dashed lines indicate the acoustic propagation paths, each with a corresponding time of flight, t_i. The black outlined rectangles schematically represent the array elements. The recorded waveforms for each element are shown as a single-cycle pulse arriving at different times. (B) When $\overrightarrow{r}$ corresponds to the source location and is used to compute the time delays to shift the waveforms, the waveforms will sum constructively. (C) When $\overrightarrow{r}$ is a location away from the source, the time-delayed waveforms do not add constructively and the summed waveform has a lower amplitude and less energy.

As described in Section I, there are many advantages to creating the image in the frequency domain. The frequency-domain algorithm relies on the equivalence between a time delay in the time domain and a phase shift in the frequency domain. Using the continuous Fourier transform, $\mathfrak{F}\{\diamond \}$, of ⋄, the relationship between time delays and phase shifts is:

$$\mathfrak{F}\{x_l(t+t\prime )\}=X_l(f)\cdot e^{i2\pi ft\prime },$$ (2)

where the finite-duration continuous-time Fourier transform X_l(f) is defined as:

$$\mathfrak{F}\{x_l(t)\}=X_l(f)={\displaystyle {\int }_{t_o}^{t_f}{x}_l(t)e^{-i2\pi ft}dt},$$ (3)

f is frequency, and t_o and t_f define the start and end of the duration of the signal x_l(t), respectively. Applying a Fourier transform and (2) to (1) yields the frequency-domain equation for creating a passive cavitation image, $B(f,\overrightarrow{r})$:

$$B(f,\overrightarrow{r})={\left|{\displaystyle \sum _{l=1}^L{X}_l(f)\cdot e^{i2\pi f\frac{\left|{\overrightarrow{r}}_l-\overrightarrow{r}\right|}{c}}}\right|}^2,$$ (4)

where X_l(f) is the frequency domain representation of the signal received on the l^th element of the passive array. An image is created by computing (4) for all values of $\overrightarrow{r}$ that are of interest. These computations are performed using a single data set. Note that because a summation is performed over the received signals on each element, any signals that are incoherent across the elements (such as electronic noise) will be reduced.

A multi-frequency composite image can be formed by integrating $B(f,\overrightarrow{r})$ over the frequency band(s) of interest:

$$B(\overrightarrow{r})={\displaystyle {\int }_{f_1}^{f_2}B(f,\overrightarrow{r})}df,$$ (5)

where f₁ and f₂ define the lower and upper frequency band limits, respectively. If the integral is performed for all frequencies between negative infinity and positive infinity, (5) yields the same result as (1). Composite images are useful when the bandwidth of interest is finite. Furthermore, incoherent noise will be reduced in multi-frequency composite images relative to a single-frequency image.

Example duplex B-mode and passive cavitation images are shown in Fig. 2. Details of the experimental setup can be found in [42]. The data was acquired using a P4-1 phased array (Philips, Bothell, WA, USA). The region over which the passive data was beamformed is delineated with a cyan box. A peristaltic pump induced flow (from left to right) of a microbubble-saline mixture through latex tubing. Microbubble cavitation and destruction was initiated by 500 kHz pulsed ultrasound. The latex tube was suspended in degassed water. The passive cavitation images were formed from ultraharmonics of the fundamental, indicative of stable cavitation (Fig. 2A), or inharmonics of the fundamental (i.e., frequency bands not harmonically related to the fundamental), representative of the broadband emissions that are indicative of inertial cavitation (Fig. 2B). The relative strength of the different frequency components at two different locations are shown in representative energy spectra (Fig. 2C). These spectra demonstrate the ability of passive cavitation imaging to localize different types of cavitation emissions. The loss of echogenicity due to microbubble destruction from ultrasound insonation is observed as a relative hypoechogenicity in the tube lumen downstream (to the right) of the cavitation activity. It can be seen that cavitation activity is mapped to regions outside the latex tube. This imaging artifact is due to the poor axial resolution of the algorithm for diagnostic phased and linear arrays, which is described in more detail in section IV-A. For both images, there are pixels outside the tube with an amplitude that is within −3 dB of the maximum pixel value in the image. This strong signal outside of the tube would still be seen if the images were shown on a linear scale [33], [40], [52], [53].

Fig. 2.

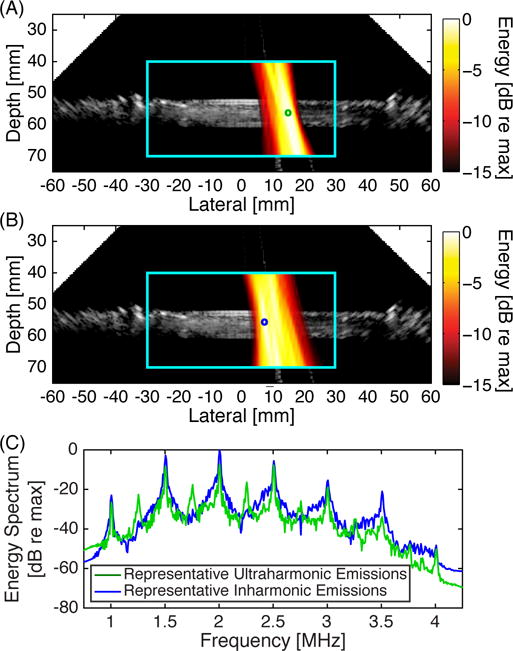
Example duplex images showing a passive cavitation image (hot colormap) superimposed onto a B-mode ultrasound image using a Philips P4-1 phased array. The cyan box delineates the region of interest over which the passive cavitation image was formed. The passive cavitation images were formed by summing over multiple frequency bands corresponding to (A) ultraharmonic frequencies relative to the insonation frequency (2.23 MHz to 2.27 MHz, 2.73 MHz to 2.77 MHz, and 3.23 MHz to 3.27 MHz) and (B) inharmonic frequencies relative to the insonation frequency (2.105 MHz to 2.145 MHz, 2.605 MHz to 2.645 MHz, and 3.105 MHz to 3.145 MHz). Each passive cavitation image has 15 dB of dynamic range with 0 dB corresponding to the maximum pixel value in each image. (C) Representative energy spectra used to form the passive cavitation images at two different locations, denoted by the green and blue circles in panels A and B, respectively. Note the spatial variation of ultraharmonic and inharmonic components. All of the plots are derived from the same data set.

B. Voltage to Energy Conversion

Often x_l(t) is recorded in units of volts and is the system-generated voltage in response to the l^th element passively receiving ${\overline{p}}_l(t)$, the average incident acoustic pressure over the element surface [62]. To convert x_l(t) to units of pressure, a complex calibration factor is necessary. The calibration factor (units of volts per unit pressure) consists of physical scalars and a frequency-dependent system calibration factor M_l(f) to account for the receive sensitivity and electronic noise characteristics of an element, as well as signal filtering and any other components that influence the acquired signal. Using M_l(f), the Fourier transform of ${\overline{p}}_l(t)$ is related to the Fourier transform of x_l(t) by:

$${\overline{P}}_l(f)=\frac{X_l(f)}{M_l(f)},$$ (6)

where ${\overline{P}}_l(f)$ is the Fourier transform of ${\overline{p}}_l(t)$ [63]. The receive sensitivity component of M_l(f) can be characterized using scattering [64], [65], pulse-echo, and pitch-catch [66] measurement techniques.

For the l^th calibrated element, the energy associated with the received pressure spatially integrated over the surface S_l in a frequency band f₁ ≤ f ≤ f₂ is referred to as the incident acoustic energy, E_l. E_l is determined by integrating the magnitude squared of the Fourier transform and multiplying by the surface area of the element divided by the acoustic impedance:

$$E_l={\displaystyle {\int }_{f_1}^{f_2}\frac{S_l}{{\rho }_{0}c}}{\left|\frac{X_l(f)}{M_l(f)}\right|}^{2}df,$$ (7)

where ρ₀ is the density of the medium and c the speed of sound of the medium [67], [68]. The integrand is the energy density spectrum, EDS_l(f), of ${\overline{p}}_l(t)$. For frequencies outside the nominal bandwidth of the receive element, M_l(f) approaches zero and the signal to noise ratio of X_l(f) will be poor. For these out-of-bandwidth frequencies, the noise will contribute substantially to the calculated energy, limiting the accuracy of the energy calculation. It should also be noted that when x_l(t) is a real-valued voltage signal as assumed here, the conjugate symmetry of the Fourier transform spreads energy equally between positive and negative frequencies (i.e., |X_l(f_o)| = |X_l(−f_o)|) [68]. If f₁ and f₂ are both positive, the energy calculated using (7) must be multiplied by two to achieve equivalence with a time-domain signal that has been bandpass filtered between f₁ and f₂ [69]. If f₁ is negative infinity and f₂ is positive infinity then (7) needs no modification to calculate the total energy.

Combining (4), (6), and (7) allows for the derivation of a passive cavitation image with correct physical units (energy per unit frequency) based on the energy density spectrum:

$$I(f,\overrightarrow{r})=\frac{1}{{\rho }_{o}cS}{\left|{\displaystyle \sum _{l=1}^L{S}_l\frac{X_l(f)}{M_l(f)}\cdot e^{i2\pi f\frac{\left|{\overrightarrow{r}}_l-\overrightarrow{r}\right|}{c}}}\right|}^2,$$ (8)

where S is the summed surface area of the active elements.

The incident energy within a frequency band of interest can be estimated by integrating $I(f,\overrightarrow{r})$ over that frequency band. The energy density spectrum associated with the total incident energy on the array can be computed using Parseval’s theorem applied to the signals received by all of the elements:

$${\text{EDS}}_{\text{inc}}(f)=\frac{1}{{\rho }_{o}c}{\displaystyle \sum _{l=1}^L{S}_l}{\left|\frac{X_l(f)}{M_l(f)}\right|}^2.$$ (9)

If the summands of (8) and (9) are independent of l, then $I(f,\overrightarrow{r})$ is equal to EDS_inc(f). The summands of (8) and (9) are independent of l when the radiated energy originates from a single point source, the receiving elements are omnidirectional, amplitude variations from spherical spreading are negligible, and the signals are beamformed to the location of the point source. In practice, these assumptions may be violated (e.g., multiple microbubbles cavitating, non-point-source cavitation emissions [70], or directional receiving elements [71]) and thus the beamformed signal is only an approximation for the energy incident on the array. This error is further discussed in the Appendix and supplemental m-files. Note that this error occurs regardless of whether the beamforming is performed in the frequency domain or the time domain.

To estimate the energy radiated by the source, it is necessary to account for spreading of the source waveform, the diffraction-derived directional receive sensitivity of each element, and the attenuation of cavitation emissions through the medium. Spherical spreading of emissions can be compensated by multiplying the signal strength by the distance between the receive element and source [64], [72]. The effect of the diffraction pattern can be compensated by incorporating the receive sensitivity of each element as a function of location into each element’s system calibration factor (i.e., $M_l(f)\to M_l(f,\overrightarrow{r})$). When the receive elements can be approximated as omnidirectional point receivers, the system calibration factors are independent of $\overrightarrow{r}$. Frequency-dependent attenuation can be compensated by standard derating procedures [64], [73].

Even if the above compensation factors are included, the finite size of the spatial spread of energy due to the algorithm’s point-spread function results in artifactual mapping of energy to locations without a true source. For example, if the point-spread functions corresponding to two point sources overlap, then the energy at each source will be incorrect. Correcting for this inaccuracy is a significant challenge for quantitative passive imaging of cavitation sources because many cavitation sources are spatially and temporally stochastic. However, computing the energy incident on the array is valuable as it allows for quantitative comparison of results from different setups or laboratories.

As noted by Norton et al. [26], the algorithm in (8) results in a “DC bias” that can be removed for each frequency by subtracting the total incident energy density spectrum (9). Thus, a passive cavitation image at a given frequency, based on the incident energy density spectrum without bias, is given by:

$$I_{\text{unbiased}}(f,\overrightarrow{r})=I(f,\overrightarrow{r})-{\text{EDS}}_{\text{inc}}(f).$$ (10)

Note that removal of the “DC bias” can result in small nonphysical negative energy at some locations away from sources.

III. Passive Cavitation Imaging of Discrete-Time Signals

The passive cavitation image obtained using (10) requires a continuous frequency signal. In practice, signals are digitized for recording and often are processed. In this section, normalization factors will be derived to account for discretization of the received signal, zero padding, and windowing. At the end of the section, equations are provided for forming a quantitative passive cavitation image using discretized signals.

A. Effect of Discretization

The finite-duration continuous-time Fourier transform, (3), can be transformed into a summation, based on the fact that x_l(t) is sampled at the time points:

$$n=\text{round}\left(\frac{t-t_o}{\mathrm{\Delta }t}\right),$$ (11)

where n is the sample index and the sampling period Δt is the inverse of the sampling frequency f_s. It will be assumed that Δt is small enough to satisfy the Nyquist criterion. Under this transformation, dt → Δt and x_l(t) → x_l[n]:

$$\begin{array}{l}{X}_l(f)\approx {\displaystyle \sum _{n=0}^{N-1}{x}_l[n]}{e}^{-i2\pi f(n\cdot \mathrm{\Delta }t+t_o)}\mathrm{\Delta }t\\ =\frac{1}{f_s}{\displaystyle \sum _{n=0}^{N-1}{x}_l[n]e^{-i2\pi \frac{f}{f_s}n}{e}^{-i2\pi f{t}_o}},\end{array}$$ (12)

where square brackets denote a function of a discrete variable and N = round(T/Δt).

Next, X_l(f) needs to be discretized with respect to f. Δf is the sampling step size for the frequency domain discretization and is taken to be 1/T. The discretized frequency values are f_k = k·Δf, where k indexes the frequency values from 0 ≤ f_k < f_s:

$$\begin{array}{l}{X}_l(f_k)\approx \frac{1}{f_s}{\displaystyle \sum _{n=0}^{N-1}{x}_l[n]}{e}^{-i2\pi \frac{k\cdot \mathrm{\Delta }f}{f_s}n}{e}^{-i2\pi (k\cdot \mathrm{\Delta }f)t_o}\\ =e^{-i2\pi (k\cdot \mathrm{\Delta }f)t_o}\frac{1}{f_s}{\displaystyle \sum _{n=0}^{N-1}{x}_l[n]e^{-i2\pi kn/N}}.\end{array}$$ (13)

Note that both n and k have N steps. Thus Δf·N = f_s, which has been used to simplify the above equation. The discrete Fourier transform is defined as:

$$X_l[k]={\displaystyle \sum _{n=0}^{N-1}{x}_l[n]e^{-i2\pi kn/N}.}$$ (14)

Comparing (13) and (14), the relationship between X_l(f_k) and X_l[k] is:

$$X_l(f_k)\approx \frac{1}{f_s}{e}^{-i2\pi (k\cdot \mathrm{\Delta }f)t_o}{X}_l[k].$$ (15)

Note that the discrete Fourier transform, X_l[k], has units of volts while the continuous Fourier transform, X_l(f), has units of volts-seconds.

The discrete-time system calibration factor, M_l[k], can be defined in an analogous manner to the continuous-time system calibration factor (6). M_l[k] has units of volts per pascal, like M_l(f). Because X_l[k] and P_l[k] are both scaled by 1/f_s, M_l[k] is not scaled by 1/f_s.

The acoustic energy in the frequency band f₁ ≥ f ≥ f₂ that is incident on an element can be computed by discretizing (7) and using (15) and the discrete-time system calibration factor:

$$E_l={\displaystyle \sum _{k=k_1}^{k_2}\left(\frac{S_l}{{\rho }_{0}c}\frac{1}{f_s^2}{\left|\frac{X_l[k]}{M_l[k]}\right|}^2\right)}\mathrm{\Delta }f.$$ (16)

The term in parentheses represents the discretized energy density spectrum for the l^th element at frequency k. The energy density spectrum is sometimes called the energy spectral density or energy spectrum [68], [74]. Note that in many digital signal processing books, the authors work in normalized units. As a result, their definition of the energy density spectrum drops the $1/f_s^2$. To work in physical (and dimensionally correct) units, it is important to include this factor.

The prior relationships for energy and energy density spectrum are for the signal recorded. This may or may not correspond to the total incident acoustic energy depending on whether the memory size is adequate to record the entire duration of the emissions. If the acoustic emission duration temporally extends beyond what was recorded and it is a stationary signal, then the time-averaged energy can be computed and used to estimate the total acoustic energy.

The power density spectrum (PDS) is defined as the energy density spectrum divided by a relevant time (which should always be defined for clarity). One logical choice is the signal duration, T (i.e., the green and yellow shaded regions in Fig. 3). Another common choice is the interval of interest over which there are detectable acoustic emissions, T_IOI (i.e., the green shaded region in Fig. 3). Using T, the power density spectrum is given by:

$${\text{PDS}}_l[k]=\frac{S_l}{{\rho }_{0}c}\frac{1}{T{f}_s^2}{\left|\frac{X_l[k]}{M_l[k]}\right|}^2.$$ (17)

Fig. 3.

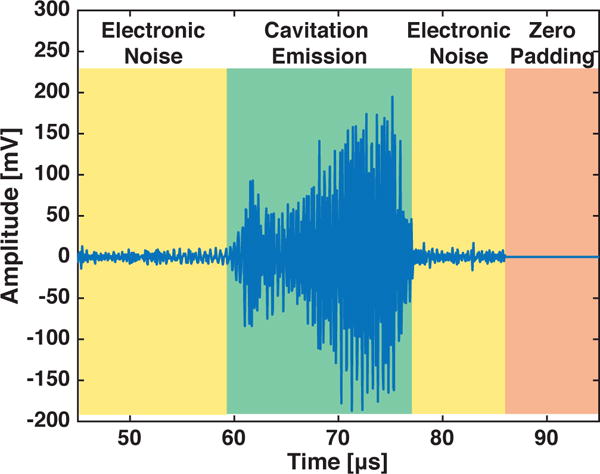
An example recorded signal is shown. The signal includes times when only electronic noise was measured by the system (yellow shading), when zero padding as a post-processing step was implemented (orange shading), and when cavitation emissions were recorded (green shading). Only the green shaded region would be including when determining T_IOI.

B. Effect of Zero Padding

Often, a signal will be zero padded (Fig. 3) to increase the total time duration recorded and thus decrease Δf for better apparent resolution or so that data points fall exactly on the center frequency of a transmitted signal, which is particularly useful for quasi-continuous-wave insonations. It should be noted that zero padding does not increase the resolution of the spectrum because the technique effectively just interpolates between existing bins. Zero padding to adjust the discrete frequencies in the spectrum can be convenient, but it is not strictly necessary if one is interested in computing the total energy or power in a frequency band. Based on Parseval’s theorem, no energy in the signal is lost in the process of performing a Fourier transform. If a single tone burst at frequency f_o is transmitted, but the sampling is such that there is not a frequency point exactly at f_o, the energy from f_o will be distributed about the frequencies nearest f_o. Thus, the energy and power can be obtained by summing over the appropriate spectral densities (including the appropriate scalars, as defined above) for a band that covers the spread of the frequency-domain signal.

Zero padding changes the value of N and T by increasing the duration of the signal when the signal amplitude is zero. Therefore, care needs to be taken when computing the energy and power. In (16), the value of Δf needs to reflect the smaller frequency bin spacing due to the zero padding. Additionally, when computing the power density spectrum, T should be replaced by T_IOI.

C. Effect of Windowing

Recorded signals are commonly windowed to reduce the sidelobes in the frequency domain. However, windowing reduces the energy in the original time-domain signal. It is often desirable to compensate for this energy reduction. Additionally, the window acts to blur the energy at a single frequency over nearby frequencies. This sub-section discusses both of these issues. For simplicity, the scaling factors S_l/(ρ_oc), M_l[k], and Δt are not included.

1) Compensation for energy reduction due to windowing

Because windowing reduces the energy at different times within a signal, if the frequency content of the signal varies with time, the windowing may preferentially affect certain frequencies. Compensating for this effect can be difficult. To avoid this complexity, we will assume that that any subset within x[n] has the same frequency content and energy as any other subset. This assumption implies that windowing only scales the total energy in the signal:

$$\text{Energy}={\displaystyle \sum _n{\left|x[n]\right|}^2}=C\cdot {\displaystyle \sum _n{\left|x[n]\cdot w[n]\right|}^2},$$ (18)

where w[n] is the window function and C is the scalar used to compensate for the window. If the amplitude of the window w[n] is assumed to vary slowly with increasing values for n as compared to the recorded signal x[n], the signal energy can be written as a summation over M intervals of length P = N/M, chosen such that the value of w[n] is approximately constant over each interval:

$$\begin{array}{l}\text{Energy}=C\cdot {\displaystyle \sum _{m=0}^{M-1}\left({\displaystyle \sum _{n=mP}^{(m+1)P-1}{\left|x[n]\cdot w[n]\right|}^2}\right)}\\ \approx C\cdot {\displaystyle \sum _{m=0}^{M-1}\left({\left|w[mP]\right|}^2{\displaystyle \sum _{n=mP}^{(m+1)P-1}\left|x{[n]}^2\right|}\right)}.\end{array}$$ (19)

Because it was assumed that the energy density spectrum of x[n] is approximately constant for each of the M intervals then:

$$\begin{array}{l}\text{Energy}\approx C\cdot \left(\frac{1}{M}{\displaystyle \sum _{m=0}^{M-1}{\left|w[mP]\right|}^2}\right)\left(M{\displaystyle \sum _{n=0}^P{\left|x[n]\right|}^2}\right)\\ \approx C\cdot \overline{{\left|w\right|}^2}\left({\displaystyle \sum _{n=0}^N{\left|x[n]\right|}^2}\right),\end{array}$$ (20)

where $\overline{{\left|w\right|}^2}$ is the mean-square value of the window function w[n]. Thus, the constant C in (18) is identified as $C=1/\overline{{\left|w\right|}^2}$. Note that the window function is dimensionless.

2) Spectral leakage due to windowing

A second effect of windowing is that energy becomes blurred over neighboring frequencies. This effect derives from the fact that two signals multiplied together in the time domain are equivalently convolved in the frequency domain. Fortunately, the blurring process conserves energy. As a result, the energy can be computed by summing over the band containing the spread (assuming that multiple bands of interest do not overlap):

$$\text{Energy}=\frac{1}{\overline{{\left|w\right|}^2}}{\displaystyle \sum _k\text{EDS}[k]\cdot \mathrm{\Delta }f}.$$ (21)

This equation includes the $1/\overline{{\left|w\right|}^2}$ windowing compensation factor from the prior sub-section. A similar equation can be derived for calculating the power. The size of the band can be determined empirically, by noting when the signal has fallen to an adequately small value (say 1% of the maximum). Alternatively, tables (e.g., Table I) can be used to determine the approximate width over which the energy is spread. In Table I, the approximate width given is the distance between the first positive and negative zeros of W[k], where W[k] is the discrete Fourier transform of the window function, w[n].

TABLE I.

Width Between the First Positive and Negative Zeros of W[k] and Peak Sidelobe Height of w[k] for Some Commonly Used Window Functions. T is the Duration of the Window, Which is Typically T_IOI.

Window Type	Width (Hz)	Peak Sidelobe (dB)
Rectangular	2T	−13.3
Bartlett	4T	−26.5
Hann	4T	−31.5
Hamming	4T	−44.0
Blackman	6T	−58.1

Often when measuring broadband signals, different frequency components, such as a harmonic and ultraharmonic, might bleed into each other due to the spectral leakage. In these cases, it might be most appropriate to select the signal width empirically so that inappropriate signal is not included in the band of interest. If one is interested in relative power measurements across different signals or frequency bands that are all recorded and processed identically, it may be best to only use the peak value within each frequency band of interest to minimize the effects of spectral leakage from neighboring frequency components. Alternatively, signal processing using alternate transformations, such as wavelets [75], [76], or modeling [50] can be used to estimate frequency components within received cavitation emissions.

In some cases, windowing can be designed to substantially reduce the effects of spectral leakage. This reduction is possible when received acoustic emissions contain narrow-band, harmonically related components of known frequencies, as in continuous-wave sonication for thermal ablation. The energy of each narrow-band component will be contained within a single bin in the Fourier domain if a rectangular window (w[n] = 1 and no zero padding) is selected that is an integer number of periods for all frequency components of interest. The key to this approach is ensuring that the frequency bins fall exactly at the harmonically related components. For example, in one study employing 3.1 MHz, continuous-wave sonication [78], acoustic emissions were analyzed using rectangular windows of length 100 μs, equal to 155 cycles of the 1.55 MHz subharmonic. In the resulting spectra, all measurable subharmonic energy was contained in the single bin centered at 1.55 MHz, with any spectral leakage falling below the electronic noise floor.

D. Summary Equation for Passive Cavitation Imaging of Discretized Signals

To compute a passive cavitation image based on the incident energy density spectrum without a DC bias, the normalization factors that should be applied to correct for signal discretization and windowing are, respectively:

$$\frac{1}{f_s^2}\text{and}\frac{1}{\overline{{\left|w\right|}^2}}.$$ (22)

If the received discretized signal has been recorded for the entire duration of the emissions or thereafter, has been potentially zero padded and windowed, and was not attenuated, then applying discretization and the normalization factors to (8), (9), and (10) yields the following expression for the amplitude of the passive cavitation imaging, $I[k,\overrightarrow{r}]$, at location $\overrightarrow{r}$:

$$\begin{array}{c}I[k,\overrightarrow{r}]=\frac{1}{\overline{{\left|w\right|}^2}{\rho }_{o}c{f}_s^{2}S}{[\left|{\displaystyle \sum _{l=1}^L{S}_l\frac{X_l[k]}{M_l[k]}{e}^{-i2\pi k\mathrm{\Delta }f\frac{[{\overrightarrow{r}}_l-\overrightarrow{r}]}{c}}}\right|}^2\\ -{{\displaystyle \sum _{l=1}^L\left|S_l\frac{X_l[k]}{M_l[k]}\right|}}^2],\end{array}$$ (23)

for frequency kΔf using discretized signals. Note that Δf should include zero padding. To compute a passive cavitation image based on power spectrum density, $I[k,\overrightarrow{r}]$ should be divided by T_IOI. It is also of note that the normalization factors and conversion to energy can be applied to a passive cavitation detection signal received by a single-element transducer. An image that is composed of multiple frequencies can be computed using:

$$I[\overrightarrow{r}]={\displaystyle \sum _{k}I[k,\overrightarrow{r}]}\cdot \mathrm{\Delta }f.$$ (24)

The frequency bins over which the summation is performed do not need to be contiguous. For instance, the bins may correspond to a summation over frequency bands corresponding to multiple ultraharmonics.

Proper normalization when transforming to the frequency domain can be determined based on the variance of the time-domain signal being equivalent to the summation of the power density spectrum. Ultrasound signals are commonly zero-mean, and thus the variance of the time-domain signal is equal to the mean-square value of the time-domain signal. The normalization factors can then be confirmed using the following equation:

$$\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}{\left(x[n]\right)}^2}\approx \frac{1}{\overline{{\left|w\right|}^2}T{f}_s^2}{\displaystyle \sum _{k=0}^{N-1}{\left|X_w[k]\right|}^2\mathrm{\Delta }f,}$$ (25)

where X_w[k] is the Fourier transform of x[n]·w[n].

E. Example of Passive Cavitation Imaging

In cavitation-based therapies, it is advantageous to analyze specific emission frequency bands because different bands correspond to different modes of cavitation, which correlate with different bioeffects [8], [12], [17], [20]. Examples of beamforming different frequencies from the same data set are shown in Fig. 4. Emissions were generated by albumin-coated microbubbles with an air core, produced in house, exposed to 2 MHz pulses at one of four insonation pressures. The microbubbles were pumped through tubing using a peristaltic pump. The insonation pressures were selected to produce neither ultraharmonics nor broadband emissions (peak rarefaction pressure 190 kPa), ultraharmonics alone without broadband emissions (peak rarefaction pressure 260 kPa), ultraharmonics and broadband emissions (peak rarefaction pressure 400 kPa), or broadband emissions alone without ultraharmonic emissions (peak rarefaction pressure 760 kPa). All pressure measurements were made in a free-field environment. The acoustic emissions from the insonation were received with a Philips L7-4 linear array (Bothell, WA, USA) and beamformed using (23) without compensating for the frequency sensitivity of the array. Emissions at an ultraharmonic frequency (7 MHz) were used to characterize stable cavitation, and emissions at an inharmonic frequency (4.5 MHz) were used to characterize inertial cavitation. A time-domain beamforming algorithm [30], indicative of the total energy, was also implemented.

Fig. 4.

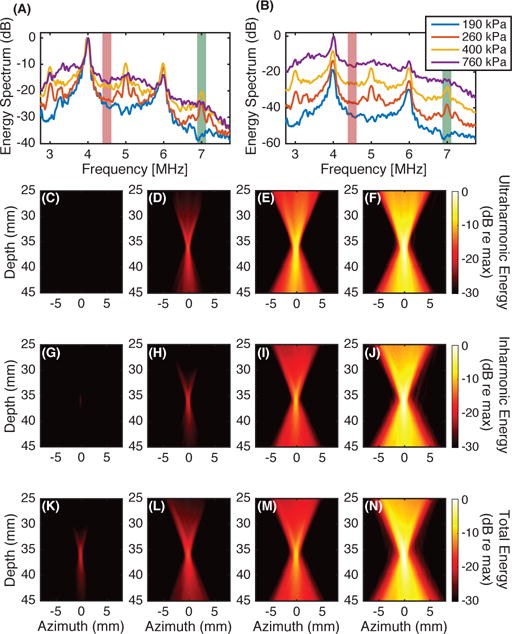
Microbubbles were insonified with a 2 MHz pulse of duration 14.4 μs at one of four different pressure amplitudes. The computed energy spectra at the location of the pixel with the maximum amplitude in passive cavitation images is shown (A, B). The energy spectra are plotted on a decibel scale relative to the energy at 4 MHz for each insonation pressure amplitude (A) or relative to the energy at 4 MHz for the 760 kPa insonation (B). Passive cavitation images were formed for each insonation pressure amplitude from the energy at the ultraharmonic frequency of 7 MHz, shown with green shading [(C), (D), (E), (F), respectively] and the inharmonic frequency of 4.5 MHz shown with red-orange shading [(G), (H), (I), (J), respectively]. For comparison, subfigures (K), (L), (M), and (N) are formed using a time-domain algorithm, which beamforms all frequencies. For a given bandwidth, each image was normalized by the maximum energy in the image formed from data obtained while insonifying with a 760 kPa peak rarefactional pressure amplitude.

Each of the columns in Fig. 4 were beamformed from the same data set (i.e., Figs. 4C, 4G, and 4K were beamformed from a data set obtained from exposure to a peak rarefactional pressure of 190 kPa; Figs. 4D, 4H, and 4L were beamformed from a 260 kPa exposure; Figs. 4E, 4I, and 4M were beamformed from a 400 kPa exposure; and Figs. 4F, 4J, and 4N were beamformed from a 760 kPa exposure). As the insonation pressure increased (i.e., for a fixed row in Figs. 4C–4N), the maximum amplitude within the passive cavitation images increased. Note that the signal is below the −30 dB dynamic range that is plotted for the ultraharmonic and inharmonic frequency bands at the lowest pressure amplitude exposure, 190 kPa (Figs. 4C and 4G, respectively). The threshold for ultraharmonic frequency emissions was exceeded for the 260 kPa insonation, as evident in the spectrum in Fig. 4A and beamformed image in Fig. 4D.

Care must be used to avoid false interpretation of spectral data used to create passive cavitation images. Three potential pitfalls include spectral leakage, analysis of spectral waveform shape, and nonlinear propagation and scattering. Note that inharmonic frequency emissions are mapped at 260 kPa (Fig. 4H), which are artifactual due to spectral leakage from the harmonic at 4 MHz (Fig. 4A). This example demonstrates that spectral leakage from the fundamental, harmonics, or ultraharmonics may produce artifacts in passive cavitation imaging. Windowing (Section III-C2) can be used to reduce spectral leakage.

Regarding analysis of spectral waveform shape, Fig. 4F shows ultraharmonic frequency emissions produced by insonation at 760 kPa. The spectrum in Fig. 4B at 7 MHz is dominated by broadband emissions corresponding to inertial cavitation and not stable cavitation. Careful attention to the shape of the spectral components is important for correct interpretation of the corresponding microbubble dynamics. Exclusion of the broadband contribution at the ultraharmonic frequencies helps to ensure appropriate mapping of stable cavitation [15].

If harmonics are produced via nonlinear propagation or nonlinear scattering from objects other than bubbles, the passive imaging algorithm will not be able to differentiate between these sources and cavitation. For example, Fig. 4N could include harmonic contributions due to scattering from the tubing. The ability to beamform emissions originating from sources other than microbubbles can, however, be useful, such as in mapping the field of a transducer (see for example, [79], [80], or Fig. 7 from [61]).

IV. Image Quality

A. Image Resolution

As has been previously noted [31], [61], the resolution of the algorithm described in (23) is defined by the diffraction pattern of the receiving array. For low f-number hemispherical arrays, the resolution is high in all directions [51], [52]. The diffraction pattern for many diagnostic linear and phased arrays results in an axial resolution that is significantly worse than the lateral resolution. For a linear array, which can be approximated as an unapodized line aperture, the lateral −6 _dB beamwidth, W₋₆ dB, when z ≫ λ, where z is the axial distance of an imaged point source from the array and λ is the wavelength at the frequency of interest, can be approximated as [81]:

$$W_{-6\text{dB}}=\frac{1.21\lambda z}{L_o},$$ (26)

where L_o is the length of the line aperture. In many imaging applications, z and L_o are within an order of magnitude of each other. Therefore the lateral resolution is within an order of magnitude of λ.

The corresponding axial resolution can be estimated from an analytic expression [31] for a passive image of a point source, based on the Fresnel approximation for the diffraction pattern of a rectangular aperture [71]. On axis, for an unapodized line aperture cylindrically focused at the depth of the imaged point source, the axial −6 dB depth of field, D_{−6 dB}, under the Fresnel approximation is:

$$D_{-6\text{dB}}=\frac{9.69\lambda z^2}{L_o^2}.$$ (27)

Unlike B-mode imaging, the axial resolution does not depend on the insonation pulse duration or shape, but only the frequency-dependent diffraction pattern of the array [61].

As an example, the L7-4 array used in Fig. 4 has a length of 38.14 mm and the source was located at a depth of 35 mm. The ultraharmonic was analyzed at 7 MHz (λ = 0.218 mm), yielding estimated lateral and axial beamwidths of 0.24 mm and 1.78 mm, respectively. The inharmonic was analyzed at 4.5 MHz (λ = 0.339 mm), yielding estimated lateral and axial beamwidths of 0.38 mm and 2.76 mm, respectively. For the time-domain image, the dominant frequency is 4 MHz (λ = 0.381 mm). The estimated lateral and axial beamwidths at 4 MHz are 0.42 mm and 3.11 mm, respectively. The lateral beamwidths measured from the passive cavitation images formed from Figs. 4F, 4J, and 4N are 0.65 mm, 0.81 mm, and 0.91 mm, respectively. The experimental result follows the trend of smaller beamwidths with increasing frequency. The lateral beamwidths are not the same as what would be predicted using (26) because of the finite beamwidth of the ultrasound insonation. For complex array geometries or computing the resolution for locations in the image where there is no longer symmetry about the array, simulated cavitation images (see the Appendix) may be the easiest approach to determining the image resolution [51], [61].

Because the diffraction pattern is frequency-dependent, with improved resolution obtained by the inclusion of higher frequencies, techniques to increase the bandwidth of the received signal can be advantageous. Gyöngy and Coviello [55] achieved this goal by employing two sparsity-preserving techniques, matching pursuit and basis pursuit, to deconvolve inertial cavitation emissions. For matching pursuit deconvolution, the resolution (both axial and lateral) was improved, but at the expense of eliminating or incorrectly localizing some cavitation events. Basis pursuit deconvolution led to cavitation maps that could be used to resolve neighboring sources more clearly but did not affect the resolution for a single cavitation source. Both approaches relied on the assumption that the cavitation events were temporally sparse, which may not be the case in the presence of sustained stable cavitation [82].

B. Apodization

Implicitly assumed in the beamforming equation (23) is that the elements that form the passive array are omnidirectional receivers and that the propagation medium has no attenuation, neither of which are true in practice. To account for these effects, an apodization scalar $a_l({\overrightarrow{r}}_l,\overrightarrow{r},k)$ can be utilized. Correcting for the frequency dependent attenuation of the propagation path has been reported in [83], [84]. The directionality of the individual elements, which can be measured using a hydrophone, can be used to set the apodization. If the elements are rectangular in shape, the directionality of the elements can be estimated using the Fresnel approximation [71], [85]. Apodization may also be applied to reduce the formation of grating lobes that will occur if the element spacing is greater than one-half of a wavelength, where the wavelength should be computed for the highest frequency of interest [61].

Apodization can also be used to improve the image resolution. The apodizations described in the previous paragraph for delay, sum, and integrate approaches utilize a predefined, data-independent apodization of each element to weight the received signals during beamforming. An alternative approach is adaptive beamforming algorithms, such as Capon beamforming [86], that use the same time delays but apodize the weighting of the elements differently for each pixel in the image based on the signals received on each element and the pixel location. The weights are selected via optimization to minimize signal contributions originating from locations other than the location corresponding to the pixel being computed, while simultaneously constraining the weights for unity gain in the direction of the pixel [23]. Capon beamforming processes have been primarily designed to improve the lateral resolution in an image, but improved axial resolution can also be achieved [87].

Though Capon beamforming can reduce the elongation of the point-spread function relative to traditional delay and sum algorithms, the image is susceptible to artifacts arising from variability of the array elements (e.g., sensitivity or position), variability in the sound speed of the path between pixel and element location, and interference from scatterers within the imaging location. Stoica et al. [88] developed the robust Capon beamformer (RCB) that allowed the distance between each element and the pixel to vary by a set parameter, ε, when computing the apodization weights. Coviello et al. [40] utilized the Capon beamformer and the RCB for passive cavitation imaging in a flow phantom perfused with Sonovue microbubbles in vitro. The Capon beamformer mapped cavitation activity predominantly outside the flow phantom due, in part, to an inactive element on the imaging array that confounded the Capon beamformer algorithm. The passive cavitation images created via the RCB significantly reduced the axial elongation artifacts compared to the delay, sum, and integrate method [40]. Drawbacks to the RCB are that it is more computationally intensive than traditional delay and sum algorithms and requires empirical determination of ε. However, graphics processing unit implementation of the RCB has enabled real-time performance for cardiac B-mode ultrasound imaging [89].

V. Experimental Considerations

A. Hardware

Passive cavitation imaging has been reported on multiple systems, including those produced by Zonare Medical Systems (Z.one Imaging System, Mountain View, CA, USA) [30], [33]–[35], [39], [40], [45], [49], [61], Ardent Sound (Iris 2 Ultrasound Imaging System, Mesa, AZ, USA) [31], [37], Terason (Terason 2000 Ultrasound System, Burlington, MA, USA) [32], Verasonics (V-1 and Vantage sytems, Bothell, WA, USA) [36], [38], [42], [47], [59], and Ultrasonix, now BK Ultrasound, (SonixDAQ, Richmond, BC, Canada) [52], [54]. Some of the systems, such as the Z.one, Vantage, and Sonix-DAQ provide direct access to pre-beamformed radio frequency or in-phase and quadrature signals so that the beamforming can be performed using the researchers’ algorithms. Direct access to pre-beamformed signals provides researchers with more flexibility in beamforming, such as windowing, apodization, and nonlinear approaches. These systems have been used to beamform emissions induced by pulsed ultrasound at a variety of duty cycles [45]–[47], [49], [53], [61].

Other systems provide access to beamformed data, such as the Terason 2000 and the Iris 2. Farny et al. [32] implemented a modified B-mode imaging algorithm based on delay and sum beamforming to monitor cavitation activity across a span of lateral locations at a single depth from the imaging array. They noted that the beamforming performed by the Terason 2000 caused temporal and spatial variations in the mapped field when a constant source was used to generate acoustic emissions. To avoid variations of the beamformed data not associated with changes in the cavitation source, Farny et al. only used subsets of the collected cavitation emissions. Salgaonkar et al. [31] and Haworth et al. [37] employed an Iris 2 system to record emissions during a continuous-wave insonation. The system architecture of the Iris 2 allowed a discrete set of pixels to be beamformed according to (1). However each pixel within the image was formed from data acquired sequentially. Thus the images were formed from a composite set of data, analogous to standard B-mode imaging rather than a single data set akin to plane-wave B-mode imaging. As in standard B-mode imaging, artifacts can occur when the medium changes between each data acquisition. To minimize the potential for these artifacts, a large axial pixel spacing was used to reduce the number of data sets (and thus the amount of time) necessary to create the images. Additionally, several frames of data were averaged together to reduce variability associated with the stochastic nature of cavitation.

A limitation associated with data acquisition using the Terason 2000 [32], Iris 2 [31], [37], and Z.one [61] systems was that synchronization between the therapy insonation pulse and the passive data acquisition was not implemented. Although the passive algorithm (23) does not use absolute time-of-flight information during beamforming, synchronization is useful to ensure that the passive recording time coincides with the time when the emissions are incident on the passive receive array. Farny et al. [32], Salgaonkar et al. [31], and Haworth et al. [37] used continuous-wave insonation and assumed statistically stationary cavitation emissions. This assumption allows the data acquisition to occur at any time and the images created from multiple data sets can be averaged together to obtain the mean cavitation emissions. For pulsed-wave insonations, a lack of time-synchronization makes it more difficult to capture emissions as the recording buffer needs to be long enough to store data over the entire insonation pulse repetition period, or the frame rate can be carefully selected to ensure that some cavitation emissions will occur during the passive acquisition [61]. If the data acquisition system can only provide a synchronization output signal, the output signal can be used to trigger the insonation system. This scenario limits the insonation protocol, which may or may not be acceptable depending on the goals of the ultrasound insonation (e.g., a therapeutic endpoint). Even when a system allows for synchronization between the insonation and receive transducers, (23) does not use absolute time-of-flight information. Therefore the traditional trade-off between axial resolution and frequency resolution in B-mode or Doppler imaging does not occur. However, (23) is susceptible to an ambiguity in spatially-mapping cavitation activity as described in section II-B.

Requirements for the passive array are similar to those for active imaging systems, including having precise knowledge of the array’s geometry and frequency characteristics to calculate phase shifts accurately and correct for frequency sensitivity. Element spacing should be one-half wavelength or less to ensure no grating lobes. When this is not feasible, apodization or limited-angle beamforming may be necessary to reduce grating lobe artifacts. The frequency bandwidth of the passive array must contain the frequencies of interest. It should be noted that the frequency bandwidth does not need to include the insonation fundamental frequency. It may be advantageous to use an array that has a frequency bandwidth that does not include the fundamental frequency if harmonic, ultraharmonic, subharmonic, or inharmonic frequencies are of primary interest because these signals are often much smaller in amplitude than the fundamental. If the fundamental is outside the frequency bandwidth of the array, the fundamental component will be attenuated and the gain applied to the received signals can be increased to maximize the signal to noise ratio of other frequencies of interest without saturating the digitizers [42], [78]. If however, the frequency bandwidth of the passive array causes any Fourier domain signal components to be attenuated to a level below the electronic noise floor, then the received voltage signal will not be converted accurately to a received pressure or energy.

B. Geometric Considerations

A primary consideration for determining the clinical utility of passive cavitation imaging is to assess the potential distribution of cavitation activity within the body and determine the optimal orientation of the array in order to resolve cavitation activity over that area. The prior text focused predominantly on the temporal characteristics of the data acquisition. However, the geometry of the therapeutic insonation and the passive receive array is also a crucial consideration (Fig. 5).

Fig. 5.

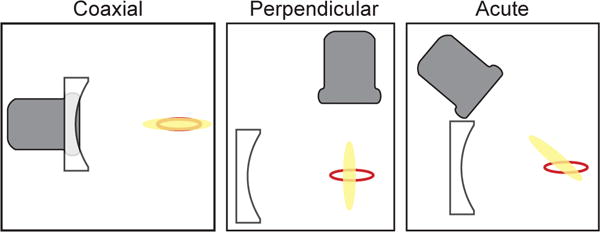
Schematics of possible alignment strategies between the imaging array (gray) and insonation transducer (white). The perimeter of the focal volume of the insonation transducer is denoted by the red line. The point-spread-function of the imaging array is shown as yellow shading. Jensen et al., [34] used a coaxial alignment, which relies on a single acoustic window (or path) through the body. However, the point-spread-function of the imaging array overlaps entirely with the focus of the insonation transducer, preventing resolution of cavitation activity at different locations within the focal volume. Perpendicular alignments have enabled the resolution of cavitation activity within the focus, but require separate acoustic paths to enable colocation of the foci [37], [43]. The acute alignment, such as the experimental setup used by Choi et al., [45] provides another option for co-alignment to resolve cavitation activity within the insonation transducer focal volume.

If the passive receive array is a standard one-dimensional clinical imaging array (e.g., a linear array or a phased array), the axial resolution of passive cavitation imaging is relatively poor due to the diffraction pattern of the array (section IV-A). Some therapy transducers have a larger axial than lateral beamwidth. Coaxial placement of the passive array with the insonation transducer will result in a limited ability to resolve cavitation activity along the axial beamwidth (see for example [34]). Depending on the clinical application, the imaging array could be oriented perpendicular to the axis of the therapy transducer. The fine lateral spatial resolution of the passive cavitation image would enable resolving cavitation along the insonation axial beamwidth [37]. A suitable acoustic window may not be available with this perpendicular setup, however. For vascular applications employing ultrasound contrast agents flowing in the lateral direction of the image, cavitation can be reasonably expected to be confined to a vessel lumen. Thus the axial resolution of the passive cavitation image is not critical, and a coaxial orientation of the array might provide the necessary image resolution along the length of the vessel (or vessel phantom) [45], [49]. Orienting the therapy transducer and the passive receive array at an acute angle may provide an acceptable compromise in certain circumstances [42], [45]. Other orientations are also possible. The diffraction pattern of hemispherical arrays [46], [52] or other geometries [90] can provide fine axial and lateral resolution for passive cavitation imaging.

C. Computational Speed

The practical implementation of (23) is fairly straightforward with an example provided in the Appendix. The application of the phase-shift at each frequency for each element can be carried out using vectorization in MATLAB to decrease the computational time (e.g., supplemental m-files). Additionally, it can been seen that each pixel is calculated independently. Therefore, the algorithm is well suited to parallelization. MATLAB offers many functions that can take advantage of parallel computing, such as general-purpose computing on graphics proocessing units (GPGPU). Additionally, the use of dedicated hardware for beamforming could further decrease processing times.

VI. Alternative Methods of Forming Passive Cavitation Images

Alternative frequency-domain approaches have also been described. Within the underwater acoustics literature, an approach termed frequency-sum beamforming was described [91]. Abadi et al. [91] had a stated goal of using delay, sum, and integrate beamforming at high frequencies to improve localization of an underwater sound source. However these authors noted that as the center frequency of the emission increases, the algorithm is more susceptible to imaging artifacts originating from inhomogeneities in the propagation path. Their approach sought to manufacture higher frequencies from a source emitting a relatively low frequency. To manufacture the higher frequencies, they proposed squaring the time-delayed signals before summation:

$${{\displaystyle \sum _{l=1}^L\left(X_l[k]\cdot e^{i2\pi k\mathrm{\Delta }f\frac{\left|{\overrightarrow{r}}_m-\overrightarrow{r}\right|}{c}}\right)}}^2.$$ (28)

When the square is propagated to each term, the exponential now has a factor of 2·k, effectively doubling the frequency and creating the higher manufactured frequency. Abadi et al. [91] were able to show that the image resolution improved by a factor of 2 as a result. Additionally, they demonstrated a fourth-order version that further improved the image resolution. However, they noted that when working with noisy data, the sidelobes had a larger amplitude with the manufactured high frequencies. Haworth et al. [56] reported that frequency-sum imaging could be implemented with a diagnostic ultrasound array and cavitation emissions from a single finite location. However when cavitation emissions originated from two discrete locations, the received emissions, X_l[k], were effectively composed of two sources, that when squared resulted in cross-terms. These cross-terms mapped cavitation activity to a location that was halfway between the sources, creating an artifact that limits the utility of this approach to cases where it is known that the acoustic emissions originate from one finite location.

Arvanitis et al. [59] recently described a passive cavitation imaging approach based on the angular spectrum method. The angular spectrum method was used to back-propagate the passively recorded cavitation emissions in the spatial frequency domain to form an image. The use of an angular spectrum method was reported to decrease the computational time by a factor of 2 or more relative to the frequency-domain delay, sum, and integrate approach when the same frequency bands were beamformed in each approach. This approach could be extended to more general wavenumber beamforming algorithms, such as the Stolt f-k migration, which have recently been explored in pulse-echo ultrasound imaging [92], [93]. Similar to Jones et al. [51], [52], [54], aberration correction can be applied to reduce imaging errors caused by propagation through a skull bone [53].

VII. Conclusion

Passive cavitation imaging is a relatively new approach that is gaining increased adoption for beamforming cavitation and other acoustic emissions. It yields spatially-resolved information about acoustic emissions. In principle, the approach can be used any time passive cavitation detection over a finite spatial extent would be useful. The approach is relatively easy to implement provided the appropriate hardware is available to record passive emissions simultaneously on the elements of an imaging array. In order to make absolute quantitative statements about the acoustic emissions, the array must be calibrated and the Fourier transforms carried out with appropriate normalization factors. The frequency domain delay, sum, and integrate approach can be used to differentiate between cavitation types at different locations simultaneously.

Biographies

Kevin J. Haworth (s’07, M’10) received the B.S. degree in physics from Truman State University in 2003 and the M.S. and Ph.D. degrees in applied physics from the University of Michigan, Ann Arbor, MI, in 2006 and 2009, respectively. Following his graduate studies he performed a postdoctoral fellowship under the tutelage of Christy K. Holland at the University of Cincinnati. He is now an Assistant Professor of Internal Medicine and Biomedical Engineering at the University of Cincinnati. He is currently directing and conducting research in medical ultrasound including the use of bubbles for diagnostic and therapeutic applications. His work includes studies of cavitation imaging and acoustic droplet vaporization for gas scavenging and imaging. Dr. Haworth is a member of the IEEE, Acoustical Society of America (ASA), and American Institute of Ultrasound in Medicine (AIUM). He serves on the Bioeffects Committee for the AIUM and on the Biomedical Acoustic Technical Committee and Public Relations Committee for the ASA.

Kenneth B. Bader received a B.S. degree in physics from Grand Valley State University in 2005 and the M.A. and Ph.D. degrees in physics from the University of Mississippi, Oxford, MS, in 2007 and 2011, respectively. Following his graduate studies he performed a postdoctoral fellowship under the tutelage of Christy K. Holland at the University of Cincinnati. He is now an Assistant Professor of Radiology at the University of Chicago. He is currently directing and conducting research in image-guided focused ultrasound therapies. Dr. Bader is a member of the Acoustical Society of America (ASA), where he serves on the Biomedical Acoustic Technical Committee and the Task Force for Membership Engagement and Diversity for the ASA.

Kyle T. Rich received the B.S. degree in physics from Northern Kentucky University in 2008. He is currently pursuing a Ph.D. degree in the Biomedical Engineering Program at the University of Cincinnati, working in the Biomedical Acoustics Lab under the direction of Dr. T. Douglas Mast. His current research includes monitoring and detection techniques for analyzing acoustic emissions from cavitation.

Christy K. Holland attended Wellesley College where she majored in Physics and Music and received the B. A. degree in 1983. Thereafter she completed an M.S. (1985), M.Phil. (1987), and Ph.D. (1989) at Yale University in Engineering and Applied Science. Dr. Holland is a Professor in the Department of Internal Medicine, Division of Cardiovascular Health and Disease, College of Medicine and Biomedical Engineering Program (BME) in the College of Engineering and Applied Science at the University of Cincinnati (UC). She directs the Image-Guided Ultrasound Therapeutics Laboratories in the UC Cardiovascular Center, which focus on applications of biomedical ultrasound including sonothrombolysis, ultrasound-mediated drug and bioactive gas delivery, development of echogenic liposomes, early detection of cardiovascular diseases, and ultrasound-image guided tumor ablation. Prof. Holland serves as the Scientific Director for the Heart, Lung, and Vascular Institute, a key component of efforts to align the UC College of Medicine and UC Health around research, education, and clinical programs. She is a fellow of the Acoustical Society of America, the American Institute of Ultrasound in Medicine, and the American Institute for Medical and Biological Engineering. She assumed the editorship of Ultrasound in Medicine and Biology, the official Journal of the World Federation for Ultrasound in Medicine and Biology, in 2006. Prof. Holland currently serves as Past-President of the Acoustical Society of America.

T. Douglas Mast (M’98) was born in St. Louis, Missouri in 1965. He received the B.A. degree (Physics and Mathematics) in 1987 from Goshen College, received the Ph.D. degree (Acoustics) in 1993 from The Pennsylvania State University, and was a postdoctoral fellow with University of Rochester’s Ultrasound Research Laboratory until 1996. From 1996 until 2001, he was with the Applied Research Laboratory of The Pennsylvania State University, where he was Research Associate and Assistant Professor of Acoustics. He was a Senior Electrical and Computer Engineer for Ethicon Endo-Surgery in Cincinnati, Ohio from 2001 until 2004. In 2004, he joined the Biomedical Engineering faculty at the University of Cincinnati, where he is currently Professor and Program Chair. His research interests include ultrasound image guidance for minimally invasive therapy, cavitation detection and imaging, therapeutic ultrasound for cancer treatment and drug delivery, simulation of ultrasound-tissue interaction, image-based biomechanics measurements, and inverse scattering. He is a Fellow of the Acoustical Society of America and a Senior Member of the American Institute of Ultrasound in Medicine.

Appendix Matlab Code for Passive Cavitation Imaging

To assist the reader in developing a better practical understanding of implementing (23) to form a passive cavitation image, four supplemental files are provided to create passive cavitation images in MATLAB. File ‘PCIBeamforming_Simulation.m’ beamforms simulated received acoustic emissions using either data saved in the matfile ‘SimData.mat’ or data that can be created de novo using the local functions ‘pelement.m’ [71] and ‘cerror.m’ [94] within ‘PCIBeamforming_Simulation.m’. The simulated data provided in ‘SimData.mat’ corresponds to a point source emitting a 20-cycle tone burst with a center frequency of 6 MHz at a distance 26 mm from a Philips L7-4 linear array. The source is centered about the linear array. The received signals were simulated using the Fresnel approximation [71] and assume transmit-receive reciprocity for the elements.

As mentioned in section II-B, the beamformed pixel amplitude is an estimation of incident energy. For the simulation provided above, the difference between the incident energy and the estimated energy is 7.4% (0.3 dB). The error is due to the signal received on each element having a different amplitude because of the complex diffraction pattern of the receive elements. If the 6 MHz signal is replaced by a 2 MHz signal, the error reduces to 1.6% (0.07 dB) because the complex diffraction pattern of the receive elements has a smaller angular dependence at lower frequencies. The simulation also can be used to obtain estimates for the point-spread function of the L7-4 array. The point-spread function associated with other array designs can be obtained by modifying the m-file to account for the appropriate receive element geometries and positions.

File ‘PCIBeamforming_Experiment.m’ beamforms experimentally measured acoustic emissions that are in file ‘ExpData.mat’. The emissions were recorded using a V-1-256 ultrasound research scanner (Verasonics Inc., Bothell, WA, USA) and a Philips L7-4 linear array. The cavitation emissions originated from Definity microbubbles (Lantheus Medical Imaging, Inc., N. Billerica, MA, USA) pumped through tubing and insonified with 6 MHz pulsed ultrasound at a pressure amplitude sufficient to produce subharmonic emissions (indicative of stable cavitation). The scattered emissions include both cavitation emissions and scattering from the tubing.

Both beamforming m-files neglect the element sensitivity, M[k], in (23). For plotting the images on a decibel scale, the small non-physical negative energies that occur due to the “DC bias” subtraction are set to small positive values. An optional flag allows the user to decide whether they wish to include cosine apodization across the receive elements (see section IV-B). The m-files use the ability of MATLAB to implement vectorization to remove <ms>for</ms> loops and decrease the computational time.