Abstract

Cellulose is the most abundant biopolymer on Earth. Cellulose fibers, such as the one extracted form cotton or woodpulp, have been used by humankind for hundreds of years to make textiles and paper. Here we show how, by engineering light–matter interaction, we can optimize light scattering using exclusively cellulose nanocrystals. The produced material is sustainable, biocompatible, and when compared to ordinary microfiber-based paper, it shows enhanced scattering strength (×4), yielding a transport mean free path as low as 3.5 μm in the visible light range. The experimental results are in a good agreement with the theoretical predictions obtained with a diffusive model for light propagation.
Keywords: cellulose nanocystals, photonics, scattering, photonic glass, diffusion, disorder
Introduction
With the term “paper”, we include a large variety of cellulose-based composite materials that find use in everyday life such as packaging and printing. Recently, paper-based technologies have captivated increasing interest not only due to their applications in sensing1−3 and lasing,4 but also in 3D cell scaffolding.5 Cellulose can be easily functionalized to produce materials with enhanced mechanical, optical, and chemical properties because of its intrinsic fibrillary morphology and consequent porosity. These new materials are particularly attractive from an industrial point of view thanks to their low production costs.6
The main component of paper is cellulose.7 Natural cellulose can be extracted from different sources: ranging from plants (such as wood pulp or cotton) to bacteria, to invertebrates and some marine animals,8 nonetheless it is consistently found to have fibrillary nature.9 Such natural fibers are generally composed of amorphous and crystalline regions, see Figure 1a. In the paper-manufacturing process, moist cellulose fibers extracted from natural sources are compressed together and dried. The thickness of the fibers and their packing density determine the optical response of the material.7 Conventional fibers in paper are several tens of microns in diameter and therefore, they are not ideal to produce a strong scattering response, Figure 1b–d. By acid hydrolysis, a crystalline region, called cellulose nanocrystals (CNCs) can be extracted and suspended in water.8 CNCs can be considered as rod-shaped colloidal particles typically 150 nm in length and a few nm in diameter10 (Figure 1e), with a significantly high refractive index (about 1.55 in the visible range). CNCs have received an increase interest in photonics, because of their colloidal behavior and their ability to self-assemble into cholesteric optical films.11,12
Figure 1.
Structure and fabrication. A molecular chain of cellulose and a diagram showing the hierarchical structure of a cellulose chain is illustrated in panel a. Cellulose fiber is composed of fibrils (orange cylinder) with alternating crystalline (dark green rods) and amorphous (light green spheres) sections. On the top, (b) cellulose fibers used to fabricate (d) white paper whose fibrous structure is shown in (c) the SEM image. On the bottom, (e) cellulose nanocrystals that can be (g) self-assembled in the shape of a photonic glass structure by polystyrene sphere templating, and (f) the respective SEM image.
Although CNCs have been intensively studied for structural color applications,13 such materials have never been exploited to maximize scattering. Maximal scattering strength is, in fact, challenging to obtain. Optimal scattering design comes from the balance of scatterers’ size, refractive index contrast and filling fraction. Therefore, it is fulfilled for dielectric particles of diameters comparable with the wavelength of light packed with maximal density assuring also a high refractive index contrast between the scatters and their surrounding environment.
Scattering is measured
via the transport mean free path (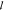 t), the length beyond which the
propagation is randomized, which for paper is typically of the order
of 20 μm.14 Maximal scattering, which
means minimal
t), the length beyond which the
propagation is randomized, which for paper is typically of the order
of 20 μm.14 Maximal scattering, which
means minimal 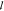 t, is an important technological
goal for producing whiter and more opaque materials. More efficient
scattering implies that a smaller quantity of material is needed to
achieve the same white coating.
t, is an important technological
goal for producing whiter and more opaque materials. More efficient
scattering implies that a smaller quantity of material is needed to
achieve the same white coating.
Here, we report the bottom-up fabrication technique for the production of a new scattering paper-like material. Unlike conventional paper, our starting material is the smallest constituent of cellulose: the cellulose nanocrystal11 (Figure 1a). We produce a nanostructure made solely of CNCs capable of improved light–matter interactions, due to its much smaller feature size (Figure 1e–g).
Results
By characterizing the scattering response of the CNC-based photonic glass we obtain 400% stronger scattering than for standard cellulose fiber paper. The experimental results compare well with a diffusive model. Furthermore, we estimate the optimum fabrication conditions for maximum scattering and opacity, and point out a possible strategy to minimize costs.
A cellulose inverse photonic glass15,16 is fabricated using a templating technique that consists in the codeposition of monodisperse PS spheres and CNCs and subsequential chemical etching of the PS spheres. This geometry is particularly convenient to optimize light-matter interaction because provides the right balance between the size of the scattering elements (at the edge of the spherical voids), and a high filling fraction.16 Commercial cellulose nanocrystals (Forest Product Laboratory Canada) are extracted by sulfuric acid treatment of wood-pulp, leaving negative charged sulfate half-esters which are neutralized with Na+ ions. The dimension of the colloids is around 5 nm in diameter and ranges from 150 to 200 nm in length. The pH of the suspension is neutral, whereas the surface change is 278 ± 1 mmol/kg estimated by conductometric titration.17 The scanning electron microscope (SEM) image in Figure 1e shows the characteristic needlelike geometry of the CNCs.
A 4%wt CNCs aqueous solution (deionized water) is mixed with colloidal monodisperse polystyrene (PS) spheres of diameter d = 1.27 μm (Micro particles GmbH), such that the dry weight ratio between CNCs and PS spheres is 2:3, respectively. The obtained suspension is then cast into a hollow Teflon cylinder attached to a glass substrate with PS as in reference.18 Prior to this, the Teflon cylinder is immerged in a NaOH bath to improve the hydrophilicity of its surfaces, while the glass is coated with PS to stabilize the film (to avoid cracking during drying).
The samples are kept in partially sealed containers and dried for 1–2 week(s) in a quasi-saturated water vapor atmosphere kept at a constant temperature (30 °C). Such conditions allow a slow evaporation rate which further improves the film quality by avoiding cracking and delamination. Once the sample is dry, the PS spheres are selectively etched in a bath of toluene for approximately 3–9 h, depending on the sample thickness (50–500 μm). Toluene also removes the PS coating substrate and separates the Teflon cylinder from the glass; this facilitates the detachment of the sample, yielding a free-standing cellulose inverse photonic glass, a nanostructured paper (Figure 1g). The CNCs properties are unaffected by the toluene bath,19,20 as confirmed by the transmission experiments conducted for a timespan of over 10 h, showing no significant transmission change.
After the drying process, a random close-pack arrangement is formed, confirmed by SEM inspection (Figure 1f) and optically by the lack of iridescence and enhanced normal reflection. The only observable change is a minor reflection from the surface in contact with the glass i.e. where the cellulose layer is more compact. The resulting cellulose inverse photonic glass is shown in Figure 2. An SEM image of the structure reveals spherical voids of diameter around 1.3 μm (where the PS spheres were present prior to etching), as well as circular openings characteristic of a close packed structure, (in correspondence of the position where the PS spheres touched each other before template removal). We observe that such topology is homogeneous throughout the sample, as further confirmed by transmission studies on different areas of the sample (see later). In addition, a photograph of one of the samples fabricated is shown in Figure 1g (approximately 1.5 cm in diameter and 100 μm thick): the increased opaqueness of the photonic glass paper is visible even by the naked eye, when compared to conventional paper of similar thickness (Figure 1d).
Figure 2.

Sample morphology. The panel on the top reports an overview of the sample showing it is porous on a large scale. When imaged at higher magnification (bottom panel), it is possible to observe the micrometre-sized voids formed around the etched spheres. Smaller pores connecting the voids are visible, formed when the PS spheres were touching. The larger voids in the image are introduced when the sample is cut and prepared for SEM imaging.
We compare the scattering
properties of CNCs photonic glass and
common cellulose fiber paper by measuring 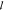 t, by means of total transmission
measurements (T) performed with an integrating sphere
which collects the transmitted flux over all angles.20 The measured light is sent to a spectrometer which provides
spectral information. The photonic Ohm’s law,21,22 which is described by the change in total transmission (T) as a function of the sample thickness (L), is obtained via the stationary solution of the diffusion equation
(assuming a slab geometry)15,21
t, by means of total transmission
measurements (T) performed with an integrating sphere
which collects the transmitted flux over all angles.20 The measured light is sent to a spectrometer which provides
spectral information. The photonic Ohm’s law,21,22 which is described by the change in total transmission (T) as a function of the sample thickness (L), is obtained via the stationary solution of the diffusion equation
(assuming a slab geometry)15,21
| 1 |
where α
= 1/ 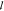 a is the reciprocal of the absorption
length
a is the reciprocal of the absorption
length 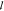 a,ze is the extrapolation length and zp is
the penetration length, typically taken to be equal with
a,ze is the extrapolation length and zp is
the penetration length, typically taken to be equal with 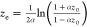 and
and 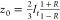 . R is the averaged reflectivity
(R = 0.39 assuming a filling fraction of ∼55%
and n = 1.55).
. R is the averaged reflectivity
(R = 0.39 assuming a filling fraction of ∼55%
and n = 1.55).
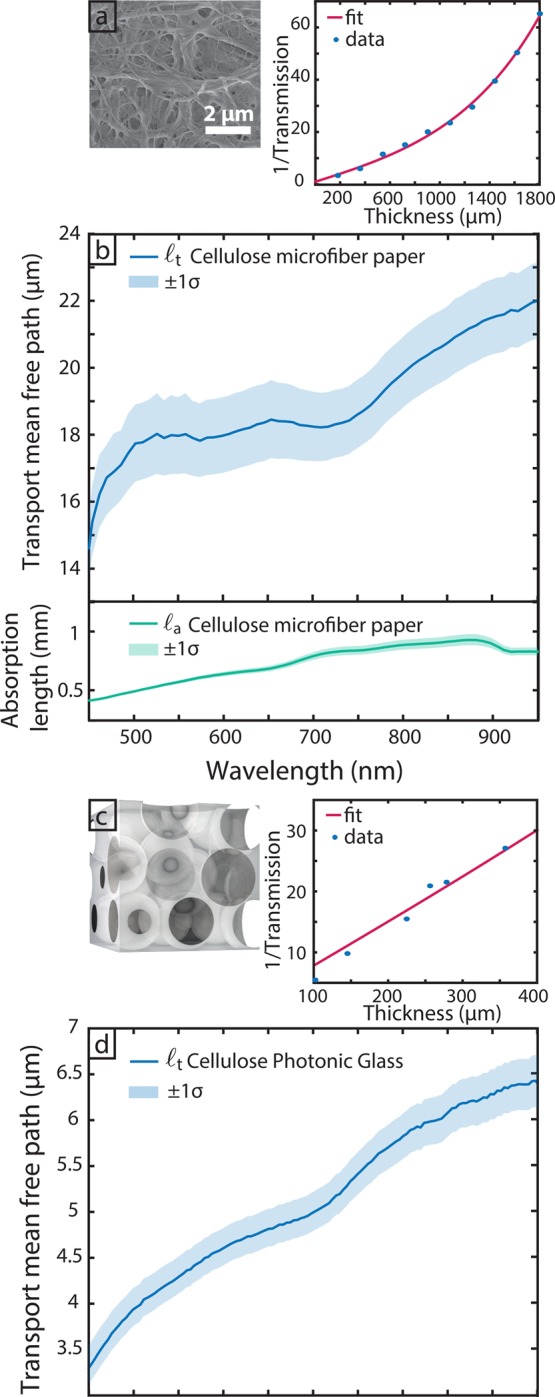
The microfiber paper used is
Whatman filter paper, grade 1, with
a reported thickness of 180 μm confirmed by SEM inspection.
While for the paper photonic glass it was possible to produce samples
of different thicknesses, for cellulose fiber paper multiple sheets
of paper had to be compressed together in order to increase the overall
thickness. The transmission spectra of cellulose fiber paper, averaged
over 3 measurements, were fitted with eq 1 for each wavelength as shown in Figure 3a and b. A typical fit at λ = 600 nm
is plotted in Figure 3a highlighting the exponential dependence of the inverse transmission
(1/T) on the thickness (L) due to
absorption. Here, 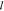 t and
t and 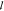 a are estimated by a two-parameter
fit of eq 1. We use a
multistep fitting routing: 1.
a are estimated by a two-parameter
fit of eq 1. We use a
multistep fitting routing: 1. 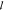 t and
t and 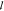 a are taken as free parameters
of the fit to obtain approximate values for each wavelength; 2. each
parameter is fitted independently using the other parameter as an
input, until convergence is achieved (after 4 iterations). Furthermore,
the fitted value from each wavelength is used as the starting point
of the consequent one to improve the convergence. The measured
a are taken as free parameters
of the fit to obtain approximate values for each wavelength; 2. each
parameter is fitted independently using the other parameter as an
input, until convergence is achieved (after 4 iterations). Furthermore,
the fitted value from each wavelength is used as the starting point
of the consequent one to improve the convergence. The measured 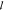 t ranges between 15 and 22 μm
in the visible spectra as depicted in Figure 3b), whereas
t ranges between 15 and 22 μm
in the visible spectra as depicted in Figure 3b), whereas 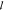 a is of the order of a millimeter.
The measured
a is of the order of a millimeter.
The measured 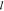 t is an underestimation of the
actual value, although the air gaps between the sheets are expected
to increase the apparent
t is an underestimation of the
actual value, although the air gaps between the sheets are expected
to increase the apparent 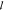 t, we estimate by microscopy
inspection that they are less than 10% of the sample thickness. The
reflection at each interface (about 40% for each sheets), on the other
hand, is a more significant effect that increases the total reflectivity,
thus lowering the transmission and increasing the measured
t, we estimate by microscopy
inspection that they are less than 10% of the sample thickness. The
reflection at each interface (about 40% for each sheets), on the other
hand, is a more significant effect that increases the total reflectivity,
thus lowering the transmission and increasing the measured 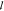 t.
t.
Figure 3.
Measured scattering strength. (a) Cellulose microfibre paper SEM and fit of the total transmission data at different thicknesses (λ = 600 nm). (b) Measurement of the light transport mean free path (blue) and absorption length (green) for microfiber paper. The error bars are shown by the shaded area around the lines, for both fitting parameters. (c) Model of structure of a cellulose inverse photonic glass and fit of the total transmission data at different thicknesses (λ = 600 nm). (d) Measurements of the light transport mean free path for the inverse cellulose photonic glass. The error bars are shown by the blue shaded area around the line.
The measurement of 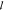 t in the case of the photonic
glass paper was performed by comparing samples with different thicknesses
(Figure 3c) in the
range 100–400 μm. Such thicknesses are estimated by SEM.
The values of the thickness are averaged over different areas on the
sample, with an error of around 5%. The transmission spectra of the
cellulose photonic glass are averaged over different regions of the
sample and a dispersion less than 5% is measured. Using the same procedure
depicted above, the data is fitted with eq 1. As
t in the case of the photonic
glass paper was performed by comparing samples with different thicknesses
(Figure 3c) in the
range 100–400 μm. Such thicknesses are estimated by SEM.
The values of the thickness are averaged over different areas on the
sample, with an error of around 5%. The transmission spectra of the
cellulose photonic glass are averaged over different regions of the
sample and a dispersion less than 5% is measured. Using the same procedure
depicted above, the data is fitted with eq 1. As 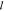 a in these samples is much larger
than the sample thickness, lossless Ohm’s law is valid, as
shown in Figure 3c.
Therefore, for simplicity and stability of the fit, we choose α
= 0. Figure 3d shows
a in these samples is much larger
than the sample thickness, lossless Ohm’s law is valid, as
shown in Figure 3c.
Therefore, for simplicity and stability of the fit, we choose α
= 0. Figure 3d shows 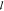 t obtained as a function of wavelength.
The statistical error of the fit, accredited to minor sample-to-sample
variation, is estimated to be less than 10%. As expected,
t obtained as a function of wavelength.
The statistical error of the fit, accredited to minor sample-to-sample
variation, is estimated to be less than 10%. As expected, 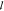 t decreases toward shorter wavelengths
as predicted by Mie theory (see later). The measured
t decreases toward shorter wavelengths
as predicted by Mie theory (see later). The measured 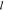 t is in the range
t is in the range 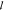 t ≈ 3–7 μm
for the visible range with very shallow resonances. The lack of resonances
is expected, as air voids in a higher refractive index matrix are
poor resonators, in contrast with high refractive index spheres which
show appreciably stronger resonances.15,18 The scattering
strength of the photonic glass paper is significantly stronger:
t ≈ 3–7 μm
for the visible range with very shallow resonances. The lack of resonances
is expected, as air voids in a higher refractive index matrix are
poor resonators, in contrast with high refractive index spheres which
show appreciably stronger resonances.15,18 The scattering
strength of the photonic glass paper is significantly stronger: 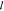 t is 4 times smaller than that
measured for cellulose fiber paper.
t is 4 times smaller than that
measured for cellulose fiber paper.
The theoretical calculations are performed via Mie theory and independent scattering approximation, taking into account the polydispersity of the PS spheres.23,24 Comparing to previous work16 we expect the photonic glass paper to have a filling fraction around f = 50–55%, smaller than the theoretical limit for hard-sphere random packing.25 The comparison between the theoretical results for different degrees of polydispersity is shown in Figure 4. Because the resonances are weak, they are unaffected by the small polydispersity.
Figure 4.
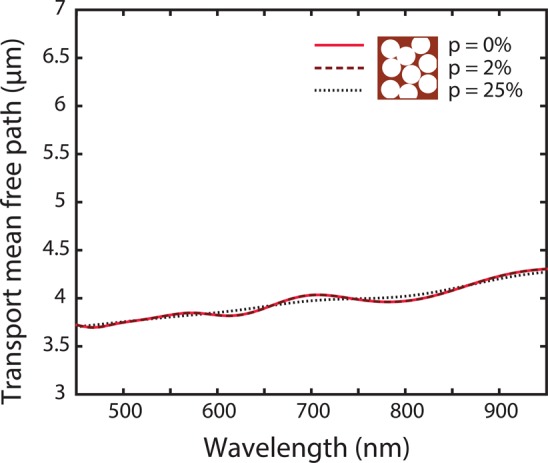
Modeling experimental results. Theoretical transport mean free path calculated for air spheres in cellulose matrix ncellulose = 1.55 at a filling fraction of f = 0.55 as a function of wavelength (full red line) assuming polydispersity of 2% (dashed red line) and assuming a polydispersity of 25% (dashed black line).
We use the Mie model
to investigate the optimum void diameter required
to maximize scattering. Figure 5 plots  t for different void diameters
(at a wavelength of λ = 600 nm), both in the absence of polydispersity
and at 2% polydispersity. At d = 250 nm,
t for different void diameters
(at a wavelength of λ = 600 nm), both in the absence of polydispersity
and at 2% polydispersity. At d = 250 nm,  t is at its lowest value, around
1.3 μm, whereas for smaller diameters,
t is at its lowest value, around
1.3 μm, whereas for smaller diameters,  t increases rapidly for decreasing d, as dictated
by Rayleigh scattering. Although scattering
may be increased by using smaller PS sphere to nanostructure the CNCs,
smaller CNCs than the ones used here are required to ensure maximal
close-packing of the sphere and consequently stronger scattering and
a lower
t increases rapidly for decreasing d, as dictated
by Rayleigh scattering. Although scattering
may be increased by using smaller PS sphere to nanostructure the CNCs,
smaller CNCs than the ones used here are required to ensure maximal
close-packing of the sphere and consequently stronger scattering and
a lower  t.
t.
Figure 5.
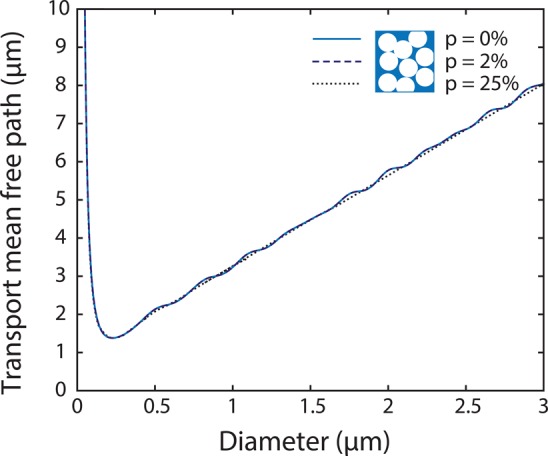
Theoretical scattering strength with different void diameter. Theoretical transport mean free path calculated for air spheres in cellulose matrix ncellulose = 1.55 at a filling fraction of f = 0.55, as a function of different void diameters at λ = 600 nm.
Polydisperse PS spheres are cheaper
and easier to produce than
its monodisperse counterpart, therefore we explore here the effect
of polydispersity in the templating matrix. Our calculations show
that even for large polydispersity, as high as 25%, the average value
of  t is unaffected, only the resonances
are damped, as shown by the dotted black line in Figure 4 and 5.
t is unaffected, only the resonances
are damped, as shown by the dotted black line in Figure 4 and 5.
Conclusions
In conclusion, we have presented a highly scattering
nanostructured
CNCs paper with  t = 3–7 μm. The
inverse photonic glass made of CNC scatters 4 times more than standard
cellulose fiber paper. By post-treatment of the film, or by adding
other materials in suspension, the properties of the produced photonic
glass can be further improved in terms of mechanical properties and
moisture-resistance.26−29 Increased scattering implies that the same visual contrast and whiteness
can be achieved in a thinner sample. With a simple theoretical model,
we identify the optimum sphere diameter of about half the light wavelength,
for which the scattering strength can be maximized. Large scattering
strength allows for larger contrast in sensors, thinner paper, which
would reduce coating and packaging. Furthermore, nanophotonic enhanced
paper offers the additional benefit of large porosity together with
increased light–matter interaction.
t = 3–7 μm. The
inverse photonic glass made of CNC scatters 4 times more than standard
cellulose fiber paper. By post-treatment of the film, or by adding
other materials in suspension, the properties of the produced photonic
glass can be further improved in terms of mechanical properties and
moisture-resistance.26−29 Increased scattering implies that the same visual contrast and whiteness
can be achieved in a thinner sample. With a simple theoretical model,
we identify the optimum sphere diameter of about half the light wavelength,
for which the scattering strength can be maximized. Large scattering
strength allows for larger contrast in sensors, thinner paper, which
would reduce coating and packaging. Furthermore, nanophotonic enhanced
paper offers the additional benefit of large porosity together with
increased light–matter interaction.
Acknowledgments
The authors thank Michele Gaio, Giulia Guidetti, and Bruno Frka-Petesic for the fruitful discussions. This research was funded by the EPSRC (EP/M027961/1), the Leverhulme Trust (RPG-2014-238), Royal Society (RG140457), the BBSRC David Phillips fellowship (BB/K014617/1), and the European Research Council (ERC-2014-STG H2020 639088). All data created during this research are provided in full in the results section and Supporting Information. They are openly available from figshare and can be accessed at ref (30).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.6b15986.
Additional figure (PDF)
Author Present Address
‡ M.P. is currently at Institute of Science and Technology Austria (IST Austria), 3400 Klosterneuburg, Austria
The authors declare no competing financial interest.
Supplementary Material
References
- Nie Z.; Nijhuis C. A.; Gong J.; Chen X.; Kumachev A.; Martinez A. W.; Narovlyansky M.; Whitesides G. M. Electrochemical Sensing in Paper-based Microfluidic Devices. Lab Chip 2010, 10, 477–483. 10.1039/B917150A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delaney J. L.; Hogan C. F.; Tian J.; Shen W. Electrogenerated Chemiluminescence Detection in Paper-Based Microfluidic Sensors. Anal. Chem. 2011, 83 (4), 1300–1306. 10.1021/ac102392t. [DOI] [PubMed] [Google Scholar]
- Yan C.; Wang J.; Kang W.; Cui M.; Wang X.; Foo C. Y.; Chee K. J.; Lee P. S. Highly Stretchable Piezoresistive Graphene-Nanocellulose Nanopaper for Strain Sensors. Adv. Mater. 2014, 26, 2022–2027. 10.1002/adma.201304742. [DOI] [PubMed] [Google Scholar]
- Derda R.; Laromaine A.; Mammoto A.; Tang S. K. Y.; Mammoto T.; Ingber D. E.; Whitesides G. M. Paper-supported 3D Cell Culture for Tissue-based Bioassays. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (44), 18457–18462. 10.1073/pnas.0910666106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viola I.; Ghofraniha N.; Zacheo A.; Arima V.; Conti C.; Gigli G. Random Laser Emission from a Paper-based Device. J. Mater. Chem. C 2013, 1, 8128–8133. 10.1039/c3tc31860e. [DOI] [Google Scholar]
- Moon R. J.; Martini A.; Nairn J.; Simonsen J.; Youngblood J. Cellulose Nanomaterials review: Structure, properties and Nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. 10.1039/c0cs00108b. [DOI] [PubMed] [Google Scholar]
- Hubbe M. A.; Pawlak J. J.; Koukoulas A. A. Paper’s appearance: A review. BioResources 2008, 3 (2), 627–665. [Google Scholar]
- Habibi Y.; Lucia L. A.; Rojas O. J. Cellulose Nanocrystals: Chemistry, Self-assembly, and Applications. Chem. Rev. 2010, 110 (6), 3479–3500. 10.1021/cr900339w. [DOI] [PubMed] [Google Scholar]
- Eichhorn S. J.; Dufresne A.; Aranguren M.; Marcovich N. E.; Capadona J. R.; Rowan S. J.; Weder C.; Thielemans W.; Roman M.; Renneckar S.; Gindl W.; Veigel S.; Keckes J.; Yano H.; Abe K.; Nogi M.; Nakagaito A. N.; Mangalam A.; Simonsen J.; Benight A. S.; Bismarck A.; Berglund L. A.; Peijs T. Review: Current International Research into Cellulose Nanofibres and Nanocomposites. J. Mater. Sci. 2010, 45, 1–33. 10.1007/s10853-009-3874-0. [DOI] [Google Scholar]
- Mariano M.; El Kissi N.; Dufresne A. Cellulose Nanocrystals and Related Nanocomposites: Review of some Properties and Challenges. J. Polym. Sci., Part B: Polym. Phys. 2014, 52, 791–806. 10.1002/polb.23490. [DOI] [Google Scholar]
- Fernandes S. N.; Almeida P. L.; Monge N.; Aguirre L. E.; Reis D.; de Oliveira C. L. P.; Neto A. M. F.; Pieranski P.; Godinho M. H. Mind the Microgap in Iridescent Cellulose Nanocrystal Films. Adv. Mater. 2017, 29, 1603560. 10.1002/adma.201603560. [DOI] [PubMed] [Google Scholar]
- Shopsowitz K. E.; Qi H.; Hamad W. Y.; MacLachlan M. J. Free-standing Mesoporous Silica Films with Tunable Chiral Nematic structures. Nature 2010, 468, 422–425. 10.1038/nature09540. [DOI] [PubMed] [Google Scholar]
- Middleton R.; Steiner U.; Vignolini S. In Bio-inspired Polymers; Bruns N., Kilbinger A. F. M., Eds.; The Royal Society of Chemistry: Croydon, U.K., 2017; Chapter 17, pp 555–585. [Google Scholar]
- Burresi M.; Cortese L.; Pattelli L.; Kolle M.; Vukusic P.; Wiersma D. S.; Steiner U.; Vignolini S. Bright-white Beetle Scales Optimise Multiple Scattering of light. Sci. Rep. 2014, 4, 6075. 10.1038/srep06075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia P. D.; Sapienza R.; Bertolotti J.; Martín M. D.; Blanco Á.; Altube A.; Viña L.; Wiersma D. S.; López C. Resonant Light Transport through Mie Modes in Photonic Glasses. Phys. Rev. A: At., Mol., Opt. Phys. 2008, 78, 023823. 10.1103/PhysRevA.78.023823. [DOI] [Google Scholar]
- Garcia P. D.; Sapienza R.; Blanco Á.; López C. Photonic Glass: A Novel Random Material for Light. Adv. Mater. 2007, 19, 2597–2602. 10.1002/adma.200602426. [DOI] [Google Scholar]
- Beck S.; Methot M.; Bouchard J. General Procedure for Determining Cellulose Nanocrystal Sulfate Half-Ester Content by Conductometric Titration. Cellulose 2015, 22, 101–116. 10.1007/s10570-014-0513-y. [DOI] [Google Scholar]
- Caixeiro S.; Gaio M.; Marelli B.; Omenetto F. G.; Sapienza R. Silk-Based Biocompatible Random Lasing. Adv. Opt. Mater. 2016, 4 (7), 998–1003. 10.1002/adom.201600185. [DOI] [Google Scholar]
- Heux L.; Chauve G.; Bonini C. Nonflocculating and Chiral-Nematic Self-ordering of Cellulose Microcrystals Suspensions in Nonpolar Solvents. Langmuir 2000, 16 (21), 8210–8212. 10.1021/la9913957. [DOI] [Google Scholar]
- Frka-Petesic B.; Jean B.; Heux L. First Experimental Evidence of a Giant Permanent Electric-dipole Moment in Cellulose Nanocrystals. EPL 2014, 107, 28006. 10.1209/0295-5075/107/28006. [DOI] [Google Scholar]
- Garcia N.; Genack A. Z.; Lisyansky A. A. Measurement of the Transport Mean Free Path of Diffusing Photons. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46, 14475. 10.1103/PhysRevB.46.14475. [DOI] [PubMed] [Google Scholar]
- Durian D. J. Influence of Boundary Reflection and Refraction on Diffusive Photon Transport. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1994, 50, 857–866. 10.1103/PhysRevE.50.857. [DOI] [PubMed] [Google Scholar]
- Bohren C. F.; Huffman D. In Absorption and Scattering of Light by Small Particles; Wiley: New York, 1983. [Google Scholar]
- Gaio M.; Peruzzo M.; Sapienza R. Tuning Random Lasing in Photonic Glasses. Opt. Lett. 2015, 40 (7), 1611–1614. 10.1364/OL.40.001611. [DOI] [PubMed] [Google Scholar]
- Song C.; Wang P.; Makse H. A. A Phase Diagram for Jammed Matter. Nature 2008, 453, 629–632. 10.1038/nature06981. [DOI] [PubMed] [Google Scholar]
- Giese M.; Blusch L. K.; Khan M. K.; Hamad W. Y.; MacLachlan M. J. Responsive Mesoporous Photonic Cellulose Films by Supramolecular Cotemplating. Angew. Chem., Int. Ed. 2014, 53, 8880–8884. 10.1002/anie.201402214. [DOI] [PubMed] [Google Scholar]
- Guidetti G.; Atifi S.; Vignolini S.; Hamad W. Y. Flexible Photonic Cellulose Nanocrystal Films. Adv. Mater. 2016, 28 (45), 10042–10047. 10.1002/adma.201603386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gicquel E.; Martin C.; Yanez J. G.; Bras J. Cellulose Nanocrystals as New Bio-based Coating Layer for Improving Fiber-based Mechanical and Barrier Properties. J. Mater. Sci. 2017, 52 (6), 3048–3061. 10.1007/s10853-016-0589-x. [DOI] [Google Scholar]
- Rodionova G.; Lenes M.; Eriksen O.; Gregersen O. Surface Chemical Modification of Microfibrillated Cellulose: Improvement of Barrier Properties for Packaging Applications. Cellulose 2011, 18, 127–134. 10.1007/s10570-010-9474-y. [DOI] [Google Scholar]
- Caixeiro S.; Peruzzo M.; Onelli O. D.; Vignolini S.; Sapienza R. Disordered Cellulose-based Nanostructures for Enhanced Light-scattering. ACS Appl. Mater. Interfaces 2017, 10.1021/acsami.6b15986. [DOI] [PMC free article] [PubMed] [Google Scholar]; See Figshare DOI: 10.6084/m9.figshare.4598239.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



