Significance
When making decisions, humans and other primates move their eyes freely to gather information about their environment. A large literature has explored the factors that determine where the eyes fall during natural scene perception and visual search, concluding that deviant or surprising perceptual information attracts attention and gaze. Here, we describe a sampling policy that paradoxically shows that in a decision-making task, the eyes are attracted to expected rather than unexpected information: When classifying the average of an array of numbers, human observers looked by preference at the numbers that were closest to the mean. This policy drove a behavioral tendency to discount the influence of outliers when making choices, leading to “robust” choices about the stimulus array.
Keywords: decision-making, categorization, eye movements, numerical averaging, information sampling
Abstract
Humans move their eyes to gather information about the visual world. However, saccadic sampling has largely been explored in paradigms that involve searching for a lone target in a cluttered array or natural scene. Here, we investigated the policy that humans use to overtly sample information in a perceptual decision task that required information from across multiple spatial locations to be combined. Participants viewed a spatial array of numbers and judged whether the average was greater or smaller than a reference value. Participants preferentially sampled items that were less diagnostic of the correct answer (“inlying” elements; that is, elements closer to the reference value). This preference to sample inlying items was linked to decisions, enhancing the tendency to give more weight to inlying elements in the final choice (“robust averaging”). These findings contrast with a large body of evidence indicating that gaze is directed preferentially to deviant information during natural scene viewing and visual search, and suggest that humans may sample information “robustly” with their eyes during perceptual decision-making.
A well-validated computational framework argues that decisions are made by integrating information toward a threshold, at which point a response is made (1, 2). Within this integration-to-bound framework, decisions are optimized by sequential sampling, at the cost of delaying responding (3). Studies using this framework in conjunction with psychophysical tasks have suggested that humans and monkeys make approximately optimal perceptual category judgments, with choice accuracy limited mainly by sensory noise or uncertainty in the external world (2, 4, 5). These psychophysical studies have been argued to offer a window on the general mechanisms by which humans make decisions (6).
However, paradigms in which stimulation is continuously available and controlled exclusively by the experimenter differ from everyday choices in real-world environments. For example, in the random dot motion (RDM) paradigm, subjects passively sample from a single, continuous, centrally presented stream of information and decide whether average dot motion tends in one direction or another (7). By contrast, decisions about the average feature in a natural scene are made by actively saccading (or covertly attending) to successive image locations and sampling the subset of information that is available there. For example, a foraging monkey might move its eyes freely to several locations in the forest canopy and average the available fruit yield to decide where to move. Real-world category decisions, thus, are affected not only by the quality of the sensory information and the dynamics of integration, but also by the policy that dictates how information is sampled and weighted when forming a decision. However, the nature of this policy remains largely unknown.
The determinants of saccadic eye movements have been extensively investigated during visual search (8) and natural scene perception (9). In visual search tasks, eye movements are attracted to image locations that contain perceptually salient or surprising items (10, 11) or to those points at which task-relevant information is maximal (12–15). In value-based choice tasks, in which for example participants judge which of two or more food items is preferred, choices and eye movements are interlinked, in that items that are fixated more frequently are chosen more often (16, 17). Other models have suggested that more uncertain sources are sampled more thoroughly with the eyes (18) or that decisions and information-gathering mutually drive one another in a reciprocal cascade (19). However, little is known about the policy by which participants sample information during choice tasks that involve integrating decision information from multiple locations across the visual field. Various studies have investigated the sampling policy in differing domains, such as category learning (20) and classification tasks (21). Recently, researchers have highlighted the importance of investigating evidence accumulation as an active sampling process (22). We investigated this sampling process by measuring eye movements while human participants performed a categorization task that involved averaging numbers in a spatial array. We used fully visible symbolic numbers as stimuli, allowing us to assess how gaze placement was determined by the statistics of decision information, rather than the perceptual arrangement of the stimulus array.
When averaging perceptual features across multiple locations under central fixation, participants tend to downweight or ignore extreme values, such as a deviant expression in a crowd of faces (23) or outlying color values in an array of shapes (24). This has led to the proposal that “inlying” items (those that are closer to the category boundary) are processed with higher gain than outliers (24, 25). However, a related possibility is that observers tend to sample by preference those items that are closer to the category boundary. Testing this theory, we found humans prefer to fixate the inlying items in a stimulus array during a perceptual decision-making task—a policy that contradicts the well-established preference for fixating deviant items in visual search tasks. This “robust” sampling policy drove decisions to ignore or discount outlying information during perceptual decisions.
Results
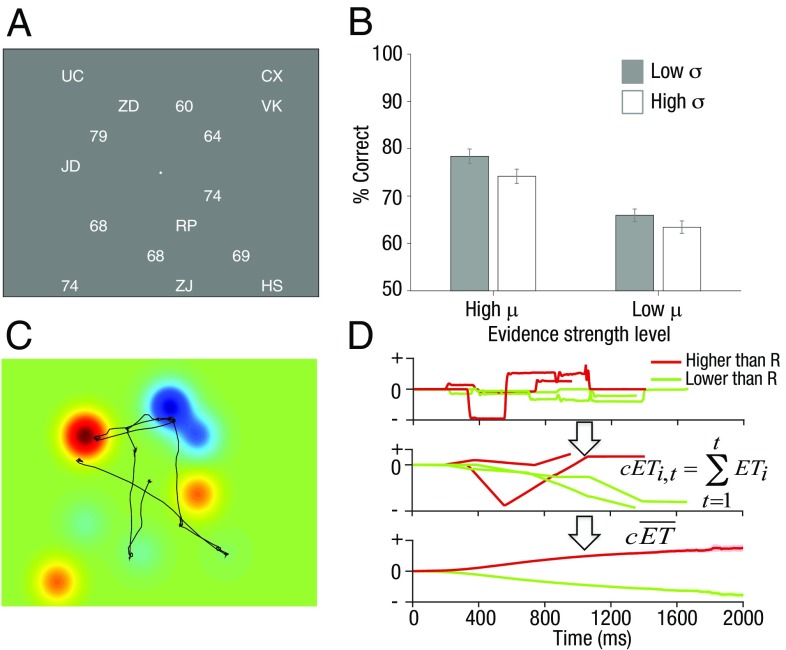
Participants (n = 54) viewed eight two-digit numbers distributed quasirandomly around the screen (Fig. 1A). Numbers were drawn from a distribution with mean µ and SD σ, and participants were asked to compare their average to a reference value R that varied across blocks (µ = R ± 2 or R ± 4 in low and high µ trials, respectively, and σ = 6 or 12 in low and high σ trials, respectively). Half of the participants indicated whether the average was higher (or not) than the reference; the others indicated whether the average was lower (or not). Numbers were interspersed among task-irrelevant items (letters), which introduced a gentle crowding effect and encouraged shifts of gaze during decision formation. By tracking gaze during task performance, we were able to ask how the information sampled with the eyes related to decisions, with a focus on whether participants sampled by preference those numbers that were inlying (close to reference) or outlying (far from reference).
Fig. 1.
Average accuracy and demonstration of the landscape approach. (A) Example trial display. Participants could sample the numbers freely by moving their eyes and had to indicate whether the average of all of the numbers on the screen was higher or lower than the reference value. (B) Performance increased for higher µ and lower σ. Bars are shown with 95% confidence intervals. (C) Landscape was created by convolving each stimulus location with a bivariate Gaussian basis function. Evidence landscape was created by setting the height of the Gaussian associated with each number location equal to the number value – reference value (Vk – R). The integral of gaze (black line) under these landscapes is used to calculate the ET. (D, Top) ET over time for four example trials (lines). (Middle) The cumulative ET over time (t) for these four example trials (i). (Bottom) The cumulative ET time series averaged across trials. Cumulative ET is on average positive when participants responded higher than reference and negative when participants responded lower than reference (green).
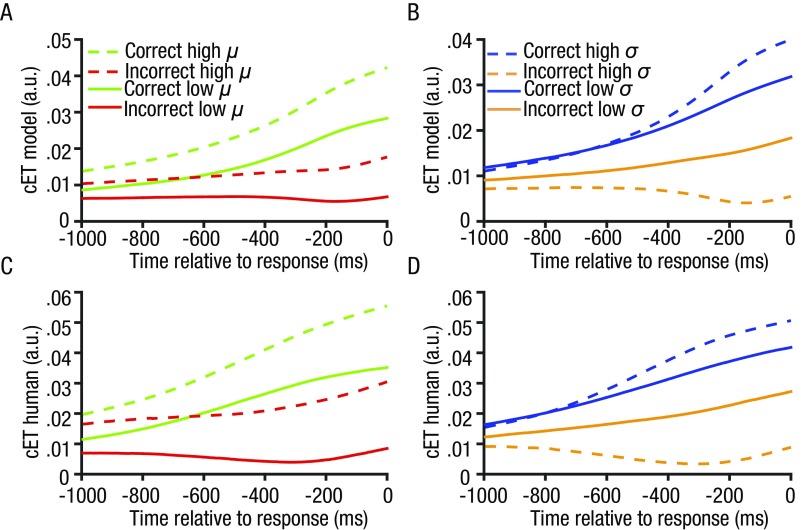
We report data collapsed over two experiments that differed only in terms of the response deadline (3,000 ms and 5,000 ms in experiment 1 and experiment 2, respectively). Overall mean accuracy was 70.5% (n = 54). Performance depended on both the mean and variance of the distribution from which the numbers were drawn (Fig. 1B for accuracy and Table S1 for response time). Accuracy increased on high µ trials compared with low µ trials [F(1, 53) = 76, P < 0.001] and decreased on high σ (more variable evidence) trials compared with low σ trials [F(1, 53) = 47, P < 0.001], as previously reported (24).
Table S1.
Influence of evidence strength (µ) and reliability (σ) on reaction times
| Experiment | σ | High µ | Low µ | Effect on RT | Significance |
| 1 | High σ | 1.57 ± 0.27 s | 1.61 ± 0.27 s | µ ↑ → RT ↓ | F(1, 25) = 31, P < 0.001 |
| Low σ | 1.62 ± 0.27 s | 1.67 ± 0.28 s | σ↑ → RT ↓ | F(1, 25) = 33, P < 0.001 | |
| 2 | High σ | 2.05 ± 0.55 s | 2.1 ± 0.60 s | µ ↑ → RT ↓ | F(1, 27) = 19, P < 0.001 |
| Low σ | 2.11 ± 0.58 s | 2.18 ± 0.62 s | σ↑ → RT ↓ | F(1, 27) = 25, P < 0.001 |
Mean reaction times (RTs) and SD are shown per condition. RTs decreased on high µ trials compared with low µ trials and RTs decreased on high σ trials compared with low σ trials, which is in contrast with previous studies of feature-averaging using color and shape (25). No significant interaction effects were found for either accuracy or RT.
Gaze Trajectories.
We developed an approach to analyzing eye-tracking data (“landscape analysis”) that measured the decision information sampled by the eyes as a continuous, time-varying quantity (the “evidence trajectory,” or ET) across each trial (Fig. S1 and SI Methods for a detailed description of the analysis method). We first converted the stimulus array on each trial to a smooth topography (or landscape) of decision values, with peaks or troughs centered on the spatial position of each element and a height and sign that was determined by the difference between each element Vk and the reference R (positive peaks favoring the decision “higher than reference,” negative troughs favoring “lower”; Fig. 1C). The momentary evidence at each point in time was defined as the landscape value under the gaze location, and the ET constituted the time-series of values obtained as the eyes moved across the stimulus array on each trial (Fig. 1D and SI Methods). This is equivalent to conceiving of the gaze as a “soft” (or smooth) information-harvesting spotlight moving across the screen, allowing evidence to be accumulated up to a decision threshold. The width of the spotlight was estimated independently of further analyses under the assumption that participants’ gaze maximized the acquisition of total sensory evidence. We fit this value by searching for values that maximized “quality trajectory” (QT)—that is, the extent to which items were viewed irrespective of their task-relevant values (SI Methods). We also validated all analyses using a “hard” spotlight—that is, an aperture of fixed width with no spatial smoothing, obtaining qualitatively identical results (Fig. S2).
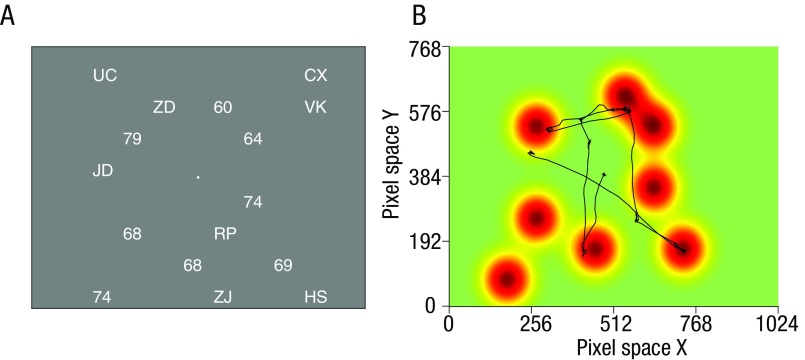
Fig. S1.
Landscape and prototypicality analysis. Our landscape analysis converts the stimulus array (A) on each trial to a topography of to-be-sampled decision values spanning the 1024 × 768 pixel space constituting the screen (B). The landscapes are created by convolving each stimulus location (i.e., the x and y coordinates of each number in pixel space) with a bivariate Gaussian basis function. Each Gaussian has an SD s and height g, with the latter reflecting some information conveyed by the stimulus. In the simplest case (B), g = 1 and s is a constant (e.g., 50 pixels). An example of such a landscape is shown in B (for the corresponding stimulus array shown in A). The estimated quality trajectory, or QTt, which represents the total information available to the participant at any time point t, can thus be quantified as the landscape value at the current eye position (x, y) at that time point (black line in B). Across each trial, this provides a vector of values that indicate whether the participant is looking directly at a stimulus (QTt, ∼1) or away from a stimulus (QTt, ∼0) at each point in time following array onset. The parameter s of the Gaussian can be seen as a proxy of how much information participants can harvest around their fixation. For convenience of display, we conduct this analysis by assuming a “smooth” topography in the stimulus space. However, this is equivalent to a Gaussian filter spotlight of width s, centered at the x, y position of gaze, moving across the landscape and integrating the sum of all values under the spotlight. In this approach, the values under the spotlight are scaled by their distance to the center of the spotlight. A more in depth explanation of the landscape analysis is available in SI Methods.
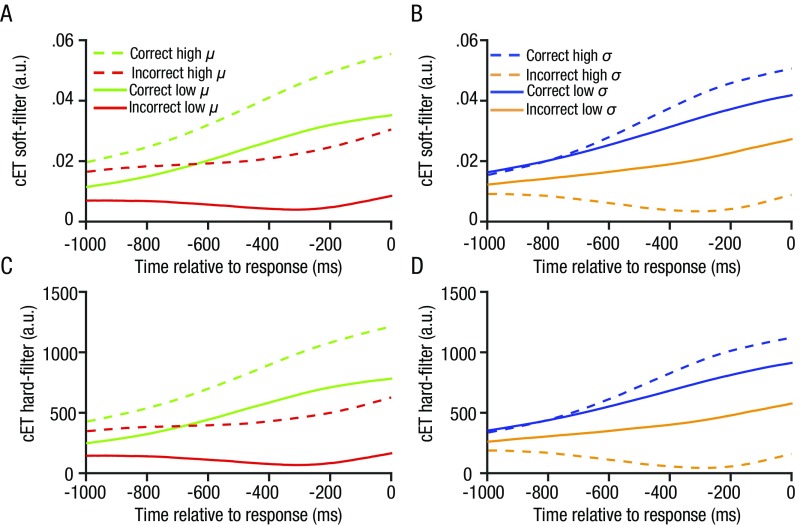
Fig. S2.
Qualitatively identical ETs under soft (A and B) and hard (C and D) information harvesting spotlights. A hard information harvesting spotlight assumes that information within that spotlight that is proximal and distal to the point of gaze contributes equally to decisions. The plots are split by accuracy, mean (µ, A–C) and variance (σ, B–D) of the numbers on each trial. The soft and hard information harvesting spotlights show qualitatively identical patterns.
Decisions Depend on Gaze Location.
Using this approach, we first compared cumulative ET on trials where participants responded “higher” and those where they responded lower, correcting for differences in available information on “high” and “low” trials (SI Methods). As expected, choices depended strongly on the decision information sampled, with average cumulative ET building up steadily until the response: participants responded lower when the sampled evidence was lower than the reference and higher when the sampled evidence was higher than the reference (Fig. 1D, Bottom). In other words, consistent with previous findings, choices were strongly affected by where participants looked (16).
Gaze Is Directed Preferentially to Inliers Over Outliers.
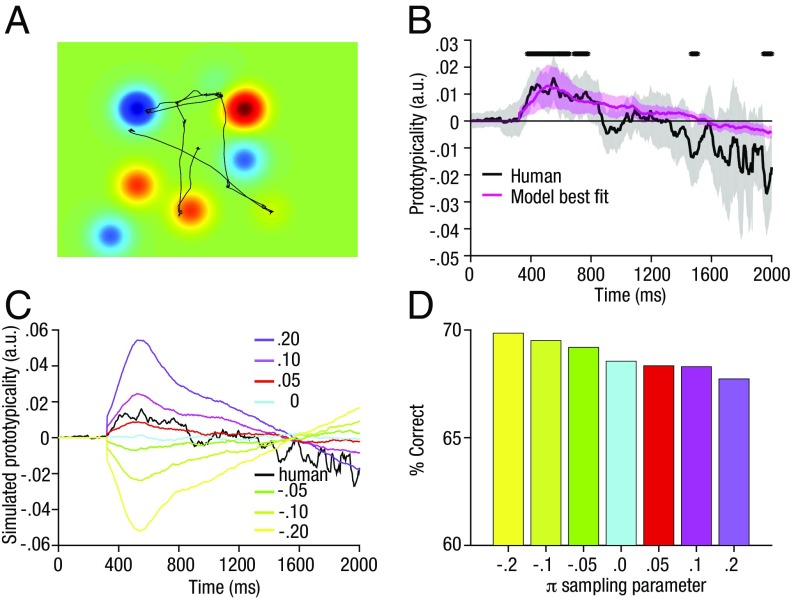
Next, we used a similar landscape approach to determine the extent to which participants’ gaze favored items that were inlying or outlying (numerically closer or further from the reference). We generated a new set of landscapes in which the topography on each trial was determined by the rank of the absolute value of each element (number) within the stimulus array, so that more inlying elements had higher values and more outlying elements had lower values (Fig. 2A; similar results were obtained when this analysis was carried out using the absolute values instead of the ranks). The integral of the eye movement trajectory under these landscapes, which we call the “prototypicality trajectory” (PT), thus encoded participants’ time-varying preference to fixate those elements that were numerically similar (inliers; denoted by positive values) or dissimilar (outliers; negative values) to the reference. We found that inlying items were sampled preferentially, from 400 to 800 ms poststimulus presentation, indicated by a significantly positive PT value (Fig. 2B, black line and shading). This result survived correction for multiple comparisons across time points using a well-validated cluster-based approach (26).
Fig. 2.
PTs for the human and model data. (A) Prototypicality landscape for the example trial from Fig. 1. This landscape is created by setting the height of the Gaussian (gk) associated with each number location equal to the prototypicality value Pk = 4.5 – tiedrank(|Vk – R|). (B) PT over time. Inlying items were viewed by preference from ∼400–800 ms poststimulus presentation, indicated by a significantly positive PT value (black). Significant clusters (P < 0.05, corrected for multiple comparisons) are marked by black bars (Methods). Shading around the lines signify 95% confidence intervals. The magenta line shows the predicted values for PT over time for the best fitting sampling strategy (determined per subject) of the model. (C) Simulated PTs for different sampling strategies (π) in the model. More positive values indicate a preference to sample inlying items first; more negative values indicate a preference to sample outlying items first. (D) Accuracy of the model under different sampling policies. Performance is lower for a sampling policy preferentially sampling inliers first (positive π) compared with sampling outliers first (negative π).
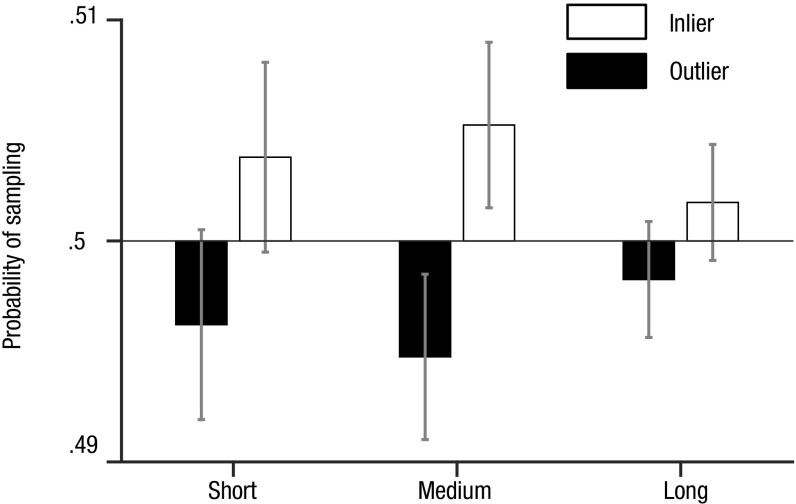
Next, we evaluated this preference for inliers using a different approach. On each fixation, we defined the item being viewed as that which was closest to the current gaze location, allowing us to calculate the probability of gaze moving from an item of one rank (i.e., ordinal position in the array) to another. To avoid any biases that may arise from nonindependence of nearby items, we constructed a null distribution specific to our experiment by randomly permuting item-location assignments on each trial and repeating the analysis 1,000 times. Next, we computed the difference between gaze-transition probabilities in our dataset and under the null distribution. Finally, we calculated the probability for a single fixation to go to an inlier/outlier, split for short, medium, and long Euclidean distance in pixels on the screen between the currently and subsequently fixated items (Fig. 3). The main effect of preference to sample inliers (sampling policy) was significant [F(1, 53) = 8.58, P < 0.01]. This effect was largely driven by fixations of medium distance [t(53) = 2.74, P < 0.01] in comparison with short and long distances (both P > 0.05). The main effect of distance [F(1.9, 100.67) = 1.71, P > 0.05] and its interaction with sampling policy [F(1.89, 100.38) = 1.168, P > 0.05] were not significant.
Fig. 3.
Preference to fixate inlying items: the probability to sample inliers/outliers on each fixation in the real human data in comparison with the null distribution. Probabilities higher than 50% show an increase of sampling relative to the null distribution (and vice versa). The main effect of preference to sample inliers was significant [F(1, 53) = 8.58, P < 0.01]. The medium Euclidean distance fixations largely drove this effect [t(53) = 2.74, P < 0.01], whereas the effect was not significant for short and long distances (P > 0.05). The main effect of distance [F(1.9, 100.67) = 1.71, P > 0.05] and its interaction with sampling policy [F(1.89, 100.38) = 1.168, P > 0.05] were not significant. Bars are shown with 95% confidence intervals across the cohort.
These findings obtained using discrete fixations rather than the landscape approach demonstrate that observers exhibited a tendency to shift their gaze toward inliers rather than merely dwelling for longer while viewing these items. Unsurprisingly, these effects diminished for long Euclidean distances between previous and current fixations, as the decision information associated with distant items cannot be evaluated through parafoveal processing. Thus, the data suggest that participants’ parafoveal processing is not unbounded but occurs within a fixed range, and the sampling bias (moving to inlying information) is only possible for items falling within this range.
Humans Show Robust Averaging of Number.
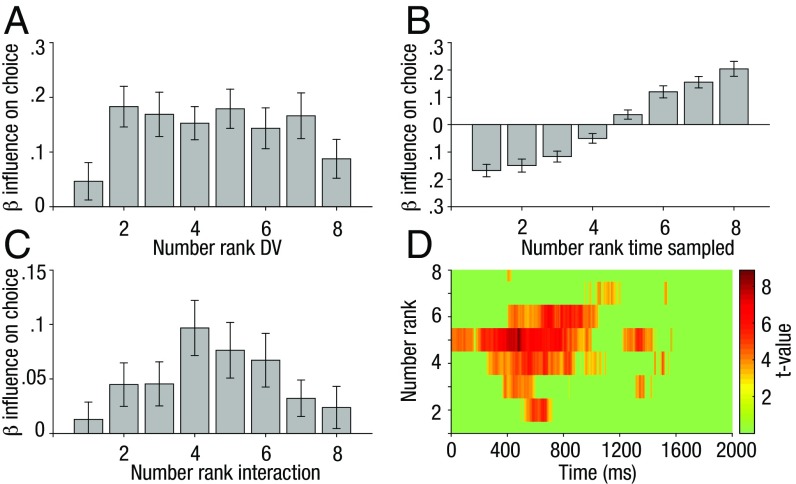
Next, we investigated whether participants’ decisions show evidence of robust averaging—that is, a decision policy in which outliers carry less weight than inliers. We used probit regression to predict human choices as a function of (i) the numbers associated with each item (ranked from lowest to highest), (ii) the time spent sampling those numbers, and (iii) the interaction between these two factors, all entered as competitive predictors in the predictor matrix (Fig. 4 A–C and Methods). The weighting function plotted in Fig. 4A shows the main effect of stimulus—that is, the weight given to each number as a function of its rank within the numerical array. The inverted-u shape indicates that outliers are downweighted. This observation is qualified by a statistical comparison between the weight given to inlying ranks [3, 4, 5, 6] and outlying ranks [1, 2, 7, 8], t(53) = 3.72, P < 0.001. This finding of robust averaging with numbers complements earlier reports with color, shape, and facial expression, confirming that outliers carry less influence during perceptual averaging across domains and task settings (24, 25).
Fig. 4.
Robust averaging of decision information. (A) Weights associated with each item rank, calculated by sorting the numbers associated with each item, and using probit regression to predict participants’ choices. The inverted-u shape over ranks shows evidence for robust averaging (larger weights for inliers). (B) Weights associated with the time spent sampling each number rank. More time spent sampling low-ranked led to a tendency to respond lower than higher and vice versa. (C) Weights associated with the interaction between number rank and the time spent sampling these numbers. The inverted-u shape over ranks shows evidence that robust averaging is mediated by gaze duration. (D) Robust averaging due to the sampling policy as a function of time. Ranks are now shown on the y axis and t values by the green–red color scale. Robust averaging due to preferential sampling of inliers was maximal during the 400–800 ms time frame (larger weights for inliers). Bars on A–C are shown with 95% confidence intervals.
Linking Sampling Policy and Human Decisions.
Next, we show how the main effect of sampled information influenced choices, finding that the resulting estimates grew with rank: sampling low numbers was associated with a propensity to respond low, and sampling high numbers was associated with responding high (Fig. 4B). This is expected from the ET analyses above (Fig. 1D), which show that the information sampled was strongly predictive of the response (high vs. low). Critically, the third predictor (interaction term) in the regression allowed us to assess how the weight given to each stimulus rank was modulated by gaze duration, over and above the influence of stimulus value. Ranks where this term differs positively from zero are those where directing gaze to the relevant numbers amplifies their weight multiplicatively. For example, if gaze were merely a filter that acted equally for all numbers irrespective of their rank, we would see weights that are equal for all ranks. However, this is not what is observed (Fig. 4C). The time spent sampling inlying items enhances the effect that they will have on choice (compared with outlying items) above and beyond what would be predicted simply by their values alone [inlying vs. outlying: t(53) = 5.10, P < 0.001]. We note that this finding is not simply due to a logarithmic (Weber-like) compression of the number line, because it occurred both for those participants that were asked whether the average was higher than the reference [t(28) = 4.99, P < 0.001] and those that reported whether the average was lower than the reference [t(24) = 2.18, P = 0.039], a framing variable that we counterbalanced over participants (Methods). This result also persisted when we used the average (rather than total) ET calculated over the trial, suggesting that it is not simply due to different sampling policies being deployed on trials with short and long RTs.
Given that the prototypicality analysis (above) showed that inlying items were preferentially viewed 400–800 ms poststimulus, we examined whether this downweighting, due to preferential sampling, is also most apparent in this time period. To do this, we conducted the previous regression for each sampling time point individually and tested which of these resulting coefficients (for the Gaze × Stimulus interaction) were significantly different from zero. In Fig. 4D, these are plotted (t values > 3) on a heat map, showing that this downweighting of outliers effect is also maximally depended on gaze during this 400–800 ms timeframe. These results suggest that robust averaging is due at least in part to the sampling policy with which participants actively sample inlying rather than “outlying” information.
Together, Fig. 4 A and C show that (i) inlying stimuli (i.e., those close to the reference) have a stronger influence on choice than outlying stimuli (i.e., those that are much larger or much smaller than the reference) and (ii) that this effect is multiplicatively enhanced by gaze. Thus, any tendency that inlying stimuli might have had to drive choices more strongly is exaggerated when they are fixated, but this is not true for outlying stimuli. In other words, human observers are not only “robust averagers” but also “robust samplers”—selectively viewing inlying category information and thereby ensuring that this information is a more potent driver of choice. In further control analyses, we ruled out the possibility that this effect was due to a “counting” strategy, in which all items above or below the reference contributed equally to decisions (Fig. S3).
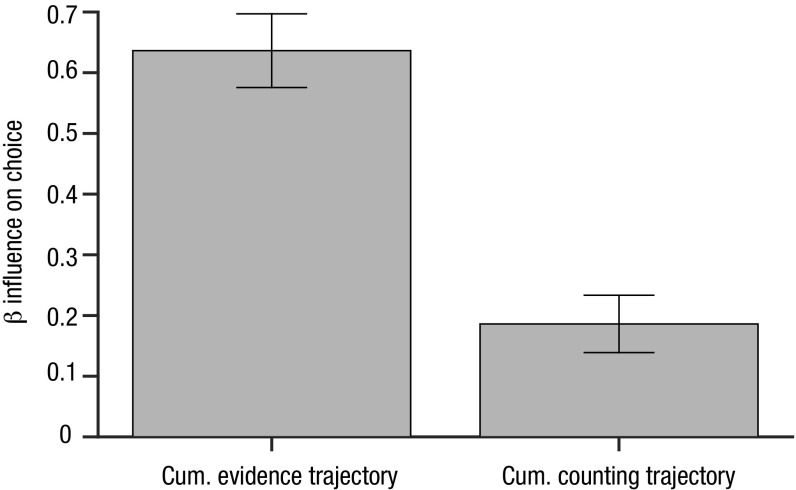
Fig. S3.
Counting strategy as an alternative explanation. Robust sampling cannot be explained by an alternative counting strategy, in which participants only keep track of the number of elements higher/lower than the reference. In past work, our laboratory has shown that down-weighting of outliers can be explained by a nonlinear (sigmoidal) transformation of the decision information before averaging, over and above any counting (24). To test this alternative explanation in the current study, we generated new landscapes in which the decision value is the same positive value (+1) for all values above the reference and the same negative value (–1) for all values below. We then used both the cumulative ET values and the cumulative counting ET values from each trial (averaged up to the response) to predict human choices, in a competitive regression. Predictors were standardized (z-scored) to allow comparison. The resulting coefficients (betas) for these two predictors are shown in the bar plot above. Both the cumulative ET and the cumulative counting ET predicted choice [t(53) = 20.53, P < 0.001 and t(53) = 7.72, P < 0.001, respectively]. This is both consistent with previous work (in which counting accounted for some of the variance in our data) and also with the results described in Fig. 4A, which show that there is a residual “squashing” that occurs beyond the sampling stage (i.e., over and above the Gaze × Decision Information weights, we still see robust averaging). Importantly, the cumulative ET was a significantly better predictor of choice than the cumulative counting ET [t(53) = 9.08, P < 0.001]. Bars are shown with 95% confidence intervals.
Computational Simulations.
Next, to validate our approach, we used computational simulations to estimate how the ET and PT should vary under differing sampling policies. Using distributions of decision information (i.e., numbers) identical to those viewed by human participants (i.e., same µ and σ), we constructed simulated ET and PT vectors consisting of alternating periods of fixation and eye movements, prefixed by a delay period. The duration of all of these periods (initial delay, fixation, eye movement) was sampled from the distributions exhibited by human participants. During simulated fixations, simulated ET was set to the decision values Vk – R (where Vk is the numerical value of item k), and during delay and eye movements, ET values were set to zero. Simulated PT was constructed in the same manner by setting PT during a fixation of stimulus k to its value ranked within the array, as for the human analyses. Model choices occurred when the cumulative simulated ET reached a fixed threshold, as in standard integration-to-bound models (2). The sign of the cumulative ET at this fixed threshold determined model choice and thus accuracy. To ensure that human PT and model PT values were on the same scale, we multiplied the model PT with the average QT for the corresponding participant.
This framework allowed us to manipulate the model sampling policy—that is, to simulate the order in which the array items were sampled. We implemented this via a single parameter π that dictated whether the observer preferred to view inliers before outliers (π > 0), outliers before inliers (π < 0), or sampled the elements in random order (π ∼ 0). The parameter π encodes the (positive or negative) correlation between the observed sampling order and the most “prototypical” ordering—that is, from most inlying to most outlying. In Fig. 2C, we plot simulated PT for different values of π. The best fitting parameterization was determined per subject by calculating the mean squared error (MSE) between human and simulated PT for each value of π. Fig. 2B shows the simulated values of PT for the best fitting average π value over subjects (magenta line) plotted against human data. Human PT curves were best accounted for by positive π values, consistent with a policy that involved sampling inliers before outliers and thus with the analyses described above. Fig. S4 shows the distribution of best fitting values for π over subjects. Next, using the best fitting π values for each subject, we returned to the analysis of ET and compared the human and simulated ET values for the different conditions—that is, for different means µ and SDs σ of the decision values with respect to the reference. We observed a striking convergence between the human and model ET values (Fig. S5), providing an independent validation of our best fitting model.
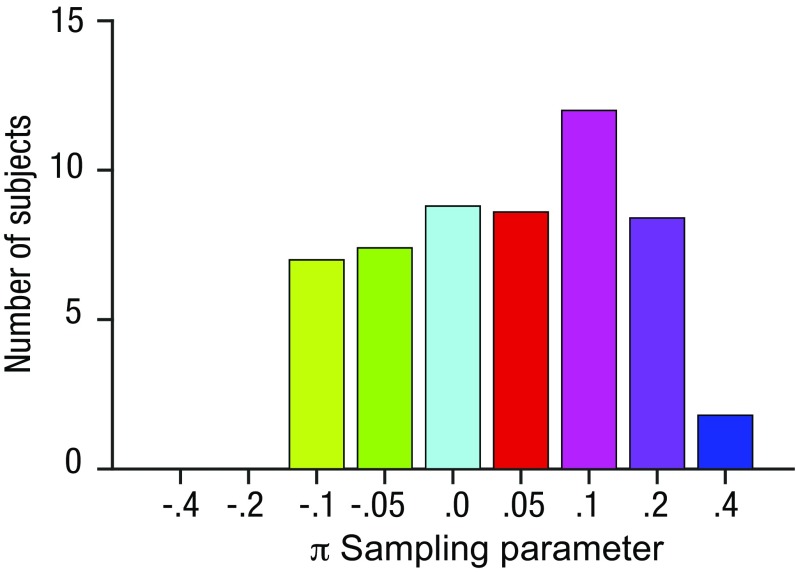
Fig. S4.
Histogram of the best fitting parameter values π from the model, over the human cohort. Because of random noise in the model, results varied slightly each time the model was fit, and so the results shown were obtained by fitting the model 10 times and averaging the number of subjects. Note that the x axis is an ordinal, not interval scale. The best fitting sampling parameter was significantly more positive than 0 (P < 0.05; on average, ∼57% of participants had a positive best fitting π—i.e., values of either 0.05, 0.1, 0.2, or 0.4—whereas 27% had a negative best-fitting π—i.e., values of either –0.05 or –0.1), indicating a tendency to preferentially sample inlying items.
Fig. S5.
Cumulative ETs from the landscape analysis for simulated model (A and B) and human data (C and D). The plots are split by accuracy, mean (µ, A–C) and variance (σ, B–D) of the numbers on each trial. The simulated and human cumulative ET show very similar qualitative patterns.
Determinants of Human and Model Performance.
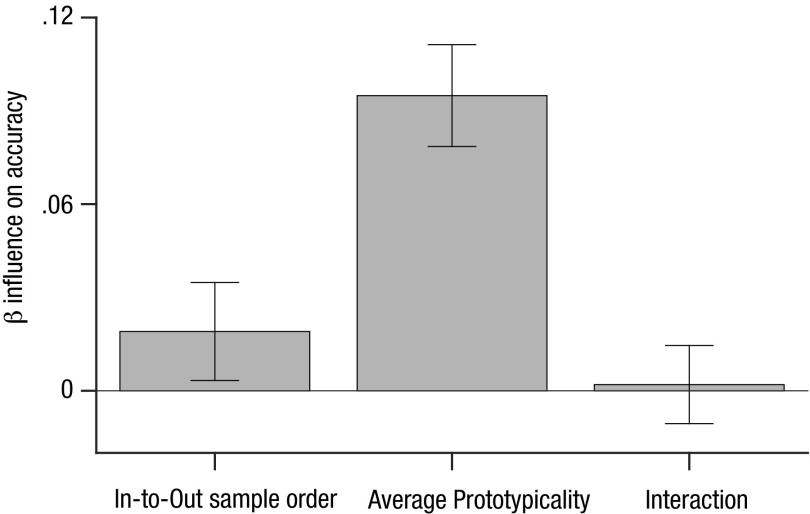
Finally, we tested how model performance (accuracy) varied with π. Interestingly, performance for the model linearly decreased as the sampling policy π changed from a policy to sample outlying information first to a policy to sample inlying information (Fig. 2D). Thus, for an “ideal” model—in which decisions are only limited by the quality of information that is sampled from the screen—a policy that preferentially samples inlying information incurs a model performance cost relative to random sampling. To test whether this was the case for human observers, we conducted an additional analysis that evaluated how estimated human values of π predicted accuracy at the single-trial level. We computed single-trial estimates of π by correlating the order in which items were actually sampled with their ranked equivalent and then used logistic regression to estimate how these values predicted choice accuracy (Fig. S6). Both the sampling policy π [t(53) = 2.37, P < 0.05] and the average prototypicality [t(53) = 11.3, P < 0.001] were positive predictors of accuracy, indicating that unlike the model, participants performed better as they exhibited more robust sampling.
Fig. S6.
Predicting human accuracy based on the sampling policy (preference for in- vs. outlying elements). Single-trial estimates of π are computed by correlating the order in which items were actually sampled with their ranked equivalent. To quantify the effect of sampling policy on accuracy in our dataset, we regressed this single-trial value of π (given the eye-movement trajectory on each trial) and the average prototypicality against accuracy—that is, used a probit regression to determine the extent to which these variables predicted whether participants would be correct (1) or not (0). Both the sampling policy [t(53) = 2.37, P < 0.05] and the average prototypicality [t(53) = 11.3, P < 0.001] show positive parameter estimates, indicating that participants were more likely to be correct when they pursued a policy of sampling inliers over outliers (positive values of π).
SI Methods
We exhaustively computed the QT across a space of possible parameter values (range 0–100) for s and identified the value of s that maximized QT. In other words, we made the assumption that participants move their eyes to locations that maximize available information (QT), irrespective of any decision values (ET or PT). Note that an excessively narrow spotlight would lead to items even close to the point of gaze being neglected, whereas (because landscapes were normalized to have a mean of zero) an excessively broad spotlight would lead to large portions of uninformative space being sampled, reducing the overall level of information (QT) obtained. The aperture size s that maximizes QT is the one that maximizes this trade-off. The resulting function was found to be concave with a peak at 50 pixels.
The QT-maximizing SD of the Gaussian for the entire cohort (50 pixels) was used for subsequent analyses. This approach thus defines the width of the information-processing spotlight within the same task but in a way that is independent of all key analyses described in the paper, which related to the decision values (numbers relative to the reference) rather than the position of the items on the screen. We opted to develop this specific ad hoc computation of the width of the information-harvesting spotlight for two reasons. First, this approach assumes that information falling further from the point of gaze has a weaker influence on choices than that falling directly under a fixation point rather than assuming that all information within a fixed window contributes equally to choices. Second, recent work has suggested that sampling policies are not always well predicted by mapping retinal sensitivity based on independent data from a task with different constraints (38).
In a subsequent step, we used a variant of this method to obtain real-time measures of the decision information available at each point in the trial, a quantity we call ET. To this end, we set the height of the Gaussian gk associated with each item k equal to Vk – R, where Vk is the value (number) of each item and R is the reference value. As a consequence, peaks in the landscape are located at numbers higher than the reference value, and troughs are located at numbers lower than the reference value (Fig. 1C). The amplitude of peaks (red) and troughs (blue) depended linearly on the difference between each number and the reference point. These values were inverted for participants in the lower framing group, such that positive deflections in each landscape were always in the frame of reference of the choice, not the absolute number. Time point-by-time point measures of decision information are then obtained by defining gaze trajectory as the temporal sequence of landscape values falling under the observer’s gaze at each time point t. We averaged the resulting ET curves across trials and conditions (for each chosen response) to assess how decision information is sampled across time during trials and how it relates to behavior.
The approach we use here has some drawbacks. Notably, we assume that all information falling under the gaze trajectory contributes to the decision, in direct proportion to its viewing time, an assumption that is probably incorrect; it is known that participants are blind to information arriving at the retina during saccades (39). However, using a standard analysis approach, in which we defined fixations using Eyelink preset criteria (velocity threshold of 30, acceleration threshold of 8,000, and a saccade motion threshold of 0.1), saccadic trajectories accounted for only 18.75% of time points, and as these were largely made across the space separating stimuli, they contributed only 0.00004% to the final decision value, so any bias that arises by accounting for inputs from between fixations is likely to be negligible. However, our approach has the major benefit that it allows us to characterize, in real time on each trial, information that is available to the participant and thus to explore how stimulation and gaze interact in determining choices. It is also immune to otherwise arbitrary choices that might have to be made during a more standard fixation analysis, such as the size and shape of the window that surrounds each stimulus or the criteria for determining dwell times. Moreover, we provide multiple validation analyses that show that our approach offers sensible information about how people move their eyes and how this determines choices.
Nevertheless, to verify that our findings were not in some way specific to our use of this “landscape” approach, we repeated the analysis using a more conventional method of defining an aperture with fixed width. In this “hard” filter approach, the landscape is composed of a series of circular “cylinders” placed at the x, y position of each item k, with height ck corresponding to the quantityVk – R and width s, where s is a free parameter fit to the QT as for standard landscape analysis. The QT values are computed in the same way as for the “soft” filter approach—that is, as the integral under the eye movement trace. The two methods thus differ in that here, any time the gaze trajectory falls within the space defined by a cylinder, the ET value is incremented by ck, rather than depending on its distance to the x, y position. All of the results were replicated using a hard information-harvesting spotlight (i.e., a spotlight of fixed width with no spatial smoothing), and the ETs under both approaches were qualitatively identical (Fig. S2).
Having developed and tested the landscape approach, we then used it to assess our main question of interest: Do participants sample preferentially from those numbers that are inlying or outlying with respect to the reference? To this end, we defined a new quantity, protypicality or p, that encoded how inlying or outlying each sample was:
where Pk is calculated by computing the ranks for each item k (tied ranks are set to their average rank) and subtracting 4.5 from this value. Thus, Pk is more positive for inlying items and more negative for outlying items.
Next, we set the height of the Gaussian gk associated with each item k equal to this prototypicality Pk. As a consequence, peaks in the landscape are located at more inlying numbers, and troughs are located at more outlying numbers. Time point-by-time point measures of PT are then obtained as above, by defining gaze trajectory as the temporal sequence of landscape values falling under the observer’s gaze at each time point t. For the results shown in Fig. 2, we averaged the resulting PT curves across trials and conditions (up to each chosen response) to assess the prototypicality of the sampling process across the trial and how this relates to behavior.
To assess statistical significance (i.e., deviation from zero of PT) in a manner that corrected for multiple comparisons across time points, we used a nonparametric cluster-correction method. First, we constructed a null distribution of cluster sizes by sampling randomly from the t distribution at each time point and logging the maximum cluster size (i.e., greatest number of contiguous significant time points) for each of 1,000 random samples. We then report only significant (P < 0.05) clusters with a length that fell within the top 50 (5%) of this null distribution (26).
Discussion
In real-world settings, information arises in crowded natural scenes, replete with multiple features and objects that compete to drive decisions. Studies of saccadic control have revealed that attention is automatically captured by perceptually salient information, such as a target defined by a unique color in a visual search experiment (27), and may also be captured by semantically deviant information, such as an object in an unusual context (e.g., a sofa on the beach), although the latter claim remains controversial (11). However, the task at hand is a key determinant of saccadic control, and the eyes are drawn to those scene elements that are task-relevant, or valuable, or to those locations where the most information can be gleaned (10, 12–15, 28). Nevertheless, most decision-making studies either use a single, centrally presented source of information (such as a dot motion stimulus) precluding the detailed investigation of the policy by which participants sample decision information or assume that gaze allocation is a stochastic process that drives a preference for fixated alternatives, rather than vice versa (16, 17). Recently, researchers have highlighted the importance of investigating evidence accumulation as an active sampling process (22).
Here, we reveal an aspect of the sampling policy that determines where gaze is allocated during decision-making: faced with multiple spatially distinct sources of decision information, observers tend to ignore those sources that carry the most extreme information and focus instead on the inlying decision information—that is, that falling closest to the boundary that segregates one choice from another (or close to the mode of the overall information presented on one trial; our approach was not designed to distinguish these possibilities). This is surprising given that participants exhibit a well-characterized policy to saccade toward perceptually deviant information during natural scene viewing, or visual search (10, 11). The focus on inlying elements influenced human choices, with gaze driving a multiplicative effect to weight inlying elements more heavily, which in turn drove “robust averaging” in perceptual choices made during the experiment.
Robust averaging of perceptual information has been described before, for faces (23) and for colors and shapes (24, 25). Here, we add to these findings, revealing that humans engage in robust averaging of symbolic number. Importantly, we assumed that participants used an approximate number sense, meaning that numbers are treated as noisy estimates of magnitude, which can be averaged like continuous sensory signals (29). This assumption follows from the short duration for which numerical information was available and the low average dwell times observed for each number, which would preclude overt arithmetic approaches. Previous studies have left unresolved the question of whether robust averaging occurs because inlying items are sampled (i.e., overtly attended) by preference or whether the influence of outliers is attenuated at a later decision stage. For example, one model proposes that observers simply compute a posterior likelihood ratio conditional on the past distribution of features and their associated responses. This is equivalent to using a nonlinear decoder that “squashes” outlying information, muting its influence in the average and prolonging response latencies when decision information is heterogeneous (24). However, here we show that the robust averaging is driven at least in part by the policy with which gaze is directed during information integration. In other words, humans are not just robust averagers but robust samplers of decision information.
Why do humans sample and average robustly? We describe a computational simulation of the sampling policy adopted during our spatial averaging task that was able to faithfully recreate the relationship between the evidence sampled and the choices made by humans. Exploring model performance under a range of policies (spanning a tendency to sample inliers or outliers by preference) revealed that for an ideal model limited only by the information available on the screen, sampling outliers rather than inliers by preference boosted performance. This is consistent with the observation that when assigning samples to one of two Gaussian-distributed classes, eccentric or “off-channel” features are most diagnostic of the correct response (30, 31). It is very different, however, from the optimal policy that emerges as participants gradually learn a category boundary through repeated sampling (32) (Fig. S7 for discussion).
Fig. S7.
Adaptation of the sampling policy as a function of the sampled evidence. Previous research on category learning has shown evidence for enhanced attention near the category boundary (32). One key difference is that in this line of research, the category boundary is unknown to the participant and must be learned by sampling information. By contrast, in our task, participants were fully aware of the bound (i.e., the reference value on each block), and no further learning about the bound occurs during sampling, because feedback was only administered at the end of the trial, after participants had discontinued sampling. When the boundary is unknown, it is optimal to sample items that fall close to the current estimate of its location, to gather the most information (i.e., reduce uncertainty) about its precise location. Adaptive gain theory has shown evidence for up-weighting of decision information that is consistent with the overall information shown thus far (40). To investigate whether participants adapt their sampling policy as a function of the sampled evidence, we again characterized discrete fixations larger than 100 ms using Eyelink preset criteria. Next, we quantified the information value of each fixation based on each fixation’s coordinates on the TE landscape. By comparing the sign of the information value of each fixation, we could check whether each fixation confirmed (i.e., same sign of the information value; =1) or disconfirmed (i.e., opposite sign; = –1) their current hypothesis (i.e., confirmation, defined as the running mean of the fixations so far). After calculating the average of these values per trial, this yields a quantitative measure of whether participants adapted their sampling policy as a function of the sampled evidence on each trial. Next, we constructed a null-distribution specific to our experiment by randomly permuting the numbers of each trial and repeating the analysis 1,000 times, to carefully control for any possible correlations in the values. Thus, each fixation had a different TE, whereas the information sampling characteristics remained the same. We then compared the average confirmation of each fixation (sorted by position in which they occurred) in our experiment to the one found under this null distribution by calculating the average difference score between them for each fixation (positive scores indicating confirmation, negative scores indicating disconfirmation, and zero indicating sampling independent of the previously sampled information). Critically, this figure shows significant evidence for confirming evidence seeking—that is, a tendency for humans to sample information that confirms the running hypothesis up to but not including that sample. This was true for each of the fixations made from the third to the ninth (all P < 0.05, d = 0.43). In other words, participants view by preference information that confirms their running hypothesis over all samples viewed thus far. *P = 0.021; **P = 0.006; ***P < 0.001. Bars are shown with 95% confidence intervals. This suggests that participants are indeed adapting their sampling policy as new information arrives with each successive fixation, consistent with an adjustment of the sampling policy toward the mean of the trial, rather than to the reference alone.
However, in the human data, a tendency to sample inliers was a positive predictor of accuracy at the single-trial level (Fig. S6). This implies that a robust sampling policy has evolved to counter additional sources of loss that arise during the decision process, such as “late” noise that corrupts the information of integration, perhaps due to capacity limits on attention and working memory processes. For example, robust policies may lead to more stable estimates of decision information, just as nonparametric statistical inference is robust to the inclusion of aberrant data points. Other recent work has suggested that apparent “suboptimalities” in human judgment may in fact maximize performance when this late noise is taken into account (33, 34). The effect of the interplay between the decision environment (i.e., task characteristics) and cognitive constraints on the relative (sub)optimality of various sampling policies is an interesting avenue for future research.
In summary, the current results highlight that perceptual judgments are not only constrained by the quality of the sensory information and the dynamics of integration but also by the sampling policy, which dictates how the information is selected for entry into the decision process. However, other questions remain open. In particular, the information processing steps by which fixations are guided to subsequent inliers remain unclear in our work, although this presumably relies on parafoveal processing of nonfixated locations. One possibility is that covert attention is first shifted to candidate items and the eyes are then “pulled” to this location (35, 36). Nor does our study directly address how saccade placement varies according to the spatial arrangement of items on the screen. For example, participants may prefer to saccade toward the center of mass of clusters of objects (37). Thus, gaze can indeed be driven by the spatial arrangement of items on the screen, but gaze is additionally driven by the decision values of the available evidence, exhibited in this work via a preference to sample inlying samples.
Methods
Participants.
Sixty healthy human participants with normal or corrected-to-normal vision were recruited in two experiments (experiment 1, n = 30; experiment 2, n = 30). Participants provided written consent beforehand, and the study was approved by the Oxford University Medical Sciences Division Ethics Committee (approval no. MSD-IDREC-C1-2009-1). There were only minor differences between the two experiments (highlighted below), and so we collapse across their results. Six participants whose performance failed to differ from chance were excluded from all further analyses, leaving n = 54.
Stimuli.
On each trial, participants viewed an array composed of eight two-digit numbers. Stimuli were generated using PsychToolbox (psychtoolbox.org/) for MATLAB (Mathworks) and presented on a 17-inch screen (resolution, 1024 × 768) viewed from a distance of 60 cm. Numbers (∼1.15° horizontal and ∼0.95° vertical visual angle) were presented at randomly selected locations within an invisible 8 × 8 grid. Eight additional randomly selected grid locations contained letter pairs, which were distracters. No letter or number pairs were presented within the central four grid locations. An example stimulus array can be seen in Fig. 1A.
At the start of each block of 96 trials, participants were informed of the reference value, against which they compared the average number for all trials across that block. Subsequently, each trial began with the onset of a central fixation cross (500 ms), followed by the stimulus array, which remained on the screen for either up to 3,000 ms (experiment 1) or up to 5,000 ms (experiment 2). During array presentation, participants freely moved their eyes across the screen and chose which was higher (lower): the reference number or the average of the number array. The decision framing (decide whether numbers higher vs. lower than reference) was counterbalanced across participants within each experiment. Participants could respond at any point during the array presentation by pressing one of two keys (“F” or “J”), and they received auditory feedback in the form of a high or low tone lasting 100 ms (800/400 Hz, correct/incorrect). In experiment 2 only, participants were additionally paid in proportion to their accuracy. In the high frame, participants received a bonus corresponding to their choice (reference vs. numbers, in pence) on 20 randomly selected trials. In the low frame, the reward of participants started at £20, from which their choice was deducted on 20 randomly selected trials. Participants earned £10 on average for their participation. Participants performed eight blocks of 96 trials (768 trials in total) in an experiment lasting ∼50 min.
Design.
The reference number R on each block was drawn randomly from a uniform distribution between 25 and 75. The sample numbers were drawn from one of eight Gaussian distributions whose mean µ differed from R by either ±2 or ±4 and whose SD σ was either 6 or 12. Sample values were resampled to ensure that the sample mean and variance fell within the desired value for that trial with a tolerance of 0.7 and 0.1, respectively. Each of the eight trial types occurred equally often, and their presentation order within a block was random.
Eye-Tracking.
All eye movement data were recorded monocularly using an SR Research EyeLink 1000 eye-tracking system at a sampling rate of 1,000 Hz. Participants placed their heads on a chin rest that was mounted on the table at a fixed distance of 68 cm from the screen. Before the start of each new block, a standard calibration/validation procedure was executed, in which participants tracked a dot that appeared at 13 evenly spaced locations across the screen. Data were converted to vectors of x, y position in the frame of reference of the screen exported to MATLAB using the EyeLink toolbox and analyzed using in-house scripts. Missing data (due to blinks or eye movements away from the screen) were ignored (i.e., set to NaN) in all analyses. Eye movement traces were cut off at reaction time for all analyses described above. All of our analyses assume that the eye-tracker faithfully estimates the pixel position of the gaze on the screen.
Analysis.
We analyzed the eye-tracking data using both a combination of conventional methods (e.g., identifying the location and dwell time of individual fixations) and a technique that treated the stimulus array as a topography of decision information that was sampled continuously with the gaze (landscape analysis). We describe this method in detail in SI Methods (Fig. S1). The methods associated with other analyses are detailed in accompanying supplementary sections that are referenced in the main text (Figs. S3, S6, and S7).
Weighting of Decision Information on Choice.
Probit regression was used to predict human choices (higher or lower than reference) as a function of three sets of predictors: (i) the decision values of each number ranked from lowest to highest, (ii) QT for each number QTk (once again, with k ranked from lowest to highest), and (iii) the interaction between these two quantities. The QT for each number QTk was computed as the sum of the integral under an element-specific QT landscape—that is, a landscape constructed using each element in isolation (with the height of the Gaussian set to 1)—up to the response time (Fig. S1). QTk is then proportional to the time spent sampling element k.
The regression model we used was as follows, where in each case:
where ϕ denotes the cumulative normal distribution, k the sample number, and t the time point of the QT vector. For the data shown in Fig. 4 A–C, we dropped the indexing by t and used the sum of QT for all time points up to the response.
Acknowledgments
This work was supported by European Research Council Starter Grant 281628 (to C.S.), Economic and Social Research Council Funding Award 1369566 (to H.V.), and Wellcome Trust Grant 0099741/Z/12/Z (to S.H.C.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.G. is a Guest Editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1613950114/-/DCSupplemental.
References
- 1.Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- 2.Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Comput. 2008;20(4):873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced-choice tasks. Psychol Rev. 2006;113(4):700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- 4.Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends Cogn Sci. 2001;5(1):10–16. doi: 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- 5.Beck JM, et al. Probabilistic population codes for Bayesian decision making. Neuron. 2008;60(6):1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shadlen MN, Kiani R. Decision making as a window on cognition. Neuron. 2013;80(3):791–806. doi: 10.1016/j.neuron.2013.10.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Newsome WT, Paré EB. A selective impairment of motion perception following lesions of the middle temporal visual area (MT) J Neurosci. 1988;8(6):2201–2211. doi: 10.1523/JNEUROSCI.08-06-02201.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eckstein MP. Visual search: A retrospective. J Vis. 2011;11(5):14. doi: 10.1167/11.5.14. [DOI] [PubMed] [Google Scholar]
- 9.Torralba A, Oliva A, Castelhano MS, Henderson JM. Contextual guidance of eye movements and attention in real-world scenes: The role of global features in object search. Psychol Rev. 2006;113(4):766–786. doi: 10.1037/0033-295X.113.4.766. [DOI] [PubMed] [Google Scholar]
- 10.Towal RB, Mormann M, Koch C. Simultaneous modeling of visual saliency and value computation improves predictions of economic choice. Proc Natl Acad Sci USA. 2013;110(40):E3858–E3867. doi: 10.1073/pnas.1304429110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Võ ML-H, Henderson JM. The time course of initial scene processing for eye movement guidance in natural scene search. J Vis. 2010;10(3):1–13. doi: 10.1167/10.3.14. [DOI] [PubMed] [Google Scholar]
- 12.Itti L, Baldi P. Bayesian surprise attracts human attention. Vision Res. 2009;49(10):1295–1306. doi: 10.1016/j.visres.2008.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Eckstein MP, Schoonveld W, Zhang S, Mack SC, Akbas E. Optimal and human eye movements to clustered low value cues to increase decision rewards during search. Vision Res. 2015;113(Pt B):137–154. doi: 10.1016/j.visres.2015.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Navalpakkam V, Koch C, Rangel A, Perona P. Optimal reward harvesting in complex perceptual environments. Proc Natl Acad Sci USA. 2010;107(11):5232–5237. doi: 10.1073/pnas.0911972107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Manohar SG, Husain M. Attention as foraging for information and value. Front Hum Neurosci. 2013;7:711. doi: 10.3389/fnhum.2013.00711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Krajbich I, Armel C, Rangel A. Visual fixations and the computation and comparison of value in simple choice. Nat Neurosci. 2010;13(10):1292–1298. doi: 10.1038/nn.2635. [DOI] [PubMed] [Google Scholar]
- 17.Krajbich I, Rangel A. Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions. Proc Natl Acad Sci USA. 2011;108(33):13852–13857. doi: 10.1073/pnas.1101328108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cassey TC, Evens DR, Bogacz R, Marshall JA, Ludwig CJ. Adaptive sampling of information in perceptual decision-making. PLoS One. 2013;8(11):e78993. doi: 10.1371/journal.pone.0078993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shimojo S, Simion C, Shimojo E, Scheier C. Gaze bias both reflects and influences preference. Nat Neurosci. 2003;6(12):1317–1322. doi: 10.1038/nn1150. [DOI] [PubMed] [Google Scholar]
- 20.Rehder B, Hoffman AB. Eyetracking and selective attention in category learning. Cognit Psychol. 2005;51(1):1–41. doi: 10.1016/j.cogpsych.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 21.Meier KM, Blair MR. Waiting and weighting: Information sampling is a balance between efficiency and error-reduction. Cognition. 2013;126(2):319–325. doi: 10.1016/j.cognition.2012.09.014. [DOI] [PubMed] [Google Scholar]
- 22.Gottlieb J, Hayhoe M, Hikosaka O, Rangel A. Attention, reward, and information seeking. J Neurosci. 2014;34(46):15497–15504. doi: 10.1523/JNEUROSCI.3270-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Haberman J, Whitney D. The visual system discounts emotional deviants when extracting average expression. Atten Percept Psychophys. 2010;72(7):1825–1838. doi: 10.3758/APP.72.7.1825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.de Gardelle V, Summerfield C. Robust averaging during perceptual judgment. Proc Natl Acad Sci USA. 2011;108(32):13341–13346. doi: 10.1073/pnas.1104517108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Michael E, de Gardelle V, Nevado-Holgado A, Summerfield C. Unreliable evidence: 2 sources of uncertainty during perceptual choice. Cereb Cortex. 2015;25(4):937–947. doi: 10.1093/cercor/bht287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maris E, Oostenveld R. Nonparametric statistical testing of EEG- and MEG-data. J Neurosci Methods. 2007;164(1):177–190. doi: 10.1016/j.jneumeth.2007.03.024. [DOI] [PubMed] [Google Scholar]
- 27.Yarbus AL. Eye Movements During Perception of Complex Objects. Springer; New York: 1967. [Google Scholar]
- 28.Najemnik J, Geisler WS. Eye movement statistics in humans are consistent with an optimal search strategy. J Vis. 2008;8(3):1–14. doi: 10.1167/8.3.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brezis N, Bronfman ZZ, Usher M. Adaptive spontaneous transitions between two mechanisms of numerical averaging. Sci Rep. 2015;5:10415. doi: 10.1038/srep10415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Navalpakkam V, Itti L. Search goal tunes visual features optimally. Neuron. 2007;53(4):605–617. doi: 10.1016/j.neuron.2007.01.018. [DOI] [PubMed] [Google Scholar]
- 31.Scolari M, Serences JT. Adaptive allocation of attentional gain. J Neurosci. 2009;29(38):11933–11942. doi: 10.1523/JNEUROSCI.5642-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Markant DB, Settles B, Gureckis TM. Self-directed learning favors local, rather than global, uncertainty. Cogn Sci. 2016;40(1):100–120. doi: 10.1111/cogs.12220. [DOI] [PubMed] [Google Scholar]
- 33.Tsetsos K, et al. Economic irrationality is optimal during noisy decision making. Proc Natl Acad Sci USA. 2016;113(11):3102–3107. doi: 10.1073/pnas.1519157113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Howes A, Warren PA, Farmer G, El-Deredy W, Lewis RL. Why contextual preference reversals maximize expected value. Psychol Rev. 2016;123(4):368–391. doi: 10.1037/a0039996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Inhoff AW, Rayner K. Parafoveal word processing during eye fixations in reading: Effects of word frequency. Percept Psychophys. 1986;40(6):431–439. doi: 10.3758/bf03208203. [DOI] [PubMed] [Google Scholar]
- 36.Henderson JM, Ferreira F. Effects of foveal processing difficulty on the perceptual span in reading: Implications for attention and eye movement control. J Exp Psychol Learn Mem Cogn. 1990;16(3):417–429. doi: 10.1037//0278-7393.16.3.417. [DOI] [PubMed] [Google Scholar]
- 37.He PY, Kowler E. The role of location probability in the programming of saccades: Implications for “center-of-gravity” tendencies. Vision Res. 1989;29(9):1165–1181. doi: 10.1016/0042-6989(89)90063-1. [DOI] [PubMed] [Google Scholar]
- 38.Morvan C, Maloney LT. Human visual search does not maximize the post-saccadic probability of identifying targets. PLOS Comput Biol. 2012;8(2):e1002342. doi: 10.1371/journal.pcbi.1002342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dodge R. Visual perception during eye movement. Psychol Rev. 1900;7(5):454. [Google Scholar]
- 40.Cheadle S, et al. Adaptive gain control during human perceptual choice. Neuron. 2014;81(6):1429–1441. doi: 10.1016/j.neuron.2014.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]