Abstract
Key points
The ductal system of the pancreas secretes large volumes of alkaline fluid containing HCO3 − concentrations as high as 140 mm during hormonal stimulation.
A computational model has been constructed to explore the underlying ion transport mechanisms. Parameters were estimated by fitting the model to experimental data from guinea‐pig pancreatic ducts.
The model was readily able to secrete 140 mm HCO3 −. Its capacity to do so was not dependent upon special properties of the cystic fibrosis transmembrane conductance regulator (CFTR) anion channels and solute carrier family 26 member A6 (SLC26A6) anion exchangers.
We conclude that the main requirement for secreting high HCO3 − concentrations is to minimize the secretion of Cl− ions.
These findings help to clarify the mechanism responsible for pancreatic HCO3 − secretion, a vital process that prevents the formation of protein plugs and viscous mucus in the ducts, which could otherwise lead to pancreatic disease.
Abstract
A computational model of guinea‐pig pancreatic duct epithelium was developed to determine the transport mechanism by which HCO3 − ions are secreted at concentrations in excess of 140 mm. Parameters defining the contributions of the individual ion channels and transporters were estimated by least‐squares fitting of the model predictions to experimental data obtained from isolated ducts and intact pancreas under a range of experimental conditions. The effects of cAMP‐stimulated secretion were well replicated by increasing the activities of the basolateral Na+‐HCO3 − cotransporter (NBC1) and apical Cl−/HCO3 − exchanger (solute carrier family 26 member A6; SLC26A6), increasing the basolateral K+ permeability and apical Cl− and HCO3 − permeabilities (CFTR), and reducing the activity of the basolateral Cl−/HCO3 − exchanger (anion exchanger 2; AE2). Under these conditions, the model secreted ∼140 mm HCO3 − at a rate of ∼3 nl min−1 mm−2, which is consistent with experimental observations. Alternative 1:2 and 1:1 stoichiometries for Cl−/HCO3 − exchange via SLC26A6 at the apical membrane were able to support a HCO3 −‐rich secretion. Raising the HCO3 −/Cl− permeability ratio of CFTR from 0.4 to 1.0 had little impact upon either the secreted HCO3 − concentration or the volume flow. However, modelling showed that a reduction in basolateral AE2 activity by ∼80% was essential in minimizing the intracellular Cl− concentration following cAMP stimulation and thereby maximizing the secreted HCO3 − concentration. The addition of a basolateral Na+‐K+‐2Cl− cotransporter (NKCC1), assumed to be present in rat and mouse ducts, raised intracellular Cl− and resulted in a lower secreted HCO3 − concentration, as is characteristic of those species. We conclude therefore that minimizing the driving force for Cl− secretion is the main requirement for secreting 140 mm HCO3 −.
Keywords: bicarbonate secretion, computational model, pancreatic duct
Key points
The ductal system of the pancreas secretes large volumes of alkaline fluid containing HCO3 − concentrations as high as 140 mm during hormonal stimulation.
A computational model has been constructed to explore the underlying ion transport mechanisms. Parameters were estimated by fitting the model to experimental data from guinea‐pig pancreatic ducts.
The model was readily able to secrete 140 mm HCO3 −. Its capacity to do so was not dependent upon special properties of the cystic fibrosis transmembrane conductance regulator (CFTR) anion channels and solute carrier family 26 member A6 (SLC26A6) anion exchangers.
We conclude that the main requirement for secreting high HCO3 − concentrations is to minimize the secretion of Cl− ions.
These findings help to clarify the mechanism responsible for pancreatic HCO3 − secretion, a vital process that prevents the formation of protein plugs and viscous mucus in the ducts, which could otherwise lead to pancreatic disease.
Abbreviations
- AE2
anion exchanger 2
- CFTR
cystic fibrosis transmembrane conductance regulator
- NBC1
Na+‐HCO3 − cotransporter 1
- NHE1
Na+/H+ exchanger 1
- NKCC1
Na+‐K+‐Cl− cotransporter 1
- SLC26A6
solute carrier family 26 member A6
Introduction
The human pancreas secretes a large volume of alkaline isotonic fluid (2–3 l day–1) containing important digestive enzymes. The HCO3 − concentration of the pancreatic juice reaches ∼140 mm under stimulation and the HCO3 −‐rich fluid is secreted mainly by the epithelial cells lining the ductal tree (Argent et al. 2012; Lee et al. 2012). HCO3 − secretion depends critically upon the activity of the cystic fibrosis transmembrane conductance regulator (CFTR) anion channel. In cystic fibrosis, the pancreatic duct epithelium secretes severely reduced amounts of fluid, with neutral or acidic pH, which results in obstruction of the duct lumen by protein plugs or viscous mucus (Scheele et al. 1996; Quinton, 2008).
Over the last 20 years, experimental studies on isolated pancreatic ducts and duct cells, using microfluorometry and electrophysiology, have determined the membrane localization of several H+ and HCO3 − transporters, K+ channels and CFTR (Steward et al. 2005; Steward & Ishiguro, 2009; Argent et al. 2012; Lee et al. 2012). It is now generally accepted that HCO3 − accumulation across the basolateral membrane is mediated by HCO3 − uptake via a Na+‐HCO3 − cotransporter (NBC1) and indirectly by H+ extrusion via a Na+/H+ exchanger (NHE1). In the guinea‐pig duct, which is the preferred experimental model for studies of HCO3 − secretion, NBC1 is activated by stimulation with secretin, as well as by low intracellular Cl− concentrations (Shcheynikov et al. 2015), and contributes more to HCO3 − accumulation than NHE1 (Ishiguro et al. 1996a). HCO3 − secretion across the apical membrane can be mediated both by the HCO3 − conductance of CFTR and by Cl−/HCO3 − exchange. Measurements of the electrochemical gradient for HCO3 − (Ishiguro et al. 2002b) and the HCO3 − permeability of CFTR in the apical membrane suggest that CFTR is the dominant pathway during maximal secretion (Ishiguro et al. 2009).
To investigate how the pancreatic duct epithelium generates a HCO3 −‐rich fluid, previous studies constructed an early computational model of electrolyte transport based on simple kinetic descriptions of the component ion channels and transporters (Sohma et al. 1996, 2000). Although the model was capable of simulating HCO3 − secretion at concentrations typical of rat and mouse pancreas (up to ∼70 mm) (Mangos et al. 1973; Sewell & Young, 1975), it was unable to achieve the higher concentrations observed in other species, including the guinea‐pig and human. By raising the permeability of CFTR, the activity of NBC1, and the apical to basolateral ratio of Cl−/HCO3 − exchanger activity, the epithelial model could secrete up to ∼120 mm HCO3 −. However, to secrete 140 mm HCO3 −, a second stage was deemed necessary in which the distal parts of the ductal system would need a much reduced apical Cl− permeability and reduced apical Cl−/HCO3 − exchanger activity (Sohma et al. 2000). However, a two‐stage mechanism such as this would be inconsistent with the observed ability of sealed, isolated duct segments to generate high luminal HCO3 − concentrations in situ (Ishiguro et al. 1996b; Ishiguro et al. 1998).
When the model was published in 2000 (Sohma et al. 2000), the available information was limited to the membrane localization of the main H+ and HCO3 − transporters and numerical values for the membrane potentials in ducts isolated from rat pancreas which, as already mentioned, secretes only ∼70 mm HCO3 −. Subsequently, there have been a number of important developments. First, measurements of intracellular pH (pHc), Cl− concentration ([Cl−]c) and membrane potential (E) have been obtained in microperfused interlobular ducts isolated from guinea‐pig pancreas, a species that is capable of secreting ∼140 mm HCO3 − (Padfield et al. 1989; Ishiguro et al. 2000; Ishiguro et al. 2002a, 2002b; Ishiguro et al. 2009). Second, the HCO3 −/Cl− permeability ratio (P HCO3/P Cl) of CFTR has been shown to be regulated by [Cl−]c‐sensitive kinases, and is capable of rising to 1.0 or more when [Cl−]c is low (Park et al. 2010). Third, the transporter responsible for apical Cl−/HCO3 − exchange activity has been identified as solute carrier family 26 member A6 (SLC26A6) (Wang et al. 2006; Ishiguro et al. 2007a) and shown to be electrogenic with a 1:2 Cl−/HCO3 − exchange stoichiometry (Shcheynikov et al. 2006), raising the possibility that this might help to raise luminal HCO3 − to a higher concentration than previously assumed (Steward et al. 2005). Fourth, gastric and non‐gastric H+,K+‐ATPases have been detected in rat and human pancreatic ducts, and shown to make a significant contribution to fluid secretion in the rat (Novak et al. 2011; Wang et al. 2015). Finally, K+ channels have been identified at the apical membrane of guinea‐pig duct cells (Venglovecz et al. 2011; Venglovecz et al. 2015).
The transporters and channels included in our current model of guinea‐pig pancreatic duct epithelium (Fig. 1) are broadly similar to those in the model by Sohma et al. (2000). At the apical membrane, we have examined the potential advantages of 1:2 Cl−/HCO3 − exchange via SLC26A6 over the previously assumed 1:1 stoichiometry of the apical exchanger. The CFTR channel is assumed to have both Cl− and HCO3 − permeabilities, and so we have explored the effects of varying the HCO3 −:Cl− permeability ratio. At the basolateral membrane, we have focused particularly on the contribution of the anion exchanger 2 (AE2) Cl−/HCO3 − exchanger and we have also introduced a Na+‐K+‐2Cl− cotransporter (NKCC1) to test the hypothesis that its activity could account for the lower concentrations of HCO3 − in rat and mouse pancreatic juice (Fernández‐Salazar et al. 2004). The possible contributions of apical K+ channels and H+,K+‐ATPases located at both basolateral and apical membranes have also been considered.
Figure 1. Transport pathways included in the computational model of guinea‐pig pancreatic duct epithelium.
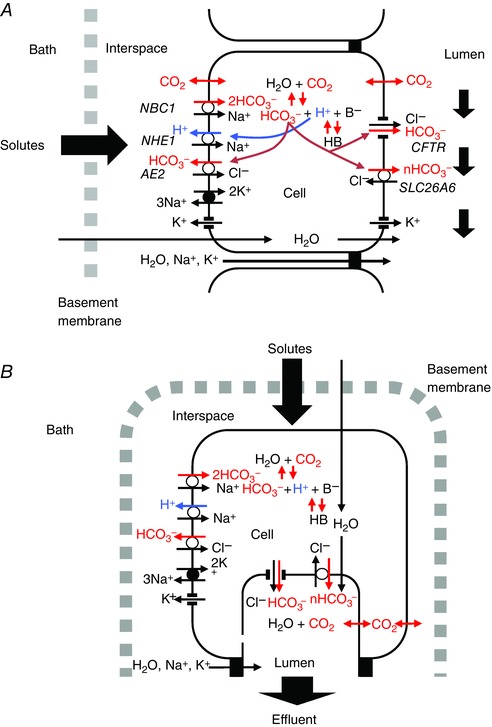
A, perfused duct model. The epithelium is bathed on both sides with solutions of fixed composition. This corresponds to the microperfused, isolated duct configuration. B, secreting duct model. Here, the basolateral bathing solution has a fixed composition but the small luminal space contains the secreted fluid whose composition may change with time. This corresponds to the in vivo situation. Basolateral transporters include an Na+‐2HCO3 − cotransporter (NBC1), an Na+/H+ exchanger (NHE1), a Cl−/HCO3 − exchanger (AE2) and an Na+,K+‐ATPase. Apical transporters include the Cl− and HCO3 − conductances of CFTR and a Cl−/nHCO3 − exchanger (SLC26A6, n = 1 or 2). Both apical and basolateral membranes have CO2 and H2O permeabilities, a K+ conductance and a small H+ conductance. Intracellular pH is buffered by HCO3 −/CO2 and by an intrinsic (B−/HB) buffering system. The paracellular pathway is represented by Na+ and K+ conductances at the tight junction. In addition to the transporters shown, we examined the effect of introducing H+,K+‐ATPase activity at both apical and basolateral membranes, as well as Na+‐K+‐2Cl− cotransporter (NKCC1) activity at the basolateral membrane in some of the simulations. [Color figure can be viewed at wileyonlinelibrary.com]
Our strategy has been to use a large set of experimental data obtained from isolated guinea‐pig ducts to find best‐fit parameter values for the model in both the unstimulated and secretin‐stimulated conditions. The crucial factor in achieving a HCO3 −‐rich secretion is that Cl− uptake across the basolateral membrane should be minimal. In the guinea‐pig, this requires the suppression of basolateral Cl−/HCO3 − exchange via AE2 during secretin‐stimulated secretion.
Methods
Model structure
The pancreatic duct epithelium is represented as a four‐compartment system (Fig. 1) comprising the basolateral bathing fluid (represented by the suffix b), the lateral intercellular space (‘interspace’, i), the cytoplasm (c) and the lumen (l). Each compartment is assumed to be well stirred; no correction is made for possible unstirred‐layer effects. Movements of water, solutes and electrical charge occur across four barriers: the basement membrane (bm), the basolateral membrane (bl), the apical membrane (ap) and the tight junction (tj).
In running model simulations, the composition of the luminal fluid may be set to pre‐defined values to simulate perfused duct experiments (Fig. 1 A). Alternatively, the composition of the luminal fluid is allowed to evolve with time and is defined by the fluid secreted by the epithelial cells, thus simulating secreting duct experiments (Fig. 1 B). In both versions of the model, the basolateral bathing fluid is a large volume of pre‐defined composition, uninfluenced by the transepithelial fluxes. The compositions of the solutions used in the model simulations are shown in Table 1.
Table 1.
Composition of solutions
| Hepes | Na+‐free Hepes | Low HCO3 – | High HCO3 – | |
|---|---|---|---|---|
| [K+] (mm) | 5 | 5 | 5 | 5 |
| [Na+] (mm) | 140 | 0.1 | 140 | 140 |
| [Cl–] (mm) | 141 | 141 | 124 | 24 |
| [HCO3 –] (mm) | 0.1 | 0.1 | 25 | 125 |
| [HEPES] (mm) | 10 | 10 | – | – |
| [X] (mm) | 12 | 152 | 12 | 12 |
| pH | 7.40 | 7.40 | 7.42 | 8.12 |
| pCO2 (mmHg) | 0.1 | 0.1 | 38 | 38 |
Cell, lumen and interspace geometry
All extensive variables and parameters (fluxes, currents, permeabilities and transporter activities) are normalized to the luminal surface area of the epithelium. Based on morphological data from rat pancreatic ducts (Argent et al. 1986), the apical and basolateral membrane area factors (A ap and A bl) are set at 1.0 and 14.3 (cm2 membrane per cm2 epithelium), respectively. The initial cell volume is 1.1 μl cm−2, corresponding to a cell height of 10 μm. The luminal volume is 0.11 μl cm−2, corresponding to a luminal diameter of ∼10 μm, as found in the smaller intralobular ducts where most of the secreted fluid is thought to arise (Burghardt et al. 2003). The initial interspace volume was set at 0.011 μl cm−2, which is 1% of the cell volume.
Transporter kinetics
We have used a number of simplifying assumptions to minimize the number of unknown or poorly‐defined parameter values in the model. For transporters, we assume instantaneous binding and dissociation at substrate binding sites, and symmetrical dissociation constants for inward‐ and outward‐facing conformations. For the ion channels and tight junctions, we use the Goldman–Hodgkin–Katz equation. Simple flux equations may not give entirely accurate descriptions, although they do ensure that reversal conditions are precisely defined and that the turnover rates and fluxes increase the further the substrate gradients are from equilibrium. The magnitudes of the fluxes are determined by permeability coefficients (P) and activity coefficients (G), which combine the protein expression densities and unit permeabilities and activities of individual channels and transporters.
Although the P and G values for seven of the channels and transporters were allowed to vary during the optimization of the model, the other kinetic parameters (e.g. dissociation constants) were fixed at estimated values based on published data wherever possible.
Flux equations
CO2 and NH3 diffusion
Permeant, uncharged solutes CO2 and NH3 are assumed to cross the apical and basolateral membranes by simple diffusion at rates determined by Fick's first law. Thus, for example, the flux of CO2 across the apical membrane is:
| (1) |
where is the permeability coefficient and A ap is the apical membrane area factor. (Fluxes and currents from interspace to cell and cell to lumen take positive values.)
Values for and (Table 2) were obtained by fitting the perfused duct model to experimental data from perfused guinea‐pig ducts (Ishiguro et al. 2000). In those experiments, changes in pHc were recorded when the luminal perfusate was switched from a Hepes‐buffered solution to a normal HCO3 –‐buffered solution. In the model simulations, the size of the initial drop in pHc was found to be relatively insensitive to the absolute CO2 permeability values but quite sensitive to the apical/basolateral permeability ratio. The best fit was obtained when was 0.7. The absolute value of was taken to be 1 cm s−1, which is comparable with values reported for the erythrocyte membrane (Forster et al. 1998).
Table 2.
Fixed parameters in the pancreatic duct model
| Parameter | Value | Unit | |
|---|---|---|---|
| Apical membrane | |||
| SLC26A6 | n | 2 / 1* | |
| K Cl | 5 | mm | |
| K HCO3 | 12 / 6* | mm | |
| CFTR | P HCO3 /P Cl | 0.4 | |
| H+,K+‐ATPase | K H | 5 × 10−4 | mm |
| K K | 3 | mm | |
| H+ permeability | P H | 10−3 | cm s−1 |
| CO2 permeability | P CO2 | 0.7 | cm s−1 |
| NH3 permeability | P NH3 | 0.1 | cm s−1 |
| Water permeability | L p | 3 × 10−5 | cm s−1 atm−1 |
| Basolateral membrane | |||
| NBC1 | K Na | 500 | mm |
| K HCO3 | 30 | mm | |
| R l / k | 100 | ||
| K als | 10.2 | mm | |
| n Cl | −1 | ||
| NHE1 | G NHE | 0.485 | nmol s−1 cm−2 |
| K Na | 100 | mm | |
| K H | 5 × 10−4 | mm | |
| K als | 1.4 × 10−4 | mm | |
| n H | 2.5 | ||
| AE2 | K Cl | 10 | mm |
| K HCO3 | 1 | mm | |
| NKCC1 | K Na | 63.3 | mm |
| K K | 108 | mm | |
| K Cl | 4.6 | mm | |
| Na+,K+‐ATPase | E rev | −200 | mV |
| K K | 1.4 | mm | |
| K Na | 25 | mm | |
| H+,K+‐ATPase | K H | 5 × 10−4 | mm |
| K K | 3 | mm | |
| H+ permeability | P H | 10−3 | cm s−1 |
| CO2 permeability | P CO2 | 1 | cm s−1 |
| NH3 permeability | P NH3 | 0.1 | cm s−1 |
| Water permeability | L p | 3 × 10−5 | cm s−1 atm−1 |
| Tight junction | |||
| K+ permeability | P K | 6 × 10−3 | cm s−1 |
| Na+ permeability | P Na | 6 × 10−3 | cm s−1 |
| Basement membrane | |||
| H+ permeability | P H | 1 | cm s−1 |
| CO2 permeability | P CO2 | 103 | cm s−1 |
| NH3 permeability | P NH3 | 103 | cm s−1 |
| Other solute permeabilities | P S | 10−3 | cm s−1 |
| Water premeability | L p | 102 | cm s−1 atm−1 |
*Alternative values are shown for the 1:2 and 1:1 Cl–/HCO3 – stoichiometries of SLC26A6.
For the purpose of simulating the changes in pHc evoked by exposure to an NH4 + pulse, the NH3 permeability of the apical and basolateral membranes (P NH3) was taken to be 0.1 cm s−1 (Star et al. 1987). This value is from a study of renal collecting duct epithelium and may not be truly representative of the pancreatic duct. However, the good fit of the rise and fall of the NH4 + pulse simulations to the experimental data suggests that it is in the right range.
Water flow
Water flow across the apical and basolateral membranes was assumed to be driven by both osmotic and hydrostatic pressure gradients, although, in practice, the latter contribute very little. Thus, the volume flow across the basolateral membrane, for example, was described by the equation:
| (2) |
where is the hydraulic conductivity of the membrane, Osm c and Osm i represent the intracellular and interspace osmolarities, and P i is the hydrostatic pressure in the interspace. Hydrostatic pressures in the cell, basal bath and lumen were taken to be zero.
Osmolarity was calculated as the sum of the molar concentrations of all the ions and other solutes in each compartment. For simplicity, no adjustment was made for the osmotic coefficients of the different solutes, and their reflection coefficients at the apical and basolateral membranes were all set at 1.
The possible contribution of the paracellular pathway to water flow across secretory epithelial remains a contentious issue (Burghardt et al. 2006). In this model, we have made no assumptions about whether water flow is predominantly transcellular, paracellular or follows both pathways. Although we chose routinely to assign water permeability to the apical and basolateral membranes rather than the tight junctions, identical results were obtained when the transepithelial water permeability was assigned exclusively to the tight junctions. This is because the osmotic gradients between the well‐stirred interspace and luminal compartments are the same, regardless of whether the water flow is transcellular or through the tight junctions.
The value of L p for the apical and basolateral membranes was estimated from measurements of the osmotic permeability of isolated rat ducts (Burghardt et al. 2006). It was assumed to be the same, per unit membrane area, for both membrane domains (Table 2); thus, the overall basolateral permeability is ∼14 times greater than the apical permeability. Using these values, the fluid generated by the secreting‐duct configuration of the model is ∼3% hypertonic at maximal secretory rates. There are no accurate values in the literature for the magnitude of the hypertonicity of the secreted fluid, although this value represents a typical upper limit for ‘isotonic’ fluid transport across epithelia.
Water flow across the basement membrane is driven solely by the hydrostatic pressure gradient:
| (3) |
The hydraulic conductivity was set at a value based upon measurements on isolated basement membranes prepared from kidney tubules (Welling & Grantham, 1972; Welling & Welling, 1978). In the pancreatic duct model, the hydrostatic pressure in the basal bath is taken to be zero, and so a negative pressure P i has to develop in the interspace in order to drive the flow of water from basal bath to interspace.
Ion channels
Similar to Sohma et al. (2000), we have used the Goldman–Hodgkin–Katz flux equation to describe the movement of K+, Cl– and HCO3 – through the basolateral K+ and apical CFTR channels, and also the movement of Na+ and K+ through the tight junctions. Thus, for example, the flux of Cl– through the apical CFTR channels is given by:
| (4) |
where is the Cl– permeability coefficient of CFTR and E ap is the apical membrane potential. z, F, R and T have their usual meanings.
The HCO3 –/Cl– permeability ratio of CFTR was initially set at the published value of ∼0.4 for guinea‐pig CFTR (O'Reilly et al. 2000). It was subsequently varied from 0 to 2 to take account of evidence that the ratio may increase significantly when the extracellular Cl– concentration is low (Park et al. 2010). Absolute values for the CFTR and K+ channel permeabilities were obtained in the course of model optimization.
The Na+ and K+ permeabilities of the tight junctions were assumed to be equal and set to values (Table 2) that yielded transepithelial potential differences similar to those measured in guinea‐pig pancreatic ducts (Ishiguro et al. 2009). The transepithelial electrical resistance of the model was estimated to be 32 Ω cm2, which is comparable with values of ∼50 Ω cm2 reported for isolated rat ducts (Novak & Greger, 1991).
Small apical and basolateral permeabilities to H+ were also included to improve the stability of the model in simulations of HCO3 –‐free experiments. The H+ permeability coefficient (P H) was set at 10−3 cm s−1, a value typical of biological membranes (Nichols & Deamer, 1980).
Basolateral Na+,K+‐ATPase
The equation for the turnover rate of the Na+,K+‐ATPase is based on the simple kinetic description of (Hartmann & Verkman, 1990):
| (5) |
where G NaK is the activity coefficient (combining the spatial density of the pump in the membrane with the unit activity), K Na and K K are the saturation constants for intracellular Na+ and extracellular K+, and E rev is a notional reversal potential.
Values for K Na, K K and E rev (Table 2) are taken from Sohma et al. (1996). The pump is assumed to move 3 Na+ ions out of, and 2 K+ ions into, the cell in each cycle. The activity coefficient G NaK was obtained in the course of model optimization.
Basolateral Na+/H+ exchanger (NHE1)
Our kinetic description of NHE1 is based on a simple, generic model for neutral cation or anion exchange (Sohma et al. 1996). An additional term, based on the Hill equation, has been included to represent the allosteric effect of the intracellular modifier site which gives the exchanger a steeper dependence on pHc (Cha et al. 2009). The turnover rate is thus given by:
| (6) |
where N and H represent [Na+]/K Na and [H+]/K H (i.e. the Na+ and H+ concentrations divided by their respective dissociation constants), K als is the dissociation constant for H+ binding at the allosteric modifier site, and n H is the Hill coefficient.
Values for K Na and K H are those used by Sohma et al. (1996). K als and n H were determined by fitting the NHE1 flux equation to published Na+ flux data from NHE1‐transfected fibroblasts (Wakabayashi et al. 1992). The activity coefficient G NHE1 was estimated by fitting the perfused duct model to data from Ishiguro et al. (2000) describing the recovery of pHc from intracellular acidification when Na+ was restored to the basolateral solution. All of the NHE1 parameter values are listed in Table 2.
Basolateral Na+‐HCO3 – cotransporter (NBC1)
NBC1 activity in epithelial cells is now known to be steeply regulated by intracellular Cl− concentration (Shcheynikov et al. 2015). To simulate the inhibitory effect of Cl−, an allosteric term, based on the Hill equation, was added to the flux equation used by Sohma et al. (2000):
| (7) |
B (for bicarbonate) represents [HCO3 –]/K HCO3, and R l / k is the ratio of the rate constants for the conformational changes of the loaded and unloaded carrier. The corresponding parameter values (Table 2) are taken from Sohma et al. (2000). The Cl− dissociation constant K als at the allosteric site has been estimated to be 10.2 mm (Shcheynikov et al. 2015) and we have obtained the Hill coefficient n Cl, by fitting our model to NBC1 current data from the same study. The NBC1 activity coefficient G NBC1 was obtained in the optimization of the model.
Basolateral Cl–/HCO3 – exchanger (AE2)
Following Sohma et al. (1996), the turnover rate for AE2 is given by:
| (8) |
where C represents [Cl–]/K Cl. Values for K Cl and (Table 2) are taken from Sohma et al. (1996). The activity coefficient G AE2 was determined in the optimization of the model.
Basolateral Na+‐K+‐2Cl– cotransporter (NKCC1)
The flux equation for this transporter is based upon the same kinetic principles as for NBC1 and is given by:
| (9) |
where K represents [K+]/K K. Values for K Na, K K and K Cl (Table 2) are taken from (Benjamin & Johnson, 1997). The activity coefficient of NKCC1, G NKCC1, was set to zero for most of the work reported here, although we did examine the effect of increasing its value on the behaviour of the secreting duct model.
Basolateral H+,K+‐ATPase
The flux equation for H+,K+‐ATPase was based on the Hartmann and Verkman
(1990) equation for Na+,K+‐ATPase (see above) assuming an electroneutral 2:2 stoichiometry:
| (10) |
Although there is no evidence for Na+ independent acid extrusion in guinea‐pig pancreatic duct cells (Ishiguro et al. 1996), it has been observed in studies of the rat pancreatic duct (Novak et al. 2011) and the human ductal cell line Capan‐1 (Wang et al. 2015), and attributed to an omeprazole‐sensitive H+,K+‐ATPase. An approximation for the activity coefficient G HK was obtained by fitting the pancreatic duct model to data for the recovery of pHc from acidification in Capan‐1 cells in the absence of Na+ (Wang et al. 2015). Values for the saturation coefficients K H and K K (Table 2) were estimated from the literature (Van der Hijden et al. 1990).
For most of the present study, G HK was set to zero. However, to explore the possible contribution of a basolateral H+,K+‐ATPase, we examined the effect of introducing basolateral G HK values comparable with that estimated for Capan‐1 cells. A possible contribution from apical H+,K+‐ATPase activity (Novak et al. 2011) was modelled in exactly the same way.
Apical Cl–/HCO3 – exchanger (SLC26A6)
The kinetic scheme used for SLC26A6, allowing for its possible electrogenicity, is shown in Fig. 2 A. We made certain simplifying assumptions: (i) there is a single binding site for either one Cl– ion or n HCO3 – ions (n = 1 or 2), which has to be fully occupied for translocation to occur; (ii) the velocity constants for the forward and backward translocation steps are the same at E ap = 0 mV; (iii) the charge on the unloaded carrier is +1 (thus translocation is voltage independent except when carrying two HCO3 – ions); (iv) the dissociation constants for Cl– and HCO3 – (K Cl and ) are the same for the inward‐ and outward‐facing orientations of the binding site. The turnover rate of the exchanger is therefore:
| (11) |
Figure 2. Estimation of SLC26A6 kinetic parameters.
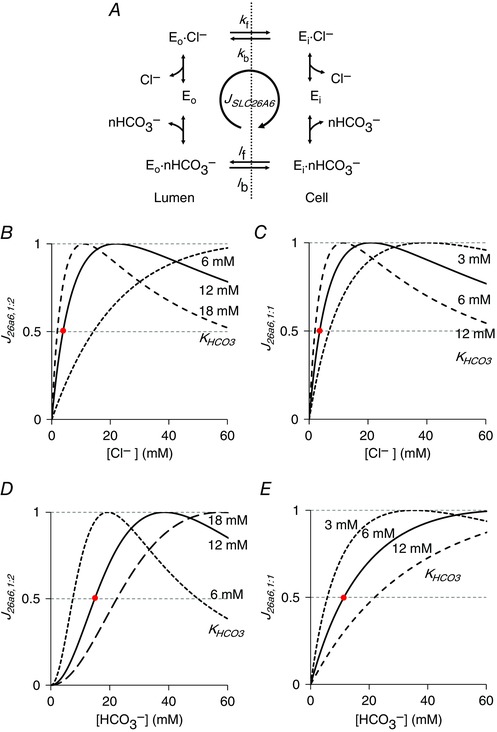
A, kinetic model for the apical Cl–/HCO3 – exchanger SLC26A6 where Eo and Ei represent the outward‐ and inward‐facing conformations. In this simplified model, the forward (subscript f) and backward (subscript b) rate constants for the Cl–‐loaded (k) and HCO3 –‐loaded (l) transporters are all assumed to be identical. The Cl–:HCO3 – stoichiometry is 1:n, where n may be 1 or 2. B–E, estimation of the HCO3 – dissociation constant (). SLC26A6 flux (J 26A6), expressed as a fraction of its maximum value, is plotted as a function of Cl– concentration (B and C) and HCO3 – concentration (D and E) for the 1:2 (B and D) and 1:1 (C and E) stoichiometries. Values for (12 mm for 1:2, and 6 mm for 1:1) and K Cl (5 mm for both) were selected that gave a reasonable fit (intersection points in red) to the apparent affinity of the guinea‐pig exchanger for Cl– (≈ 4.5 mm) (Stewart et al. 2011) and of the human SLC26A3 exchanger for HCO3 – ( ≈ 20–30 mm) (Lamprecht et al. 2006). In (B) and (C), [HCO3 –]l = 25 mm and [HCO3 –]c = 20 mm. In (D) and (E), [Cl–]l = 104 mm and [Cl–]c = 30 mm. In (B) and (D), E ap = −40 mV. [Color figure can be viewed at wileyonlinelibrary.com]
where C and B represent [Cl–]/K Cl and [HCO3 –]/ as before.
Using physiological ranges for the intracellular and extracellular Cl– and HCO3 – concentrations, the flux equation was used to estimate dissociation constants for Cl– and HCO3 – (Fig. 2 B–E). Values were obtained (Table 2) that were in broad agreement with the apparent Cl– affinity (the Cl– concentration giving half‐maximal turnover) of guinea‐pig SLC26A6 ( ≈ 4.5 mm) (Stewart et al. 2011) and, in the absence of any data for SLC26A6, the apparent HCO3 – affinity of the related SLC26A3 (DRA) exchanger ( ≈ 20–30 mm) (Lamprecht et al. 2006). Different K HCO3 values were required for the alternative 1:1 and 1:2 Cl–:HCO3 – stoichiometries proposed for SLC26A6. The activity coefficient G 26A6 was determined in the optimization of the model.
Basement membrane solute fluxes
All solutes are assumed to cross the basement membrane by a combination of diffusion and convection (solvent drag). We assume that there is no electrical potential gradient, and so the flux of solute S, whether charged or not, is given by the convection–diffusion equation (Hertz, 1922):
| (12) |
For simplicity, the solute permeability coefficient P S takes the same value for all solutes. The reflection coefficient for solvent drag σS is taken to be zero.
H+ buffering
Intracellular H+ buffering in the pancreatic duct model comprises both HCO3 –‐CO2 and intrinsic, non‐CO2 buffering systems. The model also includes an NH3‐NH4 + buffering system for the simulation of experiments used to determine the intrinsic buffering capacity. Rate constants for the intracellular buffering reactions are set to sufficiently high values to ensure almost instantaneous buffering, although not so high that the differential equations become stiff.
Intrinsic buffering
Intrinsic buffering is modelled as the equilibrium between a single weak base B– and its conjugate weak acid HB:
| (13) |
where the total buffer concentration ([B]t = [HB] + [B–]) is constant. The reaction rates for H+ and B– generation are given by:
| (14) |
where k f and k b are the forward and backward rate constants defined by a single effective pK value, and V f is the volume of the fluid (cytoplasmic) component of the cell.
Values of pK and [B]t (Table 3) were obtained by least‐squares fitting of the perfused duct model to experimental measurements of intrinsic buffering capacity βint in guinea‐pig pancreatic duct cells (Szalmay et al. 2001). In the model simulations, as in the experiments, bath and lumen were initially exposed to a Na+‐free, Hepes‐buffered solution with the result that pHc decreased to a low, steady‐state value. Increasing concentrations of NH4 + were then added to bath and lumen, and values of βint were obtained over a range of different pHc values from the changes in pHc evoked by step changes in intracellular NH4 + concentration using:
| (15) |
Table 3.
Parameters in H+ buffering systems
| Intrinsic B–/HB | [B]t | 95 | mm |
| pK | 6.4 | ||
| k f | 3.981 | s−1 | |
| k b | 107 | M−1 s−1 | |
| Intracellular and interspace | pK’ | 6.1 | |
| HCO3 –/CO2 | k f | 79.43 | s−1 |
| k b | 108 | M−1 s−1 | |
| Luminal HCO3 –/CO2 | pK’ | 6.1 | |
| k f | 79.43 × 10−4 | s−1 | |
| k b | 104 | M−1 s−1 | |
| NH3/NH4 + | pK | 8.9 | |
| k f | 0.1259 | s−1 | |
| k b | 108 | M−1 s−1 |
Values of βint were assigned to the mid point of the corresponding pHc change.
HCO3 –/CO2 buffering
For the intracellular HCO3 –/CO2 buffering system:
| (16) |
the reaction rates for H+ and HCO3 – generation are given by:
| (17) |
where k f and k b have large values that are consistent with published pK’ values (Table 3).
NH3/NH4 + buffering
The intrinsic intracellular buffering capacity of the duct model, and its pH dependence, were determined by simulating the application of a range of extracellular NH4 + concentrations. To replicate the effects of NH3 entry on pHc, the model includes an intracellular NH3/NH4 + buffering system:
| (18) |
The reaction rates for H+ and NH3 generation are given by:
| (19) |
where k f and k b have large values that are consistent with published pK values (Table 3).
Luminal and interspace HCO3 –/CO2 buffering
The HCO3 –/CO2 buffering reaction in the lumen and interspace is described in the same way as in the cytoplasm. The reaction rate for H+ and HCO3 − generation in the lumen, for example, is given by:
| (20) |
where V l is the luminal volume. The rate constants in the lumen are reduced by a factor of 104 relative to the cytoplasm (Table 3) to reflect the lower extracellular carbonic anhydrase activity (Endeward & Gros, 2005).
Intracellular solute concentrations
The cell content of each solute S is computed by integrating the net solute flux J S into the cell. For most of the solutes, there are several pathways for entry or exit across the apical and basolateral membranes. Fluxes from bath to interspace, interspace to cell, cell to lumen and interspace to lumen (through the tight junction) are treated as positive. Solutes such as H+ and HCO3 − may also be generated or consumed by buffering reactions within the cell, lumen and interspace.
The net fluxes of the solutes into the cell across apical and basolateral membranes, and from buffering reactions, are:
| (21) |
The intracellular concentration of each solute S is calculated by dividing the total cell content of that solute by the fluid volume of the cell V f (defined below), thus:
| (22) |
where is the initial cell content of S.
Cell volume
It is assumed that 40% of the initial volume of the cell () is occupied by non‐fluid constituents, and that the size of this component remains constant. The fluid component of the cell volume V f, however, varies with time and is computed by integrating the volume fluxes (water fluxes expressed in units of volume) across the apical and basolateral membranes, and , respectively:
| (23) |
Total cell volume is therefore:
| (24) |
Interspace ion concentrations, volume and pressure
The interspace content of solute S is computed by integrating the net solute flux J S into the interspace. This comprises fluxes from bath to interspace, interspace to cell, and interspace to lumen. Solutes such as H+ and HCO3 − are also generated and consumed by buffering reactions.
The net fluxes of the solutes into the interspace are:
| (25) |
The concentration of S in the interspace is calculated by dividing the interspace content of that solute by the interspace volume V i (defined below), thus:
| (26) |
Interspace volume varies with time and is computed by integrating the net volume flow into the space:
| (27) |
where is the initial volume of the interspace and and are the volume flows across the basement and basolateral membranes. The hydrostatic pressure in the interspace P i, which plays a critical role in drawing water through the basement membrane, is calculated using an approximation of the pressure–volume characteristics of a thin‐walled elastic tube (Spring & Hope, 1978):
| (28) |
where the constants α and β take the values 8.6 and 0.38 respectively. The third constant is calculated using:
| (29) |
to ensure that the initial interspace pressure, at the start of each simulation, is close to zero.
Luminal ion concentrations
In the secreting duct configuration, the luminal content of each solute S is computed by integrating the net fluxes into the lumen across the apical membrane and tight junction, and , respectively, and the solute lost in the ductal effluent :
| (30) |
where is the effluent volume flow from the duct lumen.
Because the volume of the luminal space V l is fixed (Fig. 1 B), the effluent volume flow is equal to the volume inflow across the apical membrane . Thus the luminal concentration of S is given by:
| (31) |
where is the initial luminal content of S.
Currents and membrane potentials
Total currents across apical and basolateral membranes and via the tight junctions are:
| (32) |
| (33) |
where the currents follow the same sign convention as the fluxes i.e. positive in the secretory direction across each barrier.
Apical and basolateral membrane potentials (E ap and E bl) and the transepithelial potential difference (E tj) are computed by integrating the net currents across the apical membrane (I ap), basolateral membrane (I bl) and tight junction (I tj):
| (34) |
| (35) |
| (36) |
where C m is the specific capacitance of the membrane (1 μF cm−2).
The basement membrane has a high, non‐selective permeability to all of the solutes in this model, so the differences in concentrations between interspace and basal bath are very small. We therefore assume that there is no significant electrical potential difference across the basement membrane.
Computational methods
The model was constructed as a set of simultaneous ordinary differential equations in MATLAB (MathWorks, Natick, MA, USA) using the Simulink interface to provide a modular structure and facilitate the simulation of time‐course experiments. The ode23s solver, based on a modified Rosenbrock formula of order 2, was used and the relative and absolute tolerances were set at 10−5.
Permeability and activity coefficients of seven channels and transporters were estimated by least‐squares optimization to minimize the residual errors between the predictions of the model and a set of 21 experimental measurements as listed in Table 4. In most cases, the SEM values obtained in the experimental studies were used to weight the data for optimization. The weighting factors for pHc, [Cl−]c and J v, however, were increased slightly to improve the fit to these critical variables. Other parameters (Table 2) were fixed at values obtained from the literature or derived unambiguously from our own experimental data.
Table 4.
Experimental data used for parameter estimation
| Resting | Stimulated | |||
|---|---|---|---|---|
| Mean | SEM | Mean | SEM | |
| Perfused duct – low luminal [HCO3 −] | ||||
| pHc | 7.34a | 0.001* | 7.32a | 0.001* |
| E bl (mV) | −60.6b | 2.6 | −52.5b | 2.3 |
| [Na+]c (mm) | 11.7c | 1.2 | 17.2c | 1 |
| [Cl–]c (mm) | 31.2d | 1.3* | 35.5d | 1.7* |
| ∆[Cl–]c with luminal H2DIDS | 1d | 0.7 | 6d | 0.6 |
| ∆[Cl–]c with basolateral H2DIDS | 7.1d | 0.7 | 0d | 0.3 |
| Perfused duct – high luminal [HCO3 −] | ||||
| pHc | 7.34a | 0.01 | 7.32a | 0.01 |
| E bl (mV) | −64.3b | 2.7 | −61.8b | 2.4 |
| [Cl–]c (mm) | 12.5d | 1.6* | 6.7d | 0.7 |
| Secreting duct | ||||
| J v (nl min−1 mm−2) | 2.02e | 0.052* | 3.52e | 0.041* |
| [HCO3 –]l (mm) | – | – | 140f | 1 |
Simple sensitivity analyses were performed to assess the relative importance of the various transporter parameters in defining the steady‐state values of key cellular variables such as ion concentrations, membrane potentials and secretory fluxes. Individual parameters P were altered by ±1% and the resulting fractional changes in the cellular variable X were used to calculate the scaled sensitivity R:
| (37) |
Results
Experimental data from studies on isolated interlobular ducts (Ishiguro et al. 1996a, 1996b; Ishiguro et al. 2000; Ishiguro et al. 2002a, 2002b) and isolated, perfused guinea‐pig pancreas (Padfield et al. 1989) were used to determine best‐fit values for seven key transport parameters in our computational model of pancreatic duct epithelium. The chosen data (Table 4) included steady‐state intracellular ion concentrations, membrane potentials and volume flow rates from luminally perfused ducts and from secreting (i.e. non‐perfused) ducts under a variety of experimental conditions.
The transport parameters estimated by optimization of the model are listed in Table 5. They represent the activities and permeabilities of the main transporters and channels involved in ductal electrolyte secretion. Optimization was performed for both the 1:2 and 1:1 stoichiometries proposed for Cl−/HCO3 − exchange by SLC26A6, and in the presence and absence of cAMP stimulation.
Table 5.
Estimated parameter values in resting and stimulated conditions for the alternative 1:2 and 1:1 stoichiometries of SLC26A6
| Resting | Stimulated* | ||||||
|---|---|---|---|---|---|---|---|
| 1:2 | 1:1 | 1:2 | 1:1 | Unit | |||
| Apical membrane | |||||||
| SLC26A6 activity | G 26A6 | 0.43 | 1.36 | 5.19 (×12) | 19.4 (×14) | nmol s−1 cm−2 | |
| CFTR permeability |
|
8.58 | 9.22 | 60.8 (×7) | 68.0 (×7) | 10−6 cm s−1 | |
| K+ channel permeability† |
|
0.36 | 0.33 | 0.36 (×1) | 0.33 (×1) | 10−6 cm s−1 | |
| Basolateral membrane | |||||||
| NBC1 activity | G NBC1 | 91.1 | 91.3 | 402 (×4) | 401 (×4) | nmol s−1 cm−2 | |
| AE2 activity | G AE2 | 0.164 | 0.197 | 0.046 (×0.3) | 0.045 (×0.2) | nmol s−1 cm−2 | |
| Na+,K+‐ATPase activity | G NaK | 4.37 | 3.90 | 4.37 (×1) | 3.90 (×1) | nmol V−1 s−1 cm−2 | |
| K+ channel permeability† |
|
1.01 | 0.98 | 2.45 (×2) | 2.26 (×2) | 10−6 cm s−1 | |
*Values in parenthesis show the approximate fold changes in the resting parameter values required to represent the stimulated condition.
†The ratio of apical K+ permeability to whole‐cell K+ permeability (taking into account membrane area factors) was fixed at 0.01 for optimization of the model in the stimulated condition.
As expected, the parameter changes required to simulate cAMP stimulation included significant increases in SLC26A6 activity and CFTR permeability at the apical membrane. Smaller increases in NBC1 activity and basolateral K+ permeability, and, importantly, a decrease in AE2 activity, were also necessary at the basolateral membrane. The main differences in the results obtained with the alternative stoichiometries for SLC26A6 are that the activity of a 1:1 exchanger would have to be two to three times greater than that of a 1:2 exchanger. This is not surprising when considering that a 1:2 exchanger secretes twice as much HCO3 − per transport cycle.
NBC1, SLC26A6 and CFTR dominate HCO3 − transport in the perfused duct
Luminal perfusion of isolated ducts allows separate manipulation of the solutions bathing the apical and basolateral membranes. Simulation of perfused duct experiments using the computational model allowed us to compare the time courses of the changes in variables, as well as the steady‐state values, with experimental data.
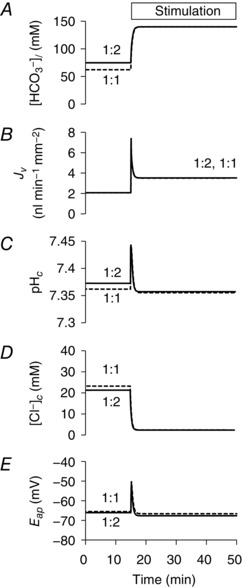
Figure 3 shows the changes in [Cl−]c, E bl and pHc evoked in the model by cAMP stimulation, as well as by raising the luminal HCO3 − concentration from 25 to 125 mm in both resting and stimulated conditions. The time courses of these changes compare remarkably well with the corresponding experimental data: thus, [Cl−]c rises slightly when cAMP stimulation is applied, it drops when luminal HCO3 − is raised, and this drop occurs more rapidly following stimulation (Ishiguro et al. 2002a); E bl depolarizes following stimulation, and the hyperpolarizing effect of raising luminal HCO3 − is then larger and faster (Ishiguro et al. 2002b); and, finally, pHc is relatively unchanged following stimulation (Ishiguro et al. 1996a) and only slightly increased when luminal HCO3 − is raised (Ishiguro et al. 2000). Figure 3 also shows that very similar time courses and steady‐state values are predicted using either of the alternative 1:2 and 1:1 stoichiometries for SLC26A6.
Figure 3. Changes in key variables in the perfused duct model evoked by cAMP stimulation and exposure to high luminal HCO3 − concentration.
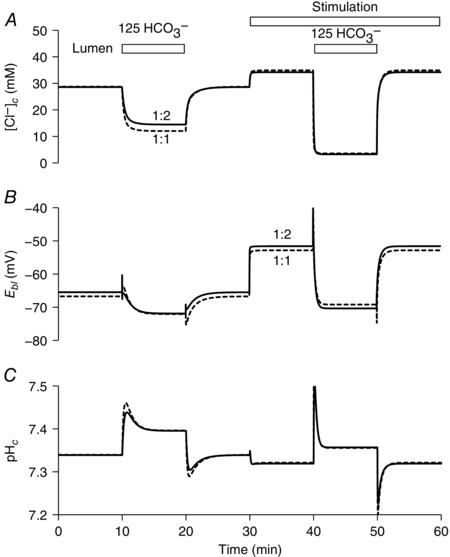
Time course of changes in intracellular Cl− concentration ([Cl−]c) (A), basolateral membrane potential (E bl) (B) and intracellular pH (pHc) (C). The lumen is perfused initially with the normal HCO3 − solution (containing 25 mm HCO3 − and 124 mm Cl−). At 10 and 40 min, the luminal perfusate is switched to a high‐HCO3 − solution (125 mm HCO3 − and 24 mm Cl−) for 10 min. Transporter activities are altered from 30 min to represent cAMP stimulation. The solid and dashed lines show the slightly different predictions for the 1:2 and 1:1 Cl−:HCO3 − stoichiometries of the SLC26A6 exchanger.
Steady‐state fluxes of HCO3 − via the apical and basolateral transporters in the perfused duct model are shown schematically in Fig. 4. For both the 1:2 and 1:1 stoichiometries of SLC26A6 (Fig. 4 A and B, respectively) we show the progression from the resting condition to cAMP stimulation, initially with the low luminal HCO3 − (25 mm) and then with the high luminal HCO3 − (125 mm). This sequence replicates, in a perfused duct experiment, the changes that are assumed to occur with the onset of cAMP‐stimulated secretion in vivo and the subsequent rise in luminal HCO3 −.
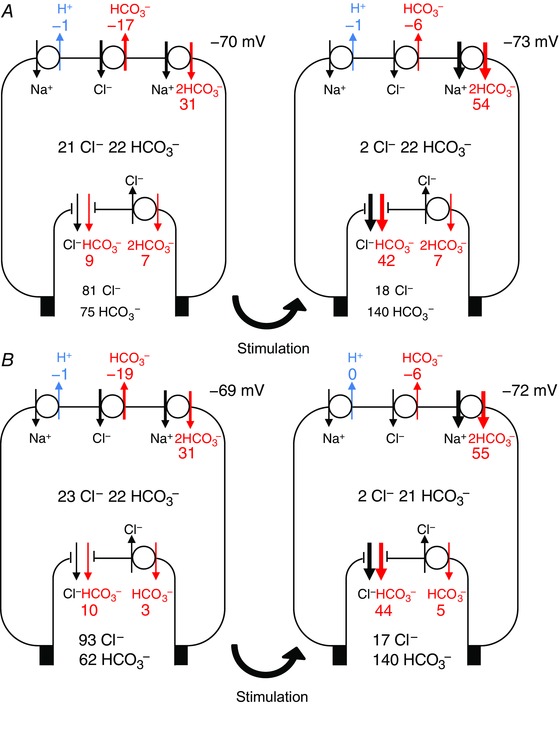
Figure 4. Steady‐state HCO3 − fluxes in the perfused duct model at rest, and following cAMP stimulation and elevation of the luminal HCO3 − concentration.
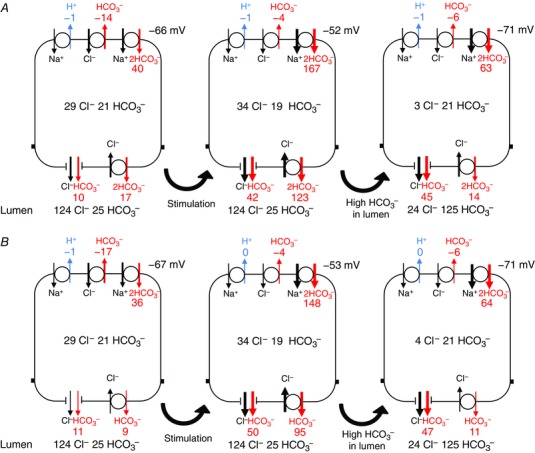
Steady‐state fluxes of HCO3 − mediated by (clockwise from top left) NHE1, AE2, NBC1, SLC26A6 and CFTR. Fluxes correspond to the steady‐state values attained in Fig. 3. Results are shown for both the 1:2 Cl−:HCO3 − stoichiometry of SLC26A6 (A) and for the 1:1 stoichiometry (B). In each case, the first panel represents the unstimulated duct perfused with the normal 25 mm HCO3 − solution, the second panel shows the effect of altering the transporter activities to represent cAMP stimulation, and the third panel shows the effect of raising the luminal HCO3 − concentration to 125 mm. Fluxes are given in nmol min−1 cm−2. Also shown are the steady‐state intracellular concentrations of Cl− and HCO3 − (mm) and the basolateral membrane potential. [Color figure can be viewed at wileyonlinelibrary.com]
For both of the SLC26A6 stoichiometries, the basolateral uptake of HCO3 − is predominantly via NBC1, with some loss via AE2, and apical efflux is via both CFTR and SLC26A6. When the luminal HCO3 − is low, cAMP stimulation causes a large increase in apical efflux via SLC26A6 (particularly with the 1:2 stoichiometry) and only a moderate increase via CFTR. When the luminal HCO3 − is raised to 125 mm, however, the net apical efflux of HCO3 − becomes slower and is predominantly (∼80%) via CFTR rather than SLC26A6. Under these conditions, the driving force for the exchanger is reduced because the Cl− and HCO3 − concentration gradients are approaching equilibrium values.
Interestingly, the alternative mechanism for HCO3 − uptake at the basolateral membrane (H+ efflux via NHE1 combined with hydration of intracellular CO2) contributes very little to the supply of HCO3 − for secretion. This is consistent with previous experimental observations suggesting the dominance of NBC1 during stimulated secretion (Ishiguro et al. 1996a) and is probably a result of the relatively high pHc under these conditions being above the set‐point for NHE1 activity.
Steady‐state values for other cellular variables, as predicted by the model, are given in Table 6. A sensitivity analysis, showing the effects of small changes in the fitted transport parameters on key cellular variables (data not shown) highlights the importance of the NBC1 and SLC26A6 activities, and the basolateral K+ permeability (presumably in maintaining membrane potential), particularly during the rapid phase of stimulated HCO3 − secretion when luminal HCO3 − is still relatively low.
Table 6.
Steady‐state values of variables in the perfused duct model in resting and stimulated conditions for the alternative 1:2 and 1:1 stoichiometries of SLC26A6
| Resting | Stimulated | ||||||
|---|---|---|---|---|---|---|---|
| [HCO3 –]l | Experimental data | 1:2 | 1:1 | Experimental data | 1:2 | 1:1 | |
| [K+]c (mm) | – | 126.4 | 126.4 | – | 116.6 | 116.9 | |
| [Na+]c (mm) | 11.7 ± 1.2a | 9.9 | 10.0 | 17.2 ± 1.0a | 19.4 | 19.3 | |
| [Cl–]c (mm) | low | 31.2 ± 2.6b | 28.6 | 28.7 | 35.5 ± 3.4b | 33.6 | 34.2 |
| high | 12.5 ± 3.2b | 14.5 | 12.0 | 6.7 ± 0.7b | 3.2 | 3.5 | |
| [HCO3 –]c (mm) | low | 20.7 | 20.7 | 19.2 | 19.3 | ||
| 20.7* | 19.8* | ||||||
| high | 23.6 | 23.7 | 21.4 | 21.3 | |||
| [X]c (mm) | – | 120.0 | 119.7 | – | 115.5 | 114.8 | |
| Osm c (mOsm) | – | 305.6 | 305.6 | – | 304.4 | 304.6 | |
| pHc | low | 7.34 | 7.34 | 7.31 | 7.31 | ||
| 7.34 ± 0.01a | 7.32 ± 0.01a | ||||||
| high | 7.39 | 7.40 | 7.35 | 7.35 | |||
| E bl (mV) | low | −59.5 ± 3.6c | −65.5 | −66.7 | −52.5 ± 2.3c | −52.0 | −53.3 |
| high | −64.3 ± 2.7c | −71.9 | −72.1 | −61.8 ± 2.4c | −70.5 | −69.5 | |
| E tj (mV) | – | −2.1 | −1.9 | – | −8.8 | −7.7 | |
| V c (μl cm−2) | – | 1.08 | 1.08 | – | 1.11 | 1.11 | |
SLC26A6 stoichiometry has little effect on volume flow and secreted HCO3 − concentration
In the secreting duct version of the model, the luminal fluid is generated by secretion rather than being defined by luminal perfusion. Using the same optimal parameter values in the model, the predicted changes in cellular variables evoked by cAMP stimulation are shown in Fig. 5. Experimental data for the secreted HCO3 − concentration and volume flow rates were used in the optimization process, and so the fit to these variables is necessarily good. However, the changes in other variables, such as pHc, [Cl−]c and E ap, are consistent with experimental data from perfused duct studies in which luminal HCO3 − was raised following cAMP stimulation (Ishiguro et al. 2000; Ishiguro et al. 2002a, 2002b). The relatively high luminal HCO3 − concentration predicted for spontaneous (unstimulated) secretion (Fig. 5 A) is also consistent with in vivo data (Padfield et al. 1989) and with measurements of luminal pH in sealed, isolated ducts (Ishiguro et al. 1996b; Ishiguro et al. 1998).
Figure 5. Changes in key variables in the secreting duct model following cAMP stimulation.
Time course of changes in secreted HCO3 − concentration ([HCO3 −]l) (A), secretory volume flow (J v) (B), intracellular pH (pHc) (C), intracellular Cl− concentration ([Cl−]c) (D) and apical membrane potential (E ap) (E). Transporter activities are altered from 15 min to represent cAMP stimulation. The solid and dashed lines show the slightly different predictions for the 1:2 and 1:1 Cl−:HCO3 − stoichiometries of the SLC26A6 exchanger.
The most interesting finding is that the two versions of the model, optimized for the alternative 1:2 and 1:1 stoichiometries of SLC26A6, are equally capable of fitting the experimental observations. Although there are small differences in the predicted values of [HCO3 −]l, pHc and [Cl−]c in unstimulated conditions (Fig. 5 A, C and D), there is almost no difference following cAMP stimulation. The reason for this becomes clear when we consider the steady‐state HCO3 − fluxes via the different transporters in the model. As shown in Fig. 6, the apical HCO3 − flux in unstimulated conditions is divided between CFTR and SLC26A6, with a slightly a larger contribution from the latter when the stoichiometry is 1:2 (40% rather than 20%). However, in the stimulated duct, the flux of HCO3 − is predominantly (∼90%) via CFTR rather than SLC26A6, regardless of its stoichiometry. Steady‐state values for other cellular variables and ion fluxes, as predicted by the secreting duct model, are given in Tables 7 and 8.
Figure 6. Steady‐state HCO3 − fluxes in the secreting duct model at rest, and following cAMP stimulation.
Steady‐state fluxes of HCO3 − mediated by (clockwise from top left) NHE1, AE2, NBC1, SLC26A6 and CFTR. Fluxes correspond to the steady‐state values attained in Fig. 5. Results are shown for both the 1:2 Cl−:HCO3 − stoichiometry of SLC26A6 (A) and for the 1:1 stoichiometry (B). In each case, the first panel represents the unstimulated duct and the second panel shows the effect of altering the transporter activities to represent cAMP stimulation. Fluxes are given in nmol min−1 cm−2. Also shown are the steady‐state intracellular and secreted (luminal) concentrations of Cl− and HCO3 − (mm) and the basolateral membrane potential. [Color figure can be viewed at wileyonlinelibrary.com]
Table 7.
Steady‐state values of variables in the secreting duct model in resting and stimulated conditions for the alternative 1:2 and 1:1 stoichiometries of SLC26A6
| Resting | Stimulated | |||
|---|---|---|---|---|
| 1:2 | 1:1 | 1:2 | 1:1 | |
| Lumen | ||||
| [K+]l (mm) | 5.4 | 5.4 | 5.5 | 5.5 |
| [Na+]l (mm) | 150.0 | 150.0 | 151.6 | 151.6 |
| [Cl–]l (mm) | 80.8 | 93.3 | 17.5 | 17.3 |
| [HCO3 –]l (mm) | 74.7 | 62.1 | 139.6 | 139.8 |
| Osm l (mOsm) | 310.9 | 310.9 | 314.2 | 314.2 |
| pHl | 7.90 | 7.83 | 8.17 | 8.17 |
| E tj (mV) | −3.4 | −3.4 | −4.8 | −4.8 |
| Cell | ||||
| [K+]c (mm) | 127.2 | 126.8 | 121.3 | 120.8 |
| [Na+]c (mm) | 9.0 | 9.5 | 11.6 | 12.2 |
| [Cl–]c (mm) | 21.3 | 23.3 | 2.4 | 2.4 |
| [HCO3 –]c (mm) | 22.4 | 21.9 | 21.5 | 21.4 |
| [X]c (mm) | 126.4 | 124.9 | 149.7 | 149.8 |
| Osm c (mOsm) | 306.3 | 306.3 | 306.5 | 306.5 |
| pHc | 7.37 | 7.36 | 7.35 | 7.35 |
| V c (μl cm−2) | 1.05 | 1.06 | 0.96 | 0.96 |
| E bl (mV) | −69.5 | −68.9 | −72.6 | −71.7 |
| Interspace | ||||
| [K+]i (mm) | 5.0 | 5.0 | 5.0 | 5.0 |
| [Na+]i (mm) | 140.0 | 140.0 | 140.0 | 140.0 |
| [Cl−]i (mm) | 124.0 | 124.0 | 124.2 | 124.2 |
| [HCO3 −]i (mm) | 24.9 | 25.0 | 24.8 | 24.8 |
| [X]i (mm) | 12.0 | 12.0 | 12.0 | 12.0 |
| Osm i (mOsm) | 306.0 | 306.0 | 306.0 | 306.0 |
| pHi | 7.41 | 7.41 | 7.41 | 7.42 |
| V i (μl cm−2) | 0.011 | 0.011 | 0.011 | 0.011 |
| P i (10−5 cmH2O) | −1.2 | −1.2 | −2.0 | −2.0 |
Table 8.
Steady‐state fluxes in the secreting duct model in resting and stimulated conditions for the alternative 1:2 and 1:1 stoichiometries of SLC26A6
| Resting | Stimulated | ||||
|---|---|---|---|---|---|
| 1:2 | 1:1 | 1:2 | 1:1 | ||
| Apical membrane | |||||
| CFTR | J Cl | 20.0 | 22.4 | 9.7 | 11.0 |
| J HCO3 | 8.9 | 9.7 | 41.6 | 43.9 | |
| SLC26A6 | J Cl | −3.3 | −3.1 | −3.6 | −5.0 |
| J HCO3 | 6.5 | 3.1 | 7.3 | 5.0 | |
| K+ channel | J K | 0.3 | 0.3 | 0.2 | 0.2 |
| Volume flow | J v | 206.7 | 206.6 | 349.8 | 349.4 |
| Basolateral membrane | |||||
| AE2 | J Cl | 16.7 | 19.3 | 6.1 | 6.1 |
| J HCO3 | −16.7 | −19.3 | −6.1 | −6.1 | |
| NBC1 | J Na | 15.6 | 15.6 | 27.0 | 27.4 |
| J HCO3 | 31.2 | 31.1 | 54.0 | 54.9 | |
| NHE1 | J Na | 1.0 | 1.1 | 1.1 | 0.1 |
| J H | −1.0 | −1.1 | −1.1 | −0.1 | |
| K+ channel | J K | −10.8 | −10.8 | −18.5 | −18.1 |
| Na+,K+‐ATPase | J K | 11.1 | 11.1 | 18.7 | 18.4 |
| J Na | −16.6 | −16.6 | −28.1 | −27.5 | |
| Volume flow | J v | 206.7 | 206.6 | 349.8 | 349.4 |
| Tight junction | |||||
| K+ permeability | J K | 0.8 | 0.8 | 1.7 | 1.7 |
| Na+ permeability | J Na | 31.0 | 31.0 | 53.0 | 53.0 |
Units are nmol min−1 cm−2 with the exception of volume flow (nl min−1 cm−2).
Reduced AE2 activity is essential for secretion of high HCO3 − concentrations
A sensitivity analysis of the secreting duct model, showing the effects of small changes in the fitted transport parameters on the volume flow rate J v and secreted HCO3 − concentration, is shown in Table 9 where the more significant dependencies are highlighted in bold. Not surprisingly, the permeability of CFTR and activity of NBC1 have positive influences on J v in both resting (spontaneously secreting) and cAMP‐stimulated ducts. So too does the activity of the basolateral Cl−/HCO3 − exchanger AE2. The explanation for this is that Cl− uptake via this pathway helps to maintain an electrochemical gradient for Cl− secretion. Secretion of Cl− across the apical membrane via CFTR provides an additional drive for osmotically coupled fluid secretion.
Table 9.
Sensitivity analysis of the secreting duct model in resting and stimulated conditions for the alternative 1:2 and 1:1 stoichiometries of SLC26A6
| Resting | Stimulated | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Jv | [HCO3 –]l | Jv | [HCO3 –]l | ||||||
| 1:2 | 1:1 | 1:2 | 1:1 | 1:2 | 1:1 | 1:2 | 1:1 | ||
|
|
0.31 | 0.37 | 0.14 | 0.29 | 0.38 | 0.41 | 0.06 | 0.06 | |
| G 26A6 | 0.08 | 0.03 | 0.11 | 0.07 | 0.05 | 0.01 | 0.01 | 0.00 | |
|
|
0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| G AE2 | 0.38 | 0.37 | −0.37 | −0.49 | 0.17 | 0.15 | −0.09 | −0.10 | |
| G NBC1 | 0.09 | 0.10 | 0.05 | 0.07 | 0.02 | 0.02 | 0.00 | 0.00 | |
|
|
−0.01 | −0.02 | 0.01 | −0.01 | 0.04 | 0.04 | 0.01 | 0.01 | |
| G NaK | 0.10 | 0.11 | 0.05 | 0.08 | 0.22 | 0.23 | 0.03 | 0.03 | |
| G NHE1 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 | 0.00 | |
Although AE2 activity has a positive effect on J v, it markedly reduces the secreted HCO3 − concentration. This is shown graphically in Fig. 7, which illustrates the effect of progressively reducing AE2 activity from its unstimulated value to zero. As AE2 activity is reduced, [HCO3 −]l increases from ∼110 mm to > 150 mm, whereas J v falls by ∼40%. The points marked in the graphs in Fig. 7 represent the 70–80% inhibition of AE2 that is required by the model (Table 5) to achieve a secreted HCO3 − concentration of 140 mm at observed volume flow rates following cAMP stimulation. Also shown in Fig. 7 are the changes in apical membrane potential and pHc, which indicate a small hyperpolarization and alkalinization, respectively, as AE2 inhibition is increased. Note that, once again, the predictions of the 1:2 and 1:1 versions of the model are very similar.
Figure 7. Effect of varying the attenuation of AE2 activity on key variables in the secreting duct model following cAMP stimulation.
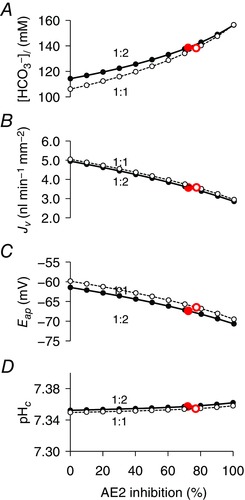
Steady‐state values of secreted HCO3 − concentration ([HCO3 −]l) (A), secretory volume flow (J v) (B), apical membrane potential (E ap) (C) and intracellular pH (pHc) (D). The solid and dashed lines show the slightly different predictions for the 1:2 and 1:1 Cl−:HCO3 − stoichiometries of the SLC26A6 exchanger. The filled and open circles indicate the attenuation levels obtained by optimization of the secreting duct model for the 1:2 and 1:1 stoichiometries, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
The implication of this result is that a high secreted HCO3 − concentration is most easily achieved by minimizing the driving force for Cl− secretion. This requires suppression of AE2, which is the main, and possibly only, pathway for Cl− uptake across the basolateral membrane in guinea‐pig ducts. The trade‐off, however, is that the overall volume flow is somewhat lower than it would be if more Cl− secretion occurred in parallel with the secretion of HCO3 −.
CFTR selectivity changes have little effect on secreted HCO3 − concentration
Another factor that might favour the secretion of HCO3 − at high concentrations would be the reported increase in the relative permeability of CFTR to HCO3 − when intracellular Cl− concentration is low (Park et al. 2010). The effect of raising the HCO3 − permeability of CFTR relative to Cl− (P HCO3/P Cl), at the same time as keeping the total anion permeability (P HCO3 + P Cl) constant, is shown in Fig. 8. Up to this point, the value of P HCO3/P Cl used in the model had been set at 0.4 according to published values (O'Reilly et al. 2000). Raising this to ∼1.0, as may occur when [Cl−]c is low (Park et al. 2010), has remarkably little effect on the secreted HCO3 − concentration (Fig. 8 A) and causes only a small increase (∼15%) increase in J v (Fig. 8 B). Under these conditions, slightly more of the secreted HCO3 − crosses the apical membrane via CFTR, and slightly less via SLC26A6 (Fig. 8 C), and there is a slight depolarization of the apical membrane (Fig. 8 D), although raising P HCO3/P Cl even as high as 2.0 has very little effect on the volume and composition of the secreted fluid.
Figure 8. Effect of varying the HCO3 −/Cl− permeability ratio of CFTR on key variables in the secreting duct model.
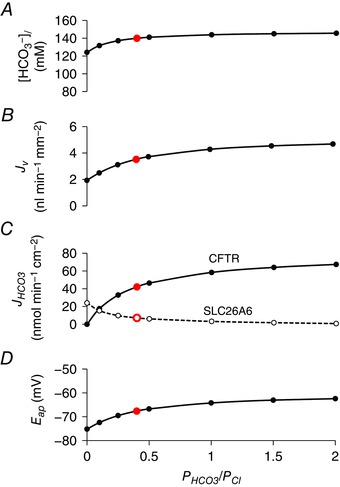
Steady‐state values in the stimulated condition of secreted HCO3 − concentration ([HCO3 −]l) (A), secretory volume flow (J v) (B), net apical HCO3 − fluxes via CFTR and SLC26A6 (J HCO3) (C) and apical membrane potential (E ap) (D) as a function of the HCO3 −/Cl− permeability ratio (P HCO3/P Cl) of CFTR. The sum of the permeabilities (P HCO3 + P Cl) is maintained at a constant value and the Cl−:HCO3 − stoichiometry of the SLC26A6 exchanger was assumed to be 1:2. [Color figure can be viewed at wileyonlinelibrary.com]
This result again supports the idea that reducing the driving force for Cl− secretion, which is determined primarily at the basolateral membrane, is the main prerequisite for the secretion of 140 mm HCO3 −.
Basolateral NKCC1 activity reduces the secreted HCO3 − concentration
To further test this hypothesis, we explored the effect of adding a Na+‐K+‐2 Cl− cotransporter (NKCC1) at the basolateral membrane of the duct model. We have previously suggested that rat and mouse ducts secrete lower HCO3 − concentrations than guinea‐pig because basolateral NKCC1 activity generates a significant driving force for Cl− secretion across the apical membrane in those species (Fernández‐Salazar et al. 2004). No such activity has been detected in guinea‐pig pancreatic duct.
Using the optimal parameters for the stimulated secreting duct model, in which NKCC1 activity was previously set to zero, Fig. 9 shows the effect of gradually increasing NKCC1 activity over a logarithmic scale. As G NKCC1 was raised, the secreted HCO3 − concentration decreased markedly and the Cl− concentration increased reciprocally (Fig. 9 A). The volume flow rate increased almost three‐fold over this range (Fig. 9 B). These changes were clearly a result of the increased driving force for Cl− secretion arising from a marked increase in [Cl−]c (Fig. 9 D) that was only partially offset by depolarization of the apical membrane (Fig. 9 C). Although the secreted HCO3 − concentration declined, the secretory flux of HCO3 − was actually maintained, despite the apical membrane depolarization, as a result of a significant increase in pHc.
Figure 9. Effect of basolateral NKCC1 activity on key variables in the secreting duct model.
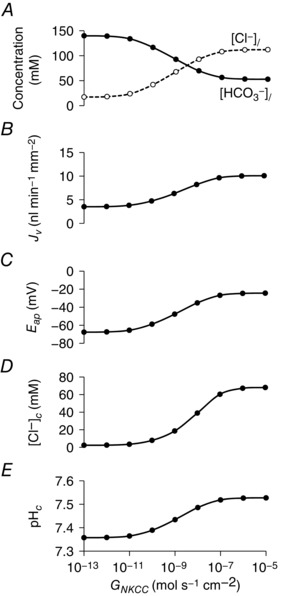
Steady‐state values in the stimulated condition of secreted Cl− and HCO3 − concentrations ([Cl−]l and [HCO3 −]l) (A), secretory volume flow (J v) (B), apical membrane potential (E ap) (C), intracellular Cl− concentration ([Cl−]c) (D) and intracellular pH (pHc) (E) for a range of NKCC1 activities (G NKCC1). The Cl−:HCO3 − stoichiometry of the SLC26A6 exchanger was assumed to be 1:2.
Taken together, these results indicate that basolateral Cl− uptake, whether via AE2 or NKCC1 (in rat and mouse), is the main threat to the secretion of a HCO3 −‐rich fluid.
H+,K+‐ATPases contribute little to HCO3 − and fluid secretion
Although previous work on guinea‐pig ducts indicates that HCO3 − accumulation across the basolateral membrane is entirely Na+‐dependent and does not involve H+ pumps (Ishiguro et al. 1996a), there is evidence for a significant contribution of gastric and non‐gastric H+,K+‐ATPases to fluid secretion in rat pancreas (Novak et al. 2011; Wang et al. 2015). Therefore, following the same approach as for NKCC1, we investigated the effect of introducing increasing levels of H+,K+‐ATPase activity on the behaviour of the secreting duct model.
First, an estimate of H+,K+‐ATPase activity (G HK) in human pancreatic duct cells was obtained by fitting the model to published data for the recovery of pHc in the absence of Na+ in acid‐loaded Capan‐1 cells (Wang et al. 2015). Figure 10 shows the effect of varying basolateral H+,K+‐ATPase activity on the secreted HCO3 − concentration, secretory volume flow and pHc in the secreting duct model. Although it is clear that a basolateral H+,K+‐ATPase can enhance both fluid and HCO3 − secretion, this only becomes apparent when G HK is raised at least 100‐fold above the estimate from Capan‐1 cells.
Figure 10. Effect of basolateral and apical H+,K+‐ATPase activity on key variables in the secreting duct model.
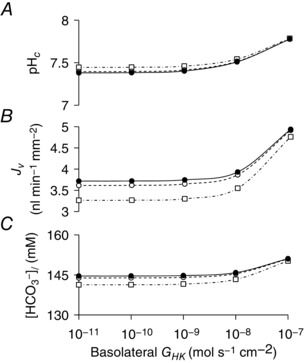
Steady‐state values in the stimulated condition of intracellular pH (pHc) (A), secretory volume flow (J v) (B), and secreted HCO3 − concentration ([HCO3 −]l) (C) for a range of basolateral and apical H+,K+‐ATPase activities (G HK). Curves are plotted against basolateral G HK (abscissa) for three different apical G HK values: 10−10 (filled circles), 10−8 (open circles) and 10−7 mol s−1 cm−2 (open squares). The Cl−:HCO3 − stoichiometry of the SLC26A6 exchanger was assumed to be 1:2.
Figure 10 also shows the effects of increasing apical H+,K+‐ATPase activity on fluid and HCO3 − secretion. Again, these only become apparent when the activity is raised more than 100‐fold above the estimate from Capan‐1 cells. Not surprisingly, the changes this time are decreases in the secreted HCO3 − concentration and volume flow.
Apical K+ conductance
To explore the influence of apical K+ channels on fluid and HCO3 − secretion, we varied the fraction of the whole‐cell K+ permeability that was assigned to the apical membrane. For optimization of the model, this fraction was fixed at 0.01 in the stimulated condition ‐ based on estimates from electrophysiological studies of rat ducts (Novak & Greger, 1991). The whole‐cell permeability was then held at its optimized value while the apical fraction was varied from 0 (K+ permeability all at the basolateral membrane) to 1 (all at the apical membrane). Figure 11 shows that varying this fraction had almost no effect on fluid and HCO3 − secretion, nor on the apical membrane potential.
Figure 11. Effect of varying the distribution of K+ permeability between apical and basolateral membranes on key variables in the secreting duct model.
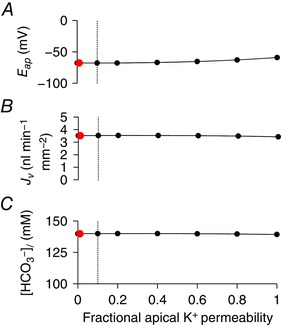
Steady‐state values in the stimulated condition of apical membrane potential (E ap) (A), secretory volume flow (J v) (B) and secreted HCO3 − concentration ([HCO3 −]l) (C) for a range of apical K+ permeability values expressed as a fraction of the whole‐cell K+ permeability, which was maintained at a constant value. The red data points show the value (0.01) used for optimization. The vertical dotted lines show the maximum value (0.1) estimated for rat pancreatic duct cells (Novak & Greger, 1991). The Cl−:HCO3 − stoichiometry of the SLC26A6 exchanger was assumed to be 1:2. [Color figure can be viewed at wileyonlinelibrary.com]
Basement membrane permeability
Finally, we examined the influence of the basement membrane on the secretory performance of the model. Using estimates of basement membrane solute permeability and hydraulic conductivity derived from measurements on other epithelia (Welling & Grantham, 1972; Welling & Welling, 1978), the differences in solute concentration between interspace and basal bath were found to be very small. The hydrostatic pressure difference required to draw water flow through the basement membrane in the stimulated, secreting duct was 2 × 10−5 cmH2O, and the decrease in interspace volume required to achieve this was infinitesimally small. Reducing the hydraulic conductivity by several orders of magnitude had no significant effect on fluid and HCO3 − secretion; it merely increased the negative hydrostatic pressure required in the interspace and consequently reduced the interspace volume (Fig. 12).
Figure 12. Effect of varying basement membrane hydraulic conductivity on key variables in the secreting duct model.
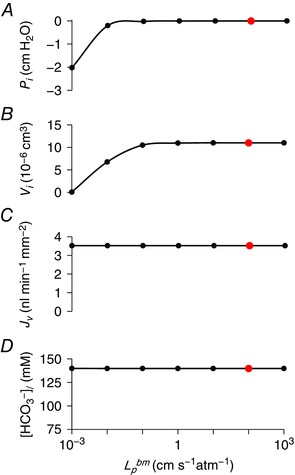
Steady‐state values in the stimulated condition of interspace hydrostatic pressure (P i) (A), interspace volume (V i) (B), secretory volume flow (J v) (C) and secreted HCO3 − concentration ([HCO3 −]l) (D) for a range of basement membrane hydraulic conductivity values (). The red data points show the value (102 cm s−1 atm−1) used for optimization. The solute permeability of the basement membrane was set at 10−3 cm s−1. The Cl−:HCO3 − stoichiometry of the SLC26A6 exchanger was assumed to be 1:2. [Color figure can be viewed at wileyonlinelibrary.com]
Discussion
Three previous studies have used computational modelling to investigate how pancreatic duct epithelium secretes HCO3 − ions at concentrations of 140 mm or more (Sohma et al. 1996, 2000; Whitcomb & Ermentrout, 2004). The reason why this has been a challenge is that the principal anion transporters at the apical membrane comprise a CFTR anion channel that was assumed to be significantly more permeable to Cl− than HCO3 − and a Cl−/HCO3 − exchanger that would be expected to reabsorb rather than secrete HCO3 − during maximal secretion.
The modelling studies of Sohma et al. (1996, 2000) showed that, although it was relatively easy to explain the secretion of ∼70 mm HCO3 − by the rat pancreatic duct, it was much more difficult to account for the higher concentrations (∼140 mm) secreted by other species including guinea‐pig and human. To achieve this, Sohma et al. (2000) proposed a sequential model in which the transport properties of the epithelium changed and favoured additional HCO3 − secretion in the more distal segments. Whitcomb et al. (2004), on reviewing the findings of Sohma et al. (2000), suggested that perhaps ‘the only way to increase bicarbonate concentrations is to remove chloride from the system’. Using a simplified version of Sohma's model, Whitcomb et al. (2004) showed that a secreted HCO3 − concentration of 140 mm could easily be attained by ‘disabling’ the basolateral Cl−/HCO3 − exchanger, which is an idea previously suggested by our own studies (Ishiguro et al. 2001).
In the last 15 years, a large amount of experimental data has been obtained from studies on isolated guinea‐pig ducts (Ishiguro et al. 2007b; Steward & Ishiguro, 2009). The apical anion exchanger has been identified as SLC26A6 and shown to be electrogenic (Wang et al. 2006; Ishiguro et al. 2007a); the HCO3 −:Cl− permeability ratio of CFTR has been shown to increase when intracellular [Cl−]c is low (Park et al. 2010); and a K+ conductance has been identified at the apical membrane (Venglovecz et al. 2011). Furthermore, studies on rat and mouse ducts have implicated basolateral Na+‐K+‐2Cl− cotransporters (Fernández‐Salazar et al. 2004) and H+,K+‐ATPases (Novak et al. 2011; Wang et al. 2015) that appear to be absent or inactive in guinea‐pig ducts. It therefore seemed timely to construct a computational model of the guinea‐pig duct cell incorporating these new findings to determine which, if any of them, might account for the higher HCO3 − concentrations secreted by guinea‐pig ducts.
We also took the opportunity to add a basement membrane to the original Sohma (2000) model, thus separating the basal bath solution from the interspace. Fluid transport in absorptive epithelia, such as gall bladder epithelium, is known to be associated with an expansion of the interspace as a consequence of the hydrostatic pressure required to force water through the basement membrane (Whitlock & Wheeler, 1964; Spring & Hope, 1978). Secretory epithelia face the opposite problem in that a negative hydrostatic pressure is required to draw water into the interspace, and this will tend to have the effect of collapsing the space. Using estimates of basement membrane permeability from other epithelia, we find that the pressures required are small and have no significant effect on fluid secretion. Nonetheless, the results indicate the probable importance of the extracellular matrix in preventing the collapse of the interspace and the resulting access problems for solutes taken up at the lateral surfaces of the cells (Gawenis et al. 2004).
As far as modelling methodology is concerned, we consider the present study to be the first time that an automated fitting routine has been used to estimate the activities and permeabilities of the individual channels and transporters from experimental data. Construction of the model inevitably required many simplifying assumptions to keep the number of poorly defined parameters to a minimum. Furthermore, our approach has mainly focused on fitting the model to steady‐state data, although some of the fixed parameter values were based on transient responses. Nonetheless, the match between the predictions of the optimized model and the original time‐course data from experiments appears to be good.
Prior to the identification of the apical Cl−/HCO3 − exchanger as SLC26A6, it was widely assumed that it would have the same electroneutral 1:1 stoichiometry as the AE (solute carrier family 4; SLC4) family exchangers (Romero et al. 2013). Using best estimates of the intracellular Cl− and HCO3 − concentrations (5 and 20 mm, respectively) we predicted that HCO3 − efflux across the apical membrane would reverse if the luminal HCO3 − concentration rose above ∼128 mm (Steward et al. 2005). This posed real problems for the traditional model of HCO3 − secretion in which the exchanger was expected to carry a vigorous HCO3 − flux into a lumen containing 140 mm HCO3 −.
The discovery that SLC26A6 was electrogenic (Ko et al. 2002; Xie et al. 2002) and had a probable stoichiometry of 1Cl−:2HCO3 − (Shcheynikov et al. 2006) raised the possibility that this would allow the secretion of HCO3 − against a steeper concentration gradient. Assuming a membrane potential of −60 mV, and the same intracellular Cl− and HCO3 − concentrations as before, the exchanger would now reverse at a slightly higher luminal HCO3 − concentration of ∼136 mm (Steward et al. 2005), which is better than 128 mm but still not sufficiently high. Unfortunately, these calculations were very sensitive to the values assumed for [Cl−]c, which was difficult to measure accurately at such low concentrations (Ishiguro et al. 2002a). Furthermore, there were some conflicting reports suggesting that the stoichiometry of SLC26A6 might after all be 1:1, at least in some species (Chernova et al. 2005; Clark et al. 2008) and it has proved difficult to determine the stoichiometry of the guinea‐pig orthologue (Stewart et al. 2011).
Because of these uncertainties, it made sense to compare the behaviour of our guinea‐pig duct model using the alternative 1:1 and 1:2 stoichiometries for apical Cl−/HCO3 − exchange. Perhaps surprisingly, good fits to the experimental data were obtained using both stoichiometries, which suggests that the 1:2 stoichiometry is not an absolute requirement for the secretion of 140 mm HCO3 −. Using both stoichiometries, the model predicts that SLC26A6 activity has to increase 10‐ to 20‐fold upon stimulation with cAMP, consistent with its synergistic interactions with CFTR (Ko et al. 2002).
SLC26A6 evidently plays an important role in raising the luminal HCO3 − concentration, both at the onset of stimulated secretion, which is consistent with the effects of luminal inhibitors in isolated ducts (Ishiguro et al. 1996b; Ishiguro et al. 1998), and during sustained secretion in the initial segments of the ductal tree, where there is probably a steady supply of Cl− ions from the acinar cells. However, in the more distal regions of the ductal tree, where the luminal concentration of HCO3 − has already risen to ∼140 mm, the continuing secretion of HCO3 − will be mediated almost entirely (∼90%) by CFTR (Fig. 6). This is consistent with the results of our previous experimental studies assessing the electrochemical gradient for HCO3 − and the HCO3 − permeability of CFTR at the apical membrane of guinea‐pig duct epithelium (Ishiguro et al. 2002b; Ishiguro et al. 2009).
The reason why there is no significant reabsorption of HCO3 − under these conditions, regardless of the SLC26A6 stoichiometry, is that the model predicts that [Cl−]c falls to very low levels (∼2 mm) (Fig. 6 and Table 7). The only measurements that we have for [Cl−]c were obtained from perfused ducts using the fluoroprobe MEQ, which is notoriously difficult to calibrate at low Cl− concentrations (Ishiguro et al. 2002a). Those values are slightly higher than the predictions of the current model under comparable conditions (Table 6) and a small difference in [Cl−]c could significantly alter the secreted HCO3 − concentration. This apparent discrepancy highlights the importance of obtaining more accurate experimental data. Another factor, not tested in the present study, is that SLC26A6 activity may also be inhibited by Cl−‐sensitive kinases when [Cl−]c falls to low levels (Park et al. 2010).
The relative permeability of CFTR to HCO3 − compared with Cl− has been estimated in several tissues and expression systems with varying results, although all of them suggest that the permeability ratio PHCO3/PCl is in the range 0.2–0.4 (Poulsen et al. 1994; Linsdell et al. 1997; Illek et al. 1999; O'Reilly et al. 2000). There have also been reports that P HCO3/P Cl may change in response to intracellular regulatory factors (Reddy & Quinton, 2003) and extracellular Cl− concentration (Shcheynikov et al. 2004). The most striking effect, and certainly the most relevant in the present context, is the observation that low [Cl−]c, by activating Cl−‐sensitive kinases, causes CFTR to become markedly more permeable to HCO3 −. P HCO3/P Cl values greater than 1.0 were observed in patch‐clamp studies of guinea‐pig duct cells when [Cl−]c was reduced to 4 mm (Park et al. 2010).
Perhaps surprisingly, raising P HCO3/P Cl from 0.4 (as previously reported for CFTR in guinea‐pig ducts (O'Reilly et al. 2000)) to 1.0 or more does not significantly alter the behaviour of our computational model (Fig. 8). With P HCO3/P Cl set at 0.4, the HCO3 − flux is already predominantly via CFTR rather than SLC26A6 during cAMP‐stimulated secretion. Increasing the ratio to 1.0 has little effect on either the volume or composition of the secreted fluid. From this, we can conclude that a rise in P HCO3/P Cl is not a prerequisite for the secretion of HCO3 −‐rich fluid by guinea‐pig ducts.
Gastric and non‐gastric H+,K+‐ATPases are expressed in rat and human pancreatic duct cells and have been shown to make a significant contribution to secretion in the rat pancreas (Novak et al. 2011; Wang et al. 2015). However, the addition of basolateral H+,K+‐ATPase activity to the guinea‐pig duct model made little difference to its capacity to secrete fluid and HCO3 −. Only when its activity was raised to unrealistic values was there a small increase in volume flow and secreted HCO3 − concentration. Such high activity levels would be incompatible with the observed lack of any significant recovery from acid loading in the absence of Na+ (Ishiguro et al. 1996a). This apparent dichotomy between species is presumably a result of differences in the relative contributions of NBC1, NHE1 and H+,K+‐ATPase to basolateral HCO3 − uptake. This in turn may reflect differences in expression levels, intracellular signalling factors, and the dependence of transporter/pump activity on pHc.
Given the dominant role of NBC1 in HCO3 − secretion by guinea‐pig pancreatic ducts, it is perhaps surprising that there is no evidence of pancreatic dysfunction in human patients lacking NBC1 activity (Seki et al. 2013), nor of pancreatic histopathology in NBC1−/− mice (Gawenis et al. 2007). To simulate this situation, we examined the effect of reducing the activity of NBC1 to zero in the guinea‐pig duct model. In the stimulated secreting duct, volume flow was reduced by 69% and the secreted HCO3 − concentration fell from 140 to 106 mm. In the absence of NBC1, HCO3 − accumulation was maintained through a 14‐fold increase in the efflux of H+ via the basolateral NHE1 as a result of a drop in pHc from 7.35 to 6.95. Thus, the redundancy of acid/base transporters at the basolateral membrane ensures that secretory function is retained, albeit at a reduced rate, in the absence of NBC1. In real life, we would also expect upregulation of other transporters such as NKCC1 that would help to maintain secretion (Gawenis et al. 2007).
Pancreatic duct cells express a variety of K+ channels at both apical and basolateral membranes (Hayashi & Novak, 2013; Venglovecz et al. 2015). Electrophysiological studies on rat duct cells indicate that ‘far less than 10%’ of the whole‐cell conductance is located at the apical membrane (Novak & Greger, 1991). Nonetheless, it has recently been suggested that stimulation of apical BK K+ channels in guinea‐pig ducts may enhance HCO3 − secretion by as much as 50% (Venglovecz et al. 2011). Varying the apical K+ permeability fraction in the duct model, however, showed very little effect on fluid or HCO3 − secretion, even when the total K+ conductance of the cell was relocated to the apical membrane. This is not surprising given that the main role of the K+ channels is to maintain the membrane potential and, consequently, the driving forces for Cl− and HCO3 − secretion. In low‐resistance epithelia, apical and basolateral membrane potentials are closely linked, and the luminal and basal K+ concentrations are very similar, and so it makes little difference where the channels are located. A previous theoretical study has shown that apical K+ channels can have a small (∼5%) stimulatory effect on secretion, although this is less pronounced in low‐resistance epithelia such as the pancreatic duct (Cook & Young, 1989).
The most important factor in secreting 140 mm HCO3 − appears to be the suppression of Cl− uptake across the basolateral membrane. This is not a new idea. In Calu‐3 airway epithelial cells, the balance between Cl− and HCO3 − secretion via CFTR at the apical membrane depends upon the relative activities of the Cl− and HCO3 − uptake mechanisms at the basolateral membrane (Devor et al. 1999). Similarly, in pancreatic duct cells, as long as intracellular pH is maintained at ∼7.3, and membrane potential is −50 mV or lower, there is a sustained driving force for HCO3 − secretion, even into a luminal fluid containing 140 mm HCO3 − (Ishiguro et al. 2002b). However, when Cl− uptake across the basolateral membrane is reduced, the driving force for Cl− secretion decreases as [Cl−]c falls (Ishiguro et al. 2002a) and the secreted fluid becomes increasingly HCO3 −‐rich.
This hypothesis is also supported by the experimental finding that ducts isolated from rat and mouse, but not guinea‐pig, can secrete fluid in the absence of HCO3 − by a mechanism that is driven by basolateral Na+‐K+‐2Cl− cotransport via NKCC1 (Fernández‐Salazar et al. 2004). In other words, ducts from those species have an additional basolateral pathway for Cl− uptake that is absent or inactive in guinea‐pig. As we show in this modelling study (Fig. 9), introduction of basolateral NKCC1 activity (i.e. to replicate the situation in rat and mouse ducts) raises the driving force for Cl− secretion and consequently reduces the secreted HCO3 − concentration. It would be interesting to determine whether inhibition of NKCC1 by bumetanide enables rat or mouse pancreas to secrete higher concentrations of HCO3 −.
In guinea‐pig ducts, the only pathway for basolateral Cl− uptake is via the AE2 Cl−/HCO3 − exchanger, and so it is not surprising that a 70–80% decrease in AE2 activity in the model is an absolute requirement for the secretion of 140 mm HCO3 −. At present, the only experimental evidence in support of this comes from measurements of [Cl−]c in perfused ducts (Ishiguro et al. 2002a). These show that inhibition of AE2 with H2DIDS resulted in a fall in [Cl−]c in unstimulated ducts, whereas it had no effect on [Cl−]c in cAMP‐stimulated ducts, suggesting that AE2 was indeed less active under those conditions.
Future experiments should clearly focus on the regulation of AE2 and explore the underlying signalling pathways. It will also be interesting to examine further the species differences in the expression and activity of NKCC1 to see how well this correlates with their capacity to secrete high HCO3 − concentrations. Computational modelling studies performed in parallel with experimental work have the potential to identify critical new experiments, and the results of those experiments will help to improve and refine the model. There is still the possibility that HCO3 − secretion in vivo depends upon sequential changes as the secretion flows from intercalated ducts to intralobular and interlobular ducts. To model this adequately will require more information about the longitudinal distribution of the channels and transporters, and the geometry of the ductal system.
Within the constraints of the present study, however, our main conclusion is that neither the 1:2 stoichiometry of SLC26A6, nor the increased HCO3 − permeability of CFTR at low [Cl−]c significantly alters the behaviour of the model. The main requirement for the secretion of 140 mm HCO3 − is that the driving force for Cl− secretion is minimized. This means that basolateral Cl− uptake, whether via AE2 or NKCC1, must be suppressed during maximal secretion.
Additional information
Competing interests
The authors declare that they have no competing interests.
Author contributions
Experiments were performed in Department of Human Nutrition, Nagoya University Graduate School of Medicine, and Faculty of Life Sciences, University of Manchester. All authors participated in the planning and design of the experiments. MY, MCS, KS, YS, AY and SBHK analysed and interpreted the data. HI interpreted the data. MY, TK and HI drafted the article. MCS revised the article. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Funding
Supported by grants from the Hori Sciences and Arts Foundation, the Research Committee of Intractable Pancreatic Diseases (principal investigator: Yoshifumi Takeyama) provided by the Ministry of Health, Labour, and Welfare of Japan, JSPS KAKENHI Grant number 23118714 and 25293049 (YS), Keio Gijuku Fukuzawa Memorial Fund for the Advancement of Education and Research (YS) and Keio Gijuku Academic Development Funds (YS).
References
- Argent BE, Arkle S, Cullen MJ & Green R (1986). Morphological, biochemical and secretory studies on rat pancreatic ducts maintained in tissue culture. Q J Exp Physiol 71, 633–648. [DOI] [PubMed] [Google Scholar]
- Argent BE, Gray MA, Steward MC & Case RM (2012). Cell physiology of pancreatic ducts In Physiology of the Gastrointestinal Tract, 5th edn, ed. Johnson LR, pp. 1399–1423. Academic Press, Amsterdam. [Google Scholar]
- Benjamin B & Johnson E (1997). A quantitative description of the Na‐K‐2Cl cotransporter and its conformity to experimental data. Am J Physiol Ren Physiol 273, F473–F482. [DOI] [PubMed] [Google Scholar]
- Burghardt B, Elkjær ML, Kwon TH, Rácz GZ, Varga G, Steward MC & Nielsen S (2003). Distribution of aquaporin water channels AQP1 and AQP5 in the ductal system of human pancreas. Gut 52, 1008–1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burghardt B, Nielsen S & Steward MC (2006). The role of aquaporin water channels in fluid secretion by the exocrine pancreas. J Membr Biol 210, 1–11. [DOI] [PubMed] [Google Scholar]
- Cha CY, Oka C, Earm YE, Wakabayashi S & Noma A (2009). A model of Na+/H+ exchanger and its central role in regulation of pH and Na+ in cardiac myocytes. Biophys J 97, 2674–2683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernova MN, Jiang LW, Friedman DJ, Darman RB, Lohi H, Kere J, Vandorpe DH & Alper SL (2005). Functional comparison of mouse slc26a6 anion exchanger with human SLC26A6 polypeptide variants – differences in anion selectivity, regulation, and electrogenicity. J Biol Chem 280, 8564–8580. [DOI] [PubMed] [Google Scholar]
- Clark JS, Vandorpe DH, Chernova MN, Heneghan JF, Stewart AK & Alper SL (2008). Species differences in Cl– affinity and in electrogenicity of SLC26A6‐mediated oxalate/Cl– exchange correlate with the distinct human and mouse susceptibilities to nephrolithiasis. J Physiol 586, 1291–1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook DI & Young JA (1989). Effect of K channels in the apical plasma membrane on epithelial secretion based on secondary active Cl transport. J Membr Biol 110, 139. [DOI] [PubMed] [Google Scholar]
- Devor DC, Singh AK, Lambert LC, DeLuca A, Frizzell RA & Bridges RJ (1999). Bicarbonate and chloride secretion in Calu‐3 human airway epithelial cells. J Gen Physiol 113, 743–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endeward V & Gros G (2005). Low carbon dioxide permeability of the apical epithelial membrane of guinea‐pig colon. J Physiol 567, 253–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández‐Salazar MP, Pascua P, Calvo JJ, López MA, Case RM, Steward MC & San Román JI (2004). Basolateral anion transport mechanisms underlying fluid secretion by mouse, rat and guinea‐pig pancreatic ducts. J Physiol 556, 415–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forster RE, Gros G, Lin L, Ono Y & Wunder M (1998). The effect of 4,4‘‐diisothiocyanato‐stilbene‐2,2’‐disulfonate on CO2 permeability of the red blood cell membrane. Proc Natl Acad Sci USA 95, 15815–15820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawenis LR, Boyle KT, Palmer BA, Walker NM & Clarke LL (2004). Lateral intercellular space volume as a determinant of CFTR‐mediated anion secretion across small intestinal mucosa. Am J Physiol Gastrointest Liver Physiol 286, G1015–G1023. [DOI] [PubMed] [Google Scholar]
- Gawenis LR, Bradford EM, Prasad V, Lorenz JN, Simpson JE, Clarke LL, Woo AL, Grisham C, Sanford LP, Doetschman T, Miller ML & Shull GE (2007). Colonic anion secretory defects and metabolic acidosis in mice lacking the NBC1Na+/HCO3 – cotransporter. J Biol Chem 282, 9042–9052. [DOI] [PubMed] [Google Scholar]
- Hartmann T & Verkman AS (1990). Model of ion transport regulation in chloride‐secreting airway epithelial cells. Integrated description of electrical, chemical, and fluorescence measurements. Biophys J 58, 391–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi M & Novak I (2013). Molecular basis of potassium channels in pancreatic duct epithelial cells. Channels 7, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertz G (1922). Ein neues Verfahren zur Trennung von Gasgemischen durch Diffusion. Physikalishes Zeitschrift 23, 433–434. [Google Scholar]
- Illek B, Tam AW‐K, Fischer H & Machen TE (1999). Anion selectivity of apical membrane conductance of Calu 3 human airway epithelium. Pflügers Arch 437, 812–822. [DOI] [PubMed] [Google Scholar]
- Ishiguro H, Namkung W, Yamamoto A, Wang ZH, Worrell RT, Xu J, Lee MG & Soleimani M (2007a). Effect of Slc26a6 deletion on apical Cl–/HCO3 – exchanger activity and cAMP‐stimulated bicarbonate secretion in pancreatic duct. Am J Physiol Gastrointest Liver Physiol 292, G447–G455. [DOI] [PubMed] [Google Scholar]
- Ishiguro H, Naruse S, Kitagawa M, Mabuchi T, Kondo T, Hayakawa T, Case RM & Steward MC (2002a). Chloride transport in microperfused interlobular ducts isolated from guinea‐pig pancreas. J Physiol 539, 175–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiguro H, Naruse S, Kitagawa M, Suzuki A, Yamamoto A, Hayakawa T, Case RM & Steward MC (2000). CO2 permeability and bicarbonate transport in microperfused interlobular ducts isolated from guinea‐pig pancreas. J Physiol 528, 305–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiguro H, Naruse S, San Román JI, Case RM & Steward MC (2001). Pancreatic ductal bicarbonate secretion: past, present and future. JOP Journal of the Pancreas (Online) 2, 192–197. [PubMed] [Google Scholar]
- Ishiguro H, Naruse S, Steward MC, Kitagawa M, Ko SBH, Hyakawa T & Case RM (1998). Fluid secretion in interlobular ducts isolated from guinea‐pig pancreas. J Physiol 511, 407–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiguro H, Steward M & Naruse S (2007b). Cystic fibrosis transmembrane conductance regulator and SLC26 transporters in HCO3 – secretion by pancreatic duct cells. Acta Physiol Sinica 59, 465–476. [PubMed] [Google Scholar]
- Ishiguro H, Steward MC, Lindsay ARG & Case RM (1996a). Accumulation of intracellular HCO3 – by Na+‐HCO3 – cotransport in interlobular ducts from guinea‐pig pancreas. J Physiol 495, 169–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiguro H, Steward MC, Naruse S, Ko SB, Goto H, Case RM, Kondo T & Yamamoto A (2009). CFTR functions as a bicarbonate channel in pancreatic duct cells. J Gen Physiol 133, 315–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiguro H, Steward MC, Sohma Y, Kubota T, Kitagawa M, Kondo T, Case RM, Hayakawa T & Naruse S (2002b). Membrane potential and bicarbonate secretion in isolated interlobular ducts from guinea‐pig pancreas. J Gen Physiol 120, 617–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiguro H, Steward MC, Wilson RW & Case RM (1996b). Bicarbonate secretion in interlobular ducts from guinea‐pig pancreas. J Physiol 495, 179–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko SBH, Shcheynikov N, Choi JY, Luo X, Ishibashi K, Thomas PJ, Kim JY, Kim KH, Lee MG, Naruse S & Muallem S (2002). A molecular mechanism for aberrant CFTR‐dependent HCO3 – transport in cystic fibrosis. EMBO J 21, 5662–5672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamprecht G, Schaefer J, Dietz K & Gregor M (2006). Chloride and bicarbonate have similar affinities to the intestinal anion exchanger DRA (down regulated in adenoma). Pflügers Arch 452, 307–315. [DOI] [PubMed] [Google Scholar]
- Lee MG, Ohana E, Park HW, Yang D & Muallem S (2012). Molecular mechanism of pancreatic and salivary gland fluid and HCO3 – secretion. Physiol Rev 92, 39–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linsdell P, Tabcharani JA, Rommens JM, Hou YX, Chang XB, Tsui LC, Riordan JR & Hanrahan JW (1997). Permeability of wild‐type and mutant cystic fibrosis transmembrane conductance regulator chloride channels to polyatomic anions. J Gen Physiol 110, 355–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangos JA, McSherry NR, Nousia‐Arvanitakis S & Irwin K (1973). Secretion and transductal fluxes of ions in exocrine glands of the mouse. Am J Physiol 225, 18–24. [DOI] [PubMed] [Google Scholar]
- Nichols JW & Deamer DW (1980). Net proton‐hydroxyl permeability of large unilamellar liposomes measured by an acid‐base titration technique. Proc Natl Acad Sci USA 77, 2038–2042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak I & Greger R (1991). Effect of bicarbonate on potassium conductance of isolated perfused rat pancreatic ducts. Pflügers Arch 419, 76–83. [DOI] [PubMed] [Google Scholar]
- Novak I, Wang J, Henriksen KL, Haanes KA, Krabbe S, Nitschke R & Hede SE (2011). Pancreatic bicarbonate secretion involves two proton pumps. J Biol Chem 286, 280–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Reilly CM, Winpenny JP, Argent BE & Gray MA (2000). Cystic fibrosis transmembrane conductance regulator currents in guinea pig pancreatic duct cells: inhibition by bicarbonate ions. Gastroenterology 118, 1187–1196. [DOI] [PubMed] [Google Scholar]
- Padfield PJ, Garner A & Case RM (1989). Patterns of pancreatic secretion in the anaesthetised guinea pig following stimulation with secretin, cholecystokinin octapeptide, or bombesin. Pancreas 4, 204–209. [DOI] [PubMed] [Google Scholar]
- Park HW, Nam JH, Kim JY, Namkung W, Yoon JS, Lee JS, Kim KS, Venglovecz V, Gray MA, Kim KH & Lee MG (2010). Dynamic regulation of CFTR bicarbonate permeability by [Cl–]i and its role in pancreatic bicarbonate secretion. Gastroenterology 139, 620–631. [DOI] [PubMed] [Google Scholar]
- Poulsen JH, Fischer H, Illek B & Machen TE (1994). Bicarbonate conductance and pH regulatory capability of cystic fibrosis transmembrane conductance regulator. Proc Natl Acad Sci USA 91, 5340–5344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinton PM (2008). Cystic fibrosis: impaired bicarbonate secretion and mucoviscidosis. Lancet 372, 415–417. [DOI] [PubMed] [Google Scholar]
- Reddy MM & Quinton PM (2003). Control of dynamic CFTR selectivity by glutamate and ATP in epithelial cells. Nature 423, 756–760. [DOI] [PubMed] [Google Scholar]
- Romero MF, Chen AP, Parker MD & Boron WF (2013). The SLC4 family of bicarbonate (HCO3 –) transporters. Mol Asp Med 34, 159–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheele GA, Fukuoka SI, Kern HF & Freedman SD (1996). Pancreatic dysfunction in cystic fibrosis occurs as a result of impairments in luminal pH, apical trafficking of zymogen granule membranes, and solubilization of secretory enzymes. Pancreas 12, 1–9. [DOI] [PubMed] [Google Scholar]
- Seki G, Horita S, Suzuki M, Yamazaki O, Usui T, Nakamura M & Yamada H (2013). Molecular mechanisms of renal and extrarenal manifestations caused by inactivation of the electrogenic Na+‐HCO3 – cotransporter NBCe1. Front Physiol 4, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sewell WA & Young JA (1975). Secretion of electrolytes by the pancreas of the anaesthetized rat. J Physiol 252, 379–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shcheynikov N, Kim KH, Kim K‐M, Dorwart MR, Ko SBH, Goto H, Naruse S, Thomas PJ & Muallem S (2004). Dynamic control of cystic fibrosis transmembrane conductance regulator Cl–/HCO3 – selectivity by external Cl– . J Biol Chem 279, 21857–21865. [DOI] [PubMed] [Google Scholar]
- Shcheynikov N, Son A, Hong JH, Yamazaki O, Ohana E, Kurtz I, Shin DM & Muallem S (2015). Intracellular Cl− as a signaling ion that potently regulates Na+/HCO3 − transporters. Proc Natl Acad Sci USA 112, E329–E337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shcheynikov N, Wang Y, Park M, Ko SBH, Dorwart M, Naruse S, Thomas PJ & Muallem S (2006). Coupling modes and stoichiometry of Cl–/HCO3 – exchange by slc26a3 and slc26a6. J Gen Physiol 127, 511–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohma Y, Gray MA, Imai Y & Argent BE (1996). A mathematical model of the pancreatic ductal epithelium. J Membr Biol 154, 53–67. [DOI] [PubMed] [Google Scholar]
- Sohma Y, Gray MA, Imai Y & Argent BE (2000). HCO3 – transport in a mathematical model of the pancreatic ductal epithelium. J Membr Biol 176, 77–100. [DOI] [PubMed] [Google Scholar]
- Spring KR & Hope A (1978). Size and shape of the lateral intercellular spaces in a living epithelium. Science 200, 54–58. [DOI] [PubMed] [Google Scholar]
- Star RA, Kurtz I, Mejia R, Burg MB & Knepper MA (1987). Disequilibrium pH and ammonia transport in isolated perfused cortical collecting ducts. Am J Physiol Ren Physiol 253, F1232–F1242. [DOI] [PubMed] [Google Scholar]
- Steward MC & Ishiguro H (2009). Molecular and cellular regulation of pancreatic duct cell function. Curr Opin Gastroent 25, 447–453. [DOI] [PubMed] [Google Scholar]
- Steward MC, Ishiguro H & Case RM (2005). Mechanisms of bicarbonate secretion in the pancreatic duct. Annu Rev Physiol 67, 377–409. [DOI] [PubMed] [Google Scholar]
- Stewart AK, Shmukler BE, Vandorpe DH, Reimold F, Heneghan JF, Nakakuki M, Akhavein A, Ko S, Ishiguro H & Alper SL (2011). SLC26 anion exchangers of guinea pig pancreatic duct: molecular cloning and functional characterization. Am J Physiol Cell Physiol 301, C289–C303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szalmay G, Varga G, Kajiyama F, Yang XS, Lang TF, Case RM & Steward MC (2001). Bicarbonate and fluid secretion evoked by cholecystokinin, bombesin and acetylcholine in isolated guinea‐pig pancreatic ducts. J Physiol 535, 795–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Hijden HTWM, Grell E, Depont JJHHM & Bamberg E (1990). Demonstration of the electrogenicity of proton translocation during the phosphorylation step in gastric H+K+‐ATPase. J Membr Biol 114, 245–256. [DOI] [PubMed] [Google Scholar]
- Venglovecz V, Hegyi P, Rakonczay Z, Tiszlavicz L, Nardi A, Grunnet M & Gray MA (2011). Pathophysiological relevance of apical large‐conductance Ca2+‐activated potassium channels in pancreatic duct epithelial cells. Gut 60, 361–369. [DOI] [PubMed] [Google Scholar]
- Venglovecz V, Rakonczay Z, Jr. , Gray MA & Hegyi P (2015). Potassium channels in pancreatic duct epithelial cells: their role, function and pathophysiological relevance. Pflügers Arch 467, 625–640. [DOI] [PubMed] [Google Scholar]
- Wakabayashi S, Fafournoux P, Sardet C & Pouyssegur J (1992). The Na+/H+ antiporter cytoplasmic domain mediates growth‐factor signals and controls H+‐sensing. Proc Natl Acad Sci USA 89, 2424–2428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Barbuskaite D, Tozzi M, Giannuzzo A, Sorensen CE & Novak I (2015). Proton pump inhibitors inhibit pancreatic secretion: role of gastric and non‐gastric H+/K+‐ATPases. PLoS ONE 10, e0126432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang YX, Soyombo AA, Shcheynikov N, Zeng WZ, Dorwart M, Marino CR, Thomas PJ & Muallem S (2006). Slc26a6 regulates CFTR activity in vivo to determine pancreatic duct HCO3 – secretion: relevance to cystic fibrosis. EMBO J 25, 5049–5057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welling LW & Grantham JJ (1972). Physical properties of isolated perfused renal tubules and tubular basement membranes. J Clin Invest 51, 1063–1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welling LW & Welling DJ (1978). Physical properties of isolated perfused basement membranes from rabbit loop of Henle. Am J Physiol Endocrinol Metab 234, F54–F58. [DOI] [PubMed] [Google Scholar]
- Whitcomb DC & Ermentrout GB (2004). A mathematical model of the pancreatic duct cell generating high bicarbonate concentrations in pancreatic juice. Pancreas 29, e30–e40. [DOI] [PubMed] [Google Scholar]
- Whitlock RT & Wheeler HO (1964). Coupled transport of solute and water across rabbit gallbladder epithelium. J Clin Invest 43, 2249–2265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Q, Welch R, Mercado A, Romero MF & Mount DB (2002). Molecular characterization of the murine SLC26A6 anion exchanger: functional comparison with SLC26A1. Am J Physiol Ren Physiol 283, F826–F838. [DOI] [PubMed] [Google Scholar]


