Accurate self-correction of errors in long reads using de Bruijn graphs

Abstract

Motivation

New long read sequencing technologies, like PacBio SMRT and Oxford NanoPore, can produce sequencing reads up to 50 000 bp long but with an error rate of at least 15%. Reducing the error rate is necessary for subsequent utilization of the reads in, e.g. de novo genome assembly. The error correction problem has been tackled either by aligning the long reads against each other or by a hybrid approach that uses the more accurate short reads produced by second generation sequencing technologies to correct the long reads.

Results

We present an error correction method that uses long reads only. The method consists of two phases: first, we use an iterative alignment-free correction method based on de Bruijn graphs with increasing length of k-mers, and second, the corrected reads are further polished using long-distance dependencies that are found using multiple alignments. According to our experiments, the proposed method is the most accurate one relying on long reads only for read sets with high coverage. Furthermore, when the coverage of the read set is at least 75×, the throughput of the new method is at least 20% higher.

Availability and Implementation

LoRMA is freely available at http://www.cs.helsinki.fi/u/lmsalmel/LoRMA/.

1 Introduction

With the diminishing costs, high-throughput DNA sequencing has become a commonplace technology in biological research. Whereas the second generation sequencers produced short but quite accurate reads, new technologies such as Pacific Biosciences and Oxford NanoPore are producing reads up to 50 000 bp long but with an error rate at least 15%. Although the long reads have proven to be very helpful in applications like genome assembly (Koren and Philippy, 2015; Madoui et al., 2015), the error rate poses a challenge for the utilization of this data.

Many methods have been developed for correcting short reads (Laehnemann et al., 2016; Yang et al., 2013) but these methods are not directly applicable to the long reads because of their much higher error rate. Moreover, most research of short read error correction has concentrated on mismatches, the dominant error type in Illumina data, whereas in long reads indels are more common. Recently, several methods for error correction of long reads have also been developed. These methods fall into two categories: either the highly erroneous long reads are self-corrected by aligning them against each other, or a hybrid strategy is adopted in which the long reads are corrected using the accurate short reads that are assumed to be available. Most standalone error correction tools like proovread (Hackl et al., 2014), LoRDEC (Salmela and Rivals, 2014), LSC (Au et al., 2012) and Jabba (Miclotte et al., 2015) are hybrid methods. PBcR (Berlin et al., 2015; Koren et al., 2012) is a tool that can employ either the hybrid or self-correction strategy.

Most hybrid methods like PBcR, LSC and proovread are based on the mapping approach. They first map the short reads on the long reads and then correct the long reads according to a consensus built on the mapped short reads. PBcR extends this strategy to self-correction of PacBio reads by computing overlaps between the long reads using probabilistic locality-sensitive hashing and then correcting the reads according to a consensus built on the overlapping reads. As the mapping of short reads is time and memory consuming, LoRDEC avoids the mapping phase by building a de Bruijn graph (DBG) of the short reads and then threading the long reads through this graph to correct them. Jabba is a recent tool that is also based on building a DBG of short reads. While LoRDEC finds matches of complete k-mers in the long reads, Jabba searches for maximal exact matches between the k-mers and the long reads allowing it to use a larger k in the DBG.

In this paper, we present a self-correction method for long reads that is based on DBGs and multiple alignments. First our method performs initial correction that is similar to LoRDEC, but uses only long reads and performs iterative correction rounds with longer and longer k-mers. This phase considers only the local context of errors and hence it misses the long-distance dependency information available in the long reads. To capture such dependencies, the second phase of our method uses multiple alignments between carefully selected reads to further improve the error correction.

Our experiments show that our method is currently the most accurate one relying on long reads only. The error rate of the reads after our error correction is less than half of the error rate of reads corrected by PBcR using long reads only. Furthermore, when the coverage of the read set is at least 75×, the size of the corrected read set of our method is at least 20% higher than for PBcR.

2 Overview of LoRDEC

LoRDEC (Salmela and Rivals, 2014) is a hybrid method for the error correction of long reads. It presents the short reads in a DBG and then maps the long reads to the graph. The DBG of a read set is a graph whose nodes are all k-mers occurring in the reads and there is an edge between two nodes if the corresponding k-mers overlap by k − 1 bases. LoRDEC classifies the k-mers of long reads as solid if they are in the DBG and weak otherwise. The correction then proceeds by replacing the weak areas of the long reads by solid ones. This is done by searching paths in the DBG between solid k-mers to bridge the weak areas between them. If several paths are found, the path with the shortest edit distance as compared to the weak region is chosen to be the correct sequence, which replaces the weak region of the long read. The weak heads and tails of the long reads are the extreme regions of the reads that are bordered by just one solid k-mer in the beginning (resp. end) of the read. LoRDEC attempts to correct these regions by starting a path search from the solid k-mer and choosing a sequence that is as close as possible to the weak head or tail.

Repetitive regions of the genome can make the DBG tangled. The path search in these areas of the DBG can then become intractable. Therefore, LoRDEC employs a limit on the number of branches it explores during the search. If this limit is exceeded, LoRDEC checks if at least one path within the maximum allowed error rate has been found and then uses the best path found for correction. If no such path has been found, LoRDEC starts a path search similar to the correction of the head and tail of the read, to attempt a partial correction of the weak region.

Some segments of the long reads remain erroneous after the correction. LoRDEC outputs bases in upper case if at least one of the k-mers containing that base is solid, i.e. it occurs in the DBG of the short reads, and in lower case otherwise. For most applications, it is preferable to extract only the upper case regions of the sequences as the lower case bases are likely to contain errors.

3 Self-correction of long reads

In this section, we will show how an error correction procedure similar to LoRDEC can be used to iteratively correct long reads without short read data. We will use LoRDEC* to refer to LoRDEC in this long reads only mode. Then, we further describe a polishing method to improve the accuracy of correction. Figure 1 shows the workflow of our approach.

Fig. 1.

Workflow of error correction. LoRDEC* is first applied iteratively to the read set, with an increasing k. The corrected reads are further corrected by LoRMA, which uses multiple alignments to find long-distance dependencies in the reads

3.1 Iterative correction

To describe how LoRDEC can be adapted for self-correction of read sets, let Q be a set of long reads to be corrected, and let integer h be the abundancy threshold that is used in choosing the k-mers to the DBG. The correction procedure repeats for an increasing sequence $k=k_1,\dots ,k_t$ the following steps 1–3:

1. Construct the DBG of set Q using as the nodes the k-mers that occur in Q at least h times;

2. Correct Q using the LoRDEC algorithm with this DBG;

3. Replace Q with the corrected Q.

After the final round, the regions of the reads identified as correct in the last iteration are extracted for further correction with the multiple alignment technique by LoRMA.

As the initial error level is assumed high, the above iterations have to start with a relatively small k = k₁. With a suitable abundancy threshold h, the DBG should then contain most of the correct k-mers (i.e. the k-mers of the target genome) and a few erroneous ones. Although path search over long weak regions may not be feasible because of strong branching of the DBG, shorter paths are likely to be found and hence, short weak regions can be corrected. After the first round, the correct regions in the reads have become longer because close-by correct regions have been merged whenever a path between them has been found, and thus, we can increase k. Then, with increasing ks, the DBG gets less tangled and the path search over the longer weak regions becomes feasible allowing for the correction of the complete reads. A similar iterative approach has previously been proposed for short read assembly (Bankevich et al., 2012; Peng et al., 2010).

When the path search is abandoned because of excessive branching, the original LoRDEC algorithm still uses the best path found so far to correct the region. Such a greedy strategy improves correction accuracy in a single run, but in the present iterative approach false corrections start to accumulate. Therefore, we make a correction only if it is guaranteed that the correction is the best one available in the DBG, i.e. all branches have been explored.

Abundancy threshold h controls the quality of the k-mers that are used for correction. In our experiments, we used a fixed threshold of h = 4 in all iterations, meaning that the k-mers with less than four occurrences in the read set were considered erroneous.

To justify the value of h, we need to analyse how many times a fixed k-mer of the genome is expected to occur without any error in the reads. Then an h that is about one or two standard deviations below the expected value should give a DBG that contains the majority of the correct k-mers and not too many erroneous ones. We will use an analysis similar to Miclotte et al. (2015).

Let $C_{\ell \ge k}$ denote the coverage of a genomic k-mer by exact regions of length at least k. Here exact region refers to a continuous maximal error-free segment of some read in our read set. Figure 2 gives an example of exact regions. Let us add a $ character to the end of each read, and then consider the concatenation of all these reads. In this sequence, an exact region (of length 0 or more) ends either at an error or when encountering the $ character. Let n denote the number of reads, N the length of the concatenation of all reads and p the error rate. Then the probability for an exact region to end at a given position of the concatenated sequence is $q=(pN+n)/(N+n)$. As the reads are long and the error rate is high, we have $q\approx p$. The length of the exact regions is distributed according to the geometric distribution $\text{Geom}(q)$_, and therefore, the probability of an exact region to have length i is $P(i)={(1-q)}^{i}q$. The expected number of exact regions is Nq. An exact region is maximal if it cannot be extended to the left or right. Let R_i be the random variable denoting the number of maximal exact regions of length i. Then $E(R_i)=NqP(i)=N{q}^2{(1-q)}^i$.

Fig. 2.

Division of a read into maximal exact regions, shown as boxed areas. The shaded boxes give the regions that could cover a 4-mer

Let $C_{\ell =i}$ denote the coverage of a k-mer in the genome by maximal exact regions of length i, and let r_i denote the number of maximal exact regions of length i. An exact region of length i, $i\ge k$, covers a fixed genomic k-mer (i.e. the read with that exact region is read from the genomic segment containing that k-mer) if the region starts in the genome from the starting location of the k-mer or from some of the i − k locations before it. Assuming that the reads are randomly sampled from the genome, this happens with probability $(i-k+1)/G$, where G is the length of the genome. Therefore, $C_{\ell =i}$ is distributed according to the binomial distribution $\text{Bin}(r_i,(i-k+1)/G)$ (independence of locations of exact regions is assumed), and the expected coverage of a genomic k-mer by maximal exact regions of length i is

$$\begin{array}{cc}E(C_{\ell =i})& ={\displaystyle \sum _{r_i=0}^{\infty }P}(R_i=r_i)·r_i·\frac{i-k+1}{G}\\ & =\frac{i-k+1}{G}E(R_i)\\ & =\frac{N}{G}{q}^2{(1-q)}^i·(i-k+1).\end{array}$$

By the linearity of expectation, the expected coverage of a genomic k-mer by exact regions of length at least k is

$$\begin{array}{c}E(C_{\ell \ge k})={\displaystyle \sum _{i=k}^{\infty }E}(C_{\ell =i})\\ =\frac{N}{G}{\displaystyle \sum _{i=k}^{\infty }{q}^2}{(1-q)}^i·(i-k+1).\end{array}$$

Because $(i-k+1)/G$ is small, we can approximate the binomial distribution of $C_{\ell =i}$ with the Poisson distribution. Therefore, ${\sigma }^2(C_{\ell =i})=E(C_{\ell =i})$.

Assuming that the coverages of a genomic k-mer by maximal exact regions of different lengths are independent, the variance of the coverage by exact regions of length at least k is ${\sigma }^2(C_{\ell \ge k})=\sum _{i\ge k}{\sigma }^2(C_{\ell =i})=E(C_{\ell \ge k})$.

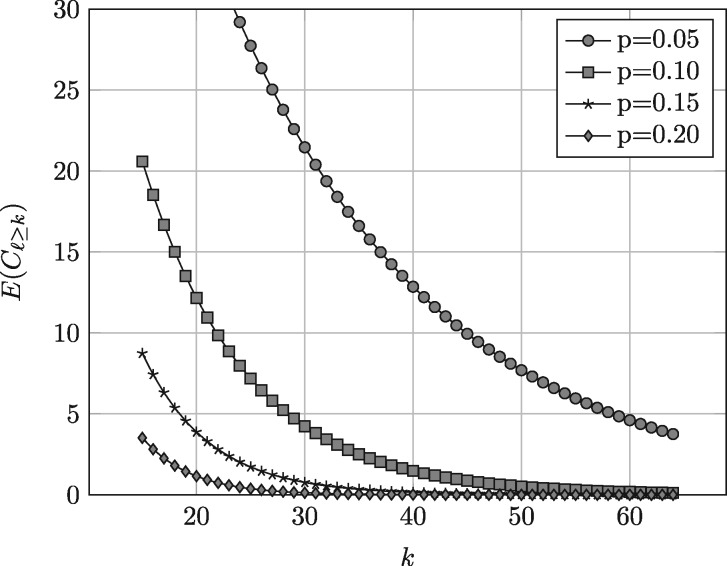
Figure 3 illustrates $E(C_{\ell \ge k})$ for various k and $q\approx p$, with 100× original coverage of the target. Note that original coverage of the target genome by the read set is N/G. For the three datasets in our experiments (Table 1), with coverages 200×, 208× and 129×, the expected coverage $E(C_{\ell \ge k})$ has values 9.12, 9.48 and 5.89, respectively, for our initial k = 19 and for our assumed error rate p = 0.15. Hence, our adopted threshold h = 4 is from 0.8 to 1.8 standard deviations below the expected coverage meaning that most of the correct k-mers should be distinguishable from the erroneous ones.

Fig. 3.

Expected coverage of a genomic k-mer by exact regions of length at least k for a read set with coverage 100× for different error rates p

Table 1.

Datasets used in the experiments

	E.coli (simulated)	E.coli	Yeast
Reference organism
Name	Escherichia coli	Escherichia coli	Saccharomyces cerevisiae
Strain	K-12 substr. MG1655	K-12 substr. MG1655	W303
Reference sequence	NC_000913	NC_000913	CM001806-CM001823
Genome size	4.6 Mbp	4.6 Mbp	12 Mbp
PacBio data
Number of reads	92 818	89 481	261 964
Avg. read length	9997	10 779	5891
Coverage	200×	208×	129×
Illumina data
Accession number	–	ERR022075	SRR567755
Number of reads	–	2 316 613	4 503 422
Read length	–	100	100
Coverage	–	50×	38×

3.2 Polishing with multiple alignments

The error correction performed by LoRDEC* does not make use of long range information contained in the reads. In particular, approximate repeats of the target are collapsed in the DBG into a path with alternative branches. In practice, such repeat regions are corrected towards a copy of the repeat but not necessarily towards the correct copy. However, the correct copy is more likely uncovered because we choose the path that minimizes the edit distance between the weak region to be corrected and the sequence spelled out by the path. Therefore, if we have several reads from the same location, the majority of them are likely corrected towards the correct copy.

Our multiple alignment error correction exploits the long range similarity of reads by identifying the reads that are likely to originate from the same genomic location. If the reads contain a repeat area, the most abundant copy of the repeat present in the reads is likely the correct one. Then by aligning the reads with each other we can correct them towards this most abundant copy. The approach we use here bears some similarity to the method used in Coral (Salmela and Schröder, 2011).

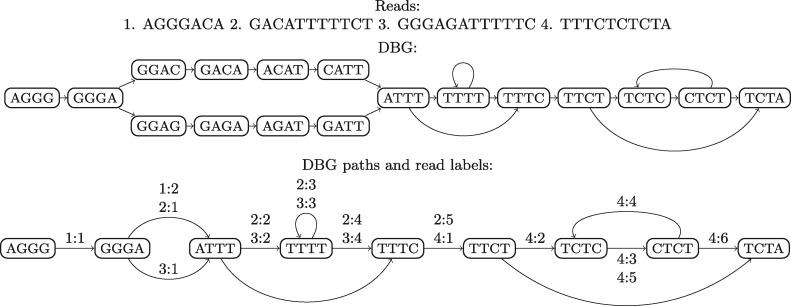
As preprocessing phase for the method, we build a DBG of all the reads using abundancy threshold h = 1 to ensure that all k-mers present in the reads are indexed. Then we enumerate the simple paths of the DBG and find for each read the unique path that spells it out. Each such path is composed of non-overlapping unitig segments that have no branches. We call such segments the parts of a path. We associate to each path segment (i.e. a unitig path of the DBG) a set of triples describing the reads traversing that segment. Each triple consists of read id, part id and the direction of the read on this path. Hence, the path for a read i consists of segments who have a triplet with i as the read id and with part id values 1, 2,…, the path being composed of these segments in the order of the part id value (Fig. 4). Using this information, it is now possible to reconstruct each read from the DBG except that the reads will be prefixed (suffixed) by the complete simple path that starts (ends) the read.

Fig. 4.

Augmented DBG. For simplicity, reverse complements are not considered. The lower graph only shows the branching nodes of the DBG and the labels on the paths/edges are of the form read id: read part id. For example, the path for read 2 consists of segments with labels 2:1, 2:2, 2:3, 2:4 and 2:5

In the second phase of our method, we take the reads one by one and use the DBG to select reads that are similar to the current read. We follow the path for the current read and gather the set of reads sharing k-mers with it, which can be done using the triplets of the augmented DBG. Out of these reads, we then first select each read R such that the shared k-mers span at least 80% of the shorter one of the read R and the current read. Furthermore, out of these reads, we select those that share the most k-mers with the current read. We call this read set the friends of the current read. The number of selected reads is a parameter of our method (by default 7).

We then proceed to compute a multiple alignment of the current read and its friends. To keep the running time feasible, we use the same simple method as in Coral (Salmela and Schröder, 2011). First, the current read is set to be the initial consensus. Then we take each friend of the current read one by one, align them against the current consensus using banded alignment, and finally update the consensus according to the alignment. Finally, we inspect every column of the multiple alignment and correct the current read towards the consensus if the consensus is supported by at least two reads.

We implemented the above procedure in a tool called Long Read Multiple Aligner (LoRMA) using the GATB library (Drezen et al., 2014) for the implementation of the DBG.

4 Experimental results

We ran experiments on three datasets that are detailed in Table 1. The simulated Escherichia coli dataset was generated with PBSIM (Ono et al., 2013) using the following parameters: mean accuracy 85%, average read length 10 000, and minimum read length 1000. The other two datasets are real data. Although our method works solely on the PacBio reads, the table also includes statistics of complementary Illumina reads that were used to compare our method against hybrid methods that need also short reads. All experiments were run on 32 GB RAM machines equipped with 8 cores.

4.1 Evaluation of the quality of error correction

In the simulated dataset, the genomic position where each read derives from is known. Therefore, the quality of error correction on the simulated dataset is evaluated by aligning the corrected read against the corresponding correct genomic sequence. We allow free deletions in the flanks of the corrected read because the tools trim regions they are not able to correct. To check if the corrected reads align to the correct genomic position, we aligned the corrected reads on the reference genome with BLASR (Chaisson and Tesler, 2012) keeping only a single best alignment for each read. The following statistics were computed:

• Size: The relative size of the corrected read set as compared to the original one.

• Error rate: The number of substitutions, insertions and deletions divided by the length of the correct genomic sequence.

• Correctly aligned: The relative number of reads that align to the same genomic position where the read derives from.

To evaluate the quality of error correction on the real datasets, we used BLASR (Chaisson and Tesler, 2012) to align the original and corrected reads on the reference genome. For each read, we used only a single best alignment because a correct read should only have one continuous alignment against the reference. Thus, chimeric reads will be only partially aligned. We computed the following statistics:

• Size: The relative size of the corrected read set as compared to the original one.

• Aligned: The relative size of the aligned regions as compared to the complete read set.

• Error rate: The number of substitutions, insertions and deletions in the aligned regions divided by the length of the aligned regions in the reference sequence.

• Genome coverage: The proportion of the genome covered by the aligned regions of the reads.

Together, these statistics measure three aspects of the quality of error correction. Size measures the throughput of the method. Aligned and error rate together measure the accuracy of correction. Finally genome coverage estimates if reads deriving from all regions of the genome are corrected.

4.2 Parameters of our method

We ran experiments on the real E.coli dataset to test the effect of parameters on the performance of our method. First, we tried several progressions of k in the first phase where LoRDEC* is run iteratively. We started all iterations with k = 19 because given the high error rate of the data k must be small for correct k-mers to occur in the read data. The results of these experiments are presented in Table 2. With more iterations, the size of the corrected read set and the aligned proportion of reads decrease, but the aligned regions are more accurate. The decrease in the size of the corrected read set may be a result of better correction because PacBio reads have more insertions than deletions. However, the decrease in the aligned proportion of the reads may indicate some accumulation of false corrections. The runtime of the method increases with the number of iterations but later iterations take less time as the reads have already been partially corrected during the previous rounds. To balance out these effects, we chose to use a moderate number of iterations, i.e. k = 19, 40, 61, by default, which also optimizes the error rate of the aligned regions.

Table 2.

The progression of k for the iterations of LoRDEC*

k progression	Size (%)	Aligned (%)	Error rate (%)	Elapsed time (h)
19	64.901	99.499	0.294	4.08
19,22,25,28,31	66.702	99.302	0.276	12.97
19,22,25,28,31,34,37,40,43,46	66.630	99.311	0.274	20.65
19,22,25,28,31,34,37,40,43,46, 49,52,55,58,61	66.546	99.296	0.271	27.53
19,26,33	66.401	99.329	0.274	9.58
19,26,33,40,47	66.230	99.298	0.271	13.07
19,26,33,40,47,54,61	66.144	99.283	0.266	16.08
19,33	66.705	99.358	0.277	7.68
19,33,47	66.178	99.352	0.268	10.58
19,33,47,61	65.991	99.301	0.261	11.92
19,40	66.619	99.360	0.272	8.32
19,40,61	66.223	99.317	0.257	10.30

LoRMA also builds a DBG of the reads and thus we need to specify k. We investigated the effect of the value of k on the E.coli dataset. Table 3 shows the effect of k on the performance of LoRMA. Because the DBG is only used to detect similar reads in LoRMA, the performance is not greatly affected by the choice of k. There is a slight decrease in the throughput of the method as k increases as well as a slight increase in runtime but these effects are very modest. For the rest of the experiments, we set k = 19.

Table 3.

The effect of the k-mer size in LoRMA. The elapsed time is the runtime of LoRDEC*+LoRMA

k	Size	Aligned	Error rate	Elapsed time	Memory peak
	(%)	(%)	(%)	(h)	(GB)
19	66.238	99.306	0.256	10.38	17.197
40	66.170	99.309	0.258	10.53	16.958
61	65.941	99.313	0.261	13.87	16.908

Another parameter of the method is the size of the set of friends of the current read (-friends parameter). We tested also the effect of this parameter on the E.coli dataset. As the optimal value of this parameter might depend on the coverage of the dataset, we created several subsets of this dataset with different coverage to investigate this. Table 4 shows the results of these experiments. We can see that the accuracy of the correction increases as the size of the friends set increases. However, for the dataset with the lowest coverage, 75×, the coverage of the genome by the corrected reads decreases when the size of the friends set is increased indicating that lower coverage areas are not well corrected. We can also see that increasing the size of the friends set increases the running time of the method. To keep the running time reasonable, we decided to set the default value of the parameter at a fairly low value, 7.

Table 4.

The effect of the size of the friends set on the quality of the correction. The elapsed time is the runtime of LoRDEC*+LoRMA

Friends	5	7	10	15	20
Coverage 75×
Size (%)	59.173	59.164	59.146	59.109	59.085
Aligned (%)	98.894	98.983	99.099	99.192	99.226
Error rate (%)	0.169	0.156	0.148	0.131	0.128
Gen. cov. (%)	90.918	90.907	90.900	90.888	90.884
Elapsed time (h)	1.13	1.22	1.53	1.88	2.27
Memory (GB)	14.522	14.518	14.522	14.515	14.525
Disk (GB)	1.076	1.076	1.076	1.076	1.076
Coverage 100×
Size (%)	65.759	65.738	65.723	65.670	65.607
Aligned (%)	98.091	98.317	98.491	98.556	98.620
Error rate(%)	0.152	0.140	0.134	0.114	0.110
Gen. cov. (%)	99.404	99.403	99.405	99.403	99.405
Elapsed time (h)	2.53	3.32	4.32	5.80	7.08
Memory (GB)	14.720	14.720	14.712	14.723	14.720
Disk (GB)	1.417	1.416	1.417	1.416	1.416
Coverage 175×
Size (%)	66.933	66.906	66.905	66.852	66.816
Aligned (%)	98.927	98.973	99.153	99.011	99.104
Error rate(%)	0.222	0.194	0.191	0.140	0.133
Gen. cov. (%)	100.000	100.000	100.000	100.000	100.000
Elapsed time (h)	6.77	8.35	10.62	14.07	17.22
Memory (GB)	16.009	16.016	16.003	16.002	16.006
Disk (GB)	2.361	2.361	2.362	2.362	2.362

4.3 Comparison against previous methods

We compared our new method against PBcR (Berlin et al., 2015; Koren et al., 2012) which is to the best of our knowledge, the only previous self-correction method for long reads, and LoRDEC (Salmela and Rivals, 2014), proovread (Hackl et al., 2014) and Jabba (Miclotte et al., 2015) which also use short complementary reads. Table 5 shows the results on the simulated dataset comparing our new method to PBcR using long reads only. Table 6 shows the results of the comparison of our new method against previous methods on the real datasets. In the following, we will use LoRDEC to refer to the hybrid correction method using also short reads and LoRDEC*+LoRMA for our new method in which LoRDEC* is run in long reads selfcorrection mode followed by LoRMA.

Table 5.

Comparison of LoRDEC*+LoRMA against PBcR (PacBio only) on the simulated E. coli dataset

Tool	Size	Error rate	Correctly aligned	Correctly aligned	Elapsed time	Memory peak	Disk peak
	(%)	(%)	(%)	$\ge$2000 bp (%)	(h)	(GB)	(GB)
Original	100.000	13.015	99.997	99.997	–	–	–
PBcR (PacBio only)	92.457	0.604	99.953	99.984	2.63	9.066	17.823
LoRDEC${}^{*}+$LoRMA	94.372	0.109	96.866	99.987	14.30	17.338	3.192

Table 6.

Comparison of both hybrid and self-correction tools on PacBio data

	Tool	Size	Aligned	Error rate	Genome coverage	Elapsed time	Memory peak	Disk peak
		(%)	(%)	(%)	(%)	(h)	(GB)	(GB)
E. coli	Original	100.000	71.108	16.9126	100.000	–	–	–
	LoRDEC	65.672	98.944	0.1143	99.820	0.96	0.368	1.570
	proovread	61.590	98.603	0.2789	99.728	28.65	9.522	7.174
	PBcR (with Illumina)	52.103	98.507	0.0682	98.769	15.13	17.429	160.154
	Jabba	2.873	99.945	0.0003	99.745	0.02	0.168	0.606
	PBcR (only PacBio)	51.068	86.023	0.6905	100.000	1.68	22.00	16.070
	LoRDEC*+LoRMA	66.223	99.318	0.2572	100.000	10.40	16.984	2.824
Yeast	Original	100.000	89.929	16.8442	99.974	–	–	–
	LoRDEC	75.522	97.337	0.9987	99.833	3.17	0.451	2.776
	proovread	0.306	97.156	0.8004	20.346	11.18	4.764	7.162
	PBcR (with Illumina)	57.337	98.100	0.3342	99.652	22.05	20.085	157.726
	Jabba	24.979	99.484	0.1279	99.900	0.17	1.031	0.993
	PBcR (only PacBio)	60.065	95.822	2.1018	99.907	4.42	9.571	24.610
	LoRDEC*+LoRMA	71.987	98.088	0.3644	99.375	21.08	17.968	4.852

Results for tools utilizing also Illumina data are shown on a grey background

PBcR pipeline from Celera Assembler version 8.3rc2 was run without the assembly phase and memory limited to 16 GB. PBcR was run both only using PacBio reads and by utilizing also the short read data. For PBcR utilizing also short read data, the PacBio reads were divided into three subsets each of which was corrected in its own run. Proovread v2.12 was run with the sequence/fastq files chunked to 20M as per the usage manual and used 16 mapping threads. LoRDEC used an abundancy threshold of 3 and k-mer size was set to 19 similar to the experiments by Salmela and Rivals (2014). Jabba 1.1.0 used k-mer size 31 and short output mode. LoRMA was run with 6 threads. The k-mer sizes for LoRDEC*+LoRMA iteration steps were chosen 19, 40 and 61. For proovread and LoRDEC, we present results for trimmed and split reads.

Table 5 shows that on the simulated data both PBcR and LoRDEC*+LoRMA are able to correct most of the data. Our new method achieves a lower error rate and higher throughput. We see that the fraction of corrected reads aligning to the correct genomic position is lower for LoRDEC*+LoRMA than for PBcR when all reads are considered, which suggests that LoRDEC*+LoRMA tends to overcorrect some reads. However, for corrected reads longer than 2000 bp this difference disappears, and thus, we can conclude that the overcorrected reads are short. When compared to the other selfcorrection method, PBcR, our new tool has a higher throughput and produces more accurate results on both real datasets as shown in Table 6. Out of the hybrid methods, Jabba has a lower error rate than LoRDEC*+LoRMA but its throughput is lower. When compared to the other hybrid methods, LoRDEC*+LoRMA has comparable accuracy and throughput. All hybrid methods produce corrected reads that do not cover the whole E.coli reference, which could be a result of coverage bias in the Illumina data. On the yeast data proovread produced few corrected reads and thus the coverage of the corrected reads is very low.

Table 6 shows that our method is slower and uses more memory than PBcR in self-correction mode but its disk usage is lower. On the E.coli dataset our new method is faster than proovread and PBcR utilising short read data but slower than LoRDEC, Jabba or PBcR using only PacBio data. On the yeast dataset, we are faster than PBcR in hybrid mode but slower than the others.

On the E.coli and yeast datasets, LoRDEC*+LoRMA uses 45% and 37%, respectively, of its running time on LoRDEC* iterations. On both datasets, the error rate of the reads after LoRDEC* iterations and trimming was 0.5%.

4.4 The effect of coverage

Especially for larger genomes, it is of interest to know how much coverage is needed for the error correction to succeed. We investigated this by creating random subsets of the E.coli dataset with coverages 25×, 50×, 100× and 150×. We then ran our method and PBcR (Berlin et al., 2015; Koren et al., 2012) on these subsets to investigate the effect of coverage on the error correction performance. Table 7 shows the results of these experiments. The other tools, LoRDEC, Jabba and proovread, use also the complementary Illumina reads and the coverage of PacBio reads does not affect their performance.

Table 7.

The effect of coverage of the PacBio read set on the quality of the correction

	LoRDEC*+LoRMA					PBcR
Coverage	25×	50×	100×	150×	208×	25×	50×	100×	150×	208×
Size (%)	3.105	30.348	65.739	67.198	66.223	31.132	44.190	48.391	50.284	51.068
Aligned (%)	99.400	99.663	98.328	98.748	99.318	99.941	99.794	95.966	90.003	86.023
Error rate (%)	0.329	0.187	0.140	0.159	0.257	2.224	1.396	0.874	0.757	0.6905
Gen. cov. (%)	3.886	45.763	99.403	99.999	100.000	94.638	100.000	100.000	100.000	100.000
Time (h)	0.10	0.32	3.30	7.17	10.40	0.08	0.18	0.47	0.93	1.68
Memory (GB)	14.165	14.275	14.718	15.415	16.984	7.851	9.020	9.706	9.931	22.00
Disk (GB)	0.272	0.655	1.416	2.024	2.824	1.232	2.443	3.714	7.114	16.070

When the coverage is high, the new method retains a larger proportion of the reads than PBcR and is more accurate, whereas when the coverage is low, PBcR retains more of the data and a larger proportion of it can be aligned. However, the error rate remains much lower for our new tool. The reads corrected by PBcR also cover a larger part of the reference when the coverage is low.

5 Conclusions

We have presented a new method for correcting long and highly erroneous sequencing reads. Our method shows that efficient alignment free methods can be applied to highly erroneous long read data. The current approach needs alignments to take into account the global context of errors. Reads corrected by the new method have an error rate less than half of the error rate of reads corrected by previous self-correction methods. Furthermore, the throughput of the new method is 20% higher than previous self-correction methods with read sets having coverage at least 75×.

Recently several algorithms for updating the DBG instead of constructing it from scratch when k changes have been proposed (Boucher et al., 2015; Cazaux et al., 2014). However, these methods are not directly applicable to our method because also the read set changes when we run LoRDEC* iteratively on the long reads.

Our method works solely on the long reads, whereas many previous methods require also short accurate reads produced by e.g. Illumina sequencing, which can incorporate sequencing biases in PacBio reads. This could have very negative effect on sequence quality, especially since Illumina suffers from GC content bias and some context-dependent errors (Nakamura et al., 2011; Schirmer et al., 2015).

As further work, we plan to improve the method to scale up to mammalian size genomes. We will investigate a more compact representation of the path labels in the augmented DBG to replace the simple hash tables currently used. Construction of multiple alignment could also be improved by exploiting partial order alignments (Lee et al., 2002) which have been shown to work well with PacBio reads (Chin et al., 2013).

Another direction of further work is to investigate the applicability of the new method on long reads produced by the Oxford NanoPore MinION platform. Laver et al. (2015) have reported an error rate of 38.2% for this platform and they also observed some GC content bias. Both of these factors make the error correction problem more challenging, and therefore, it will be interesting to see a comparison of the methods on this data.

Funding

This work was supported by the Academy of Finland (grant 267591 to L.S.), ANR Colib’read (grant ANR-12-BS02-0008), IBC (ANR-11-BINF-0002) and Défi MASTODONS to E.R., and EU FP7 project SYSCOL (grant UE7-SYSCOL-258236 to E.U.).

Conflict of Interest: none declared.