Compressed Sensing for Body MRI

Abstract

The introduction of compressed sensing for increasing imaging speed in MRI has raised significant interest among researchers and clinicians, and has initiated a large body of research across multiple clinical applications over the last decade. Compressed sensing aims to reconstruct unaliased images from fewer measurements than that are traditionally required in MRI by exploiting image compressibility or sparsity. Moreover, appropriate combinations of compressed sensing with previously introduced fast imaging approaches, such as parallel imaging, have demonstrated further improved performance. The advent of compressed sensing marks the prelude to a new era of rapid MRI, where the focus of data acquisition has changed from sampling based on the nominal number of voxels and/or frames to sampling based on the desired information content. This paper presents a brief overview of the application of compressed sensing techniques in body MRI, where imaging speed is crucial due to the presence of respiratory motion along with stringent constraints on spatial and temporal resolution. The first section provides an overview of the basic compressed sensing methodology, including the notion of sparsity, incoherence, and non-linear reconstruction. The second section reviews state-of-the-art compressed sensing techniques that have been demonstrated for various clinical body MRI applications. In the final section, the paper discusses current challenges and future opportunities.

Magnetic Resonance Imaging (MRI) is a powerful imaging modality for noninvasive examination of the body. It does not require the use of ionizing radiation and provides superior soft-tissue characterization with flexible image-contrast parameters. These properties allow good visualization of anatomical structure, physiological function, blood flow, and metabolic information, making MRI compelling in a variety of clinical applications. However, the incorporation of body MRI into routine clinical practice has been relatively slow compared to other imaging modalities such as computed tomography (CT). This barrier largely derives from stringent constraints on MR imaging speed, which result in relatively long examination times (with correspondingly high cost), limited spatiotemporal resolution and volumetric coverage, and sensitivity to respiratory motion.

Since the introduction of MRI, efforts have been devoted to improving imaging speed, and the speed at which MR images can be acquired today has increased dramatically with a combination of advances in MR hardware and innovations in both imaging acquisition and reconstruction strategies. For example, fast switching magnetic field gradients have substantially reduced the time intervals separating adjacent data points. The invention of fast imaging strategies, such as Fast Low Angle SHot (FLASH) imaging (1), Fast Spin-Echo (FSE) imaging (2), Echo-Planar Imaging (EPI) (3) and many others, has further increased imaging efficiency and motivated many new MR applications. Beginning in the late 1990s, a variety of so-called parallel-imaging techniques were proposed to accelerate data acquisition in MRI using arrays of receiver coils with spatially-varying sensitivities (4–6). Multiple coils with different spatial sensitivity profiles can be employed to perform part of the spatial encoding process that is conventionally accomplished via magnetic field gradients (7). Parallel imaging with multiple coils can reconstruct unaliased images from a subset of k-space data using sensitivity encoding (SENSE)-type algorithms (5), which operate in image space to undo the aliasing, or generalized autocalibrating partially parallel acquisitions (GRAPPA)-type algorithms (6,8), which operate in k-space to fill in missing points. The advent of parallel imaging has enabled significant advances in MR imaging speed beyond previous hardware and pulse sequence limitations, and has also led to development of various fast and ultrafast imaging techniques, such as temporal parallel imaging (9,10) and spatiotemporal acceleration techniques (11–13) that are often referred to as k-t imaging techniques. The underlying principle behind these techniques is the use of spatial and/or temporal redundancy of the MR images to accelerate MR image acquisition.

The concept of compressed sensing, which was originally proposed in the early 2000s by Donoho (14) and Candès et al (15), and was soon translated to MRI by Lustig et al. (16), represents another powerful approach for increasing imaging speed in MRI by exploiting image redundancy in a different way. Compressed sensing takes advantage of the fact that an image is usually sparse in some appropriate transform basis and enables reconstruction from a reduced number of k-space samples if they are taken in an incoherent fashion. Incoherence is a key component that aims to break the usual regularity in sampling patterns and enables the use of sparsity-based reconstructions. The introduction of compressed sensing to MRI has initiated a large body of research across multiple clinical applications, ranging from cardiovascular imaging to body imaging to neuroimaging and spectroscopic imaging (17). Moreover, appropriate combinations of compressed sensing and parallel imaging have been shown to enable further increases in imaging speed beyond what is possible with either method alone (8,18–22).

This work aims to summarize the rapidly growing topic of compressed sensing and to present a brief review of its clinical applications in body MRI. We begin with an overview of compressed sensing basics, describing the requirements for successful implementation of the technique. Then, we describe and discuss several state-of-the-art compressed sensing techniques that have been developed and demonstrated for different clinical body MRI applications. Finally, we conclude by outlining current challenges and future opportunities for compressed sensing in body imaging. In order to narrow the scope of this review, many promising applications of compressed sensing in cardiovascular imaging are not included.

Sparse MRI: A Brief Overview

Introduction to Compressed Sensing

The Nyquist-Shannon sampling theorem establishes a sufficient condition at which a signal can be reconstructed without ambiguity from a series of measurements. In MRI, a 2D image corresponds to a 2D signal, whereas a 3D image and a 2D dynamic image series correspond to 3D signals, etc. Unfortunately, fulfilling the Nyquist criterion is often time-consuming and data-intensive, and has posed a challenge for data storage and transmission as well as sampling-system design in many applications. This logistical and computational challenge can be addressed by first mapping a signal to an appropriate basis that provides a sparse representation, where the information is contained in only a few high-valued coefficients and most of the low-valued coefficients can be discarded with little or no perceptible loss of information. This process, known as signal (e.g., image or video) compression, has been widely used in the JPEG, JPEG2000, and MPEG standards. The fact that an image or a video can be compressed efficiently raises an interesting question: instead of first sampling a signal at a high sampling rate and then discarding most of the coefficients, why not directly acquire the data in a compressed form at a lower sampling rate? In other words, since information content of any given signal is usually lower than the number of coefficients required to characterize an arbitrary signal completely, can we integrate the compression process directly into the data acquisition, so that one can sample a signal at its information rate instead of the Nyquist rate?

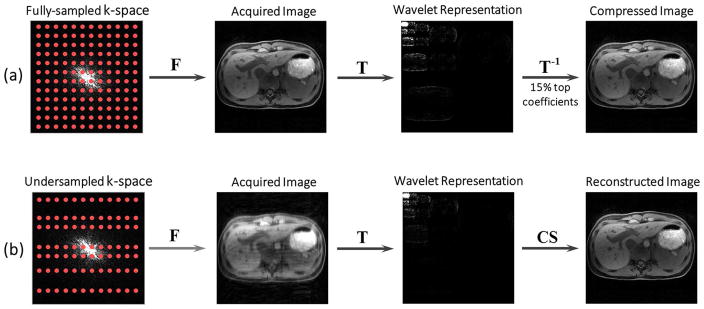
The fact that images are compressible has been known for years, but it seemed impossible to know in advance which samples to choose without knowledge of the original image. The breakthrough came with the notion of incoherence. If one chooses the samples in an irregular manner such that they do not replicate image features in the sparse domain and resulting undersampling artifacts appear as low-value coefficients, a reconstruction algorithm that enforces sparsity is able to recover the sparse representation from fewer samples than are required by the nominal Nyquist rate. Figure 1 compares (a) standard sensing and post-compression with (b) compressed sensing of an MR image. Standard sensing and post-compression methods acquire fully-sampled data and then compress the resulting image using a sparsifying transformation. This type of compression does not decrease acquisition time. In contrast, compressed sensing methods directly acquire subset of measurements in an incoherent way (e.g., random undersampling as will be discussed later), and remove undersampling artifacts in the reconstruction step.

Figure 1.

Comparison of standard image compression (a) and compressed sensing (b). Image compression first acquires a fully-sampled image and then compresses it in the second step. Compressed sensing, on the other hand, builds the compression into the encoding process, thus acquiring only a subset of the encoding steps in a random pattern. The image is subsequently reconstructed from undersampled data with a suitable nonlinear algorithm. F: Fourier transform; T: sparsifying transform; CS: compressed sensing.

The application of compressed sensing has three basic requirements: i) sparsity or transform sparsity of the target image, ii) incoherent sampling (here, incoherence is assessed between the sampling basis and the sparse basis), and iii) use of a reconstruction algorithm that enforces sparsity constrained by data consistency. The following subsections will briefly describe the practical implementation of these requirements for MR imaging. More comprehensive information on each of these components can be found in the literature (16,23,24).

Sparse MRI

Sparsity

An image is said to be sparse when it can be characterized by only a small number of non-zero coefficients, as compared with the total number of voxels. A typical example is MR angiography, where background tissue is suppressed and only vessels show signal. Thus, an MR angiography image is already sparse in image domain. This, of course, does not apply to all MR images. However, given structural correlation in MR images, there is usually a mathematical transformation that will produce a sparse representation of the image. Transformations that are known from data compression, such as the discrete wavelet transform (DWT), the discrete cosine transform (DCT), the fast Fourier transform (FFT), finite difference operations, and many others, can be used for this purpose. A high degree of sparsity is desired, since it implies that information content can be represented by a small sample of data, and this is directly related to the maximal achievable acceleration factor (23). For example, higher sparsity is obtained when processing multidimensional images, such as dynamic imaging, because the temporal dimension is typically highly compressible. This enables higher acceleration for dynamic imaging compared to static imaging.

Figure 2 shows examples of transform sparsity of a static liver image in wavelet space (a) and transform sparsity of a dynamic contrast-enhanced (DCE) liver imaging series in x–y-f (two spatial dimensions + temporal frequency dimension) space with a FFT performed along the temporal dimension (b).

Figure 2.

MR images can be considered sparse in an appropriate transform domain. A liver image has as parse representation (i.e. a representation with a small number of high-value coefficients) in the wavelet space (a), and a dynamic contrast-enhanced image series has a sparse representation in the x-y-f (two spatial dimensions + temporal frequency dimension) space, with a FFT (fast Fourier transform) performed along the temporal dimension (b).

Incoherence

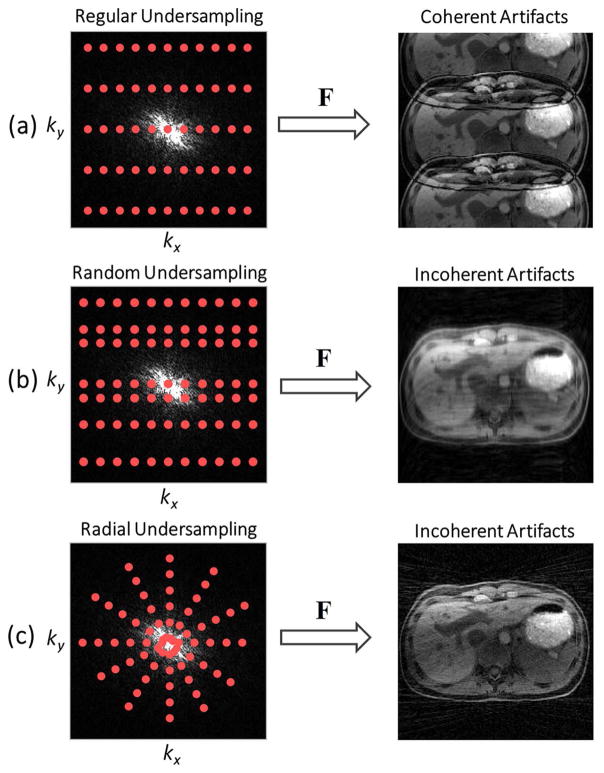
Another requirement for successful application of compressed sensing is that undersampling artifacts must be incoherent, i.e. that they must appear as noise-like patterns in the sparse domain. This criterion excludes regular undersampling schemes commonly used with parallel imaging, because the resulting artifacts manifest as coherent replicas of the signal structure, as shown in Figure 3a. Various undersampling strategies have been proposed to meet the incoherence requirement. The most popular scheme is Cartesian k-space undersampling in a random fashion (16), where some portion of the phase-encoding steps are randomly skipped, resulting in incoherent artifacts (Figure 3b). Non-Cartesian sampling (e.g., radial sampling) is an attractive alternative due to its highly incoherent undersampling behavior (21) (Figure 3c), which will be described in more detail in subsequent sections.

Figure 3.

(a) Regular undersampling generates coherent replicas of the signal structure; (b) Random undersampling generates incoherent artifacts that appear like added noise; (c) radial sampling permits undersampling along both spatial dimensions and thus enables a higher level of incoherence.

Image Reconstruction

A compressed sensing reconstruction enforces sparsity of the solution to suppress the incoherent aliasing artifacts, and maximizes data consistency between the solution and the available undersampled data. Mathematically, this can be achieved by solving the following constrained optimization problem:

$$\begin{array}{c}\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{Tm}\left|\right|}_1\\ s.t.{\left|\right|\mathbf{y}-\mathbf{Fm}\left|\right|}_2^2\le \epsilon \end{array}$$ [1]

Here, m is the image or image series to be reconstructed, F is the Fourier transform operator that maps between k-space and image space, y is the acquired k-space data, T is the sparsifying transform and ε is the estimated noise level. Data consistency is enforced via the ℓ₂-norm, which quantifies squared absolute error between the acquired measurements and the solution estimate. Sparsity is promoted by minimization of the ℓ₁-norm, which is defined as the sum of the absolute values of all coefficients. Among all solutions that are consistent with the acquired data with an error below the noise level, Equation 1 aims to find the solution that has the minimum ℓ₁-norm in the sparse domain.

The ℓ₁-minimization has been widely used in compressed sensing reconstruction because the resulting reconstruction optimization (Equation 1) is convex and the optimal solution is then guaranteed (25). Nonetheless, ℓ₁-norm minimization is not the only choice for sparse signal recovery. Reconstruction methods that enforce an ℓ_p-norm minimization with 0 ≤ p<1 have also been proposed. These methods are expected to require fewer measurements than reconstructions based on the ℓ₁-norm. However, a substantial challenge associated with such type of methods is that the resulting optimization is non-convex and thus the convergence to the global minimum, which is the optimal solution, is not always guaranteed. Moreover, the performance of non-convex methods relies on the selection of an appropriate initial solution.

The constrained optimization problem in Equation 1 is often relaxed to an unconstrained optimization problem by using Lagrange multipliers:

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{y}-\mathbf{FM}\left|\right|}_2^2+\lambda {\left|\right|\mathbf{Tm}\left|\right|}_1$$ [2]

The optimization problem in this form can be solved efficiently with iterative algorithms such as gradient descent, conjugate gradient, and many other methods. These iterative algorithms start with an aliased image and progressively remove aliasing artifacts. The regularization parameter λ controls the trade-off between data consistency (ℓ₂-norm) and the promotion of sparsity (ℓ ₁-norm).

The theory of compressed sensing states that the number of samples required to perform accurate reconstructions using ℓ₁-norm minimization is about three to five times the number of sparse coefficients (15,26). Using a multi-coil array for data reception, the combination of compressed sensing and parallel imaging can enable additional acceleration (18,19,22), as will be described later in more detail. It has been shown that the number of samples required for accurate image reconstruction with combined compressed sensing and parallel imaging can be reduced to close to the number of sparse coefficients in an ideal case (19,27).

Selection of Sparsifying Transform

The selection of a sparsifying transform should be made based on the target clinical application and either generic mathematical transforms or transforms learned from the acquired data can be used. For example, first-order finite differences have been employed for accelerated brain imaging due to the assumption that brain images are piecewise constant to some degree and exhibit a sparse representation after subtraction of adjacent pixels along the spatial dimensions (21). Here, minimization of the ℓ ₁-norm of finite differences is known as total variation (TV) constraint. However, for many applications, the assumption of a piecewise-constant signal is not valid. As a consequence, applying finite differences tends to smooth images and cause image blurring due to the loss of high-resolution information. For these applications, a combination of wavelet transform with finite differences has been shown to provide better performance, and has commonly been used in accelerated static imaging (16). In addition, the concept of total generalized variation (TGV), which has been introduced to model the characteristics of MR images more accurately, has shown improved performance over conventional transforms such as first-order finite differences (28). For dynamic imaging, transforms can be applied along the temporal dimension, which improves performance over pure spatial constraint due to a high level of temporal correlations (29). Popular temporal sparsifying transforms for accelerated dynamic imaging including the temporal FFT (19,30) and first-order temporal finite differences (31–33). In addition to the generic transforms described above, many adaptive sparsifying transforms have been shown to provide superior performance in compressed sensing reconstructions. For example, the Karhunen–Loeve transform (KLT), also known as principle component analysis (PCA), is a widely used transform in data compression and has been applied for dynamic compressed-sensing MRI (34). Unlike FFT or finite differences, KLT/PCA is a data-dependent transform and can achieve higher performance in many applications such as parameter mapping (35,36) or flow imaging (37). Moreover, another type of adaptive techniques, which is known as dictionary learning (38,39), has also been proposed for compressed sensing reconstructions. In dictionary learning, a training process is performed such that an optimal sparsifying transform can be adaptively learned from an overcomplete set of basis functions to better characterize a particular image with sparser representation. In many proposed methods, a dictionary is trained from a set of overlapping image patches, so that local image features can be captured and local image sparsity can be exploited. For practical implementations, image reconstruction and the training process can also be performed simultaneously in a joint iterative reconstruction framework.

Reconstruction Algorithm

The optimization problem in Equation 2 is non-linear due to the ℓ₁-term. Therefore, a corresponding non-linear reconstruction algorithm must be used to find a solution. Many existing algorithms can be chosen for this task, which differ in efficiency of convergence and effort of implementation. Popular optimization algorithms for compressed sensing MRI with available MATLAB implementations are listed as follows:

1. Non-linear conjugate gradient with backtracking line search (Non-linear-CG): http://people.eecs.berkeley.edu/~mlustig/Software.html

2. Iterative shrinkage-thresholding (ISTA) http://people.eecs.berkeley.edu/~mlustig/Software.html

3. Fast Iterative shrinkage-thresholding (FISTA) https://github.com/ryotat/OPT09/blob/master/matlab/fistalrl1.m

4. Limited-memory Broyden-Fletcher-Goldfarb-Shanno (l-BFGS): https://software.sandia.gov/trac/poblano/

5. Alternating directions of multiple multipliers (ADMM): https://web.stanford.edu/~boyd/papers/admm/

6. Bregman iterative algorithm: http://www.caam.rice.edu/~optimization/L1/bregman/

Sparse Body MRI: State-of-the-Art Techniques

This section describes state-of-the-art compressed sensing techniques that have been proposed for different body MRI applications. It is divided into three subsections, including data acquisition, image reconstruction, and motion compensation.

Data Acquisition

As mentioned in the previous section, compressed sensing requires incoherent undersampling to preserve sparsity and produce uncorrelated aliasing artifacts. The following subsections discuss different sampling schemes proposed for compressed sensing MRI.

Cartesian Sampling

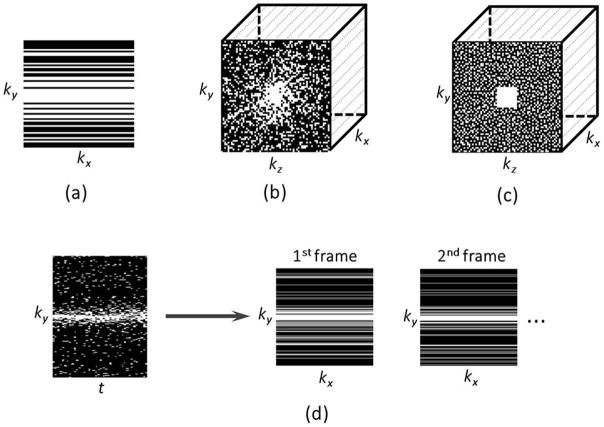
Random undersampling is the usual way to break the regularity of Cartesian k-space sampling and to produce noise-like aliasing artifacts. However, not all random schemes meet the incoherence requirement. Given that the signal intensity decreases from the center of k-space to the periphery, a variable-density random undersampling pattern usually results in a high degree of incoherence (dense sampling at the center and increased undersampling at the periphery, as shown in Figure 4a). Mathematically, the low frequency Fourier basis functions (center of k-space) are highly correlated with the basis functions of most sparsifying transformations (40), and thus improved reconstruction performance can be obtained with dense sampling of low frequency region. Since undersampling the frequency-encoding dimension does not reduce acquisition time, only 1D-sparsity and incoherence along the phase-encoding (k_y) dimension can be exploited in 2D Cartesian imaging. 3D imaging offers more possibilities due to the additional slice-encoding dimension (k_z), which allows undersampling along both k_y and k_z dimensions (Figure 4b), enabling use of two-dimensional sparsity and incoherence (23).

Figure 4.

(a) 2D Cartesian undersampling pattern, where undersampling is only performed along the phaseencoding dimension (ky); (b) 3D Cartesian undersampling pattern, where undersampling can be performed along two spatial dimensions (ky and kz); (c) 3D Cartesian undersampling pattern based on the Poisson-disc distribution, which limits the distances between samples across the entire k-space, with full sampling in a small central region; (d) 2D dynamic Cartesian undersampling pattern, where a different sampling pattern can be employed in each temporal frame to provide additional temporal incoherence. White lines or points indicate acquired data.

Poisson-disc sampling represents an alternative randomization approach that limits the distance between adjacent samples (8). It is important to avoid large gaps in k-space, which may destabilize the reconstruction when using combination of compressed sensing with parallel imaging. Figure 4c shows a 3D Cartesian sampling scheme in which Poisson-disc sampling is implemented in the k_y–k_z plane with a fully sampled small central k-space region.

Dynamic imaging provides higher flexibility in the design of sampling trajectories because a different incoherent undersampling pattern can be used for each temporal frame, as shown in Figure 4d (29,30). This introduces additional temporal incoherence that can be exploited to further improve the performance of compressed sensing reconstruction.

Non-Cartesian Sampling

Non-Cartesian sampling (e.g., radial or spiral sampling) is an attractive alternative, as the k-space samples are not directly acquired on a Cartesian grid. Therefore, even regular undersampling of non-Cartesian trajectories offers inherent incoherence. Skipping measurements in radial or spiral sampling effectively undersamples all spatial dimensions simultaneously and distributes the overall acceleration accordingly, resulting in a lower level of aliasing artifacts (21,33), as previously shown in Figure 3c. It has been shown that non-Cartesian MRI is also less sensitive to motion than many Cartesian approaches (41). Furthermore, repeated sampling of the k-space center offers the possibility of extracting motion signals (e.g., respiratory motion), which can be used for self-navigation or motion compensation (42–44). In addition, non-Cartesian trajectories can be designed with angular rotation of adjacent measurements by the golden angle (45) (e.g., 111.246^o in the case of 2D radial sampling), which offers several attractive properties. For example, each acquired measurement provides complementary information to the previous k-space coverage, and the measurements never repeat. Golden-angle sampling ensures approximately uniform k-space coverage for many useful subsets of acquired data. This enables dynamic imaging studies with continuous data acquisition and retrospective reconstruction of image series with flexible temporal resolution by grouping a different number of consecutive measurements into each temporal frame (33).

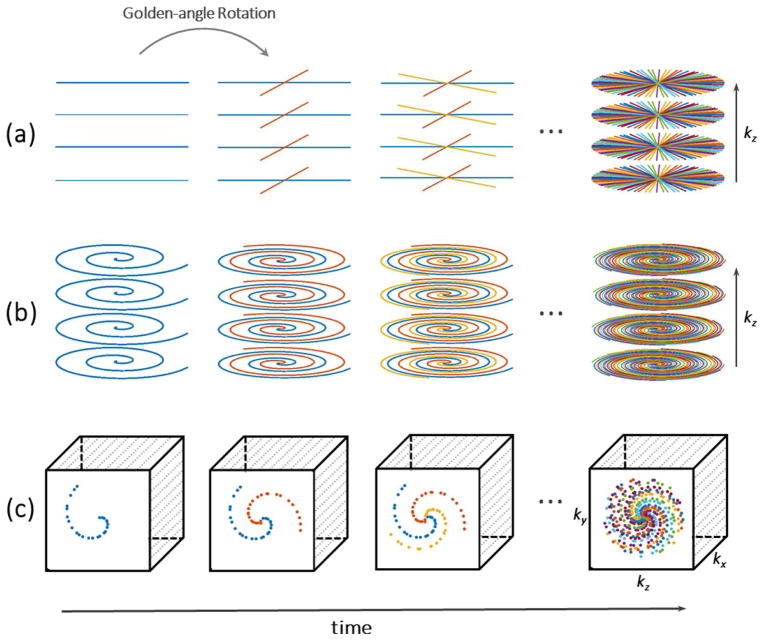
For volumetric imaging, radial and spiral trajectories are often combined with Cartesian sampling in hybrid sampling schemes, which are known as stack-of-stars (46) or stack-of-spiral (47) sampling. Figure 5a and 5b show examples of golden-angle stack-of-stars and stack-of-spiral sampling patterns. Here, radial or spiral sampling is performed in the k_x–k_y plane while Cartesian sampling is employed along the k_z dimension. Compared with full non-Cartesian 3D sampling (e.g., “koosh-ball” 3D radial trajectories), such hybrid schemes provide better performance for fat saturation, reduced sensitivity to eddy-currents and k-space discontinuities, and data acquisitions with flexible slice resolution. Furthermore, because the k-space trajectory for each slice is identical, Fourier encoding along k_z can be disentangled with a 1D Fourier transform as an initial processing step, which enables reconstruction of different slices in parallel.

Figure 5.

Various 3D golden-angle sampling schemes. (a) Stack-of-stars scheme, in which radial sampling is implemented in the kx–ky plane and Cartesian sampling is implemented in the kz plane; (b) Stack-of-spiral scheme, in which spiral sampling is implemented in the kx–ky plane and Cartesian sampling is implemented in the kz plane; (c) 3D Cartesian sampling, in which the k-space sampling in the ky–kz plane is segmented into multiple interleaves rotated by a golden-angle.

Variable-Density Cartesian Sampling with Golden-Angle View Ordering

Inspired by the beneficial features of golden-angle sampling, several studies have adapted the scheme for 3D Cartesian sampling. Here, phase-encoding steps in the k_y–k_z plane are segmented into multiple radial– or spiral-like interleaves, and each interleave is rotated by the golden angle from previous one, as shown in Figure 5c. This sampling strategy maintains a variable-density pseudorandom distribution of the measurements, allows for flexible acceleration (either isotropic or anisotropic), and supports continuous data acquisition. Because k-space samples are acquired directly on a Cartesian grid, this approach ensures faster and simpler reconstruction than conventional golden-angle radial or spiral sampling. However, since the frequency-encoding dimension is fully sampled (as in all Cartesian sampling schemes), acceleration performance along this dimension is limited. The performance of such sampling patterns also depends on the number of acquired slices, as a reduced number of slices decrease the ability to exploit sparsity and incoherence along the slice dimension. Examples of this sampling approach include Variable-Density sampling and Radial view ordering (VDRad) (48), CIRcular Cartesian UnderSampling (CIRCUS) (49), Golden angle Cartesian acquisition with Spiral Profile ordering (G-CASPR) (50), GOlden-angle CArtesian Randomized Time-resolved (GOCART) sampling (51) and spiral phyllotaxis sampling on Cartesian grid (52).

Image Reconstruction

Combination of Compressed Sensing and Parallel Imaging

Compressed sensing can be performed separately for each individual coil element. However, as image sparsity and coil sensitivity encoding are complementary sources of information, these two approaches can be synergistically combined (8,19,20). On one hand, the additional spatial encoding capabilities of multiple receiver coils in parallel imaging allow exploitation of joint sparsity in multi-coil images with reduced levels of incoherent aliasing artifact, resulting in higher achievable acceleration rates. On the other hand, compressed sensing can serve as a regularizer for the inverse problem in parallel imaging to prevent spurious noise amplification (53).

The combination with parallel imaging can be performed in a SENSE-like framework known as SPARSE-SENSE (20) for static imaging and k-t SPARSE-SENSE (19) for dynamic imaging. The SPARSE-SENSE reconstruction is formulated by incorporating coil sensitivities into Equation 2:

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{y}-\mathbf{FCm}\left|\right|}_2^2+\lambda {\left|\right|\mathbf{Tm}\left|\right|}_1$$ [3]

Here, C are the coil sensitivity maps, usually calculated from additional reference data, and T is the sparsifying transform applied in the spatial dimension. The reconstructed image m , in this case, is a single image that represents the combination from all coils. k-t SPARSE-SENSE shares the same reconstruction framework except that m is the dynamic image series to be reconstructed, and T is applied along the temporal dimension to exploit temporal correlations. Golden-angle RAdial Sparse Parallel (GRASP) MRI (33) is an extension of the k-t SPARSE-SENSE framework for golden-angle radial sampling. The synergistic combination of compressed sensing, parallel imaging, and golden-angle radial sampling has been shown to provide promising combinations of temporal resolution, spatial resolution, and volumetric coverage for dynamic MRI studies without the need for breath-holding. Furthermore, GRASP represents a new paradigm for clinical workflow, enabling continuous data acquisition and retrospective reconstruction with flexible temporal information such as temporal resolution, temporal location, and number of temporal frames.

As an alternative to the SPARSE-SENSE framework, auto-calibrating parallel imaging approaches such as SPIRiT (8) can also be combined with compressed sensing, in an approach commonly known as L₁-SPIRiT (8,54). The corresponding reconstruction problem is formulated as

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{y}-\mathbf{Fm}\left|\right|}_2^2+\alpha {\left|\right|(\mathbf{G}-\mathbf{I})\mathbf{m}\left|\right|}_2^2+\lambda \text{Joint}{\ell }_1(\mathbf{Tm})$$ [4]

Here, m is the reconstructed multi-coil image (concatenated and uncombined), and G is the SPIRiT kernel computed from calibration data, which is usually obtained from a small fully-sampled region around the k-space center. L₁-SPIRIT enforces coil-by-coil data consistency (left-hand term), kernel consistency (center-term) and joint sparsity on the multi-coil image (right-hand term). The joint sparsity term ( Joint ℓ₁ (·) ) is a combined ℓ₂-ℓ₁ norm, where the ℓ₂-norm works along the coil dimension and the ℓ₁-norm operates along the voxel dimension, as defined in the following equation:

$$\text{Joint}{\ell }_1(m)=\sum _r\sqrt{\sum _c{\mid m_{rc}\mid }^2}$$ [5]

where c is the coil index and r is the spatial index. An additional regularization parameter α is needed to control the balance between data consistency and calibration consistency.

Compressed sensing has also been combined with a recently introduced parallel imaging technique called ESPIRiT (55), which is an auto-calibrating approach that links GRAPPA and SPIRiT to SENSE-based reconstruction techniques. ESPIRiT estimates coil-sensitivity maps through an eigenvalue decomposition of the data from a compact calibration region in k-space, and the sensitivity maps are subsequently used in a SENSE-based reconstruction algorithm. Since this approach enforces relaxed sensitivity constraints in a SENSE framework without the need to explicitly calculate the coil sensitivities from additional reference data, it can potentially avoid errors that may occur in conventional SENSE reconstruction, such as aliased coil sensitivities caused by a small field of view (FOV). The combination of ESPIRiT and compressed sensing is known as L₁-ESPIRiT (55). The reconstruction framework is similar to Equation 3 except for the algorithm that estimates the coil sensitivity maps C.

Advanced Sparsity Constraints

This section describes novel constraints that extend the idea of sparsity to different data structures.

Locally Low-Rank Constraint

Dynamic image series can be sorted as a Casorati matrix, where each temporal frame corresponds to a column. Given the extensive spatial and temporal correlations, the space-time Casorati matrix is usually of low rank, which means that the number of linearly independent rows/columns is lower than the total number of rows/columns. This low-rank property can be exploited in compressed sensing (56,57) and it is related to the Karhunen–Loeve transform/PCA described earlier. The corresponding reconstruction problem, known as low-rank matrix completion (58), can be formulated as optimization problem:

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{y}-\mathbf{FCm}\left|\right|}_2^2+\lambda {\left|\right|\mathbf{m}\left|\right|}_{\ast }$$ [6]

Unlike in Equation 2, sparsity is enforced here via minimization of the nuclear norm (||m||) of the image, which is defined as sum of the singular values of an image matrix. When the low-rank property is enforced on the entire images, the method is referred to as a globally low-rank approach. Recent work suggests that the performance of compressed sensing can be further improved by using locally low-rank constraints to exploit spatiotemporal correlations within different small regions separately (59–62). This is achieved by solving the following optimization problem:

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{y}-\mathbf{Fm}\left|\right|}_2^2+\lambda \sum _{n=1}^N{\left|\right|{\mathbf{B}}_{\mathbf{n}}\mathbf{m}\left|\right|}_{\ast }$$ [7]

Here B_n is an operator that selects an image block and N is the total number of image blocks with a size ranging from 8x8 to 16x16 (61). The underlying principle of this approach is that the dynamics of adjacent image pixels are often similar, and therefore the redundancy is higher within local image regions than in the entire image.

Low-Rank Plus Sparse Matrix Decomposition

Low-rank plus sparse matrix decomposition (L+S) (63) is another compressed-sensing reconstruction technique that goes beyond the original idea of enforcing sparsity in a transform domain. The L+S model reconstructs dynamic images as the superposition of a background low-rank component with sparse innovations on that background. The reconstruction is performed by solving the following optimization problem:

$$[\mathbf{L},\mathbf{S}]=\underset{\mathbf{L},\mathbf{S}}{argmin}{\left|\right|\mathbf{y}-\mathbf{F}(\mathbf{L}+\mathbf{S})\left|\right|}_2^2+{\lambda }_L{\left|\right|\mathbf{L}\left|\right|}_{\ast }+{\lambda }_S{\left|\right|\mathbf{TS}\left|\right|}_1$$ [8]

L+S decomposition effectively combines the ideas of compressed sensing and low-rank matrix completion, providing improved performance compared to individual application of the techniques. It can also be combined with the idea of locally low-rank constraints. Moreover, the L+S reconstruction allows for automatic background suppression without the need for subtraction of a reference image, as the S component will be reconstructed without the background, which makes it particularly useful for applications such as MR angiography.

Motion Compensation

Respiratory motion is one of the most common sources of artifacts in body MRI and remains a major challenge for clinical exams. Although successful suspension of breathing during MR scans can prevent artifacts, breath-hold capabilities are subject-dependent and can be significantly limited in many patients. Furthermore, typical breath-hold durations (10–15 seconds) limit the achievable spatial resolution and volumetric coverage. Therefore, free-breathing MRI techniques are desirable. The most popular approach is to use either navigator signals or respiratory bellows to follow the respiratory motion and to acquire data only at a specific respiratory state (e.g., end-expiration). However, gated data acquisition reduces the imaging efficiency significantly, prolongs the total examination time, and is incompatible with applications such as DCE-MRI, where the passage of a contrast agent needs to be captured quickly and in real-time. This section describes several alternatives that have been proposed to overcome the abovementioned problems in free-breathing body MRI exams.

Soft-Gating

The soft-gating method has recently been introduced as a simple but effective way to reduce respiratory motion blurring in MRI (61,64,65). Based on a navigator signal, which can be obtained either from external devices or from acquired k-space data, a motion-weighting function is generated. This function is then incorporated into the data consistency term to enforce a weighted data consistency. Image reconstruction with soft-gating can be adapted from Equation 2 as follows:

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{W}(\mathbf{y}-\mathbf{Fm})\left|\right|}_2^2+\lambda {\left|\right|\mathbf{Tm}\left|\right|}_1$$ [9]

Here, W is a matrix containing motion weights in a range between 0 and 1. Measurements with weight 1 are considered consistent with the respiratory phase to be reconstructed (e.g., end-expiration) and will therefore have higher impact on the solution. On the contrary, a weight close to 0 means that the corresponding data are motion-corrupted and therefore their impact on the reconstruction will be reduced. Compared with standard gating approaches, which simply discard motion-corrupted measurements, soft-gating achieves improved scan efficiency by including all acquired data into the reconstruction in a weighted fashion. Figure 6a shows an example of k-space weighting using a respiratory motion signal.

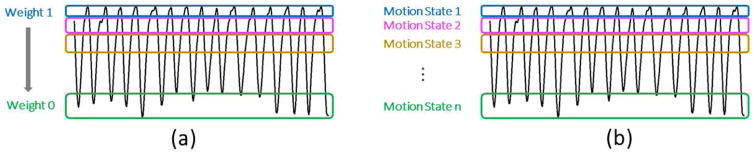
Figure 6.

Comparison of soft-gating with XD-GRASP sorting. Soft-gating (a) reduces motion blurring by binning the acquired k-space and then weighting them according to their motion state in the reconstruction process. XD-GRASP (b) sorts the acquired k-space data into multiple separated motion states and creates an additional motion dimension. Compressed sensing is performed to exploit correlations along the new dimension.

Motion Correction

Another strategy to correct for respiratory motion is to integrate image registration into the reconstruction process, such that images reconstructed in different motion states can be combined into a final result in a single motion state. This approach has been demonstrated for respiratory-motion correction in many cardiovascular applications (44,66–68), where the movement of the heart during respiration is quite rigid. Application to abdominal imaging is more challenging due to the larger deformation of the abdominal organs. Therefore, a robust deformable registration technique is needed to account for the non-rigid body motion (69–71). The non-rigid motion can also be approximated as localized linear translations, and a method called localized autofocusing has been proposed for respiratory motion correction by applying the appropriate linear-phase correction in k-space (72). This imaging technique has been demonstrated in free-breathing pediatric imaging in sedated patients where respiration patterns are largely predictable (64). Some approaches, such as motion-guided L+S reconstruction (73), are able to learn the motion fields to guide the image reconstruction, not only correcting for motion but also providing access to motion information. However, motion-correction schemes require use of specific motion models in the corresponding warping and unwarping operations for each iteration of the reconstruction procedure, and therefore are highly dependent on the respiration pattern. Thus, registration may not always suffice to account for the complex movement of organs during respiration, particularly for patients with deep and/or irregular breathing pattern.

Image Reconstruction with Extra Motion Dimensions

Recently, a novel approach has been described that handles respiratory motion by performing golden-angle radial data acquisition with compressed sensing reconstruction of one or more extra motion-state dimensions (74). A respiratory motion signal, which can be obtained from acquired k-space data, is used to sort the continuously acquired golden-angle radial dataset into multiple motion states to generate an extra respiratory motion dimension. A compressed sensing reconstruction is then performed on the sorted dataset to exploit the correlations generated along the respiratory dimension:

$$\underset{\mathbf{m}}{argmin}{\left|\right|\mathbf{y}-\mathbf{Fm}\left|\right|}_2^2+{\lambda }_1{\left|\right|{\mathbf{T}}_1\mathbf{m}\left|\right|}_1+{\lambda }_2{\left|\right|{\mathbf{T}}_2\mathbf{m}\left|\right|}_1\cdots$$ [10]

Here, m is the dataset with the extra dimensions to be reconstructed, and T₁ is the sparsifying transformation performed along the new respiratory dimension. If the dataset has more than one dynamic dimension (e.g., cardiac, contrast enhancement, or multiple echoes), additional sparsifying transformations (T₂ ) can be added. Because this approach extends the previously described GRASP reconstruction with extra dimensions, it is referred to as XD-GRASP (eXtra-Dimensional GRASP).

Figure 6b shows the k-space data-sorting procedure based on a respiratory motion signal in XD-GRASP. The data sorting is usually performed such that the number of k-space points at each motion state is the same, to ensure the same acceleration rate at each motion state.

Data Acquisition and Image Reconstruction Software for Sparse Body MRI

Some of the techniques described in this section are available for free download, including:

1. Sparse MRI: http://people.eecs.berkeley.edu/~mlustig/Software.html

2. k-t SPARSE-SENSE: http://cai2r.net/resources/software/k-t-sparse-sense-matlab-code

3. L₁-SPIRiT: http://people.eecs.berkeley.edu/~mlustig/Software.html

4. L₁-ESPIRiT: http://people.eecs.berkeley.edu/~mlustig/Software.html

5. GRASP: http://cai2r.net/resources/software/grasp-matlab-code

6. XD-GRASP: http://cai2r.net/resources/software/xd-grasp-matlab-code

7. L+S: http://cai2r.net/resources/software/ls-reconstruction-matlab-code

8. Locally low-rank sparse MRI: http://web.stanford.edu/~tzhang08/software.html

9. VDRad sampling: http://mrsrl.stanford.edu/~jycheng/software.html

10. Poisson disc sampling: https://people.eecs.berkeley.edu/~mlustig/Software.html

11. Autofocusing: http://mrsrl.stanford.edu/~jycheng/software.html

Sparse Body MRI: Clinical Applications

The sparse imaging techniques described in the previous section have been applied for a number of clinical applications in body MRI, in order to increase imaging speed and improve performance (61,64,75–86). These studies include accelerated 3D abdominal MRI, free-breathing DCE-MRI, abdominal 4D flow imaging. Table 1 summarizes studies that have been conducted in a clinical setting and this section describes representative examples selected from Table 1.

Table 1.

Author	Year	Applications	Sampling Scheme	Sparsity Constraint	Reconstruction Scheme	Motion Compensation Scheme
* Cheng JY et al64	2015	Pediatric Abdominal MRI	VDRad	3D Wavelet	L1-ESPIRiT	Soft-gating + Autofocusing
* Chandarana H et al75	2016	MRCP	Variable-density Poisson-disc	3D Wavelet	SPARSE-SENSE	Breath-hold
Zhang T et al76	2014	DCE-MRI of the pediatric abdomen	Variable-density Poisson-disc	3D Wavelet	L1-SPIRiT	Anesthesia for respiration suspension
Zhang T et al77	2015	DCE-MRA of the pediatric abdomen	VDRad	Locally low-rank	L1-ESPIRiT	Soft-gating
* Zhang T et al61	2015	DCE-MRI of the pediatric abdomen	VDRad	Locally low-rank	L1-ESPIRiT	Soft-gating
* Chandarana H et al78	2013	DCE-MRI of the liver	Golden-angle stack-of-stars	Temporal TV	GRASP	Radial sampling
* Chandarana H et al79	2015	DCE-MRI of the liver	Golden-angle stack-of-stars	Temporal TV	XD-GRASP	Extra respiratory dimension
Ream J et al80	2015	DCE-MRI of the small bowel	Golden-angle stack-of-stars	Temporal TV	GRASP	Radial sampling
Rosenkrantz A et al81	2015	DCE-MRI of the prostate	Golden-angle stack-of-stars	Temporal TV	GRASP	Radial sampling
Riffel P et al82	2016	DCE-MRI of the kidney	Golden-angle stack-of-stars	Temporal TV	GRASP	Radial sampling
Chandarana H et al 83	2015	Liver perfusion imaging	Golden-angle stack-of-stars	Temporal TV	GRASP	Radial sampling
Parikh et al84	2016	Bladder perfusion imaging	Golden-angle stack-of-stars	Temporal TV	GRASP	Radial sampling
* Dyvorne H et al85	2014	Abdominal 4D flow imaging	Golden-angle stack-of-spiral	Global low-rank	k-t SPARSE-SENSE	Breath-hold
Mann LW et al86	2016	Liver steatosis measurement	Variable-density Poisson-disc	3D Wavelet	L1-ESPIRiT	Breath-hold

Accelerated 3D Abdominal MRI

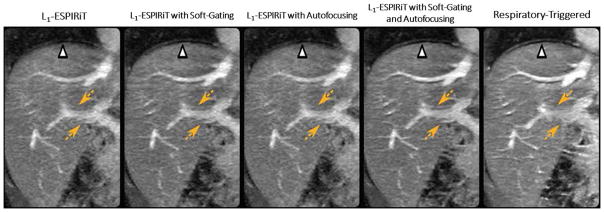
Abdominal imaging is one area with a need for scan speed due to the presence of respiratory motion. The combination of compressed sensing with free-breathing techniques, in particular, has been a popular research topic addressed by many groups. In the study of Cheng et al (64), an imaging technique was proposed for free-breathing pediatric abdominal MR exams. The VDRad sampling scheme was applied for continuous data acquisition, and a butterfly navigator (72) was implemented for respiratory motion detection. Motion compensation was performed through a combination of soft-gating and localized autofocusing, and the L₁-ESPIRiT algorithm was applied to reconstruct the undersampled dataset. As shown in Figure 7, L₁-ESPIRiT with either soft-gating or autofocusing achieved better image quality of the hepatic arteries than L₁-ESPIRiT without motion compensation (yellow dashed arrows). A combination of soft-gating and autofocusing enabled further improvement in delineation of the liver dome (white arrow) and the hepatic vessels (yellow dashed arrows) comparing to L₁-ESPIRiT with soft-gating or autofocusing alone, and also achieved better delineation of the hepatic arteries than the respiratory triggered reference.

Figure 7.

L₁-ESPIRiT with either soft-gating or autofocusing achieved better image quality of the portal vein than L₁-ESPIRiT without motion compensation (yellow dashed arrows). A combination of soft-gating and autofocusing enabled further improvement in delineation of the liver dome (white arrow) and the hepatic vessels (yellow dashed arrows) compared to L₁-ESPIRiT with soft-gating or autofocusing alone, and also achieved better delineation of the hepatic vessels than the respiratory triggered reference. (Images were obtained from the Figure 4 in Cheng JY et al. J Magn Reson Imaging. 2015 2015 Aug;42(2):407–20 and were reproduced with permission from the authors and the journal.)

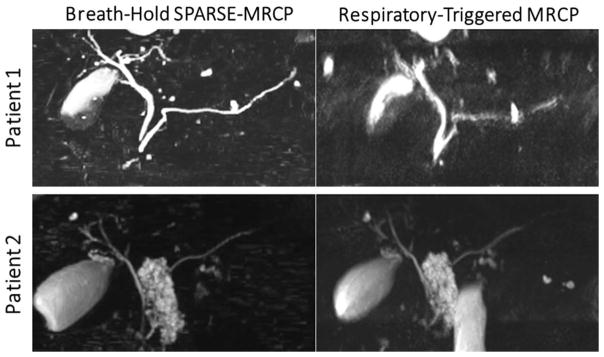
In the study of Chandarana et al (75), accelerated 3D MR Cholangiopancreatography (MRCP) images were obtained within a single breath-hold, approximately 20-fold faster than conventional respiratory-triggered acquisition. MRCP is well suited for CS reconstruction as images are inherently sparse, because the strong T₂-weighting suppresses background tissue, and biliary and pancreatic ducts that have fluid signal are visualized. In the proposed method, a variable-density Poisson-disc sampling scheme was employed for data acquisition and images were reconstructed with SPARSE-SENSE. The results were compared to free-breathing respiratory-triggered MRCP, which is the conventional imaging technique used in clinical exams. Figure 8 shows comparison of maximum intensity projection (MIP) images between breath-held SPARSE-MRCP and respiratory-triggered MRCP in two patients. In patient 1, breath-held SPARSE-MRCP achieved better image quality than free-breathing respiratory-triggered MRCP, which showed significant motion blurring due to poor respiratory triggering. In patient 2, breath-held SPARSE-MRCP demonstrated image quality comparable to that of the respiratory-triggered MRCP.

Figure 8.

Comparison of maximum intensity projection (MIP) images between breath-held SPARSE-MRCP (MR Cholangiopancreatography) and respiratory-triggered MRCP in two patients. In patient 1, breath-held SPARSE-MRCP achieved better image quality (despite approximately 17-fold acceleration) than freebreathin respiratory-triggered MRCP, which showed significant residual motion blurring due to poor respiratory triggering. In patient 2, breath-held SPARSE-MRCP demonstrated image quality comparable to that of the respiratory-triggered MRCP. (Images were modified from the Figure 2 and Figure 4 in Chandarana H et al. Radiology. 2016 Aug;280(2):585–94 and were reproduced with permission from the authors and the journal.)

Free-Breathing Dynamic Contrast-Enhanced MRI

DCE-MRI is an integral part of routine abdominopelvic MRI examinations and is essential for identifying and characterizing lesions and tumors. Since tumor have a different contrast-enhancement pattern than normal tissues, images need to be acquired at multiple time following the injection of the contrast agent. Therefore, rapid imaging is necessary to capture the temporal changes after injection of the contrast agent. In current clinical exams, a separate 3D image set at each enhancement phase is obtained during one breath-hold, and the acquisitions are usually accelerated using commercially available parallel imaging approaches. DCE-MRI is an ideal candidate for compressed sensing because of extensive spatiotemporal correlations and smooth signal changes during contrast enhancement. Several sparse body imaging techniques have been developed and applied to speed up data acquisition in DCE-MRI. The acquisitions for these techniques usually use a golden-angle ordering scheme, so that k-space data can be acquired continuously without the need to predefine temporal frames or temporal resolution. Images at different contrast phases can then be retrospectively reconstructed to answer specific clinical questions.

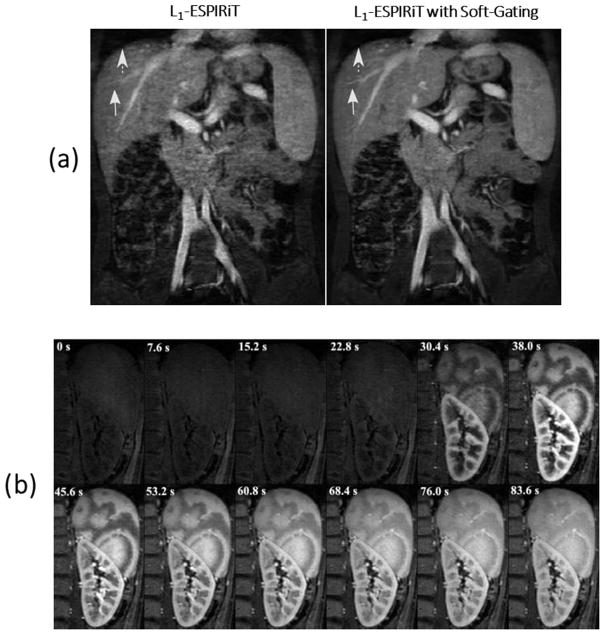
In the study of Zhang et al (61), a technique was developed for free-breathing contrast-enhanced pediatric MRI. The VDRad sampling pattern with butterfly navigator was used for continuous data acquisitions. Respiratory motion compensation was performed through soft-gating, and the L₁-ESPIRiT algorithm was used for image reconstruction with a locally low-rank sparsity constraint. Conventional respiratory triggered was chosen as a reference for comparison. Figure 9a shows L₁-ESPIRiT reconstruction with no motion weighting (left) and with soft respiratory gating (right). As indicated by the arrows, soft-gating improves the delineation of the liver edge and the hepatic vessels. Figure 9b shows zoomed and cropped image of the spleen and kidney at different contrast enhancement phases with a spatial resolution of 1.1x1.1 mm². The progressive enhancement from cortical to medullary region of the kidney, as well as the perfusion pattern of the spleen can be seen in the images.

Figure 9.

(a) L₁-ESPIRiT reconstruction with no motion weighting (left) and with soft respiratory gating (right). Soft-gating improves the delineation of the liver edge (dashed arrows) and the hepatic vessels (solid arrows). (b) Zoomed and cropped image of the spleen and kidney at different contrast enhancement phases with a spatial resolution of 1.1x1.1 mm2. The time of acquisition is shown on top of each contrast phase. Images show the progressive enhancement from cortical to medullary region of the kidney, as well as the perfusion pattern of the spleen. (Images were obtained from the Figure 2c and Figure 5a in Zhang T et al. J Magn Reson Imaging. 2015 Feb;41(2):460–73 and were reproduced with permission from the authors and the journal.)

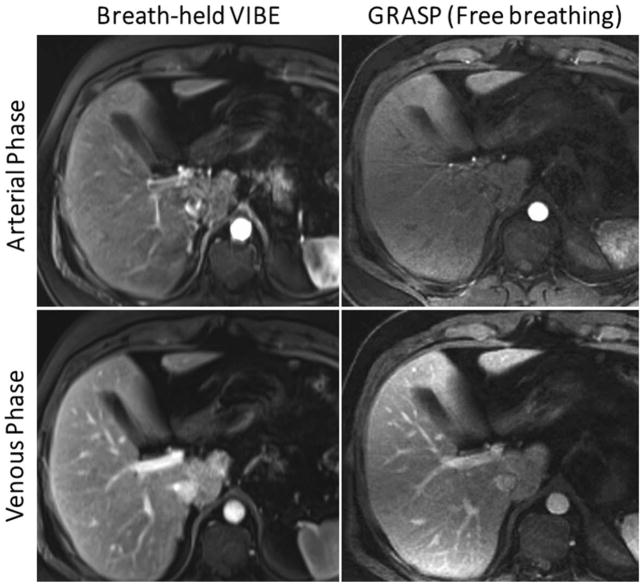
In the study of Chandarana et al (78), the GRASP technique was used for free-breathing DCE-MRI of the liver (33) and the results were compared to conventional breath-held VIBE (Volumetric Interpolated Breath-hold Examination) acquisitions. A temporal TV constraint was employed to minimize the first-order differences between consecutive temporal frames along the contrast-enhancement dimension. Due to low sensitivity to respiratory motion with radial sampling, good image quality could be achieved without need for additional motion compensation. Golden-angle stack-of-stars sampling, as implemented in GRASP, enabled continuous data acquisition and reconstruction with flexible temporal resolution for different clinical studies. As shown in Figure 10, GRASP achieves comparable image quality to breath-held scans in both arterial and venous phases.

Figure 10.

Comparison of conventional breath-hold VIBE (left) with free-breathing GRASP (right) in the arterial phase (top row) and the venous phase (bottom row). GRASP achieved image quality comparable to that of the breath-hold references in healthy volunteers who have excellent breath-holding capacity. (Images were obtained from the Figure 4 and Figure 5 in Chandarana H et al. Invest Radiol. 2013 Jan;48(1):10–6 and were reproduced with permission from the authors and the journal.)

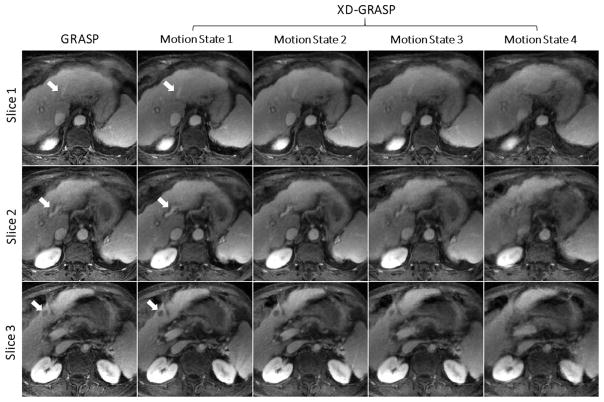
The same authors later extended the GRASP technique into XD-GRASP for improved reliability of free-breathing DCE-MRI of the abdomen (74,79). A TV constraint was enforced along both the contrast-enhancement dimension and the newly created respiratory-motion dimension. The XD-GRASP technique was compared to the original GRASP approach, showing improved image quality with higher image sharpness, better vessel-tissue contrast and greater delineation of a suspected lesion, as illustrated in Figure 11.

Figure 11.

Comparison of GRASP without motion compensation to XD-GRASP with reconstruction of an extra respiratory motion for three image slices. XD-GRASP achieved improved vessel-tissue contrast and vessel sharpness (white arrows in slice 1 and slice 2), and better delineation of hepatocellular carcinoma previously treated with chemoembolization (white arrow in slice 3).

Flow Imaging

Flow imaging is a promising technique for assessment of abdominal vessel hemodynamics, and it can be used for the diagnosis of liver pathologies such as cirrhosis (87). In MRI studies, phase-contrast (PC) imaging is usually applied to evaluate the blood flow. However, data acquisition for PC imaging is relatively time-consuming because one phase-reference image and up to three additional velocity-encoded images must be acquired to obtain the flow information. In PC imaging, the background signal is static and the temporal signal variation only occurs in blood vessel regions. As a consequence, the resulting images exhibit a high level of sparsity in an appropriate transform domain, enabling high acceleration factors using compressed sensing.

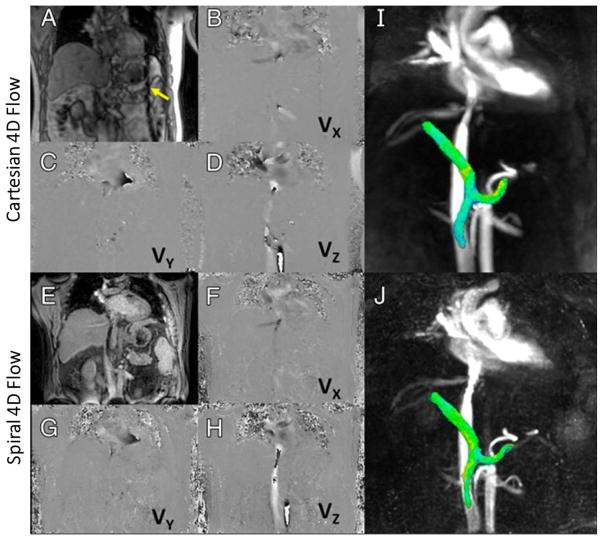
Dyvorne et al proposed an accelerated imaging technique for 4D flow imaging within a single breath hold (85). Golden-angle stack-of-spiral sampling was employed for data acquisition and images were reconstructed using the k-t SPARSE-SENSE framework. The results were compared to free-breathing Cartesian 4D flow imaging with respiratory navigator gating. Figure 12 shows images obtained with Cartesian (A–D, I) and spiral (E–H, J) 4D flow techniques. Magnitude images are shown in A and E and phase-difference images are shown in B–D and F–H. V_X, V_Y, and V_Z correspond to velocity measured with motion-encoding gradients in right-left, anterior-posterior, and foot-head directions, respectively. I and J are 3D angiograms showing segmented views of portal, splenic, and superior mesenteric veins with comparable quality and conspicuity.

Figure 12.

Representative results obtained with Cartesian (A–D, I) and spiral (E–H, J) 4D flow imaging techniques. Magnitude images are shown in A and E and phase-difference images are shown in B–D and F–H. VX, VY, and VZ correspond to velocity measured with motion-encoding gradients in right-left, anteriorposterior, and foot-head directions, respectively. I and J are 3D angiograms showing segmented view of portal, splenic, and superior mesenteric veins with comparable quality and conspicuity. Dark lines proximal to spleen on Cartesian series (yellow arrow) show cross-beam navigator used for respiratory gating in Cartesian acquisition. (Images were obtained from the Figure 2 in Dyvorne H et al. Radiology 2015 Apr;275(1):245–54 and were reproduced with permission from the authors and the journal.)

Sparse Body MRI: Challenges and Opportunities

Challenges and Potential Solutions

There are several challenges for the application of compressed sensing techniques in routine clinical practice. A major limitation is the relatively long computation time currently required for non-linear iterative reconstruction processes. Large data sizes, which occur, for example, in dynamic imaging, impose additional computational burdens and require adequate hardware support and dedicated software implementations. One potential solution to improve reconstruction speed is to implement the reconstruction algorithms on graphical processing units (GPUs), which can provide high performance for computation of highly-parallel transforms such as FFT, wavelets, and the gridding operation for non-Cartesian sampling. This has already been demonstrated for iterative reconstruction methods such as L₁-SPIRiT (88–90), where online reconstructions in clinically feasible runtimes can be achieved. Given the latest advances in GPU devices, GPU-based computations are expected to play an important role in the translation of compressed sensing methods into clinical routine. In addition to parallel implementation of algorithms, coil compression (76,91) and numerical optimization algorithms with faster convergence can also contribute to achieving shorter reconstruction time. Cloud-based computing offers additional possibilities, which has already been demonstrated for reconstruction and post-processing of cardiac exams (92). Despite all these hardware and software implementations, the calculation speed can still be insufficient for directly reconstructing images online at the scanner. To address this problem and to enable wider use of compressed sensing reconstructions in clinical routine, software tools have been developed to transfer data to dedicated workstations and send the reconstructed images back to PACS (picture archiving and communication systems). This allows reconstruction of images offline on external high-performance computing servers without interrupting clinical MR workflow. Existing software tools for this purpose include the Gadgetron framework (93) (https://github.com/gadgetron) and the Yarra framework (94) (https://yarra.rocks), which are available online for free download.

A second obstacle for clinical implementation is the requirement to select appropriate regularization parameters (e.g., λ in Equation 2), which control the balance between data consistency and promotion of sparsity in the cost function. An excessively high regularization parameter value can lead to excessive removal of low-value coefficients in the sparse domain, resulting in image blurring or loss of small image features. On the other hand, an excessively low regularization parameter value will lead to incomplete removal of incoherent artifacts, which in turn degrades image quality for clinical diagnosis. Although, in theory, parameter values can be selected based on the noise level of the samples, values are often chosen empirically by trained readers. Specifically, parameters can be determined by repeating the same reconstruction for one or multiple sample datasets with a range of different values. The value that achieves the highest image quality is then selected and applied to the reconstruction of other datasets for the same clinical application. However, although many studies have shown that such a selection scheme is adequate for qualitative assessment of reconstructed images, large-scale patient studies are necessary to fully evaluate clinical utility, reliability and reproducibility for quantitative evaluation in these cases. Alternatively, approaches such as the L-curve method (95) may be used to automate the selection of regularization parameters in an optimization problem

In addition to the high computational effort and the challenge of selecting proper regularization parameters, the lack of a suitable metric for image quality assessment constitutes another practical challenge for compressed sensing techniques. Conventional metrics, such as the signal-to-noise ratio (SNR), are not adequate due to the non-linear nature of compressed sensing reconstruction, and these metrics generally do not capture typical failure modes. For example, a “clean” image with very high SNR can be generated simply by increasing the regularization parameter to a large value, but the result would be unrealistic, as small details would be removed and image contrast perturbed. Currently, a common approach to assess image quality is qualitative evaluation of the reconstructed images by experienced radiologists who evaluate the diagnostic image quality in a blinded-reader fashion. However, further studies to evaluate specific artifact behavior in different clinical applications are needed, and an automated method to measure image quality and to characterize lesions, in particular, would be highly desirable.

Emerging Image Reconstruction Strategies

Many of the previously mentioned reconstruction techniques have been tested in clinical applications, and some are being translated into routine clinical body MR exams. Recently, a number of new sparse MRI methods have been presented. Although most of them have only been tested in research settings so far, they have great potential to change clinical body imaging in the future. One promising example is the incorporation of a specific signal model into the reconstruction problem, in which parameter maps can be estimated directly from the acquired k-space data. For example, separated water and fat maps can be directly estimated from the acquired k-space data in chemical shift imaging (96–99). Perfusion maps with parameters such as K_trans and V_e, can be estimated directly by including perfusion tracer-kinetic models into the reconstruction process (100). Moreover, motion models, either rigid or non-rigid, can also be integrated to guide the image reconstruction and to determine motion fields for certain applications (73). Other examples include T₁ and T₂ encoding (101), diffusion encoding (102), and flow encoding (103). These models are expected to improve the sparsity conditions and the performance of sparsity-enforcing reconstructions.

Although non-Cartesian sampling has shown benefits in several MRI applications, it also poses several challenges compared to Cartesian sampling, including sensitivity to off-resonances, gradient delays, and non-ideal gradient-amplifier responses. These system imperfections may result in image distortion or blurring if not corrected properly. However, they can be corrected with separate gradient calibration or trajectory measurements (104,105) Furthermore, correction of these errors can also be included directly into the reconstruction of non-Cartesian images, which makes separate calibration scans unnecessary (106). Such approach can theoretically also be combined with compressed sensing and/or parallel imaging, making it promising for future use.

Another direction is to combine motion-correction algorithms with the XD-GRASP framework. For example, Rank et al recently proposed a four-dimensional joint motion-compensated high dimensional total variation (4D joint MoCo-HDTV) algorithm (70), which alternates between motion-compensated image reconstruction and respiratory motion estimation at multiple spatial resolution levels. The reconstruction is performed progressively starting from a low spatial resolution series, based on the assumption that the low-resolution images with less undersampling artifacts enable better estimation of the motion. The algorithm has been tested for radial MR data of the upper abdomen with very high acceleration rates.

An Outlook for the Future

There has been a rapid growth of compressed sensing MRI techniques in the past decade. Although implementations are mainly limited to research applications, these early studies have demonstrated the feasibility of new applications with previously inaccessible imaging performance. The translation of these methods into routine clinical practice is expected and some subset of these methods will be available as commercial products from vendors.

Although many imaging techniques described in this paper have been implemented initially for T₁-weighted body imaging, typical clinical body MR protocols also include T₂-weighted and diffusion-weighted acquisitions, and research to incorporate these weightings is underway. Another promising research direction involves combination of MR fingerprinting (MRF) (107) concepts with some of the continuous imaging approaches outlined previously, to enable comprehensive model-based reconstructions for the quantitative characterization of the tissues and tumors.

Such considerations make it clear that the application of sparsity in MRI can go beyond pure acceleration of image acquisition. Rapid imaging can be combined with continuous data acquisition both to enhance information content and to simplify the imaging paradigm. The use of the golden-angle ordering scheme with sparse imaging techniques is one example that promises more than mere acceleration of existing imaging protocols. It could represent a shift of the day-today clinical workflow from conventional time-consuming and tailored acquisitions towards rapid and continuous volumetric acquisitions with flexible reconstruction that can be adapted retrospectively for diverse clinical or research needs (108).

Summary

Compressed sensing represents a major step forward in the development of rapid MRI techniques, with its capabilities being investigated in numerous applications. The methods and applications surveyed in this paper represent significant progress toward clinical implementations for body imaging. In the future, sparsity-based techniques have the potential to shift the body MR imaging exam from its current time-consuming and cumbersome form to a new paradigm of continuous and comprehensive data acquisition with flexible image reconstruction. This shift will transform the experience as well as the information content of everyday clinical imaging, for clinicians, radiographers, and patients alike.