Abstract
Adhesion of circulating tumor cells (CTCs) to the microvessel wall largely depends on the blood hydrodynamic conditions, one of which is the blood viscosity. Since blood is a non-Newtonian fluid, whose viscosity increases with hematocrit, in the microvessels at low shear rate. In this study, the effects of hematocrit, vessel size, flow rate and red blood cells (RBCs) aggregation on adhesion of a CTC in the microvessels were numerically investigated using dissipative particle dynamics. The membrane of cells was represented by a spring-based network connected by elastic springs to characterize its deformation. RBCs aggregation was modelled by a Morse potential function based on depletion-mediated assumption and the adhesion of the CTC to the vessel wall was achieved by the interactions between receptors and ligands at the CTC and those at the endothelial cells forming the vessel wall. The results demonstrated that in the microvessel of 15μm diameter, the CTC has an increasing probability of adhesion with the hematocrit due to a growing wall-directed force, resulting in a larger number of receptor-ligand bonds formed on the cell surface. However, with the increase in microvessel size, an enhanced lift force at higher hematocrit detaches the initial adherent CTC quickly. If the microvessel is comparable to the CTC in diameter, CTC adhesion is independent of Hct. In addition, the velocity of CTC is larger than the average blood flow velocity in smaller microvessels and the relative velocity of CTC decreases with the increase in microvessel size. An increased blood flow resistance in the presence of CTC was also found. Moreover, it was found that the large deformation induced by high flow rate and the presence of aggregation promote the adhesion of CTC.
Keywords: Adhesion, Aggregation, Circulating tumor cell, Dissipative particle dynamics, Red blood cell
1 Introduction
CTCs are caused by the tumor cell intravasation into the blood stream from the original tumor. Such CTCs are transported by the blood flow to the distant organs through the vasculature to form secondary tumors. During the blood circulation, the tumor cell must suffer the hydrodynamic shear stresses, and local forces due to neighboring cells. In order to step out of the flow, a very important step is the so called “adhesion cascade” (Guo et al. 2004; Haier and Nicolson 2001; Stroka and Konstantopoulos 2014; Wirtz et al. 2011). Most previous studies have experimentally (Cheung et al. 2011; Fu et al. 2015; Guo et al. 2014; Yan et al. 2012; Zhang et al. 2016) and numerically (Rejniak 2012; Yan et al. 2012; Yan et al. 2010) investigated the process of cell adhesion to the blood vessel. The numerical studies simply regarded the blood as a homogenous Newtonian fluid (Rejniak 2012; Yan et al. 2010). However, under shear flow, shear stresses acting on the CTCs largely depend on blood viscosity. As a matter of fact that the blood was tested in a viscometer and revealed to behave like a non-Newtonian fluid (Fung 1993) in small blood vessels at the relatively low shear rates, and its viscosity increases markedly with the increase of hematocrit. Furthermore, CTCs rolling along the vessel wall can greatly increase the vascular resistance and modify the blood flow and biophysical conditions to affect adhesive interactions. Although the interactions between the tumor cell and red blood cells in the blood stream remain partly unclear, some similarities with the interactions between white blood cells (WBCs) and RBCs may be found.
The moving RBCs were proved to promote WBC adhesion either by causing margination of leukocytes or by initiating adhesion and stabilizing attachment (Abbitt and Nash 2003; Munn et al. 1996). During microcirculation, the trend of RBCs flowing to the center of the vessels tends to push leukocytes toward the endothelium, leading to the process of margination. Previous studies have shown that leukocyte margination largely depends on the blood properties, including shear rate, hematocrit and RBC aggregation. Fedosov and Gompper (2014) numerically analyzed the mechanism of three-dimensional leukocyte margination toward the vessel wall and showed that WBC marginates to the wall at a region of intermediate hematocrits, Hct=0.2~0.4, under relatively low flow rates corresponding to the venular shear rate and RBCs aggregation is unnecessary for margination at high hematocrit values. Likewise, Takeishi et al. (2014) showed that leukocytes rarely approach the wall surface within microvilli length (less than 0.5μm) when numerically investigated margination of leukocytes at arteriole shear rate (670/s), but lower shear rate enables the leukocytes contact the wall. Similarly, shear flow induces the deformation of CTCs and the margination of CTCs towards the vessel wall is also expected primarily in the venular part of microcirculation, which would imply that the tissue invasion by tumor cells in blood largely occurs from venules (Firrell and Lipowsky 1989). In fact, CTCs prefer to adhere to the small venules with relatively low blood flow rates (Guo et al. 2014; Zhang et al. 2016). Moreover, the increase of WBC margination with reduction in shear rate (<50s−1) (Nash et al. 2008) is strongly dependent on the occurrence of RBC aggregation. Also increasing the extent of RBC aggregation increases the firm adhesion of WBCs to the endothelium because of an enhanced probability of contact between leukocytes and the vessel wall (Abbitt and Nash 2003; Munn and Dupin 2008; Pearson and Lipowsky 2000; Sun and Munn 2006). In addition to this, the leukocyte adhesion increases at the hematocrit ranging from 10% to 30% (Abbitt and Nash 2003). It has been found that the WBC rolling speed increases with RBC concentration because it is affected by the RBC-WBC collision frequency and blunting of the velocity profile (Sun and Munn 2005). Still, the rolling velocity of a WBC is strongly dependent on the local WBC concentration. The velocity fluctuation decreases as the WBC concentration increases. Equally, the rolling velocity and velocity fluctuation decreases with increasing cell deformability (Pappu et al. 2008). Recently, the forces exerted by the flowing blood on an adherent rigid WBC was estimated and it is found that RBCs not only enlarge the streamwise forces, impairing the WBC binding, but also cause an average wall-directed force, which is expected to enhance binding (Isfahani and Freund 2012).
Based on many similarities in the processes of margination and adhesion, models developed for leukocytes can be applied to CTCs. King et al. (2015) experimentally and numerically investigated the CTC dynamics in the microvasculature and the numerical findings demonstrated that single CTC with more rigid membrane marginates quicker than the softer one while the experimental results showed that the rolling velocity of cancer cells increases with the number of cells or aggregates. However, for the process of adhesion, softer cell flattening enables adherent cells to avoid high shear forces within the center of the parabolic curve of fluid flow. Takeishi et al. (2015) demonstrated that the cell margination depends on its relative size to the vessels. When the discrepancy in the radiuses between vessel and tumor cell exceeds the thickness of red blood cell, tumor cell tends to margination. In addition to tumor cell properties, the vessel geometry could contribute to tumor cell adhesion (Weiss 1992). In vivo experiments (Guo et al. 2014; Yan et al. 2012; Zhang et al. 2016) have demonstrated that tumor cells prefer to adhere to the curved vessels and at the bifurcations of microvasculature. Previous findings provide valuable premises for the tumor cell firm adhesion. As limited studies have been conducted on how the tumor cell switches from the initial attachment to firm adhesion in the presence of RBCs, we focus on the effects of flowing RBCs on the adhesion of a CTC to the vessel wall.
In this study, the blood is modeled by a suspension of RBCs. Dissipative particle dynamics method combined with a spring-based network cell model is employed to carry out 3D simulations of motion of a rolling tumor cell in microvessels constructed by the straight tubes. Cell-cell interaction is represented by a Morse-potential function based on a depletion model. Then the simulation results of motion of tumor cell in blood flow at different hematocrits in the tube ranging from 10 to 20μm are given. Next, the effects of hematocrit, vessel size, tumor cell deformability as well as RBC aggregation on the motion of the rolling CTC are investigated. Finally, summary and conclusions are presented.
2 Model and methods
The blood flow is modeled by using dissipative particle dynamics, which has been adopted in our previous study (Xiao et al. 2016). Details of DPD method have been introduced (Espanol 1995; Groot and Warren 1997; Hoogerbrugge and Koelman 1992). In brief, each DPD particle represents a soft lump of atoms and interacts with surrounding particles through three simple pairwise additive forces: conservative force, dissipative force and random force. Particle motion follows Newton’s law. In the following, the cell models employed in the simulations are specifically described.
2.1 Cell membrane model
In simulations, the cell membrane is discretized into a collection of particles connected by elastic springs. A spring-based network model endowed with in-plane and bending energy as well as constraint of surface area and volume has been introduced by Boey et al. (1998) to describe RBC initially. A systematic coarse-grained procedure was introduced by Pivkin and Karniadakis (2008) to reduce the number of degrees of freedom dramatically in the RBC model. This coarse-grained model was further improved by Fedosov et al. (2010), yielding accurate mechanical response. The total energy of the network is defined as
| (1) |
where ri represents the vertex coordinates and the in-plane elastic energy for WLC-POW model is given by
| (2) |
where xl = l/lmax ∈ (0,1) xl = l/lmax ∈ (0,1), lmax is the maximum spring extension, which is equal to 2.2 times equilibrium spring length for the WLC model, p is the persistence length, kB is Boltzmann constant and T is temperature of the system, which is equal to 310K. kp is a POW force coefficient and m is a specified exponent, here we set it to 2 (Fedosov et al. 2010).
The bending energy stored in the adjacent triangular elements is defined by
| (3) |
where kbend is a bending modulus; θαβ is the instantaneous angle formed between the outer normal vectors of two adjacent triangles α, β sharing the common edge; θ0 is the spontaneous angle.
The area and volume conservation constraints are
| (4) |
| (5) |
where , karea and kvolume are constraint constants for global area, local area, and volume; Atot and V are the instantaneous membrane area and the cell volume; and are their respective specified total area and volume values. A, A0 are the instantaneous and initial local area.
Nodal forces are derived from the total energy as follows:
| (6) |
The elasticity of the network is based on the linear analysis of a two-dimensional sheet of springs built with equilateral triangles (Dao et al. 2006). The linear shear modulus of the WLC-POW model is
| (7) |
The linear area compression modulus is defined as
| (8) |
The Young’s modulus Y for the two-dimensional sheet can be expressed through the shear and area-compression moduli as follows
| (9) |
And the Poisson’s ratio ν is given by
| (10) |
Based on the incompressibility assumption is set, so Y →4G and ν→1.
The relationship between bending modulus kbend and the macroscopic membrane bending rigidity kc is derived for the case of a spherical shell in the Helfrich bending energy, as follows:
| (11) |
2.2 RBC aggregation model
To analyze the RBC aggregation, the depletion model introduced by Liu et al. (2004) is employed. In this model a Morse potential function ψ(r) is used to model the interaction energy
| (12) |
where r is the distance between two plane elements of the opposing RBCs directly facing each other, r0 is the zero force length, De is the intercellular interaction strength, and β is the scaling factor controlling the interaction decay behavior. Therefore, the total interaction energy (Ye et al. 2014) of a triangulated cell is expressed by
| (13) |
where rjk is the local distance between the jth and kth triangles located in cells 1 and 2 respectively. Nt is the number of the triangle elements which are linked by particle i. nj and nk are the outward unit normal vectors to the those curved elements, Ij and Ik stand for the unit vectors parallel to the line joining the centers of two cells and directed toward each other, which are based on the DLVO (Derjaguin-Landau-Verwey-Overbeek) theory (Bhattacharjee et al. 1998) to describe the interaction energy between two curved surfaces. Aj is the area of jth triangle of cell 1. The interaction force acting on the membrane particle i in cell1 is given by:
| (14) |
It has been shown that the intercellular interaction force is simply illustrated as a weak attractive force at far distance, but a strong repulsive force at near distance. In the numerical model, in order to save the computational cost, a cut-off distance is defined as zero force separation threshold, set to be 1.5, beyond which the intercellular force is assumed to be zero.
2.3 CTC adhesion model
Adhesion of cells to the vessel wall is mediated by the interactions between receptors and ligands at the CTC and those at the endothelial cells forming the vessel wall. The adhesion model provides the rules of formation and dissociation of bonds between receptors and ligands. The probabilistic model developed by Hammer and Apte (1992) is commonly used in simulations and is known as adhesive dynamics. If the distance between a receptor and a free ligand is less than the reactive distance don, a new bond may form with the association rate kon. A free ligand refers to that it is not bound to any receptors. A preexisting bond is ruptured with off-rate koff or if its length exceeds the rupture distance doff. The rates kon and koff are computed as:
| (15) |
where and are the unstressed reaction rates at the distance between a receptor and a ligand with the equilibrium spring length . The effective on and off strengths σon and σoff define a decrease or an increase of the corresponding rates within the interaction lengths don and doff. A spring force acted on the receptors and ligands linked by an existing bond is calculated from the Hooke’s law
| (16) |
where ks is the spring constant. The binding force can be derived as . The probability of the formation of a new bond and that of the breakage of an existing bond are given by
| (17) |
where Δt is the time interval. At a given time instance, two random numbers ξ1 and ξ2 uniformly distributed on [0, 1] are generated. An existing bond is ruptured if ξ1 < Poff and left unchanged otherwise. A bond formation is allowed for each found receptor according to the relationship Pon > ξ2.
2.4 Model and physical units scaling
In order to keep the simulation system consistent with the real system, the physical properties should be mapped onto the dimensionless properties in the model. A scaling procedure has been presented by Fedosov et al. (2010), which relates the model’s non-dimensional units to physical units. The length scale is given by:
| (18) |
where the superscripts M and P denote “model” and “physical”. The energy scale is provided as follows
| (19) |
The force scale is defined by
| (20) |
The scaling between model and physical times is defined as follows
| (21) |
3 Results and discussion
3.1 Simulation setup and modeling parameters
The tumor cells arrest and adhesion experiment was performed, in which the individual trajectories of tumor cells in the blood flow can be measured by labeling them with the fluorescent dye. A certain portion of tumor cells were found to be arrested at the postcapillary venules, as shown in Fig. 1, where there is no size restriction and the flow rate is relatively low. Based on the experimental observation, the motion of a rolling tumor cell under blood flow with a low velocity in a microvessel with a diameter ranging from D = 10 ~ 20μm and a length of L = 45μm were simulated, as illustrated in Fig. 2.
Fig. 1.
CTC adhesion at a postcapillary venule. The adherent CTC is labeled with the fluorescent dye. The blood flow direction is indicated by a yellow arrow.
Fig. 2.
Schematic illustration of computational domain
The blood is modeled as a suspension of RBCs. Each RBC consists of 640 particles and is 7.82μm in diameter. It has a thickness at the thickest point of 2.5μm and a minimum thickness in the center of 1μm. A breast tumor cell is of spherical shape with a diameter of 9μm, constructed by 1170 particles. The nucleus of tumor cell is neglected for simplicity in this study. Both the RBCs and CTC are filled with a Newtonian fluid with a viscosity of μi = 6×10−3 Pa·s and they are based on the spring-based network model. To validate the CTC model, the shape of the CTC passing through a narrow slit obtained in our previous numerical findings (Xiao et al. 2016) is compared with that of the captured CTC in experimental results. Lv et al. (2013) analyzed the fluorescence result of the captured CTC in the microfluidic chip. Figure 3a shows that the cell of interest (the Hela CTC) is marked with red fluorescence, which has similar characteristics to the breast cancer cell. Figure 3b shows the result that is obtained using the Dissipative Particle Dynamics combined with the spring-based network model. Figure 3c compares the experimentally obtained shape of CTC indicated by the blue solid line with the numerically obtained shape labeled by the red dotted line. It can be seen that they are nearly in agreement with each other, showing that the spring-based network model can capture the deformation of CTC.
Fig. 3.
(a) Bright field and fluorescence and merged images in the microfluidic chip (Lv et al. 2013). Hela CTC is marked with red fluorescence. Scale bar is 10μm; (b) Shape of CTC obtained using numerical simulation (Xiao et al. 2016); (c) Comparison of captured CTC in the experiment conducted by Lv et al. (2013) (blue solid line) and numerical results using Dissipative Particle Dynamics (red dotted line)
The parameters of plasma, RBCs and CTC are listed in Table 1. The attachment of CTC to the vessel wall is achieved by the adhesive dynamics model. As the CTC is based on a coarse-grained cell model, the densities for the receptor and ligand are smaller. Nevertheless, an effective receptor-ligand bond in simulations may be equivalent to several physical bonds. When the RBC aggregation is taken into consideration, the intercellular interaction energy is characterized by the Morse potential function. Different types of DPD particles are employed to distinguish different components in the computational domain, enabling the fluid-structure interactions easier to deal with. For the suspending fluid and cytoplasm particles, only DPD forces are considered. For the RBC membrane particles, the deformation of the cell membrane and intercellular interaction forces are involved in addition to the DPD forces. While for the CTC membrane particles, the deformation of membrane, adhesion forces as well as DPD forces are included. No-slip boundary condition is imposed near the wall and a periodic boundary condition is applied along the flow direction. Bounce-back reflection is exerted on the surface of the cell membrane to ensure its impenetrability. To drive the flow, a uniform body force is applied to all particles in the flow direction, which is equivalent to the pressure gradient ΔP/L=ρf, where ΔP is the pressure drop over the tube length and ρ is the suspension’s mass density. As the tumor cell margination and adhesion is expected to occur at a lower flow rate, the shear rates are set to below 20s−1.
Table 1.
Simulation parameters for cell membrane and plasma
| Parameter | Simulation | Physical values |
|---|---|---|
| Blood plasma density (ρ) | 6 | 1.0 × 103 kg/m3 (Skalak and Jian 1987) |
| Blood plasma viscosity (μ) | 20.4 | 1.2 × 10−3 Pa·s (Skalak and Jian 1987) |
| Temperature (T) | 0.0828 | 310K |
| Membrane Young’s modulus for RBCs (YR) | 369 | 18.9μN/m (Suresh et al. 2005) |
| Membrane Young’s modulus for CTC (YT) | 80.5~8050 | 4.16 ~ 416μN/m |
| Membrane bending modulus for RBC ( ) | 5.364 | 2.8 × 10−19 J (Fedosov et al. 2010) |
| Membrane bending modulus for CTC ( ) | 69.28 | 3.6 × 10−18 J |
| Intercellular energy density (De) | 3.872 | 0.2μJ/m2 (Zhang et al. 2009) |
| Scaling factor (β) | 7.68 | 7.68μm−1 |
| Zero force distance (r0) | 0.3 | 0.3μm (Fedosov et al. 2011) |
| Time step (Δt) | 0.001 | 0.00114ms |
| Global area constraint constant ( ) | 5 × 104 | 2.58 × 10−3 N/m |
| Local area constraint constant (karea) | 100 | 5.2μN/m |
| Volume constraint constant (kvolume) | 5 × 104 | 3.35 × 10−3 N/m |
| Unstressed on rate ( ) | 11.3 | 104s−1(Schwarz and Alon 2004) |
| Unstressed off rate ( ) | 0.023 | 20s−1(Alon et al. 1997) |
| On strength (σon) | 9.68 | 0.5μN/m (Dembo et al. 1988) |
| Off strength (σoff) | 0.968 | 0.05μN/m (Dembo et al. 1988) |
| Association length (don) | 0.1 | 0.1μm |
| Disassociation length (doff) | 0.1 | 0.1μm (Marshall et al. 2006) |
| Spring constant (ks) | 1.55 × 105 | 8 × 10−3 N/m (Fritz et al. 1998) |
| Equilibrium spring length ( ) | 0.025 | 0.025μm (Dembo et al. 1988) |
| Receptor density (nr) | 4.6 | 4.6/μm2 |
| Ligand density (nl) | 4 | 4/μm2 |
Initially, CTC was released near the wall with a distance of 50nm to facilitate binding by the receptor-ligand formation. When the flow was turned on, the suspension began to flow and the adherent tumor cell rolled along the wall. Representative snapshots of the simulated CTC and RBCs motion within the microvessels with a diameter of 15μm were presented in Fig. 4. The RBCs are scattered in the flow at low flow rates, so the particulate nature of the blood is pronounced. The CTC was found to move faster than the RBCs by comparing the trajectories of CTC and the green RBC. When the RBCs were overtaken by the CTC, most RBCs approached the upper end of the CTC. The forces induced by the collision of these RBCs push the CTC toward the wall in further, as illustrated in Fig. 4d. As the adhesion of CTC in the blood flow is a complex process, which is greatly affected by the properties of the blood, the following sections will analyze the effect of hematocrit, CTC deformability, vessel size, flow rate as well as RBCs aggregation on the CTC adhesion in detail.
Fig. 4.
Representative images of the motion of a CTC (blue) and RBCs (red) in the microvessel with a diameter of 15μm at (a) t=0s; (b) t=0.25s; (c) t=0.5s; (d) t=0.75s. The green RBC represents a reference
3.2 Dependence on hematocrits and tumor cell deformability
The motion of a rolling CTC in the flow with hematocrits ranging from 0.1 to 0.3 in a microvessel of 15μm in diameter was simulated firstly. The results demonstrate that at a lower hematocrit (Hct = 0.1, 0.2), the rolling tumor cell might be pulled off the vessel by the intercellular interactions, as shown in Fig. 5a. However, at Hct = 0.3, the CTC maintains to roll along the wall (Fig. 5b), resulting in a larger number of receptor-ligand bonds formed on the cell surface compared with the cases of Hct =0.1 and Hct =0.2, as shown in Fig. 5c. The force on the CTC is defined by the cumulative force generated by the interactions with the RBC and plasma. The positive force implies a lift force pointing to the vessel center while the negative value refers to a wall-directed force. Due to the particulate nature of blood, the CTC has a lower collision frequency with RBCs and subjects to a weaker wall-directed force (Fig. 5d) at lower hematocrits. However, at Hct = 0.3, a stronger wall-directed force inhibits detachment of CTC from the vessel wall. The maximum pressure normal to the wall on the adhered leukocyte has been estimated as about 30Pa (Isfahani and Freund 2012). This pressure is equivalent to the maximal force divided by the CTC surface area, so the value of 118Pa was obtained, which is larger than that estimated value. That is because the CTC is larger and the hematocrit is higher compared to the simulations of Hct =0.25 conducted by Isfahani and Freund (2012).
Fig. 5.
Simulation snapshots of RBCs (red) and a CTC (blue) at Hct= 0.2 (a) and Hct =0.3(b); and the variations of number of receptor-ligand bonds formed on the surface of CTC (c) and of the force on the CTC (d) at different hematocrits in a microvessel of 15μm in diameter
Then, the effects of CTC deformability on its deformation and adhesion in a microvessel of 15μm diameter were investigated. Three values of elastic modulus Y = 416μN/m, 41.6μN/m and 4.16μN/m were employed to represent different deformabilities. For the adherent CTC, the shearing forces from the suspending fluid extend the CTC and the wall-directed forces from the RBCs compress the CTC. Since the CTC deforms with constant volume, its elongation in the flow direction may accompany a reduction in the height. To quantify the deformation of a rolling CTC, the deformation indexes HT/DT and LT/DT are used to characterize the deformation of CTC along the radial direction and flow direction respectively, where HT, LT and DT are defined as the height, length, and initial diameter of the deformed CTC, as shown in Fig. 6a and Fig. 6b. It can be found that there is a slighter fluctuation in the evolution of the deformation in the CTC with Y = 416μN/m . But when the Young’s modulus decreases by 10 times, the CTC deforms significantly within 8%. The shear deformation during rolling may be of importance in adhesion owing to their direct effect on contact area correlated with the number of receptor-ligand bonds. Figure 6c shows the time history of number of receptor-ligand bonds formed on the surface of the CTC with different deformabilities. It seems that the softer cell with Y = 41.6μN/m has the largest number of bonds compared to the other two cases especially after t=0.2s. This is because that the deformation of this soft cell along tube axis is larger than the stiff one (Y = 416μN/m). For the softest cell, the lift force increases the cell height, leading to the decline in the length and the number of bonds. Despite the discrepancies on the deformation for the CTC with different deformabilities have been observed, the deformation is so small by virtue of the low shear rate, compared to the deformation up to 40% at 800s−1 (Pearson and Lipowsky 2000). Consequently, the deformability has no significant effect on the CTC displacement along the flow direction, as shown in Fig. 6d. The CTC was found to move at a constant velocity.
Fig. 6.
Deformation of a rolling CTC (a) along the radial direction HT/DT and (b) along the flow direction LT/DT, and the receptor-ligand number of bonds formed on the cell surface (c) as well as cell position in the flow direction (d) at Hct = 0.3 in a microvessel of 15 μm as a function of CTC membrane deformability.
3.3 Dependence on the microvessel size
Since the vessel size has a great effect on the adhesion of CTC flowing in the blood flow (Takeishi et al. 2015; Wirtz et al. 2011), the flow of the CTC in different microvessels of various diameters ranging from 10 to 20μm were simulated. The blood flow parameters are summarized in Table 2. The mean flow velocity is vaverage = Q/A = ∫A v(r)dAc/Ac, where Q is volume flow rate and Ac is the area of cross section. The mean shear rate is defined as γ = vaverage/D, and pressure gradient is expressed by ΔP/L. As the CTC adhesion is expected at lower shear rates, the mean shear rates are less than 20s−1. The capillary number defined by Ca=μiγDR/2GR, is less than 0.075. Here, R represents the RBC, the diameter of RBC is DR=7.82μm, and the shear modulus for RBC is GR = 6.3μN/m.
Table 2.
Blood flow parameters for different hematocrit values and different tube diameters. D is the tube diameter, Hct is the tube hematocrit, γ is the mean shear rate, ΔP/L is the pressure gradient, vp is the average velocity for the blood flow without CTC
| D (μm) | Hct | vaverage (mm/s) | γ (1/s) | ΔP/L (Pa/m) | vp (mm/s) |
|---|---|---|---|---|---|
| 10 | 0.1 | 0.116 | 11.63 | 2.44E+05 | 0.140 |
| 10 | 0.2 | 0.074 | 7.43 | 2.44E+05 | 0.137 |
| 10 | 0.3 | 0.043 | 4.31 | 2.44E+05 | 0.121 |
| 15 | 0.1 | 0.131 | 8.74 | 1.08E+05 | 0.139 |
| 15 | 0.2 | 0.076 | 5.04 | 1.08E+05 | 0.099 |
| 15 | 0.3 | 0.040 | 2.66 | 1.08E+05 | 0.054 |
| 20 | 0.1 | 0.121 | 6.05 | 6.10E+04 | 0.084 |
| 20 | 0.2 | 0.070 | 3.51 | 6.10E+04 | 0.071 |
| 20 | 0.3 | 0.044 | 2.20 | 6.10E+04 | 0.051 |
For D = 20μm, the initial adherent CTC is more likely to detach from the vessel at higher hematocrit, which can be seen in Fig. 7a. Figure 7c shows the variation of number of bonds at different hematocrits for D = 20 μm. The initial adherent CTC can be found to be peeled off from the vessel for all cases during rolling along the wall. But at higher hematocrit, the CTC cannot arrive at the vessel again during this simulation time period. Under the low shear flow rate, the weak tendency of RBC flowing towards the center of microvessel inhibits the margination of CTC. Instead, the effect of particulate nature is so pronounced that RBCs in the blood flow are distributed separately and the number of RBCs near the wall is larger compared to the lower hematocrits, leading to an enhanced lift force (Fig. 7d). Therefore, the CTC nearly cannot reach the vessel wall at high hematocrit (Hct = 0.3), as shown in Fig. 5a. While at a low concentration of RBCs (Hct = 0.1), the detached CTC can easily reapproach the vessel wall (Fig. 7b) under the pushing force exerted by the RBCs.
Fig. 7.
Simulation snapshots of RBCs (red) and a CTC (blue) at Hct= 0.3 (a) and Hct =0.1(b); and variation of number of receptor-ligand bonds formed on the surface of CTC (c) and of the force on the CTC (d) at different hematocrits in a microvessel of 20μm in diameter
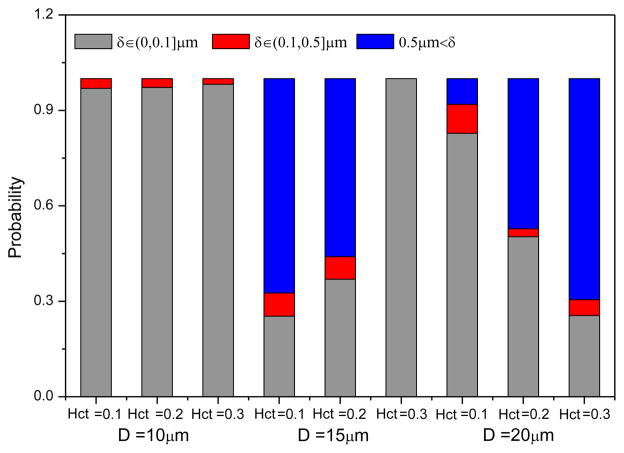
To trace the radial position of the CTC in the blood flow, a separation distance δ is introduced, which is defined by the closest distance between the CTC membrane and the vessel wall surface. Here, δ≤0.1μm indicates that the CTC attaches to the vessel wall as the association length is set to 0.1μm. Figure 8 illustrates the probability of separation distance computed over a time period of 0.9s for D =10, 15 and 20 μm at the hematocrits ranging from 0.1 to 0.3. From the bar chart, it can be seen that for D = 10μm, the initial adherent CTC nearly attaches to the vessel wall, which is independent on the hematocrit. This is due to the fact that the CTC has a stronger confinement DT/D = 0.9. That’s why the tumor cell extravasation is expected in the microvessels with a diameter less than the cell diameter. With the decrease in the hematocrit, the probability of CTC detachment from the vessel improves for D = 15μm. Interestingly, the relation between the probabilities of separation length and hematocrits for D =15μm is reverse to that for D = 20μm, which is consistent with the findings on the variation of formed bonds number.
Fig. 8.
Probability of the separation distance between the CTC membrane and the wall surface for different sized vessels at Hct =0.1, 0.2 and 0.3
3.4 CTC velocity and effect of CTC motion on the flow resistance
The velocity of CTC is an important indicator of CTC adhesion especially in larger microvessels. If the CTC maintain to attach the vessel, its velocity may be lower than the average blood velocity. Otherwise, according to the Fahraeus effect, an increased discharge hematocrit is expected when the cells leave the outlet due to its tendency of migrating toward the vessel center, the CTC flows faster than the blood stream. The translational velocity of CTC was examined by normalizing the CTC velocity VT to the average blood velocity vaverage. Figure 9 shows that the normalized CTC velocity for different values of Hct and diameter. It suggests that in smaller microvessels (D ≤ 15μm), the CTC flows faster than the average blood velocity, also can be observed in Fig. 4. This is consistent with the previous finding of VT/vaverage>1 when D/DT<2.0 (Takeishi et al. 2015). That is because that the CTC may be located nearer to the center of the vessel, even attached to the vessel. But when the vessel diameter increases further, the normalized CTC velocity decreases to around the unity at higher hematocrits. Particularly, the CTC moves slower than the blood stream at Hct =0.1 in microvessel of 20μm, which means that the CTC probably moves near the vessel wall. Moreover, the normalized CTC velocity increases with hematocrit, but this tendency becomes weak in larger microvessel. Owing to the fact that an increased cellular force with the growing number of RBCs leads to larger traction, which has been reported by Isfahani and Freund (2012), CTC adhesion may be inhibited. In fact, a larger CTC velocity than the average blood velocity is expected to prevent the firm adhesion in CTC metastasis.
Fig. 9.
Ratio of CTC velocity to the average blood velocity for different microvessels at various hematocrits
The effect of the CTC on the blood flow resistance was quantified by introducing the relative flow resistance, which is the ratio of the computed apparent viscosity for the blood flow with a CTC to that for the blood flow without a CTC (Fedosov and Gompper 2014). Here, the computed apparent viscosity is defined by ηapp = πΔPD4/128QL . Figure 10 presents the relative flow resistance for blood flow in microvessels with a CTC. Generally, the presence of CTC increases the flow resistance, resulted from the increasing volume fraction of cells. This effect is more pronounced in smaller microvessels because of the larger relative volume fraction of CTC compared to that in large microvessel. In smaller microvessels, the larger probability of CTC adhesion induced by the stronger CTC confinement at high hematocrit leads to a larger flow resistance. However, in microvessels of 20μm, the flow resistance is larger at Hct =0.1 due to CTC has a larger adhesion probability (Fig. 8), which is consistent with Fig. 7.
Fig.10.
Relative flow resistance for blood flow in different microvessels with a CTC at various hematocrits
3.5 Dependence on RBCs aggregation at different flow rates
It should be noted that the above findings are based on the condition of low flow rates and without considering the RBCs aggregation. Under such a low flow rate, the RBCs scatter in the flow without RBCs aggregation, which is not consistent with the real blood. In this section, the effects of flow rate combined with RBCs aggregation on the adhesion of the CTC in the microvessel (D = 20μm) were investigated.
Firstly, for the case without RBC aggregation, by comparing the variation of the number of receptor-ligand bonds over the time period of around 0.8s at different flow rates, Figure 11 shows that at high flow rate (γ=17.72s−1), the initial adherent CTC detaches from the wall quickly due to the increasing lift force. But after a short time, the RBCs flowing towards the vessel center expel the CTC from the RBC core and further initiate the adhesion of the CTC to the vessel wall, as shown in Fig. 12c. In addition, the number of formed bonds is more than that at the low flow rate due to the large deformation resulting from the large shear deformation, as plotted in Fig. 11b. The CTC retains its original spherical shape at the low flow rate as the value of LT/DT=1
Fig. 11.
Variation of number of receptor-ligand bonds (a) and the deformation of CTC along the flow direction (b) for the cases of RBC aggregation and non-aggregation at different flow rates
Fig. 12.
Snapshots of the flow of a CTC and RBCs for the cases of (a) γ=2.2s−1, without RBC aggregation, (b) γ=2.2s−1, with RBC aggregation, (c) γ=17.72s−1, without RBC aggregation, (d) γ=17.72s−1, with RBC aggregation
The main effect of RBCs aggregation is that the time of CTC contact to the vessel extends and the presence of RBCs aggregation provides an additional wall-directed force to compress the adherent CTC (Fig. 12b and Fig. 12d), leading to an increasing number of receptor-ligand bonds. At the low flow rate (γ=2.2s−1), the RBC aggregation enables the CTC to stably roll along the surface of the vessel wall with a certain number of bonds. Nevertheless, the weak deformation inhibits the formation of firmed adhesion. However, the large deformation induced by the high flow rate increases the CTC contact area, thus the number of bonds increases considerably, which can be seen at t = 0.4s for the case of RBC aggregation in Fig. 11. If the adhesive force is larger than the hydrodynamic force exerted on the CTC, firm adhesion may be formed.
4 Conclusions
The effects of flowing RBCs on the adhesion of CTC in microvessels were examined in terms of the hematocrit, vessel size, flow rate and RBC aggregation. At the low flow rates, increasing the hematocrit can detach the initial adherent CTC from the vessel wall due to the enhanced lift force in larger microvessels, while an inverse effect was found in smaller microvessels. This is because in a stronger confinement, a growing wall-directed force on the CTC is expected at higher hematocrit. Also, the velocity of CTC is larger than the average blood velocity in smaller microvessels but the ratio of CTC velocity to the mean blood velocity drops to around 1 in larger microvessel and even the CTC flows slower than the blood stream at Hct =0.1 as the CTC nearly moves near the vessel wall. In addition, the presence of CTC increases the blood resistance, which is more pronounced for the case of CTC adhesion. Lastly, the strong tendency of RBCs migrating towards the vessel in higher flow rate enables the detached CTC to contact with the vessel wall again. And the induced large deformation increases the number of receptor-ligand bonds for the adherent CTC. By adding the RBCs aggregation, an enhanced CTC adhesion can be found because it enables the CTC to stably roll along the vessel wall at the low flow rate. And an additional wall-directed force further compresses the CTC, leading to an increasing number of receptor-ligand bonds.
It should be noted that the data analyses are based on the entire time of computation. As the flow of RBCs suspension without CTC can reach the steady state at t=0.4s. The time period of all the simulation cases is about 0.9s, the blood flow experiences from developing to fully developed state. From the numerical simulation data, it can be seen that the conclusions for the developing stage is nearly the same as that for the stage of fully developed.
Acknowledgments
Supports given by HKRGC PolyU 5202/13E, PolyU G-YBG9, National Natural Science Foundation of China (Grant No. 51276130), and NIH SC1 CA153325-01 are gratefully acknowledged.
References
- Abbitt KB, Nash GB. Rheological properties of the blood influencing selectin-mediated adhesion of flowing leukocytes. Am J Physiol-Heart C. 2003;285:H229–H240. doi: 10.1152/ajpheart.00408.2002. [DOI] [PubMed] [Google Scholar]
- Alon R, Chen SQ, Puri KD, Finger EB, Springer TA. The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling. J Cell Biol. 1997;138:1169–1180. doi: 10.1083/jcb.138.5.1169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharjee S, Elimelech M, Borkovec M. DLVO interaction between colloidal particles: Beyond Derjaguin’s approximation. Croat Chem Acta. 1998;71:883–903. [Google Scholar]
- Boey SK, Boal DH, Discher DE. Simulations of the erythrocyte cytoskeleton at large deformation. I. Microscopic models. Biophys J. 1998;75:1573–1583. doi: 10.1016/S0006-3495(98)74075-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung LSL, et al. Adhesion dynamics of circulating tumor cells under shear flow in a bio-functionalized microchannel. J Micromech Microeng. 2011:21. [Google Scholar]
- Dao M, Li J, Suresh S. Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mat Sci Eng C-Bio S. 2006;26:1232–1244. [Google Scholar]
- Dembo M, Torney DC, Saxman K, Hammer D. The Reaction-Limited Kinetics of Membrane-to-Surface Adhesion and Detachment. Proc R Soc Ser B-Bio. 1988;234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- Espanol P. Hydrodynamics from Dissipative Particle Dynamics. Phys Rev E. 1995;52:1734–1742. doi: 10.1103/physreve.52.1734. [DOI] [PubMed] [Google Scholar]
- Fedosov DA, Caswell B, Karniadakis GE. Systematic coarse-graining of spectrin-level red blood cell models. Comput Method Appl M. 2010;199:1937–1948. doi: 10.1016/j.cma.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedosov DA, Gompper G. White blood cell margination in microcirculation. Soft Matter. 2014;10:2961–2970. doi: 10.1039/c3sm52860j. [DOI] [PubMed] [Google Scholar]
- Fedosov DA, Pan WX, Caswell B, Gompper G, Karniadakis GE. Predicting human blood viscosity in silico. P Natl Acad Sci USA. 2011;108:11772–11777. doi: 10.1073/pnas.1101210108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firrell JC, Lipowsky HH. Leukocyte Margination and Deformation in Mesenteric Venules of Rat. Am J Physiol. 1989;256:H1667–H1674. doi: 10.1152/ajpheart.1989.256.6.H1667. [DOI] [PubMed] [Google Scholar]
- Fritz J, Katopodis AG, Kolbinger F, Anselmetti D. Force-mediated kinetics of single P-selectin ligand complexes observed by atomic force microscopy. P Natl Acad Sci USA. 1998;95:12283–12288. doi: 10.1073/pnas.95.21.12283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu BM, Yang JL, Cai B, Fan J, Zhang L, Zeng M. Reinforcing endothelial junctions prevents microvessel permeability increase and tumor cell adhesion in microvessels in vivo. Sci Rep-Uk. 2015;5 doi: 10.1038/Srep15697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung YC. Biomechanics : mechanical properties of living tissues. 2. Springer-Verlag; New York: 1993. [Google Scholar]
- Groot RD, Warren PB. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J Chem Phys. 1997;107:4423–4435. [Google Scholar]
- Guo HL, et al. Mechanical properties of breast cancer cell membrane studied with optical tweezers. Chinese Phys Lett. 2004;21:2543–2546. [Google Scholar]
- Guo P, Cai B, Lei M, Liu Y, Fu BMM. Differential arrest and adhesion of tumor cells and microbeads in the microvasculature. Biomech Model Mechan. 2014;13:537–550. doi: 10.1007/s10237-013-0515-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haier J, Nicolson GL. Tumor cell adhesion under hydrodynamic conditions of fluid flow. Apmis. 2001;109:241–262. doi: 10.1034/j.1600-0463.2001.d01-118.x. [DOI] [PubMed] [Google Scholar]
- Hammer DA, Apte SM. Simulation of Cell Rolling and Adhesion on Surfaces in Shear-Flow - General Results and Analysis of Selectin-Mediated Neutrophil Adhesion. Biophys J. 1992;63:35–57. doi: 10.1016/S0006-3495(92)81577-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoogerbrugge PJ, Koelman JMVA. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys Lett. 1992;19:155–160. [Google Scholar]
- Isfahani AHG, Freund JB. Forces on a Wall-Bound Leukocyte in a Small Vessel Due to Red Cells in the Blood Stream. Biophys J. 2012;103:1604–1615. doi: 10.1016/j.bpj.2012.08.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King MR, et al. A physical sciences network characterization of circulating tumor cell aggregate transport. American journal of physiology Cell physiology. 2015;308:C792–802. doi: 10.1152/ajpcell.00346.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu YL, Zhang L, Wang XD, Liu WK. Coupling of Navier-Stokes equations with protein molecular dynamics and its application to hemodynamics. Int J Numer Meth Fl. 2004;46:1237–1252. [Google Scholar]
- Lv P, Tang Z, Liang X, Guo M, Han RP. Spatially gradated segregation and recovery of circulating tumor cells from peripheral blood of cancer patients. Biomicrofluidics. 2013;7:34109. doi: 10.1063/1.4808456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall BT, Sarangapani KK, Wu JH, Lawrence MB, McEver RP, Zhu C. Measuring molecular elasticity by atomic force microscope cantilever fluctuations. Biophys J. 2006;90:681–692. doi: 10.1529/biophysj.105.061010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munn LL, Dupin MM. Blood cell interactions and segregation in flow. Ann Biomed Eng. 2008;36:534–544. doi: 10.1007/s10439-007-9429-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munn LL, Melder RJ, Jain RK. Role of erythrocytes in leukocyte-endothelial interactions: Mathematical model and experimental validation. Biophys J. 1996;71:466–478. doi: 10.1016/S0006-3495(96)79248-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nash GB, Watts T, Thornton C, Barigou M. Red cell aggregation as a factor influencing margination and adhesion of leukocytes and platelets. Clin Hemorheol Micro. 2008;39:303–310. [PubMed] [Google Scholar]
- Pappu V, Doddi SK, Bagchi P. A computational study of leukocyte adhesion and its effect on flow pattern in microvessels. J Theor Biol. 2008;254:483–498. doi: 10.1016/j.jtbi.2008.05.020. [DOI] [PubMed] [Google Scholar]
- Pearson MJ, Lipowsky HH. Influence of erythrocyte aggregation on leukocyte margination in postcapillary venules of rat mesentery. Am J Physiol-Heart C. 2000;279:H1460–H1471. doi: 10.1152/ajpheart.2000.279.4.H1460. [DOI] [PubMed] [Google Scholar]
- Pivkin IV, Karniadakis GE. Accurate coarse-grained modeling of red blood cells. Phys Rev Lett. 2008:101. doi: 10.1103/PhysRevLett.101.118105. [DOI] [PubMed] [Google Scholar]
- Rejniak KA. Investigating dynamical deformations of tumor cells in circulation: predictions from a theoretical model. Frontiers in oncology. 2012;2:111. doi: 10.3389/fonc.2012.00111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz US, Alon R. L-selectin-mediated leukocyte tethering in shear flow is controlled by multiple contacts and cytoskeletal anchorage facilitating fast rebinding events. P Natl Acad Sci USA. 2004;101:6940–6945. doi: 10.1073/pnas.0305822101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skalak R, Jian S. Handbook of bioengineering. McGraw-Hill; New York: 1987. [Google Scholar]
- Stroka KM, Konstantopoulos K. Physical Biology in Cancer. 4. Physical cues guide tumor cell adhesion and migration. Am J Physiol-Cell Ph. 2014;306:C98–C109. doi: 10.1152/ajpcell.00289.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun C, Munn LL. Influence of erythrocyte aggregation on leukocyte margination in postcapillary expansions: A lattice Boltzmann analysis. Physica A: Statistical Mechanics and its Applications. 2006;362:191–196. doi: 10.1016/j.physa.2005.09.027. [DOI] [Google Scholar]
- Sun CH, Munn LL. Particulate nature of blood determines macroscopic rheology: A 2-D lattice Boltzmann analysis. Biophys J. 2005;88:1635–1645. doi: 10.1529/biophysj.104.051151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suresh S, et al. Connections between single-cell biomechanics and human disease states: gastrointestinal cancer and malaria. Acta Biomater. 2005;1:15–30. doi: 10.1016/j.actbio.2004.09.001. [DOI] [PubMed] [Google Scholar]
- Takeishi N, Imai Y, Nakaaki K, Yamaguchi T, Ishikawa T. Leukocyte margination at arteriole shear rate. Physiological reports. 2014:2. doi: 10.14814/phy2.12037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeishi N, Imai Y, Yamaguchi T, Ishikawa T. Flow of a circulating tumor cell and red blood cells in microvessels. Phys Rev E. 2015:92. doi: 10.1103/PhysRevE.92.063011. [DOI] [PubMed] [Google Scholar]
- Weiss L. Biomechanical Interactions of Cancer-Cells with the Microvasculature during Hematogenous Metastasis. Cancer Metast Rev. 1992;11:227–235. doi: 10.1007/BF01307179. [DOI] [PubMed] [Google Scholar]
- Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nature reviews Cancer. 2011;11:512–522. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao LL, Liu Y, Chen S, Fu BM. Numerical simulation of a single cell passing through a narrow slit. Biomech Model Mechanobiol. 2016 doi: 10.1007/s10237-016-0789-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan WW, Cai B, Liu Y, Fu BM. Effects of wall shear stress and its gradient on tumor cell adhesion in curved microvessels. Biomech Model Mechan. 2012;11:641–653. doi: 10.1007/s10237-011-0339-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan WW, Liu Y, Fu BM. Effects of curvature and cell-cell interaction on cell adhesion in microvessels. Biomech Model Mechan. 2010;9:629–640. doi: 10.1007/s10237-010-0202-1. [DOI] [PubMed] [Google Scholar]
- Ye T, Phan-Thien N, Khoo BC, Lim CT. Dissipative particle dynamics simulations of deformation and aggregation of healthy and diseased red blood cells in a tube flow. Phys Fluids. 2014:26. [Google Scholar]
- Zhang JF, Johnson PC, Popel AS. Effects of erythrocyte deformability and aggregation on the cell free layer and apparent viscosity of microscopic blood flows. Microvasc Res. 2009;77:265–272. doi: 10.1016/j.mvr.2009.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Zeng M, Fu BM. Inhibition of endothelial nitric oxide synthase decreases breast cancer cell MDA-MB-231 adhesion to intact microvessels under physiological flows. American journal of physiology Heart and circulatory physiology:ajpheart. 2016:00109–02016. doi: 10.1152/ajpheart.00109.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]