Abstract
Measuring gender inequality and women’s empowerment is essential to understand the determinants of gender gaps, evaluate policies and monitor countries’ progress. With this aim, over the past two decades, research has mainly been directed towards the development of composite indices. The purpose of this paper is to introduce a new and interdisciplinary perspective to the current debate on measuring gender inequality in human development. As a starting point, we develop a simple macroeconomic model of the interdependence between human development and gender inequality. We then introduce a biometric indicator, based on the ratio of female to male body mass index, to measure women’s empowerment at the country level. Finally, by using the latest available data, we examine the ability of this biometric indicator to capture countries’ performance in achieving gender equality. We obtain five main results: 1) we provide a theoretical framework to explain the joint determination of human development and gender inequality; 2) we show how to use this framework to simulate the impact of exogenous shocks or policy changes; 3) we demonstrate that exogenous changes have a direct and a multiplier effect on human development and gender inequality; 4) we find that the distribution of obesity between the female and male populations represents a useful proxy variable for measuring gender equality at the country level; 5) finally, we use these results to integrate and develop existing knowledge on the ‘ecological’ approach to the overweight and obesity pandemic.
Keywords: Social sciences, Economics, Health sciences, Public health
1. Introduction
Equality between men and women, in terms of both opportunities and outcomes, is a fundamental dimension of human development (UNDP, 1995). Since the Beijing Declaration in 1995 (United Nations, 1996), significant progress has been made worldwide towards more gender-equal societies (World Bank, 2011). However, forms of gender discrimination still remain unquestionable realities in most parts of the world, particularly in developing countries (United Nations, 2014). The development of ‘gender-equity-sensitive’ indicators, albeit difficult, is an essential task to gain a better understanding of the determinants of gender gaps, evaluate policies and monitor countries’ progress (Beneria and Permanyer, 2010). With this aim and to capture a complex multi-dimensional phenomenon, research has mainly focused on the use of composite indices (Anand and Sen, 1995). As a result of broad collective efforts, several composite measures of gender disparities are now available to researchers and policymakers (van Staveren, 2013).
The purpose of this paper is to introduce a new perspective to the current debate on the measurement of gender inequality in human development (Human Development Report Office, 2015). So far, there has been little discussion of the possible use of biometric indicators to measure gender disparities at the country level. However, research has shown that the patterning of obesity prevalence across countries is gendered (Kanter and Caballero, 2012) and also that international differences in obesity prevalence between men and women are significantly associated with several countries’ measures of gender inequality (Garawi et al., 2014).
This study takes an interdisciplinary approach to explore the relationship between gender inequality and gender disparities in overweight and obesity. As a starting point, we sketch a simple macroeconomic model to analyse the two-way interplay between human development and gender inequality. We then introduce a basic indicator − based on the ratio of female to male body mass index − to measure gender inequality at the country level. Finally, by using the latest available data, we examine the ability of this biometric indicator to predict countries’ performance in achieving gender equality, as compared to the six most common indices of gender discrimination currently available to the international research community.
We obtain five main results. First, we provide an economic framework to explain the joint determination of human development and gender inequality. Second, we show how this framework can be used to simulate the impact of exogenous shocks (due, for instance, to policy changes). Third, we demonstrate that exogenous shocks (such as an action to promote women’s empowerment) have both a direct as well as an indirect (i.e. ‘multiplier’) effect on human development and gender inequality. Fourth, we find that the distribution of obesity between the female and male populations represents a useful proxy variable for measuring gender equality at the country level. Fifth, and finally, we use these results to develop existing knowledge on the ‘ecological’ approach to the current overweight and obesity pandemic (Egger and Swinburn, 1997).
2. Theory
2.1. Multiplier effects in the interplay between human development and gender inequality
A useful way of addressing the relationship between gender discrimination and human development is to look at gender equality both as an input and as an outcome of society’s reproduction process (Weil, 2005). From this viewpoint, eliminating barriers that limit women’s capabilities, opportunities and empowerment has been shown to generate a positive feedback loop between women’s conditions, economic growth and human development (Cuberes and Teignier, 2013; Kabeer and Natali, 2013). Specifically, promoting gender equality tends to improve women’s health and education. These improvements in women’s stock of human capital positively affect the political and economic empowerment of the female population (Galor and Weil, 1996; Lagerlöf, 2003). As a result, countries are able to make more efficient use of their human resources. Finally, a full and better use of human resources fosters economic growth (Esteve-Volart, 2004; Hsieh et al., 2013); in turn, the growth process may support a virtuous circle in which increasing income per capita stimulates further progress in human development and gender equality (Becker, 1991; Doepke and Tertilt, 2009; Greenwood et al., 2005).
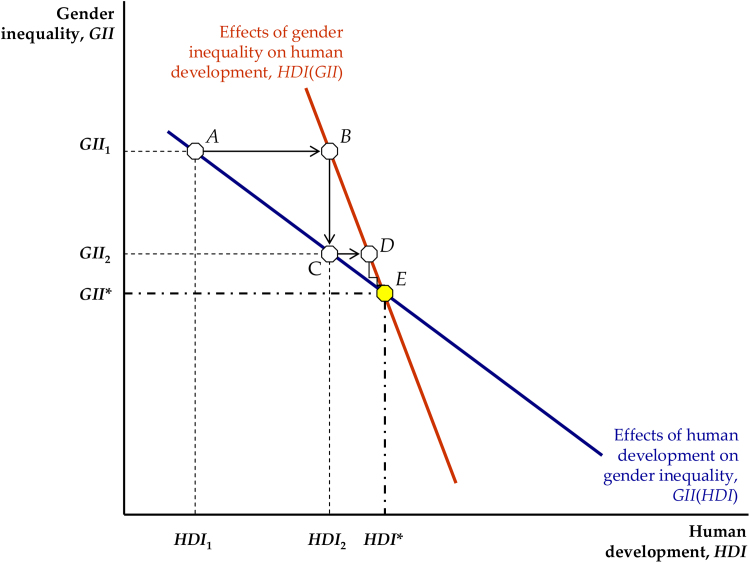
Fig. 1 illustrates a simplified macroeconomic model of human development and gender inequality as being determined simultaneously. The horizontal axis indicates the level of human development and the vertical axis indicates the level of gender inequality. Specifically, we measure human development and gender inequality using the UNDP’s Human Development Index (HDI) and Gender Inequality Index (GII), respectively (UNDP, 2014). To simplify, let us consider linear relationships. On the one hand (i.e. from the gender inequality perspective), the effect of higher human development in improving gender equality is represented by the function GII(HDI), depicted in blue. This function is downward sloping, showing that improvements in a population’s health, education and economic conditions (i.e. a rightward movement along the x-axis) normally translate, at least partially, into lower discrimination against women. On the other hand (i.e. from the human development perspective), the effect of better gender equality in promoting human development is represented by the function HDI(GII), depicted in red. This function − plotted in the space (HDI, GII) for ease of exposition − is also downward sloping because greater gender discrimination (i.e. an upward movement on the y-axis) means an increasingly inefficient use of human resources that hinders economic growth and negatively affects the level of human development. Finally, the different slope of the two functions reflects the fact that − all other things being equal − a one-unit increase in human development has an effect on gender inequality which is not generally of the same magnitude as the effect on human development of a one-unit increase in gender inequality (Kabeer and Natali, 2013).
Fig. 1.
The interaction between human development and gender inequality.
In this model, human development and gender discrimination are both endogenous variables and their equilibrium levels (HDI* and GII*) are determined by the intersection of the two curves (point E in Fig. 1) as a result of the interplay between the GII(HDI) and HDI(GII) functions. This process can be described as follows. Given the impact of human development on gender inequality − i.e. given the blue GII(HDI) curve − a level of human development below the equilibrium (for instance HDI1 < HDI*) determines a level of gender inequality above the equilibrium value (here equal to GII1, point A). However, given the impact of gender inequality on human development − i.e. given the red HDI(GII) curve − GII1 implies a level of human development equal to HDI2 (point B) that is greater than HDI1, but still less than HDI*. In turn, HDI2 allows society to reduce gender inequality until GII2 (point C) by moving downward along the blue GII(HDI) curve. Again, this leads to a further increase in human development (point D on the HDI(GII) red curve) and so forth. This process continues, reducing gender inequality and increasing human development, until both variables converge to their long-run equilibrium values (precisely HDI* and GII*) and vice-versa for any level of human development above HDI*.
Movements along given functions, as shown in Fig. 1, illustrate the recursive nature of the relationship between human development and gender inequality. Conversely, exogenous changes in the level of human development, or in that of gender inequality, result in a shift in either or both functions (i.e. these are shocks that shift the entire function). In order to analyse the impact of an exogenous shock, we may rewrite our two basic functions as GII(HDI, α) and HDI(GII, β), in which α and β are catchall variables that act as ‘shifters’ of the respective curves. More specifically, α stands for all factors, other than human development, that may affect gender inequality (such as policy or cultural changes), whereas β stands for all factors, other than gender inequality, that may affect human development (such as economic or institutional changes).
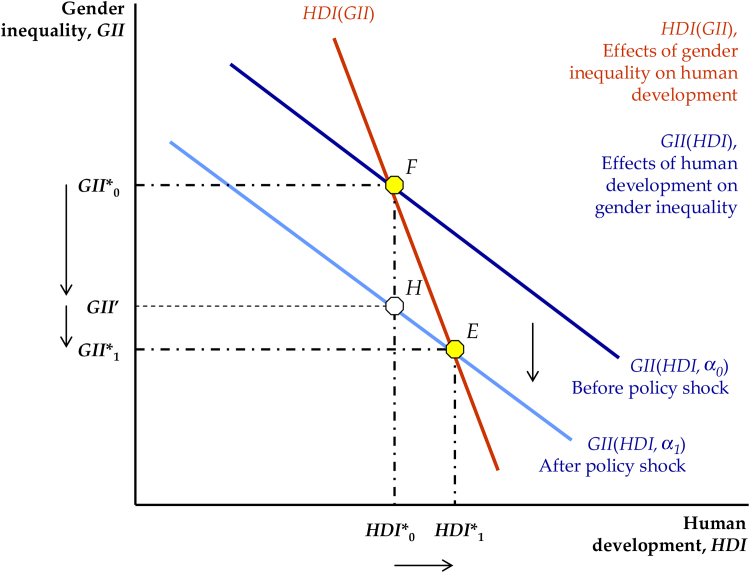
Let us consider, for example, a country where a new and progressive government puts through a women-friendly reform programme that eliminates legal barriers to women’s inclusion. An exogenous improvement in gender equality, as shown in Fig. 2, shifts downward − from the original dark blue GII(HDI, α0) curve to the new light blue curve GII(HDI, α1) − the relationship that shows the effect of human development on gender inequality. In other words, after the policy shock, there is less gender discrimination for any given level of human development. If there were no effects of women’s conditions on human development, the decrease in gender inequality would simply match the direct effect of the reform programme on GII (this is shown as the movement from point F to point H and thus from GII*0 to GII’ in Fig. 2). However, the model also shows a ‘multiplier effect’. The decrease in discrimination against women − via the human capital channel − promotes economic growth and human development. These improved general economic and social conditions feed back to generate an indirect additional decrease in gender discrimination (this is shown as the movement from H to E, i.e. from GII’ to GII*1). As a result, the long-run equilibrium level of gender inequality and human development ends up in E (HDI*1, GII*1).
Fig. 2.
The effects of an exogenous change in gender inequality.
We can similarly use our model to figure out the effects of a negative exogenous shock on gender inequality − i.e. a shock that shifts the GII(HDI, α) function upward − due, for example, to the rise of a radical interpretation of religious doctrines (as suggested by the recent experience of several North African and Middle East countries, resulting from the failure of the so-called ‘Arab Springs’), or even to a government's severe cuts in social programmes against gender discrimination as a response to tightening public budget constraints (as in the case of some southern European countries in the aftermath of the ‘Great Recession’ of 2008–09). These negative shocks increase gender inequality for any given level of human development and give rise to a negative feedback loop: i.e. greater inequality undermines human development, providing the conditions for even greater gender inequality, and so on.
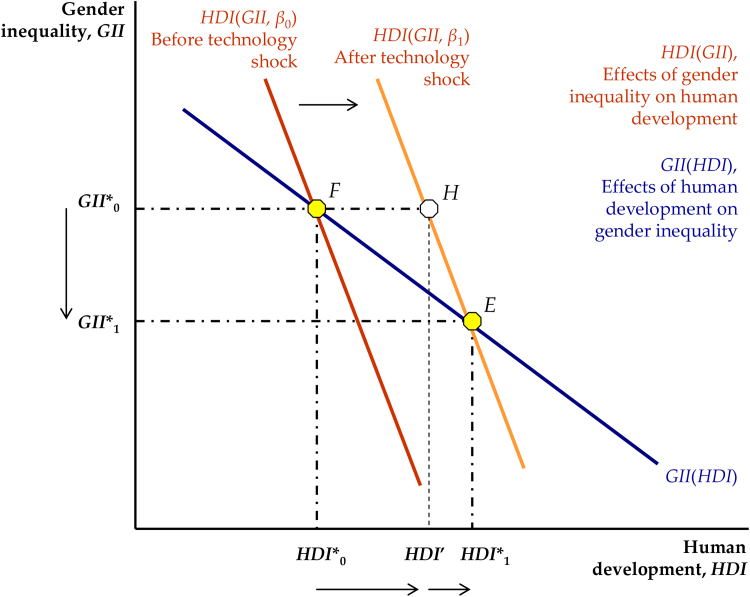
This model is also able to explain the direct and indirect effects on gender inequality of an exogenous change in human development due, for instance, to a change in the economic environment (such as the development of new technologies that allow labour, and other factors of production, to be used more effectively boosting economic growth). In this case, as shown in Fig. 3, the HDI(GII, β) curve shifts rightward, indicating a higher level of human development for any given value of gender inequality. This kind of shock generates positive feedback effects that move the long-run equilibrium levels of gender inequality and human development from the initial point F to the final point E, as the sum of a direct effect (from F to H) and an indirect (i.e. a multiplier) effect (from H to E). It is worth noting that in both cases (Figs. 2 and 3), when one of the two functions shifts, the magnitudes of the resulting equilibrium HDI and GII change depending on two factors, namely the size of the shift and the steepness of the function that does not change. Specifically, the former determines the size of the direct effect, whereas the latter determines the size of the multiplier effect.
Fig. 3.
The effects of an exogenous change in human development.
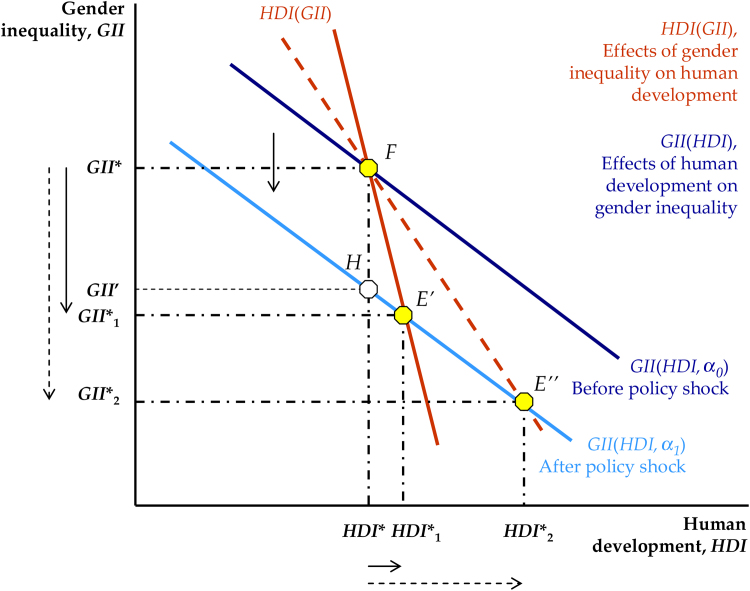
To provide a better understanding of the difference between these two (direct and indirect) effects, let us consider again the impact of a programme to reduce gender disparity. Fig. 4 reproduces the comparative statics analysis from Fig. 2. Now the government may introduce a ‘minor’ reform (e.g. in December 2003 Norway passed a law that requires large companies to have at least 40% of company board members to be women (Smith, 2014)), or a major reform (e.g. in December 2015 women in Saudi Arabia took part in the country's elections, as both voters and candidates for the first time ever (BBC, 2015)). In both cases, on the one hand, the extent of the reform determines the size of the downward shift of the GII(HDI, α) curve and on the other hand, for any given shift of the GII(HDI, α) curve − for instance from GII(HDI, α0) to GII(HDI, α1) − the slope of the HDI(GII, β) curve determines whether the policy change leads to a relatively small or large multiplier effect. Specifically, if the HDI(GII, β) function that shows the impact of gender inequality on human development is relatively flat (such as the dashed red curve in Fig. 4), the equilibrium changes from initial point F to final point E”, and the positive multiplier effect of the reform on both gender inequality and human development will be relatively large (from GII’ to GII*2 and from HDI* to HDI*2, respectively). Conversely, if the HDI(GII, β) function is relatively steep (such in the case of the solid red curve), the same reform will exert a small effect on the final HDI and GII equilibrium values and, under this conditions, society moves from initial point F to the final point E’.
Fig. 4.
The reactivity of human development to gender inequality.
The slope of the HDI(GII, β) curve measures the reactivity of human development to changes in gender inequality. This reactivity is affected by many interrelated cultural, economic and social factors. Therefore, the impact of a given policy in reducing gender discrimination and improving human development (for instance, the introduction of gender quotas on boards of directors) may vary significantly depending on the country’s specific characteristics (such as the existence of family-friendly employment regulations, a well-functioning labour market, a meritocratic recruitment system and so forth). Finally, the same analysis holds for a rightward shift in the HDI(GII, β) function, where a flatter (steeper) GII(HDI, α) curve results in smaller (larger) changes in the final equilibrium level of gender inequality and human development.
3. Calculation
3.1. Human development and gender disparities in obesity
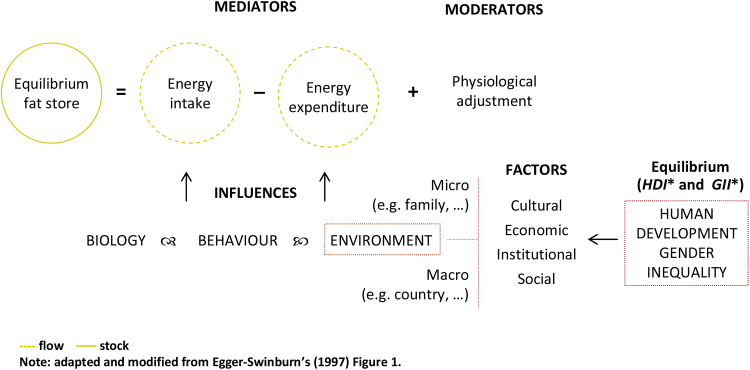
Unequal health outcomes between men and women reflect the interplay between biological sex and societal gender differences (Annandale and Hunt, 2000). Overweight and obesity are typical, complex, multifactorial diseases in which the inborn genetic characteristics of individuals interact with a wide range of cultural, social and economic variables (Akabas et al., 2011; Hu, 2008). In particular, the abnormal or excessive fat accumulation, as shown in Fig. 5, results from a positive energy imbalance between calorie intake and calorie expenditure. Both mediators of this stock-flow relationship are moderated by physiological adjustments. According to the ‘ecological’ approach to the problems of overweight and obesity (Kickbusch, 1989), however, calorie intake and expenditure are also subject to biological, behavioural and environmental influences (Egger and Swinburn, 1997), (Fig. 5 is adapted and modified from Egger & Swinburn’s Fig. 1.). These environmental influences, in turn, are the result of the interference of a wide range of economic, institutional and socio-cultural factors that operate at both the micro- and the macroeconomic levels (e.g. at individual, family and local community level, and at population or country level).
Fig. 5.
An improved ecological approach to the overweight and obesity pandemic.
The ecological paradigm takes the macroeconomic environment as given. One of the main purposes of this study is to integrate this approach by explicitly introducing the determination of human development and gender inequality, and their impact on the diffusion of overweight and obesity between the male and female populations. To this aim, we define and compute the ‘gender overweight and obesity ratio’ (GOOR) as the ratio between the prevalence of overweight and obesity in female (OOF) and male (OOM) populations (i.e. GOOR = OOF/OOM). The essential Food and Nutrition in Numbers 2014, recently published by the Food and Agriculture Organization of the United Nations (FAO, 2014) provides comprehensive country profile indicators, including World Health Organization (WHO, 2014) estimates of overweight and obesity prevalence − measured by the % of adults (ages 20+) who have a BMI (Body Mass Index, kg/m2) greater than 25 (overweight) or greater than 30 (obese) − for 158 countries worldwide in 2014.
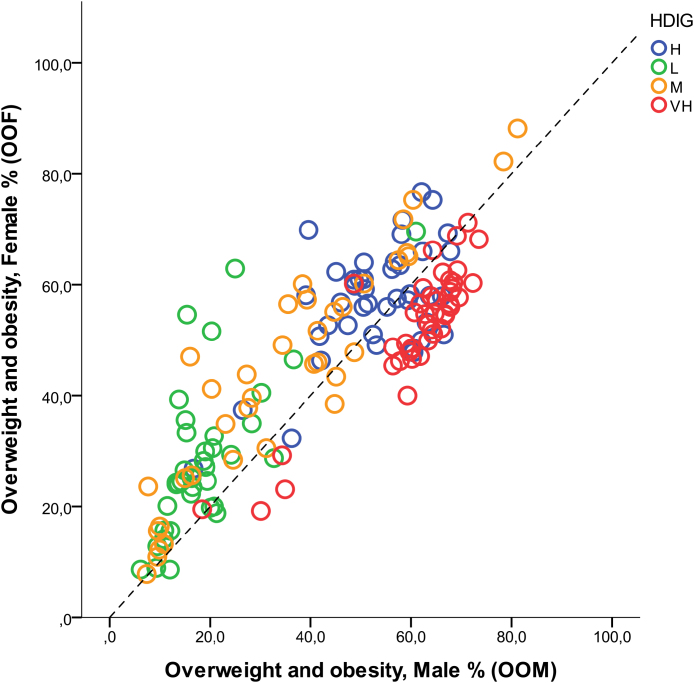
A simple way to capture the ‘gender dimension’ of these nutrition-related health outcomes is to examine the impact of human development on the prevalence of overweight and obesity in male and female populations around the world. In Fig. 6, in which OOM and OOF are measured on the horizontal and vertical axes respectively, each dot indicates a country, classified by the level of human development − i.e. very high, high, medium and low − according to their HDI (UNDP, 2014). If the GOOR index were around 1–that is, if the process of social and economic development did not have any appreciable influence on nutrition-related health outcomes − all points should line up close to the grey 45-degree line. But as a matter of fact, the data points lie above the line (GOOR > 1) for the vast majority of low-, medium- and high-HDI countries and below the line (GOOR < 1) for almost all very high-HDI countries (a paired samples t-test confirms this intuition: differences between the mean values of OOM and OOF in each HDI group are highly significant, as shown in Table D, S1 File (.XLS) in the Supplementary Content section).
Fig. 6.
The gender overweight and obesity ratio (GOOR).
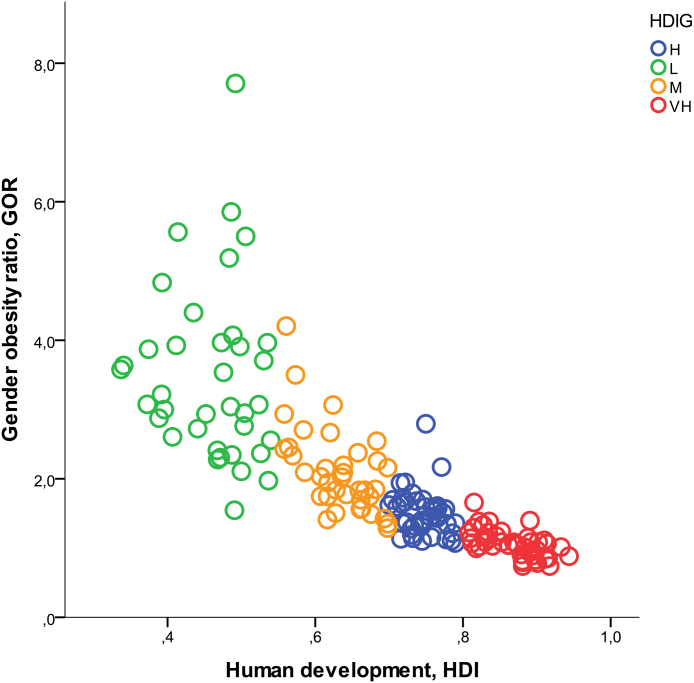
The impact of human development on BMI can be further illustrated by focusing on obesity alone (again, measured by the % of adults (ages 20+) who have a BMI (kg/m2) greater than 30). Using the same FAO (2014) and WHO (2014) datasets, we thus compute the ‘gender obesity ratio’ (GOR), as the ratio between the prevalence of obesity in female (OF) and male (OM) populations: i.e. OF/OM = GOR. Fig. 7 plots the GOR on the vertical axis against the HDI on the horizontal axis. The scatter plot highlights that there is a strong negative relationship between HDI and GOR, and also that countries are clearly clustered by their level of development (with an intra-group variability that decline sharply as human development increases). These findings confirm a ‘stylized fact’: as countries move towards higher levels of economic and social development the prevalence of obesity tends to shift from the female to the male population (Kanter and Caballero, 2012).
Fig. 7.
Human development (HDI) and the gender obesity ratio (GOR).
3.2. Gender disparities in obesity and gender inequality
In attempting to ‘engender human development’, the international research community has developed various country-level measures of women’s conditions. Over the past two decades, in particular, several leading institutions and organizations have proposed their own indices for measuring gender equality and women’s empowerment. Now, six countries’ measures of gender discrimination are available for international comparison, i.e. the Gender Inequality Index (GII), the new Gender Development Index (GDI), the Global Gender Gap Index (GGGI), the Gender Equity Index (GEI), the Social Institutions and Gender Index (SIGI) and the Women’s Economic Opportunities Index (WEOI). All these statistics are composite indices that measure gender equality (or inequality) on a scale between 0 and 1 (except for the GDI) and in the latest available versions they cover a number of countries worldwide that range from 102 to 143, over the period 2012–14 (a full list of the variables used in this paper and their acronyms is included in Table A, S1 File (.XLS) in the Supplementary Content section).
More particularly, the GII is calculated for the Human Development Reports (HDRs) (UNDP, 2014; Gaye et al., 2010) within the United Nations Development Programme (UNDP); it focuses on women’s empowerment and measures gender inequality by using five indicators on three key dimensions (reproductive health, political and educational empowerment and labour market participation). The HDRs also provide the new GDI, by computing the ratio of female to male Human Development Index (UNDP, 2014). The GGGI and GEI are instead published by the World Economic Forum (WEF, 2014) and the Social Watch research group (Social Watch, 2012), respectively. They both aim to capture gender disparities. However, the GGGI uses 14 indicators for four (economic, education, health and political) dimensions, whereas the GEI is composed of 7 indicators on three dimensions (education, economic participation and women’s empowerment). The SIGI is calculated by the Organisation for Economic Co-operation and Development (OECD), mainly for developing countries, and focuses on social norms that constrain women’s lives and on women’s discrimination in social institutions (OECD, 2014). Finally, the WEOI of the Economist Intelligence Unit (EIU, 2012) is specifically designed to determine whether a country’s legal, social and political environment is more or less favourable to women’s economic empowerment (a full description of each index can be found in the issue paper prepared by the HDR for the 2015 meeting on the measurement of gender equality in human development (Human Development Report Office, 2015) and in the van Staveren (2013) recent comparative analysis of gender indices).
We compute the Spearman's rank-order correlation coefficients to test the strength of the association between these six composite indices and our two biometric measures of gender inequality (that is, GOOR and GOR). The results are collected in Table 1. It is apparent that there is a strong correlation between the biometric and the composite measures of gender inequality. All the Spearman’s coefficients are highly significant (p < 0.01). They range from 0.30 to 0.83 for the gender overweight and obesity ratio and from 0.40 to 0.89 for the gender obesity ratio. The association is particularly strong between GOR and WEOI (ρ = –0.83) and especially between GOR and GII (ρ = 0.89) (the latter is a positive correlation because higher GII values mean a more unequal society, and vice-versa for the former).
Table 1.
Spearman’s rho correlation coefficients between GOOR, GOR and gender inequality indices.
| GOOR | GII | GDI | GGGI | GEI | SIGI | WEOI | ||
|---|---|---|---|---|---|---|---|---|
| GOOR | Correlation coefficient, ρ | 1.000 | 0.802** | –0.483** | –0.341** | –0.546 | 0.512** | –0.702** |
| Sig. (2-tailed) | .000 | .000 | .000 | .000 | .000 | .000 | ||
| n | 159 | 139 | 138 | 134 | 143 | 102 | 118 | |
| GOR | GII | GDI | GGGI | GEI | SIGI | WEOI | ||
| GOR | Correlation coefficient, ρ | 1.000 | 0.888** | –0.653** | –0.400** | –0.629** | 0.615** | –0.831** |
| Sig. (2-tailed) | .000 | .000 | .000 | .000 | .000 | .000 | ||
| n | 159 | 139 | 138 | 134 | 143 | 102 | 118 |
Correlation is significant at the 0.01 level (2-tailed).
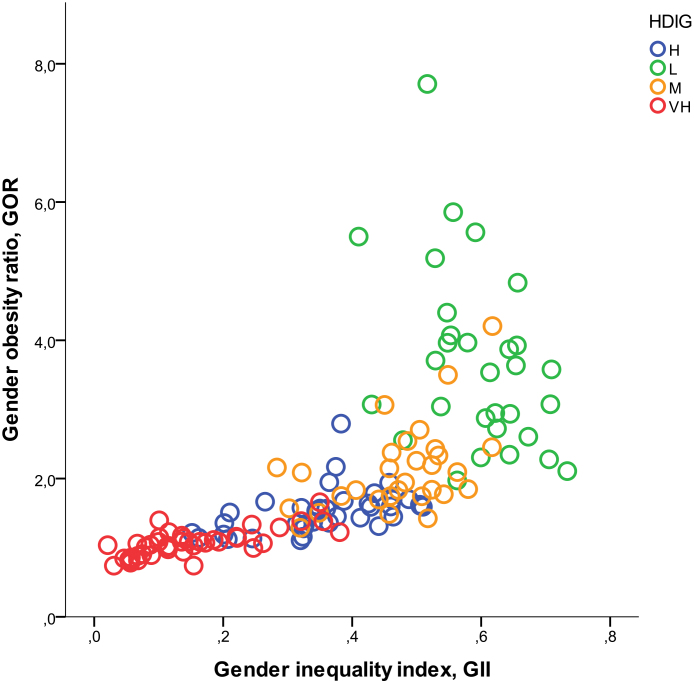
Focusing in particular on the association between the UNDP’s Gender Inequality Index (GII) and the gender obesity ratio (GOR) − given that GII is the most widely used ‘general index’ of gender inequality and that it covers a large number of both developed and developing countries worldwide − Fig. 8 plots the level of gender inequality (GII) against the level of gender disparities in obesity (GOR), with countries classified according to their human development group. There is a clear positive relationship between GII and GOR, especially in very high, high and medium HDI countries. It can be seen from these data that discrimination against women in the social dimension tends to translate into the biometric dimension: i.e. females are more likely to be obese with respect to males in societies in which women suffer from forms of discrimination in the economic, education, health and political dimensions.
Fig. 8.
Gender inequality (GII) and gender disparities in obesity (GOR).
4. Results and discussion
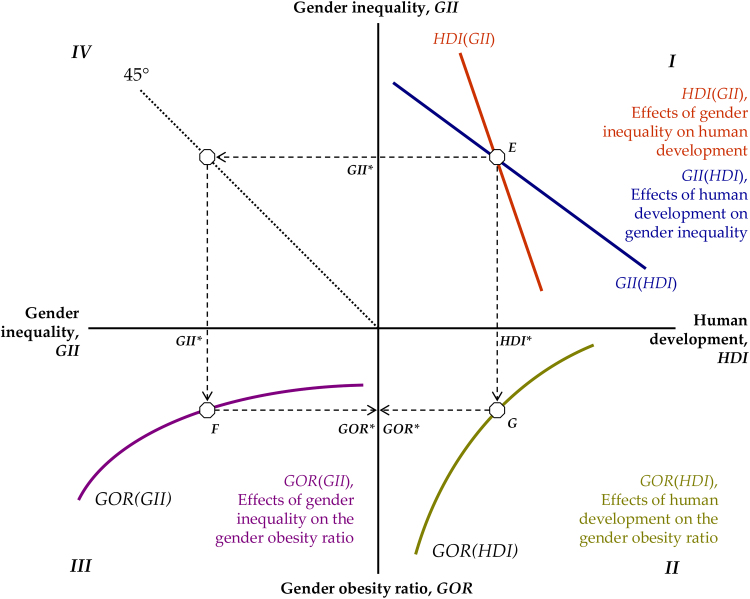
The empirical evidence presented here can be combined with our theoretical framework. In Fig. 9, quadrant I reproduces the joint determination of human development and gender inequality (i.e. Fig. 1), whereas quadrants II and III reproduce − in a stylized form − the relationship between gender disparities in obesity and human development (GOR(HDI), i.e. Fig. 7) and that between gender disparities in obesity and gender inequality (GOR(GII), i.e. Fig. 8), respectively.
Fig. 9.
Human development, gender inequality and gender disparities in obesity.
The interplay between the GII(HDI) and HDI(GII) functions − as previously explained in Fig. 1–determines the long-run levels of human development and gender inequality (point E in quadrant I). With each pair of a country’s gender inequality and human development equilibrium values (GII* and HDI*) is associated a given level of gender disparity in obesity, that is a specific distribution of the obesity prevalence between the female and male populations. This resulting equilibrium level of the gender obesity ratio (GOR*) can be derived from both the inequality perspective, in quadrant III, along the GOR(GII) relationship (via the 45-degree dotted line), or equivalently from the development perspective, in quadrant II, along the GOR(HDI) relationship (points F and G, respectively).
The causal relationship goes from human development and gender inequality to gender disparities in obesity. For measurement purposes, however, this diagrammatical exposition suggests the possible use of the gender obesity ratio as a ‘proxy variable’ to predict gender inequality in the broader sense. Table 2 presents the results obtained by regressing each of the six indices of gender inequality against the gender obesity ratio (with a flexible log-quadratic specification that allows different non-linear relationships to be dealt with). Except for the Gender Equity Index (GEI), variations in the gender obesity ratio predict from one-third to nearly four-fifths of the variations in gender inequality at large. The GOR performs particularly well in predicting the level of gender inequality as measured by three leading indices: SIGI, WEOI and GII (the adjusted R2 is equal to 0.56, 0.65 and 0.78 respectively, and all coefficients are significantly different from zero, p < 0.01).
Table 2.
Regression results: using GOR as a proxy variable to predict gender inequality.
| constant | Log(GOR) | Log(GOR)2 | Adj. R2 | n | |
|---|---|---|---|---|---|
| 1. Gender Inequality Index, GII | –2.08 | 2.75* | –1.14* | 0.78 | 139 |
| Std. Error | 0.19 | 0.12 | |||
| t-Statistic | 14.19 | –9.62 | |||
| 2. Gender Development Index, GDI | –0.01 | –0.16* | 0.05* | 0.31 | 138 |
| Std. Error | 0.03 | 0.02 | |||
| t-Statistic | –4.93 | 2.36 | |||
| 3. Global Gender Gap Index, GGGI | –0.31 | 0.23* | 0.13* | 0.29 | 134 |
| Std. Error | 0.03 | 0.02 | |||
| t-Statistic | –7.05 | 5.80 | |||
| 4. Gender Equity Index, GEI | –0.32 | –0.99 | 0.51 | 0.05 | 143 |
| Std. Error | 0.26 | 0.19 | |||
| t-Statistic | –3.80 | 2.76 | |||
| 5. Social Institutions and Gender Index, SIGI | –4.17 | 4.90* | –2.07* | 0.56 | 102 |
| Std. Error | 0.65 | 0.33 | |||
| t-Statistic | 7.57 | –6.24 | |||
| 6. Women’s Economic Opportunities Index, WEOI | –0.34 | –0.85* | 0.29* | 0.65 | 118 |
| Std. Error | 0.08 | 0.06 | |||
| t-Statistic | –10.76 | 5.07 |
Note: Estimated using White's coefficient covariance matrix.
= p < 0.01.
Finally, in order to test the ability of the gender obesity ratio to replicate the ranking of countries based on a general inequality index, Table 3 compares the rankings of the last 20 countries according to their levels of GII and GOR (that is, the 20 countries with the smallest GII and GOR values). It is worth noting that there is a substantial overlap between the two rankings. With only small differences in ranking positions, the first 10 places are occupied by the same 8 countries. Furthermore, within the first 20 positions, only 5 countries (those labelled in red) appear only in one ranking. A more exhaustive comparison between the two rankings is illustrated in Figure A (S1 File (.XLS) in the Supplementary Content section), where the absolute difference between each country’s position in the GII and GOR ranking (DRANK = GII rank − GOR rank) is plotted against the country’s position in the gender obesity ratio (for the full sample of 139 worldwide countries). Despite some outliers (for example, Rwanda and Samoa at −62 and +46 respectively), about 75% of the observations fall in the range of +20 and −20 positions. In other words, ranking countries by the ratio of the obesity prevalence between the female and male populations returns nearly the same results as a country’s ranking based on a general composite measure of gender inequality, such as the UNDP’s Gender Inequality Index.
Table 3.
Country ranking according to GII and GOR.
| Country | GII | Country | GOR | ||
|---|---|---|---|---|---|
| 1 | Slovenia | 0.021 | 1 | Switzerland | 0.740 |
| 2 | Switzerland | 0.030 | 2 | Luxembourg | 0.741 |
| 3 | Germany | 0.046 | 3 | Denmark | 0.783 |
| 4 | Sweden | 0.054 | 4 | Austria | 0.795 |
| 5 | Austria | 0.056 | 5 | Belgium | 0.816 |
| 6 | Denmark | 0.056 | 6 | Sweden | 0.827 |
| 7 | Netherlands | 0.057 | 7 | Germany | 0.845 |
| 8 | Italy | 0.067 | 8 | Netherlands | 0.855 |
| 9 | Norway | 0.068 | 9 | Norway | 0.882 |
| 10 | Belgium | 0.068 | 10 | Iceland | 0.892 |
| 11 | Finland | 0.075 | 11 | Finland | 0.907 |
| 12 | France | 0.080 | 12 | Japan | 0.941 |
| 13 | Czech Republic | 0.087 | 13 | Ireland | 0.977 |
| 14 | Iceland | 0.088 | 14 | Hungary | 0.996 |
| 15 | Spain | 0.100 | 15 | France | 1.008 |
| 16 | Korea (Republic of) | 0.101 | 16 | Australia | 1.014 |
| 17 | Israel | 0.101 | 17 | Portugal | 1.025 |
| 18 | Australia | 0.113 | 18 | Estonia | 1.032 |
| 19 | Ireland | 0.115 | 19 | Slovenia | 1.037 |
| 20 | Lithuania | 0.116 | 20 | Czech Republic | 1.042 |
Countries that appear in only one ranking are in bold.
These findings corroborate the results of previous research (Kanter and Caballero, 2012; Wells et al., 2012; Garawi et al., 2014) and are consistent with the ecological approach to the problems of overweight and obesity (Swinburn et al., 2011). By stressing the importance of environmental influences (i.e. cultural, economic, institutional and social influences), the ecological approach regards obesity as a ‘normal’ response to an abnormal micro- and macro-environment (Egger and Swinburn, 1997). We are able to enhance this approach and thus our understanding of the obesity pandemic. Specifically, in this study, the macro-environment is no longer an exogenous variable. The levels of human development and gender inequality result from the balancing of the forces that express the two-way linkages between a country’s development stage and the conditions of its female population. Individuals make choices within this context and their health outcome in terms of BMI (that is, being normal weight, overweight or obese) is a response to a more or less ‘obesogenic environment’ (i.e. the brown side of Fig. 5). This environment may be biased towards the male or female population according to society’s general level of human development and gender inequality. As a result, the gender obesity ratio that we observe at a given time and in a given society, summarizes in a single biometric statistic some of the most important dimensions of gender discrimination, and thus it may provide a ‘rule of thumb’ for measuring women’s empowerment and gender equality.
An important policy implication of our findings concerns the role of gender differences in devising and designing innovative strategies for reducing the worldwide prevalence of overweight and obesity. Especially in low- and medium-development countries − where the burden of obesity is predicted to affect an increasing percentage of the female population (WHO, 2014) − effective strategies to tackle overweight and obesity should not neglect the gender dimension (and vice versa, as without substantial progress in the economic and social condition of the female population, the effectiveness of any action against obesity will be severely reduced). However, the results of this study, are limited by the use of a simplified macroeconomic model. Linear relationships, in particular, may fail to account for intersectionality within a given society and for cultural differences in the nature and extent of gender inequality between countries. Thus, further research on this topic should be designed around the specific characteristics of homogeneous populations, using a more complex (i.e. non-linear) set of relationships and taking advantage of disaggregated microeconomic datasets.
Declarations
Author contribution statement
Fabrizio Ferretti: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Michele Mariani: Analyzed and interpreted the data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Appendix A. Supplementary data
The following are Supplementary data to this article:
References
- Akabas S., Lederman S.A., Moore B.J., editors. Wiley-Blackwell; London: 2011. Textbook of obesity: Biological, psychological and cultural influences. [Google Scholar]
- Anand S., Sen A. United Nations Development Programme (UNDP); Washington, D.C: 1995. Gender inequality in human development: Theories and measurement. UNDP Occasional Paper, 19. [Google Scholar]
- Annandale E., Hunt K. Open University Press − Taylor & Francis Group; London: 2000. Gender inequalities in health. [Google Scholar]
- BBC . BBC World News; 2015. Saudi Arabia's women vote in election for first time. Dec 12, 2015.http://www.bbc.com/news/world-middle-east-35075702 Accessed: March 2, 2016. [Google Scholar]
- Becker G.S. Harvard University Press; Cambridge, MA: 1991. A treatise on the family. [Google Scholar]
- Beneria L., Permanyer I. The measurement of socio-economic gender inequality revisited. Dev. Change. 2010;41(3):375–399. [Google Scholar]
- Cuberes D., Teignier M. Gender inequality and economic growth: A critical review. J. Int. Dev. 2013;26(2):260–276. [Google Scholar]
- Doepke M., Tertilt M. Women’s liberation: What’s in it for men? Q. J. Econ. 2009;124(4):1541–1591. [Google Scholar]
- EIU . The Economist - Economist Intelligence Unit; London: 2012. Women’s economic opportunity 2012. [Google Scholar]
- Egger G., Swinburn B. An ecological approach to the obesity pandemic. BMJ. 1997;315(7106):477–480. doi: 10.1136/bmj.315.7106.477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esteve-Volart B. The Suntory Centre − London School of Economics and Political Science; London: 2004. Gender discrimination and growth: Theory and evidence from India (Working Paper DEDPS 42) [Google Scholar]
- FAO . Food & Agriculture Organization of the United Nations; Rome: 2014. Food and nutrition in numbers 2014. [Google Scholar]
- Galor O., Weil D. The gender gap, fertility, and growth. Am. Econ. Rev. 1996;85(3):374–387. [Google Scholar]
- Garawi F., Devries K., Thorogood N., Uauy R. Global differences between women and men in the prevalence of obesity: Is there an association with gender inequality? Eur. J. Clin. Nutr. 2014;68(10):1101–1106. doi: 10.1038/ejcn.2014.86. [DOI] [PubMed] [Google Scholar]
- Gaye A., Klugman J., Kovacevic M., Twigg S., Zambrano E. United Nations Development Programme (UNDP); Washington, D.C: 2010. Measuring key disparities in human development: The gender inequality index (Human Development Research Paper) [Google Scholar]
- Greenwood J., Seshadri A., Yorukoglu M. Engines of liberation. Rev. Econ. Stud. 2005;72(1):109–133. [Google Scholar]
- Hsieh C.T., Hurst E., Jones C., Klenow P. National Bureau of Economic Research (NBER); Washington, D.C: 2013. The allocation of talent and U.S. economic growth. (NBER Working Paper No. 18693.) [Google Scholar]
- Hu F.B. Oxford University Press; New York: 2008. Obesity epidemiology: Methods and applications. [Google Scholar]
- Human Development Report Office . United Nations; Washington, D.C: 2015. Gender equality in human development. Measurement revisited (Issue paper prepared for the 2015 Expert group meeting) [Google Scholar]
- Kabeer N., Natali L. Institute of Development Studies; Brighton, UK: 2013. Gender equality and economic growth: Is there a win-win? (IDS Working Paper – No 417 ed.) [Google Scholar]
- Kanter R., Caballero B. Global gender disparities in obesity: A review. Advances in Nutrition: An International Review Journal. 2012;3(4):491–498. doi: 10.3945/an.112.002063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kickbusch I. Approaches to an ecological base for public health. Health Promot. Int. 1989;4(4):265–268. [Google Scholar]
- Lagerlöf N.-P. Gender equality and long-run growth. J. Econ. Growth. 2003;8(4):403–426. [Google Scholar]
- OECD . Organisation for Economic Co-operation and Development; Paris: 2014. Social institutions and gender index. [Google Scholar]
- Social Watch . The Social Watch Research Group; Montevideo, Uruguay: 2012. Measuring inequity: The 2012 gender equity index. [Google Scholar]
- Smith N. Gender quotas on boards of directors. IZA World of Labour. 2014;7:1–10. [Google Scholar]
- Swinburn B.A., Sacks G., Hall K.D., McPherson K., Finegood D.T., Moodie M.L., Gortmaker S.L. The global obesity pandemic: Shaped by global drivers and local environments. The Lancet. 2011;378(9793):804–814. doi: 10.1016/S0140-6736(11)60813-1. [DOI] [PubMed] [Google Scholar]
- United Nations . Diane Publishing Company for the United Nations Entity for Gender Equality and Women Empowerment; New York: 1996. The Beijing declaration and the platform for action: Fourth world conference on women, Beijing, China, 4-15 September 1995. [Google Scholar]
- United Nations . United Nations; Washington, D.C: 2014. The millennium development goals report 2014. [Google Scholar]
- UNDP . Oxford University Press for the United Nations Development Programme; New York: 1995. Human development report 1995. [Google Scholar]
- UNDP . United Nations; Washington, D.C: 2014. Human development report 2014: Sustaining human progress – Reducing vulnerability and building resilience. [Google Scholar]
- van Staveren I. To measure is to know? A comparative analysis of gender indices. Rev. Soc. Econ. 2013;71(3):339–372. [Google Scholar]
- Weil D.N. Pearson Education; New York: 2005. Economic Growth. [Google Scholar]
- Wells J.C.K., Marphatia A.A., Cole T.J., McCoy D. Associations of economic and gender inequality with global obesity prevalence: Understanding the female excess. Soc. Sci. Med. 2012;75(3):482–490. doi: 10.1016/j.socscimed.2012.03.029. [DOI] [PubMed] [Google Scholar]
- World Bank . World Bank Publications; Washington, D.C: 2011. World development report 2012: Gender equality and development. [Google Scholar]
- WEF . World Economic Forum; Geneva: 2014. The global gender gap report 2014. [Google Scholar]
- WHO . World Health Organization; Geneva: 2014. Global status report on non-communicable diseases 2014. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.