Water clusters in nonpolar cavities

Abstract

We explore the structure and thermodynamics of water clusters confined in nonpolar cavities. By calculating the grand-canonical partition function term by term, we show that small nonpolar cavities can be filled at equilibrium with highly structured water clusters. The structural and thermodynamic properties of these encapsulated water clusters are similar to those observed experimentally in the gas phase. Water filling is highly sensitive to the size of the cavity and the strength of the interactions with the cavity wall. Water penetration into pores can thus be modulated by small changes in the polarity and structure of the cavity. Implications on water penetration into proteins are discussed.

Hydrophobic literally means water repelling. So are nonpolar cavities hydrophobic, i.e., devoid of water? Answering this question profoundly impacts our understanding of the role of water in protein function. Although some weakly polar cavities created inside proteins by mutations were indeed found to be empty (1), recent studies using crystallography (2–4), NMR (5, 6), and simulations (7) show that water molecules may be present at least transiently. Evidence for a functional role of water in the nonpolar interior of proteins is also accumulating. Water has been implicated as the mediator for proton transfer through the nonpolar interior channels of the proton pumps cytochrome c oxidase (8) and bacteriorhodopsin (9), and the monooxygenase cytochrome P450 (10, 11), with water detected in trapped intermediates (9, 10), but empty channels in crystal structures of the resting enzymes.

Water permeation of carbon nanotubes (12–14) and the dewetting of hydrophobic surfaces (15–17) have been studied recently, but the thermodynamic driving forces for water filling nonpolar cavities remain poorly understood. The loss of hydrogen-bond energy should render the transfer of a single water molecule into a nonpolar environment energetically unfavorable (18). Moreover, multiple water molecules confined into narrow spaces will form highly ordered structures, resulting in unfavorable entropies of transfer. However, mounting experimental evidence for water penetrating into weakly polar cavities in the protein interior (2–6, 9, 10, 19) suggests that this simple reasoning must be incomplete.

To investigate the hydration of nonpolar cavities, we reverse the extensively studied process of nonpolar solvation in water (20, 21) and study instead the more poorly understood transfer of water into a nonpolar environment (18). We demonstrate that water can fill nonpolar cavities at ambient conditions, with entropy and “weak” van der Waals interactions playing a critical role, and that the strong water–hydrogen-bond interactions lead to the formation of unique water clusters similar in topology to the gas-phase structures detected spectroscopically (22–27).

We study the stability and structure of water in nonpolar cavities of varying size by Monte Carlo simulations, effectively by constructing a grand canonical ensemble. This approach allows us to compute the free energy of transfer of water from the bulk phase into cavities with diameters ranging from 0.9 to 1.19 nm. We also calculate the entropy and energy of transfer from the temperature dependence of the occupancy probabilities, as well as the specific heat, to clarify the factors that determine the formation and stability of the water clusters. The 3D structures of the more stable clusters in the cavities are examined and compared with water clusters studied experimentally in the gas phase (26).

Methods

The water occupancy of a cavity is determined by the balance of the excess chemical potentials of water inside the cavity and in the bulk fluid outside. We restrict our analysis to spherical cavities with smooth walls and rigid fullerenes to elucidate the fundamental aspects of filling thermodynamics and structure. In the grand-canonical ensemble, water molecules inside a cavity are in thermal and chemical equilibrium with the surrounding bulk fluid. The occupancy probabilities P(N) for finding exactly N particles in the volume V are related through (28)

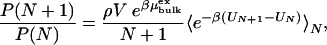[1]

where ρ is the number density of the bulk phase, 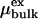is the corresponding excess chemical potential, β = 1/k_BT with k_B being Boltzmann's constant and T being the absolute temperature, U_N is the potential energy of the N-particle system, and 〈e^{–β(U_N+1–U_N)}〉_N is a canonical test-particle average for an (N + 1)th water molecule randomly inserted into the cavity containing N water molecules. This expression allows us to calculate the occupancy probabilities P(N) successively, starting from N = 1, by a combination of test-particle insertion and the method of overlapping histograms (28, 29). The probability of finding an empty cavity, P(0), is obtained by normalization. The free energy ΔA_N of filling the cavity with exactly N water molecules from bulk phase is related to the occupancy probabilities P(N) by ΔA_N = A_N – A₀ = –k_BT ln P(N)/P(0), neglecting a pressure-volume term that is small near ambient conditions (28). From the temperature dependence of ΔA_N = ΔU_N – TΔS_N, we can estimate the internal energy ΔU_N and entropy ΔS_N =–∂ΔA_N/∂T of the water clusters inside the cavities relative to bulk water.

The occupancy probabilities P(N) were evaluated by performing Monte Carlo simulations of water molecules in the canonical ensemble (28) for four different spherical cavities with diameters of 0.9, 1.0, 1.04, and 1.19 nm at temperatures of T = 280, 290, 298, 310, and 320 K. The free volume of the cavities, defined by a 1 k_BT energy surface for the water-cavity interaction, ranges from 0.02 to 0.13 nm³ for diameters between 2R = 0.9 and 1.19 nm.

Data were collected over half a million Monte Carlo steps after an initial equilibration of 100,000 steps. Additional simulations were performed for water inside rigid fullerenes C₁₄₀ and C₁₈₀ with diameters of ≈1.04 and ≈1.19 nm, respectively. We are not concerned here with the actual mechanism of how water gets into or out of the cavities. As in our earlier studies of carbon nanotubes (12, 13), we used the three-point transferable intermolecular potential function (TIP3P) model (30) to describe water, and the sp² “graphene” carbon type of amber (parm94) (31) with Lennard–Jones parameters for the carbon–water interaction of ε = 0.114333 kcal/mol and σ = 0.327521 nm. As before, we also considered a modified potential in which the attractive interaction with the carbons is approximately reduced by half (ε = 0.06461 kcal/mol and σ = 0.34138 nm). The water molecules in the smooth cavities were confined by a potential u(r),

[2]

that was obtained by spherically averaging over sp² carbon atoms uniformly distributed on a sphere of radius R with a surface density κ corresponding to that of a graphene sheet of bond length 0.14 nm. r is the radial distance of water oxygen atoms from the center of the cavity. The electrostatic interactions between the water molecules were treated with the full 1/r interaction. For water in the bulk phase, we use the experimental density ρ (32). The experimental excess chemical potential 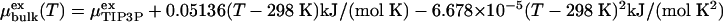is shifted to the value of TIP3P water at ambient conditions, 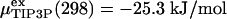(12, 28).

Results

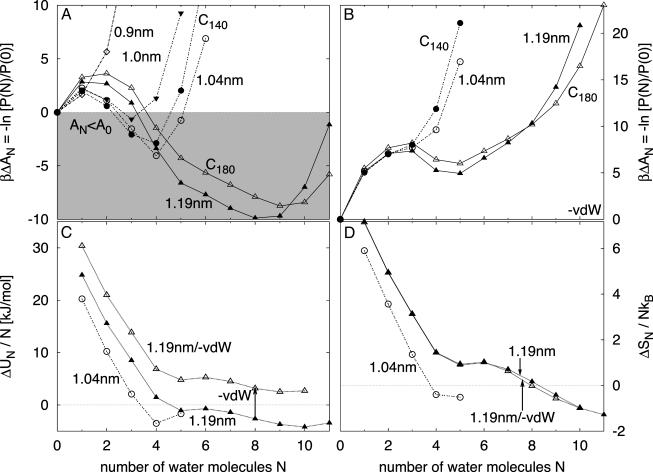
Thermodynamics of Cavity Filling. Fig. 1 summarizes the thermodynamics of water inside the nonpolar cavities. The free energy profiles as a function of the number N of water molecules in the cavities reflect two-state behavior with minima corresponding to empty (N = 0) and filled (N > 0) states. As the size of the cavity increases, the filled state becomes more populated and its free energy decreases. For the graphene potential (Fig. 1 A), the filled state is preferred over the empty states for cavities of 1.0 and 1.04 nm in diameter that contain clusters of three and four water molecules, respectively. Reducing the van der Waals attraction between water and the cavity wall makes filling unfavorable at all cavity sizes considered (Fig. 1B). For both types of cavity–water interactions, C₁₄₀ and C₁₈₀ fullerenes give results similar to those of smooth spherical cavities of corresponding size.

Fig. 1.

Thermodynamics of water filling nonpolar cavities at 298 K. (A) Free energy of water filling of smooth graphene-like spherical cavities with diameters between 0.9 and 1.19 nm, and fullerenes C₁₄₀ and C₁₈₀ with diameters ≈1.04 and ≈1.19 nm, respectively. The shaded area indicates thermodynamically favorable filling. (B) Free energy of water filling corresponding cavities with less attractive van der Waals interactions between water and the cavity walls. (C) Internal energy per water molecule inside cavities with diameters of 1.04 and 1.19 nm. The filled and open triangles show the internal energy for the 1.19-nm cavity with graphene-like and less attractive potentials, respectively. The arrow indicates the shift expected from first-order perturbation theory with respect to the van der Waals attraction. (D) Entropy per water molecule inside the cavities of C.

To identify the thermodynamic driving forces of the filling process, we calculate the energy and entropy of filling from the temperature dependence of the free energy. As the water occupancy N rises, the initially unfavorable energy decreases (Fig. 1C), reflecting the formation of hydrogen bonds between the water molecules. The magnitude of the transfer energy is sensitive to the water–cavity interaction strength. Differences between the graphene-like cavity of diameter 1.19 nm (with the N = 8 filled state favored over the empty state by ≈9.9 k_BT) and the less attractive cavity (with the empty state favored by ≈4.9 k_BT) can be explained quantitatively by first-order perturbation theory with respect to the water–wall van der Waals interaction energy (Fig. 1C). In contrast to the energy, the entropy of transfer is insensitive to changes in the water–cavity potential (Fig. 1D). As the occupancy N rises, the entropy per molecule decreases, reflecting the formation of hydrogen-bonded water structures and a reduction in free volume.

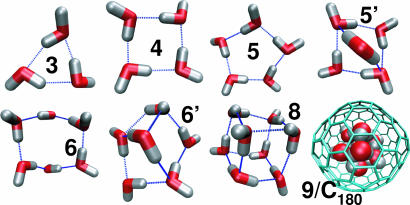
Structures of Encapsulated Water Clusters. The structures of the encapsulated water clusters help us to understand their stability and highlight the relationship to experimentally studied water clusters in the gas phase (26). Fig. 2 shows clusters of N = 3 to eight water molecules inside the smooth cavities and a nine-water cluster corresponding to the filling free energy minimum of the C₁₈₀ fullerene. For Fig. 2, low-energy structures were selected by tracing the energy landscape of equilibrated clusters during the Monte Carlo simulations.

Fig. 2.

Representative structures of clusters of three to eight water molecules inside spherical cavities and nine water molecules inside a C₁₈₀ fullerene. Blue dashed lines indicate hydrogen bonds. Water oxygen and hydrogen atoms are shown in red and white, respectively, and carbon atom bonds of C₁₈₀ are shown in light blue. Clusters are labeled with the number of water molecules.

The structures of the water clusters formed inside the large nonpolar cavity are strikingly similar to the structures deduced from gas-phase spectroscopy (26). The water clusters are all hydrogen-bonded, beginning with the dimer, and evolve through the trimer to the pentamer as cyclic structures with each water monomer donating a hydrogen bond to one nearest neighbor and accepting a hydrogen bond from the other. In gas-phase experiments, the free hydrogens of each monomer in the ring lie alternately above and below the plane of the oxygen atoms, thus creating a frustrated structure for the trimer. In our simulations using the TIP3P model for water, the free hydrogens are nearly planar and are perfectly planar at a T = 0 K structure. In simulations using the anisotropic site–site potential (ASPW4) (33) which is a refinement of the Millot–Stone potential (34, 35) with superior performance for water clusters, we found alternating out-of-plane dangling hydrogens in the confined C₁₈₀ water tetramer, as observed experimentally in gas phase. In the encapsulated pentamer, ring strain is relieved by displacing one of the water molecules out of the plane of the other oxygens, as seen in gas-phase experiments (24). These features lead to transitions in the gas phase that have been observed in the spectra of Keutsch and Saykally (26).

As in the gas-phase experiments, our simulations of the water hexamer in the large cavities signal a crossover from cyclic to cage-like hydrogen-bonded clusters. We find coexistence between the two types of hexamers in the simulations (6 and 6′ in Fig. 2). This degeneracy is the origin of the inflection point in the energy and entropy of transfer as the occupancy increases from five to seven (see Fig. 1 C and D). Continuing on to octamers we see exclusively cage-like hydrogen-bonded clusters. The octamer in the large cavity has the oxygen atoms at the vertices of a cube with S₄ symmetry (25), as shown in Fig. 2. In the simulations, we also find water octamers forming cubes with D_2d symmetry.

We calculate the configurational specific heat of the encapsulated water in fullerenes from the fluctuations in the potential energy collected over a million Monte Carlo steps at each temperature after equilibration. The kinetic energy contribution given by the equipartition theorem is not included. As seen before in simulations of gas-phase clusters (36), a plot of the specific heat versus temperature indicates a “melting” transition near 180 K of the water octamer encapsulated into C₁₈₀ (Fig. 3). The corresponding transition occurs near 400 K for the water tetramer in C₁₄₀. The nearly cubic hydrogen-bonded octamer is transformed into a mostly disordered liquid with broken hydrogen bonds above the “melting” temperature of 180 K, with only infrequent occurrence of the ordered clusters. Such melting has been studied previously (36–38). The melting of the tetramer, which occurs at a higher temperature of 400 K, is likewise characterized by the breakup of its ring structure. To our knowledge this has not been observed in the gas phase.

Fig. 3.

Configurational-specific heat of the water octamer encapsulated into C₁₈₀ (○) and the water tetramer in C₁₄₀ (•). (Insets) Low-energy structures at the temperatures indicated by arrows.

Concluding Remarks

Our studies show that water molecules can fill even small nonpolar cavities at equilibrium and ambient conditions. The smallest stable water cluster in a spherical cavity (1.0 nm) is the trimer with three hydrogen bonds, one per water molecule. A dimer with only a single hydrogen bond is easily accommodated in a smaller cavity of 0.9-nm diameter, but is not thermodynamically stable (Fig. 1 A). Linear chains of water molecules inside a narrow cylindrical pore are less stable than the water clusters in a spherical nonpolar cavity of comparable volume (28). All of the stable structures found in the spherical cavities have at least one hydrogen bond per water molecule; i.e., each water molecule is involved in two or more hydrogen bonds, a minimum number seen also for water molecules in proteins (39) and in the water chains formed inside nanotubes (12).

The stability of encapsulated water clusters depends critically on cavity size and the strength of the attractive interactions with the cavity walls. The sensitivity of filling to changes in the water–wall interactions is consistent with water filling of protein cavities upon slight increases in polarity. For instance, during the catalytic cycle of cytochrome P450, cryocrystallography (10) indicates that the amide hydrogen of a threonine is exposed to a narrow cavity that becomes filled with a water molecule (10, 11). As indicated by our simulations using the highly accurate ASPW4 potential (33), improved water models will certainly change details of the structures and thermodynamics of water clusters in cavities but are unlikely to alter our general conclusions about water in nonpolar cavities. The spectroscopic study of water clusters trapped in cavities should be of great interest in better characterizing water in a biologically relevant environment (40). Although encapsulation into fullerenes using, for instance, molecular beams or hydrothermal preparations will be challenging, other systems, in particular protein cavities, are more amenable.