Abstract
Amyloid formation is implicated in a number of human diseases, and is thought to proceed via a nucleation-dependent polymerization mechanism. Experimenters often wish to relate changes in amyloid formation kinetics, for example, in response to small molecules to specific mechanistic steps along this pathway. However, fitting kinetic fibril formation data to a complex model including explicit rate constants results in an ill-posed problem with a vast number of potential solutions. The levels of uncertainty remaining in parameters calculated from these models, arising both from experimental noise and high levels of degeneracy or codependency in parameters, is often unclear. Here, we demonstrate that a combination of explicit mathematical models with an approximate Bayesian computation approach can be used to assign the mechanistic effects of modulators on amyloid fibril formation. We show that even when exact rate constants cannot be extracted, parameters derived from these rate constants can be recovered and used to assign mechanistic effects and their relative magnitudes with a great deal of confidence. Furthermore, approximate Bayesian computation provides a robust method for visualizing uncertainty remaining in the model parameters, regardless of its origin. We apply these methods to the problem of heparin-mediated tau polymerization, which displays complex kinetic behavior not amenable to analysis by more traditional methods. Our analysis indicates that the role of heparin cannot be explained by enhancement of nucleation alone, as has been previously proposed. The methods described here are applicable to a wide range of systems, as models can be easily adapted to account for new reactions and reversibility.
Introduction
Amyloid deposition is associated with a number of severe degenerative disorders, including major public health concerns such as Alzheimer’s disease, Parkinson’s disease, and type II diabetes (1, 2). The amyloid fold, with its characteristic fibrillar, cross-β structure, can be adopted by a wide range of proteins (3, 4). Amyloid formation by proteins is often modeled in terms of a nucleated polymerization mechanism, which was first proposed by Tobacman and Korn (5) and Oosawa and Asakura (6) as a model for actin self-assembly. In the initial step, referred to as “primary nucleation”, small concentrations of energetically unfavorable nuclei begin to form. These nuclei are typically defined as the highest-energy intermediates along the aggregation trajectory and may be monomeric or oligomeric. Once a critical nucleus size nc is reached, rapid and highly favorable elongation follows by addition of a more soluble monomer to the nuclei/fibril ends. Amyloid formation differs from canonical nucleated polymerization (as in the case of actin) in one important aspect: for many systems, a single (primary) nucleation process is insufficient to account for the level of cooperativity in aggregation kinetics observed experimentally (7). As such, other secondary nucleation pathways, e.g., fragmentation of existing fibrils to form new nuclei (7, 8, 9, 10, 11), or nucleation from the surface of existing fibrils (12), are often invoked (Fig. 1). Nucleated conformational conversion mechanisms, which involve relatively rapid formation of nonfibrillar oligomers followed by a rate-determining conversion into β-sheet-rich states that can nucleate further fibrillization (13), have also been advanced for a variety of amyloid-forming systems (14, 15, 16).
Figure 1.
Scheme of nucleated polymerization models used in this work. Reactions and relevant rate constants are labeled. (A) Our ODE model. Soluble monomers (m) form aggregation-prone nuclei (nuc) at a rate kn. Active nuclei, newly formed or at the ends of fibrils catalyze the formation of fibrilized species (M) from more monomer at a rate ke1, which can dissociate from the fiber at a rate . Note that elongation is only allowed at a single fibril end in this case, and that monomer dissociation from fibrils is approximated as a bimolecular reaction; is an apparent bimolecular rate constant and represents a convolution of rate constants for different fibril lengths and end concentrations. Finally, fibrils may break, allowing formation of more nuclei (blue) from fibrilized species at a rate kf. (B) N-E-F model based on Knowles et al. (7). Soluble monomers form energetically unstable nuclei at a rate kn, similar to the ODE model. Soluble monomers may add irreversibly to either end of the growing fibril at a rate k+, to form fibrils of length i. These fibrils may break in one of two places at a rate k− to form two fibrils of length j and i − j. Equation 2 results from integration of the corresponding master differential equation over all fibril lengths. To see this figure in color, go online.
Detailed analysis of amyloid formation kinetics is a nontrivial problem. Typically, the progress of amyloid formation is monitored with respect to fibrillar mass (M), which is assumed to be proportional to whatever signal is measured. Numerous techniques are available to characterize amyloid fibrils and their in vitro assembly kinetics, including bulk and single molecule fluorescence, light scattering, and electron microscopy (17, 18). Nonetheless, data relating to relevant rate constants and to the exact nature of the species formed along the reaction pathway are often sparse, and fitting data to a specific fibril formation model (most straightforwardly a set of linked ordinary differential equations, ODEs) almost always results in an ill-posed problem with a wide range of rate constants capable of giving rise to identical data. Care must also be taken to collect sufficient complementary information (i.e., structural data, evidence for intermediates, concentration dependence, etc.) to support the proposed model, as diverse assembly mechanisms can generate roughly similar sigmoidal kinetics. The amount of uncertainty remaining in model parameters calculated from fits to experimental data is also unclear in many cases.
Amyloid formation kinetics (19, 20, 21) are commonly analyzed by fitting to generic sigmoidal equations to extract descriptive, empirical parameters as in Eq. 1 (where and denote fibril mass as a function of time and the monomer concentration, respectively). These parameters may include the midpoint and steepness of the transition, and the lag time before the aggregation begins (τlag), which can be calculated from the former two. Such approaches have a long history in the protein aggregation field, and have been used to develop many of the fundamental aspects of the amyloid paradigm. They are analytically straightforward, and do not impose a specific model on the data. Empirical sigmoidal analyses are therefore well suited for comparative studies of, for example, the effects of different inhibitors on the aggregation of a target protein:
| (1) |
In and of themselves, the empirical parameters provide relatively little mechanistic insight into the process of fiber formation or changes in the underlying elementary rate constants. A richer understanding of amyloid formation can be achieved through the use of more complex models (22, 23, 24, 25, 26), such as an elegant analytical nucleation-elongation-fragmentation (N-E-F) model developed by Knowles et al. (7). Based upon substantial empirical evidence, this model assumes that amyloid formation occurs via nucleated polymerization, with fragmentation as a secondary nucleation process (outlined above). This treatment allows for explicit calculation of parameters including nucleus size (nc), primary (kn) and secondary (k−) nucleation rate constants, and elongation rate constant (k+):
| (2) |
where (simplified for M(0) = 0) and .
Given the complexity of the amyloid formation pathway, it is unsurprising that evaluation of protein fibrillization with respect to time in closed form is far from trivial. It is therefore difficult for the non-mathematician to extend an analytical model such as N-E-F to account for new processes or modulators of the system, and to account for codependency or degeneracy of the underlying constants.
Another, related approach is numerical modeling via a system of differential equations describing nucleation, elongation, and any other processes that may be at play (12, 19, 27, 28, 29). Modern computing resources make it possible to directly use these numerical models for data fitting along with rigorous statistical analyses, even in the absence of closed-form analytical solutions. Using an ecosystem of well-established tools (30, 31), creation of numerical models and modification and extension of reaction pathways is facile. The standardized Systems Biology Markup Language (SBML) format (32) used by most biology-geared numerical modeling software allows for easy editing, publication, and transfer of these models (33). However, this approach shares some of the drawbacks of analytical treatments like N-E-F: fundamental model parameters are degenerate, and it is difficult to recover rigorous estimates of the uncertainty in the resulting parameter values.
Approximate Bayesian computation (ABC) (34, 35, 36, 37) is useful for parameter inference in these cases, as the remaining uncertainty in model parameters (here, the rate constants) is clearly outlined in the form of posterior distributions. The shape of these distributions gives additional information on the nature of the rate constants’ covariance. As the name implies, ABC makes use of Bayes’ theorem:
| (3) |
to infer the most likely values for a set of parameters (the posterior distribution, ), from a range of possibilities (the prior distribution, ). In other words, the most likely values for a parameter set Θ given some observed data can be found by multiplying the prior distribution by a function describing the likelihood of those data having been produced by the parameter set Θ. This likelihood function is not known a priori, but is instead iteratively approximated by simulating a model dataset using a parameter set Θ∗ sampled randomly from the prior distribution . The Euclidian (i.e., root-mean-square) distance ε between and is a convenient proxy of likelihood: the smaller the value of ε, the greater the agreement between observed and modeled data, and the greater the probability that the parameter set Θ∗ reflects the posterior distribution . Parameter sets that give rise to datasets with ε below a certain defined cutoff are included in , while those with ε values too large are rejected. For computational efficiency, the prior distribution is iteratively sampled, refined to resemble , and sampled again. This generates ensembles of parameter sets Θ∗ that satisfy progressively smaller cutoff values of ε (referred to as the “ε schedule”), until a user-defined minimum, εfinal, is reached. If is sampled thoroughly, reflects the full range of parameter sets compatible with both the observed data and any prior knowledge of the system (38).
Here, we demonstrate the value of applying numerical modeling approaches, built using the COPASI software package (30), in combination with ABC techniques implemented in the ABC-SysBio software package developed by Liepe et al. (39, 40), to the inverse problem of recovering relative changes in rate constants in a model of amyloid formation. We show as a proof-of-concept that it is possible to identify with confidence relatively small changes in each rate constant without the need to solve for their explicit values. We offer a comparison between a combined ODE numerical modeling/ABC strategy and analysis using the N-E-F model. The technique presented here allows the experimenter to easily make changes to models and visualize the resulting effects on parameter relationships and uncertainty, with minimal need for further mathematical manipulation or transformation.
We finally apply ODE/ABC analysis to kinetic data to elucidate the mechanism of inducer-mediated amyloid formation by tau protein. Neural amyloid deposits of this microtubule-associated protein are implicated in a number of neurodegenerative disorders, including Alzheimer’s disease and chronic traumatic encephalopathy (41, 42, 43). Several anionic cofactors have been shown to be effective in inducing tau aggregation in in vitro assays (44, 45, 46), while native tau alone is highly soluble and does not assemble into amyloid over experimentally tractable periods of time. A number of models have been proposed to describe the complex behavior of tau protein in the presence of heparin, though its exact mechanism remains unclear (47, 48, 49, 50, 51). Here the fibrillization kinetics exhibited by the four-repeat domains of htau40, tau244–372 (52), are examined in the presence of heparin sodium. While we propose that heparin has effects on primary nucleation in agreement with previously published models (50, 53), we also demonstrate that the effects of this inducer cannot be restricted to this process alone.
Materials and Methods
Model building
Models for tau244–372 assembly were built in COPASI (30), assuming a nucleation-dependent polymerization mechanism as outlined in Results. Synthetic data were simulated in COPASI using a 2000 s time step over 150,000 s, for a total of 76 data points.
Least-squares analysis
Least-squares fitting of the kinetic data to Eqs. 1 and 2 was carried out in GraphPad Prism 6 (GraphPad Software, La Jolla, CA).
Approximate Bayesian computation
Rate constant distributions were generated using the ABC-SysBio software package according to published protocols (39, 40). Computation was performed on local workstations and using the Amazon Elastic Compute Cloud service. Input SBML files were generated in COPASI and modified such that log10 values of each rate constant were the parameters of interest. This allowed the use of a log-uniform prior parameter distribution, which greatly improved sampling of parameter space as well as computation time. ABC was performed using a timestep of 10 s using prior distributions spanning the ranges indicated in Table S3 in the Supporting Material. Appropriate values were defined based on RMSD calculated by least-squares fitting to Eq. 1, with the relationship:
| (4) |
where n is the number of data points in the timecourse. Schedules of decreasing cutoff ε-values were assigned by empirical adjustment and are also available in Table S3. Because weighting of individual data points in the fitting process was not readily implemented, the use of distributions with was required in some cases.
Purification of tau244–372
The plasmid for the tau244–372 fragment (the four repeat domain K18 construct of htau40) was a kind gift from the Rhoades lab at the University of Pennsylvania. Protein expression and purification was based on published protocols (54). Briefly, tau244–372 was transformed into BL21(DE3) cells and used to inoculate 1 L cultures in Luria-Bertani medium. Cells were grown in baffled flasks to OD ∼0.6–0.7 at 32°C. Cultures were cooled to 16°C and induced with the addition 1 mM IPTG, followed by overnight growth at 16°C. Cells were harvested by centrifugation, and resuspended in 30 mL lysis buffer: 50 mM tris pH 8 at 4°C, 500 mM NaCl, 10 mM imidazole, 1× Halt protease inhibitor cocktail (EDTA free; Thermo Fisher Scientific, Waltham, MA), 0.1 mg/mL of DNase, and 0.1 mg/mL of RNase per 1 L of growth. A quantity of 300 μL of a saturated solution of PMSF was added, lysis was achieved via French press, and the lysate clarified by centrifugation at 9000g for 45 min. The supernatant was passed through a 0.8 μm filter (Sigma-Aldrich, St. Louis, MO) before application to a 5 mL Ni-NTA agarose column (GE Healthcare, Pittsburgh, PA). Protein was eluted using a gradient from 10 to 250 mM imidazole, then exchanged back into imidazole-free buffer using a 3 kDa MWCO centrifugal filter (EMD Millipore, Billerica, MA). Dithiothreitol was added to a final concentration of 1 mM, followed by 250 μL of TEV protease at 2.8 mg/mL. The solution was dialyzed against 500 mL lysis buffer without protease inhibitors, then the protein was reapplied to the Ni column. Flowthrough was collected, concentrated to 1–2 mL using a centrifugal filter, and fractionated on a 25 mL S200 Extend gel filtration column (GE Healthcare) using 25 mM tris pH 8 at 4°C, 500 mM NaCl, 1 mM EDTA, and 0.5 mM TCEP as the mobile phase. Purity was confirmed by SDS-PAGE. Protein was concentrated as above to ∼500 μM, flash-frozen, and stored at −80°C before use. Aliquots were thawed immediately before use, and used only once.
Fibrillization assay
All fibrillization reactions were carried out at 37°C at pH 7.4, in buffer containing 25 mM Tris-HCL, 50 mM NaCl, 1 mM dithiothreitol, and 50 μM Thioflavin T. A quantity of 100 μL aliquots of tau244–372 at twice the desired final concentration was added in triplicate to the wells of black-walled polystyrene 96-well plates (Corning Life Sciences, Tewksbury, MA). Equal volumes of unfractionated heparin sodium (Acros Organics, Morris Plains, NJ) at twice the desired final concentration were added to the wells to initiate the reactions. Reaction progress was monitored by increase in Thioflavin T fluorescence with λex = 440 nm and λem = 485 nm in a BioTek Synergy HTX (BioTek, Winooski, VT) plate reader. Reads were taken every 2 min after 3 s agitation, over 4 h. Experiments were performed in triplicate, with two separate protein preparations. Data presented are the average of three separate experiments.
Seeding experiments
Seeds were prepared from freshly fibrilized material (see Fibrillization Assay). After 4 h, fibrilized material was harvested by centrifugation at 20,000g for 1 h. The supernatant was removed, and pelleted material resuspended in an equal volume of fresh aggregation buffer without heparin. Fibrils were sonicated in a bath sonicator for 2 min followed by vortexing for 10 s, repeated for a total of five cycles. Seeds were added to the reactions at the indicated final weight percent, with initiation of the reactions and monitoring of fibrillization carried out as indicated above. Experiments were performed in triplicate.
Determination of extent of fibrillization
Aliquots of the completed fibrillization reactions (above) were centrifuged at 20,000g for 1 h to remove aggregated material, and the supernatants analyzed either by tyrosine fluorescence or reverse-phase HPLC. Tyrosine fluorescence of the supernatants was measured with λex = 280 nm and λem = 315 nm and compared to a standard curve of tau244–372 in the absence of heparin. Alternatively, HPLC was performed on an UltiMate 3000 HPLC system (Dionex, Sunnyvale, CA) using an analytical 4.6 × 50 mm Hypersil BDS C18 column (Thermo Fisher Scientific) with a linear gradient of 0–95% acetonitrile + 0.1% TFA as the mobile phase. Separation was monitored by absorbance at 220 and 280 nm, and [tau244–372] in the supernatants was calculated by comparing integrated peak areas with tau244–372 standards treated identically to the samples, except without heparin.
All reagents were purchased from Sigma-Aldrich or Thermo Fisher Scientific unless otherwise noted, and were of ACS reagent grade or higher purity.
Results
Minimal model for heparin-induced tau244–372 polymerization
The behavior we observe in our tau244–372 fibrillization reactions can be defined with a mechanism consisting of as few as three steps, modeled by the following reactions:
Nucleation
| (5) |
Elongation
| (6) |
Fragmentation
| (7) |
Here, m, nuc, and M indicate the soluble, nucleus (or fibril ends), and fibrilized (bound within a fibril) forms of the protein, respectively. This scheme is reminiscent of the minimal model proposed in 1997 by Watzky and Finke (55), with two important exceptions: firstly, the elongation step is assumed to be reversible. Secondly, fragmentation is modeled here as a separate step and is therefore not kinetically hidden as it is in the model by Watzky and Finke.
This simple model is fully capable of describing our observations, but entails two noteworthy simplifications. The first is that nucleation and fragmentation are treated as irreversible. While the reverse reactions may occur, the fact that the forward nucleation and fragmentation reactions are slow relative to elongation means that the overall reaction trajectory is negligibly sensitive to the reverse rate constant of either process (data not shown). The second simplification is that we treat elongation as a reversible bimolecular reaction that is, in essence, the nucleus-catalyzed generation of fibrillar material. The reversibility of this reaction (56) is required to account for the varying final ratios of soluble material to fibrils that we observe; the N-E-F model in its originally published form (7) assumes that elongation is irreversible, and that fibril formation thus always proceeds to completion. For simplicity, we treat the back-reaction as bimolecular as well. This approach obviates the need to account for fibrils of different lengths, and allows for more straightforward conservation of mass in our simulations. The apparent rate constant () of the reverse reaction derived from this treatment should be thought of as a convolution of multiple rate constants for different fiber lengths and fiber end concentrations, rather than a single elementary value.
The concentration of each reaction component can be calculated with respect to time using the following linked ODEs:
| (8) |
| (9) |
| (10) |
Using this system, it is possible to recapitulate all of the features of interest of our sigmoidal kinetic data, including τlag, , M∞, and . The SBML file for this model is available in Table S1. Note that many analytical models make predictions of fibril number concentrations (as opposed to mass concentrations) and fibril length distributions over time (7, 25, 26), both of which can be valuable experimentally observable parameters. While it is possible to estimate fibril number and mean length from the concentration of nuc in Eqs. 8–10, in this work we limit ourselves to considering fibril mass concentrations.
Synthetic data: a comparison of fitting to Eq. 2 and ABC analysis
As a proof of concept, we utilized our ODE model to generate a number of simulated timecourses (76 points each) with systematically varied rate constants. The rate constants used to generate the base timecourse are provided in Table 1, and were chosen to model aggregation behavior similar to that typically observed experimentally (sigmoidal fibrillization occurring over a few hours). The forward and reverse elongation rate constants, ke1 and , were set equal to best demonstrate the effect of changes in either with respect to endpoint fibril concentration. We attempted to recover these constants by fitting our ODE-derived synthetic data to the analytical N-E-F model using the standard Levenberg-Marquardt approach, as well as to the original numerical ODE model using ABC. Note that both the N-E-F and ODE models are ill posed, meaning that even very large changes in one parameter can be completely compensated for by changes in other parameters, and it is impossible to uniquely identify the underlying rate constants from a single dataset. Therefore, we limit ourselves to comparing derived parameters composed of appropriate ratios or products of fundamental rate constants.
Table 1.
Rate Constants Used to Simulate the Base Synthetic Timecourse, Subsequently Varied to Test N-E-F and ODE-Based Fitting Approaches
| kn (s−1) | 10−15 |
| ke1 (μM−1 s−1) | 103 |
| (μM−1 s−1) | 103 |
| kf (s−1) | 10−12 |
Fitting to the analytical N-E-F model
The synthetic timecourses are shown in the left column of Fig. 2. All forward rate constants contribute to the length of the lag phase; the ratio ke1/, is equivalent to the KA of the elongation process and governs the extent of fibrillization. The solid lines show fits to the analytical N-E-F model (Eq. 2). The change in derived parameters as rate constants are varied is plotted in the right column of Fig. 2; values for kn are listed in Table 2, and the full set is given in Table S2. Each panel shows the log (fold-change) in the derived parameters kn/k− and k+k− in response to changes in one or more of the input rate constants of the ODE model (kn, kf, ke1, ).
Figure 2.
The analytical N-E-F model (Eq. 2) accurately describes many features of simulated fibrillization kinetics. (Left column) Simulated data (circles) with indicated rate constants at base levels, increased by twofold, fivefold, and 10-fold. Every second data point is plotted for ease of inspection. Refer to Table 1 for base rate constants used to simulate data. (Solid lines) Fits to the N-E-F model (Eq. 2). (Right column) Fold-changes in rate constants recovered from fits to Eq. 2. Error bars (in many cases smaller than the points) reflect the standard errors of fitting generated by the Levenberg-Marquardt algorithm. (Dotted lines) No change in derived parameter from base timecourse (black); twofold increase or decrease (dark gray); fivefold increase or decrease (medium gray); 10-fold increase or decrease (light gray). Refer to Table 2 for derived parameters recovered from fits. Note that, for example, as kn is increased, the derived parameter kn/k− also increases by the expected amount (data points all align with expected values shown in dotted lines). Meanwhile, the parameter k+k−, which is independent of kn, does not change (data points lie along zero line). To see this figure in color, go online.
Table 2.
Derived Parameters for Increasing kn from Least-Squares Fitting to Eq. 2, and from ODE/ABC Analysis
| Derived Parameter | Base | kn × 2 | kn × 5 | kn × 10 | |
|---|---|---|---|---|---|
| N-E-F | log(kn/k−) | −2.43 ± 0.02 | −2.15 ± 0.02 | −1.78 ± 0.01 | −1.49 ± 0.01 |
| log(k+k−) | −9.104 ± 0.006 | −9.108 ± 0.006 | −9.116 ± 0.006 | −9.127 ± 0.006 | |
| ODE | log(kn/kf) | −3.09 ± 0.03 [−3.00] | −2.78 ± 0.03 [−2.70] | −2.59 ± 0.05 [−2.30] | −2.06 ± 0.02 [−2.00] |
| log(ke1kf) | −8.98 ± 0.01 [−9.00] | −8.98 ± 0.01 [−9.00] | −8.91 ± 0.02 [−9.00] | −8.97 ± 0.01 [−9.00] | |
| log(kf) | −8.98 ± 0.01 [−9.00] | −8.98 ± 0.01 [−9.00] | −8.91 ± 0.02 [−9.00] | −8.98 ± 0.01 [−9.00] | |
| log(ke1kn) | −12.07 ± 0.02 [−12.00] | −11.76 ± 0.02 [−11.70] | −11.50 ± 0.03 [−11.30] | −11.04 ± 0.01 [−11.00] | |
| log(kn) | −12.07 ± 0.02 [−12.00] | −11.76 ± 0.02 [−11.70] | −11.50 ± 0.03 [−11.30] | −11.04 ± 0.01 [−11.00] | |
| log(ke1/) | −0.0003 ± 0.002 [0] | −0.001 ± 0.001 [0] | −0.002 ± 0.002 [0] | 0.001 ± 0.001 [0] |
Reported errors indicate standard errors of fitting for N-E-F parameters, and mean ± SE of the derived parameter posterior distributions for ODE (n = 100). Also for ODE, italicized values in brackets indicate the expected value of the derived parameter used to generate a synthetic timecourse.
The N-E-F model accurately captures some changes to the input parameters but not others. For instance, kn/k− increases linearly with kn, and both kn/k− and k+k− change (in opposite directions, as expected) with changes in kf. Similarly, k+k− changes linearly as ke1 is increased, either in isolation or in combination with . One complicating factor is that the N-E-F model does not account for dissociation of monomers from fibril ends (corresponding to ) and therefore does not accommodate changes in this parameter; instead, kn/k− and k+k− both increase roughly with ()0.7.
Note that the ratio ke1/ is equivalent to an association constant (KA) for elongation, and reflects the free energy driving the aggregation process. We highlight the importance of measuring the concentration of free monomer at the end of a fibrillization reaction, which constrains this ratio and thus determines this key aspect of aggregation behavior. Because the N-E-F model assumes that aggregation proceeds to completion, for the fits in Fig. 2 it was necessary to permit the total protein concentration ( in Eq. 2) to float rather than fixing it to the true value of 10 μM used in the input simulations.
Given these limitations, it is encouraging that N-E-F is able to capture some valuable information regarding changes in fundamental rate constants. However, other important aspects of aggregation behavior such as incomplete fibrillization remain inaccessible (57), and the least-squares fitting approach substantially underestimates the uncertainty in recovered parameters (58).
Fitting to the ODE model using ABC
For each synthetic data curve evaluated, our ABC analysis returns 100 distinct sets of parameters (i.e., kn, ke1, , and kf) that each give rise to model datasets with ε ≤ εfinal. Five of these model datasets were arbitrarily selected and used in our ODE model to generate the curves shown in Fig. 3 A (thin lines). Also shown are representative posterior distributions generated by ABC from fits to synthetic data, with one input model parameter (in this case, kn) systematically varied. Each panel plots a pair of output model parameters against each other; each point represents a parameter set that fits the data at least as well as εfinal. Appropriate derived parameters were calculated for each output parameter set, and are plotted as histograms for different values of kn in Fig. 3 B.
Figure 3.
ODE/ABC analysis of simulated data reveals codependency and uncertainty in model parameters. (A) Comparison of synthetic data (circles) and five representative timecourses (randomly selected from 100 total) simulated using sets of kn, ke1, , and kf returned by the ABC inference procedure (lines). For ease of inspection, data is separated into two plots, and every second synthetic data point is plotted. (B) Parameter distributions for simulated data with systematically varied kn. Note that parameter distributions shift as anticipated when kn is increased; uncertainty is reflected by the breadth of the histograms. To see this figure in color, go online.
The posterior distribution plots reveal a few important points. First, the strong correlations between the fundamental model parameters immediately point to the relevant derived parameters (i.e., ratios or products) that must be used to account for their codependency. Second, the breadth of the histograms of the derived parameters (given a suitable value of ε) more accurately reflects uncertainty due to experimental noise, model structure, and parameter degeneracy than the standard errors typically estimated in nonlinear fitting (38). Third, we observe that all of the derived parameters that depend on nucleation rate constant (kn/kf, ke1kn, and kn) change, while all of the other derived parameters (ke1/, ke1k, and kf) stay constant. This unambiguously indicates that the value of kn alone varies for the input data sets, as is indeed the case.
The means and standard errors of the derived parameters are summarized in Table 2, with input values included in italics for comparison. In general, the extracted and input values agree very well. Fig. 4 shows how each of the derived parameters changes with the input model parameters. We see that, in all cases, the derived parameters increase as expected from our model. The uncertainty in these values increases for input data sets with sharp transitions defined by few simulated points (e.g., high values of kf or simultaneously high values of ke1 and ). ODE/ABC is thus able to effectively identify degeneracies in model parameters, define appropriate derived parameters, estimate the uncertainty in their values, and accurately capture perturbations to a simple model of amyloid formation.
Figure 4.
Derived parameters from ODE/ABC fits of simulated data accurately capture changes in the underlying rate constants. Derived parameters can also be recovered when two are changed simultaneously (ke1 and ). Shown are change in values for log(derived parameters) recovered from ABC for each systematically varied rate constant (see Fig. 2 for coloring). Error bars reflect mean ± SE. (Dotted lines) No change from base timecourse, twofold increase/decrease, fivefold increase/decrease, or 10-fold increase/decrease from base timecourse. Refer to Table 2 for derived parameters from fits (increasing kn only). To see this figure in color, go online.
In general, the parameters recovered from fits using either method agree with the input rate constants, and the agreement between observed and modeled data is well within typical experimental error. The slight differences in derived parameters between the ODE and N-E-F model are in many cases a result of subtle disparities in the interpretation of these rate constants. For example, kn is roughly equivalent in both models. However, the fragmentation rate constant (kf) in our model is defined with respect to fibrilized monomer concentration, whereas the fragmentation rate constant (k−) in N-E-F is defined with respect to fibril concentration (7) (refer to Fig. 1). This is particularly clear upon comparison of kn/kf in the ODE model with the analogous N-E-F parameter kn/k− (Table 2); kn/k− is ∼0.6–0.7 log units larger than kn/kf, although the fold changes in each in response to increasing kn are nearly identical.
Remarkably, ODE/ABC analysis and the N-E-F model are nevertheless able to distinguish an increase in kf from simultaneous increases in ke1 and . Empirical fits to equations such as Eq. 1 indicate similar decreases in t50 and increases in for both perturbations, and cannot differentiate between them (see Fig. S1; Table S4). The advantage of the ODE approach is that it can be trivially extended by the experimenter to describe more complex behavior (e.g., multiple tau isoforms, ligand effects, membrane binding) by adding appropriate equations to the original system of linked ODEs (Eqs. 8–10).
Analysis of inducer-mediated tau244–372 fibrillization
We applied the ABC analysis to fibrillization data of tau244–372 in the presence of heparin, a polyanion commonly used to induce amyloid formation in a number of proteins (44, 59, 60, 61). It has been demonstrated previously that addition of heparin up to a saturating point significantly speeds the process of fibril formation, while addition beyond the point of saturation begins to slow the process (48, 50). We therefore used ABC analysis to determine the effect of heparin at a range of concentrations on tau244–372 aggregation, assuming that the process can be modeled using our simple scheme. Fitting to the N-E-F model is complicated by the fact that complete fibrillization is predicted in all cases by that model, but is only observed at the highest concentrations of heparin; it is thus not possible to predict extent of fibrillization from starting monomer concentration alone.
The results of our ABC analysis are shown in Fig. 5, with derived parameters listed in Table 3. Particularly striking is the steep anticorrelation of the derived parameters ke1/ and kf, indicating that a change in is largely responsible for the behavior observed at lower concentrations of heparin. Apparent changes in kn are also observed (Fig. 6, top panel). These data suggest a mechanism by which heparin modestly increases nucleation while also strongly decreasing .
Figure 5.
Effects of heparin on tau244–372 fibril formation analyzed by ODE/ABC. (A) Titration of heparin sodium into 20 μM tau244–372. (Circles and shaded areas) Mean and standard deviation, respectively, of three independent experiments. Heparin increases the amount of fibrilized material up to a saturation point, then begins to slow fibrillization. (As in Fig. 3, lines represent data simulated using five parameter vectors randomly selected from 100 generated by ABC analysis.) (B) Rate distributions and histograms of derived parameters. Note strong changes in that are particularly obvious in the ke1/ distribution. To see this figure in color, go online.
Table 3.
Parameters Recovered from tau244–372 Aggregation Data by ODE/ABC Analysis
| [Heparin] (μg/mL) | log(ke1kn) | log(kn) | log(ke1kf) | log(kf) | log(kn/kf) | log(ke1/) |
|---|---|---|---|---|---|---|
| 7.5 | −8.93 ± 0.04 | −8.55 ± 0.04 | −6.77 ± 0.03 | −6.39 ± 0.03 | −2.16 ± 0.07 | −0.380 ± 0.002 |
| 15 | −8.46 ± 0.04 | −8.71 ± 0.04 | −6.79 ± 0.04 | −7.04 ± 0.05 | −1.67 ± 0.08 | 0.243 ± 0.009 |
| 30 | −8.18 ± 0.03 | −9.38 ± 0.04 | −6.82 ± 0.03 | −8.02 ± 0.07 | −1.36 ± 0.06 | 1.20 ± 0.05 |
| 60 | −8.59 ± 0.03 | −9.98 ± 0.06 | −7.20 ± 0.03 | −8.59 ± 0.09 | −1.39 ± 0.06 | 1.39 ± 0.07 |
Figure 6.
Heparin effects on ODE/ABC-derived parameters. (Top) Change in derived parameters in response to heparin. Most dramatic is the apparent decrease in dissociation of monomer from fibrils at higher concentrations of heparin. Refer to Table 3 for derived parameters from ABC fitting to the ODE model. (Bottom left) Linear extrapolation to [heparin] = 0 reveals an intrinsic log(KA) = −0.86. (Bottom right) Changes in calculated by linear extrapolation cannot account for complete lack of fibrillization observed experimentally. Data were simulated from five parameter sets selected from ABC analysis of 20 μM tau244–372 in the presence of 7.5 μg/mL, with adjusted to reflect the extrapolated value. To see this figure in color, go online.
As the concentration dependence of log(KA) on heparin is roughly linear under this regime, it is tempting to speculate that extrapolation back to [heparin] = 0 might reflect the intrinsic KA for fibril elongation. This treatment is commonly applied to chemical denaturation data to extract the free energy of protein folding, under the assumption that denaturation is a reversible, two-state process (62). The extrapolated value corresponds to a decrease in KA in going from 7.5 to 0 μg/mL of roughly half an order of magnitude (Fig. 6, lower left); according to our model, this modest change in is insufficient to account for the complete absence of fibrillization observed experimentally (Fig. 6, lower right). This suggests that heparin’s effect must stem from enhancement of both nucleation and elongation, and is consistent with a mechanism by which heparin promotes intermolecular contacts. Heparin could accelerate fibrillization by binding multiple copies of tau244–372 and relieving electrostatic repulsion, thereby increasing the local concentration of protein.
The behavior observed at higher concentrations of heparin is difficult to interpret under the conditions used here, but suggests that an excess could act to both inhibit nucleation processes and slow elongation. One possibility is that heparin stabilizes fibrils at higher concentrations, resulting in less fragmentation and therefore fewer nuclei. Another possibility is that, at higher stoichiometries, heparin could bind to tau in a weak (potentially nonspecific) mode that sequesters monomers and inhibits self-association. The latter explanation seems more likely, as previous studies have demonstrated that small species, as opposed to longer fibrils, are observed at high concentrations of inducers (48).
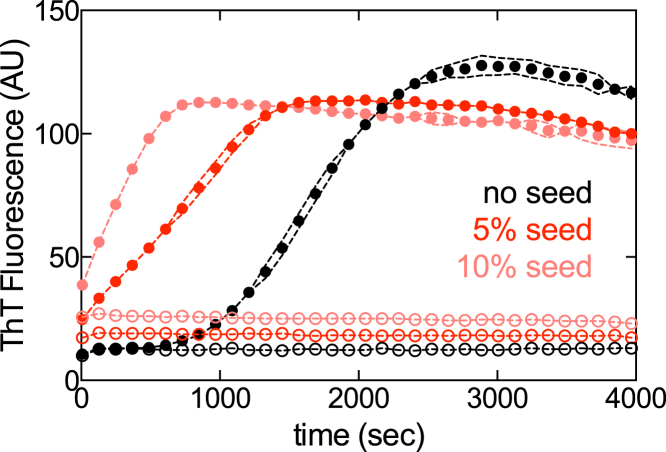
Regardless of the precise mechanism, our results clearly indicate that the effect of this inducer is not confined solely to enhancement of nucleation, as has been previously suggested (50, 53). As a direct test of this hypothesis, we carried out seeding experiments in the presence and absence of heparin: if its effects were restricted to kn alone, no additional heparin should be required to trigger assembly of tau244–372 so long as sufficient amounts of seeding material are present at the beginning of the reaction. As shown in Fig. 7, addition of up to 10 wt % preformed fibrils had no effect on soluble tau244–372 in the absence of heparin. Fibrillization in the presence of heparin exhibited the typical decrease in lag phase with increasing seed concentration, highlighting the requirement of heparin for elongation to continue.
Figure 7.
Seeding does not promote tau244–372 assembly in the absence of heparin. 5 μM tau244–372 was incubated in the presence (solid circles) or absence (open circles) of 7.5 μg/mL heparin sodium, including 0%, 5%, or 10% prefibrilized seed material. Data from one representative experiment is shown; (dotted lines) SD. To see this figure in color, go online.
Comparison to global analysis
Simultaneous fitting of aggregation measurements collected over a range of protein concentrations (or while varying some other experimental parameter) improves the accuracy and precision of least-squares approaches, and enables more robust model selection (7, 57). We therefore compared ABC analysis to local and global fitting using the N-E-F model (Eq. 2) and to global fitting implemented in the AmyloFit server (57). We first analyzed synthetic timecourses generated using the rate constants in Table 1 and protein concentrations ranging from 2.5 to 20 μM (Fig. S2). Compared to local fitting of the 10 μM trace alone, global fitting to Eq. 2 decreased the standard error in the recovered parameters by approximately twofold, and global fitting in AmyloFit produced parameters in good agreement with the latter. In a Bayesian framework, global analysis can be performed simply by looking for the overlap in the posterior distributions obtained from each of the individual datasets (Fig. S3). This overlap defines the range of parameters consistent with all the observed data, and more closely reflects the true distribution of parameters than any of the individual posterior distributions. Finally, we performed a similar comparison of local and global fitting based on experimental aggregation timecourses over a range of tau244–372 concentrations while maintaining a constant protein/heparin ratio (Fig. S4). Again, global fitting to Eq. 2 or using AmyloFit decreased standard errors of fitting by at least twofold relative to local analysis, and the overlap in the Bayesian posterior distributions (Fig. S5) further narrowed the range of model parameters consistent with our observations. ABC analysis thus easily allows for global analysis of data, with similar improvements in robustness and precision as conventional least-squares approaches.
Discussion
We have shown that fibril formation can be modeled well by a simple three-step model containing four rate constants, even when approximations are made to avoid the issue of tracking fibril lengths explicitly. The addition of reversibility to the elongation process was essential in this case, as it accommodates the experimentally observed variations in extent of fiber formation under different conditions. This model also displays the features of amyloid formation behavior predicted by well-established approaches such as assumed scaling (29) and the analytical N-E-F model (7). It is important to note that classical analyses are invaluable in the initial model building process.
We have also combined ABC analysis with ODE-based numerical modeling to approach the issue of calculating rate constants for amyloid formation processes. ABC provides a straightforward way to visualize the relationships among a given model’s parameters, changes in their values, and estimates of their uncertainties, all without the need for extensive mathematical expertise or closed-form analytical solutions. The theoretical analysis of amyloid formation is an active field of study, with recent advances including the development of a Hamiltonian framework that extends N-E-F-type approaches to describe a variety of nucleated polymerization models with a single master equation (63), and the use of Smoluchowski kinetics to quantitatively compare nucleated polymerization and nucleated conformational conversion paradigms (64). While elegant and clearly powerful, these analytical methods are each subject to their own simplifying assumptions and approximations. ODE models can be constructed to describe diverse fibrillization mechanisms from both the nucleated polymerization and conformational conversion families, and can be tractably and robustly fit to experimental data using ABC. Thus, ODE/ABC is not necessarily an alternative to analytical approaches or empirical sigmoidal fitting, but may serve as an excellent complementary technique, particularly when a model must be extended to account for new observations, or when a number of possible models are to be ranked and compared. We are able to recover relative changes in rate constants and identify which constant changed with confidence, despite the fact that precise values for the constants are not known.
Finally, we have used ODE/ABC to bring to light the fact that the effects of the inducer heparin on tau244–372 cannot be restricted to acceleration of the nucleation process. Our analysis suggests that at low concentrations, heparin exerts its effects by enhancing nucleation and lowering the dissociation rate of monomer from fibril ends. At saturating concentrations, it may bind nonspecifically to monomeric protein and inhibit primary nucleation and elongation. Additionally, heparin’s involvement in elongation processes is directly demonstrable through seeding experiments in the presence and absence of inducer, a finding consistent with recent single-molecule observations of tau aggregation (65). In that case, the authors propose a conformational conversion mechanism without secondary nucleation, while a secondary nucleation process (modeled as fragmentation in our simple nucleated polymerization model) was required to adequately describe our data. Bayesian model comparison based on ODE/ABC analysis could help reconcile these observations in future studies.
The techniques developed here could be of particular use in the screening of potential drugs against amyloid formation, where the ability to identify the mechanistic effects of small molecule inhibitors is of great importance. They additionally lay the groundwork for the use of Bayesian model selection methods to rank models of amyloid formation, facilitating quantitative comparisons of the numerous models for amyloid formation that have been proposed.
Author Contributions
E.N.-W. and A.N. designed research, analyzed data, and wrote the article, and E.N.-W. performed research.
Acknowledgments
We thank Profs. Elizabeth Rhoades, Ursula Jakob, Jason Gestwicki, and Hong Qian for helpful discussions.
We gratefully acknowledge support from the University of Washington Royalty Research Fund, and the Brady Fund for Natural Products Research (UW Medicinal Chemistry). This publication was supported by the National Center for Advancing Translational Sciences of the National Institutes of Health under award No. KL2TR000421.
Editor: James Shorter.
Footnotes
Five figures and five tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30106-6.
Supporting Material
References
- 1.Koo E.H., Lansbury P.T., Jr., Kelly J.W. Amyloid diseases: abnormal protein aggregation in neurodegeneration. Proc. Natl. Acad. Sci. USA. 1999;96:9989–9990. doi: 10.1073/pnas.96.18.9989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Glabe C.G. Common mechanisms of amyloid oligomer pathogenesis in degenerative disease. Neurobiol. Aging. 2006;27:570–575. doi: 10.1016/j.neurobiolaging.2005.04.017. [DOI] [PubMed] [Google Scholar]
- 3.Vendruscolo M., Knowles T.P.J., Dobson C.M. Protein solubility and protein homeostasis: a generic view of protein misfolding disorders. Cold Spring Harb. Perspect. Biol. 2011;3:a010454. doi: 10.1101/cshperspect.a010454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Eichner T., Radford S.E. A diversity of assembly mechanisms of a generic amyloid fold. Mol. Cell. 2011;43:8–18. doi: 10.1016/j.molcel.2011.05.012. [DOI] [PubMed] [Google Scholar]
- 5.Tobacman L.S., Korn E.D. The kinetics of actin nucleation and polymerization. J. Biol. Chem. 1983;258:3207–3214. [PubMed] [Google Scholar]
- 6.Oosawa F., Asakura S. Academic Press; New York: 1975. Thermodynamics of the Polymerization of Protein. [Google Scholar]
- 7.Knowles T.P.J., Waudby C.A., Dobson C.M. An analytical solution to the kinetics of breakable filament assembly. Science. 2009;326:1533–1537. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 8.Aguzzi A. Understanding the diversity of prions. Nat. Cell Biol. 2004;6:290–292. doi: 10.1038/ncb0404-290. [DOI] [PubMed] [Google Scholar]
- 9.Toyama B.H., Kelly M.J.S., Weissman J.S. The structural basis of yeast prion strain variants. Nature. 2007;449:233–237. doi: 10.1038/nature06108. [DOI] [PubMed] [Google Scholar]
- 10.Tanaka M., Collins S.R., Weissman J.S. The physical basis of how prion conformations determine strain phenotypes. Nature. 2006;442:585–589. doi: 10.1038/nature04922. [DOI] [PubMed] [Google Scholar]
- 11.Collins S.R., Douglass A., Weissman J.S. Mechanism of prion propagation: amyloid growth occurs by monomer addition. PLoS Biol. 2004;2:e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ruschak A.M., Miranker A.D. Fiber-dependent amyloid formation as catalysis of an existing reaction pathway. Proc. Natl. Acad. Sci. USA. 2007;104:12341–12346. doi: 10.1073/pnas.0703306104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Serio T.R., Cashikar A.G., Lindquist S.L. Nucleated conformational conversion and the replication of conformational information by a prion determinant. Science. 2000;289:1317–1321. doi: 10.1126/science.289.5483.1317. [DOI] [PubMed] [Google Scholar]
- 14.Lee J., Culyba E.K., Kelly J.W. Amyloid-β forms fibrils by nucleated conformational conversion of oligomers. Nat. Chem. Biol. 2011;7:602–609. doi: 10.1038/nchembio.624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wei L., Jiang P., Pervushin K. The molecular basis of distinct aggregation pathways of islet amyloid polypeptide. J. Biol. Chem. 2011;286:6291–6300. doi: 10.1074/jbc.M110.166678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Thakur A.K., Jayaraman M., Wetzel R. Polyglutamine disruption of the huntingtin exon 1 N-terminus triggers a complex aggregation mechanism. Nat. Struct. Mol. Biol. 2009;16:380–389. doi: 10.1038/nsmb.1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nilsson M.R. Techniques to study amyloid fibril formation in vitro. Methods. 2004;34:151–160. doi: 10.1016/j.ymeth.2004.03.012. [DOI] [PubMed] [Google Scholar]
- 18.Frieden C. Protein aggregation processes: in search of the mechanism. Protein Sci. 2007;16:2334–2344. doi: 10.1110/ps.073164107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Murphy R.M. Kinetics of amyloid formation and membrane interaction with amyloidogenic proteins. Biochim. Biophys. Acta. 2007;1768:1923–1934. doi: 10.1016/j.bbamem.2006.12.014. [DOI] [PubMed] [Google Scholar]
- 20.Miranker A.D. Unzipping the mysteries of amyloid fiber formation. Proc. Natl. Acad. Sci. USA. 2004;101:4335–4336. doi: 10.1073/pnas.0401163101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wetzel R. Kinetics and thermodynamics of amyloid fibril assembly. Acc. Chem. Res. 2006;39:671–679. doi: 10.1021/ar050069h. [DOI] [PubMed] [Google Scholar]
- 22.Crespo R., Rocha F.A., Martins P.M. A generic crystallization-like model that describes the kinetics of amyloid fibril formation. J. Biol. Chem. 2012;287:30585–30594. doi: 10.1074/jbc.M112.375345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gillam J.E., MacPhee C.E. Modelling amyloid fibril formation kinetics: mechanisms of nucleation and growth. J. Phys. Condens. Matter. 2013;25:373101. doi: 10.1088/0953-8984/25/37/373101. [DOI] [PubMed] [Google Scholar]
- 24.Buell A.K., Dobson C.M., Knowles T.P.J. The physical chemistry of the amyloid phenomenon: thermodynamics and kinetics of filamentous protein aggregation. Essays Biochem. 2014;56:11–39. doi: 10.1042/bse0560011. [DOI] [PubMed] [Google Scholar]
- 25.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. From macroscopic measurements to microscopic mechanisms of protein aggregation. J. Mol. Biol. 2012;421:160–171. doi: 10.1016/j.jmb.2012.02.031. [DOI] [PubMed] [Google Scholar]
- 26.Morris A.M., Watzky M.A., Finke R.G. Protein aggregation kinetics, mechanism, and curve-fitting: a review of the literature. Biochim. Biophys. Acta. 2009;1794:375–397. doi: 10.1016/j.bbapap.2008.10.016. [DOI] [PubMed] [Google Scholar]
- 27.Xue W.-F., Homans S.W., Radford S.E. Systematic analysis of nucleation-dependent polymerization reveals new insights into the mechanism of amyloid self-assembly. Proc. Natl. Acad. Sci. USA. 2008;105:8926–8931. doi: 10.1073/pnas.0711664105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee C.-C., Nayak A., McRae G.J. A three-stage kinetic model of amyloid fibrillation. Biophys. J. 2007;92:3448–3458. doi: 10.1529/biophysj.106.098608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Flyvbjerg H., Jobs E., Leibler S. Kinetics of self-assembling microtubules: an “inverse problem” in biochemistry. Proc. Natl. Acad. Sci. USA. 1996;93:5975–5979. doi: 10.1073/pnas.93.12.5975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hoops S., Sahle S., Kummer U. COPASI—a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- 31.Li H., Cao Y., Gillespie D.T. Algorithms and software for stochastic simulation of biochemical reacting systems. Biotechnol. Prog. 2008;24:56–61. doi: 10.1021/bp070255h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hucka M., Finney A., Wang J. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics. 2003;19:524–531. doi: 10.1093/bioinformatics/btg015. [DOI] [PubMed] [Google Scholar]
- 33.Hucka M., Finney A., Kitano H. Evolving a lingua franca and associated software infrastructure for computational systems biology: the Systems Biology Markup Language (SBML) project. Syst. Biol. (Stevenage) 2004;1:41–53. doi: 10.1049/sb:20045008. [DOI] [PubMed] [Google Scholar]
- 34.Tavaré S., Balding D.J., Donnelly P. Inferring coalescence times from DNA sequence data. Genetics. 1997;145:505–518. doi: 10.1093/genetics/145.2.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Owen J., Wilkinson D.J., Gillespie C.S. Likelihood free inference for Markov processes: a comparison. Stat. Appl. Genet. Mol. Biol. 2015;14:189–209. doi: 10.1515/sagmb-2014-0072. [DOI] [PubMed] [Google Scholar]
- 36.Toni T., Welch D., Stumpf M.P. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface. 2009;6:187–202. doi: 10.1098/rsif.2008.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Toni T., Stumpf M.P.H. Simulation-based model selection for dynamical systems in systems and population biology. Bioinformatics. 2010;26:104–110. doi: 10.1093/bioinformatics/btp619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hines K.E. A primer on Bayesian inference for biophysical systems. Biophys. J. 2015;108:2103–2113. doi: 10.1016/j.bpj.2015.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liepe J., Barnes C., Stumpf M.P.H. ABC-SysBio--approximate Bayesian computation in PYTHON with GPU support. Bioinformatics. 2010;26:1797–1799. doi: 10.1093/bioinformatics/btq278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liepe J., Kirk P., Stumpf M.P.H. A framework for parameter estimation and model selection from experimental data in systems biology using approximate Bayesian computation. Nat. Protoc. 2014;9:439–456. doi: 10.1038/nprot.2014.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ramachandran G., Udgaonkar J.B. Mechanistic studies unravel the complexity inherent in tau aggregation leading to Alzheimer’s disease and the tauopathies. Biochemistry. 2013;52:4107–4126. doi: 10.1021/bi400209z. [DOI] [PubMed] [Google Scholar]
- 42.Lee G., Leugers C.J. Tau and tauopathies. Prog. Mol. Biol. Transl. Sci. 2012;107:263–293. doi: 10.1016/B978-0-12-385883-2.00004-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hasegawa M. Molecular mechanisms in the pathogenesis of Alzheimer’s disease and tauopathies-prion-like seeded aggregation and phosphorylation. Biomolecules. 2016;6:24. doi: 10.3390/biom6020024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pérez M., Valpuesta J.M., Avila J. Polymerization of tau into filaments in the presence of heparin: the minimal sequence required for tau-tau interaction. J. Neurochem. 1996;67:1183–1190. doi: 10.1046/j.1471-4159.1996.67031183.x. [DOI] [PubMed] [Google Scholar]
- 45.Goedert M., Jakes R., Crowther R.A. Assembly of microtubule-associated protein tau into Alzheimer-like filaments induced by sulphated glycosaminoglycans. Nature. 1996;383:550–553. doi: 10.1038/383550a0. [DOI] [PubMed] [Google Scholar]
- 46.Kampers T., Friedhoff P., Mandelkow E. RNA stimulates aggregation of microtubule-associated protein tau into Alzheimer-like paired helical filaments. FEBS Lett. 1996;399:344–349. doi: 10.1016/s0014-5793(96)01386-5. [DOI] [PubMed] [Google Scholar]
- 47.Barghorn S., Biernat J., Mandelkow E. Purification of recombinant tau protein and preparation of Alzheimer-paired helical filaments in vitro. Methods Mol. Biol. 2005;299:35–51. doi: 10.1385/1-59259-874-9:035. [DOI] [PubMed] [Google Scholar]
- 48.Carlson S.W., Branden M., Gamblin T.C. A complex mechanism for inducer mediated tau polymerization. Biochemistry. 2007;46:8838–8849. doi: 10.1021/bi700403a. [DOI] [PubMed] [Google Scholar]
- 49.Barghorn S., Mandelkow E. Toward a unified scheme for the aggregation of tau into Alzheimer paired helical filaments. Biochemistry. 2002;41:14885–14896. doi: 10.1021/bi026469j. [DOI] [PubMed] [Google Scholar]
- 50.Ramachandran G., Udgaonkar J.B. Understanding the kinetic roles of the inducer heparin and of rod-like protofibrils during amyloid fibril formation by Tau protein. J. Biol. Chem. 2011;286:38948–38959. doi: 10.1074/jbc.M111.271874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kuret J., Chirita C.N., Zhong Q. Pathways of tau fibrillization. Biochim. Biophys. Acta. 2005;1739:167–178. doi: 10.1016/j.bbadis.2004.06.016. [DOI] [PubMed] [Google Scholar]
- 52.Gustke N., Trinczek B., Mandelkow E. Domains of tau protein and interactions with microtubules. Biochemistry. 1994;33:9511–9522. doi: 10.1021/bi00198a017. [DOI] [PubMed] [Google Scholar]
- 53.Friedhoff P., von Bergen M., Mandelkow E. A nucleated assembly mechanism of Alzheimer paired helical filaments. Proc. Natl. Acad. Sci. USA. 1998;95:15712–15717. doi: 10.1073/pnas.95.26.15712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Elbaum-Garfinkle S., Cobb G., Rhoades E. Tau mutants bind tubulin heterodimers with enhanced affinity. Proc. Natl. Acad. Sci. USA. 2014;111:6311–6316. doi: 10.1073/pnas.1315983111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Watzky M.A., Finke R.G. Transition metal nanocluster formation kinetic and mechanistic studies. A new mechanism when hydrogen is the reductant: slow, continuous nucleation and fast autocatalytic surface growth. J. Am. Chem. Soc. 1997;119:10382–10400. [Google Scholar]
- 56.Carulla N., Caddy G.L., Dobson C.M. Molecular recycling within amyloid fibrils. Nature. 2005;436:554–558. doi: 10.1038/nature03986. [DOI] [PubMed] [Google Scholar]
- 57.Meisl G., Kirkegaard J.B., Knowles T.P.J. Molecular mechanisms of protein aggregation from global fitting of kinetic models. Nat. Protoc. 2016;11:252–272. doi: 10.1038/nprot.2016.010. [DOI] [PubMed] [Google Scholar]
- 58.Donaldson J.R., Schnabel R.B. Computational experience with confidence regions and confidence intervals for nonlinear least squares. Technometrics. 1987;29:67–82. [Google Scholar]
- 59.Suk J.Y., Zhang F., Kelly J.W. Heparin accelerates gelsolin amyloidogenesis. Biochemistry. 2006;45:2234–2242. doi: 10.1021/bi0519295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Iannuzzi C., Irace G., Sirangelo I. The effect of glycosaminoglycans (GAGs) on amyloid aggregation and toxicity. Molecules. 2015;20:2510–2528. doi: 10.3390/molecules20022510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Motamedi-Shad N., Monsellier E., Chiti F. Amyloid formation by the model protein muscle acylphosphatase is accelerated by heparin and heparan sulphate through a scaffolding-based mechanism. J. Biochem. 2009;146:805–814. doi: 10.1093/jb/mvp128. [DOI] [PubMed] [Google Scholar]
- 62.Pace C.N., Shaw K.L. Linear extrapolation method of analyzing solvent denaturation curves. Proteins. 2000;41(Suppl 4):1–7. doi: 10.1002/1097-0134(2000)41:4+<1::aid-prot10>3.3.co;2-u. [DOI] [PubMed] [Google Scholar]
- 63.Michaels T.C.T., Cohen S.I.A., Knowles T.P.J. Hamiltonian dynamics of protein filament formation. Phys. Rev. Lett. 2016;116:038101. doi: 10.1103/PhysRevLett.116.038101. [DOI] [PubMed] [Google Scholar]
- 64.Schreck J.S., Yuan J.-M. A kinetic study of amyloid formation: fibril growth and length distributions. J. Phys. Chem. B. 2013;117:6574–6583. doi: 10.1021/jp401586p. [DOI] [PubMed] [Google Scholar]
- 65.Shammas S.L., Garcia G.A., Klenerman D. A mechanistic model of tau amyloid aggregation based on direct observation of oligomers. Nat. Commun. 2015;6:7025. doi: 10.1038/ncomms8025. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.