Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Feb 17;139(10):3697–3705. doi: 10.1021/jacs.6b11717

Bulk Heterojunction Morphologies with Atomistic Resolution from Coarse-Grain Solvent Evaporation Simulations

Riccardo Alessandri †,‡, Jaakko J Uusitalo †,‡, Alex H de Vries †,‡, Remco W A Havenith †,§,∥, Siewert J Marrink †,‡,*
PMCID: PMC5355903  PMID: 28209056

Abstract

graphic file with name ja-2016-117179_0006.jpg

Control over the morphology of the active layer of bulk heterojunction (BHJ) organic solar cells is paramount to achieve high-efficiency devices. However, no method currently available can predict morphologies for a novel donor–acceptor blend. An approach which allows reaching relevant length scales, retaining chemical specificity, and mimicking experimental fabrication conditions, and which is suited for high-throughput schemes has been proven challenging to find. Here, we propose a method to generate atom-resolved morphologies of BHJs which conforms to these requirements. Coarse-grain (CG) molecular dynamics simulations are employed to simulate the large-scale morphological organization during solution-processing. The use of CG models which retain chemical specificity translates into a direct path to the rational design of donor and acceptor compounds which differ only slightly in chemical nature. Finally, the direct retrieval of fully atomistic detail is possible through backmapping, opening the way for improved quantum mechanical calculations addressing the charge separation mechanism. The method is illustrated for the poly(3-hexyl-thiophene) (P3HT)–phenyl-C61-butyric acid methyl ester (PCBM) mixture, and found to predict morphologies in agreement with experimental data. The effect of drying rate, P3HT molecular weight, and thermal annealing are investigated extensively, resulting in trends mimicking experimental findings. The proposed methodology can help reduce the parameter space which has to be explored before obtaining optimal morphologies not only for BHJ solar cells but also for any other solution-processed soft matter device.

Introduction

Organic solar cells (OSCs)1 are among the new generation photovoltaic (PV) technologies which could be employed to convert solar energy to electricity. Their main advantage over more traditional PV cells is the solution processability of the layers that compose the device. Moreover, the potential mechanical flexibility and low weight of organic PV panels may enable the introduction of innovative new products.2,3 The most efficient OSCs require a bulk heterojunction (BHJ),4,5 an active layer composed of intimately intermixed electron acceptors and electron donors. Not only their electronic properties6 but also the morphology of the active layer7,8 will determine the final device efficiency. These two different but entangled aspects of a chosen donor–acceptor system along with the many degrees of freedom offered by organic materials translate into a vast multiparameter optimization space which, despite extensive research efforts, has not yet led to efficiencies which can compete with inorganic PV technologies. Design principles for bringing BHJ solar cells to a substantially higher performance level are still sought after.9

In OSCs the absorption of light leads to the formation of excitons. These have to dissociate at a donor–acceptor interface before the resultant free carriers can be transported to the electrodes. A large donor–acceptor interfacial area must therefore be present for efficient exciton dissociation;10 second, both phases need to be continuous and well-connected to the respective electrode for adequate charge collection. Furthermore, a high degree of crystallinity is usually beneficial, as it increases charge mobility, while the active layer needs to be at least ∼80–100 nm thick so as to absorb an adequate amount of light. From these conditions stems the need for a bicontinuous interpenetrating network of donor and acceptor phases. Such networks, usually achieved by spin coating or doctor blading, are generally believed to be a kinetically trapped state, as they are formed during the rapid solidification of a thin layer of solution cast on a substrate.11 Many processing conditions11−15 have been found critical for the resulting morphology, but determining a priori those which will lead to an optimal morphology when the two constituting materials are modified is still not possible.7,9

A number of techniques have been employed to acquire structural information on BHJs. Atomic force microscopy,11,12,16 and transmission17−19 and scanning16 electron microscopy have been used to image BHJs but provide only limited insights about the nature of the interpenetrating network. Electron tomography has therefore been developed19 to study the 3D morphology. However, the inherently poor contrast due to the weak electron scattering of organic materials leads to a limited and complex interpretation of the 3D-reconstructed morphology. Techniques used to quantify the crystallinity of BHJs are grazing-incidence X-ray diffraction (GIXD)20 and grazing-incidence small-/wide-angle X-ray scattering (GISAXS/GIWAXS).21 The valuable information provided by these techniques represents, however, averages over the irradiated area of the sample, thus preventing real space localization of nanocrystallites.

Computational modeling provides atomistic detail and thereby has the potential to bridge the gap between experimental and molecular length scales. In particular, coarse-grain (CG) molecular dynamics (MD) simulations are often employed to model BHJs,22−26 being able to capture the morphology at relevant length scales while still retaining a molecular description (as opposed to Monte Carlo simulated annealing27−29 or mean field30 approaches where that is lost). However, CG models developed to date are not readily transferable.22−25 This hinders their potential use within a high-throughput screening scheme aimed at optimizing the morphology of a novel donor–acceptor blend. Furthermore, CG models currently applied in this field often22,23,26 simplify the description of donor and acceptor molecules too severely: while this allows reaching length scales which are comparable to real device thicknesses,26 the loss of detail hampers the discrimination of different donor (acceptor) structures and does not allow for direct retrieval of atom-resolved structural information. Such structures are needed as input for higher level of theory, e.g., quantum mechanical (QM), calculations31−33 that address the electronic states involved in the charge separation. Finally, simulated annealing is usually employed24−26 to obtain CG morphologies. This does not reflect the morphological evolution taking place during the solution processing of BHJs, hence making the link between experimental fabrication conditions and simulations more elusive. Importantly, Lee and Pao have recently developed34 a method to generate morphologies which remedy this: during a standard MD simulation, the solvent is slowly removed, thus simulating the experimental evaporation process. The evolution of the BHJ morphology during solution processing can therefore be studied, and a direct link to experimental conditions can be made.

In the present work, we employ CG models which retain a sizable degree of chemical specificity to simulate the large scale organization of polymer–fullerene systems during solution processing, which results in a predictive tool for BHJ morphologies. The method follows the one developed by Lee and Pao,34 but differs from it in the nature of the CG models employed, namely finer CG models based on the Martini CG force field.35 The chemical specificity of this force field implies the possibility to use it for rational design of donor (acceptor) compounds which differ only slightly in chemical nature. Moreover, Martini gives ready access to fully atomistic detail through backmapping,36 opening the way for improved QM calculations. As a first case study, we chose to simulate the poly(3-hexyl-thiophene) (P3HT)–phenyl-C61-butyric acid methyl ester (PCBM) mixture. The validity of the method is assessed by comparing the outcome of simulations to a variety of experimental data available for this well-studied system. Simulations predict morphologies in agreement with published data in the literature. The effect of drying rate, polymer molecular weight, and thermal annealing are investigated extensively, resulting in trends in accordance with experimental observations. Finally, the atomistic detail of the whole blend is directly retrieved by means of backmapping. Together, the results presented in this contribution show the potential of the proposed methodology to get insight into larger scale morphological organization while, at the same time, obtaining atom-resolved structural information on, for example, donor–acceptor interfaces where such details are vital to solve the puzzle of the charge separation mechanism.

Results and Discussion

Evolution of Bulk Heterojunction Morphologies during Simulated Solution Processing

Solvent evaporation CG MD simulations were performed using newly developed Martini37 CG models of P3HT, PCBM, and chlorobenzene (CB). The atomistic structures along with schematic representations of the CG models are presented in Figure 1. On average, 4 atoms are mapped to one CG particle, while bond, angle, and dihedral potentials are used to have the CG models reproduce the structure and flexibility of the corresponding atomistic models. Interactions have been calibrated by using experimental free energy of transfer data as reference. A detailed description of the CG models, atomistic models which aided the parametrization and validation of the CG models, as well as the parametrization and validation procedures themselves are presented in the Methods section and in the Supporting Information.

Figure 1.

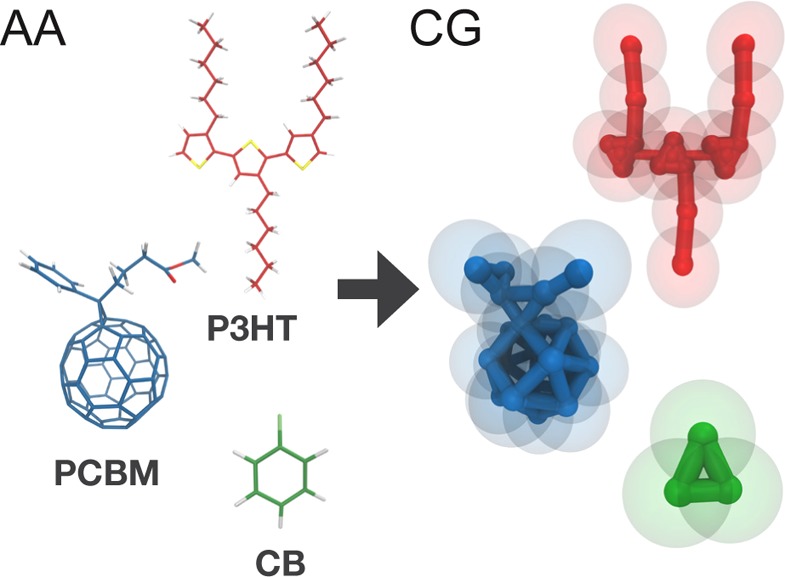
Figure 1

Open in a new tab

All-atom structures (left) and corresponding coarse-grain models (right) for P3HT (in red; a trimer is shown), PCBM (in blue), and CB (in green). The connectivity between the coarse-grain interaction sites is highlighted, while the actual size of the beads is shown with semitransparent spheres.

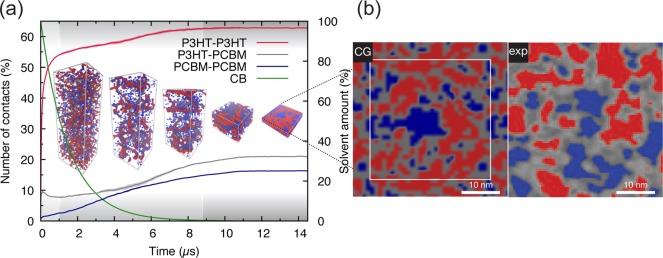
In Figure 2, a prototypical solvent evaporation simulation is illustrated (see also video in the Supporting Information), and the resulting BHJ morphology compared to experimental data from ref (38). In particular, Figure 2b shows a comparison between the morphology obtained via an evaporation simulation (where the molecular weight (MW) of P3HT is 8 kDa) and an energy-filtered scanning electron microscopy (EFSEM) image taken by Masters et al.38 of an as-cast P3HT–PCBM blend (P3HT MW of 54 kDa) spin-coated from CB. The P3HT–PCBM weight ratio is 1:0.8 in both cases. The experimental EFSEM image contains gray zones which Masters et al. ascribed to mixed polymer–fullerene phases.38 In these areas, fullerene and P3HT are close to each other and give rise to an average signal, which thus cannot be resolved. By contrast, simulations allow resolution of structures up to the level of single CG particles (the CG particle-resolved morphology is shown in Figure S1a). To account for this discrepancy, and for the escape depth of secondary electrons from P3HT (found to be between around 20–30 Å),38 a ∼2.5 nm thick layer taken from the CG morphology has been spatially discretized in polymer, fullerene, and mixed phases, following the procedure outlined in the Methods section. A comparison of the resulting image (left-hand side of Figure 2b) to the experimental one (right-hand side of Figure 2b) suggests that obtained donor and acceptor domain sizes are in qualitative agreement with the experimental ones. However, it is important to stress that the close agreement between the experimentally and computationally obtained morphologies is somewhat unexpected, given the difference in processing conditions. A first difference is in the way the solvent evaporation takes place. In spin coating, the solvent evaporates from the surface of the blend, whereas in our simulations solvent is taken out of the system randomly. The latter approach leads to a more uniform distribution of the molecular components along the sample normal. A revised protocol in which surface evaporation is taken into account is currently being developed to quantify this effect in future studies. A more serious concern is the considerable differences in time and length scales. Experimentally, solvent evaporation takes place on the time scale of seconds, whereas the simulations are necessary limited to the sub-millisecond range. The length scale of the experimental samples is also larger, with typical sample areas of ∼1 cm2, compared to 900 nm2 in the simulated samples. Note that the polymer chains in the simulation are smaller than those used in experiment (8 kDa vs 30–50 kDa), compensating, at least to some extent, for the shorter time scale. Apparently, the primary driving forces governing morphology formation in real blends act on time and length scales accessible by our simulations. Further details about these driving forces during the evaporation process are discussed below.

Figure 2.

Figure 2

Open in a new tab

Simulation of the evolution of a P3HT:PCBM bulk heterojunction during solution-processing (a) and comparison to experimental data (b). The evolution of P3HT-P3HT, P3HT-PCBM, and PCBM–PCBM contacts and of the solvent amount during drying are plotted (a), and snapshots at different times during the simulation are shown (P3HT chains are rendered in red while PCBM molecules are in blue; solvent molecules are not shown for clarity). The three stages of BHJ morphology evolution (see text) are indicated with different shades of gray. (b) Visual comparison between a spatially discretized morphology obtained via the solvent evaporation protocol (left-hand side; the thin white square shows the repeating unit cell) and a spin-coated blend imaged by EFSEM (right-hand side; close up of Figure 7c of ref (38), reproduced under the Creative Commons Attribution 4.0 International License).

The evolution of the morphology during the evaporation can be followed by computing the number of P3HT–P3HT, P3HT–PCBM, and PCBM–PCBM contacts during the drying process. These have been calculated as described in detail in the Methods section and are plotted in Figure 2a. Three evaporation stages can be distinguished. Within the first microsecond, a first phase where molecules are still in solution and thus relatively free to diffuse can be identified: during this phase, a substantial increase in the number of P3HT-P3HT contacts due to the aggregation of P3HT chains to form ordered nanostructures (which will be discussed more extensively in the following sections) is observed. Consequently, PCBM–P3HT contacts initially decrease as PCBM molecules are deprived of P3HT neighboring molecules (as these aggregate). Fullerene molecules are found to be considerably more soluble in CB and do not show aggregation propensity. This is consistent with the experimental solubility of P3HT in CB (∼16 mg/mL for P3HT with MW of ∼65 kDa) being lower than the one of PCBM (∼60 mg/mL).39 In the second stage, which starts already after 1 μs when the amount of solvent is less than 60% of the initial amount, the diffusion processes become much slower (time scale of hundreds of nanoseconds to microseconds) due to the increased size of P3HT nanostructures and the ever-decreasing quantity of solvent, which starts to reduce dramatically the mobility of the molecules. As a consequence, in this phase the number of contacts between all compounds steadily increases. These aggregation processes become gradually more stagnant and essentially stop when the solvent weight content is about 1%. At this point, in the third and final stage, the blend is in an almost frozen state where the free energy barriers to even minimal rearrangement are very high. These observations agree with the drying dynamics observed experimentally by GIXD and GIWAXS/GISAXS during spin-coating40 or printing.41,42 The studies follow the evolution of the P3HT X-ray scattering peaks. Four drying stages are commonly individuated: a first stage in which no scattering is detected and where thus the molecules are considered being dispersed in solution; a second stage in which the P3HT crystals start to nucleate and grow; a third stage, also called the solvent swollen glassy state,42 where the mobility of the molecules is already compromised by the low amount of solvent and where, therefore, no new crystals can form but the existing ones continue drying; a last stage where the film is practically dry and close to the final structure. In the present simulations, aggregation of P3HT is observed from the beginning, which seems not to be consistent with experimental findings. However, the aggregation of P3HT molecules may be happening earlier also in experiments, but the P3HT crystals have to reach a certain size in order to be detected by X-ray scattering techniques. Moreover, the initial P3HT concentration in the simulations (∼39 mg mL–1) is higher than the one commonly used in experiments (∼15 mg mL–1), positioning P3HT already beyond the solubility limit.

In summary, the driving force for the (modest) phase separation observed during the solvent evaporation simulation is the self-organization propensity of P3HT. This process can be hampered by a faster evaporation and/or entanglement of polymer chains, as explored in the next sections. It is crucial also to realize that, due to the relatively good affinity of PCBM and P3HT, large-scale phase separation does not occur.

Effect of Drying Rate and Polymer Molecular Weight

Slow drying, also called solvent annealing43 or solvent-assisted annealing,19 has been shown to allow for structure reorganization, leading the P3HT:PCBM blend to approach a degree of phase separation closer to thermodynamic equilibrium. Lower MW (up to 10 kDa) P3HT has been found to have a stronger tendency to phase separate during the solvent evaporation process44 than higher MW fractions, likely due to an increased capability to crystallize. To investigate the effect of drying rate and polymer length on the as-cast morphologies, we performed two additional sets of simulations: one in which the rate of solvent evaporation was varied, and another where this was kept fixed while varying the polymer MW.

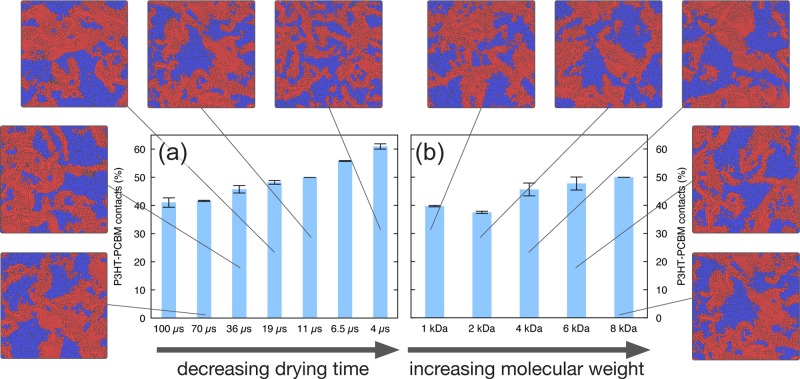
To quantify the degree of phase separation, the number of P3HT–PCBM contacts in the dried morphologies has been computed. The number of polymer–fullerene contacts correlates with the extent of donor–acceptor interface present in the blend. The minimal amount of polymer–fullerene contacts is obtained for a planar heterojunction morphology where only one interface is present (see Figure S10); on the opposite end, the maximum amount of contacts is found in a completely intermixed morphology. This has been built as a random mixture, as explained in more detail in the Supporting Information. The numbers of contacts in the planar heterojunction and intermixed extremes, respectively, have been used as references to normalize the computed fraction of P3HT-PCBM contacts. Using this scale, Figure 3a and 3b show how the number of polymer–fullerene contacts varies with the drying rate and with the polymer molecular weight, respectively. In the latter case, simulations with the same number of P3HT monomers are compared.

Figure 3.

Figure 3

Open in a new tab

Effect of the drying rate and polymer molecular weight on the morphology. Normalized number of P3HT–PCBM contacts expressed in percentage (where 0 is taken as the number of contacts in a planar heterojunction and 100 is the one computed for a finely intermixed morphology) are shown as blue bars. Top views of representative morphologies are shown for the various drying rates (increasing drying rate from bottom left to top, clockwise) and for various polymer molecular weights (increasing polymer weight from top to bottom right, clockwise).

Faster drying leads to less phase separation. Faster evaporation does not allow for polymer crystals to grow, which therefore end up having smaller dimensions (and, as a consequence, PCBM domains remain smaller as well). This result is consistent with the hypothesis that P3HT–PCBM blends are an example of blends which do not (liquid–liquid or solid–liquid) phase separate considerably during spin coating.30 Even though fast drying of a P3HT:PCBM mixture leads to an intimately mixed blend, larger-scale phase separation would occur on a longer time scale. Simulations also predict that longer polymeric chains lead to less phase-separated morphologies (Figure 3b). Slower diffusion and more chain entanglement decelerate the aggregation of longer polymer chains. However, the trend is not so pronounced, which may be due to the limited range of MWs considered in the present contribution (1 to 8 kDa). In fact, Liu et al.44 reported that blends with a P3HT MW up to 10 kDa practically behave indistinguishably during spin coating.

Thermal Annealing and Crystallinity of the Morphologies

P3HT–PCBM solar cells require an annealing step in order to reach their full potential.45 The improved power conversion efficiency is well documented and has been shown to involve polymer crystallization—which increases optical absorption and improves charge transport—and optimized phase segregation, leading to more efficient charge separation. The width of polymer and fullerene domains is known to increase upon annealing, up to dimensions in the 10–20 nm range.21,46,47 Various nanoscopic views on the thermal annealing process have been proposed. The mobility of PCBM molecules or small aggregates has been demonstrated by several studies.48−50 It is often concluded to result from crystallization of P3HT disordered domains which expel fullerene loading.44,48−50 In particular, diffusion of fullerenes appears to occur only through the disordered regions of P3HT.50 Conjectures about polymer crystal growth during annealing inhibiting18 or competing with21 the formation of large fullerene domains are also found in the literature. In order to investigate the effect of thermal annealing on the obtained morphologies, a thermal annealing protocol has been applied by carrying out MD simulations with an increased temperature, as described in detail in the Methods section.

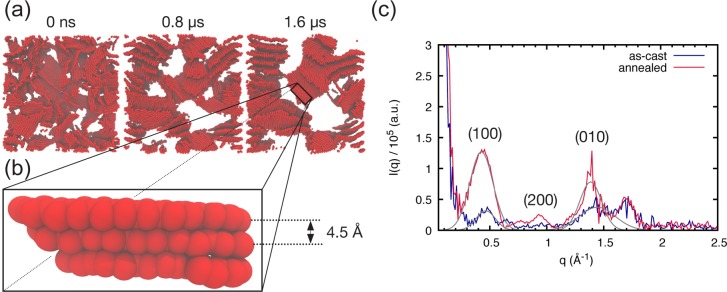
Figure 4a shows three snapshots taken at different times during an annealing simulation for a P3HT–PCBM blend (MWP3HT = 4 kDa). Only P3HT backbones are shown to highlight the increased ordering in the P3HT phase upon annealing. The voids between P3HT sheets are, in general, occupied by P3HT side chains, while the bigger white areas denote the presence of PCBM domains (compare to Figure S2). Chain alignment increases dramatically upon annealing. Domain segregation is also observed, leading to sharper interfaces and larger domains. These results are not surprising and are in line with experimental findings. When P3HT is given more time for reorganization, crystallinity increases and domain segregation is enhanced.45 The simulations further provide insight into the driving force for the morphology evolution upon annealing. Following what is also observed during the solvent evaporation simulations, P3HT drives the domain segregation as P3HT crystals grow and therefore expel PCBM molecules. No breaking of P3HT stacks is observed, corroborating the hypothesis that diffusion of fullerene takes place through amorphous domains.50

Figure 4.

Figure 4

Open in a new tab

Morphology evolution during thermal annealing and associated computed scattering curves. Snaphots at different times during the annealing process (a) where only the P3HT backbones are shown. White areas denote the location of P3HT side chains or PCBM domains (compare to Figure S2). A zoom in on the blend reveals a stack of 3 P3HT chains (b) reporting the observed CG stacking distance of 4.5 Å. (c) The corresponding computed scattering profiles are shown; Gaussian fits to the (100) and (010) peaks are shown in gray.

Scattering curves have been computed as described in the Methods section and are shown in Figure 4c. Note that only thiophene rings are considered in the simulated scattering curves. Upon annealing, the intensities of the (100) (or lamellar) and (010) (or stacking) peaks, which are fairly weak in the as-cast scattering curve, increase considerably, in agreement with experimental observations.51 This confirms the visual inspection of the morphologies indicating increased P3HT crystallinity. The obtained peaks can be fitted with a Gaussian function to obtain peak positions. The sharper (100) and (010) peaks observed for the annealed blend, qualitatively indicating a higher degree of crystallinity, are located at positions q ≈ 0.426 Å–1 and q ≈ 1.385 Å–1, respectively. These values correspond to a lamellar distance of 14.7 Å and a stacking distance of 4.5 Å (highlighted in Figure 4b). The discrepancy with the experimental stacking distance value of 3.8 Å52 is due to the too large radius of CG beads, which does not allow for a ring thickness which matches the all-atom one; the lamellar distance is instead underestimated (16.5 Å, experimentally52). Such discrepancies, inherent to the current Martini CG force field (see also the Methods section), do not, however, impact the nanomorphology evolution.

The effect of P3HT MW on the annealing process has also been investigated by simulated annealing of blends containing P3HT with a MW ranging from 2 to 8 kDa. Lower MW P3HT is found to both crystallize and promote a phase-separated morphology more readily, as can be seen in Figure S3, where annealing results are shown for blends with varying P3HT MW (2–8 kDa). In particular, P3HT chains with MWs in the 2–4 kDa range respond similarly to annealing, as quantified by the decrease in P3HT–PCBM contacts shown in Figure S3. When the MW is raised to 8 kDa, a lower decrease of P3HT–PCBM contacts is observed (Figure S3): the blend responds less promptly to thermal annealing due to a slowed down dynamics caused by the increased molecular weight. Moreover, in this latter case amorphous regions can still be observed (Figure S3c), while in the former case the P3HT phase is almost completely crystalline. We can therefore conclude that lower (up to 4 kDa) MW P3HT shows a higher stacking efficiency. Low-MW P3HT films (<4 kDa) are known to be more sensitive to processing conditions. Those protocols which give more time for molecules to approach thermodynamic equilibrium (e.g., slow growth, thermal annealing) lead to more crystalline phases,53 as the molecules diffuse relatively fast due to their small size. By contrast, polymer chain entanglement54 and lower mobility slow the kinetics of ordering and, consequently, the phase separation process in high (>30 kDa) MW P3HT films.53 The present data are also in agreement with GIXD findings by Liu et al.44 which show how low-MW (up to 5 kDa) P3HT, both in pure P3HT films and when blended with PCBM, shows considerable reorientation freedom upon annealing, while this effect is considerably reduced already at MW of 10 kDa.

The observed P3HT structures correspond to the well-characterized 2D sheets in which the polymer is known to self-organize.52,55 The strong tendency of P3HT to self-organize is well-known,52,55 and it is evident from the outcome of the simulations that the model also strongly favors aggregation. This self-organizing propensity seems to be induced by the geometrical features of P3HT chains. It should be stressed that no explicitly ad-hoc anisotropic interaction has been introduced between thiophene rings, in contrast to the strategy proposed by Carrillo et al.26 in order to improve the “ultra” CG model of Lee et al.22 (also referred to as the LPC model26). In that model, representing thiophene units with single beads sacrifices one of the characteristic features of this polymer, namely the planar thiophene backbone. In the present model, the employed finer mapping preserves the thiophene planarity, and thus anisotropy, which evidently contains the driving force for P3HT self-organization.

Backmapping CG Morphologies to Atomistic Resolution

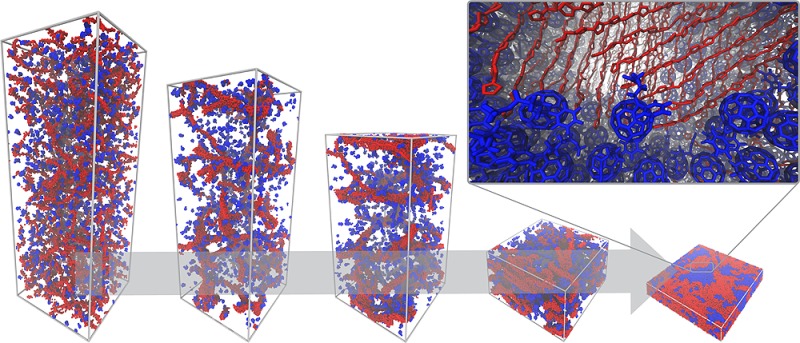
The CG morphologies obtained have finally been backmapped to atomistic—also termed all-atom (AA)—resolution by employing a published protocol36 described in the Methods section. A snapshot of a CG donor–acceptor interface for an annealed blend along with its atom-resolved counterpart is shown in Figure 5. In this procedure, the fully relaxed atomistic configuration is obtained by placing atoms in positions consistent with the CG beads that represent them and then relaxing the structure to the local atomistic energy minimum. Such a direct backmapping methodology differs from the ones employed by, for example, Carrillo et al.,26 where only a qualitative estimation of the donor–acceptor interface configuration can be made from the large-scale CG simulations. In that case, the obtained CG morphologies cannot be unambiguously backmapped to AA resolution due to too severe loss of detail inherent to the LPC model. The qualitative information can only be used to “manually” assemble an atomistic interface. Such a procedure is closer to strategies used to build idealized donor–acceptor interfaces, such as the one of Liu et al., where an idealized donor–acceptor interface is assembled by putting together P3HT and PCBM crystals.56 While there are always multiple AA structures corresponding to the same CG configuration, the present finer CG models restrict their number and allow for the use of a semiautomatized procedure for the direct retrieval of structural detail. This can pave the way to QM calculations which can fully benefit from large-scale derived structural information. In particular, the investigation of the local dielectric response of organic photovoltaic blends upon changes in the electronic density is of notable interest, as the dielectric screening of charges is crucial for the exciton splitting and recombination processes.57 Promisingly, previous studies on model systems have shown how the reorientation of dipole moments can stabilize the charge separated state33,58 relative to the lowest charge transfer state, thereby making the exciton dissociation enthalpically favorable.

Figure 5.

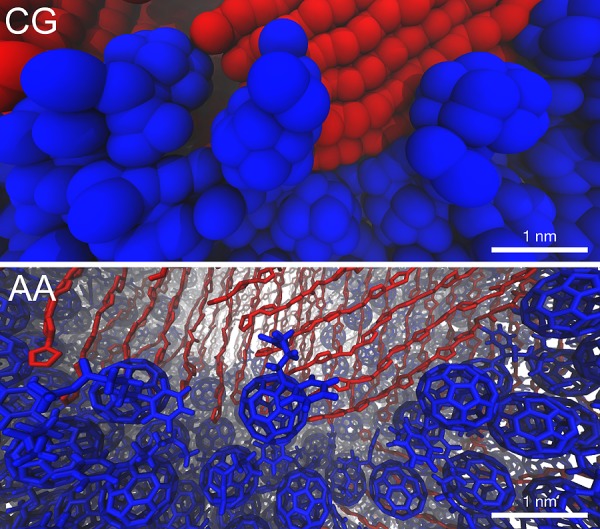
Figure 5

Open in a new tab

Close up of a donor–acceptor interface at different resolutions. The coarse-grain morphology (top) has been backmapped to atomistic resolution (bottom). In both cases, only P3HT backbones (in red) are shown to ease the view. PCBM molecules are depicted in blue.

Conclusions

We presented a CG MD based method which is able to capture the kinetically trapped nature of spin-coated bulk heterojunction morphologies with direct access to atom-resolved structural information. Simulations predict morphologies in agreement with experimental findings. The effects of slow-drying and annealing follow what is known for P3HT:PCBM solar cells. The nanoscopic picture which emerges from the simulations suggests that the (moderate) phase separation which is observed for P3HT:PCBM blends is driven by the self-organization propensity of P3HT. The good affinity between P3HT and PCBM does not allow for complete phase separation on spin coating time scales.

The resolution mapping scheme of the Martini CG force field represents a favorable compromise between the speedup of CG models and the preservation of chemical detail; moreover, the existence of a robust backmapping protocol ensures the retrieval of the atomistic structures underlying the CG ones, opening the way for a molecular view on an in silico solution-processed bulk heterojunction.

As a whole, this work proposes a predictive methodology for obtaining morphologies of solution-processed soft matter systems with atomistic resolution. The morphologies can subsequently serve as a starting point for QM calculations on excitonic properties, or be used to compute the mechanical response59,60 of BHJ materials.

Methods

CG Models

CG MD simulations have been run using models which are based on the Martini CG force field.37 Developed initially for biomolecules,37,61−64 this CG force field has been later extended to nonbiological systems, including various polymers65−68 and carbon-based nanostructures.69−72 As a general rule, four heavy atoms are coarse-grained to one interaction site (bead). Finer mapping is, however, allowed for ring systems, where an interaction site may represent two or three atoms. The PCBM model makes use of the Martini “F16” model,69 a 16 beads representation of C60 fullerene, while the oligothiophene amphiphile Martini model73 has been used as starting point for the P3HT CG model. Experimental transfer free energies were the main target of the Martini force field parametrization.37 This (top-down) approach is used to obtain nonbonded interactions between CG particles. These are determined by the type of beads which are used to describe the molecules, the choice of which is made on the basis of experimental free energy of transfer data. Bonded parameters between the beads are instead obtained by matching bond and angle distributions of atomistic simulations (bottom-up). The AA models used are based on the GROMOS 53A6 force field.74 See the Supporting Information for detailed description of the AA and CG models.

Both CG and AA models have first been validated by comparing computed free energies of transfer between different solvents to experimental data for various molecular fragments. The results, collected in Table S6, show good agreement between experiments and simulations. Interactions between the molecules studied here were further validated by comparing dimerization potentials of mean force (PMFs) at the CG level with the corresponding AA ones. PMFs were calculated for the dimerization of two 3HT molecules, two PCBM molecules, and the 3HT-PCBM pair, all in CB solution. Figure S7 shows that CG PMFs are well in line with atomistic ones. A thorough description of the free energy of transfer and PMF calculations can be found in the Supporting Information.

As already hinted previously, the Martini CG force field parametrization, based on a four heavy atoms to one CG site mapping scheme, brings with it a bead size which is too large to accurately reproduce the thickness of ring structures. This causes the discrepancy in the CG stacking distance observed in the simulated morphologies (and also seen in the potential of mean force of dimerization of two P3HT monomers in the Supporting Information, Figure S7). The bead radius is part of the Martini CG force field and cannot be tweaked arbitrarily without disrupting the carefully parametrized Martini partitioning equilibria. Work in our research group is being carried out on improving properties of Martini CG ring models. Nevertheless, the increased thickness of thiophene rings at the CG level does not affect the nature of P3HT self-assembly, which is evident from the simulations and which gives rise to structures in agreement with experiments.

Simulated Solvent Evaporation

The approach follows the one recently developed by Lee and Pao.34 Starting from a simulation box (30 × 30 × 88 nm3) containing a ternary mixture P3HT–PCBM–CB (∼39 mg mL–1 in P3HT and ∼31 mg mL–1 in PCBM for a 1:0.8 weight ratio), 1.25% of the solvent (i.e., CB) is removed every time interval t until a dried blend is obtained (30 × 30 × ∼5 nm3). The degrees of polymerization N of (regioregular) P3HT employed are 6, 12, 24, 36, and 48, approximately corresponding to molecular weights of 1000, 2000, 4000, 6000, and 8000 Da. Various sizes for the system have been tested, and the simulations have been found not to suffer from finite size effects (see the Supporting Information). The largest size which could be exhaustively simulated was chosen. 3D periodic boundary conditions are applied. After every solvent removal, 4 ns of NPT equilibration are run followed by a run 180, 120, 60, 30, 15, 7.5, or 3 ns long. This leads to total drying times of 100, 70, 36, 19 11, 6.5, and 4 μs, respectively. The equations of motion were integrated with a time step of 30 or 20 fs (the latter employed in the equilibration and often in the second half of the evaporation to avoid numerical instabilities). The box dimensions were fixed in the lateral directions by setting the compressibility to 0 bar–1. The Verlet neighbor search algorithm is employed to update the neighbor list.75 Lennard-Jones potentials and forces are cut off at 1.1 nm; “potential modifiers” are used to shift the potentials to zero at the cut off.76 The velocity-rescaling thermostat77 and the Parrinello–Rahman barostat78 are employed to maintain pressure and temperature, respectively, with coupling parameters of 1.0 and 12.0 (or 15.0) ps–1. These parameters follow the standard “new” Martini set of run parameters.76 All the evaporation simulations were run using the GROMACS 5.x package.79 All the run parameter files, as well as the solvent evaporation protocol, implemented as a bash script (which assumes the use of GROMACS), are available for download as part of the Supporting Information and on the Martini portal http://cgmartini.nl. More details on the implementation can be found in the Supporting Information.

Simulated Annealing

Dried configurations have been annealed by running MD simulations at higher temperature. The temperature has been raised gradually, in the following way: 20 ns at 498 K, 180 ns at 598 K, and up to 1.8 μs at 698 K. This led to a total simulation time of 2 μs for the full annealing cycle. The parameters employed for the run are the same as the ones employed in the solvent evaporation simulations (with the exception of the temperature). The employed simulated annealing temperature is higher than the temperatures commonly employed in experiments (∼420 K).80 However, time scales are also different, as blends are usually annealed for time scales currently not available for CG modeling (5–10 min80). A direct comparison between CG and experimental conditions is therefore not trivial.

Simulated Diffraction Pattern

The distances between all the N thiophene centers of mass have been computed. The N by N obtained distance matrix is, evidently, symmetric and thus contains N(N – 1)/2 unique distances. These distances have been binned in a histogram (occurrence vs distance; bin width = 1 nm). Subsequently, the Fourier transform of this distribution has been computed. This is done in the following way: the atoms are considered as point scatterers located at points in the real space given by the coordinates obtained by the MD simulations. If so, the scattering intensity I(q) in the 3D reciprocal space is given by81

graphic file with name ja-2016-117179_m001.jpg 1

where q is the reciprocal space vector, rj is the position vector of atom j, and Zj is the atomic number of atom j. In this particular case, we will make use of a one-dimensional version of eq 1. Moreover, as we consider identical atoms (i.e., the thiophene centers of mass), the factor Zj can be omitted. The procedure, which makes use of the MDAnalysis package,82,83 has been implemented in a Jupyter/IPython notebook available for download as part of the Supporting Information.

Backmapping

The procedure developed by Wassenaar et al.36 has been employed for the backmapping. Briefly, mapping files, i.e., initial positioning of atoms expressed on the CG particles space, have been defined for P3HT and PCBM. The program backward.py places the atoms according to the definitions contained in the mapping files. A series of energy minimizations is then carried out (as implemented in the bash script initram.sh) until a relaxed atomistic morphology is obtained. Further details are described in the Supporting Information. The programs are available for download as part of the Supporting Information and on the Martini portal http://cgmartini.nl.

Calculation of Number of Contacts

The number of contacts between molecules A and B in the simulations were calculated by counting one contact for each CG bead belonging to a molecule B within a sphere of radius 0.6 nm from each CG bead belonging to a molecule A. The cutoff distance of 0.6 nm comprises the nearest neighbor CG sites around a CG particle, with the radius of Martini S-particles being 0.24 nm (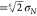Inline graphic where σN = 0.43 nm). When counting contacts, the counting of intramolecular contacts is avoided. More details on the computation of the number of contacts and generation of the planar heterojunction and intermixed morphology used to normalize the number of contacts can be found in the Supporting Information.

Spatial Discretization Scheme and Rendering

From each obtained dried BHJ (of dimensions 30 × 30 × ∼5 nm3), two slabs (of dimensions 30 × 30 × ∼2.5 nm3) have been extracted. The thickness of these slabs (2.5 nm), and consequently of the voxels into which the slabs are divided, has been chosen based on the P3HT escape depth of secondary electrons in the EFSEM measurements (found to be between around 20–30 Å38) to which the spatially discretized morphologies are compared. The morphology slabs have been therefore converted to a grid of polymer (red), fullerene (blue), and mixed (gray) domains employing the following algorithm: the simulation box is divided into voxels of dimensions 1 × 1 × 2.5 nm3; the number of P3HT (NP3HT) and PCBM (NPCBM) particles is then computed for each i,j voxel, and a color assigned to the voxel based on the relative number of polymer and fullerene CG particles contained in the voxel. In particular, the following ratio is evaluated:

graphic file with name ja-2016-117179_m003.jpg

A xi,j fraction higher (lower) than 0.6 (−0.6) has been assigned to the polymer (fullerene) phase, while fractions between 0.6 and −0.6 (included) have been assigned to the mixed phase. Simulations were visualized and rendered using VMD84 and the Tachyon ray-tracer.85

Acknowledgments

R.A. thanks The Netherlands Organisation for Scientific Research NWO (Graduate Programme Advanced Materials, No. 022.005.006) for financial support, Ria Broer, Paulo C. T. Souza, and Carsten F. E. Schroer for fruitful discussions, and Jonathan Barnoud for providing useful scripts. Dainius Janeliunas is acknowledged for the pioneering work on the polythiophene backbone model. J.J.U. was supported by a young researcher scholarship by Emil Aaltonen Foundation. The research has been carried out in affiliation with the FOM Focus Group “Next Generation Organic Photovoltaics” in Groningen. Computational resources for this work were partly provided by the Dutch National Supercomputing Facilities through NWO.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b11717.

  • Additional results, additional figure renderings; CG and AA force field details and validation (free energy of transfer and dimerization potentials of mean force data); simulation, backmapping and analysis details (PDF)

  • Evaporation simulation files, backmapping programs, Simulated scattering Jupyter/IPython notebook (ZIP)

  • Evaporation video (AVI)

The authors declare no competing financial interest.

Supplementary Material

ja6b11717_si_001.pdf (10.7MB, pdf)
ja6b11717_si_002.zip (5.5MB, zip)
ja6b11717_si_003.avi (9.3MB, avi)

References

  1. Brabec C. J.; Sariciftci N. S.; Hummelen J. C. Adv. Funct. Mater. 2001, 11, 15–26. . [DOI] [Google Scholar]
  2. Lee M. R.; Eckert R. D.; Forberich K.; Dennler G.; Brabec C. J.; Gaudiana R. A. Science 2009, 324, 232–235. 10.1126/science.1168539. [DOI] [PubMed] [Google Scholar]
  3. Kaltenbrunner M.; White M. S.; Głowacki E. D.; Sekitani T.; Someya T.; Sariciftci N. S.; Bauer S. Nat. Commun. 2012, 3, 770. 10.1038/ncomms1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Yu G.; Gao J.; Hummelen J. C.; Wudl F.; Heeger A. J. Science 1995, 270, 1789–1790. 10.1126/science.270.5243.1789. [DOI] [Google Scholar]
  5. Halls J. J. M.; Walsh C. A.; Greenham N. C.; Marseglia E. A.; Friend R. H.; Moratti S. C.; Holmes A. B. Nature 1995, 376, 498–500. 10.1038/376498a0. [DOI] [Google Scholar]
  6. Scharber M. C.; Muhlbacher D.; Koppe M.; Denk P.; Waldauf C.; Heeger A. J.; Brabec C. J. Adv. Mater. 2006, 18, 789–794. 10.1002/adma.200501717. [DOI] [Google Scholar]
  7. Huang Y.; Kramer E. J.; Heeger A. J.; Bazan G. C. Chem. Rev. 2014, 114, 7006–7043. 10.1021/cr400353v. [DOI] [PubMed] [Google Scholar]
  8. Jackson N. E.; Savoie B. M.; Marks T. J.; Chen L. X.; Ratner M. A. J. Phys. Chem. Lett. 2015, 6, 77–84. 10.1021/jz502223t. [DOI] [PubMed] [Google Scholar]
  9. Scharber M. C. Adv. Mater. 2016, 28, 1994–2001. 10.1002/adma.201504914. [DOI] [PubMed] [Google Scholar]
  10. Clarke T. M.; Durrant J. R. Chem. Rev. 2010, 110, 6736–6767. 10.1021/cr900271s. [DOI] [PubMed] [Google Scholar]
  11. Chirvase D.; Parisi J.; Hummelen J. C.; Dyakonov V. Nanotechnology 2004, 15, 1317–1323. 10.1088/0957-4484/15/9/035. [DOI] [Google Scholar]
  12. Shaheen S. E.; Brabec C. J.; Sariciftci N. S.; Padinger F.; Fromherz T.; Hummelen J. C. Appl. Phys. Lett. 2001, 78, 841–843. 10.1063/1.1345834. [DOI] [Google Scholar]
  13. Zhang F.; Jespersen K. G.; Bjoerstroem C.; Svensson M.; Andersson M. R.; Sundström V.; Magnusson K.; Moons E.; Yartsev A.; Inganäs O. Adv. Funct. Mater. 2006, 16, 667–674. 10.1002/adfm.200500339. [DOI] [Google Scholar]
  14. Li G.; Shrotriya V.; Huang J.; Yao Y.; Moriarty T.; Emery K.; Yang Y. Nat. Mater. 2005, 4, 864–868. 10.1038/nmat1500. [DOI] [Google Scholar]
  15. Padinger F.; Rittberger R. S.; Sariciftci N. S. Adv. Funct. Mater. 2003, 13, 85–88. 10.1002/adfm.200390011. [DOI] [Google Scholar]
  16. Hoppe H.; Niggemann M.; Winder C.; Kraut J.; Hiesgen R.; Hinsch A.; Meissner D.; Sariciftci N. S. Adv. Funct. Mater. 2004, 14, 1005–1011. 10.1002/adfm.200305026. [DOI] [Google Scholar]
  17. Yang C. Y.; Heeger A. J. Synth. Met. 1996, 83, 85–88. 10.1016/S0379-6779(97)80058-6. [DOI] [Google Scholar]
  18. Yang X.; Loos J.; Veenstra S. C.; Verhees W. J. H.; Wienk M. M.; Kroon J. M.; Michels M. A. J.; Janssen R. A. J. Nano Lett. 2005, 5, 579–583. 10.1021/nl048120i. [DOI] [PubMed] [Google Scholar]
  19. van Bavel S. S.; Sourty E.; Loos J. Nano Lett. 2009, 9, 507–513. 10.1021/nl8014022. [DOI] [PubMed] [Google Scholar]
  20. Kim Y.; Cook S.; Tuladhar S. M.; Choulis S. A.; Nelson J.; Durrant J. R.; Bradley D. D. C.; Giles M.; McCulloch I.; Ha C.-S.; Ree M. Nat. Mater. 2006, 5, 197–203. 10.1038/nmat1574. [DOI] [Google Scholar]
  21. Wu W.-R.; Jeng U.-S.; Su C.-J.; Wei K.-H.; Su M.-S.; Chiu M.-Y.; Chen C.-Y.; Su W.-B.; Su C.-H.; Su A.-C. ACS Nano 2011, 5, 6233–6243. 10.1021/nn2010816. [DOI] [PubMed] [Google Scholar]
  22. Lee C.-K.; Pao C.-W.; Chu C.-W. Energy Environ. Sci. 2011, 4, 4124–4132. 10.1039/c1ee01508g. [DOI] [Google Scholar]
  23. Huang D. M.; Faller R.; Do K.; Moulé A. J. J. Chem. Theory Comput. 2010, 6, 526–537. 10.1021/ct900496t. [DOI] [PubMed] [Google Scholar]
  24. Jankowski E.; Marsh H. S.; Jayaraman A. Macromolecules 2013, 46, 5775–5785. 10.1021/ma400724e. [DOI] [Google Scholar]
  25. To T.; Adams S. Phys. Chem. Chem. Phys. 2014, 16, 4653–4663. 10.1039/c3cp54308k. [DOI] [PubMed] [Google Scholar]
  26. Carrillo J.-M. Y.; Seibers Z.; Kumar R.; Matheson M. A.; Ankner J. F.; Goswami M.; Bhaskaran-Nair K.; Shelton W. A.; Sumpter B. G.; Kilbey S. M. ACS Nano 2016, 10, 7008–7022. 10.1021/acsnano.6b03009. [DOI] [PubMed] [Google Scholar]
  27. Peumans P.; Uchida S.; Forrest S. R. Nature 2003, 425, 158–162. 10.1038/nature01949. [DOI] [PubMed] [Google Scholar]
  28. Koster L. J. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 205318. 10.1103/PhysRevB.81.205318. [DOI] [Google Scholar]
  29. Moench T.; Friederich P.; Holzmueller F.; Rutkowski B.; Benduhn J.; Strunk T.; Koerner C.; Vandewal K.; Czyrska-Filemonowicz A.; Wenzel W.; Leo K. Adv. Energy Mater. 2016, 6, 1051280. 10.1002/aenm.201501280. [DOI] [Google Scholar]
  30. Kouijzer S.; Michels J. J.; van den Berg M.; Gevaerts V. S.; Turbiez M.; Wienk M. M.; Janssen R. A. J. J. Am. Chem. Soc. 2013, 135, 12057–12067. 10.1021/ja405493j. [DOI] [PubMed] [Google Scholar]
  31. Yost S. R.; Wang L.-P.; van Voorhis T. J. Phys. Chem. C 2011, 115, 14431–14436. 10.1021/jp203387m. [DOI] [Google Scholar]
  32. Liu T.; Troisi A. J. Phys. Chem. C 2011, 115, 2406–2415. 10.1021/jp109130y. [DOI] [Google Scholar]
  33. de Gier H. D.; Broer R.; Havenith R. W. A. Phys. Chem. Chem. Phys. 2014, 16, 12454–12461. 10.1039/C4CP01070A. [DOI] [PubMed] [Google Scholar]
  34. Lee C.-K.; Pao C.-W. J. Phys. Chem. C 2014, 118, 11224–11233. 10.1021/jp501323p. [DOI] [Google Scholar]
  35. Marrink S. J.; Tieleman D. P. Chem. Soc. Rev. 2013, 42, 6801–6822. 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
  36. Wassenaar T. A.; Pluhackova K.; Böckmann R. A.; Marrink S. J.; Tieleman D. P. J. Chem. Theory Comput. 2014, 10, 676–690. 10.1021/ct400617g. [DOI] [PubMed] [Google Scholar]
  37. Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
  38. Masters R. C.; Pearson A. J.; Glen T. S.; Sasam F.-C.; Li L.; Dapor M.; Donald A. M.; Lidzey D. G.; Rodenburg C. Nat. Commun. 2015, 6, 6928. 10.1038/ncomms7928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Machui F.; Langner S.; Zhu X.; Abbott S.; Brabec C. J. Sol. Energy Mater. Sol. Cells 2012, 100, 138–146. 10.1016/j.solmat.2012.01.005. [DOI] [Google Scholar]
  40. Richter L. J.; DeLongchamp D. M.; Bokel F. A.; Engmann S.; Chou K. W.; Amassian A.; Schaible E.; Hexemer A. Adv. Energy Mater. 2015, 5, 1400975. 10.1002/aenm.201400975. [DOI] [Google Scholar]
  41. Pröller S.; Liu F.; Zhu C.; Wang C.; Russell T. P.; Hexemer A.; Müller-Buschbaum P.; Herzig E. M. Adv. Energy Mater. 2016, 6, 1501580. 10.1002/aenm.201501580. [DOI] [Google Scholar]
  42. Gu X.; Yan H.; Kurosawa T.; Schroeder B. C.; Gu K. L.; Zhou Y.; To J. W. F.; Oosterhout S. D.; Savikhin V.; Molina-Lopez F.; Tassone C. J.; Mannsfeld S. C. B.; Wang C.; Toney M. F.; Bao Z. Adv. Energy Mater. 2016, 6, 1601225. 10.1002/aenm.201601225. [DOI] [Google Scholar]
  43. Li G.; Yao Y.; Yang H.; Shrotriya V.; Yang G.; Yang Y. Adv. Funct. Mater. 2007, 17, 1636–1644. 10.1002/adfm.200600624. [DOI] [Google Scholar]
  44. Liu F.; Chen D.; Wang C.; Luo K.; Gu W.; Briseno A. L.; Hsu J. W. P.; Russell T. P. ACS Appl. Mater. Interfaces 2014, 6, 19876–19887. 10.1021/am505283k. [DOI] [PubMed] [Google Scholar]
  45. Brabec C. J.; Heeney M.; McCulloch I.; Nelson J. Chem. Soc. Rev. 2011, 40, 1185–1199. 10.1039/C0CS00045K. [DOI] [PubMed] [Google Scholar]
  46. Shih M.-C.; Huang B.-C.; Lin C.-C.; Li S.-S.; Chen H.-A.; Chiu Y.-P.; Chen C.-W. Nano Lett. 2013, 13, 2387–2392. 10.1021/nl400091f. [DOI] [PubMed] [Google Scholar]
  47. Su Y.-W.; Chiu M.-Y.; Wei K.-H. In Progress in High-Efficient Solution Process Organic Photovoltaic Devices: Fundamentals, Materials, Devices and Fabrication; Yang Y., Li G., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2015; pp 251–271. [Google Scholar]
  48. Erb T.; Zhokhavets U.; Gobsch G.; Raleva S.; Stühn B.; Schilinsky P.; Waldauf C.; Brabec C. J. Adv. Funct. Mater. 2005, 15, 1193–1196. 10.1002/adfm.200400521. [DOI] [Google Scholar]
  49. Jo J.; Na S.-I.; Kim S.-S.; Lee T.-W.; Chung Y.; Kang S.-J.; Vak D.; Kim D.-Y. Adv. Funct. Mater. 2009, 19, 2398–2406. 10.1002/adfm.200900183. [DOI] [Google Scholar]
  50. Treat N. D.; Brady M. A.; Smith G.; Toney M. F.; Kramer E. J.; Hawker C. J.; Chabinyc M. L. Adv. Energy Mater. 2011, 1, 82–89. 10.1002/aenm.201000023. [DOI] [Google Scholar]
  51. Chiu M.-Y.; Jeng U.; Su C.-H.; Liang K. S.; Wei K.-H. Adv. Mater. 2008, 20, 2573–2578. 10.1002/adma.200703097. [DOI] [Google Scholar]
  52. Brinkmann M.; Wittmann J.-C. Adv. Mater. 2006, 18, 860–863. 10.1002/adma.200501838. [DOI] [Google Scholar]
  53. Kline R. J.; McGehee M. D.; Kadnikova E. N.; Liu J.; Fréchet J. M. J.; Toney M. F. Macromolecules 2005, 38, 3312–3319. 10.1021/ma047415f. [DOI] [Google Scholar]
  54. Tummala N. R.; Risko C.; Bruner C.; Dauskardt R. H.; Brédas J.-L. J. Polym. Sci., Part B: Polym. Phys. 2015, 53, 934–942. 10.1002/polb.23722. [DOI] [Google Scholar]
  55. Sirringhaus H.; Brown P. J.; Friend R. H.; Nielsen M. M.; Bechgaard K.; Langeveld-Voss B. M. W.; Spiering A. J. H.; Janssen R. A. J.; Meijer E. W.; Herwig P.; de Leeuw D. M. Nature 1999, 401, 685–688. 10.1038/44359. [DOI] [Google Scholar]
  56. Liu T.; Cheung D. L.; Troisi A. Phys. Chem. Chem. Phys. 2011, 13, 21461–21470. 10.1039/c1cp23084k. [DOI] [PubMed] [Google Scholar]
  57. Koster L. J. A.; Shaheen S. E.; Hummelen J. C. Adv. Energy Mater. 2012, 2, 1246–1253. 10.1002/aenm.201200103. [DOI] [Google Scholar]
  58. de Gier H. D.; Jahani F.; Broer R.; Hummelen J. C.; Havenith R. W. A. J. Phys. Chem. A 2016, 120, 4664–4671. 10.1021/acs.jpca.5b09279. [DOI] [PubMed] [Google Scholar]
  59. Tummala N. R.; Bruner C.; Risko C.; Bredas J.-L.; Dauskardt R. H. ACS Appl. Mater. Interfaces 2015, 7, 9957–9964. 10.1021/acsami.5b02202. [DOI] [PubMed] [Google Scholar]
  60. Root S. E.; Savagatrup S.; Pais C. J.; Arya G.; Lipomi D. J. Macromolecules 2016, 49, 2886–2894. 10.1021/acs.macromol.6b00204. [DOI] [Google Scholar]
  61. Marrink S. J.; de Vries A. H.; Mark A. E. J. Phys. Chem. B 2004, 108, 750–760. 10.1021/jp036508g. [DOI] [Google Scholar]
  62. Monticelli L.; Kandasamy S. K.; Periole X.; Larson R. G.; Tieleman D. P.; Marrink S. J. J. Chem. Theory Comput. 2008, 4, 819–834. 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
  63. López C. A.; Rzepiela A. J.; de Vries A. H.; Dijkhuizen L.; Hünenberger P. H.; Marrink S. J. J. Chem. Theory Comput. 2009, 5, 3195–3210. 10.1021/ct900313w. [DOI] [PubMed] [Google Scholar]
  64. Uusitalo J. J.; Ingólfsson H. I.; Akhshi P.; Tieleman D. P.; Marrink S. J. J. Chem. Theory Comput. 2015, 11, 3932–3945. 10.1021/acs.jctc.5b00286. [DOI] [PubMed] [Google Scholar]
  65. Lee H.; de Vries A. H.; Marrink S. J.; Pastor R. W. J. Phys. Chem. B 2009, 113, 13186–13194. 10.1021/jp9058966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Rossi G.; Monticelli L.; Puisto S. R.; Vattulainen I.; Ala-Nissila T. Soft Matter 2011, 7, 698–708. 10.1039/C0SM00481B. [DOI] [Google Scholar]
  67. Panizon E.; Bochicchio D.; Monticelli L.; Rossi G. J. Phys. Chem. B 2015, 119, 8209–8216. 10.1021/acs.jpcb.5b03611. [DOI] [PubMed] [Google Scholar]
  68. Vögele M.; Holm C.; Smiatek J.. J. Chem. Phys. 2015, 143, 243151. 10.1063/1.4937805 [DOI] [PubMed] [Google Scholar]
  69. Monticelli L. J. Chem. Theory Comput. 2012, 8, 1370–1378. 10.1021/ct3000102. [DOI] [PubMed] [Google Scholar]
  70. Baoukina S.; Monticelli L.; Tieleman D. P. J. Phys. Chem. B 2013, 117, 12113–12123. 10.1021/jp405732k. [DOI] [PubMed] [Google Scholar]
  71. Lelimousin M.; Sansom M. S. P. Small 2013, 9, 3639–3646. 10.1002/smll.201202640. [DOI] [PubMed] [Google Scholar]
  72. Hu Q.; Jiao B.; Shi X.; Valle R. P.; Zuo Y. Y.; Hu G. Nanoscale 2015, 7, 18025–18029. 10.1039/C5NR05401J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Janeliunas D.Self-Assembly of Facial Oligothiophene Amphiphiles; Ph.D. Dissertation, Delft University of Technology, TU Delft, 2014. [Google Scholar]
  74. Oostenbrink C.; Villa A.; Mark A. E.; van Gunsteren W. F. J. Comput. Chem. 2004, 25, 1656–1676. 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
  75. Verlet L. Phys. Rev. 1967, 159, 98. 10.1103/PhysRev.159.98. [DOI] [Google Scholar]
  76. de Jong D. H.; Baoukina S.; Ingólfsson H. I.; Marrink S. J. Comput. Phys. Commun. 2016, 199, 1–7. 10.1016/j.cpc.2015.09.014. [DOI] [Google Scholar]
  77. Bussi G.; Donadio D.; Parrinello M. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  78. Parrinello M.; Rahman A. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  79. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. SoftwareX 2015, 1, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  80. Dang M. T.; Hirsch L.; Wantz G. Adv. Mater. 2011, 23, 3597–3602. 10.1002/adma.201100792. [DOI] [PubMed] [Google Scholar]
  81. Kimminau G.; Nagler B.; Higginbotham A.; Murphy W. J.; Park N.; Hawreliak J.; Kadau K.; Germann T. C.; Bringa E. M.; Kalantar D. H.; Lorenzana H. E.; Remington B. A.; Wark J. S. J. Phys.: Condens. Matter 2008, 20, 505203. 10.1088/0953-8984/20/50/505203. [DOI] [Google Scholar]
  82. Michaud-Agrawal N.; Denning E. J.; Woolf T. B.; Beckstein O. J. Comput. Chem. 2011, 32, 2319–2327. 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  83. Gowers R. J.; Linke M.; Barnoud J.; Reddy T. J. E.; Melo M. N.; Seyler S. L.; Dotson D. L.; Domanski J.; Buchoux S.; Kenney I. M.; Beckstein O.. MDAnalysis: a Python package for the rapid analysis of molecular dynamics simulations; Proceedings of the 15th Python in Science Conference, Austin, TX, 2016; Benthall S., Rostrup S., Eds.; Scipy: 2016; pp 98–105.
  84. Humphrey W.; Dalke A.; Schulten K. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  85. Stone J.An Efficient Library for Parallel Ray Tracing and Animation; Master’s thesis, Computer Science Department, University of Missouri-Rolla, 1998. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja6b11717_si_001.pdf (10.7MB, pdf)
ja6b11717_si_002.zip (5.5MB, zip)
ja6b11717_si_003.avi (9.3MB, avi)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES