Self-referential phase reset based on inferior olive oscillator dynamics

Abstract

The olivo-cerebellar network is a key neuronal circuit that provides high-level motor control in the vertebrate CNS. Functionally, its network dynamics is organized around the oscillatory membrane potential properties of inferior olive (IO) neurons and their electrotonic connectivity. Because IO action potentials are generated at the peaks of the quasisinusoidal membrane potential oscillations, their temporal firing properties are defined by the IO rhythmicity. Excitatory inputs to these neurons can produce oscillatory phase shifts without modifying the amplitude or frequency of the oscillations, allowing well defined time-shift modulation of action potential generation. Moreover, the resulting phase is defined only by the amplitude and duration of the reset stimulus and is independent of the original oscillatory phase when the stimulus was delivered. This reset property, henceforth referred to as selfreferential phase reset, results in the generation of organized clusters of electrically coupled cells that oscillate in phase and are controlled by inhibitory feedback loops through the cerebellar nuclei and the cerebellar cortex. These clusters provide a dynamical representation of arbitrary motor intention patterns that are further mapped to the motor execution system. Being supplied with sensory inputs, the olivo-cerebellar network is capable of rearranging the clusters during the process of movement execution. Accordingly, the phase of the IO oscillators can be rapidly reset to a desired phase independently of the history of phase evolution. The goal of this article is to show how this selfreferential phase reset may be implemented into a motor control system by using a biologically based mathematical model.

Coordinated motor control signals addressing large numbers of muscles at a given time must implement strict temporal coherence, also known as “temporal motor binding,” to generate appropriate motricity (1). Electrophysiological studies have indicated that such motor intention patterns require proper olivocerebellar system function (1–4). And, in particular, sets of time-coherent inferior olive (IO) action potentials reach given motor neuron pools by means of the cerebellar nuclei (1, 5–7). To provide the required synchrony of muscle activation, the IO signals must be temporally coherent at the final motor path regardless of the distance between the activated muscle groups. As such, then, the main coherence control parameter is the mutual temporal shifts among sequences of action potentials innervating different muscles. Recent experimental work indicates that such a temporal signal mechanism is provided by the sequence of oscillatory events in the olivo-cerebellar system (7). The possibility that a “universal control system,” based on olivo-cerebellar physiology, may be implemented in analog hardware electronic chips has been proposed (8).

Indeed, temporal motor intention patterns may be formed as oscillatory phase clusters in the IO (9–12). Because IO neurons in vivo may be considered close to 10-Hz oscillators that generate action potentials at the peaks of subthreshold oscillations (9–11), oscillation phase shifts would uniquely define the time shift between spikes. Olivo-cerebellar inhibitory feedback and sensory inputs are capable of reconfiguring IO oscillatory phase and thus of setting the required phase cluster pattern. Once attained, a given cluster phase is sustained by the internal mechanism of IO neuron synchronization. Local oscillation synchrony is provided through dendritic gap junctions that are formed among ≈50 neighboring cells (13, 14). Obviously, such local coupling can provide neither global coherence nor the transition from one cluster configuration to another at sufficiently fast time scales. Rather, the reset of the IO oscillators phases occurs through sensory signals from effector feedback. Accordingly, the IO reconfigures the oscillation, automatically evolving to an optimal cluster configuration.

Analysis of intracellular recordings from in vitro IO neurons has shown that phase reset in the IO oscillators differs from typical oscillatory systems (12). Phase reset is controlled by input parameters and does not depend on the time moment (initial phase) when the input is received. In this sense, the phase reset is self-referential and ignores the “history” of the system. This is a key property that makes IO neuronal oscillators extraordinarily flexible and able to process a forthcoming motor command in accordance with current environment conditions. Moreover, uncoupled oscillators located at distant places can be rapidly synchronized in phase if they receive the same stimulus.

Here, we propose a physiologically based mathematical model of the IO that is capable of self-referential phase reset (SPR). We describe SPR mechanisms and discuss the applications of the phase control strategy for artificial automatic control systems by using phase synchronization.

Methods and Results

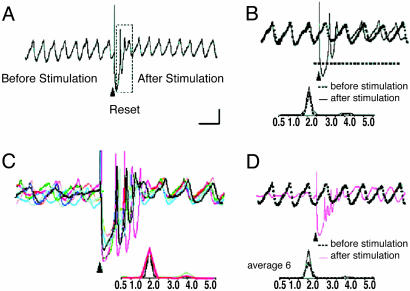
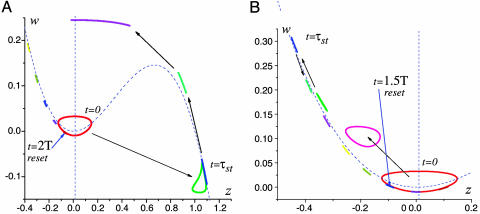
Phase Reset Effect. The experimental basis for the model is summarized in Fig. 1 (12). In agreement with previous results (9), spontaneous IO neuronal oscillations are interrupted by an extracellular stimulus (Fig. 1 A, boxed area) and resume with a different phase without affecting their frequency or amplitude (Fig. 1B). Thus, the stimulus phase reset can be obtained repeatedly in any given cell. The stimulation-induced shift in the oscillation phase is remarkably similar and independent from stimulus time onset. This result is illustrated in Fig. 1C, where an average of six individual stimulus-evoked oscillatory reset results with the same average frequency and similar phase indicates that the reset is independent of the original phase. Thus, the phase reset has two basic features. (i) The poststimulus phase is independent of the initial phase and can be controlled by the characteristics of the stimulus. (ii) The same stimulus resets all of the cells to the same phase, i.e., it synchronizes them.

Fig. 1.

Intracellular inferior olive oscillations recorded in vitro. (A) Spontaneous oscillations are interrupted by an extracellular stimulus (arrowhead), delivered to the dorsal border of the IO nucleus. After stimulation, the oscillations were interrupted for 750 ms (boxed area) before resuming. (B) Superposition of recordings of spontaneous (dashed line) and stimulus-evoked (solid line) oscillations from the same cell. Note that extracellular stimulation modified only the phase of spontaneous oscillations without affecting their amplitude or frequency. (C) Superposition of six (color-coded) individual intracellular traces of stimulus-evoked oscillations from the same cell are superimposed on the left. Note that the frequency of all of the stimulation-evoked oscillations is 2.0 Hz, and the stimulation-induced shift in the oscillatory phase is similar. Oscillations are clearly seen after the stimulus induced reset but can be barely detected before the stimulation. (D) Superposition of mean stimulus-evoked oscillations (n = 6, red line) and spontaneous oscillations (dashed black line). Note that the average trace has the same frequency and amplitude as the spontaneous oscillations and differs only in the phase shift. [Calibration bar: 1 mV; 1s (A), 500 ms (B and D), and 415 ms (C).] (Modified from ref. 9.)

IO Neuron Model. We have developed a mathematical model that reproduces the key IO neuron electrophysiological properties (8, 15) and the SPR effect. In particular, the model comprises two sets of functionally coupled equations where the oscillations of a supercritical Andronov–Hopf bifurcation in the first set drive the dynamics of the second set of parameters. Because spike threshold occurs mostly at the peak of a subthreshold oscillation, spike onset is determined by the subthreshold oscillation. Depending on the values of the control parameters, the model qualitatively reproduces the spontaneous and stimuli-induced oscillations observed in IO neurons (8, 15). A mathematical model comprising a set of four nonlinear differential equations can describe these properties:

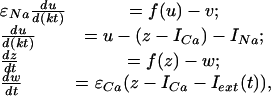[1]

where the variables z and w are responsible for the subthreshold oscillations and low-threshold (Ca-dependent) spiking, and the variables u and v describe the higher-threshold (Na⁺-dependent) spiking. The parameters ε_Ca and ε_Na control the oscillation time scales; I_Ca and I_Na drive the depolarization level of the two blocks; f is a cubic shape nonlinearity, f(x) = x (x – a)(1 – x); the parameter k sets a relative time scale between the two blocks. Function I_ext(t) describe the extracellular stimulus. It has nonzero value, I_ext(t) = I_st only when the stimulus has been applied, t_i < t < t_i + t_st. Here I_st and t_st are constants describing the magnitude and duration of the stimulus pulse arriving at the time instants t_i.

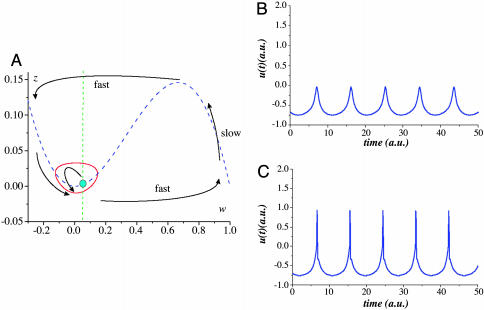
The oscillations appear in the (z, w) subsystem with a frequency and amplitude that is controlled by the depolarization parameter, I_Ca. The shape of the corresponding limit cycle in the (z, w) phase plane is shown in Fig. 2A. The oscillations are close to sinusoidal shape; however, they have a sharper peaks for the z-variable. These peaks provide sharper pedestals for the Na⁺ pulses when reaching the threshold potential in the (u, v) subsystem (Fig. 2 B and C). Due to these pedestals (Ca²⁺-dependent spikes), IO spiking has a precise timing. The timing of the spikes can be associated with subthreshold oscillation phase. Let us define the phase j as the phase shift with a reference oscillator, R:(z̃, w̃), whose dynamics is described by Eqs. 1 with I_ext(t) = 0. This shift can be determined by calculating the oscillation peak times:

[2]

where t and t_r are the peak times of the subthreshold oscillations and the reference oscillations, respectively (16). Note that the oscillation phase ϕ is a free parameter and can be set to an arbitrary value from 0 to 2π (corresponds to the zero Lyapunov exponent of the limit cycle).

Fig. 2.

Subthreshold oscillatory properties. (A) Qualitative phase portrait of (z, w)-subsystem. The nullclines are shown by the dashed curves. The arrows illustrate fast and slow motions. Stable limit cycle corresponding to the subthreshold oscillations appears from Andronov–Hopf bifurcation that happens when the fixed point loses its stability at the minimum of the u-nullcline curve. (B) Oscillations (u-variable) of model 1. Subthreshold oscillations with Ca²⁺-dependent spiking [(u, v) subsystem is unexcited]. Parameter values: ε_Na = 0.001; ε_Ca = 0.02; k = 0.1; I_Ca = 0.018; I_Na =–0.61; a = 0.01. (C) Spiking (Na⁺-dependent) at the peaks of subthreshold oscillations. Parameter values: ε_Na = 0.001; ε_Ca = 0.02; k = 0.1; I_Ca = 0.018; I_Na = –0.59; a = 0.01.

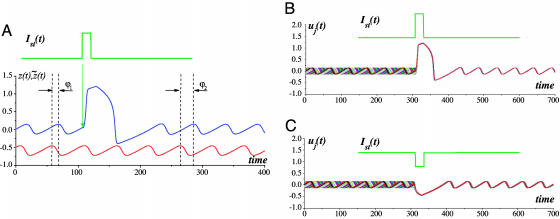
Stimulus-Induced Phase Reset. To study phase reset effects, we set the unit parameters to the following values: ε_Na = 0.001; ε_Ca = 0.02; k = 0.1; I_Ca = 0.01; I_Na =–0.11; a = 0.01. Fig. 3 illustrates the reset properties of the model (Eqs. 1) when an extracellular stimulus of I_st > 0 and τ_st = 0.4T was applied. This stimulus arrived in-phase with the reference oscillator, i.e., it corresponds to a peak of z̃. Let the IO oscillator have an initial phase shift ϕ₁ relative to the reference unit (Eq. 2). After a short transient process, the oscillation recovers its shape and frequency, approaching the resulting phase ϕ₂ (Fig. 3A).

Fig. 3.

Oscillatory reset. (A) Phase reset in the IO oscillatory unit. The phase computed according to formula 2 is reset from the initial value ϕ₁ to the value ϕ₂. The lower oscillation trace corresponds to the base oscillator staying unperturbed. The upper signal corresponds to the stimulus. (B) Excitatory stimulus-induced SPR effect in the IO unit. Superimposed traces from n = 20 initial phases uniformly distributed illustrate that the reset phase is almost the same for all initial phases. Parameter values: I_st = 1.15, τ_st = 0.4T, T ≈ 51.1. (C) Inhibitory stimulus-induced SPR effect. Superimposed traces from n = 20 initial phases uniformly distributed. Parameter values: I_st = –1, τ_st = 0.4T, T ≈ 51.1.

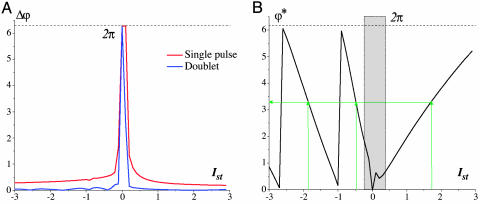
Let us now change the initial phase. Fig. 3B shows superimposed traces from 20 initial phases uniformly distributed within the interval [0, 2π]. Their reset phases are localized in the small neighborhood of the mean phase ϕ*. Indeed, the reset properties are independent of the initial state of the oscillator. Fig. 4A illustrates the dependence of the reset phase deviation (the difference between maximum and minimum values of the reset phases) on the stimulus amplitude, I_st, for a fixed stimulus pulse duration of τ_st = 0.4T. The phase deviation decreases for increasing stimulus amplitudes. For longer values of τ_st, stimulusduration-dependent deviation vanishes (data not shown). Note that the deviation can be significantly decreased if one or more additional pulses are applied (Fig. 4A, blue curve). Note also that, for small stimulus amplitudes, the reset phases are distributed within the whole interval [0, 2π], and the SPR effect disappears. In the SPR state the reset phase is controlled only by the characteristics of the stimulus.

Fig. 4.

Characteristics of the SPR effect. (A) Deviation of the reset phase (red curve) depending on the stimulus amplitude for fixed stimulus duration τ_st = 0.4T, T = 51.1. The deviation Δϕ is defined as the difference between the maximum and minimum reset phase values. The blue curve corresponds to the doublet stimulation for interpulse interval 12T. n = 100 initial phases have been uniformly distributed in the interval [0, 2π]. (B) Stimulus amplitude – reset phase dependence for fixed stimulus duration τ_st = 0.4T, T = 51.1. The reset phase ϕ* is computed as the mathematical average from n = 100 oscillation traces. The green arrows show how the desired value of the reset phase can be obtained by the appropriate choice of stimulus amplitude for excitatory, I_st > 0, and inhibitory, I_st < 0, stimulation.

Thus, the phase response curve (representing the dependence of the reset phase on the initial phase) is close to the constant line ϕ*. Fig. 4B shows how the value of the mean reset phase, ϕ*, changes with increasing stimulus amplitude. Because the curve covers the whole interval [0, 2p], there is a point-by-point correspondence between the stimulus amplitude and the reset phase. Any desired value of the oscillation phase can be set by an appropriate choice of stimulus amplitude. Consequently, at any moment, one can control the oscillation phase independently on the “history” of the system. The SPR effect also takes place for an inhibitory extracellular stimulus, i.e., for I_st < 0, (Figs. 3C and 4A).

SPR Mechanism. The SPR effect can be explained as follows. Consider Eqs. 1 for the (z, w) subsystem (Fig. 2 A). Numerical solutions (Fig. 5A) illustrate how n = 100 points, uniformly distributed along the limit cycle, are transformed by the excitatory stimulus. After the stimulation, the phase volume occupied by the limit cycle becomes strongly compressed and converges to the reset point. A similar compression occurs for inhibitory stimuli. Fig. 5B illustrates the phase volume transformation. In this case, the reset occurs faster (the excursion of the points is shorter) but with less precision. There are two basic mechanisms leading to the reset: one for short pulses and another for long pluses. In the case of relatively short pulses (less than oscillation period), due to the small parameter ε_Ca « 1, its trajectories have fast and slow time scales. The trajectories slow down in the neighborhood of the nonlinear curve z = f(w) and speed up out of this neighborhood. Because the limit cycle is located within this neighborhood, the oscillation has a relatively slow time scale. When a sufficiently strong stimulus is applied, the w-nullcline is shifted either to the right portion of the nonlinear curve for an excitatory stimulus or to the left for an inhibitory stimulus. Thus, any trajectory initiated at the limit cycle circle goes into the fast motion region approaching either the left or the right branches of nonlinear curve f(u). The transformation of the circle can be estimated by the value of the appropriate Lyapunov exponent. Note that, due to different time scales, the initial circle becomes strongly compressed. This compression can be treated with Lyapunov exponents, indicating an exponential change in the phase volume along the trajectories. The slow motions manifold located near the nonlinear curve z = f(w) has quite a large transverse Lyapunov exponent, λ, corresponding to the manifold stability relative to the fast motions. The value of λ can be estimated by using Eqs. 1.

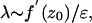[3]

where z₀ is the coordinate of the points at the manifold. Then, for the outer parts of the nonlinear curve f′(z₀) < 0, and the Lyapunov exponent is strongly negative for small ε. This result corresponds to the strong phase volume compression in the transverse direction when the trajectories evolve near the manifold (Fig. 5 A and B). The volume becomes elongated near the manifolds. Then, for excitatory stimuli, the trajectories jump once more into the fast motion region, elongating in the horizontal direction. The phase volume is again compressed near the left stable compartment of the manifold (Fig. 5A). Such a double compression provides better reset precision, compared with the inhibitory case (Fig. 5B). All points return to the limit cycle almost in-phase when the stimulus ends. If the stimulation is longer, τ_st » T, the reset mechanism drives system relaxation to a stable fixed point. Let us suppose that I_st > z_max – I_Ca, where z_max is the coordinate of the maximum of f(z) (Fig. 2 A). When the system is being stimulated the (z, w)-subsystem of Eqs. 1 has a stable fixed point located on the right part of the nonlinear curve f(z) attracting all trajectories. If the stimulation is long enough, all points from the limit cycle (different initial phases) asymptotically tend to this fixed point. That is, the phase volume (the limit cycle circle) is compressed to this point. When the system is released, the oscillation recovers with the same phase. In the case of inhibitory pulses, the condition of the reset is I_st > z_max – I_Ca and provides the stability of the fixed point during the stimulation. In this case, phase volume compression is provided by the Lyapunov eigenvalues of the stable fixed point that appears due to the stimulus.

Fig. 5.

SPR mechanism illustrated in the (z, w) phase plane of Eqs. 1. n = 100 initial points are uniformly distributed along the limit cycle. Due to the stimulation, the initial circle is strongly compressed during the excursion in the phase plane. (A) Sequence of snapshots of initial circle transformation under the excitatory stimulus. The circle is compressed while evolving along the right and left compartment of the slow motions manifold located near z-nullcline (dashed curve). After the excursion, the trajectories return to the limit cycle almost in-phase. Parameter values: I_st = 1.15, τ_st = 0.4T, T ≈ 51.1. (B) Circle transformation under inhibitory stimulus. The reset is faster but less precise. The circle is compressed only near the left compartment of the slow motions manifold. Parameter values: I_st = –1, τ_st = 0.4T, T ≈ 51.1.

SPR-Induced Synchronization. When the SPR effect is applied to large ensembles of oscillatory units, it can provide their phase synchronization. Indeed, if the same pulse stimulates a large number of isolated IO units, they will return to the same phase and becoming mutually synchronized (Fig. 3 B and C). By contrast, with classical examples of networks of intercoupled units (ensembles of electrically coupled oscillators) (16), the SPR-induced synchronization is coupling-independent, and so even spatially distant cells can be phase synchronized by just one or a few stimulation pulses. Moreover, for appropriate stimulus parameters (amplitude and duration), the oscillators in the network can be set to any value of mutual phase lag (Fig. 4B). In this fashion, phase clusters of any complex spatial configuration can be formed. By changing the stimulus parameters, the cluster configuration can be easily rearranged, irrespective of prior clusters configuration. Transient isolation of individual IO neurons is accomplished through inhibitory feedback that interrupts interunit coupling. During the short time IO neurons are electrically uncoupled, they may receive direct sensory feedback that can provide the desired cluster configuration. The olivocerebellar cluster-based universal control system (UCS) has been described in detail (8). SPR-induced synchronization as implemented with the UCS architecture is illustrated in Fig. 6. A square network of 200 × 200 locally coupled IO oscillators is stimulated by a given input pattern. The stimulus has a fixed duration τ_st = 0.4T and variable amplitudes 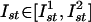. As shown in Fig. 4B, each unit will be reset to a certain phase. We take as the stimulus pattern the grayscale picture of a scarab digitized and mapped into the interval of amplitudes 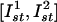. Starting from an initial random oscillatory phase distribution, the network evolves to the phase distribution corresponding to the scarab picture (Fig. 6). Note that, in the case of excitatory stimulation (Fig. 6 B and C), the picture is positive because the amplitude-phase curve has a positive slope (Fig. 4B). For the inhibitory stimulus pattern, the slope is negative; hence, the image would appear inverted (negative). Note also that the amplitude-phase curves are, in fact, piece-wise linear. Therefore, the nonlinear image distortions during the transformation are negligible.

Fig. 6.

Stimulus-induced pattern formation in the network of 200 × 200 IO oscillatory units. During the stimulation, the units are uncoupled. The initial phases are randomly distributed in the interval [0, 2π]. The stimulus has fixed duration τ_st = 0.4T, T = 51.1 and variable amplitudes. The stimulus amplitude pattern is taken from digitized grayscale 200 × 200 image, 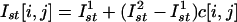, where c[i, j] ∈ [0,1] is the matrix of real numbers corresponding to the grayscale levels. The image c[i, j] contains a picture reproduced with permission from www.beautifulbugs.com. (A) Initial random distribution. (B and C) Phase cluster formation for excitatory stimulus pattern, I¹_st = 0.4, I²_st = 3.5. Phase distribution after the stimulation nicely reproduces the desired bug picture. After the stimulus, the oscillators group with required phases. The images are plotted with the same grayscale grade as the phase values interval [0,2π].

The phase distribution in the network is further translated to corresponding action potential patterns when the IO units fire Na-dependent spikes [the (u, v)–variables in Eqs. 1 at the peak times of the oscillations (Fig. 2C)]. When they are stimulated, the units are effectively uncoupled by the inhibitory feedback. When synchronized to the desired cluster configuration, the system tends to sustain this configuration if no other stimuli are applied. Because in-phase oscillators have a shorter coupling inhibition than out-of-phase oscillators, IO cells become effectively coupled, sustaining the synchronization. When the oscillators are phase-shifted, there is prolonged coupling inhibition because the inhibition periods are summarized from the two units. Thus, they stay effectively uncoupled, sustaining the phase shift. The example of SPR effect in the universal control system-based network represents the mechanism of sensory-motor transformation in the brain. The sensory information arriving as sequences of action potentials appropriately resets the motor control oscillators to a phase pattern that further converts to a space-time distribution of action potentials that implements a motor execution pattern.

Chaotic Modes. New functionally significant properties appear when shorter stimulation impulses τ_st « T applied to oscillatory component (Ca²⁺/K⁺) of the system (1):

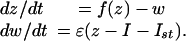[4]

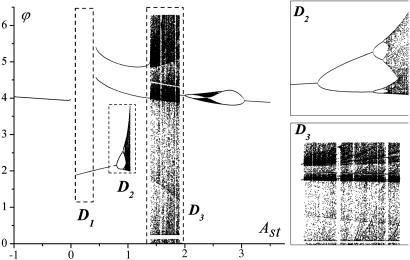
This case is biologically important because a stimulus may arrive to an IO neuron by means of synaptic input as a single or several action potentials. Action potentials have a characteristic time ≈1/100th of a period subthreshold oscillation of membrane potential. For our computer simulations, we chose the stimulation duration τ_st = 0.01T. In such a case, when stimulated with frequency not higher than frequency of subthreshold oscillations, the evolution of system's phase is defined by the sequent iterations of the phase response curve. The bifurcation diagram shown in Fig. 7 illustrates different attractor regions that correspond to different amplitude A_st of external stimulus I_st.

Fig. 7.

Bifurcation diagram of the reset phase for τ_st = 0.01T. D_i are the regions described in the main text. (Insets) The chaotic regions D₁ and D₂.

Three regions present main interest are designated as D₁, D₂, and D₃. In region D₁, the stable fixed point seems to attract all map trajectories with n → ∞. In this case, the map derivative T′(f) is close to 1, and therefore the map trajectories have quite a long transition before reaching the fixed point. The selfreferential phase reset occurs, but it takes longer for a system to “forget” the initial state. The regions D₂ and D₃ present special interest (Fig. 7 Insets). In D₂, a classical period doubling bifurcation occurs, and the map exhibits a chaotic behavior coexisting with period 2 stable limit cycles. Hence, there are an infinite number of 2^m (m = 1, 2,..., 8) coexisting orbits, and changing the stimulus amplitude can stabilize each orbit. After each stimulus, the oscillation phase jumps along the orbit. Therefore, spiking behavior of the IO neuron displays the spike consequences encoded by the orbits and represents the built-in mechanism for information encoding in the oscillatory neurons when the spike timings is associated with well defined stimulus-dependent phase reset. In the region D₃ (Fig. 7), the attractors are characterized by intermittent behavior. The map trajectories stay for a long time near the saddle-node bifurcation point, followed by long excursions in the whole [0,2π] region. The regions of chaotic behavior alternate with windows of stable periodic orbits. Each orbit also represents the encoded phase sequences realized for particular values of stimulus amplitude.

Discussion

In a previous study (17), we demonstrated that IO neurons have robust but sensitive subthreshold oscillation dynamics modulated by mutual electrotonic coupling. From that study, we learned that these dynamics intrinsically exhibit weakly chaotic properties, allowing almost regular periodic oscillations, while also supporting nonlinear sensitivity to initial conditions, resulting in the fast renewal of the system's memory (at ≈4 ms). Indeed, the phase plane portrait of the oscillation demonstrates radial trajectory divergence (stretching and folding) with little azimuthal divergence, as the result of the channels kinetics responsible for the membrane potential oscillation. These experimental findings were supported by a formal model of the IO neuron's subthreshold oscillations by using a Rössler-type nonlinear system (17).

Recently, using a nonlinear dynamical system (8), we modeled the SPR effect, originally observed experimentally in IO neurons (9–12). The results of the present study demonstrate an excellent fit to the experimental data. The SPR property has true nontrivial attributes concerning the type of global motor control function implemented by the olivo-cerebellar network. Because its response is independent of the IO oscillatory phase when the stimulus arrives, the system demonstrates extraordinary flexibility in organizing a given motor intention and in modifying its activity on-line according to sensory feedback. The system does not need an operational memory. This result makes it very reliable and prevents “computational overloads” that appear when memorizing the states. In fact, the speed of the SPR operation (of order of an oscillation period) is limited only by the oscillatory frequency and so it can operate many times faster than the actuators it controls.

The SPR property of IO oscillator can be very powerful in artificial control systems. Indeed, the oscillator represents a phase controller. One can set and maintain a required phase by delivering to the oscillator an appropriate stimulus pulse. Then, if the phase is associated with any given physical parameter (e.g., position, velocity, angle, or temperature), the phase controller can maintain it at a desired level. In contrast with standard control systems, the controlling principle here deals with a “motor recovery response” (16). Within limits, a walking animal may stumble without falling, in which case it promptly recovers its walking rhythm irrespective of when an obstacle is encountered during the stride. Such synchronization of large oscillator array requires only a synchronous reset stimulus and does not require to be electrically coupled. A fundamental aspect concerns the possibility of phase encoding when the map has both periodic orbits and chaotic attractors. In this case, the phase resets associated with these orbits are naturally transformed into neuron spiking. In turn, neurons fire spike trains with interspike intervals that are directly correlated with the orbits (18). Finally, the SPR effect can be viewed as an effective tool to represent and/or store information in the form of oscillatory clusters. In contrast to Hopfield gradient networks (19), cluster reorganization can be extremely fast because the oscillator frequency may be moved up to the limits of the constituent materials. Compared with Kuramoto-like oscillatory systems, where a complex coupling matrix should be applied to form the clusters (Hebbian learning rule), the SPR-based pattern formation can work directly with digitized information converted to the stimulus template.