Image-based gradient non-linearity characterization to determine higher-order spherical harmonic coefficients for improved spatial position accuracy in magnetic resonance imaging

Abstract

Purpose

Spatial position accuracy in magnetic resonance imaging (MRI) is an important concern for a variety of applications, including radiation therapy planning, surgical planning, and longitudinal studies of morphologic changes to study neurodegenerative diseases. Spatial accuracy is strongly influenced by gradient linearity. This work presents a method for characterizing the gradient non-linearity fields on a per-system basis, and using this information to provide improved and higher-order (9th vs 5th) spherical harmonic coefficients for better spatial accuracy in MRI.

Methods

A large fiducial phantom containing 5229 water-filled spheres in a grid pattern is scanned with the MR system, and the positions all the fiducials are measured and compared to the corresponding ground truth fiducial positions as reported from a computed tomography (CT) scan of the object. Systematic errors from off-resonance (i.e., B0) effects are minimized with the use of increased receiver bandwidth (±125 kHz) and two acquisitions with reversed readout gradient polarity. The spherical harmonic coefficients are estimated using an iterative process, and can be subsequently used to correct for gradient non-linearity. Test-retest stability was assessed with five repeated measurements on a single scanner, and cross-scanner variation on four different, identically-configured 3T wide-bore systems.

Results

A decrease in the root-mean-square error (RMSE) over a 50 cm diameter spherical volume from 1.80 mm to 0.77 mm is reported here in the case of replacing the vendor’s standard 5th order spherical harmonic coefficients with custom fitted 9^th order coefficients, and from 1.5mm to 1mm by extending custom fitted 5th order correction to the 9th order. Minimum RMSE varied between scanners, but was stable with repeated measurements in the same scanner.

Conclusions

The results suggest that the proposed methods may be used on a per-system basis to more accurately calibrate MR gradient non-linearity coefficients when compared to vendor standard corrections.

1. Introduction

There are a variety of applications for which spatial position accuracy in magnetic resonance imaging (MRI) is particularly critical, including surgical planning[1], radiation therapy planning[2], longitudinal studies of neurodegenerative disease[3,4], and MR-PET attenuation correction[5]. In each of these applications, the soft tissue contrast of MRI is desired in order to obtain the necessary information, but the spatial distortion of the MR image presents a barrier to adoption[6,7].

MRI is particularly attractive for proton beam therapy because of its ability to clearly demarcate the target from surrounding radiosensitive organs at risk[8]. There is also interest in using MR imaging alone, without a corresponding pre-treatment computed tomography (CT) exam, for both photon and proton radiation therapy planning[6,9,10]. A major technical challenge in utilizing MRI lies in determining the geometric accuracy of the tissues that are to be targeted or avoided during radiation therapy.

A primary source of error affecting the geometric accuracy of an MR image is the spatial distortion caused by spatial gradient nonlinearity (GNL). Imaging gradients ideally are designed to vary linearly across the magnet’s diameter of spherical volume (DSV) and the associated maximum field-of-view (FOV). However, due to the constrained geometry of the gradient coils, design or engineering trade-offs, and limitations imposed by Maxwell’s equations, residual GNL will be present within the imaging volume. If gradient nonlinearity is not accounted for during image reconstruction, the generated MR images will exhibit geometric spatial distortion. This distortion can be retrospectively corrected after via image-based interpolation[11], or circumvented by using a model-based inverse problems framework that prospectively accounts for GNL[12–14]. If GNL is not accounted for in any manner, however, the generated images will exhibit severe geometric spatial distortion, which typically manifests as either a “barrel” or “pincushion” type of effect. In certain instances, even GNL-corrected images exhibit some residual distortion, particularly if the supplied nonlinearity map was insufficiently accurate or the maximum spatial order of the polynomial fit is not sufficiently high. As the magnitude of gradient nonlinearity increases with distance from gradient isocenter, this effect is more pronounced towards the edges of the FOV, and especially when a large FOV is prescribed. Position errors up to 5 mm from truth have been reported[15], potentially impairing the accuracy of radiation therapy treatment planning. Previous work has shown improved GNL correction for a compact 3T system using an asymmetric gradient design for the transverse axes and a 26 cm DSV[16]. In that work the ADNI phantom was used as a reference and up to 10th order GNL correction was studied[17]. The present work extends those methods to whole body systems with large (e.g., up to 50 cm) FOV imaging.

2. Methods

This work utilizes a large 3D-printed fiducial phantom[18] that has been previously utilized for assessing gradient nonlinearity in large FOV MRI applications. The phantom consists of a three-dimensional array of 5229 MR visible water-based paintballs (Rap4, Modern Combat Solutions, Gilroy, CA) uniformly distributed throughout. Each paintball has a diameter of 6 mm and the center-to-center distance between each neighbor is 25 mm in each orthogonal direction. Applying RAS (Right, Anterior, Superior) coordinates to the phantom placed in a supine, head-first orientation, the total MR visible extent (marker center-to-center) of the phantom is 52.5 cm superior/inferior, 47.5 cm left/right, and 35 cm anterior/posterior. The matrix is made up of low density foam, and secured with acrylic rods.

MR images of the phantom were acquired with a 3D gradient-echo sequence with 614 mm square FOV, 1.2 mm acquired and reconstructed isotropic voxels in all three axes and ±125 kHz receiver bandwidth (readout L/R, phase A/P, slab S/I) utilizing the body coil for transmit and receive on a 3T scanner (Discovery MR750w, software version DV25.0, GE Healthcare, Waukesha WI) with a nominal 50cm imaging DSV and 70cm patient bore aperture. The phantom was placed at magnet/gradient isocenter in S/I and L/R, and aligned as closely as possible with the physical axes by iterative positioning with a 2D 3-plane gradient-echo localizer scan through aligning the center of the grid with isocenter. In order to minimize any effects of main magnetic field (B0) inhomogeneity the imaging was done at the maximum available receiver bandwidth. Additionally, paired image sets were acquired using the identical imaging parameters, but with the polarity of the readout gradient direction reversed[19]. Thus, two scans are required for each experiment, both the DICOM image output including the vendor GNL correction and the raw MR data are saved for use in the calibration procedure. Total acquisition time for both 3D scans was approximately 71 minutes (35.5 minutes each gradient readout polarity).

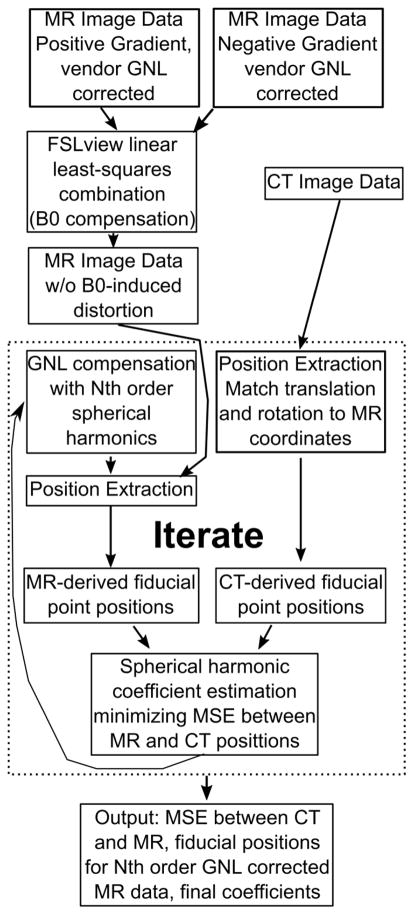
As an overview, Figure 1 shows a schematic representation of the calibration process. To determine the true positions of the fiducial markers, the phantom was scanned with X-ray CT (SOMATOM Definition AS, Siemens, Erlagen, Germany). Images were acquired with 1.27 mm in-plane resolution with a 0.6 mm slice thickness using 120 kVp. The fiducial positions in the CT data were determined using software associated with the phantom design [18], which is a vendor-provided tool. This process could be brought in house with some effort, but the existing code was well validated.

Figure 1.

An overview of the calibration process. Briefly, the MR image data before any corrections are registered together in FSLview via the “topup” command, which creates a single 3D volume without off-resonance induced shifts. These data are then corrected via industry standard interpolative warping with the vendor-supplied spherical harmonic coefficients as a bootstrapping technique to get closer to the mean-square-error-optimal solution. The CT and MR image data are then processed to extract the fiducial positions, with the CT data translated and rotated via and singular value decomposition-based technique. These positions are compared and new spherical harmonic coefficients are estimated on the criteria that they minimize the mean square error between the MR and CT fiducial positions. These coefficients are then used to correct the original MR data after off-resonance correction, and the positions re-estimated. This process continues until convergence.

Whereas historically the vendor-provided spherical harmonic model coefficients typically have been specified only up to 5^th order[11], we utilized an independent calibration tool to generate 3^rd, 5^th, 7^th, and 9^th order model coefficient sets as follows: In all cases, iterative calibration process was initialized with the vendor-provided spherical harmonic coefficients in order to bootstrap the process for faster convergence, as the vendor coefficients are available and the residual warp field between the vendor correction and the fitted positions can be calculated. The standard- and reversed-readout gradient polarity acquisitions were mutually registered before any GNL correction was applied using the FMRIB Software Library tools “topup” linear estimator[20,21]. This estimator attempts to fit the underlying off-resonance field which, when applied to the image data, causes the observed image distortions, and using that field solves for a single off-resonance corrected volume. This is done to account for any B0 off-resonance based geometric distortion in the image, as the reversed gradient polarity acquisition would result in a positional shift equal in magnitude, but opposite in direction from the “normal” gradient polarity acquisition. This effect is well known [19], but must be compensated before gradient non-linearity calibration procedure to ensure B0 effects do not corrupt the GNL model coefficients.

Spherical harmonics as a basis function for characterizing gradient non-linearity has roots in a justification that they provide a solution for Laplace’s equation. These are usually described in spherical coordinates[22], and are expressed through the associated Legendre polynomials. In more detail, the displacement due to gradient non-linearity at any point d_k (x⃑) for the k-axis where k is the X, Y or Z gradient coil can be described by

$$d_k(\stackrel{\rightharpoonup }{x})=\sum _{n=0}^N\sum _{m=0}^n{r}^n(\stackrel{\rightharpoonup }{x})P_{nm}\left(cos\left(\theta (\stackrel{\rightharpoonup }{x})\right)\right)\left[A_{nm}^k\mathit{cos}\left(m\phi (\stackrel{\rightharpoonup }{x})\right)+B_{nm}^k\mathit{sin}\left(m\theta (\stackrel{\rightharpoonup }{x})\right)\right]$$

where x⃑ is the true position in the volume, r(x⃑), θ(x⃑), and φ(x⃑) are the polar coordinate representation of the position x⃑, N is the model order, with $A_{nm}^k$ and $B_{nm}^k$ representing coefficients with order n and degree m for the k-axis gradient coil. P_nm represents the aforementioned associated Legendre polynomial with the noted order and degree. The model fitting was performed using a subset of spherical harmonic polynomial basis: one polynomial term corresponding to a certain degree (m) in each order was used for each gradient coil (i.e., A_n,1 for x gradient, B_n,1 for y gradient, and A_n,0 for z gradient). This configuration is consistent with the standard practice on GE’s gradient system[23] and is incorporated in their gradient coil design [24] with a maximum order 5 [11]. We are now free to choose the maximum order N for which we will characterize the gradient field. Note also that we limit the basis set to odd n, as this is a design constraint for the gradient coils under investigation.

The off-resonance corrected image sets were then analyzed using in-house developed Matlab-based position estimation software to identify fiducial markers in the MRI data, estimate their spatial locations, and compare these physical values against the CT reference. Fiducial marker identification and position estimation in the position tracking software was performed using a 3D Hough transform[25,26], and was re-estimated at each iteration. Using these nominal MR image based marker position estimates and presuming CT identified positions as the gold standard, a finite-order spherical harmonic model[22] of the distortion field was estimated using the iterative RMSE minimization scheme proposed by Trzasko et al. [17].

Briefly, the fitting procedure minimizes residual mean-square-error between the CT and MR position and alters the spherical harmonic coefficients via Gauss-Newton iteration. Note that rotations and translations of the MR data compared to the CT data are tracked and compensated in the fitting process using a singular value decomposition-based method[27], which seeks the rigid transformation matrix minimizing the least-square difference between the fiducial positions in the CT and MRI data sets. This fitting procedure was performed (as separate trials) over three different diameter spherical volumes (DSVs), 340 mm, 420 mm, and 500 mm. It was previously shown that 10 iterations is sufficient for convergence[17]. On a dual eight-core Xeon system with 128 GB of RAM, each iteration of this procedure required 25 minutes of computation, or about 4.2 hours for the entire fitting process. Using the field distortion maps generated from these coefficients, the raw MR images were resampled to correct for the observed gradient nonlinearity. Resampling was done in the image-domain using cubic spline interpolation[11]. Finally, the 3D magnitude displacement compared to the CT image of each fiducial marker interrogated by the fitting routine was plotted to generate position dependent accuracy figures.

To test inter-scanner variation of the GNL coefficients, we performed the above-described procedure across a total of four MR units of the same model at our institution. These data were acquired to investigate whether gradient nonlinearity varies appreciably even between like scanners, e.g., due to manufacturing variances such as coil winding errors[22].

To investigate test-retest repeatability of the measurements, we performed this same experiment five times on a single MR system over two sessions. The phantom was completely removed from and then replaced in the scanner bore between each run to simulate an independent experiment in an effort to validate repeatability and invariance to small unavoidable translations and rotations of the phantom.

3. Results

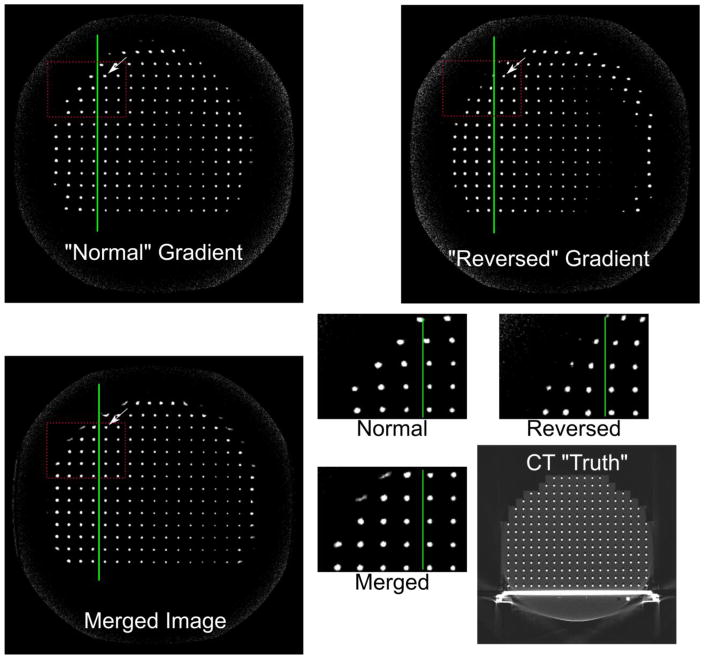
An example of the off-resonance effect is shown in Figure 2, where the standard and reverse readout polarities manifest opposite shifts in the frequency-encoded direction of fiducial markers at the points indicated by arrows in the large set of images. The insets show a magnified portion denoted by dashed lines, clearly indicating the off-resonance effect in shifting fiducials, especially towards the superior edge of the phantom, with these images acquired at approximately 10 cm off-isocenter. The inset on the bottom right shows magnified views of part of the image.

Figure 2.

Off resonance artifact and correction demonstration. Note that in the normal vs. reversed gradient polarity the fiducial markers along the green line shift along the frequency-encoded direction (right-left). The magnified insets emphasize this effect. These images are reconstructed with the vendor standard 5^th order gradient non-linearity correction method in order to demonstrate the B0 off resonance effect, but the correction itself is done on non-GNL compensated data.

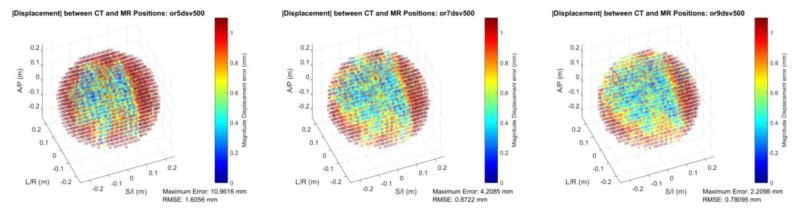
Figure 3 shows spatial accuracy in the form of root-summed-squared (RSS) error vs. the CT position reference for a 340 mm DSV, comparing the fitted 5^th, 7^th, and 9^th order corrections. Additionally, Figure 4 shows the fitted 5,7,9^th order corrections for a 500mm DSV. Both figures also include the maximum error from the interrogated fiducials, as well as the RMS spatial error over all fiducials. The 340 mm DSV results show that there is little to no improvement in the RMSE when moving from 5^th to 9^th order fitted corrections. Considering the 500 mm DSV dataset, there is a large change in RMSE from the fitted 5^th to the fitted 9^th order correction, and the maximum error is also reduced substantially from 10.96 to 2.21 mm.

Figure 3.

Color-coded, magnitude displacement error of the fiducial phantom MRI reconstruction as compared to the CT-measured ground truth positions for a 340 mm DSV and three different model orders used for gradient nonlinearity correction. The 5^th, 7^th, and 9^th order corrections are shown from left-to-right. Reported in the inset are the RMSE and maximum error of the dataset.

Figure 4.

Color-coded, magnitude displacement error of the fiducial phantom MRI reconstruction compared to the CT-measured ground truth positions for a 500 mm DSV across three different model orders used for gradient nonlinearity correction. Note the improved spatial accuracy moving from 5th to 7th, then to 9th order corrections. Reported in the inset are the RMSE and maximum error of the dataset.

Figure 5 shows MR images at axial planes approximately 14 cm inferior to isocenter, and coronal planes approximately through isocenter corrected with the fitted up to 5^th, 7^th and 9^th order models respectively. The two image planes are shown to illustrate that there is an improvement in gradient linearity in all three dimensions. Note the fiducial markers in the 7^th and 9^th order case, vs 5^th order are properly reconstructed to the imaging plane at the FOV boundaries and the reduced pincushion effects. The improvement is evidenced in the axial plane by the increased number of fiducials visible in what is a planar array of fiducials in 3D space. In the 5^th order case, many of the fiducial markers have been pulled out of plane by uncompensated gradient nonlinearity. As the distortion correction moves to include higher order basis functions, the reconstructed image becomes more planar, thus the image includes the truly planar fiducial grid.

Figure 5.

5^th, 7^th, and 9^th order axial and coronal views of the fiducial phantom. Note that with increasing model order, the number of visible paintballs increases due to the improved out-of-plane non-linearity correction. Axial and coronal planes are presented to illustrate distortion correction in all three dimensions.

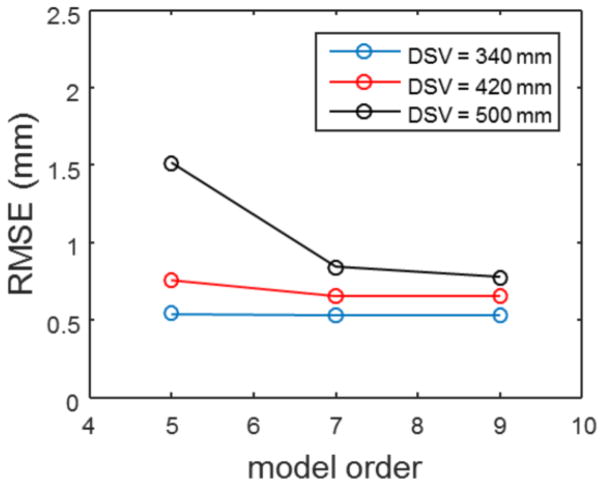
Figure 6 shows the RMS spatial error comparison as a function of spherical harmonic model order used for a single system across the three different diameter spherical volumes. The smallest diameter spherical volume shows minimal differences in RMSE across the different model orders. However, the larger DSVs show improved accuracy with the 9^th order correction verses the two lower model order cases.

Figure 6.

RMSE verses model order and DSV. Note the relatively flat response to model order by the smallest volume interrogated. The large DSV sees the most improvement when going to a higher order set of coefficients.

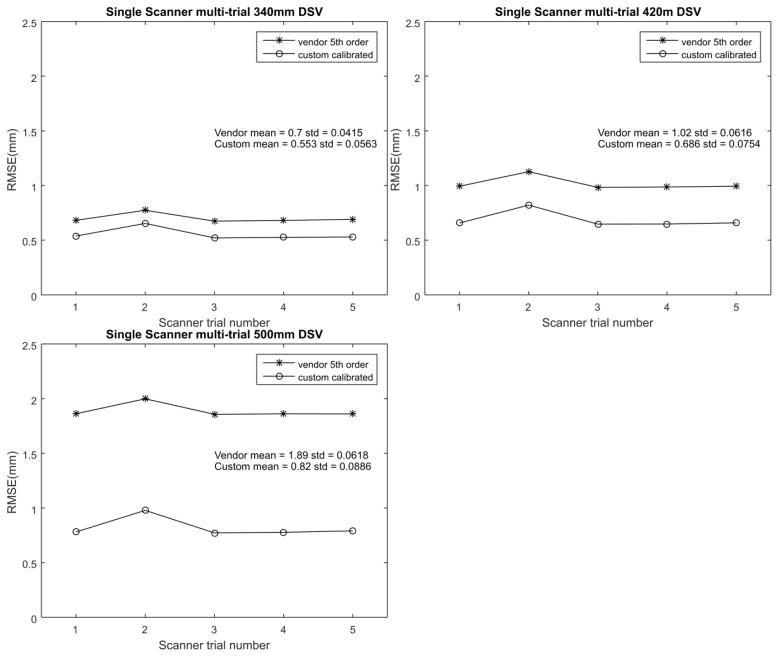
Figure 7 shows each of the 5 trials comparing the RMSE values of fitted 9^th order verses vendor standard 5^th order on the single scanner tested. The fitted coefficients produce a lower RMSE compared to the vendor’s standard 5^th order correction.

Figure 7.

RMSE verses scanner trial broken up by DSV. Each of these compares the 9^th order fitted with the standard 5^th order vendor supplied correction. Note that the standard deviation of the measured RMSE is an order of magnitude below the mean.

Table 1 shows results of the spherical harmonic fitting process for the intra-scanner comparison from N = 5 experiments. For sake of readability, we have included only the superior/inferior coefficients for the 9^th order fitting. Compared to the multi-scanner results we note a reduction in coefficient of variability, suggesting that 1) our estimation procedure is robust, with high repeatability, and 2) that individual system characterization can provide some additional benefit, verses one set of coefficients per scanner model. The full set of coefficients is available in Table S1 in the supplementary materials.

Table 1.

DSV	Superior/Inferior coefficients for 9th order fitting with different calibration volumes – Intra-scanner comparison
	9th Order Maximum
3rd order	Mean	Std Dev	CoV
340mm	−1.194E-04	8.217E-07	−0.0069
420mm	−1.192E-04	1.102E-07	−0.0009
500mm	−1.191E-04	1.315E-07	−0.0011
5th order
340mm	−1.759E-08	1.319E-09	−0.075
420mm	−1.795E-08	1.786E-10	−0.01
500mm	−1.794E-08	6.182E-11	−0.0034
7th order
340mm	9.681E-12	1.514E-12	0.1564
420mm	9.990E-12	3.575E-13	0.0358
500mm	9.993E-12	7.026E-14	0.007
9th order
340mm	−1.700E-16	4.313E-16	−2.5368
420mm	−6.760E-16	1.352E-16	−0.2
500mm	−7.245E-16	1.689E-17	−0.0233

Table 2 shows results of the spherical harmonic fitting with 9 orders considered for the N = 4 multi-scanner comparison. For sake of readability, we have included only the superior/inferior coefficient set. Note that the lower order coefficients are much larger compared to the higher orders, and also have a lower coefficient of variability. We note that increasing the interrogated DSV from 340 to 420 or 500mm increases the stability of the coefficient estimation. The full set of coefficients is available in Table S2.

Table 2.

DSV	Superior/Inferior coefficients for 9th order fitting with different calibration volumes – Inter-scanner comparison
	9th Order Maximum
3rd order	Mean	Std Dev	CoV
340mm	−1.186E-04	2.685E-07	−0.0023
420mm	−1.193E-04	2.565E-07	−0.0022
500mm	−1.193E-04	1.912E-07	−0.0016
5th order
340mm	−1.832E-08	4.868E-10	−0.0266
420mm	−1.818E-08	8.290E-11	−0.0046
500mm	−1.797E-08	8.994E-11	−0.005
7th order
340mm	1.065E-11	4.520E-13	0.0424
420mm	1.043E-11	2.549E-13	0.0244
500mm	1.009E-11	1.018E-13	0.0101
9th order
340mm	−1.033E-15	1.122E-15	−1.0862
420mm	−8.132E-16	1.835E-16	−0.2256
500mm	−7.387E-16	2.755E-17	−0.0373

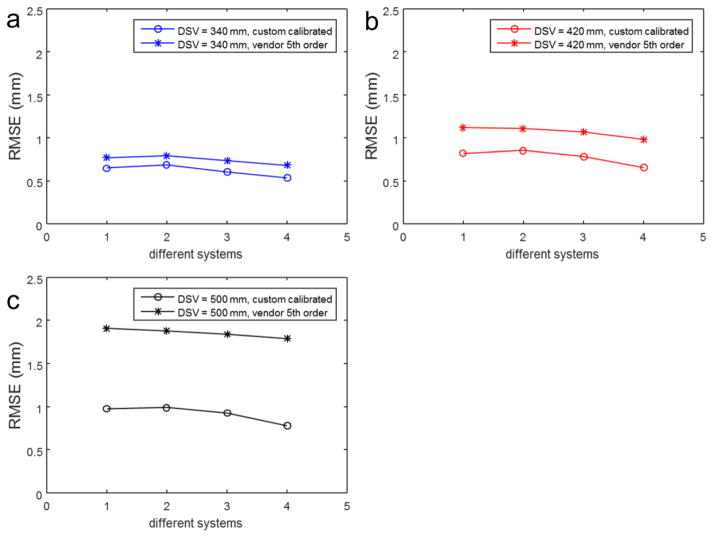
Figure 8 shows the RMS spatial error across multiple MR scanners of the same hardware configuration for three different DSVs for the 9^th order fitted coefficients verses the vendor standard 5^th order coefficients.

Figure 8.

RMSE with calibrated 9th order coefficients vs. vendor supplied 5^th order coefficients, also compared across the 4 identical MR systems investigated. Note that for smaller DSV, the difference in RMSE is less pronounced as opposed the larger 500 mm DSV. Additionally, note that system 4 appears to have somewhat more correctable non-linearity versus systems 1–3. These differences highlight the importance of performing the calibration on a per-system basis.

4. Discussion

We have applied an imaging-based method for characterizing and correcting gradient non-linearity of whole-body scanners on a per-system basis. This adaptive calibration capability reduces the RMS spatial error substantially from standard non-adaptive 5^th order GNL correction that is conventionally used in routine clinical MRI, potentially allowing for a higher level of confidence when using MR images for radiation therapy planning. The use of 3D MRI acquisition (i.e., with two phase encoding directions) avoided B0 errors in the two orthogonal phase-encoding directions. By acquiring two sets of images which are identical, except for the polarity of the readout gradient, we minimized any confounding off-resonance effects on the locations of the fiducial markers measured with MRI in the readout direction. Use of a single readout polarity would have mixed gradient non-linearity effects and the off-resonance effects. This would have been particularly problematic for large FOV acquisitions and as well acquisitions for which shimming is difficult, like the paintball phantom utilized in this work. Note that there may be some limit to the off resonance correction, as the fiducials near the superior and inferior edges of the large DSV studies show consistently worse error. This may be due to gross, uncorrectable off resonance effects. In other works the forward and reversed gradient readout polarity images themselves are subjected to a position estimation step, and then those positions are averaged to find an off-resonance free distortion map[28]. We chose to do the B0 correction upfront and perform a single position estimation step, but the other method could be used as well.

An important consideration was the limitation of the model to a maximum of order 9. Figure S3 shows the RMSE for orders up to and including 11th order, as well as the 13th order. To investigate this further, we have applied the coefficients estimated from a single trial of the single-scanner experiments to different datasets within that trial. Table S1 shows the results of this fitting process. Note: the fitting for 11th order was stable on the largest (500 mm DSV) but unstable at the smaller DSVs. This leads to the conclusion that the large size of the phantom is essential to the success of this fitting process. Note also the decrease in RMSE as order increases from 5th to 7th to 9th to 11th grows smaller with each increment, and the increment to 11th order is on the micron level. Given the difficulty in obtaining the fits, we believe the 9th order fitting is sufficient. The residual distortion can be due to a series of effects, such as the residual off resonance distortion, numerical estimation accuracy in fiducial tracking, as well as other residual system imperfections like eddy current, although these are minimized by optimizing the acquisition protocol. Note that the calibration was performed with odd order terms excluding the even-orders to minimize the impact from these effects, which is in consistent with the state-of-the-industry.

We note that the single scanner calibration results show magnitude of coefficients of as order of magnitude below the coefficients of variation for the between-scanner results. This order-of-magnitude difference suggests that 1) the iterative gradient nonlinearity estimation method[17] exhibits reproducible performance and capability, and 2) the coefficients of gradient nonlinearity distortion field models can and should be optimized for individual MRI scanner systems. We remark that these observations are based on heuristic assessment of the results in presented in Tables 1 and 2, rather than formal statistical testing. Due to the relatively small number of coefficients in the evaluated distortion field models, there was insufficient power to make a statistical significance argument between them. The improved root-mean-square-error results shown in Figure 7, however, demonstrate the value of calibration on a per-system basis.

While we did compensate for translations and rotations from the MR coordinates to the CT coordinates, it is likely that small positioning inconsistencies in the MR data may influence the calibration – see results number two in Figure 7 detailing the RMSE for one of five runs on a single scanner. These small translations and rotations may result in minute differences in whether a few fiducials are recoverable in the fitting process. Some fiducials located around the edge of the imaging volume experience dramatically changing distortion field from GNL, and slight change of phantom positioning (translation and rotation) may render these fiducials to be unrecoverable. It may well be that there is a better position for the phantom to be in order to best characterize the gradient field, but we attempted to align with system axis in the isocenter. Limiting the spherical harmonic model to the 1st degree was also done to allow for rotational invariance with the fitting and increasing robustness to slight positioning errors and potential over-fitting to distortions caused by other physical effect (i.e. eddy current).

Maximum error is reported for each case in Figures 2 and 3. We note that this metric is of interest especially for radiation therapy planning, as it can serve as a metric for “worst case” in dose delivery. We note that this maximum error is quite stable for the 340 mm DSV across all model orders, but that it decreases quite dramatically as model order increases for the large 500 mm DSV. This further demonstrates the value in higher order calculations with these large FOVs. Another consequence of this result is that imaging near the isocenter of the magnet results in less gradient non-linearity. As is well known, imaging near the isocenter should be considered whenever practical.

Note in Figure 5 the subtly increased background noise near the edges of the FOV in the identically window/leveled images with the higher order correction. This artifact is due to an increase compensation term from “spreading out” image intensity from previously overlapping pixels in the image-based correction for gradient nonlinearity. This suggests the utility of an integrated gradient nonlinearity correction and image reconstruction[29] that has previously been shown to decrease image blurring, to further improve image quality.

In other work[18] it has been demonstrated that a template-based ground truth approach could be taken to determine initial fiducial positions. To account for possible manufacturing errors in the phantom, we elected to use a CT scan as the gold standard for position. Any errors in the CT position information would degrade our measurements, but the CT scan was done at a 1.2 mm in-plane spatial resolution, with about 0.6 mm through plane resolution. This is substantially smaller than the paintball (6mm diameter) and the spacing (25mm) between paintballs. Additionally, the 3D Hough transform method has been shown to localize the shapes of interest to sub-voxel precision[30].

An interesting application of this work is to calibrate multiple systems across many sites using the described procedure, such that gradient nonlinearity correction processes account for system-specific deviations, as opposed to the “one size fits all” coefficients derived from the standard electromagnetic calculations. Further deployment of this technique would allow for sufficient statistical power to examine the significance of system-by-system deviation. Future work to measure GNL on other systems from other vendors would also be of interest.

While this work does account for gross off-resonance effects caused by imperfections in the B0 shim during the gradient non-linearity estimation it does not seek to characterize or correct for patient-induced susceptibility effects[31]. In general, those spatial distortions caused by off resonance are treated independently from GNL calibration and correction, e.g., by tailoring the readout bandwidth to the specific patients acquisition.

The proposed calibration and correction could be practical to implement on a per-system basis across a wide fleet of MR scanners. While the phantom is somewhat bulky, it only weighs 14 kg. The total acquisition time to acquire the MR data is 71 minutes per system. The data analysis can be done off-line, and once the GNL coefficients are determined for a particular MR system, we expect they will remain valid indefinitely, or until the gradient coil is replaced, as has been previously demonstrated for an MR system[32]. That is to say, since the gradient coils are fixed on the installation of the scanner, this procedure could be incorporated into the clinical acceptance of the system, subject to coordination with the install and maintenance teams. We do note that the current implementation takes a long time to process, but the current implementation is a hybrid single-threaded MATLAB analysis suite which requires a large amount of small file reading and writing. Some additional time polishing the implementation would significantly decrease the calibration time. The technique can be useful in multi-site MRI studies where consistent spatial accuracy is desired among sites. This is also beneficial for longitudinal clinical MR studies where high level of spatial accuracy is needed, as the same patient may get scanned on different scanner for repeated sessions. This method has not currently implemented into clinical workflow, as IRB approval would be needed to collect raw data and then reconstruct with the modified non-linearity corrections. However, the interpolative gradient non-linearity correction is of relatively low computational cost, and it takes on the order of seconds. The overall correction time would be dominated by system I/O, i.e., saving raw data, transferring to server, and DICOM pullback to the scanner host computer’s DICOM database. Analogous processes have been used for other IRB-approved applications at our site, and all steps routinely are accomplished for more computationally intensive datasets and algorithms in under five minutes.

5. Conclusion

In this work, we have demonstrated improved geometric accuracy and precision for large FOV MRI by a per-system, calibration and fitting procedure for GNL coefficients. The results show improvement in geometrical accuracy not only by going to higher spatial order (e.g., from 5^th to 9^th order), but also comparing 5^th order corrections with the custom-fit and vendor supplied coefficients.

This work has application in a variety of areas, including pre-surgical planning, and particularly to radiation therapy planning.

Supplementary Material

1

Figure S1: RMSE for a given iteration set of three different DSV’s. Note that the method appears to converge after about 5 iterations, and does not change after about ten. Based on these results, we settled on ten iterations as suitable for the calibration process.

Figure S2: Axial fiducial images for the three different model orders presented. Note that there is significant residual gradient non-linearity present at the edge of the FOV (Approximately 26cm superior from isocenter). There is significantly worse out-of-plane distortion on the lower model order results, which improves with increasing model order.

Figure S3: RMSE curves vs. iteration for a given dataset with terminal orders of 9, 11, and 13. Note that for order 13 the fitting process becomes unstable. We also refer to Table S1, and note that the RMSE for the 11^th order fit is only improved by about 1%, but the fitting becomes unstable at smaller DSV analysis volumes.

Table S1: RMSE from a given dataset analyzed up to the 11th order. The dashed lines in the bottom right indicate that the fit process was unstable for the given calibration DSV. We note the decreasing RMSE improvement, as well as the fitting instability as a good criterion to stop the fitting at order 9..