Summary
The fluorescence microscopy methods presently used to characterize protein motion in cells infer protein motion from indirect observables, rather than measuring protein motion directly. Operationalizing these methods requires expertise that can constitute a barrier to their broad utilization. Here, we have developed PIPE (photo-converted intensity profile expansion) to directly measure the motion of tagged proteins and quantify it using an effective diffusion coefficient. PIPE works by pulsing photo-convertible fluorescent proteins, generating a peaked fluorescence signal at the pulsed region, and analyzing the spatial expansion of the signal. We demonstrate PIPE’s success in measuring accurate diffusion coefficients in silico and in vitro and compare effective diffusion coefficients of native cellular proteins and free fluorophores in vivo. We apply PIPE to measure diffusion anomality in the cell and use it to distinguish free fluorophores from native cellular proteins. PIPE’s direct measurement and ease of use make it appealing for cell biologists.
Keywords: fluorescence-based techniques, molecular diffusion, protein mobility, photo-conversion, anomalous diffusion, molecular crowding, protein oligomerization, protein quality control, protein aggregation, Sod1
Graphical Abstract
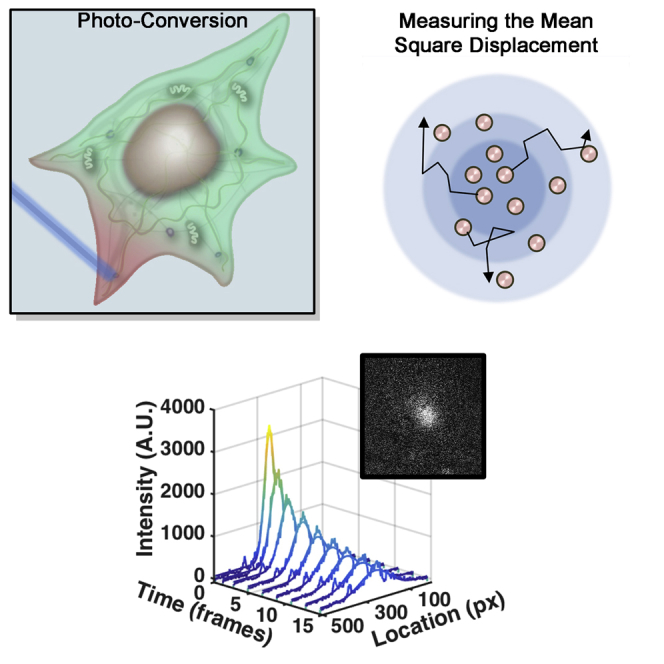
Highlights
-
•
PIPE directly measures rapid motion of proteins in the cell cytoplasm
-
•
PIPE aids users in understanding the analysis and assessing the results’ quality
-
•
We observe slower motion of aggregation-prone Sod1 mutants compared with wild-type Sod1
-
•
We measure diffusion anomality of free fluorophores and cellular proteins in vivo
Gura Sadovsky et al. present a fluorescence microscopy method that directly measures rapid protein motion in the cytoplasm using photo-convertible fluorophores and fast imaging. The method provides cell biologists with easily accessible and reliable quantitative measurements of protein motion in their chosen systems of interest.
Introduction
Protein motion plays an important role in biological function at a range of scales. Starting from the single-protein level, enzyme motion has been shown to accelerate in vitro when substrate concentration is higher (Riedel et al., 2015). On the pathway level, substrate motion affects the likelihood of enzyme binding (Gabison et al., 2006, Takahashi et al., 2010), which, in turn, affects pathway efficiency (Castellana et al., 2014). Finally, on the cellular level, protein motion changes under global cellular perturbations, including hyperosmotic stress (Miermont et al., 2013), unfolded-protein stress (Lai et al., 2010), and heat shock (English et al., 2011).
Unlike the simple motion of proteins in buffer, protein motion in the cell cytoplasm is complexly modulated by interactions with cellular components. In buffer, protein motion is driven by thermal fluctuations delivered through interaction with water molecules. This motion is accurately described by the Fickian diffusion equation, whose only parameter is the diffusion coefficient. In contrast, proteins in the cell cytoplasm interact not only with water molecules, but also with various biomolecules and cellular structures that densely populate the cytoplasm (Luby-Phelps, 2000). These interactions significantly affect protein motion: binding to large complexes may transiently trap proteins, slowing them down (Saxton, 1996), while interacting with ATP-driven components such as molecular motors and fluctuating cytoskeletal fibers may speed proteins up or constrain their motion to specific directions (Guo et al., 2014a). The complex nature of protein motion in the cytoplasm is not easily captured by simple models. Fickian diffusion, reaction-diffusion equations (Engelke et al., 2009), and anomalous diffusion (Saxton, 2012, Weiss et al., 2004) have all been used to describe effective parameters of protein motion, such as diffusion coefficients, binding and unbinding rates, and anomalous exponents, but none of these models is regarded as adequately describing protein motion (Saxton, 2012).
To test models of cytoplasmic protein motion against experimental data, researchers have developed quantitative fluorescence microscopy methods, including correlation-based and perturbation-based methods (see Table 1). Correlation-based methods, such as fluorescence correlation spectroscopy (FCS), extract information about protein motion from the autocorrelation of the fluorescence signal. The autocorrelation can be analytically calculated given the model of motion, and doing so enables users to test the model by fitting the calculated expression to the imaging data. Correlation-based methods have been used in vitro to measure reduced diffusion of biomolecules due to molecular crowding (Engelke et al., 2009). These methods have also been used extensively in vivo, for example, in characterizing the dynamics of human islet amyloid polyprotein interaction with the cell membrane (Guo et al., 2014c), in measuring diffusion of paxillin near focal adhesions (Digman et al., 2008) and in determining the interactions of the polyprotein Gag with cytoplasmic complexes (Larson et al., 2003). In comparison with correlation-based methods, perturbation-based methods implement a more active approach, using a laser pulse to perturb the fluorescent sample and image it as diffusion smooths out the perturbation. Usually, the laser pulse depletes fluorescence from the perturbed region through photo-bleaching, and the observable analyzed is either the recovery of fluorescence at the bleached region (as in fluorescence recovery after photo-bleaching [FRAP]) or the loss of fluorescence outside that region. In samples containing photo-convertible fluorophores, the laser pulse generates a fluorescence signal rather than depleting it, and the observable analyzed is the subsequent decay of fluorescence at the photo-converted region (Calvert et al., 2007, Ehrlicher et al., 2011, Mazza et al., 2008). In all of these cases, models can be tested by fitting the measured observable to a predicted analytical expression. Perturbation-based methods are convenient to apply to cytoplasmic proteins, because these methods work well with high protein concentrations, which usually characterize cytoplasmic proteins.
Table 1.
Comparison of PIPE with Popular Fluorescence Microscopy Methods for Measuring Protein Motion in the Cell
| Method | Observable | Requirements | Photo-Bleaching Sensitivity | Ease of Use |
|---|---|---|---|---|
| FCS | autocorrelation of fluorescence fluctuations (indirect) | continuous point imaging, low fluorophore concentration, calibration of point spread function | not sensitive to mild and uniform bleaching | easy acquisition and analysis, but assessment of output quality requires expertise |
| SPT | trajectories of single fluorophores (direct) | fast or stroboscopic imaging for cytoplasmic proteins, low fluorophore concentration | sensitive to photo-bleaching and blinking | requires acquisition of many trajectories per experiment |
| FSM | trajectories of co-localized fluorophore clusters (direct) | most suitable for studying motion of polymers, microinjection of fluorophores is often needed | not sensitive to mild and uniform bleaching | similar to SPT |
| FRAP | recovery of average fluorescence in photo-bleached region (indirect) | calibration of beam width | sensitive to reversible photo-bleaching | easy acquisition and analysis, but assessment of output quality requires expertise |
| FRAPa/FLAC/FDAP | decay of average fluorescence in photo-converted region (direct) | photo-convertible fluorophores, calibration of beam width | sensitive to photo-bleaching | easy acquisition and analysis, but assessment of output quality requires expertise |
| PIPE | spreading of initially localized photo-converted fluorophores (direct) | photo-convertible fluorophores | not sensitive to mild and uniform bleaching | easy acquisition and analysis, quality assessment is intuitive |
These methods are in addition to confinement by cell membrane, which interferes with all ensemble methods applied to cytoplasmic proteins. FLAC, fluorescence loss after photo-conversion. FDAP, fluorescence decay after photo-activation.
Each of these methods can be challenging to operationalize in a research setting. First, each of the methods requires either a calibration of the excitation beam width or a careful measurement of the microscope point-spread function (Petrášek and Schwille, 2008). Second, users find it challenging to assess the accuracy of the methods in a given instance. For example, FRAP results may be skewed by reversible photo-bleaching, i.e., spontaneous turning on of photo-bleached fluorophores within the pulsed region. Most users cannot assess whether reversible photo-bleaching skews a particular instance of their FRAP analysis merely by looking at the results. FRAP presents users with a single fluorescence recovery curve and a model that was fitted to it. Since the model consists of a complex expression, it is hard to judge the quality of the fit and, in turn, the accuracy of the analysis. In other words, FRAP functions as a black box, in that it does not offer tools to assess the quality of its output.
Single-particle tracking (SPT) offers an alternative to these methods. Rather than measuring an indirect observable and fitting it to a model to infer the underlying motion, SPT directly measures the trajectories of individual proteins, which allows a phenomenological description of their motion. Examples include distinguishing directed from non-directed trajectories (Monnier et al., 2015), identifying trajectory symmetry with respect to organelles (Jaqaman et al., 2011), and characterizing the temporal scaling of the trajectory mean-square displacement (MSD) (Bronstein et al., 2009, Guo et al., 2014a).
Unfortunately, it is challenging to apply SPT to monomeric proteins in the cytoplasm. SPT requires imaging thousands of trajectories, many of which end prematurely due to photo-bleaching, blinking, or exiting the field of view. Moreover, the typical speed of monomeric proteins in the cytoplasm renders SPT even harder to use (compared to cases such as membrane proteins and large organelles or beads), since distinguishing individual trajectories requires a low concentration of tagged proteins, which results in fewer trajectories per movie and thus in more imaging work (English et al., 2011). Some of these challenges are resolved in fluorescence speckle microscopy (FSM), which tracks fluorophores incorporated into macromolecular structures (Waterman-Storer et al., 1998, Cameron et al., 2011). As part of large structures, these fluorophores move more slowly compared to monomeric fluorophores in the cytoplasm. Thus, FSM can correctly identify each speckle from frame to frame, even when speckles densely populate the field of view. In addition, FSM is less sensitive to photo-bleaching and blinking than SPT, because speckles often consist of a few fluorophores, which bleach more slowly than single fluorophores and rarely blink simultaneously. FSM has been primarily used to investigate the dynamics of polymers, such as microtubules (Waterman-Storer et al., 1998), meiotic spindles (Yang et al., 2007), and F-actin (Ponti et al., 2003) and has also been used to analyze membrane receptor motion (Jaqaman et al., 2011). However, FSM is not suitable for studying monomeric proteins in the cytoplasm, as they move quickly and do not form stable speckles.
Here, we propose photo-converted intensity profile expansion (PIPE) as a method for direct measurement of rapid protein motion in the cytoplasm. PIPE works by applying a laser pulse to a sample of photo-convertible fluorophores, generating a peaked fluorescence signal at the pulsed region and imaging the signal expanding as the photo-converted fluorophores move away from that region. This expansion shows proteins moving in different directions and through different parts of the cytoplasm. To make the measurement useful for cell biologists, the data are processed to a single number, the effective diffusion coefficient (EDC). This number allows users to compare the rate of expansion of different proteins or of the same proteins under different conditions. Rather than claiming that protein motion obeys a simplified diffusion model, the EDC provides a phenomenological description of the imaging data.
PIPE shares the advantages of other methods and avoids their drawbacks (see Table 1). Like SPT, PIPE images protein motion directly, rather than inferring it from indirect observables. Unlike SPT, PIPE can be easily applied to rapid cytoplasmic proteins. PIPE is similar to FRAP in its applicability to high protein concentrations but differs from FRAP in user accessibility: PIPE uses simple fitting functions and presents data at several stages of the analysis, helping users assess the output quality. In addition, PIPE requires no calibration of the excitation beam width. Finally, PIPE is robust against some forms of photo-bleaching, which can skew FRAP results.
To further demonstrate PIPE’s usefulness in generating biological insight, we applied PIPE to questions about proteins’ anomalous diffusion. Whether or not anomalous diffusion of biomolecules takes place in the cell has been much debated among biologists (Hihara et al., 2012, Malchus and Weiss, 2010, Pawar et al., 2014). Anomalous subdiffusion is characterized by slower motion to long distances compared to Brownian motion, and anomalous subdiffusion in the cell may reflect the spatial organization within cellular compartments, which has implications to chromatin accessibility (Hihara et al., 2012), directional motion along the mitotic spindle (Pawar et al., 2014), and search efficiency of binding sites (Guigas and Weiss, 2008). While microscopy methods like FCS have been used to measure anomalous diffusion in the cell, some claim that these results originate from artifacts in the data analysis (reviewed in Saxton, 2012). Unlike most existing methods, PIPE directly accesses the property of motion that defines anomalous diffusion, i.e., the mean-square displacement of the protein ensemble and how it scales with time. Thus, PIPE provides distinctive opportunities for measuring anomalous diffusion in the cell.
Results
PIPE Calculates Correct Diffusion Coefficients from Simulated Data
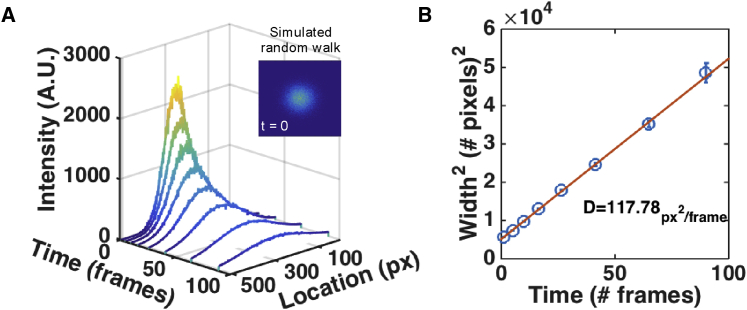
To test how well PIPE analyzes data in non-ideal yet controlled environments, we applied PIPE to computer simulations that imitate photo-conversion experiments and explored how the output of PIPE changes with various perturbations modeled in these simulations (Figure 1). We found that PIPE extracted the correct diffusion coefficient at an average error of 3%, under a wide range of values of different parameters, including the random walk step size distribution (which determines the diffusion coefficient), shot noise, and background noise. We further found that the extracted diffusion coefficients changed by less than 4% under a wide range of photo-bleaching rates (0.01%–1% bleaching probability per fluorophores per time step), except under a very high rate (10% probability) that depleted much of the signal before the end of the simulation. In addition, since the theory behind PIPE assumes that the initial intensity profile has a Gaussian shape, we tested PIPE against a rectangular initial profile with width of 3 μm and found that the diffusion coefficient changed by less than 6% on average for high diffusion coefficients (10–100 μm2/s), although the change went up to ∼30% for low diffusion coefficients (0.1–1 μm2/s). One interesting parameter that did affect PIPE’s output was the initial width of the protein ensemble, relative to the width of the field of view. The greater this parameter was, the wider the confidence intervals for the diffusion coefficient became (although the mean diffusion coefficient remained within the aforementioned 3% error bound). This insight aided us in designing real photo-conversion experiments, since this ratio of widths can be controlled by the microscope zoom and by the power and duration of the photo-conversion pulse.
Figure 1.
PIPE Analysis of Simulated Data Correctly Recovers Diffusion Coefficients
(A) A time series of one-dimensional intensity profiles chosen from a two-dimensional simulation of stochastic random walk. Raw data and Gaussian fits are shown at each time point. Inset: an image representing the simulated fluorescence intensity at t = 0. The intensity profiles shown in (A) were taken from a horizontal cross-section that passes through the center of the peak.
(B) The square widths of the Gaussian fits from (A) are presented as a function of time. Error bars represent 1σ confidence intervals. A fitted linear model is plotted as a solid line, and the diffusion coefficient is stated, calculated as the slope of the line times one-quarter. The value of the diffusion coefficient is presented in square pixels per frame.
PIPE Reproducibly Measures Expected Diffusion Coefficients of Purified Proteins in Solution
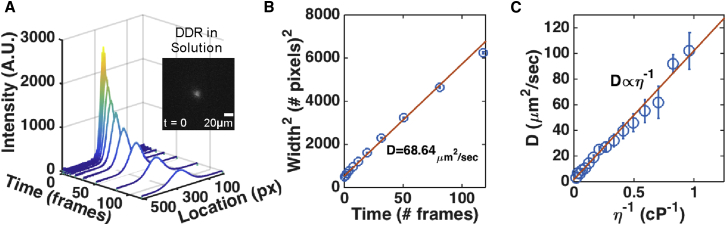
To test the capability of PIPE to extract correct diffusion coefficients from real microscopy data, we conducted and analyzed photo-conversion experiments in solution. For these experiments, we purified the photo-convertible fluorescent protein Dendra2 (DDR) from bacteria transformed with a DDR-encoding plasmid. To assess the robustness of PIPE against fluctuating system variables, we repeated the measurements under a range of photo-bleaching rates (1%–100% laser power), DDR concentrations (0.4–40 μM), and durations of the photo-conversion pulse (50–500 ms). As the theory behind PIPE suggests, we found no dependence of the diffusion coefficients on either of these variables (data not shown). We then turned to measure the accuracy of PIPE in confirming a known dependence of the diffusion coefficient on media viscosity. In dilute media, protein diffusion obeys the Stokes-Einstein relation , where is Boltzmann’s constant, is the Stokes radius of the particle, and and are the temperature and viscosity of the media, respectively. We changed the media viscosity by titrating glycerol into the DDR solution, measured the diffusion coefficients using PIPE, and fitted them to a linear function of . The model fit the data well (R2 = 0.98), passing close to the origin, as predicted by the Stokes-Einstein relation (Figure 2C). Plugging the slope of the fitted line into the Stokes-Einstein relation, we calculated the Stokes radius of DDR to be 2.4 ± 0.2 nm. This result agrees with the geometric radius of DDR, R = 2.25 nm, which we extracted from the crystal structure 2VZX (Adam et al., 2009, PDB file was downloaded from http://www.rcsb.org/pdb/home/home.do, and R was extracted by calculating the longest distance in each coordinate (x, y, z) between α-Carbons atoms within each monomer in the PDB file and averaging over these distances).
Figure 2.
PIPE Confirms that Purified DDR in Solution Satisfies the Stokes-Einstein Relation
Purified DDR and glycerol were mixed to produce solutions of known viscosities. Photo-conversion experiments were performed in these solutions, and the diffusion coefficients of DDR were obtained using PIPE.
(A) A typical intensity profile expansion series. Inset: the red channel image at t = 0. Scale bar, 20 μm.
(B) The square width of each Gaussian fit from (A) as a function of time. The extracted diffusion coefficient is in units of μm2/s. Error bars denote 1σ confidence intervals.
(C) The diffusion coefficients of DDR as measured by PIPE presented as a function of the inverse viscosity. The data fit well to a straight line that passes close to the origin, as predicted by the Stokes-Einstein relation. Error bars, SE.
Finally, we compared our results to previously reported diffusion coefficients. Since we were not familiar with reports on the diffusion coefficient of DDR, we focused on GFP, which resembles DDR in size and structure (Adam et al., 2009). The reported diffusion coefficient of GFP (see Table 2) had been measured in water at room temperature, i.e., at viscosity ∼0.89 cP. Since our purification media contained glycerol, which increased the viscosity, we obtained the diffusion coefficient of DDR at 0.89 cP by extrapolating from the fitted Stokes-Einstein model and got DDDR–0.89 cP = 115 ± 11 μm2/s, in agreement with the overall set of previously measured diffusion coefficients of GFP. Taken together, these results demonstrate that PIPE is capable of measuring diffusion coefficients of proteins in dilute solutions.
Table 2.
Summary of Diffusion Coefficients Measured for DDR and GFP in Solution
| Protein | D (m ± SE) μm2/s | Temperature (°C) | Method | Rh–effnm | Reference |
|---|---|---|---|---|---|
| DDR | 115 ± 11a | 25 | PIPE | 2.4 ± 0.2 | this work |
| EGFP | 95 | 22.5 | sFCS | 2.42 | Petrášek and Schwille (2008) |
| EGFP | 94b | 22 | FCS | 2.42 | Schenk et al. (2004) |
| GFP | 87 | 25 | FCS | 2.82 | Terry et al. (1995) |
| GFP | 130 | 20 | FRAP | 1.66c | Busch et al. (2000) |
| EGFP | 87 | RT | FRAP | Swaminathan et al. (1997) |
sFCS, scanning fluorescence correlation spectroscopy.
This value was extrapolated from the Stokes-Einstein relation measured using glycerol titration. The error reflects the range of parameter values of the linear regression used to fit the Stokes-Einstein relation, within 2σ confidence intervals.
The original value of 63 μm2/s was corrected after publication.
The authors verified the Stokes radius using dynamic light scattering (DLS).
PIPE Establishes Baseline EDCs for Proteins of Different Sizes in the Cytoplasm
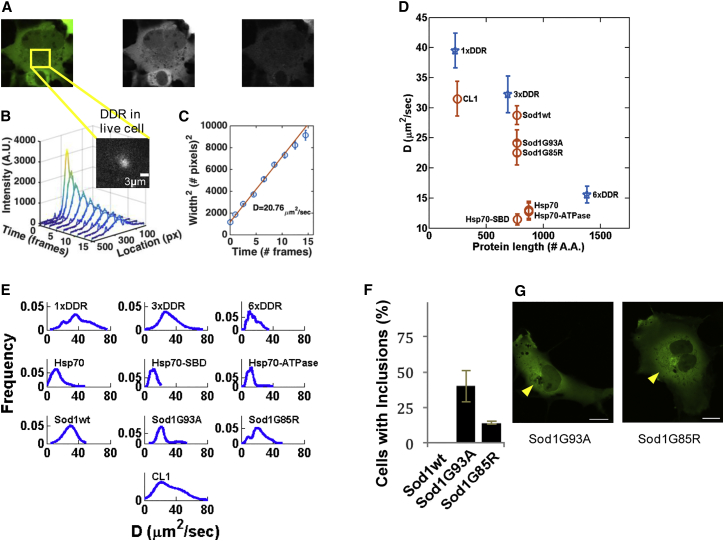
Having demonstrated the capability of PIPE to measure protein diffusion in solution, we turned to using it to measure protein motion in the cytoplasm of living cells. While in dilute media the diffusion coefficient is determined mainly by the viscosity and the protein size, in the crowded cytoplasm the EDC may reflect additional factors, including binding to and unbinding from other proteins, complexes, and intracellular structures. To probe the scaling of the EDC with protein size, we applied PIPE to photo-conversion experiments of DDR repeats of variable length (denoted as NxDDR, where N = 1, 3, 6), which we transiently expressed in COS7 cells. The EDCs we obtained from different cells for each protein spanned a wide range of values (Figure 3E), with a coefficient of variation of ∼0.3. The EDC range of 1xDDR included published diffusion coefficients of GFP in the cytoplasm of mammalian cells (Table 3). The average EDCs (denoted for convenience) of NxDDR decreased with increasing N, which is consistent with the prediction that larger proteins move more slowly. For the rest of this report, we will use as a rough baseline for EDCs at different protein sizes, to which we can compare EDCs of other proteins with similar sizes.
Figure 3.
Using PIPE to Measure Diffusion Coefficients in the Cytoplasm of COS-7 Cells
(A) A typical DDR-expressing COS7 cell is shown before photo-conversion. Left, signal from green- and red-emitting DDR is shown in pseudo color. Middle, signal from green-emitting DDR is shown in grayscale. Right, signal from red-emitting DDR is shown in grayscale. The frame on the left panel marks the area in which a photo-conversion experiment was imaged.
(B) An intensity profile expansion series of photo-converted DDR in a typical cell. Inset: signal from red-emitting DDR at the moment of photo-conversion in the region framed in (A). Scale bar, 3 μm.
(C) The square widths of the Gaussian fits from (B) are plotted as a function of time. The extracted D is stated in units of μm2/s.
(D) Average diffusion coefficients ±SE of NxDDR (blue stars) and DDR-tagged proteins (orange circles) in the cytoplasm are plotted against the size of each protein in amino acids.
(E) The weighted probability distribution of all the measured diffusion coefficients is plotted for each protein from (D), assuming that the error of each measurement is normally distributed. The number of measurements (one to three per cell) included in each distribution is shown row by row from left to right: 31, 17, 32, 29, 21, 21, 27, 31, 21, 34.
(F) Morphology of SOD1 aggregates: about 40% of cells expressing Sod1-G85R had large juxtanuclear inclusions compared to only 14% of Sod1-G93A-expressing cells. Error bars denote SE.
(G) The juxtanuclear inclusions of Sod1-G93A appeared smaller and subtler than that of Sod1-G85R. Yellow arrows point to the juxtanuclear inclusions. Scale bar, 20 μm.
Table 3.
Comparison of EDC Measured for DDR with Literature Values of Diffusion Coefficients of GFP in the Cytoplasm of Mammalian Cells
| Protein | D (m ± SE) μm2/s | Cell Type | Method | Reference |
|---|---|---|---|---|
| DDR | 38 ± 3 | COS7 | PIPE | this work |
| EGFP | 22 ± 7 | CHO-K1 | STICS | Hedde et al. (2015) |
| GFP | 21/17a | U2OS | FRAP/FLIP | Guo et al. (2014b) |
| GFP | 26 ± 3 | A549 | Line FRAP | Braeckmans et al. (2007) |
| GFP | 15 | mouse adenocarcinoma | FRAP | Sprague et al. (2004) |
| GFP | 25 | HeLa | FCS | Elsner et al. (2003) |
| EGFP | 23 ± 4 | HeLa | FCS | Ruan et al. (2002) |
Measurements were performed at 22°C.
Having used PIPE to measure baseline EDCs for DDR repeats, we continued by measuring EDCs of DDR-tagged native proteins and compared the results to the baseline. We focused on proteins from the mammalian protein-folding quality-control system: the amyotrophic lateral sclerosis (ALS)-associated protein Sod1wt and its aggregation-prone mutants Sod1G93A and Sod1G85R, the molecular chaperone Hsp70, and the short degradation signal CL1 (Gilon et al., 1998), which has been shown to convert GFP to an aggregation prone protein. The measured for these proteins and for NxDDR are shown in Figure 3D.
We first applied PIPE to measure the motion of Sod1 variants and found that Sod1 mutants stimulate the protein-folding quality-control system and move more slowly than wild-type Sod1. Sod1 is known to form tight homodimers, which stay associated even when tagged with a fluorescent protein (Grad et al., 2014). Our results supported this finding, as lay much closer to the NxDDR baseline if plotted against the size of two Sod1-DDRs compared with the size of one Sod1-DDR (Figure 3D). To compare the aggregation propensity of Sod1 variants, we compared their EDCs and counted the number the cells that formed a juxtanuclear inclusion, which demonstrates the large number of misfolded proteins in these cells. 24 hr after the cells began expressing Sod1G85R or Sod1G93A, we found that inclusions formed in 40% ± 11% of the cells expressing Sod1G85R, but only in 14% ± 1% of the cells expressing Sod1G93A. Moreover, Sod1G93A inclusions appeared much smaller and dimmer compared to Sod1G85R inclusions (Figure 3F). Interestingly, both mutants had decreased mobility compared to Sod1wt , a claim we supported with a t test that enabled us to reject the null hypothesis that each of the mutant EDC samples and the wild-type EDC sample were drawn from the same underlying distribution (p value = 0.0007 for comparing Sod1wt and Sod1G85R, and p value = 0.046 for comparing Sod1wt and Sod1G93A). We interpret this result to mean that the aggregation of the Sod1 mutants slows down the motion of the entire Sod1 ensemble in the cytoplasm, and this effect is detectable by PIPE.
Our next result showed that the degradation signal CL1 fused to DDR had an EDC similar to 3xDDR, , while the number of amino acids in DDR-CL1 is much smaller than in 3xDDR. This result suggests that the effective size of DDR-CL1 is bigger than what one would expect based on the number of amino acids in DDR-CL1. This hypothesis is compatible with the observation that CL1 expression promotes the formation of large perinuclear fluorescent aggregates in the cell cytoplasm (data not shown).
Last, we found that Hsp70 diffuses much more slowly than the baseline, with , while for the similar-sized 3xDDR . This result can be explained by the fact that Hsp70 frequently binds other proteins, either misfolded substrates as part of its chaperone activity, or non-substrate molecules, including other Hsp70 units. To test the former hypothesis, we compared the EDC of wild-type Hsp70 with two Hsp70 mutants: Hsp70 substrate binding domain mutant (Hsp70-SBD) and Hsp70 ATPase domain mutant (Hsp70-ATPase). Hsp70-SBD is a truncated 543 amino acids Hsp70 where the last 98 amino acids of the SBD containing the helical lid subdomain (HLS) have been removed. HLS has been shown to play a crucial key role in substrate binding (Aprile et al., 2013), and Hsp70-SBD was measured, using FRAP, to move faster than wild-type Hsp70 (Kim et al., 2002). Unlike Kim et al., we did not measure faster motion of Hsp70-SBD compared to wild-type (, and t test comparing the Hsp70wt and Hsp70-SBD EDC samples returned p value = 0.37). We also measured the EDC of the Hsp70-ATPase (A72W). ATP is crucial for Hsp70 activity and allows Hsp70 to rapidly bind and release substrates. If the deviation of Hsp70 from the NxDDR baseline was due to its substrate binding, we should expect to measure different EDCs for Hsp70-ATPase, either higher EDCs if the mutant cannot bind substrate or lower EDCs if the mutant cannot release substrate. However, we observed the same EDCs as measured for Hsp70wt . We concluded that the deviation of Hsp70 from the NxDDR baseline is not due to its interaction with misfolded substrate, but perhaps due to interaction with non-substrate proteins, like other Hsp70 units (Aprile et al., 2013).
PIPE Discovers Different Degrees of Diffusion Anomality for DDR Repeats and Native Proteins
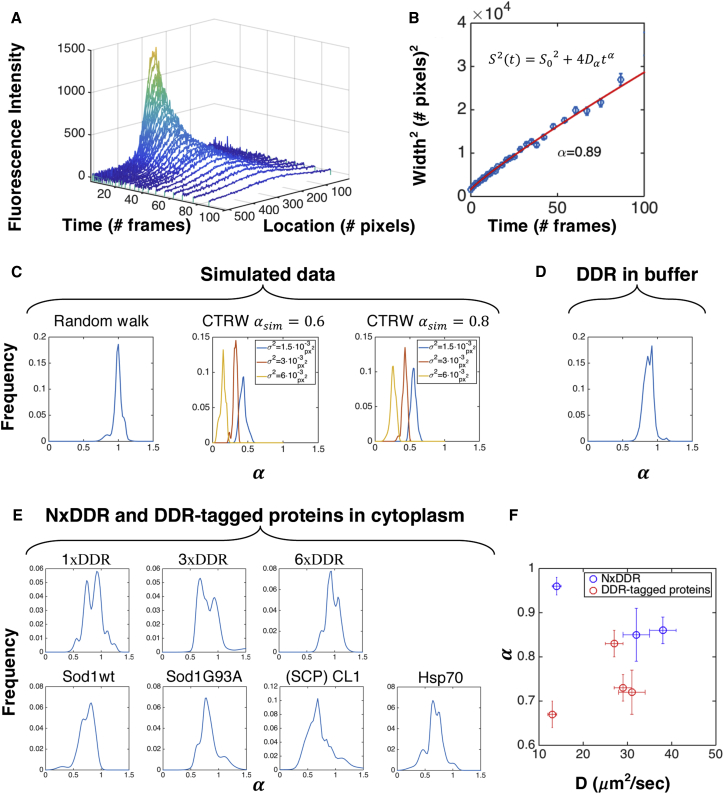
To further demonstrate PIPE’s usefulness in generating new biological insight, we applied PIPE to assessing whether protein diffusion in the cytoplasm is normal or anomalous and found that the diffusion of the native cellular proteins is more anomalous than the diffusion of the DDR repeats.
To test the capability of PIPE to distinguish normal from anomalous diffusion, we applied it to control data in silico and in vitro. First, we simulated data of classic random walk (see Supplemental Information) and continuous time random walk (CTRW), which is an anomalous subdiffusion model that requires less computational resources to simulate compared with other models. PIPE extracted different anomalous exponents from the two types of simulations, demonstrating success in distinguishing normal from anomalous diffusion in silico. From classical random walk simulations, we obtained an anomalous exponent of , as expected. From CTRW data, we obtained , also as expected. However, the values of α calculated from CTRW data deviated from the simulated values , and depended on the distribution of step sizes (Figure 4C, and see Supplemental Information for discussion of this result). We then applied PIPE to photo-conversion experiments on purified DDR in buffer. In this dilute media, we expected to observe normal diffusion and therefore to measure . However, we measured (Figure 4D). This downward shift in measured anomalous exponents may be explained by protein oligomerization or non-linearity in fluorescence detection, which we explore in the Supplemental Information (Figure S3). Even with this downward shift, can be used to distinguish between diffusion anomality of different proteins; importantly, we observed no dependence of α on the photo-bleaching rate, DDR concentration, or the EDC (which we modulated by changing media viscosity, as in Figure 2C).
Figure 4.
Using PIPE to Measure Diffusion Anomality
(A) A typical expansion series of intensity profiles of purified DDR in vitro, including raw data and Gaussian fits.
(B) The widths of the Gaussian fits in (A) are fitted to a power law as a function of time. The fitted model and the scaling exponent α are stated.
(C–E) Distributions of the α measurements are shown. To visualize each distribution, each measurement of α was treated as a Gaussian with SD that equals to the 1σ confidence interval of the fitted α, and then all the Gaussians were summed. (C) Simulated data of classical random walk and CTRW with . For CTRW, distributions of are shown for several values of the random walk step size variance σ2. (D) Microscopy data of purified DDR in vitro. n = 127. (E) Microscopy data of DDR repeats and DDR-tagged proteins in the cytoplasm of COS7 cells. n = 40, 17, 24, 27, 31, 68, 34 (row by row, left to right). (F) α is shown as a function of the diffusion coefficient from Figure 3 for proteins from (E). Error bars denote SE.
We then used PIPE to discover differences in the diffusion anomality of different proteins in the cytoplasm. We reanalyzed the microscopy movies showing motion of NxDDR and DDR-tagged proteins in the cytoplasm and measured the α values that describe this motion (Figures 4E and 4F). For NxDDR, we observed slightly sublinear scaling, similar to the results we obtained in vitro: , and . For the DDR-tagged quality-control proteins, we obtained lower exponents: , , , and . To test whether the two protein groups differ in their mean , we executed a two-sample t test. The test resulted in p value = 0.013, which allowed us to reject the hypothesis that the two groups are described using the same distribution of . To check for a possible artifact of data sampling (since different proteins have different EDCs but for all the proteins we only analyzed the first ten to 15 frames of each movie), we calculated the correlation between α and the EDCs. The correlation was 0.13, which has a probability of 0.78 to occur at random (0.13 or higher and −0.13 or lower) for the same number of points sampled from the same plotted value range, which suggests that differences in data sampling do not artifactually distinguish between the DDR repeats and the native cellular proteins. These results suggest that the native cellular proteins diffuse with a greater degree of anomality compared to the free fluorescent probes.
Discussion
Distinctiveness of PIPE
PIPE is not the first technique to use photo-convertible proteins (Calvert et al., 2007, Ehrlicher et al., 2011, Mazza et al., 2008) or to analyze the time evolution of spatial intensity profiles (Berk et al., 1993, Tardy et al., 1995). Rather, PIPE’s distinctiveness lies in the synthesis that it implements between a direct measurement of protein motion in the cytoplasm and an intuitive and detailed output that aids the users in assessing the measurement’s quality.
In principle, PIPE analysis can be applied to photo-bleaching experiments that are normally analyzed using FRAP. However, doing so would effectively mean quantifying the expansion of the lack of fluorophores, rather than the fluorophores themselves. Such a measurement would miss the advantage of directly quantifying the motion of the tagged proteins and would instead provide an indirect description of how the tagged proteins flow into the bleached area. Moreover, applying PIPE to photo-bleaching data tends to yield inaccurate results, because the fitted signal is inverted, where the point of maximal depletion lies at the peak of the Gaussian, and points of higher fluorescence lie at the tail. While this inversion may seem like a minor issue, it significantly changes the noise distribution along the intensity profile; since photon shot noise scales with the number of fluorophores, the tails of the intensity profile are much noisier in photo-bleaching experiments, where they consist of many fluorophores, compared to photo-conversion experiments, where the tails consists of a few fluorophores. Therefore, despite the theoretical possibility of applying PIPE to photo-bleaching data, doing so in practice is less favorable from both a conceptual and a technical point of view.
PIPE Guides Users in Assessing Quality of Results
In most existing methods, assessing the quality of output can be challenging. While method developers are aware of the assumptions that each method makes about the imaging system and underlying biological processes and use each method in the appropriate setup, other users may be less meticulous when they use a method as a part of a larger body of work. This situation can lead to ambiguous output being misinterpreted, especially if the method does not provide tools to assess output quality.
With this challenge in mind, we designed PIPE to be as intuitive and user friendly as possible. First, PIPE directly measures the motion of the tagged proteins. This capability is enabled largely due to the use of advanced imaging technology and photo-convertible proteins. Second, the computational analysis of PIPE merely makes a quantitative measurement of an effect that is already qualitatively visible in the microscopy images. Third, PIPE calculates the EDC from a single movie, which obviates the need for calibration of the beam width or the point spread function. Last, PIPE presents its output to the users at several stages of the analysis, allowing the users to examine the shapes of the intensity profiles and the fitting quality and to rerun the analysis with different parameters if needed.
Do Native Cellular Proteins Undergo Anomalous Diffusion?
Expanding beyond the framework of the EDC, we used PIPE to find out whether proteins in the cytoplasm undergo normal or anomalous diffusion. We measured significantly lower values for native cellular proteins compared with NxDDR, which suggests that the former are more subdiffusive than the latter, and therefore that the native cellular proteins we examined are subdiffusive.
There may be several objections to this interpretation:
-
1.
Does the downward shift in undermine the distinction between the different protein groups? When testing PIPE, we only obtained the expected values from simulations of normal diffusion, while we obtained lower values than expected from simulations of anomalous diffusion and from in vitro microscopy data. Nevertheless, we did obtain significantly lower values for anomalous diffusion compared to normal diffusion in silico. This suggests that downward shift in does not undermine PIPE’s ability to measure differences in diffusion anomality between different protein groups.
-
2.
Could NxDDR be superdiffusive in the cytoplasm, in which case the native proteins’ lower values would not necessarily mean that they are subdiffusive? It is unlikely that NxDDR is superdiffusive, because (1) no mechanisms are currently known to cause such motion of small proteins in the cell, and (2) NxDDR shared similar values with purified DDR in vitro, which is likely to undergo normal diffusion, and not superdiffusion. Therefore, NxDDR most probably undergoes either normal diffusion or subdiffusion, which leads us to interpret the lower values of the native cellular proteins as subdiffusive.
-
3.
Are measured values dominated by artifacts, so a lower does not necessarily mean a lower anomalous exponent? While our measured might be lower than the anomalous exponent, it is still a meaningful characteristic of the analyzed motion, because (1) different movies with the same protein and under the same conditions give similar values, and (2) even movies under different conditions (DDR in buffers of different viscosities) or of different proteins (1xDDR and 3xDDR) share similar values. The similarity in under different conditions shows that it is unlikely that values are dominated by artifacts. Therefore, we claim that differences in represent real differences in diffusion anomality.
Experimental Procedures
Cell Culture
COS7 cells were cultured in DMEM high glucose (Sigma) supplemented with 10% certified fetal bovine serum (Biological Industries), and 10 mL/L penicillin-streptomycin (P4333 Sigma). Cells were maintained and imaged at 37°C in a humidified incubator with 5% carbon dioxide.
COS7 cells were transiently transfected by seeding cells in 35-mm glass-bottom plates (Greiner Bio One) 24–48 hr before imaging. For transfections, 50%-confluent cells were incubated for 12–18 hr with 1–2 μL polyethylenimine (PEI) 0.1% (w/v) and 1 μg of plasmid DNA for each plasmid construct. Following PEI incubation, the mixture was replaced with fresh medium for 6–12 hr before imaging.
Plasmid Constructs
A CMV-driven expression plasmid, pDendra2-N, was used to fuse wild-type Hsp70, Hsp70 substrate binding domain deletion mutant (Hsp70-SBD), Hsp70 ATPase domain mutant (Hsp70-ATPase), Sod1, Sod1G85R, and Sod1G93A to the N terminus of the photo-convertible fluorescent protein DDR. Constructs containing Hsp70-SBD and Hsp70-ATPase sequences were kindly provided by Richard Morimoto’s lab (Northwestern University). CL1 sequence was fused to the C terminus of DDR vector pDendra2-C, and the CMV promoter of pDendra2-C was exchanged for the stronger SCP3 promoter (Even et al., 2016), which enhanced expression by 2- to 4-fold compared to CMV (Figure S2). In addition, using pDendra2-C, three constructs with a variable number of DDR repeats (1, 3, and 6, denoted 1xDDR, 3xDDR, and 6xDDR) were cloned.
A trc-driven expression plasmid containing 6x His tag and protein Biotinylation Tag fused to DDR was kindly provided by Carlos Bustamante’s lab (UC-Berkeley) for the purpose of DDR purification.
Protein Samples
For in vitro experiments, DDR was purified from bacteria by transformation of the His-tag DDR plasmid DNA into DH5α bacterial cells. The transformed bacteria were seeded in suspension media and incubated for 12–24 hr at 37°C before 0.5 mM isopropyl β-D-1-thiogalactopyranoside (IPTG) was added to induce DDR expression. The suspension media with DDR-expressing bacteria was then left overnight and centrifuged the next day to extract a pellet. The pellet was resuspended in lysis buffer (50 mM sodium phosphate [pH 7.4], 300 mM NaCl, 10 mM imidazole, 5% glycerol) and lysed using a microfluidizer device (Microfluidics). The lysate was then centrifuged to separate soluble proteins (supernatant) from insoluble proteins. The supernatant was loaded into a NiSephB column and eluted by an elution buffer (50 mM sodium phosphate [pH 7.4], 300 mM NaCl, 300 mM imidazole, 5% glycerol). The eluted protein was then dialyzed against a dialysis buffer (50 mM sodium phosphate [pH 7.4], 300 mM NaCl). Protein concentration was quantified by absorption at 488 nm, where the extinction coefficient of DDR is known (McKinney et al., 2009). The eluted DDR was then used to prepare working solutions of different viscosity by titrating in glycerol.
Microscopy
Time-lapse images were acquired with a NIKON A1 confocal microscope. A CFI Plan Apo Lambda 60× oil objective was used in all in vivo experiments. In in vitro experiments, either the oil objective or a CFI Plan Apo IR SR 60×WI water objective was used. While using oil objectives in an aqueous environment may lead to optical aberrations caused by mismatched refractive indices, we found no significant change when comparing diffusion coefficients between oil and water objectives (<10%, data not shown).
Imaging was performed using a 488-nm laser (COHERENT, 50 mW) prior to photo-conversion and using a 561-nm laser (COHERENT, 50 mW) for excitation of the photo-converted DDR. Fluorescence emission was detected through a 525/50- and 595/50-nm band-pass filters, respectively.
While we developed PIPE using a specific confocal imaging system, PIPE is usable with any commercial confocal, total internal reflection fluorescence (TIRF), or epifluorescence microscope with a capability to apply localized photo-conversion pulses.
Photo-Conversion
For photo-conversion experiments, we used the NIKON A1 resonant scan mode. The resonant scan mode, combined with bi-directional scanning and an ROI of 512 × 512 pixels, allowed for an imaging rate up to 30 frames per second. In theory, this imaging rate enables measuring diffusion coefficients up to 104 μm2/s, which is well above the diffusion coefficients of biomolecules. For other systems, the frame rate should allow for at least ten time points to be acquired between the end of the photo-conversion pulse and when the signal is no longer visible.
Photo-conversion was executed using a 406-nm laser (COHERENT, 50 mW), a 488-nm laser (COHERENT, 50 mW), or both lasers simultaneously. Depending on the efficiency of photo-conversion, the percentage of photo-converted molecules is expected to be significantly smaller than that of the fluorescent molecules prior to photo-conversion. Therefore, as a rule of thumb, the power settings for the 561-nm excitation laser, which was used to image to photo-converted DDR, was set to be two to three times greater than that of the 488-nm excitation laser, which was used to image the cell prior to photo-conversion. This allowed the pulse to be imaged for relatively long time intervals after the initial pulse without saturating the acquired image. The photo-conversion pulse was directed at a single spot, without scanning, and was stopped after 100 or 300 ms, depending on the concentration of DDR. The point of photo-conversion was selected at the center of the cells cytoplasm such that the signal expansion time will be maximized before reaching the outer bilayer membrane and nucleus. About 100 frames were acquired prior to the photo-conversion pulse to measure the baseline fluorescence. Immediately after photo-conversion ten to 100 frames were typically acquired, which corresponds to 300–3,000 ms in our system. The photo-conversion time lapse analysis is performed using homemade software written in MATLAB (MathWorks).
To test the consistency and evenness of illumination of the excitation laser, an autofluorescent plastic slide (CHROMA) was used. We found slight variations in the imaging intensity, which were mostly pronounced around the edges of the imaging field. Far away from these edges, the intensity was uniform, suggesting that the illumination of the sample is even. We recommend that users test their imaging systems this way, since non-uniform illumination may lead to an asymmetric intensity profile, resulting in changes to the Gaussian distribution signal that are unrelated to the underlying protein diffusion. Correcting for non-uniform illumination post-acquisition may eliminate the distortions that arise due to non-uniformity of photon emission rate. However, it will not eliminate distortions due to bleaching in a non-uniform excitation light, which leads to parts of the imaging field bleaching faster than others, therefore distorting accordingly the distribution of fluorescent proteins. Consequently, if a certain imaging system has severely non-uniform illumination, we recommend that the excitation laser power be kept low to avoid rapid bleaching. In such cases, the rate of bleaching can be estimated by measuring the average intensity in the time interval required for the Gaussian distribution to reach the edge of the image plane. Alternatively, a reference with similar diffusion coefficient can be used to test the validity of applying PIPE in such cases.
Principles of PIPE and the Effective Diffusion Coefficient
Immediately after photo-conversion, one-dimensional intensity profiles at different time points were fitted to Gaussian functional forms. The square width of these Gaussians as a function of time was then fitted using linear regression, and the EDC was extracted from the slope of the linear fit. This is one way out of many possible ways to quantify the expansion of the intensity profiles, but this is a useful way in that it provides means to validate the accuracy of PIPE in vitro, where protein motion obeys Fickian diffusion, and the EDC is the actual diffusion coefficient, and is related to the media viscosity by the Stokes-Einstein relation. Calculating the diffusion coefficient considers the fluorophore concentration as a solution to the diffusion equation
where is the fluorophore concentration and is the fluorophore’s diffusion coefficient. The photo-conversion pulse generates a perturbed red fluorescence concentration field, whose profile can be approximated as a Gaussian localized at point with width and amplitude . Plugging this initial condition into the diffusion equation above, we derived the time evolution of this perturbation according to the diffusion equation:
where is the number of spatial dimensions and . Thinking about the above solution as the time evolution of the spatial fluorescence profile , we can calculate the MSD of this profile. When is treated as a probability distribution (which is justified because it is just a normalized Gaussian, where ), the definition of the MSD is
Plugging into this definition, we obtain
It follows that by measuring the width of the profile () we directly measure its MSD. Importantly, as seen from the expression of above, this quantity scales linearly in regardless of the dimensionality . This means that measuring along as little as a single spatial dimension is sufficient to obtain the EDC.
Based on this analytical prediction, the intensity profile at each time point was fitted to the Gaussian function , where is the index of the pixel in the intensity profile and are fitting parameters, which generally change with time. Last, the square of the parameter was fitted as a function of time using linear regression to the function , extracting the diffusion coefficient . In movies where diffusion time was short (, where is the frame size and is the time to acquire one image), the Gaussian amplitude decreased quickly, and data points at late times were dominated by noise. Only the first 15 frames after were analyzed. This was done in most of the in vivo data, whenever plots of showed an initial monotonous increase and low error bars followed by flattening of the values or by values with high error bars. To check how analyzing only 15 frames affects the results, we analyzed in vitro movies both at full length and limited to 15 frames. We found that the EDCs increased by ∼20% when only the first 15 frames were analyzed, compared with cases where the whole movie was analyzed. More information about this procedure and about differences between in vitro and in vivo data is provided in the Supplemental Information.
Expanding beyond the EDC, when measuring diffusion anomality, the width as a function of time was fitted to a power law instead of a straight line, and the anomalous exponent was extracted from the power law. An anomalous exponent α < 1 indicates subdiffusive motion, while α = 1 means that diffusion is not anomalous, as the MSD grows linearly with time.
Robustness to Photo-Bleaching and Blinking
Incorporating spatial information into the analysis makes PIPE robust against photo-bleaching and blinking, given that the illumination of the microscope excitation laser is spatially uniform. Under such illumination, rates of blinking, reversible photo-bleaching, and irreversible photo-bleaching of a single fluorophore are usually independent of fluorophore concentration, and therefore these processes are modeled as time-dependent functions . Thus, the diffusion-bleaching solution is , which only affects the amplitude of the Gaussian and not the width . Since the EDC is calculated solely from , the EDC is not affected by blinking and bleaching. In contrast, other perturbation-based methods, including FRAP, do not use spatial information and are therefore more sensitive to photo-bleaching. See Results for results from testing PIPE’s sensitivity to photo-bleaching.
Technical Limitations of PIPE
Certain experimental conditions must be met for PIPE to provide accurate results. First, microscopy movies that depict the expansion of a photo-conversion profile are analyzable only until the photo-converted proteins approach the cell boundaries. At that moment, the profile’s expansion slows down due to confinement. Therefore, if users try to analyze the expansion past that moment, the resulting EDC would be smaller compared to the EDC of the same protein whose expansion was not confined by the cell boundaries. To avoid such inaccuracy in our work, we chose to image only big cells, whose boundaries lay at least 10 μm away from the edge of the field of view. (The entire field of view defined an area of ∼30 × 30 μm.) As a rule of thumb, we recommend that users analyze data up to the point when the width of the Gaussian profile is equal to the distance between the peak of the Gaussian and the nearest boundary in the imaged plane.
Second, the concentration of photo-convertible protein should be high enough so that enough protein is photo-converted to be detected. We tested PIPE in vitro at DDR concentrations that range from about 100 nM to 40 μM with no effect on the EDC (data not shown). We note that much higher concentrations may promote aggregation and can also cause quenching between colliding DDR molecules, which can lead to error in the measured EDC. However, for fluorescent proteins in which access to the chromophore is protected by a cylindrical beta barrel structure, this effect can be neglected for submillimolar concentration (Gather and Yun, 2014), which is often the case for transient or stable transfection in mammalian cells.
Random Walk Simulations
To test how PIPE’s accuracy is affected by various types of noise and potential artifacts, we imitated imaging data by simulating diffusion starting from a Gaussian initial condition, which approximates the shape of the imaged protein distribution in our experiments immediately after photo-conversion. See Supplemental Information for a detailed description of the random walk simulations we performed.
Author Contributions
Conceptualization, all authors; Methodology, all authors; Software, R.G.S.; Validation, R.G.S. and S.B.; Formal Analysis, R.G.S.; Investigation, R.G.S. and S.B.; Resources, D.K. and J.L.E.; Data Curation, R.G.S. and S.B.; Writing – Original Draft, R.G.S. and S.B.; Writing – Review and Editing, R.G.S. and S.B.; Visualization, R.G.S. and S.B.; Supervision, D.K. and J.L.E.; Project Administration, all authors; Funding Acquisition, D.K. and J.L.E. PIPE’s source code and user manual can be found at http://www.englandlab.com/.
Acknowledgments
We thank Dr. Mario Lebendiker from HUJI for help with protein purification. We thank Dr. Carlos Bustamante from UC-Berkeley and Dr. Richard Morimoto from Northwestern University for sharing materials. We thank Tamar Juven-Gershon for sharing the SCP promoter. D.K. was supported by the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC-StG2013 337713 DarkSide starting grant, as well as an Israel Science Foundation Grant ISF 843/11, a German Israel Foundation Grant GIFI-1201-242.13/2012, a Niedersachsen-Israel Research Program grant, an Abisch-Frenkel Foundation grant, and a joint Israel-Italy cooperation grant from the Israeli Ministry of Science, Technology, and Space. This is an EU Joint Programme – Neurodegenerative Disease Research (JPND) 2 project.
Published: March 14, 2017
Footnotes
Supplemental Information includes Supplemental Experimental Procedures, three figures, and one table and can be found with this article online at http://dx.doi.org/10.1016/j.celrep.2017.02.063.
Contributor Information
Daniel Kaganovich, Email: dan@cc.huji.ac.il.
Jeremy L. England, Email: jengland@mit.edu.
Supplemental Information
References
- Adam V., Nienhaus K., Bourgeois D., Nienhaus G.U. Structural basis of enhanced photoconversion yield in green fluorescent protein-like protein Dendra2. Biochemistry. 2009;48:4905–4915. doi: 10.1021/bi900383a. [DOI] [PubMed] [Google Scholar]
- Aprile F.A., Dhulesia A., Stengel F., Roodveldt C., Benesch J.L.P., Tortora P., Robinson C.V., Salvatella X., Dobson C.M., Cremades N. Hsp70 oligomerization is mediated by an interaction between the interdomain linker and the substrate-binding domain. PLoS ONE. 2013;8:e67961. doi: 10.1371/journal.pone.0067961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berk D.A., Yuan F., Leunig M., Jain R.K. Fluorescence photobleaching with spatial Fourier analysis: Measurement of diffusion in light-scattering media. Biophys. J. 1993;65:2428–2436. doi: 10.1016/S0006-3495(93)81326-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braeckmans K., Remaut K., Vandenbroucke R.E., Lucas B., De Smedt S.C., Demeester J. Line FRAP with the confocal laser scanning microscope for diffusion measurements in small regions of 3-D samples. Biophys. J. 2007;92:2172–2183. doi: 10.1529/biophysj.106.099838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bronstein I., Israel Y., Kepten E., Mai S., Shav-Tal Y., Barkai E., Garini Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 2009;103:018102. doi: 10.1103/PhysRevLett.103.018102. [DOI] [PubMed] [Google Scholar]
- Busch N.A., Kim T., Bloomfield V.A. Tracer diffusion of proteins in DNA solutions. 2. Green fluorescent protein in crowded DNA solutions. Macromolecules. 2000;33:5932–5937. [Google Scholar]
- Calvert P.D., Peet J.A., Bragin A., Schiesser W.E., Pugh E.N., Jr. Fluorescence relaxation in 3D from diffraction-limited sources of PAGFP or sinks of EGFP created by multiphoton photoconversion. J. Microsc. 2007;225:49–71. doi: 10.1111/j.1365-2818.2007.01715.x. [DOI] [PubMed] [Google Scholar]
- Cameron L.A., Houghtaling B.R., Yang G. Fluorescent speckle microscopy. Cold Spring Harb. Protoc. 2011 doi: 10.1101/pdb.top106. Published online May 11, 2011. [DOI] [PubMed] [Google Scholar]
- Castellana M., Wilson M.Z., Xu Y., Joshi P., Cristea I.M., Rabinowitz J.D., Gitai Z., Wingreen N.S. Enzyme clustering accelerates processing of intermediates through metabolic channeling. Nat. Biotechnol. 2014;32:1011–1018. doi: 10.1038/nbt.3018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Digman M.A., Brown C.M., Horwitz A.R., Mantulin W.W., Gratton E. Paxillin dynamics measured during adhesion assembly and disassembly by correlation spectroscopy. Biophys. J. 2008;94:2819–2831. doi: 10.1529/biophysj.107.104984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrlicher A.J., Nakamura F., Hartwig J.H., Weitz D.A., Stossel T.P. Mechanical strain in actin networks regulates FilGAP and integrin binding to filamin A. Nature. 2011;478:260–263. doi: 10.1038/nature10430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsner M., Hashimoto H., Simpson J.C., Cassel D., Nilsson T., Weiss M. Spatiotemporal dynamics of the COPI vesicle machinery. EMBO Rep. 2003;4:1000–1004. doi: 10.1038/sj.embor.embor942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelke H., Dorn I., Rädler J.O. Diffusion and molecular binding in crowded vesicle solutions measured by fluorescence correlation spectroscopy. Soft Matter. 2009;5:4283–4289. [Google Scholar]
- English B.P., Hauryliuk V., Sanamrad A., Tankov S., Dekker N.H., Elf J. Single-molecule investigations of the stringent response machinery in living bacterial cells. Proc. Natl. Acad. Sci. USA. 2011;108:E365–E373. doi: 10.1073/pnas.1102255108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Even D.Y., Kedmi A., Basch-Barzilay S., Ideses D., Tikotzki R., Shir-Shapira H., Shefi O., Juven-Gershon T. Engineered Promoters for Potent Transient Overexpression. PLoS ONE. 2016;11:e0148918. doi: 10.1371/journal.pone.0148918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabison L., Chiadmi M., Colloc’h N., Castro B., El Hajji M., Prangé T. Recapture of [S]-allantoin, the product of the two-step degradation of uric acid, by urate oxidase. FEBS Lett. 2006;580:2087–2091. doi: 10.1016/j.febslet.2006.03.007. [DOI] [PubMed] [Google Scholar]
- Gather M.C., Yun S.H. Bio-optimized energy transfer in densely packed fluorescent protein enables near-maximal luminescence and solid-state lasers. Nat. Commun. 2014;5:5722. doi: 10.1038/ncomms6722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilon T., Chomsky O., Kulka R.G. Degradation signals for ubiquitin system proteolysis in Saccharomyces cerevisiae. EMBO J. 1998;17:2759–2766. doi: 10.1093/emboj/17.10.2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grad L., Yerbury J.J., Turner B.J., Guest W.C., Pokrishevsky E., O’Neill M.A., Yanai A., Silverman J.M., Zeineddine R., Corcoran L. Intercellular propagated misfolding of wild-type Cu/Zn superoxide dismutase occurs via exosome-dependent and –independent mechanisms. Proc. Natl. Acad. Sci. USA. 2014;111:3620–3625. doi: 10.1073/pnas.1312245111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guigas G., Weiss M. Sampling the cell with anomalous diffusion—the discovery of slowness. Biophys. J. 2008;94:90–94. doi: 10.1529/biophysj.107.117044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo M., Ehrlicher A.J., Jensen M.H., Renz M., Moore J.R., Goldman R.D., Lippincott-Schwartz J., Mackintosh F.C., Weitz D.A. Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell. 2014;158:822–832. doi: 10.1016/j.cell.2014.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo M., Gelman H., Gruebele M. Coupled protein diffusion and folding in the cell. PLoS ONE. 2014;9:e113040. doi: 10.1371/journal.pone.0113040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo S.-M., Bag N., Mishra A., Wohland T., Bathe M. Bayesian total internal reflection fluorescence correlation spectroscopy reveals hIAPP-induced plasma membrane domain organization in live cells. Biophys. J. 2014;106:190–200. doi: 10.1016/j.bpj.2013.11.4458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedde P.N., Stakic M., Gratton E. Rapid measurement of molecular transport and interaction inside living cells with single plane illumination microscopy. Biophys. J. 2015;4 doi: 10.1038/srep07048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hihara S., Pack C.-G., Kaizu K., Tani T., Hanafusa T., Nozaki T., Takemoto S., Yoshimi T., Yokota H., Imamoto N. Local nucleosome dynamics facilitate chromatin accessibility in living mammalian cells. Cell Rep. 2012;2:1645–1656. doi: 10.1016/j.celrep.2012.11.008. [DOI] [PubMed] [Google Scholar]
- Jaqaman K., Kuwata H., Touret N., Collins R., Trimble W.S., Danuser G., Grinstein S. Cytoskeletal control of CD36 diffusion promotes its receptor and signaling function. Cell. 2011;146:593–606. doi: 10.1016/j.cell.2011.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S., Nollen E.A.A., Kitagawa K., Bindokas V.P., Morimoto R.I. Polyglutamine protein aggregates are dynamic. Nat. Cell Biol. 2002;4:826–831. doi: 10.1038/ncb863. [DOI] [PubMed] [Google Scholar]
- Lai C.W., Aronson D.E., Snapp E.L. BiP availability distinguishes states of homeostasis and stress in the endoplasmic reticulum of living cells. Mol. Biol. Cell. 2010;21:1909–1921. doi: 10.1091/mbc.E09-12-1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson D.R., Ma Y.M., Vogt V.M., Webb W.W. Direct measurement of Gag-Gag interaction during retrovirus assembly with FRET and fluorescence correlation spectroscopy. J. Cell Biol. 2003;162:1233–1244. doi: 10.1083/jcb.200303200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luby-Phelps K. Cytoarchitecture and physical properties of cytoplasm: Volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 2000;192:189–221. doi: 10.1016/s0074-7696(08)60527-6. [DOI] [PubMed] [Google Scholar]
- Malchus N., Weiss M. Elucidating anomalous protein diffusion in living cells with fluorescence correlation spectroscopy-facts and pitfalls. J. Fluoresc. 2010;20:19–26. doi: 10.1007/s10895-009-0517-4. [DOI] [PubMed] [Google Scholar]
- Mazza D., Braeckmans K., Cella F., Testa I., Vercauteren D., Demeester J., De Smedt S.S., Diaspro A. A new FRAP/FRAPa method for three-dimensional diffusion measurements based on multiphoton excitation microscopy. Biophys. J. 2008;95:3457–3469. doi: 10.1529/biophysj.108.133637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinney S.A., Murphy C.S., Hazelwood K.L., Davidson M.W., Looger L.L. A bright and photostable photoconvertible fluorescent protein. Nat. Methods. 2009;6:131–133. doi: 10.1038/nmeth.1296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miermont A., Waharte F., Hu S., McClean M.N., Bottani S., Léon S., Hersen P. Severe osmotic compression triggers a slowdown of intracellular signaling, which can be explained by molecular crowding. Proc. Natl. Acad. Sci. USA. 2013;110:5725–5730. doi: 10.1073/pnas.1215367110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monnier N., Barry Z., Park H.Y., Su K.-C., Katz Z., English B.P., Dey A., Pan K., Cheeseman I.M., Singer R.H., Bathe M. Inferring transient particle transport dynamics in live cells. Nat. Methods. 2015;12:838–840. doi: 10.1038/nmeth.3483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawar N., Donth C., Weiss M. Anisotropic diffusion of macromolecules in the contiguous nucleocytoplasmic fluid during eukaryotic cell division. Curr. Biol. 2014;24:1905–1908. doi: 10.1016/j.cub.2014.06.072. [DOI] [PubMed] [Google Scholar]
- Petrášek Z., Schwille P. Precise measurement of diffusion coefficients using scanning fluorescence correlation spectroscopy. Biophys. J. 2008;94:1437–1448. doi: 10.1529/biophysj.107.108811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponti A., Vallotton P., Salmon W.C., Waterman-Storer C.M., Danuser G. Computational analysis of F-actin turnover in cortical actin meshworks using fluorescent speckle microscopy. Biophys. J. 2003;84:3336–3352. doi: 10.1016/S0006-3495(03)70058-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedel C., Gabizon R., Wilson C.A.M., Hamadani K., Tsekouras K., Marqusee S., Pressé S., Bustamante C. The heat released during catalytic turnover enhances the diffusion of an enzyme. Nature. 2015;517:227–230. doi: 10.1038/nature14043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruan Q., Chen Y., Gratton E., Glaser M., Mantulin W.W. Cellular characterization of adenylate kinase and its isoform: Two-photon excitation fluorescence imaging and fluorescence correlation spectroscopy. Biophys. J. 2002;83:3177–3187. doi: 10.1016/S0006-3495(02)75320-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton M.J. Anomalous diffusion due to binding: A Monte Carlo study. Biophys. J. 1996;70:1250–1262. doi: 10.1016/S0006-3495(96)79682-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton M.J. Wanted: A positive control for anomalous subdiffusion. Biophys. J. 2012;103:2411–2422. doi: 10.1016/j.bpj.2012.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schenk A., Ivanchenko S., Röcker C., Wiedenmann J., Nienhaus G.U. Photodynamics of red fluorescent proteins studied by fluorescence correlation spectroscopy. Biophys. J. 2004;86:384–394. doi: 10.1016/S0006-3495(04)74114-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprague B.L., Pego R.L., Stavreva D.A., McNally J.G. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 2004;86:3473–3495. doi: 10.1529/biophysj.103.026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swaminathan R., Hoang C.P., Verkman A.S. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: Cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 1997;72:1900–1907. doi: 10.1016/S0006-3495(97)78835-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K., Tănase-Nicola S., ten Wolde P.R. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc. Natl. Acad. Sci. USA. 2010;107:2473–2478. doi: 10.1073/pnas.0906885107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tardy Y., McGrath J.L., Hartwig J.H., Dewey C.F. Interpreting photoactivated fluorescence microscopy measurements of steady-state actin dynamics. Biophys. J. 1995;69:1674–1682. doi: 10.1016/S0006-3495(95)80085-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terry B.R., Matthews E.K., Haseloff J. Molecular characterisation of recombinant green fluorescent protein by fluorescence correlation microscopy. Biochem. Biophys. Res. Commun. 1995;217:21–27. doi: 10.1006/bbrc.1995.2740. [DOI] [PubMed] [Google Scholar]
- Waterman-Storer C.M., Desai A., Bulinski J.C., Salmon E.D. Fluorescent speckle microscopy, a method to visualize the dynamics of protein assemblies in living cells. Curr. Biol. 1998;8:1227–1230. doi: 10.1016/s0960-9822(07)00515-5. [DOI] [PubMed] [Google Scholar]
- Weiss M., Elsner M., Kartberg F., Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004;87:3518–3524. doi: 10.1529/biophysj.104.044263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G., Houghtaling B.R., Gaetz J., Liu J.Z., Danuser G., Kapoor T.M. Architectural dynamics of the meiotic spindle revealed by single-fluorophore imaging. Nat. Cell Biol. 2007;9:1233–1242. doi: 10.1038/ncb1643. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.