Signal-independent noise in intracortical brain-computer interfaces causes movement time properties inconsistent with Fitts’ law

Abstract

Objective

Do movements made with an intracortical BCI (iBCI) have the same movement time properties as able-bodied movements? Able-bodied movement times typically obey Fitts’ law: MT = a + b log₂(D/R ) (where MT is movement time, D is target distance, R is target radius, and a,b are parameters). Fitts’ law expresses two properties of natural movement that would be ideal for iBCIs to restore: (1) that movement times are insensitive to the absolute scale of the task (since movement time depends only on the ratio D/R) and (2) that movements have a large dynamic range of accuracy (since movement time is logarithmically proportional to D/R).

Approach

Two participants in the BrainGate2 pilot clinical trial made cortically controlled cursor movements with a linear velocity decoder and acquired targets by dwelling on them. We investigated whether the movement times were well described by Fitts’ law.

Main Results

We found that movement times were better described by the equation MT = a + bD + cR⁻², which captures how movement time increases sharply as the target radius becomes smaller, independently of distance. In contrast to able-bodied movements, the iBCI movements we studied had a low dynamic range of accuracy (absence of logarithmic proportionality) and were sensitive to the absolute scale of the task (small targets had long movement times regardless of the D/R ratio). We argue that this relationship emerges due to noise in the decoder output whose magnitude is largely independent of the user’s motor command (signal-independent noise). Signal-independent noise creates a baseline level of variability that cannot be decreased by trying to move slowly or hold still, making targets below a certain size very hard to acquire with a standard decoder.

Significance

The results give new insight into how iBCI movements currently differ from able-bodied movements and suggest that restoring a Fitts’ law-like relationship to iBCI movements may require nonlinear decoding strategies.

Introduction

Able-bodied reaching movements towards stationary targets typically obey Fitts’ law:

$$MT=a+b{log}_2(\frac{D}{R}),$$

where MT is movement time, D is target distance, R is target radius, and a,b are parameters (Fitts 1954). Tasks where Fitts’ law has been shown to be a good descriptor of movement times include using a stylus to tap a target region of a predefined size (Fitts 1954), transferring pins to holes of different sizes (Fitts 1954), grasping objects (Bootsma et al. 1994), using a joystick or mouse to move a cursor on a monitor (Jagacinski, Hartzell, and Ward 1978; Epps 1986; Kantowitz and Elvers 1988), and making pointing movements with a variety of joints (Michmizos and Krebs 2014; Langolf, Chaffin, and Foulke 1976; Corcos, Gottlieb, and Agarwal 1988; Leisman 1989). Fitts’ law expresses two properties of the able-bodied motor system that hold generally (though not always strictly) across a wide range of tasks:

1. Scale invariance. According to Fitts’ law, only the ratio of target distance to target radius affects movement time. Shrinking or expanding the task by a constant scale factor should therefore not affect movement time. This invariance to motor scale is similar to the sensory system’s ability to operate at an equivalent relative accuracy over many orders of magnitude (Weber’s law).

2. High dynamic range. Fitts’ law describes movement time as a logarithmic function of D/R, reflecting the ability of the motor system to complete tasks requiring orders of magnitude more relative accuracy (larger D/R ratios) without taking orders of magnitude more time to complete them.

Scale invariance and high dynamic range are useful properties that enable the able-bodied motor system to achieve good performance over a wide range of tasks occurring at different absolute scales and demanding different relative levels of accuracy. With the stated goal of many iBCI studies being to close the existing performance gap between iBCI-controlled movements and able-bodied movements [e.g. (Collinger et al. 2013; Gilja et al. 2012)], it is natural to ask: do iBCI-controlled movements currently obey a Fitts’ law-like movement time relationship that would be indicative of scale invariance and high dynamic range? If not, can investigating this discrepancy teach us something new about iBCIs and give insight into how to further improve them?

Several studies have used Fitts’ law as a tool to quantify iBCI performance (Simeral et al. 2011; Gilja et al. 2012; Gilja et al. 2015) and have reported data that is reasonably consistent with Fitts’ law for a limited range of target distances, radii, and gains (speed scaling parameters). One recent study tested the validity of Fitts’ law explicitly and showed that in one rhesus macaque, iBCI movement times were better described by the Shannon-Welford model in one of the five experimental sessions considered (Matlack, Chizeck, and Moritz 2016). The Shannon-Welford model relaxes the scale invariance assumption of Fitts’ law by having separate terms for the effect of target distance and radius on movement time. While statistically significant, the departure from Fitts’ law observed in that study was relatively small in magnitude, on the order of what is sometimes seen in able-bodied movements (Shoemaker et al. 2012). Therefore, as previous iBCI studies have not reported a substantial departure from Fitts’ law, one might conclude that movement time properties for iBCIs may be quite similar to natural movements. Alternatively, this lack of departure may be because Fitts’ law was not tested over a wide enough range of target radii and gains (particularly, smaller targets and faster gains, which would enable task difficulties and movement times similar to those found in studies on able-bodied movements).

In this study, to test whether iBCI-commanded movement exhibit different movement time properties from natural movements, we collected and use data from fifteen research sessions from two participants of the BrainGate2 pilot clinical trial in which iBCI control was tested under a wide range of parameters. In the first half of the study, we demonstrate substantial departures from Fitts’ law when participants use a linear decoder to acquire targets with a computer cursor. We found that the participants’ movement times were inconsistent with both the scale invariance and high dynamic range properties expressed by Fitts’ law, and that these inconsistencies were substantially greater than smaller violations sometimes found for able-bodied movements (Shoemaker et al. 2012). We propose a new movement time equation to describe what we observed.

In the second half of the study, we investigate why Fitts’ law does not generally hold for iBCI-controlled cursor movements. It is thought that signal-dependent motor noise (motor noise that scales in proportion to the magnitude of the motor command) underlies both the scale invariance and dynamic range properties of able-bodied movements by enabling a person to achieve greater precision by moving more slowly or by making smaller movements (Meyer et al. 1988; Harris and Wolpert 1998; Tanaka, Krakauer, and Qian 2006; Guigon, Baraduc, and Desmurget 2008; Bye and Neilson 2008). Signal-dependent noise explains scale invariance because movements made at smaller scales have a proportionally smaller amount of noise (thus keeping the relative size of the noise constant across scales). Signal-dependent noise also explains the high dynamic range of able-bodied movement, since targets demanding high accuracy can be achieved by slowing down and making small corrective movements.

Could signal-independent noise in iBCI- controlled movements be the underlying reason for a departure from Fitts’ law? To our knowledge, there is no direct evidence in the literature concerning the signal-dependency of unintended variability (“noise”) in the decoder output during control of an iBCI, though when discussing and simulating iBCI movements researchers often model the decoding noise as signal-independent (Willett et al. 2017; Marathe and Taylor 2015; Rouse and Schieber 2015).

Here, we directly analyze the decoder output and simulate iBCI movements in several ways to show that signal-independent decoding noise is indeed the root cause of the non-standard movement time properties we observed. Finally, we quantitatively compare the noise properties of iBCI movements to those of the able-bodied motor system, and conclude that new decoding approaches may be required to impart Fitts’ law properties to iBCI commanded movements.

Methods

Permission for these studies was granted by the US Food and Drug Administration (Investigational Device Exemption #G090003) and the Institutional Review Boards of University Hospitals Case Medical Center (protocol #04-12-17), Stanford University (protocol #20804), Partners Healthcare/Massachusetts General Hospital (2011P001036), Providence VA Medical Center (2011-009), and Brown University (0809992560). All participants were enrolled in a pilot clinical trial of the BrainGate Neural Interface System (http://www.clinicaltrials.gov/ct2/show/NCT00912041). Informed consent, including consent to publish, was obtained from the participants prior to their enrollment in the study.

Participants

This study includes data from two participants (T6, T8), both of whom have chronic tetraplegia and received intracortical implants as part of the BrainGate2 pilot clinical trial. T6 and T8 had one and two 96 channel intracortical microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT), respectively, implanted in the hand area of dominant motor cortex (1.0-mm electrode length for T6, 1.5-mm length for T8). T6 is a 52-year-old woman diagnosed with ALS. T6 received the intracortical array on December 7, 2012 and data in this study are from T6’s trial days 727 to 837. Participant T8 is a 53-year-old man with cervical spinal cord injury (C4, ASIA A). T8 received the intracortical arrays on December 1, 2014 and data in this study are from T8’s trial days 101 to 354. Surgery details can be found in (Gilja et al. 2015; Simeral et al. 2011; Hochberg et al. 2006).

Note that we sometimes used different parameter settings (specified below) for each participant. This was done in attempt to optimize decoding performance for each participant’s unique neural signals and to keep consistent with what each participant was accustomed to from previous studies. We do not believe that any of these differences are a confounding factor, and consistent results were found despite these minor differences.

Study design and task

We analyzed 3 center-out-and-back and 12 random target sessions of closed loop neural control of a 2D computer cursor. Participants were instructed to imagine using the thumb and index finger to control the cursor (T6) or attempt to make arm movements to control the cursor (T8), consistent with how each participant was accustomed to controlling the cursor from previous studies (Jarosiewicz et al. 2015; Gilja et al. 2015).

Each session began with an open loop block where participants watched the cursor automatically complete a center-out-and-back target acquisition task while attempting to make the cursor movements shown. We used this data to calibrate the decoding matrix. Then, participants completed a series of closed loop neural control blocks with computer assistance that were used to re-calibrate the decoder. Finally, the decoder was held fixed and participants completed a series of 4 or 5 minute closed-loop blocks with no computer assistance. Data reported in the study are from these later closed-loop blocks.

Participants acquired targets by holding the cursor in unbroken contact with the target region for a specified dwell-time (which we sometimes varied from session to session). A trial was failed and the cursor was reset to the target position if a maximum movement time of 8 to 12 seconds (depending on the session) was exceeded. After a target was acquired, another target appeared after a 200 to 300 ms delay (T6) or immediately afterwards (T8). In the random target task, targets appeared in a random location within a square workspace with uniform probability (but were constrained to appear far enough away from the cursor so as not to overlap it). Targets appeared with a radius chosen from a set of 1 of 3 possible radii. Note that when reporting target radius and testing Fitts’ law, we use the “effective” target radius (actual target radius plus cursor radius) which defines the size of the target acquisition region. Supplementary tables 1 and 2 summarize the parameters used for each dataset.

Decoding architecture

We used a reparameterized, steady-state Kalman filter to enable real-time neural control of cursor velocity (Jarosiewicz et al. 2015; Gilja et al. 2015; Fan et al. 2014; Gilja et al. 2012; Malik et al. 2011). We reparameterized the Kalman filter to separate its dimensionality reduction step (linearly mapping the high-dimensional neural feature space to a two-dimensional control signal) from its filtering dynamics (gain, smoothing, and integrating velocity to get position) following the methods of (Willett et al. 2017). This reparameterization allowed us to clearly isolate and define the cursor gain, which was important for testing Fitts’ law.

Dimensionality reduction

Our signal processing and neural feature extraction methods followed closely those of (Willett et al. 2017; Jarosiewicz et al. 2015). Every 20 millisecond time step, threshold crossing counts and power in the spike frequency band (250–5000 Hz) were computed for each channel. Threshold crossing counts were defined as the number of times that the voltage time series on a given channel crossed a negative threshold ( −3.25 × RMS for T6, who did not have many discernable single-unit spikes, and −4.5 × RMS for T8, who did). The RMS for each channel was computed at the beginning of the session using one minute of data. High frequency power was defined as the root mean square of the signal in the spike band during each 20 ms time step. These neural features were concatenated into a 2N × 1 feature vector (where N is the number of microelectrode array channels) and normalized by subtracting their mean and dividing by their standard deviation.

At each time step, we mapped the neural features to a decoded “control” vector with the equation

$$u_t=D{f}_t,$$

where f_t is a 2N × 1 neural feature vector, D is a 2 × 2N decoding matrix, and u_t is a 2 × 1 decoded control vector.

To account for changes in the mean value of neural features over time that can cause an offset (bias) to appear in u_t (Perge et al. 2013), we updated our estimate of the feature means over the course of the session using methods similar to Jarosiewicz et al. 2015. We also used a “bias corrector” during blocks of closed-loop control to detect and remove biases in u_t not accounted for by updating the feature means (Jarosiewicz et al. 2015).

Decoder calibration

To build the decoding matrix, we made the assumption that u_t pointed straight from the cursor to the target at each time step with a constant magnitude of 1. To build the decoder, we used all open loop and closed-loop calibration data (2 to 7 blocks, each five minutes long). The matrix D was solved for using either “reverse regression” with T6 (Kass, Ventura, and Brown 2005), or “full OLE” with T8 (Chase, Schwartz, and Kass 2009). The regressions were done on the raw, 20 ms time step data (and not the trial averages). To exclude data where the control vector may have decreased in magnitude near the target (violating the assumption that the control vector is of constant magnitude), we excluded time steps after the first 1.8 (T6) or 1.5 (T8) seconds of the trial.

Cursor gain and smoothing

The decoded control vector u_t was smoothed using a first-order low-pass filter (equivalent to the kind of smoothing done by a steady-state Kalman filter) and mapped to cursor velocity with the equation

$$v_{t+1}=\alpha v_t+(1-\alpha )\beta u_t,$$

where v_t is cursor velocity, α ∈ [0,1) parameterizes the amount of low-pass smoothing and β ∈ (0, ∞) can be used to vary the cursor gain.

Importantly, we normalized the decoding matrix D (see Section 1 of the Supplement) so that β alone parameterized the maximum speed of the cursor. When D is normalized, β defines the cursor’s “terminal velocity”, or the (average) speed that the cursor would asymptotically approach if the user pointed u_t in the same direction forever. We report cursor gain as this maximum speed, reported in units of workspace widths per second (WW/s).

Computer simulation of iBCI cursor movements with signal-independent noise

We propose a simple computer model of iBCI cursor movements that can explain the movement time properties we observed and that is consistent with the hypothesis that signal-independent noise is the root cause of those properties. In the model, the cursor is a massless particle whose velocity at each time step is equal to signal-independent, Gaussian noise plus neural modulation that pushes the cursor straight towards the target at a constant magnitude. To simulate movements with this model, we set α=0 (which simplifies the model by removing all smoothing dynamics) and generated u_t at each time step according to the following equation:

$$u_t=\frac{g_t-p_t}{\Vert g_t-p_t\Vert }+e_t,$$

where g_t is the target position, p_t is the cursor position, and e_t is normally distributed (signal-independent) white noise with a standard deviation equal to 1.5. Note that similar results can be obtained with α>0 (not shown). We chose to report results for α=0 to highlight that the movement time properties we observed can be explained solely by signal-independent noise and a constant “neural push”.

We performed three separate simulations to show that the model can reproduce the empirical movement time properties shown in figures 2, 3 and 4 (simulation results are shown in figure 5). To reproduce figure 2, we simulated 100 movements under each of 5 gain settings to a target with a radius of 0.095 workspace widths (WW) and a distance of 0.58 WW. To reproduce figure 3, we simulated 100 movements under 18 target distance and radius conditions and 3 different gain conditions (full factorial design with 3 radii, 6 distances and 3 gains). To reproduce figure 4, we simulated 100 movements under 64 target distance and radius conditions (full factorial design with 8 radii and 8 distances).

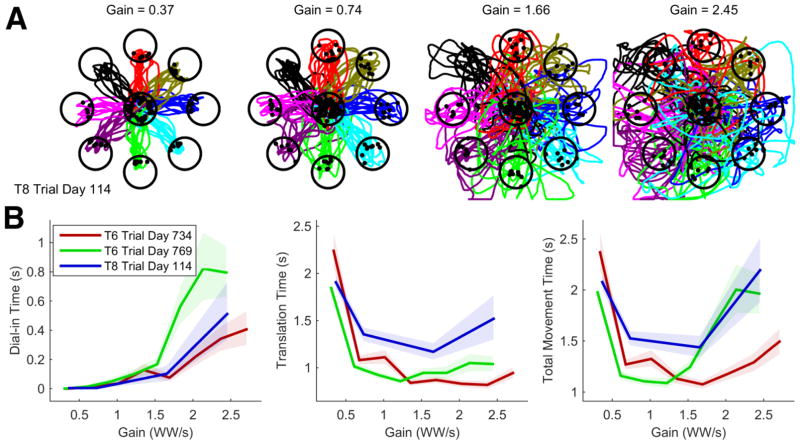
Figure 2.

Effect of cursor gain on iBCI movements. (A) Cursor trajectories (colored by target) made by T8 under four different cursor gains. Cursor movements made at higher gains are faster but lack accuracy; the cursor takes curved paths towards the target and circles around it instead of coming to a complete stop on top of it. (B) Dial-in Time, Translation Time, and Movement Time as a function of cursor gain (reported in workspace widths per second at terminal speed) for three sessions (2 with T6, 1 with T8). Error regions are 95% confidence intervals for the mean. Cursor gain has a large effect on movement time, in contrast to the scale invariance predicted by Fitts’ law.

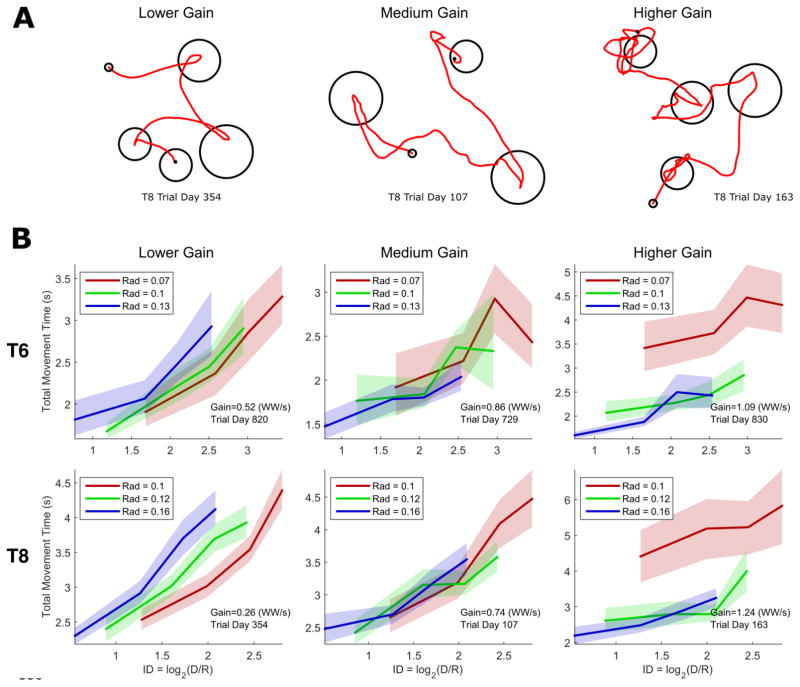
Figure 3.

(A) Example cursor movements made by T8 in the random target task under three different gain conditions. (B) Index of difficulty (ID) vs. movement time plots for 6 example conditions (3 from T6 on the top row, 3 from T8 on the bottom row). One “ID vs. movement time” line is plotted for each target radius and illustrates the average movement time for four target distance bins. If Fitts’ law holds, all three radius lines should lie on top of one another. Divergent lines (left and right columns) indicate that index of difficulty alone cannot describe how movement time varies as a function of target distance and radius. Error regions represent 95% confidence intervals. Each line contains data from four distinct target distance bins (with bin edges at 0.15, 0.3, 0.45, 0.6, and 0.75 workspace widths).

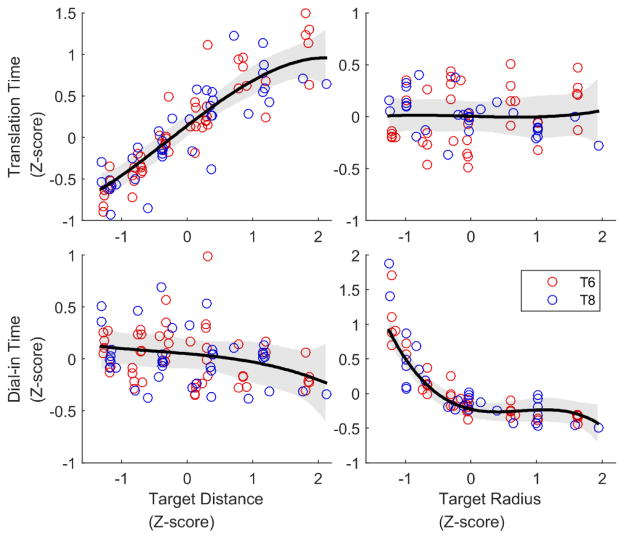
Figure 4.

Main effect of target distance (left column) and target radius (right column) on translation time (top row) and dial-in time (bottom row) across all sessions and conditions. Each circle indicates the average dial-in time or translation time for movements corresponding to a single “dataset” (a unique session date and dwell time setting). Variables have been normalized (z-score) to enable comparison across data with different absolute levels of performance and target characteristics. The thick black lines with gray 95% CI regions were generated by fitting a third-order polynomial for visualization purposes. They indicate that translation time is a linear function of target distance and that dial-in time is a power law function of target radius.

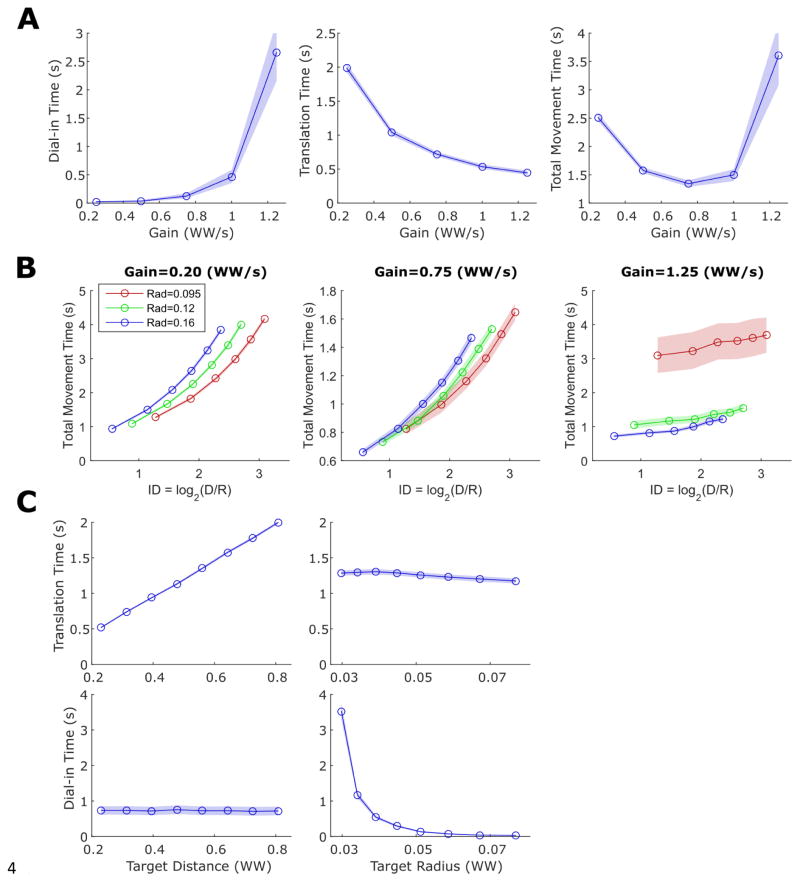
Figure 5.

A highly simplified computer model of iBCI cursor movements featuring signal-independent decoding noise reproduces all of the movement time relationships we empirically observed in figures 2–4. One hundred movements were simulated for each condition and the shaded regions indicate 95% confidence intervals. (A) Simulated gain vs. movement time curves are U-shaped, as in figure 2. (B) The simulated ID vs. movement time curves diverge for low and high gains, as in figure 3. (C) Simulated dial-in time is a power law function of radius (independently of distance) and simulated translation time is a linear function of distance (independently of radius), as in figure 4.

Simulation of iBCI cursor movements with able-bodied volunteers

To further investigate the effect of signal-independent and dependent noise on movement times, we constructed a simulation of iBCI cursor movements that consisted of able-bodied volunteers controlling cursors using a joystick. We collected data from three able-bodied volunteers (2 male and 1 female graduate students at Case Western Reserve University, ages 22 to 25) that were naïve to the purpose of the experiment. Informed consent was obtained from the participants and approval was obtained from the Institutional Review Board at University Hospitals Case Medical Center (protocol #11-12-27).

Each volunteer completed 12 blocks of 200 cursor movements each (2400 movements total) under different noise and cursor gain conditions. The “position” of the joystick at each time step (i.e. the X and Y offset of the stick from its center position, as returned by the device) was substituted for u_t in the velocity update equation, so that the velocity smoothing dynamics were identical to those in the iBCI system. The joystick position was normalized to have a maximum magnitude of 1. We set the smoothing coefficient (α) equal to 0.94 and varied the cursor gain (β) from 0.385 to 3.85 WW/s. We preferred using a joystick to using the position of a computer mouse because (1) the joystick position is physically bounded, thus simulating bounds on the neural population activity, and (2) the springs in the joystick automatically guide it back to its equilibrium position that corresponds to zero velocity, so that the user does not have to guess or memorize where the zero position is.

We tested three different noise conditions. In the “no noise” condition, no noise was added to u_t beyond that introduced by the participant’s own motor system. In the “signal-independent noise” condition, we added white noise to u_t at each time step that was normally distributed with a standard deviation of 1.0 (compare to figure 6F) In the “signal-dependent noise” condition, we added white noise to u_t at each time step that was normally distributed with a standard deviation equal to 2 times the magnitude of u_t as determined by the joystick.

Figure 6.

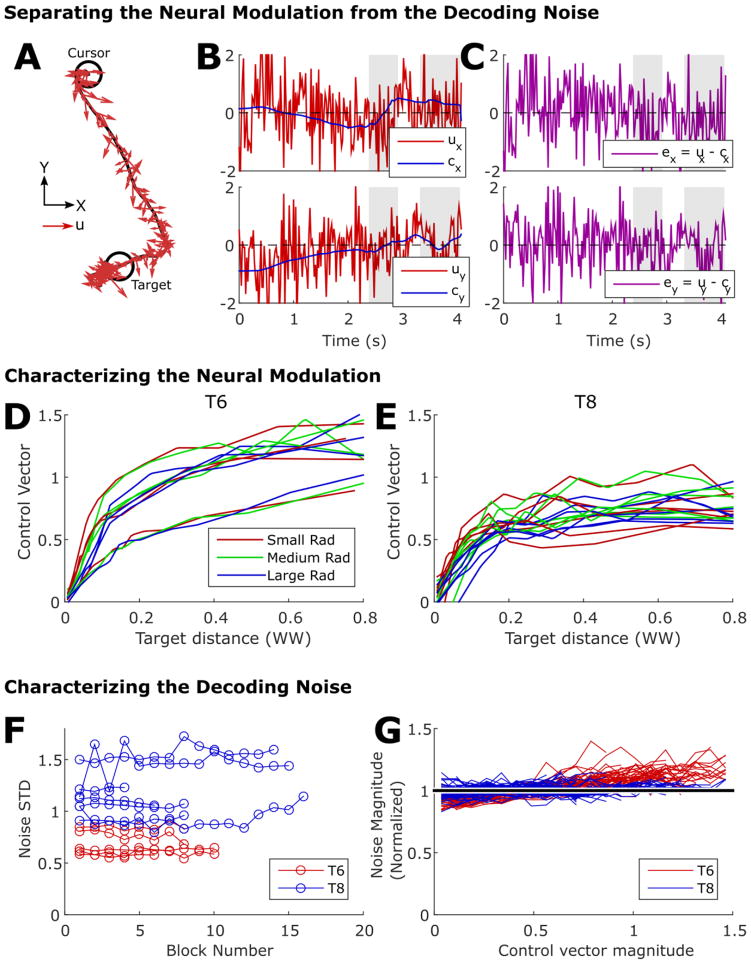
Verifying that the participants’ neural modulation and decoding noise is consistent with the computer model of iBCI cursor movements. (A–C) Before analysis can be done, the output of the decoder must first be decomposed into a volitional modulation component and a noise component. Panel A shows an example cursor movement from a random target session with T8, illustrating the trajectory (black line) plus the pre-smoothed output of the decoder at each time step along the trajectory (red vectors). Panel B shows the same decoder output (u) as a time series plotted against what we estimated to be the volitional component (c, which we call the “encoded control vector”). Panel C shows the noise component (e) obtained by subtracting c from u. Gray regions indicate when the cursor is on top of the target. (D,E) Size of the control vector as a function of target distance and radius for T6 and T8. Each line is estimated from a different session of the random target task. Consistent with the computer model, modulation is independent of target radius and is relatively flat when not near the target. (F) Magnitude of the noise (characterized by standard deviation) for each block of the random target task included in the study (blocks from the same session are connected with a line). The noise magnitude is comparable to that of the volitional modulation. (G) Normalized noise magnitude as a function of control vector magnitude for each block of data. Each curve was normalized by dividing by its mean value. Consistent with our hypothesis, the noise is largely signal-independent.

Results

I. Effect of gain on movement time

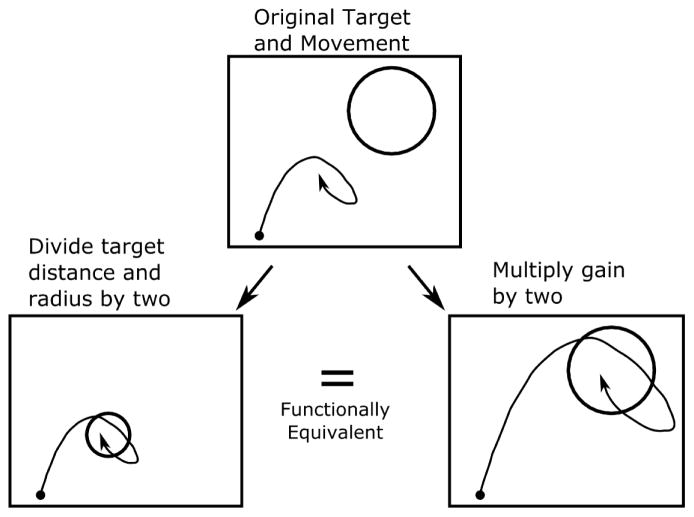
If iBCI movements are scale invariant (as Fitts’ law predicts), then their duration should be invariant to “cursor gain” (also called the control display gain, or speed scaling). This is because changing the cursor gain by a factor of g has functionally the same effect as scaling both the target distance and radius by a factor of 1/g (e.g., doubling the cursor gain is functionally the same as halving both the target distance and radius, see figure 1 for an illustration). Fitts’ law would then predict that movement time will remain unchanged (since $\frac{D/g}{R/g}=\frac{D}{R}$ for any g).

Figure 1.

Diagram illustrating how increasing (decreasing) the cursor gain is equivalent to shrinking (expanding) both the target distance and radius. We study the effect of cursor gain on iBCI movement times as a way of testing the scale invariance predicted by Fitts’ law.

Figure 2 illustrates how changing the cursor gain affected movement time for three experimental sessions of a standard center-out-back task. In this task, participants T6 and T8 controlled the velocity of the cursor using a reparameterized, steady-state Kalman filter that decodes velocity (Gilja et al. 2015; Jarosiewicz et al. 2015; Hochberg et al. 2012; Malik et al. 2011) and acquired targets by hovering the cursor over the target for a specified dwell-time.

In contrast to able-bodied movements, where movement accuracy can remain roughly equivalent over a wide range of gains (Kantowitz and Elvers 1988; Lin, Radwin, and Vanderheiden 1992; Bohan et al. 2003; van Doorn and Unema 2005; Casiez et al. 2008), we found that movement accuracy sharply decreased for iBCI movements as gain was increased. Cursor movements made at higher gains were fast and inaccurate, orbiting uncontrollably in and around the target region instead of stopping precisely on top of it (figure 2a).

We used three metrics to quantify each movement: translation time (time taken to first reach the target), dial-in time (time spent trying to dwell on the target beyond the necessary dwell time; Gilja et al., 2012), and total movement time (time taken to acquire the target). As the gain was increased, dial-in time (figure 2b, left) and translation time (figure 2b, middle) traded off with each other and caused the total movement time curve to be U-shaped, with an optimal point where dial-in time trades off in a balanced way with translation time (figure 2b, right). This is evidence that iBCI movements may not have the scale invariance property implied by Fitts’ law; if they did, the gain vs. movement time curves would be horizontal lines (implying a constant movement time) instead of U-shaped. For able-bodied movements this is typically the case; able-bodied gain vs. movement time curves are mostly flat with movement time varying only slighty (e.g., by 0–10%) in spite of a 2, 4, or even 10 fold increase in gain (Kantowitz and Elvers 1988; Lin, Radwin, and Vanderheiden 1992; Bohan et al. 2003; van Doorn and Unema 2005; Casiez et al. 2008).

Note that we define movement time here to include both the translation and dial-in portion of the movement. Including the dial-in time is important for measuring movement accuracy and is consistent with literature on Fitts’ law where a “dial-in” phase of the task is typically included [e.g., requiring participants to place a pin accurately in a hole (Fitts 1954)].

II. Effect of target distance and radius on movement time

To measure the effect of target distance and radius on movement time, we asked T6 and T8 to acquire targets in a “random target” task (Simeral et al. 2011) where each new target appeared in a random location with one of three possible sizes (figure 3A shows example movements made by T8). Results from twelve sessions of the random target task demonstrate that iBCI movement times can sometimes substantially depart from Fitts’ law (Figure 3B). To be consistent with Fitts’ law, movement times must be linearly proportional to ${log}_2(\frac{D}{R})$ (called the “index of difficulty”). We tested this by plotting movement time vs. index of difficulty (ID) for each of the three target sizes separately; if Fitts’ law holds, these three lines should lie on top of each other.

We found that for conditions with higher cursor gains, target radius had a disproportionately large effect on movement time. Targets with small radii were much more difficult to acquire than those with larger radii, adding more movement time than Fitts’ law expects and shifting the index of difficulty (ID) vs. movement time lines upwards for smaller targets (right column of figure 3). This departure from Fitts’ law was substantially greater than the smaller violations of Fitts’ law previously demonstrated for able-bodied pointing movements (Shoemaker et al. 2012; Matlack, Chizeck, and Moritz 2016); in supplemental figure 1 we demonstrate this quantitatively.

For conditions with lower cursor gains, smaller targets posed no extra difficulty and so the target radius had little effect on the movement time, leaving the effect of target distance to dominate (left column of figure 3). As we discuss later, the cursor seems to approach maximum velocity before reaching the target, causing movement time to increase linearly with target distance (instead of logarithmically as expected by Fitts’ law). The linear effect of distance and the non-existent effect of radius at lower gains causes the ID vs. movement time curves to shift towards the right. However, when the effect of target radius was approximately balanced with that of target distance, Fitts’ law did appear to hold (middle column of figure 3).

Supplemental figure 2 shows the ID vs movement time curves for all parameter settings included in all twelve sessions. We varied the target radii, dwell times, and cursor gains across sessions and sometimes tested multiple conditions within a single session. For some settings, Fitts’ law is a reasonable approximation of the data, while for others gross violations can be seen, particularly when the gain is higher or the dwell time is long. At higher gains, both T6 and T8 were unable to make the cursor slow down enough to make the cursor stop within the smaller target without continually leaving the target area. Supplemental figure 3 confirms that the lack of overlap for the radius-specific ID vs. movement time lines is not affected by the placement of the bin edges (it holds for both linearly and logarithmically spaced edges).

III. A new movement time equation for iBCIs

Since we found that Fitts’ law was sometimes substantially violated by iBCI movement times (figures 2 and 3), we sought to find a new equation that could better explain iBCI movement times and, in doing so, offer new insight into the properties of iBCI-commanded movements.

We designed a new equation by examining the main effect of target radius and distance on translation time and dial-in time as observed in the random target task (figure 4). For sessions with more than one gain condition, we combined the data across conditions by dividing the target distances and radii by the cursor gain (since changing the gain by a factor of g has the same functional effect as scaling the task by a factor of 1/g). Doing so increased the number of target distance and radius pairs available for fitting from 12 pairs in a single-gain condition to 24 or 36 pairs in a multi-gain combined condition. However, data collected during the same session but with a different dwell time setting could not be combined in the same way; we therefore examined each unique combination of session date and dwell time separately as its own dataset.

Figure 4 illustrates that translation time appears to vary linearly as a function of target distance and to be independent of target radius. In contrast, dial-in time appears to vary as a power law function of target radius and to be independent of target distance. Assuming that translation time and dial-in time sum linearly to determine the total movement time yields the following equation:

$$MT=a+bD+c{R}^{-2},$$

where a, b, and c are parameters, D is target distance, R is target radius, and MT is average movement time.

The proposed relationship (which we call “LinPow”) implies that movement time is a linear function of target distance (bD), but a power law function of target radius (cR⁻²). In contrast to Fitts’ law, LinPow is scale sensitive as opposed to scale invariant (since it has separate terms for D and R). It also implies a smaller dynamic range of accuracy than Fitts’ law (R⁻² grows much faster than log₂(1/R) when R is small; see Section 2 of the Supplement for how we determined the −2 exponent for the cR⁻² term). LinPow can therefore describe the sharp increase in movement time we observed when target radius becomes too small (supplemental figure 4A and 4B show examples).

To validate LinPow, we performed a cross-validated comparison of its ability to predict movement times vs. Fitts’ law. LinPow outperformed Fitts’ law for 14 out of 14 datasets (trials corresponding to a unique session date and dwell time combination). On average, Fitts’ law explained 46% of the variance in movement time as a function of target distance and radius, while LinPow explained 78%. Supplemental figure 5 shows prediction performance for each dataset and compares LinPow to four additional movement time equations in the literature, including the recently proposed Shannon-Welford model (Matlack, Chizeck, and Moritz 2016; Shoemaker et al. 2012). LinPow outperformed these models as well.

An additional advantage of LinPow is that it explains how movement time varies as a function of cursor gain for a fixed target distance and radius (supplemental figure 4C shows how LinPow can fit the U-shaped movement time vs. gain curves observed in figure 3B, while Fitts’ law and the Shannon-Welford model cannot).

IV. A computer model of iBCI cursor movements featuring signal-independent noise

We now turn our attention to explaining why Fitts’ law did not hold for the iBCI cursor movements we studied. In this section, we propose a simple model of iBCI cursor movements that can explain why iBCI movement times follow the form of the LinPow equation.

We hypothesize that when attempting to dwell on the target using a standard linear decoder, the user continually adjusts their neural activity using visual feedback to counteract signal-independent decoding noise perturbations that push the cursor about randomly. Instead of stopping definitively, the cursor moves about in a cloud centered on the target. As the radius of the target becomes small enough, the probability that the cursor will pop outside of the target at some point during the dwell time increases rapidly (power law), causing the R⁻² term in the LinPow equation. This phenomenon has no analog in able-bodied movements, where a person can come to a nearly complete stop since motor noise is small when no motor command is being executed (signal-dependent noise). For example, one study showed that the average hand acceleration during rest caused by physiologic tremor was around 0.02 m/s² (Morrison and Newell 2000), while peak accelerations during arm movements can easily reach 10 m/s² (Gordon et al. 1994).

To explain the linear D term in the movement time equation, we turn to the specifics of the user’s neural modulation and the exponential smoothing dynamics imposed by the Kalman filter decoder. Unless the smoothing is pronounced, it doesn’t take long to accelerate the cursor to near max speed. Since cursor movements typically occur over longer time scales (several seconds), the cursor will travel for much of the time at a relatively constant (on average) speed that is determined by the magnitude of the neural activity. If we assume that the user applies a “neural push” to the cursor that has a constant magnitude for any target distance or radius, then the cursor will cover distance linearly with respect to time, independently of target radius.

This model of iBCI cursor movements can be distilled into a simplified form: the movement of the cursor at each time step is equal to a Gaussian white noise vector (representing signal-independent decoding noise) plus a vector of constant magnitude that points from the cursor to the target (representing a volitional neural push that directs the cursor towards the target). Results from simulating this model, shown in figure 5, reproduce the departures from Fitts’ law empirically observed in figures 2–4. We simulated movements under different gains to reproduce the U-shaped movement time curves demonstrated in figure 2, and simulated movements to targets of different radii and distances to reproduce the divergent ID vs. movement time curves demonstrated in figure 3 and the dial-in time and translation time curves demonstrated in figure 4.

V. Verifying the computer model of cursor movement

The simplified computer model of iBCI cursor movements reproduces the movement time properties we observed, but is it also consistent with our participants’ neural modulation and decoding noise properties? To answer this, we directly examined the decoding noise properties of the iBCI and the user’s neural modulation strategy for moving the cursor to see if they matched the model.

To perform the analysis, we first needed to separate the output of the decoder into a noise component and a “volitional” component intended to push the cursor towards the target. To do so, we followed the approach taken in (Willett et al. 2017) and modeled the pre-smoothed output of the decoder (called the decoded control vector) as the sum of population-level neural modulation (called the encoded control vector) and decoding noise (unintended variability). In equation form:

$$u_t=c_t+e_t,$$

where u_t is the decoded control vector at time step t, c_t is the encoded control vector (representing volitional neural modulation) and e_t is the decoding noise.

We assumed that the encoded control vector points straight from the cursor to the target with a magnitude that is a nonlinear function of the distance between the cursor and the target [which is a simplified form of the feedback control model presented in (Willett et al. 2017)]. We empirically fit this distance weighting function to the data and used it to decompose u_t into c_t and e_t (see Section 3 of the Supplement for details). Panels A, B and C of figure 6 illustrate the results of this decomposition for an example cursor movement and highlight how large the decoding noise is compared to the signal. In addition to being large, it also appears pre-dominantly signal-independent; that is, the noise does not seem to attenuate very much when the cursor is on top of the target and the user is trying to hold still (and therefore presumably outputting a smaller motor command).

Figure 6D and 6E summarize, for each target radius, the magnitude of the encoded control vector as the cursor approaches the target. The analysis reveals that the participants did not change their behavior as a function of target radius (i.e., they did not attempt to move more slowly to acquire smaller targets) and that the control vector magnitudes remained fairly constant as a function of target distance [except when the cursor was near to the target, consistent with results from center-out datasets analyzed in (Willett et al. 2017)]. Figure 6F summarizes the magnitude of the noise (often comparable to or greater than the signal) and figure 6G summarizes its signal-dependency (weak or non-existent). In sum, the computer model appears to be consistent not only with the observed movement times, but also the user’s neural modulation and decoding noise.

VI. A model of how signal-independent decoding noise can arise from neurons with signal-dependent noise

The dominant presence of signal-independent decoding noise identified in figure 6 may seem at odds with the known fact that the variability of individual neurons increases with their mean firing rate in a signal-dependent manner [e.g. by following a Poisson distribution (de Ruyter van Steveninck et al. 1997; Paninski 2004; Maimon and Assad 2009)]. We investigated the signal-dependent variability of the neural features we used for decoding (threshold crossing rates and spike band power) to confirm that, similar to individual neurons, their variability increases with their mean (supplemental figure 6). How then can the output of a linear decoder, which is only a weighted sum of individual neural features, have largely signal-independent variability while the individual features have signal-dependent variability?

One possible explanation is that, as the encoded control vector becomes larger, features whose preferred directions align with the control vector increase their level of activity while other features with the opposite preferred direction decrease their activity. The corresponding increases and decreases in variance then cancel each other out, causing the decoding noise to be predominantly signal-independent. One caveat to this explanation is that some studies suggest that during movement the overall firing rate of neurons increases relative to baseline (Moran and Schwartz 1999; Churchland and Shenoy 2007; Perel et al. 2015) even though some features decrease their firing rate. This phenomenon could introduce some signal-dependency to the decoding noise; however, it would only dominate if the increase in firing rate were substantially larger than the baseline firing rate, which causes a floor of signal-independent noise.

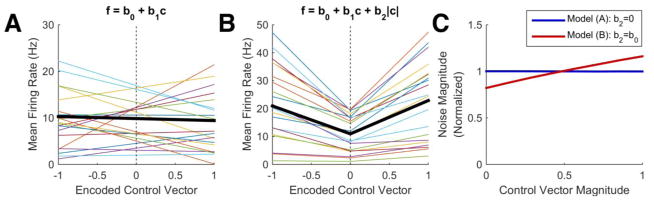
To test that this is a plausible explanation for the largely signal-independent decoding noise we observed, we simulated an ensemble of 60 Poisson-distributed neural features whose mean firing rate varied as a linear function of the encoded control vector and its magnitude. Linear tuning is a simple approximation that captures how neural activity might be expected to adapt to a linear decoder and is also consistent with aspects of neural activity elucidated in previous reports (Moran and Schwartz 1999; Perel et al. 2015). We used the following equation:

$$f=b_0+b_{1}c+b_2\mid c\mid ,$$

where f is the mean firing rate of a neural feature, c is the (one-dimensional) control vector, and b₀, b₁ and b₂ are feature-specific tuning coefficients. The linear tuning to magnitude, b₂|c|, can describe an overall increase in firing rate with the strength of the motor command (when b₂>0). We considered only a single dimension of the control vector to simplify the simulation.

Figure 7 shows results consistent with our expectation: when neural activity is tuned purely to the control vector (b₂=0, figure 7A), increases and decreases in firing rate cancel each other and the decoding noise is purely signal-independent (blue line in figure 7C). When there is also an overall increase in firing rate with control vector magnitude (b₂>0, figure 7B), the decoding noise is weakly signal-dependent (red line in figure 7C). For Poisson-distributed noise, the standard deviation of the noise increases with the square root of the mean. Thus, although we simulated a 100% increase in firing rate from no motor command to full motor command (b₂=b₀), the decoding noise increased only by a factor of $\sqrt{2}\approx 1.41$. In Section 5 of the Supplement we give more simulation details and in Section 6 we give a complementary statistical analysis.

Figure 7.

Decoding from a simulated ensemble of Poisson-distributed neural features. (A, B) Thin colored lines illustrate the mean firing rate of example features as a function of the encoded control vector. The thick black lines show the mean firing rate across the entire ensemble. The features in (A) are tuned only to the control vector (b₂=0), while those in (B) are tuned to the control vector and its magnitude independently (b₂=b₀), causing the mean firing rate of the ensemble to increase with the control vector magnitude. (C) A linear decoding matrix was calibrated with the same mathematical methods used with our participants and then applied to the neural ensemble. The standard deviation of the decoding noise is plotted as a function of control vector magnitude, showing that the noise is purely signal-independent (model A, blue line) or predominantly signal-independent (model B, red line).

VII. Able-bodied joystick movements under different noise properties

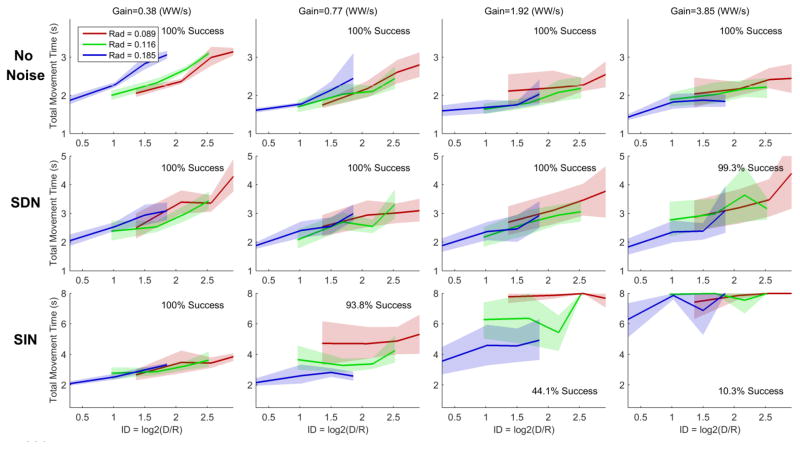
We studied joystick movements made by able-bodied volunteers to confirm that (1) Fitts’ law accurately describes movement times for our random target task when the cursor is controlled by able-bodied movement, (2) that adding large amounts of signal-dependent noise does not cause Fitts’ law to break down in the ways we observed for iBCI movements (and thus could not be an alternative explanation for the results), and (3) that adding signal-independent noise causes a breakdown of Fitts’ law as expected.

Figure 8 illustrates the results for one able-bodied volunteer, who controlled the cursor with joystick movements under different gain and noise conditions. Fitts’ law appears to hold in both the no noise and signal-dependent noise conditions under a wide range of gains, with the exception of the lowest gain setting (low gain results with no noise are similar to the left column of figure 3). While large amounts of signal-dependent noise caused movement times to increase overall as compared to the no noise condition, movement times remained stable for higher gains (scale invariance was preserved). On the other hand, when signal-independent noise was added, performance rapidly deteriorated for higher gains and Fitts’ law ceased to be a good descriptor of movement times. Supplemental figure 7 and supplemental figure 8 show similar results for the other two able-bodied volunteers.

Figure 8.

Movement time data from participant A (1 of 3 able-bodied volunteers) using a joystick to complete the random target task under different gain and artificial noise conditions. The cursor’s velocity is smoothed and integrated in the same way as it is under iBCI control, but the output of the decoder is determined by the joystick position instead of neural activity. Performance is relatively robust to gain under the no noise and signal-dependent noise (SDN) conditions, but rapidly deteriorates as gain is increased under the signal-independent noise (SIN) condition. Consequently, Fitts’ law is a good descriptor of movement times in the no noise and signal-dependent noise conditions, but breaks down when signal-independent noise is added (the radius-specific lines do not overlap). Note that failed trials (where movement time exceeded 8 seconds) are reported as 8 second movement times.

VIII. Quantitative comparison of the noise properties of the Kalman iBCI and the able-bodied motor system

Our results indicate that the decoding noise of the iBCI is large (significantly higher than the variability of able-bodied movements) and is largely signal-independent, in contrast to the largely signal-dependent noise of able-bodied movements. In this section, we quantify this comparison using able-bodied motor performance data available in the literature.

In figure 9A we illustrate the size of the decoding noise for T6 and T8 compared to that of the able-bodied motor system in various motor tasks (hand force impulses, wrist rotations, stylus movements, and arm movements) (Schmidt et al. 1979; Meyer et al. 1988; Young, Pratt, and Chau 2009; Liao and Kirsch 2014). We defined SNR as the size of the signal divided by the standard deviation of the noise. To estimate the SNR for iBCI movements, we averaged the pre-smoothed decoder output (u_t) in a 300 ms time window at the beginning of each movement (beginning after a reaction time interval) and modeled it as the sum of a vector pointing straight from the cursor to the target (signal) and neural variability (noise). Similarly, the able-bodied noise distributions were estimated using the first 100 to 300 ms of the movement only (i.e. the “ballistic” portion of the movement before fine corrections could be made) and the SNR was computed by dividing the amplitude of the movement by its variability (more methodological details are reported in Section 4 of the Supplement).

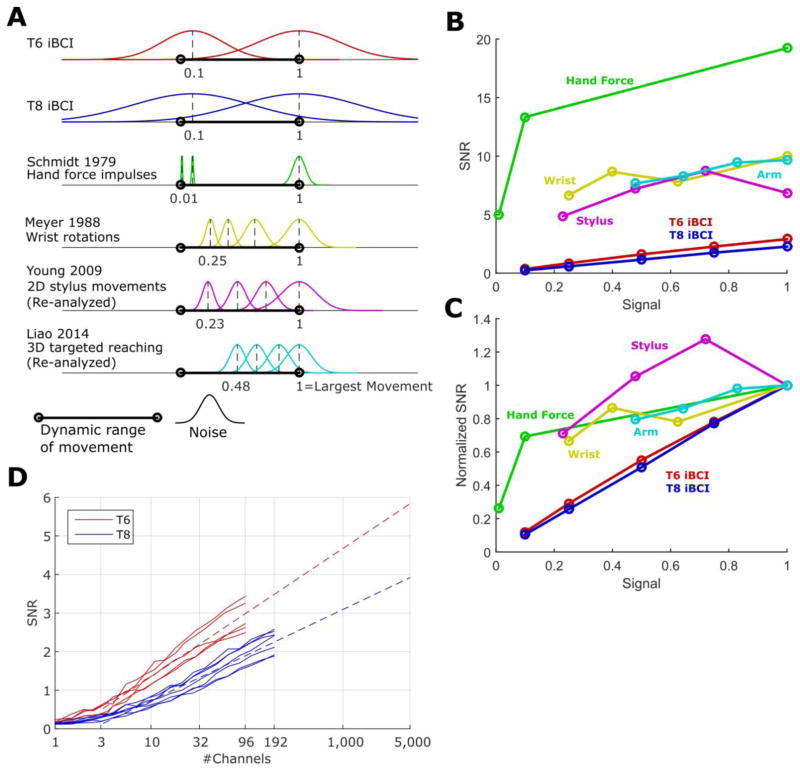
Figure 9.

Signal-to-noise ratio (signal strength divided by noise standard deviation) of our iBCI compared to the able-bodied motor system. iBCI and able-bodied SNRs are computed using a small time window of movement (100 ms to 300 ms) representing the “ballistic” phase of motion. (A) The decoding noise of iBCI cursor movements is compared to the variability of able-bodied motion. The standard deviation of the noise at different movement magnitudes is illustrated with a Gaussian probability density function (normalized to unit height). Movement magnitudes have been normalized so that 1 corresponds to the largest movement studied in a given experiment. (B) The signal-to-noise ratios implied by the data shown in A, plotted as a function of signal strength. (C) The same SNR curves as in B, but normalized to the SNR at full signal strength, revealing the relative fall-off of SNR as the signal strength declines. For purely signal-independent noise, the curve would lie on the unity line. (D) How many more recording electrodes would be needed for iBCI movements to approach the SNR of able-bodied movements using the decoder studied here? To answer this, we plot the signal to noise ratio as a logarithmic function of the number of recording channels included in the decoder (computed offline). One line is drawn for each session, and linear extrapolations are drawn as dashed lines (a linear model was fit to the session-specific lines using least squares regression and then extrapolated).

Note how, for able-bodied movements, the magnitude of the noise clearly declines as the movements become smaller. Figure 9B and 9C plot the SNR as a function of signal strength; not only are the SNRs of the able-bodied motor system considerably higher, they decay more slowly as signal strength declines (i.e. the SNR vs. signal strength curves are flatter for the able-bodied motor system). For movements perfectly obeying Fitts’ law (where the relative accuracy is constant regardless of the movement scale), we would expect a perfectly flat SNR curve.

Finally, in figure 9D we analyze how the SNR of the iBCI decoder output varies as a function of the number of recording electrodes included in the decoder (these curves were generated by cross-validated offline decoding, see Section 4 of the Supplement). Based on linear extrapolations of the session-speceific curves in figure 9D, with current decoding and recording methods about 5,000 to 10,000 channels would be required to restore an SNR approaching that of able-bodied motion (an SNR of 5 or 6). To restore that same SNR for a variety of signal strengths (thus enabling the user to make smaller movements while maintaining a high relative accuracy), even more channels would be needed. For example, when the noise is signal-independent, a base SNR of 10 would be needed to ensure an SNR > 5 for a signal strength of either 0.5 or 1.

Discussion

Overview

We examined whether iBCI cursor movements have the movement time properties described by Fitts’ law. With data from two participants in the BrainGate2 pilot clinical trial, we showed that, inconsistent with Fitts’ law, iBCI cursor movements made with a standard linear velocity decoder are significantly scale sensitive (figure 2) and have a smaller dynamic range of accuracy than do able-bodied movements (movement time increases very sharply for small targets, figure 3). We introduced a new movement time equation that can describe these departures from Fitts’ law.

To explain how this equation comes about, we proposed a highly simplified computer model of iBCI cursor movement that reproduces all the phenomena we observed (figure 5) and is based on two main assumptions: large, signal-independent decoding noise and neural modulation that is the same regardless of the target radius or the distance to the target. We verified the model by characterizing the participants’ neural modulation (figure 6) and by reproducing the same movement time phenomena when signal-independent (but not dependent) noise was added to able-bodied joystick movements (figure 8). We also explained how neural features with signal-dependent variability (e.g. Poisson-distributed neurons) could be consistent with signal-independent decoding noise (figure 7). Finally, we compared the noise properties of iBCI movements to those of able-bodied movements based on motor performance data available in the literature (figure 9).

Restoring Fitts’ law properties to iBCI-controlled movements

Fitts’ law describes two properties of able-bodied movements: scale invariance (the ability to make movements at different scales with similar relative accuracy) and a high dynamic range (the ability to acquire small targets without a large sacrifice in movement time). Ideally, iBCIs would be capable of restoring movements with these properties, thus enabling the user to operate effectively over a wide range of tasks that occur at different scales and demand different levels of relative accuracy.

One straightforward way to restore Fitts’ law properties might be to reduce the amount of signal-independent decoding noise by recording from more electrodes (figure 9). Through cross-validated, offline decoding we demonstrated that the signal-to-noise ratio of a linear decoder increases steadily as a function of the number of electrodes used, though it does so rather slowly (logarithmically) as a function of the number of electrodes, echoing what others have observed (Carmena et al. 2003; Li et al. 2009; Fitzsimmons et al. 2009; Lebedev and Nicolelis 2011). The trends shown in figure 9 suggest that it would require 5,000 or 10,000 electrodes to approach the SNR of able-bodied movements for a single movement scale using a linear velocity decoder. It would require even more electrodes to reduce the signal-independent noise enough to enable a high relative accuracy for both small movements and large movements (thus restoring scale invariance). Given the current state of recording technology, recording from more than 10,000 microelectrodes may prove challenging in the near term.

Another way to reduce the amount of signal-independent noise while still using the same linear decoding architecture could be to improve how the decoder is calibrated, so that there is a better match between the decoder coefficients and the neural activity (and thus, in theory, a higher SNR). There have been several reports of improved performance obtained by improving the calibration procedure, for example by better estimating the user’s intention (Shanechi, Orsborn, and Carmena 2016; Fan et al. 2014; Gilja et al. 2012) and by updating decoder parameters during the course of a session to track non-stationarities in the neural activity (Jarosiewicz et al. 2015). Recently, it was reported that there can be a substantial mismatch between the subject’s “internal model” and the decoder (Golub, Yu, and Chase 2015), implying that there may be significant room for improvement in calibration (at least for the calibration procedure tested in that study). How best to calibrate linear decoders, and how much improvement still stands to be made, is still an open question.

However, there may be a limit to what can be achieved with a linear decoder architecture alone, given that neural features behaving under standard assumptions cause predominantly signal-independent noise when passed through a linear decoder (figure 7). A relatively simple way to restore more scale invariance and dynamic range may be to apply a non-linear transformation to the output of a linear decoder. Recently, an improved ability to stop the cursor on smaller targets was reported when a standard Kalman filter was modified to attenuate cursor speed in the presence of fast changes in the direction of the decoded velocity (which occur more frequently when the user is trying to stop on the target) (Golub et al. 2014). Another method could be to apply a static non-linear transformation, such as squaring the decoded velocity, to create signal-dependent decoding noise (Rouse and Schieber 2015). Signal-dependent noise in the able-bodied motor system is believed to come primarily from the distribution of sizes and the recruitment order of motor units (smaller motor units are more common and are recruited first) (Jones, Hamilton, and Wolpert 2002). When generating small forces, many small motor units participate together, reducing variability by enabling noise in single motor units to be averaged out. When generating large forces, there are fewer large motor units that can be recruited, leading to more variability. Typical iBCIs, consisting of a linear decoder combined with linear smoothing, do not have this same structure. In theory, a static non-linear transformation could increase the user’s ability to hold still on small targets by reducing noise when their neural command signal is small, at the cost of reducing the user’s SNR when trying to move.

Finally, another way to restore signal-dependency might be to use a different decoder architecture altogether that can extract more information about stopping or the intended scale of the movement from the neural activity. Recently, a non-linear, two state decoder that can switch between a postural decoder and a movement decoder (Sachs et al. 2015) increased the ability of the user to stop on smaller targets. More generic non-linear decoders could automatically extract information about stopping or about movement scale in general, if it exists (Sussillo et al. 2012; Li et al. 2009). There is evidence that the speed or scale of a movement may be encoded somewhat separately from its direction in a way that a linear velocity decoder might not be able to use optimally (Moran and Schwartz 1999; Churchland and Shenoy 2007; Perel et al. 2015). Using a different decoding architecture to extract such a “scaling” signal, and using it to gate the output of a typical linear decoder, might restore some scale invariance to iBCI movements.