Bridging the physical scales in evolutionary biology: From protein sequence space to fitness of organisms and populations

Abstract

Bridging the gap between the molecular properties of proteins and organismal/population fitness is essential for understanding evolutionary processes. This task requires the integration of the several physical scales of biological organization, each defined by a distinct set of mechanisms and constraints, into a single unifying model. The molecular scale is dominated by the constraints imposed by the physico-chemical properties of proteins and their substrates, which give rise to trade-offs and epistatic (non-additive) effects of mutations. At the systems scale, biological networks modulate protein expression and can either buffer or enhance the fitness effects of mutations. The population scale is influenced by the mutational input, selection regimes, and stochastic changes affecting the size and structure of populations, which eventually determine the evolutionary fate of mutations. Here, we summarize the recent advances in theory, computer simulations, and experiments that advance our understanding of the links between various physical scales in biology.

Introduction

The direction of evolution is shaped by the interplay of mutations and selection. These two factors operate on vastly different scales: While mutations perturb the biophysical properties of proteins, potentially altering their structure, function and intracellular abundances, selection operates directly on the phenotypes and its outcome depends on fitness of organisms and populations. Understanding the link between the molecular effect of mutations and their fitness effect, the genotype-phenotype gap, is a major problem in biology. The relationship between the biophysical properties of macromolecules and their fitness effects is complex [1] and is influenced by various mechanisms operating at the molecular, systems, organismal, and, finally, population scales [2,3,4••,5,6,7•,8•,9,10,11,12,13,14]. Although each scale of biological organization is usually studied independently by traditional scientific disciplines, it is becoming clear that more accurate understanding of evolutionary processes will depend on integrating these scales into a unified model [10].

A useful concept to visualize the linkage between genotype and phenotype in biology is fitness landscape. The concept was originally introduced by Sewall Wright in the early 1930s [15]. Wright’s landscape can be easily imagined in three dimensions (in reality it is highly multidimensional) where axes x and y represent allele frequencies at loci 1 and 2, while axis z (the height) represents the mean fitness of a population. In such a representation peaks and valleys describe, respectively, high and low mean fitness of a population. Selection is viewed as a force driving the allele frequencies to increase a population’s mean fitness over time. However, if the landscape is rugged, i.e., is characterized by multiple peaks, selection is most likely to push a population to the nearest peak (local optimum), thus, effectively, locking it in a suboptimal fitness [16]. Climbing to the highest peak of the landscape (the global optimum) would require passing through a fitness valley that is disfavoured by selection.

The common use of the ‘fitness landscape’ metaphor often involves discrete values of fitness that correspond to specific alleles [16,17,18], or, more generally, discrete sequence variants [17,18]. However, such representations are limited to known variants and, as such, their predictive power of the effects and evolutionary consequences of de novo mutations are limited. Conversely, full representation of the fitness landscape in sequence space is still extremely challenging due to extremely high dimensionality of such mapping.

It is important to note that the term ‘fitness’ is often used in a variety of contexts that might be different from the traditional use of the term by Wright who defined fitness as a quantity that is proportional to the mean number of produced viable and fertile progeny [19]. For example, ‘fitness’ can stand in the literature for an organismal phenotype, systems level response, biological function of a protein, and, in case of sequence space-based landscapes, a molecular property that directly affects a protein’s biological function [20,21,22]. Thus, the concept of ‘fitness’ is often interpreted to mean functional rather than reproductive capacity. However, in our view, such broad definition of fitness detracts from the main conundrum in evolution that mutations and selection are separated by several levels of biological organization. To that end, we will exclusively use the term “fitness” in the traditional sense close to Wright’s as a phenotypic trait that is under selection and, as such, determines the outcome of a competitive evolutionary scenario in the wild, or in laboratory experiments. In the subsequent discussion we focus on organism-based definition of fitness as a reproductive capacity or related phenotypic traits of an organism related to its specific genotype rather than a more traditional Wright’s view of fitness as mean reproductive capacity of a population. We also note that specific phenotypic traits that are most relevant for the outcome of a competition might depend on the environment and ecological scenarios under which the competition occurs.

Another challenge that limits our ability to predict the direction and outcomes of evolution is that structure of a population has a crucial effect on how it evolves on the fitness landscape. Theoretical population genetics predicts that population size controls the balance between the forces of selection and random genetic drift; this eventually determines the direction of evolution on the fitness landscape. Earlier studies appreciated the role of population size, deriving an “effective population size” to fit the genetics or the evolutionary data to existing population genetics models [23]. Nevertheless, direct experimental evidence for this fundamental concept is very scarce due to the inherent difficulty of simultaneously controlling the population size and obtaining tractable molecular readouts of evolutionary processes in a configurable and reproducible environment of a laboratory experiment, or in multiscale organism-based simulations.

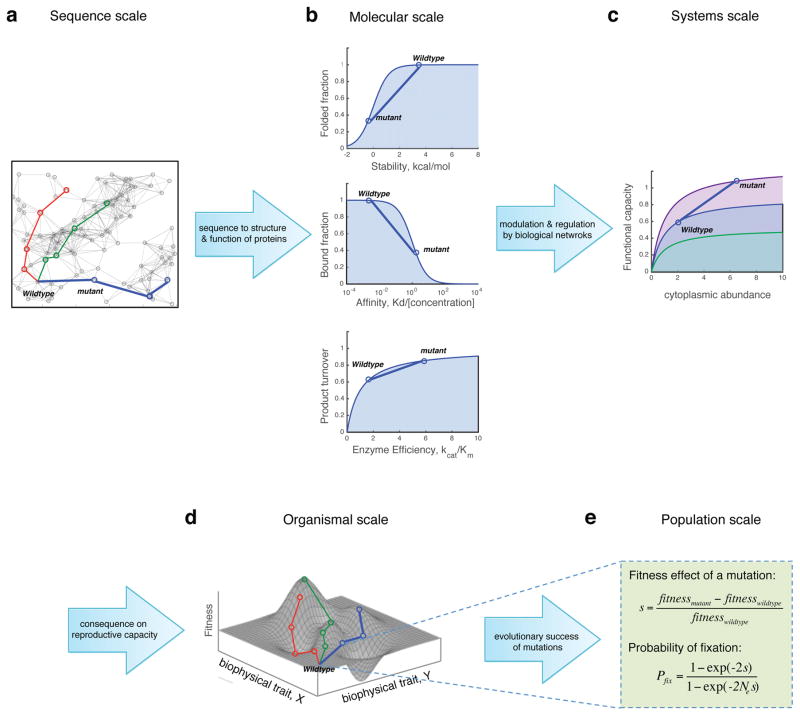
To address these challenges, several authors have recently introduced the concept of a ‘biophysical fitness landscape’. The key premise of biophysical fitness landscape is that the gap between genotype and fitness is closed through the intermediate phenotype-molecular biophysical properties of proteins (Figure 1). In this approach the sequence-fitness gap might be overcome in two (or more) steps: A) from variation of sequence to variation of molecular and systems-level properties of proteins (panels a–c on Fig. 1), and B) from variation of molecular (stability, activity etc.) and systems-level properties (e.g. abundances) to organismal fitness effects reflected in biophysical fitness landscape (panel d on Fig. 1) to the fate of a mutation in population (fixation or loss, panel e on Fig. 1), The key assumption of this approach is that the complexity of mapping sequence variation to changes in molecular properties (step A above, from panel a to panels b,c on Fig. 1)) is at the root of the complexity of the sequence-fitness relationship (‘ruggedness of fitness landscape’). Molecular effects of mutations are complex, degenerate and epistatic: similar molecular effects can be caused by different mutations and they strongly depend on the molecular background (epistasis) [9,22,24,25•]. However, at the next level(s) (step B), the relationship between changes in the molecular properties (stability, activity, aggregation propensity) cellular (intracellular abundance), and the ensuing phenotypic effects might be much less degenerate and predictive giving rise to a smooth fitness landscape in space of molecular properties of proteins (Figure 1). It is also important to note that pleiotropy, when mutations have conflicting effects on different molecular traits, is another major source of epistasis. In terms of biophysical fitness landscape this means that projection of individual mutational effects could lead to complex trajectories in the space of biophysical parameters. In this review we present recent theoretical, computational and experimental studies that elaborate on and further develop these ideas.

Figure 1. Biophysics as a stepping stone between sequence and phenotype.

Closing the genotype-phenotype gap is facilitated by an intermediate projection of organismal fitness to biophysical properties of macromolecules. While the effect of sequence variation (panel a) on molecular traits (e.g. folding stability, binding affinity, catalytic activity, panel b) might be complex, the ensuing relation between variation of the observable biophysical traits (vertical axes in panel b) and their fitness effect on the organism might be simple and predictable in some cases (panel d and Figure 2). The effects of mutations are also modulated by a regulation of biological networks (panel c) that might also have simple integrative effect on fitness. On the level of populations, the probability of fixing a specific mutation is a function of the effect of a mutation (selection coefficient) and an effective population size (N_e). Note a different interpretation of fitness landscape in (panel d) from classical Wright’s where mean fitness of the population vs allele frequencies is usually plotted.

From protein sequence space to protein biophysics

Maynard Smith was first to suggest that evolution can be viewed as a walk through a protein sequence space [26]. Assuming an L-residue long protein sequence, its sequence space will constitute a network of 20^L sequences interconnected through edges, each representing a change in a single residue. Each of the sequences is assigned a value (a molecular property such as thermodynamic stability, or function), thus forming a discrete landscape of the sequence space. Because mutations are rare, evolutionary trajectories are thought to traverse the sequence space by single mutation steps, without passing through non-functional intermediates. The resulting accessible fraction of the interconnected functional sequences constitutes the (nearly) neutral protein network [27,28,29,30]. If the effect of each mutation on fitness is independent on the genetic background on which it occurs, the resulting fitness landscape contain a single peak populated by optimal sequences with multiple evolutionary trajectories leading to it. Conversely, should epistasis (non-additivity of mutations) be prevalent, fitness effect of a mutation might be beneficial or detrimental depending on the genetic background [31,32•]. Epistasis can severely constrain the accessible evolutionary pathways, and create a rugged fitness landscape with multiple local optima separated from each other and the global fitness peak by trajectories passing through non-functional sequence states [33,34,35]. Kaltenbach et al. [33••] examined the evolutionary reversibility of phosphotriesterase that was evolved by directed evolution to arylesterase and back, and found that many of the original amino acid exchanges between the new and original function could not be tolerated, and an alternative set of mutations was needed to restore the phosphodiesterase activity. Extensive epistasis made the adaptive fitness landscape in sequence space highly rugged, and, although the evolutionary trajectories were phenotypically (at the level of protein phenotype, i.e. function) reversible, the genotypic trajectory became irreversible, suggesting that the new and the original activities constitute separate fitness peaks [36].

Which biophysical properties determine the epistatic interaction between mutations? Various mechanisms were proposed, including protein-ligand or protein-DNA binding [25,37,38••], protein conformation [33,39], and allostery [40]. However, protein stability appears to be the most prevalent mechanism of intramolecular epistasis [7,41••,42,43]. Since most mutations destabilize protein structures [14,44], it was asserted that protein evolution is often accompanied by stability-activity trade-offs [45]. Indeed, Gong et al.[41••] demonstrated that evolution of influenza nucleoprotein is constrained by a stability-related epistasis: Acquisition of stabilizing mutations was required prior to obtaining the adaptive substitutions, which, on their own, caused adverse effects due to destabilization of the nucleoprotein and, therefore, were evolutionary inaccessible. Stability activity trade-off is often cast as the effect of stabilizing mutations on “flexibility” of the protein which is detrimental to “functional protein dynamics” [46,47]. Experimental studies indeed showed that mutations introduced in the active site of a protein stabilize the protein yet make it less or completely inactive [48]. However more comprehensive analyses where mutations were introduced throughout the protein, and not just in the active site, showed no inverse relation between stability and activity [36,49]. Moreover, a weak positive correlation between activity and stability was observed for multiple variants of Dihydrofolate Reductase (DHFR) from E. coli [36]. However, a highly stabilizing mutation in the active site of DHFR, D27F, completely eliminated its function [36], similar to what was observed for another enzyme in [48]. The apparent disparity of the conclusions from substitutions in/near the active site and elsewhere in the protein can be rationalized by the observation that most “random” mutations in proteins are destabilizing [13,44,50]. Carving an active site on an enzyme requires several functional substitutions, which, from the point of view of an independent trait – stability – could be random or even detrimental (e.g., placing charged residues in partly buried areas of the protein). Thus, activity-stability trade-off could be real for substitutions in the active sites. However, it disappears or reverses itself for substitutions outside the active sites. Two possibilities can be raised to explain this finding: 1) that global stability of a protein against unfolding might not be relevant for its global dynamics in the native state, and 2) that global dynamics might not determine functionality, as was indeed argued in [51]. To illustrate these arguments, the following analogy with building a house might be offered. In order for a house to be livable, it must have windows. Windows certainly diminish structural integrity of the building (decreased “stability”). However, that does not mean that a building must be structurally shaky to be livable. What it does imply, though, is that other parts of the building must be reinforced to allow for windows to be carved in the walls without the building falling apart completely – the analogy with the need to make stabilizing mutations elsewhere in the protein to evolve functional variants [49,52]. A strong evidence that overall stabilization of proteins does not come at a detriment to its function comes from long term evolutionary experiments with E. coli [53]. Most lines that evolved at 20 °C lost fitness relative to the ancestor when they competed at 40°C and above [88], whereas most lines that evolved at 41.5 °C did not lose fitness at 20 °C and below [54].

The prevalence of epistasis, and its impact on evolution is still debated. Some describe it as rampant [38] and pervasive [55], or even consider it a determining factor of the molecular evolution [22,56], whereas others view it as less important [57,58]. We return to the discussion of prevalence and mechanisms of epistasis later, after introducing the theoretical foundation of protein biophysics-population genetics mapping.

From protein biophysics to organismal fitness

Although insightful and informative, evolutionary studies that focus entirely on the protein sequence space landscapes have one major disadvantage – being purely phenomenological, they are oblivious to the biophysical mechanisms on the molecular and systems scales that determine fitness effects of mutations [59]. Indeed, biological networks are responsible for the striking capacity of organisms, on one hand, to limit the enormous fitness cost of the mutational load [60,61], and, on the other hand, to harness its evolutionary potential [62]. A major role in modulating the mutational effects at a systems scale is played by Protein Quality Control (PQC). In general, molecular chaperones constituting the PQC can serve as a buffer against the deleterious effects of mutations, thus they are less likely to be purged by purifying selection [12,63]. This lead to the view that certain elements of the PQC act as “capacitors” of genetic variability that broadly reshape the biophysical properties – organismal fitness map[12,64,65,66,67] and control the rate of protein evolution [63,68,69,70,71,72]. Recently, PQC was also identified as imposing a global barrier to functional integration of horizontally transferred genes in bacteria because the newly acquired genes were found to be incompatible with the elements of PQC of the host [73••].

Rodrigues et al. [4••] have recently demonstrated that it is possible to incorporate the pleiotropic effects of mutations originating in the PQC interaction with the mutant proteins into a model that correctly predicts organismal fitness entirely from the biophysical characteristics. The model is based on the relationship between fitness and metabolic flux [74,75]:

$$\mathit{fitness}~\mathit{flux}=a·E/(B/E),$$ [Eq.1]

where E is the functional capacity of a protein in the enzymatic chain, a denotes maximal fitness at the highest flux, and B is the constant related to the effect of all other proteins in an enzymatic chain. The functional capacity is proportional to the product of the net intracellular abundance of the functional protein molecules (E₀) and its catalytic efficiency (k_cat/K_M):

$$E~E_0\frac{k_{\mathit{cat}}}{K_M}.$$ [Eq.2]

In the presence of a competitive inhibitor Eq.2 can be further modified as:

$$E_{\mathit{eff}}~E_0\frac{k_{\mathit{cat}}}{K_m}{K}_i,$$ [Eq.3]

where K_i is the enzyme inhibition constant, and E_eff is the effective functional capacity. Rodrigues et al. [4] chose DHFR as a convenient model, since bacterial fitness can be accurately predicted from the metabolic flux through DHFR according to Eq.1 [2,12,73] (Figure 2). They showed that mutations conferring trimethoprim resistance in DHFR are highly pleiotropic, i.e., simultaneously affecting multiple molecular traits: catalytic efficiency, trimethoprim binding K_i, and protein stability, thus rendering the biophysical fitness landscape multidimensional. While k_cat/K_m and K_i can be measured in vitro, the successful implementation of the model also requires the knowledge of the functional intracellular abundance E₀ (Eq.3). Apart from the thermodynamic stability that determines the fraction of the folded protein molecules at equilibrium [76], protein abundance, E_0, also depends on the interaction with PQC [12]. Rodrigues et al. [4••] showed that this latter quantity can be accurately predicted from the in vitro measurements of the population of the Molten-Globule-like state of the mutant proteins, in agreement with theoretical predictions from the dynamic turnover model [12]. Using the model, Rodrigues et al. [4••] successfully predicted the fitness effects (IC₅₀) of the trimethoprim-resistance conferring mutations entirely from the molecular properties of mutant DHFRs in a broad range of conditions.

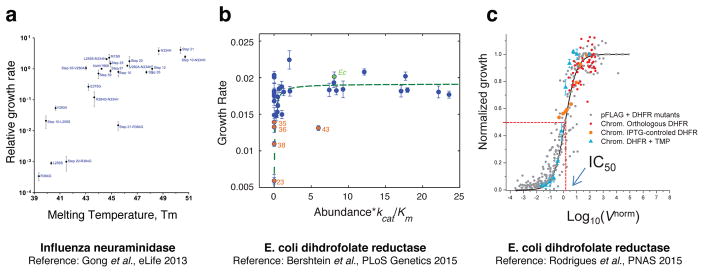
Figure 2. Experimentally derived biophysical fitness landscape in viruses and microorganisms.

A, Fitness of influenza from strain Aichi/1968 to strain Brisbane/2007 is mapped to the thermal stability of its neuraminidase domain [41••]. Viral fitness is defined as the number of particles that are able to productively infect cells and transcribe high levels of GFP from viral RNA. B, Fitness of E. coli (defined as growth rate) is mapped to the effective functional capacity (Abundance*Kcat/Km) of dihydrofolate reductase, a core metabolic enzyme. Points correspond to strains where the chromosomal copy of DHFR was replaced with an ortholog to mimic xenologous horizontal gene transfer [73••]. C, Fitness of E. coli under antibiotic resistance (defined as IC50) is mapped to the rate of DHFR catalyzed reaction. Points correspond to strains/conditions where the E. coli DHFR has been mutated and/or its abundance has been titrated [4••].

The map between the biophysical to systems to organismal scales can also be assessed quantitatively by global transcriptomics and proteomics techniques [2,77,78]. Bershtein et al. [2] demonstrated that local perturbation of a central metabolic enzyme by chromosomal incorporation of destabilizing mutations produced a global perturbation of protein abundances for a large number of genes well beyond the local metabolic neighbourhood of the enzyme. An empirical quantitative relation was established between the biophysical properties of the mutants (change in thermodynamic stability), global proteome response to the destabilizing mutations (measured as standard deviations of the distributions of logarithms of relative to wild-type protein abundances), and bacterial fitness of the mutant strains (approximated as growth rates).

Altogether, these works, as well as the recent studies of viral fitness [41••], demonstrate the utility of biophysical fitness landscapes in providing the predictive quantitative multiscale relationships between variation of the molecular properties and the ensuing fitness effects. Figure 2 summarizes the recent examples of biophysical fitness landscapes where simple deterministic relationships between certain combinations of physical traits and fitness were established.

From protein biophysics to population genetics

Mapping of the observed molecular biophysical properties of proteins to evolutionary history of populations is one of the most challenging aspects of the evolutionary studies. The difficulty of theoretical analyses stems from the fact that factors affecting the fixation probabilities of mutations at a population scale, such as mutation rate, effective population size, drift, selection regimes, etc., are i) stochastic, and ii) are of non-biophysical nature. The experimental difficulty is rooted, on one hand, in the inherent complexity of the living systems that makes it very difficult to disentangle the pure biophysical properties of the evolving proteins from the pleiotropic influences, and on the other hand, in the scarcity of the data on the evolutionary intermediates. Considerable progress in the field in the last decade [6,7,9,14,50,79,80] came from the theoretical synthesis of the population genetics theory [81] with statistical thermodynamics of protein stability and folding [82].

Regardless of a specific function, globular proteins must be stable enough in order to preserve their native structure and function. Thus, from a molecular biophysics perspective, protein thermodynamic stability (described as Gibbs free energy difference between folded and unfolded states, ΔG), is one of the major determinants of sequence evolution [50,83,84,85]. Under a selection pressure to maintain protein stability, fitness of an organism, F, is assumed to be proportional to the number of the folded proteins: F ~ P_nat, where P_nat is the probability to find protein in its native state at equilibrium, given the two-state model of protein folding [86]:

$$P_{\mathit{nat}}=\frac{1}{1+e^{\frac{\mathrm{\Delta }G}{kT}}}.$$ [Eq.4]

The effect of an accrued mutation on protein stability is calculated as:

$$\mathrm{\Delta }{G}_{\mathit{after}}=\mathrm{\Delta }{G}_{\mathit{before}}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{mutation}},$$ [Eq.5]

were ΔΔG_mutation stands for the change in ΔG upon mutation, and can be directly estimated using force field based stability predictors [87,88], calculated by summing the contact energies of all of the pairs of contact-making residues in a conformation [89], or, in a more phenomenological approach, drawn from a Gaussian distribution with mean 1 kcal/mol, and SD=1.7 kcal/mol [9,50], - parameters that are derived from empirical studies [90] and computational estimates [45]. The strong non-linearity of the Fermi-Dirac function Eq.4 makes the fitness effects of stability-changing mutations inherently epistatic: fitness effects of mutations are more pronounced on low stability backgrounds [9,76]. However, because of the assumed additivity of ΔΔG values [91], the model cannot account explicitly for the instances of site-site epistasis. To this end, additional terms correcting for the site-site epistasis in the energy function were suggested [11,43].

An arising mutation would have a selection coefficient, s, defined as [9,11]:

$$s=\left(F_{\mathit{after}}-F_{\mathit{before}}\right)/F_{\mathit{before}}~e^{\frac{\mathrm{\Delta }{G}_{\mathit{before}}}{kT}}e\left(1+e^{\frac{\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{mutation}}}{kT}}\right).$$ [Eq.6]

Importantly, Eq.6 allows establishing a direct link between a biophysical property of a protein afflicted by a mutation and the probability of fixation of the mutation (P_fix) in a monoclonal population with an effective population size N_eff [92]:

$$P_{\mathit{fix}}=\left(1-e^{-2s}\right)/\left(1-e^{-2\mathit{sNeff}}\right).$$ [Eq.7]

Eq.4–6. lay the theoretical foundation for theory and evolutionary simulations in the class of models where fitness is directly linked to stabilities of proteins encoded in genomes of organisms, and populations of such organisms are subjected to mutations, drift, and selection [6]. This approach provided important evolutionary insights into the distribution of fitness effects of mutations [9,80], the molecular determinants of the rate of protein evolution [93,94], the genetic variation in coding regions [79], and the observed thermodynamic and structural properties of proteins in nature [11,95]. The key insight from these studies is the realization that “marginal” stabilities of natural proteins is a direct consequence of mutation-selection balance [11,95], rather than selection against an excessive protein stability. The theory based on mutation-selection balance quantitatively predicts the distribution of protein stabilities in a remarkable agreement with experiments [9,50]. Additionally, the integration of protein folding stability and population genetics leads to some major insights in molecular evolution. First, the selection for protein folding stability (or its contrapositive, selection against protein misfolding) could explain the genomics observations of the rate of protein evolution (dN and dS). These trends, observed across all kingdoms of life, include the observation that highly expressed proteins tend to evolve slowly [94,96,97], and the apparent universality of the log-normal distribution of evolutionary rates [98]. Second, selection for folding stability has also been shown to predominantly shape the pattern of polymorphisms in the protein coding regions [79]. Third, it has also been theoretically shown that on the biophysical fitness landscape defined by folding stability there exists a mathematical relationship between the folding stability of a protein, its abundance in the cell, and the effective population size of the organism [9,95]. This mathematical relationship is important because, for the first time, it quantifies (in units of energy) the contribution of variables, such as population size and protein abundance, to the observed folding stability of proteins in nature. Altogether, these mechanistic insights on the rate of protein evolution and patterns of polymorphisms arising from integrating biophysics and population genetics could have fundamental practical application on the statistical tools used to infer selection and adaptive evolution of sequencing data. We note that inference of evolutionary forces based on observed genetic variation are largely based on the Neutral Theory (neutrality tests such as dN/dS, McDonald-Kreitman, Hudson-Kreitman-Aguade (HKA), etc.) that altogether ignores these mechanistic aspects of protein evolution.

Lastly, Eq. 4–6 also provide for the simple and universal mechanism of epistasis on the biophysical fitness landscape. The mapping between the effect of mutations on folding stability (ΔΔG) and the selection coefficient (s) depends on the wildtype (or background) folding stability ΔΔG_before. In particular, when the proteins are sufficiently stable (ΔG_before≪−5 kcal/mol), the factor e^ΔGbefore/RT approaches zero, which then renders most mutations neutral (s~0). Alternatively, when the proteins are close to being unfolded, the non-zero factor the e^ΔGbefore/RT modulates the effect of ΔΔG_mutation on s. Indeed, by running explicit evolutionary simulations on biophysical fitness landscape determined by folding stability, Eqs 4–6 Serohijos et al. showed that epistasis is prevalent but generally weak [79]. Interestingly, by using deep mutational screening analysis on GB1 protein, a technique allowing a comprehensive characterization of pairwise epistasis [99,100], Olson et al. have arrived to a similar conclusion [42]. They showed that strong epistasis is relatively rare (~ 5% of pairwise interaction), whereas weak epistasis is widespread (~ 30%). Additionally, according to Olson et al. there is a strong epistasis among destabilizing mutations, but not among stabilizing mutations. This again finds an explanation in the biophysical fitness landscape based on protein folding thermodynamics. Two stabilizing mutations bring the protein to the flatter part of the landscape, hence less epistasis, but two destabilizing mutations shift it to the more curved part of the landscape, hence stronger epistasis. In a similar vein, Bloom and coauthors showed that stability-mediated weak epistasis of the type described in [79] is prevalent in evolution of influenza nucleoprotein [41••].

Recently, these ideas were extended to a multidimensional biophysical fitness landscape that encompasses several molecular traits. Interaction with other proteins is almost as universal a trait as protein folding. Cheron et al studied a biophysical fitness landscape of viral proteins escaping antibody stressors [101]. They used a simple biophysics-based model of viral fitness which assumed that successful escape from antibody required that viral proteins maintain their folded state while decreasing the affinity of the antibody to the viral antigen and showed how viral demographics affects evolution of stability of the viral antigen and its binding to antibody. Further, they showed how evolutionary dynamics on biophysical fitness landscape determines optimal (for the viral escape) mutations rates. Another interesting example of the interplay between folding and binding on biophysical fitness landscape is given in [8,102] where binding affinity to other proteins can evolve as an evolutionary spandrel to maintain stable folding of proteins.

Conclusions and Outlook

The concept of biophysical fitness landscape is helping to advance our understanding of the interplay of mutation and selection in determining the course and outcomes of evolution [10]. Several examples of simple quantitative and predictive relationships between biophysical properties of proteins and fitness contributed to mechanistic understanding of how Darwinian selection at the population level shapes the evolution of molecular properties of enzymes [10]. The availability of quantitative biophysical fitness landscape opens up an exciting opportunity to develop accurate multiscale models to predict evolutionary dynamics from first biophysical principles. Important applications include bacterial and viral escape from stressors such as antibiotic, antibody [101] and thermal adaptation [103]. The challenges ahead include extension of biophysical fitness landscape from metabolic enzymes to other functional classes, including accurate fitness models of gene expression and integrating system level global effects on metabolic and proteomic states of cells. We expect that combination of predictive biophysical models, biophysical fitness landscape with advances in genomics and proteomics will bring quantitative ab initio prediction of evolution within the reach of many applications of fundamental and translational significance.

Highlights.

• Biophysical fitness landscapes (BFL) map fitness to molecular and system-level traits

• BFL of a bacterial enzyme provides accurate prediction of antibiotic resistance

• Protein quality control plays key role in shaping BFL

• BFL show how population-scale evolutionary dynamics shapes properties of proteins