Dynamical effects of calcium‐sensitive potassium currents on voltage and calcium alternans

Abstract

Key points

• A mathematical model of a small conductance Ca^{2 +}‐activated potassium (SK) channel was developed and incorporated into a physiologically detailed ventricular myocyte model.

• Ca²⁺‐sensitive K⁺ currents promote negative intracellular Ca²⁺ to membrane voltage (CA_i ²⁺→ V_m) coupling.

• Increase of Ca²⁺‐sensitive K⁺ currents can be responsible for electromechanically discordant alternans and quasiperiodic oscillations at the cellular level.

• At the tissue level, Turing‐type instability can occur when Ca²⁺‐sensitive K⁺ currents are increased.

Abstract

Cardiac alternans is a precursor to life‐threatening arrhythmias. Alternans can be caused by instability of the membrane voltage (V _m), instability of the intracellular Ca²⁺ (${\mathrm{Ca}}_{\mathrm{i}}^{2+}$) cycling, or both. V _m dynamics and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ dynamics are coupled via Ca²⁺‐sensitive currents. In cardiac myocytes, there are several Ca²⁺‐sensitive potassium (K⁺) currents such as the slowly activating delayed rectifier current (I _Ks) and the small conductance Ca²⁺‐activated potassium (SK) current (I _SK). However, the role of these currents in the development of arrhythmias is not well understood. In this study, we investigated how these currents affect voltage and Ca²⁺ alternans using a physiologically detailed computational model of the ventricular myocyte and mathematical analysis. We define the coupling between V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling dynamics (${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling) as positive (negative) when a larger Ca²⁺ transient at a given beat prolongs (shortens) the action potential duration (APD) of that beat. While positive coupling predominates at baseline, increasing I _Ks and I _SK promote negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling at the cellular level. Specifically, when alternans is Ca²⁺‐driven, electromechanically (APD–Ca²⁺) concordant alternans becomes electromechanically discordant alternans as I _Ks or I _SK increase. These cellular level dynamics lead to different types of spatially discordant alternans in tissue. These findings help to shed light on the underlying mechanisms of cardiac alternans especially when the relative strength of these currents becomes larger under pathological conditions or drug administrations.

Key points

• A mathematical model of a small conductance Ca^{2 +}‐activated potassium (SK) channel was developed and incorporated into a physiologically detailed ventricular myocyte model.

• Ca²⁺‐sensitive K⁺ currents promote negative intracellular Ca²⁺ to membrane voltage (CA_i ²⁺→ V_m) coupling.

• Increase of Ca²⁺‐sensitive K⁺ currents can be responsible for electromechanically discordant alternans and quasiperiodic oscillations at the cellular level.

• At the tissue level, Turing‐type instability can occur when Ca²⁺‐sensitive K⁺ currents are increased.

Abbreviations

AP

action potential

APD

action potential duration

${\mathrm{Ca}}_{\mathrm{i}}^{2+}$

intracellular Ca²⁺

DI

diastolic interval

g_ks

slowly activating delayed rectifier conductance

g_sk

small conductance Ca²⁺‐activated potassium conductance

I_Ks

slowly activating delayed rectifier current

I_CaL

L‐type Ca²⁺ current

I_SK

small conductance Ca²⁺‐activated potassium current

NCX

Na⁺–Ca²⁺ exchanger

PCL

pacing cycle length

SR

sarcoplasmic reticulum

V_m

membrane voltage

Introduction

Ventricular arrhythmia is a major cause of sudden cardiac death. It has been shown that a precursor to life‐threatening arrhythmia formation is the development of cardiac alternans, a sequence of paired long and short action potentials (APs) (Pastore et al. 1999; Garfinkel et al. 2000; Fox et al. 2002 b; Hayashi et al. 2007; Groenendaal et al. 2014). However, physiological and dynamical mechanisms are not fully understood (Weiss et al. 2006, 2011; Wilson et al. 2006; Laurita & Rosenbaum, 2008; Merchant & Armoundas, 2012; Sato & Clancy, 2013; Kanaporis & Blatter, 2015; Valdivia, 2015). At the cellular level, alternans can be caused by instability of membrane voltage (V _m) due to steep action potential duration (APD) restitution (Nolasco & Dahlen, 1968; Hayashi et al. 2007), instability of intracellular calcium (${\mathrm{Ca}}_{\mathrm{i}}^{2+}$) cycling due to steep sarcoplasmic reticulum (SR) Ca²⁺ release dependence on Ca²⁺ load/refractoriness, or both (Chudin et al. 1999; Shiferaw et al. 2003, 2005; Picht et al. 2006; Groenendaal et al. 2014; Wang et al. 2014). Dynamical systems of V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ are coupled via Ca²⁺‐sensitive currents. We previously investigated the role of the major Ca²⁺‐sensitive currents, the L‐type Ca²⁺ current (I _CaL) and sodium(Na⁺)–Ca²⁺ exchanger (NCX) (Shiferaw et al. 2005; Sato et al. 2006, 2007, 2013). However, the slowly activating delayed rectifier current (I _Ks) is a Ca²⁺‐sensitive current, and recent experimental studies showed that the small conductance Ca²⁺‐activated potassium (SK) channels exist in cardiac myocytes and play an important role in regulating APs (Xu et al. 2002; Tuteja et al. 2005; Zhang et al. 2008; Li et al. 2009; Hsueh et al. 2013; Chang et al. 2013 a; Chang & Chen, 2015; Yu et al. 2015; Zhang et al. 2015). Yet, little is known about the role of these Ca²⁺‐sensitive K⁺ currents in the formation of alternans. In this study, we investigate dynamical effects of Ca²⁺‐sensitive K⁺ currents on V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ alternans and show how ion channel/current level modifications lead to various phenomena at cellular and tissue levels including electromechanically (APD–Ca²⁺) discordant alternans and spatially discordant alternans.

Methods

In order to investigate the dynamical and physiological mechanisms of alternans, we used a physiologically detailed mathematical model of AP and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling of the ventricular myocyte developed by Shiferaw et al. (2005). Figure 1 A shows the schematic diagram of the currents and fluxes that regulate V _m dynamics and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling. The membrane potential is governed by

$$\frac{\mathrm{d}{V}_{\mathrm{m}}}{\mathrm{d}t}=-\frac{\sum I}{C_{\mathrm{m}}},$$

where V _m is the membrane potential, C _m is the cell capacitance and I represents the transmembrane currents. The details of the model are described in the online Supporting information, Data S1.

Figure 1. Physiologically detailed mathematical model.

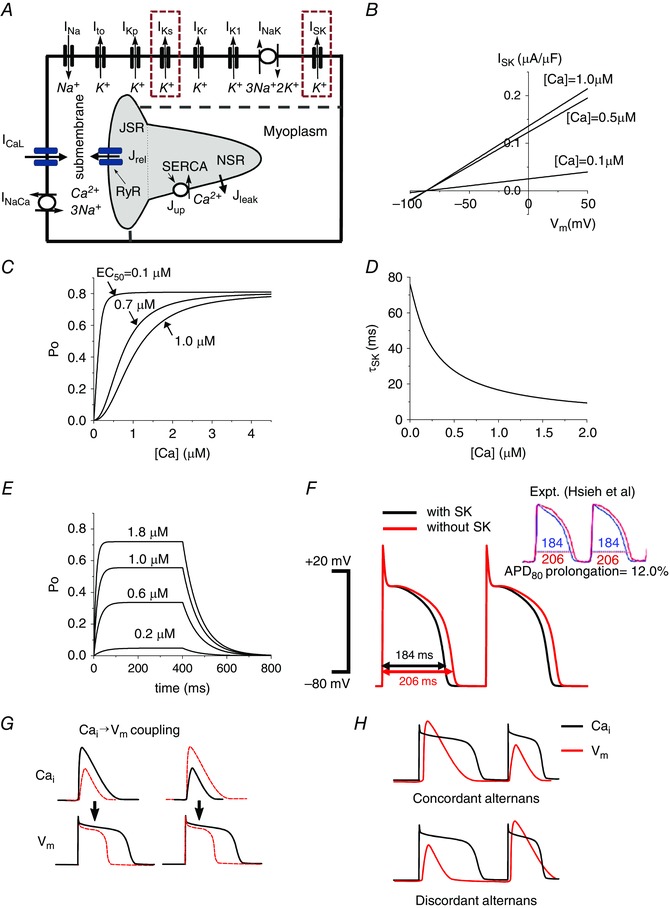
A, schematic diagram of the currents and fluxes that regulate V _m dynamics and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling. B, model of the SK channel: I _SK vs. V _m when [Ca²⁺] is 0.1, 0.5 and 1.0 μm. C, channel open probability as a function of intracellular Ca²⁺. D, inverse relationship between intracellular Ca²⁺ and the SK time constant (τ_SK2). E, open probability (P _o) vs. time when various test [Ca²⁺] pulses are applied. [Ca²⁺] was changed from 0 μm to test [Ca²⁺] for 400 ms, and then changed to 0 μm. F, transmembrane voltage plotted against time demonstrating the decrease in APD from baseline (red) to inclusion of the SK channel (black). When g _sk = 0.8 μS μF⁻¹ and EC₅₀ = 0.7 μm are chosen, the model shows 12% difference of APDs, which was shown by Hsieh et al. experimentally (Hsueh et al. 2013), by copyright permission of the American Heart Association, Inc. G, positive and negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling. H, electromechanically concordant (large APD→large Ca²⁺ transient, small APD→small Ca²⁺ transient) alternans and discordant (large APD→small Ca²⁺ transient, small APD→large Ca²⁺ transient) alternans.

The formula of the Ca²⁺ dependence of I _Ks from Mahajan et al. (2008) was incorporated into this model. I _Ks is given by

$$\begin{array}{ccc}\hfill I_{\mathrm{Ks}}& =& g_{\mathrm{ks}}{x}_{\mathrm{s}1}{x}_{\mathrm{s}2}{q}_{\mathrm{Ks}}\left(V_{\mathrm{m}}-E_{\mathrm{Ks}}\right),\hfill \\ \hfill q_{\mathrm{Ks}}& =& 1+\frac{0.8}{1+{\left(\frac{K_{\mathrm{m}}}{c_{\mathrm{s}}}\right)}^3},\hfill \end{array}$$

where g _ks is the maximum conductance of I _Ks, q _Ks is the Ca²⁺ dependence, x _s1 and x _s2 are the time‐dependent gating variables, E _Ks is the reversal potential of I _Ks, and K _m controls the affinity of Ca²⁺. We varied g _Ks and K _m to explore the effects of I _Ks on alternans.

The SK channel has been recently described in atrial and ventricular myocytes (Xu et al. 2002; Tuteja et al. 2005; Zhang et al. 2008; Li et al. 2009; Hsueh et al. 2013; Chang et al. 2013 a; Chang & Chen, 2015; Yu et al. 2015; Zhang et al. 2015). In this study we develop a novel computational model of the SK channel and integrate it with a physiologically detailed ionic model of a ventricular myocyte. We used the Ca²⁺ dependence formulation by Hirschberg et al. (1998). The governing equations for the SK channel are

$$\begin{array}{ccc}\hfill I_{\mathrm{SK}}& =& g_{\mathrm{sk}}{x}_{\mathrm{sk}}\left(V_{\mathrm{m}}-E_{\mathrm{K}}\right)\hfill \\ \hfill x_{\mathrm{sk}}& =& \frac{x_{\mathrm{sk}\infty }-x_{\mathrm{sk}}}{{\tau }_{\mathrm{sk}}}\hfill \\ \hfill x_{\mathrm{sk}\infty }& =& 0.81\frac{c_{\mathrm{s}}^n}{c_{\mathrm{s}}^n-{\mathrm{EC}}_{50}^n}\hfill \\ \hfill {\tau }_{\mathrm{sk}}& =& \frac{1.0}{\left(0.047c_{\mathrm{s}}+\frac{1}{76}\right)}\hfill \end{array}$$

where g _sk is the maximum conductance, E _K is the reversal potential, and EC₅₀ controls the affinity of Ca²⁺. Several experimental studies have reported the EC₅₀ of the SK channel in cardiac cells. Hongyuan et al. have reported that the EC₅₀ of the SK channel in rat ventricles is 0.23–0.59 μm (Hongyuan et al. 2016). Chang et al. have reported that the EC₅₀ of the SK channel in human ventricles is 0.35–0.6 μm (Chang et al. 2013 b). In this study, we varied the EC₅₀ from 0.1 to 1.0 μm to cover the whole range of physiological and pathophysiological conditions. In experimental studies, the SK current (I _SK) shows weak (or sometimes reverse) rectification (Lu et al. 2007; Zhang et al. 2008; Hsieh et al. 2013). Thus, in this study we chose a linear current–voltage relationship (Fig. 1 B). Rectification properties can affect our results quantitatively. However, they did not affect our results qualitatively. Ca²⁺ dependence and its time constant are plotted in Fig. 1 C and D. Figure 1 E shows the open probability (P _o) of the SK channel when various test [Ca²⁺] pulses are applied. Some reported g _sk values in ventricular myocytes are as high as 10 μS μF⁻¹ (Lu et al. 2007; Zhang et al. 2008; Chang et al. 2013 b; Hongyuan et al. 2016), which would profoundly shorten APD. We have chosen a range of g _sk more conservatively (from 0.4 to 4 μS μF⁻¹), based on apamin effects on APD. Hsieh et al. showed a 12% prolongation of APD when apamin was applied (pacing cycle length, PCL = 300 ms, heart failure rabbit ventricular myocyte) (Hsueh et al. 2013). When g _sk is 0.8 μS μF⁻¹ and EC₅₀ is 0.7 μm, the model also showed 12% difference between AP with I _SK (Fig. 1 F black) and AP without I _SK (Fig. 1 F red).

Tissue simulations were performed in a mono‐domain one‐dimensional cable. The governing equation for the membrane potential V _m of a cell in tissue is

$$C_{\mathrm{m}}\frac{\mathrm{d}{V}_{\mathrm{m}}}{\mathrm{d}t}=-I_{\mathrm{ion}}+I_{\mathrm{coupling}},$$

where C _m is the membrane capacitance, I _ion is the total ionic current through the membrane, and I _coupling is the current that comes from the neighbouring cells through the gap junctions. This equation was solved by an operator splitting method (Qu & Garfinkel, 1999; Xie et al. 2004).

At the cellular level, alternans can be caused by instability of V _m due to steep APD restitution. We call this V _m‐driven alternans. To alter the steepness of the restitution slope, we varied the time constant of the voltage‐dependent inactivation of the L‐type Ca²⁺ channel (τ_f) (Shiferaw et al. 2005). Alternans can also be caused by instability of ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling due to a steep SR Ca²⁺ release vs. SR Ca²⁺ load relationship and Ca²⁺ restitution properties. We call this ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven alternans (Chudin et al. 1999; Shiferaw et al. 2003, 2005). To alter the instability of ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling, we varied the gain of the SR Ca²⁺ release function (u) (Shiferaw et al. 2005).

Coupling of Ca²⁺ on the APD (${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling) is defined as positive (negative) if a large Ca²⁺ transient prolongs (shortens) the APD of the same beat (Shiferaw et al. 2005; Weiss et al. 2006) (Fig. 1 G). In our previous study (Shiferaw et al. 2005), we controlled ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling with a varying relative contribution of I _CaL and NCX by changing the Ca²⁺‐induced inactivation strength (γ). As γ is increased, I _CaL dominates and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling becomes more negative. The ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is positive when γ is 0.7. By fixing γ = 0.7 and varying Ca²⁺‐sensitive K⁺ currents, we demonstrate that Ca²⁺‐sensitive K⁺ currents can change the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling.

V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ alternans can be electromechanically concordant (a Long–Short–Long–Short APD sequence corresponding to a Large–Small–Large–Small Ca²⁺ transient sequence) or discordant (a Long–Short–Long–Short APD sequence corresponding to a Small–Large–Small–Large Ca²⁺ transient sequence) (Fig. 1 H). These phenomena depend on the underlying instability mechanisms (V _m‐driven or ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven) and the coupling between V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling.

Results

I _SK is an outward current during the AP. Introduction of the SK channel, while keeping all other parameters constant as in Shiferaw et al. (2005) was shown to shorten the APD (Fig. 1 F) similar to other outward currents.

Introduction of I _SK increases the area of stable APs with three distinct modes of oscillations at the stability boundary

By varying the instability factors of V _m (τ_f) and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling (u), we plotted the stability diagram (Fig. 2 A and B) for the pacing cycle length (PCL) of 300 ms.  Without I _SK (Fig. 2 A), the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is positive and alternans was always electromechanically concordant regardless of the instability mechanism. When I _SK was introduced (g _sk = 4 μS μF⁻¹, EC₅₀ = 0.7 μm), the area of the stable APs (i.e. periodic APs) was increased, evident from Fig. 2 A and B. In addition, three distinct modes of oscillations, electromechanically concordant alternans, quasiperiodic oscillations and electromechanically discordant alternans, occurred at the stability boundary, as labelled in Fig. 2 B (as C, D, E). The relation between peak [Ca²⁺]_i and APD was plotted, with (C) corresponding to electromechanically concordant alternans, (D) representing electromechanically discordant alternans as seen by the negative relation between peak [Ca²⁺]_i and APD, while (E) shows the quasiperiodic oscillation with corresponding orbit in peak [Ca²⁺]_i–APD plane (Fig. 2 E right panel). From our previous study (Shiferaw et al. 2005) three modes of oscillations implies that the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is negative.

Figure 2. Effects of I _SK at the cellular level.

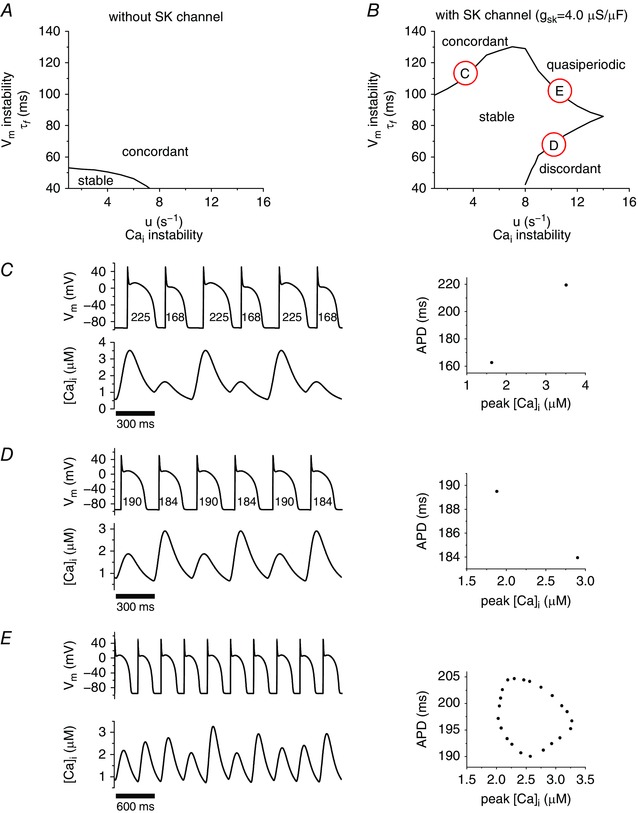
Stability boundaries were numerically determined for both the baseline system and the baseline plus SK, as seen in A and B, respectively. A demonstrates one mode of instability, namely concordant alternans, while B shows three distinct modes of instability; concordant alternans (C), discordant alternans (D), and quasiperiodic oscillation (E).

Affinity of [Ca²⁺] also affects V _m–${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ dynamics

Figure 3 A shows how the stability boundary curves (at PCL = 300 ms) shift with increasing I _SK conductance (g _sk). Figure 3 B shows how these curves shift as the I _SK [Ca²⁺]_i dependence (EC₅₀) is altered from 0.1 to 1.0 μm. When Ca²⁺ affinity is high (lower EC₅₀), I _SK shortens both short AP and long AP regardless of the amplitude of the Ca²⁺ transient. However, when Ca²⁺ affinity becomes lower (higher EC₅₀), I _SK shortens only when the amplitude of the Ca²⁺ transient is large. This means that the change in the APD becomes larger even when the change in the amplitude of the Ca²⁺ transient is the same. This promotes negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling (ΔAPD vs. Δpeak [Ca²⁺]_i will become steeper).

Figure 3. Effects of the maximum conductance and Ca²⁺ affinity of I _SK .

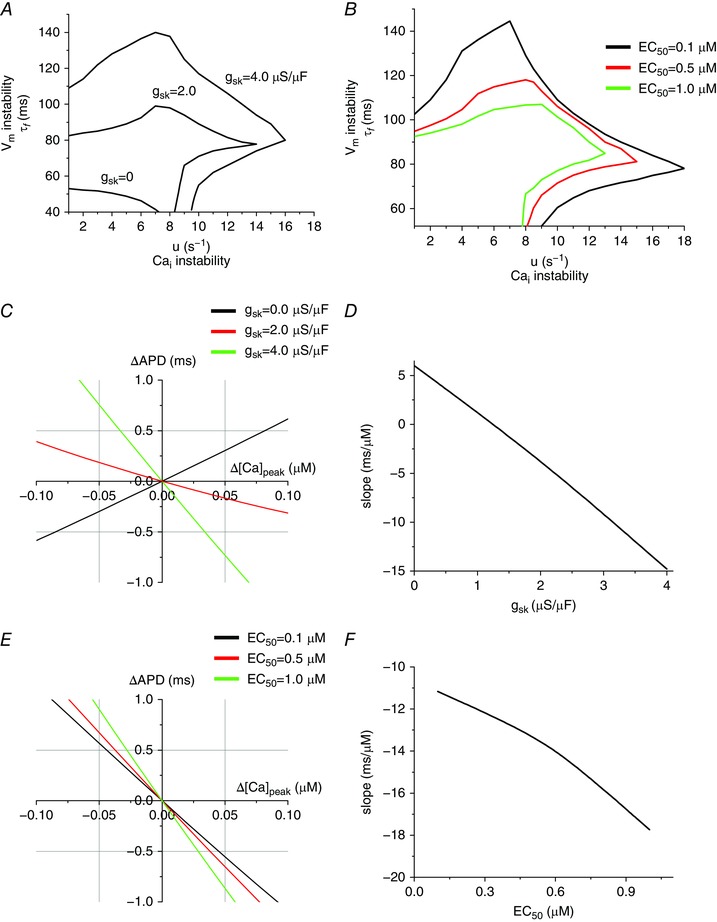
A, stability boundaries plotted for three g _sk, with values of 0, 2.0 and 4.0 μS μF⁻¹. B, stability boundaries plotted for three EC₅₀ values of 1.0, 0.5 and 0.1 μm corresponding to the black, red and green curves, respectively. C, the slope of ΔAPD vs. Δ[Ca²⁺]_peak indicates the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling. When g _sk = 0 μS μF⁻¹, the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is positive, while when g _sk = 4.0 μS μF⁻¹, the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is negative. EC₅₀ is 0.7 μm. D, slope (ΔAPD/Δ[Ca²⁺]_peak) vs. g _sk. E, ΔAPD vs. Δ[Ca²⁺]_peak when EC₅₀ is varied. g _sk is 4.0 μS μF⁻¹. F, slope (ΔAPD/Δ[Ca²⁺]_peak) vs. EC₅₀.

To test this idea of coupling change, we plotted ΔAPD vs. peak [Ca²⁺]_i (Fig. 3 C) for small changes in [Ca²⁺]_i. Peak [Ca²⁺]_i was varied by changing initial (diastolic) SR Ca²⁺ load. Without I _SK the positive slope indicates positive ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling, but as g _sk increases the slope flattens and by g _sk = 4 μS μF⁻¹, the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling becomes substantially negative (Fig. 3 C). The sign was changed around g _sk = 1 μS μF⁻¹ (Fig. 3 D). Higher Ca²⁺ affinity also makes the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling more negative (Fig. 3 E and F).

I _Ks is also Ca²⁺ sensitive. As expected, qualitatively similar results are seen with increasing I _Ks as were seen with I _SK. When the maximum conductance of I _Ks (g _ks) is reduced by half, we observed electromechanically concordant alternans at the stability boundaries (Fig. 4 A). On the other hand, when g _ks is increased to 300%, we observed three modes of oscillations (Fig. 4 B). These modes are plotted in Fig. 4 C (electromechanically concordant alternans), Fig. 4 D (electromechanically discordant alternans), and Fig. 4 E (quasiperiodic oscillations).

Figure 4. Effects of I _Ks at the cellular level.

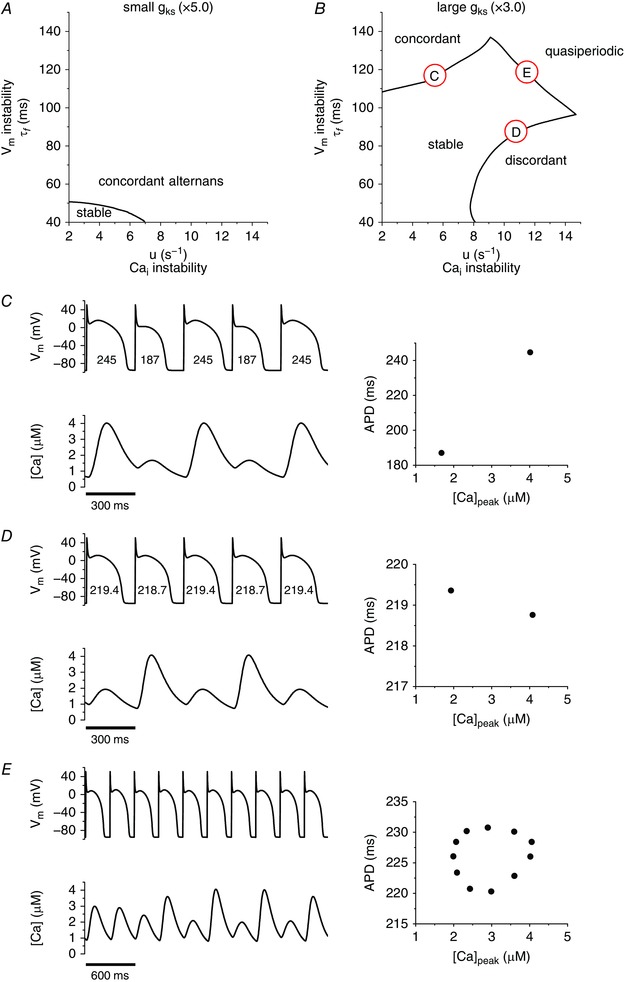
A, stability diagram when g _ks is small (50% of the original value, the original g _ks is 0.0245 mS μF⁻¹). Alternans is always electromechanically concordant. B, stability diagram when g _ks is large (300% of the original value). In this case, there are three distinct modes of instability; electromechanically concordant alternans (C), electromechanically discordant alternans (D), and quasiperiodic oscillation (E).

Both the maximum conductance (g _ks) and Ca²⁺ sensitivity affect the stability boundaries and the modes of oscillations

When g _ks was increased from 50 to 300%, it not only increased the stable area but also induced three modes (Fig. 5 A). On the other hand, when Ca²⁺ sensitivity was decreased, it suppressed electromechanically concordant and discordant alternans but promoted quasiperiodic oscillations (Fig. 5 B). This indicates that Ca²⁺ sensitivity changed only the coupling without changing V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ instabilities. Figure 5 C and D shows positive ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling when I _Ks is small (g _ks × 0.5) and negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling when I _Ks is large (g _ks × 3).

Figure 5. Effects of the maximum conductance and Ca²⁺ affinity of I _Ks .

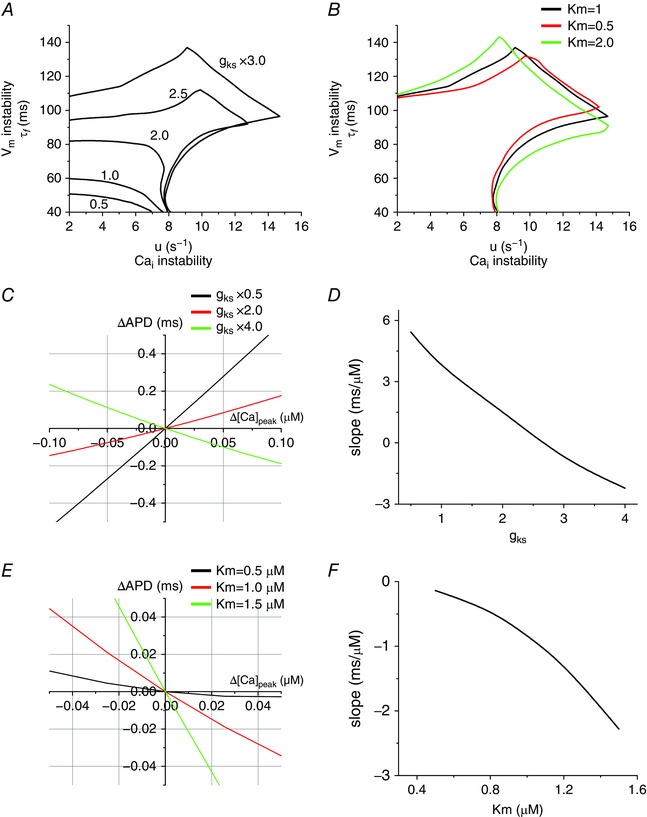
A, stability boundaries plotted for multiple g _ks, with values of 50, 100, 200, 250 and 300% of the original value (0.0245 mS μF⁻¹). B, stability boundaries plotted for three K _m, with values of 1.0, 0.5 and 2.0 μm corresponding to the black, red and green curves, respectively. C, ΔAPD vs. Δ[Ca²⁺]_peak when g _ks is varied. D, slope (ΔAPD/Δ[Ca²⁺]_peak) vs. g _ks. E, ΔAPD vs. Δ[Ca²⁺]_peak when K _m is varied. F, slope (ΔAPD/Δ[Ca²⁺]_peak) vs. K _m.

From these single cell simulations, we summarize as follows. If alternans is ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven (small τ_f and large u, along the abscissa in Figs 2, 3, 4), increasing the maximum conductance of I _SK or I _Ks promotes electromechanically discordant alternans (Fig. 6 A). On the other hand, if alternans is V _m‐driven (large τ_f and small u, along ordinate in Figs 2, 3, 4), electromechanically concordant alternans remains electromechanically concordant even when the maximum conductance of I _SK or I _Ks is increased (Fig. 6 B).

Figure 6. Summary of the effects of Ca²⁺ ‐sensitive K⁺ currents.

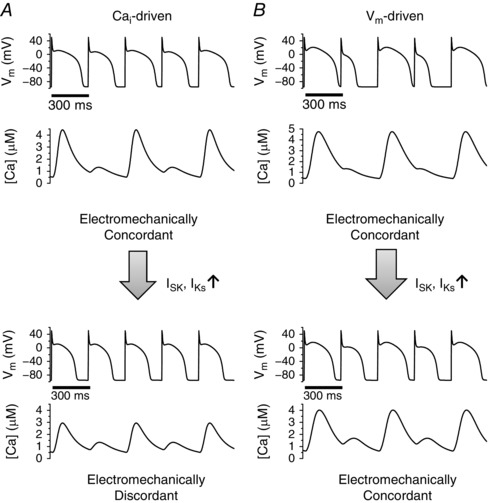
A, if alternans is ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven, Ca²⁺‐sensitive K⁺ currents promote electromechanically discordant alternans. B, if alternans is V _m‐driven, electromechanically concordant alternans remains electromechanically concordant even when Ca²⁺‐sensitive K⁺ currents are increased.

At the tissue level, increasing I _SK or I _Ks leads to different types of spatially discordant alternans

In tissue, cellular level instability mechanisms lead to different alternans. We paced the left‐most five cells of the 6 cm (400 cell) homogeneous cable. First, we paced the cable at a PCL of 600 ms until it reached the steady state. At this PCL, there is no alternans. Then, the PCL was decreased to 300 ms. Alternans gradually developed. When all cells in the cable reached the steady state, we plotted APD and peak [Ca²⁺]_i along the cable (Fig. 7).

Figure 7. Effects of I _SK and I _Ks at the tissue level.

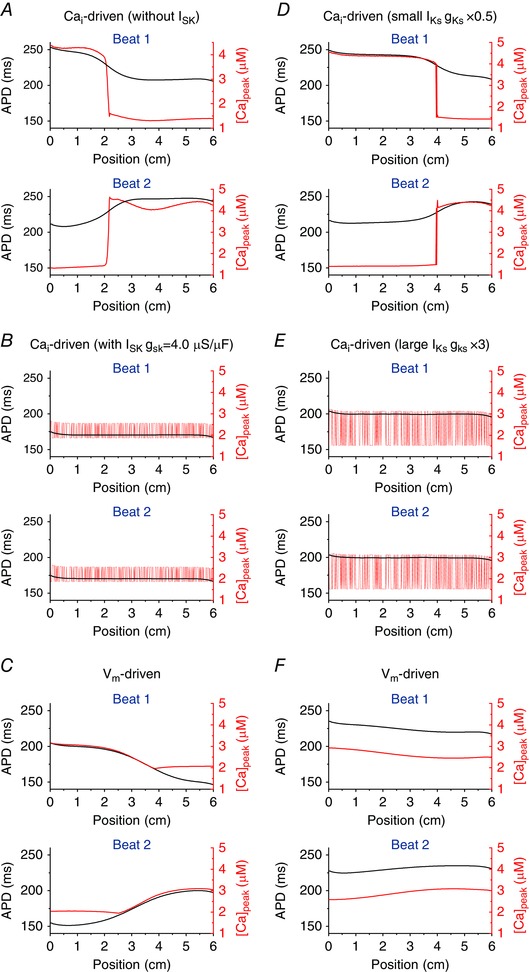
A, Ca²⁺‐driven alternans without I _SK. The mechanism of spatially discordant alternans is competition between synchronization due to diffusive coupling and desynchronization due to stochasticity. B, Ca²⁺‐driven alternans with I _SK. The mechanism of spatially discordant alternans is Turing‐type instability. C, V _m‐driven alternans. The mechanism of spatially discordant alternans is interaction between APD and conduction velocity restitution. When alternans is V _m‐driven, changing the magnitude of I _SK does not change the mechanism of spatially discordant alternans. In this simulation, g _sk is 4.0 μS μF⁻¹. D, Ca²⁺‐driven alternans when g _ks is small (50% of the original value). The mechanism of spatially discordant alternans is competition between synchronization due to diffusive coupling and desynchronization due to stochasticity. E, Ca²⁺‐driven alternans when g _ks is large (300% of the original value). The mechanism of spatially discordant alternans is Turing‐type instability. F, V _m‐driven alternans. The mechanism of spatially discordant alternans is interaction between APD and conduction velocity restitution. When alternans is V _m‐driven, changing the magnitude of I _Ks does not change the mechanism of spatially discordant alternans. In this simulation, g _ks is 300% of the original value.

When alternans are ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven (small τ_f and large u), if these currents are small, the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is positive and the mechanism of spatially discordant alternans is due to competition between synchronization due to diffusive electrical coupling and desynchronization due to Ca²⁺‐related stochasticity (Sato et al. 2013). The mechanism of spatially discordant alternans does not depend on the details of the ionic currents. This occurs whenever the cellular level instability mechanism is ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven and the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling is positive. In this case, the spatial scale of phase reversal of ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ alternans is short (Sato et al. 2007) (Fig. 7 A and D), where spatially discordant alternans is shown. However, when I _SK or I _Ks becomes large, the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling becomes negative and the mechanism of spatially discordant alternans is due to Turing‐type instability (instability due to electrotonic coupling) (Sato et al. 2006) (Fig. 7 B and E). The mechanism of this spatially discordant alternans is also model independent and requires only ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven instability and negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling. If alternans is V _m‐driven, the mechanism of spatially discordant alternans is due to interaction between APD and conduction velocity restitution (Echebarria & Karma, 2002, 2007)(Fig. 7 C and F). In this case, the spatial scales of phase reversal of ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ alternans is large (e.g. vs. that in Fig. 7 A and D) (Sato et al. 2007).

Discussion

In this study, we have shown that Ca²⁺‐sensitive K⁺ currents I _Ks and I _SK promote negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling, which creates three modes of instability at the cellular level and Turing‐type instability at the tissue level.

In 1968, Nolasco and Dahlen used APD restitution, which is the relationship between APD and the previous diastolic interval (DI), APD(n + 1) = Function (F) (DI(n)), to demonstrate that the formation of alternans occurs when the slope of the APD restitution curve exceeds unity (Nolasco & Dahlen, 1968). This interpretation provides a model for the relationship of V _m and APD stability. However, this one‐dimensional map cannot explain the existence of three distinct modes (electromechanically concordant/discordant alternans and quasiperiodicity) of instability (Shiferaw et al. 2005), which have been shown experimentally (Rubenstein & Lipsius, 1995; Gilmour et al. 1997; Walker & Rosenbaum, 2003).

One possible mechanism for these multiple modes is the interactions between V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling. ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling can be unstable when the myocyte is Ca²⁺ overloaded or RyRs are sensitized. ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling can also be unstable when the cell is rapidly paced. In fact, Chudin et al. have demonstrated that ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ transients exhibit alternans even with AP clamp waveform (i.e. APs are periodic) (Chudin et al. 1999). This implies that ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling has its own non‐linear dynamics (Dilly & Lab, 1988; Hall et al. 1999; Hall & Gauthier, 2002; Fox et al. 2002 a; Pruvot et al. 2004; Picht et al. 2006; Wang et al. 2014).

In the present study, we used a computational model which shows both non‐linearities of V _m and ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$ cycling. These two non‐linear systems are coupled via Ca²⁺‐sensitive currents. As the myocyte experiences a large Ca²⁺ transient, the open probability of the Ca²⁺‐sensitive K⁺ channel will increase, increasing outward K⁺ current. This larger Ca²⁺ transient also promotes Ca²⁺‐dependent inactivation of L‐type Ca²⁺ channels, limiting inward Ca²⁺ current, so both K⁺ and Ca²⁺ current effects tend to promote negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling. However, Ca²⁺‐dependence increases in inward current via NCX (due to changes in electrochemical driving force) promoting positive ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling. Net changes in the competition between these Ca²⁺‐dependent currents produces the transition from positive to negative ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling. Any increase in Ca²⁺‐dependent K⁺ current (I _Ks or I _SK) would tend to shift the coupling negative. Moreover, increasing either I _Ks or I _SK reveals three modes of instability. As the ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$→V _m coupling becomes more negative (with rising I _Ks or I _SK), the slope of ΔAPD vs. ΔCa²⁺ is negative, and three distinct modes of alternans are induced: (1) V _m‐driven electromechanically concordant alternans (large τ_f, small u), (2) ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven electromechanically discordant alternans (small τ_f, large u), and (3) quasiperiodic oscillation (large τ_f, large u)). All three of these modes of instability have been observed in both voltage and Ca²⁺ recordings (Dilly & Lab, 1988; Hall et al. 1999; Hall & Gauthier, 2002; Fox et al. 2002 a; Pruvot et al. 2004).

Another important point of this study is that we introduced a novel model of the SK channel. Using this model, we demonstrate that its Ca²⁺ dependence (Hirschberg et al. 1998) is responsible for the observed existence of three distinct modes of instability.

Typical healthy myocytes show electromechanically concordant alternans during fast pacing. We found that as the maximum conductance of I _SK was increased, electromechanically concordant alternans became electromechanically discordant when alternans is ${\mathrm{Ca}}_{\mathrm{i}}^{2+}$‐driven. These findings shed light on the underlying mechanisms of cardiac alternans, especially for failing hearts since I _SK was shown to be up‐regulated in ventricular myocytes in heart failure (Yu et al. 2015). In this study, we used a ventricular AP model. Alternans have also been observed in atrial cells (Kanaporis & Blatter, 2015). We expect I _SK to have the same dynamical effects on alternans in atrial cells, and may be even more impactful there because of higher basal density of I _SK in atrial vs. ventricular myocytes (Xu et al. 2003). Finally, our study also provides insights into the non‐linearities of cardiac tissue behaviour and a potential link between molecular processes within the cell to the development of disorders of the organ itself.

Additional information

Competing interests

None declared.

Author contributions

All authors contributed ideas and discussion. M.K. and D.S. performed computer simulations and mathematical analysis. All authors wrote the manuscript, approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by National Institutes of Health grant R00‐HL111334, American Heart Association Grant‐in‐Aid 16GRNT31300018 and Amazon AWS Cloud Credits for Research program (D.S.); R01‐HL105242 (D.M.B.); and R01‐HL085844 (N.C.).

Translational perspective

Recent experimental studies showed that I _SK becomes extremely large in failing hearts. Thus, understanding the role of the SK channel in alternans dynamics is potentially important to develop new drugs and therapies for heart failure. In this study, we investigated the role of Ca²⁺‐sensitive K⁺ channels (I _SK and I _Ks) on V _m and Ca²⁺ dynamics. An increase of Ca²⁺‐sensitive K⁺ currents can be responsible for electromechanically discordant alternans and quasiperiodic oscillations at the cellular level and Turing‐type spatially discordant alternans in tissue. These results provide theoretical bases to understand and interpret experimental and clinical results.

Supporting information

Disclaimer: Supporting information has been peer‐reviewed but not copyedited.

Data S1: Details of the model.