Data integration in physiology using Bayes’ rule and minimum Bayes’ factors: deubiquitylating enzymes in the renal collecting duct

Abstract

A major challenge in physiology is to exploit the many large-scale data sets available from “-omic” studies to seek answers to key physiological questions. In previous studies, Bayes’ theorem has been used for this purpose. This approach requires a means to map continuously distributed experimental data to probabilities (likelihood values) to derive posterior probabilities from the combination of prior probabilities and new data. Here, we introduce the use of minimum Bayes’ factors for this purpose and illustrate the approach by addressing a physiological question, “Which deubiquitylating enzymes (DUBs) encoded by mammalian genomes are most likely to regulate plasma membrane transport processes in renal cortical collecting duct principal cells?” To do this, we have created a comprehensive online database of 110 DUBs present in the mammalian genome (https://hpcwebapps.cit.nih.gov/ESBL/Database/DUBs/). We used Bayes’ theorem to integrate available information from large-scale data sets derived from proteomic and transcriptomic studies of renal collecting duct cells to rank the 110 known DUBs with regard to likelihood of interacting with and regulating transport processes. The top-ranked DUBs were OTUB1, USP14, PSMD7, PSMD14, USP7, USP9X, OTUD4, USP10, and UCHL5. Among these USP7, USP9X, OTUD4, and USP10 are known to be involved in endosomal trafficking and have potential roles in endosomal recycling of plasma membrane proteins in the mammalian cortical collecting duct.

a major challenge in physiology is to exploit the many large-scale data sets available from “-omic” studies to seek answers to key physiological questions. “-Omic” data include output from protein mass spectrometry, deep DNA sequencing, DNA microarrays, and genome-wide association studies, for example. One approach that has been employed for large-scale data integration is the use of Bayes’ theorem to link together multiple diverse data sets. Bayes’ theorem has not been used extensively in physiology but has been widely employed in the field of medicine. For example, the then-controversial conclusion that smoking causes cancer was reached in the 1950s using data integration from multiple sources via Bayesian statistics (14). More recently, the Bayesian approach has been employed to address risks and benefits of screening mammography (2) and to address whether measurements of prostate-specific antigen (PSA) should be used for routine screening for prostatic cancer (37). An example of use of Bayes’ theorem in kidney physiology ranked all protein kinases coded by the mammalian genome with regard to likelihood of phosphorylating the renal water channel, aquaporin-2 (AQP2) (6, 38). The method was also used to rank all ubiquitin E3 ligases with regard to likelihood of ubiquitylating AQP2 (24). In addressing questions like these, Bayes’ Theorem can be viewed as a mathematical operator (Fig. 1) with an input of two vectors of equal length (a prior probability vector and a likelihood vector from a new data set), which outputs a new vector of the same length, the posterior probability vector (6). For protein kinases, the vector dimension is 521 because there are 521 protein kinases coded by mammalian genomes. For ubiquitin E3 ligases, the dimension is 377 (24).

Fig. 1.

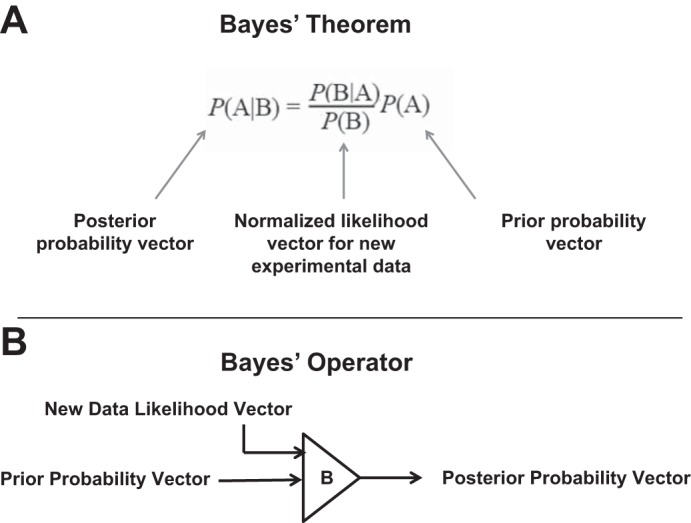
Bayes theorem. A: new experimental data are represented as a normalized likelihood vector P(B|A)/P(B). The vector dimension is equal to the number of genes/proteins that are candidates for a particular physiological role. B: viewed from the perspective of linear algebra, the application of Bayes’ theorem can be viewed as an operator that takes 2 equal-sized vectors as inputs (the prior probability vector and the normalized likelihood vector and produces a “posterior probability” vector of the same size. The vector size for the physiological example given in this paper is 110 (equal to the number of deubiquitylating enzymes coded by mammalian genomes).

One limitation of the Bayesian method used so far in modeling the renal collecting duct is in the assignment of likelihood values that map experimental data to a set of probabilities describing the strength of the evidence (Fig. 1). For example, transcriptomic data can be used to estimate the likelihood that a given gene is expressed in collecting duct cells: High values are compatible with the classifier “expressed” and low values with the classifier “not expressed.” However, such classification must be viewed as probabilistic, since unknown technical limitations may cast uncertainty on the interpretation. To assign likelihood values, prior studies have utilized assignment tables to map experimental values to probabilities that are determined somewhat subjectively based on experience (6, 24, 38). This approach classifies the data according to user-defined threshold values that are assigned, somewhat subjectively, based on knowledge of the method used to generate the data. In this paper, we introduce an alternative approach, the use of so-called “minimum Bayes’ factors” (17, 18) to calculate the likelihood vectors from quantitative data. This approach assigns likelihood values based on assignment of a single parameter, a noise threshold that is experimentally determined from the appropriate large-scale data set (Table 1).

Table 1.

Data sets used and method for calculating likelihood values

Data set	Rationale	Assignment of Likelihood Values: P(B|A)	Noise Threshold
Mouse mpkCCD transcriptome	The ability of a DUB to deubiquitinate plasma membrane transporters depends on whether or not it is expressed in collecting duct cells.	complements of minimal Bayes' factors (Z* = value/noise)	0.4
Mouse mpkCCD proteome	The ability of a DUB to deubiquitinate plasma membrane transporters depends on whether or not it is expressed in collecting duct cells.	complements of minimal Bayes' factors (Z* = value/noise)	26,251 (10th percentile value)
Annotated subcellular localization from Uniprot protein records	The ability of a DUB to deubiquitinate plasma membrane transporters depends on whether or not it is expressed in the same subcellular compartment.	if “cytoplasm,” “cytosol,” “lysosome,” “endosome,” “Golgi,” P(B|A) = 0.95; if not, P(B|A) = 0.1; if no annotation, P(B|A) = 0.5	none
Subcellular colocalization with plasma membrane proteins based on dot products of DUBs with the Na-K-ATPase (Atp1a1) and AQP2	The ability of a DUB to deubiquitinate plasma membrane transporters depends on whether or not it is expressed in the same subcellular compartment.	complements of minimum Bayes' factors = 1 – exp(–[Z*]2/2), for each DUB where Z* is the ratio of each value to the intrinsic noise in the measurement	0.05
CCD transcriptome from native rat	The ability of a DUB to deubiquitinate plasma membrane transporters depends on whether or not it is expressed in collecting duct cells.	complements of minimum Bayes' factors = 1 – exp(–[Z*]2/2), for each DUB where Z* is the ratio of each value to the intrinsic noise in the measurement	RPKM = 1

DUB, deubiquitylating enzyme; AQP2, aquaporin-2; CCD, cortical collecting duct; RPKM, reads per kilobase of transcript per million mapped reads.

To illustrate the physiological use of Bayes’ theorem with minimum Bayes’ factors, we addressed the question, “Which deubiquitylating enzymes (DUBs) encoded by mammalian genomes are most likely to regulate plasma membrane transport processes in renal cortical collecting duct principal cells?” Protein ubiquitylation is already known to play important roles in the regulation of several plasma membrane transporters in the renal collecting duct, including the water channel AQP2 (20), individual subunits of the epithelial sodium channel ENaC (15, 26, 32), the urea channel UT-A1 (10, 33), the potassium channels KCNQ1 (1) and KCNJ1 (22), and the tight junction proteins claudin-8 (16) and occludin (27). Membrane transporters are integral membrane proteins (IMPs). With IMPs, ubiquitylation typically directs the targeted protein to degradation in the lysosome via endosomal trafficking (25), and this appears to be true of ENaC (32), UT-A1 (33), and AQP2 (20). Ubiquitylation of IMPs, however, does not invariably result in degradation. They can instead be recycled as a result of deubiquitylation by deubiquitinating enzymes (DUBs) (8, 12). Here, we use Bayes’ theorem to integrate several large-scale data sets to identify the DUBs most likely to regulate plasma membrane protein recycling in the renal collecting duct.

A necessary first step in such an analysis is to compile a list of all DUB genes present in mammalian genomes. Accordingly, we have assembled a list of 110 DUBs (as well as 12 similar enzymes that remove SUMO or Nedd8 from their attachments to proteins) and have made the list available as a publically accessible web page, providing a new systems-biological tool. In the absence of additional data, each of these 110 DUBs can be considered as candidates to play regulatory roles in the renal collecting duct.

The list can be sorted with regard to likelihood of roles in regulation of transport across the plasma membrane through use of large-scale data sets from transcriptomic and proteomic studies of renal collecting duct cells. As in our prior studies (6, 24, 38), this can be achieved through repeated application of Bayes’ theorem to sequentially incorporate information from different data sets obtained using protein mass spectrometry, Affymetrix expression arrays, and RNA-Seq analysis in renal collecting duct cells. Although these data sets have been published (41), they have been only minimally exploited for physiological modeling, e.g., for identification of physiological roles for DUBs in the renal collecting duct. Thus, large-scale data integration using Bayes’ rule provides a means for mining data to draw new physiological conclusions.

The present paper has four aims: 1) to introduce the use of the minimum Bayes’ factor to map experimental data to a set a likelihood values for the application of Bayes’ theorem; 2) to curate a list of DUBs present in the mammalian genome and make the information available via a publicly accessible webpage; 3) to provide an example of the application of Bayes’ rule to a physiological question “What DUBs interact with plasma membrane proteins in the renal cortical collecting duct?”; and 4) to relate the predictions made via Bayesian analysis to the reductionist literature on regulation of transport in collecting duct principal cells.

METHODS

Database of mammalian DUBs.

Application of Bayes’ theorem to large-scale data integration in physiology requires a list of all candidate genes/proteins as a starting point. To illustrate the use of Bayes’ theorem in this paper, we use it to ask what DUBs may play roles in regulation of plasma membrane transporters in renal cortical collecting duct cells. To provide an initial list of DUBs, we assembled a comprehensive database of human and mouse DUBs (https://hpcwebapps.cit.nih.gov/ESBL/Database/DUBs/) using several bioinformatic tools as follows. We collated an initial list from several data resources, viz. the DUDE v. 1.0 Database (http://www.dude-db.org/) (19), and the literature (7, 30). The tools used to collect related information are BLAST (https://blast.ncbi.nlm.nih.gov/Blast.cgi), ABE (Automated Bioinformatics Extractor, https://hpcwebapps.cit.nih.gov/ESBL/ABE/) (34), and BIG (https://big.nhlbi.nih.gov/) (41).

Application of Bayes’ rule to large-scale data integration.

To determine the DUBs most likely to regulate plasma membrane transport processes in the renal cortical collecting duct, we used data from multiple sources to rank all mammalian DUBs using Bayes’ theorem (6) (see Supplemental Data Set 1 for details of calculations). (The online version of this article contains supplemental material.) Bayes’ theorem (Fig. 1) can be formulated as P(A|B) = P(B|A) × P(A)/P(B), where P(A|B) is the probability of A given B, P(B|A) is the probability of B given A, P(A) is the prior probability for A, and P(B) is the sum of probabilities of B over all A (13). From a practical perspective, P(B|A) represents new experimental data being integrated at a given step after mapping it to probability (likelihood) values (range 0 to 1). For this mapping, we introduce in this paper the use of complements of minimum Bayes’ factors (see below). Thus, as illustrated in Fig. 1, the application of Bayes’ theorem can be viewed in the context of linear algebra as an “operator” that takes a set of ‘prior probabilities’ [P(A) vector] and a set of new data likelihood values [P(B|A) vector] and generates a set of “posterior probabilities” [P(A|B vector]. This Bayes’ operator can be applied sequentially to integrate multiple data sets, using posterior probabilities from one step as prior probabilities in the next step (Fig. 2). The operator is commutative, so the order of data integration does not affect the final values.

Fig. 2.

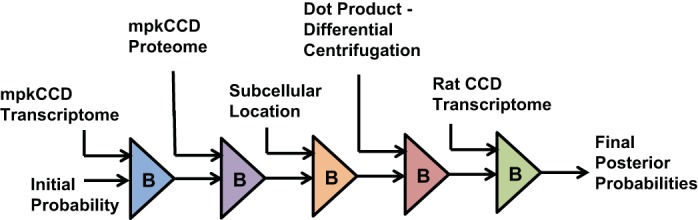
Analysis of deubiquitylating enzymes (DUBs) most likely to be involved in regulation of plasma membrane transporters uses repeated application of Bayes’ theorem to integrate various data sets from large-scale proteomics and transcriptomics studies. In each case, the posterior probability from one step becomes the prior probability for the next. The calculation is commutative meaning that the result is independent of the order of data integration.

The application of Bayes’ rule provides a systematic means of utilizing existing data to provide answers to biological questions via a process that simulates the way that humans normally integrate multiple pieces of information. To provide a practical example of the use of Bayes’ theorem for large-scale data integration in physiology, we used it to estimate our degree of confidence regarding whether any particular DUB could deubiquitylate and regulate plasma membrane proteins in renal cortical collecting duct cells.

For this calculation (Supplemental Data Set 1), we started with all 110 DUBs, assigning them the same prior probabilities P(A) of 1/110 and used Bayes’ theorem to update the values from sets of likelihood values, P(B|A), based on different experimental data sets. The data sets used were: 1) the mouse mpkCCD transcriptome (39) downloaded from https://esbl.nhlbi.nih.gov/mpkCCD-transcriptome/; 2) the mouse mpkCCD proteome (38), downloaded from https://helixweb.nih.gov/ESBL/Database/mpkCCD_Protein_Abundances/; 3) annotated subcellular localization from Uniprot protein records to determine what subcellular compartments each of the DUB proteins are found in; 4) calculated dot product of DUBs vs. representative plasma membrane proteins (ATP1A1 and AQP2) in mouse mpkCCD subcellular fractions (27) downloaded from https://hpcwebapps.cit.nih.gov/ESBL/Database/mpkFractions/; and 5) RNA-Seq data reporting levels of DUB transcripts in microdissected rat cortical collecting ducts downloaded from https://hpcwebapps.cit.nih.gov/ESBL/Database/NephronRNAseq/All_transcripts.html. The rationales for the use of these data sets and the method of calculating likelihood values from the data are shown in Table 1. In the case of quantitative data, we use minimum Bayes’ factors to assign likelihood values based on Goodman (17) and Held (18). Specifically, we used the complement of the minimum Bayes’ factor to calculate likelihoods, i.e., 1 – exp(– [Z*]²/2), for each DUB where Z* is the ratio of each value to the intrinsic noise in the measurement (Table 1). The overall approach is “unbiased,” meaning that each of the 110 DUBs is assumed to have the same prior probability before being updated with experimental data.

Functional annotation of the top-ranked DUBs were obtained from the “[FUNCTION]” field of individual UniProt Protein records, as well as through use of “Biological Information Gatherer - Kidney” (41) (BIG, see https://big.nhlbi.nih.gov/index.jsp) to extract information from previous studies of renal collecting duct cells.

RESULTS

Database of mammalian DUBs.

To illustrate the use of Bayes’ theorem for large-scale data integration, we focused on identification of DUBs that may play a role in the regulation of transport across the plasma membranes of the renal cortical collecting duct. To do such an analysis, a list of all DUBs and related enzymes present in mammalian genomes was a prerequisite. However, because of the lack of a readily accessible, fully curated list of known DUBs, we compiled our own list (methods) containing 110 mammalian DUBs. In addition we identified 12 related enzymes that cleave the small ubiquitin-like proteins SUMO or Nedd8, including nine desumolylating enzymes and three deneddylating enzymes. This data set has been made available as a freely accessible database located at https://hpcwebapps.cit.nih.gov/ESBL/Database/DUBs/. A screenshot of the database webpage is shown in Fig. 3. A link is provided to allow users to download the data into an electronic spreadsheet (A). The webpage can be searched (B) using the browser’s intrinsic search command (Shortcut: Ctrl-F).

Fig. 3.

A publicly available webpage was created to provide users with a comprehensive list of 110 mammalian DUBs as well as 12 similar enzymes that remove SUMO or Nedd8 from their attachments to proteins. Access to this webpage can be found at https://helixweb.nih.gov/ESBL/Database/DUBs/. A: data can be downloaded as a spreadsheet. B: the webpage can be searched using the browser Find command (Ctrl-F).

Specifying likelihood vectors from experimental data using minimum Bayes’ factors.

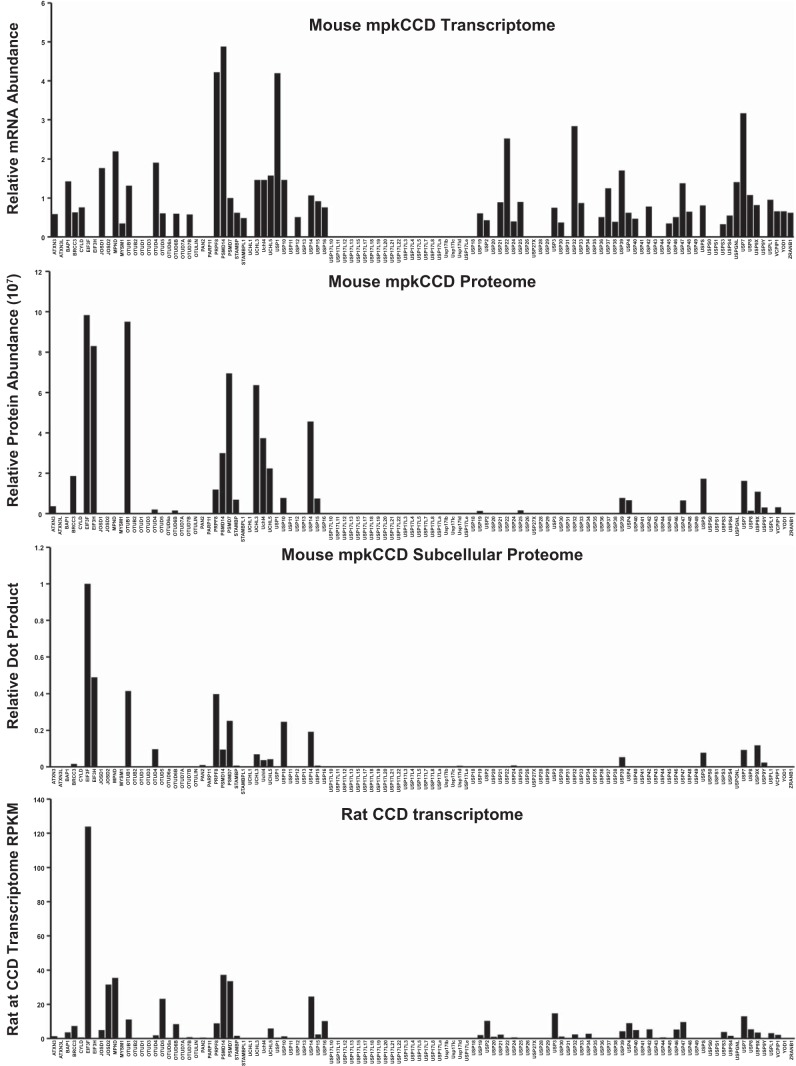
We started with the assumption of equal prior probabilities for each DUB in the curated database (Table 2, column 3), and using Bayes’ theorem, we sequentially updated all probabilities using the large-scale data sets listed in Table 1. Figure 4 shows a summary of the source data for all DUBs from four different data sets. Application of Bayes’ theorem to large-scale data integration in physiology requires a method to translate quantitative experimental data to likelihood values that represent probabilities that a particular descriptor applies (Fig. 1). In this paper, we introduce the use of minimum Bayes’ factors (17, 18) for this purpose. Figure 5 illustrates the method using one of the data sets, viz. the “rat CCD transcriptome” (Table 1) generated by Lee et al. (21) to classify DUB genes as “expressed” or “not expressed,” This classification is relevant to the question of which DUBs regulate plasma membrane transporters in the renal cortical collecting duct, because those not expressed are unlikely to deubiquitylate proteins in these cells. The data are from experiments in microdissected rat cortical collecting duct segments using RNA-Seq (deep DNA sequencing) to quantify relative mRNA abundances across the genome. The graph in Fig. 5 shows how use of the complement of minimum Bayes’ factors maps normalized RNA-Seq data to likelihood values. The mapping uses a single parameter, the intrinsic noise in the measurement (here RPKM = 1.0), which reflects a threshold data value identified in the experimental study (21) as the limit of reliable detectability. As can be seen, for all data values substantially above the noise level, the complements of the minimum Bayes’ factors are all essentially equal because the function asymptotically approaches the value of 1. Conversely, likelihood values for mRNAs levels substantially below the noise level approach the value of zero. The greatest discrimination is appropriately around the defined noise level.

Table 2.

The 20 top ranked DUBs base on probability of interacting with plasma membrane transporters

Rank	2 Gene Symbol	3 Initial Probability	4 mpkCCD Transcriptome	5 mpkCCD Proteome	6 UniProt Subcellular Location	7 Dot Product	8 Rat CCD Transcriptome	9 Final Posterior Prob.
1	OTUB1	0.0091	0.0195	0.0340	0.0428	0.0944	0.1203	0.1203
2	USP14	0.0091	0.0191	0.0332	0.0428	0.0921	0.1173	0.1173
3	PSMD7	0.0091	0.0188	0.0327	0.0428	0.0907	0.1155	0.1155
4	PSMD14	0.0091	0.0196	0.0342	0.0427	0.0795	0.1012	0.1012
4	USP7	0.0091	0.0196	0.0342	0.0427	0.0786	0.1001	0.1001
6	USP9X	0.0091	0.0172	0.0300	0.0427	0.0783	0.0996	0.0996
7	OTUD4	0.0091	0.0196	0.0342	0.0427	0.0805	0.0876	0.0876
8	USP10	0.0091	0.0196	0.0341	0.0427	0.0947	0.0709	0.0709
8	UCHL5	0.0091	0.0196	0.0342	0.0426	0.0294	0.0375	0.0375
8	PRPF8	0.0091	0.0196	0.0342	0.0416	0.0100	0.0127	0.0127
11	EIF3F	0.0091	0.0020	0.0034	0.0416	0.0095	0.0121	0.0121
12	USP47	0.0091	0.0196	0.0341	0.0409	0.0095	0.0120	0.0120
13	USP8	0.0091	0.0191	0.0333	0.0397	0.0092	0.0118	0.0118
14	USP15	0.0091	0.0182	0.0317	0.0394	0.0088	0.0105	0.0105
14	BRCC3	0.0091	0.0139	0.0243	0.0375	0.0067	0.0086	0.0086
16	USP4	0.0091	0.0137	0.0239	0.0373	0.0066	0.0084	0.0084
17	OTUD6B	0.0091	0.0132	0.0231	0.0318	0.0064	0.0082	0.0082
18	VCPIP1	0.0091	0.0146	0.0254	0.0304	0.0071	0.0081	0.0081
18	UCHL3	0.0091	0.0196	0.0341	0.0299	0.0585	0.0074	0.0074
18	USP5	0.0091	0.0171	0.0298	0.0299	0.0585	0.0074	0.0074

The 20 DUBs most likely to interact with plasma membrane proteins based on Bayesian analysis. The Bayesian analysis is sequential. Columns 4–8 show the Bayesian posterior probabilities for DUB interaction with plasma membrane proteins in the cortical collecting duct using the data sets described in Table 1.

Fig. 4.

Data used to estimate likelihood vectors for Bayes’ analysis of deubiquitylating enzymes (DUBs) involved in regulation of plasma membrane transporters in cortical collecting duct principal cells. Horizontal axis lists each of the 110 DUBs in the same order. Data sources are listed in main text.

Fig. 5.

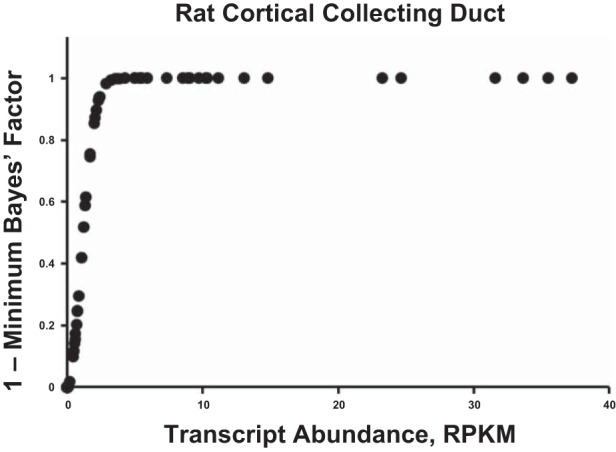
Example of the conversion of experimental data to likelihood values using the complements of minimum Bayes’ factors. The data are mRNA abundance levels measured as RPKM obtained using RNA-Seq in microdissected cortical collecting ducts from rats. The conversion uses the equation: 1 – exp(– [Z*]²/2), for each DUB where Z* is the ratio of each value to the intrinsic noise in the measurement (Table 1).

Likelihood assignments for all data sets (Table 1) employed complements of minimum Bayes’ factors with the exception of “Annotated Subcellular Localization from Uniprot Protein Records.” For this data set, we extracted data from the “Subcellular Localization” fields of UniProt protein records, classifying each DUB with regard to whether or not the strings corresponding to nonnuclear structures “cytoplasm,” “cytosol,” “lysosome,” “endosome,” or “Golgi” were found. This classification is relevant to the question of which DUBs regulate plasma membrane transporters in the renal cortical collecting duct, because those present exclusively in the nucleus are unlikely to interact physically with plasma membrane transporters. For these data, we made discrete likelihood assignments (Table 1).

Ranking DUBs in the renal cortical collecting duct.

Which of the 110 DUBs in the mammalian genome are most likely to interact with plasma membrane transporters in the renal cortical collecting duct? We started with the assumption of equal prior probabilities for each DUB in the curated database (Table 2, column 3) and using Bayes’ theorem, we sequentially updated all probabilities using the large-scale data sets listed in Table 1. (See Supplemental Data Set 1 for details of calculations.) After integration of all data sets, we obtained a final ranked list of DUBs (Table 2, last column) most likely to interact with plasma membrane transporters in the renal collecting duct, headed by OTUB1, USP14, PSMD7, PSMD14, USP7, USP9X, OTUD4, USP10, and UCHL5. Figure 6 shows the progression of change of posterior probabilities for the 20 highest ranked DUBs throughout the calculation. The other 90 DUBs have extremely low probability values and many are not even expressed in collecting duct cells. A listing of the key characteristics of the top-ranked DUBs is given in Table 3.

Fig. 6.

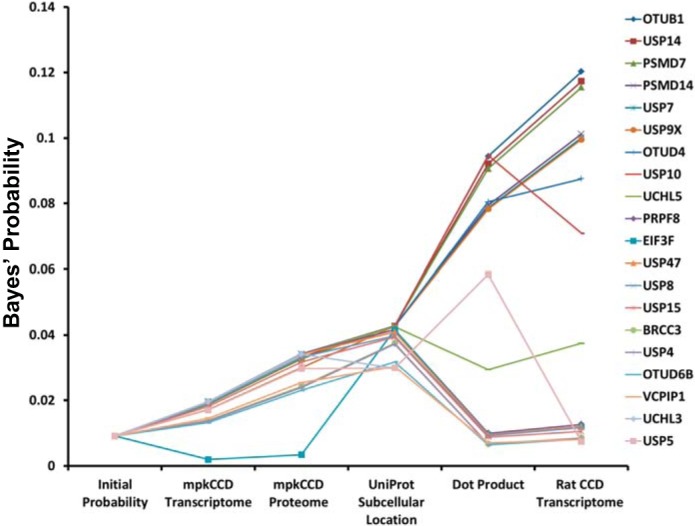
Sequential application of Bayes’ rule using data from indicated sources discriminates DUBs with highest probability of interacting with plasma membrane transporters in renal collecting duct cells. Data for only the 20 highest ranked DUBs are shown (listed in order in the right-hand column).

Table 3.

Description of the top-ranked DUBs from Table 2

Gene Symbol	Ubiquitin Chain Specificity	Cell Component	Class	Physiological Role
OTUB1	Lys-48	cytoplasm	OTU	Regulates RNF128-mediated ubiquitination but does not deubiquitinate polyubiquitinated RNF128; deubiquitinates estrogen receptor alpha (ESR1) (31); overexpression in mesangial cells enhanced the ubiquitination and degradation of decorin (40).
USP14	Lys-48 & Lys-63	proteasome	USP	Proteasome-associated deubiquitinase that releases ubiquitin from the proteasome targeted ubiquitinated proteins; ensures the regeneration of ubiquitin at the proteasome.; undergoes a reciprocal abundance change in the 200,000 g cytosolic fraction [down] and the 200,000 g pellet fraction [up] in mpkCCD cells in response to vasopressin (38); is a major regulator of the proteasome and one of three proteasome-associated deubiquitinating enzymes.
PSMD7	Lys-63	proteasome	JAMM	Acts as a regulatory subunit of the 26S proteasome.
PSMD14	Lys-63	proteasome	JAMM	Component of the 26S proteasome.; identified in or attached to the apical plasma membrane by surface biotinylation in cultured mouse mpkCCD cells (23).
USP7	Lys-48>Lys-63	endosome	USP	Undergoes a reciprocal abundance change in the 1,000 g pellet fraction [down] and the 200,000 g cytosolic fraction [up] in response to vasopressin (38).; protein has a half-life of 28.8 h in mouse mpkCCD cells (28); deubiquitylates and regulates FOXO4 transcriptional activity (36).
USP9X	Lys-29; Lys-33	endosome, plasma membrane, cytosol	USP	Processing of both ubiquitin precursors and of ubiquitinated proteins.; prevents degradation of proteins through the removal of conjugated ubiquitin; vasopressin administration for 7 days increased mRNA abundance of Usp9x in mouse renal inner medulla (9).
OTUD4	Lys-48	endosome?	OTU	Undergoes a reciprocal abundance change in the 200,000 g pellet fraction [down] and the 17,000 g membrane fraction [up] in response to vasopressin (38); development role: interaction with Tsc22d3 (GILZ) to affect BMP signaling (35); GILZ positively regulates ENaC (29).
USP10	Lys-48	endosome	USP	Deubiquitinates CFTR in early endosomes, enhancing its endocytic recycling (4); Usp10 protein has a half-life of 26.2 h in mouse mpkCCD cells in the absence of vasopressin and a half-life of 29.3 h in presence of vasopressin (28).
UCHL5	Lys-48	proteasome	UCH	Associated with the 19S regulatory subunit of the 26S proteasome.

“Physiological Role” is an annotated function obtained from “[FUNCTION]” field of individual UniProt Protein records and the output of BIG (41).

To compare the results using the complements of minimum Bayes’ factors to the prior method of likelihood assignments using assignment tables, we repeated the calculation using discrete likelihoods assigned as described previously (6, 24, 38) (see Supplementary Data Set 2). Among the top 10 DUBs in the current analysis, nine are in the top 10 of the assignment table-based analysis, although the order is changed (OTUB1 > [PSMD14 = USP14 = USP7] > [UCHL5 = OTUD4 = USP10] > PSMD7 > EIF3F > USP9X).

To test the relative information in each data set used for the ranking of DUBs with regard to likelihood of interacting with plasma membrane transporters in collecting duct cells, we carried out a sensitivity analysis in which we dropped each data set from the analysis in turn and recalculated the rankings (Table 4). Dropping each alone had relatively little effect on the ranking, especially for the top-ranked DUBs, indicating consistency among the data sets and a robust methodology.

Table 4.

Sensitivity analysis

Gene Symbol	None Excluded	mpkCCD Transcriptome Excluded	mpkCCD Proteome Excluded	Subcellular Localization Excluded	Dot Product Excluded	Rat CCD Transcriptome Excluded
OTUB1	1	1	1	2	5	2
USP14	2	4	2	3	7	3
PSMD7	3	3	3	4	8	4
USP7	5	7	5	6	2	7
USP9X	6	5	6	7	9	8
OTUD4	7	8	7	8	>10	5
USP10	8	9	8	9	>10	1
UCHL5	9	10	9	>10	3	>10
PRPF8	10	>10	10	1	>10	>10

Values are ranks when the indicated data sets are dropped from the Bayes’ theorem-based calculation.

In addition, we carried further sensitivity analysis to test the effect of doubling and halving the noise threshold assignments (Supplemental Data Set 3). Halving the threshold did not affect the top 10 DUBs. Doubling the threshold resulted in a minor reordering of the top 11. Thus, the calculations did not depend critically on the exact assignments of noise threshold.

DISCUSSION

This paper reports the use of so-called minimum Bayes’ factors to translate continuously distributed experimental data into probabilities for large-scale data integration using Bayes’ theorem (also known as Bayes’ rule). We illustrate the overall approach by addressing a physiological problem, “Which DUBs are most likely to interact with (and deubiquitylate) plasma membrane transporters in the renal cortical collecting duct?” In this application, Bayes’ rule is used to integrate several large-scale data sets from proteomics and transcriptomics studies to rank the DUBs. As an initial step, we curated a comprehensive list of DUBs coded by mammalian genomes and made this information available via a publically accessible website (https://hpcwebapps.cit.nih.gov/ESBL/Database/DUBs/). The list also includes several enzymes that are similar to DUBs but carry out deneddylation or desumoylation.

Bayes’ theorem and integration of data from multiple sources.

In this study, we used Bayes’ theorem to address a physiological question. The method is akin to the thought process that occurs with normal human reasoning. First, by creating a list of all DUBs in mammalian genomes, we have narrowed the possibilities for interaction with plasma membrane transporters to 110 candidates out of ~24,000 protein-coding genes. From there, incorporation of transcriptomics and proteomics data sets from the analysis of whole collecting duct cells further reduced the number of possible candidates by virtually eliminating any DUBs that were not found to be expressed. Then, the analysis used subcellular proteomics data to further narrow the candidates down to a few that are in the same subcellular fractions as plasma membrane transporters and therefore are most likely to encounter these transporters in collecting duct cells. We have used similar methodology in the past to identify protein kinases (6, 38) and ubiquitin E3 ligases (24) most likely to interact with AQP2. The innovation here is a new method to assign values to the likelihood vector based on experimental data. For quantitative data in which a characteristic noise level can be identified, we calculated minimum Bayes’ factors (17, 18) to provide a means of assessing strength of evidence (Table 1). The use of minimum Bayes’ factors obviates the need to assign subjective threshold values in the conversion of experimental values to probabilities. When the calculations were done by the prior method, very similar results were obtained.

Top-ranked DUBs and the reductionist literature on DUBs in epithelial cells.

Table 3 lists the properties of the top-ranked DUBs: OTUB1, USP14, PSMD7, PSMD14, USP7, USP9X, OTUD4, USP10, and UCHL5. With regard to membrane trafficking of transporters, the DUBs known to be associated with endosomal trafficking may be of greatest interest, viz. USP7, USP9X, OTUD4, and USP10. USP7 is strongly expressed in mouse mpkCCD collecting duct cells and has been reported to translocate from membrane fractions into the cytosolic fraction in response to vasopressin in these cells (38). USP9X has been shown to bind to the plasma membrane urea channel UT-A1 in rat IMCD cells although a regulatory role has not been demonstrated (11). Vasopressin administration for 7 days increased mRNA abundance of USP9X in mouse renal inner medulla (9). OTUD4 is known to bind to and interact with Tsc22d3 (also known as “GILZ”) to affect bone morphogenetic protein (BMP) signaling during embryonic development (35). In the collecting duct, GILZ positively regulates ENaC (29). USP10 deubiquitinates CFTR in early endosomes, enhancing its endocytic recycling (3), (4). USP10 protein and mRNA levels are markedly increased by vasopressin in cultured cortical collecting duct cells (mCCDcl cell line), and its overexpression markedly increases ENaC-mediated Na⁺ transport, not by deubiquitylating ENaC, but indirectly by deubuiquitylating sorting nexin 3 (5). Thus, it appears possible that all four of these DUBs play important roles in collecting duct cells to regulate plasma membrane transport proteins including AQP2. In addition to the top ranked DUBs, two additional endosomal DUBs that regulate ENaC recycling have been identified, namely UCHL3 (8) and USP8 (42). These DUBs were ranked 19th and 13th, respectively.

The current study uses a mathematical modeling approach to identify candidates for important regulatory roles in the transport of water and solutes by collecting duct principal cells. The approach takes advantage of the large amount of underinterpreted data from proteomics and transcriptomics studies that already exist. A long-term goal is to extend the approach to other regulatory processes in the cell including those that mediate posttranslational modifications such as protein acetylation, methylation, glycosylation, ribosylation, etc. In the meantime, we hope that the new database of DUBs and the accompanying analysis provide a useful framework for reductionist-oriented studies of cell physiology.

GRANTS

The study was carried out in the Division of Intramural Research of the National Heart, Lung, and Blood Institute (projects HL-001285 and HL-006129, M. A. Knepper).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).