A multivariate computational method to analyze high-content RNAi screening data

Abstract

High-content screening (HCS) using RNA interference (RNAi) in combination with automated microscopy is a powerful investigative tool to explore complex biological processes. However, despite the plethora of data generated from these screens, little progress has been made in analyzing HC data using multivariate methods that exploit the full richness of multidimensional data. We developed a novel multivariate method for HCS, Multivariate Robust Analysis Method (M-RAM), integrating image feature selection with ranking of perturbations for hit identification, and applied this method to a HC RNAi screen to discover novel components of the DNA damage response in an osteosarcoma cell line. M-RAM automatically selects the most informative phenotypic readouts and time points to facilitate the more efficient design of follow-up experiments and enhance biological understanding. Our method outperforms univariate hit identification and identifies relevant genes that these approaches would have missed. We found that statistical cell-to-cell variation in phenotypic responses is an important predictor of ‘hits’ in RNAi-directed image-based screens. Genes that we identified as modulators of DNA damage signaling in U2OS cells include B-Raf, a cancer driver gene in multiple tumor types, whose role in DNA damage signaling we confirm experimentally, and multiple subunits of protein kinase A.

INTRODUCTION

Image-based HC RNAi screening is an effective experimental approach to elucidate the functions of genes on the systems level by investigating the phenotypes of a large number of living cells in culture. HC perturbation assays generate large amounts of high-resolution image-data that is converted into multidimensional numeric data by image processing software. The resulting features are numeric representations of a variety of phenotypic readouts of cells, such as cellular morphology measurements or the intensity of stains of cellular DNA or specific proteins, and permit the identification of genes that are involved in complex biological pathways. Although univariate computational methods, i.e. methods that only make use of a single feature, can suffice to identify a limited number of the most salient hits in HCS, it was conclusively demonstrated that multivariate hit identification methods, i.e. methods that exploit multiple numeric features, outperform univariate methods¹.

A recent review lists over a dozen studies in which multivariate techniques were applied to HC RNAi screens². In the vast majority of these and other relevant studies, multivariate analysis was either a complicated, multi-step procedure that involved an extended sequence of separate computational steps for hit identification and dimensionality reduction^3–7, lacking non-greedy/ad-hoc feature selection^8,9, or both^10–12.

As a potential result, the majority of researchers pursuing HCS still rely on univariate methods to analyze multidimensional screening data. Analyzing multidimensional data with univariate methods is a self-imposed bottleneck that makes HC assays factually low-content. A meta-analysis of 118 published papers to investigate how many features were actually used for hit identification in different HC screens found that even as recently as 2012 only 25% of HC screens were analyzed using multivariate methods, rendering the information content of these experiments much lower than their potential¹³. We believe that the reason for the underwhelming popularity of multivariate methods in HCS is their extensive complexity. A powerful but easy-to-use multivariate method would encourage more researchers to get more actual content out of their HC screens.

Moreover, to gain real insight into the biological mechanisms of identified hits from these HC screens, secondary screens and follow-up experiments are required. The majority of dimensionality reduction methods previously used in HCS, such as in factor analysis¹⁴ or principal component analysis⁵, construct novel “meta-features” by linear combination of the original features. While these techniques successfully reduce the screening data’s dimensionality, they do not necessarily reduce the actual number of features (and therefore the number of phenotypic readouts) required for hit identification. Hence, even after dimensionality reduction, a large number of features needs to be re-screened in secondary screens. Selecting the minimum number of the most informative original features at the most informative time points would greatly reduce the effort in biological follow-up experiments since only a subset of the original phenotypic readouts at a limited number of time points would have to be recorded without any significant loss of important biological information.

To address these challenges, we developed M-RAM (Multivariate Robust Analysis Method), a novel computational technique for the multivariate analysis of biological perturbation screens and applied this method to a HC screen recently performed in our laboratory to discover novel regulators of the DNA damage response (DDR)¹⁵. M-RAM consists of two components: dRIGER, which condenses the effects of all of the shRNAs for any particular gene into a single value for each of the features analyzed in the images, and logistic regression paired with the Least Absolute Shrinkage and Selection Operator (Lasso), an effective, integrated regularization method for feature selection¹⁶. M-RAM predicts hits and simultaneously selects a limited number of the most informative original features and time points in one single step. Therefore, this method is fast, elegant, and easy to use. We anticipate that M-RAM will find wide acceptance in the HCS community due to its simplicity and interpretability.

MATERIALS AND METHODS

High-content screen

To investigate new aspects of the DNA damage response in molecular detail, an RNAi-based HC screen was performed, as described previously¹⁵. In brief, U2OS cells in 44,384 well plates (Supp. Tab. 1) were infected with varying numbers of lentiviral shRNAs (Supp. Fig. 1), irradiated with 10 Gy of ionizing radiation (IR), and immunostained for phenotypic readouts of DNA double-strand breaks (histone H2AX phosphorylated on serine-139, γH2AX), progression through the cell cycle (DNA content), mitotic entry (phosphohistone H3, pHH3), apoptotic cell death (cleaved caspase 3, CC3), and cytoskeletal changes within cells (tubulin) immediately before IR (0h) and at 1, 6, and 24h after IR. Furthermore, each screened plate contained varying numbers of positive controls (caffeine and ATM) and negative controls (GFP, RFP, and lacZ) (Supp. Tab. 2) that were used to normalize between plates. For each screened well, a robotic Cellomics Arrayscan automated microscope outfitted with Zeiss optics acquired six non-overlapping images in four fluorescent channels at four time points. A 20× Plan Neofluar objective lens with N.A. 0.4 was used for all images, resulting in typical nuclei sizes between 20 and 100 pixels, and damage foci between two and six pixels (see Supp. Mat.). As a result, over 1.2 million images that captured over half a billion single cells and nuclei were generated. Assay validation suggests high reproducibility of our screen (Supp. Fig. 2).

Directional RIGER

A new, extended derivation of RNAi Gene Set Enrichment (RIGER)¹⁷, directional RIGER (dRIGER), was used to transform normalized (see Supp. Mat.) shRNA-level data into gene-level data by computing directional normalized enrichment scores (dNES). dRIGER quantifies both the magnitude and the consistency of the phenotypic effects of multiple shRNAs targeting the same specific gene using a Kolmogorov-Smirnov motivated running-sum test statistic. Multiple shRNAs inducing a moderate but consistent phenotypic effect receive a higher dNES than a set of highly inconsistent shRNAs with one very strong outlier. Briefly, dRIGER, like RIGER, first rank-orders all screened shRNA values from largest to smallest and sequentially traverses each rank in this list from beginning to end (top to bottom) to compute a list of positional ES (one positional ES for each rank). A rank’s positional ES reflects how many shRNAs from the set targeting the gene of interest were previously encountered in the list and how many are still ahead in the list. This procedure quantifies whether the shRNAs targeting a gene of interest are clustered towards the top/beginning of the list. In dRIGER, but not in RIGER, the rank-ordered list is then similarly traversed from end to beginning (bottom to top) to compute a second list of positional ES that quantify whether the shRNAs of interest are clustered towards the bottom/end of the list. Therefore, two positional ES, henceforth called directional positional ES, are computed for every single rank. Finally, the single largest directional positional ES is normalized as in Gene Set Enrichment Analysis¹⁸ and selected as dNES. If the dNES was found by traversing from end to beginning (bottom to top), its sign is set to negative to indicate bottom-of-list enrichment. dNES were computed for each feature and each gene at each time point.

Mathematically, positional hit scores (P_H) and miss scores (P_M) were calculated at each position i in a rank-ordered list of length L based on the ranks of the screened shRNAs targeting the gene of interest, G_f,t = (h₁, …, h|_Gf,t|), where each h ∈ G_f,t represents the rank of an shRNA targeting gene G in the rank-ordered list for feature f at time point t, and |G_f,t| refers to the number of shRNAs targeting gene G:

$$P_H\left(G_{f,t},i\right)=\sum _{h_{j\le i}\in G_{f,t}}\frac{h_j}{{\sum }_{h\in G_{f,t}}h}$$ (1)

$$P_M\left(G_{f,t},i\right)=\sum _{h_{j\le i}\notin G_{f,t}}\frac{1}{L-\left|G_{f,t}\right|}$$ (2)

Similarly, inverse positional ES were computed to test for rank enrichment at the bottom/end of the rank-ordered list using an inverse shRNA rank set $G_{f,t}^I$ where

$$G_{f,t}^I=L-G_{f,t}+1$$ (3)

Finally, dES were computed as

$${\epsilon }_d\left(G_{f,t}\right)=max\left[max\left({\overrightarrow{P}}_H\left(G_{f,t}\right)-{\overrightarrow{P}}_M\left(G_{f,t}\right)\right),max\left({\overrightarrow{P}}_H\left(G_{f,t}^I\right)-{\overrightarrow{P}}_M\left(G_{f,t}^I\right)\right)\right]$$ (4)

and multiplied with −1 if the inverse directional ES was greater than the directional ES. A Java implementation of the dRIGER algorithm is available at http://yaffelab.mit.edu/driger/.

Logistic regression and Lasso

A logistic regression model with Lasso regularization¹⁶ (Lasso model) was used for integrated feature selection and hit identification. Feature weights were computed as

$$\text{arg}\underset{\overrightarrow{\beta }}{\text{min}}\sum _{i=1}^{N}log\left(1+e^{-y_i\overrightarrow{\beta }{\overrightarrow{x}}_i}\right)+\lambda \sum _{j=1}^F\left|{\beta }_j\right|$$ (5)

where β⃗ = (β₁, …, β_F) are the weights of the F features, (y_i, …, y_k) are the labels of the training set with K genes, x⃗_i = (x_i.1, …, x_i.F) are the dNES of all features for gene i in the training set, λ is the Lasso tuning parameter, and log refers to the decadic logarithm here and in the rest of this paper. If no convergence was achieved, the positive observations in the training set were up-sampled two-fold and the model was refit. The optimal λ was identified by trying 100 different λ from a geometric sequence of values between 1 and 10⁻⁴. The Lasso then selected the λ that produced the model with the minimum expected model deviance (the optimal model) using tenfold cross validation. The model deviance was measured using the mean squared error (MSE), which is defined as

$$\mathit{MSE}=\frac{1}{n}\sum _{i=1}^n{\left({\widehat{Y}}_i-Y_i\right)}^2$$ (6)

where n is the number of observations in the test data, Ŷi is the model’s prediction for observation i, and Y_i is the actual label of observation i. A suboptimal, larger λ was selected to produce a sparser Lasso model. To compute this suboptimal λ, the standard error of the model deviances for all λ was computed. Then, the largest λ that produced the model with the largest deviance within one standard error of the minimum deviance was chosen as the λ for the selective model. The selective model tolerated a worse fit in exchange for fewer selected features. Finally, each selected set of features formed a readout profile whose statistical significance was evaluated based on the profile’s entropy (see Supp. Mat.)

Network analysis

SteinerNet¹⁹, an implementation of the Prize-Collecting Steiner Tree (PCST) algorithm, was used to produce a focused view of a protein-protein interaction network of interest. Interactions and genes were annotated with edge costs and node prizes, respectively, and fed into SteinerNet (see Supp. Mat.).

RESULTS AND DISCUSSION

To identify novel molecular components of the DNA damage response after IR, we performed an image-based HC RNAi screen, looking for unknown DDR modulators in seven functional categories (kinases, phosphatases, chromatin modifiers, RNA binding proteins, DDR modulators, oncogenic regulators, and miRNA machinery). For this multidimensional HC assay, we screened five distinct phenotypic readouts (DNA content,γH2AX, pHH3, CC3, and tubulin) at four time points (before IR, and 1, 6, and 24h after IR) to systematically quantify both temporal and spatial changes in the DDR, thus enabling a sophisticated understanding of the signal transduction network that governs the cell’s response to DNA damage.

dRIGER transforms shRNA-level into gene-level data

In order to capture the consistency of the differential knock-down effects of multiple shRNAs targeting the same specific gene, we developed dRIGER, an extension of the GSEA-based RIGER^17,18. We developed this method because RIGER was originally designed for continuous signal-to-noise ratios or (log) fold-changes. Inherently, RIGER does not capture the enrichment of ranks of shRNAs targeting the same specific gene towards the bottom of a rank-ordered list of all screened shRNAs. Our new method, dRIGER, computes directional normalized enrichment scores (dNES) to quantify the enrichment of ranks of shRNAs targeting the same specific gene towards both the top and the bottom of a rank-ordered list of all screened shRNAs, therefore capturing the consistency of both increased and decreased phenotypic knock-down responses.

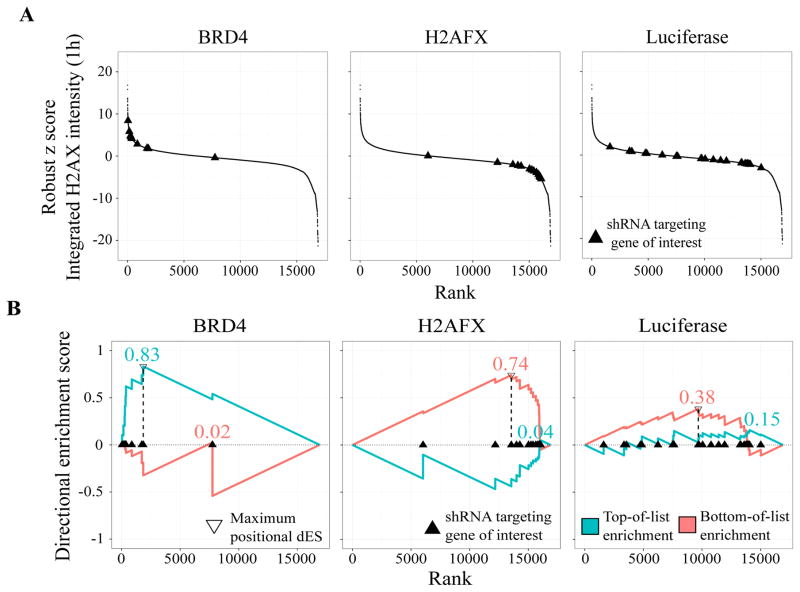
We applied dRIGER to all genes on all screened plates to compute dNES for each feature at each time point. To demonstrate how dRIGER captures both statistical location and statistical spread of differential knock-down phenotypes of shRNAs targeting specific genes, we computed dNES for the integrated γH2AX intensity feature 1h after IR for a small number of selected genes. We chose Brd4, H2AFX, and the negative control luciferase because the phenotypic responses to H2AFX and Brd4 knock-down are well characterized^15,20. As expected, knockdown of H2AFX substantially decreased recorded γH2AX intensity 1h after IR and Brd4 knockdown substantially increased it (Figure 1A). Although the majority of shRNAs targeting Brd4 and H2AFX induced a consistent phenotypic effect, outliers existed in both cases. Negative control knock-downs induced a wide range of phenotypic effects, from increased to decreased γH2AX intensities (Figure 1A). dRIGER effectively captured these variable phenotypic effects and assigned high dNES to the H2AFX and the Brd4 knock-down, but a low dNES to the negative control knock-down (Figure 1B). dRIGER successfully quantified statistical location and statistical spread–or the lack thereof–for known DDR modulators and negative controls. At the same time, dRIGER transformed shRNA-level data (67,584 rows) into gene-level data (10,892 rows), which led to a more than six-fold reduction of our data’s dimensionality. All subsequent analyses were performed on gene-level data.

Figure 1.

Directional RNAi Gene Enrichment Ranking (dRIGER) captures the consistency of differential effects of multiple shRNAs and transforms shRNA-level data into gene-level data.

(A) S-curves of shRNAs targeting the genes Brd4, H2AFX, and the negative control luciferase, for integrated γH2AX intensity 1h after IR. As expected, knock-down with most shRNAs targeting the chromatin modifier Brd4 leads to vastly increased γH2AX intensity while most shRNAs targeting H2AFX have the opposite knock-down effect. shRNAs targeting the negative control luciferase surprisingly induce a wide variety of different phenotypic responses, including increased and decreased γH2AX intensities.

(B) Directional ES (dES) of Brd4, H2AFX, and the negative control luciferase for integrated γH2AX intensity 1h after IR. dRIGER rewards strong, consistent knock-down phenotypes with high dES. shRNAs targeting Brd4 and H2AFX are enriched at the top and bottom of the rank-ordered list of all screened shRNA respectively, resulting in high dES. shRNAs targeting luciferase are widely spread over the entire list, resulting in a substantially lower dES.

Feature selection with the Lasso

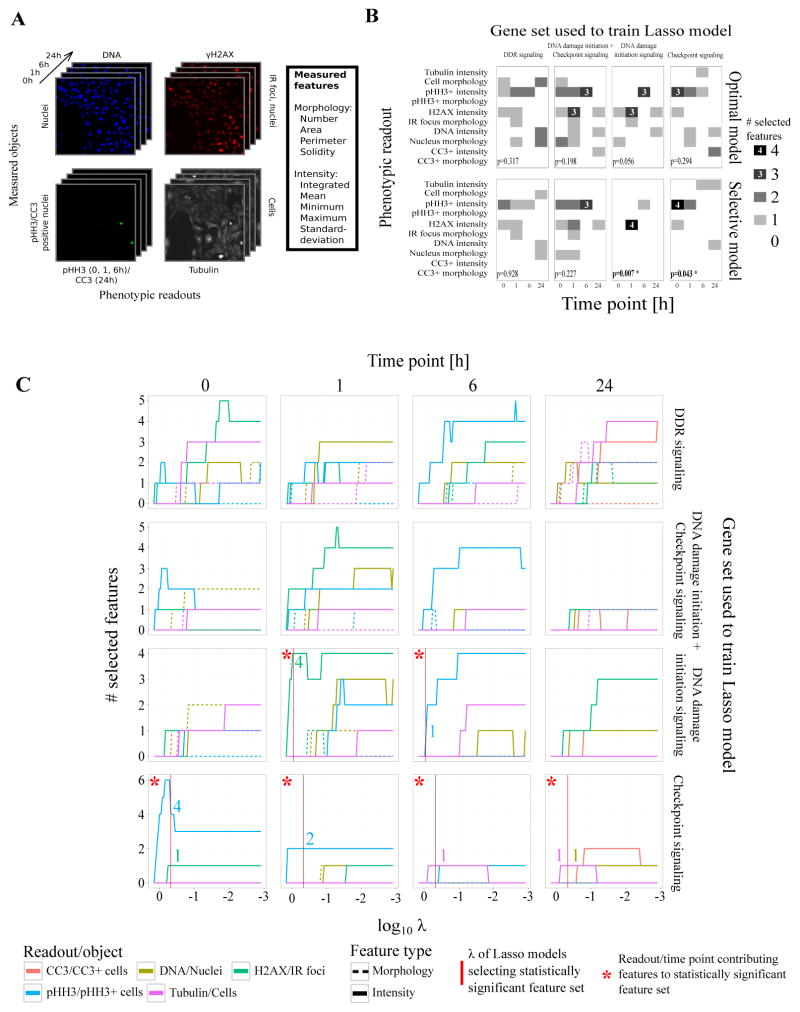
As M-RAM’s explicit purpose is to generate more reliable hypotheses for follow-up experiments, we wanted to select the phenotypic readouts and time points for which these follow-up experiments would prove most successful from the set of all screened readouts and time points (Figure 2A). To select the features that were most predictive for DDR modulators and discard features mainly capturing noise, we used a logistic regression model with Lasso regularization (Lasso model).

Figure 2.

Logistic regression with Lasso regularization selects the most informative phenotypic readouts and time points that best capture the differences between a knocked-down gene and negative controls.

(A) Images of four fluorescent channels recorded by automated microscopy capturing five phenotypic readouts at four time points. Each readout is used to identify different biological objects (DNA: nuclei; γH2AX: IR-induced foci; pHH3/CC3: pHH3/CC3 positive cells; tubulin: cells). Cell Profiler was used to generate 60 numeric features capturing morphological and intensity characteristics of each recorded object.

(B) Readout profiles for feature sets selected by the optimal and selective Lasso models for four different sets of genes. A readout profile describes how many features were selected for each phenotypic readout at each time point. Only functionally coherent gene sets (DNA damage initiation signaling and checkpoint signaling) led to models that selected statistically significant feature sets with a confidence level of 95%. Readout-time point combinations with more than two selected features were additionally labeled for improved readability. P-values reflect the statistical significance of a readout profile’s Shannon entropy.

(C) Readout traces for different Lasso models as function of the tuning parameter λ at four time points (0, 1, 6, 24h). Colored lines represent the number of selected features per readout for any given λ. They indicate what readouts and time points best capture the phenotypic characteristics that differentiate knocked-down genes from negative controls. As λ increases, fewer features are selected. For DNA damage initiation signaling genes, the γH2AX readout at the 1h time point and the pHH3 readout at the 6h time point are most predictive.

First, we wanted to investigate whether a feature set existed that was able to capture a putative “über-phenotype” shared among all the knock-downs of a large set of functionally diverse DDR modulators. We trained our Lasso model on a training set consisting of 17 genes known to play a prominent role in various aspects of the DDR (Supp. Tab. 4) and three negative control genes (GFP, RFP, lacZ). To determine the optimal Lasso tuning parameter λ, we ten-fold cross-validated our model and identified the minimum-deviance model (the optimal model) by selecting the λ that produced the model with the optimal fit (Supp. Fig. 4). We then selected a larger tuning parameter λ to produce an even sparser model with suboptimal fit (the selective model). The models selected sixteen and ten out of the 60 features respectively (Supp. Fig. 5). Surprisingly, in both cases the extracted readout profile, a tabular representation of the selected features grouped by phenotypic readout and time point, was not statistically significant with a confidence level of 95% (Figure 2B).

We hypothesized that the different and diverse functions of the various DDR modulators used as positive observations in the Lasso model’s training set were the reason for the lack of statistical significance of the selected feature set, and postulated that our predictive models might be better at successfully capturing knock-down phenotypes of more functionally coherent gene sets. Knock-down of genes that are functionally coherent–i.e. participate in a similar process within the larger set of molecular events which constitute the DDR–is likely to induce similar phenotypic responses that can be captured by automated microscopy and subsequently numerically captured in the extracted features. We therefore trained Lasso models for DNA damage initiation signaling, checkpoint signaling, and, as a stringent control, the union of these two, to test our hypothesis. As before, GFP, RFP, and lacZ served as negative observations in the training sets. All Lasso models converged (Supp. Fig. 4), selecting varying numbers of features (Supp. Fig. 5) from different phenotypic readouts (Figure 2C). However, only the readout profiles identified by the selective model for DNA initiation signaling alone and checkpoint signaling alone were statistically significant with a confidence level of 95% (Figure 2B). We therefore focused all subsequent analyses on the selective models. The selective model for DNA initiation signaling identified five features (Table 1), resulting in a dimensionality reduction by a factor of 12. Four of these five features belonged to the γH2AX readout 1h after IR. This statistically significant feature set re-confirmed the extreme importance of γH2AX intensity as a marker of DNA damage initiation signaling activity, consistent with our prior selection of γH2AX metrics for a more basic analysis of the high-throughput RNAi screen for DDR genes¹⁵.

Table 1.

Features selected by the selective Lasso models trained on DNA damage initiation and checkpoint signaling genes. Scaled weights represent feature weights that were normalized to sum to 100 for better readability.

DNA damage initiation signaling
Readout	Time	Feature	Weight	Scaled weight
H2AX	1	Maximum nucleic intensity	0.039715	46
		Standard deviation of foci intensity	0.022996	27
		Standard deviation of nuclei intensity	0.012257	14
		Number of foci	0.010534	12
pHH3	6	Number of pHH3+ nuclei	0.000333	1

Checkpoint signaling
Readout	Time	Feature	Weight	Scaled weight
H2AX	0	Number of foci	0.007222	3
pHH3	0	Standard deviation of pHH3+ nuclei	0.047811	22
		Minimum nucleic intensity	0.015302	7
		Maximum pHH3+ nucleic intensity	0.014266	7
		Mean nucleic intensity	0.004452	2
	1	Number of pHH3+ nuclei	0.057373	26
		Integrated pHH3+ nucleic intensity	0.042539	19
DNA	24	Integrated nucleic intensity	0.006422	3
Tubulin	6	Minimum cellular intensity	0.013966	6
	24	Mean cellular intensity	0.011349	5

Surprisingly, only two features of the five selected features were canonical features likely to be picked manually. These two features, the number of γH2AX foci 1h after IR and the number of pHH3 positive nuclei 6h after IR, received the lowest feature weights in the Lasso model. The three remaining features, all γH2AX features 1h after IR (maximum nucleic intensity, standard deviation of IR foci intensity, and standard deviation of nucleic intensity), received significantly higher weights (Table 1). These features either directly captured information about the statistical spread of γH2AX intensities (standard deviations) within segmented nuclei or foci or were highly sensitive to outliers and increased statistical spread (maximums). This analysis reveals that the statistical spread of intensities within each object better captured knock-down phenotypes of DNA damage initiation signaling genes than estimators for statistical location such as average γH2AX intensity.

One potential cause for the importance of statistical spread estimators over statistical location estimators is the wide variety of RNAi-induced changes on the single-cell level. The microenvironment of cells that are subject to RNAi can be a potential source of the stochasticity of differential phenotypic responses¹². Additional contributors to this intra-nuclear or intra-foci variation in γH2AX intensity include varying levels of shRNA integration and expression or stochastic effects of equally expressed shRNAs on protein expression, particularly if these effects result in local alterations in chromatin structure or DNA damage repair efficiency. Indeed, image analysis on the single cell level visually confirmed a high variability of phenotypes of single cells that were targeted by the same shRNA²¹. Imperfect knock-down and puromycin selection can also lead to multiple subpopulations of cells that exhibit more variable and convoluted phenotypic effects at the single cell level. We therefore propose that features that capture statistical spread might be able to better quantify the resulting variability of knock-down effects and thus better identify hits in RNAi screens.

It should be noted that the entirety of phenotypic information in a HC screen can only be captured on the single-cell level by analyzing distributions of populations of individual cells in screened wells. However, as each well frequently contains large numbers of individual cells, single-cell analysis would potentially increase the computational effort required to analyze the data by multiple orders of magnitude. We consider statistical spread in combination with statistical location as a good compromise to estimate characteristics of cell population distributions in HC screens such as ours where the richness and amount of data render single-cell analysis impractical.

The selective Lasso model for DNA damage initiation signaling did not select γH2AX intensity features at the 6h time point, meaning that γH2AX features did not reliably differentiate DNA damage initiation signaling genes from negative control genes at this time point. In our previous study¹⁵, we simply hand selected three image features (integrated γH2AX intensity, number of IR foci per nucleus, and mean IR foci area) at 1h and 6h after IR as a metric to rank chromatin modifier genes using quartile thresholding. This basic thresholding method selected Brd4 as top hit, as did M-RAM. However, some of the chromatin modifier genes ranked in the top and bottom quartile using these metrics were not in the top or bottom quartile of M-RAM-ranked genes. Since half of the thresholds in our previous analysis were applied to imaging features from the 6h time point, a time point shown by M-RAM to be entirely unpredictive, the lack of perfect agreement in gene ordering between these two lists can be attributed to the ad-hoc nature of our selection process for image features and time points used in our previous analysis.

To learn if a simple method like quartile thresholding would exhibit increased performance after automatic feature selection, we dropped the 6h time point as suggested by our model. Quartile thresholding of the three features at the 1h time point alone led to a relative increase in sensitivity by 11.2% and a relative decrease in specificity by 0.53% as compared to thresholding at both time points. Therefore, even simple hit identification methods such as quartile thresholding may benefit from a priori feature selection.

The selective Lasso model for checkpoint signaling also produced a statistically significant readout profile with a confidence level of 95% (Figure 2B). 60% of the profile’s features were derived from the pHH3 readout, and two thirds of these specifically captured pHH3 before IR although the highest scoring features were selected at the 1h time point (Table 1). The high prevalence of pHH3 features before IR likely reflected the importance of CHEK1 and CHEK2 in cell cycle control even in the absence of exogenous DNA damage. This finding suggests that intrinsic DNA damage in an unperturbed cell cycle in these cells is already sufficient to control cell cycle progression rates through CHEK1 and CHEK2.

Furthermore, we investigated whether images of cells treated with shRNAs targeting genes in the training set for DNA damage initiation signaling (H2AFX, ATM) and cells treated with shRNAs targeting genes in the training set for checkpoint signaling (CHEK1, CHEK2) would have similar phenotypes within their respective functionally coherent groups. Indeed, knock-down of γH2AX and ATM led to a decrease in IR-induced γH2AX foci 1h after IR, while knock-down of CHEK1 and CHEK2 resulted in an increased number of mitotic cells (Supp. Fig. 6).

The readout profiles of the control model trained on the union of DNA damage initiation and checkpoint signaling genes were not statistically significant (Figure 2B). Therefore, we conclude that statistical significance of the selected feature sets depended on functional coherence of the positive observations in the training sets. This finding is important because it shows that broad computational approaches to identify complex phenotypes cannot be blindly performed using a diverse set of genes which are important in various different parts of a biological process. Instead, only genes that function together to control a limited portion of a complex phenomenon are likely to be useful in training predictive models that capture their more well defined phenotypes. To capture a complex biological process in its entirety it will likely be necessary to use smaller subsets of the whole, each representing a functionally coherent subcomponent.

M-RAM identifies DDR modulators missed by univariate methods

We used the selective Lasso model for DNA damage initiation signaling with the selected feature set (Table 1) to identify novel DDR modulators. Intuitively, this Lasso model ranked all screened genes based on how much their knock-down phenotype resembled the knock-down phenotypes of genes in the DNA damage initiation signaling training set (Supp. Tab. 4). Genes were ranked from strongest phenotypic resemblance (intuitively corresponding to low γH2AX 1h after IR) to strongest opposite phenotype. Genes at the top and bottom of the list are therefore likely to be true ‘hits’. In agreement with this, the top ten and bottom ten ranked genes (Table 2) contained numerous canonical DDR signaling components, many of which were not part of the training set.

Table 2.

Best-ranked hits that resemble the knock-down phenotype of DNA damage initiation signaling genes (top) or the opposite phenotype (bottom).

Top ten hits
Gene symbol	Gene name	M-RAM rank	2BHM rank
H2AFX	Histone H2A.X	1	120
ATM	Ataxia telangiectasia mutated	2, 5	203, 1232
PRKACG	cAMP-dependent protein kinase catalytic subunit γ	3	537
TEX14	Testis expressed 14	4	2338
BRCA2	Breast cancer 2	6	8
PRKAR1A	cAMP-dependent protein kinase type I-α regulatory subunit	7	442
EXO1	Exonuclease 1	8	11
CCND1	Cyclin D1	9	18
CHEK2	Checkpoint kinase 2	10	17

Bottom ten hits
Gene symbol	Gene name	M-RAM rank	2BHM rank
BRD4	Bromodomain-containing protein 4	1, 4	12, 49
EPHA2	EPH receptor A2	2	1
GRK1	Rhodopsin kinase	3	254
PI4K2A	Phosphatidylinositol 4-kinase type 2 α	5	246
PFKFB1	6-phosphofructo-2-kinase/fructose-2,6-biphosphatase 1	6	98
PIKFYVE	PI-3-phosphate/PI 5-kinase, type III	7	25
PRKCI	Protein kinase C ι	8	633
MID2	Midline 2	9	29
BRAF	V-raf murine sarcoma viral oncogene homolog B1	10	82

To establish a baseline for comparisons with M-RAM, we applied a popular method for identifying hits in HC RNAi screens, the 2nd best hairpin method (2BHM) (see Supp. Mat.), to our normalized HC data set. Using 2BHM on the integrated γH2AX intensity 1h after IR ranked the negative control lacZ as top hit (Supp. Fig. 8). Moreover, other negative control shRNAs were also widely spaced over the rank-ordered list of second best shRNAs.

No sound justification exists to select the second best shRNA, and not the best, third best, or any other. Selecting one arbitrary, single shRNA makes the implicit assumption that all other shRNAs with stronger or weaker effects do not contribute useful information. A single shRNA, by definition, can only be a measure of statistical location but not statistical spread. High spread implies inconsistent knock-down effects that should decrease the confidence in an identified hit. This highly important aspect of hit identification is completely lost using 2BHM but captured by shRNA aggregation methods such as dRIGER.

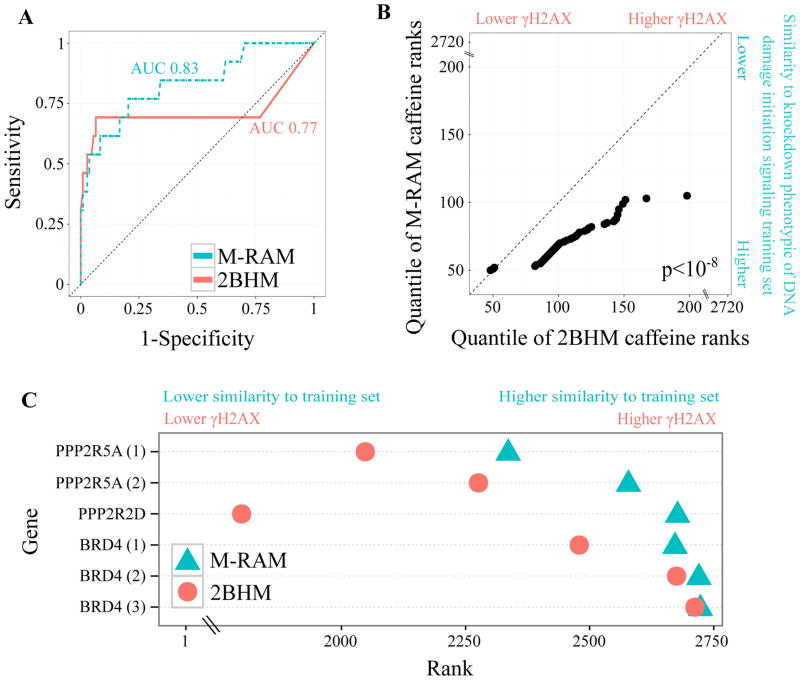
To compare M-RAM’s and 2BHM’s classification performance, we performed leave-one-out cross validation on the training set of DNA damage initiation signaling genes. The selective Lasso model outperformed 2BHM (area under the receiver operating characteristic (ROC) curve (AUC) 0.83 and 0.77 respectively) (Figure 3A). M-RAM consistently ranked independent caffeine controls closer to the top of the hit list (where one would expect knockdowns that decrease γH2AX) than 2BHM (Figure 3B). Additionally, it ranked Brd4 and selected protein phosphatase 2 (PP2A) subunits²² closer to the bottom of the list (where one would expect knock-downs that increase γH2AX) than 2BHM (Figure 3C).

Figure 3.

M-RAM outperforms 2BHM.

(A) ROC curve comparing M-RAM’s (selective Lasso model for DNA damage initiation signaling) and 2BHM’s performance using leave-one-out cross validation. M-RAM provides superior sensitivity and specificity. AUC refers to area under the receiver operating characteristic (ROC) curve.

(B) Q-Q plot comparing the ranking of independent caffeine controls by M-RAM and 2BHM. M-RAM ranks the independent caffeine controls more accurately than 2BHM (closer to zero which indicates lower γH2AX and higher similarity to knock-down of genes belonging to DNA damage initiation signaling). Additionally, M-RAM ranks the controls more precisely (ranks provided by M-RAM have less than half the statistical spread than ranks provided by 2BHM). The p-value was computed using a Wilcoxon rank-sum test.

(C) Dot plot of Brd4 and selected PP2A subunit ranking as provided by M-RAM and 2BHM. As in (B), M-RAM ranks the genes more precisely and more accurately than 2BHM. Brd4 and PPP2R5A are displayed more than once because they were independently screened on multiple different plates.

Lastly, we used dRIGER to rank screened genes based on their integrated γH2AX intensity 1h after IR to investigate whether dRIGER provides potential performance gains over 2BHM, even in the absence of systematic feature selection. Top and bottom of the list of screened genes ranked by their dNES were heavily enriched in genes known to be involved in the DDR and oncogenic processes (Supp. Tab. 6). Additionally, dRIGER alone ranked independent caffeine controls better than 2BHM but worse than M-RAM (Supp. Fig. 9). Therefore, although dRIGER alone outperforms 2BHM, M-RAM provides even better performance than dRIGER due to its integrated feature selection step.

Network analysis puts identified hits into context

To generate even more reliable hypotheses about how the hits previously identified by M-RAM potentially interact among themselves and with known DDR modulators, we investigated how these hits could be tied into known protein-protein interaction networks that were enriched with kinase-substrate predictions. We anticipated that the most tightly connected network structures would suggest potential mechanisms of DDR signaling. For this purpose, we employed the Prize-Collecting Steiner Tree (PCST), a network flow algorithm successfully applied in the biological domain²³ by using M-RAM to assign prize values to genes in the shRNA screen.

First, we constructed a base network from four sources, a prior knowledge network (PKN), the screened genes, the filtered STRING interactome, and Scansite²⁴ predictions. We defined a small, tightly connected network, the PKN, that represented well established DNA damage initiation signaling genes^20,25,26 (Supp. Fig. 10). We speculated that genes closely connected to the PKN were more likely to play a role in DNA damage initiation signaling. In order to connect putative M-RAM hits with the PKN, we filtered the STRING interactome²⁷ for experimentally verified, high-confidence interactions. The filtered STRING interactome had 9,857 nodes and 483,940 edges. We placed our screened genes and the PKN in this large network (see Methods). To expand our network analysis beyond static protein-protein interactions, we used 70 position-specific scoring matrices (PSSMs) in Scansite to predict putative substrates of kinases and putative binding partners of proteins for which PSSMs were available. 4,517 high-confidence interactions were predicted and added to our base network. Because the resulting base network was of prohibitively high complexity, we reduced it to screened genes and STRING interactome genes that were closely connected to the PKN. The extracted subnet had 4,719 nodes (half of the number of the base network’s nodes) and 52,834 edges (nearly ten times fewer edges than the base network), representing a substantial reduction of complexity.

Since the filtered base network was still far too complex to allow its intuitive interpretation and visualization, we employed the PCST to extract the most confident subnetwork. We rewarded high confidence in a gene with high node prizes, and high confidence in an interaction with low edge cost. The PCST extracted a network consisting of the six genes from the PKN, 35 screened genes, and six genes from the filtered STRING interactome which we visualized with a hive plot²⁸ (Supp. Fig. 11). Three of the extracted screened genes were originally ranked below 100 by the selective Lasso model. All three were previously described as being involved in the DDR (Supp. Tab. 7). Furthermore, all six genes extracted from the filtered STRING interactome were implicated in the DDR (Supp. Fig. 11; Supp. Tab. 8).

B-Raf is involved in the DDR

M-RAM identified the knock-down phenotype of B-Raf in U2OS cells as similar to that of Brd4 (Table 2, bottom ten hits), a chromatin modifying protein whose knock-down we recently showed results in expanded chromatin architecture and enhanced DNA damage signaling with elevated γH2AX foci intensity⁵. Importantly, B-Raf’s knock-down phenotype was ranked significantly worse by 2BHM because no single shRNA induced an exceptional signal although the vast majority of its shRNAs had a highly consistent, positive effect (Supp. Fig. 7).

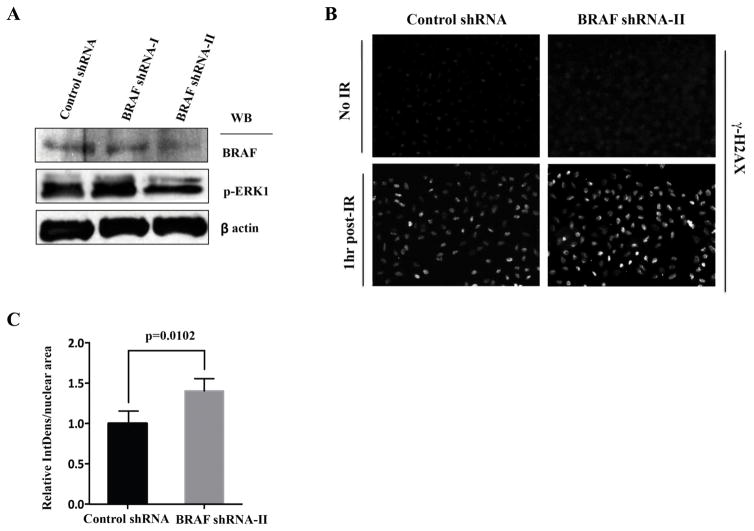
To independently verify the knock-down effects of B-Raf on γH2AX foci intensity, we used additional shRNA sequences against B-Raf that differed from those used in the high-throughput screen (see Supp. Mat.). Note that M-RAM’s selection of the most informative phenotypic readouts at the most informative time points vastly reduced the effort of follow-up experiments by allowing us to focus on the γH2AX readout at the 1h time point. shRNA-II, but not shRNA-I, resulted in a 74% reduction in B-Raf protein levels and a corresponding decrease in the levels of phospho-Erk (Figure 4A). Importantly, the B-Raf shRNA-II knock-down cells showed a marked increase in γH2AX foci intensity at 1h following application of 10 Gy of IR (Figure 4B and C) when compared to the control shRNA knock-down cells at the same time point after IR. Quantification of the resultant images verified a statistically significant ~40% increase in the intensity of γH2AX foci per nucleus or per nuclear area (thereby excluding the possibility that the B-Raf knock-down caused an increase in γH2AX indirectly through changing the nuclear size).

Figure 4.

Validation of B-Raf as a modifier of the DDR in U2OS cells.

(A) U2OS cells were infected with retroviruses encoding control and B-Raf-directed shRNAs, harvested 72h after the final infection, and lysates analyzed for B-Raf and phosphor-Erk levels by immunoblotting.

(B) Control and BRAF-shRNA-II infected cells were fixed before and 1h after irradiation with 10 Gy of IR, and stained for γH2AX.

(C) γH2AX staining intensity was quantified using four representative fields containing greater than 100 nuclei total, from three independent experiments. Shown are integrated γ^H2AX intensity per nuclear area, normalized to that measured in the control shRNA-infected cells at 1 h after IR. Values are mean ± SEM, with p-values calculated using a Student’s unpaired t-test.

M-RAM also identified DNA damage signaling alterations following knock-down of various components of protein kinase A (PKA) complexes. These components were missed by 2BHM for the same reasons described above (Supp. Fig. 7). Knock-down of the PKA less active catalytic subunit γ²⁹ and PKA type I-α regulatory subunit closely resembled the knock-down phenotype of DNA damage initiation signaling components (Table 2, top ten hits), whereas knock-down of the more active catalytic α and β subunits displayed the opposite phenotype, showing increased γH2AX and DNA damage signaling (Supp. Tab. 5). While the role of PKA signaling in the DDR is complex and remains poorly understood, our findings are consistent with two recent studies. Cho et al. (2014)³⁰ reported that PKA activity stimulates PP2A to dephosphorylate γH2AX and suppress ATM signaling after IR, while Jarrett et al. (2014)³¹ showed that PKA phosphorylation of ATR promotes recruitment of xeroderma pigmentosum complementation group A (XPA) to UV-induced DNA damage sites to enhance DNA repair and clear DNA lesions. Both of these studies can rationalize the lower levels of γH2AX signals when the net catalytic activity of PKA complexes within the cell is high, and the converse when it is low. Additional studies, however, are clearly required to more thoroughly characterize the involvement of specific PKA subcomplexes in the DDR.

In conclusion, we conducted an image-based HC RNAi screen to identify novel regulators of the DDR. We then proceeded to develop M-RAM, a novel computational method to tap the full potential of this and similar HC screens. Employing dRIGER, an enhanced version of RIGER, we significantly reduced the dimensionality of the screening data. We transformed shRNA-level data into gene-level data, capturing consistency and variability of differential shRNA effects, and achieved a nearly seven-fold reduction in dimensionality. Lasso models selected the most predictive features at the applicable time points. In case of DNA damage initiation signaling, the feature selection step resulted in a more than fifty-fold dimensionality reduction. Functional coherence of training sets–that is, the specific selection of genes for a training set that function together within a single process within a much larger multi-process phenomenon such as the DDR–was required to select statistically significant feature sets. The resulting selective logistic regression model generated a rank-ordered list from which hits could be selected for further analysis and verification. Canonical DDR regulators were highly clustered towards the top and bottom of this hit list. Comparison of the sensitivity and specificity of M-RAM with the 2BHM demonstrated that our method provides superior performance. Additionally, our method ranked independent controls better than 2BHM. Lastly, we applied a PCST to a network consisting of our weighted hits, Scansite predictions, and the filtered STRING interactome to narrow down the hit list and generate hypotheses about how the hits might modulate the DDR. M-RAM identified both B-Raf and specific subunits of PKA as hits that were missed by 2BHM. Follow-up experiments further verified that B-Raf knock-down in U2OS cells indeed markedly increased γH2AX 1h after IR, a finding that has potentially important clinical applications for the addition of radiation therapy in the treatment of B-Raf mutant tumors that are being concurrently treated with B-Raf inhibitors³¹.

We believe that M-RAM has two important advantages over other published multivariate approaches for the analysis of HC screens. First, M-RAM elegantly combines hit identification and feature selection in one single computational step. Other multivariate approaches treat feature selection and hit identification as a multi-step procedure in the HCS data analysis pipeline, complicating implementation and interpretation of results. Furthermore, M-RAM only requires the selection of the Lasso tuning parameter λ. The appropriate λ can be easily determined using cross validation and by computing the statistical significance of the resulting readout profiles. While we did not implement a rigid binary computational classification for ‘hit’ selection, as we believe this is best done in consultation with biologists familiar with the process being studied, we do provide an explicit method for doing so using the resulting rank ordered list to place the genes in a relevant signaling network based on pre-existing knowledge with a PCST algorithm.

Second, our method provides integrated feature selection, not dimensionality reduction like principal component analysis or factor analysis. The inherent objective of computational methods for the analysis of HC screens is to generate hypotheses for follow-up experiments from primary HC data. It is essential to reduce the number of screened phenotypic readouts and the number of time points without losing essential biological information to save experimentalists the effort of re-screening all of them. Our method efficiently selects the most predictive phenotypic readouts at the most predictive time points, therefore vastly simplifying confirmatory experiments. Hence, we believe that M-RAM will find more widespread adoption than other published multivariate approaches.