Using a network-based approach and targeted maximum likelihood estimation to evaluate the effect of adding pre-exposure prophylaxis to an ongoing Test-and-Treat trial

Abstract

Background

Several cluster randomized trials are underway to investigate the implementation and effectiveness of a universal test-and-treat strategy on the HIV epidemic in sub-Saharan Africa. We consider nesting studies of pre-exposure prophylaxis (PrEP) within these trials. PrEP is a general strategy where high risk HIV- persons take antiretrovirals daily to reduce their risk of infection from exposure to HIV. We address how to target PrEP to high risk groups and how to maximize power to detect the individual and combined effects of universal test-and-treat and PrEP strategies.

Methods

We simulated 1000 trials, each consisting of 32 villages with 200 individuals per village. At baseline we randomized the universal test-and-treat strategy. Then after three years of follow-up, we considered four strategies for targeting PrEP: (i) all HIV- individuals who self-identify as high risk, (ii) all HIV- individuals who are identified by their HIV+ partner (serodiscordant couples), (iii) highly connected HIV- individuals, and (iv) the HIV- contacts of a newly diagnosed HIV+ individual (a ring-based strategy). We explored two possible trial designs, and all villages were followed for a total of seven years. For each village in a trial, we used a stochastic block model to generate bipartite (male-female) networks and simulated an agent-based epidemic process on these networks. We estimated the individual and combined intervention effects with a novel targeted maximum likelihood estimator, which used cross-validation to data-adaptively select from a pre-specified library the candidate estimator that maximized the efficiency of the analysis.

Results

The universal test-and-treat strategy reduced the three-year cumulative HIV incidence by 4.0% on average. The impact of each PrEP strategy on the four-year cumulative HIV incidence varied by the coverage of the universal test-and-treat strategy with lower coverage resulting in a larger impact of PrEP. Offering PrEP to serodiscordant couples resulted in the largest reductions in HIV incidence (2% reduction), and the ring-based strategy had little impact (0% reduction). The joint effect was larger than either individual effect with reductions in the seven-year incidence ranging from 4.5% to 8.8%. Targeted maximum likelihood estimation, data-adaptively adjusting for baseline covariates, substantially improved power over the unadjusted analysis, while maintaining nominal confidence interval coverage.

Conclusions

Our simulation study suggests that nesting a PrEP study within an ongoing trial can lead to combined intervention effects greater than those of universal test-and-treat alone and can provide information about the efficacy of PrEP in the presence of high coverage of treatment for HIV+ persons.

Introduction

Despite the ongoing scale-up of antiretroviral therapy, an estimated 2 million people became infected with HIV and 1.2 million died of AIDS-related illnesses in 2014.¹ Mounting evidence suggests that early HIV diagnosis combined with immediate antiretroviral therapy could slow the spread of HIV.^2;3 In particular, the TEMPRANO and START trials reported that early treatment initiation (regardless of disease stage) resulted in improved health outcomes for HIV+ people.^4;5 Furthermore, the HPTN052 study confirmed that sustained antiretroviral therapy sharply reduces the risk of HIV transmission between serodiscordant couples.⁶

Synthesizing these data with prior studies, the WHO recently recommended antiretroviral therapy for all persons living with HIV regardless of clinical stage and at all CD4 levels.³ These recommendations are in line with the UNAIDS 90-90-90 cascade target: 90% of all HIV+ people know their status, 90% of those with known HIV+ status are on sustained antiretroviral therapy, and 90% of those on antiretroviral therapy are virally suppressed.⁷ Both organizations are calling for implementation of a universal test-and-treat strategy: early HIV diagnosis and immediate antiretroviral therapy initiation for all HIV+ people. Such a strategy is expected to not only preserve the health of HIV+ people but also protect their partners and children.^4–6;8;9

At the time of the WHO and UNAIDS guidelines, four cluster randomized trials were underway to investigate the population-level impact of universal test-and-treat. Specifically, the ANRS12249 TasP trial is ongoing in South Africa (NCT01509508);¹⁰ the BCPP trial in Botswana (NCT01965470);¹¹ the HPTN071 PopART trial in South Africa and Zambia (NCT01900977);¹² and the SEARCH trial in Uganda and Kenya (NCT01864603).¹³ These studies are cluster randomized trials, wherein the unit of randomization are communities or villages. The primary outcome of HIV incidence captures not only the direct effect of the intervention at the individual-level, but also indirect and spillover effects among individuals within a cluster.

In light of the recent recommendations, several questions arise regarding the relevance and power of these studies. These trials will provide estimates of the population-level effect of universal test-and-treat on HIV incidence as well as other health, economic and educational outcomes. Furthermore, these trials will provide information on how best to implement universal test-and-treat in resource-limited settings as well as guidance on the feasibility and sustainability of the strategy in diverse contexts. However, as countries embrace the new WHO guidelines, the control arm for each of these trials will more closely resemble the intervention arm. This change in standard of care will attenuate the randomized effects and threaten statistical power. Finally, it is unknown whether universal test-and-treat alone is sufficient; once the UNAIDS 90-90-90 target has been reached, what other strategies will be needed to achieve 0 new infections?

In this paper, we consider adding targeted pre-exposure prophylaxis (PrEP) to an ongoing test-and-treat trial. PrEP refers to the provision of antiretroviral therapy to high risk HIV- people to reduce risk of infection from exposure to HIV. Recent studies have indicated that PrEP can sharply reduce HIV transmission when taken regularly.^14–17 Formal evaluation of PrEP in the context of universal test-and-treat is especially pressing given the WHO guidelines, recommending PrEP as an “additional prevention choice for people at ‘substantial risk’”.³ Using a network-based approach to simulation, we consider (i) targeting PrEP to people at substantial risk; (ii) the impact of adding a targeted PrEP strategy to an ongoing cluster randomized trial; and (iii) the best design and analysis to maximize power to detect the individual and joint effects of test-and-treat and PrEP.

Methods

Targeted PrEP strategies

Ideal candidates for PrEP are HIV- individuals who are at high risk of acquiring HIV. We consider four strategies for targeting PrEP:

• On-demand: HIV- individuals who self-identify as being high risk

• Couples: HIV- individuals who are identified by their HIV+ partner

• Degree: HIV- individuals who report having 2+ partners

• Ring: HIV- partners of a newly diagnosed HIV+ individual.

The feasibility, cost and acceptability of each strategy will vary by epidemiological context. On-demand PrEP relies on measuring demographic characteristics and providing PrEP education to these key populations or vulnerable groups (e.g. young women¹⁸). As a result, implementation of On-demand PrEP may not require any additional data collection, but may also be poorly targeted. There is strong evidence that Couples PrEP reduces the HIV transmission when adherence is high.^14–17 This strategy could be implemented, for example, in the SEARCH trial where serodiscordant couples are identified through annual community-based testing programs.^19;20 Degree PrEP is in line with the 2014 Clinical Practice Guidelines²¹ and also relies on self-report. Misreporting the number of sexual partners could result in poor targeting. Ring PrEP is inspired by the recent success of the vaccine effectiveness trial against Ebola Virus Disease in Guinea.²² This approach requires contact tracing or identification (at least in part) of the underlying sexual networks.²³ Both Couples and Ring PrEP are expected to have the greatest impact if the index case is detected during the acute and early phases of infection when transmission rates are the highest.²⁴ As a result, these targeting strategies fit well within ongoing test-and-treat trials, where population-wide testing is regularly occurring.^19;20

Trial design

To investigate the impact of each PrEP strategy, we simulate 1000 cluster randomized trials. In each trial, there are 32 villages (experimental units) with 200 individuals each. At baseline the test-and-treat assignment is randomized among villages with balanced allocation: 16 intervention and 16 control. We parameterize coverage as the proportion of village members who would successfully complete the care cascade (testing, treatment, retention and adherence) for antiretroviral therapy or PrEP, as appropriate. The test-and-treat intervention provides universal eligibility for antiretroviral therapy at a high coverage: 85% of HIV+ patients on treatment and suppressed. To capture the evolving landscape of HIV prevention and to reflect baseline trial data,^3;25–27 the test-and-treat control arm also provides universal eligibility for antiretroviral therapy, but with lower coverage: 55% of HIV+ patients on treatment and suppressed.

After three years of follow-up, we modify the trial to account for uptake of the WHO guidelines.³ Specifically, we consider a second randomization to investigate the effect of a targeted PrEP strategy versus the standard of care. We explore two trial designs: Design 1 randomizes a given PrEP strategy within the test-and-treat intervention arm (8 targeted PrEP and 8 standard of care, total); Design 2 ramps up coverage of antiretroviral therapy in the test-and-treat control arm from 55% to 85% and randomizes the PrEP strategy within each test-and-treat trial arm separately (16 targeted PrEP and 16 standard of care, total). In both designs, we assume high coverage in the PrEP intervention arm: 85% of all individuals who are eligible under a given strategy are on PrEP and adherent. To reflect the ongoing trials, the standard of care for PrEP is 0% coverage. If in the future PrEP were regularly offered, the control arm as the standard of care would reflect this change in eligibility and therefore coverage. This complexity, however, is ignored here. All villages are followed for four additional years after the second randomization.

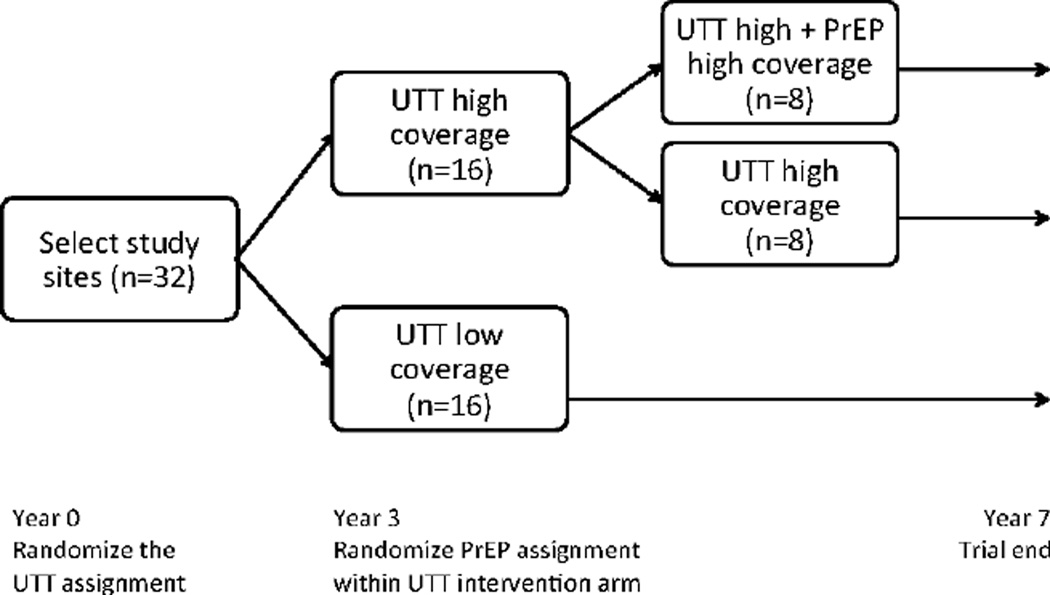
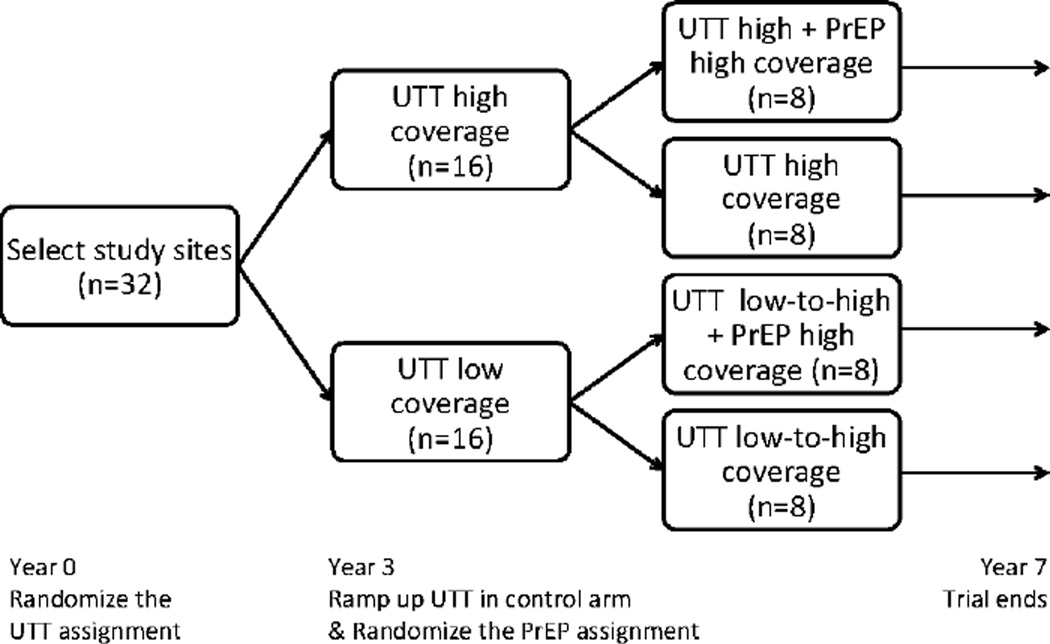
Designs 1 and 2 are shown in Figures 1 and 2, respectively. The first design might be favored when resources prohibit simultaneous scale-up of both antiretroviral therapy and PrEP. The latter design reflects the recent modifications to the SEARCH trial^*.²⁸ Both designs constitute a sequentially randomized trial, wherein the units (villages) are randomized first at baseline and subsequently at follow-up year three. Unlike a sequential multiple assignment randomized trial,²⁹ however, the second randomization is not adaptive – it does not depend on the outcomes in the first phase. Design 2 is similar to a 2x2 factorial design;^30;31 all the relevant combinations of the treatment are present and the effect of individual components and their interactions can be examined. However, unlike a standard factorial design, the second experimental condition (PrEP) is introduced part way through the trial.

Figure 1.

Proposed Design 1: The universal test-and-treat (UTT) assignment (high vs. lower coverage) is randomized with balanced allocation to the 32 villages. After three years of follow-up, the PrEP assignment (high vs. no coverage) is randomized within the UTT intervention arm (high coverage). All villages are followed for four additional years after the second randomization.

Figure 2.

Proposed Design 2: The universal test-and-treat (UTT) assignment (high vs. lower coverage) is randomized with balanced allocation to the 32 villages. After three years of follow-up, the coverage of antiretroviral therapy is scaled-up in the UTT control arm (from low to high coverage), and the PrEP assignment (high vs. no coverage) is randomized within both UTT arms separately. All villages are followed for four additional years after the second randomization.

Network generation

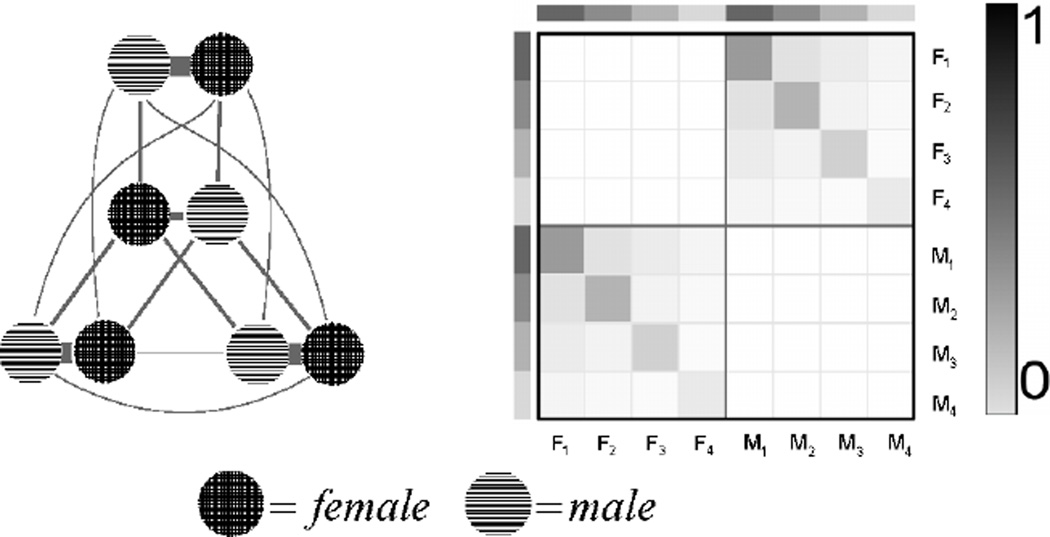
For each village in a trial, we generate an underlying sexual network with a degree-corrected, bipartite (female/male) stochastic block model.³² Each individual (node) has an expected number of partners (degree) and belongs to a block. An individual’s degree is distributed according to a powerlaw with exponent 2.5. Block structure represents the sexual mixing patterns among discrete demographic groups. The probability of a connection (edge) between two individuals depends on their expected number of partners and their probabilities of connecting within or across blocks. Our structure is specified to create three blocks where relationships mainly occur within block pairs, and two blocks that mix heavily with others. A schematic of the block matrix and the mixing diagram are in Figure 3, and further details are in the Supplementary Material.

Figure 3.

Mixing diagram (left) and the block matrix (right) for our bipartite, degree-corrected, stochastic block model. On the mixing diagram, line thickness represents the proportion of edges (connections) between each block. For the block matrix, F₁ – F₄ represent the four female blocks, and M₁ – M₄ represent the four male blocks, and the shading represents the propensity to mix (form connections) within or across blocks.

Epidemic dynamics

For each village in a trial, we simulate an infectious spread on the network with a susceptible-infected-recovered compartmental model.³³ We select time steps of one year to aid in interpretation. At each time step, an HIV+ individual could infect each of his/her susceptible partners (degree infectivity). The probability of transmission depends on the infectiousness of the HIV+ individual and the susceptibility of his/her HIV- partner. We model the probability that an HIV+ individual is in the acute phase and thereby highly infectious²⁴ with an independent Bernoulli process. We assume antiretroviral therapy reduces the risk of an HIV+ individual’s infecting others at each time step by 90%.⁶ We also assume that 10% of the HIV+ population have a low viral load without treatment and their risk of infecting others is reduced by 90%.^34–36 Finally, we assume high adherence to PrEP, reducing susceptibility by 90% in both men and women in heterosexual relationships.^14–17

To initiate the epidemic, we randomly select 10% of village members to be infected. The infectious process then spreads until reaching an average pre-trial prevalence of 25%. We then begin the trial and generate the counterfactual outcomes under the treatment arms (described above). We also include a time-lag between treatment eligibility and uptake with an independent Bernoulli process. To reflect ongoing HIV prevention and treatment efforts, 55% of HIV+ individuals are assumed to be on antiretroviral therapy and suppressed prior to the study start.^25–27 Full Python code to generate networks and simulate the epidemic are given in Staples.³⁷

Causal effects

Let A1 be an indicator of the first randomized assignment with A1 = 1 for universal test-and-treat with high coverage and A1 = 0 for universal test-and-treat with lower coverage. Similarly, let A2 indicate the second randomization with A2 = 1 for PrEP with high coverage and A2 = 0 for standard of care PrEP. We denote the joint treatment assignment as A = (A1, A2). As outlined in Table 1, the proposed trials allow for effect estimation of various treatment combinations.

Table 1.

Some possible effects of interest: When the control arm differs, we show the description of Design1/Design2.

	Description of Study Arms & Treatment Regimes				Trial	Units (Int. x Con.)
Effects	Intervention		Control		Yrs	Design1	Design2
UTT before PrEP	UTT hia	A1 = 1	UTT lowb	A1 = 0	0–3	16x16	16x16
PrEP in UTT intervention arm	UTT hia+PrEP hic	A = (1, 1)	UTT hia	A = (1, 0)	3–7	8x8	8x8
PrEP in UTT control arm	UTT low-to-hid+PrEP hic	A = (0, 1)	UTT low-to-hid	A = (0, 0)	3–7	NA	8x8
UTT without PrEP	UTT hia	A = (1, 0)	UTT lowb/low-to-hid	A = (0, 0)	0–7	8x16	8x8
UTT with PrEP	UTT hia+PrEP hic	A = (1, 1)	UTT low-to-hid+PrEP hic	A = (0, 1)	0–7	NA	8x8
Main PrEP effecte	PrEP hic	A2 = 1	Std. of care PrEP	A2 = 0	3–7	NA	16x16
Main UTT effectf	UTT hia	A1 = 1	UTT low-to-hid	A1 = 0	0–7	NA	16x16
Joint UTT & PrEP effect	UTT hia+PrEP hic	A = (1, 1)	UTT lowb/low-to-hid	A = (0, 0)	0–7	8x16	8x8

Int.: Intervention arm; Con.: Control arm; Yrs.: Years; UTT: universal test-and-treat; hi: high; Std.: Standard

A1: first randomization assignment; A2: second randomization assignment; A = (A1, A2): joint treatment assignment

^aUTT with high coverage: 85% of HIV+ on antiretroviral therapy & suppressed

^bUTT with low coverage: 55% of HIV+ on antiretroviral therapy & suppressed

^cPrEP with high coverage: 85% of eligible HIV- on PrEP & adherent

^dUTT with low coverage (55%) until year 3, then UTT with high coverage (85%) - Design 2 only

^eThis comparison averages or collapses over the UTT arms: A = (1, 1) & A = (0, 1) versus A = (1, 0) & A = (0, 0)

^fThis comparison averages or collapses over the PrEP arms: A = (1,1) & A = (1,0) versus A = (0,1) & A = (0,0)

First, we can estimate the effect of test-and-treat with high coverage (A1 = 1) compared to lower coverage (A1 = 0) on the three-year cumulative HIV incidence from study start to year three. This “universal test-and-treat before PrEP” effect estimate is based all 32 villages. We can also estimate the effect of a given PrEP strategy with high and sustained coverage of test-and-treat on the four-year cumulative incidence from study year three to study termination. This comparison utilizes 16 villages: 8 intervention A = (1,1) and 8 control A = (1,0). Within Design 2, we can estimate the PrEP effect with initially lower and then scaled-up coverage of test-and-treat on the four-year cumulative incidence; this comparison utilizes 16 villages: 8 intervention A = (0,1) and 8 control A = (0, 0). Also within Design 2, we can estimate the “main”^30;31 PrEP effect on the four-year incidence. This is the effect of targeted PrEP versus the standard of care averaging over the test-and-treat arms and utilizes all 32 villages: 16 intervention A2 = 1 and 16 control A2 = 0. We can estimate the analogous test-and-treat effects (within and collapsing over PrEP arms) on the seven-year cumulative incidence. Finally, with both designs, we can estimate the joint effect of high coverage of both test-and-treat and PrEP A = (1,1) versus (initially) low coverage of test-and-treat A = (0, 0) on the seven-year incidence.

We define these effects as contrasts between counterfactual outcomes.^38;39 Let A* be the treatment indicator, equaling 1 for the relevant intervention combination and 0 for the relevant control combination. For example, for the PrEP effect within the test-and-treat intervention arm, A* would equal 1 for high coverage of both test-and-treat and PrEP and 0 for high coverage of only test-and-treat. Further let Y_k(a*) represent the counterfactual cumulative incidence that would have been observed for village k if possibly contrary-to-fact the village received treatment combination A* = a*. The average difference in these counterfactual outcomes captures the effects of interest. We focus on the sample average treatment effect: ^40–45

$$\text{SATE}=\frac{1}{K}\sum _{k=1}^K[Y_k(1)-Y_k(0)]$$

where k = {1,…, K} indexes the villages with the relevant treatment combinations. For example, the PrEP effect within the test-and-treat intervention arm is the average difference in the counterfactual four-year cumulative incidence with high coverage of test-and-treat and PrEP versus high coverage of test-and-treat only for the K = 16 villages with the relevant treatment combinations. Using the sample effect obviates the need to assume the existence of and generalization to some hypothetical target population of villages. Of course, we only observe the counterfactual outcome corresponding to the observed treatment history. The observed outcome Y_k equals the counterfactual outcome Y_k(a*) when village k receives the treatment combination A_k = (a1, a2) corresponding to A* = a*. Finally, let W_k denote the set of baseline covariates.

Estimation and inference

Since our design is a two-phase randomized trial, the unadjusted estimator – the difference in the average outcomes among intervention units and the average outcomes among control units – provides an unbiased estimate of the treatment effect:

$$\text{Unadj}.=\left[\frac{{\sum }_{k=1}^K𝕀(A_k^{*}=1)Y_k}{{\sum }_{k=1}^K𝕀(A_k^{*}=1)}\right]-\left[\frac{{\sum }_{k=1}^K𝕀(A_k^{*}=0)Y_k}{{\sum }_{k=1}^K𝕀(A_k^{*}=0)}\right]=\widehat{𝔼}(Y|A^{*}=1)-\widehat{𝔼}(Y|A^{*}=0)$$

where k = {1,…, K} indexes the villages with the relevant treatment combinations. When baseline characteristics predict the outcome, this simple difference-in-means estimator can be inefficient as it fails to adjust for measured covariates. In general, adjusting for baseline covariates during the analysis can reduce variance without creating bias, even in small trials.^46–51

We compare the unadjusted estimator with targeted maximum likelihood estimation, a general method for the construction of double robust, semi-parametric, efficient substitution estimators.^39;45 Briefly, the algorithm updates an initial estimator of the expected outcome, given the treatment assignment and covariates 𝔼(Y|A*, W), with information in the known or estimated treatment mechanism ℙ(A*|W). This targeting step is used to achieve the optimal bias-variance trade-off for the parameter of interest and to solve the efficient score equation. A point estimate is given by the average difference in the targeted predictions:

$$\text{TMLE}=\frac{1}{K}\sum _{k-1}^K{\widehat{𝔼}}^{*}(Y_k|A_k^{*}=1,W_k)-{\widehat{𝔼}}^{*}(Y_k|A_k^{*}=0,W_k)$$

where again k = {1,…, K} indexes the villages with the relevant treatment combinations and where 𝔼̂*(Y|A*,W) denotes a targeted estimate of the conditional mean outcome.

With few independent units (villages), we are limited to the size of the adjustment set (i.e. variables included in the outcome regression model or in estimation of the known treatment mechanism). Therefore, we apply the targeted maximum likelihood estimator described in Balzer et al.,⁵² to select from a pre-specified library the candidate estimator that maximizes precision. We consider the following individual-level candidate adjustment variables:

• Nothing

• Demographic risk group: indicator of belonging to the high risk block

• Degree: number of partners

• Number of partners (network neighbors) infected at baseline.

We also include the following village-level candidate adjustment variables:

• Village HIV prevalence at baseline

• Assortativity: degree-degree correlation taken over all network connections (edges)

• Number of components: number of distinct groups with no connections (edges) between members of different groups.

Here, “baseline” refers to study year zero for the test-and-treat and joint effects and to study year three for the PrEP effects. Our candidates include a mix of variables that are fairly easy to collect (demography, degree, village prevalence), are more difficult (number of partners infected, assortativity), and possibly unknowable (number of components). We note that measurement of a full sexual²³ or social¹³ contact network would allow for adjustment for potentially very predictive covariates.^53;54

Both the unadjusted estimator and the targeted estimator are asymptotically linear; their limiting distributions are normal with mean zero and variance given by the variance of their influence curves (Section 4.2 of Balzer et al.⁴⁵). To account for limited numbers of independent units in these simulations, the Student’s t-distribution is used in place of the standard normal^28;55;56 when constructing Wald-type 95% confidence intervals and testing the null hypothesis of no average effect for the study units. To the best of our knowledge, this is the first application of the hierarchical targeted maximum likelihood estimator, proposed in Balzer et al.,⁵⁷ to make full use of individual-level data when estimating the cluster-level effect. Further details are given in the Supplementary Material, and full R code is available in Balzer.⁵⁸

Results

Our main simulation results are summarized in Table 2. We focus on the test-and-treat effect before PrEP, the PrEP effects and the joint effect. Additional results are given in the Supplementary Material. For each effect, we show the average cumulative HIV incidence for each intervention and control scenario and the average value of the sample effect across 1000 simulated trials. For estimator performance, we give the mean squared error, the 95% confidence interval coverage, and the attained power. For simplicity, we only present the results from Design 1 if they differ meaningfully from Design 2.

Table 2.

Selected effects and performance of the unadjusted estimator and targeted maximum likelihood estimator over 1000 simulated trials. We only present the results from Design1 when there is a meaningful difference in performance from Design2.

	True Values			Unadjusted Estimator			Targeted Estimator
	Inta	Conb	SATEc	MSEd	Cove	Powerf	MSEd	Cove	Powerf
UTT before PrEP on the three-year cumulative HIV incidence
Design2:	5.2	9.2	−4.0	1.9E-4	96	76	8.3E-5	98	95
PrEP in UTT intervention arm on the four-year cumulative HIV incidence
Design2: Ring	2.8	2.8	−0.0	8.1E-5	98	6	8.6E-5	96	7
Design2: On-demand	2.3	2.8	−0.5	6.2E-5	98	7	3.7E-4	97	9
Design2: Degree	1.5	2.8	−1.3	4.5E-5	97	28	7.3E-5	96	33
Design2: Couples	1.1	2.8	−1.7	4.3E-5	97	51	2.4E-4	94	55
PrEP in UTT control arm on the four-year cumulative HIV incidence
Design2: Ring	3.5	3.5	0.0	9.7E-5	98	4	1.0E-4	97	7
Design2: On-demand	2.8	3.5	−0.6	8.2E-5	98	9	8.4E-5	97	11
Design2: Degree	1.9	3.4	−1.6	6.3E-5	98	30	9.2E-5	96	34
Design2: Couples	1.4	3.4	−2.0	5.4E-5	98	54	7.4E-5	97	60
Main PrEP effect on the four-year cumulative HIV incidence
Design2: Ring	3.1	3.1	0.0	4.4E-5	98	5	3.1E-5	99	5
Design2: On-demand	2.6	3.1	−0.6	3.6E-5	98	11	2.8E-5	98	13
Design2: Degree	1.7	3.1	−1.4	2.8E-5	98	54	2.3E-5	98	62
Design2: Couples	1.2	3.1	−1.9	2.5E-5	98	83	2.0E-5	98	90
Joint (UTT + PrEP) effect on the seven-year cumulative HIV incidence
Design1: Ring	7.7	15.0	−7.3	4.8E-4	97	83	2.6E-4	98	95
Design1: On-demand	7.3	15.0	−7.7	3.9E-4	98	89	2.0E-4	98	97
Design1: Degree	6.6	15.0	−8.4	3.9E-4	96	94	1.9E-4	98	99
Design1: Couples	6.2	15.0	−8.8	3.9E-4	97	96	1.9E-4	98	100
Design2: Ring	7.8	12.3	−4.5	6.0E-4	96	38	3.4E-4	97	56
Design2: On-demand	7.3	12.3	−5.0	5.4E-4	96	45	3.2E-4	97	63
Design2: Degree	6.5	12.2	−5.7	5.1E-4	96	57	2.8E-4	97	76
Design2: Couples	6.2	12.3	−6.1	5.2E-4	96	62	5.6E-4	96	80

Int.: Intervention arm; Con.: Control arm; SATE: sample average treatment effect; UTT: universal test-and-treat

^aAverage cumulative HIV incidence under the intervention scenario (%)

^bAverage cumulative HIV incidence under the control scenario (%)

^cAverage value of the SATE (%)

^dMSE: mean squared error (bias² + variance) (%)

^eCoverage: Proportion of times the 95% confidence intervals contained the true value (%)

^fAttained power: proportion of times the false null hypothesis was rejected (%)

The test-and-treat intervention reduces the cumulative incidence in the first three years of the trial by 4.0% on average. We have 76% power to detect this effect with the unadjusted estimator and 95% power with the targeted estimator using adaptive pre-specification to select the adjustment set for the outcome regression 𝔼(Y|A*, W) and treatment mechanism ℙ(A*|W). In this case, the number of partners infected at baseline is selected as the adjustment variable for the outcome regression in 82% of the trials (Supplementary Table 1). Through adjustment, targeted estimation improves performance by reducing the estimator’s variability (smaller mean squared error) and by providing a less conservative variance estimator⁴⁵ and hence higher power.

For Design 2, the impact of a given PrEP strategy on the four-year incidence varies by the test-and-treat arm. Initially lower antiretroviral therapy coverage results in a larger impact of each PrEP strategy. For example, Couples PrEP results, on average, in a 1.7% reduction in incidence in the test-and-treat intervention arm where antiretroviral therapy coverage is always at 85%, and in a 2% reduction in the test-and-treat control arm where antiretroviral therapy coverage is initially at 55% and then ramps up to 85%. Consistently, the largest impact is with Couples PrEP, and there is no impact of Ring PrEP in these simulations. These results are robust to the assumed coverage of antiretroviral therapy and PrEP (Supplementary Figure 1). We further note that in these simulations, the Couples strategy requires the largest person-years on PrEP, and the Ring strategy fails to put high risk individuals on PrEP (Supplementary Figure 1).

For these effects, the targeted estimator is slightly more variable than the unadjusted (larger mean squared error) possibly due to a large library for data-adaptive estimation and only 16 independent units. Nonetheless, the targeted estimator still results in slightly more power. The number of partners infected and the village HIV prevalence at baseline (here, year 3) are selected for adjustment in ≈48% and ≈13% of the trials, respectively. This suggests that including time-updated covariates in the candidate adjustment set is important to maximize power to detect the PrEP effects.

For the main effect of PrEP on the four-year incidence, the largest impact is associated with the Couples strategy (−1.9% on average), followed by the Degree strategy (−1.4% on average), the On-demand strategy (−0.6% on average), and finally the Ring strategy (0% on average). As noted above, the main PrEP effect is the impact of a given strategy averaged over the test-and-treat arms. For these effects, improved performance with targeted estimation is demonstrated by smaller mean squared errors and higher power. For example, to detect the main effect of Couples PrEP, the unadjusted approach provides 83% power and targeted estimation 90%. For these effects, the number of partners infected and the village HIV prevalence at baseline (here, year three) are selected as the adjustment variable for the outcome regression in 58% and 18% of the trials, respectively.

For the joint effect of high coverage of both test-and-treat and PrEP on the seven-year incidence from study start to termination, there is a notable impact of the trial design. Recall the test-and-treat control arm in Design 1 provides lower coverage of antiretroviral therapy for the trial duration, whereas the test-and-treat control arm for Design 2 provides lower coverage for years zero to three and then scales up to high coverage. As a result, there is a larger joint effect of each test-and-treat and PrEP strategy combination in Design 1 than in Design 2. Indeed, the joint effect ranges from −7.3% to −8.8% in Design 1 and from −4.5% to −6.1% in Design 2. The basis for estimation of these effects involves 24 villages in Design 1 and only 16 in Design 2 (Table 1). As a consequence, we are well-powered to detect these joint effects with both estimators under Design 1, but only achieved 80% power to detect the joint effect of test-and-treat and Couples PrEP with targeted estimation in Design 2. In all cases, the joint effect of test-and-treat and PrEP is larger than either individual effect on the seven-year incidence (Supplementary Table 2). Again, targeted estimation tends to provide a lower mean squared error and always yields more power than does the unadjusted. Throughout confidence interval coverage is near or above nominal rate of 95%.

Discussion

We propose four strategies to target PrEP and study their impact within an ongoing test-and-treat trial. Our strategies range from simple (On-demand) to harnessing information in the underlying sexual network (Ring). We propose two modifications to the ongoing trials in response to the WHO’s recommendations and the evolving landscape of HIV prevention and treatment. Investigators may favor one design over the other depending on resource constraints and their primary scientific questions.

To study the PrEP strategies and these designs, we simulate underlying sexual networks using a degree-corrected stochastic block model. While this network generation is highly idealized, it allows us to investigate the spread of epidemics across networks and the use of network information to target interventions and to improve the analysis. We simulate the infectious process within each village (network) using an agent-based compartmental model. Our epidemic model could be more closely calibrated to specific settings (e.g. accounting for variability in viral load evolution over time and its impact on transmission).^59–62 Nonetheless, our idealized models capture the stochastic variation inherent in epidemics occurring on networks⁶³ and provide a framework for investigating pressing questions in HIV prevention and treatment. For estimation and inference, we compare the unadjusted estimator to a new targeted maximum likelihood estimator, data-adaptively adjusting for baseline covariates measured at both the individual and cluster-level. The latter consistently leads to notable gains in attained power, while maintaining nominal confidence interval coverage.

There are several areas of future work. First, we focus on trials where universal test-and-treat was randomized to the study villages in a parallel design. This work can be adopted to other common designs, such as stepped wedge and pair-matched trials. We also study a high prevalence setting wherein an average of 25% of village members were infected at baseline. Future studies will examine a lower prevalence setting; we suspect that impact of test-and-treat and PrEP will vary by context. Finally, we focused on estimation and inference of the sample average treatment effects on the village-level outcome (cumulative HIV incidence). There are many other interesting causal parameters, such as the effect on the individual-level outcome. Nonetheless, the implemented targeted maximum likelihood estimator is able to make full use of the individual-level data and could also easily accommodate additional complications due to right-censoring and informative drop-out.^39;57;58

Overall, our work suggests that nesting a PrEP study within an ongoing universal test-and-treat trial will answer timely questions in HIV prevention and treatment as well as lead to combined effects greater than those of test-and-treat alone. While the impact of PrEP varied by test-and-treat intervention arm, offering PrEP to HIV- partners in serodiscordant couples consistently led to the greatest reductions in incidence.