Optimizing MR Scan Design for Model-Based T₁, T₂ Estimation from Steady-State Sequences

Abstract

Rapid, reliable quantification of MR relaxation parameters T₁ and T₂ is desirable for many clinical applications. Steady-state sequences such as Spoiled Gradient-Recalled Echo (SPGR) and Dual-Echo Steady-State (DESS) are fast and well-suited for relaxometry because the signals they produce are quite sensitive to T₁ and T₂ variation. However, T₁, T₂ estimation with these sequences typically requires multiple scans with varied sets of acquisition parameters. This paper describes a systematic framework for selecting scan types (e.g., combinations of SPGR and DESS scans) and optimizing their respective parameters (e.g., flip angles and repetition times). The method is based on a Cramér-Rao Bound (CRB)-inspired min-max optimization that finds scan parameter combinations that robustly enable precise object parameter estimation. We apply this technique to optimize combinations of SPGR and DESS scans for T₁, T₂ relaxometry in white matter (WM) and grey matter (GM) regions of the human brain at 3T field strength. Phantom accuracy experiments show that SPGR/DESS scan combinations are in excellent agreement with reference measurements. Phantom precision experiments show that trends in T₁, T₂ pooled sample standard deviations reflect CRB-based predictions. In vivo experiments show that in WM and GM, T₁ and T₂ estimates from a pair of optimized DESS scans exhibit precision (but not necessarily accuracy) comparable to that of optimized combinations of SPGR and DESS scans. To our knowledge, T₁ maps from DESS acquisitions alone are new. This example application illustrates that scan optimization may help reveal new parameter mapping techniques from combinations of established pulse sequences.

I. Introduction

Fast, accurate quantification of spin-lattice and spin-spin relaxation parameters T₁ and T₂ has been of longstanding interest in MRI. Many researchers have suggested that T₁, T₂ maps may serve as biomarkers for monitoring the progression of various disorders [1]. Neurological applications include: lesion classification in multiple sclerosis [2]; tumor characterization [3, 4]; and symptom onset prediction in stroke [5, 6]. In addition, T₁, T₂ have shown promise for detecting hip and knee cartilage degeneration [7, 8] and for assessing cardiac dysfunction due to iron overload [9] or edema [10]. Motivated by this broad interest in T₁, T₂ mapping, this paper describes a systematic method to guide MR scan design.

Classical pulse sequences such as inversion/saturation recovery (IR/SR) or (single) spin echo (SE) yield relatively simple methods for T₁ or T₂ estimation, respectively; however, these methods require several scans, each with long repetition time T_R, leading to undesirably long acquisitions. Numerous modifications such as the Look-Locker method [11], multi-SE trains [12], or fast k-space trajectories [13–15] have been proposed to accelerate T₁ [16–19] and T₂ [20–23] relaxometry with these classical sequences. These techniques are more sensitive to model non-idealities [24–26], and are still speed-limited by the long T_R required for (near)-complete T₁ recovery.

Steady-state (SS) pulse sequences [27, 28] permit short T_R, and are thus inherently much faster than classical counterparts. SS techniques are well-suited for relaxometry because the signals produced are highly sensitive to T₁ and T₂ variation. However, short T_R times also cause SS signals to be complex functions of both desired and undesired (nuisance) parameters, complicating quantification. Furthermore, some such methods [29, 30] still require scan repetition, though individual scans are now considerably shorter. Despite these difficulties, the potential for rapid scanning with high T₁, T₂ sensitivity has motivated numerous SS relaxometry studies [29–38].

The dual-echo steady-state (DESS) sequence [39] was recently proposed as a promising SS imaging technique for T₂ estimation [35]. Because it produces two distinct signals per excitation, the DESS sequence can reduce scan repetition requirements by recording twice as much data per scan. As with other SS methods, the resulting signals [40, 41] are complicated functions of T₁, T₂, and other parameters. Prior works have isolated T₂ dependencies using either algebraic manipulations of the first- and second-echo signals [35, 36] or separate scans to first estimate nuisance parameters [42]. Although DESS concurrently encodes rich T₁ and T₂ information, these methods have shied away from using DESS for T₁ estimation, either through bias-inducing approximations, or noise-propagating sequential estimation, respectively.

Whether it be with DESS, other sequences, or even combinations thereof, it is generally unclear how to best assemble a scan profile (i.e., a collection of scans) for a fixed amount of scan time. Furthermore, for a given scan profile, it is typically not obvious how to best select acquisition parameters (e.g., flip angles, repetition times, etc.) for relaxometry. In this paper, the term scan design refers to the related problems of scan profile selection and scan parameter optimization.

Historically, scan design for relaxometry has predominantly been explored using figures of merit related to estimator precision. In particular, several studies have used the Cramér-Rao Bound (CRB), a statistical measure that bounds the minimum variance of an unbiased estimator. Earlier works have used the CRB and variations to select inversion times for recovery experiments [43, 44], flip angles for spoiled gradient-recalled echo (SPGR) sequences [45], and echo times for SE experiments [46]. More recent studies have considered additional scan design challenges, including scan time constraints [47], multiple latent parameters [48], multiple scan parameter types [49], and latent parameter spatial variation [50, 51].

The aforementioned studies consider scan parameter optimization for profiles consisting of only one pulse sequence. In contrast, this paper introduces a general framework for robust, application-specific scan design for parameter estimation from combinations of pulse sequences. The framework first finds multiple sets of scan parameters that achieve precise estimation within a tight, application-specific range of object parameters (e.g., T₁, T₂, etc.). The framework then chooses the one scan parameter set most robust to estimator precision degradation over a broader range of object parameters. As a detailed example, we optimize three combinations of DESS and SPGR sequences for T₁, T₂ mapping. For a fixed total scan time, we find that well-chosen DESS scans alone can be used to estimate both T₁ and T₂ with precision and robustness comparable to combinations of DESS and SPGR. This example illustrates that, with careful scan profile design, well-established pulse sequences can find use in new estimation problems.

This paper is organized as follows. Section II uses a general signal model to describe a CRB-inspired min-max optimization problem for robust, application-specific scan optimization. Section III adapts the DESS signal models to our framework and optimizes three practical DESS/SPGR combinations to show that, even in the presence of radiofrequency (RF) field inhomogeneity, DESS is a promising option for T₁, T₂ relaxometry. Section IV describes simulation, phantom, and in vivo experiments and discusses corresponding results. Section V discusses practical challenges and suggests future directions. Section VI summarizes key contributions.

II. A CRB-Inspired Scan Selection Method

A. A Generalized Signal Model

A broad class of MR pulse sequences useful for parameter mapping produce, after reconstruction, a set of noisy images y_d(·) that can be described with the following general model:

$$y_d(\mathbf{r})=f_d(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),{\mathbf{p}}_d)+{\epsilon }_d(\mathbf{r}),d=1,\dots ,D,$$ (1)

where x(r) ∈ ℂ^L collects L latent object parameters, at position r; ν(r) ∈ ℂ^K gathers K known object parameters at r; p_d ∈ ℝ^P denotes a set of P scan parameters chosen for the dth dataset; f_d : ℂ^L×ℂ^K ×ℝ^P ↦ ℂ is a (pulse-sequence dependent) function that models the noiseless signal obtained from the dth dataset; and ${\epsilon }_d~ℂ\mathcal{N}(0,{\sigma }_d^2)$ is assumed, for sake of simplicity, to be independent, complex Gaussian noise¹ [54, 55]. (As a concrete example, for T₂(·) mapping from single SE datasets, x(·) could collect spin density and T₂(·); ν(·) could collect known off-resonance and RF field inhomogeneities; and p_d could assign the dth echo time, chosen to yield image y_d(·).)

A scan profile consists of D datasets from a combination of pulse sequences. Let y(r) := [y₁(r),…, y_D(r)]^⊤ ∈ ℂ^D collect the noisy signals at r from all datasets, P := [p₁,…, p_D] ∈ ℝ^P×D gather the corresponding scan parameters, and vector function f : ℂ^L × ℂ^K × ℝ^P×D ↦ ℂ^D naturally extend scalar function f, where (·)^⊤ denotes vector transpose. Then the log-likelihood function is (to within a constant independent of x(r)):

$$lnL(\mathbf{x}(\mathbf{r}))=-\frac{1}{2}{\Vert \mathbf{y}(\mathbf{r})-\mathbf{f}(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P})\Vert }_{{\mathbf{\sum }}^{-1/2}}^2,$$ (2)

where covariance matrix $\mathbf{\sum }:=\text{diag}\left({\sigma }_1^2,\dots ,{\sigma }_D^2\right)$ is diagonal due to the assumption of independence between scans.

Under suitable regularity conditions², the Fisher information matrix I(x(r); ν(r),P) ∈ ℂ^L×L [56] is a measure useful for characterizing the precision of unbiased estimates of x(r) from y(r), given ν(r) and P:

$$\begin{array}{c}\mathbf{I}(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P}):=\mathbb{E}\left({[{\nabla }_{\mathbf{x}}lnL(\mathbf{x}(\mathbf{r}))]}^{†}[{\nabla }_{\mathbf{x}}lnL(\mathbf{x}(\mathbf{r}))]\right)\\ ={[{\nabla }_{\mathbf{x}}\mathbf{f}(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P})]}^{†}{\mathbf{\sum }}^{-1}[{\nabla }_{\mathbf{x}}\mathbf{f}(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P})],\end{array}$$ (3)

where 𝔼(·) denotes expectation; ∇_x denotes a row gradient with respect to x at fixed r; and (·)^† denotes Hermitian transpose. In particular, the matrix Cramér-Rao Bound (CRB) [57] ensures that any unbiased estimator x̂(r) satisfies

$$cov(\widehat{\mathbf{x}}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P})\underset{\_}{\succ }{\mathbf{I}}^{-1}(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P}),$$ (4)

where for arbitrary, equally sized matrices A and B, matrix inequality A ⪰ B means A − B is positive semi-definite. In the following, we design an optimization problem based on the CRB to guide MR scan design for relaxometry.

B. Min-max Optimization Problem for Scan Design

Following [58], we focus on minimizing a weighted average of the variances in each of the L latent object parameter estimates. A reasonable objective function for overall estimator precision is therefore given by

$$\mathrm{\Psi }(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P})=\text{tr}({\mathbf{WI}}^{-1}(\mathbf{x}(\mathbf{r});\mathit{\nu }(\mathbf{r}),\mathbf{P}){\mathbf{W}}^{\perp }),$$ (5)

where W ∈ ℝ^L×L is a diagonal, application-specific matrix of weights, preselected to control the relative importance of precisely estimating the L latent object parameters; and tr (·) denotes the matrix trace operation. For scan design, we would like to minimize (5) with respect to scan parameters P.

The CRB depends not only on P but also on the spatially varying object parameters x(·) and ν(·). Thus, one cannot perform scan design by “simply” minimizing Ψ over the scan parameters P. Instead, we pose a practical and application-dependent min-max optimization problem for scan design: we seek candidate scan parameters P̆ over a search space ℘ that minimize the worst-case, i.e., maximum cost Ψ̃^t, as viewed over “tight” parameter ranges 𝒳_t and 𝒩_t:

$$\stackrel{⌣}{\mathbf{P}}\in \underset{\mathbf{P}\in \mathcal{P}}{argmin}{\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{t}}(\mathbf{P}),\text{where}$$ (6)

$${\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{t}}(\mathbf{P})=\underset{\begin{array}{l}\mathbf{x}\in {\mathcal{X}}_{\mathrm{t}}\\ \mathit{\nu }\in {\mathcal{N}}_{\mathrm{t}}\end{array}}{max}\mathrm{\Psi }(\mathbf{x};\mathit{\nu },\mathbf{P}).$$ (7)

Here, we select latent object parameter set 𝒳_t based on the application and known parameter set 𝒩_t based on the spatial variation typically observed in the known parameters ν(·). Min-max approach (6) should ensure good estimation precision over a range of parameter values.

Since Ψ is in general non-convex with respect to P, it may have multiple global minimizers as well as other scan parameters that are nearly global minimizers. To improve robustness to object parameter variations, we form an expanded set of candidate scan parameters by also including scan parameters that yield costs to within a tolerance δ ≪ 1 of the optimum. Mathematically, we define this expanded set of candidate scan parameter combinations (for a given scan profile) as

$$\mathcal{S}:=\left\{\mathbf{P}:{\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{t}}(\mathbf{P})-{\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{t}}(\stackrel{⌣}{\mathbf{P}})\le \delta {\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{t}}(\stackrel{⌣}{\mathbf{P}})\right\}.$$ (8)

To select amongst these candidate scan parameters, we employ a robustness criterion: we select the single scan parameter P^* that degrades the least when the worst-case cost is viewed over widened object parameter sets 𝒳_b ⊇ 𝒳_t and 𝒩_b ⊇ 𝒩_t:

$${\mathbf{P}}^{\ast }=\underset{\mathbf{P}\in \mathcal{S}}{argmin}{\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{b}}(\mathbf{P}),\text{where}$$ (9)

$${\stackrel{\sim }{\mathrm{\Psi }}}^{\mathrm{b}}(\mathbf{P})=\underset{\begin{array}{l}\mathbf{x}\in {\mathcal{X}}_{\mathrm{b}}\\ \mathit{\nu }\in {\mathcal{N}}_{\mathrm{b}}\end{array}}{max}\mathrm{\Psi }(\mathbf{x};\mathit{\nu },\mathbf{P}).$$ (10)

To compare different scan profiles, we select corresponding search spaces ℘ to satisfy acquisition constraints (e.g., total scan time), but otherwise hold optimization parameters W, δ, 𝒳_t,b, and 𝒩_t,b fixed. Since Ψ is data-independent, we can solve (6) and (9) offline for each scan profile. The result of each profile’s min-max optimization process (9) is a corresponding optimized scan parameter matrix P^* that is suitable for the range of latent x and known ν object parameters specified in 𝒳_t and 𝒩_t, and is robust to variations in those parameters over broader sets 𝒳_b and 𝒩_b, respectively.

III. Application: Optimizing SS Sequences for T₁, T₂ Relaxometry in the Brain

This section applies the methods of Section II.B to the problem of scan design for joint T₁, T₂ estimation from combinations of SS sequences. Section III.A presents a brief overview of the DESS signals, formulating models to permit estimation of as few nuisance parameters as possible. Section III.B details how we use optimization problems (6) and (9) to tailor three combinations of DESS and SPGR scans for precise T₁, T₂ estimation in white matter (WM) and grey matter (GM) regions of the human brain. Section III.C compares the predicted performance of the three optimized scan profiles.

A. The DESS Signal Model

The DESS sequence interlaces RF excitations with unbalanced spoiler gradients of fixed area [39] to produce two distinct signals per excitation. If the gradient lobe area is carefully chosen to dominate through-voxel field inhomogeneity gradients, yet not introduce significant diffusive effects [59–61], the bulk steady-state signal s_D (from a voxel centered at position r) immediately before (t ≈ 0⁻) and after (t ≈ 0⁺) an RF excitation centered at time t = 0 can be written as

$$s_{\mathrm{D}}(\mathbf{r},0^{-})=-i{M}_0(\mathbf{r})tan\frac{\alpha (\mathbf{r})}{2}[1-\eta (\mathbf{r},T_{\mathrm{R}})]\text{and}$$ (11)

$$s_{\mathrm{D}}(\mathbf{r},0^{+})=+i{M}_0(\mathbf{r})tan\frac{\alpha (\mathbf{r})}{2}\left[1-\frac{\eta (\mathbf{r},T_{\mathrm{R}})}{\xi (\mathbf{r},T_{\mathrm{R}})}\right];\text{where}$$ (12)

$$\eta (\mathbf{r},t):=\sqrt{\frac{1-E_2^2(\mathbf{r},t)}{1-E_2^2(\mathbf{r},t)/{\xi }^2(\mathbf{r},t)}},\text{and}$$ (13)

$$\xi (\mathbf{r},t):=\frac{1-E_1(\mathbf{r},t)cos\alpha (\mathbf{r})}{E_1(\mathbf{r},t)-cos\alpha (\mathbf{r})}.$$ (14)

Here, E_u (r, t) := exp (−t/T_u(r)) for u ∈ {1, 2} describes longitudinal or transverse relaxation at time t, respectively; M₀(r) ∈ ℂ is proportional to spin density; flip angle α(r) = α₀κ(r) is decomposed as a nominal (prescribed) value α₀ with spatial variation κ(r) ≈ 1 due to RF field inhomogeneities; T_R is repetition time; and $i:=\sqrt{-1}$. Signal models (11) and (12) neglect relaxation and off-resonance effects during each (short) RF pulse³, and assume RF rotations about the î-axis.

We model each voxel’s macroscopic broadening distribution to be Cauchy (ω̄(r), $R_2^{\prime }(\mathbf{r})$), where ω̄(r) denotes median off-resonance frequency and $R_2^{\prime }(\mathbf{r})$ is the broadening bandwidth. If we time readout gradients to form echoes symmetrically centered at echo time T_E before and after RF excitation, then the noiseless DESS signals are well approximated as

$$s_{\mathrm{D}}(\mathbf{r},-T_{\mathrm{E}})\approx s_{\mathrm{D}}(\mathbf{r},0^{-})E_2^{-1}(\mathbf{r},T_{\mathrm{E}})e^{-(R_2^{\prime }(\mathbf{r})+i\overline{\omega }(\mathbf{r}))T_{\mathrm{E}}}$$ (15)

$$s_{\mathrm{D}}(\mathbf{r},+T_{\mathrm{E}})\approx s_{\mathrm{D}}(\mathbf{r},0^{+})E_2(\mathbf{r},T_{\mathrm{E}})e^{-\left(R_2^{\prime }(\mathbf{r})-i\overline{\omega }(\mathbf{r})\right)T_{\mathrm{E}}}.$$ (16)

In (15) and (16), nuisance parameters M₀(r), $R_2^{\prime }(\mathbf{r})$, κ(r), and ω̄(r) complicate estimation of T₁(r) and T₂(r). For simplicity, we take κ(r) to be known from a separately acquired RF transmit field $B_1^{+}(\mathbf{r})$ scan. To avoid (separate or joint) ω̄(r) estimation, we choose to use magnitude DESS data, at the expense of slight model mismatch (studied with simulations in Section IV.A) in (1) due to Rician noise. By fixing T_E across acquisitions and defining

$$M_{\mathrm{E}}(\mathbf{r}):=M_0(\mathbf{r})E_2(\mathbf{r},T_{\mathrm{E}})e^{-R_2^{\prime }(\mathbf{r})T_{\mathrm{E}}},$$ (17)

we can rewrite magnitude signals as functions of L = 3 latent and K = 1 known object parameters, collected as x(r) := [M_E(r), T₁(r), T₂(r)]^⊤ and ν(r) := κ(r), respectively:

$$f_1(\mathbf{x}(\mathbf{r});\nu (\mathbf{r}),\mathbf{p}):=\mid s_{\mathrm{D}}(\mathbf{r},-T_{\mathrm{E}})\mid =M_{\mathrm{E}}(\mathbf{r})tan\frac{\alpha (\mathbf{r})}{2}{E}_2^{-2}(\mathbf{r},T_{\mathrm{E}})[1-\eta (\mathbf{r},T_{\mathrm{R}})]$$ (18)

$$f_2(\mathbf{x}(\mathbf{r});\nu (\mathbf{r}),\mathbf{p}):=\mid s_{\mathrm{D}}(\mathbf{r},+T_{\mathrm{E}})\mid =M_{\mathrm{E}}(\mathbf{r})tan\frac{\alpha (\mathbf{r})}{2}\left[1-\frac{\eta (\mathbf{r},T_{\mathrm{R}})}{\xi (\mathbf{r},T_{\mathrm{R}})}\right];$$ (19)

where p := [α₀, T_R]^⊤ collects the P = 2 scan parameters we are free to optimize. From here, we use the scan design method described in Section II to select an optimized p corresponding to each DESS scan within a particular scan profile.

B. Scan Design Details

There are numerous candidate scan profiles involving DESS and/or other pulse sequences that may be useful for fast, accurate T₁, T₂ mapping. In this work, we consider combinations of DESS and SPGR scans [63]. With proper RF phase cycling and gradient spoiling, the SPGR signal s_S can be expressed without any explicit T₂(r) dependence:

$$s_{\mathrm{S}}(\mathbf{r},T_{\mathrm{E}})=\frac{i{M}_{\mathrm{E}}(\mathbf{r})sin\alpha (\mathbf{r})(1-E_1(\mathbf{r},T_{\mathrm{R}}))}{1-E_1(\mathbf{r},T_{\mathrm{R}})cos\alpha (\mathbf{r})}.$$ (20)

SPGR’s reduced dependence on spatially varying unknowns is reason for its use for T₁ mapping [30–32] and subsequent T₂ mapping from other sequences [29, 42]. In a similar spirit, we examine scan profiles containing SPGR over other SS sequences because we predict that the SPGR sequence’s T₂-independence may help estimators disentangle T₂ from other unknown sources of DESS signal contrast.

As written in (20), each SPGR scan also leaves p = [α₀, T_R]^⊤ as P = 2 scan parameters available to optimize. A given scan profile consisting of C_SPGR SPGR and C_DESS DESS scans yields D = C_SPGR + 2C_DESS datasets. We optimize such a scan profile by solving (9) over a dimension-PD = 2(C_SPGR + 2C_DESS) space of scan parameters.

We select constraints on search space ℘ based on hardware limitations and desired scan profile properties. Since each pair of DESS signals must share the same choice of p, the search space is reduced to ${\mathcal{A}}_{0,\text{SPGR}}^{C_{\text{SPGR}}}\times {\mathcal{A}}_{0,\text{DESS}}^{C_{\text{DESS}}}\times {\mathcal{T}}_{\mathrm{R},\text{SPGR}}^{C_{\text{SPGR}}}\times {\mathcal{T}}_{\mathrm{R},\text{DESS}}^{C_{\text{DESS}}}$ (superscripts denote Cartesian powers). We assign flip angle ranges 𝒜_0,SPGR = 𝒜_0,DESS ← [5, 90]° to restrict RF energy deposition. We set feasible T_R solution sets 𝒯_R,SPGR ← [12.2,+∞)ms and 𝒯_R,DESS ← [17.5,+∞)ms based on pulse sequence designs that control for other scan parameters. These control parameters are described in further detail in Section IV, and are held fixed in all subsequent SPGR and DESS experiments. To equitably compare optima from different scan profiles, we require T_R := [T_R,1,…, T_R,CSPGR, T_R,CSPGR+1,…, T_{R,CSPGR+CDESS}]^⊤ to satisfy a total time constraint, ||T_R||₁ ≤ T_R,max. For a scan profile consisting of C_SPGR SPGR and C_DESS DESS scans, these constraints collectively reduce the search space dimension from PD to 2(C_SPGR + C_DESS) − 1.

Prior works have considered T₁ or T₂ estimation from as few as 2 SPGR [29, 45] or 1 DESS [35] scan(s), respectively. We likewise elect to optimize the (C_SPGR,C_DESS) ← (2, 1) scan profile as a benchmark. We choose T_R,max ← 2(12.2)+ 1(17.5) = 41.9ms and select other scan profiles capable of meeting this time constraint. Requiring that candidate profiles contain C_DESS ≥ 1 DESS scans for T₂ contrast and satisfy D ≥ L(= 3) for well-conditioned estimation, we note that (1, 1) and (0, 2) are the only other eligible profiles.

In the ensuing experiments, we focus on precise T₁, T₂ estimation in the brain and design latent object parameter ranges 𝒳_t = ℳ_E,t × 𝒯_1,t × 𝒯_2,t and 𝒩_t = 𝒦_t accordingly. Noting that T₁ ~ 10T₂, we choose W ← diag (0, 0.1, 1) in (5) to place roughly equal importance on precise T₁ vs. T₂ estimation. Since W places zero weight on M_E estimation (obviating the need for complex differentiation in (3)), it is easily shown that Ψ depends on M_E only through a constant scale factor; thus it suffices to consider ℳ_E,t ← 1. We select 𝒯_1,t ← [800, 1400]ms and 𝒯_2,t ← [50, 120]ms to correspond with WM and GM regions of interest (ROIs) at 3T [64, 65].We take 𝒦_t ← [0.9, 1.1] to account for 10% spatial variation in flip angle. Broadened ranges 𝒳_b ← 1×[400, 2000]ms×[40, 200]ms and 𝒦_b ← [0.5, 2] are constructed to encourage solutions robust to a wide range of object parameters. We assume constant noise variance ${\sigma }_1^2=\cdots ={\sigma }_D^2:={\sigma }^2$, where σ² ← 1.49 × 10⁻⁷ is selected to reflect measurements from normalized phantom datasets (cf. Sections IV.B.1 and S.V.A-S. V.B for acquisition details). Lastly, we set δ ← 0.01 to select a robust scan parameter P^* with associated worst-case cost Ψ̃^t(P^*) within 1% of global optimum Ψ̃^t(P̆).

C. Scan Profile Comparisons

We solve (6) and (9) via grid search to allow illustration (§S.I in Supplement⁴) of Ψ̃^t(P) as well as worst-case T₁, T₂ standard deviations ${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{t}}(\mathbf{P})$ and ${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{t}}(\mathbf{P})$, each defined as

$${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{t}}(\mathbf{P}):=\underset{\begin{array}{l}\mathbf{x}\in {\mathcal{X}}_{\mathrm{b}}\\ \mathit{\nu }\in {\mathcal{N}}_{\mathrm{b}}\end{array}}{max}{\sigma }_{T_1}(\mathbf{x};\mathit{\nu },\mathbf{P})\text{and}$$ (21)

$${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{t}}(\mathbf{P}):=\underset{\begin{array}{l}\mathbf{x}\in {\mathcal{X}}_{\mathrm{b}}\\ \mathit{\nu }\in {\mathcal{N}}_{\mathrm{b}}\end{array}}{max}{\sigma }_{T_2}(\mathbf{x};\mathit{\nu },\mathbf{P}),$$ (22)

where σ_T1 (x; ν, P) and σ_T2 (x; ν, P) are corresponding diagonal elements of inverse Fisher matrix I⁻¹(x; ν, P). Grid searches for the (2, 1), (1, 1), and (0, 2) profiles each took about 4, 43, and 28 minutes, respectively. All experiments described hereafter were carried out using MATLAB^® R2013a on a 3.5GHz desktop with 32GB RAM.

Table I compares optimized scan parameters for profiles consisting of (2, 1), (1, 1), and (0, 2) SPGR and DESS scans, respectively. In addition to ${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{t}}({\mathbf{P}}^{\ast })$ and ${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{t}}({\mathbf{P}}^{\ast })$, Table I presents analogous worst-case standard deviations ${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{b}}(\mathbf{P})$ and ${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{b}}(\mathbf{P})$ over 𝒳_b × 𝒦_b to show how each estimator degrades over the broadened object parameter range. When viewed over tight range 𝒳_t × 𝒦_t, the (0, 2) profile provides a 11.5% reduction in worst-case cost over the other choices. Extending to broadened range 𝒳_b×𝒦_b, this reduction grows dramatically to 31.4%. We thus observe that while the different optimized profiles afford similar estimator precision over a narrow range of interest, the (0, 2) profile may be preferable due to its robustness to a wide range of object parameters.

TABLE I.

Performance summary of different scan profiles, optimized by solving (9) subject to scan time constraint T_R,max = 41.9ms. The first column defines each profile. The next four columns describe P^*. The latter three pairs of columns show how worst-case σ̃_T1 σ̃_T2, and Ψ̃ values degrade from tight to broad ranges. Flip angles are in degrees; all other values are in milliseconds.

Scan	${\widehat{\alpha }}_0^{\text{spgr}}$	${\widehat{\alpha }}_0^{\text{dess}}$	${\widehat{T}}_R^{\text{spgr}}$	${\widehat{T}}_R^{\text{dees}}$	${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{t}}({\mathbf{P}}^{\ast })$	${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{b}}({\mathbf{P}}^{\ast })$	${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{t}}({\mathbf{P}}^{\ast })$	${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{b}}({\mathbf{P}}^{\ast })$	Ψ̃t(P*)	Ψ̃b(P*)
(2, 1)	(15, 5)°	30°	(12.2, 12.2)	17.5	28	154	1.3	9.1	4.0	17.7
(1, 1)	15°	10°	13.9	28.0	27	169	2.8	8.8	4.9	17.9
(0, 2)	–	(35, 10)°	–	(24.4, 17.5)	21	113	1.5	6.0	3.5	12.2

As the DESS sequence has already found success for T₂ mapping from even one scan [35], it is reassuring but unsurprising that our analysis finds two DESS scans to yield the most precise T₂ estimates. More interestingly, our methods suggest that, with a minimum C_DESS = 2 scans, DESS can be used to simultaneously estimate T₁ as well. In fact, for certain choices of parameter ranges, a second DESS scan is predicted to afford T̂₁ precision comparable to two SPGR scans.

IV. Experimental Validation and Results

To test our approach to optimized scan design (described in Section II.B), we next estimate T₁ and T₂ maps (using maximum-likelihood (ML) and regularized least squares (RLS) methods detailed in Section S.II) from datasets collected using the scan profiles optimized in Section III. In Section IV.A, we study estimator statistics from simulated data. In Sections IV.B–IV.C, we progress to phantom and in vivo datasets to evaluate scan profile performance and estimator robustness under increasingly complex settings. For the latter experiments, we use reference parameter maps from classical (long) pulse sequences, in lieu of ground truth maps.

A. Numerical Simulations

We select T₁ and T₂ WM and GM values based on previously reported measurements at 3T [64, 65] and extrapolate other unimportant latent object parameters M₀ and $T_2^{\ast }$ from measurements at 1.5T [66]. We assign these parameter values to the discrete anatomy of the BrainWeb digital phantom [66, 67] to create ground truth M₀, T₁, T₂, and ${\mathbf{T}}_2^{\ast }$ maps. We then choose acquisition parameters based on Table I (with fixed T_E = 4.67ms) and apply models (20) and (15)–(16) to the 81st slices of these true maps to compute noiseless 217×181 SPGR and DESS image-domain data, respectively.

For each scan profile, we corrupt the corresponding (complex) noiseless dataset F with additive complex Gaussian noise, whose variance σ² ← 1.49 × 10⁻⁷ is set to match CRB calculations. This yields realistically noisy datasets Y ranging from 105–122 SNR, where SNR is defined here as

$$\text{SNR}(\mathbf{F},\mathbf{Y}):=\frac{{\Vert \mathbf{F}\Vert }_F}{{\Vert \mathbf{Y}-\mathbf{F}\Vert }_F}.$$ (23)

We use each profile’s noisy magnitude dataset |Y| to compute estimates M̂_E, T̂₁, and T̂₂ (images and histograms in Section S.III). We then evaluate estimator bias and variance from latent ground truth T₁ and T₂ maps.

In these simulations, we intentionally neglect to model a number of physically realistic effects because their inclusion would complicate study of estimator statistics. First and foremost, we assume knowledge of a uniform transmit field, to avoid confounding $B_1^{+}$ and T₁, T₂ estimation errors. For a similar reason, spatial variation in the sensitivity of a single receive coil is also not considered. We omit modeling partial volume effects to ensure deterministic knowledge of WM and GM ROIs. We will explore the influence of these (and other) nuisance effects on scan design in later subsections.

To isolate bias due to estimator nonlinearity from regularization bias, we minimize the ML initialization cost (S.1) only, and do not proceed to solve RLS problem (S.2). This permits consideration of T₁, T₂ estimation from each of the 7733 WM or 9384 GM data points as voxel-wise independent realizations of the same estimation problem. To minimize quantization bias, we optimize (S.1) using a very finely spaced dictionary of signal vectors from 1000 T₁ and T₂ values logarithmically spaced between [10², 10^3.5] and [10¹, 10^2.5], respectively. Using 10⁶ dictionary elements, solving (S.1) took less than 7 minutes for each tested scan design P^*.

Table II⁵ verifies that, despite model nonlinearity and Rician noise, estimation bias in WM- and GM-like voxels is negligible. Sample standard deviations are consistent with ${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{t}}$ and ${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{t}}$ (cf. Table I). In WM and GM, we observe that the (1, 1) and (0, 2) profiles afford high ${\widehat{\mathbf{T}}}_1^{\text{ML}}$ precision, while the (2, 1) and (0, 2) scans afford high ${\widehat{\mathbf{T}}}_2^{\text{ML}}$ precision. In agreement with the predictions of Ψ̃^t and Ψ̃^b, these simulation studies suggest that at these SNR levels, an optimized profile containing 2 DESS scans can permit T₁ and T₂ estimation precision in WM and GM comparable to optimized profiles containing SPGR/DESS combinations.

TABLE II.

Sample means ± sample standard deviations of T₁ and T₂ ML estimates in WM and GM ROIs of simulated data, compared across different optimized scan profiles. Sample means exhibit insignificant bias, and sample standard deviations are consistent with worst-case standard deviations ${\stackrel{\sim }{\sigma }}_{T_1}^{\mathrm{t}}$ and ${\stackrel{\sim }{\sigma }}_{T_2}^{\mathrm{t}}$ reported in Table I. All values are reported in milliseconds.

Scan	(2, 1)	(1, 1)	(0, 2)	Truth
WM ${\widehat{T}}_1^{\text{ML}}$	830 ± 17	830 ± 15	830 ± 14	832
GM ${\widehat{T}}_1^{\text{ML}}$	1330 ± 30.	1330 ± 24	1330 ± 24	1331
WM ${\widehat{T}}_2^{\text{ML}}$	80. ± 1.0	80. ± 2.1	79.6 ± 0.94	79.6
GM ${\widehat{T}}_2^{\text{ML}}$	110. ± 1.4	110. ± 3.0	110. ± 1.6	110

B. Phantom Experiments

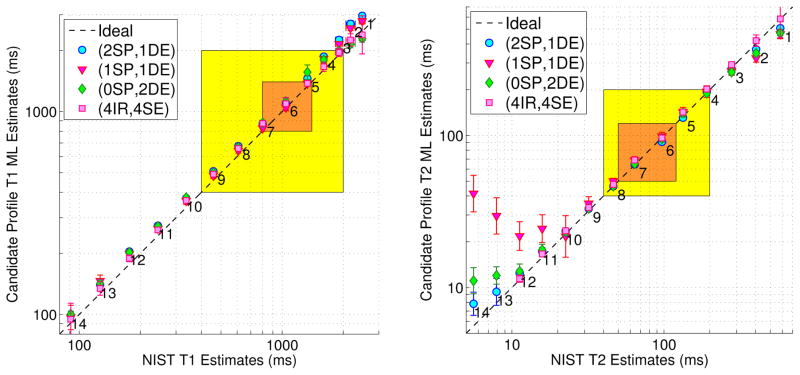
This subsection describes two experiments. In the first experiment, we compare the SPGR/DESS scan profiles described in Table I (as well as a reference profile consisting of IR and SE scans) against nuclear magnetic resonance (NMR) measurements from the National Institute for Standards and Technology (NIST) [68]. These measurements provide information about ROI sample means and ROI sample standard deviations (Fig. 1), which we define as first- and second-order statistics computed across voxels within an ROI. In the second experiment, we repeat the SPGR/DESS scan profiles 10 times and compute sample standard deviation maps across repetitions (not shown). Taking ROI sample means of these maps gives pooled sample standard deviations (Table III), which indicate relative scan profile precision.

Fig. 1.

Phantom within-ROI sample statistics of T₁ and T₂ ML estimates from optimized SPGR/DESS and reference IR/SE scan profiles, vs. NIST NMR measurements [68]. Markers and error bars indicate ROI sample means and ROI sample standard deviations within the 14 labeled and color-coded vials in Fig. S.7. Tight 𝒳_t and broad 𝒳_b latent parameter ranges are highlighted in orange and yellow, respectively. Fig. S.8 provides analogous plots for RLS estimates. Table S.2 replicates sample statistics within Vials 5–8. Our MR measurements are at 293K, while NIST NMR measurements are at 293.00K. Within the designed parameter ranges, estimates from different acquisitions are in reasonable agreement with NIST measurements.

TABLE III.

Phantom pooled sample standard deviations ± pooled standard errors of sample standard deviations, from optimized SPGR/DESS scan profiles. Each entry is a measure of uncertainty of a typical voxel’s T₁ or T₂ ML estimate. For sake of brevity, sample statistics corresponding only to phantom vials within (or nearly within) tight design range 𝒳_t (color-coded orange in Fig. S.7) are reported. ‘V#’ abbreviates vial numbers. All values are reported in milliseconds.

	(2SP,1DE)	(1SP,1DE)	(0SP,2DE)
V5 ${\widehat{\sigma }}_{{\widehat{T}}_1^{\text{ML}}}({\mathbf{P}}^{\ast })$	50 ± 12	40 ± 10.	39 ± 9.4
V6 ${\widehat{\sigma }}_{{\widehat{T}}_1^{\text{ML}}}({\mathbf{P}}^{\ast })$	70 ± 18	60 ± 15	70 ± 16
V7 ${\widehat{\sigma }}_{{\widehat{T}}_1^{\text{ML}}}({\mathbf{P}}^{\ast })$	60 ± 13	50 ± 13	50 ± 13
V8 ${\widehat{\sigma }}_{{\widehat{T}}_1^{\text{ML}}}({\mathbf{P}}^{\ast })$	23 ± 5.4	20. ± 4.7	18 ± 4.3

	(2SP,1DE)	(1SP,1DE)	(0SP,2DE)
V5 ${\widehat{\sigma }}_{{\widehat{T}}_2^{\text{ML}}}({\mathbf{P}}^{\ast })$	2.6 ± 0.63	6 ± 1.4	3.5 ± 0.84
V6 ${\widehat{\sigma }}_{{\widehat{T}}_2^{\text{ML}}}({\mathbf{P}}^{\ast })$	1.9 ± 0.46	5 ± 1.1	2.3 ± 0.54
V7 ${\widehat{\sigma }}_{{\widehat{T}}_2^{\text{ML}}}({\mathbf{P}}^{\ast })$	1.4 ± 0.34	3.4 ± 0.80	1.5 ± 0.35
V8 ${\widehat{\sigma }}_{{\widehat{T}}_2^{\text{ML}}}({\mathbf{P}}^{\ast })$	1.1 ± 0.26	3.5 ± 0.84	1.4 ± 0.33

1) Within-ROI Statistics

We acquire combinations of (2, 1), (1, 1), and (0, 2) SPGR and DESS coronal scans of a High Precision Devices^® MR system phantom T₂ array. For each scan profile, we prescribe the optimized flip angles α̂₀ and repetition times T̂_R listed in Table I, and hold all other scan parameters fixed. We achieve the desired nominal flip angles by scaling a 20mm slab-selective Shinnar-Le Roux excitation [69], of duration 1.28ms and time-bandwidth product 4. For each DESS (SPGR) scan, we apply 2 (10) spoiling phase cycles over a 5mm slice thickness. We acquire all steady-state phantom and in vivo datasets with a 256 × 256 × 8 matrix over a 240 × 240 × 30 mm³ field of view (FOV). Using a 31.25kHz readout bandwidth, we acquire all data at minimum T_E ← 4.67ms before or after RF excitations. To avoid slice-profile effects, we sample k-space over a 3D Cartesian grid. After Fourier transform of the raw datasets, only one of the excited image slices is used for subsequent parameter mapping. Including time to reach steady-state, each steady-state scan profile requires 1m37s scan time.

To validate a reference scan profile for use in in vivo experiments, we also collect 4 IR and 4 SE scans. For (phase-sensitive, SE) IR, we hold (T_R, T_E) ← (1400, 14)ms fixed and vary (adiabatic) inversion time T_I ∈ {50, 150, 450, 1350}ms across scans. For SE, we similarly hold T_R ← 1000ms fixed and vary echo time T_E ∈ {10, 30, 60, 150}ms across scans. We prescribe these scan parameters to acquire 256×256 datasets over the same 240 × 240 × 5 mm³ slice processed from the SPGR/DESS datasets. Each IR and SE scan requires 5m58s and 4m16s, for a total 40m58s scan time.

We additionally collect a pair of Bloch-Siegert shifted 3D SPGR scans for separate ${\mathbf{B}}_1^{+}$ estimation [70]. We insert a 9ms Fermi pulse (peak amplitude $B_1^{\text{pk}}\leftarrow 0.075\mathrm{G}$) at ±8 kHz off-resonance into an SPGR sequence immediately following on-resonant excitation. We estimate regularized ${\widehat{\mathbf{B}}}_1^{+}$ maps [71] from the resulting pair of datasets. We then estimate flip angle variation κ̂ as ${\widehat{\mathbf{B}}}_1^{+}/B_1^{\text{pk}}$, calibrate κ̂ (via separate measurements described in Section S.IV), and thereafter take κ as known. For consistency, we account for flip angle variation when estimating T₁ and T₂ from both the candidate (SPGR/DESS) and reference (IR/SE) aforementioned scan profiles. With a repetition time of 21.7ms, this ${\mathbf{B}}_1^{+}$ mapping acquisition requires 1m40s total scan time.

Fig. 1 plots sample means and sample standard deviations computed within circular ROIs of phantom T₁ and T₂ ML estimates (reconstruction details, analogous plots for RLS estimates, and images in Sections S.V.A–S.V.C). The highlighted orange and yellow parameter spaces correspond to design ranges 𝒳_t and 𝒳_b. T₁ estimates from both the candidate (2, 1), (1, 1), and (0, 2) (SPGR, DESS) and reference (4, 4) (IR, SE) profiles are in reasonable agreement with NIST estimates [68] across the vial range. T₂ estimates from all profiles are also in good agreement with NIST for vials within 𝒳_b. SPGR/DESS profiles likely underestimate large T₂ values (≥200ms) due to greater influence of diffusion in DESS [59–61]. SPGR/DESS profiles possibly overestimate and the IR/SE profile likely underestimates short (≤30ms) and very short (≤15ms) T₂ values, respectively, due to poorly conditioned estimation.

2) Across-Repetition Statistics

In a second study, we repeat the (2, 1), (1, 1), and (0, 2) scan profiles 10 times each and separately estimate T₁ and T₂ for each repetition of each scan profile. We then estimate the standard deviation across repetitions on a per-voxel basis, to produce sample standard deviation maps for each profile. Each ROI voxel of the sample standard deviation map is a better estimate of the population standard deviation (which the CRB characterizes) than the ROI sample standard deviation from a single repetition, because the latter estimate is contaminated with slight spatial variation of voxel population means (due to imaging non-idealities such as Gibbs ringing due to k-space truncation).

Table III reports pooled sample standard deviations and pooled standard errors of the sample standard deviations (computed via expressions in [72]) for phantom vials within (or nearly within) tight design range 𝒳_t (marked orange in Fig. S.7). Due to error propagation from coil combination and κ̂ estimation, pooled ML sample standard deviations cannot be compared in magnitude to worst-case predicted standard deviations (Table I); however, trends of empirical and theoretical standard deviations are overall similar. In particular, the optimized (0, 2) DESS-only scan profile affords T₁ ML estimation precision (in vials whose T₁, T₂ is similar to that of WM/GM) comparable to optimized (2, 1) and (1, 1) mixed (SPGR, DESS) profiles. Also in agreement with predictions, the optimized (2, 1) and (0, 2) profiles afford greater T₂ ML estimation precision than the optimized (1, 1) profile.

C. In Vivo Experiments

In a single long study of a healthy volunteer, we acquire the same optimized scan profiles containing (2, 1), (1, 1), and (0, 2) SPGR and DESS scans (cf. Table I), as well as the reference profile containing (4, 4) IR and SE scans. We obtain axial slices from a 32-channel Nova Medical^® receive head array. To address bulk motion between acquisitions and to compare within-ROI statistics, we rigidly register each coil-combined image to an IR image (details in Section S.V.D) prior to parameter mapping. All acquisition (cf. Section IV.B.1) and reconstruction (cf. Sections S.V.A–S.V.B) details are otherwise the same as in phantom experiments.

Fig. 2 compares brain T₁ and T₂ ML estimates from optimized scan profiles (Fig. S.9 and Fig. S.10 provide corresponding colorized and grayscale RLS estimates, respectively). Though in-plane motion is largely compensated via registration, through-plane motion and non-bulk motion likely persist, and will influence ROI statistics. Due to motion (and scan duration) considerations, we examine within-ROI statistics from a single repetition as in Section IV.B.1, and do not attempt across-repetition statistics as in Section IV.B.2.

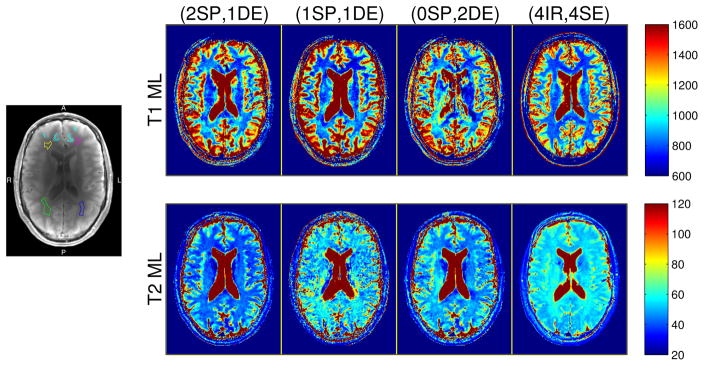
Fig. 2.

Left: WM and GM ROIs, overlaid on a representative anatomical (coil-combined IR) image. Separate WM ROIs are distinguished with anterior/posterior (A/P) and right/left (R/L) directions. Four small anterior cortical GM polygons are pooled into a single ROI (cyan). Right: Colorized T₁ and T₂ ML estimates from the brain of a healthy volunteer. Columns correspond to profiles consisting of (2 SPGR, 1 DESS), (1 SPGR, 1 DESS), (0 SPGR, 2 DESS), and (4 IR, 4 SE) acquisitions. Parameter maps are cropped in post-processing for the purpose of display. Figs. S.9 (colorized) and S.10 (grayscale) provide analogous full-FOV maps estimated via both ML and RLS estimators. Colorbar ranges are in milliseconds.

Visually, T̂₁ maps from steady-state profiles exhibit similar levels of contrast in WM/GM regions well away from cerebrospinal fluid (CSF) as that seen in the reference T̂₁ estimate. Since we did not optimize any scan profiles for estimation in high-T₁ regions, it is expected that greater differences may emerge in voxels containing or nearby CSF. In particular, T₁ is significantly underestimated within and near CSF by the (0, 2) DESS-only profile. This suggests that with the signal models used in this work, including at least one SPGR scan in an optimized profile may offer greater protection against estimation bias in high-T₁ regions.

Table IV summarizes within-ROI sample means and sample standard deviations computed⁶ over four separate WM ROIs containing 96, 69, 224, and 148 voxels and one pooled cortical GM ROI containing 156 voxels (cf. Fig. 2). Within-ROI T̂₁ sample standard deviations are comparable across steady-state profiles. In agreement with Table I, T₂ estimates from the optimized (1, 1) scan profile exhibit higher within-ROI sample variation than corresponding (2, 1) and (0, 2) T̂₂ maps.

TABLE IV.

Within-ROI sample means ± within-ROI sample standard deviations of T₁ and T₂ ML estimates from the brain of a healthy volunteer. Sample statistics are computed within ROIs indicated in Fig. 2. All values are reported in milliseconds.

	ROI (color)	(2SP,1DE)	(1SP,1DE)	(0SP,2DE)	(4IR,4SE)
${\widehat{T}}_1^{\text{ML}}$	anterior right WM (yellow)	840 ± 32	770 ± 31	840 ± 43	780 ± 22
	anterior left WM (magenta)	740 ± 61	660 ± 45	740 ± 55	760 ± 24
	posterior right WM (green)	890 ± 88	860 ± 72	960 ± 84	810 ± 26
	posterior left WM (blue)	860 ± 70.	850 ± 61	880 ± 79	820 ± 37
	anterior GM (cyan)	1200 ± 210	1200 ± 230	1300 ± 230	1300 ± 180
${\widehat{T}}_2^{\text{ML}}$	anterior right WM (yellow)	40. ± 1.3	54 ± 3.8	46 ± 1.5	55 ± 1.9
	anterior left WM (magenta)	40. ± 1.7	50. ± 4.5	44 ± 1.7	53 ± 1.8
	posterior right WM (green)	43 ± 2.7	60. ± 6.9	51 ± 3.6	59 ± 2.1
	posterior left WM (blue)	43 ± 1.8	57 ± 4.9	49 ± 2.5	57 ± 1.8
	anterior GM (cyan)	50 ± 12	60 ± 15	60 ± 11	59 ± 6.0

In most cases, T̂₁ within-ROI sample means from optimized SPGR/DESS scan profiles do not deviate substantially from each other or from reference IR/SE measurements. Two notable exceptions are ${\widehat{T}}_1^{\text{ML}}$ in anterior left and posterior right WM from (1, 1) and (0, 2) profiles: these estimates are significantly lower and higher than analogous estimates from other profiles, respectively. Results thus suggest that the optimized (2, 1) scan profile yields WM ${\widehat{T}}_1^{\text{ML}}$ estimates that are more consistently similar to IR WM ${\widehat{T}}_1^{\text{ML}}$ estimates than other optimized SPGR/DESS profiles.

Systematic differences in T̂₂ sample means are evident across scan profiles, particularly within WM ROIs. Curiously, the (1, 1) profile agrees most consistently (in WM/GM ${\widehat{T}}_2^{\text{ML}}$ within-ROI sample mean) with reference estimates, though with relatively high sample variation. The (2, 1) and (0, 2) SPGR/DESS profiles produce consistently lower WM ${\widehat{T}}_2^{\text{ML}}$ than the reference IR/SE profile, though the (0, 2) profile is in reasonable agreement with other steady-state estimates [73].

These discrepancies may due to differences in sensitivity to multi-compartmental relaxation [74]. Specifically, different signal models with different scan parameter choices might be more or less sensitive to the model mismatch incurred by neglecting to distinguish the multiple T₂ components within each voxel. Section S.VI studies T₂ estimation bias due to multi-compartmental relaxation in more detail.

V. Discussion and Future Work

Phantom experiments show that optimized scan profiles consisting of (2, 1), (1, 1), and (0, 2) (SPGR, DESS) scans yield accurate WM/GM T₁, T₂ estimates, and that empirical precision trends across profiles agree reasonably with CRB-based predictions. However, in vivo experiments reveal that even with scan optimization, it may be challenging to achieve clinically viable levels of precision from the aforementioned steady-state profiles, at least at 3T. At the expense of greater scan time, it is of course possible that optimized profiles containing greater numbers of SPGR, DESS, and/or other steady-state scans can provide clinically acceptable precision levels. For these and other more complicated scan profiles, estimator dependence on scan parameters becomes even less intuitive, increasing the need for scan design.

The proposed scan design framework addresses spatial variation in object parameters through a min-max design criterion. The min-max criterion guarantees an upper bound on a weighted sum of variances and assumes no prior knowledge of distributions. However, in general it is non-differentiable in P, precluding gradient-based optimization. Furthermore, it is conservative by nature, and often selects scan parameters based on corner cases of the object parameter space. To reduce the influence of corner cases, it may be desirable to instead construct a cost function related to the coefficient of variation as in [44, 46–48], perhaps by setting parameter weights W⁻¹ ← diag (x) for x ≠ 0 in (5).

As a less conservative alternative to min-max design, other recent works [50, 51] have addressed object parameter spatial variation by instead constructing cost functions related to the Bayesian CRB [75], which characterizes the expected precision with respect to a prior distribution on object parameters. Bayesian cost functions are usually differentiable and can also, with appropriate priors, penalize object parameter coefficients of variation instead of variances, as in [50]. However, prior distributions are generally unknown, and may need to be estimated from data, as in [51].

Careful calibration of flip angle scaling κ is essential for accurate T₁,T₂ estimation from SPGR/DESS scan profiles. In this work, we estimate κ from separate acquisitions and adjust nominal flip angles prior to reconstruction, but acknowledge that non-idealities in those separate acquisitions may themselves cause resultant ${\widehat{\mathbf{B}}}_1^{+}$ errors to propagate into our T₁,T₂ estimates. To reduce error propagation, it may be desirable to instead design scan profiles to permit joint estimation of κ, in addition to other latent object parameters. Unfortunately, we find that optimizing the (2, 1) or (0, 2) profile to allow for four-parameter x(r) := [M_E(r), T₁(r), T₂(r), κ(r)]^⊤ estimation results in unacceptably high amplification of the worst-case T₁ standard deviation. (Incidentally, precise T₂ ML and RLS estimation alone from the (2, 1) or (0, 2) profile is possible [42].) It remains an open scan design question as to whether time spent collecting Bloch-Siegert data for separate ${\mathbf{B}}_1^{+}$ mapping could instead be better spent collecting additional SPGR, DESS, and/or other data for joint estimation.

By working with closed-form signal expressions, we neglect to model several higher-order effects. However, it is apparent that the nonlinear estimation procedures required for many mapping problems can amplify the influence of these secondary effects, often inducing substantial bias. Since the CRB (as described) applies only to unbiased estimators, it is thus desirable to use signal models that are as complete as possible for CRB-based scan design. In theory, scan optimization approach (9) is even compatible with acquisitions where a closed-form model relating data to latent and scan parameters is unknown, as in [22, 76]. In practice, difficulties arise in efficient computation of signal gradients required in (3), which may demand more specialized techniques, as in [77]. Designing scan profiles involving such complex signal models would likely necessitate optimization techniques more involved than the simple grid searches used in this work.

VI. Conclusion

We have introduced a CRB-inspired min-max optimization approach to aid robust, application-specific MR scan selection and optimization for precise parameter estimation. As a detailed example, we have optimized combinations of fast SPGR and DESS scans for T₁, T₂ relaxometry in WM and GM regions of the human brain at 3T. Numerical simulations show that at typical noise levels and with accurate flip angle prior knowledge, WM- and GM-like T₁, T₂ ML estimates from optimized scans are nearly unbiased, and so worst-case CRB predictions yield reliable bounds on ROI sample variances. Phantom accuracy experiments show that optimized combinations of (2, 1), (1, 1), or (0, 2) (SPGR, DESS) scans are in excellent agreement with NIST and IR/SE measurements over the designed latent object parameter range of interest. Phantom precision experiments show that these SPGR/DESS combinations exhibit trends in pooled sample standard deviations that reasonably reflect CRB predictions. In vivo experiments suggest that with optimization, the (0, 2) profile can yield comparable T̂₁, T̂₂ precision to the more conventional (2, 1) [42] scan profile in well-isolated WM/GM ROIs; however, the (0, 2) T₁ estimates are unreliable within and near the CSF and do not agree with IR measurements in WM as consistently as the (2, 1) profile. This and other disagreements across profiles in vivo may be attributable to differences in signal model sensitivities to neglected higher-order effects. Nevertheless, this simple example application illustrates that scan optimization may enable new parameter mapping techniques from established pulse sequences.