HIV-1 Capsid Function is Regulated by Dynamics: Quantitative Atomic-Resolution Insights by Integrating Magic-Angle-Spinning NMR, QM/MM, and MD

Abstract

HIV-1 CA capsid protein possesses intrinsic conformational flexibility, which is essential for its assembly into conical capsids and interactions with host factors. CA is dynamic in the assembled capsid, and residues in functionally important regions of the protein undergo motions spanning many decades of timescales. Chemical shift anisotropy (CSA) tensors, recorded in magic-angle-spinning NMR experiments, provide direct residue-specific probes of motions on nano- to microsecond timescales. We combined NMR, MD, and Density-Functional-Theory calculations, to gain quantitative understanding of internal backbone dynamics in CA assemblies, and found that the dynamically averaged ¹⁵N CSA tensors calculated by this joined protocol are in remarkable agreement with experiment. Thus, quantitative atomic-level understanding of the relationships between CSA tensors, local backbone structure and motions in CA assemblies is achieved, demonstrating the power of integrating NMR experimental data and theory for characterizing atomic-resolution dynamics in biological systems.

Graphical Abstract

INTRODUCTION

HIV-1 capsids, assembled from ~1,500 copies of the capsid (CA) protein, are an internal part of mature virions (Figure 1).^1,2 Conical in shape, capsids enclose the viral genome together with several proteins that are essential for viral replication.³ During HIV-1 entry, intact capsids are released into the cytoplasm of the host cell, followed by disassembly (uncoating), which takes place in a tightly orchestrated fashion. The net result of these events is the integration of the reverse transcribed viral DNA into the host genome, necessary for viral replication.^4,5

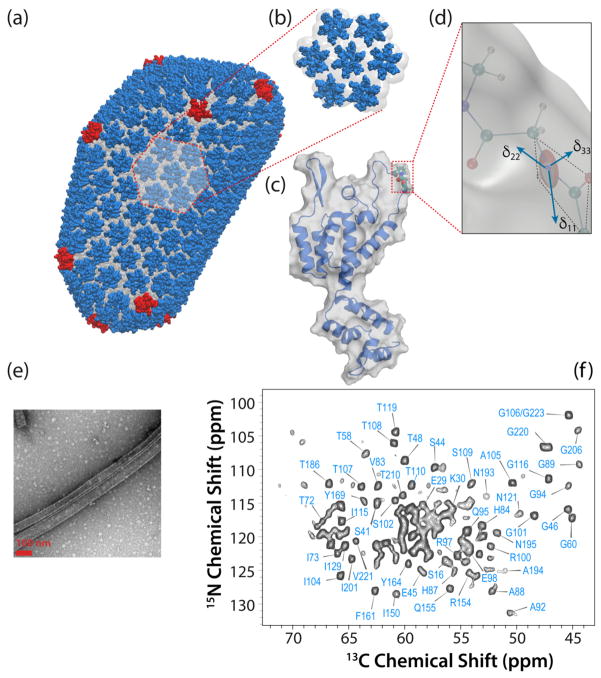
Figure 1.

a) All-atom model of mature HIV-1 capsid determined by an integrated cryo-ET, solution NMR, and MD approach (PDBID: 3J3Y ⁶). Hexameric (predominant) and pentameric (minor) building blocks are shown in blue and red, respectively. b) Hexamer of hexamers (HOH), a predominant structural element of the capsid. c) 3D structure of an HIV-1 CA monomer (PDB file 3NTE). d) Illustration of a backbone ¹⁵N^H CSA tensor and its orientation in the protein molecular frame, e) Transmission electron microscopy (TEM) image of tubular assemblies of CA HXB2. f) A 2D NCA spectrum of tubular assemblies of U-¹³C, ¹⁵N CA, recorded at 21.1 T and the MAS frequency of 14 kHz.

Capsids are pleomorphic comprised of varied number of copies of CA protein structural blocks, with variable curvature in the capsid shell and overall appearance. Pleomorphism is directly related to the conformational plasticity of the CA protein.⁷ Remarkably, in the assembled state, CA is dynamic over a range of timescales from nano- to milliseconds.^6,8–10 Specifically, motions in the linker, which connects the CA’s N- and C-terminal domains (NTD and CTD) occur on the milliseconds timescale, and are directly linked to capsid’s ability to assemble into varied morphologies.⁸ These motions, coupled with pH-dependent electrostatic interactions may contribute to assembly control, involving a molecular switch.⁸

In the host cells, capsid interacts with host proteins. These interactions can either facilitate or inhibit the HIV-1 replication. One such protein is Cyclophilin A (CypA), which is required for the virus to be active in certain cell types.^11,12 CypA interacts with the capsid by binding to the CypA loop located in CA’s NTD, and mutants in the CypA loop can escape from CypA dependence. For instance, the A92E and G94D CA escape mutants are fully infectious when CypA/CA interactions are inhibited, while in the presence of CypA these mutants retain only ~10% of infectivity. It has been proposed that CypA plays a role in stabilizing the capsid through a novel binding interface, where one CypA molecule bridges two CA hexamers, along the highest-curvature direction.¹³

CA/CypA interactions modulate capsid dynamics, and the virus takes advantage of this effect to escape from the CypA dependence. Specifically, CypA binding attenuates the motions of the CypA loop and also induces allosteric conformational changes in other regions of the protein. Remarkably, the dynamic behavior A92E and G94D CA mutants closely resembles that of the CA/CypA assembly, and dynamic allosteric regulation mechanism was proposed to explain the capsid’s escape from CypA dependence.¹⁰

Internal dynamics of CA also play a role in HIV-1 maturation. Initially, during virus budding from the host cell, the Gag polyprotein, which contains the main structural proteins of HIV (MA, CA, MA, NC, and p6), is a single polypeptide chain. During maturation, Gag is proteolytically cleaved into the individual domains by the HIV protease in an orderly, stepwise fashion. The final step is the cleavage of a 14-residue spacer peptide 1 (SP1) from the CA-SP1 maturation intermediate to release CA, which in turn organizes into the conical cores characteristic of mature virions. In CA-SP1, the SP1 peptide is highly flexible and its presence affects the mobility of distal residues, such as those in the CypA loop.¹⁴ Clearly, dynamic regulation is an important ingredient in the final maturation step, and the above-described studies highlight the importance of understanding residue-specific conformational dynamics in HIV-1 capsid assemblies, given the direct relationship between dynamics and virus function.

Previously, we analyzed ¹H-¹⁵N/¹H-¹³C/¹⁵N-¹³C dipolar interactions as well as resonance intensities and linewidths, demonstrating the power of combining MAS NMR and MD simulations for determining the motional modes of the individual residues. Here, we focus on ¹⁵N chemical shift anisotropy (CSA) tensors as sensitive probes of nano- to microsecond dynamics in HIV-1 capsid assemblies. We integrate quantum mechanics/molecular mechanics (QM/MM) calculations of magnetic shielding anisotropy, using Density Functional Theory (DFT), with MD simulations and MAS NMR to gain quantitative insights into the effects of dynamic averaging on CSA tensors. We show that the experimental and calculated ¹⁵N CSA tensors are in remarkable agreement, including those for dynamic residues, such as in the CypA-binding loop, and that dynamic averaging of chemical shifts has to be taken into account. The integrated approach described here is broadly applicable to any system and is particularly important in NMR-based structure determination of dynamic regions in protein assemblies.

RESULTS AND DISCUSSION

Experimental NMR parameters

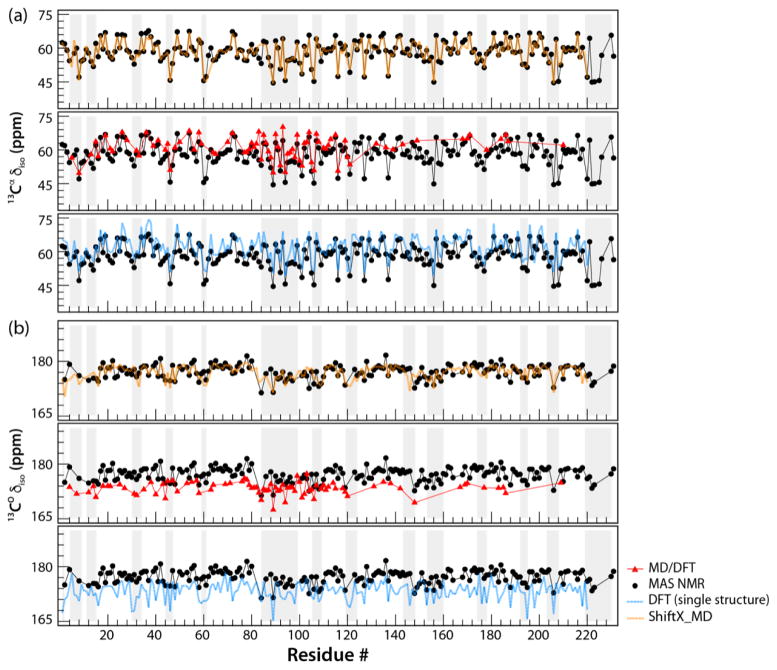
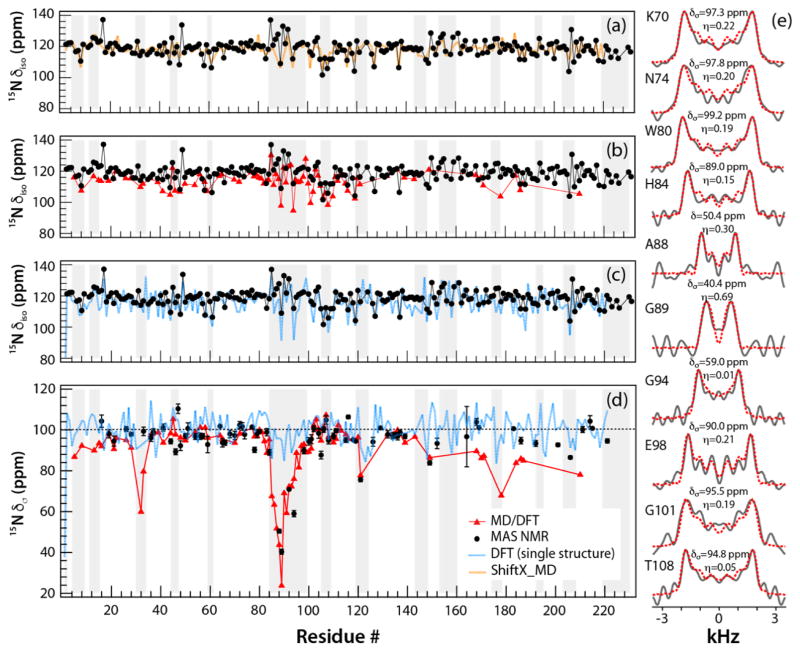
Tubular assemblies of HIV-1 CA yield highly resolved MAS NMR spectra (Figure 1), and permitted assignments ¹³C^α, ¹³C° and ¹⁵N chemical shifts for 222, 188, and 210 residues, respectively. Backbone ¹⁵N CSA tensors for individual residues were derived from a 3D R14₂⁵-symmetry based RNCSA experiment.^15,16 The experimental ¹⁵N, ¹³C^α, and ¹³C° isotropic chemical shifts, δ_iso are plotted vs. residue number in Figure 2 and 3, and reduced anisotropy parameters in Fig. 3d as well as CSA lineshapes are shown in Fig. 3e and Fig. S1 (Supplementary Information).

Figure 2.

The backbone isotropic chemical shift parameters in tubular assemblies of CA, plotted as a function of the residue number: (a) ¹³C^α δ_iso and (b) ¹³C° δ_iso. The parameters are shown as follows: isotropic chemical shifts recorded from NMR experiments, black; calculated by MD/DFT, red; calculated by DFT from a single X-ray structure, blue; calculated by ShiftX, orange. The grey rectangles denote the loop regions of CA protein.

Figure 3.

The backbone ¹⁵N^H chemical shift parameters in tubular assemblies of CA, plotted as a function of the residue number: δ_iso (a–c) and δ_σ (d). The parameters are shown as follows: isotropic chemical shifts or reduced chemical shift anisotropy recorded from 3D RNCSA NMR experiments, black; calculated by MD/DFT, red; calculated by DFT from a single X-ray structure, blue; calculated by ShiftX, orange. The error bars are shown on the experimental δ_σ values. The grey rectangles denote the loop regions of CA protein, (e) Experimental (solid black lines) and simulated (dashed red lines) ¹⁵N^H RNCSA lineshapes plotted for selected CA residues; the best fit CSA parameters are indicated above each spectrum.

It is well known from solution NMR studies that isotropic chemical shifts are modulated by dynamics,¹⁷ and MD simulations in conjunction with empirical ShiftX-based calculations were reported to explain the dynamic averaging of δ_iso in RNaseH.¹⁸ Here, for CA assemblies, large variation in ¹⁵N, ¹³C^α, and ¹³C° δ_iso is seen for the different residues, and the extent of variability is generally greater for the loop vs. the helical regions of CA (Fig. S2, Supplementary). However, no obvious trends that would suggest the presence of motions in specific regions of the protein can be noted. In contrast, the experimental reduced anisotropy parameters of the ¹⁵N CSA tensors, δ_σ, are dramatically different along the CA sequence, see Fig. 3d. Most notably, the residues in CypA loop exhibit low δ_σ values for A88, G89, A92, and G94 of 50.4, 40.3, 70.9, and 59.0 ppm, respectively (the corresponding rigid-limit values are 96.0, 95.3, 102.6, and 92.8 ppm, based on a DFT calculation using X-ray structure geometry; PDBID: 3NTE). While it is known that differences in the secondary structure and local interactions (hydrogen bonding and solvent interactions) affect the ¹⁵N CSA tensors in proteins,^19,20 the dramatic reduction of δ_σ observed for the residues in the CypA loop residues, compared to the rigid value limits, cannot be explained by a structural effect alone. Greatly attenuated δ_σ values were also observed for several other residues, primarily in loop regions of both, the NTD and CTD.

We previously demonstrated via a combined MAS NMR and MD simulations approach, using ¹H-¹⁵N/¹³C^α dipolar tensors, that residues in loop regions are mobile, with those in the CypA loop unusually flexible on the nano- to microseconds timescale.¹⁰ Therefore, we hypothesized that these internal motions may cause partial averaging of the backbone CSA tensors, similar to the dynamic effects on CSA tensors observed in other proteins.^21,22 This notion was examined in the present study.

Understanding the Mechanism of Dynamic CSA Averaging by Integrating NMR, MD, and QM/MM Calculations

To test the hypothesis that dynamics influence CSA tensors in CA assemblies in a major way, we computed CSA tensors using a QM/MM approach, with the quantum region being treated at the DFT level. In parallel we also calculated isotropic shifts by ShiftX.²³ These calculations were carried out for a monomer extracted from the CA X-ray structure (PDBID: 3NTE) as well as for individual CA substructures, using the reported 100-ns MD trajectories.¹⁰

As evidenced from the data in Fig. 2 and Fig. 3, the ShiftX-based predictions of isotropic chemical shifts agree well with the NMR experiments, because these calculations, by nature of their database driven properties, take into account dynamic averaging of isotropic shifts for mobile regions, as reported previously by several groups.^24–27 On the other hand, DFT-calculated values based on the CA X-ray structure are not in agreement with experiment, neither for the reduced anisotropy parameters nor the isotropic shifts. For example, the experimental ¹⁵N δ_σ vary over a large range, from 40.4 ppm to 106.3 ppm, while the calculated ¹⁵N δ_σ exhibit only small variations (99.0 ± 15.4 ppm). RMSD values from DFT calculations are 6.2, 4.4, and 12.6 ppm for ¹⁵N δ_σ, ¹³C δ_iso, and ¹⁵N δ_σ, respectively. Furthermore, no correlation with secondary structure is seen and residues in CypA-binding loop were not predicted to have uniquely attenuated anisotropy. Likewise, the calculated isotropic ¹⁵N, ¹³C^α, and ¹³C° shifts do not reproduce the experimental parameters.

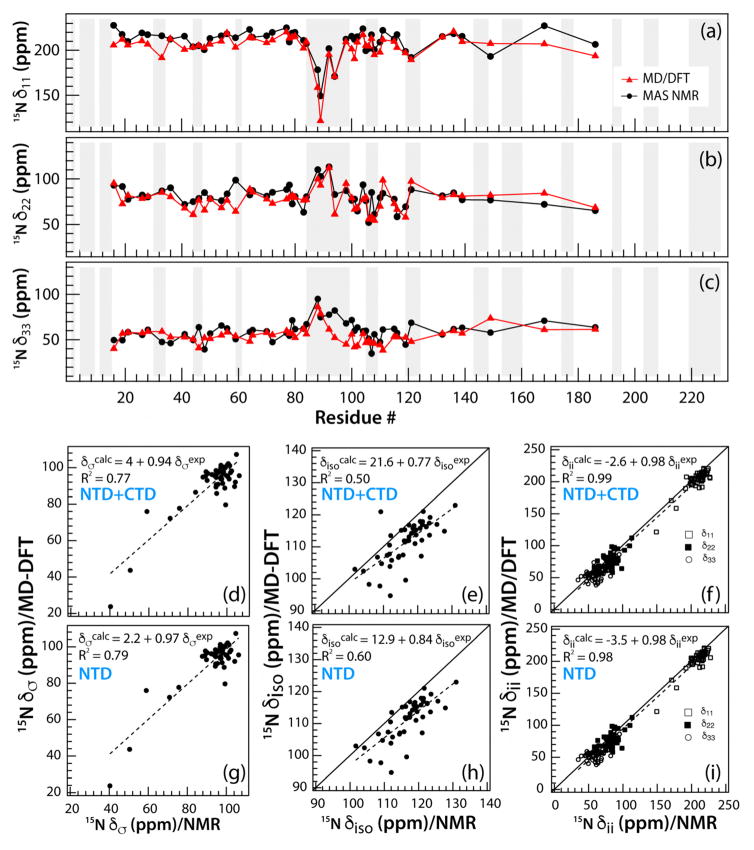
In contrast, the dynamically averaged ¹⁵N CSA tensors computed by MD/DFT are generally in remarkably good agreement with experiment, as shown in Figures 3–4. Importantly, the dramatic reduction in ¹⁵N δ_σ values for the CypA-loop residues that was observed experimentally is captured in the computations, indicating that this decrease is caused by internal loop dynamics rather than by structural effects. This finding is consistent with our prior results from dipolar tensors.¹⁰ In addition, the extent of CSA averaging increases for the residues in the middle of the CypA loop, where the largest motional amplitudes and extensive sampling of conformational space is expected.¹⁰ An outlier in that regard is G89, for which the computational results suggest a considerably smaller ¹⁵N δ_σ (23.75 ppm) than the experimentally observed value (40.3 ppm). While such a deviation in δ_σ values is generally considered to be acceptable for quantum mechanical calculations, it may also be the result of insufficient sampling, due to the length of the MD trajectory.

Figure 4.

(a–c) The backbone ¹⁵N^H principal components of the CSA tensors, δ_ii, in tubular assemblies of CA, plotted as a function of the residue number. The experimental values obtained from 3D RNCSA are shown in black; the values calculated by MD/DFT are in red. (d–i) The MD-DFT calculated CSA tensor parameters, δ_σ, δ_iso, and δ_ii, plotted vs. the corresponding experimental parameters. The parameters for both NTD and CTD are displayed in (d–f); those for NTD only are shown in (g–i).

The overall agreement between the experimental and MD/DFT computed δ_iso is poorer than that for δ_σ, see Fig. 2–3 and 4e. Considerable scatter is noted, and the slope of 0.77 and offset of 21.6 ppm are significantly greater than those reported for previous DFT calculations of ¹⁵N chemical shifts for 20 structurally characterized proteins.²⁸ To gain further insights into the effect of dynamic averaging on the ¹⁵N CSA tensors we analyzed their experimental and computed principal components, δ₁₁, δ₂₂, and δ₃₃. These are plotted vs. the residue number in Fig. 4a–c. The experimental and calculated δ_ii correlate well, see Fig. 4f: the slope is 0.98, and a negligible offset of −2.6 ppm is seen (1.3% of the entire range of δ_ii values). The largest scatter for any principal component is observed for δ₃₃ (Fig. S3, Supplementary), suggesting that reorientation of the CSA tensor due to motion affects most prominently the principal component perpendicular to the amide plane (Fig. 1d). These results highlight the importance of measuring CSA tensors, not only isotropic shifts, for systems that possess internal dynamics.

Another interesting observation in this study relates to the finding that better agreement between the experiment and calculations is seen for NTD residues, compared to the CTD. This is evident from the data depicted in Fig. 4, both, for δ_iso and δ_σ. We observed a similar effect in our studies of ¹H-¹⁵N/¹³C^α dipolar tensors, where alignments were carried out for the individual domains in the calculations in order to eliminate overall translational and rotational motions.¹⁰ The NTD and CTD are connected by a flexible linker, which is mobile on the slow-microsecond to millisecond timescales.⁸ CTD residues are more rigid according to the experimental CSA parameters than those computed by MD/QM/MM. Since MD/QM/MM calculations were conducted on monomeric CA, the intermolecular CTD-CTD interactions, which are essential for the capsid assembly and stability,⁶ could not be captured, rendering the CTD in the MD/QM/MM calculations more flexible than in tubular assemblies studied by MAS NMR.

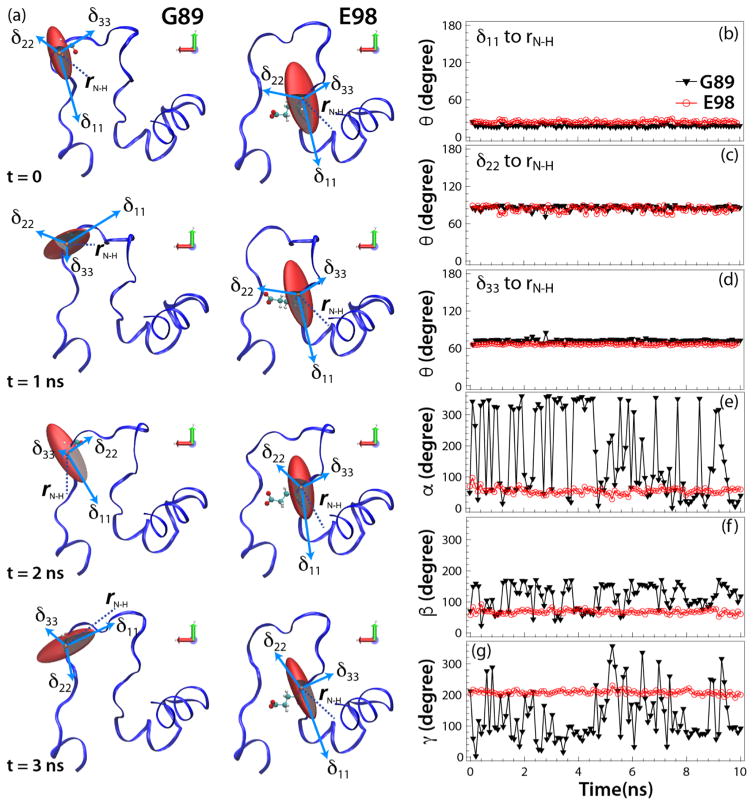
To understand how the CSA tensors are affected by the reorientation of the corresponding residues during local motions, we examined the computed principal components of the ¹⁵N CSA tensors, δ_ii, and the isotropic shifts, δ_iso, for each residue along the MD trajectory. In Fig. S3 Supplementary) we illustrated the results for two residues: G89 in the tip of the CypA-binding loop, which is highly mobile, and the more rigid E98. Interestingly, the variations in the principal CSA components are relatively modest, and independent of whether the corresponding residue is dynamic or static. However, as shown in Fig. 5, for the dynamic G89 very large changes in the Euler angles (α, β, γ) are observed, associated with different orientations of the CSA tensors in the individual substructures in the MD trajectory. These kinds of motions are expected to attenuate the observed CSA tensors (see an illustration for a spin model in Fig. S4. Supplementary). Conversely, for the static E98 these variations are much smaller. The polar angles θ, which relate each δ_ii to the N-H bond vector, on the other hand, are similar for both static and dynamic residues, see Fig. 5. This indicates that motions exert larger effects on the relative orientations of the individual CSA tensors, while the individual principal components of the diagonal CSA tensor are affected less. This is vividly seen when the individual components of a non-diagonal CSA tensor, δ_ij (where i/j=x,y,z) are plotted in the molecular fixed frame (MFF) representation (Fig. S5, Supplementary), with variations predominantly being caused by the changing Euler angles. (MFF here coincides with the lab frame since only one protein molecule is considered in calculations.) The dynamic averaging of the ¹⁵N CSA tensors is illustrated in Fig. 6a–f for representative CypA-loop residues. The differences between mobile and rigid residues are also apparent when comparing experimental δ_iso values with those computed by MD/DFT and MD/ShiftX (Fig. S2, Supplementary). Not surprisingly, loop residues that are mobile exhibit broad distributions, while residues in helices possess narrow chemical shift ranges. The corresponding residue-specific distributions computed by MD/ShiftX (Fig. S6, Supplementary) reveal that the width of the CS distribution correlates with the conformational space sampled by each residue in the course of MD trajectory. This result is consistent with our prior findings for dipolar tensors¹⁰ and with solution-NMR studies of RNaseH.¹⁸

Figure 5.

(a) The amplitudes and orientations of backbone ¹⁵N^H CSA tensors for G89 (left) and E98 (right) in HIV-1 CA protein with respect to the molecular frame, for the individual structures along the MD trajectory at t = 0, 1, 2, and 3 ns (from top to bottom, respectively). (b–d) Plots of the relative angles between the principal components of the ¹⁵N CSA tensor, δ_ii, and the N-H bond, r_N-H. (e–g) Euler angles for the backbone ⁵N^H CSA tensors in the molecular frame. The CSA parameters and relative tensor orientations were calculated by QM/MM (at the DFT level) for the individual structures along the MD trajectory as a function of time, as shown for G89 (black triangles) and E98 (red circles).

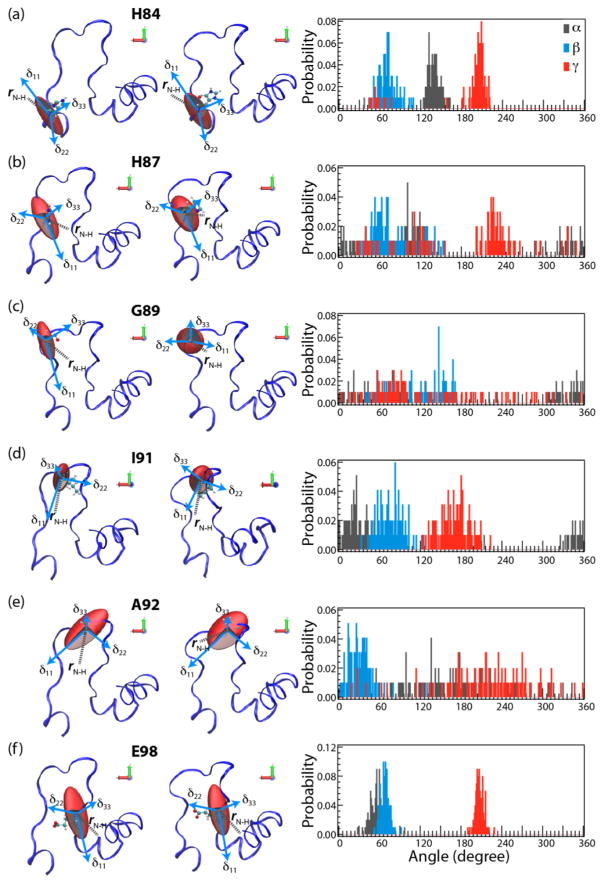
Figure 6.

Left two panels: The plots of the amplitudes and orientations of the backbone ¹⁵N^H CSA tensors in HIV-1 CA, in the molecular frame, calculated by QM/MM (at the DFT level) for the starting structure (left) and averaged along the MD trajectory (right). Right panel: probability distributions for Euler angles α (black), β (blue), and γ (red) over the course of MD trajectory. The plots are shown for selected CA residues: (a) H84, (b) H87, (c) G89, (d) 191, (e) A92, and (f) E98.

Given the computationally expensive nature of QM/MM CSA tensor calculations, it is important to evaluate whether the number of MD frames and the sampling intervals, which are required to accurately represent the accessible conformational space for each residue, are sufficient. Such analysis was carried out for the highly mobile G89 and rigid E98 residues (Fig. S7, Supplementary). Interestingly, for both residues we find that averaging either 100 or 200 frames from a 100-ns trajectory (1- or 0.5-ns sampling interval, respectively) yields similar δ_σ values (±2%), essentially identical within experimental error. Averaging 100 frames from the first 10 ns of the MD trajectory yields essentially identical δ_σ values for the static E98, while a difference of 5.4 ppm is observed for the dynamic G89. Therefore, it appears that longer MD trajectories are required to reach more quantitative agreement with experiment.

To rule out that details of the particular DFT methodology used in the current calculations for G89 biased the resulting CSA parameters, we applied three commonly used density functionals: B3LYP, OLYP, and 03LYP. All three yield δ_σ values to within 4%, i.e. vary less than the difference between the experimental and the calculated values, confirming that all three functionals are indistinguishable in outcome (Fig. S8, Supplementary).

Overall, the differences observed here between computations and experiment for certain residues highlight the importance of long trajectories and the development of MD protocols that enhance sampling of biologically relevant states. With computational cost decreasing rapidly, they should no longer be an impediment to calculate dynamically averaged CSA calculations by quantum mechanical methods. Such calculations are feasible and represent the method of choice for a rigorous analysis of the structural vs. dynamic contributions to chemical shifts, as demonstrated here.

CONCLUSIONS AND FUTURE OUTLOOK

Residue-specific ¹⁵N, ¹³C, and ¹H CSA tensors are readily accessible using contemporary multidimensional RNCSA methods,^15,16,29 even for large protein assemblies. These experiments provide uniquely rich information about the geometry, electronic structure, and dynamics. ¹⁵N CSA tensors provide a direct and sensitive probe of internal residue backbone dynamics occurring on timescales of nano- to microseconds. For tubular assemblies of the HIV-1 CA protein, investigated here, residues in the mobile CypA-binding loop exhibit dramatic decreases in ¹⁵N chemical shift anisotropy. The reduced anisotropy parameters, δ_σ, unequivocally report on the presence of motions, unlike isotropic chemical shifts, where dynamic effects are not immediately obvious. Knowledge of dynamic regions in proteins and assemblies thereof is invaluable for accurate interpretation of chemical shifts in terms of geometric structure. The integrated analysis of combined experimental MAS NMR data, MD simulations as well as QM methods for calculating chemical shifts in proteins using Density Functional Theory, provides rich and in-depth atomic-level information on the inter-relatedness of internal motions and local structure. Here we show that the dynamic averaging of the CSA parameters results from Euler angle changes rather than variations in the principal components of the CSA tensor. This finding has important implications for the analysis of dynamics by solution NMR relaxation methods, where the shift anisotropy is taken as a constant.³⁰ The integrated MAS NMR and MD/DFT approach developed and illustrated here is a powerful tool for atomic-resolution characterization of structure and dynamics of biological assemblies.

MATERIALS AND METHODS

Protein expression, purification and NMR sample preparation were performed as described previously³¹. CA was expressed in E. coli Rosetta 2 (DE3), cultured in Luria-Bertani or modified minimal media, after induction with 0.4 mM IPTG at 23 °C for 16h. The purification was performed with cation exchange column chromatography with 0–1 M NaCI gradient in a buffer containing 25 mM sodium phosphate pH 5.8, 1 mM DTT, and 0.02% NaN₃. Uniform ¹⁵N- and ¹³C-labeling was performed using ¹⁵NH₄CI and ¹³C₆-glucose as sole nitrogen and carbon sources. Tubular assemblies of CA protein were prepared from 30 mg/mL protein solution in 25 mM phosphate buffer (pH5.5) containing 1M NaCI. The solution was incubated at 37 °C for 1 h and stored at 4 °C for subsequent NMR experiments. The incubated CA sample was pelleted by centrifugation at 6,000 G for 15 minutes, the supernatant was removed, and 15 mg (0.59 mmoles) of full-length tubular WT CA assemblies were packed into a Varian 3.2 mm MAS rotor. The rotor was sealed using an upper spacer and a top spinner.

MAS NMR experiments were carried out on a 21.1 T ultra-wide bore spectrometer outfitted with a 3.2 mm HXY Enhanced-Design Low-E MAS probe designed and built at NHMFL.³² Larmor frequencies were 899.1 MHz (¹H), 226.1 MHz (¹³C), and 91.1 MHz (¹⁵N). The MAS frequency was set at 14 kHz for all experiments, and was controlled to within ± 5 Hz by a Bruker MAS controller. KBr was used as temperature sensor, and the actual temperature of the sample was maintained to within 4 ± 0.1 °C using the Bruker temperature controller. ¹³C and ¹⁵N chemical shifts were referenced with respect to the external standards adamantane and NH₄CI, respectively. In ¹⁵N RNCSA 3D experiment, the typical 90° pulse lengths were 2.5 μs (¹H), 3 μs (¹³C), and 5 μs (¹⁵N), and the contact time of ¹H-¹⁵N cross polarization (CP) was 1.0 ms. ¹H-¹⁵N CP employed a linear amplitude ramp on the ¹H channel with the center Hartmann-Hahn matched to the first spinning side band. The band-selective magnetization transfer from ¹⁵N to ¹³C^α was realized through a 4.5 ms SPECIFIC-CP with a tangent amplitude ramp on the ¹⁵N channel (49 kHz rf field center) and a constant rf field on the ¹³C channel (35 kHz). High-power ¹H continuous wave (CW) decoupling (110 kHz) was applied during the SPECIFIC-CP period, and SPINAL-64 decoupling (100 kHz) was applied during the direct (t₃) and indirect (t₂) acquisition periods. R14₂⁵-based symmetry sequence was used to reintroduce ¹⁵N CSA interaction during the t₁ evolution period, and the phase-alternated (±5Π/14 or ± 64.29°) rf field irradiation (49 kHz) was applied on the ¹⁵N channel. Simultaneous Π pulses were applied on the ¹³C channel at the center of every two rotor periods to decouple ¹⁵N-¹³C dipolar interactions, and ¹H CW was applied to decouple ¹H-¹⁵N dipolar interactions.

Numerical simulations of ¹⁵N RNCSA lineshapes were performed with the SIMPSON software package, versions 2.0. To produce a powder average, 320 pairs of {α, β} angles generated according to the REPULSION algorithm and 16 γ angles (resulting in a total of 5,120 angle triplets) were used for all simulations. Haberlen-Mehring-Spiess convention was followed to define the CSA parameters in the present work, where the isotropic chemical shift δ_iso, the reduced anisotropic chemical shift δσ, and the asymmetry parameter η, are related to the principal elements δ_ii (i = 1, 2 or 3) of the chemical shift tensor according to |δ₁₁ - δ_iso| ≥ |δ₃₃ - δ_iso| ≥ |δ₂₂ - δ_iso|, δ_iso = ⅓ (δ₁₁+δ₂₂+δ₃₃), δ_σ = δ₁₁ - δ_iso, and $\eta =\raisebox{1ex}{$({\delta }_{22}-{\delta }_{23})$}\!\left/ \!\raisebox{-1ex}{$({\delta }_{11}-{\delta }_{\mathit{iso}})$}\right.$. For extracting the best-fit ¹⁵N CSA NMR parameters (δ_σ, η), all of the experimental and processing parameters (i.e., Larmor frequency, MAS frequency, RF field strength, number of t₁ points, finite pulse lengths, zero-filling, line broadening, etc.) were taken into account in the simulations. With the attainable sensitivity and resolution, a total of 76 non-overlapping ¹⁵N CSA lineshapes were extracted and fitted.

Molecular dynamics simulations of the wild type CA monomer (HXB2 polymorph, PDB ID 3NTE) were performed using ACEMD as reported previously.¹⁰ Ions in close proximity to the protein were placed using the CIONIZE routine in VMD, bulk waters and Na/CI ions were then added using VMD^33,34, setting the total concentration of NaCI to 1M. The system was then equilibrated using NAMD 2.9 with the CHARMM36FF at 300 K for 100 ns.

QM/MM calculations of magnetic shielding anisotropy tensors were carried out in Gaussian09,³⁵ and automated fragmentation quantum mechanics/molecular mechanics approach (AF-QM/MM) from AFNMR package²⁵ of ShiftS was used to divide the entire protein system into nonoverlapping fragments, in which QM region included a fragment within 4 or 3 Å from the target residue (without or with protons included, respectively). MM region included the rest residues beyond the core and the buffer regions. AF-QM/MM was performed to generate individual spin system for each target residue. In this work, the DFT calculations of the NMR calculations were performed by the GIAO method using the OLYP density functional and the TZVP basis set, and all of the calculated ¹⁵N magnetic shieldings were referenced to the isotropic shielding constant of 237.8 ppm, as reported previously for the computations at the same level of theory in Ubiquitin (PDB ID: 1D3Z); the calculated 13C magnetic shieldings were referenced to the isotropic shielding constant of 190.8 ppm, according to the RMSD-based referencing method³⁶.

Averaged chemical shift tensor calculations were performed by combining QM/MM calculations with MD simulations. A total of 100 frames were extracted from first 10 ns from the 100 ns MD trajectory. For each frame, the AF-QM/MM was performed to generate individual spin system for each target residue. For each target residue, we performed the 100 QM/MM calculations using Gaussion09, and the backbone ¹⁵N chemical shielding tensors for the target residue were extracted from each calculation, as follows:

$${\mathit{\sigma }}^i=\left[\begin{array}{ccc}{\sigma }_{xx}^i& {\sigma }_{xy}^i& {\sigma }_{xz}^i\\ {\sigma }_{yx}^i& {\sigma }_{yy}^i& {\sigma }_{yz}^i\\ {\sigma }_{zx}^i& {\sigma }_{zy}^i& {\sigma }_{zz}^i\end{array}\right]$$ (1)

where i denotes the index of the frame extracted from the MD trajectory.

The magnetic shielding anisotropy tensor is expressed in its principal axes system (PAS) as

$${\mathbf{\Lambda }}^i=\left[\begin{array}{ccc}{\sigma }_{11}^i& 0& 0\\ 0& {\sigma }_{22}^i& 0\\ 0& 0& {\sigma }_{33}^i\end{array}\right]$$ (2)

The dynamically averaged ¹⁵N chemical shielding tensor for each residue was then obtained by linear averaging of its nine elements extracted from the QM/MM calculations for each of the 100 individual substructures in the MD trajectory,

$$\langle \mathit{\sigma }\rangle =\frac{1}{N}·\left[\begin{array}{lll}{\sum }_{i=1}^N{\sigma }_{xx}^i\hfill & {\sum }_{i=1}^N{\sigma }_{xy}^i\hfill & {\sum }_{i=1}^N{\sigma }_{xz}^i\hfill \\ {\sum }_{i=1}^N{\sigma }_{yx}^i\hfill & {\sum }_{i=1}^N{\sigma }_{yy}^i\hfill & {\sum }_{i=1}^N{\sigma }_{yz}^i\hfill \\ {\sum }_{i=1}^N{\sigma }_{zx}^i\hfill & {\sum }_{i=1}^N{\sigma }_{zy}^i\hfill & {\sum }_{i=1}^N{\sigma }_{zz}^i\hfill \end{array}\right]$$ (3)

where N denotes the number of total frames taken for QM/MM calculations for the residue of interest; in the present work N=100. The averaged ¹⁵N chemical shielding tensors were referenced to the isotropic shielding constant of 237.8 ppm to obtain the motion-averaged chemical shift tensor, 〉δ〈, and the principal components, δ_ii, for each target residue.

To obtain the time-dependent orientation of the chemical shielding tensors in the laboratory frame, for each target residue, rotations in Cartesian space were used to express the orientation relative to the stationary set of axes in each frame. These were parameterized by three Euler angles α, β, and γ, according to the standard notation:³⁷

$${\mathit{\sigma }}^i={\mathit{R}}^i·{\mathbf{\Lambda }}^i·{({\mathit{R}}^i)}^{-1}$$ (4)

where R denotes the corresponding rotation matrix, expressed as

$$\mathit{R}=\left[\begin{array}{ccc}cos\alpha cos\beta cos\gamma -sin\alpha sin\gamma & sin\alpha cos\beta cos\gamma +cos\alpha sin\gamma & -sin\beta cos\gamma \\ -cos\alpha cos\beta sin\gamma -sin\alpha cos\gamma & -sin\alpha cos\beta sin\gamma +cos\alpha cos\gamma & sin\beta sin\gamma \\ cos\alpha sin\beta & sin\alpha sin\beta & cos\beta \end{array}\right]$$ (5)

Chemical shift prediction ShiftX was also used to calculate the dynamically averaged ¹⁵N isotropic chemical shifts for the individual 5000 frames during the 100 ns MD trajectory.