Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jul 4;4:5573. doi: 10.1038/srep05573

A design principle underlying the paradoxical roles of E3 ubiquitin ligases

Daewon Lee 1, Minjin Kim 1, Kwang-Hyun Cho 1,a
PMCID: PMC5381699  PMID: 24994517

Abstract

E3 ubiquitin ligases are important cellular components that determine the specificity of proteolysis in the ubiquitin-proteasome system. However, an increasing number of studies have indicated that E3 ubiquitin ligases also participate in transcription. Intrigued by the apparently paradoxical functions of E3 ubiquitin ligases in both proteolysis and transcriptional activation, we investigated the underlying design principles using mathematical modeling. We found that the antagonistic functions integrated in E3 ubiquitin ligases can prevent any undesirable sustained activation of downstream genes when E3 ubiquitin ligases are destabilized by unexpected perturbations. Interestingly, this design principle of the system is similar to the operational principle of a safety interlock device in engineering systems, which prevents a system from abnormal operation unless stability is guaranteed.

The ubiquitin-proteasome system (UPS) is primarily known as an important part of the protein degradation (proteolysis) machinery. The proper and timely degradation of proteins is critical to maintaining the homeostasis of biological systems, and a failure of the UPS can cause abnormal development1 and devastating diseases such as cancer2,3,4, neurodegeneration5, cardiac diseases6,7, autoimmunity, and inflammatory diseases8,9.

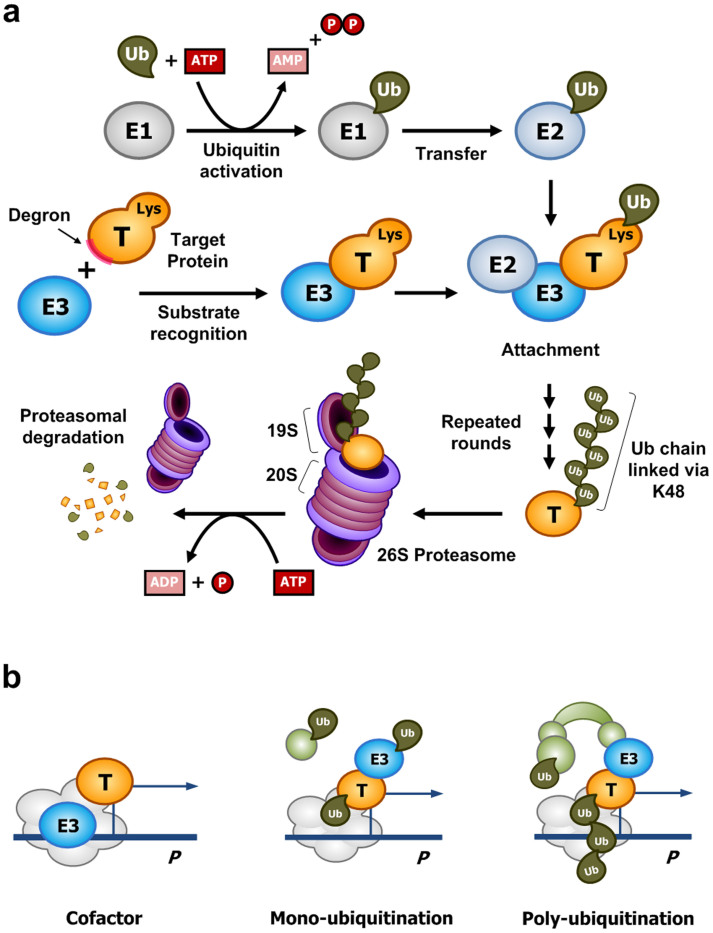
UPS-dependent proteolysis requires the attachment of multiple ubiquitin molecules to a target protein, which results in the subsequent degradation of the polyubiquitinated target protein through the 26S proteasome complex (Fig. 1a)3,10,11,12,13. The ubiquitination step involves at least three enzymes: a ubiquitin-activating enzyme (E1), a ubiquitin-conjugating enzyme (E2), and a ubiquitin-protein ligase (E3). E1 activates a ubiquitin molecule via an ATP-dependent reaction, forming a high-energy thioester linkage between E1 and a ubiquitin. The activated ubiquitin is transferred to E2; subsequently, E3, supported by E2, attaches the ubiquitin to a lysine residue of the substrate protein or a lysine residue of the previously attached ubiquitin. E3, in particular, plays a key role in the recognition of the amino acid sequence of a target protein, which is called a “degron.” Thus, E3 determines the specificity for the “death” of the target protein molecule. Finally, the polyubiquitinated protein is recognized by a specific subunit of the 19S regulatory particle of the proteasome and is degraded by the 20S core subunit in an ATP-dependent manner.

Figure 1. E3 ubiquitin ligases in the ubiquitin-proteasome system (UPS) play paradoxical roles in proteolysis and transcription.

Figure 1

Open in a new tab

(a) Protein degradation mediated by the UPS. E3 ubiquitin ligases determine the substrate specificity of UPS-dependent proteolysis. The specific biochemical reactions depend on the type of proteins in the UPS. (b) An E3 ubiquitin ligase can participate in the transcriptional activation of transcription factors, which also undergo proteolysis facilitated by the same E3 ligase.

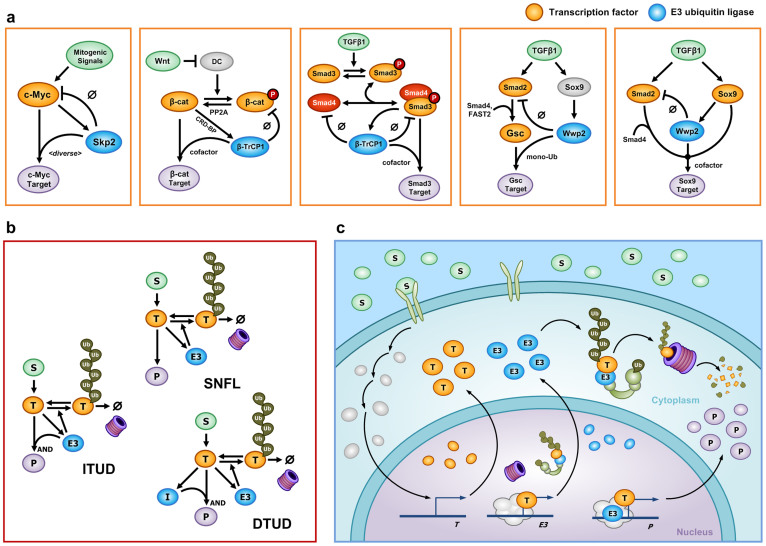
Several recent studies have demonstrated that the UPS plays a role in transcriptional activation (Fig. 1b)13. For example, the UPS was found to activate a transcription factor on the promoter of a target gene via ubiquitination14,15,16,17. Other studies have indicated that E3 ubiquitin ligases can act as transcription cofactors in the absence of ubiquitin ligase activity18,19. In addition, it was found that a certain type of polyubiquitination does not promote the degradation of a transcription factor but rather stabilizes it20,21. Figure 2a presents examples in which E3 ubiquitin ligases facilitate both proteolysis and transcription in various signaling pathways. (1) Skp2 not only promotes the degradation of Myc but also enhances the transcription of a subset of Myc target genes with or without ubiquitin ligase activity14,15,19. (2) The regulatory relationship of β-catenin and β-TrCP1 (also known as Fbw1a) in the canonical Wnt pathway22 is similar to that of Myc and Skp218; the major difference is that the Wnt/β-catenin pathway involves phosphorylation for the recognition of β-catenin by β-TrCP123. (3) β-TrCP1 also facilitates the proteolysis of Smad4 and the Smad3/Smad4 complex24,25,26, whereas it participates in the transcriptional activation of Smad3 without ubiquitin ligase activity18. (4) For Smad2 and Wwp2 (also known as AIP2), Wwp2 oppositely regulates TGF-β signal transduction to its target genes by participating in both the proteolysis of Smad227,28 and the transcriptional activity of Goosecoid (Gsc)17 or Sox929 (see Supplementary Methods (section S1) for details).

Figure 2. Biological examples and the generic mathematical model.

Figure 2

Open in a new tab

(a) Examples of E3 ubiquitin ligases (blue) that play paradoxical roles in proteolysis and transcriptional activation of a transcription factor (orange). (b) The mathematical model of ITUD. For comparative analysis, SNFL and DTUD are introduced as alternatives. Basal production and degradation of each component are not denoted in this diagram. (c) A detailed illustration of ITUD in a cell. This schematic diagram depicts a RING-type E3 ubiquitin ligase and its role as a cofactor in transcriptional activation. Other types of E3 proteins can be described differently. (b–c) S is an upstream signal; T is a transcription factor; E3 is an E3 ubiquitin ligase; P is the final product (system output); and I is an intermediate node.

We were intrigued as to why a single protein, i.e., the E3 ubiquitin ligase, participates in both proteolysis and transcriptional activation (i.e., the downregulation and upregulation, respectively, of a signal transduction pathway), which are apparently opposing reactions. In particular, we wondered what would be the advantage of simultaneously promoting both processes via this single component of the UPS. To decipher the design principles underlying these paradoxical roles of E3 ubiquitin ligases, we developed a generic mathematical model that represents the essential dynamics of the signaling pathways exemplified in Figure 2a, which we call integrated transcription and UPS-dependent degradation (ITUD)18 (Fig. 2b). For comparison, we considered a simple negative feedback loop (SNFL) and dissociated transcription and UPS-dependent degradation (DTUD) as alternative models of the ITUD (Fig. 2b). Based on a mathematically controlled comparison of these models, we found that only the ITUD system can suppress abnormal responses under unexpected downregulation of the E3 ubiquitin ligase by which the cognate transcription factor might be excessively stabilized. We further confirmed these characteristics of ITUD at the cell population level using in silico cell proliferation and migration experiments. Interestingly, the design principle that underlies the paradoxical roles of the E3 ubiquitin ligase in the ITUD model is similar to the operational principle of a safety interlock device in engineering systems in which any unexpected perturbation of the safety device results in the system shutdown to prevent abnormal operation.

Results

The mathematical model of ITUD

ITUD is the core structure of the signaling networks presented in Figure 2a, which includes only the essential components for investigation of the underlying design principles of biological systems30,31,32,33,34,35,36 (see Methods and Supplementary Table S1). The ITUD system consists of five components: the signal (S), the transcription factor (T), polyubiquitinated T (ubT), E3 ubiquitin ligase (E3), and the target gene product (P) (Fig. 2b and 2c). The signal, S, is an extracellular ligand or a subcellular biomolecule, which increases the amount of T. T is a transcription factor that promotes the expression of the target gene P. It is assumed that T can undergo UPS-dependent proteolysis promoted by E3 in both cytoplasm and nucleus. ubT is the polyubiquitinated form of T, which undergoes proteasomal degradation. E3 is an E3 ubiquitin ligase that not only facilitates the ubiquitin-proteasomal degradation of T but also ‘paradoxically' aids in the transcriptional function of T. It is assumed that the stability of T is not affected by either the proteolytic or the nonproteolytic function of E3 in transcription37,38 (see Supplementary Methods (section S1 and S2)). E3 is also transactivated by T, and therefore, E3 and T form a negative feedback loop by which the appropriate level of T is maintained. For instance, Skp2 is a direct target gene of c-Myc in leukemia39 and melanoma cells40. P is the final product, or the output of the system, whose expression is activated by both T and E3.

We employed the method of mathematically controlled comparison (MCC), which identifies the essential characteristics of a mathematical model by comparison with alternative models according to a set of mathematical criteria and statistical methods41,42,43,44. To understand the essential characteristics of ITUD, we compared it with two alternative systems having different configurations: SNFL and DTUD (Fig. 2b). SNFL represents a negative feedback loop where E3 does not participate in the transcriptional activation of P. In SNFL, T transactivates E3 and the enhanced E3 only regulates T through UPS-dependent proteolysis as a feedback control. In DTUD, the proteolysis of T and the transcriptional activation of P by T are processed by different components: E3 only participates in the degradation of T, and another component, I (i.e., the intermediate node), assumes the role of E3 for the transcriptional activation of P. We developed mathematical models for SNFL, DTUD, and ITUD such that the mathematical terms of the biochemical reactions and their common parameters were established to be comparable on the basis of MCC (Supplementary Table S1, Table S2, and Supplementary Methods (section S2)).

Identification of the critical determinants of ITUD in comparison to SNFL and DTUD

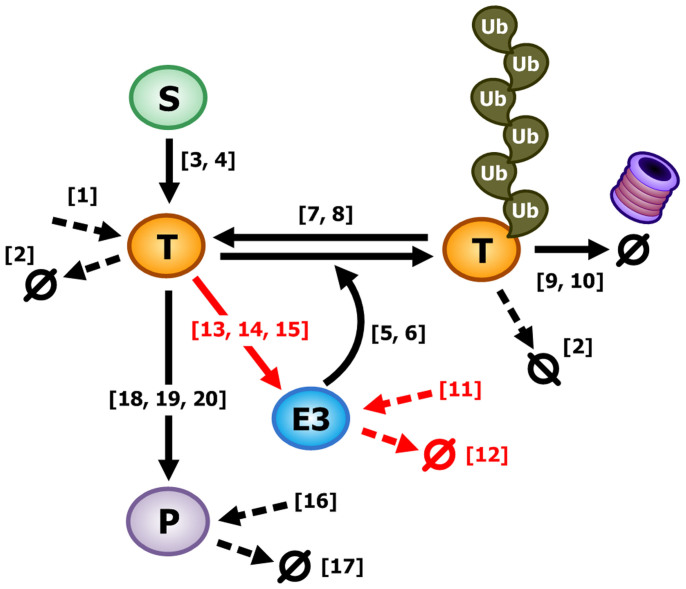
We wondered what distinguishes ITUD from the alternative systems. To answer this question, we explored the critical determinants that characterize ITUD. Specifically, we analyzed how these three systems differently respond to an identical small perturbation of each kinetic parameter (i.e., local sensitivity analysis, LSA), in which the system output is the steady-state level of P (Pss). Among the 20 common kinetic parameters, five parameters (ID: 11–15) exhibited a noticeable difference (i.e., <20%) in the ratio of the sensitivities between ITUD and the other two systems (Table 1 and Fig. 3). The ratio of sensitivities denotes the ratio of how the steady-state level of P changes between the two systems in response to a small perturbation on the same parameter. So, a small ratio of the sensitivities means that the two systems have a large difference in their responses to the change of the parameter value. To overcome the limitations of using specific values for a parameter set, we further performed LSA based on MCC over a wide range of parameter values (see Methods). The five parameters (ID: 11–15) also exhibited different patterns as compared to the remaining parameters (Supplementary Fig. S1). These five parameters are involved in the regulation of the level of E3 and, thus, are important for the stability of E3; i.e., ITUD and the other two systems differently respond to a change in the level of E3. Specifically, βE3 (ID: 11) and αE3 (ID: 12) represent the basal production and degradation rates, respectively, which determine the basal level of E3. βTE3 (ID: 13), KTE3 (ID: 14), and nTE3 (ID: 15) represent the maximum transactivation rate, half-maximal occupancy, and Hill-coefficient, respectively, in the regulation of E3 by T. Among the five parameters, βTE3 (ID: 13) and KTE3 (ID: 14) are the critical determinants because βE3 (ID: 11) and αE3 (ID: 12) do not affect the signal transduction from S to E3, and the Hill coefficient represents the cooperativity of ligand binding45, which is not within the primary scope of this study. Therefore, the regulation (represented by the two kinetic parameters, βTE3 and KTE3) of E3 by T distinguishes ITUD from the two alternative systems, and we can conclude that the two kinetic parameters are critical determinants.

Table 1. Identification of the kinetic parameters that characterize the ITUD system. We determined the kinetic parameters that discriminate the output of the ITUD system from those of the alternative systems when a small perturbation was given. The ratio of the sensitivities were obtained using a positive (+1%) and a negative (−1%) perturbation. The five parameters (ID: 11–15) displayed noticeable differences (<20% vs. >60% of the others).

ID Parameter Perturbation
    Positive (+1%) Negative (−1%)
I/S (%) I/D (%) I/S (%) I/D (%)    
1 βT 60.42 100 60.42 100
2 αT 60.48 100 60.37 100
3 kST 60.26 100 60.59 100
4 Km_ST 60.48 100 60.37 100
5 kE3T 60.57 100 60.28 100
6 Km_E3T 60.37 100 60.47 100
7 Vm_ubT 60.39 100 60.46 100
8 Km_ubT 60.43 100 60.41 100
9 Vm_pro 60.43 100 60.42 100
10 Km_pro 60.42 100 60.42 100
11 βE3 10.78 17.85 10.76 17.80
12 αE3 9.43 15.65 12.07 19.92
13 βTE3 12.04 19.88 9.43 15.65
14 KTE3 10.43 17.28 11.10 18.36
15 nTE3 10.99 18.18 10.54 17.46
16 βP 100 100 100 100
17 αP 100 100 100 100
18 βTE3P 100 100 100 100
19 KTP 100 100 100 100
20 nTP 100 100 100 100
Open in a new tab

I, S, and D: The sensitivity of ITUD, SNFL, and DTUD, respectively.

Figure 3. Graphical representation of the major parameters commonly used in SNFL, DTUD, and ITUD.

Figure 3

Open in a new tab

The numbers in brackets are parameter IDs and the dotted arrows represent the basal production or degradation rates. The red arrows represent the regulations which involve the identified five parameters, of which βTE3 (ID: 13) and KTE3 (ID: 14) are defined as the critical determinants.

Steady-state analysis with respect to the critical determinants

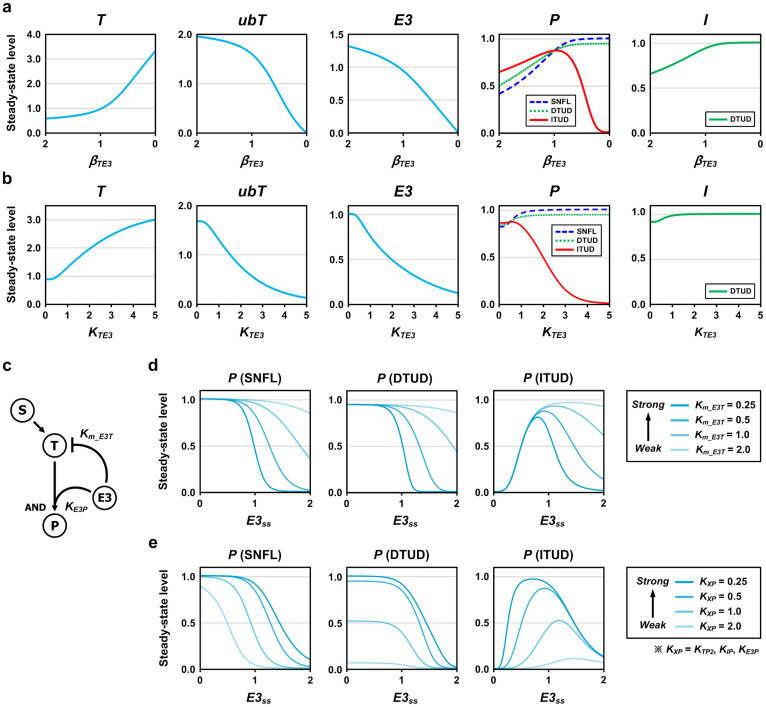
We further investigated how the critical determinants (i.e., βTE3 and KTE3) characterize ITUD in comparison to the two alternative systems. In contrast to the small discrete perturbation in LSA, we perturbed E3 by continuously varying βTE3 or KTE3 such that E3 was upregulated initially and downregulated subsequently, and measured the steady-state levels of the system components. Pss rose gradually until βTE3 was decreased to the nominal value of 1.0 in all systems (Fig. 4a). However, below the nominal value, Pss was dramatically decreased in ITUD, whereas it is finally saturated in the other two systems. For KTE3, the increasing phase of Pss in ITUD was observed within a small range, and the decreasing phase began near the nominal value of 0.5 (Fig. 4b). This result suggests that ITUD exhibits a biphasic response with respect to the factors that alter the stability of E3 and that the output level is lowered only in ITUD when the amount of E3 is reduced by perturbations.

Figure 4. The effects of the critical determinants on the three systems at steady state.

Figure 4

Open in a new tab

We examined the effects of the critical determinants (i.e., βTE3 and KTE3) on the steady-state outputs of the three systems under the activating signal (S = 1.0). E3 was perturbed by continuously varying (a) βTE3 and (b) KTE3 such that E3 was initially upregulated and subsequently downregulated. The decrease of βTE3 leads to the downregulation of E3, and thereby the horizontal axis of (a) is set in a descending order (from 2.0 to 0). (c) The regulation of E3 by T was removed to observe the system response with respect to the steady-state level of E3 (E3ss). The Km_E3T and KE3P represent the binding affinities (or the reaction intensities) of E3 for proteolysis and transcription, respectively. (d) The curves of the steady-state level of P (Pss) generated by varying Km_E3T under the activating signal (S = 1.0). (e) Identical curves generated by varying KXP. KTP2 and KIP are the kinetic parameters that correspond to KE3P of ITUD in SNFL and DTUD, respectively.

To explore the biphasic characteristics of ITUD with respect to the level of E3, we applied the steady-state analysis solely on the ITUD system through direct manipulation of the steady-state E3 level (E3ss). The regulation of E3 by T was deliberately removed to modulate the E3ss irrespective of the signal S (Fig. 4c). At the higher E3ss, the outputs of all three systems decreased due to the enhanced proteolysis facilitated by an excess of E3. However, at the lower E3ss, only ITUD demonstrated a decreasing phase, whereas the other two systems exhibited saturated responses (Fig. 4d and 4e). Thus, ITUD demonstrates a differential behavior as compared to the alternative systems at a lower E3 level.

We also examined how binding affinities (or reaction intensities) of E3 for T in proteolysis (Km_E3T) and transcription (KE3P) affect the shapes of the response curves. In all three systems, increasing Km_E3T (i.e., decreasing proteolysis) reduced the sharpness of the curves, whereas KE3P primarily altered the amplitudes of the curves. In addition, the effect of Km_E3T on the response curves was large at the higher E3ss, whereas that of KE3P was prominent at the lower E3ss. Similar patterns of the biphasic response were also observed in the intact ITUD (Supplementary Fig. S2). These results suggest that the biphasic characteristics of the ITUD system are tunable by modulating the regulatory mechanisms involved in proteolysis and transcription such as posttranslational modifications or subcellular localization.

The effects of the critical determinants on temporal dynamics

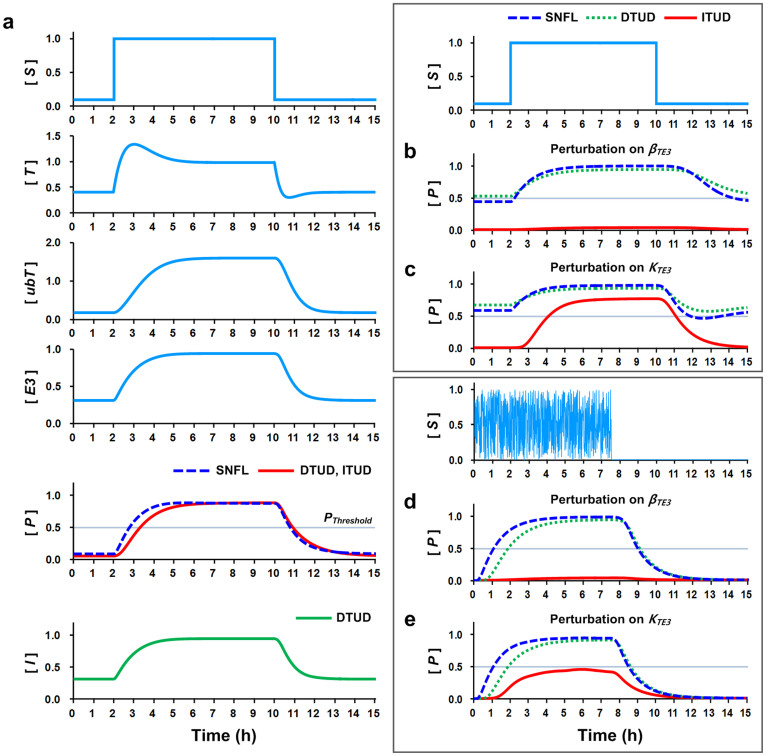
Having identified the critical determinants that characterize the biphasic responses of ITUD at the steady state, we sought to determine how the critical determinants affect the temporal dynamics. Hence, we observed the temporal profile of the three systems under the perturbation of the critical determinants. As the signal S increased, T was activated, and subsequently the levels of E3, ubT, and P were also increased in the control condition (no perturbation) (Fig. 5a). The three systems exhibited the identical temporal dynamics for T, ubT, and E3 because they share the negative feedback loop comprising T, ubT, and E3. However, the output responses of DTUD and ITUD were slower than that of SNFL, in which the response time was defined as the time required for a system output to exceed the activation threshold (i.e., PThreshold = 0.5; approximately half of the maximum level of P at the control condition) after the input signal was applied. This slower response is attributable to a “sign-sensitive delay” of the AND-gated coherent feed-forward loop46,47 embedded in DTUD and ITUD. The presence of a sign-sensitive delay means that the output response is delayed to an extent almost identical to the duration for the expression of intermediate components such as E3 and I if the input signal is increased (plus), whereas it is not delayed when the input is decreased (minus). By contrast, when S was diminished T was rapidly degraded by E3 and exhibited undershooting dynamics. The decreasing dynamics of P was similar in all three systems. Notably, the three systems also exhibited similar overall dynamics over a wide range of kinetic parameter values with or without noise in the signal (Supplementary Fig. S3, control).

Figure 5. Temporal dynamics under the perturbation of the critical determinants.

Figure 5

Open in a new tab

(a) Temporal dynamics of the perturbation-free condition (control). The signal S changes from a low to a high level (specific values: 0.1 to 1.0). The temporal dynamics of the common negative feedback loop involving T, ubT, and E3 are identical in the three systems. The activation threshold (PThreshold = 0.5, gray line) is defined as the threshold that the system output, P, must exceed to activate the system. (b) Temporal dynamics under the perturbation of βTE3, which was decreased by 80% (0.2-fold). (c) Identical to (b), except the perturbation was applied on KTE3, which was increased by 150% (2.5-fold). (d–e) Temporal dynamics under identical perturbations in (b–c) with noise in signal S. The initial states are all zero.

In the perturbation condition, we perturbed the critical determinants (i.e., βTE3 and KTE3) toward the downregulation of E3. The perturbation for the upregulation of E3 was not considered because it did not noticeably distinguish ITUD at the higher E3ss in the steady-state analysis (Fig. 4). When βTE3 was decreased by 80% (0.2-fold), the outputs of SNFL and DTUD nearly reached the activation threshold even at a low signal S level (Fig. 5b). By contrast, ITUD was irresponsive to the signal. When KTE3 was increased by 150% (2.5-fold), SNFL and DTUD exhibited similar overactivated dynamics as in the βTE3 perturbation case (Fig. 5b), in which the outputs exceeded the activation threshold even at the low S level (Fig. 5c). However, ITUD exhibited an attenuated response (a response time of 2.09 h in comparison to 1.33 h in the control).

The temporal dynamics under the perturbation of the critical determinants were also investigated using a noisy signal because biological environments fluctuate and are noisy48,49. The dynamics of SNFL and DTUD under the perturbation of βTE3 or KTE3 were similar to those of the control condition in Figure 5a (Fig. 5d and 5e). However, ITUD under the perturbation of βTE3 with a noisy signal was irresponsive, as shown in Figure 5b (Fig. 5d). For KTE3, the output of ITUD failed to exceed the activation threshold (Fig. 5e), suggesting that ITUD lost its functionality under this condition. The difference between ITUD and the other two systems was more evident upon variation of the kinetic parameters with or without noise in the signal (Supplementary Fig. S3). Therefore, the temporal dynamics results suggest that the speed and amplitude of the system response is attenuated only in ITUD, whereas the other two systems are overactivated when the E3 ubiquitin ligase is destabilized and thus fail to regulate the transcription factor.

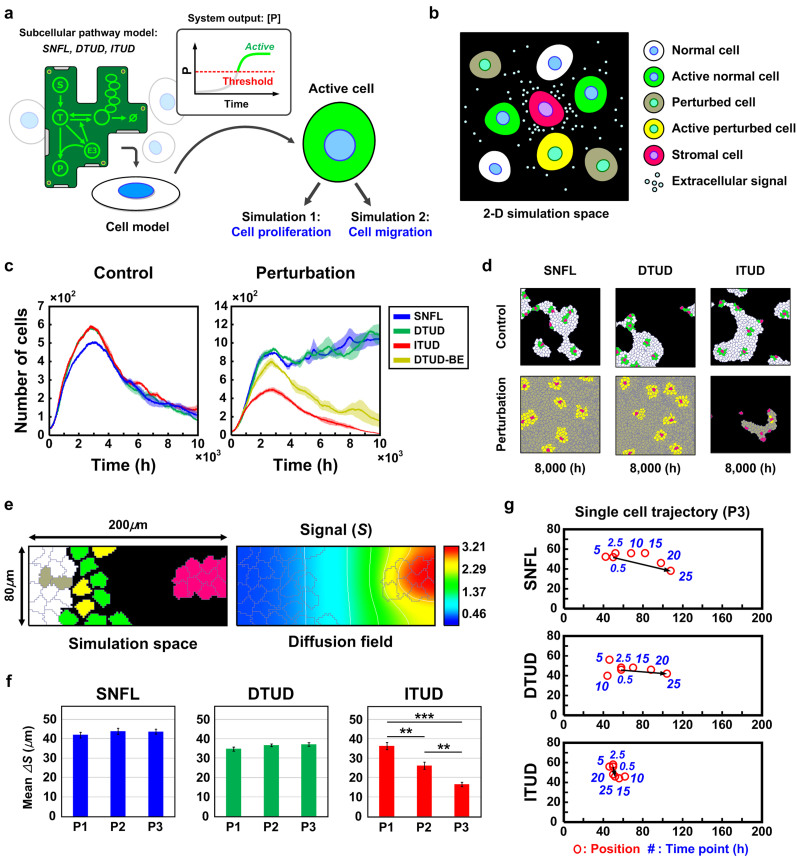
In silico cell population dynamics for proliferation and migration

The analyses of the steady-state response and the temporal dynamics suggest that ITUD is characterized by the critical determinants that dominate the stability of E3 under the effect of signal S at the single-cell level. To understand the characteristics of ITUD at the cell population level, we performed in silico analysis of the cell population dynamics50,51,52,53,54. Because the downstream genes or cellular functions activated by the signaling pathways in Figure 2a are primarily related to cell proliferation55,56, migration, or metastasis19,57, we designed the simulations for two in silico experiments: 1) cell proliferation and 2) cell migration. The SNFL, DTUD, or ITUD system is implemented in a cell model (see Supplementary Methods (section S3)) as a subcellular pathway (Fig. 6a). In a two-dimensional simulation space, the cell population consists of five types of cells: 1) normal cells, 2) active normal cells, 3) perturbed cells, 4) active perturbed cells, and 5) stromal cells (Fig. 6b and Supplementary Methods (section S3)). Stromal cells secrete the signal molecule S but do not possess any subcellular pathway. The other cells receive the signal to be activated, and only the active cells are capable of cell division or chemotaxis-driven migration. The activation of each cell is determined by measuring the output of its subcellular pathway (i.e., the level of P) (Fig. 6a). The cell population was configured to receive a stochastic signal and perturbation of the critical determinants toward the downregulation of E3. Thus, the subcellular pathway in each cell exhibited similar temporal dynamics, as shown in Figure 5d and 5e.

Figure 6. In silico cell population dynamics for cell proliferation and migration.

Figure 6

Open in a new tab

(a) The cell model includes SNFL, DTUD or ITUD as a subcellular pathway. The level of P in the subcellular pathway determines the activation of a cell. (b) The types of cells that comprise the cell population. (c) Cell proliferation dynamics under the perturbation of the critical determinants (i.e., βTE3 and KTE3). The shade of each curve represents standard errors at the respective time point (n = 3). For ‘DTUD-BE', refer to the main text. (d) Snapshots of the cell population at 8,000 h in the cell proliferation dynamics. (e) The simulation space of 200 μm × 80 μm for cell migration dynamics. The diffusion field of the signal molecule is shown in the right panel. (f) Mean displacement of the migrating 25 cells (n = 5). P1, P2, and P3 represent perturbation probabilities of 0.001, 0.01, and 0.1, respectively, in the unit simulation step. (g) Trajectory of a single cell migration in the harshest environment (P3). A red circle represents the position of the cell that is tracked at each time point (a blue number). Arrows indicate the displacement of the cell migration. ** P < 0.01 and ***P < 0.001.

In the absence of perturbation, the cell populations of all three systems grew rapidly but gradually declined after reaching the maximum population due to cellular senescence and apoptosis (Fig. 6c, left and Supplementary Fig. S4a). Conversely, in the perturbation condition, the cell populations of SNFL and DTUD continuously increased despite cellular senescence and apoptosis. These increases in the SNFL and DTUD populations are akin to tumorigenic cell proliferation. However, the ITUD population exhibited dynamics with a smaller peak in comparison to the control condition (Fig. 6c, right and Supplementary Fig. S4b). Notably, when the perturbation effect of DTUD was reduced to half by introducing a ‘buffering effect' (DTUD-BE) through the intermediate node (I), the population dynamics was similar to that of ITUD in the perturbation condition with a larger peak (Fig. 6c, right). This result demonstrates that a ‘semi-integration' of proteolysis and transcription in DTUD-BE under the perturbation (i.e., the perturbation of both I and E3) can prevent uncontrolled proliferation that was observed in the cell population of the intact DTUD. The results of the in silico cell proliferation dynamics are also provided as snapshots and movies (Fig. 6d and Supplementary Movies S1–S2).

For in silico cell migration experiments, cells were laid in a 200 μm × 80 μm space and were attracted by signal S that was secreted by stromal cells (Fig. 6e). We varied the probability of the perturbation occurrence (i.e., P1, P2, and P3; see Supplementary Methods (section S3)) and observed the cell migration. When the perturbation occurred more frequently, the mean displacement of cells possessing SNFL or DTUD was slightly increased. Conversely, the cell population of ITUD exhibited a significantly reduced migration (Fig. 6f and Supplementary Movies S3–S4). We also tracked the migration of a single cell for the most frequent perturbation (P3). In the 25-h simulation, SNFL and DTUD cells moved toward stromal cells, whereas the ITUD cell wandered around its initial position (Fig. 6g). This result suggests that cell migration can also be attenuated by ITUD if the E3 ubiquitin ligase is destabilized and thereby fails to regulate the transcription factor that drives cell migration.

In vitro cell proliferation and migration experiments

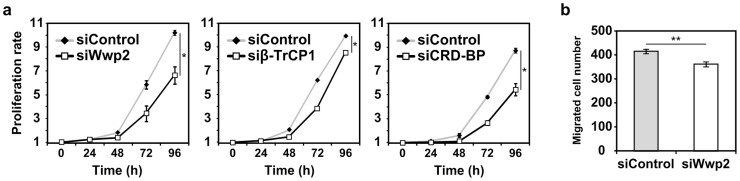
To experimentally validate our results obtained from the in silico analysis at the population level, we performed in vitro cell proliferation and migration experiments in HEK293T cells. These experiments were confined to ITUD only since there is a limitation in preparing experimental systems that exactly correspond to the three mathematical models (see Supplementary Note 1). The perturbation of the critical determinants was provided through the knockdown of E3 ubiquitin ligases (e.g., Wwp2 and β-TrCP1) or a protein that regulates the production of E3 proteins (e.g., CRD-BP) (Fig. 2a). Subsequently, cell proliferation or migration was observed, as shown in Figure 6.

The proliferation of HEK293T cells was significantly reduced when we transiently knocked down Wwp2, β-TrCP1, or CRD-BP (after 96-h culture: 65.2%, 85.9%, and 62.5% of the control, respectively) (Fig. 7a). For cell migration, we considered Wwp2 in the Smad2/Gsc pathway (Fig. 2a, fourth panel). Gsc has been reported to promote EMT (epithelial-mesenchymal transition), migration, and metastasis of breast cancer cells57. In addition, Wwp2 transactivates Gsc17. Thus, we knocked down Wwp2 in HEK293T cells, expecting that the transcriptional effects of Gsc on cell migration would be attenuated through the downregulation of Wwp2. The migration of HEK293T cells was found to be significantly reduced through the knockdown of Wwp2 (Fig. 7b). The efficiency of RNAi-mediated knockdown of Wwp2, β-TrCP1, and CRD-BP transcripts is shown in Supplementary Figure S5a–c.

Figure 7. In vitro experiments for cell proliferation and migration.

Figure 7

Open in a new tab

(a) Proliferation rates of HEK293T cells under the knockdown of Wwp2, β-TrCP1, or CRD-BP relative to the control. (b) Wwp2 was knocked down, and the migrated HEK293T cells were counted after TGF-β stimulation. * P < 0.05 and ** P < 0.01.

We also observed the expression of target genes that were expected to be affected by the knockdown of Wwp2, β-TrCP1, or CRD-BP in the cell proliferation and migration assays. The known pro-proliferative gene c-Jun58 was selected as a target gene (P) of Gsc(T)/Wwp2(E3) and Smad3(T)/β-TrCP1(E3)59. The knockdown of Wwp2 or β-TrCP1 resulted in the reduced expression of c-Jun (Supplementary Fig. S5a and S5b). The knockdown of CRD-BP, which is in the Wnt/β-catenin pathway (Fig. 2a, second panel), efficiently decreased β-TrCP1 and thereby the expression of CyclinD1, a pro-proliferative target gene of β-catenin (Supplementary Fig. S5c). For the cell migration assay, Wwp2 knockdown upregulated FGF2 which was reported to inhibit cell migration in breast cancer cells60,61 and MEF cells62 (Supplementary Fig. S5a). These experimental results are consistent with our simulation results indicating that cell proliferation and migration are significantly reduced through the downregulation of E3 in ITUD. However, the results are not entirely attributable to the effects of ITUD because E3 proteins possess many substrates, and, thus, might have pleiotropic effects on cellular functions3,4,63,64,65.

We further investigated whether the decreasing phase of ITUD caused by the enhanced proteolysis of T by an excess of E3 (Fig. 4d and 4e) can also be observed in the target gene expression and the actual cell proliferation. For this purpose, we overexpressed CRD-BP to stabilize β-TrCP1 mRNA in HEK293T cells, which corresponds to an increase of βTE3 in ITUD. Consequently, the overexpression of CRD-BP reduced both the proliferation rate of HEK293T cells (Supplementary Fig. S5d) and CyclinD1 expression (Supplementary Fig. S5e), which is consistent with our simulation results.

Discussion

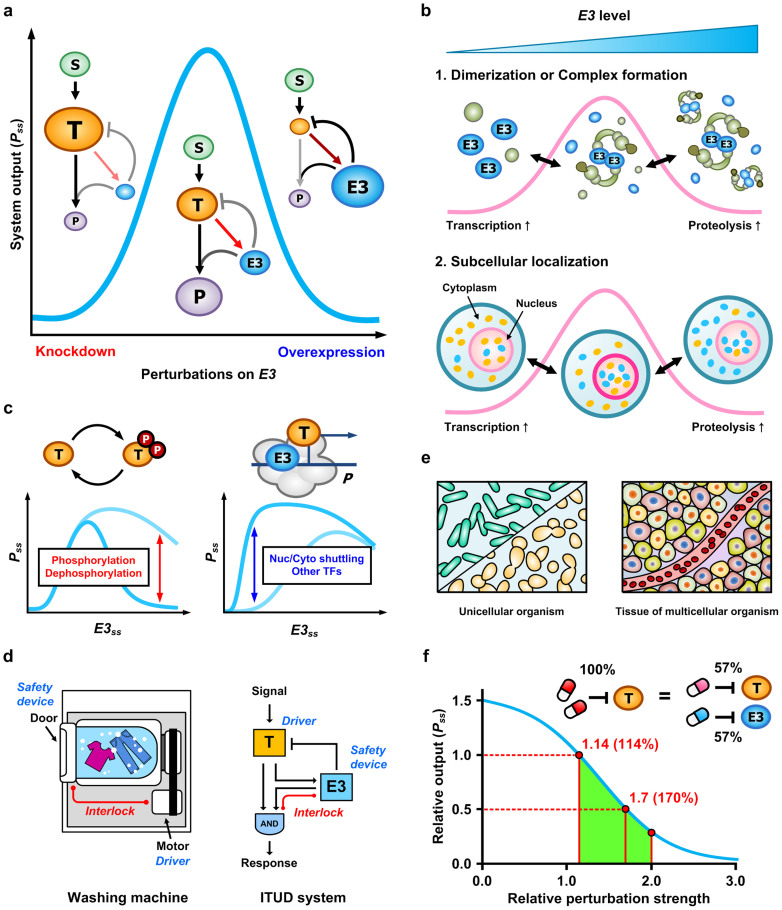
Perturbation of the critical determinants for both downregulation and upregulation of E3 (corresponding to the increase and decrease of T, respectively) reduced the output of the ITUD system (Fig. 8a). The maximum output of ITUD is achieved by an intricate balance between T and E3. Thus, ITUD exhibits biphasicity with respect to the stability of the E3 ubiquitin ligase. We suggest two molecular mechanisms underlying the biphasicity of ITUD. The first mechanism involves complex formation or dimerization of the E3 ubiquitin ligase (Fig. 8b, top). Some E3 ubiquitin ligases must form a complex to achieve their proteolytic function. β-TrCP1 or Skp2, for example, interacts with Skp1 to form an SCF complex for proteolysis3, whereas these proteins can also participate in transcription without complex formation18,19. In addition, dimerization is necessary for some E3 proteins to achieve ubiquitin ligase activity (Table 2). This evidence indicating the necessity of the dimerization of and complex formation by E3 proteins for their proteolytic function suggests that the maximum, or the optimal response of the ITUD system, may be established by a subtle balance between the monomeric form for transcription and the oligomeric form for proteolysis. The second mechanism is based on subcellular localization (Fig. 8b, bottom). Several isoforms of β-TrCP1 and β-TrCP2 have been reported to predominantly localize in the nucleus66,67. Assuming that proteolysis is facilitated primarily in the cytoplasm, transcriptional activation may be initially promoted by a small amount of E3 proteins that preferentially localize in the nucleus. Eventually, the accumulation of the E3 ubiquitin ligase in the cytoplasm and nucleus would enhance proteolysis, which prevents the transcription factor from entering the nucleus to participate in transcription, thereby suppressing transcriptional activation (these two mechanisms can be classified as Type I and Type IV biphasic regulation according to Levchenko et al.68).

Figure 8. The design principles of the ITUD system.

Figure 8

Open in a new tab

(a) Biphasic response of ITUD with respect to the perturbation on E3. (b) Possible mechanisms underlying the biphasicity of ITUD mediated by E3 ubiquitin ligases. (c) Possible regulatory mechanisms that affect the shapes of the biphasic response in the ITUD system (d) A representative example of a safety interlock device can be found in a clothes washing machine (left). The E3 ubiquitin ligase in the ITUD system can serve as a safety interlock device based on its integrated roles in proteolysis and transcription (right). (e) ITUD may support tissue homeostasis in multicellular organisms. (f) Combinatorial therapy based on ITUD. The relative output is the ratio of Pss between the inhibition of only T (single perturbation) and the inhibition of both T and E3 (dual perturbation) in the ITUD system. Perturbation strength is the percentage change of a kinetic parameter value to the perturbation of a system component, and the relative perturbation strength is the ratio between the single and dual perturbation strengths (see Methods for details).

Table 2. An example of the dimerization required for the ubiquitin ligase activity of E3 proteins.

E3 ubiquitin ligase Target Reference
β-TrCP* IκBα 94
Fbw7 Cyclin E 95
Cdc4 Sic peptide 95
Fbx4 CyclinD1 96,97
TRAF6 TRAF6 (autoubiquitination) 98
Open in a new tab

*The homodimer of β-TrCP1 or β-TrCP2 was able to bind to phosphorylated IκBα, although the heterodimers failed to be recruited.

We suppose that the characteristics of the biphasic response in ITUD might be modulated by regulating the extent of phosphorylation/dephosphorylation or nuclear-cytoplasmic shuttling. For example, the proteolysis of β-catenin by β-TrCP1 requires the phosphorylation of β-catenin, and the phosphorylation can be reversed by a phosphatase such as PP2A. Therefore, the intensity of phosphorylation/dephosphorylation of the transcription factor by an upstream enzyme determines both the timing and the extent of E3-mediated proteolysis, which consequently alters the biphasic response (Fig. 8c, left). This effect was observed by varying Km_E3T in ITUD (Fig. 4d). Alternatively, nuclear-cytoplasmic shuttling is another possible mechanism that exemplifies the effects of varying KE3P in ITUD (Fig. 4e). For example, the nuclear-cytoplasmic shuttling of Skp2 is regulated by phosphorylation of Akt69 or the acetylation of p30070. The upstream signals of Akt or p300 may modulate the biphasic response by regulating the nuclear-cytoplasmic shuttling of Skp2 for its transcriptional activation (Fig. 8c, right).

Biological circuits employ elaborate structures and dynamic properties to achieve specialized functions31. Interestingly, such circuits also possess mechanisms to protect the biological systems from intrinsic or extrinsic perturbations. A representative example is the DNA repair system, which ensures the integrity of genetic information71. Another intriguing example is the responsive backup circuit of genetic redundancy, in which any problem that reduces the stability of the activator is buffered by a functionally redundant partner to guarantee a robust output72,73,74. This principle is comparable to the redundancy of critical components for system reliability in engineering. We suggest that the apparently paradoxical roles of E3 ubiquitin ligases in ITUD may represent a safety interlock device that prevents the overactivation of a molecular or cellular function due to the destabilization of E3. A safety interlock device does not allow the entire system to operate unless the safety condition is satisfied. A familiar example of a safety interlock device is the door of a washing machine (Fig. 8d, left). In the washing machine, the door is interlocked with the motor so that the motor can operate only if the door safety is guaranteed. E3 and the transcription factor in ITUD correspond to the door and motor of the washing machine, respectively (Fig. 8d, right). So, E3 ubiquitin ligase functions as a safety interlock device which prevents a devastating overactivation as observed in SNFL and DTUD (Fig. 5 and 6), by controlling an appropriate level of the transcription factor through UPS-dependent proteolysis. If E3 is not functional due to a certain perturbation in ITUD, transcription should be attenuated in this case since ‘proteolysis for safety' is not guaranteed. Together, we find that both washing machine and ITUD can cope with the breakdown of safety device by shutting down the system to avoid its abnormal operation.

The design principles of ITUD may also represent an important mechanism used to prevent potentially dangerous functions in multicellular organisms (Fig. 8e). Proliferation or migration of cells in a tissue should be tightly regulated because the overactivation of such cellular functions can disrupt tissue homeostasis and even result in death. A typical example is the manifestation of abnormal cellular physiology in cancer development75. The strategy of ITUD in support of tissue homeostasis is that of “if impossible to control potentially dangerous cellular functions such as cell division or migration, it would be better not to activate it.” If the stability of E3 ubiquitin ligase in a cell collapses owing to any perturbation, ITUD suppresses transcriptional activation (Fig. 5b–e) and, therefore, the corresponding cellular functions (Fig. 6c and 6f). This preventive strategy of ITUD may represent one of the mechanisms for cellular dormancy under harsh environments76. Moreover, the paradoxical bifunctionality of E3 ubiquitin ligases presents an interesting example of the utility of paradoxical components77 to ensure the prevention of disastrous consequences in the cell population.

The consideration of E3 ubiquitin ligases as targets for cancer treatment relates to the successful application of the proteasome inhibitor bortezomib (commercialized name, Velcade®) for multiple myeloma78. The rationale for the development of therapeutics targeting E3 proteins is based on enhancing the specificity of the drug to reduce the side effects due to proteasome inhibition. However, targeting an E3 protein, particularly the SCF E3 ubiquitin ligase, can cause unpredictable effects because a single E3 is able to promote the proteolysis of both oncogenes and tumor-suppressor genes3. Therefore, we suggest a combinatorial therapy to downregulate both oncogenes and cognate E3 proteins by exploiting the E3 function as the safety interlock device in the ITUD system. Targeting of a single oncogene or a specific signal transduction pathway based on the rationale of “oncogene addiction” is one of the basic approaches in cancer treatment79. However, this approach typically includes drawbacks such as dose toxicity80 and drug resistance81. To mitigate such problems in a given ITUD signaling pathway, we can distribute the perturbation strength from an addictive oncogene to the E3 ubiquitin ligases to reduce toxicity and to diversify targets to block as many escape routes as possible. A toy example of the steady-state analysis in ITUD system indicated that 114% (i.e., 57% for each T and E3) of the single perturbation strength on T is required to inhibit both T and E3 to attain an identical result (Fig. 8f and see Methods for further details). If the dose required to cause this perturbation in clinical treatment is known, our approach can represent a promising strategy for the treatment of cancer or other obstinate diseases.

In this study, the role of E3 in transcription was limited to the transcriptional activation. However, E3 ubiquitin ligases can also participate in transcriptional repression independent of proteolysis82,83,84. In yeast, Met30, an SCF E3 ubiquitin ligase, not only promotes the UPS-dependent proteolysis of Met4, a transcriptional activator85,86,87,88,89, but also represses the transcriptional activity of Met4 through non-proteolytic ubiquitination84. In this case, the roles of E3 in transcription and proteolysis are not paradoxical, but consistent in inhibiting the function of the cognate transcription factor. On the other hand, BRCA1, a tumor suppressor E3 in breast cancers, can activate or repress transcription pre-initiation complex depending on the context82,90. Therefore, the effects of BRCA1 should be carefully interpreted in consideration of the cellular environment. Although the design principle of ITUD that we unraveled in this study cannot be generalized to expound all the complicated roles of E3 in transcription and proteolysis, it is still useful to get a new insight into the apparently paradoxical roles of E3. We need to further investigate the design principles underlying the other roles of E3 as in the case of Met30.

Methods

Numerical methods

Numerical solutions and random numbers were obtained using MATLAB® 2012a (64 bit). The fsolve and ode15s/ode45 functions were used for steady-state analysis and temporal dynamics, respectively. For the noise signal in temporal dynamics (Fig. 5d and 5e), we generated a random number that is uniformly distributed on (0, 1) as an amplitude of the signal for each time point using rand function.

Mathematical model of subcellular pathways

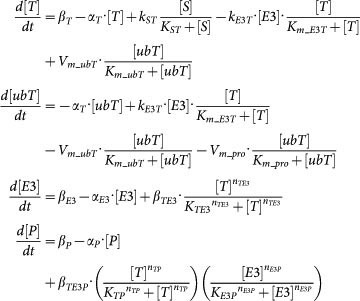
Mathematical models of SNFL, DTUD, and ITUD are systems of ordinary differential equations as follows (the ordinary differential equations for T, ubT, E3 of SNFL and DTUD are the same as those of ITUD):

ITUD:

graphic file with name srep05573-m7.jpg

SNFL:

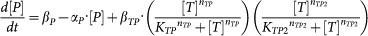graphic file with name srep05573-m8.jpg

DTUD:

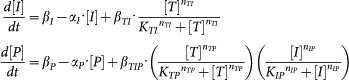graphic file with name srep05573-m9.jpg

The individual biological processes are described by typical kinetic terms such as Michaelis-Menten type kinetics and Hill equation. Refer to Supplementary Methods (section S2) for model derivation and major assumptions.

In silico cell population dynamics

The models of the cell population dynamics were developed on the basis of the CompuCell3D multiscale modeling platform91. Refer to Supplementary Methods (section S3) for additional details.

Sensitivity analysis for identifying critical determinants

In this study, local sensitivity was defined as the relative change in the system output (i.e., the steady-state level of P) when a small perturbation (±1%) was imposed on a single kinetic parameter92. The relative local sensitivity coefficient was approximated by the following formula:

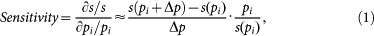graphic file with name srep05573-m1.jpg

where s is the system output, and pi is a parameter of ID number i. The steady-state levels of the system components were numerically solved, and thus, did not rely on the use of power-law formalism and an analytic solution93.

We sampled 5000 sets of parameter values for the steady-state analysis over a wide range of parameter values (Supplementary Fig. S1). The parameter values were generated using a uniform random variable on [0.01, 100]. Subsequently, we calculated M and R, which are defined as

graphic file with name srep05573-m2.jpg

where M is the relative sensitivity coefficient, as previously defined, and R is the ratio of two Ms between ITUD and an alternative system such as SNFL and DTUD. Therefore, R represents the ratio of the rate of change in the system outputs as follows:

graphic file with name srep05573-m3.jpg

The external equivalence of MCC was achieved for each parameter set (see Supplementary Methods (section S2)). The 5000 data entities of a pair (M, R) were sorted according to MITUD, and the moving quantile method with a window size of 1000 was applied as in the method of Alves and Savageau42, in which the median of R (i.e., quantile 0.5) and its corresponding MITUD were obtained from a subset of the data extracted by the sliding window. Thus, we finally obtained 4001 data entities for <R> and <M> (the total number of windows is “sample size − window size + 1”; i.e., 5000 − 1000 + 1). To exclude extreme cases, 10% of each end in the total windows was trimmed (i.e., 80% of 4001 windows ≒ 3200 windows remaining), and density plots were generated (Supplementary Fig. S1).

Combinatorial therapy based on the ITUD system

We first applied the perturbation on T by disrupting the signal flow from S to T (single perturbation), which was implemented by increasing the parameter value of Km_ST (ID: 4). Next, both values of Km_ST (ID: 4) and KTE3 (ID: 14) were increased for the inhibition of both T and E3 (dual perturbation). We defined a perturbation strength (PS) as the percentage change of a kinetic parameter value to the perturbation of a system component (e.g., T or E3) as follows:

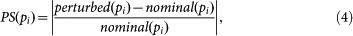graphic file with name srep05573-m4.jpg

where perturbed(pi) and nominal(pi) are perturbed and nominal value of parameter pi, respectively. Therefore, the single perturbation strength (PSs) of Km_ST, when it is perturbed from the nominal value 0.5 (Supplementary Table S2) to 1.5, is calculated as follows:

graphic file with name srep05573-m10.jpg

In this case, Pss under single perturbation is 0.0721, which is decreased by 91.8% (0.08 fold) from Pss without any perturbation (i.e., 0.8781). The relative perturbation strength (RPS) was obtained based on the ratio between the single and dual perturbation strengths as follows:

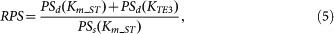graphic file with name srep05573-m5.jpg

where PSd(pi) represents the dual perturbation strength for a given parameter pi with the inhibition of both T and E3. For example, if we change Km_ST from 0.5 to 1.5 as the single perturbation and both Km_ST and KTE3 from 0.5 to 0.75 as the dual perturbation, the relative perturbation strength in Figure 8f is calculated as follows:

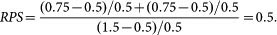graphic file with name srep05573-m11.jpg

For simplicity, the perturbation strengths of Km_ST and KTE3 were set to be identical in the dual perturbation. So, RPS was calculated as follows:

graphic file with name srep05573-m6.jpg

where PSd = PSd(Km_ST) = PSd(KTE3). The relative output in Figure 8f represents the ratio of Pss between the single and dual perturbation. Pss under single perturbation is 0.0721, so the relative output 0.5 means that Pss under dual perturbation is 0.5 × 0.0721 = 0.03605.

In vitro experiments

Refer to Supplementary Methods (section S4) for cell culture and transfection, RNA isolation and qRT-PCR, cell proliferation assay, and cell migration assay.

Supplementary Material

Supplementary Information

Supplementary Information

srep05573-s1.pdf (4.6MB, pdf)
Supplementary Information

Movie S1

Download video file (7.1MB, avi)
Supplementary Information

Movie S2

Download video file (7.1MB, avi)
Supplementary Information

Movie S3

Download video file (7.1MB, avi)
Supplementary Information

Movie S4

Download video file (5.6MB, avi)

Acknowledgments

This work was supported by grants from the National Research Foundation of Korea (NRF), which is funded by the Korean Government, the Ministry of Science, ICT & Future Planning (MSIP) (2010-0017662 and 2013M3A9A7046303). This work was also supported by the “Systems biology infrastructure establishment grant” provided by Gwangju Institute of Science and Technology in 2014. We thank Tae-Hwan Kim and Taejun Park for their critical reading and valuable comments.

Footnotes

The authors declare no competing financial interests.

Author Contributions K.-H.C. designed the project and supervised the research; D.L. and K.-H.C. performed the mathematical modeling and analysis; M.K. performed the experiments; and D.L. and K.-H.C. wrote the manuscript.

References

  1. Naujokat C. & Saric T. Concise review: role and function of the ubiquitin-proteasome system in mammalian stem and progenitor cells. Stem Cells 25, 2408–2418; 10.1634/stemcells.2007-0255 (2007). [DOI] [PubMed] [Google Scholar]
  2. Mani A. & Gelmann E. P. The ubiquitin-proteasome pathway and its role in cancer. J. Clin. Oncol. 23, 4776–4789; 10.1200/JCO.2005.05.081 (2005). [DOI] [PubMed] [Google Scholar]
  3. Nakayama K. I. & Nakayama K. Ubiquitin ligases: cell-cycle control and cancer. Nat. Rev. Cancer 6, 369–381; 10.1038/nrc1881 (2006). [DOI] [PubMed] [Google Scholar]
  4. Frescas D. & Pagano M. Deregulated proteolysis by the F-box proteins SKP2 and beta-TrCP: tipping the scales of cancer. Nat. Rev. Cancer 8, 438–449; 10.1038/nrc2396 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ciechanover A. & Brundin P. The ubiquitin proteasome system in neurodegenerative diseases: sometimes the chicken, sometimes the egg. Neuron 40, 427–446; 10.1016/S0896-6273(03)00606-8 (2003). [DOI] [PubMed] [Google Scholar]
  6. Powell S. R. The ubiquitin-proteasome system in cardiac physiology and pathology. Am. J. Physiol. Heart Circ. Physiol. 291, H1–H19; 10.1152/ajpheart.00062.2006 (2006). [DOI] [PubMed] [Google Scholar]
  7. Zolk O., Schenke C. & Sarikas A. The ubiquitin-proteasome system: focus on the heart. Cardiovasc. Res. 70, 410–421; 10.1016/j.cardiores.2005.12.021 (2006). [DOI] [PubMed] [Google Scholar]
  8. Liu Y. C. Ubiquitin ligases and the immune response. Annu. Rev. Immunol. 22, 81–127; 10.1146/annurev.immunol.22.012703.104813 (2004). [DOI] [PubMed] [Google Scholar]
  9. Malynn B. A. & Ma A. Ubiquitin makes its mark on immune regulation. Immunity 33, 843–852; 10.1016/j.immuni.2010.12.007 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Glickman M. H. & Ciechanover A. The ubiquitin-proteasome proteolytic pathway: destruction for the sake of construction. Physiol. Rev. 82, 373–428; 10.1152/physrev.00027.2001 (2002). [DOI] [PubMed] [Google Scholar]
  11. Meusser B., Hirsch C., Jarosch E. & Sommer T. ERAD: the long road to destruction. Nat. Cell Biol. 7, 766–772; 10.1038/ncb0805-766 (2005). [DOI] [PubMed] [Google Scholar]
  12. Hochstrasser M. Origin and function of ubiquitin-like proteins. Nature 458, 422–429; 10.1038/nature07958 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Geng F., Wenzel S. & Tansey W. P. Ubiquitin and proteasomes in transcription. Annu. Rev. Biochem. 81, 177–201; 10.1146/annurev-biochem-052110-120012 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kim S. Y., Herbst A., Tworkowski K. A., Salghetti S. E. & Tansey W. P. Skp2 regulates Myc protein stability and activity. Mol. Cell 11, 1177–1188; 10.1016/S1097-2765(03)00173-4 (2003). [DOI] [PubMed] [Google Scholar]
  15. von der Lehr N. et al. The F-box protein Skp2 participates in c-Myc proteosomal degradation and acts as a cofactor for c-Myc-regulated transcription. Mol. Cell 11, 1189–1200; 10.1016/S1097-2765(03)00193-X (2003). [DOI] [PubMed] [Google Scholar]
  16. Wu R. C., Feng Q., Lonard D. M. & O'Malley B. W. SRC-3 coactivator functional lifetime is regulated by a phospho-dependent ubiquitin time clock. Cell 129, 1125–1140; 10.1016/j.cell.2007.04.039 (2007). [DOI] [PubMed] [Google Scholar]
  17. Zou W. et al. The E3 ubiquitin ligase Wwp2 regulates craniofacial development through mono-ubiquitylation of Goosecoid. Nat. Cell Biol. 13, 59–65; 10.1038/ncb2134 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kimbrel E. A. & Kung A. L. The F-box protein beta-TrCp1/Fbw1a interacts with p300 to enhance beta-catenin transcriptional activity. J. Biol. Chem. 284, 13033–13044; 10.1074/jbc.M901248200 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Chan C. H. et al. Deciphering the transcriptional complex critical for RhoA gene expression and cancer metastasis. Nat. Cell Biol. 12, 457–467; 10.1038/ncb2047 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Popov N., Schulein C., Jaenicke L. A. & Eilers M. Ubiquitylation of the amino terminus of Myc by SCF(beta-TrCP) antagonizes SCF(Fbw7)-mediated turnover. Nat. Cell Biol. 12, 973–981; 10.1038/ncb2104 (2010). [DOI] [PubMed] [Google Scholar]
  21. Bres V. et al. A non-proteolytic role for ubiquitin in Tat-mediated transactivation of the HIV-1 promoter. Nat. Cell Biol. 5, 754–761; 10.1038/ncb1023 (2003). [DOI] [PubMed] [Google Scholar]
  22. MacDonald B. T., Tamai K. & He X. Wnt/beta-catenin signaling: components, mechanisms, and diseases. Dev. Cell 17, 9–26; 10.1016/j.devcel.2009.06.016 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Winston J. T. et al. The SCFbeta-TRCP-ubiquitin ligase complex associates specifically with phosphorylated destruction motifs in IkappaBalpha and beta-catenin and stimulates IkappaBalpha ubiquitination in vitro. Genes Dev. 13, 270–283 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fukuchi M. et al. Ligand-dependent degradation of Smad3 by a ubiquitin ligase complex of ROC1 and associated proteins. Mol. Biol. Cell 12, 1431–1443 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wan M. et al. Smad4 protein stability is regulated by ubiquitin ligase SCF beta-TrCP1. J. Biol. Chem. 279, 14484–14487; 10.1074/jbc.C400005200 (2004). [DOI] [PubMed] [Google Scholar]
  26. Wan M. et al. SCF(beta-TrCP1) controls Smad4 protein stability in pancreatic cancer cells. Am. J. Pathol. 166, 1379–1392 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Chantry A. WWP2 ubiquitin ligase and its isoforms New biological insight and promising disease targets. Cell Cycle 10, 2437–2439; 10.4161/cc.10.15.16874 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Soond S. M. & Chantry A. Selective targeting of activating and inhibitory Smads by distinct WWP2 ubiquitin ligase isoforms differentially modulates TGFbeta signalling and EMT. Oncogene 30, 2451–2462; 10.1038/onc.2010.617 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Nakamura Y. et al. Wwp2 is essential for palatogenesis mediated by the interaction between Sox9 and mediator subunit 25. Nat Commun 2, 251; 10.1038/ncomms1242 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Brandman O., Ferrell J. E. Jr, Li R. & Meyer T. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science 310, 496–498; 10.1126/science.1113834 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Alon U. An Introduction to Systems Biology: Design Principles of Biological Circuits. (Chapman & Hall/CRC, 2007). [Google Scholar]
  32. Kim J. R., Yoon Y. & Cho K. H. Coupled feedback loops form dynamic motifs of cellular networks. Biophys. J. 94, 359–365; 10.1529/biophysj.107.105106 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ma W., Trusina A., El-Samad H., Lim W. A. & Tang C. Defining network topologies that can achieve biochemical adaptation. Cell 138, 760–773; 10.1016/j.cell.2009.06.013 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sneppen K., Krishna S. & Semsey S. Simplified models of biological networks. Annu Rev Biophys 39, 43–59; 10.1146/annurev.biophys.093008.131241 (2010). [DOI] [PubMed] [Google Scholar]
  35. Kim J. R., Shin D., Jung S. H., Heslop-Harrison P. & Cho K. H. A design principle underlying the synchronization of oscillations in cellular systems. J. Cell Sci. 123, 537–543; 10.1242/jcs.060061 (2010). [DOI] [PubMed] [Google Scholar]
  36. Ratushny A. V., Saleem R. A., Sitko K., Ramsey S. A. & Aitchison J. D. Asymmetric positive feedback loops reliably control biological responses. Mol. Syst. Biol. 8, 577; 10.1038/msb.2012.10 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lipford J. R. & Deshaies R. J. Diverse roles for ubiquitin-dependent proteolysis in transcriptional activation. Nat. Cell Biol. 5, 845–850; 10.1038/ncb1003-845 (2003). [DOI] [PubMed] [Google Scholar]
  38. Muratani M. & Tansey W. P. How the ubiquitin-proteasome system controls transcription. Nat. Rev. Mol. Cell Biol. 4, 192–201; 10.1038/nrm1049 (2003). [DOI] [PubMed] [Google Scholar]
  39. Bretones G. et al. SKP2 oncogene is a direct MYC target gene and MYC down-regulates p27(KIP1) through SKP2 in human leukemia cells. J. Biol. Chem. 286, 9815–9825; 10.1074/jbc.M110.165977 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Qu X. et al. A signal transduction pathway from TGF-beta1 to SKP2 via Akt1 and c-Myc and its correlation with progression in human melanoma. J. Invest. Dermatol. 134, 159–167; 10.1038/jid.2013.281 (2014). [DOI] [PubMed] [Google Scholar]
  41. Savageau M. A. [Ch. 10. Genetic Regulation: Repressible Systems]. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology [pp. 306–334] (Addison-Wesley Pub. Co., Advanced Book Program, 1976). [Google Scholar]
  42. Alves R. & Savageau M. A. Comparing systemic properties of ensembles of biological networks by graphical and statistical methods. Bioinformatics 16, 527–533; 10.1093/bioinformatics/16.6.527 (2000). [DOI] [PubMed] [Google Scholar]
  43. Alves R. & Savageau M. A. Systemic properties of ensembles of metabolic networks: application of graphical and statistical methods to simple unbranched pathways. Bioinformatics 16, 534–547 (2000). [DOI] [PubMed] [Google Scholar]
  44. Alves R. & Savageau M. A. Extending the method of mathematically controlled comparison to include numerical comparisons. Bioinformatics 16, 786–798 (2000). [DOI] [PubMed] [Google Scholar]
  45. Weiss J. N. The Hill equation revisited: uses and misuses. FASEB J. 11, 835–841 (1997). [PubMed] [Google Scholar]
  46. Mangan S., Zaslaver A. & Alon U. The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks. J. Mol. Biol. 334, 197–204; 10.1016/j.jmb.2003.09.049 (2003). [DOI] [PubMed] [Google Scholar]
  47. Nakakuki T. et al. Ligand-specific c-Fos expression emerges from the spatiotemporal control of ErbB network dynamics. Cell 141, 884–896; 10.1016/j.cell.2010.03.054 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Raj A. & van Oudenaarden A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216–226; 10.1016/j.cell.2008.09.050 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Balazsi G., van Oudenaarden A. & Collins J. J. Cellular decision making and biological noise: from microbes to mammals. Cell 144, 910–925; 10.1016/j.cell.2011.01.030 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Anderson A. R., Weaver A. M., Cummings P. T. & Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 127, 905–915; 10.1016/j.cell.2006.09.042 (2006). [DOI] [PubMed] [Google Scholar]
  51. Chaudhary S. U., Shin S. Y., Won J. K. & Cho K. H. Multiscale modeling of tumorigenesis induced by mitochondrial incapacitation in cell death. IEEE Trans. Biomed. Eng. 58, 3028–3032; 10.1109/TBME.2011.2159713 (2011). [DOI] [PubMed] [Google Scholar]
  52. Deisboeck T. S., Wang Z., Macklin P. & Cristini V. Multiscale cancer modeling. Annu Rev Biomed Eng 13, 127–155; 10.1146/annurev-bioeng-071910-124729 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Hester S. D., Belmonte J. M., Gens J. S., Clendenon S. G. & Glazier J. A. A multi-cell, multi-scale model of vertebrate segmentation and somite formation. PLoS Comput. Biol. 7, e1002155; 10.1371/journal.pcbi.1002155 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Goni-Moreno A. & Amos M. A reconfigurable NAND/NOR genetic logic gate. BMC Syst. Biol. 6, 126; 10.1186/1752-0509-6-126 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Logan C. Y. & Nusse R. The Wnt signaling pathway in development and disease. Annu. Rev. Cell Dev. Biol. 20, 781–810; 10.1146/annurev.cellbio.20.010403.113126 (2004). [DOI] [PubMed] [Google Scholar]
  56. Dang C. V. MYC on the path to cancer. Cell 149, 22–35; 10.1016/j.cell.2012.03.003 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Hartwell K. A. et al. The Spemann organizer gene, Goosecoid, promotes tumor metastasis. Proc. Natl. Acad. Sci. U. S. A. 103, 18969–18974; 10.1073/pnas.0608636103 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Shaulian E. & Karin M. AP-1 in cell proliferation and survival. Oncogene 20, 2390–2400; 10.1038/sj.onc.1204383 (2001). [DOI] [PubMed] [Google Scholar]
  59. Wong C. et al. Smad3-Smad4 and AP-1 complexes synergize in transcriptional activation of the c-Jun promoter by transforming growth factor beta. Mol. Cell. Biol. 19, 1821–1830 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Korah R. M., Sysounthone V., Golowa Y. & Wieder R. Basic fibroblast growth factor confers a less malignant phenotype in MDA-MB-231 human breast cancer cells. Cancer Res. 60, 733–740 (2000). [PubMed] [Google Scholar]
  61. Korah R., Choi L., Barrios J. & Wieder R. Expression of FGF-2 alters focal adhesion dynamics in migration-restricted MDA-MB-231 breast cancer cells. Breast Cancer Res. Treat. 88, 17–28; 10.1007/s10459-004-6006-2 (2004). [DOI] [PubMed] [Google Scholar]
  62. Kottakis F. et al. FGF-2 regulates cell proliferation, migration, and angiogenesis through an NDY1/KDM2B-miR-101-EZH2 pathway. Mol. Cell 43, 285–298; 10.1016/j.molcel.2011.06.020 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Skaar J. R., D'Angiolella V., Pagan J. K. & Pagano M. SnapShot: F Box Proteins II. Cell 137, 1358, 1358 e1351; 10.1016/j.cell.2009.05.040 (2009). [DOI] [PubMed] [Google Scholar]
  64. Skaar J. R., Pagan J. K. & Pagano M. SnapShot: F box proteins I. Cell 137, 1160–1160 e1161; 10.1016/j.cell.2009.05.039 (2009). [DOI] [PubMed] [Google Scholar]
  65. Silverman J. S., Skaar J. R. & Pagano M. SCF ubiquitin ligases in the maintenance of genome stability. Trends Biochem. Sci. 37, 66–73; 10.1016/j.tibs.2011.10.004 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Seo E. et al. Multiple isoforms of beta-TrCP display differential activities in the regulation of Wnt signaling. Cell. Signal. 21, 43–51; 10.1016/j.cellsig.2008.09.009 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Putters J., Slotman J. A., Gerlach J. P. & Strous G. J. Specificity, location and function of betaTrCP isoforms and their splice variants. Cell. Signal. 23, 641–647; 10.1016/j.cellsig.2010.11.015 (2011). [DOI] [PubMed] [Google Scholar]
  68. Levchenko A., Bruck J. & Sternberg P. W. Regulatory modules that generate biphasic signal response in biological systems. Syst. Biol. (Stevenage) 1, 139–148; 10.1049/sb:20045014 (2004). [DOI] [PubMed] [Google Scholar]
  69. Lin H. K. et al. Phosphorylation-dependent regulation of cytosolic localization and oncogenic function of Skp2 by Akt/PKB. Nat. Cell Biol. 11, 420–432; 10.1038/ncb1849 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Inuzuka H. et al. Acetylation-dependent regulation of Skp2 function. Cell 150, 179–193; 10.1016/j.cell.2012.05.038 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Alberts B. et al. [Ch. 5. DNA Replication, Repair, and Recombination]. Molecular Biology of the Cell 5th ed. [pp. 295–304] (Garland Science, 2008). [Google Scholar]
  72. Kafri R., Levy M. & Pilpel Y. The regulatory utilization of genetic redundancy through responsive backup circuits. Proc. Natl. Acad. Sci. U. S. A. 103, 11653–11658; 10.1073/pnas.0604883103 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Haldar M., Karan G., Tvrdik P. & Capecchi M. R. Two cell lineages, myf5 and myf5-independent, participate in mouse skeletal myogenesis. Dev. Cell 14, 437–445; 10.1016/j.devcel.2008.01.002 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Kafri R., Springer M. & Pilpel Y. Genetic redundancy: new tricks for old genes. Cell 136, 389–392; 10.1016/j.cell.2009.01.027 (2009). [DOI] [PubMed] [Google Scholar]
  75. Hanahan D. & Weinberg R. A. Hallmarks of cancer: the next generation. Cell 144, 646–674; 10.1016/j.cell.2011.02.013 (2011). [DOI] [PubMed] [Google Scholar]
  76. Aguirre-Ghiso J. A. Models, mechanisms and clinical evidence for cancer dormancy. Nat. Rev. Cancer 7, 834–846; 10.1038/nrc2256 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Hart Y. & Alon U. The utility of paradoxical components in biological circuits. Mol. Cell 49, 213–221; 10.1016/j.molcel.2013.01.004 (2013). [DOI] [PubMed] [Google Scholar]
  78. Adams J. & Kauffman M. Development of the proteasome inhibitor Velcade (Bortezomib). Cancer Invest. 22, 304–311; 10.1081/CNV-120030218 (2004). [DOI] [PubMed] [Google Scholar]
  79. Weinstein I. B. & Joe A. Oncogene addiction. Cancer Res. 68, 3077–3080; 10.1158/0008-5472.CAN-07-3293 (2008). [DOI] [PubMed] [Google Scholar]
  80. Hutson T. E., Figlin R. A., Kuhn J. G. & Motzer R. J. Targeted therapies for metastatic renal cell carcinoma: an overview of toxicity and dosing strategies. Oncologist 13, 1084–1096; 10.1634/theoncologist.2008-0120 (2008). [DOI] [PubMed] [Google Scholar]
  81. Torti D. & Trusolino L. Oncogene addiction as a foundational rationale for targeted anti-cancer therapy: promises and perils. EMBO Mol. Med. 3, 623–636; 10.1002/emmm.201100176 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Horwitz A. A., Affar el B., Heine G. F., Shi Y. & Parvin J. D. A mechanism for transcriptional repression dependent on the BRCA1 E3 ubiquitin ligase. Proc. Natl. Acad. Sci. U. S. A. 104, 6614–6619; 10.1073/pnas.0610481104 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  83. Ehrlund A. et al. E3 ubiquitin ligase RNF31 cooperates with DAX-1 in transcriptional repression of steroidogenesis. Mol. Cell. Biol. 29, 2230–2242; 10.1128/MCB.00743-08 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  84. Ndoja A., Cohen R. E. & Yao T. Ubiquitin signals proteolysis-independent stripping of transcription factors. Mol. Cell 53, 893–903; 10.1016/j.molcel.2014.02.002 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  85. Chandrasekaran S. et al. Destabilization of binding to cofactors and SCFMet30 is the rate-limiting regulatory step in degradation of polyubiquitinated Met4. Mol. Cell 24, 689–699; 10.1016/j.molcel.2006.10.028 (2006). [DOI] [PubMed] [Google Scholar]
  86. Rouillon A., Barbey R., Patton E. E., Tyers M. & Thomas D. Feedback-regulated degradation of the transcriptional activator Met4 is triggered by the SCF(Met30) complex. EMBO J. 19, 282–294; 10.1093/emboj/19.2.282 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Menant A., Baudouin-Cornu P., Peyraud C., Tyers M. & Thomas D. Determinants of the ubiquitin-mediated degradation of the Met4 transcription factor. J. Biol. Chem. 281, 11744–11754; 10.1074/jbc.M600037200 (2006). [DOI] [PubMed] [Google Scholar]
  88. Lee T. A. et al. Dissection of combinatorial control by the Met4 transcriptional complex. Mol. Biol. Cell 21, 456–469; 10.1091/mbc.E09-05-0420 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. McIsaac R. S., Petti A. A., Bussemaker H. J. & Botstein D. Perturbation-based analysis and modeling of combinatorial regulation in the yeast sulfur assimilation pathway. Mol. Biol. Cell 23, 2993–3007; 10.1091/mbc.E12-03-0232 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  90. Horwitz A. A., Sankaran S. & Parvin J. D. Direct stimulation of transcription initiation by BRCA1 requires both its amino and carboxyl termini. J. Biol. Chem. 281, 8317–8320; 10.1074/jbc.C500475200 (2006). [DOI] [PubMed] [Google Scholar]
  91. Swat M. H. et al. Multi-scale modeling of tissues using CompuCell3D. Methods Cell Biol. 110, 325–366; 10.1016/B978-0-12-388403-9.00013-8 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Ingalls B. Sensitivity analysis: from model parameters to system behaviour. Essays Biochem. 45, 177–193; 10.1042/BSE0450177 (2008). [DOI] [PubMed] [Google Scholar]
  93. Savageau M. A. Power-law formalism: a canonical nonlinear approach to modelingand analysis. Proceedings of the first world congress on World congress of nonlinear analysts '92, volume IV, Tampa, Florida, USA. 3323–3334, Hawthorne, NJ, USA: Walter de Gruyter & Co. (Dec 1 1995). [Google Scholar]
  94. Suzuki H. et al. Homodimer of two F-box proteins betaTrCP1 or betaTrCP2 binds to IkappaBalpha for signal-dependent ubiquitination. J. Biol. Chem. 275, 2877–2884; 10.1074/jbc.275.4.2877 (2000). [DOI] [PubMed] [Google Scholar]
  95. Hao B., Oehlmann S., Sowa M. E., Harper J. W. & Pavletich N. P. Structure of a Fbw7-Skp1-cyclin E complex: multisite-phosphorylated substrate recognition by SCF ubiquitin ligases. Mol. Cell 26, 131–143; 10.1016/j.molcel.2007.02.022 (2007). [DOI] [PubMed] [Google Scholar]
  96. Barbash O. & Diehl J. A. SCF(Fbx4/alphaB-crystallin) E3 ligase: when one is not enough. Cell Cycle 7, 2983–2986; 10.4161/cc.7.19.6775 (2008). [DOI] [PubMed] [Google Scholar]
  97. Barbash O. et al. Mutations in Fbx4 inhibit dimerization of the SCF(Fbx4) ligase and contribute to cyclin D1 overexpression in human cancer. Cancer Cell 14, 68–78; 10.1016/j.ccr.2008.05.017 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  98. Yin Q. et al. E2 interaction and dimerization in the crystal structure of TRAF6. Nat. Struct. Mol. Biol. 16, 658–666; 10.1038/nsmb.1605 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep05573-s1.pdf (4.6MB, pdf)
Supplementary Information

Movie S1

Download video file (7.1MB, avi)
Supplementary Information

Movie S2

Download video file (7.1MB, avi)
Supplementary Information

Movie S3

Download video file (7.1MB, avi)
Supplementary Information

Movie S4

Download video file (5.6MB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES