In-silico prediction of concentration-dependent viscosity curves for monoclonal antibody solutions

ABSTRACT

Early stage developability assessments of monoclonal antibody (mAb) candidates can help reduce risks and costs associated with their product development. Forecasting viscosity of highly concentrated mAb solutions is an important aspect of such developability assessments. Reliable predictions of concentration-dependent viscosity behaviors for mAb solutions in platform formulations can help screen or optimize drug candidates for flexible manufacturing and drug delivery options. Here, we present a computational method to predict concentration-dependent viscosity curves for mAbs solely from their sequence—structural attributes. This method was developed using experimental data on 16 different mAbs whose concentration-dependent viscosity curves were experimentally obtained under standardized conditions. Each concentration-dependent viscosity curve was fitted with a straight line, via logarithmic manipulations, and the values for intercept and slope were obtained. Intercept, which relates to antibody diffusivity, was found to be nearly constant. In contrast, slope, the rate of increase in solution viscosity with solute concentration, varied significantly across different mAbs, demonstrating the importance of intermolecular interactions toward viscosity. Next, several molecular descriptors for electrostatic and hydrophobic properties of the 16 mAbs derived using their full-length homology models were examined for potential correlations with the slope. An equation consisting of hydrophobic surface area of full-length antibody and charges on V_H, V_L, and hinge regions was found to be capable of predicting the concentration-dependent viscosity curves of the antibody solutions. Availability of this computational tool may facilitate material-free high-throughput screening of antibody candidates during early stages of drug discovery and development.

Abbreviations

cP

Centipoise

mAb

Monoclonal antibody

SCM

Spatial Charge Map

Fv

Variable Fragment

UF/DF

Ultrafiltration/Diafiltration

η₀

Viscosity of platform formulation buffer

η

Viscosity of antibody solution

c

Concentration of an antibody

MOE

Molecular Operating Environment

GB/VI

Generalized Born/volume integral

RMSG

Root mean square gradient

MD

Molecular dynamics

CDR

Complementarity determining region

Fc

Crystalizable portion of the antibody

IMGT®

The international ImMunoGeneTics information system®

e

Charge on an electron

Z_VH

Charge on V_H region

Z_VL

Charge on V_L region

Z_Fc

Charge on Fc region

Z_CL

Charge on C_L region

Z_CH1

Charge on C_H1 region

Z_Hinge

Charge on hinge region

Z_mAb

Total charge on the antibody molecule

pI_Sequence

Sequence-based pI of the antibody molecule

pI_Structure

Structure-based pI of the antibody molecule

AP_Tango

Normalized aggregation propensity of the antibody sequence calculated using TANGO

AP_Waltz

Normalized aggregation propensity of the antibody sequence calculated using WALTZ

vdwA

Van der Waals surface area of the antibody molecule

ASA_hyd

Hydrophobic surface area of the antibody molecule

ASA_hphil

Hydrophilic surface area of the antibody molecule

D_mAb

Dipole moment of the antibody molecule

ζ_mAb

Zeta potential of the antibody molecule

IgG

Immunoglobulin G

LOO

Leave one out

D₀

diffusion coefficient at the limit concentration → 0

Introduction

In recent years, monoclonal antibody (mAb)-based therapeutic products have gained greater representation in the pipelines of pharmaceutical companies. For example, the total number of antibody molecules in clinical pipelines increased from ∼350 in 2013¹ to ∼470 in 2016.² MAb-based therapeutics can target a wide variety of disease conditions³ with high target specificity⁴ and low non-mechanism toxicity.⁵ Often, such products need to be administered at high concentrations to improve patient compliance, ease of administration, and to save on treatment costs.⁶ But, in some cases these high concentration antibody solutions can become highly viscous, leading to challenges in manufacturing, storage and administration. Therefore, low viscosities at high concentrations of antibody solutions are desired for successful product development of mAb-based therapeutics.

Typical approaches to ensure low viscosity of antibody solutions depend upon the stage of drug product development.⁶ If the product is in late stages of development, then optimization of formulation can be pursued. However, re-formulation requires additional material and resources, which adds to the already high cost of drug product development. Therefore, rationally prioritizing/optimizing antibody candidates at early discovery stages is preferred. At the early stages, material available for experimental testing is limited. Computational tools require no material, and are therefore ideally suited for early stage developability assessments of mAb candidates.

Computational tools for viscosity prediction of small molecules were developed several decades ago,^7-9 but only a few studies of biologics have been reported so far in the literature. Li and coworkers¹⁰ pioneered the efforts to predict viscosity of highly concentrated mAb solutions using their calculated molecular properties. These authors experimentally measured concentration-dependent viscosity behaviors of 11 different mAbs under standardized conditions and found correlations with computationally estimated molecular descriptors such as charge, zeta-potential and aggregation propensity of variable fragments (Fv regions) of the antibodies. Antibody molecules whose formulations demonstrate high viscosities at 150 mg/mL contain negatively charged patches on their Fv regions. This is because pIs of these Fv regions are lower than the pH of formulation buffer. Sharma and coworkers¹¹ also used computationally estimated molecular descriptors to predict viscosity at 180 mg/mL concentration in different formulation conditions than those used by Li and coworkers.¹⁰ These authors also predicted plasma clearance difference between human and cynomolgus monkeys, and chemical stability against tryptophan oxidation and aspartic acid isomerization using molecular dynamics (MD) simulations. In a third study, Trout and coworkers¹² developed a spatial charge map (SCM) tool for screening antibody solutions using information about the charge distribution on the Fv portions of mAbs. The authors validated their method using data on mAbs being developed at 3 pharmaceutical companies. Furthermore, Nichols et al.¹³ used a molecular model of the Fv portion of a viscosity-challenged IgG₁λ mAb to rationally design point mutations that improved its viscosity behavior. Recently, Geoghegan et al.¹⁴ also demonstrated that rational structure-based re-engineering of the Fv portion of an IgG₁ mAb can help mitigate its viscosity and tendencies to form reversible self-associations. These studies demonstrate utility of molecular modeling and simulations toward developability assessments of therapeutic antibody candidates.

The studies described above focused on predicting and improving the viscosity of mAbs at high concentrations using molecular models of the Fv regions only, while the viscosity data were collected using experiments performed on the full-length mAbs. Use of molecular models for Fv regions alone neglects contributions of the constant regions toward concentration-dependent viscosity behaviors of full-length antibodies. The effects on viscosity behaviors due to variations in antibody isotypes are also ignored. In contrast, coarse-grained simulations of antibody solutions performed by Buck et al.¹⁵ showed that inter-domain interactions involving both the variable (Fv) and the constant (C_L, C_H1, and Fc) regions engage in the formation of transient intermolecular networks, and therefore contribute toward increased viscosity of antibody solutions at high concentrations. This observation motivated us to use full-length antibody models in the present investigation.

Knowledge of the viscosity behaviors of antibody solutions not only at one arbitrarily chosen high concentration, but over a wide range of concentrations is desirable during drug development. Antibody solutions are concentrated to different extents during manufacturing, drug substance storage, drug product presentations and administration. Prior knowledge of concentration-dependent viscosity behaviors can be very useful at all these steps. Here, we present an algorithm to predict entire concentration-dependent viscosity curves for different mAbs in the same formulation solely from their amino acid sequences and homology-based structural models. Experimentally determined concentration-dependent viscosity curves for 16 different antibody molecules were combined with molecular descriptors computed from their full-length homology-based structural models to construct this algorithm. While contributions of the electrostatic interactions toward viscosity behaviors of antibody solutions have been emphasized in earlier studies,^6,10-13 this analysis demonstrates that hydrophobicity also makes important contributions to protein:protein interactions that eventually lead to high viscosities in certain concentrated antibody solutions.

Results

In this report, we describe our attempts to predict concentration-dependent viscosity curves for mAbs solely from their sequence and structural attributes. To enable this, concentration-dependent viscosity curves for 16 different antibodies were determined experimentally under standardized conditions as described earlier.¹⁰ Next, homology-based structural models of all 16 antibodies in our data set were built and used for calculation of hydrophobic and electrostatic properties for these antibodies. The sequence-based analyses for calculating aggregation propensities were also performed.

Observations from concentration-dependent viscosity curves for 16 mAbs

Concentration-dependent viscosity curves for 16 mAbs formulated in the same buffer were analyzed using Eqs 2 and 3 (see Materials and Methods section for details). Briefly, the relationship between solution viscosity and solute concentration is exponential (Eq. 2), which can be linearized via logarithmic manipulation (Eq. 3). Here, the experimental data on each antibody (Table 1) were used to obtain the values of intercept (lnA) and slope (B) via linear regression of Eq. 3. These values are presented in Table 2.

Table 1.

Concentration dependent viscosity data on 16 mAbs used in this study.^*

Name	C20	η (cP)	C50	η (cP)	C60	η (cP)	C75	η (cP)	C100	η (cP)	C125	η (cP)	C150	η (cP)	C175	η (cP)	C200	η (cP)
mAb1	19	1.1 ± 0.0	49	1.5 ± 0.0					98	2.6 ± 0.0	126	3.7 ± 0.0	153	5.4 ± 0.1	172	8.0 ± 0.1	204	13.5 ± 0.2
mAb2	18	1.2 ± 0.0	52	1.6 ± 0.0					97	2.7 ± 0.0	127	3.7 ± 0.1	149	5.4 ± 0.1	171	8.1 ± 0.2	195	13.3 ± 0.7
mAb3	23	1.2 ± 0.0	46	1.5 ± 0.0					95	2.9 ± 0.1	126	4.0 ± 0.0	148	6.2 ± 0.1	171	11.1 ± 0.6	198	19.1 ± 3.7
mAb4			51	1.9 ± 0.4					102	2.9 ± 0.0	133	4.7 ± 0.5	161	6.8 ± 0.2			198	21.3 ± 0.4
mAb5	19	1.1 ± 0.0	45	1.4 ± 0.0					99	2.7 ± 0.0	126	4.1 ± 0.1	147	6.6 ± 0.1	176	12.2 ± 0.6	196	20.4 ± 0.9
mAb6	21	1.2 ± 0.0	48	1.7 ± 0.0			74	2.3 ± 0.0	98	3.3 ± 0.0	129	5.3 ± 0.0	150	8.4 ± 0.1	175	14.1 ± 0.2	203	28.9 ± 0.8
mAb7	19	1.2 ± 0.0	46	1.7 ± 0.0					101	3.7 ± 0.0	124	6.1 ± 0.0	150	10.7 ± 0.3	176	19.2 ± 0.6	206	39.1 ± 2.4
mAb8	17	1.2 ± 0.0	43	1.5 ± 0.0			91	3.3 ± 0.0	114	5.0 ± 0.1	137	8.3 ± 0.1	160	14.5 ± 1.1			189	33.0 ± 2.7
mAb9	25	1.3 ± 0.0	49	1.7 ± 0.0					105	3.9 ± 0.0	127	6.9 ± 0.0	153	12.9 ± 0.1	183	27.6 ± 0.2
mAb10	25	1.3 ± 0.0	50	1.7 ± 0.0					107	4.2 ± 0.1	134	7.6 ± 0.1	155	15.6 ± 0.6			191	44.9 ± 1.8
mAb11	19	1.1 ± 0.0	53	1.5 ± 0.0					96	3.2 ± 0.2	125	6.4 ± 0.6	150	13.9 ± 0.5	170	27.3 ± 4.5
mAb12	18	1.2 ± 0.0	46	1.6 ± 0.0					99	4.0 ± 0.0	126	7.0 ± 0.1	148	13.7 ± 0.2	172	31 ± 0.6	212	113 ± 2.7
mAb13	20	1.3 ± 0.0	40	1.9 ± 0.0	61	3.1 ± 0.03	83	5.8 ± 0.0	102	11.0 ± 0.1	126	28.9 ± 3.2	132	33.5 ± 2.4
mAb14	20	1.6 ± 0.0	41	3.4 ± 0.0	62	7.5 ± 0.03	81	15.4 ± 0.1	106	30.2 ± 0.2	130	57.9 ± 0.5	150	103.6 ± 1.0
mAb15			51	1.9 ± 0.0					91	5.0 ± 0.0	122	13.2 ± 2.2	149	29 ± 2.9	172	70.5 ± 0.6	199	226 ± 16.0
mAb16	19	1.2 ± 0.0	52	2.5 ± 0.0					103	15.4 ± 0.2	131	43.6 ± 0.6	149	94.7 ± 0.6

^*A total of 105 concentration-antibody measurements were performed. Each viscosity value is an average of 3 independent measurements.

Table 2.

Experimentally observed values of parameters A and B for the 16 mAbs.^*

	Number of viscosity measurement points	ln A	A	B	R2	Heavy chain germline	Light chain germline	Isotype	D0 (10−7 cm2/s)
mAb1	7	−0.37	0.69	0.0133	0.98	IGHV3–23*03	IGKV2–30*02	IgG1κ	4.1
mAb2	7	−0.33	0.72	0.0133	0.98	IGHV3–11*05	IGKV1D-33*01	IgG1κ	4.3
mAb3	7	−0.44	0.64	0.0154	0.97	IGHV1–2*05	IGKV4–1*01	IgG4κ	4.6
mAb4	5	−0.52	0.59	0.0159	0.92	IGHV1–2*02	IGKV2–29*02	IgG1κ	n.d.
mAb5	7	−0.54	0.59	0.0163	0.97	IGHV4-b*01	IGLV3–19*01	IgG1λ	4.2
mAb6	8	−0.47	0.62	0.0171	0.98	IGHV3–23*04	IGKV1–39*01	IgG1κ	4.3
mAb7	7	−0.49	0.62	0.0187	0.99	IGHV1–46*03	IGKV1–39*01	IgG4κ	4.5
mAb8	7	−0.52	0.59	0.0192	0.98	IGHV3–48*01	IGKV1–39*01	IgG4κ	4.5
mAb9	6	−0.53	0.59	0.0193	0.98	IGHV1–2*02	IGLV1–40*01	IgG1λ	4.5
mAb10	6	−0.62	0.54	0.0208	0.96	IGHV1-f*01	IGKV1–16*01	IgG2κ	4.6
mAb11	6	−0.73	0.48	0.0213	0.96	IGHV1–18*04	IGKV4–1*01	IgG2κ	4.5
mAb12	7	−0.74	0.48	0.0233	0.96	IGHV1–46*03	IGKV3–20*01	IgG1κ	4.3
mAb13	7	−0.67	0.51	0.0299	0.99	IGHV1–46*03	IGKV1–6*01	IgG2κ	4.2
mAb14	7	−0.17	0.84	0.032	0.99	IGHV3–43D*01	IGLV6–57*01	IgG1λ	2.6
mAb15	6	−1.34	0.26	0.0321	0.99	IGHV3–23*04	IGKV3–11*01	IgG2κ	4.3
mAb16	5	−0.79	0.46	0.0341	0.99	IGHV1–46*03	IGLV3–1*01	IgG1λ	4.1
Average values	6.56±0.79 (Total: 105)	−0.58±0.26	0.58±0.13	0.021±0.0069

^*Values for parameters A and B for all antibodies in the database were obtained by linear regressions to experimental data shown in Table 1. Each linear regression was performed for logarithm of relative viscosity versus concentration (Eq. 3). R² is the linear correlation coefficient obtained from each regression. The number of different concentrations at which viscosity was measured for each mAb is listed in the second column. In total, 105 different antibody and concentration combinations were used for viscosity measurements and each measurement reports average of 3 independent observations. The germlines of both the chains of the antibody molecules in this database were identified using IgBLAST¹ that is based on IMGT® classification system (http://www.imgt.org). The D₀ value for mAb4 was not determined (n.d.) due to lack of material.

Parameter A is nearly constant

Most antibodies in the current data set have similar values for the intercept, lnA (Table 2 and Fig. 1). The average value for intercept (lnA) is −0.58±0.26 (range: −0.17 to −1.34). Upon taking the antilog, the average value for parameter A is 0.58±0.13 (range: 0.26–0.84; standard deviation to mean ratio = 22%). Two antibodies, mAbs 14 and 15 show significantly different values for parameter A than the remaining 14 mAbs (A = 0.84 for mAb 14 and 0.26 for mAb 15). If these 2 outliers are removed, the average value for parameter A for the remaining 14 mAbs becomes 0.58±0.079 (range = 0.46–0.72; standard deviation to mean ratio = 13%). These observations suggest that the intercept for the antibodies studied here is nearly constant. As noted by Li et al.,¹⁰ parameter A is the intrinsic relative viscosity of an antibody dissolved in infinitely dilute solution. The intrinsic relative viscosity of a solute (mAb in our case) is related to diffusion coefficient of the solute via the Stokes-Einstein equation,¹⁰ which also considers the solute's molecular size. Even though the antibodies studied in this work differ from one another in terms of the number of residues, germlines and isotypes, they all have overall similar molecular shapes and sizes. Therefore, it is expected that they have similar intrinsic relative viscosity values (intercept, lnA). To further explore the connection between lnA and D₀, we determined the D₀ values for the antibodies, except mAb4, used in this study via the dynamic light scattering experiments.¹³ The D₀ value for mAb4 was not determined because material was not available. The measured D₀ values for all mAbs, except for mAb14, fall in the range 4.0–4.6 × 10⁻⁷ cm²/s (Table 2). These values are similar to those reported in the literature. For example, Saltzman et al.¹⁶ reported the D₀ value for a mAb to be 4.4 ± 1.3 × 10⁻⁷ cm²/s, while Connolly et al.¹⁷ reported a range of 3.9–4.8 × 10⁻⁷cm²/s. The average measured D₀ values for the mAbs included in this study (excluding mAb14) is 4.4 ± 0.17 × 10⁻⁷ cm²/s with a standard deviation to mean ratio = 3.9%. Therefore, the measured D₀ values behave similarly to the lnA values.

Figure 1.

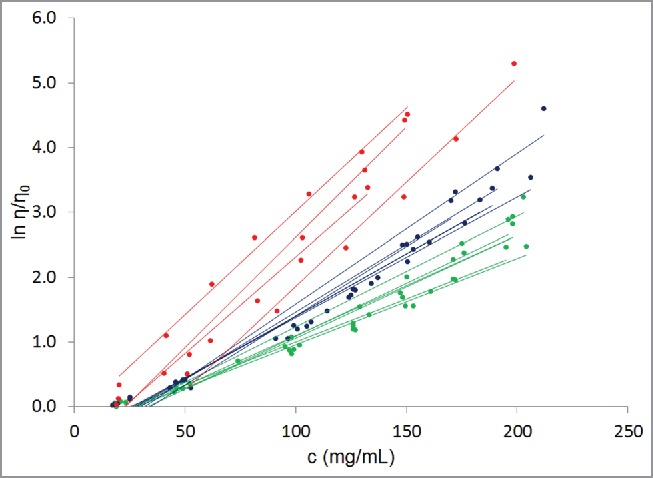
Experimentally determined concentration-dependent viscosity behaviors for the 16 antibodies in our database (Table 1). Dots are experimentally obtained data points while lines are least square fits to the data using equation 3. c is the concentration of the antibody in the solution, η is the viscosity of the solution, and η₀ is the viscosity of the platform formulation buffer. All the antibody molecules show exponential dependence of viscosity on concentration, as is clear from the R² values in Table 2. As a guide to the eye, well-behaved antibodies are shown in green, poorly-behaved antibodies are shown in red, and rest of the antibodies are shown in blue.

The greater than average A value for mAb14 (A = 0.84 for mAb14) is consistent with a slower diffusion coefficient for this mAb under the dilute conditions. The D₀ (diffusion coefficient at the limit concentration → 0) value for this mAb, measured using DLS experiments, is 2.6 × 10⁻⁷ cm²/s, which is significantly smaller than those for the other mAbs in this study (Table 2). On the other hand, the smaller than average value of the parameter A for mAb15 (A = 0.26) does not correspond to a relatively larger value for D₀. The measured D₀ value for mAb15 is 4.3×10⁻⁷ cm²/s, which is similar to D₀ values for the other mAbs (Table 2). These observations suggest that the relationship between D₀ and the parameter A may not be a simple one. More experimental data are needed to understand this relationship before it can be used for the prediction of parameter A. At present, we have used the average value of A while predicting the antibody viscosity curves (described below).

Parameter B varies significantly

In comparison to ln A, the values for the slope parameter B show larger variations from antibody to antibody (Table 2 and Fig. 1). Parameter B varies by ∼260%, ranging from 0.0133 for mAbs 1 and 2 to 0.0341 for mAb16 in our data set (Table 2). The average value for the parameter B is 0.021±0.007 (standard deviation to mean ratio = 33%). The first quartile, median, and third quartile B values are 0.0159, 0.0192, and 0.0233, respectively. The interquartile range between first and third quartile is 0.0074. The variation in parameter B does not shrink when the data on mAbs 14 and 15 is excluded (Average B = 0.0198±0.0059; range = 0.0133–0.0341; standard deviation to mean ratio = 30% for the remaining 14 mAbs). The observation of large variations in values of parameter B is important because the slope governs the rate of increase in logarithm of relative viscosity with antibody concentration. In other words, it determines the curvature of the exponential concentration-dependent viscosity curve. In physical chemistry, the curvature is a measure of solute:solute interactions in a solution.^10,17,18 Moreover, Connolly et al. have provided experimental evidence that the curvature is related to diffusion interaction parameter (k_D), which is a measure of antibody:antibody interactions in solution.¹⁷ Therefore, large variations in the values of slope (parameter B) suggest that antibody self-associations are formed to different extents in different antibody solutions at the same solute (antibody) concentration. Because all the antibodies in this study had the same formulation, the differences in their viscosity behaviors (different B values) must arise from the differences in their molecular sequence and structural attributes.

Taken together, these observations show that it is feasible to estimate entire concentration-dependent viscosity curve for an antibody dissolved in a platform formulation provided that the value of its slope can be derived from sequence-structural attributes of the antibody. In the next section, several different molecular properties of antibodies will be examined for correlations with the parameter B and the prediction of parameter B.

Prediction of the parameter B

Germlines and isotypes do not correlate with viscosity behaviors of mAbs

The isotypes, germlines of the variable regions, and experimentally derived values for parameters A and B for the 16 mAbs studied here are shown in Table 2. It can be seen that the data set of 16 mAbs contains antibodies of diverse isotypes and germlines. However, there is no correlation between germlines/isotypes and parameter B. For example, 4 mAbs (mAb5, mAb9, mAb14, and mAb16) are of isotype IgG₁λ, but their concentration-dependent viscosity behaviors are significantly different from one another. mAb5 and mAb9 show lower viscosity in comparison to mAb14 and mAb16 (see Fig. 2). Similarly, mAb6 and mAb15 have the same heavy chain germline, IGHV3–23*04, but mAb15 shows considerably poorer concentration-dependent viscosity behavior than mAb6. These observations are consistent with those made by Li et al.,¹⁰ and suggest that the viscosity behaviors of antibody molecules are encoded in their amino acid sequences at a finer level than germlines or isotypes.

Figure 2.

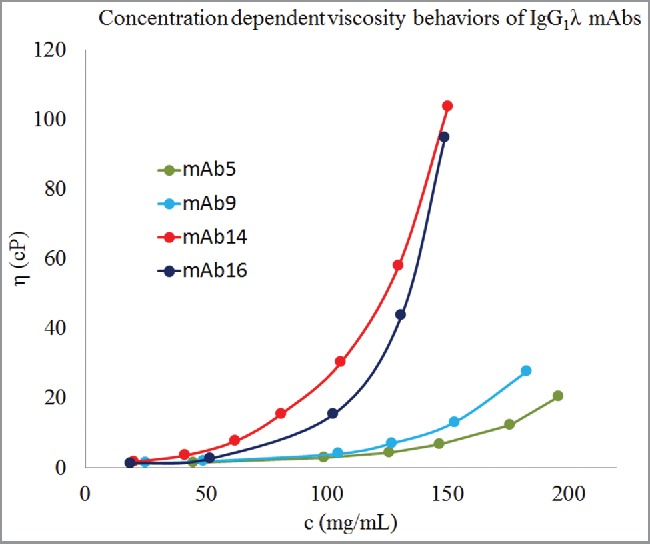
Concentration-dependent viscosity behaviors of 4 antibodies of IgG₁λ isotype. Dots represent experimental data, c is concentration in mg/mL, and η is viscosity in cP. Lines are guide to the eye. These 4 mAbs of the same isotype show different concentration-dependent viscosity behaviors. mAb5 and mAb9 have considerably lower viscosity behaviors than mAb14 and mAb16. Therefore, viscosity behaviors of antibody molecules are encoded in their amino acid sequences at a finer level than isotypes.

No single molecular descriptor is capable of predicting parameter B reliably

Full-length homology-based structural models were built for all 16 antibodies in our data set by following the procedures described in the methods section. These models were used to compute several descriptors, e.g., charge, pI, zeta-potential, dipole moments, hydrophobic surface area, hydrophilic surface area, according to the methods described by Long et al.¹⁹ These descriptors represent both electrostatic and hydrophobic properties of the mAbs. Amino acid sequences of the mAbs were also used to compute additional descriptors such as aggregation propensity. The Methods sections presents all the descriptors calculated for each antibody. The square of linear correlation coefficient (R²) values for linear correlation coefficients obtained from regressions between parameter B and various descriptors calculated from homology models and amino acid sequences of the 16 mAbs are shown in Table 3. Plots showing the linear relationships between the slope parameter B and the descriptors are also shown in Fig. S1 of the Supporting Information. Student's t-tests were performed to determine if these linear relationships obtained from analyses of the 16 mAbs are statistically significant and will also be present in larger data sets. The descriptors whose correlations with the parameter B show R² values > 0.18 (r < −0.42 or r > +0.42) are statistically significant at a 95% confidence level, and the descriptors whose correlations with the parameter B show R² values > 0.38 (r < −0.62 or r > 0.62) are statistically significant at a 99.5% confident level (see materials and methods). No single descriptor shows strong linear correlation with the parameter B that is significant at 99.5% confidence level (Table 3). However, aggregation propensity calculated using WALTZ, hydrophobic and van der Waals surface areas, charges on V_H and V_L regions, total charge on the full-length antibody, Z_mAb, sequence- and structure-based pIs, and dipole moment of the full-length antibody with the parameter B show statistically significant linear correlations with the parameter B, at 95% confidence level (Table 3).

Table 3.

Correlation coefficient (R), square of correlation coefficient (R²) obtained from a linear regression between experimentally derived value of parameter B and each computationally estimated descriptor. The results from t-tests for the significance of the correlations are also shown and significant correlations are highlighted. ^*

Computationally estimated descriptors	R	R2	Parameter Index	t value	p value
ZVH (Charge on VH region)	−0.49	0.24	x3	2.1032	0.0258
ZVL (Charge on VL region)	−0.48	0.23	x7	2.0473	0.0287
ZmAb (Charge on the antibody)	−0.43	0.18	x2	1.7821	0.0469
ZHinge (Charge on the hinge region)	−0.20	0.04	x5	0.7638	0.2281
ZCH1 (Charge on the CH1 region)	−0.21	0.04	x4	0.8037	0.2167
ZFc (Charge on the Fc region)	0.22	0.05	x6	0.8438	0.2056
ZCL (Charge on the CL region)	0.31	0.10	x8	1.22	0.1201
APTango (Aggregation propensity predicted by TANGO)	−0.21	0.04	x9	0.8037	0.2167
APWaltz (Aggregation propensity predicted by WALTZ)	0.56	0.32	x10	2.5291	0.0112
pISequence (Sequence-based pI)	−0.48	0.23	x11	2.0473	0.0287
pIStructure (Structure-based pI)	−0.41	0.17	x1	1.6819	0.0560
ASAhyd (Hydrophobic surface area)	0.54	0.29	x13	2.4006	0.0144
vdwA (van der Waals surface area)	0.43	0.19	x12	1.7821	0.0469
ASAhlic (Hydrophilic surface area)	0.25	0.06	x14	0.9661	0.1742
DmAb (Dipole moment of the antibody)	−0.50	0.25	x15	2.1602	0.0231
ζmAb (Zeta potential of the antibody)	−0.43	0.18	x16	1.7821	0.0469

^*The straight line fits are shown in Supplemental Material.

The correlation between AP_Waltz and B is particularly interesting, considering that the aggregation process can involve non-native molecular conformations.²⁰ In our experience, aggregation and viscosity, particularly at high concentrations, are related (our unpublished experimental data). In some cases, antibodies that demonstrate high viscosity are also more aggregation prone, but this is not a perfect trend. In highly concentrated antibody solutions, it is conceivable that a certain extent of conformational diversity around the native state of the antibody molecular structure exists.²¹ These near-native antibody molecules could form weak intermolecular interactions and then networks leading to increased viscosity.¹⁵ If the antibody concentration continues to rise, these interactions could trigger aggregation and precipitation of the antibody molecules. However, it is difficult to quantify conformational diversity in antibody molecules at high concentrations in the absence of multi-copy atomistic simulations of antibody solutions. Such simulations are computationally very expensive and out of the scope of this investigation.

In summary, these results show that concentration-dependent viscosity behaviors of antibody solutions depend on several factors and individual descriptors show only weak correlations with parameter B. This is a reasonable observation from the physical perspective because intermolecular interactions, underpinning solution behaviors of antibodies, are defined by several hydrophobic and electrostatic properties of the individual antibodies.⁶

Multivariate analysis of parameter B

Several independent mathematical models using all or subsets of the descriptors were built and compared for their abilities to predict the parameter B. Different mathematical models were compared for their adjusted R², RMSE, p-values, as well as performance on leave-one-out (LOO) analysis. The best performing model is discussed below in this section and a subset of the remaining models is listed in Section 5 of the Supporting Information. The final model selected by stepwise linear regression routine in the software MATLAB²² as the best performing model for the prediction of parameter B is shown in the Eq. 1.

$$\text{B} = 1+ \text{x}3*\text{x}7 +\text{x}3*\text{x}13 +\text{x}5*\text{x}7 +\text{x}7*\text{x}13$$ (1)

where x3, x5, x7, and x13 have the same meaning as in Table 3. That is, x3 is the net charge on V_H domain (Z_VH), x5 is the net charge on the Hinge region (Z_Hinge), x7 is the net charge on the V_L domain (Z_VL), and x13 is the solvent accessible hydrophobic surface area of the full-length antibody (ASA_hyd). The coefficients of this final model are listed Table S1. The Eq. 1 is presented in Wilkinson notation.²³ Briefly, x3*x7 means x3 + x7 + x3 × x7 in this notation. All the intermediate steps taken by MATLAB²² to reach Eq. 1 are listed in Table S2 of Supporting Information.

Equation 1 was found to be the best performing mathematical model for prediction of the parameter B from molecular descriptors because: 1) it shows high value for adjusted R²; 2) it has low root mean square error (RMSE); 3) it has low p-value; and most importantly, 4) it performs very well in LOO cross-validations. An R² of 0.885 and adjusted R² of 0.754 were obtained for this model. The F-statistic and p-value for the model in Eq. 1 are 6.75 and 0.0104, respectively. Therefore, the null hypothesis that Eq. 1 is not capable of predicting the parameter B, is rejected at 95% level of confidence (p-value <0.05). The RMSE for the Eq. 1 is 0.00344, which is an order of magnitude lower than experimental values of parameter B. Furthermore, LOO cross-validations were performed by excluding one antibody molecule from the training set at a time to assess the robustness of the model. This exercise was repeated 16 times by leaving out the experimental data on a different mAb each time. During the LOO cross-validations, the adjusted R² values ranged from 0.676 to 0.891 and the R² values ranged from 0.861 to 0.953. The RMSEs ranged from 0.00216 to 0.0037, while the p-values of F-tests for significance in linear relationship ranged from 0.00184 to 0.0385. These results show that Eq. 1 represents a statistically significant predictive model between the computationally obtainable descriptors and the slope parameter B. It is pertinent to note here that the total number of different viscosity measurements were 105 (Table 1) and each value of the parameter B represents the entire concentration-dependent viscosity curve for an antibody.

The mathematical model (Eq. 1) derived here was used to make predictions for parameter B. Fig. 3(a) shows a comparison between predicted and experimentally observed values for parameter B. The R² value for correlation between experimental and predicted values for parameter B is 0.8718 with RMSE 0.002276. The t-value is 9.70 and p-value is 2.0934 × 10⁻⁸. Fig. 3(b) shows the comparison between predicted and experimentally observed values for B-parameter by LOO cross-validation analyses. In this case, the R² value for correlation between experimental and predicted values for parameter B is 0.2864 with RMSE 0.0073. The t-value is 2.3570 and p-value is 0.0157. Both these figures show that the agreements between predictions from the mathematical model derived in this work and the experimental values are statistically significant at 95% confidence (both the p-values < 0.05) level.

Figure 3.

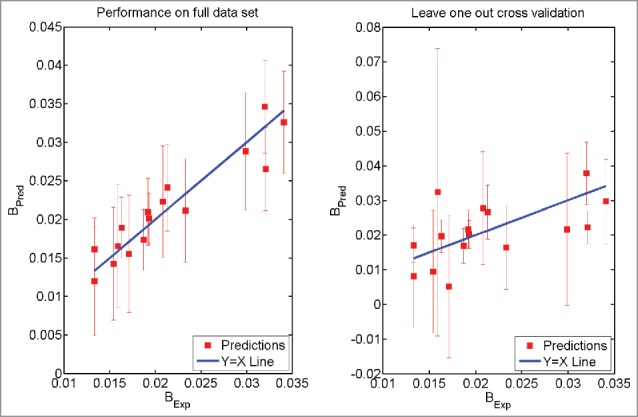
Prediction using Eq. 1. The model was trained on the full data set (Left Panel). The model was trained after leaving one antibody molecule out of the data set (Right Panel). The error bars have the same size as 95% confidence intervals. B_Exp refers to the experimentally obtained values of the parameter B while B_Pred refers to the prediction made using Eq. 1.

To further test the validity of the mathematical model, predicted concentration-dependent viscosity curves were constructed for all 16 antibodies using average values for the intercept (lnA) and the predicted values for parameter B. These curves were then compared with experimentally obtained viscosity curves in each case. Figs. 4(a–c) show comparisons between experimental and predicted concentration-dependent viscosity curves for 3 representative mAbs that demonstrate good (low viscosities at high concentrations, mAb3), moderate (moderate viscosities at high concentrations, mAb9) and poor (high viscosities at high concentrations, mAb16) concentration-dependent viscosity behaviors. Figs. 4 (a–c) show that predictions are in reasonable agreement with experimentally observed viscosity behaviors. Moreover, experimentally observed viscosity behaviors are always within the error bars of the predicted viscosity behaviors. We note that for mAb3, the agreement between predicted viscosity behaviors and experimentally observed viscosity behavior is relatively less accurate at concentrations higher than 150 mg/mL. In our training data set experimental measurements on antibody solutions greater than 150 mg/mL are sparse. This is because it is often difficult to perform experiments at such high concentrations particularly when antibody solutions are highly viscous. Therefore, it is expected that predictions become relatively less accurate at concentrations above 150 mg/mL in some cases. The comparisons between predicted and experimentally obtained viscosity curves for the remaining 13 antibodies are shown in the Section 3 of Supplementary Information. These figures show that the mathematical model derived in our study can reasonably predict the concentration-dependent viscosity behaviors of all the 16 antibodies in the data set. Moreover, we note that for the poorly behaved antibody molecules the differences between predictions using the average value of the parameter A and the experimentally obtained values of the parameter A tend to be high (mAb14 and mAb15 in Fig. S2).

Figure 4.

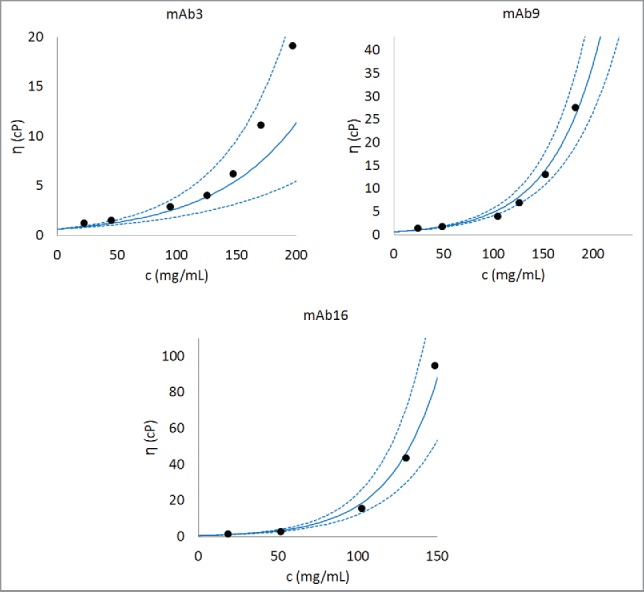
Comparison of experimentally observed and predicted concentration-dependent viscosity behaviors of 3 representative antibodies. The parameter B is obtained after training Eq. 1 on the complete data set. The parameter A is taken as the average of A values for all the antibodies (i.e., 0.58, as listed in Table 2). An antibody with low viscosity (mAb3), an antibody with moderate viscosity (mAb9), and an antibody with high viscosity (mAb16) are shown in this figure. Dashed lines are predictions made using one standard deviation about the predicted value of B. Similar concentration-dependent viscosity behavior curves can be constructed for any antibody in the database after the parameter B is predicted using Eq. 1. Further examples for predicted concentration-dependent viscosity behaviors are provided in Section 3 in Supporting Information.

Further test of predictability of Eq. 1

Equation 1 was tested further by predicting concentration-dependent viscosity behavior of an antibody molecule (TestmAb) that was not part of the 16 mAbs used for developing the predictive model described in Eq. 1 (i.e., TestmAb is not listed in Table 1). TestmAb is an IgG₁κ Pfizer proprietary antibody currently in drug product development. The heavy chain of TestmAb is 86% to 95% similar to the IgG₁ heavy chains and the light chain is 77% to 92% similar to the kappa light chains in our training data set of 16 mAbs. Its concentration-dependent viscosity behavior was measured in platform formulation and the values of the parameters A and B were calculated using Eq. 1. The calculated values of parameters A and B for this antibody are 0.73 and 0.0179, respectively. A homology model for this antibody was built following the same procedure as for the 16 mAbs in the training data set (described in Methods section). Descriptors listed in Table 2 were calculated from this homology model and Eq. 1 was used to predict the parameter B. The predicted value of B was 0.0166 with 1 standard deviation error bar of 0.008. Equation 1 was used to construct the concentration-dependent viscosity behavior of TestmAb from the predicted B and average value of A (i.e., 0.58, as listed in Table 2.) and real value of A (0.73). The result of this analysis is presented in Fig. 5. It is clear from Fig. 5 that Eq. 1 is capable of predicting the concentration-dependent viscosity behavior of TestmAb. However, the predictability improved significantly when the real value of A (0.73) was used. Even using the real A, the experimental and predicted viscosity values still show differences at concentrations above 100 mg/mL. However, these differences fall within the error limits (dotted red lines in Fig. 5), obtained from uncertainties in the B-value estimates. In summary, the ability of Eq. 1 to correctly predict the concentration-dependent viscosity behavior of an antibody molecule that was not in the training data set provides greater support for the validity of the scheme developed here. Further testing of this predictive method is currently underway in our laboratory.

Figure 5.

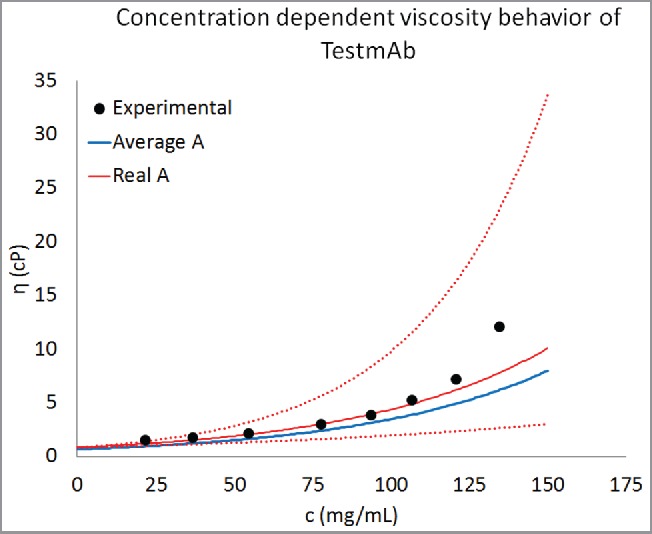
Prediction of concentration-dependent viscosity behavior of an antibody currently under development at Pfizer. The experimental data are shown as black circles and the predictions are shown as curve. The parameter B was predicted using Eq. 1. This predicted value of B and average value of A (Table 2) was used for creating the concentration-dependent viscosity curves from Eq. 2. For comparison predictions using the real value of A for TestmAb (0.73) are also shown. Equation 1 is correctly able to predict the concentration-dependent viscosity behavior of TestmAb. Moreover, the agreement between predicted and experimentally observed viscosity behavior improves when the real value of A for TestmAb is used. The dotted red lines are viscosity predictions using the real value of A for TestmAb (0.73) and within one standard deviation about the predicted value of B.

Physical insights gained from the mathematical model for prediction of parameter B

The mathematical model described above is phenomenological in nature. However, it does lead to improved understanding of the molecular origins of protein:protein interactions that underpin concentration-dependent viscosity behaviors of antibody solutions. Most importantly, no descriptor alone can fully explain concentration-dependent viscosity behavior of antibody molecules, and therefore models that utilize a broader set of physical descriptors may achieve greater success in explaining molecular origins of concentration-dependent viscosity behaviors of antibody molecules. The profile-based scheme is one such method that seeks to qualitatively explain concentration-dependent viscosity behavior by striking a balance between electrostatic interactions and hydrophobic interactions. Moreover, quantitative methods developed by Li et al.¹⁰ and Sharma et al.¹¹ used this balance while predicting the viscosity of antibody solutions at higher concentrations by using electrostatic and hydrophobic interactions originating from the Fv portions of the antibody molecules.

Consistent with earlier studies that relied on molecular models of the Fv regions,^10,11 the model presented in Eq. 1 also suggests that net values of the charge on the V_H and V_L domains in the Fv regions play important roles in determining concentration-dependent viscosity behaviors of the antibody solution. In addition to the charge on Fv region, a role for hydrophobicity in viscosity behaviors of antibodies is also suggested by inclusion of hydrophobic surface area of the full-length antibody in the model (see Eq. 1). This new finding justifies use of full-length antibody structural models in this work because large solvent-exposed hydrophobic patches (> 100 Ų) were found on both the variable and the constant regions of antibody molecules in our database. Our earlier report¹⁰ did discuss a role for hydrophobicity, but hydrophobic surface area was not explicitly included in the previous model. While both hydrophobicity and electrostatics contribute to intermolecular interactions, and therefore viscosity behaviors of antibody solutions, none of the currently available experimental methods is capable of separating their individual percent contributions. It may be feasible to estimate these percentages and identify the nature of dominant interactions via multi-copy antibody atomistic simulations. However, such simulations are extremely computationally expensive and out of the scope of this investigation.

Moreover, the effect of the heavy chain isotype of an antibody molecule on its viscosity behavior was also incorporated in this model through the charge on the hinge region. The isotypes IgG₁, IgG₂, and IgG₄ have different amino acid sequences and disulfide bond patterns in their hinge regions as is shown in Fig. 6.²⁴

Figure 6.

Hinge region sequence alignment of human IgG₁, IgG₂, and IgG₄ antibodies. Note that number of charged residues in the hinge regions of different isotypes is different.

Discussion

Antibody-based therapeutics are an important segment of the drug development pipelines of biopharmaceutical companies. To increase patient compliance, adherence, and ease of administration, subcutaneous administration of highly concentrated (typically above 100 mg/mL) antibody solutions is preferred.⁶ However, the undesirably high viscosity (viscosity greater than 20 cP) demonstrated by certain antibody solutions can lead to challenges in manufacturing and administration, and thereby delay the progression of a drug candidate through development.⁶ Methods to forecast concentration-dependent viscosity behavior of antibody solutions are required for proactive elimination or optimization of antibody-based drug candidates that are likely to show undesirably high viscosities at high concentrations. Here, we developed a computational scheme to predict concentration-dependent viscosity behavior of mAb solutions solely from their molecular sequence and structural attributes. It correlates experimentally observed viscosity behaviors of mAbs with computationally estimated molecular descriptors from their homology-based structural models. This scheme can be used early in the discovery and formulation development stages where material available for experimental testing is scarce. The computational approaches such as the one we developed do not need any material and can be used to prioritize antibody candidates based on their predicted concentration-dependent viscosity behaviors, even before any material becomes available to perform experiments.

In our previous work,¹⁰ we developed a scheme to predict viscosity of antibody solutions at a given concentration using the properties of the Fv region. We found that the computationally estimated charge on the Fv region of an antibody can be used to predict viscosity of antibody solutions at 150 mg/mL. In addition to this, we also rationalized the differences in viscosity behaviors of antibody molecules by developing a qualitative profile-based screening method. Here, we made 2 significant improvements over our previous work. First, we are now able to predict the viscosity behaviors of antibody solutions at all concentrations. Second, the calculations of the macromolecular descriptors now utilize the homology models of full-length antibodies. To our knowledge, this study is the first reported attempt to quantitatively predict the entire concentration-dependent viscosity curves for mAbs. The utility of full-length antibody models in viscosity prediction is reflected in the finding that total hydrophobic surface area is an important component of the model. This implies that hydrophobic effects are important aspects of protein:protein interactions that contribute toward viscosity behaviors of the mAbs. This model also explicitly takes into account the charge on the hinge region of the antibodies to account for presence of antibodies with different isotypes in our data set. These insights could not have been gained from use of molecular models for just the Fv portions.^10,11

Although the current model is significantly improved, the scheme presented here has the following 5 limitations, and therefore, scope for further improvements. First, a bigger and more diversified training data set is needed to increase the robustness of the scheme. Only 16 antibody molecules, most of them well behaved, were used in this analysis. While this is an improvement over the 11 mAbs used in our previous effort, the number of antibodies whose concentration-dependent viscosity curves have been determined under standardized experimental conditions and procedures remains small. Second, in this work, we relied on physically intuitive correlations between computationally estimated molecular descriptors and experimentally observed viscosity behaviors of antibody solutions. We realize that many other more sophisticated statistical and machine learning methods, such as support vector machine, principal component regression, random forest regression, least absolute shrinkage and selection operator (LASSO) regression, partial least squares regression, could have been also used in this work and mathematical models derived from these methods could have been compared with one another. However, this is out of scope for the current work. Third, homology-based molecular models of full-length antibodies were constructed and used to obtain values for various descriptors of the molecular properties used in this work. However, mAbs are inherently dynamic macromolecules. Therefore, use of average values for these descriptors derived from conformational ensembles of the mAbs may have improved the performance of this scheme. The conformational ensembles for protein molecules can be obtained via MD simulations, but such simulations of full-length antibody molecules are computationally time consuming and resource intensive at present. For example, in our ongoing unpublished work, atomistic representation of a full-length antibody molecule in explicit solvent led to approximately 900,000 atoms in the simulation box and the simulation required approximately 2 days to complete one nanosecond run, using a 2 femtosecond time-step on a 12 CPU machine supported with 2 K5000 NVIDIA graphics processing units (GPUs). Wang and coworkers²⁵ also reported that 1.5 computer days were needed to complete one nanosecond of MD simulations on a murine antibody on a 32 CPU cluster. At this time, we found use of energy minimized homology structures as a reasonable first step toward the prediction of concentration-dependent viscosity behaviors of the mAb solutions. The fourth limitation is that the mathematical model obtained for viscosity prediction in one platform formulation condition is not transferrable across different formulations. Analogous schemes for each different formulation need to be derived so that they can accurately account for inclusion/exclusion of various formulation components, along with the change in buffers and pH. A step-by-step guide to develop a viscosity prediction algorithm for a different formulation is provided in Table 4. The fifth limitation is that our analysis is based on correlations observed among molecular descriptors and viscosity of antibody solutions. While the correlations are physically meaningful, they do not imply causal relationships. Therefore, we caution that phenomenological models alone may be insufficient to conclusively prove or disprove potential hypotheses regarding the molecular origins of high viscosity in concentrated antibody solutions. Moreover, viscosity, solubility, and aggregation are interrelated phenomena because they all arise from protein:protein interactions. Molecular descriptors calculated here may correlate with more than one of these phenomena.

Table 4.

Steps followed in this scheme to develop viscosity prediction algorithm. Analogous schemes can be used to develop predict viscosity behaviors of antibodies for different formulations (different buffers, excipients and pH).

Step	Action
I	Collect concentration dependent viscosity curves for different antibodies in the same buffer under the same formulation conditions following the same experimental protocol by performing experiments
II	Build full-length homology models of those antibodies in step I
III	Computationally estimate various descriptors listed in Table 3
IV	Fit the concentration dependent viscosity behavior observed in step 1 to the Eq. 3 to identify the intercept and slope parameters
V	Perform linear regression of the slope parameter (response variable) with the descriptors identified in step IV (predictor variables)

In spite of these limitations, this work presents a consistent scheme and promises improvements as greater experimental data becomes available. Here, our quest for developing highly accurate viscosity prediction algorithms was tempered by the practical immediate need for such predictive tools. However, we have explored how this scheme might be used to provide an additional input during the developability assessment of antibody molecules. As an example, 3 antibodies that target proprotein convertase subtilisin/kexin type 9 (alirocumab (Sanofi-Aventis and Regeneron Pharmaceuticals, Praluent), bococizumab (Pfizer, PF-04950615), and evolucumab (Amgen, Repatha)), were chosen for a hypothetical developability assessment for viscosity behaviors. Molecular descriptors of these antibodies were calculated using the same procedure as described in the previous sections. The predicted viscosity curves for the 3 antibodies, if they were formulated in the same way as the 16 mAbs in our data set, are shown in Fig. 7. All 3 antibodies are predicted to demonstrate low viscosities at 150 mg/mL, but the trends suggest that concentrating 2 of them further (> 200 mg/mL) leads to unacceptably high viscosities. It must be emphasized that these viscosity curves are hypothetical and actual viscosities for these antibody products at high concentrations may vary significantly since their formulations are different. Notwithstanding this, Fig. 7 describes how Eq. 1 can be used to forecast and compare concentration-dependent viscosity behaviors of multiple antibody candidates, against a given target antigen, under standardized formulation conditions. This information, if available at the early stages of biologic drug development, can be used as an additional input to the lead candidate selection/optimization process. Such an input becomes invaluable if the target product profile involves high concentration drug product development. Therefore, the scheme developed here can provide a time- and cost-effective screening technique for formulation development of antibody-based therapeutics.

Figure 7.

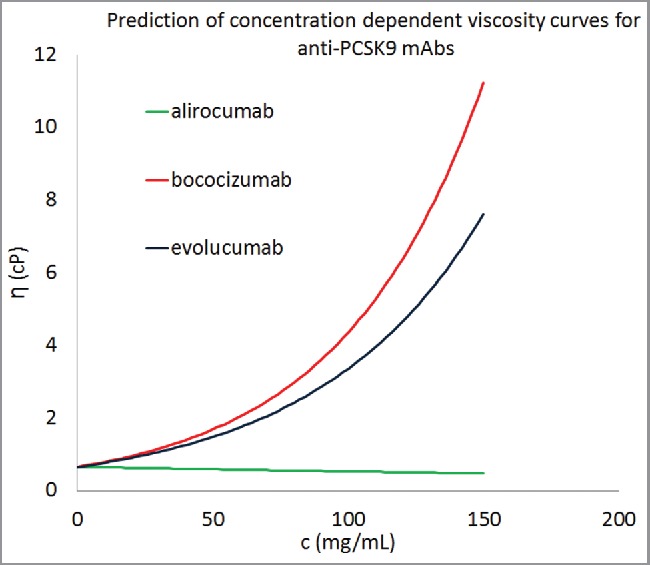
Concentration-dependent viscosity curves for 3 commercially developed antibody molecules using the descriptors from homology models. Equation 1 was used to predict the parameter B for these antibody molecules and average values of A was taken from Table 2. All 3 antibody molecules were predicted to show viscosity less than 20 cP at concentrations greater than 150 mg/mL.

Materials and methods

Five of 16 drug product development-stage Pfizer proprietary antibodies used in this study are IgG₁κs, 4 are IgG₁λs, 4 are IgG₂κs, and 3 are IgG₄κs.

Experimental methods

Experimental data on concentration-dependent viscosity curves for 16 Pfizer proprietary antibodies under platform formulation was collected by following the procedures described earlier.¹⁰ Experimental data on concentration-dependent diffusion behaviors of antibody molecules under platform formulation were collected using dynamic light scattering in a manner described by Nichols et al.¹³

Mathematical modeling

Concentration-dependent viscosity behavior

The following equation was used for mathematical modeling of concentration-dependent viscosity behavior of antibody molecules:¹⁰

$$\frac{\eta }{{\eta }_0}= A\mathrm{ exp }Bc$$ (2)

This equation can be linearized as follows:

$$\text{ln}\frac{\eta }{{\eta }_0}=\ln \mathrm{ A} +Bc$$ (3)

Where η is the viscosity of an antibody solution with concentration c; ${\eta }_0$ is the viscosity of the platform buffer; ln A and B are intercept and slope of the linear regression.

The experimental data (presented in Table 1) was used to obtain the values of A and B for each antibody.

Concentration-dependent diffusion behavior

The experimentally observed concentration-dependent diffusion behaviors were fit to the following equation proposed by Harding et. al.²⁶ to calculate D₀:

$$D_c=D_0 \left(1+k_{D}c\right)$$ (4)

Where k_D is the diffusion interaction parameter, c is the concentration of the antibody molecules, D_c is the diffusion coefficient of antibody molecules at concentration c, and D₀ is the diffusion coefficient of the antibody molecules in the limit of zero concentration. This equation assumes a linear relationship between diffusion coefficient and concentration, and is usually valid for antibody solutions with antibody concentration lower than 10 mg/mL. All antibodies in our data set exhibited linear relationship between D_c and c. The linear relationship improved considerably after one outlier D_c was removed from the linear fits for mAb6, mAb9, mAb10. The D₀ values thus calculated are listed in Table 2.

Computational methods

Homology modeling

The software Molecular Operating Environment (MOE)²⁷ from Chemical Computing Group (Montreal, Canada) was used for constructing homology-based models of full-length antibody structures and for computing molecular properties from these structural models.²⁷ Amber10:EHT force field as implemented in MOE²⁷ was used. Protein internal and external dielectrics were set to 4 and 80, respectively. Homology-based structural models for Fabs were built first. These models were then used to build chimeric templates for full-length antibody structural models. Antibody modeler in MOE²⁷ was used for building homology models of the Fabs, while protein modeler in MOE²⁷ was used for building the full-length antibody models.

Homology modeling of fabs

Homology-based structural models for Fab regions were built using MOE antibody modeler by searching for appropriate templates frameworks in the antibody database. The templates for CDR loops were manually assigned. The maximum number of main chain models was set to 25 and the number of side chain models per main chain was also set to 25. Up to 625 intermediate models were built for each Fab. GB/VI solvation was used for ranking the intermediate models for each Fab. The model with the best GB/VI score was chosen for each Fab. In the next step, the Fab models with the best GB/VI scores were energy minimized.

Homology modeling for full-length models for the antibodies

As stated earlier, the isotypes, IgG₁, IgG₂, and IgG₄ are represented in the data set of 16 mAbs studied here. Therefore, the following crystal structures for full-length antibodies available in the Protein Data Bank (http://www.rcsb.org/pdb/home/home.do) were used for constructing chimeric templates for homology-based models for full-length antibodies: 1HZH²⁸ for IgG₁ mAbs, 1IGT²⁹ for IgG₂ mAbs and 5DK3³⁰ for IgG₄ antibodies. Note that 1IGT is the crystal structure for a murine IgG₂a antibody. To our knowledge, no crystal structures for a human or humanized IgG₂ mAb are publicly available.

The procedure to build chimeric templates published by Guo et al.³¹ was followed with some modifications. In each case, the chimeric templates were constructed by superposing the previously built Fab models on both the Fabs present in the crystal structures of the full-length antibodies. The sequence identities between target antibodies and chimeric templates were as follows: > 98% for IgG₁ heavy chains, > 99% for IgG₁ light chains, > 77% for IgG₂ heavy chains, > 99% for IgG₂ light chains, > 99% for IgG₄ heavy chains and 100% for IgG₄ light chains. For each target full-length antibody, the query coverage of the chimeric template was almost 100%. The sequence identity for IgG₂ heavy chains was lower because IGT is a murine IgG₂a antibody. It has a different disulfide bonding pattern than a human IgG₂ antibody because murine IgG₂a antibodies have 3 disulfide bonds in their hinge regions, while human IgG₂ antibodies have 4 disulfide bonds (for further details, see Fig. S2 in Wang et al.³² and Fig. S6 in Supporting Information.) Moreover, for IgG₂ molecules, the disulfide bond between Cys128 of the heavy chain (the first Cys of the C_H1 domain) and the Cys214 of the light chain (the last Cys of the light chain) in 1IGT was preserved while building the chimeric template by grafting the residues near Cys128 in the heavy chain of 1IGT onto the Fab of the chimeric molecule. Each chimeric template was then used to build the full-length antibody structure in MOE.²⁷ The number of main chain models was set to 100 and number of sidechain models was set to 10. Therefore, 1000 intermediate models were made for each molecule and ranked according to their GB/VI implicit solvation energies in MOE.²⁷ The model with the best GB/VI implicit solvation energy was selected as the final model. The final model for each mAb was further optimized via energy minimizations to an RMSG below 0.00001 kcal mol⁻¹ Å⁻². An extra step was taken in the case of IgG₂ molecules before energy minimization. As noted above, 1IGT has a different disulfide bond structure than a human antibody. Because of this, homology modeling for IgG₂ molecules resulted in unpaired cysteines in the hinge region. These cysteines were paired by building disulfide bonds manually before energy minimizing the structure.

Computation of molecular descriptors

The structural model for each mAb was protonated to pH 5.8 and salt concentration of 10 mM, and was again energy minimized to an RMSG below 0.00001 kcal mol⁻¹ Å⁻². These models were used to compute several molecular descriptors, such as charge, pI, ξ-potential, dipole moment, solvent exposed polar and nonpolar surface areas for each mAb. The protein properties were calculated using MOE Protein Properties module at pH 5.8 and 10 mM salt concentrations (refer to MOE help pages and Long et. al.¹⁹ for further description of the computed protein properties). The formulation buffer used in the experiments contained no salt. However, a low ionic strength was used in the calculations to take into account any residual ions that may have been carried over from the purification trains. In addition to the protein properties computed using MOE protein properties module, the charges on residues were summed up to obtain charges on different regions of the mAbs, namely, V_H, V_L, C_L, C_H1, Hinge, and Fc. These charges were calculated within the context of the full-length models and are therefore different in magnitudes from the values of charges calculated based on the models of the individual regions outside the context of the mAb structure. The definitions for different antibody regions were taken from a review by Padlan.³³ These regions were automatically identified for all antibodies using an in-house script written in Python (https://www.python.org/). In addition to the above described structure-based properties, aggregation propensities for each antibody heavy and light chain in our data set were calculated using WALTZ³⁴ at a pH of 5.8 and 10 mM salt concentration. AP_Waltz, aggregation propensity of an antibody based on WALTZ scores, was calculated in a manner similar to Eq. 4 in Li et al.,¹⁰ i.e., by adding the aggregation propensities of heavy and light chains of the antibody and then by dividing it with the number of residues in the antibody. AP_Tango was calculated following the same procedure after obtaining aggregation propensities using the software TANGO.³⁵

Identification of germlines and isotypes

The germlines of both the chains of the antibody molecules in this database were identified using IgBLAST,³⁶ which is based on the IMGT® classification system (http://www.imgt.org). The heavy chain and light chain isotypes were identified manually according to the definitions given in the review by Padlan.³³

t-test for significance in correlation

t-tests were performed to determine if the correlations (R²) between the parameter B and the computationally estimated descriptors are statistically significant. A significant correlation is more likely to hold for larger data sets. These tests were performed in the manner described in Kumar et al.³⁷ Briefly, t values were calculated first as follows:

$$tvalue=\left|R\right|\frac{\sqrt{(n-2)}}{\sqrt{(1-R^2)}}$$ (5)

Where n is the total number of antibodies in the data set, i.e., 16. From these t values, the values of cumulative distribution function of the Student's t distribution for 16 (n = 16) degrees of freedom were calculated using the function tcdf() in the software MATLAB.²² These calculated values of cumulative distribution function were subtracted from 1 to calculate the p value. A p value of 0.05 is significant at 95% confidence level. The |R| and t value of 0.423 and 1.7467, respectively, correspond to a p value = 0.05 when n = 16. Therefore, |R| ≥ 0.423 is statistically significant at a 95% confidence level.

F-test for linear regression

F-tests were performed to evaluate goodness of the linear fit. These tests were automatically performed in the software MATLAB.²² A significant p value means that the linear relationship is significant and the goodness of fit is high. In the F-test, F-statistic is calculated as follows:³⁸

$$\text{F}-\text{Statistic }= \frac{{\text{RSS}}_{\text{Null}}-{\text{RSS}}_{\text{Alt}}}{{\text{RSS}}_{\text{Alt}}} \times \frac{{\text{d}}_{\text{Alt}}}{{\text{d}}_{\text{Null}}-{\text{d}}_{\text{Alt}}}$$ (6)

Where, RSS_Null, RSS_Alt, d_Null, and d_Alt are residual sum of squares of the null model, residual sum of squares of the alternative model, degree of freedom of the null model, and degree of freedom of the alternative model, respectively. The null model is a model that has no descriptors in it, i.e., the null model is a constant term. The alternative model is the model that is being tested. If the F-statistics is high and the corresponding p-value is low, then the hypothesis that the null model is better than the alternative model is rejected. Further details about the implementation of F-test in the software MATLAB,²² can be found in a tutorial on the software's website (http://www.mathworks.com/help/stats/f-statistic-and-t-statistic.html?requestedDomain=www.mathworks.com).

Prediction of B from computationally estimated molecular descriptors

Stepwise linear regression was performed to identify an equation that uses the smallest number of computationally estimated descriptors to reliably predict the parameter B. These analyses were performed in the software MATLAB.²² Adjusted R² was used as a criterion to add or remove a term from the model to avoid over-fitting the data because adjusted R² penalizes a model for adding a new term, and it only increases when the goodness of fit is statistically significant.³⁹ The starting model was a constant term. Descriptors were added or removed by using the default settings for adjusted R² in the software MATLAB.²²

Disclosure of potential conflicts of interest

DST, LL, MPB, NGL, CTB, and SK are employees of Pfizer Inc. SKS is an employee of Lonza AG. The authors declare no potential conflict of interest.

Acknowledgments

The authors thank numerous Pfizer colleagues for their inputs at various stages of this work. Dr. Brajesh Rai is thanked for his advice and discussions on data analysis. DST thanks Pfizer Postdoctoral program for financial support.