On the Interpretation of the Hazard Ratio and Communication of Survival Benefit

This article highlights the importance of the difference between a relative hazard and a relative risk, especially as related to the interpretation of risk reductions.

Abstract

This brief communication will clarify the difference between a relative hazard and a relative risk. We highlight the importance of this difference, and demonstrate in practical terms that 1 minus the hazard ratio should not be interpreted as a risk reduction in the commonly understood sense of the term. This article aims to provide a better understanding of the type of risk reduction that a hazard ratio implies, thereby clarifying the intent in the communication among practitioners and researchers and establishing an accurate and realistic foundation for communicating with patients.

Introduction

It is a common practice when reporting results of cancer clinical trials to express survival benefit based on the hazard ratio (HR) from a survival analysis as a “reduction in the risk of death,” by an amount equal to 100 × (1 − HR) %. Stating, for instance, that “drug X reduces the risk of dying by 40%,” based on an observed survival HR of 0.60, is a typical way of communicating survival benefit. Special care is needed in interpreting such statements, since a reduction in the “hazard” of an event implies a reduction in risk only in a particular, restricted sense. This paper will clarify the difference between a relative hazard and a relative risk. Expanding on previous brief explanations offered in [1], [2], we highlight the importance of this difference and demonstrate in practical terms that 1 minus the HR should not be interpreted as a risk reduction in the commonly understood sense of the term. The goal of this paper is thus to foster a better understanding of the type of risk reduction that a hazard ratio implies, thereby clarifying the intent in the communication among practitioners and researchers and establishing an accurate and realistic foundation for communicating with the most important stakeholders—the patients.

If qualified no further, a “reduction in the risk” of an event conveys an implied durability of effect in the sense that one is led to believe that for a fraction of the population the therapeutic intervention in question is able to eliminate the chance of the event occurring. This may be an accurate way of summarizing survival benefit in an acute risk setting, at an appropriate landmark time point beyond which that acute risk has been practically overcome. Thus, in studying outcomes in severe sepsis, for instance, it is appropriate to assess survival benefit by comparing the proportion of deaths in an experimental and control arm at 28 days post‐randomization in the intensive care unit and compute a true relative risk or risk reduction. Survival curves in this setting are biphasic and after a rapid fall off plateau. The implicit assumption is that the death rate due to the acute sepsis event after 28 days is very low compared to the initial 4‐week window, and that 28 days is therefore a reasonable time point at which to assess the durable benefit of the intervention.

However, in settings like end‐stage metastatic cancer, where disease‐related (and all too often, proximate) death is a reality for the vast majority of patients, the concept of a reduction in the risk of death as described above is not applicable. Rather, the hazard of death, and any relative hazard reduction (as measured by 1 minus the HR) due to a particular treatment, becomes more relevant. The “hazard” is an instantaneous, as opposed to a cumulative, risk. In lay terms, the hazard of an event at some time point t may be thought of as the chance of that event occurring at time t, given event‐free survival up to t (see also the explanations in [2], [3]). This risk is small over any very short time interval, but has a significant cumulative effect over time—effectively it describes an event rate. A reduction in the hazard (rate) of death means that survival is prolonged, but not that the risk of death has been averted. As an example, suppose a particular disease diagnosis carries with it a 1% hazard of dying, per day. This means that the chances of surviving 1 day with this diagnosis are 99%. The following day carries the same survival chances, given this hazard assumption, so the chances of surviving 2 days are 0.99 × 0.99 = 0.98. With each day carrying a 99% chance of survival, the likelihood of surviving 2 weeks is 0.99¹⁴ = 0.87, and the 6‐month and 1‐year survival chances can be shown to be 0.16 and 0.03, respectively. If an effective treatment reduces the hazard of death by 40% (i.e., results in an HR of 0.60), the hazard is only 0.6% per day, meaning the chances of surviving 1 day with this diagnosis are 99.4%, the chances of surviving 2 days are 0.994 × 0.994 = 0.988, and so forth. Continuing to multiply these probabilities out, the 6‐month and 1‐year survival chances can be shown to be 0.33 and 0.11. So, while a 40% hazard reduction (HR = 0.60) is undoubtedly an impressive treatment effect, survival chances beyond 1 year are slim in both treatment arms in this example, and at no point in following the patient is the relative reduction in risk of death equal to 40%. A more formal illustration clarifying the implications of this example is given in the next section.

Example Based on Exponential Survival

In planning oncology trials with survival endpoints, exponential event times are typically assumed and often a reasonable approximation, especially for overall survival. Within this framework, consider a hypothetical control cohort with median overall survival of 6 months and a comparative group of patients whose treatment results in a 40% reduction in the hazard of death, that is, an HR = 0.60. Figure 1 shows the resulting survival distributions for the experimental (a) and control (b) group, denoted by $S_E(x)$ and $S_C(x)$, respectively. The relative reduction in risk of death up to any time point $x$ is given by 1 minus the proportion of patients who have died up to time $x$ on the treatment arm versus the control arm. This can be expressed as

$$\text{Relative} \text{Risk} \text{Reduction} \text{at} \text{time} x = \frac{S_E(x)-S_C(x)}{1-S_C(x)}.$$ (Eq. 1)

Figure 1.

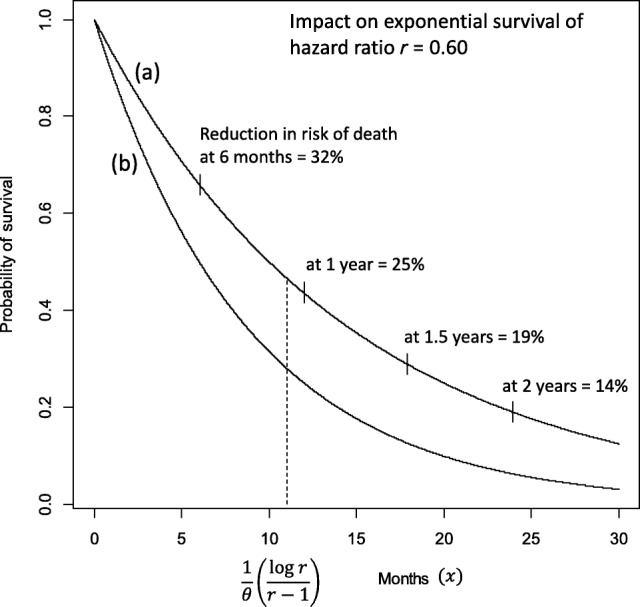
Exponential survival distributions for an experimental arm (a) and a control arm (b). Distributional forms are $S_E(x)=\exp (-r\theta x)$ for (a) and $S_C(x)=\exp (-\theta x)$ for (b), assuming hazard rate $\theta$= 0.116 for the control arm (yielding median survival of 6 months) and hazard ratio $r$= 0.60. Absolute survival benefit is maximized at $x=(1/\theta )(\log r/(r-1))$.

It can be shown that this risk reduction is less than $1-r$ at all post‐baseline observation points and for any hazard ratio $r<1$ (see Appendix). In other words, the relative reduction in risk of death is always less than the hazard ratio implies. It is also a decreasing function of the time point at which it is assessed. For instance, in the example in Figure 1, a 40% hazard reduction implies risk reductions of 25% and only 14% in the 1‐year and 2‐year mortality rates, respectively.

An alternative way of assessing treatment benefit is to consider the relative survival at a given point in time, expressed as the ratio of the survival proportion on the control arm to that on the experimental arm. This too is sometimes brought into connection with the hazard ratio, although it is a measure of relative survival chances (control versus experimental treatment) rather than a measure of relative risk of death (experimental versus control treatment). The advantage of this perspective is that it follows naturally from a consideration of the survival distributions and does not require “inversion” to calculate mortality rates. But the connection between the hazard ratio and relative survival rates is also weak. Under the assumption of exponential survival, there is only one post‐baseline point $x$ at which the relative survival (ratio of control versus experimental arm) equals the hazard ratio. This can be shown to be the case for $x_r=\frac{1}{\theta }\left(\frac{\log r}{r\hspace{0.17em}-\hspace{0.17em}1}\right)$, where $\theta$ is the hazard rate of the control survival distribution. An interesting feature of exponential survival is that $x_r$ is also the point at which the absolute survival difference between the experimental and control distributions is maximized (see Appendix). At this point of greatest separation, by some accounting the most favorable point at which to assess survival benefit, the relative survival ratio equals the hazard ratio $r$, but the relative risk of death (experimental versus control) is considerably greater than $r$, that is, the risk reduction is much smaller than $1-r$. In the example of Figure 1 with $r$= 0.60, the absolute survival benefit is maximized at $x_r=$11 months, at which point the reduction in risk of death is 26%.

Having shown that the relative risk reduction up to any point $x$ is a decreasing function of $x$ with maximum value equal to 1 – HR only at $x$= 0, and also that relative survival (control versus experimental arm) equals the HR at only one specific post‐baseline point, it is also important for fair balance to point out that the relative increase in survival (ratio of experimental versus control arm) up to point $x$ is an increasing function of $x$, from a minimum of 1.0 at $x$= 0. The implication of this is that at time points distant from baseline, although the relative reduction in risk of death is very small, this is essentially a feature of the small proportion of surviving patients in both arms, and the relative increase in survival is quite large. In the example of Figure 1, the relative reduction in risk of death at 2 years is 14%, but the likelihood of survival up to that point in the experimental arm is over three times greater than in the control arm (19% versus 6%).

Discussion

The results presented here show that when we speak of a risk reduction based on a hazard ratio, we mean a reduction in the instantaneous risk of the event at any given point in time, or the reduction in the rate of the event, not the chances of obtaining a durable benefit. Throughout this paper we have used exponentially distributed survival times, implying constant hazards as well as hazard ratios (proportional hazards) over time [3], [4]. However, the arguments made apply more generally. Note that equation (1) holds for any distribution of the experimental and control survival times, illustrating that a relative risk reduction based on these survival distributions is not a measure of overall treatment benefit like the hazard ratio, but defined for a particular observation time. This implies that the interpretive differences between hazard ratios and risk reductions apply under broader circumstances than the ones considered in this paper.

Moreover, for much clinical research requiring survival analysis, the assumption of proportional hazards and the computation of a hazard ratio is practically reasonable, and the HR clearly remains an appropriate, clinically relevant measure of overall effect. Given the central role of the HR in communicating survival benefits, it is worthwhile to appreciate the facts highlighted here. Whereas understanding the HR is arguably somewhat challenging, it is therefore also worthwhile to consider its implications through other effect measures that are more intuitive and also commonly used. For instance, the difference in median survival or absolute risk differences at specific points in time are important alternative expressions of the effect of an intervention. Snappin and Jiang [5] discuss these measures of assessing clinical meaning but, interestingly, also point to interpretive challenges with each of them. There is an apparent contradiction in that with modest hazard rates, for any given HR, differences in medians tend to be large but absolute risk differences are small, whereas with larger hazard rates, differences in medians decrease, but absolute risk differences increase. This is simply a characteristic of survival distributions and does not detract from the usefulness of these absolute measures. Rather, it further underscores the inherent complexity in interpreting results from survival analyses and suggests that a complete understanding of treatment effect is best achieved by considering multiple relevant measures, including the hazard ratio, as well as differences in medians and other measures of absolute or relative benefit.

See http://www.TheOncologist.com for supplemental material available online.

Disclosures

The authors indicated no financial relationships.