Disentangling polydispersity in the PCNA−p15^PAF complex, a disordered, transient and multivalent macromolecular assembly

Abstract

The intrinsically disordered p15^PAF regulates DNA replication and repair when interacting with the Proliferating Cell Nuclear Antigen (PCNA) sliding clamp. As many interactions between disordered proteins and globular partners involved in signaling and regulation, the complex between p15^PAF and trimeric PCNA is of low affinity, forming a transient complex that is difficult to characterize at a structural level due to its inherent polydispersity. We have determined the structure, conformational fluctuations, and relative population of the five species that coexist in solution by combining small-angle X-ray scattering (SAXS) with molecular modelling. By using explicit ensemble descriptions for the individual species, built using integrative approaches and molecular dynamics (MD) simulations, we collectively interpreted multiple SAXS profiles as population-weighted thermodynamic mixtures. The analysis demonstrates that the N-terminus of p15^PAF penetrates the PCNA ring and emerges on the back face. This observation substantiates the role of p15^PAF as a drag regulating PCNA processivity during DNA repair. Our study reveals the power of ensemble-based approaches to decode structural, dynamic, and thermodynamic information from SAXS data. This strategy paves the way for deciphering the structural bases of flexible, transient and multivalent macromolecular assemblies involved in pivotal biological processes.

INTRODUCTION

During the last decade, bioinformatics analyses have predicted that many key proteins involved in cell signaling and regulation are disordered or contain large disordered regions under physiological conditions (1,2). These Intrinsically Disordered Proteins or Regions (IDPs/IDRs) are more abundant in eukaryotes than in prokaryotes, thereby suggesting a correlation between disorder and the complexity of biological processes. The discovery of biological functions for non-globular proteins required a reformulation of the traditional structure/function paradigm (3).

The amino acid sequences and the structural features of IDPs have evolved to execute specialized functions that complement those performed by their globular counterparts (4). The biological function of many IDPs is manifested when they recognize their biological folded partners. This recognition frequently involves linear motifs of the disordered chain. Upon binding, these motifs adopt relatively fixed conformations adapted to the structural and chemical signatures of the partner, while the rest of the IDP remains flexible in the context of the complex (5,6). The reduction of the conformational fluctuations of recognition elements upon interaction with the partner implies an entropic cost that often leads to low to intermediate affinity complexes. This entropic modulation of the interaction is a key contributor to achieving tunable responses to changes in environmental conditions or external signals, thereby explaining the prevalent role of disordered proteins in signaling processes (2).

Due to the transient nature of the interaction and the distinct hydrodynamic properties of the globular and disordered parts of the complex, high-resolution Nuclear Magnetic Resonance (NMR) generally detects only those regions that remain flexible upon binding. In certain cases, it has been possible to crystallize the globular partner in the presence of a small peptide corresponding to the interacting region of the IDP. Therefore, X-ray crystallography provides an atomic resolution picture of the interacting regions that is complementary to NMR since the two techniques probe non-overlapping parts of the same entity. Nevertheless, their inclusion in a common model is not straightforward due to the lack of information on the complete assembly.

Small-Angle X-ray Scattering (SAXS) has emerged as a powerful tool to study the structure and dynamics of biomolecular systems (7–9). SAXS probes the size and shape of molecules in solution at low-resolution (12–20 Å) and has thus become a key tool through which to characterize biomolecular complexes and highly flexible proteins (10,11). Importantly, under the concentrations required for SAXS experiments (from μM to mM range), low to intermediate affinity complexes are likely to be polydisperse since free and bound states coexist in the sample. Since SAXS curves are population-weighted averages over all the species present in solution, SAXS data in a polydisperse scenario provide information about the structure and relative concentration of all these species. However, disentangling this information is a considerable challenge. The magnitude of this challenge increases when the species involved are conformationally heterogeneous. The use of structural models that describe all the species in the mixture is a powerful strategy to tackle these complex systems (12,13). However, there are two main difficulties that need to be overcome when using such an approach. First, it is necessary to generate representative structural models that include the conformational heterogeneity of all the potential species present in the equilibrium. Second, it is crucial to calculate accurate theoretical scattering profiles from all individual conformations.

The interaction between the Proliferating Cell Nuclear Antigen (PCNA) and the intrinsically disordered PCNA-associated factor p15 (p15^PAF, hereafter named p15) is an example of a flexible and transient biomolecular complex. PCNA is a DNA sliding clamp found in all kingdoms of life that is involved in multiple DNA metabolic processes including replication and repair, chromatin assembly and remodeling, and cell cycle control and survival (14–18). PCNA acts as a platform where enzymes and regulatory proteins bind and perform specific actions on DNA (19). Human PCNA is a homotrimeric assembly of 86 kDa, with protomers binding in a head-to-tail fashion to form a well structured and stable negatively charged ring with an internal diameter of 35 Å and a positively charged inner surface (Figure 1). This asymmetric charge distribution is considered essential to ensure that PCNA can slide along double stranded DNA (dsDNA) (20). Many proteins interacting with PCNA share a consensus amino acid sequence known as a PIP-box (PCNA-Interacting Protein-box), whose pattern is QXXhXXaa, where h is hydrophobic, a is aromatic (F, W or Y), and X is any of the 20 proteinogenic residues (21). Often located at the disordered C-terminal end of folded PCNA-interacting proteins, PIP-boxes recognize a hydrophobic pocket located at the front face of the ring. The structural details of the interaction of PCNA with several proteins have been revealed by crystallography. The crystallographic structures available correspond to PIP-box peptides derived from seven IDPs or IDRs, namely p21 (22), Polδ p66 (23), FEN1 (24), RNaseH2B (25), Polη (26), Polκ (26) and p15 (27). PIP-boxes display similar structural characteristics in the bound state, featuring a short 3₁₀ helix but diverging in the structural content and the orientation of the flanking regions (23,27). PCNA-interacting proteins show a wide range of binding affinities, spanning from nM for p21 (K_d ≈ 90 nM) (23,28,29) to mM for ING1 (28). This variability is explained by the differences in the amino acid sequence of PIP-boxes and the distinct contributions of the flanking regions to the interaction with PCNA.

Figure 1.

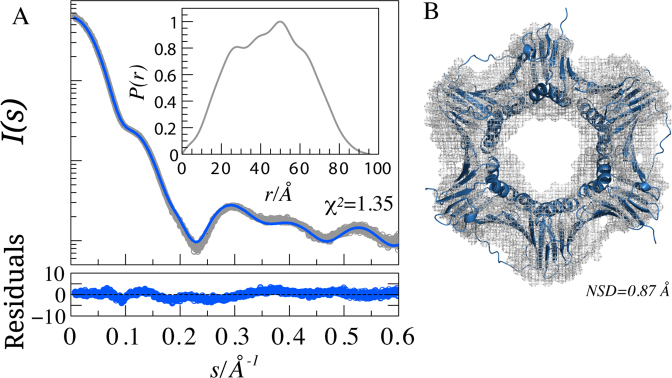
SAXS analysis of PCNA. (A) SAXS intensity profile of free PCNA (open circles), I(s), is represented in logarithmic scale as a function of the momentum of transfer, s = (4π sin θ)/λ, where 2θ is the scattering angle. The solid line corresponds to the predicted SAXS profile of the PCNA crystal structure (4D2G) (blue) with WAXSiS (χ² = 1.35). Point-by-point residuals of the fitting computed using the absolute values of the curve are displayed at the bottom. The inset shows the pair distance distribution function for PCNA calculated from the data in the range 0.068 < s < 0.5 Å⁻¹. (B) Superposition of the crystallographic structure of PCNA and the ab initio reconstruction determined using DAMMIN (42). The structures have a Normalized Spatial Discrepancy (85) (NSD) of 0.87 Å.

We have recently characterized the interaction of PCNA with p15, a 111-residue-long disordered protein involved in the regulation of DNA repair during replication. p15 functions by interacting with PCNA (30–32), and its overexpression correlates with poor prognosis in several types of cancer (33–36). The study used complementary biophysical techniques to determine the structural details of the PCNA–p15 recognition and the flexibility of the non-interacting regions of p15 (27). Isothermal Titration Calorimetry (ITC) experiments established the affinity of the complex to be K_d = 1.1 μM at 25°C and the absence of cooperativity between each of the three binding sites of PCNA. The electronic density of the complex showed that the flanking region at the N-terminus of the p15 PIP-box points towards the inside of the PCNA ring. Moreover, some NMR signals corresponding to residues at the back face of PCNA were perturbed by the addition of p15. On the basis of these two observations, we proposed that, upon binding to the front face of PCNA, the disordered N-terminal region of p15 crosses the ring and emerges on the back face. Moreover, we showed that the p15 N-terminus has direct DNA binding activity and proposed that this terminus serves as a flexible drag that regulates PCNA sliding on DNA (27). However, the ‘bead on a string’ arrangement of PCNA onto p15 could not be directly and unambiguously demonstrated due to the limitations imposed by the experimental data: the unsuccessful crystallization of the full-length p15 bound to PCNA, probably attributable to the remaining disorder, and NMR signal perturbations on the back face of the ring that could originate from long-range contacts with the flexible tails. Thus, structural information reporting on the complete PCNA–p15 biomolecular assembly would be essential to unambiguously demonstrate that p15 crosses the PCNA ring. However, the analysis of these data is challenging due to the moderate affinity of the interaction and the trimeric nature of PCNA, implying that multiple stoichiometries of the complex coexist in solution.

Here, we provide a structural description of the PCNA–p15 complex that accounts for the coexistence of several species with mixed stoichiometries, as well as for their intrinsic flexibility. The collective analysis of multiple SAXS curves measured for several mixtures of PCNA and p15 proteins demonstrates that p15 crosses the PCNA ring, thereby substantiating previous biophysical and biochemical observations (27). In order to quantitatively characterize such a flexible, transient and multivalent macromolecular assembly, reliable and accurate computational tools were required. These tools allowed us to describe the conformational landscape of p15 and PCNA and to calculate the scattering properties of individual conformations without adjustable parameters. In this context, our study demonstrates the relevance of an explicit description of the structure and dynamics of the hydration layer for interpreting SAXS data on PCNA and its complexes.

Integrative structural biology approaches that combine complementary information derived from various techniques are promising strategies through which to resolve heterogeneous ensembles such as that formed by PCNA and p15. We show that SAXS can play a crucial role in integrative approaches due to its sensitivity to molecular size and shape and its easy coupling with modeling tools and information derived from X-ray crystallography and NMR. This study presents efficient strategies to fulfill the growing need to characterize biomolecular assemblies containing IDPs in other contexts, such as in signaling and regulation.

MATERIALS AND METHODS

Protein samples

Human p15 (Uniprot: Q15004) and PCNA (UniProt: P12004) were produced in Escherichia coli and purified from the soluble fraction by several chromatographic separations, as previously described (37,27). Protein integrity was checked by MALDI-TOF, which indicated that p15 lacked the initial methionine resulting in a 110-residue long construct, and that PCNA contained three additional residues (GPH) at the N terminus. Protein stock solutions were prepared in PBS (137 mM NaCl, 2.7 mM KCl, 10 mM sodium phosphate, 2 mM potassium phosphate), pH 7.0, using desalting columns, and concentrated by ultrafiltration. The concentration was measured by absorbance at 280 nm using the corresponding extinction coefficients calculated from the amino acid compositions of the proteins (protomer concentration, in the case of PCNA).

Small-angle scattering measurement and analysis

SAXS experiments were carried out at the European Molecular Biology Laboratory beamlines X33 and P12 of DORIS and PETRAIII storage rings respectively, using the X-ray wavelengths of 1.54 and 1.24 Å and a sample-to-detector distance of 2.7 and 3.0 m, respectively (38). The scattering profiles measured at the beamline X33 covered a momentum transfer range of 0.0087 < s < 0.60 Å⁻¹, and those obtained at the beamline P12 a range of 0.0047 < s < 0.5 Å⁻¹.

SAXS data on free PCNA were collected for two series corresponding to monomeric protein concentrations of 1.3, 3.0, 5.1, 10.6, 12.7, 42.4 mg/ml, and 1.3, 5.1, 10.2, 20 mg/ml at X33 and P12 beamlines, respectively. SAXS data of the PCNA–p15 complex were collected at beamline X33 from multiple titration point mixtures at 25°C. In these experiments, the concentration of monomeric PCNA was kept constant at 150 μM for all samples with increasing amounts of p15 (30, 60, 90, 130, 200, 300 and 370 μM). The components were mixed before SAXS measurements.

The scattering patterns of the buffer solutions were recorded before and after the measurements of each protein sample. Multiple repetitive measurements were performed to detect and correct for radiation damage. Final curves at each concentration were derived after the averaged buffer scattering patterns were subtracted from the protein sample patterns using standard protocols with PRIMUS (39). No sign of aggregation was observed in any of the curves. However, noticeable repulsive inter-particle interactions were detected for PCNA alone (Supplementary Figure S4). Consequently, the final SAXS profiles were obtained by merging curves for the lowest and highest concentrations.

The forward scattering intensity, I(0), and the radius of gyration, R_g, were evaluated using Guinier's approximation (40), assuming that at very small angles (s < 1.3/R_g), the intensity can be well represented as I(s) = I(0) exp(−(sR_g)²/3). The P(r) distribution function of free PCNA was calculated by indirect Fourier Transform using GNOM (41), applying a momentum transfer range of 0.0068 < s < 0.60 Å⁻¹. Ten independent ab initio reconstructions of PCNA were built starting from a sphere of D_max = 94.1 Å with the program DAMMIN (42), and the reported structure was derived from their average.

The capacity of several programs to predict the theoretical SAXS curve from the 3D structure of PCNA was evaluated. In addition to WAXSiS (see below), we tested CRYSOL (43), AXES (44), FOXS (45), AquaSAXS (46) and SASTBX (47).

Molecular dynamics simulations

We used Gromacs 5.0.2 (48) to set up and run the Molecular Dynamics of PCNA starting from the crystal structure (27), where the flexible N- and C-terminal tails were added using Flexible-Meccano (49). The system was then solvated in a dodecahedron box with a distance of at least 1 nm from the protein. A total of 213 sodium and 162 chlorine ions were added to simulate a salt concentration around 200 mM. The use of virtual sites and bond constraints with LINCS (50) allowed a time step of 5 fs. We used particle-mesh Ewald (51–53) for electrostatic interactions and a cut-off of 1 nm for the evaluation of van der Waals interactions. The system was equilibrated for 0.1 ns in the NVT ensemble and then for 0.2 ns in the NPT ensemble with a 2 fs time-step. A Berendsen barostat (54) and a Velocity-rescale thermostat (55) kept the system in an NPT ensemble. The production run spanned 500 ns, and the last 400 ns were used for the analysis. We used the AMBER99sb-ILDN (56) force field for the protein and the ions, and TIP3P (57) for the water molecules. AMBER99sb-ILDN accurately describes folded proteins and also disordered regions, as required for the PCNA tails (58).

The superposition of structures and the calculation of the C^α root mean square fluctuations (RMSF) were done with the Theseus Maximum Likelihood algorithm (59). Theseus down-weights variable regions of the superposition and corrects for correlations among atoms, thus producing more accurate results, especially for proteins with rigid and flexible regions.

We obtained residue-specific N–H 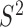values from the 400 ns trajectory by calculating the auto-correlation function, C(t), of the N–H vectors of PCNA. We first removed translations and rotations for the whole molecule and then calculated the rotational correlation function with GROMACS utilities trjconv and rotacf respectively (48,60). For each residue, three C(t) functions were computed, corresponding to each of the protomers of PCNA, and subsequently averaged. The final C(t) was fitted to a two-parameter model: 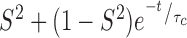(61) with the program Scipy (62).

Ensemble construction

All-atom models were used to build ensembles for p15, PCNA and the three complexes of PCNA–p15 with 3:1, 3:2 and 3:3 stoichiometries. An ensemble model of 800 conformations of free p15 was computed using Flexible-Meccano, taking into account the dihedral angle φ/ψ propensities obtained in the previously described analysis of RDCs and SAXS data (37). The PCNA complexes bound to full-length p15 were modeled with p15 termini randomly appended to the PCNA–p15^50-77 crystal structure (27) and with missing N- and C-termini tails randomly added onto each PCNA protomer. The conformation of p15^50–77 was maintained as in the crystal, and the disordered N- and C-terminal extensions were added to 1, 2 or 3 p15^50–77 peptides using Flexible-Meccano and in-house scripts. The p15 termini and also the missing tails in the PCNA structure were modeled as an ensemble of flexible polypeptide backbone segments that could attain different conformations relative to the static ring-shaped structure. For each disordered segment built, side-chains were added with SCCOMP (63). Depending on the stoichiometry of the complex (3:1, 3:2 or 3:3), p15 molecules were individually docked on PIP-box binding sites of the PCNA trimer, and those without steric clashes with PCNA and other p15-bound conformations were selected. The resulting conformations were classified as in-model or out-model in the following manner. The centre of mass of PCNA and a plane passing through this centre and perpendicular to the 3-fold symmetry axis of PCNA were defined. A p15 conformation was considered to be in-model when at least one of the heavy atoms in residues 2–50 fulfilled the following two criteria: (i) the vector connecting the centre of mass of PCNA and the heavy atom had a positive dot product with the normal to the plane directed to the back face; and (ii) the distance between the heavy atom and the PCNA center of mass was <17 Å (half the diameter of the PCNA ring) to exclude chains that comply with the first criterion but going over the ring instead of through it. Conformations not fulfilling these criteria were considered to be out-model.

Short explicit-solvent MD simulations for WAXSiS calculations

The SAXS predictions for the structural ensembles were based on a short explicit-solvent MD simulation conducted for each conformation of the different ensembles. Accordingly, each structure of the ensembles of p15, PCNA and PCNA–p15 complexes were pre-processed with Rosetta3.5 fixbb module (64) to alleviate side-chain clashes. Each structure was placed in a simulation box of a dodecahedron, solvated with the TIP3P water model (57), and neutralized with counter ions. After an energy minimization, the backbone atoms were constrained with a force constant of 100 kJ mol⁻¹ nm⁻². Each structure was simulated for 200 ps using Gromacs 4.6 (48) and the AMBER99sb-ILDN (56) force-field. NPT conditions were maintained using velocity rescaling (55) to 300 K and Berendsen barostats (54).

WAXSiS calculation of SAXS profiles

Two schemes were used to calculate SAXS curves from conformational ensembles. To compute the scattering pattern of free PCNA in the MD trajectory, 800 frames from the 400 ns trajectory described above were extracted at 500 ps intervals and used for SAXS prediction without further solvent dynamics sampling, following previous work (65). A second scheme following the WAXSiS approach (66) was used to sample solvent dynamics while preserving the coordinates of the backbone. Trajectories of 200 ps of explicit models for each p15, PCNA and PCNA–p15 complexes were generated as described in the previous paragraph with GROMACS, rather than the YASARA engine used on the WAXSiS web server. Two-hundred frames were extracted from the last 100 ps for SAXS calculation (see below).

SAXS curves were computed from the explicit solvent simulations as described previously (65). The protein conformation and also solvent atoms inside an 8 Å envelope surrounding the protein were taken into account for the SAXS calculations. The excluded solvent scattering was computed from the atoms inside the same envelope in a pure-water simulation. The electron density of the solvent was corrected to 334 e nm⁻³.

SAXS data analysis of PCNA–p15 mixtures

The P(r) functions of the mixtures of PCNA and p15 were calculated from the SAXS profiles divided by their forward scattering intensity, I(0), using the momentum transfer range 0.05 < s < 0.50 Å⁻¹, and normalized to have a constant area under the curve. R_g and D_max values of the resulting curves of the titration experiment were derived form the P(r) function. Hollow cylinders were generated using BODIES (39), and their theoretical SAXS profiles were computed with CRYSOL (43). The size and shape of the cylinder were optimized by minimizing the normalized spatial discrepancy to the ab initio reconstruction of free PCNA. Additional hollow cylinders were created with a different inner radius, but maintaining their height and outer radius.

The PCNA ring has three identical independent binding sites for p15 (27). The reactions describing the binding process are: 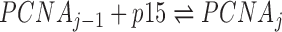, where j = 1, 2, 3 is the number of p15 molecules bound to the PCNA trimer. For a given dissociation constant K_d of p15 towards one PCNA protomer, the concentrations of individual species can be estimated by solving the following system of equations:

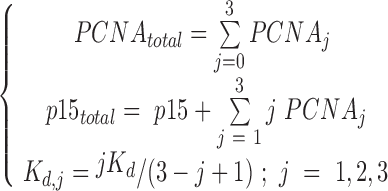(1)

where 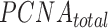and 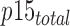correspond to the total concentration of trimeric PCNA and p15, respectively, 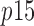is the concentration of free p15, 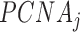is the concentration of PCNA bound to j molecules of p15 (with j = 0, 1, 2 or 3), and 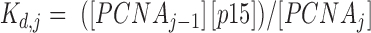is the dissociation constant of the individual complexes.

For each titration point, we calculated the populations of individual species assuming K_d values ranging from 10⁻³ to 10³ μM. Ensemble-based SAXS profiles obtained from all-atom models of individual species were linearly combined on the basis of the relative populations obtained at each titration point. The resulting weighted SAXS curves were directly compared to the experimental SAXS data. K_d optimization was performed by minimizing the χ² between the experimental data (I_exp) and theoretical (I_theor) profiles:

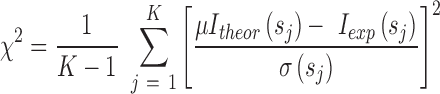(2)

where K is the number of data points, 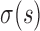are the standard deviations of the scattering intensities, and 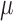is a scaling factor. 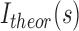is defined as follows:

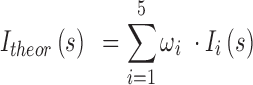(3)

where 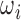is the molar fraction (i.e. relative population) of individual species, 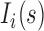is the simulated SAXS profiles of a given species ( 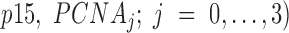obtained by averaging the scattering intensities of 800 explicit models per individual species:

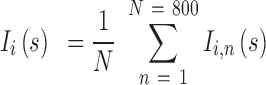(4)

To avoid inter-particle effects in PCNA–p15 samples, a momentum transfer range of 0.05 < s < 0.50 Å⁻¹ was used for the analysis.

RESULTS

SAXS analysis of PCNA

SAXS measurements of PCNA were collected at concentrations ranging from 1.3 to 42.4 mg/ml, thus providing a final SAXS curve with an excellent signal-to-noise ratio. The SAXS profile of PCNA presented features in a broad momentum transfer range, from 0.0068 to 0.6 Å⁻¹ (Figure 1A). The radius of gyration (R_g) extracted from this curve was 34.6 ± 0.3 Å and the maximum intramolecular distance, D_max, was 94.1 ± 3.0 Å. These two values are in the range previously described for PCNA (67–71). The corresponding electron pair distance distribution function, P(r), calculated using GNOM (41), had distinctive peaks and features that reported on the structure of PCNA (Figure 1A). This highly resolved P(r) was used to generate an ab initio 3D-reconstruction with DAMMIN (42). This reconstruction displayed the expected ring-shape of the protein and precisely enveloped the crystallographic structure of PCNA (PDB code: 4D2G) (27). The high quality of the reconstruction reflects the wealth of information encoded in the 1D scattering pattern of PCNA.

Before analyzing the SAXS curves of the PCNA–p15 mixtures, we assessed how accurately we could reproduce the experimental SAXS profile of human PCNA by back-calculating the scattering intensity from the atomic coordinates of its crystal structure, using available predictors with default parameters (Supplementary Figure S1). The various methods vary in the calculation of interatomic distances, in the treatment of the hydration layer, and in the calculation of the background contrast (72). WAXSiS (65,66) was the only predictor that accurately described the features present in the experimental curve. This accuracy is explained by the use of explicit atomistic descriptions for interatomic distances, the hydration layer and the excluded volume. Subsequently, a total of 10 explicit models of full-length PCNA, varying solely in their N- and C-tails of three and six residues respectively, were used as starting coordinates for short explicit solvent MD simulations, as normally done in the WAXSiS approach. The capacity of WAXSiS to describe the SAXS curve from the 3D structure of PCNA can be inferred from the low χ² values, ranging from 1.35 to 2.23 for the 10 starting structures, and from the residuals displayed in Figure 1A, which correspond to the structure with the lowest χ². This excellent agreement is a remarkable result taking into account that we did not fit any parameter, except for the arbitrary absolute scale of I(s).

Validation of PCNA molecular dynamics simulation by SAXS and NMR

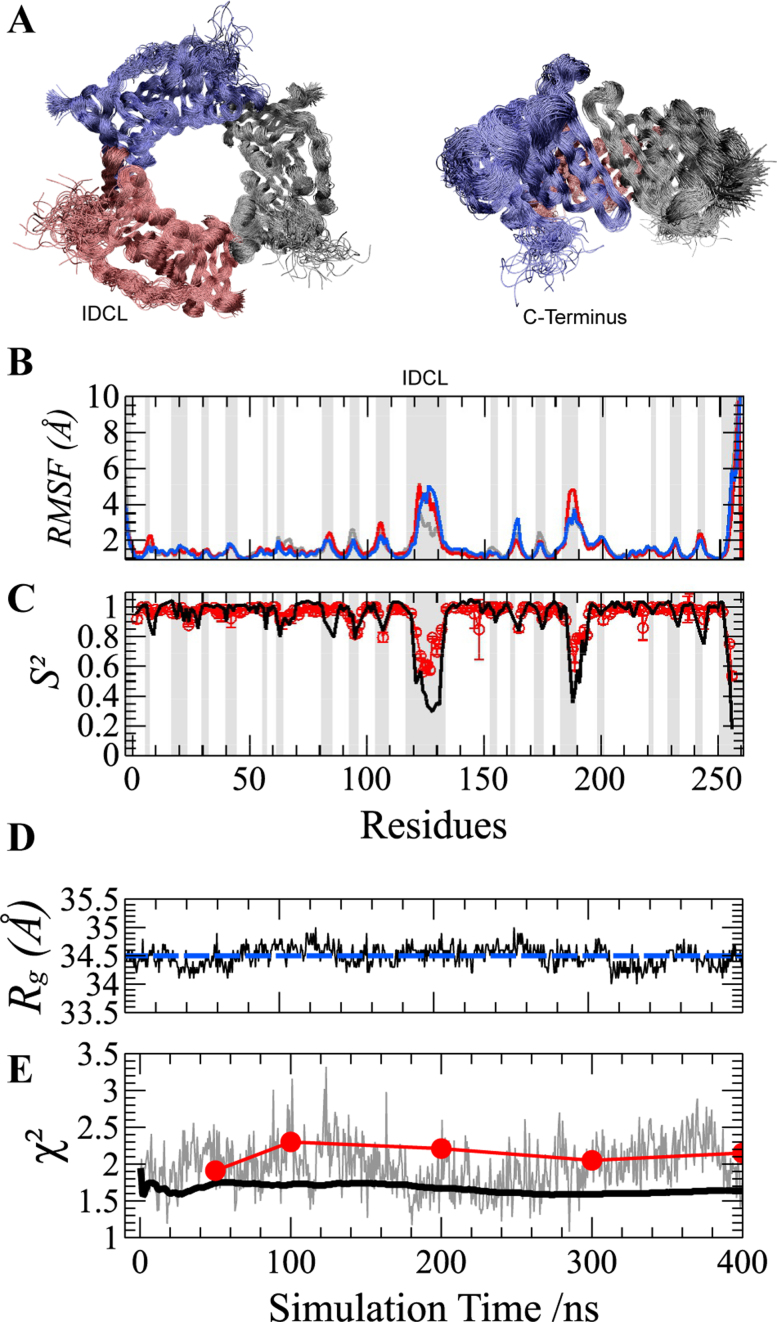
We performed a 400 ns all-atom explicit solvent MD simulation on human PCNA to obtain an atomistic description of picosecond and nanosecond fluctuations of the protein. MD-derived snapshots revealed a relatively stable PCNA ring (Figure 2A). Protein fluctuations were analyzed by computing the C^α Root Mean Square Fluctuations (RMSF) for PCNA conformations derived from the trajectory (Figure 2B). The three protomers displayed a similar level of mobility, and spatial fluctuations were located mainly in exposed loops connecting secondary structure elements, and particularly in the interdomain-connecting loop (IDCL), which is the longest loop in the protein (residues Y117-Q134), and the loop region K184-E195. The C-terminal tail presented the highest flexibility—an observation consistent with the absence of this region in the electron density maps of most crystal structures of PCNA. The residue-specific backbone N–H order parameters, S², were calculated from the MD trajectory by computing the corresponding autocorrelation functions, C(t). Note that the final C(t) corresponds to the average of those obtained for each residue in the three protomers. Computed S² values were compared with those previously determined by ¹⁵N NMR relaxation (28) (Figure 2C). Excellent agreement was found between experimental and MD-derived S² values, showing that several loop residues are mobile on the ps-ns time-scale, the regions of largest fluctuation matching those in the RMSF analysis above. Importantly, our MD trajectory captured this enhanced flexibility and is therefore an excellent model to describe fast sub-nanosecond dynamics in PCNA.

Figure 2.

Molecular Dynamics (MD) simulation of the PCNA ring. (A) Two orthogonal views of the overlay of 100 structures sampled at regular intervals during the 400 ns MD simulation. The superposition was based on a Maximum Likelihood method implemented in Theseus (59). Different protomers forming the PCNA trimer are shown in blue, red and gray. (B) C^α Root-Mean-Square Fluctuations (RMSF) and (C) N–H bond order parameters (S²) for PCNA residues. RMSF profiles of individual protomers are highlighted using the same color code as described above. MD-derived S² values (black line) are multiplied by a common scaling factor to best reproduce those obtained by model-free analysis of experimental NMR relaxation data (28) (red circles with error bars). RMSF and S² patterns show that only loops and the C-terminus display fast motions. Loops are highlighted by gray-shaded areas for reference. (D) Validation of PCNA MD by SAXS. MD-snapshots fluctuate around the experimental R_g value (blue dashed line). (E) The χ² values obtained from the comparison between the calculated SAXS curve from each MD-snapshot and the experimental one is shown in gray. The χ² values of the comparison of the experimental curve with the computed time-dependent averaging of SAXS profiles over 400 ns MD trajectory predicted including (black solid line) or not (red circles) solvent and side-chain fluctuations.

Validation of the all-atom MD simulation was further assessed by SAXS. Conformations were extracted every 500 ps along the 400 ns simulation to obtain an ensemble of 800 snapshots. SAXS profiles were computed for each snapshot using WAXSiS, and the individual R_g values were extracted using the Guinier approximation (Figure 2D). The computed R_g values were within a small range (34.2–34.7 Å), around an average value of 34.5 Å. This R_g value is in excellent agreement with the experimentally determined one, 34.6 ± 0.3 Å (Figure 2D). The consistency in R_g reflects that PCNA forms a stable ring in solution, and that the open conformations, if present, represent a very small population not detectable by SAXS, which is in agreement with previous simulations of PCNA (73).

Simulated SAXS curves of individual snapshots were found to be in agreement with the experimental curve. The average χ² among the 800 snapshots was 1.97, but fluctuations from 1.1 to 3.3 were observed in the individual χ² (Figure 2E, gray line). When averaging consecutive scattering profiles in a time-dependent manner, a systematic improvement in the description of the SAXS curve was observed, reaching a final χ² of 1.64 when the complete trajectory was taken into account (Figure 2E, black line). This observation highlights the importance of the ensemble description of PCNA to describe its SAXS properties.

In the WAXSiS protocol, the SAXS intensity of a given conformation is derived by averaging individual profiles computed from simulation frames of a short MD trajectory in which solvent molecules and protein side-chains are allowed to move freely while protein backbone atoms are restrained by a harmonic potential (65). We used the high-quality SAXS data of PCNA to evaluate the effect of such additional sampling over solvent and side-chain fluctuations. With this aim, we calculated the scattering profile derived from 800 snapshots (including water molecules) from the 400 ns trajectory, without performing the short MD simulation that would include additional water and side-chain fluctuations. These individual SAXS curves were averaged in a time-dependent manner using incremental fractions of the trajectory and compared with the experimental curve. The resulting profiles produced notably higher χ² values (Figure 2E, red dots) than those simultaneously including water and side-chain fluctuations. These results highlight the importance of capturing the coupled dynamics between the solvent and the protein. In this regard, the approach used, which properly explores both slow backbone motions, as well as fast side-chain and solvent fluctuations, provides a thorough description of the PCNA ensemble and, consequently, of the PCNA SAXS curve.

WAXSiS analysis of the intrinsically discorded protein p15

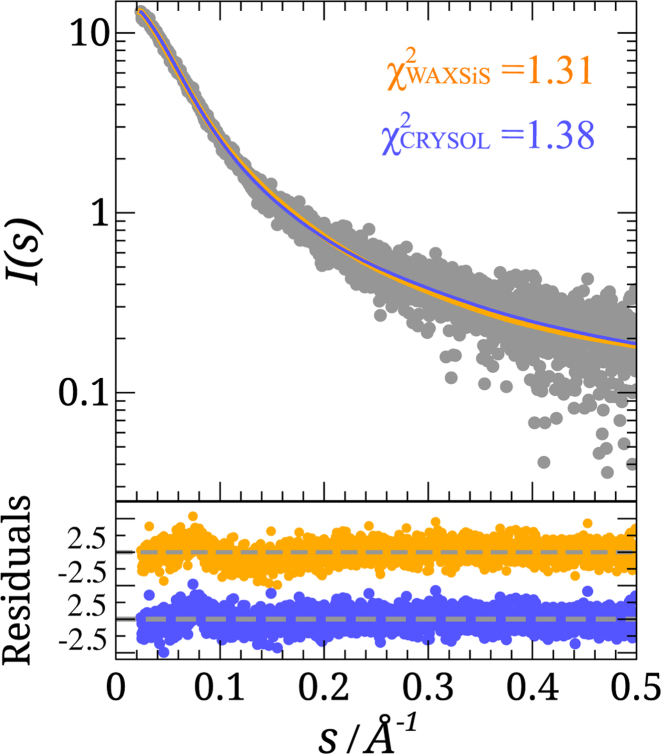
The local structural information contained in Residual Dipolar Couplings (RDCs) and the global features reported by SAXS were recently combined to study the intrinsic conformational flexibility of p15 in solution (37). Here, we tested the performance of WAXSiS, which accounts for the explicit dynamics of the hydration layer, in predicting the SAXS properties of p15. Flexible-Meccano (FM) was used to generate an ensemble of 800 conformations of p15 using the same structural bias as that derived from the RDC analysis (37). The theoretical SAXS profiles for these conformations were computed using both WAXSiS and CRYSOL (43), the latter being the software most commonly used to compute SAXS properties of disordered proteins (74,75). The resulting averaged profiles were compared with the experimental one measured in a 4.9 mg/ml p15 sample (Figure 3). Interestingly, despite the different procedures and approximations of WAXSiS and CRYSOL to compute the SAXS properties, both methods accurately reproduced the experimental SAXS curve of p15, showing χ² of 1.31 and 1.38, respectively.

Figure 3.

SAXS analysis of p15. Logarithmic-scale representation of SAXS intensity of a p15 sample at 4.9 mg/ml versus momentum transfer, s (gray circles), and the averaged back-calculated curves derived from an ensemble of 800 structures using WAXSiS (orange) and CRYSOL (blue). Residuals between simulated and experimental absolute intensities are shown below following the same color code.

SAXS analysis of the PCNA–p15 complex

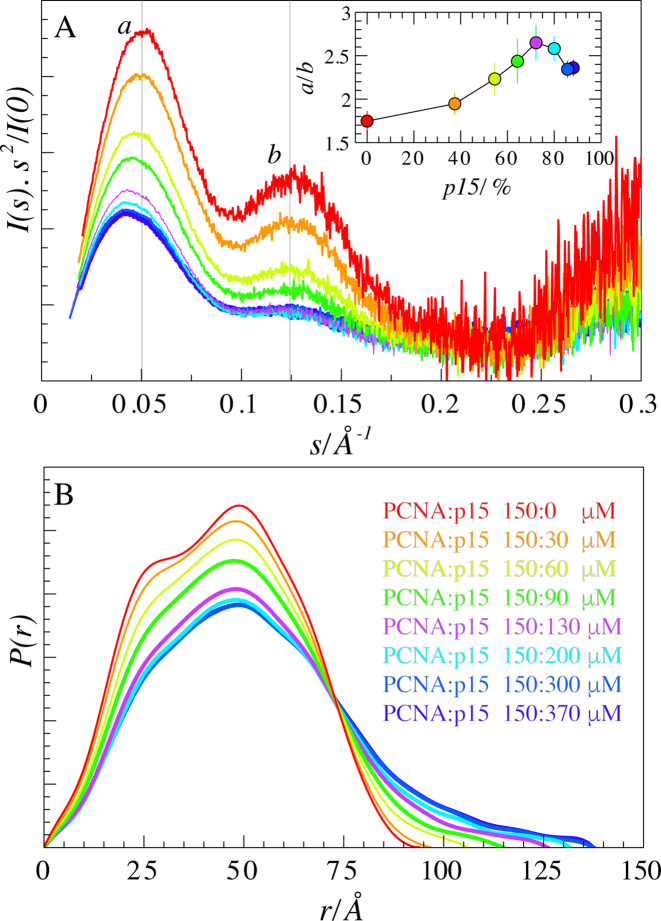
SAXS data were measured for a titration series in which increasing amounts of p15 were added to a fixed concentration of PCNA (Figure 5C). The addition of p15 to PCNA provoked specific signatures in the resulting SAXS profiles in the form of a systematic smearing of PCNA features induced by the increasing amount of protein disorder. This increase in disorder was especially evident in the Kratky representation (Figure 4A). PCNA had a bimodal bell-shaped P(r) function, which, upon addition of p15, gradually became less resolved. The distribution tailed off towards higher values of intramolecular distances, culminating at a D_max of 137.5 ± 5.0 Å for the highest p15 concentration (Figure 4B). Mixing PCNA and p15 also produced a hyperbolic increase in SAXS-derived R_g and D_max values, in correlation with the progressive saturation of PCNA binding sites by p15, which gradually populated higher molecular-weight stoichiometries (3:2 and 3:3, PCNA protomer: p15 molecule) (Supplementary Figure S2).

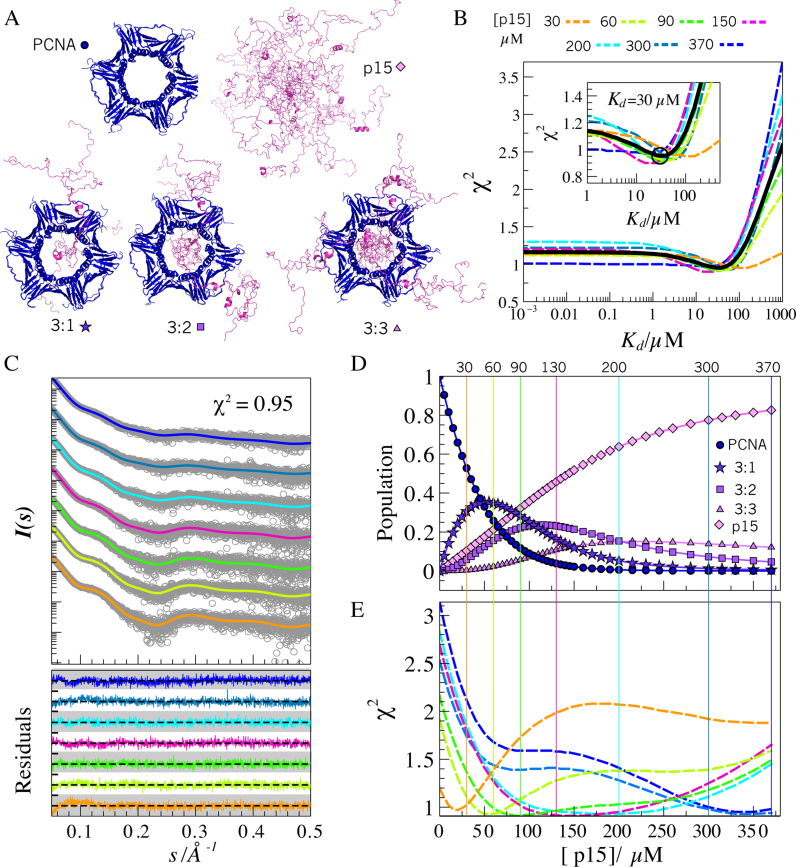
Figure 5.

SAXS modeling of PCNA–p15 mixtures. (A) Representatives of all-atom ensembles generated for the five individual coexisting species in solution. PCNA (blue) and p15 (magenta) structures are in ribbon representation. (B) χ² assessment of the screening over K_d values from 10⁻³ to 10³ μM obtained for each p15 titration point (dashed-lines): 30 (orange), 60 (yellow-green), 90 (green), 150 (pink), 200 (cyan), 300 (blue) and 370 μM (dark blue), and for all SAXS curves analyzed collectively (black solid line). Inset: Zoom of the grid-search profiles showing a minimum around K_d = 30 μM. (C) Simulated SAXS profiles (solid lines and the same color code as in panel B) for each titration point with a K_d = 30 μM, superimposed to the experimental SAXS data (gray circles). Residuals using absolute values are displayed at the bottom with the same color code, with a scale going from –4.0 to 4.0 (white and gray bands). (D) Evolution of the molar fraction of the five species over the titration, assuming a K_d = 30 μM. (E) Discrepancy (χ²) of the individual experimental SAXS curves with respect to simulated SAXS profiles in which the K_d was fixed to 30 μM and the p15 concentration was varied from 0 to 370 μM. The same color code as in panels B and C was used. Vertical lines represent the experimentally added concentration of p15 at each titration point. The coincidence of the minimum of the χ² profiles with the vertical lines of the same color substantiates the structural and thermodynamic model used to describe the titration data.

Figure 4.

SAXS of PCNA–p15 mixtures. (A) Normalized Kratky representations of scattering intensities for PCNA in the presence of increasing amounts of p15. Colors are defined in panel B. Inset: Ratio of the heights of the peaks at 0.050 and 0.125 Å⁻¹ as a function of the relative concentration of p15 with respect to trimeric PCNA. (B) Normalized pair-wise distance distribution functions, P(r), for each titration point. Peak tailing towards higher D_max values is indicative of the presence of more extended particles.

The Kratky representation of the PCNA SAXS curve presents two well-defined peaks that are differentially smeared along the titration. This is reflected in the sigmoidal shape of the ratio between the intensities of the two maxima, around 0.05 and 0.125 Å⁻¹, as a function of the concentration of p15 (Figure 4A, inset). In order to structurally explain this asymmetric decrease in Kratky intensities, we constructed a simplified geometric model of PCNA consisting in a hollow cylinder. Subsequently, we calculated the scattering profiles for this simplified model both in the presence of increasing amounts of a non-interacting Gaussian chain, which mimics the presence of p15 (Supplementary Figure S5A), and with a gradual reduction of the inner ring radius, representing the filling of the pore by p15 (Supplementary Figure S5B). In the presence of increasing amounts of the non-interacting disordered chain, the two maxima in the Kratky representation of the hollow cylinder were gradually smeared. Interestingly, the intensity ratio between the two maxima remained essentially constant over a broad range of titration points. Thus, the differential attenuation of the peaks observed in experimental Kratky plots must be interpreted in terms of a direct interaction between the two proteins. In contrast, the Kratky plots of the same hollow cylinder when reducing the radius of the inner ring showed a sigmoidal increase in the peak intensity ratio, similar to the experimental titration of p15 to PCNA. Taken together and in comparison with the experimental observations, these models suggest that titrated p15 binds to PCNA, leading to increased disorder in the system and to a gradual occlusion of the ring. This observation is fully consistent with previous NMR and crystallographic results suggesting that p15 penetrates the PCNA ring (27). However, the simplicity of the modeling strategy used cannot discard other scenarios where the partial occlusion of the ring by p15 is achieved without crossing it.

Capturing structural polydispersity within the PCNA–p15 complex using molecular models

p15 can bind each of the three PCNA monomers with moderate affinity (27). This binding action entails the presence of up to five species in equilibrium: free p15, free PCNA and PCNA bound to one (3:1), two (3:2) and three (3:3) p15 molecules (Figure 5A). The analysis of the SAXS data and the use of geometrical bodies provided insights into the interaction between p15 and PCNA but not into the structural characteristics of the coexisting species. The relative population of the different species varies over the course of the titration according to the law of mass action, which is characterized by the dissociation constant, K_d. SAXS can be used to directly interrogate each titration point about the distribution of species and their structural features. Nevertheless, the SAXS intensities measured represent averages over all coexisting species and thus cannot be used directly to assess these properties. To address this challenge, we generated explicit ensembles of 800 conformations for each of the five species (see Figure 5A and methods section for details). The complexes of PCNA bound to full-length p15 were modeled with p15 termini randomly appended to the PCNA–p15^50-77 crystal structure. In line with previous NMR and crystallographic observations, p15 was forced to cross the PCNA ring (27). The PCNA ensemble was extracted from the 400 ns trajectory, and free p15 was modeled as previously described (37). Subsequently, we computed the theoretical SAXS curve for each conformation using WAXSiS and then averaged them to derive a species-pure SAXS curve. The resulting averaged curves displayed distinct features along the whole simulated momentum transfer range that reflected an increase in the molecular weight and flexibility as the number of p15 molecules bound to PCNA increased (Supplementary Figure S3).

Simulated SAXS profiles of pure species were used to describe the experimental scattering measured along the p15 titration of PCNA. Given a K_d and the total concentrations of the two proteins, the population of each of the species can be estimated. On the basis of these populations, the species-pure curves can be linearly combined to yield the expected curve for each titration point (see experimental section). Guided by the figure of merit χ², values of K_d ranging from 10⁻³ to 10³ μM were screened to identify the value providing the best agreement for each titration point (Figure 5B). A similar trend was observed for the seven experimental χ² versus K_d profiles that displayed broad minima at intermediate binding affinities, with K_d values from 10 to 100 μM. In the high-affinity range, with K_d values from 10⁻³ to 1 μM, a flat profile of χ² values was observed, whereas the figure of merit χ² gradually worsened when moving to low-affinity complexes, with K_d values from 10² to 10³ μM. The similar range of optimal K_d values found at all titration points prompted us to perform a collective fitting of the seven titration SAXS curves that yielded a χ² minimum in the K_d range of 10–50 μM and centered at a K_d of 30 μM (Figure 5B, solid line), which is higher than the previously measured by ITC, 1.1 μM (27). For K_d values much lower than the total concentration of PCNA (i.e. K_d < 1 μM), most of the p15 molecules are bound to PCNA, thereby explaining the lack of sensitivity of χ ² to the K_d. However, at such high affinities there was poor agreement with the experimental data, presumably because the model does not account for the contribution from unbound p15 and PCNA. Similarly, for low-affinity scenarios, the species distribution differed greatly from the experimental one, with a clear underestimation of the high stoichiometry forms of the complex and an overestimation of the free forms of the two proteins. A correct description of relative populations of the five species was achieved only in the intermediate range where the individual and collective χ² minima were found.

In the optimal range of K_d values, our model encoded the polydispersity of the system and was able to describe all SAXS curves of the experimental dataset without systematic deviations in the residuals (Figure 5C). In particular, our model captured the smearing of the SAXS features upon addition of increasing amounts of p15. At the optimal K_d, the averaged collective χ² value of the complete dataset was 0.95, and the individual collective χ² values varied between 0.91 and 0.98. All titration points at a K_d of 30 μM contained non-negligible populations of several species, thereby highlighting the complexity of the system under study (Figure 5D). The robustness of the derived model was further evaluated by calculating the optimal amount of p15 able to reproduce the experimental curves at the optimal K_d. For each curve, the minimum found was in excellent agreement with the amount of p15 experimentally added (Figure 5E). Although some curves displayed a narrow collective χ ² minimum, others showed very flat and broad profiles, thereby indicating their reduced discriminatory capacity. This analysis highlights the power of the collective analysis of SAXS data to reduce inherent ambiguities of individual curves.

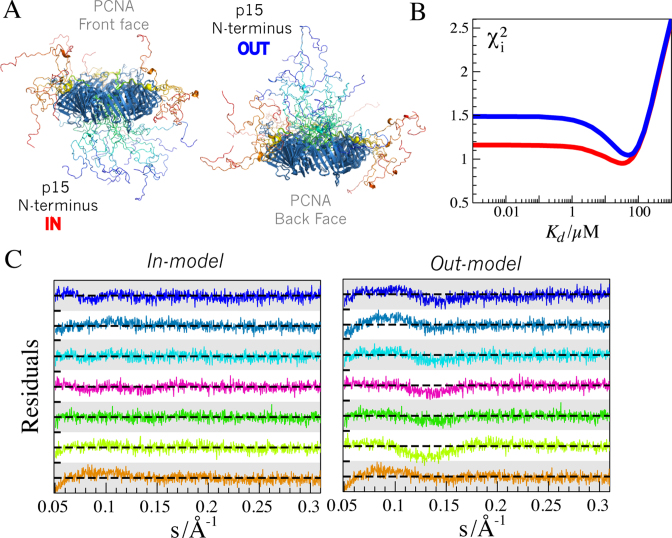
p15 crosses the PCNA ring

In all the models built for the structural analysis of the SAXS data for the PCNA–p15 complex, the disordered N-terminal region of p15 was modeled to cross the ring and emerge on the back face. This model, which we call in-model (see Figure 6A), is supported by previous NMR and X-ray crystallography data (27). However, this model was not unambiguously proven (see above), and the possibility that the N-terminus of p15 reverses its direction towards the front face of PCNA, which we call out-model (see Figure 6A), could not be discarded. We used the SAXS dataset to study this structural feature. The K_d screening analysis of the SAXS data was repeated but using the averaged curves computed from 800 models for each of the three complexes (3:1, 3:2 and 3:3), where the N-terminus of p15 sampled the front face of PCNA. For this out-model, the overall behavior of collective χ² with K_d was equivalent to that of the previously analyzed in-model, with relatively broad minimum flanked by non-sensitive region for high-affinity complexes and a marked rise in the low-affinity range (Figure 6B). Interestingly, the out-model of the complex yielded systematically higher collective χ² values than the in-model. The minimum of the grid-search for the out-model was slightly shifted towards lower affinities (K_d ∼ 50 μM) and presented a larger collective χ² compared to the in-model (1.05 and 0.95, respectively). At the optimal K_d value of 50 μM, the out-model showed systematic deviations when compared with the experimental data, as observed in the residuals (Figure 6C). These deviations were especially noticeable in the momentum transfer range 0.05 < s < 0.2 Å⁻¹ and were not present in the in-model. These observations support the notion that p15 crosses the ring and samples the space at the back face of PCNA.

Figure 6.

(A) Lateral view of an ensemble of the 3:3 complex containing five conformations of p15 on each site corresponding to the in-model (left) and the out-model (right). p15 conformations were colored according the residue number from blue to red. Notice the distinct relative orientation of the N- and C-termini of p15 and the occlusion of the PCNA ring in the two models that induce the difference in the resulting SAXS curves. (B) Averaged χ² values for the K_d screening for the in-model (red line) and the out-model (blue line). (C) Residuals computed for the fitting of the in-model (left) and the out-model (right) to the experimental SAXS curves at the optimal K_d values for each structural model (K_d = 30 μM for the in-model, and K_d = 50 μM for the out-model). Residual ranges for each curve span from -4.0 to 4.0 (white and gray bars). The momentum transfer range 0.05 < s < 0.3 Å⁻¹ is displayed to highlight the systematic deviations encountered for the out-model. Color code for p15 concentrations is the same as in Figure 5, going from low (30 μM) to high (370 μM) p15 concentration, from bottom to top.

DISCUSSION

Given the crucial role of biomolecular complexes containing disordered partners in signaling, regulation, and homeostasis, there is a growing interest in their characterization. The evolutionary pressures that stimulate faster responses to environmental changes favor low to moderate affinity interactions, forming the so-called transient complexes. Deciphering the structural characteristics of these molecular assemblies is highly challenging as they host multiple forms of heterogeneity. First, conformational heterogeneity is induced by the presence of flexible regions within complexes. Second, the polydispersity of species is caused by the coexistence of free and bound forms of the partners at the required experimental concentrations. A third source of polydispersity can also be present when any of the partners contains multiple equivalent (or similar) binding sites. These three phenomena contribute to the heterogeneity of the complex of disordered p15 and the homotrimeric PCNA. The moderate affinity of the interaction between these two proteins results in the presence of five distinct species, which correspond to the free forms of p15 and PCNA, and the three complexes with different stoichiometries (3:1, 3:2 and 3:3). Here, we demonstrate that SAXS, which is sensitive to global features of particles such as the molecular weight, the size and the shape, is highly suited to structurally probing the polydispersity of this complex. The exploitation of SAXS for structural studies of polydisperse systems requires an adequate design of the experimental measurements, the generation of atomic models of the coexisting species, and the prediction of accurate theoretical SAXS profiles from these atomic models. In our study of the PCNA–p15 assembly, we addressed these three aspects.

To derive structural information from multiple coexisting species, it is necessary to have several SAXS curves under different conditions with distinct populations of the species concerned. The titration conditions used for the PCNA–p15 complex allowed measurement of SAXS curves that contained information for all five species, thereby reducing the ambiguity of the final model (Figure 5D). As a perspective, the design of microfluidic devices coupled to automatized SAXS beam lines could provide extensive and structurally richer titration experiments (76). Although some approaches have been developed to extract pure scattering curves for multiples species in equilibrium from SAXS data (77,78), the use of atomistic models seems the most adequate strategy for complex systems such as PCNA–p15. Here, we combined MD simulation and molecular modeling with previous experimental structural data to describe PCNA, p15, and the different stoichiometric complexes. We demonstrate that the 400 ns MD trajectory captures the mobility of PCNA, as it is able to reproduce both NMR relaxation and highly precise SAXS data. In agreement with previous reports, we found that PCNA is a relatively rigid protein with fast conformational fluctuations in the following three regions: IDCL, the region encompassing K184-E195, and the C-terminus. Large protein rearrangements involving ring breakage, which in the cell requires the action of the clamp loader RFC enzyme (79) to load PCNA onto dsDNA, were not detected in the present experimental conditions. This observation is in line with extensive MD simulations that revealed that a large kinetic barrier has to be surpassed to open the ring, resulting in a considerable thermodynamic destabilization of the open form with respect to the closed one (80). While MD simulations probe fast dynamics on globular proteins, the conformational exploration of disordered proteins such as p15 and its complexes requires other approaches. Applying integrative strategies, we used previous non-overlapping NMR and crystallographic information to build accurate models for these highly flexible species. These models allowed us to simultaneously reproduce the SAXS dataset probing all species present in the mixture, thereby substantiating the quality of the models constructed. Finally, the use of atomistic models to describe transient equilibria can be achieved only when accurate approaches for computing scattering profiles from 3D models are available. Our study demonstrates the importance of properly describing protein and hydration dynamics when reproducing SAXS data. Among the software tested, WAXSiS, which performs short explicit solvent MD, was the only one with the capacity to accurately describe the SAXS data of PCNA. Our analysis highlights the relevance of sampling fluctuations in protein conformation, the hydration layer, and the excluded solvent. In this context, the use of multiple short simulations capturing the coupled motions between the solvation water shell and the protein seems to be the most appropriate strategy. We speculate that these effects are more notable in ring-shaped proteins where the water density in the ring can have strong effects on the final SAXS curve, as demonstrated by our geometric model analysis. Moreover, the highly charged nature of the ring, which prevents specific interactions with dsDNA, most probably modifies water density, thus hampering the use of programs with an implicit hydration model. In line with this hypothesis, in a recent SAXS/SANS study using three mutants of the green fluorescent protein with very different net charges (+36, –6 and –29), it was demonstrated that the hydration shell is locally denser around acidic residues than around basic and hydrophobic ones (81). Our study also shows that, for p15, WAXSiS performs as well as CRYSOL, the latter using an implicit homogeneous description of the water layer. The origin of the similarity of the resulting averaged curves for proteins with extensive solvent-accessible surfaces remains unclear. However, the observation that individual conformations provide different theoretical curves depending on the program used suggests that the effect of the hydration layer is smeared when averaging hundreds of theoretical scattering profiles. This result is important as fast computational approaches such as CRYSOL are commonly used to structurally describe highly flexible proteins with ensemble approaches (74,82,83), and the less accurate treatment of solvation does not compromise the results.

SAXS has been widely used to validate (or invalidate) 3D models of globular proteins (43–47,84). These programs generally optimize structural parameters such as atomic volume, the hydration layer contrast, or the background subtraction in order to obtain a better description of the experimental curve. However, in a disordered system, these fitting parameters cannot be optimized individually for each of the conformations, as this would increase the risk of overfitting the experimental data, and a general parametrization has to be used for all conformations. In this context, the use of SAXS prediction approaches such as WAXSiS, which does not require specific parameterization, is highly advantageous. Enabled by the use of a parameter-free predictor, here we extended the structural model validation approach to a system that, in addition to multiple conformations, presents species polydispersity. In our approach, the only adjustable parameter was the dissociation constant, K_d, which we screened from a range of values spanning six orders of magnitude. The screening of K_d values performed on the titration series highlights the distinct sensitivity of SAXS data to the binding affinities of biomolecular complexes. Not surprisingly, our results indicate that SAXS is a valuable tool to structurally characterize moderate and low affinity complexes (K_d > 1 μM). At the concentrations normally used in SAXS experiments, the K_d value for stronger affinities cannot be precisely determined and, in this scenario, SAXS can detect only the formation of the complex. The continuous improvement of SAXS beam lines and commercial detectors will decrease the amount of protein required to achieve a satisfactory signal to noise ratio, thus allowing the quantification of stronger biomolecular interactions by SAXS. Interestingly, individual curves presented distinct sensitivity to K_d depending on the species composition. Consequently, the simultaneous fitting of multiple SAXS curves facilitates the determination of the optimal K_d. Our approach could also potentially detect and quantify positive or negative cooperativity effects between binding sites. Analytical equations for distinct allosteric models can be derived and tested using a titration SAXS dataset. Despite this simultaneous analysis, the K_d value obtained is not precise. Although the minimum was found at K_d = 30 μM, values ranging from 10 to 50 μM will produce acceptable descriptions of the experimental curves. Therefore, this approach is not intended to provide precise K_d values but to validate an overall model embedding the structure, dynamics and thermodynamics of a polydisperse system. The range of acceptable K_d values derived from our analysis, 10–50 μM, is not coincident with the ITC-derived one, 1.1 μM (27). We attribute this lack of agreement to the use of techniques that are sensitive to distinct physical phenomena. For instance, the formation of an encounter complex could be probed differently by ITC and SAXS. Moreover, our approach concentrates all experimental (protein concentration estimation, concentration-dependent SAXS artifacts, experimental noise, etc.) and computational (structural bias in the ensemble generation and theoretical SAXS profile calculations) uncertainties in the definition of the K_d value, which is the only adjustable parameter of our model.

The study of the PCNA–p15 complex exemplifies the challenge posed by transient disordered complexes. Previous structural and dynamic studies of this complex focused either on the details of the interaction between the p15 PIP box with PCNA, or on p15 regions that remain flexible upon binding. The overall properties of the complex could not be addressed due to the intrinsic limitations of NMR and X-ray crystallography for studying transient disordered biomolecular complexes. In the present study, SAXS allowed us to characterize these features. Our approach validated an interaction mode whereby the N-terminal part of p15 crosses the PCNA ring and emerges at the back face of the protein. Conversely, structural models where p15 does not cross the ring but places its N- and C-termini on the front face of PCNA presented a lower agreement with the SAXS dataset. NMR chemical shift perturbation experiments and the crystallographic structure of PCNA with an enlarged version of p15 PIP region already suggested that p15 crossed the ring. Our SAXS data analysis now validates these previous observations. This interaction mode is coherent with the enhanced protection of p15 from proteasomal degradation in the presence of PCNA and suggests that the disordered chain remains partially encircled by PCNA in the unbound state due to the entropic cost of unthreading p15 chains (27). Additionally, this model provides solid bases to hypothesize that p15 act as a drag that slows down PCNA processivity along DNA facilitating actions of the repair machinery.

In summary, we have structurally characterized the interaction between p15 and PCNA, two molecules that form a disordered and transient multivalent complex presenting five coexisting species. The use of advanced modeling and computational strategies to interpret multiple SAXS curves with different relative populations of the individual species has enabled us to decipher structural features of the complex that are not accessible by other techniques. The approaches presented here, which are based on model validation, are generally applicable to the characterization of transient biomolecular interactions of disordered proteins, thus providing insights into the structural bases of fundamental biological processes linked to signaling and regulation.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

SPIN-HD – ANR Chaires d'Excellence 2011; ATIP-Avenir; French Infrastructure for Integrated Structural Biology [FRISBI – ANR-10-INSB-05-01 to P.B., CTQ2014-56966-R] from the Spanish Ministerio de Economía y Competitividad (to F.J.B.); Deutsche Forschungsgemeinschaft [HU 1971-1/1 to P.C. and J.S.H.]. Funding for open access charge: chemREPEAT-ERC-Consolidator.

Conflict of interest statement. None declared.