Abstract
The analysis of walking behavior in a physical activity intervention is considered. A Bayesian latent structure modeling approach is proposed whereby the ability and willingness of participants is modeled via latent effects. The dropout process is jointly modeled via a linked survival model. Computational issues are addressed via posterior sampling and a simulated evaluation of the longitudinal model’s ability to recover latent structure and predictor effects is considered. We evaluate the effect of a variety of socio-psychological and spatial neighborhood predictors on the propensity to walk and the estimation of latent ability and willingness in the full study.
Keywords: latent structure, intervention, physical activity, joint model, Bayesian, longitudinal data
1 Introduction
US national guidelines indicate substantial health benefits for adults who participate in at least 150 min of moderate physical activity (PA) each week.1 Despite the well-documented benefits of regular PA, data indicate that over half of all adults in the United States are not meeting national recommendations and are therefore at increased risk for developing obesity and chronic diseases.2 Perhaps even more troubling are the drastic disparities found in PA among minority groups. Recent statistics show that physical inactivity is more prevalent among African-American men and women2 and that PA declines with increasing age.3 Given that African-American adults experience higher rates of obesity and chronic diseases,4 identifying determinants of PA among older, underserved (low-income, ethnic minority) populations is a high priority.
A social ecological framework5–7 was used to develop a community-based intervention and walking program to promote walking in low income, high crime communities. The Positive Action for Today’s Health (PATH) intervention targeted three communities in South Carolina with the aim of conducting an efficacy trial to increase access and safety for walking on neighborhood walking trails.6–8 This intervention is a result of an NIH-funded community intervention study. One important endpoint of the study was defined as days of walking activity in the full intervention walking program, which received police support and social marketing grassroots efforts to support the neighborhood walking trail program. A secondary aim of the study was to assess individual- and community-level factors involved with initiation and maintenance of walking activity over 2 years.
Three communities were identified and matched on crime rates, poverty rates, PA levels, and percent minorities.7,8 Each community was randomized using a computer-generated randomized allocation sequence to receive one of three interventions: an intervention that combined a police-patrolled walking program with a social marketing intervention (full intervention), a police-patrolled walking program only, or no walking-related intervention (general health education only). The randomization was done by an independent statistician who was not connected to the trial. The trial design, power and sample size calculations are detailed elsewhere.7 The study was powered for detecting an average difference in change in moderate to vigorous physical activity from baseline to post-test of 8 min per day using accelerometer estimates. Eighty percent power was estimated with a sample size of 100 participants per community. Inclusion criteria included: (1) African-American, (2) age 18 years or older, (3) no medical condition that would limit participation in moderate intensity exercise, (4) residing in the defined census areas, (5) availability to participate in the evaluations and intervention over the study period, and (6) blood pressure (systolic <180mm Hg/diastolic <110mmHg) and blood sugar levels (<300 non-fasting mg/dL, ≤250 fasting mg/dL). The focus of this analysis is on the 133 participants who participated in the full intervention community.
A previous analysis considered individual-level motivator’s contributions to whether individuals walked at least once during the first year of the intervention and controlled for unmeasured community level variables through correlated and uncorrelated random spatial heterogeneity effects.9 This cross-sectional analysis was limited in that it could not consider the dynamic process that underlies an individual’s decision to begin and continue walking. We report here secondary data analysis that examines methods for incorporating different data sources for dynamically modeling walking behavior over time.
Comprehensive longitudinal data were recorded for individuals at up to four measurement periods over a 2-year interval. Additionally, daily logs were used to document information on attendance and walking behavior in the program, but reasons for failure to attend the walks were ambiguous (for example, individuals who moved out of the area were not able to participate in the program but may have participated had they not moved). The method proposed in the present study combines information at different orders of resolution—data-rich, information-poor daily walking records and data-poor, information-rich subject level data collected at four discrete time points—to retain the unique strengths of both data sources. Further, the use of a latent interaction construct enables investigators to assess the treatment effect in individuals with potentially insurmountable barriers to participation separately from those without barriers.
The PATH full intervention integrated principles from ecological and social marketing perspectives to development of a social marketing campaign that targeted improving perceptions of safety, access, psychosocial and social environmental barriers related to walking among residents living in low-income, high crime communities.7 Off-duty police were hired to patrol the trail during regularly scheduled walks (once daily, 6 days per week) for both trail communities. Guided by the community steering committee, a grassroots approach to social marketing was developed to motivate residents to use the identified walking path as part of the intervention program and to walk regularly with others in their communities, to increase PA and improve health.
Our approach to addressing these aims for the PATH intervention assumes a Bayesian longitudinal model for individual walking participation with linked dropout process.10–12 In addition, we also consider a linked joint model for total walkers at each observation point. Further, within our longitudinal model we account for latent structures that address the ability and willingness of participants to take part in the PA intervention. While longitudinal analysis of walking behavior is common in PA research,13 there are few examples of latent and joint modeling of the kind proposed in this paper. The structure of this paper is as follows: first, we introduce the intervention and its form. Second, we consider the latent structures that possibly exist in this study, followed by the predictor variables of interest. Third, we consider individual level models in detail and with time dependent predictors. Fourth, a simulation study is presented to evaluate the effects of latent variable assumptions. Finally, we examine the modeling scenarios with the real PATH data and present potential implications for PA and health disparities experienced by African American adults.
2 Introduction to the intervention
The PATH trial, conducted from 2008 to 2010, was designed to examine a 24-month environmental intervention for increasing PA and walking trail use in underserved communities. Assessments were conducted within each of the three communities at baseline, 12-, 18-, and 24-months. To aid in participant retention, investigators also “checked-in” with participants at 6 months when dropout was assessed. The focus of this paper is on the longitudinal walking process in the full intervention community who received a social marketing plus police supported neighborhood-walking program.
Two recruitment strategies were employed. First, participants were actively recruited from a random list of households in the census tracts that were targeted in this trial. Recruitment letters were mailed to each participant and each household received a follow-up phone call and/or personal visit from a community steering committee member. Approximately 54% of the sample was actively recruited from the random phone lists. Second, participants were recruited through volunteer advertisements. In all three communities, flyers were distributed, ads were placed in the local newspaper, and posters and banners were put up in churches, schools, and at local businesses in each community. A total of 434 participants were recruited for the project, including 133 participants in the full intervention community. Inclusion criteria included: (1) African-American (three of four grandparents of African heritage), (2) age 18 years or older, (3) no plans to move in the next 2 years, (4) no medical condition that would limit moderate intensity exercise including life-threatening illness, (5) residing in a targeted census tract, (6) available to participate in the evaluations over the study period, and (7) controlled blood pressure and blood sugar levels. Enrolled participants completed informed consent and attended biannual health screenings during which they completed anthropometric and psychosocial measures.
3 Latent population structure
Due to the mechanisms of recruiting individuals, our population potentially represents a range of participant investment in the study. For example an individual recruited through phone contact may agree to participate due to convenience, whereas a participant recruited by the fliers may have shown an active interest. Conversely, failure to observe an individual participating in the PATH walking program may have been because the conditions were such that the intervention was unsuccessful, that the individual would not participate regardless of the situation, or that the individual was lost to follow-up. As such we are characterizing the population using a hidden Markov model, which postulates that there is some underlying structure in the data that cannot be observed. Moreover, we can structure it such that individuals can move in and out of these defined states over time.
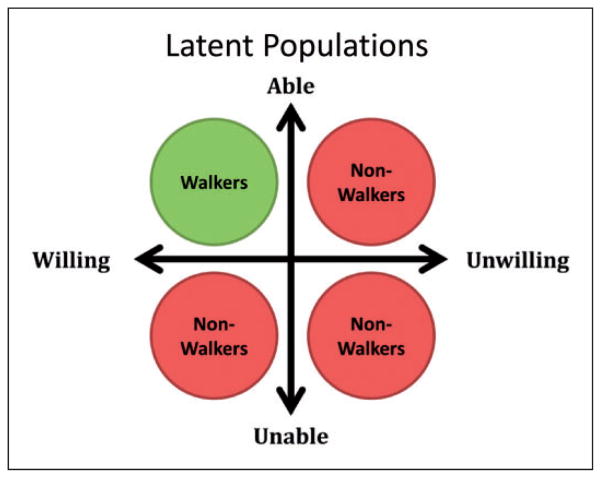
For the purposes of this study we will describe participants using two latent constructs, where an individual is grouped into one of four quadrants defined by two axes as described in Figure 1. First, an individual is either able or unable to participate (first latent construct), where we consider an individual able if they are not lost to follow up and unable if we presume that moving, health, or other circumstances have prevented the individual from responding in the study. Second, an individual is either willing or unwilling (second latent construct), where we assume that a willing individual will utilize the walking path and an unwilling individual will not utilize the walking path. In this way we can characterize factors important for intervention as those that yield a high probability for the hidden willing state of the individual to engage.
Figure 1.
Latent variable paradigm to illustrate a participant’s probability of walking based on their willingness and ability.
3.1 Variables
Due to the diversity of information available as part of the study, variables can be defined as available at the individual level, available at the block group level, or available at the walking level. For the purposes of this modeling exercise we will only consider the individual level variables; however, in section 4 we discuss how other types of variables can be integrated into the analysis.
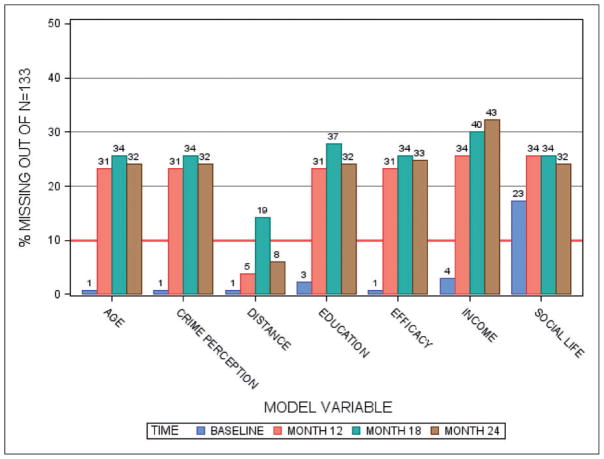
Individual level variables include demographics (e.g. sex, age, height, weight, education, marital status, income, employment, and distance to trail) and psychosocial variables (e.g. family social support, friend social support, neighbor social support, perceptions of access for walking, perceptions of crime, neighborhood social life, self-efficacy for PA). All variables were collected at baseline, 12-, 18- and 24-months. Any values that are missing are assumed to be missing completely at random (MCAR) and imputed using the mean of all continuous responses or the response with the highest frequency for categorical. Previous studies support the fact that using full imputation versus other methods does not change interpretation,9 and Figure 2 illustrates the missing present per variable. However, it should be noted that if the individual is missing data because they have been lost to follow-up (Latent Group: Unable) it is possible that the data is missing not-completely at random (NCAR), and further that it is possible that an individual has been lost to follow-up but still participates in the walking intervention (i.e. not within the scope of a zero-inflated Poisson model). It is beyond the scope of this study to consider how to handle missing data, but the authors recommend that sensitivity analysis be performed and future work will consider appropriate methods for handling NCAR data associated with the latent construct.
Figure 2.
Percentages and counts of missingness per variable using in the PATH participant data. given that there is a set of walks from which a person chooses then if we denote the walk date as tj, j = 1, …, M then we can denote yij as a binary indicator for the ith individual at the jth walk time (tj). We can assume that at this data level we have
3.2 Individual level models
The observed behavior, participation in walks, is a function both of an individual’s willingness to walk and availability to participate in the program. An interaction model allows investigators to identify modifiable risk factors of an individual’s willingness to walk, compare the probability of walking in individuals who are available but unwilling to walk versus individuals who are available and willing to walk, and identify whether it is of greater intervention interest to focus efforts on increasing willingness to walk or ability to walk (defined as the relative difference in walking probability between the four strata).
Assume that there are N participants of which Nw are walkers. We have data on walking history for the Nw walkers. The sequence of walks an individual takes is a point process in time. However,
| (1) |
The probability of walking is modulated at the latent level by the combined factors of whether an individual is willing and able. These in turn are affected by individual level effects. As such we characterize our individual level model as follows
| (2) |
In this model, the first level of the hierarchy (1) models the probability pij of the ith individual walking on the jth walk. Next in equation (2), we assume that this probability has an underlying hidden Markov state model,14 which accounts for an individual’s willingness ω1ij and ability ω2ij to participate. Note that for this we believe there is an interaction between these terms, such that the effect of someone willing and able to walk is not additive.
| (3) |
| (4) |
| (5) |
The first component ω1ij has two states and as such we model the probability that an individual is in the willing state. For this, we specify the probability that someone is willing at the first walk, π1 (3), after which we model the probability that someone is willing to walk, conditioned on their willingness state in the previous walk, θ1ij (4). Note that this probability changes for each person and each walk. Moreover, this probability (5) depends on the willingness at the previous walk ω1i(j−1), as well as individual-specific covariates zij (e.g. age, gender, height) that are allowed to vary over time. To model the covariate over time, the covariate at each visit is weighted, αti(see section 4 for details), and a single coefficient ηi is estimated. These effects are modeled through a logit link and thus, odds ratios can be reported.
For the second component, ability (ω2ij), we cannot observe the exact time at which an individual chooses to no longer participate in the walking program. Instead, we assume that this is predicted by failing to participate in a follow-up visit. To model the exact time of dropout, we assume that the latent component is a function of the individual’s dropout time ( t̃i), where an individual’s baseline ability to walk is modified by whether the ith individual has dropped out of the study by the jth given walk (6). However, since we only observe dropout at 12-, 18-, or 24- month assessments, we must impute the censoring time, t̃i using an interval censored Weibull model l (7) where t̃i,U is the follow-up visit where dropout occurred and t̃i,L is the penultimate visit. In the following equation (6), a+b represents the coefficient for ability before a subject has been censored, and a represents the coefficient for ability after a subject has been censored.
| (6) |
| (7) |
4 Time-dependent covariates
For this study, an additional complexity is the fact that predictors are only measured at discrete time points with many walks occurring during the intervening time period; thus for each covariate measured at baseline, 12-, 18-, and 24-month assessments, there is a need to define an individual’s state at unobserved intermediate time points. We expect that the behavior in these windows will be largely defined by the observed measurements recorded before and after. However, we also expect there to be some error both in terms of recall and measurement.
Consider for instance that a subject is employed at baseline but unemployed at the 12-month assessment. The question arises of how to associate the employment variable with a walk occurring at 6 months. For this study we make the assumption that an individual’s state for the current walk most closely resembles the state of the temporally most proximal visit. Thus, for continuous variables an individual’s state at a given walk was determined by a weighted average (8) of the observed state for the previous (T0) and subsequent (T1) future visit/assessment (e.g. if a participant scored 0% on the self-efficacy scale at baseline and 100% on the self-efficacy scale at the 12-month assessment, then self-efficacy at walks occurring at 90, 180, 270 days after baseline would be associated with self-efficacy scores of 25%, 50%, and 75% respectively):
| (8) |
For nominal variables, the value for a given walk was defined based on the closest assessment period (e.g. 3 months would use the baseline measure, 9 months would use the 12-month assessment measure). It should be noted that because the four time point measures are not evenly spaced, for both continuous and nominal variables, this weighting scheme implies that the four measurements will be used for different amounts in the analysis with baseline affecting 25% of the walks, Month 12 affecting 37.5% of the walks, Month 18 affecting 25% of the walks and Month 24 affecting 12.6% of the walks. This also has implications in terms of missing data since the amount of missing data may differ between follow-up visits. In addition, at each follow up, it is recorded whether the participant was available, and if the participant was lost to follow up the reason participation was terminated, when available. Since the model is generating estimates as though there were j measurements for an individual variable rather than a maximum of 5 measurements, where j is much larger than 5 (j≫>5), further simulations are necessary to assess whether the latent model appropriately measures the variance or whether the high correlation in measurements leads to an underestimate of the variances.
5 Computational considerations
In both the following simulation and the application to real PATH data we have considered the full joint posterior distribution of the individual level logistic longitudinal model jointly with the Weibull dropout model. We considered approaches to posterior sampling of this joint model. The full conditional distributions for the parameter set θ: {s, r, a, b, α, β, ω, γ …} are not all available and so Metropolis updates were performed for the relevant parameters. We used a log concave adaptive rejection sampler without fixed effect blocking. An adaptive phase of 4000 iterations was used. Convergence was assessed using multiple chain diagnostics (Brooks–Gelman–Rubin statistic: R̂). Convergence was achieved among the simulations with a burnin of 10,000 iterations. Subsequent samples were of varying size based on the number of effective parameters. For application to the real PATH data, convergence was achieved with a burnin of 8000 iterations, and the subsequent samples were of size 2000. We used a similar strategy when we introduced the joint total walkers model as described in section 7.1.
6 Simulated evaluation
Through simulation, we aim to assess the model’s ability to correctly recover an estimate of the coefficient for three key types of covariates: a constant dichotomous variable, a constant continuous variable, and a time-varying continuous variable. Note, we do not consider a time-varying categorical variable.
6.1 Variables
For the simulations, we use the model as specified in section 3.2 with the following assumptions and modifications. Due to computational time constraints and ease of model performance assessments, we consider two simple cases: a primary case with 40 participants, 10 walks, and 2 assessment visits occurring at walks 5 and 10, and a secondary case with 20 participants, 40 walks, and 4 assessment visits occurring at walks 10, 20, 30, and 40. Further we believe that the inclusion of additional data, as is the case in our observed PATH results, will only enhance the model’s ability to recover accurate estimates of the latent constructs.
For the latent willingness component of the model, we set the probability that someone is willing at the first walk, π1=0.70 (see equation (3)). Setting this probability simply means that we have fixed the probability an individual is willing to walk on the first walk; sensitivity analysis has shown that this does not have a large impact on the resulting parameter estimates. For each subsequent walk we model the probability as a function of the previous walk, and covariates (5). For the covariates, we consider three models of increasing complexity: model one that includes dichotomous variable only, model two that includes a dichotomous variable and a continuous variable, and model three that includes a dichotomous variable, a continuous variable, and a time-dependent continuous variable. Model three is the only model present in the secondary case since it is the most complex and presents the best estimates overall in the primary case; the secondary case used for the purpose of verification. The distribution of the constant dichotomous variable is modeled after the observed distribution of sex, and assumed to be distributed such that there is 1 male for every 4 females. The distribution of the constant continuous variable is modeled after the observed distribution of age, and assumed to be fixed as the first 15 participants being aged 55, the next 10 being aged 60, and the last 15 being aged 65. The distribution of the time-varying continuous variable is modeled after the observed distribution for social life, and the baseline measure is assumed to be normally distributed with mean 15 and standard deviation 5. The assumed distribution for the follow up social life values, after walk 5 and 10, is normal with the previous measure as the mean and a standard deviation of 2. Next, a weighted average of the three measurements was calculated for each participant on each walk as follows
| (9) |
The secondary case’s social life variable was calculated similarly weighted over the 4 assessment times rather than only two seen in the primary case. These three types of variables cover the range that we wish to explore through the simulation phase of analysis. Using these data together with the censoring information, we are able to derive ω1, ω2, and the probability of an individual walking on a specific walk. Finally, for each simulation, we model the probability of an individual walking on a specific walk as a Bernoulli random variable with probability derived from the lower levels of the hierarchy.
For the latent ability component of the model, we assume that for the first walk all individuals are enrolled in the study. For each subsequent walk, t̃i the dropout time is defined such that if the participant has not yet dropped out, the probability of dropping out at this time is dependent on their willingness and ability. This dropout time is determined ultimately by the specification of the lower censoring variable. We set this variable such that there is a 10% (n=4) chance of dropping out between both times 1 and 5 as well as times 5 and 10. Based on the value of the lower censoring variable, we define the upper censoring as the subsequent follow-up visit (e.g. if the lower censoring value is 1, the upper censoring value is set to 5). We set the observed censoring time as the final follow-up visit (e.g. 10) for those individuals who complete the study, and missing for those that have been censored to allow the model to impute an exact date within the censoring boundaries (i.e. dropout = It̃i=tj|tj−1 ~ Bernoulli(0.818) where I is an indicator function).
The simulation consists of 30 samples each run for 100,000 total MCMC iterations including a burn in of 20,000 iterations for a total sample size of 80,000 observed iterations. To assess whether this model can be used to accurately recover parameters for use in analyses of real data, the results consider the following performance metrics.
6.2 Assessing the effect of the time weighting scheme and coefficient recovery
To assess the model’s ability to recover the true mean value we report posterior mean estimates from the 30 simulations per each model. To recover the correct mean estimate, we ran the simulation until r̂ reached a converging value of 1. Overall, we have been able to recover the correct mean estimate since the true values do exist in 53% of the confidence intervals between the three models in the primary case and 50% for only model three in the secondary case. As far as recovering the variance is concerned, we assume that underestimation is likely due to the structure of the simulation. Further, as we have fixed the latent intercept (γ1 = −1.5), it is important to note that any time a value is fixed in place of one that truly varies, the variance will be lowered.
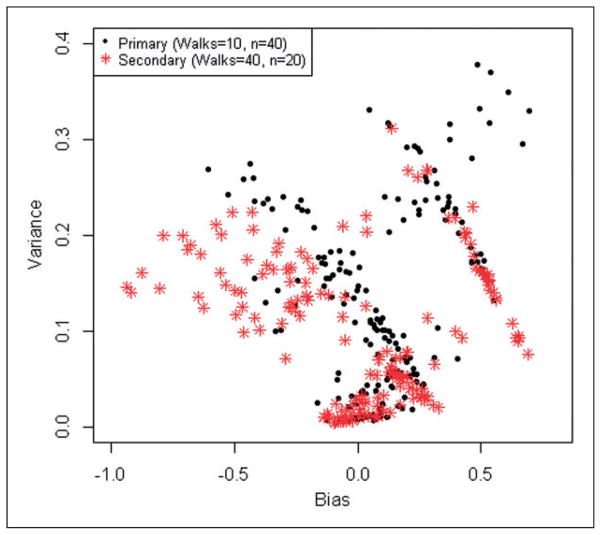
Table 1 displays the results from the simulation. Overall, the 95% credible intervals of the estimates contain the true value 53% (n=8) of the time for the primary case and 50% (n=3) in only model three for the secondary case. When comparing the models in the primary case, recovering the latent parameters proves to be the most difficult, with model three showing the best performance since 67% (n=2) of the parameters confidence intervals contain the true value compared to 0% (n=0) in each of the other models. Although, model three returns a confidence interval containing the true value most often, a second metric—the difference in the predicted mean value compared to the true mean value, would suggest that model one performs best for constant dichotomous predictors. Model three in the secondary case seems to perform better for the predictors rather than the latent parameters. Note that the mean deviances are not comparable from case to case because different data is used. Figure 3 shows a comparison of the variance and bias for model three in the primary verses secondary cases. This illustrates that the two cases behave similarly to this respect though the variance appears slightly better for the secondary case while the bias is slightly better in the primary case.
Table 1.
Posterior average estimates from 30 simulations of the model parameters for each of three models in the primary case and model three in the secondary case.
| Parameter | True value | Estimate averaged over simulations
|
||||
|---|---|---|---|---|---|---|
| Model one Primary case
|
Model two Primary case
|
Model three Primary case
|
Model three Secondary case
|
|||
| Mean deviance: 425.3 | Mean deviance: 427.6 | Mean deviance: 425.2 | Mean deviance: 859.11 | |||
| Constant dichotomous predictor | η1 | 0.3 | 0.240 (−0.011, 0.606) | 0.583 (0.032, 1.130) | 0.397 (−0.047, 0.956) | 0.038 (−0.213, 0.489) |
| Constant continuous predictor | η2 | 0.1 | – | 0.101 (0.024, 0.229) | 0.140 (0.013, 0.313) | 0.076 (−0.022, 0.230) |
| Time-varying continuous predictor | η3 | 0.5 | – | – | 0.554 (0.345, 0.882) | 0.591 (0.407, 0.897) |
| Latent willingness | γ2 | 1.5 | 1.065 (0.739, 1.481) | 1.137 (0.885, 1.451) | 1.355 (0.929, 1.681) | 1.007 (0.523, 1.380) |
| Latent ability | γ3 | 1.5 | 1.731 (1.597, 1.817) | 1.674 (1.535, 1.789) | 1.635 (1.260, 1.808) | 1.723 (1.551, 1.842) |
| Latent interaction | γ4 | 1.0 | 1.516 (1.361, 1.633) | 1.455 (1.293, 1.593) | 1.448 (1.149, 1.630) | 1.591 (1.245, 1.748) |
Figure 3.
Comparison of the variance and bias associated with the primary and secondary simulation cases for model three.
These results suggest that the inclusion of covariates and especially time-varying covariates lead to better recovery of true estimates when modeling real data; however, care must be taken as models for real data are likely to be more complex than the examples considered here. In particular, the model suggest that the recovery of each of the three types of predictors do not present an issue, though the variance is most likely underestimated as mentioned previously. The latent parameters, on the other hand, are difficult to properly estimate. These results demonstrate that the latent variables are best estimated when all three types of predictors are included in the model. Throughout all of the models, though, we see that observed predictors are consistently and accurately recovered. Each of the models produces confidence intervals that include the true predictor value, but we show the most difficulty producing a narrow interval for the parameter estimate associated with the constant dichotomous predictor especially as we add more predictors.
In assessing the model fit for the individual predictors and latent components, a model is considered to be successful if a reasonable size credible interval is produced containing the true value. Overall, we considered the simulations a success if 40% of the posterior averages produced confidence intervals that included the true value. The simulations demonstrate that we have been successful in recovering the true parameter when our Bayesian posterior estimation method is employed, though further simulation is needed to assess whether the model is successful in recovering a variance not inflated by overestimation from “generating multiple visit measures”.
6.3 Assessing the effect of assuming informative censoring
For the model specified by equation (7) we have data for whether a participant was lost at a future assessment at each of the time points (12-, 18-, and 24-months). In order to estimate the exact date when a participant decided to no longer participate in the study we had to either fully specify the functional form of the Weibull dropout distribution or we had to specify the hyperprior distributions. For instance, theory and past experience may suggest that most individuals commit to quitting the study within days of completing an assessment visit. In this scenario, a distribution which is right-skewed may be appropriate. Conversely, if most participants only decide to quit when there is an assessment visit imminently scheduled a left-skewed distribution may be more representative.
If data were collected that could help predict the precise dropout time the appropriate model would specify uninformative hyperpriors, which in turn would allow the data to specify the distribution. In our scenarios, the data was not informative enough and this approach did not lead to converged model estimates. Similarly, literature on the functional form of dropout times is sparse. As a result, we considered functional forms, that included either specifying the shape and scale parameters directly or specifying appropriate hyperpriors and evaluated the sensitivity of the model to our assumptions. The final model was fit using a Weibull distribution with shape and scale parameters of one and five respectively, implying that walkers typically dropout later in the interval (i.e. closer to the observed missing visit). The latent intercept, γ1, indicates the probability of an individual walking when he/she is neither willing nor able. For the real PATH data models, we have set γ1 ~ Uniform(−1.6, − 1.4). This suggests that when a participant is neither willing nor able to walk, the probability of them actually walking is logit−1(−1.5)=0.182. The simulation results were handled similarly for the latent intercept because we set γ1 = −1.5. For the time of censoring variable, though, all participants that complete the study have a value of 10 while the censored subjects receive “NA”. The participants that dropout must have values initialized as we are attempting to guess when during the time period they actually dropped out.
7 Application to the PATH participation data
We now consider the application of this modeling approach to data collected for the PATH trial consisting of 133 participants and 798 scheduled walks. In addition to the latent parameters discussed above, we include the following covariates to predict an individual’s willingness to walk. Sex and age are included as constant dichotomous and continuous predictors respectively. For time-varying predictors we include distance the respondent lived from the trail, crime perception, efficacy, and social life, modeled as continuous, and education (≤12 years vs. >12 years) and income (>US$10,000/year vs. >US$10,000) modeled as dichotomous.
Table 2 presents the converged posterior estimates following a burn-in of 8000 iterations, and a final sample of 2000 iterations. We assessed convergence based the R̂ measure using the built in BGR plots in WinBUGS with a value close to 1 for the majority of the parameters over the converged sample. This model estimates the probability of an individual walking using latent variables to associate the walking probability to ability and willingness as well as other descriptive covariates. The log odds of a female being willing to walk is 1.204 less than that of a man being willing to walk. For every one year increase in age, the log odds of an individual being willing to walk decreases by 0.096 (95% OR −0.105, −0.088). For participants with more than 12 years of education, the log odds of an individual being willing to walk increases by 0.289 (95% CI 0.264, 0.365) compared with those who had 12 or fewer years. For individuals with an income greater than US$10,000, the log odds of an individual being willing to walk increases by 0.108 (95% CI 0.080, 0.140) compared with those whose income is less than or equal to US$10,000. For every one mile increase in distance, the log odds of an individual being willing to walk increases by 0.316 (95% CI 0.224, 0.409). For every one unit increase in crime perception, the log odds of an individual being willing to walk is not significantly different (95% CI −0.029, 0.133). For every one unit increase in efficacy, the log odds of an individual being willing to walk increases by 0.207 (95% CI 0.206, 0.209). For every one unit increase in social life, the log odds of an individual being willing to walk decreases by 0.537 (95% CI −0.558, −0.518).
Table 2.
Converged posterior estimates for the model using PATH participant data.
| Application | Parameter | Mean |
|---|---|---|
| Walking ability | a | −1.854 (−2.00, −1.56) |
| Walking ability | b | 4.829 (4.106, 5.69) |
| Probability of walking | γ1 | −1.592 (−1.6, −1.572) |
| Probability of walking | γ2 | 0.093 (0.003, 0.266) |
| Probability of walking | γ3 | 0.014 (2.53E–04, 0.052) |
| Probability of walking | η4 | 1.978 (1.923, 1.999) |
| Sex | η1 | −1.204 (−1.409, −1.005) |
| Age | η2 | −0.096 (−0.105, −0.088) |
| Education | η5 | 0.289 (0.264, 0.326) |
| Income | η6 | 0.108 (0.080, 0.140) |
| Distance | η7 | 0.316 (0.224, 0.409) |
| Crime perception | η11 | 0.038 (−0.029, 0.133) |
| Efficacy | η12 | 0.207 (0.206, 0.209) |
| Social life | η13 | −0.537 (−0.558, −0.518) |
An individual’s walking ability is determined by a and b such that after an individual is censored, the log odds of an individual being able to walk increases by 4.829 (95% CI 4.106, 5.69). Before censoring, the odds of an individual being able to walk are −1.854 (95% CI −2.00, −1.56). The components γ1, γ2, γ3, and γ4 directly associate the individual’s ability and willingness to the probability of walking. When an individual is neither willing nor able to walk, the log odds of walking is −1.592 (95% CI −1.6, −1.572). For those willing, the log odds of an individual walking increases by 2.071 compared to those unwilling, when there is no change in ability. For each one unit increase in ability, the log odds of an individual walking increases by 1.992 when there is no change in willingness.
7.1 Total walker modeling
In our original models, we only considered the longitudinal behavior of the individual walkers without reference to the participation rate at walks. The PATH study also has recorded the total numbers of walkers at each walking event, including those members of the community not enrolled in the longitudinal study. The total count of walkers can also be thought to relate to the potential behavior of individual walkers, either as immediate or lagged encouragement or as a measure of enthusiasm within the community. Denote the walker count at the jth walk as and we assume that this has a Poisson distribution as and we assume a log link to a linear predictor of the form . Here the predictors in can represent walk-specific effects (such as weather variables, time of day, etc.). Table 3 displays the results of fitting such a model jointly with the longitudinal and the Weibull dropout model. The same method of analyzing convergence is used here as well. Note that there is a common random effect between both the total walking model and the individual model to allow for a random intercept. This random effect is applied to the total walkers model with the linear predictor such that , and in the individual model it is added to the latent effect structure as logit( pij) = f (γ*, ω*ij) + rwj.
Table 3.
Converged posterior estimates for the model using PATH participant data with a joint model for total walker participation.
| Application | Node | Mean |
|---|---|---|
| Walking ability | a | −0.354 (−1.79, 0.694) |
| Walking ability | b | 0.299 (0.003, 1.241) |
| Probability of walking | γ1 | −1.6 (−1.6, −1.6) |
| Probability of walking | γ2 | 1.18E–04 (2.23E–06, 4.50E–04) |
| Probability of walking | γ3 | 1.34E–04 (2.37E–06, 5.75E–04) |
| Probability of walking | γ4 | 2.90E–04 (4.95E–06, 0.001) |
| Sex | η1 | −0.070 (−0.187, 0.030) |
| Age | η2 | 0.412 (0.406, 0.417) |
| Education | η5 | −0.233 (−0.287, −0.195) |
| Income | η6 | −0.396 (−0.420, −0.366) |
| Distance | η7 | 0.940 (0.92, 0.965) |
| Crime perception | η11 | 0.230 (0.149, 0.331) |
| Efficacy | η12 | −0.451 (−0.454, −0.447) |
| Social life | η13 | 0.008 (−0.004, 0.019) |
The joint model is then:
In the results cited here, we have simply described the total walkers via a random component and fixed intercept, as the focus is only on individual walking behavior and we consider the individual walking behavior to be conditioned on the total walker behavior. Hence, we do not seek to explain total walking via predictors.
8 Discussion and conclusions
Community intervention trials present several unique methodological and implementation challenges far beyond those commonly identified for controlled clinical trials. These include balancing study goals and community goals, controlling for group dynamics as mediators of outcome success, and the involvement of individuals with limited previous experience in this area.15,16 Moreover, these studies often involve complex interventions that require specialized methods to account for the joint primary endpoints.17 Finally, for interventions that involved underserved or African-American communities, study recruitment and retention is often problematic and may result in biased results if the underlying cause is not considered.18–20 Specifically, for these studies it is often the case that no simple causal relationship exists, but rather represents a complex network of competing challenges many of which cannot be measured but rather inferred using latent psychological constructs.
There is a dearth of literature that addresses how to model the dynamic relationship between a measurable outcome and latent predictors, when both the predictors and outcome are confounded by participation in the study. Models exist for hidden Markov models of count14,21 or continuous data,22 or for jointly modeling latent effects and missingness,23,24 but there are no standards on modeling a binary outcome in the presence of informative missingness and latent effects that interact to create unique states of participation over time.
In this study, we have shown that variation in walking behavior can be modeled via the use of latent structures that reflect the underlying ability and willingness factors. We have also shown that the addition of another component to the walking model (that of count of walking at each walk) does help to explain some of the social aspects of walking behavior as the positive effect of larger participation is associated with masking of social life effects.
In terms of the predictors included in respective models it is clear that efficacy has a significant and positive effect on walking behavior, while social life has a significant negative effect. This mirrors the results found in Wilson et al.9 On the other hand, in the total walker joint model the effect of efficacy is negative (significant) while social life is not significant. This may be accounted for by the group effect of increased walker participation and thereby the masking of the personal effects of social life. Note that crime perception is significant and positive in both models and so walking behavior is positively associated with a more positive perception that crime was not a neighborhood safety threat. As for distance effects, there also appears to be a positive association between distance/proximity from walking trail and walking participation that is sustained across models. While income and education level are also positively related for the individual model they appear to be negatively (significant) associated with the total walkers model. This could be due to an interaction occurring between these variables and social life that was affected by the group effect of increased walker participation mentioned earlier.
For the data collected, one could consider several possible alternatives to the analysis presented above. A static cross-sectional analysis would have the benefit of easy interpretation but would most likely miss key temporal trends. Alternatively, a standard longitudinal analysis may over or underestimate parameters if latent effects truly modify the causal relationship. Our simulation results demonstrated that it is possible to estimate with reasonable accuracy the latent effects (ω, η) and further that when latent effects exist failing to account for them will result in biased estimates (results not shown). However, the simulations are limited in that they have not yet considered whether the translation of individual level covariate data at sparsely measured time points to a much larger set of outcome measures (i.e. over assessment time points walks translated to the scale of daily walking data) will underestimate the variance. In addition, because of sparse predictive data, informative distributional assumptions were made. While the simulations did test the sensitivity of these assumptions, the scope of the assessment was by no means exhaustive and it is likely the case that additional information would lead to better estimates of latent parameters (e.g. the use of weather data in addition to dropout to predict the daily latent ability component). In the real data analysis, the magnitude of the latent effects reflect the fact that at the population level the PATH participants had significant barriers to participation initiation and further that the intervention was not able to successfully motivate the community to walk. However, as demonstrated by the measured covariates that are significantly related to willingness, there are several factors at an individual level that motivated participants to walk. This is reflected by the fact that, within the study participants, individuals tended to either never walk or consistently walk (in some cases twice a day). Furthermore, these significant factors may be key components to target in future interventions. In this analysis we restricted our attention to variables that were mainly measured at a fixed time for individuals. An important aspect to consider would be the dynamic community level variables such as the interplay of participation in walking and distance (both spatially and temporally) from reported crimes. As crime could occur at different locations and at different times, if the spatio-temporal dynamic of crime were recorded then the walking behavior might be influenced by this variation. In summary, this is one of the first studies to evaluate the effect of a variety of socio-psychological and spatial neighborhood predictors on the propensity to walk and the estimation of latent ability and willingness in the full study. This approach provides a guideline for future longitudinal studies that address health disparities.
Acknowledgments
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the NIH funded PATH intervention study: R01DK067615-04: Improving Safety and Access for Physical Activity.
Footnotes
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Committee PAGA. Physical activities guidelines advisory committee report. Washington, DC: Department of Health and Human Services; 2008. [Google Scholar]
- 2.Carlson SA, Fulton JE, Schoenborn CA, et al. Trend and prevalence estimates based on the 2008 physical activity guidelines for Americans. Am J Prev Med. 2010;39:305–313. doi: 10.1016/j.amepre.2010.06.006. [DOI] [PubMed] [Google Scholar]
- 3.Hawkins MS, Storti KL, Richardson CR, et al. Objectively measured physical activity of USA adults by sex, age, and racial/ethnic groups: A cross-sectional study. Int J Behav Nutr Phys Act. 2009;6:31. doi: 10.1186/1479-5868-6-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ogden CL, Carrol MD. Prevalence of overweight, obesity, and extreme obesity among adults: United States, trends 1976–1980 through 2007–2008. Hyattsville, MD: NCHS Health E-Stat; 2010. [Google Scholar]
- 5.Bronfenbrenner U. Making human beings human: Bioecological perspectives on human development. Thousand Oaks, CA: Sage; 2005. [Google Scholar]
- 6.Griffin SF, Wilson DK, Wilcox S, et al. Physical activity influences in a disadvantaged African American community and the communities’ proposed solutions. Health Promot Pract. 2008;9:180–190. doi: 10.1177/1524839906296011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wilson DK, Trumpeter NN, St George SM, et al. An overview of the “Positive Action for Today’s Health” (PATH) trial for increasing walking in low income, ethnic minority communities. Contemp Clin Trials. 2010;31:624–633. doi: 10.1016/j.cct.2010.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Coulon SM, Wilson DK, Griffin S, et al. Formative process evaluation for implementing a social marketing intervention to increase walking among African Americans in the Positive Action for Today’s Health trial. Am J Public Health. 2012;102:2315–2321. doi: 10.2105/AJPH.2012.300758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wilson DK, Ellerbe C, Lawson AB, et al. Imputational modeling of spatial context and social environmental predictors of walking in an underserved community: the PATH trial. Spat Spatiotemporal Epidemiol. 2013;4:15–23. doi: 10.1016/j.sste.2012.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Daniels M, Hogan J. Missing data in longitudinal studies: Strategies for Bayesian modeling and sensitivity analysis. New York: Chapman & Hall/CRC; 2008. [Google Scholar]
- 11.Guo X, Carlin B. Separate and joint modeling of longitudinal and event time data using standard computer packages. Am Stat. 2004;58:1–9. [Google Scholar]
- 12.Hu W, Li G, Li N. A Bayesian apporach to joint analysis of longitudinal measurments and competing risks failure time data. Stat Med. 2009;28:1601–1619. doi: 10.1002/sim.3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hearst MO, Patnode CD, Sirard JR, et al. Multilevel predictors of adolescent physical activity: a longitudinal analysis. Int J Behav Nutr Phys Act. 2012;9:8. doi: 10.1186/1479-5868-9-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wall MM, Li R. Multiple indicator hidden Markov model with an application to medical utilization data. Stat Med. 2009;28:293–310. doi: 10.1002/sim.3463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thompson B, Coronado G, Snipes SA, et al. Methodologic advances and ongoing challenges in designing community-based health promotion programs. Annu Rev Public Health. 2003;24:315–340. doi: 10.1146/annurev.publhealth.24.100901.140819. [DOI] [PubMed] [Google Scholar]
- 16.Minkler M. Community-based research partnerships: Challenges and opportunities. J Urban Health: Bull NY Acad Med. 2003;82:ii3–ii12. doi: 10.1093/jurban/jti034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Campbell M, Fitzpatrick R, Haines A, et al. Framework for design and evaluation of complex interventions to improve health. BMJ. 2000;321:694–696. doi: 10.1136/bmj.321.7262.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Morse EV, Simon PM, Besch CL, et al. Issues of recruitment, retention, and compliance in community-based clinical trials with traditionally underserved populations. Appl Nurs Res. 1995;8:8–14. doi: 10.1016/s0897-1897(95)80240-1. [DOI] [PubMed] [Google Scholar]
- 19.Gorelick PB, Harris Y, Burnett B, et al. The recruitment triangle: Reasons why African Americans enroll, refuse to enroll, or voluntarily withdraw from a clinical trial. J Nat Med Assoc. 1998;90:141–145. [PMC free article] [PubMed] [Google Scholar]
- 20.Dancy BL, Wilbur J, Talashek M, et al. Community-based research: Barriers to recruitment of African Americans. Nurs Outlook. 2004;52:234–240. doi: 10.1016/j.outlook.2004.04.012. [DOI] [PubMed] [Google Scholar]
- 21.DeSantis SM, Bandyopadhyay D. Hidden Markov models for zero-inflated Poisson counts with an application to substance use. Stat Med. 2011;30:1678–1694. doi: 10.1002/sim.4207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hahn M, Sass J. Parameter estimation in continuous time Markov switching models: A semi-continuous Markov chain Monte Carlo approach. Bayes Anal. 2009;4:63–84. [Google Scholar]
- 23.Huang W, Zeger SL, Anthony JC, et al. Latent variable model for joint analysis of multiple repeated measures and bivariate event times. J Am Stat Assoc. 2001;96:906–914. [Google Scholar]
- 24.Lin H, McCulloch CE, Rosenheck RA. Latent pattern mixture models for informative intermittent missing data in longitudinal studies. Biometrics. 2004;60:295–305. doi: 10.1111/j.0006-341X.2004.00173.x. [DOI] [PubMed] [Google Scholar]