Studying multiprotein complexes by multisignal sedimentation velocity analytical ultracentrifugation

Abstract

Protein interactions can promote the reversible assembly of multiprotein complexes, which have been identified as critical elements in many regulatory processes in cells. The biophysical characterization of assembly products, their number and stoichiometry, and the dynamics of their interactions in solution can be very difficult. A classical first-principle approach for the study of purified proteins and their interactions is sedimentation velocity analytical ultracentrifugation. This approach allows one to distinguish different protein complexes based on their migration in the centrifugal field without isolating reversibly formed complexes from the individual components. An important existing limitation for systems with multiple components and assembly products is the identification of the species associated with the observed sedimentation rates. We developed a computational approach for integrating multiple optical signals into the sedimentation coefficient distribution analysis of components, which combines the size-dependent hydrodynamic separation with discrimination of the extinction properties of the sedimenting species. This approach allows one to deduce the stoichiometry and to assign the identity of the assembly products without prior assumptions of the number of species and the nature of their interaction. Although chromophoric labels may be used to enhance the spectral resolution, we demonstrate the ability to work label-free for three-component protein mixtures. We observed that the spectral discrimination can synergistically enhance the hydrodynamic resolution. This method can take advantage of differences in the absorbance spectra of interacting solution components, for example, for the study of protein–protein, protein–nucleic acid or protein–small molecule interactions, and can determine the size, hydrodynamic shape, and stoichiometry of multiple complexes in solution.

The reversible formation of multiprotein complexes is ubiquitous, frequently leading to very large functional assemblies that control many cellular processes. Well known examples include immunological receptor–ligand interactions (1–4), the cardiac ryanodine receptor complex (5), signal transduction complexes (6–9), transcription regulation complexes (10), and replication machinery (11, 12). Significant biophysical insight has been gained, for example, by imaging techniques and mass spectroscopy. To fully understand the interactions of the building blocks of protein complexes, the role of intermediates, and the dynamics of the assembly processes of such complexes, it is of interest to study their formation from purified components in solution. Experimentally, such studies can be very difficult because, in many cases, mixed interactions of self-associating components and complexes of more than two proteins in multiple conformations are involved, confering cooperative interactions with high dynamic complexity. For example, the detailed understanding of signal transduction requires understanding of the multiprotein complexes that form close to the cell membrane as a result of ligand binding to cell-surface receptors, and it has been established that the energetics, kinetics, allosteric interactions, and multivalent interactions of the multiprotein complexes can be critical for signal transduction (9). In many systems, even deceptively simple questions, such as the stoichiometry of the complexes formed by only two protein components, can be very difficult to address, although they are often key observations for understanding protein function, such as the influence of expression levels on the dynamics of the assembly (6).

Sedimentation velocity has historically played a central role in measuring protein sizes and shapes (13, 14). It is based on first principles, and, because in the last decade the underlying differential equations have become tractable in routine analyses, it has reemerged as a powerful tool for protein interactions and the study of the size distribution of protein complexes (15–18). In the analysis of protein interactions, when a high gravitational force is applied to an initially uniform mixture of proteins, the reversibly formed complexes sediment in a bath of the slower sedimenting components. Under suitable conditions, this process allows transient complexes to persist or reassociate during the sedimentation process. A drawback of sedimentation velocity has been that the observed sedimentation coefficient of a macromolecular species only indirectly allows conclusions about its size, shape, and, for heterogeneous protein mixtures, its composition and stoichiometry. In the present paper, we propose the use of spectral information to overcome this limitation for multicomponent mixtures.

The pioneering work of Schachman and colleagues (19, 20) in the development of an absorbance optical system for the analytical ultracentrifuge made possible the selective detection of macromolecular components, which has proven to be extremely useful in the study of proteins and protein interactions. In 1966, Steinberg and Schachman (21) developed the simultaneous detection of absorbance and refractive index profiles for the analysis of protein–small molecule interactions in terms of constituent effective molecular weights and constituent sedimentation coefficients. In the last decades, global least-squares modeling of sedimentation equilibrium profiles observed at multiple characteristic wavelengths or optical signals was used for the study of protein–protein interactions. It is well known that this global multiwavelength analysis substantially increases the potential to distinguish different protein complexes (22–28). Unfortunately, size-dependent separation in sedimentation equilibrium is very limited because of the difficulties unraveling the Boltzmann exponentials of sedimentation equilibrium. In contrast, the resolution of the size-dependent migration of sedimentation boundaries in sedimentation velocity is far superior. It can be envisioned that exploiting the additional data dimensions provided by multiwavelength or multisignal detection should permit the hydrodynamic separation of protein complexes and simultaneously the identification of their composition through spectral discrimination of the components. This approach would have the potential to facilitate the first and frequently most important step in the characterization of many protein interactions: to unravel the stoichiometry of the different complexes formed. Furthermore, if the stoichiometry of a sedimenting protein complex can be determined from the spectral signature, the molar mass can be calculated, and sedimentation coefficients directly report on the translational frictional coefficient, which provides low-resolution shape information.

In the present work, we explored this potential and monitored the evolution of the macromolecular concentration profiles during sedimentation simultaneously by UV/visible spectrum absorption and refractive index-sensitive laser interferometry optics. We developed a computational approach to integrate these signals into a multicomponent sedimentation coefficient distribution, which utilizes the previously introduced technique for deconvoluting the effects of diffusion during sedimentation to increase the hydrodynamic resolution. As test systems, we studied the label-free sedimentation of binary and ternary protein mixtures.

Materials and Methods

Experimental. Sedimentation velocity experiments were conducted with an Optima XLI (Beckman Coulter) using an An50 Ti eight-hole rotor and with seven 400-μl samples in standard double-sector Epon centerpieces equipped with sapphire windows. (Satisfactory results were also achieved with quartz windows.) Interference and absorbance data were acquired simultaneously with the absorbance scanner in the continuous mode without averaging and with radial increments of 0.003 cm. For the acquisition of multiple absorption signals, characteristic wavelengths were chosen by avoiding steep slopes of the extinction profiles of any component because of limited monochromator accuracy and bandwidth. With this precaution, the wavelength control was sufficiently accurate for the analysis described. Wavelength accuracy was also found not to be problematic when a single absorption signal was combined with interference optical data acquisition. To accommodate possible imperfections in the radial calibration of the absorbance and the interference detection system, the menisci positions in the different data sets were treated as independent parameters optimized in the fit.

IgG, rabbit muscle aldolase, and BSA were taken from gel filtration standard kits (catalog no. 17-0442-01, Amersham Pharmacia). Hen egg lysozyme (HEL) was purchased from Worthington, and D1.3 antibody was prepared as described in ref. 29. A DNA fragment encoding the SH3 domains of phospholipase Cγ1 (790–851) (PLCγ1) was cloned in the vector pGEX-4T-1(+) (Novagen) and expressed in Escherichia coli BL21-CodonPlus(DE3)-RIL cells (Stratagene). The GST–PLCγ1–SH3 fusion protein was purified by using a GSTrap FF column (Amersham Pharmacia), digested with thrombin protease (Amersham Pharmacia), and further purified by gel filtration and anion exchange chromatography. The proline-rich region of SH2-domain-containing leukocyte protein 76 (SLP-76) (158–244) was cloned in the vector pET 28a and expressed in E. coli BL21 cells. His-tagged SLP-76 protein was purified from a soluble fraction with a HisTrap HP column (Amersham Pharmacia) followed by gel filtration and anion exchange chromatography.

Multicomponent Sedimentation Coefficient Distributions. The evolution of the signals, a_λ(r, t), from observing the macromolecular concentration distributions after applying a centrifugal field is modeled as a superposition of sedimentation coefficient distributions, c_k(s), of the different macromolecular components:

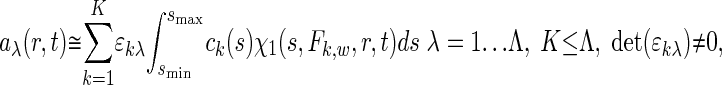[1]

with each component k contributing in a characteristic way to the signal λ according to a predetermined extinction coefficient (or molar signal increment) matrix, ε_kλ. It is assumed that the signal increments are constant, implying the absence of hyper- and hypochromicity, which can be independently verified in a spectrophotometer. (Small relative changes may be tolerable if they are small compared with the difference of the extinction coefficients of the components.) The number of signals, Λ, in current commercial instrumentation is up to four, which in theory could be used to distinguish the same number of spectrally different protein components, K. In Eq. 1, each component is represented as the distribution of noninteracting species χ₁ with different sedimentation coefficients, s, with their respective evolution described by the Lamm equation (30, 31):

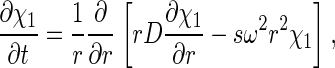[2]

where r is the distance from the center of rotation and ω is the rotor angular velocity. For each species, the diffusion coefficient, D, is calculated based on a signal-average frictional ratio, F_k,w,of all species containing component k according to the hydrodynamic scaling relationship

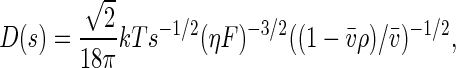[3]

where η and ρ are the solvent viscosity and density, respectively, and v̄ is the partial-specific volume of the macromolecules. This model represents a multidimensional extension of the previously introduced sedimentation coefficient distributions c(s) (32), which exploits the fact that the frictional ratio is not a strongly shape-dependent quantity to increase the hydrodynamic resolution. The best-fit weight-average frictional ratio, F_k,w, was determined by nonlinear regression (33). Results obtained were found to be similarly robust against the choice of F_k,w as described for c(s) in ref. 33.Eq. 1 was combined with Tikhonov–Phillips regularization (34), which resulted in the most parsimonious distribution that fitted the data with a quality statistically indistinguishable from the overall best fit. Eq. 1 was also combined with an algebraic elimination of the characteristic systematic noise components (35).

The global multisignal analysis provides the opportunity for a refinement by using more prior knowledge and/or the testing of specific models of interactions. If the complex sediments at a sufficiently higher rate than the free protein species, we can subdivide the s values into the ranges of free species and faster-sedimenting complexes. This approach can be combined with initial information on the composition of the complexes from inspection of the magnitude of the initial molar c_k(s) distribution. In a refined analysis, a constraint can be introduced by expressing the signal increments ε_κλ for complexes k as the stoichiometric combination of the signal increments of the protein subunits. If 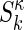reflects the number of subunits k in the complex κ, the signal increments of the complexes can be written as 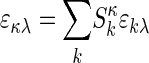, leading to the new model

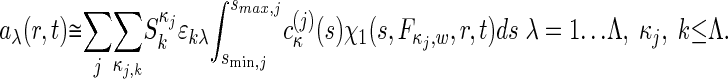[4]

Here, in each segment of the range of sedimentation coefficients, [s_min,j, s_max,j], different complexes can be described, with 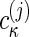now reflecting molar sedimentation coefficient distributions of the complex species with the spectral composition S^κj. Because of the nonnegativity of 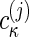, the switch from the set of spectral components ε_κλ to a new set 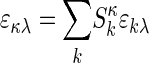can be a powerful constraint. For example, in this way, one can enforce that only complexes with stoichiometry of at least 1:1 may be present at higher s values.

A second possible refinement is the departure from the assumption of a strictly continuous range of s values. If peak regions in the initial continuous 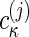distribution can be identified as a particular protein species or protein complex, this peak region can be eliminated and replaced by a discrete species (i.e., Dirac δ functions) with a corresponding molar mass, M (which may be known or treated as unknown parameter) (36). This approach allows an improvement over the approximation of the hydrodynamic scaling law (Eq. 3) by calculating the corresponding diffusion coefficient according to the Svedberg equation (13).

All computational methods, including Lamm equation solutions incorporating reaction terms and the global analysis of isotherms of signal-average sedimentation coefficients, were implemented for global modeling of ultracentrifugation data in the software sedphat (37), which is available from the authors upon request.

Results

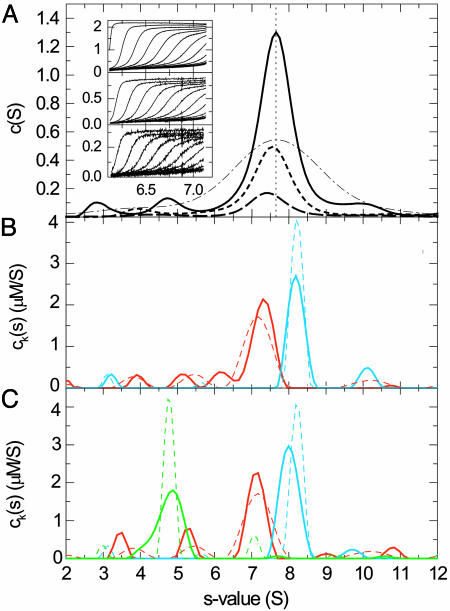
In preliminary experiments, we verified that for solutions of single-protein components, the sedimentation data acquired simultaneously by absorbance and interferometric refractive index optical systems could be modeled well with a single component sedimentation coefficient distribution c_k(s). This step also allowed the determination of the different signal increments ε_κλ of each component at each signal, which were consistent with the amino acid composition and the known spectral properties of the proteins. To test the potential of the spectral decomposition, we sedimented a mixture of two proteins (aldolase and IgG) with slightly different sedimentation coefficients, which generated a single broad sedimentation boundary, and acquired interference optical and absorbance optical data at two wavelengths (Fig. 1A Inset). Conventional c(s) analyses of each of the signals produced a single, relatively broad peak, with different heights according to the different signal intensity (Fig. 1 A). Observation of only a small shift in the peak position indicated the presence of different species that migrate at slightly different rates and contribute differently to each of the signals. In contrast, the global multisignal analysis of the mixture clearly reveals two well separated peaks correctly representing each protein component (Fig. 1B). The sedimentation coefficient distributions compare very well with those obtained from studying the individual protein samples (Fig. 1B, dotted traces). (It should be noted that the width of the distribution is governed by the regularization and the noise in the data acquisition and that the area under the peaks, not the peak heights, corresponds to the species concentrations.) This result demonstrates that the spectral decomposition can significantly enhance the hydrodynamic resolution.

Fig. 1.

Sedimentation coefficient distributions derived from sedimentation velocity profiles of a mixture of IgG and aldolase. (A Inset) The raw sedimentation signals acquired at different time points with interference (Top), absorbance at 280 nm (Middle), and absorbance at 250 nm (Bottom) at a rotor speed of 48,000 rpm at 26°C, with the signal profiles shown in units of fringes, OD₂₈₀, and OD₂₅₀, respectively, as a function of radius in centimeters. (A) c(s) distributions calculated separately for the refractive index data (solid trace), the absorbance at 280 nm (dotted trace), and the absorbance at 250 nm (dashed trace). For comparison, the apparent sedimentation coefficient distribution ls-g^*(s) (45) without diffusional deconvolution applied to the interference data set is shown (dashed-dotted trace). To facilitate comparison of the peak positions, the vertical dotted line indicates the peak of the c(s) distribution from the interference data. (B) Global multiwavelength analysis and decomposition into the component sedimentation coefficient distributions, c_k(s), for the IgG sample (red trace) and the aldolase (blue trace). The extinction coefficients for these two components at the three signals were predetermined from separate experiments with IgG and aldolase alone, which resulted in the sedimentation coefficient distributions indicated by the dotted traces. (C) Calculated component sedimentation coefficient distributions from a mixture (solid traces) of IgG (red trace), aldolase (blue trace), and BSA (green trace, 5-fold reduced scale) and comparison with the distributions obtained from the individual proteins (dotted traces).

Next, we tested whether the acquisition of three signal types can be used to distinguish three proteins on the basis of different fractions of tryptophan and tyrosine residues alone. In preliminary experiments, we found that the proteins IgG, BSA, and aldolase exhibit linearly independent and, therefore, in principle, distinguishable signal contributions with refractive index and 280- and 250-nm UV detection. Fig. 1C shows the results of the global multisignal c_k(s) analysis of the mixture. Clearly, the protein identity could be properly assigned to the different sedimenting species while the enhanced hydrodynamic resolution was maintained. Compared with the distributions from the separate experiments, slight differences in the aldolase peak position at 8S and the lack of the BSA dimer appears to indicate some correlation of the signals within the noise of the data acquisition or a limited precision of the predetermined extinction properties.

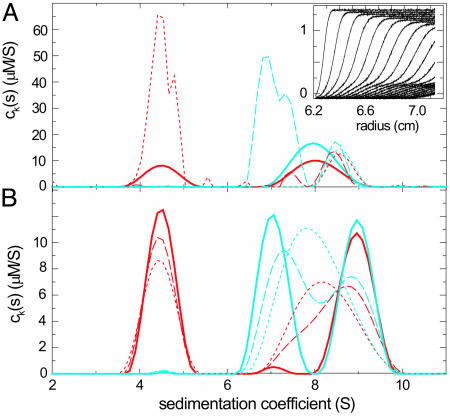
So far, we have examined mixtures of stable protein components. An important question is how chemical conversion of species on the time scale of sedimentation affects the results of the multisignal c_k(s) analysis. As predicted by Gilbert, the sedimentation boundary of systems with fast reactions can be broadened and can exhibit shapes not described by Eqs. 1 and 2 (38). Modeling such a boundary as a distribution of noninteracting species c(s) results in peaks at positions intermediate of the free and complex species, characteristic for the sedimenting system (37) (J. Dam, C.A.V., R.A.M., C. Urbanke, and P.S., unpublished data). For the multisignal c_k(s) analysis, we addressed this question by using computer simulations of a reacting system with different kinetic rate constants. The most difficult situation was observed for fast reactions at equimolar concentrations of ≈K_d or lower (Fig. 2A, solid trace). In the limit of an instantaneous reaction forming a 1:1 complex, the reaction boundary of the faster component and the complex did not hydrodynamically separate (Fig. 2 A Inset). In this case, the multisignal analysis c_k(s) was found to detect the presence of the smaller component (Fig. 2, red traces) in a larger complex and thereby qualitatively show complex formation, but the apparent s value and the apparent stoichiometry reflected that of the reaction boundary of the system. However, this problem is significantly reduced when at least one component can be used at concentrations several-fold >K_d. As illustrated in Fig. 2 A, a 5-fold molar excess of either one component led to coinciding peaks in both component c_k(s) (Fig. 2 A, dashed and dotted traces). Because the molar excess is not high enough to prevent partial dissociation of the complex during the sedimentation experiment, the peaks did not report the true sedimentation coefficient of the complex. However, they did reflect the correct stoichiometry of the complex. The situation was improved at slower reaction kinetics (see Fig. 2B): In the worst-case scenario of equimolar concentrations, at dissociation rate constants of smaller than ≈10^-4 per sec, the reactants could be hydrodynamically separated from the complex and the correct stoichiometry was obtained from the relative peak areas in the component c_k(s) distributions (Fig. 2B, dashed traces). At rate constants of 10^-5 per sec or slower (Fig. 2B, solid traces), the separation was essentially complete, and we obtained baseline-resolved peaks with the correct area and position. These results indicate that the spectral decomposition of the sedimenting components cannot overcome a lack of a hydrodynamic separation of the species for rapidly reversible systems that exhibit a reaction boundary. However, in such cases, a series of experiments at different loading concentrations and molar ratios should allow the identification of conditions that maintain a significant population of the complex throughout the experiment and permit its spectral characterization.

Fig. 2.

Simulated sedimentation of two proteins, one with 50 kDa and 4.5 S (A) and the other with 100 kDa and 7 S (B), which formed a reversible 9 S complex sedimenting at a rotor speed of 50,000 rpm. Two signals were generated by assuming molar extinction coefficients of 50,000 and 30,000 for the 50-kDa protein and 100,000 and 30,000 for the 100-kDa protein, and Gaussian noise with a rms magnitude of 0.005 was added. Component sedimentation coefficient distributions, c_k(s), were calculated from multisignal analysis for components A (red traces) and B (blue traces). (A) The effect of concentration for an instantaneous reaction equimolar at 2× K_d (solid traces), with a 5-fold molar excess of component A over component B (dotted traces), and with a 5-fold molar excess of component B over component A (dashed traces). (In both cases, the concentrations were K_d and 5× K_d, respectively). (A Inset) The second signal for the limit of an instantaneous reaction at equimolar concentration (only every second profile shown). (B) The effect of finite dissociation rate constants, log₁₀(k_off) = -3.5 (dotted traces), -4 (dashed traces), and -5 (solid traces) under the conditions of equimolar concentrations.

The practical application of the multisignal analysis to interacting proteins was tested with two model systems of known complex stoichiometry. As an example for 1:1 reaction, we studied the sedimentation of two peptides derived from adaptor protein SLP-76 and the enzyme PLCγ1, which play essential roles in signal transduction after T cell activation (39). Peptides comprising the SH3 domain of PLCγ1 and the complementary proline-rich region of SLP-76 can be expected to form a 1:1 complex, which was verified by isothermal titration calorimetry (data not shown). Accordingly, the component distributions c_k(s) revealed a complex peak at ≈1.1 S comprised of equimolar PLCγ1 and SLP-76 (Fig. 3C). It could also be seen that PLCγ1 was in molar excess in the mixture, and, from the absence of free SLP-76, it could be concluded that the concentration of PLCγ1 is significantly >K_d. Under these conditions, it was a good approximation to apply a refined analysis in which free PLCγ1 was modeled as an independently sedimenting species, and species sedimenting faster than the free species are constrained to have spectra of complexes with stoichiometries of 1:1 or higher (Fig. 3D).

Fig. 3.

Analysis of the interaction of peptides derived from the adaptor protein SLP-76 and PLCγ1. SLP-76 contains only one tyrosine and no tryptophan residues, allowing its spectral discrimination from PLCγ1. (A and B) Absorbance and interference optical signal distributions of a mixture of SLP-76 and PLCγ2 at time intervals of 2,500 sec at a rotor speed of 59,000 rpm and a temperature of 4°C, with systematic noise subtracted. The residuals are from the fit with the hybrid discrete/continuous model shown in D (see below). (C) Data in the same configuration as shown in A and B were collected for SLP-76 and PLCγ1 separately (data not shown), which led to the component distributions shown as a blue dashed trace for PLCγ1 (molar extinction coefficient, 20,060 OD₂₈₀/Mcm; F_k,w = 1.5) and a green dotted trace for SLP-76 (molar extinction coefficient, 2,550 OD₂₈₀/Mcm; F_k,w = 2.3). Alternatively, the data of SLP-76 and PLCγ1 alone could be modeled well as discrete sedimenting species with 0.6 and 0.75 S, respectively. Shown is an analysis of the mixture with component sedimentation coefficient distributions for SLP-76 (green solid trace) and PLCγ1 (blue solid trace), with a uniform frictional ratio of F_k,w = 2.0. (D) Analysis with subdivision of the s values in three ranges: (i) the buffer components at <0.4 S; (ii) the discrete free peptides with their predetermined extinction properties, molar masses, and predetermined s values of 0.6 and 0.75 S; and (iii) the continuous distribution of complexes >0.8 S, which can be constrained in their spectral properties to reflect stoichiometries of 1:1 (red trace) or 2:1 (blue trace). The interference optical data contain contributions from the sedimentation of a small buffer component (likely predominantly optically unmatched NaCl), which can be modeled well as discrete species at 0.08 and 0.3 S (black crosses with dropped lines). All units for s values are S at experimental conditions, the concentration of discrete species are in μM, and the c_k(s) distributions are in μM/S.

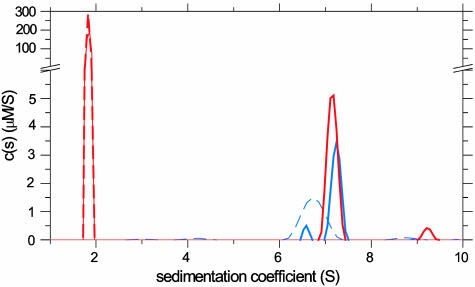
A natural test for the correct identification of protein–protein complexes with higher stoichiometries is the analysis of an antibody–antigen interaction. We examined the interaction of HEL and the monoclonal antibody D1.3 (40) (Fig. 4). Although the weight-based extinction coefficient of the proteins differs by 46%, because HEL is much smaller than the antibody, the difference of the extinction between a 2:1 complex and the free D1.3 was only 11%. Nevertheless, in the mixture HEL was clearly detected in a peak sedimenting at a slightly higher rate than the free D1.3. The areas under the peaks (1.5 μM HEL and 0.84 μM D1.3) showed the interaction to be a 2:1 complex. The same concentrations were used in the mixture and in the separate experiments, and, consistent with this design, the total concentration of IgG detected in the separate and mixed experiment was 0.90 μM and 0.92 μM, respectively. That the IgG concentrations obtained in the two experiments were similar may serve as an internal control that the spectral decomposition was successful. Some unreacted IgG was also observed, consistent with possible IgG contaminations in this D1.3 preparation. However, the spectral decomposition of the IgG dimer fraction at ≈9 S was not completely successful, which likely represents the current limitation in the details of the analysis that can be obtained with the given signal-to-noise ratio of the data. The ability to resolve the complex stoichiometry was also confirmed in a second study of an antibody–antigen interaction: the complex between a FITC-labeled IgG specific against vitronectin (data not shown).

Fig. 4.

Sedimentation velocity analysis of HEL binding to the D1.3 antibody (29) at 50,000 rpm, scanned by absorbance at 280 nm, and by refractive index detection. Shown are c_k(s) from the mixture (solid traces) and from separate experiments (dashed traces) for both HEL (red traces) and D1.3 (blue traces).

Discussion

Analytical ultracentrifugation is a classical technique of physical biochemistry, but it is still rapidly developing and regaining popularity, in particular, for the study of protein interactions in solution. Key features of this technique, including experiments covering a large concentration range at once and the characterization of protein complexes without their removal from the bath of building blocks, make it a highly useful tool for the study of high- and low-affinity interactions as well as self-association and heteroassociation processes. In the present work, we have exploited the fact that the hydrodynamic separation of protein complexes in sedimentation velocity can be combined with another dimension of separation based on absorbance spectral properties of the sedimenting species, an approach pioneered by Steinberg and Schachman (21).

The spectral discrimination should be useful, for example, for the study of protein–protein interactions, protein–nucleic acid interactions, or protein–small molecule interactions. Our results demonstrate that different weight fractions of aromatic amino acids can suffice for the discrimination of three protein components. The observed spectral resolution appears to far exceed that of sedimentation equilibrium, most likely because of the significantly larger data basis and the ability to better identify the systematic noise contributions (28) and it can be further improved, for example, by attaching chromophoric labels. One could be concerned that the time necessary to acquire multiple signals might lead to a loss of hydrodynamic information. However, in practice, loss of hydrodynamic information does not occur because the different signals report on the concentration distribution at different points in time and, therefore, in combination, report on the time-dependent migration in a similar way as one absorbance signal acquired at a single wavelength.

To fully exploit the hydrodynamic separation, the present approach was based on the technique of directly modeling the sedimentation boundary with finite element solutions of the Lamm equation, c(s), which deconvolutes effects of diffusion from the sedimentation profiles. During the past few years, the c(s) method has found many applications to the study of protein self-association and protein–protein interactions, demonstrating high resolution and sensitivity (for examples, see www.analyticalultracentrifugation.com/references.htm). In a few applications of protein–small ligand interactions, c(s) sedimentation coefficient distributions were calculated from two characteristic signals simultaneously acquired during sedimentation, and, in a secondary analysis, the signals were related to each other to obtain information on the stoichiometry of the complex (41, 42). Although this approach is only applicable in special cases and in many ways does not exploit the full potential of multisignal analysis, it clearly shows the rich information that can be gained from combining hydrodynamic and spectral resolution.

Like the original c(s) sedimentation coefficient distribution analysis, the new molar component distributions, c_k(s), are most easily applicable to species that are stable on the time scale of the sedimentation experiment, which is intrinsically the case for many high- or medium-affinity protein interactions because of a sufficiently slow dissociation rate constant. For faster reactions, the hydrodynamic separation is limited by chemical interconversion and the sedimentation is characteristic for the whole sedimenting system (38). However, by conducting sedimentation velocity experiments at a range of loading concentrations, conditions can be found for which a significant population of complexes can be maintained throughout the experiment and the model with distributions of noninteracting Lamm equation solutions is a good approximation that permits the spectral analysis and determination of their composition. In this regard, multisignal analysis should not pose difficulties in addition to those occurring in the application of the original c(s) method. It should be noted that the spectral decomposition only requires that a boundary component can be identified that reflects mostly the complexes. This is a much weaker requirement than the ability to correctly describe the hydrodynamic parameters (i.e., the s values) of the complexes, for which a much higher fractional population of the complexes would be necessary (37).

For protein interactions, the multisignal method alleviates a major difficulty in sedimentation velocity, which is the assignment of the sedimenting species to particular complexes. The information obtained on the stoichiometry of protein complexes can permit a more specific characterization of the interaction. For example, a more detailed model of the sedimentation process may be applied that explicitly considers the kinetics of reaction between discrete numbers of species in the Lamm equation (43), and a low-resolution structural model of the complexes might be calculated based on crystal structures of the components (44). However, it is the initial identification of the reaction scheme that is usually the most challenging step. Based on the hydrodynamic separation alone, initial identification can be exceedingly difficult, in particular, for multistage associations and even more for the triple or higher-order protein interactions that are emerging as key regulatory entities in many biological systems. This approach is applicable to systems of interacting proteins forming extended associations, such as the study of ternary mixtures of adaptor proteins in signal transduction complexes (J. C. D. Houtman, H. Yamaguchi, M. Barda-Saad, B. Bowden, E. Apella, P.S., and L. E. Samelson, unpublishd data) and multistage assembly of plasminogen activator inhibitor with vitronectin (K.H.M., C. R. Schar, G. E. Blouse, J. D. Shore, D. A. Lawrence, P.S., and C.B.P., unpublished data). We believe that multisignal sedimentation velocity analysis has the potential to be a valuable tool for the characterization of systems of interacting proteins with multiple coexisting reversible complexes over large size ranges and that it can provide data on assembly processes in free solution that are complementary to the existing structural, microscopic, surface-based, and mass spectroscopic approaches.