Counting the ions surrounding nucleic acids

Abstract

Nucleic acids are strongly negatively charged, and thus electrostatic interactions—screened by ions in solution—play an important role in governing their ability to fold and participate in biomolecular interactions. The negative charge creates a region, known as the ion atmosphere, in which cation and anion concentrations are perturbed from their bulk values. Ion counting experiments quantify the ion atmosphere by measuring the preferential ion interaction coefficient: the net total number of excess ions above, or below, the number expected due to the bulk concentration. The results of such studies provide important constraints on theories, which typically predict the full three-dimensional distribution of the screening cloud. This article reviews the state of nucleic acid ion counting measurements and critically analyzes their ability to test both analytical and simulation-based models.

INTRODUCTION

Double- and single-stranded DNA and RNA are all strongly negatively charged, with sub-nanometer inter-phosphate charge separations. This high charge density means that the free energy of nucleic acid (NA) interactions will be strongly influenced by electrostatics. Under physiological conditions, salt ions in solution mitigate electrostatic effects by screening the potential of the NA, reducing it from a long-range 1/r decay to an exponential decay in the far-field. Because the screening ions are free to move in solution, positive cations will accumulate near the negatively charged NA while negative anions will be repelled from its vicinity; this region of perturbed ion concentration is known as the ion atmosphere (1) and can differ significantly from the bulk concentration (2).

Because of their role in modulating electrostatic effects, a quantitative knowledge of the distribution and energetics of these screening ions is needed to understand NA self-interactions and interactions with other charged species, including the folding of ssRNA into functionally competent three-dimensional structures such as ribozymes (3) or riboswitches (4), the folding of ssDNA into biotechnologically relevant DNA origami assemblies (5) and the binding of single- and double-stranded NAs to proteins such as histones (6), ssDNA binding proteins (7) and polymerases (8,9). Beyond their biological significance, NAs are of interest to polymer physicists as models of strong polyelectrolytes (10).

We begin this article by defining the parameters used to quantify the NA ion atmosphere and discussing the methods used to experimentally measure these parameters. We then briefly review theoretical models of the ion atmosphere before surveying the existing experimental results. We will critically analyze the extent to which the experimental findings can be used to constrain the theoretical models. Throughout, we will focus on ions diffusely associated with simple single- and double-stranded structures; binding of ions to specific structural sites (11) and interaction of ions with more complicated structures (e.g., tertiary structure of folded RNAs) (12,13) are beyond the scope of this article. In addition to this Survey and Summary, which highlights recent advances and emphasizes a quantitative comparison between experiment and theory, the reader may also be interested in earlier reviews on the NA ion atmosphere, including those by Lipfert et al. (1) and Record et al. (14).

QUANTIFYING THE ION ATMOSPHERE

Three-dimensional distribution

The ion atmosphere distribution of an NA can be fully described, under given conditions, by specifying the local concentration of each ion species as a function of position. Such distributions are often the output of theoretical models of the ion atmosphere, which also make further predictions about the energetics of NA-ion interactions. An experimentally measured spatial distribution would constitute a powerful test of these theories. However, to our knowledge no experimental study has measured the full distribution of the ion atmosphere of any NA. Partial spatial information has been obtained from small-angle X-ray scattering (SAXS) experiments (15). These include anomalous SAXS (16–20), in which data are recorded at several wavelengths near an absorption transition of the ions, and heavy-atom replacement SAXS (21,22), in which the ion identity—and thus scattering cross-section—is varied. Both methods allow the scattering pattern of the ions to be isolated from that of the solvent and the NA. The spatial information in these studies is contained in the q-dependence of the scattering intensity, where q is the scattering wave vector. However, constant signal-to-noise is not seen across all values of q; in particular, robust signal is seen at small q (corresponding to large spatial length scales), whereas poor signal is seen at large q (corresponding to short length scales). This disparity occurs because smaller features in the ion distribution necessarily present smaller scattering cross-sections and means that SAXS, while an extremely powerful technique, is limited in the information it provides about short-range interactions of ions with the NA.

Ion counting

Absent the ability to measure the full distribution of the ion atmosphere across all length scales, knowledge of its composition must be pieced together from other experimental data, including both SAXS and ion counting studies. Ion counting experiments measure how many of each ion species (i.e. cation, anion) are present in the ion atmosphere. These quantities are constrained since, taken together, the NA and its ion atmosphere must be charge neutral. Measurements are typically made as a function of bulk salt concentration, ion identity, and NA structure.

The canonical ion counting experiment is Donnan equilibrium dialysis (23), sketched in its idealized form in Figure 1A. In such an experiment, two compartments—a sample compartment containing an NA solution and a reservoir with a particular bulk salt concentration—are separated by a membrane that is impermeable to the NA under study but permeable to the ions. In the absence of NA, each ion species has the same concentration on both sides of the membrane. When NA is added, electrostatic interactions with the ions lead to a higher cation concentration, and lower anion concentration, in the sample compartment compared with the bulk reservoir. This imbalance contains information about the net ion atmosphere of the NA under study, which is quantified by the preferential ion interaction coefficient, Γ, defined formally by a limiting derivative and read out experimentally as a ratio of concentrations: (24–27)

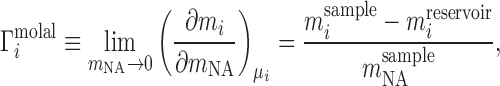(1)

where m_i and m_NA are the molal concentrations of a particular ion species (indexed by i) and of the NA, respectively. The derivative is taken at constant μ_i, the bulk chemical potential of the ion, which takes on a value corresponding to the bulk salt concentration in the experiment. We will often normalize this quantity by the number of phosphates to obtain the per-nucleotide interaction coefficient, 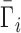; this allows for generalization and comparison of results between NAs of different lengths. Practically, Equation (1) says that, in the dilute NA limit, is equal to the change in the number of ions in the sample compartment with respect to changes in the number of NA molecules. Since it represents the number of ions in the vicinity of the NA in excess of that expected due to the bulk salt concentration alone, Γ is also referred to as the ion excess. Typically, values of the cation excess, Γ₊, will be positive and values of the anion excess, Γ₋, will be negative, as in Figure 1A, which corresponds to a toy experiment with NA charge of −4. 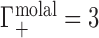In this example, the NA charge is offset by the migration of three cations into, and one anion out of, the sample compartment, meaning that and .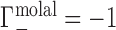

Figure 1.

Depictions of Donnan equilibrium dialysis experiments used to measure the preferential ion interaction coefficient, Γ, under (A) idealized (molal) and (B) practical (molar) conditions. In both cases, an NA-containing solution is equilibrated with a bulk salt reservoir across a membrane permeable to ions but impermeable to the NA. In the toy example illustrated, the NA has −4 charge. This charge is neutralized by electrostatic (ES) interactions: three cations are drawn into the sample compartment (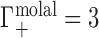) and one anion is displaced into the reservoir (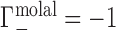). Under practical conditions, excluded volume (EV) displaces equal numbers of cations and anions across the membrane. In this case, one cation and one anion are displaced, leading to 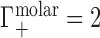and .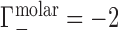

It is not generally possible, in experimental practice, to measure ion concentrations in molal units (i.e., number of ions per solvent volume); rather, molar concentrations, c, are typically reported (i.e., number of ions per solution volume, including the volume occupied by the NA). The molar analog to Equation 1 is written:

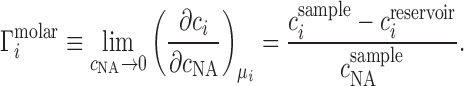(2)

When the NA excluded volume (EV) is non-negligible, 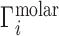exhibits the behavior sketched in Figure 1B, in which the total ion excess is the sum of the electrostatic contribution, 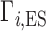, and a contribution from the ions forced across the membrane due to exclusion from the occupied volume of the NA, 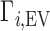. In the example of Figure 1B, the NA charge is again −4 and is again electrostatically neutralized by association of three cations and exclusion of one anion. However, in this case the non-zero EV of the NA also displaces one cation and one additional anion, meaning that 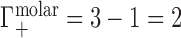and 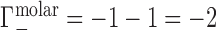. Ignoring end effects, the per-nucleotide EV contribution is not expected to vary with chain length; however, Γ_EV grows linearly with c_bulk. Because Γ_EV obscures the electrostatic effects at high salt concentration, it is often desirable to correct the experimental data into molal units by estimating 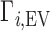and subtracting it from 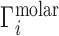(28). This correction preserves the simple interpretation of the ion excess as the number of ions surrounding the NA beyond the number expected due to the bulk concentration and allows for direct comparison with electrostatics-derived theories.

Ion excesses defined in terms of molal and molar units are related differently to the 3D ion distribution, 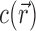. In the molar picture (i.e. including EV effects), 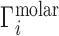is equal to the volume integral of the excess ion concentration above, or below, the bulk concentration, c_bulk: (29,30)

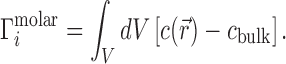(3)

This integration is over the entire volume of the system, V. EV effects are included in this integral because 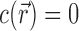within the spatial extent of the NA. In the molal picture, however, EV effects are explicitly excised by restricting the integration to the solvent-accessible volume; i.e., V → V_solvent in Equation (3). These integral relations are important in that they connect the experimental output, Γ, with the typical output of most theories, .

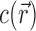THEORETICAL MODELS

We now review theoretical models of the ion atmosphere at several levels of detail and computational sophistication. We first consider simple, analytically tractable theories to predict Γ in the low- and high-salt limits. We then consider numerical theories that give the full ion distribution at all intermediate salt concentrations.

Limiting behavior: Counterion condensation and Debye-Hückel theories

The ion excess in the low-salt limit can be estimated using Oosawa–Manning counterion condensation theory, which holds that ions will tend to condense near to the surface of a cylindrical polyelectrolyte when its linear charge density exceeds a certain threshold (31–34). This theory is formally valid for c_bulk → 0 and holds, approximately, for c_bulk ≲ 10 mM (35). The phenomenon of condensation arises from the competition between the favorable electrostatic enthalpy for ions to bind to the NA and the unfavorable entropy change associated with the loss of their translational freedom in solution. When combined with Poisson-Boltzmann theory (to be further discussed in the next section), this theory gives the following expected low-c_bulk limiting behavior in monovalent salt (31,36):

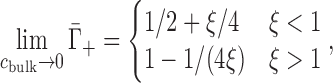(4)

where ξ = l_B/b is the Manning parameter, defined in terms of the charge spacing, b, and the Bjerrum length, l_B = e²/4πε₀εk_BT (e: elementary charge, ε₀: permitivity of free space, ε: dielectric constant, k_BT: thermal energy). The charge spacing of the dsNAs is estimated by projecting the phosphate positions onto the helical axis (dsDNA: 0.17 nm; dsRNA: 0.12 nm) and that of the ssNAs is estimated from the phosphate spacing of a fully elongated chain (ssDNA: 0.7 nm; ssRNA: 0.59 nm) (37). The assumptions underlying Equation (4) render it inappropriate for treating higher valence ions. In these cases, we can instead consider the strong coupling limit (38), in which the entire NA charge is offset by cation association (i.e., complete condensation), leading to 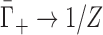, where Z is the ion valence.

In the high-salt limit, charge screening reduces the electrostatic potential to the extent that the full Poisson-Boltzmann equation can be linearized—also known as the Debye-Hückel approximation. This occurs, specifically, when eΦ ≪ k_BT (Φ: electrostatic potential), i.e. above roughly a few molar monovalent salt concentration. When Debye–Hückel holds, there is no preference for cation association versus anion exclusion and the ion excess is predicted to take on the limiting value (39,40)

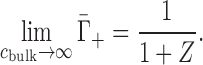(5)

Note that this high-salt limit is derived only on the basis of electrostatics, and is thus a prediction of Γ^molal, not of Γ^molar. This distinction was unimportant for Equation (4), since EV effects are negligible at low c_bulk.

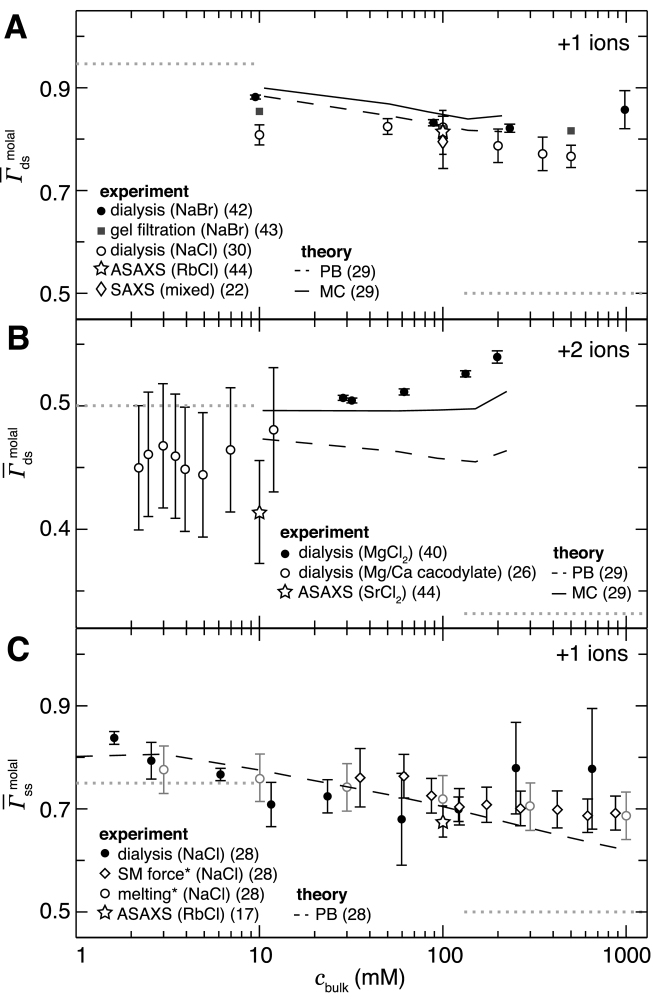
The degree to which the high- and low-salt limiting laws correctly reflect experimental results is assessed in Figure 2, in which experimental data, corrected for excluded volume effects, are compared with the relevant limits, plotted as dotted lines. We see that Equation (4), or 1/Z in the divalent case, reasonably describes the low-salt behavior; some disagreement is expected due to the assumption of cylindrical geometry. The high-salt limit is less successful. Both dsDNA and ssDNA monovalent data (Figure 2A and C) do decrease towards the expected Γ₊ → 1/2 limit, although only weakly. In contrast, the divalent data (Figure 2B) increase with c_bulk, manifestly inconsistent with the Γ₊ → 1/3 limit. This disagreement indicates that the Debye-Hückel approximation does a poor job of describing the NA-ion system, even at high salt concentration. For divalents, this is a well-known result owing to the small size and high valence of the ions (41). For monovalents, the cause of the disagreement is less obvious and may arise from finite size effects: Debye–Hückel theory is formulated for point charges, and does not, for example, consider the finite volume of an ion and its hydration shell.

Figure 2.

Molal cation excesses of dsDNA in (A) NaCl and (B) MgCl₂ and of (C) ssDNA in NaCl, compared with PB theory (dashed line) and the MC simulations of Ni et al. (29) (solid line). Molar literature values (17,22,26,29,30,40,42–44) have been corrected into molal units using the method of (28) to isolate electrostatic effects. Horizontal dotted lines represent the expected limiting behavior at low- and high-salt (Equations 4 and 5); the low-salt limit assumes a cylindrical geometry. The SAXS data of (22) uses the heavy ion replacement method and is not sensitive to differences between monovalent ion species. The divalent data of Ref. (26) are extracted from a mixed Mg^{2 +}/Ca^{2 +} competition experiment. The asterisked ssDNA studies are indirect techniques based on a thermodynamic cycle analysis.

Poisson–Boltzmann theory

More comprehensive—and complicated—theoretical models are needed to achieve quantitative precision and to map out the full salt-dependence and spatial distribution of the ion atmosphere. The first of these is Poisson–Boltzmann (PB) theory, which has at its core the mean-field approximation that the salt ions can be treated not as discrete particles but as a continuous charge density. Under this approximation, is found via a Boltzmann factor relation:

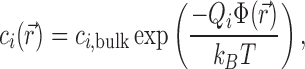(6)

where Q_i is the charge of the ion species in question. 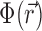is obtained by solving the PB equation, a second-order differential equation that is analytically soluble only in a few special cases (45) and, more generally, can be handled using easy-to-use numerical solvers (46). The PB equation is given by

(7)

where ρ_NA is the charge density of the NA and the summation is over all species of mobile ion in solution. Note that the Debye–Hückel approximation, used to obtain Equation (5), arises from linearizing the exponential in Equation (7).

PB calculations have been used in many studies to model the ion atmosphere of nucleic acids (2,47–54). The level of agreement between such studies and experimental results will be assessed below. In general, PB does a good job of describing the interactions of NAs with monovalent cations (e.g. Figure 2A and C), but breaks down for higher valence ions where strong ion-ion interactions render the mean-field approximation inappropriate (e.g. Figure 2B). Some enhancements to PB results can be obtained by accounting for the sizes of the mobile ions or for dielectric saturation effects (47,50,51). The fundamental mean-field limitation is addressed in the tightly bound ion (TBI) model by treating the higher-valence ions near the NA surface using a cell-binding approach (55–58). While the TBI model does a good job of reproducing experimental free energies of secondary structure formation (56) and ion binding competition curves (57), it does not allow for the full distribution of the ion atmosphere to be obtained.

Simulations

Today the benchmark method for obtaining the full distribution of the ion atmosphere is atomistic molecular dynamics (MD) simulation (59); in the past, grand-canonical Monte Carlo (MC) simulations were preferred (60). These simulations go beyond PB by explicitly accounting for ion-ion interactions (i.e. there is no mean-field approximation) as well as other non-electrostatic effects, such as interplay with the structure of water.

Unfortunately, these improvements come at a practical cost: MD simulations are vastly more computationally intensive when compared with PB, rendering impractical studies that span a wide parameter space or that probe large molecules. For this reason other more efficient models, relying on varying degrees of simplification, have been developed (61–64). Examples of such approaches include classical density functional theory (65) and the 3D reference interaction site model (3D-RISM) (66), which involve either the minimization of a free energy or the evaluation of a simplified Ornstein–Zernike equation, respectively, rather than the time-dependent Newtonian simulation of the system.

MD simulations are also susceptible to vagaries in the choice of force fields, the detailed parameters describing the microscopic molecular interactions. Different force fields have been shown to yield different ion atmosphere distributions (67). The most advanced force fields (68), parameterized against osmotic pressure data, are able to reproduce detailed ion counting results. It does remain, however, to be seen if these empirical calibrations will hold up against new and different types of measurements.

ION COUNTING EXPERIMENTS

An overview of many ion counting experiments in the literature is given in Table 1. While the results of these studies are of interest in their own right, our focus below is on a critical analysis of the degree to which they can validate or constrain the theoretical models. In limiting our discussion to ion counting methods, we leave out other techniques that also bear on understanding the ion atmosphere. Besides SAXS, these include NMR (89), gel electrophoresis (90), conductivity (91) and osmotic pressure (92) measurements.

Table 1. Overview of ion counting experiments in the literature.

	Ion valence
	+1	+2	+3/higher
Γds	Shack et al. (69)	Skerjanc and Strauss (40)	Rubin (70)
	Strauss et al. (42)	Bai et al. (26)	Braunlin et al. (71)
	Shapiro et al. (72)	Pabit et al. (18)	Plum and Bloomfield (73)
	Lindström et al. (43)	Nguyen et al. (19,44)
	Bai et al. (26)
	Pabit et al. (18)
	Kirmizialtin et al. (16)
	Nguyen et al. (19,44)
	Meisburger et al. (22)
	Gebala et al. (30)
	Gebala et al. (74)
Γss	Meisburger et al. (17)	Holland and Geiger (75)
	Jacobson and Saleh (D/R) (28)	Walter et al. (76)
ΔΓds-ss	Record (77)	Record (78)
	Record (78)	Serra et al. (79)
	Bond et al. (D/R) (80)
	Williams and Hall (R) (81)
	Owczarzy et al. (82)
	Stellwagen et al. (83)
	Reiling et al. (84)
ΔΓds-stretch	Dittmore et al. (85)		Todd and Raua (86)
	Jacobson and Saleh (D/R) (28)
ΔΓstretch-ss	Landy et al. (87)
	Jacobson et al. (R) (88)
competition	Bai et al. (26)	Bai et al. (26)	Andresen et al. (20)
	Andresen et al. (20)	Gebala et al. (74)
	Gebala et al. (74)

^a measured ΔΓ between condensed and uncondensed states of dsDNA.

All studies report data on DNA samples unless denoted (R) for RNA samples or (D/R) for both DNA and RNA samples.

Absolute ion atmosphere stoichiometry

Ion atmosphere stoichiometry experiments, like the hypothetical study of Figure 1B, measure the ion excess in molar units, 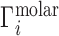, incorporating both electrostatic and excluded volume effects. These experiments are practically realized either as equilibrium dialyses (28,40,42,69) or as forced dialyses across a centrifugal filter (26,30). Concentrations are typically read out by atomic emission spectroscopy (26,73) or, alternatively, by liquid scintillation counting (72); 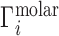is then found by evaluation of Equation (2). The experimental literature describing these measurements of Γ is summarized in rows 1 and 2 of Table 1.

Whereas these experiments measure 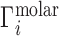, it is actually 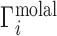that contains the purely electrostatic information that is amenable to direct comparison with electrostatics-derived theories (29). Therefore, in Figure 2, we have taken experimental literature values of 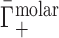for dsDNA and ssDNA in monovalent and divalent salt and applied an excluded volume correction to couch them in terms of 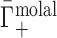. We made this correction, as in (28), by estimating the EV of dsDNA and ssDNA using structural models from the Nucleic Acid Builder package (93) and then subtracting from 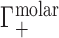the number of bulk ions contained within the NA volume, as a function of c_bulk. While such modeling allows us to expose the underlying electrostatic behavior at high salt, it is critically dependent on the structural model used to compute the EV. This can introduce systematic bias into the reported results, especially in cases where the molecular EV is not constant as a function of experimental conditions. Any such errors will be most pronounced at high salt, where the EV correction is large, and negligible at low salt.

Beyond the data of Figure 2, ion counting experiments have been carried out using a variety of salt species. Comparative studies have shown that the identities of both the cation and anion have an effect on Γ (30). Gebala et al. have recently proposed that the ion excess, especially at high c_bulk, depends strongly on the mean ion activity coefficient, γ_±, of the salt (30).

Theoretical predictions, where available, are co-plotted in Figure 2. Under monovalent salt conditions, for both dsDNA (Figure 2A) and ssDNA (Figure 2C), PB calculations (28,29) do a good job of reproducing the experimental results. This is expected, as the mean-field approximation of PB is most applicable to weakly interacting monovalent ions. Following from the same argument, it is not surprising that the PB agreement breaks down for the divalent data of Figure 2B (29), in which ion–ion interactions are expected to become significant. In fact, in divalent salt Γ₊ increases with the bulk salt concentration, an effect at odds with the expected limiting behavior but further confirmed by studies that have observed strongly favorable Mg^{2 +} binding (94,95). Although the results of both PB and the non-atomistic MC simulations of Ni et al. (29) (ions modeled as atoms, but NA as a cylinder and water as a continuum) do increase at high divalent salt concentrations, only the MC reproduces these data with reasonable accuracy. MC results are shown because we are not aware of a comparable, salt-dependent MD study.

Competition between ions

An extension of the absolute ion stoichiometry experiments discussed above are competition experiments, in which Γ_i values of two different ion species are measured as the relative bulk concentrations of those species are varied. Competition studies can directly probe the subtle effects arising from differences between ion species; these differences can include valence, hydrated radius, ion activity, and degree of dissociation. Many of these effects are expected to become most pronounced in the crowded, high-electrostatic-potential region directly adjacent to the NA. Thus, whereas absolute ion counting reports equally on all excess ions, competition experiments are expected to be most sensitive to the numerically fewer ions close to the NA. A distinct population of such closely associated ions can be seen, for example, in the dsDNA MD results of Giambaşu et al. (52), where two peaks occur in the radial distribution function of the ion atmosphere: one corresponding to tight localization in the major and minor grooves and the other to the bulk of the ion atmosphere.

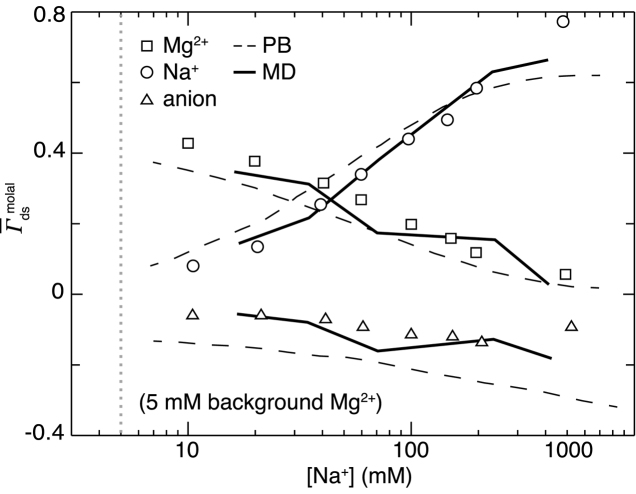
A representative competition experiment is that of Bai et al. (26). Many ion pairs were probed in this study; in Figure 3 we show the results of the Na⁺/Mg^{2 +} competition as an example. Also shown in Figure 3 are the predictions of two theoretical models. One is PB theory (26), which fails to capture the detailed shape of the curves across the full range of salt concentrations, and the other the MD results of Yoo and Aksimentiev (96) (corrected for EV into ), which show generally good agreement, e.g. in their ability to reproduce the crossover between a majority Mg^{2 +} and Na⁺ ion atmosphere composition. The disagreement between MD and experiment likely arises because of anion effects: for technical reasons related to atomic emission spectroscopy, the experimental data were collected with cacodylate as the anion, whereas the simulations were based on Cl⁻. Significant differences in the high-salt behavior of these two anions have been described by Gebala et al. (30). The lack of low-salt (i.e. large Debye length) MD data arises from the technical limitation of that method in simulating systems of large spatial extent. Note that these MD simulations used specially parameterized force fields based on independent osmotic pressure data; standard force fields would not be expected to give results that agree so well with studies including +2 or higher valence ions (68). Notwithstanding this complication, we see here another case in which PB theory breaks down in the presence of divalent ions, but a series of simulations successfully reproduces the ion counting results. The 3D-RISM model has also been tested by competition studies; those experiments were unable to reproduce the cation size dependence predicted by that theory (74).

Figure 3.

Competition experiment measuring Na⁺ and Mg^{2 +} ion excess as Na⁺ is titrated into a background of 5 mM MgCl^{2 +}. Compared are the predictions of PB theory (dashed lines) and the MD simulations of Yoo and Aksimentiev (solid lines). The anion used in the experimental study is cacodylate and in the MD is Cl⁻; this discrepancy likely explains the anomalous behavior at the highest [Na⁺]. The dashed vertical line denotes the condition [Na⁺] = [Mg^{2 +}]. We have EV-corrected the experimental and MD data into molal units. Based upon Figure 7A of (26) and Figure 4C of (96).

Changes with denaturation

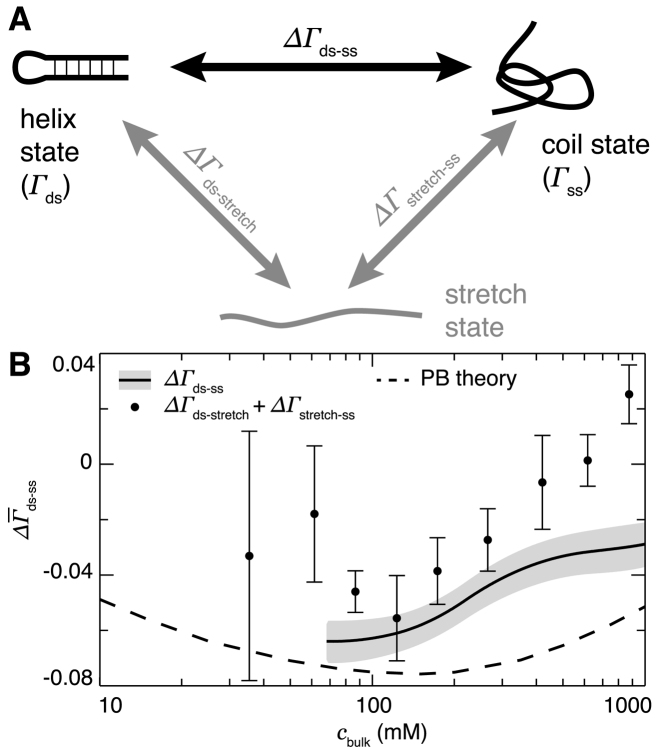
In addition to measuring the total ion excess, Γ_i, it is also possible to directly measure differences in ion excess, ΔΓ_i, between NA conformations. For example, one can measure the change in ion excess when a dsNA is denatured into its single-stranded state, when a dsNA is mechanically unfolded into a stretched, single-stranded state, or when a relaxed ssNA is stretched. The available transitions are summarized in the thermodynamic cycle of Figure 4A, and the existing experimental results are listed in rows 3–5 of Table 1. Like the competition experiments, ΔΓ measurements do not report equally on all atmospheric ions, but are most sensitive to those ions associated with structural or conformational stabilization. Beyond the information provided about the ion atmosphere stoichiometry, these measurements can also be analyzed to obtain the differential free energy of NA stabilization due to ion association (97).

Figure 4.

(A) Thermodynamic cycle of nucleic acid secondary structure formation. Ion counting measurements have been made of all indicated quantities: of both the folded, double-stranded and unfolded, single-stranded species (Γ_ds and Γ_ss, respectively) and of changes in ion atmosphere between the states, denoted ΔΓ_{i, j}. (B) Comparison of ΔΓ_ds-ss measurements of DNA made directly by melting experiments (line) (28,82) and indirectly by single-molecule force spectroscopy (points) (28,85,87) with a PB prediction based on the difference of the dsDNA and ssDNA curves from (28). Adapted from Figure 1 and S7 of (28).

In one differential technique, NA duplex melting temperatures are analyzed to obtain the change in ion excess between double- and single-stranded NAs, ΔΓ_ds-ss using (98):

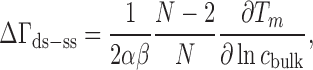(8)

where α is an ion activity correction factor (85), N is the number of base pairs, and 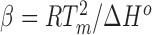is a compound constant measured by calorimetry of NA conformational transitions with value β = 55 ± 10% (14). Thus, concentration-dependent ΔΓ_ds-ss values can be obtained in an experiment that, unlike dialysis, does not involve a membrane and can be performed at arbitrarily dilute NA concentrations. Such measurements have been made for DNA in both monovalent (77,78,80,81,83,84) and divalent (78,79) salt as a function of structural parameters and ion species. In the case of NaCl, a rich dataset amenable to this analysis is that of Owczarzy et al. (82).

More recently, a second related technique has been developed that measures the change in ion excess associated with mechanically stretching an NA, ΔΓ_ds-stretch or ΔΓ_stretch-ss, by analyzing the salt dependence of the equilibrium unfolding force from single-molecule force spectroscopy experiments (97). Similar arguments have also been applied to the analysis of simulated RNA pseudoknot unfolding data by Hori et al. (99). Several thermodynamic relations can be derived to analyze the data, one of which, applicable to an NA hairpin system, is given by (85,86,97)

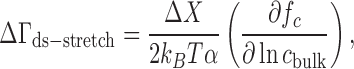(9)

where ΔX is the change in molecular extension as the hairpin construct is unfolded and f_c is the equilibrium mechanical force of unfolding. This equation is valid only in monovalent salt, but similar relations can be derived for other valences (97). Note that this relation has a similar form to Equation (8), but does not require an independently measured quantity analogous to β. Also, the single-molecule nature of these studies allows the realization of the c_NA → 0 limit in the formal definition of the ion excess (Equation 2), i.e. there is not a concern about NA–NA interactions. Relations like Equation (9) have been used to measure the association of monovalent ions to DNA (85) and RNA (28) upon folding and the binding of trivalent ions to DNA (86) upon condensation. ΔΓ_stretch-ss data can likewise be obtained by applying another ion counting relation to force spectra of intrinsically single-stranded samples (87,88). These data can be combined with ΔΓ_ds-stretch to complete the thermodynamic cycle of Figure 4A and obtain a measure of ΔΓ_ds-ss equivalent to that from the melting studies.

Results for both melting and mechanical stretching measurements of ΔΓ_ds-ss for 25 base pair DNA helices are shown in Figure 4B (28). We see that the two methods give salt-dependent values with the same general shape and trend, but that they do not agree quantitatively within uncertainty. Also plotted is a PB estimate of ΔΓ_ds-ss found by taking the difference between the PB results for dsDNA and ssDNA in Ref. (28). Even though those two PB results are, separately, in very good agreement with the absolute ion excess data, their difference is in poor agreement with the results of Figure 4B. Thus, we see that ΔΓ measurements provide an additional, and perhaps more stringent, test of the theories. Unfortunately, a lack of simulation-based studies of single-stranded NAs precludes comparing these differential data with MD or MC predictions.

DISCUSSION

We have described several types of ion counting experiments and how they can be used to critically, but not comprehensively, test theoretical models of the ion atmosphere. The data we have shown in our figures are for dsDNA and ssDNA systems, but some data are also available for RNA (Table 1). One place where a direct comparison between the two species can be made is in measurements of Γ_ss, where only slight quantitative differences are seen (28). Greater differences between DNA and RNA behavior may arise when considering more strongly interacting +2 or +3 ions, which are more sensitive to the local NA structure.

We have seen that PB theory reproduces most of the available monovalent ion counting data (except for the differential data of Figure 4B), but disagrees notably with the divalent Γ₊(c_bulk) data of Figure 2B and the mixed monovalent/divalent competition data of Figure 3, consistent with the limitations of the mean-field approximation underlying that theory.

In contrast, there exist MD and MC simulations in agreement with many of the ion counting results we have surveyed, both in monovalent and divalent salt (Figures 2 and 3). For this reason, MD predictions are often used as benchmarks against which to compare similar results from other, simpler models (2,52). However, the agreement between MD and experiment depends upon the particular parameterization of the MD force field, as discussed, for example, in the context of Figure 3. Different force fields are known to give different ion excesses and other electrostatic results (67). An extreme example is seen in Ca^{2 +}, for which standard force fields predict cation condensation to the extent that the effective charge becomes positive (100). Similar anomalies are seen for higher-valence ions as well (101,102). Thus, carefully parameterized, modern force fields must be used to quantitatively describe NA systems (68).

In addition to the need for care in choosing appropriate force fields, three further caveats accompany the acceptance of MD results. First, MD studies are computationally impractical for probing systems at low salt concentration, where electrostatic interactions are strongest, because the volume of the simulated system becomes too large. Second, while we have shown several cases where MD and experimental results do agree, nothing approaching all possible pairings (Table 1) of the two have been explored. As one example, to our knowledge no ssDNA simulations have been performed that would allow a comparison with the differential data of Figure 4. Third, even if MD simulations—with appropriate force fields—were fully validated against all possible ion counting experiments, that is not a guarantee of the accuracy of the full three-dimensional distributions. This is illustrated by comparing the MD and 3D-RISM simulations of Giambaşu et al. (52): while both simulation schemes give similar values of Γ₊, and are thus equally in agreement with experiment, their predicted radial ion distributions disagree for the ions closest to the helical axis (compare Figures 5 and 6 of that paper). It may be that MD force fields, in the current state of the art, are adequate for reproducing the ion excess but fail to capture certain subtleties of the full ion distribution.

Thus, we see that ion counting constitutes an experimentally accessible benchmark against which theoretical models must be compared. Agreement with the ion counting results is a necessary, but not sufficient, condition on the acceptability of a particular model. Some progress can be made in expanding the power of the experiments to test theory, as mentioned above, by filling in the holes in the existing ion counting corpus—the gaps in Table 1—and by conducting matching theoretical analyses; recent developments in MD force fields should render such comprehensive analyses possible (68). Beyond that, a great leap in understanding would accompany the development of an experimental technique capable of measuring the full, 3D distribution of the ion atmosphere. SAXS experiments (15,44) have come the closest to this goal, in that they give information about the distribution over moderate to long length scales. New or improved techniques will be needed, however, to probe the short length scales where subtle perturbations in the ion atmosphere could have large impacts on biomolecular interactions.

FUNDING

National Science Foundation (NSF) [DMR-1309414, DGE-1144085 to D.R.J.]. Funding for open access charge: NSF.

Conflict of interest statement. None declared.