A combination of computational and experimental approaches is used to show that the complex dynamics of dendritic filopodia, which is essential for synaptogenesis, is explained by a conceptually simple interplay among actin retrograde flow, myosin contractility, and substrate adhesion.
Abstract
Dendritic filopodia are actin-filled dynamic subcellular structures that sprout on neuronal dendrites during neurogenesis. The exploratory motion of the filopodia is crucial for synaptogenesis, but the underlying mechanisms are poorly understood. To study filopodial motility, we collected and analyzed image data on filopodia in cultured rat hippocampal neurons. We hypothesized that mechanical feedback among the actin retrograde flow, myosin activity, and substrate adhesion gives rise to various filopodial behaviors. We formulated a minimal one-dimensional partial differential equation model that reproduced the range of observed motility. To validate our model, we systematically manipulated experimental correlates of parameters in the model: substrate adhesion strength, actin polymerization rate, myosin contractility, and the integrity of the putative microtubule-based barrier at the filopodium base. The model predicts the response of the system to each of these experimental perturbations, supporting the hypothesis that our actomyosin-driven mechanism controls dendritic filopodia dynamics.
INTRODUCTION
Formation of synapses during development and their maintenance in the adult organism are required for the proper functioning of neuronal circuitry. Spines—micrometer-scale protrusions from neuronal dendrites—receive the majority of synaptic inputs in the CNS. Regulation of spine density, morphology and spatial distribution is required for synaptic stability and plasticity. Abnormal density and morphology are associated with impaired motor and cognitive functions underlying neurological disorders such as autism, schizophrenia, and fragile X syndrome (Segal, 1995; Irwin et al., 2000; Lin and Koleske, 2010; Wilson et al., 2010).
Spine morphogenesis is a delicate process that starts from the formation of the dendritic filopodium (Ziv and Smith, 1996; Hotulainen and Hoogenraad, 2010; Korobova and Svitkina, 2010). Dendritic filopodia are dynamic protrusions up to 15 μm in length that explore their extracellular environment and connect with the presynaptic axons (Kayser et al., 2008). The population of motile filopodia is highest during early neuron development and gradually decreases as the neuron ages. Starting from day in vitro 4 (DIV4) hippocampal cell culture, when neurites are fully differentiated into axons and dendrites, filopodia are numerous and highly motile (Ziv and Smith, 1996). They extend 2–10 μm away from the dendritic shaft to establish contact with nearby axons and also can retract back toward the dendrite. The protrusion/retraction cycle repeats until filopodia stabilize or dissolve back into their parent dendrite. By DIV13, most of the filopodia observed in culture are nonmotile, whether solitary or connected to an axon. In the same time frame, the first spines start to appear on the dendrites. The initial axon–dendritic contact and its stabilization are considered to be the key events in spinogenesis (Kayser et al., 2008; Hotulainen and Hoogenraad, 2010). However, the dynamics of spine morphogenesis from filopodia has not been fully characterized, and the mechanism of dendritic filopodial motility is poorly understood.
What is known is that dendritic filopodial motility is actin based. The main components of actin network dynamics in motile cells have been extensively studied, resulting in models that describe various mechanisms of leading-edge protrusion (Leibler and Huse, 1993; Mogilner and Rubinstein, 2005; Lammermann and Sixt, 2009). From models of keratocyte and nerve growth cone motility, we know that actin-based motility arises from the force that polymerizing actin filaments exerts on the membrane, which is opposed by membrane tension (Medeiros et al., 2006). Myosin II contracts the actin filaments, generating the actin retrograde flow that pulls filaments away from the leading edge (Verkhovsky et al., 1995). If the actin filament polymerization rate overcomes the retrograde flow, a local protrusion forms. How are actin polymerization, contraction, and local adhesion mechanisms marshaled to control dendritic filopodial motility and stability? Previous models of filopodial dynamics treated the system as a stiff elastic rod compressed by the membrane resistance force without considering adhesion or contractility (Mogilner and Rubinstein, 2005); others focused on the adhesion to and compliance of the substrate (Chan and Odde, 2008). These earlier studies did not consider the unique molecular composition of dendritic filopodia.
The molecular composition of the actin network in dendritic filopodia, which lack filament bundling proteins found in conventional filopodia (Korobova and Svitkina, 2010), affects the rheological properties making it more viscous than bundled actin (Kim et al., 2009). For example, the actin network in dendritic spines is four to five times more viscous than the average cell cytoskeleton (Smith et al., 2007). The actin cytoskeleton inside a dendritic filopodium consists of short, branched filaments of mixed polarity (Portera-Cailliau et al., 2003; Korobova and Svitkina, 2010), which can make them sensitive to myosin contractile stresses. Adhesion to the substrate can affect actin retrograde flow and govern the retraction phase of the filopodia motility cycle (Yamashiro and Watanabe, 2014). Furthermore, substrate adhesion is required for neurogenesis (Lin and Koleske, 2010) and may be important for dendritic filopodia behavior.
Therefore we expect the dynamics of dendritic filopodia to differ from that of conventional filopodia. Such a range of behaviors could be involved in the establishment and stabilization of initial synaptic connections in the developing nervous system (Portera-Cailliau et al., 2003). Indeed, in this article, we characterize a wide range of motility states, from nonmotile to persistently fluctuating filopodia. To understand these diverse motility behaviors, we develop a minimal mathematical model of dendritic filopodia dynamics that explains the spatiotemporal regulation of actin and myosin dynamics and describes conditions under which dynamic filopodia are maintained. The model uses partial differential equations that balance the forces of substrate adhesion, actin retrograde flow, and myosin contractility while accounting for actin polymerization and diffusion. To validate the proposed mechanism experimentally, we perturbed key model parameters using various manipulations, comparing the model predictions with the results of motility analysis of dendritic filopodia on hippocampal neurons in culture.
RESULTS
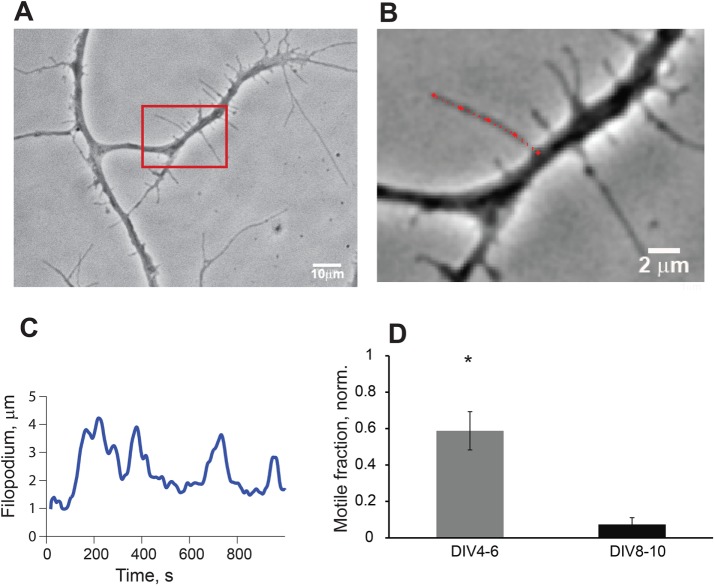
To collect sufficient data on filopodia dynamics, we performed 2-h (Δt = 1 s) time-lapse recordings of filopodia extending and retracting from the dendrites of young neurons (DIV4–12; Figure 1A). Filopodial dynamics was then quantified by tracking filopodia length automatically using our custom-written software FiloTracker (Supplemental Movie S1A and Figure 1, B and C). Having collected trajectories from 938 filopodia (83 neurons), we classified dendritic filopodia by their motility patterns into filopodia with transient and continual dynamics and nonmotile filopodia (Supplemental Figure S1, A and C). Filopodia with continual dynamics displayed lifetimes t > 20 min with regular protrusion/retraction cycles (Supplemental Figure S1A). Filopodia with transient motility were defined by irregular, short-lived bursts of motility (Supplemental Figure S1B), and filopodia with constant length did not exhibit any motility, displaying invariable length for the duration of the recording session (≥20 min; Supplemental Figure S1C). Filopodia were more dynamic during early neurodevelopment, with a motile fraction of 41 ± 22% for DIV3–9, which decreased to 11 ± 6% after DIV10 (Figure 1D). This result is consistent with the trend reported earlier (Smith et al., 2007).
FIGURE 1:
Analysis of filopodia motility with automated tracking software FiloTracker. (A) Phase-contrast image of hippocampal pyramidal neuron in culture, DIV5, with dendrites covered with filopodia; scale bar, 10 µm. (B) High-magnification image of boxed area in A during length tracking process in FiloTracker; red dotted line is a length estimate for the current frame; scale bar, 2 µm. (C) Output sample of length measurements from the filopodia in B (red); acquisition rate, 1 frame/s; periodicity of length, ∼122 ± 19 s. (D) Comparison of motile fraction of all filopodia in imaging session (t = 30 min) at DIV4–9 and DIV8–10 (t test, p < 0.05).
In all filopodia trajectories with continual dynamics, we calculated the protrusion rates (length increase per time during extension) and retraction rates (length decrease per time during retraction) with the Peakfinder algorithm, which was set to detect large changes in length (see Materials and Methods). We determined that the lengths fluctuate with similar protrusion and retraction rates of 0.37 ± 0.080 and 0.32 + 0.054 μm/s in DIV4–7, respectively.
Formulation of a model based on experimental constraints
We hypothesized that feedback among the actin retrograde flow (ARF), myosin activity, and substrate adhesion are the principal factors that drive the range of filopodia behaviors observed in primary neuron culture, and we developed a deterministic mathematical model to quantitatively explore this hypothesis. Because growth and retraction events observed in filopodia are due to stochastic events involving small numbers of molecules and filaments, the protrusion and retraction rates measured from the trajectories are expected to be higher than the rates estimated from a deterministic mathematical model. This is because the experimental procedure using the Peakfinder algorithm detects only growth or retraction events and does not account for resting phases between events. Thus the reported experimental protrusion and retraction rates will always be much faster than those produced by the deterministic model. In addition, the experimental measurements of protrusion and retraction rates were necessarily performed on motile filopodia. The deterministic model necessarily corresponds to behavior that is essentially integrated over all filopodia in a given state. However, because the simplicity of the deterministic model allows for ready analysis and exploration of hypotheses, it has real advantages for the purposes of this study. Thus the deterministic model serves well to explain the overall behavior of the system and any trends or patterns due to experimental manipulations.
We considered a minimal number of biophysical mechanisms as sufficient to describe filopodium dynamics, with its extension driven by actin polymerization and its retraction by myosin contraction. The total contractile force exerted within the filopodium is proportional to the total amount of bound myosin. When the filopodium is short, there is only a small amount of bound myosin and, consequently a small contractile force. Therefore polymerization of the actin at the tip causes the filopodium to extend. As the filopodium gets longer, the contractile force gets larger due to binding of myosin, and the tip extension slows. At some point, myosin contraction can outstrip polymerization, and the filopodium shrinks. As shrinking proceeds, the density of bound myosin increases and accelerates contraction. Ultimately, myosin dissociation reduces the contractile force, and the filopodium length reaches its minimum before extension resumes. It is therefore possible that standard actomyosin dynamics can account for all ranges of filopodia dynamics. However, other factors, such as the viscoelasticity of the actin network and the adhesion of the filopodium to the substrate, may affect the overall system behavior. These and other features of the system can be quantitatively explored with a mathematical model based on five essential processes (Figure 2): 1) polymerization of F-actin at the tip of the filopodium; 2) binding and unbinding of myosin to F-actin; 3) isotropic contractile stresses exerted by myosin on F-actin; 4) viscous flow of F-actin (ARF) induced by these contractile stresses; and 5) friction between the filopodium and the substrate due to adhesion (Kim et al., 2012).
FIGURE 2:
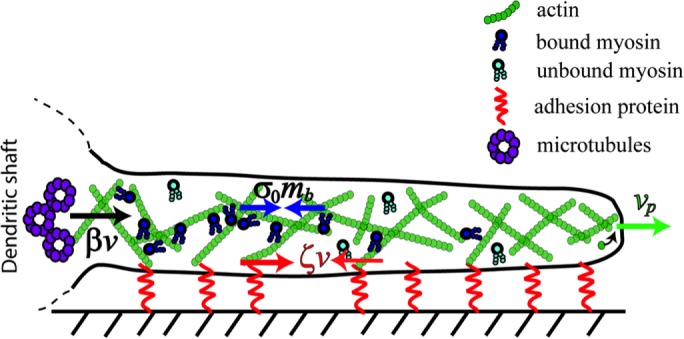
Balance of forces in a dendritic filopodium described by the minimal model. The model captures five essential processes: 1) polymerization of F-actin at the tip of the filopodium; 2) binding and unbinding of myosin to F-actin; 3) isotropic contractile stresses exerted by bound myosin on F-actin; 4) viscous flow of F-actin (ARF) induced by these contractile stresses and membrane tension; and 5) friction between the filopodium and the substrate due to adhesion. Bound myosin contractile stress is shown by blue arrows, σ0 and mb; vp, polymerization rate, direction indicated by green arrow, ζv, the substrate adhesion force, is denoted by the red arrows, and the black arrow is β v, the resistance force at the base due to the microtubule network inside the dendrite. Unbound myosin freely diffuses inside the filopodium.
We implemented the model filopodium as a linear one-dimensional (1D) object whose length, L(t), varies with time. The state of the system is described by two variables, the distribution of bound myosin, mb(x, t), and the local velocity of the actin network, v(x, t), x e [0, L], where x = 0 corresponds to the base of the filopodium and x = L to the tip. Myosin can bind and unbind from the actin cytoskeleton with rate constants kon and koff, respectively. The unbound myosin is assumed to diffuse rapidly on the length scale of the filopodium and, on the time scale of filopodial dynamics, to be in equilibrium with the large reservoir contained in the adjacent dendrite; therefore its concentration, m, is assumed to be constant.
Bound myosin moves with the F-actin at the velocity v(x) and can also diffuse due to random motion of the actin filaments (Kruse et al., 2004). The dynamics of the bound myosin is then described by the following continuity (transport) equation:
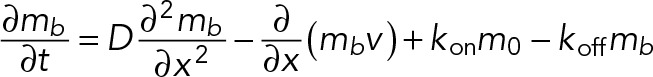 (1) (1)
|
where D is the diffusion coefficient.
The bound myosin exerts a contractile stress on the actin network. We assume that this contractile stress is isotropic and proportional to the concentration of bound myosin. On the time scales relevant to filopodial motility, the actin network can be approximated as a viscous fluid with viscosity η (Bausch et al., 1998). Adhesion between the filopodial membrane and the extracellular matrix resists the movement of the filopodium. We account for this as a resistive force proportional to the velocity. Therefore myosin contractile stresses will induce a viscous flow of F-actin governed by the mechanical balance equation,
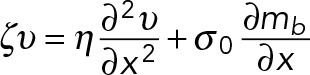 (2) (2)
|
which takes into account the three major forces present in the system: viscous stress, the contractile stress exerted by bound myosin, σ0mb, and the resistive drag force, ζν, due to adhesive interactions with the substrate. In Eq. 2, σ0 is a myosin contractility coefficient that should be approximately proportional to the maximum force that can be applied by a single myosin molecule.
Equations 1 and 2 are solved with the following initial conditions:
|
|
and L, mb, and v allowed to evolve over time and along the 1D space. With regard to boundary conditions, we assume that F-actin and its bound myosin do not flow into or out of the dendritic shaft, based on previous experimental findings (Tatavarty et al., 2012) and possibly due to a barrier formed by microtubules in the adjacent dendritic shaft (this idea will be further explored later); therefore the flux of bound myosin is zero at the base:
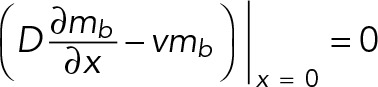 (4) (4)
|
We use a resistive force proportional to the velocity, βν, to model the stress balance at the base of the filopodium:
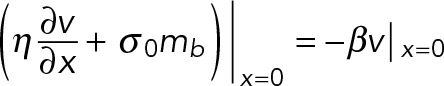 (5) (5)
|
At the tip of the filopodium, membrane tension, T, exerts a force proportional to the curvature, κ, on the actin network:
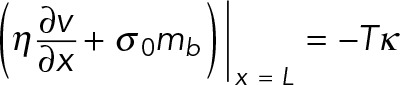 (6) (6)
|
where, effectively, Tκ is a single parameter. Using experimental data, we estimate that Tκ = 2 pN (see later discussion). In addition, we find that the model is insensitive to Tκ values in the range 0–5 pN, as demonstrated in Supplemental Figure S2A. Therefore we use this value of 2 pN in all of our calculations to simplify the number of free parameters without affecting the results.
The rate that the length of the filopodium changes is equal to the difference between the actin polymerization rate at the tip, vp, which is set to be independent of other system variables, and the retrograde velocity of the F-actin network. Thus
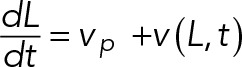 (7) (7)
|
Because the actin at the tip is newly polymerized, myosin will not have bound yet, leading to the boundary condition mb(L,t) = 0. Supplemental Table S1 lists model variables and parameters.
The model can recapitulate the experimentally observed motility behaviors
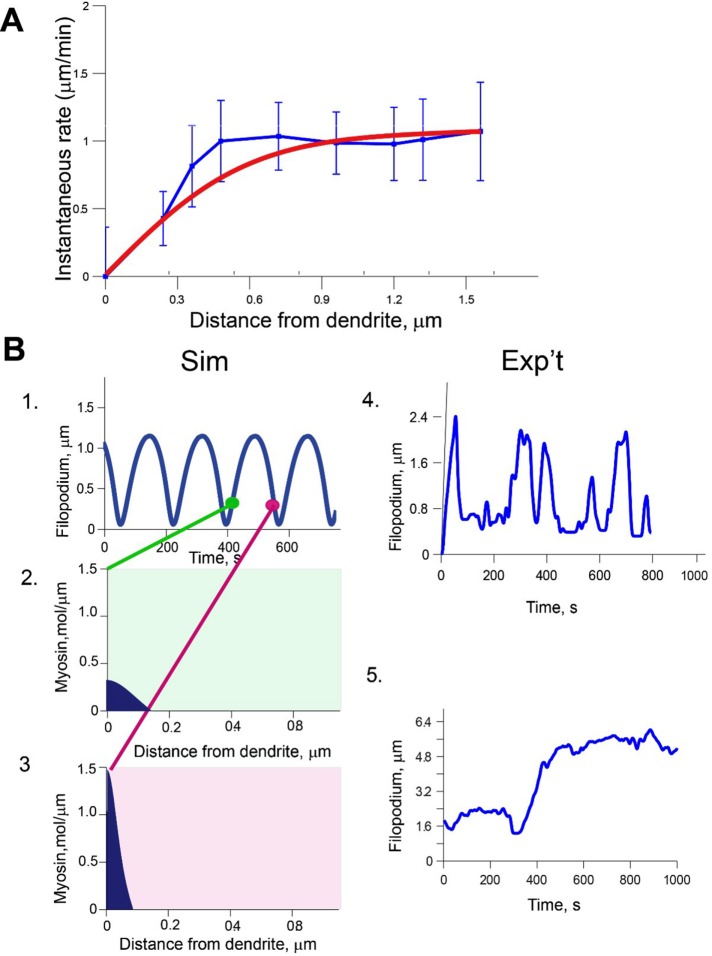
We analyzed Eqs. 1– 7 over a large range of parameters using a semi-implicit Crank–Nicolson scheme coded in MATLAB. We found that the model leads to three qualitatively different patterns of behavior: continuous increase of filopodium length, an equilibrium state with constant length, and periodic filopodium length fluctuations around a constant value. To begin, we focused on scenarios in which the filopodium length fluctuated, similar to what is observed during early neuron development (Ziv and Smith, 1996). To test the predictions of our model, we compared the model results to existing experimental measurements of ARF and myosin localization from live dendritic filopodia (Tatavarty et al., 2012). In those experiments, ARF was measured and averaged in motile and nonmotile filopodia. We compared simulated ARF over protrusion and retraction phases and found striking agreement between experiment and model over a wide range of parameter values (Figure 3A). Experimental data and calculations were used to set the parameters σ0, vp, kon, koff, ζ, η, and Tκ as described in the next section.
FIGURE 3:
Model solutions correspond to experimental data. (A) Fit of simulated actin flow velocity at steady state (red; Eq. 1) with experimental ARF distribution along normalized filopodium length (blue; Tatavarty et al., 2012). Mean ± SD. Parameter values: L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = 25, η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04. (B) (1) Simulated filopodium length fluctuations with retrograde flow from A. Myosin distribution taken close to the most rapid phases of (2) protrusion and (3) retraction. L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = 25, η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04. (4) Representative dynamics of a live filopodium traced using automated software; acquisition rate, 1 frame/s. (5) Dynamics of a live filopodium with large amplitude of fluctuations traced using automated software; acquisition rate, 1 frame/s. (Note y-axes in 4 and 5.)
Parameter justification for the dendritic filopodia model
Our actomyosin model for dendritic filopodia has the following 11 parameters: η, actin viscosity; ζ, substrate drag coefficient; σ0, myosin contractility; m0, unbound myosin concentration; vp, polymerization velocity of actin at the tip of the filopodium; T, membrane tension; κ, curvature of the membrane at the tip of the filopodium; β, drag coefficient at base of spine; D, bound myosin effective diffusion coefficient; kon, myosin on rate; and koff, myosin off rate.
Of these parameters, T and κ are not independent, as it is possible to rewrite the dynamic equations such that only the combination Tκ appears. Therefore 10 parameters determine the behavior of the model. The definitions, nominal values, and units for each parameter are provided in Supplemental Table S1. In what follows, we use experimental data from the literature to justify each of these parameters.
Actin viscosity, η. Many experiments have probed the viscosity of actin networks in cells. This literature suggests a wide range of values for the cytoskeletal viscosity. For example, Kole et al. (2005) performed passive microrheology on quiescent and motile Swiss 3T3 cells. In motile cells, they measured the actin viscosity to be ∼5 Pa·s, whereas Bausch et al. (1998) found a value of 2000 Pa s using magnetic bead microrheology. The model produces more accurate agreement with the experimental data for values of the viscosity that are closer to the larger value found by Bausch et al. (1998). We used a value of 500 Pa·s as a baseline value. This viscosity, however, represents the three-dimensional (3D) viscosity of the actin network. Because our model is 1D, we need to treat the net effect of the viscosity over the cross section of the filopodium; that is, 1D viscosity is equal to 3D viscosity times the cross-sectional area of the filopodium. If the diameter of a dendritic filopodium is ∼500 nm, then the cross-sectional area is ∼0.2 μm2 and our baseline value of the 1D viscosity is η = 100 pN·s.
Substrate drag coefficient, ζ. To our knowledge, there have not been any experiments examining the substrate drag coefficient for dendritic filopodia. However, Chan and Odde (2008) simultaneously measured the traction force generated by axonal filopodia and the retrograde flow of actin. They found traction forces of 10–50 pN with actin retrograde flow rates of 80–100 nm/s. The ratio of the traction force to the retrograde flow rate should be approximately equal to the drag coefficient times the length of the filopodium. For an axonal filopodium of length 5 μm, we estimate ζ = 100 pN·s/μm2.
The free concentration of myosin, m0. We estimate the concentration of unbound myosin molecules to be 0.5–5 μM (Wu and Pollard, 2005). In the 1D model, the myosin concentration, m0, is the number of molecules per length, which is between 6 and 60 molecules/μm.
The stress from bound myosin, σ0. In the 1D model, the combination σ0m represents the net contractile force F that would be produced by a concentration m of myosin molecules distributed over the length L of the filopodium. Therefore we estimate the total number of bound myosin molecules along the filopodium to be N ≈ m·L. Because the force from a single myosin molecule is ∼2–3 pN (Norstrom et al., 2010), the net force is F ≈ N (2–3 pN) ≈ σ0m, or σ0 ≈ L (2–3 pN). For a characteristic filopodium length of 2–3 μm, we then estimate σ0 to be ∼4–9 pN·μm. To account for some cooperative effect between myosin molecules, we use a baseline value of 25 pN·μm.
Polymerization velocity, vp. In vitro, actin filaments elongate at ∼0.1 μm/s (Kuhn and Pollard, 2005). These experiments were performed at an actin concentration of 1.5 μM, whereas concentrations of G-actin in the lamellipodia of motile cells can be as high as 150 μM (Koestler et al., 2009). In principle, then, actin polymerization in vivo could occur up to 100-fold faster than in these in vitro experiments. However, we expect the velocity at which actin elongates at the tip of the filopodium to be comparable to these values and set a baseline value vp = 0.9 μm/s.
Membrane tension times curvature, Tκ. The quantity Tκ represents the stress exerted onto the actin cytoskeleton due to the membrane tension at the tip of the filopodium. Membrane tension in neuronal growth cones was measured to be ∼3 pN/μm (Hochmuth et al., 1996). The membrane curvature at the tip of the filopod is κ = 4 μm−1 for a filopodium with a diameter of 500 nm. Therefore Tκ ≈ 12 pN/μm2. For the 1D model, we need to compute the net force that is exerted on the actin at the filopod tip due to the membrane tension and curvature. (Note that the tension in the membrane along the sides of the filopodium does not contribute any force in the 1D model because tension on one side of the filopodium cancels the tension on the other side.) Therefore the force at the tip of the filament is equal to Tκ times the cross-sectional area of the filopodium, which is then equal to 2.4 pN.
Drag coefficient at the base of the filopodium, β. We hypothesize that flow of actin out of the base of the filopodium is hindered, most likely due to steric interactions with microtubules in the dendritic shaft. We model this behavior using a resistive drag force that is proportional to the flow rate of actin (Eq. 5). To our knowledge, there are no data that will allow us to estimate a value for the constant of proportionality between the drag force and the flow rate. However, as demonstrated in Supplemental Figure S2B, the system behavior is completely insensitive to β > 100 and still displays robust oscillations with β = 0. We chose a value large enough to be well within the insensitive region of parameter space so that the actomyosin dynamics slows completely as it approaches the base of the filopodium.
Myosin diffusion coefficient, D. The diffusion coefficient, D, represents the diffusion of bound myosin on the actin. This represents random events, such as slipping of the myosin molecules and diffusion of the actin filaments. The diffusion coefficient for myosin light chain kinase moving on actin filaments was recently measured to be between 0.03 and 0.07 μm2/s (Hong et al., 2015). We use a value of D = 0.04 μm2/s.
10. Myosin on and off rates, kon and koff. Nagy et al. (2013) measured the dissociation rate constant for single myosin molecules to be ∼0.4 s−1, and Norstrom et al. (2010) measured the on-rate and off-rate of nonmuscle myosin and found them to be comparable. Based on these data, we set baseline values of koff = 0.13 s−1 and kon = 0.12 s−1.
Myosin activity is the main regulator of actin retrograde flow force. In the model, bound myosin is pushed by actin retrograde flow toward the dendrite, and accumulation of myosin at the base is largely due to the resistive barrier at the filopodium base, which prevents actin from flowing out of the filopodium (Eqs. 4 and 5). Because of the barrier at the dendrite, the bound myosin remains highly localized at the filopodium base during all phases of the motility cycle. The output of the simulated motility cycle is shown in Figure 3B1. During the initial stage of protrusion, myosin begins to bind to the actin network, which leads to generation of slow ARF and further promotes accumulation of myosin at the base of the filopodium (Figure 3B2). When the protrusion rate reaches zero at the peak of the growth phase, bound myosin localizes in high concentration right near the filopodium base, whereas low concentrations are distributed along the filopodium length and decay to 0 at the tip. During the retraction phase, the ARF is larger than during protrusion, maintaining high concentrations of myosin at the filopodium base (Figure 3B3). Although the deterministic nature of the model does not capture stochasticity present in the live filopodia movement, it does produce representative behavior between the extremes observed experimentally (see Figure 3B4 and later discussion of Figure 5).
FIGURE 5:
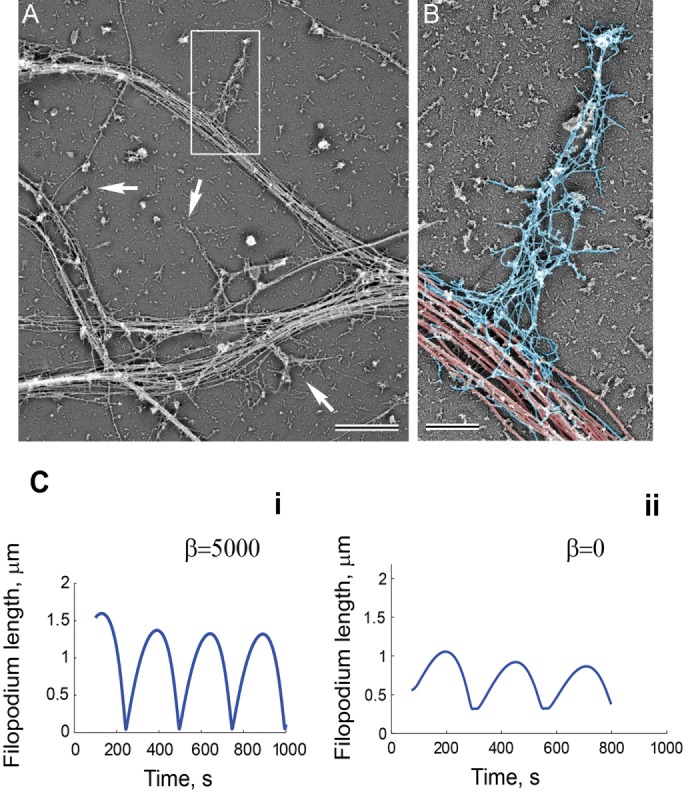
Filopodia dynamics depends on the resistive force applied at the base by the microtubule network. Cytoskeletal organization of dendritic filopodia revealed by platinum replica electron microscopy. (A) A network of dendrites from hippocampal neurons cultured for 8 DIV. Dendritic filopodia (boxed region and arrows) reside on dense arrays of microtubules in dendrites. (B) Dendritic filopodium from the boxed region in A color-coded to show microtubules in the dendrite (red) and actin filaments in the filopodium (blue). Scale bars, 2 μm (A), 0.5 μm (B). (C) Simulated filopodia dynamics with (i) and without (ii) resistive force at the barrier. (i) L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = 25, η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04. (ii) L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = 25, η = 100, ζ = 100, σ0 = 25, β = 0, and D = 0.04.
Thus our model emphasizes that maintaining myosin localization at the base is required for persistent filopodial dynamics. To validate the model’s prediction, we compared the simulated myosin gradient with the experimental results on the active myosin distribution in live filopodia. Neurons were transfected with an Eos–myosin light chain (MLC) DNA construct (Tatavarty et al., 2012). Single-molecule photoactivated localization microscopy (PALM) imaging showed localization of active myosin II near the base of the dendritic filopodia (Figure 4A). The probability of MLC residence at the base changed from almost 80% at DIV8–10 to 50% at DIV14–15 (Figure 4B). Myosin localization was measured in dynamic and nonmotile filopodia, with both measurements showing maximum myosin concentration at the base (Figure 4B). The averaged myosin distribution over the course of simulation displays a base localization pattern similar to the one from the experimental results.
FIGURE 4:
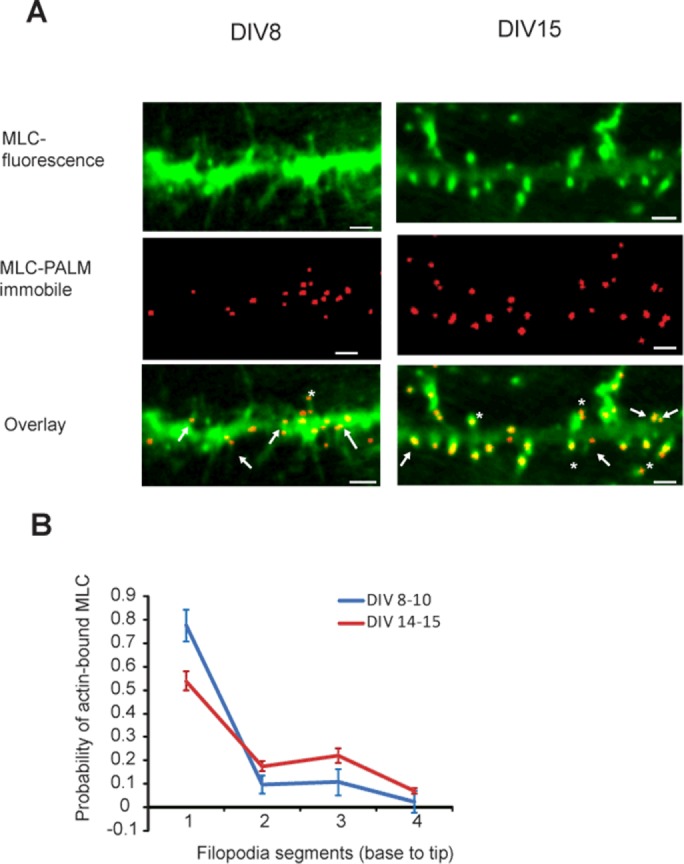
Localization of myosin (MLC) in dendrites using PALM imaging. (A) Top, epifluorescence images of neurons transfected with Eos-MLC. Middle, corresponding PALM images constructed with only the immobile subpopulation of the molecules. Bottom, overlay of the top and middle images. Arrowheads indicate immobile MLC localization in the base of the filopodia. Asterisks indicate immobile MLC localization in the spine heads. Scale bar, 3 μm. (B) Probability of MLC to be found in one of the four segments of the filopodium during early development (DIV8–10; 26 filopodia) vs. late development (DIV 14–15; 25 filopodia). Error bars represent SEM; numbers indicate relative distance from the base.
Whereas the filopodium is filled with branched filamentous actin, the dendrite contains a prominent microtubule network, as shown by electron microscopy images (Figure 5A). The dense network of microtubules runs uninterrupted in the dendrites orthogonal to the filopodial actin filaments, forming a barrier. We hypothesize that the microtubules at the base of the filopodium function as a barrier to retain bound myosin and actin inside the filopodium (Figure 5B), as expressed in the boundary condition of our model (Eqs. 4 and 5). The no-flux condition for the actomyosin network at the filopodium base (Eq. 4) prevents filopodium collapse at the end of the retraction cycle and is required for filopodium stability. By Newton’s law, the microtubule network has to exert some stress on the actin network proportional to the retrograde flow generated in the filopodium. However, it is unclear whether the stress from the microtubule network in the dendritic shaft plays any role in filopodia motility. Thus, to test the effect of the resistance force at the filopodium base, we varied the resistance parameter β and observed its effect on filopodia dynamics. Whereas all values of β resulted in motile filopodium with regular length oscillations (Figure 5Ci and Supplemental Figure S2B), removing the stress at the base by setting β = 0 produced shorter filopodia (Figure 5Cii). Therefore large β values increase filopodial lengths and increase the range of other unconstrained parameters, which results in oscillations (Supplemental Figure S2B). Furthermore, treating the filopodia with low doses of nocodazole, a microtubule-dissolving drug, abolished filopodia motility and significantly reduced their number (Supplemental Figure S3). In conclusion, our data and model are consistent with the hypothesis that the force at the base of the filopodium, proportional to the actin retrograde flow in the filopodium, stabilizes filopodial length and promotes filopodial motility.
In summary, simulated actin retrograde flow and myosin dynamics recapitulated dynamic behavior of dendritic filopodia observed in live-imaging experiments. We next explored whether the model can reproduce the effects of experimental manipulations. We chose a series of experimental manipulations that have direct correlates to the key parameters of the model.
Actin polymerization rate regulates filopodia motility
Cytochalasin D (CD) is a pharmacological agent that disrupts actin polymerization by blocking G-actin incorporation into existing filaments. To understand the effect of polymerization rate on filopodia motility, we designed experiments to decrease systematically the actin polymerization rate with CD. We then compared these experimental results with results from our simulations in which we decreased the polymerization rate, vp.
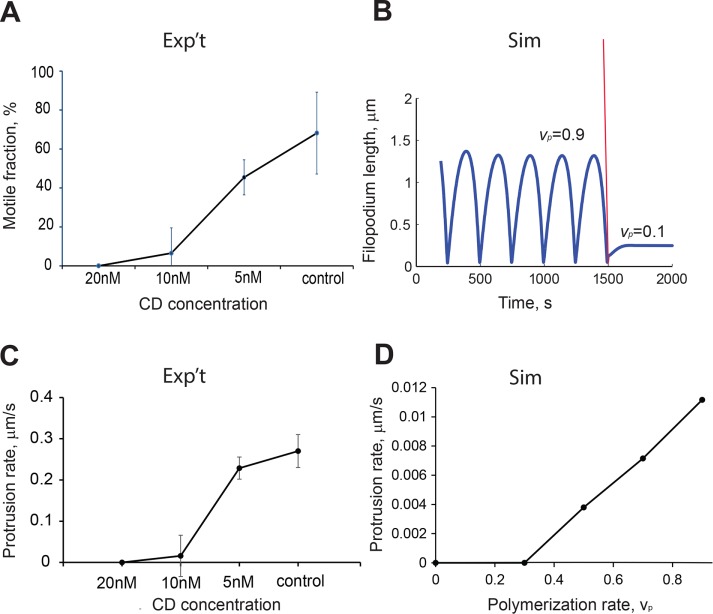
The application of 20 nM CD abolished filopodia motility at DIV9 (Supplemental Movie S2A). Treatment of neurons with lower concentrations of CD resulted in dose-dependent attenuation of filopodia motility (Supplemental Movie S2B). Whereas 20 nM CD treatment “froze” all motile filopodia, 5 nM CD resulted in a 20% reduction in the number of motile filopodia compared with control (Figure 6A). Smaller concentrations of CD (<5 nM) did not produce statistically significant effects on the motility of dendritic filopodia at DIV4–7. The low dose and short time over which cells were exposed to CD assured that the actin cytoskeleton remained intact during our measurements (Supplemental Figure S4).
FIGURE 6:
Effect of actin polymerization rate on filopodial motility. (A) Percentage of motile filopodia as a function of CD concentration; one-way ANOVA, p < 0.001 for the 20 nM dose compared with each of the lower doses (201 filopodia, 21 neurons; error bars are SD). (B) Simulated changes in filopodial motility after decreasing actin polymerization rate, vp, from 0.9 to 0.1. Other parameter values are L0 = 1, koff = 0.13, kon = 0.12, m0 = 25, η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04 (Eq. 7). (C) Effect of CD treatment on the protrusion rate of motile filopodia, one-way ANOVA, p < 0.001, for the 20 nM dose compared with each of the lower doses (124 filopodia, 18 neurons; error bars are SEM). (D) Protrusion rates from simulated filopodial dynamics using a range of polymerization rate values, vp [0–0.9]. Other parameters used in the simulations are L0 = 1, koff = 0.13, kon = 0.12,vp = 0.9, m0 = 25, η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04.
Because cytochalasin blocks incorporation of actin monomers into F-actin, the overall motility inhibiting effect of cytochalasin is not surprising (Figure 6A). However, we specifically expected that the decrease in protrusion rate is reproduced in the model simulations by perturbing polymerization rate, vp. A stepwise reduction of the parameter vp from 0.9 to 0.1 resulted in essentially nonmotile filopodia, with steady-state lengths fourfold smaller than the average lengths of filopodia at vp = 0.9 (Figure 6B). The experimental data showed a gradual decrease of protrusion rates in dendritic filopodia treated with increasing CD dose (Figure 6C). The trend we observed is reproduced by our mathematical model (Figure 6D).
The effect of substrate adhesion on filopodia dynamics is biphasic
The drag force generated by substrate adhesion inhibits actin retrograde flow and supports polymerizing actin filaments in an elongating filopodium (San Miguel-Ruiz and Letourneau, 2014). Poly-l-lysine (PLL) is a positively charged polymer that effectively mediates adhesion in cultured neurons. It stimulates integrin–substrate binding via syndecans (Beauvais and Rapraeger, 2003), and a range of PLL concentrations is used to obtain viable neurons in culture.
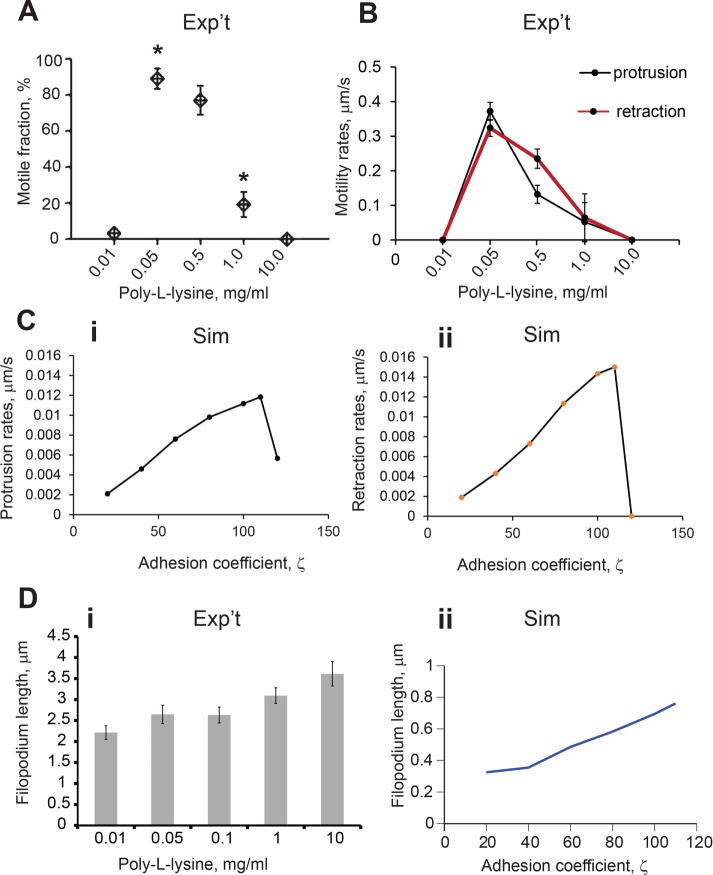
We plated hippocampal neurons on glass coverslip dishes coated with PLL concentration of 0.01, 0.05, 0.5, 1.0, or 10 mg/ml and measured filopodial density and protrusion and retraction rates using the custom-written tracking method described in Figure 1. The highest number of motile filopodia was measured at 0.05 mg/ml (Figure 7A), with significantly smaller values at 0.01 and 1.0 mg/ml (Supplemental Movies S3A–S3C). Because protrusion and retraction rates were the same for the filopodia grown on corresponding PLL substrate, all rates were compared together (Figure 7B). Motile filopodia grown on PLL applied at 0.05 mg/ml had the highest protrusion and retraction rates, 0.37 ± 0.080 and 0.32 + 0.054 μm/s, respectively, whereas filopodia grown at the other concentrations showed a significant reduction in protrusion and retraction rates (Figure 7B).
FIGURE 7:
PLL–substrate adhesion strength regulates filopodial motility. (A) The highest number of motile filopodia was observed on substrates with medium PLL concentration; using one-way ANOVA, motile fraction at 0.05 and 0.5 mg/ml were not significantly different from each other but were each significantly different from the filopodia at 0.01, 1.0, and 10.0 mg/ml (433 filopodia, 36 neurons; p < 0.001, ANOVA; error bars are SEM). (B) Protrusion and retraction rates from filopodia grown on substrates of different PLL concentration (DIV4–5, 316 filopodia, 20 neurons); using one-way ANOVA, motility rates at 0.05 and 0.5 mg/ml were significantly different from each other and were each significantly different from the less motile filopodia at 0.01, 1.0, and 10.0 mg/ml (p < 0.001; error bars are SEM). (C) Protrusion and retraction rates from simulated filopodia within adhesion coefficient range (20–115) demonstrate a biphasic relationship between adhesion forces and filopodial dynamics. The simulations are initiated with mb = 0 and L0 = 1 µm; they both quickly approach nonmotile steady-state lengths, bracketing the intermediate ζ values that produce oscillations. Other parameters in these simulations are L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = 25, η = 100, σ0 = 25, β = 5250, and D = 0.04. (D) Comparison of filopodial length change in modeling and experimental results: (i) average filopodial lengths on the range of PLL concentrations (433 filopodia, 36 neurons; ANOVA, p < 0.005; error bars are SEM; Tukey post hoc test: group 0.1 mg/ml has mean not statistically different from other groups; other four groups have means statistically different from each other. (ii) Simulated filopodia lengths in the range of the drag force parameter ζ [20, 110].
To examine whether these results correlate qualitatively with the modeling results, we simulated filopodia dynamics over a range of the drag force parameter, ζ. A greater traction force with increasing drag force parameter resulted in changes in actin retrograde flow across the adhesion drag force range. As a result, the simulated protrusion and retraction rates in filopodia followed a biphasic trend corresponding to the net sum of forces.
At ζ < 20, the force due to friction was insufficient to generate motility and resulted in nonmotile short filopodia, consistent with observations on live filopodia grown on low PLL concentrations. The protrusion and retraction rates were decreased compared with the nominal case. This phenotype can be explained by lack of traction force and inability to generate sufficient actin retrograde flow necessary for retraction. Similarly, filopodia plated on PLL at low concentrations were unable to undergo regular motility cycles and flailed during protrusion and retraction.
Filopodial protrusion rates decreased at ζ > 110, and no regular motility was observed (Figure 7Ci). Of interest, retraction rates were greater than protrusion rates (Figure 7Cii). At larger values of the drag coefficient, friction forces counteract actin retrograde flow, and the resulting protrusion rate is small and insufficient to maintain the retraction phase, which halts motile cycle. This result is congruent with the observation that filopodia grown on PLL at high concentrations were straight and immobile.
Because the effect of drag force coefficient on the filopodial motility is quite dramatic, we expected that filopodial lengths would also be affected by the changes in substrate adhesion. Indeed, on comparing experimental measurements between the lowest and highest PLL concentrations, we found filopodial lengths to increase by almost twice (Figure 7Di).
The increasing length trend was reproduced in simulations across the drag force parameter, ζ, range [20 to 120]. At ζ > 100, the steady-state length of nonmotile filopodia was greater than the average lengths of motile filopodia at lower values of ζ (Figure 7Dii).
Thus, in simulated filopodia as well as in live neurons, intermediate values of adhesion drag coefficient produced filopodia with the greatest protrusion/retraction rates undergoing regular cycles of protrusion and retraction.
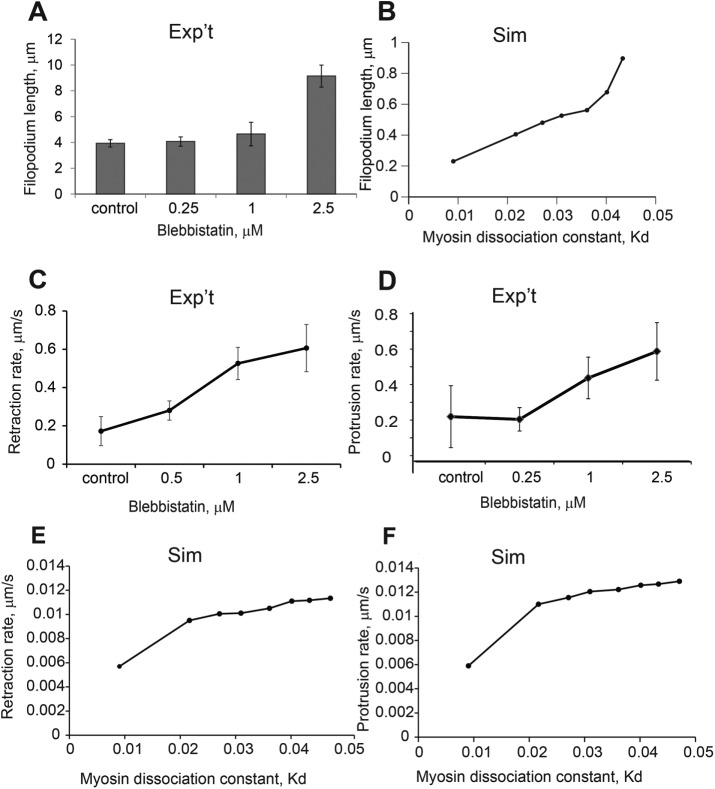
Dendritic filopodia lengths and motility are increased by blebbistatin treatment
Experimentally, it has been shown that nonmuscle myosin is a key regulating force in filopodia dynamics, and myosin inactivation by pharmacological agents, such as blebbistatin, abolishes filopodia motility (Medeiros et al., 2006; Ryu et al., 2006). The force opposing protrusion is generated by myosin contractile activity on the actin network and affects both protrusion and retraction rates of the motile system. To evaluate how the myosin–actin interaction proposed in the model predicts and explains the live filopodia motility, we treated dendritic filopodia with a range of blebbistatin concentrations. To minimize the cytotoxicity and nonspecific effects of blebbistatin (Kepiro et al., 2012), we limited the upper concentration to 2.5 µM (Supplemental Movie S4); at ≥10 µM, we observed collapse of filopodia and membrane blebbing.
The result of gradual myosin inactivation on filopodia dynamics was best captured by comparing filopodial lengths (Figure 8, A and B) and retraction/protrusion rate patterns (Figure 8, C–F) in the experiments and simulations. This is because the protrusion/retraction rates and length measurements (as opposed to the fraction of motile filopodia) are most directly compared with the output of our deterministic partial differential equation simulations. In the experiment, the filopodia were significantly longer in cells treated with 2.5 µM blebbistatin than in controls (Figure 8A). This is expected because the balance between the fixed actin polymerization rate and the decreasing myosin-induced contractility moves the system toward increased average filopodial length. Similarly, blebbistatin increases the measured (Figure 8D) protrusion rate. Surprisingly, however, blebbistatin also increases the measured average contraction rate (Figure 8C). To explain the observed trends in filopodial motility rates and lengths in terms of the drug effect on myosin activity, we looked at how simulated filopodia dynamics changes when the myosin on-rate parameter, konm0, is decreased.
FIGURE 8:
Dependence of filopodial lengths and retraction rates on myosin Kd. (A) Filopodial lengths after treatment with blebbistatin; significantly longer filopodia were observed after treatment with 1.0 and 2.5 μM doses of blebbistatin compared with control; one-way ANOVA, p < 0.001 (95 filopodia, 12 neurons); error bars are SEM. (B) Simulated filopodial lengths on the range of Kd [0.01, 0.05]. (C) Filopodial retraction rates after treatment with blebbistatin; the highest retraction rate was observed at blebbistatin treatment of 2.5 μM (DIV4–5, 78 filopodia, 12 neurons; ANOVA, p < 0.001. (D) Filopodial protrusion rates after treatment with blebbistatin; the highest protrusion rate was observed at blebbistatin treatment of 2.5 μM (DIV4–5, 78 filopodia, 12 neurons; ANOVA, p < 0.001. (E) Simulated filopodial retraction rates on the range of Kd [0.01, 0.05]; the highest retraction rate was observed at the highest Kd. Parameters used for the simulations are L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = [23–120], η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04. (F) Simulated filopodial protrusion rates on the range of Kd [0.01, 0.05]; the highest protrusion rate was observed at the highest Kd. Parameters used for the simulations are L0 = 1, koff = 0.13, kon = 0.12, vp = 0.9, m0 = [23–120], η = 100, ζ = 100, σ0 = 25, β = 5250, and D = 0.04.
Blebbistatin binds to myosin in the ADP-Pi state and interferes with the phosphate release process, locking myosin in the actin-unbound state (Kovacs et al., 2004). Thus the effect of blebbistatin can be modeled as a decreased m0 in Eq. 1, which effectively decreases the on-rate for formation of bound myosin, or, equivalently, increases the effective dissociation constant, Kd. In simulations, instantaneous protrusion rate was calculated at the half point between minimum and maximum lengths in the oscillation, and instantaneous retraction rate was calculated at the half point between the maximum and minimum lengths of the oscillation. In simulated filopodia dynamics, lower myosin on-rate resulted in longer filopodia compared with the control on-rate (Figure 8B). Satisfyingly consistent with the experiments, the protrusion and retraction rates in these filopodia were both increased as Kd increased. The time it took for the myosin to accumulate at sufficient amounts to induce retraction increases with increase in Kd; however because of the increased duration of the protrusion phase, there is actually sufficient time for a significantly increased level of bound myosin at the peak of an oscillation, resulting in a faster retraction phase. In other words, the longer duration of the growth phase, as well as the longer length of the filopodia, allows more myosin to accumulate despite the higher Kd, resulting in faster retraction (Figure 8E). Of course, if we were to decrease Kd for myosin binding still further, the system would stop oscillating, and protrusion would proceed unchecked (unpublished data). Thus the simulation and experimental results are consistent, giving us confidence that our conceptually simple model is sufficient to explain the dynamic behavior of dendritic filopodia.
DISCUSSION
In this study, we numerically simulated and experimentally characterized two types of dendritic filopodia—nonmotile and fluctuating. We demonstrated that a complex interplay among the actin retrograde flow, myosin contractility, and substrate adhesion regulates filopodia dynamics observed in primary neuron culture. Consequently we formulated a simple mechanism that explains filopodia transition from the motile to the immotile state. Understanding filopodia dynamics is necessary for developing insight into the dendritic spine plasticity and stability. Analyzing the filopodia motility in high resolution is of great utility for identification of cellular phenotypes in neurodevelopmental disorders and development of drug-screening platforms.
We found that filopodia protrusion rate is highly sensitive to actin polymerization. Cytochalasin inhibits polymerization by blocking free barbed ends, resulting in reduced filopodia protrusion rate. Similarly, in neuronal growth cones, 5 μM cytochalasin B treatment resulted in reversibly blocked motility (Medeiros et al., 2006). Treatment with CD also decreases membrane tension by as much as ∼50% (Lieber et al., 2013). We define membrane protrusion kinematically using the parameter vp, which implicitly contains the effects of membrane tension at the tip. Because the actin-generated protrusive force depends on the number of pushing actin filaments, more filaments will generate higher membrane tension values, whereas fewer filaments will yield lower membrane tension values (Lieber et al., 2013).
The drug produced a dose-dependent reduction in filopodia protrusion and retraction rates and steady-state filopodia length. Thus the actin polymerization rate at the filopodium tip is one of the key parameters that determine the filopodia dynamics and lifetime. Continuous depolymerization rate has been reported at the dendritic filopodia base, where accumulation of myosin takes place, and it is significantly smaller than the polymerization rate (Tatavarty et al., 2012). Although we did not explicitly include depolymerization rate in the model, we assumed that the vp parameter at the filopodia tip is a net actin polymerization rate and combines the polymerization and depolymerization rates. Because only the polymerization rate at the leading edge is inhibited by CD, the depolymerization rate is not affected and contributes to the filopodia retraction rate. Therefore the model can reproduce the experimental results well with the simplifying assumptions about the rates.
Next we showed that traction force due to substrate adhesion promotes filopodia motility on surfaces with intermediate adhesiveness. Filopodia protrusion/retraction rates and motile fraction exhibited a biphasic dependence on adhesion strength, with filopodia at intermediate adhesion strength displaying the highest motility rates. The results of simulations also suggested that protrusion and retraction rates in dendritic filopodia are highly sensitive to the strength of substrate adhesion. At low and high values of the adhesion coefficient, the actin retrograde flow was weaker, producing stable or slightly motile filopodia. The highest simulated motility rates were observed at intermediate values of traction force. These results are consistent with the trend in actin retrograde flow measurements on various adhesion strengths in axonal growth cones (Geraldo and Gordon-Weeks, 2009). Similarly, actomyosin-based keratocyte motility on fibronectin also shows a biphasic distribution of locomotion speed on substrates of increasing adhesion (Barnhart et al., 2011). However, although the biphasic trend is reproduced by the model, the exact relationship between PLL concentration and adhesion coefficient value is not known.
Of interest, the data suggest that the filopodia lengths are slightly greater at the high concentrations of PLL in the substrate. This effect can be due to the fact that whereas the retraction and protrusion rates are slower, the force required to overcome the friction of the substrate increases with the stickiness of the substrate, and thus the minimal length that filopodium can reach at the end of retraction phase increases, which consequently leads to longer filopodia on average.
The treatment of adhesion in our model assumes that the traction force arises from uniform adhesion between the filopodium and the substrate. The assumption can be applied only in the case of very soft or very stiff surfaces (Bangasser et al., 2013), and a more elaborate description of the interaction between the substrate and filopodial membrane will yield more accurate results for all surface types. A stochastic physical model is needed to model motor-clutch interaction of myosin-substrate linkage, where tension along the engaged clutches sums to a traction force balanced by the tension and deformation of the compliant substrate (Chan and Odde, 2008). However, in vivo substrates such as glial cells, neurons, and laminin are very soft (0.04–0.3 kPa), whereas the experimental system uses thin PLL on glass surface and is considered a stiff substrate (Engler, 2004). Thus a basic description of traction forces is relevant and recapitulates qualitatively the biphasic trend observed in the experiments. Nevertheless, measurements on the PLL substrate stiffness have not been done for the experimental system used and are necessary in deciding which model is more appropriate.
The next important parameter of filopodia dynamics is the effect of myosin activity. Experimentally, we show that bound myosin accumulates at the base (Figure 4, A and B), which is also consistent with the model simulations in which bound myosin is highly biased toward the filopodium base during oscillatory dynamics. This pattern reflects the fact that the actin filaments at the base region are the oldest and therefore have the most time to bind myosin. The myosin localization pattern maintains the actin retrograde flow, which in turn causes cyclic length contractions in filopodia.
To explore further the role of myosin for filopodium motility, we disrupted myosin binding to actin with low doses of blebbistatin (Loudon et al., 2006). Treatments with a range of increasing blebbistatin concentrations led to dendritic filopodia with increased protrusion rates (Figure 8D), which is expected because protrusion is a competition between actin polymerization at the tip and actomyosin-dependent contraction. Similarly, the average length of filopodia also increases with increased blebbistatin concentration (Figure 8A). Both of these responses to inhibition of myosin binding are recapitulated by the model (Figure 8, F and B, respectively). However, unexpectedly and remarkably, retraction rates also increased with low doses of blebbistatin (Figure 8C). Although this result seems counterintuitive, it is predicted by the model (Figure 8E). In addition, analysis of the model suggests a reason for this unexpected behavior: the longer duration of the fluctuations required to reach the maximum length when myosin binding is inhibited also gives the myosin more time to accumulate in the region of the filopodium base. Another way of thinking about this is to consider the oscillations as arising from a kinetic overshoot in the approach toward balance between actin polymerization and contractility; the overshoot is more severe when myosin binding is inhibited.
It is important to consider potential off-target effects of blebbistatin. Although it was reported previously that myosin inhibition with blebbistatin decreases myosin-dependent F-actin disassembly and thus inhibits overall actin turnover rate (Ryu et al., 2006), it was also suggested that blebbistatin decreases the actin polymerization rate as an off-target effect, which can cause the decreased motility in filopodia (Tatavarty et al., 2012). The findings also describe nonspecific effects by blebbistatin in Dictyostelium myosin II–knockout cells (Kolega, 2006). Indeed, we were unable to use blebbistatin concentrations >10 µM in our experiments because these concentrations caused complete loss of filopodia and even shrinkage of dendrites. To avoid any of these nonspecific effects, we limited our measurements to concentrations of ≤2.5 µM. Therefore we believe that the effect of blebbistatin on myosin contractility in filopodia was highly specific.
Membrane tension has been shown to play a role in regulating cell motility in rapidly moving keratocytes (Lieber et al., 2013). For thin projections like filopodia, the tension force is set by the force required to pull out a membrane tether, which depends on the membrane surface tension and the bending rigidity of the membrane (Sheetz, 2001). The force from membrane tension is proportional to the curvature of the membrane. Therefore this force can vary spatially across the membrane. Because this is a 1D model that does not account for radial forces within the filopodium, the tension is necessarily zero everywhere but at the tip.
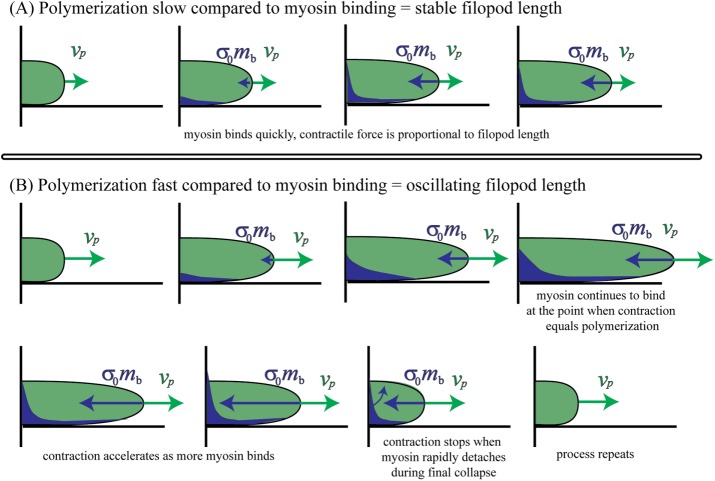
To summarize, our model reproduces experimental actin flow patterns, as well as the effects of varying myosin, adhesion, and actin polymerization that lead to emergence of dynamic filopodia through the following mechanism. Consider a filopodium with a stable steady-state length (Figure 9A). In this scenario, the actin retrograde flow due to contraction and tension balance the polymerization rate. However, this balance can be attained only if the myosin can enter and bind to the filopodial actin at a rate sufficient to keep up with the polymerization rate. Now consider a scenario in which myosin binding and unbinding are slow compared with polymerization (Figure 9B). If the polymerization velocity is fast compared with the on-rate of the myosin, then the filopodium will grow to be longer than the balance point that would have been achieved if myosin were fully bound to actin. As time progresses, however, the myosin will bind to a point at which contractile velocity is equal to polymerization velocity. However, the delay caused by the slow myosin unbinding rate is such that the myosin continues to bind, leading to “overshoot” and producing a contractile stress that overcomes the polymerization velocity (Figure 9B). At this point, the filopodium will start to contract. As the filopodium contracts, myosin continues to bind, which causes the contractile velocity to increase. In addition, as the filopodium shortens, there is less external drag (because the total external drag is proportional to the length of the filopodium). Therefore the contraction accelerates even further. In the absence of any other effects, the filopodium can end up shrinking to zero size. However, the viscosity of the actin prevents the filopodium from shrinking too quickly, and this effect increases as the filopodium gets smaller. Therefore the actin viscosity can prevent total collapse of the filopodium. Once the unbinding of myosin finally reduces contractility enough for polymerization to again dominate, the filopodium begins to grow again, and the cycle repeats.
FIGURE 9:
Summary of filopodium nonmotile (A) and motile (B) behaviors. (A) Nonmotile filopodium. The length of filopodium does not change when myosin dynamics is fast enough to counteract the protrusion rate produced by actin polymerization. (B) Motile filopodium undergoes protrusion-peak-retraction cycle. At small lengths, the total amount of bound myosin is low; hence retrograde flow is insufficient to overcome polymerization velocity, which results in gradual length increase. The filopodium reaches its maximum length when actin retrograde flow at the tip equals exactly the actin polymerization rate. Peak is followed by retraction stage, which is characterized by the large magnitudes of actin retrograde flow due to large amounts of bound myosin. The retraction lasts until the length is so small that the amount of bound myosin is low, which allows actin polymerization to increase the filopodial length and initiate the protrusion phase. This leads to the cyclical changes in filopodial length.
Whether filopodial dynamics and stability are important for spine formation is controversial (Portera-Cailliau et al., 2003; Hotulainen and Hoogenraad, 2010). Because the actin network inside the dendritic spine consists mainly of the same components as filopodia, we suggest that the factors that play important role in filopodia stability will be also important in spine morphogenesis and stability. Thus, in future studies, we plan to focus on three central aspects of spine morphogenesis: metamorphosis of filopodia into spines, diversity of spine shapes, and their stability.
MATERIALS AND METHODS
Cell culture
Hippocampal neuron cultures were prepared from E18 rat (Sprague Dawley) hippocampi obtained from BrainBits (Springfield, IL) and plated following BrainBits Kit Protocol brainbitsllc.com/brainbits-kits-primary-neuron-protocol/. Briefly, cells were plated at 20,000–30,000 cells/well on MatTek (Ashland, MA) glass-bottom culture dishes that were thoroughly cleaned by sonicating sequentially in 10% HCl, 20% NaOH, and Millipore water or in plasma cleaner and coated with PLL (Sigma-Aldrich, St. Louis, MO) overnight before use. Cell cultures were maintained for up to 25 DIV in neurobasal medium supplemented with B27.Samples were imaged with a Nikon Plan NA1.25 × 100 objective on DIV 3–12 on a Nikon diaphot 300 inverted microscope. Images were collected with a back-illuminated charge-coupled device (CCD) camera (CH350; Roper Scientific) driven by MetaMorph image acquisition and analysis software (Molecular Devices, Sunnyvale, CA).
Drug treatments
For control conditions, dimethyl sulfoxide (DMSO) was added to Hibernate E and mixed well, and the culture medium was replaced with the DMSO solution at room temperature. The cells were imaged immediately after the medium replacement for 20 min. Blebbistatin (Sigma-Aldrich, St. Louis, MO) was used at 1.0, 2.5, 5.0, 12.5, 25, and 50 μM final concentration in DMSO (2.5%), and CD (Sigma-Aldrich) was used at 5.0, 10, and 20 nM in DMSO (2%) final concentration at room temperature. At the start of the recording, cell medium was replaced with the well-mixed solution of drug dissolved in DMSO and Hibernate E. The filopodia motility was recorded for 20 min after drug administration.
Eos-MLC imaging
To express Eos-MLC fusion, a Gateway cassette (Invitrogen) was inserted to the C-terminal of the tdEos sequence (a gift from J. Wiedenmann, University of Ulm, Ulm, Germany), which converted the original vector into a Gateway vector. An entry clone of the myosin regulatory light chain, Mlrc2, was purchased from Open Biosystems (Thermo Biosystems, Huntsville, AL). The Mlrc2 sequence was then subcloned into the tdEos Gateway vector using the LR clonase (Invitrogen), following the manufacturer’s procedure, to produce the Eos-MLC fusion construct.
Single-molecule imaging of Eos-MLC was performed using a modified epifluorescence microscope (Olympus IX81; Olympus, Tokyo, Japan) equipped with 60× microscope objective (numerical aperture, 1.45; Olympus) and a thermoelectric-cooled, electron-multiplying CCD camera (PhotonMax; Roper Scientific, Trenton, NJ). A 405-nm diode laser (Cube laser system; Coherent, Santa Clara, CA) was the light source for photoactivation. The MLC-green fluorescence of unactivated Eos was excited with the 488-nm laser line from an argon ion laser (CVI Melles Griot, Albuquerque, NM). Activated single molecules were imaged with a 532-nm, diode-pumped solid-state diode laser (Lambda Photometrics, Harpenden, United Kingdom). Time-lapse images were acquired every 0.3 s with 100- to 200-ms exposure for each image. Image acquisition software was built on top of the MicroManager platform (http://micromanager.org). Image analysis was performed using a custom-built particle-tracking algorithm as previously described (Tatavarty et al., 2009). Only stationary single molecules of Eos-MLC (which moved <1 pixel) were considered for generating PALM images (MLC-PALM immobile) because this is the MLC fraction that is bound to the actin filaments (Tatavarty et al, 2012). Filopodia with length ≥2 µm were chosen for analysis and binned into four segments, each of minimum 0.5 µm. Individual immobile MLC molecules were assigned to a particular bin segment along the filopodia.
Immunostaining
Cells were washed with phosphate-buffered saline (PBS) at room temperature and fixed in gluteraldehyde 2% for 10 min at 20°C and then washed with PBS for 30 s and permeabilized with Triton X-100 0.5% in PBS for 5 min at 20°C. Cells are then rinsed with PBS twice at room temperature and incubated in bovine serum albumin for 1 h. After a 5-min wash in PBS, the cells were incubated with Acti-Stain 488 (Cytoskeleton, Denver CO) or phalloidin 555 (Cytoskeleton) for 30 min.
Staining for β-tubulin was made as described in Keating et al. (1997). Briefly, the cells were fixed with glutaraldehyde and permeabilized with Triton X-100. Imaging was performed on Zeiss LSM 780, a combined confocal/FCS/NLO system, mounted on an inverted Axio Observer Z1 with Plan Neofluar 63OilxNA1.25 objective.
Platinum replica electron microscopy
Dissociated rat embryo hippocampal neurons isolated as described previously (Wilcox et al., 1994) were obtained from the MINS Neuron Culture Service Center (University of Pennsylvania, Philadelphia, PA). In brief, hippocampi were dissected from brains of Sprague Dawley rat embryos at embryonic days 18–20 and dissociated into individual cells by incubating in a trypsin-containing solution. The cells were then washed and plated on PLL-coated (1 mg/ml) glass coverslips at a concentration of 150,000 cells per 35-mm dish in 1.5 ml of neurobasal medium (Life Technologies) with 2% B27 supplement. Sample preparation for platinum replica electron microscopy was performed as described previously (Svitkina, 2007, 2009). In brief, neuron cultures were detergent extracted for 20 s at room temperature with 1% Triton X-100 in PEM buffer (100 mM 1,4-piperazinediethanesulfonic acid–KOH, pH 6.9, 1 mM MgCl2, and 1 mM ethylene glycol tetraacetic acid) containing 2% polyethylene glycol (molecular weight 35,000), 2 μM phalloidin, and 10 μM Taxol. Detergent-extracted samples were sequentially fixed with 2% glutaraldehyde in 0.1 M Na-cacodylate buffer (pH 7.3), 0.1% tannic acid, and 0.2% uranyl acetate; critical point dried; coated with platinum and carbon; and transferred onto electron microscopic grids for observation. Samples were analyzed using JEM 1011 transmission electron microscope (JEOL USA, Peabody, MA) operated at 100 kV. Images were captured by an ORIUS 832.10W CCD camera (Gatan, Warrendale, PA) and presented in inverted contrast. Color labeling and image overlays were performed using Adobe Photoshop (Adobe Systems, Mountain View, CA), as described previously (Shutova et al., 2012).
Filopodia length tracking
Custom-written software FiloTracker was used to track individual filopodia lengths. The use of an automated procedure excluded bias in selection of filopodia and increased the data throughput. Grayscale movies were segmented in ImageJ (National Institutes of Health, Bethesda, MD) and loaded into Matlab (MathWorks, Natick, MA). The individual filopodia length was measured and recorded into output file at each frame (dt = 1 s). The program output .mat and .csv files, which were then imported into Matlab for further quantitative analysis. For a description of the FiloTracker software, refer to the Supplemental Materials (also see Supplemental Figures S5 and S6); all code is available at https://github.com/olemarch/Filopod-1D-Model. The tracks of filopodia motility were smoothed using a Gaussian filter to remove noise, and the protrusion retraction rates were computed using custom-written script. Filopodium length was estimated as maximum length from the averaged time series for each filopodium (mobile and stationary).
Computational analysis
The model is solved numerically using a semi-implicit Crank–Nicolson scheme coded in Matlab. Filopodium protrusion and retraction rates were computed using the peakfinder function by Nathan Yoder (mathworks.com/matlabcentral/fileexchange/25500-peakfinder-x0–sel–thresh–extrema–includeendpoints–interpolate-),with threshold value 75% from global minimum and maximum for finding local extremes. All code is available at https://github.com/olemarch/Filopod-1D-Model.
Statistical analysis
Statistical analysis was conducted using one-way analysis of variance (ANOVA) tests with t tests performed in Matlab. Error bars are mean ± SEM unless noted otherwise.
Supplementary Material
Acknowledgments
We thank Boris Slepchenko, Yi Wu, and Betty Eipper for valuable discussions on model validation, analysis, and interpretation.
Abbreviations used:
- ARF
actin retrograde flow
- DIV
days in vitro
- MLC
myosin light chain
- PALM
photoactivated localization microscopy
- PLL
poly-l-lysine
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E16-06-0461) on February 22, 2017.
REFERENCES
- Bangasser BL, Rosenfeld SS, Odde DJ. Determinants of maximal force transmission in a motor-clutch model of cell traction in a compliant microenvironment. Biophys J. 2013;105:581–592. doi: 10.1016/j.bpj.2013.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnhart EL, Lee K-C, Keren K, Mogilner A, Theriot JA. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bausch AR, Ziemann F, Boulbitch AA, Jacobson K, Sackmann E. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys J. 1998;75:2038–2049. doi: 10.1016/S0006-3495(98)77646-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauvais DM, Rapraeger AC. Syndecan-1-mediated cell spreading requires signaling by alphavbeta3 integrins in human breast carcinoma cells. Exp Cell Res. 2003;286:219–232. doi: 10.1016/s0014-4827(03)00126-5. [DOI] [PubMed] [Google Scholar]
- Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- Engler A. Substrate compliance vs ligand density in cell on gel responses. Biophys J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geraldo S, Gordon-Weeks PR. Cytoskeletal dynamics in growth-cone steering. J Cell Sci. 2009;122:3595–3604. doi: 10.1242/jcs.042309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochmuth F, Shao JY, Dai J, Sheetz MP. Deformation and flow of membrane into tethers extracted from neuronal growth cones. Biophys J. 1996;70:358–369. doi: 10.1016/S0006-3495(96)79577-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong F, Brizendine RK, Carter MS, Alcala DB, Brown AE, Chattin AM, Haldeman BD, Walsh MP, Facemyer KC, Baker JE, Cremo CR. Diffusion of myosin light chain kinase on actin: a mechanism to enhance myosin phosphorylation rates in smooth muscle. J Gen Physiol. 2015;146:267–280. doi: 10.1085/jgp.201511483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hotulainen P, Hoogenraad CC. Actin in dendritic spines: connecting dynamics to function. J Cell Biol. 2010;189:619–629. doi: 10.1083/jcb.201003008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irwin SA, Galvez R, Greenough WT. Dendritic spine structural anomalies in fragile-X mental retardation syndrome. Cereb Cortex. 2000;10:1038–1044. doi: 10.1093/cercor/10.10.1038. [DOI] [PubMed] [Google Scholar]
- Kayser MS, Nolt MJ, Dalva MB. EphB receptors couple dendritic filopodia motility to synapse formation. Neuron. 2008;59:56–69. doi: 10.1016/j.neuron.2008.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keating TJ, Peloquin JG, Rodionov VI, Momcilovic D, Borisy GG. Microtubule release from the centrosome. Proc Natl Acad Sci USA. 1997;94:5078–5083. doi: 10.1073/pnas.94.10.5078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepiro M, Varkuti BH, Bodor A, Hegyi G, Drahos L, Kovacs M, Malnasi-Csizmadia A. Azidoblebbistatin, a photoreactive myosin inhibitor. Proc Natl Acad Sci USA. 2012;109:9402–9407. doi: 10.1073/pnas.1202786109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim DH, Khatau SB, Feng Y, Walcott S, Sun SX, Longmore GD, Wirtz D. Actin cap associated focal adhesions and their distinct role in cellular mechanosensing. Sci Rep. 2012;2:555. doi: 10.1038/srep00555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim T, Hwang W, Lee H, Kamm RD. Computational analysis of viscoelastic properties of crosslinked actin networks. PLoS Comput Biol. 2009;5:e1000439. doi: 10.1371/journal.pcbi.1000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koestler SA, Rottner K, Lai F, Block J, Vinzenz M, Small JV. F- and G-actin concentrations in lamellipodia of moving cells. PLoS One. 2009;4:e4810. doi: 10.1371/journal.pone.0004810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kole TP, Tseng Y, Jiang I, Katz JL, Wirtz D. Intracellular mechanics of migrating fibroblasts. Mol Biol Cell. 2005;16:328–338. doi: 10.1091/mbc.E04-06-0485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolega J. The role of myosin II motor activity in distributing myosin asymmetrically and coupling protrusive activity to cell translocation. Mol Biol Cell. 2006;17:4435–4445. doi: 10.1091/mbc.E06-05-0431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korobova F, Svitkina T. Molecular architecture of synaptic actin cytoskeleton in hippocampal neurons reveals a mechanism of dendritic spine morphogenesis. Mol Biol Cell. 2010;21:165–176. doi: 10.1091/mbc.E09-07-0596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovacs M, Toth J, Hetenyi C, Malnasi-Csizmadia A, Sellers JR. Mechanism of blebbistatin inhibition of myosin II. J Biol Chem. 2004;279:35557–35563. doi: 10.1074/jbc.M405319200. [DOI] [PubMed] [Google Scholar]
- Kruse K, Joanny JF, Julicher F, Prost J, Sekimoto K. Asters, vortices, and rotating spirals in active gels of polar filaments. Phys Rev Lett. 2004;92:078101. doi: 10.1103/PhysRevLett.92.078101. [DOI] [PubMed] [Google Scholar]
- Kuhn JR, Pollard TD. Real-time measurements of actin filament polymerization by total internal reflection fluorescence microscopy. Biophys J. 2005;88:1387–1402. doi: 10.1529/biophysj.104.047399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lammermann T, Sixt M. Mechanical modes of “amoeboid” cell migration. Curr Opin Cell Biol. 2009;21:636–644. doi: 10.1016/j.ceb.2009.05.003. [DOI] [PubMed] [Google Scholar]
- Leibler S, Huse DA. Porters versus rowers: a unified stochastic model of motor proteins. J Cell Biol. 1993;121:1357–1368. doi: 10.1083/jcb.121.6.1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieber AD, Yehudai-Resheff S, Barnhart EL, Theriot JA, Keren K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Curr Biol. 2013;23:1409–1417. doi: 10.1016/j.cub.2013.05.063. [DOI] [PubMed] [Google Scholar]
- Lin Y-C, Koleske AJ. Mechanisms of synapse and dendrite maintenance and their disruption in psychiatric and neurodegenerative disorders. Annu Rev Neurosci. 2010;33:349–378. doi: 10.1146/annurev-neuro-060909-153204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loudon RP, Silver LD, Yee HF, Jr, Gallo G. RhoA-kinase and myosin II are required for the maintenance of growth cone polarity and guidance by nerve growth factor. J Neurobiol. 2006;66:847–867. doi: 10.1002/neu.20258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medeiros NA, Burnette DT, Forscher P. Myosin II functions in actin-bundle turnover in neuronal growth cones. Nat Cell Biol. 2006;8:215–226. doi: 10.1038/ncb1367. [DOI] [PubMed] [Google Scholar]
- Mogilner A, Rubinstein B. The physics of filopodial protrusion. Biophys J. 2005;89:782–795. doi: 10.1529/biophysj.104.056515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy A, Takagi Y, Billington N, Sun S, Hong D, Homsher E, Wang A, Sellers J. Kinetic characterization of nonmuscle myosin IIB at the single molecule level. J Biol Chem. 2013;288:709–722. doi: 10.1074/jbc.M112.424671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norstrom MF, Smithback PA, Rock RS. Unconventional processive mechanics of non-muscle myosin IIB. J Biol Chem. 2010;285:26326–26334. doi: 10.1074/jbc.M110.123851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portera-Cailliau C, Pan DT, Yuste R. Activity-regulated dynamic behavior of early dendritic protrusions: evidence for different types of dendritic filopodia. J Neurosci. 2003;23:7129–7142. doi: 10.1523/JNEUROSCI.23-18-07129.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryu J, Liu L, Wong TP, Wu DC, Burette A, Weinberg R, Wang YT, Sheng M. A critical role for myosin IIb in dendritic spine morphology and synaptic function. Neuron. 2006;49:175–182. doi: 10.1016/j.neuron.2005.12.017. [DOI] [PubMed] [Google Scholar]
- San Miguel-Ruiz JE, Letourneau PC. The role of arp2/3 in growth cone actin dynamics and guidance is substrate dependent. J Neurosci. 2014;34:5895–5908. doi: 10.1523/JNEUROSCI.0672-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal M. Morphological alterations in dendritic spines of rat hippocampal neurons exposed to N-methyl-D-aspartate. Neurosci Lett. 1995;193:73–76. doi: 10.1016/0304-3940(95)11665-j. [DOI] [PubMed] [Google Scholar]
- Sheetz MP. Cell control by membrane-cytoskeleton adhesion. Nat Rev Mol Cell Biol. 2001;2:392–396. doi: 10.1038/35073095. [DOI] [PubMed] [Google Scholar]
- Shutova M, Yang C, Vasiliev JM, Svitkina T. Functions of nonmuscle myosin II in assembly of the cellular contractile system. PLoS One. 2012;7:e40814. doi: 10.1371/journal.pone.0040814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith BA, Roy H, De Koninck P, Grutter P, De Koninck Y. Dendritic spine viscoelasticity and soft-glassy nature: balancing dynamic remodeling with structural stability. Biophys J. 2007;92:1419–1430. doi: 10.1529/biophysj.106.092361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svitkina T. Electron microscopic analysis of the leading edge in migrating cells. Methods Cell Biol. 2007;79:295–319. doi: 10.1016/S0091-679X(06)79012-4. [DOI] [PubMed] [Google Scholar]
- Svitkina T. Imaging cytoskeleton components by electron microscopy. Methods Mol Biol. 2009;586:187–206. doi: 10.1007/978-1-60761-376-3_10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatavarty V, Das S, Yu J. Polarization of actin cytoskeleton is reduced in dendritic protrusions during early spine development in hippocampal neuron. Mol Biol Cell. 2012;23:3167–3177. doi: 10.1091/mbc.E12-02-0165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatavarty V, Kim E-J, Rodionov V, Yu J. Investigating Sub-spine actin dynamics in rat hippocampal neurons with super-resolution optical imaging. PLoS One. 2009;4:e7724. doi: 10.1371/journal.pone.0007724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verkhovsky AB, Svitkina TM, Borisy GG. Myosin II filament assemblies in the active lamella of fibroblasts: their morphogenesis and role in the formation of actin filament bundles. J Cell Biol. 1995;131:989–1002. doi: 10.1083/jcb.131.4.989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcox KS, Buchhalter J, Dichter MA. Properties of inhibitory and excitatory synapses between hippocampal neurons in very low density cultures. Synapse. 1994;18:128–151. doi: 10.1002/syn.890180206. [DOI] [PubMed] [Google Scholar]
- Wilson CA, Tsuchida MA, Allen GM, Barnhart EL, Applegate KT, Yam PT, Ji L, Keren K, Danuser G, Theriot JA. Myosin II contributes to cell-scale actin network treadmilling through network disassembly. Nature. 2010;465:373–377. doi: 10.1038/nature08994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu JQ, Pollard TD. Counting cytokinesis proteins globally and locally in fission yeast. Science. 2005;310:310–314. doi: 10.1126/science.1113230. [DOI] [PubMed] [Google Scholar]
- Yamashiro S, Watanabe N. A new link between the retrograde actin flow and focal adhesions. J Biochem. 2014;156:239–248. doi: 10.1093/jb/mvu053. [DOI] [PubMed] [Google Scholar]
- Ziv NE, Smith SJ. Evidence for a role of dendritic filopodia in synaptogenesis and spine formation. Neuron. 1996;17:91–102. doi: 10.1016/s0896-6273(00)80283-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.