A PARTIALLY LINEAR FRAMEWORK FOR MASSIVE HETEROGENEOUS DATA

Abstract

We consider a partially linear framework for modelling massive heterogeneous data. The major goal is to extract common features across all sub-populations while exploring heterogeneity of each sub-population. In particular, we propose an aggregation type estimator for the commonality parameter that possesses the (non-asymptotic) minimax optimal bound and asymptotic distribution as if there were no heterogeneity. This oracular result holds when the number of sub-populations does not grow too fast. A plug-in estimator for the heterogeneity parameter is further constructed, and shown to possess the asymptotic distribution as if the commonality information were available. We also test the heterogeneity among a large number of sub-populations. All the above results require to regularize each sub-estimation as though it had the entire sample size. Our general theory applies to the divide-and-conquer approach that is often used to deal with massive homogeneous data. A technical by-product of this paper is the statistical inferences for the general kernel ridge regression. Thorough numerical results are also provided to back up our theory.

1. Introduction

In this paper, we propose a partially linear regression framework for modelling massive heterogeneous data. Let ${\left\{(Y_i,{\mathit{X}}_i,Z_i)\right\}}_{i=1}^N$ be samples from an underlying distribution that may change with N. We assume that there exist s independent sub-populations, and the data from the jth sub-population follows a partially linear model:

$$Y={\mathit{X}}^T{\beta }_0^{\left(j\right)}+f_0\left(Z\right)+\epsilon ,$$ (1.1)

where ε has zero mean and known variance σ². In the above model, Y depends on X through a linear function that may vary across all sub-populations, and depends on Z through a nonlinear function that is common to all sub-populations. The possibly different values of ${\beta }_0^{\left(j\right)}$ are viewed as the source of heterogeneity. We also point out that the sample sizes in some sub-populations could be extremely high in reality. Note that (1.1) is a typical “semi-nonparametric” model (Cheng and Shang, 2013) since we want to infer both commonality and heterogeneity components throughout the paper.

The model (1.1) is motivated by the following scenario: different labs conduct the same experiment on the relationship between a response variable Y (e.g., heart disease) and a set of predictors Z, X₁, X₂,...,X_p. It is known from biological knowledge that the dependence structure between Y and Z (e.g., blood pressure) should be homogeneous for all human. However, for the other covariates (e.g., certain genes), we allow their (linear) relations with Y to potentially vary in different labs. For example, the genetic functionality of different races might be heterogenous. The linear relation is assumed here for simplicity, and particularly suitable when the covariates are discrete.

Statistical modelling for massive data has attracted a flurry of recent research. For homogeneous data, the statistical studies of the divide-and-conquer method currently focus on either parametric inferences, e.g., Bag of Little Bootstraps (Kleiner et al., 2012), and parallel MCMC computing (Wang and Dunson, 2013), or nonparametric minimaxity (Zhang et al., 2013). The other relevant work includes high dimensional linear models with variable selection (Chen and Xie, 2012) and structured perceptron (McDonald et al., 2010). Heterogenous data are often handled by fitting mixture models (Aitkin and Rubin, 1985; McLachlan and Peel, 2004; Figueiredo and Jain, 2002), time varying coefficient models (Hastie and Tibshirani, 1993; Fan and Zhang, 1999) or multitask regression (Huang and Zhang, 2010; Nardi and Rinaldo, 2008; Obozinski et al., 2008). The recent high dimensional work includes Stäadler et al. (2010); Meinshausen and Bühlmann (2014). However, as far as we are aware, semi-nonparametric inference for massive homogeneous/heterogeneous data still remains untouched.

In this paper, our primary goal is to extract common features across all sub-populations while exploring heterogeneity of each sub-population. Specifically, we employ a simple aggregation procedure, which averages commonality estimators across all sub-populations, and then construct a plug-in estimator for each heterogeneity parameter based on the combined estimator for commonality. The secondary goal is to apply the divide-and-conquer method to the sub-population having a huge sample size that is unable to be processed in one single computer. The above purposes are achieved by estimating our statistical model (1.1) with the kernel ridge regression (KRR) method. The KRR framework is known to be very flexible and well supported by the general reproducing kernel Hilbert space (RKHS) theory (Mendelson, 2002; Steinwart et al., 2009; Zhang, 2005). In particular, the partial smoothing spline model (Wahba, 1990) can be viewed a special case. An important technical contribution of this paper is that a (point-wise) limit distribution of the KRR estimate is established by generalizing the smoothing spline inference results in Cheng and Shang (2013). This theoretical innovation makes our work go beyond the existing statistical study on the KRR estimation in large datastes, which mainly focus on their nonparametric minimaxity, e.g., Zhang et al. (2013); Bach (2012); Raskutti et al. (2014).

Our theoretical studies are mostly concerned with the so-called “oracle rule” for massive data. Specifically, we define the “oracle estimate” for commonality (heterogeneity) as the one computed when all the heterogeneity information are given (the commonality information is given in each-subpopulation), i.e., ${\beta }_0^{\left(j\right)}$ 's are known (f₀ is known). We claim that a commonality estimator satisfies the oracle rule if it possesses the same minimax optimality and asymptotic distribution as the “oracle estimate” defined above. A major contribution of this paper is to derive the largest possible diverging rate of s under which our combined estimator for commonality satisfies the oracle rule. In other words, our aggregation procedure can “filter out” the heterogeneity in data when s does not grow too fast with N. Interestingly, we have to set a lower bound on s for our heterogeneity estimate to possess the asymptotic distribution as if the commonality information were available, i.e., oracle rule. Our second contribution is to test the heterogeneity among a large number of sub-populations by employing the recent Gaussian approximation theory (Chernozhukov et al., 2013). The above results directly apply to the divide-and-conquer approach that deals with the sub-population with a huge sample size. In this case, the “oracle estimate” is defined as those computed based on the entire (homogeneous) data in those sub-populations. A rather different goal here is to explore the most computationally efficient way to split the whole sample while performing the best possible statistical inference. Specifically, we derive the largest possible number of splits under which the averaged estimators for both components enjoy the same statistical properties as the oracle estimators.

In both homogeneous and heterogeneous setting above, we note that the upper bounds established for s increase with the smoothness of f₀. Hence, our aggregation procedure favors smoother regression functions in the sense that more sub-populations/splits are allowed in the massive data. On the other hand, we have to admit that our upper and lower bound results for s are only sufficient conditions although empirical results show that our bounds are quite sharp. Another interesting finding is that even the semi-nonparametric estimation is applied to only one fraction of the entire data, it is nonetheless essential to regularize each sub-estimation as if it had the entire sample.

In the end, we highlight two key technical challenges: (i) nontrivial interaction between the parametric and nonparametric components in the semi-nonparametric estimation. In particular, we observe a “bias propagation” phenomenon: the bias introduced by the penalization of the nonparametric component propagates to the parametric component, and the resulting parametric bias in turn propagates back to the nonparametric component. To analyze this complicated propagation mechanism, we extend the existing RKHS theory to an enlarged partially linear function space by defining a novel inner product under which the expectation of the Hessian of the objective function becomes identity. (ii) double asymptotics framework in terms of diverging s and N. In this challenging regime, we develop more refined concentration inequalities in characterizing the concentration property of an aggregated empirical processes. These delicate theoretical analysis show that an average of s asymptotic linear expansions is still a valid one as $s\wedge N\to \infty$ .

The rest of the paper is organized as follows: Section 2 briefly introduces the general RKHS theory and discusses its extension to an enlarged partially linear function space. Section 3 describes our aggregation procedure, and studies the “oracle” property of this procedure from both asymptotic and non-asymptotic perspectives. The efficiency boosting of heterogeneity estimators and heterogenous testing results are also presented in this section. Section 4 applies our general theory to various examples with different smoothness. Section 5 is devoted to the analysis of divide-and-conquer algorithms for homogeneous data. Section 6 presents some numerical experiments. All the technical details are deferred to Section 7 or Online Supplementary.

2. Preliminaries

In this section, we briefly introduce the general RKHS theory, and then extend it to a partially linear function space. Below is a generic definition of RKHS (Berlinet and Thomas-Agnan, 2004):

Definition 2.1

Denote by $\mathcal{F}(\mathcal{S},\mathbb{R})$ a vector space of functions from a general set $\mathcal{S}$ to $\mathbb{R}$ . We say that ${\mathcal{H}}^{\ast }$ is a reproducing kernel Hilbert space (RKHS) on $\mathcal{S}$ , provided that:

• (i) ${\mathcal{H}}^{\ast }$ is a vector subspace of $\mathcal{F}(\mathcal{S},\mathbb{R})$ ;
• (ii) ${\mathcal{H}}^{\ast }$ is endowed with an inner product, denoted as ${\langle \cdot ,\cdot \rangle }_{{\mathcal{H}}^{\ast }}$ , under which it becomes a Hilbert space;
• (iii)for every $y\in \mathcal{S}$ , the linear evaluation functional defined by E_y(f) = f(y) is bounded.

If ${\mathcal{H}}^{\ast }$ is a RKHS, by Riesz representation, we have that for every $y\in \mathcal{S}$ , there exists a unique vector, $K_y^{\ast }\in {\mathcal{H}}^{\ast }$ , such that for every $f\in {\mathcal{H}}^{\ast },f\left(y\right)={\langle f,K_y^{\ast }\rangle }_{{\mathcal{H}}^{\ast }}$ . The reproducing kernel for ${\mathcal{H}}^{\ast }$ is defined as $K^{\ast }(x,y)=K_y^{\ast }\left(x\right)$ .

Denote $U≔(\mathit{X},Z)\in \mathcal{X}\times \mathcal{Z}\subset {\mathbb{R}}^p\times \mathbb{R}$ , and ${\mathbb{P}}_U$ as the distribution of U ( ${\mathbb{P}}_X$ and ${\mathbb{P}}_Z$ are defined similarly). According to Definition 2.1, if $\mathcal{S}=\mathcal{Z}$ and $\mathcal{F}(\mathcal{Z},\mathbb{R})=L_2\left({\mathbb{P}}_Z\right)$ , then we can define a RKHS $\mathcal{H}\subset L_2\left({\mathbb{P}}_Z\right)$ (endowed with a proper inner product ${\langle \cdot ,\cdot \rangle }_{\mathcal{H}}$ ), in which the true function f₀ is believed to lie. The corresponding kernel for $\mathcal{H}$ is denoted by K such that for any $z\in \mathcal{Z}$ : $f\left(z\right)={\langle f,K_z\rangle }_{\mathcal{H}}$ . By Mercer theorem, this kernel function has the following unique eigen-decomposition:

$$K(z_1,z_2)=\sum _{\ell =1}^{\infty }{\mu }_{\ell }{\varphi }_{\ell }\left(z_1\right){\varphi }_{\ell }\left(z_2\right),$$

where μ₁ ≥ μ₂ ≥ ... > 0 are eigenvalues and ${\left\{{\varphi }_{\ell }\right\}}_{\ell =1}^{\infty }$ are an orthonormal basis in $L_2\left({\mathbb{P}}_Z\right)$ . Let ${\left\{{\theta }_{\ell }\right\}}_{\ell =1}^{\infty }$ be the Fourier coefficient of f₀ under the basis ${\left\{{\varphi }_{\ell }\right\}}_{\ell =1}^{\infty }$ (given the $L_2\left({\mathbb{P}}_Z\right)$ -inner product ${\langle \cdot ,\cdot \rangle }_{L_2\left({\mathbb{P}}_Z\right)}$ ). Mercer theorem together with the reproducing property implies that ${\langle {\varphi }_i,{\varphi }_j\rangle }_{\mathcal{H}}={\delta }_{ij}∕{\mu }_i$ , where δ_ij is the Kronecker's delta. The smoothness of the functions in RKHS can be characterized by the decaying rate of ${\left\{{\mu }_{\ell }\right\}}_{\ell =1}^{\infty }$ . Below, we present three different decaying rates together with the corresponding kernel functions.

Finite rank kernel

the kernel has finite rank r if ${\mu }_{\ell }=0$ for all $\ell >r$ . For example, the linear kernel $K({\mathit{z}}_1,{\mathit{z}}_2)={\langle {\mathit{z}}_1,{\mathit{z}}_2\rangle }_{{\mathbb{R}}^d}$ has rank d, and generates a d-dimensional linear function space. The eigenfunctions are given by ${\varphi }_{\ell }\left(\mathit{z}\right)=z_{\ell }$ for $\ell =1,\dots ,d$ . The polynomial kernel K(z₁, z₂) = (1 + z₁ z₂)^d has rank d + 1, and generates a space of polynomial functions with degree at most d. The eigenfunctions are given by ${\varphi }_{\ell }=z^{\ell -1}$ for $\ell =1,\dots ,d+1$ .

Exponentially decaying kernel

the kernel has eigenvalues that satisfy ${\mu }_{\ell }\asymp c_1\exp (-c_2{\ell }^p)$ for some c₁ c₂ > 0. An example is the Gaussian kernel K(z₁, z₂) = exp(–|z₁ – z₂|²). The eigenfunctions are given by Sollich and Williams (2005)

$${\varphi }_{\ell }\left(x\right)={(\sqrt{5}∕4)}^{1∕4}{(2^{\ell -2}(\ell -1)!)}^{-1∕2}{e}^{-(\sqrt{5}-1)x^2∕4}{H}_{\ell -1}\left({(\sqrt{5}∕2)}^{1∕2}x\right),$$ (2.1)

for $\ell =1,2,\cdots$ , where $H_{\ell }(\cdot )$ is the $\ell \text{-th}$ Hermite polynomial.

Polynomially decaying kernel

the kernel has eigenvalues that satisfy ${\mu }_{\ell }\asymp {\ell }^{2\nu }$ for some ν ≥ 1/2. Examples include those underlying for Sobolev space and Besov space (Birman and Solomjak, 1967). In particular, the eigenfunctions of a ν-th order periodic Sobolev space are trigonometric functions as specified in Section 4.3. The corresponding Sobolev kernels are given in Gu (2013).

In this paper, we consider the following penalized estimation:

$$({\widehat{\beta }}^{†},{\widehat{f}}^{†})=\underset{(\beta ,f)\in \mathcal{A}}{\mathrm{argmin}}\left\{\frac{1}{n}\sum _{i=1}^n{(Y_i-{\mathit{X}}_i^T\beta -f\left(Z_i\right))}^2+\lambda {\Vert f\Vert }_{\mathcal{H}}^2\right\},$$ (2.2)

where λ > 0 is a regularization parameter and $\mathcal{A}$ is defined as the parameter space ${\mathbb{R}}^p\times \mathcal{H}$ . For simplicity, we do not distinguish $m=(\beta ,f)\in \mathcal{A}$ from its associated function $m\in \mathcal{M}≔\{{\mathit{x}}^T\beta +f\left(z\right):(\beta ,f)\in \mathcal{A}\text{and}(\mathit{x},z)\in \mathcal{X}\times \mathcal{Z}\}$ throughout the paper. We call $({\widehat{\beta }}^{†},{\widehat{f}}^{†})$ as partially linear kernel ridge regression (KRR) estimate in comparison with the nonparametric KRR estimate in Shawe-Taylor and Cristianini (2004). In particular, when $\mathcal{H}$ is a ν-th order Sobolev space endowed with ${\langle f,\tilde{f}\rangle }_{\mathcal{H}}≔{\int }_{\mathcal{Z}}{f}^{\left(\nu \right)}\left(z\right){\tilde{f}}^{\left(\nu \right)}\left(z\right)dz$ , $({\widehat{\beta }}^{†},{\widehat{f}}^{†})$ becomes the commonly used partial smoothing spline estimate.

We next illustrate that $\mathcal{A}$ can be viewed as a partially linear extension of $\mathcal{H}$ in the sense that it shares some nice reproducing properties as this RKHS $\mathcal{H}$ under the following inner product:

$${\langle m,\tilde{m}\rangle }_{\mathcal{A}}={\langle {\mathit{X}}^T\beta +f\left(Z\right),{\mathit{X}}^T\tilde{\beta }+\tilde{f}\left(Z\right)\rangle }_{L_2\left({\mathbb{P}}_U\right)}+\lambda {\langle f,\tilde{f}\rangle }_{\mathcal{H}},$$ (2.3)

where $m=(\beta ,f)\in \mathcal{A}$ and $\tilde{m}=(\tilde{\beta },\tilde{f})\in \mathcal{A}$ . Similar as the kernel function K_z, we can construct a linear operator $R_u(\cdot )\in \mathcal{A}$ such that ${\langle R_u,m\rangle }_{\mathcal{A}}=m\left(u\right)$ for any $u\in \mathcal{X}\times \mathcal{Z}$ . Also, construct another linear operator $P_{\lambda }:\mathcal{A}\mapsto \mathcal{A}$ such that ${\langle P_{\lambda }m,\tilde{m}\rangle }_{\mathcal{A}}=\lambda {\langle f,\tilde{f}\rangle }_{\mathcal{H}}$ for any m and $\tilde{m}$ . See Proposition 2.3 for the construction of R_u and P_λ.

We next present a proposition illustrating the rational behind the definition of ${\langle \cdot ,\cdot \rangle }_{\mathcal{A}}$ . Denote $\otimes$ as the outer product on $\mathcal{A}$ . Hence, ${\mathbb{E}}_U[R_U\otimes R_U]+P_{\lambda }$ is an operator from $\mathcal{A}$ to $\mathcal{A}$ .

Proposition 2.2

${\mathbb{E}}_U[R_U\otimes R_U]+P_{\lambda }=id$ , where id is an identity operator on $\mathcal{A}$ .

Proof

For any $m(\beta ,f)\in \mathcal{A}$ and $\tilde{m}=(\tilde{\beta },\tilde{f})\in \mathcal{A}$ , we have

$$\begin{array}{cc}\hfill {\langle ({\mathbb{E}}_U[R_U\otimes R_U]+P_{\lambda })m,\tilde{m}\rangle }_{\mathcal{A}}=& {\langle {\mathbb{E}}_U[R_U\otimes R_U]m,\tilde{m}\rangle }_{\mathcal{A}}+{\langle P_{\lambda }m,\tilde{m}\rangle }_{\mathcal{A}}\hfill \\ \hfill =& {\mathbb{E}}_U\left[m\left(U\right)\tilde{m}\left(U\right)\right]+\lambda {\langle f,\tilde{f}\rangle }_{\mathcal{H}}\hfill \\ \hfill =& {\langle m,\tilde{m}\rangle }_{\mathcal{A}}.\hfill \end{array}$$

Since the choice of $(m,\tilde{m})$ is arbitrary, we conclude our proof.

As will be seen in the subsequent analysis, e.g., in Theorem 3.3, the operator $\mathbb{E}[R_U\otimes R_U]+P_{\lambda }$ is essentially the expectation of the Hessian of the objective function (w.r.t. Fréchet derivative) minimized in (2.2). Proposition 2.2 shows that the inversion of this Hessian matrix is trivial when the inner product is designed as in (2.3). Due to that, the theoretical analysis of $\widehat{m}=(\widehat{\beta },\widehat{f})$ based on the first order optimality condition becomes much more transparent.

To facilitate the construction of R_u and P_λ, we need to endow a new inner product with $\mathcal{H}$ :

$${\langle f,\tilde{f}\rangle }_{\mathcal{C}}={\langle f,\tilde{f}\rangle }_{L_2\left({\mathbb{P}}_Z\right)}+\lambda {\langle f,\tilde{f}\rangle }_{\mathcal{H}},$$ (2.4)

for any $f,\tilde{f}\in \mathcal{H}$ . Under (2.4), $\mathcal{H}$ is still a RKHS as the evaluation functional is bounded by Lemma A.1. We denote the new kernel function as $\tilde{K}(\cdot ,\cdot )$ , and define a positive definite self-adjoint operator $W_{\lambda }:\mathcal{H}\mapsto \mathcal{H}$ :

$${\langle W_{\lambda }f,\tilde{f}\rangle }_{\mathcal{C}}=\lambda {\langle f,\tilde{f}\rangle }_{\mathcal{H}}\text{for any}f,\tilde{f}\in {\mathcal{H}}^{\prime },$$ (2.5)

whose existence is proven in Lemma A.2. Since ${\Vert f\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2={\sum }_{i=1}^{\infty }{\theta }_i^2$ and ${\Vert f\Vert }_{\mathcal{H}}^2={\sum }_{i=1}^{\infty }{\theta }_i^2∕{\mu }_i$ , we now have ${\Vert f\Vert }_{\mathcal{C}}^2={\sum }_{i=1}^{\infty }{\theta }_i^2(1+\lambda ∕{\mu }_i)$ by (2.4). We next define two crucial quantities needed in the construction: $B_k≔\mathbb{E}[X_k\mid Z]$ and its Riesz representer $A_k\in \mathcal{H}$ satisfying ${\langle A_k,f\rangle }_{\mathcal{C}}={\langle B_k,f\rangle }_{L_2\left({\mathbb{P}}_Z\right)}$ for all $f\in \mathcal{H}$ . Here, we implicity assume B_k is square integrable. The existence of A_k follows from the boundedness of the linear functional ${\mathcal{B}}_{k}f≔{\langle B_k,f\rangle }_{L_2\left({\mathbb{P}}_Z\right)}$ (by Riesz's representer theorem) as follows:

$$\mid {\mathcal{B}}_{k}f\mid =\mid {\langle B_k,f\rangle }_{L_2\left({\mathbb{P}}_Z\right)}\mid \le {\Vert B_k\Vert }_{L_2\left({\mathbb{P}}_Z\right)}{\Vert f\Vert }_{L_2\left({\mathbb{P}}_Z\right)}\le {\Vert B_k\Vert }_{L_2\left({\mathbb{P}}_Z\right)}{\Vert f\Vert }_{\mathcal{C}}.$$

We are now ready to construct R_u and P_λ based on ${\tilde{K}}_z$ , W_λ, B and A introduced above, where B = (B₁,..., B_p)^T and A = (A₁,...,A_p)^T. Define $\Omega =\mathbb{E}\left[(\mathit{X}-\mathit{B}){(\mathit{X}-\mathit{B})}^T\right]$ and ${\Sigma }_{\lambda }=\mathbb{E}\left[\mathit{B}\left(Z\right){(\mathit{B}\left(Z\right)-\mathit{A}\left(Z\right))}^T\right]$ .

Proposition 2.3

For any u = (x, z), R_u can be expressed as $R_u:u\mapsto (L_u,N_u)\in \mathcal{A}$ , where

$$L_u={(\Omega +{\Sigma }_{\lambda })}^{-1}(\mathit{x}-\mathit{A}\left(z\right))\text{and}{N}_u={\tilde{K}}_z-{\mathit{A}}^T{L}_u,$$

Moreover, for any $m=(\beta ,f)\in \mathcal{A}$ , P_λm can be expressed as $P_{\lambda }m=(L_{\lambda }f,N_{\lambda f})\in \mathcal{A}$ , where

$$L_{\lambda }f=-{(\Omega +{\Sigma }_{\lambda })}^{-1}{\langle \mathit{B},W_{\lambda }f\rangle }_{L_2\left({\mathbb{P}}_Z\right)}\text{and}{N}_{\lambda }f=W_{\lambda }f-{\mathit{A}}^T{L}_{\lambda }f.$$

Notation

Denote ∥ · ∥₂ and ∥ · ∥_∞ as the Euclidean L₂ and infinity norm in ${\mathbb{R}}^p$ , respectively. For any function $f:\mathcal{Z}\mapsto \mathbb{R}$ , let ${\Vert f\Vert }_{\sup }={\sup }_{z\in \mathcal{Z}}\mid f\left(z\right)\mid$ . We use ∥ · ∥ to denote the spectral norm of matrices. For positive sequences a_n and b_n, we write $a_n\lesssim b_n(a_n\gtrsim b_n)$ if there exists some universal constant constant c > 0 (c′ > 0) independent of n such that a_n ≤ cb_n (a_n ≥ c′b_n) for all $n\in \mathbb{N}$ . We denote $a_n\asymp b_n$ if both $a_n\lesssim b_n$ and $a_n\gtrsim b_n$ . We define h as the inverse of ${\sum }_{\ell =1}^{\infty }1(1+\lambda ∕{\mu }_{\ell })$ , which is known to be the “effective dimension” of a kernel K $(\mathrm{w}.\mathrm{r}.\mathrm{t}.L_2\left({\mathbb{P}}_Z\right))$ (Zhang, 2005). For any function space $\mathcal{F}$ , define

$$\omega (\mathcal{F},\delta )={\int }_0^{\delta }\sqrt{\log \mathcal{N}(\mathcal{F},\Vert \cdot \Vert {}_{\sup },ϵ)}dϵ,$$

where $\mathcal{N}(\mathcal{F},{\Vert \cdot \Vert }_{\sup },ϵ)$ is an ∈-covering number of $\mathcal{F}$ w.r.t. supreme norm. Define the following sets of functions: ${\mathcal{F}}_1=\{f\left(\mathit{x}\right)={\mathit{x}}^T\beta :{\Vert f\Vert }_{\sup }\le 1\text{for all}\mathit{x}\in \mathcal{X},\beta \in {\mathbb{R}}^p\}$ , ${\mathcal{F}}_2=\{f\in \mathcal{H}:{\Vert f\Vert }_{\sup }\le 1,{\Vert f\Vert }_{\mathcal{H}}\le h^{1∕2}{\lambda }^{-1∕2}\}$ , $\mathcal{F}≔\{f=f_1+f_2:f_1\in {\mathcal{F}}_1,f_2\in {\mathcal{F}}_2,{\Vert f\Vert }_{\sup }\le 1∕2\}$ .

3. Heterogeneous Data: Aggregation of Commonality

In this section, we start from describing our aggregation procedure and model assumptions in Section 3.1. The main theoretical results are presented in Sections 3.2–3.4 showing that our combined estimate for commonality enjoys the “oracle property”. To be more specific, we show that it possesses the same (non-asymptotic) minimax optimal bound (in terms of mean-squared error) and asymptotic distribution as the “oracle estimate” ${\widehat{f}}_{or}$ computed when all the heterogeneity information are available:

$${\widehat{f}}_{or}=\underset{f\in \mathcal{H}}{\mathrm{argmin}}\left\{\frac{1}{N}\sum _{j=1}^s\sum _{i\in L_j}{(Y_i-{\left({\beta }_0^{\left(j\right)}\right)}^T{\mathit{X}}_i-f\left(Z_i\right))}^2+\lambda {\Vert f\Vert }_{\mathcal{H}}^2\right\}.$$ (3.1)

The above nice properties hold when the number of sub-populations does not grow too fast and the smoothing parameter is chosen according to the entire sample size N. Based on this combined estimator, we further construct a plug-in estimator for each heterogeneity parameter ${\beta }_0^{\left(j\right)}$ , which possesses the asymptotic distribution as if the commonality were known, in Section 3.5. Interestingly, this oracular result holds when the number of sub-population is not too small. In the end, Section 3.6 tests the possible heterogeneity among a large number of sub-populations.

3.1. Method and Assumptions

The heterogeneous data setup and averaging procedure are described below:

1. Obverse data (X_i, Z_i, Y_i) with the known label L_i ∈ {1, 2,...,s indicating the sub-population it belongs to, for i = 1,...,N. The size of samples from each sub-population is assumed to be the same, denoted by n, for simplicity. Hence, N = n × s.

2. On the j-th sub-population, obtain the following penalized estimator:

$$({\widehat{\beta }}_{n,\lambda }^{\left(j\right)},{\widehat{f}}_{n,\lambda }^{\left(j\right)}=\underset{(\beta ,f)\in \mathcal{A}}{\mathrm{argmin}}\left\{\frac{1}{n}\sum _{i\in L_j}{({\mathit{X}}_i^T\beta +f\left(Z_i\right)-Y_i)}^2+\lambda {\Vert f\Vert }_{\mathcal{H}}^2\right\}.$$ (3.2)

3. Obtain the final nonparametric estimate¹ for commonality by averaging:

$${\stackrel{‒}{f}}_{N,\lambda }=\frac{1}{s}\sum _{j=1}^s{\widehat{f}}_{n,\lambda }^{\left(j\right)}.$$ (3.3)

We point out that ${\widehat{\beta }}_{n,\lambda }^{\left(j\right)}$ is not our final estimate for heterogeneity. In fact, it can be further improved based on f̄_N,λ; see Section 3.5.

For simplicity, we will drop the subscripts (n, λ) and (N, λ) in those notation defined in (3.2) and (3.3) throughout the rest of this paper. The main assumptions of this section are stated below.

Assumption 3.1 (Regularity Condition)

(i) ε_i's are i.i.d. sub-Gaussian random variables independent of the designs; (ii) $B_k\in L_2\left({\mathbb{P}}_Z\right)$ for all k, and $\Omega ≔\mathbb{E}\left[(\mathit{X}-\mathit{B}\left(Z\right)){(\mathit{X}-\mathit{B}\left(Z\right))}^T\right]$ is positive definite; (iii) X_i's are uniformly bounded by a constant c_x.

Conditions in Assumption 3.1 are fairly standard in the literature. For example, the positive definiteness of Ω is needed for obtaining semiparametric efficient estimation; see Mammen and van de Geer (1997). Note that we do not require the independence between X and Z throughout the paper.

Assumption 3.2 (Kernel Condition)

We assume that there exist 0 < c_ϕ < ∞ and 0 < c_K < ∞ such that ${\sup }_{\ell }{\Vert {\varphi }_{\ell }\Vert }_{\sup }\le c_{\varphi }$ and sup_z K(z, z) ≤ c_K.

Assumption 3.2 is commonly assumed in kernel ridge regression literature (Zhang et al., 2013; Lafferty and Lebanon, 2005; Guo, 2002). In the case of finite rank kernel, e.g., linear and polynomial kernels, the eigenfunctions are uniformly bounded as long as Ƶ has finite support. As for the exponentially decaying kernels such as Gaussian kernel, we prove in Section 4.2 that the eigenfunctions given in (2.1) are uniformly bounded by 1.336. Lastly, for the polynomially decaying kernels, Proposition 2.2 in Shang and Cheng (2013) showed that the eigenfunctions induced from a ν-th order Sobolev space (under a proper inner product ${\langle \cdot ,\cdot \rangle }_{\mathcal{H}}$ ) are uniformly bounded under mild smoothness conditions for the density of Z.

Assumption 3.3

For each $k=1,\dots ,p,B_k(\cdot )\in \mathcal{H}$ . This is equivalent to

$$\sum _{\ell =1}^{\infty }{\mu }_{\ell }^{-1}{\langle B_k,{\varphi }_{\ell }\rangle }_{L_2\left({\mathbb{P}}_Z\right)}^2<\infty .$$

Assumption 3.3 requires the conditional expectation of X_k given Z = z is as smooth as f₀(z). As can be seen in Section 3.4, this condition is imposed to control the bias of the parametric component, which is caused by penalization on the the nonparametric component. We call this interaction as the “bias propagation phenomenon”, and study it in Section 3.4.

3.2. Non-Asymptotic Bound for Mean-Squared Error

The primary goal of this section is to evaluate the estimation quality of the combined estimate from a non-asymptotic point of view. Specifically, we derive a finite sample upper bound for the mean-squared error $\mathrm{MSE}\left(\stackrel{‒}{f}\right)≔\mathbb{E}\left[{\Vert \stackrel{‒}{f}-f_0\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\right]$ . When s does not grow too fast, we show that MSE(f̄) is of the order $O({\left(Nh\right)}^{-1}+\lambda )$ , from which the aggregation effect on f can be clearly seen. If λ is chosen in the order of N, the mean-squared error attains the (un-improvable) optimal minimax rate. As a by-product, we establish a non-asymptotic upper bound for the mean-squared error of ${\widehat{\beta }}^{\left(j\right)}$ , i.e., $\mathrm{MSE}\left({\widehat{\beta }}^{\left(j\right)}\right)≔\mathbb{E}\left[{\Vert {\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)}\Vert }_2^2\right]$ . The results in this section together with Theorem 3.4 in Section 3.4 determine an upper bound of s under which f̄ enjoys the same statistical properties (minimax optimality and asymptotic distribution) as the oracle estimate f̂_or.

Define τ_min(Ω) as the minimum eigenvalue of Ω and $\mathrm{Tr}\left(K\right)≔{\sum }_{\ell =1}^{\infty }{\mu }_{\ell }$ as the trace of K. Moreover, let $C_1^{\prime }=2{\tau }_{\min }^{-2}\left(\Omega \right)(c_x^{2}p+c_{\varphi }^2\mathrm{Tr}\left(K\right){\sum }_{k=1}^p{\Vert B_k\Vert }_{\mathcal{H}}^2)$ , $C_1=2c_{\varphi }^2(1+C_1^{\prime }{\sum }_{k=1}^p{\Vert B_k\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2)$ , $C_2^{\prime }={\tau }_{\min }^{-2}\left(\Omega \right){\Vert f_0\Vert }_{\mathcal{H}}^2{\sum }_{k=1}^p{\Vert B_k\Vert }_{\mathcal{H}}^2$ and $C_2=2C_2^{\prime }{\sum }_{k=1}^p{\Vert B_k\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2$ .

Theorem 3.1

Suppose that Assumptions 3.1–3.3 hold. If $s=o\left(N{h}^2{(\omega (\mathcal{F},1)+\log N)}^{-2}\right)$ , then we have

$$\mathrm{MSE}\left(\stackrel{‒}{f}\right)\le C_1{\sigma }^2{\left(Nh\right)}^{-1}+2{\Vert f_0\Vert }_{\mathcal{H}}^2\lambda +C_2{\lambda }^2+s^{-1}a(n,s,h,\lambda ,\omega ),$$ (3.4)

where $a(n,s,h,\lambda ,\omega )=C{h}^{-1}{n}^{-1}{r}_{n,s}^2(\omega {(\mathcal{F},1)}^2+1)+C{h}^{-2}{\lambda }^{-1}n\exp (-c{\log }^{2}N)$ , r_n,s = (nh)^−1/2log² N + λ and C is some generic constant.

Typically, we require an upper bound for s so that the third term in the R.H.S. of (3.4) can be dominated by the first two terms, which correspond to variance and bias, respectively. Hence, we choose $\lambda \asymp {\left(Nh\right)}^{-1}$ to attain the optimal bias-variance trade-off. The resulting rate coincides with the minimax optimal rate of the oracle estimate in different RKHS; see Section 4. This can be viewed as a non-asymptotic version of the “oracle property” of f̄. In comparison with the nonparametric KRR result in Zhang et al. (2013), we realize that adding one parametric component does not affect the finite sample upper bound (3.4).

As a by-product, we obtain a non-asymptotic upper bound for $\mathrm{MSE}\left({\widehat{\beta }}^{\left(j\right)}\right)$ . This result is new, and also of independent interest.

Theorem 3.2

Suppose that Assumptions 3.1 – 3.3 hold. Then we have

$$\mathrm{MSE}\left({\widehat{\beta }}^{\left(j\right)}\right)\le C_1^{\prime }{\sigma }^2{n}^{-1}+C_2^{\prime }{\lambda }^2+a(n,s,h,\lambda ,\omega ),$$ (3.5)

where a(n, s, h, λ, ω) is defined in Theorem 3.1.

Again, the first term and second term in the R.H.S. of (3.5) correspond to the variance and bias, respectively. In particular, the second term comes from the bias propagation effect to be discussed in Section 3.4. By choosing λ= o(n^−1/2), we can obtain the optimal rate of $\mathrm{MSE}\left({\widehat{\beta }}^{\left(j\right)}\right)$ , i.e., O(n^−1/2), but may lose the minimax optimality of MSE(f̄) in most cases.

3.3. Joint Asymptotic Distribution

In this section, we derive a preliminary result on the joint limit distribution of $({\widehat{\beta }}^{\left(j\right)},\stackrel{‒}{f}\left(z_0\right))$ at any $z_0\in \mathcal{Z}$ . A key issue with this result is that their centering is not at the true value. However, we still choose to present it here since we will observe an interesting phenomenon when removing the bias in Section 3.4.

Theorem 3.3 (Joint Asymptotics I)

Suppose that Assumptions 3.1 and 3.2 hold, and that as $N\to \infty ,h{\Vert {\tilde{K}}_{z_0}\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\to {\sigma }_{z_0}^2$ , $h^{1∕2}\left(W_{\lambda }\mathit{A}\right)\left(z_0\right)\to {\alpha }_{z_0}\in {\mathbb{R}}^p$ , and $h^{1∕2}\mathit{A}\left(z_0\right)\to -{\gamma }_{z_0}\in {\mathbb{R}}^p$ . Suppose the following conditions are satisfied

$$s=o\left(N{h}^2{(\omega (\mathcal{F},1)+\log N)}^{-2}\right),$$ (3.6)

$$s{\left(Nh\right)}^{-1}{\log }^{4}N+\lambda =o\left(h^2{(\omega (\mathcal{F},1)+\log N)}^{-2}{\log }^{-2}\left(N\right)\right).$$ (3.7)

Denote $({\beta }_0^{\left(j\right)\ast },f_0^{\ast })$ as $(id-P_{\lambda })m_0^{\left(j\right)}$ , where $m_0^{\left(j\right)}=({\beta }_0^{\left(j\right)},f_0)$ . We have for any z₀ ∈ Ƶ and j = 1,...,s,

• (i)
  if s → ∞ then

  $$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)\ast }\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0^{\ast }\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Sigma }_{22}\hfill \end{array}\right)\right),$$ (3.8)

  where ${\Sigma }_{22}={\sigma }_{z_0}^2+2{\gamma }_{z_0}^T{\Omega }^{-1}{\alpha }_{z_0}+{\gamma }_{z_0}^T{\Omega }^{-1}{\gamma }_{z_0}$ ;
• (ii)
  if s is fixed, then

  $$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)\ast })\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0^{\ast }\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill s^{-1∕2}{\Sigma }_{21}\hfill \\ \hfill s^{-1∕2}{\Sigma }_{12}\hfill & \hfill {\Sigma }_{22}\hfill \end{array}\right)\right),$$ (3.9)

  where ${\Sigma }_{12}={\Sigma }_{12}^T={\Omega }^{-1}({\alpha }_{z_0}+{\gamma }_{z_0})$ .

Part (i) of Theorem 3.3 says that $\sqrt{n}{\widehat{\beta }}^{\left(j\right)}$ and $\sqrt{Nh}\stackrel{‒}{f}\left(z_0\right)$ are asymptotically independent as s → ∞. This is not surprising since only samples in one sub-population (with size n) contribute to the estimation of the heterogeneity component while the entire sample (with size N) to commonality. As n/N = s⁻¹ → 0, the former data becomes asymptotically independent of (or asymptotically ignorable to) the latter data. So are these two estimators. The estimation bias $P_{\lambda }{m}_0^{\left(j\right)}$ can be removed by placing a smoothness condition on B_k, i.e., Assumption 3.3. Interestingly, given this additional condition, even when s is fixed, these two estimators can still achieve the asymptotic independence if h → 0. Please see more details in next section.

3.4. Bias Propagation

In this section, we first analyze the source of estimation bias observed in the joint asymptotics Theorem 3.3. In fact, these analysis leads to a bias propagation phenomenon, which intuitively explains how Assumption 3.3 removes the estimation bias. More importantly, we show that f̄ shares exactly the same asymptotic distribution as f̂_or, i.e., oracle rule, when s does not grow too fast and λ is chosen in the order of N.

Our study on propagation mechanism is motivated by the following simple observation. Denote $\mathbb{X}\in {\mathbb{R}}^{n\times p}$ and $\mathbb{Z}\in {\mathbb{R}}^n$ as the designs based on the samples from the jth sub-population and let ${\epsilon }^{\left(j\right)}={\left[{ϵ}_i\right]}_{i\in L_j}\in {\mathbb{R}}^n$ . The first order optimality condition (w.r.t. β) gives

$${\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)}={\left({\mathbb{X}}^T\mathbb{X}\right)}^{-1}{\mathbb{X}}^T{\epsilon }^{\left(j\right)}-{\left({\mathbb{X}}^T\mathbb{X}\right)}^{-1}{\mathbb{X}}^T({\widehat{f}}^{\left(j\right)}\left(\mathbb{Z}\right)-f_0\left(\mathbb{Z}\right)),$$ (3.10)

where $f_0\left(\mathbb{Z}\right)$ is a n-dimensional vector with entries f₀(Z_i) for i ∈ L_j and ${\widehat{f}}^{\left(j\right)}\left(\mathbb{Z}\right)$ is defined similarly. Hence, the estimation bias of ${\widehat{\beta }}^{\left(j\right)}$ inherits from that of f̂^(j). A more complete picture on the propagation mechanism can be seen by decomposing the total bias $P_{\lambda }{m}_0^{\left(j\right)}$ into two parts:

$$\text{parametric bias}:L_{\lambda }{f}_0=-{(\Omega +{\Sigma }_{\lambda })}^{-1}{\langle \mathit{B},W_{\lambda }{f}_0\rangle }_{L_2\left({\mathbb{P}}_Z\right)},$$ (3.11)

$$\text{nonparametric bias}:N_{\lambda }{f}_0=W_{\lambda }{f}_0-{\mathit{A}}^T{L}_{\lambda }{f}_0$$ (3.12)

according to Proposition 2.3. The first term in (3.12) explains the bias introduced by penalization; see (2.5). This bias propagates to the parametric component through B, as illustrated in (3.11). The parametric bias L_λf₀ propagates back to the nonparametric component through the second term of (3.12). Therefore, by strengthening $B_k\in L_2\left({\mathbb{P}}_Z\right)$ to $B_k\in \mathcal{H}$ , i.e., Assumption 3.3, it can be shown that the order of L_λf₀ in (3.11) reduces to that of λ. And then we can remove L_λf₀ asymptotically by choosing a sufficiently small λ. In this case, the nonparametric bias becomes W_λf₀.

We summarize the above discussions in the following theorem:

Theorem 3.4. (Joint Asymptotics II)

Suppose Assumption 3.3 and the conditions in Theorem 3.3 hold. If we choose $\lambda =o({\left(Nh\right)}^{-1∕2}\wedge n^{-1∕2})$ , then

• (i)
  if s → ∞ then

  $$\begin{gathered} \left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right)-W_{\lambda }{f}_0\left(z_0\right))\hfill \end{array}\right) \\ ⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Sigma }_{22}^{\ast }\hfill \end{array}\right)\right), \end{gathered}$$ (3.13)

  where ${\Sigma }_{22}^{\ast }={\sigma }_{z_0}^2+{\gamma }_{z_0}^T{\Omega }^{-1}{\gamma }_{z_0}$ ;
• (ii)
  if s is fixed, then

  $$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right)-W_{\lambda }{f}_0\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill s^{-1∕2}{\Sigma }_{21}^{\ast }\hfill \\ \hfill s^{-1∕2}{\Sigma }_{12}^{\ast }\hfill & \hfill {\Sigma }_{22}^{\ast }\hfill \end{array}\right)\right),$$ (3.14)

  where ${\Sigma }_{12}^{\ast }={\Sigma }_{12}^{\ast T}={\Omega }^{-1}{\gamma }_{z_0}$ and ${\Sigma }_{22}^{\ast }$ is the same as in (i).

Moreover, if h → 0, then ${\Sigma }_{12}^{\ast }={\Sigma }_{21}^{\ast }=0$ and ${\Sigma }_{22}^{\ast }={\sigma }_{z_0}^2$ in (i) and (ii).

The nonparametric estimation bias W_λf₀(z₀) can be further removed by performing undersmoothing, a standard procedure in nonparametric inference, e.g., Shang and Cheng (2013). We will illustrate this point in Section 4.

By examining the proof for case (ii) of Theorem 3.4 (and taking s = 1), we know that the oracle estimate f̄_or defined in (3.1) attains the same asymptotic distribution as that of f̄ in (3.13) when s grows at a proper rate. Therefore, we claim that our combined estimate f̄ satisfies the desirable oracle property.

In Section 4, we apply Theorem 3.4 to several examples, and find that even though the minimization (3.2) is based only on one fraction of the entire sample, it is nonetheless essential to regularize each sub-estimation as if it had the entire sample. In other words, λ should be chosen in the order of N. Similar phenomenon also arises in analyzing minimax optimality of each sub-estimation; see Section 3.2.

Cheng and Shang (2013) have recently uncovered a joint asymptotics phenomenon in partial smoothing spline models: parametric estimate and (point-wise) nonparametric smoothing spline estimate become asymptotically independent after the parametric bias is removed. This corresponds to a special case of Part (ii) of Theorem 3.4 for polynomially decaying kernels with s = 1 and h → ∞. Therefore, case (ii) in Theorem 3.4 generalizes this new phenomenon to the partially linear kernel ridge regression models. When $h\nrightarrow 0$ , e.g., $h\asymp r^{-1}$ for finite rank kernel, the semi-nonparametric estimation in consideration essentially reduces to a parametric one. Hence, it is not surprising that the asymptotic dependence remains.

Remark 3.1

Theorem 3.4 implies that $\sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})⇝N(0,{\sigma }^2{\Omega }^{-1})$ when λ = o(n^−1/2). When the error ∈ follows a Gaussian distribution, it is well known that ${\widehat{\beta }}^{\left(j\right)}$ achieves the semiparametric efficiency bound (Kosorok, 2007). Hence, the semiparametric efficient estimate can be the obtained by applying the kernel ridge method. However, we can further improve its estimation efficiency to a parametric level by taking advantage of f̄ (built on the whole samples). This is one important feature of massive data: strength-borrowing.

Efficiency Boosting: from semiparametric level to parametric level

The previous sections show that the combined estimate f̄ achieves the “oracle property” in both asymptotic and non-asymptotic senses when s does not grow too fast and λ is chosen according to the entire sample size. In this section, we employ f̄ to boost the estimation efficiency of ${\widehat{\beta }}^{\left(j\right)}$ from semiparametric level to parametric level. This leads to our final estimate for heterogeneity, i.e., ${\check{\beta }}^{\left(j\right)}$ defined in (3.15). More importantly, ${\check{\beta }}^{\left(j\right)}$ possesses the limit distribution as if the commonality in each sub-population were known, and hence satisfies the “oracle rule”. This interesting efficiency boosting phenomenon will be empirically verified in Section 6.

Specifically, we define the following improved estimator for β₀:

$${\check{\beta }}^{\left(j\right)}=\underset{\beta \in {\mathbb{R}}^p}{\mathrm{argmin}}\frac{1}{n}\sum _{i\in L_j}{(Y_i-{\mathit{X}}_i^T\beta -\stackrel{‒}{f}\left(Z_i\right))}^2.$$ (3.15)

Theorem 3.5 below shows that ${\check{\beta }}^{\left(j\right)}$ achieves the parametric efficiency bound as if the nonparametric component f were known. This is not surprising given that the nonparametric estimate f̄ now possesses a faster convergence rate after aggregation. What is truly interesting is that we need to set a lower bound for s, i.e., (3.16), and thus the homogeneous data setting is trivially excluded. This lower bound requirement slows down the convergence rate of ${\check{\beta }}^{\left(j\right)}$ , i.e., √n, such that f̄ can be treated as if it were known.

Theorem 3.5

Suppose Assumption 3.1 and 3.2 hold. If s satisfies

$$s^{-1}=o\left(h^2{\log }^{-4}N\right),$$ (3.16)

$$s=o\left(N{h}^2{(\omega (\mathcal{F},1)+\log N)}^{-2}\right),$$ (3.17)

$$s{\left(Nh\right)}^{-1}{\log }^{4}N+\lambda =o\left(h^2{(\omega (\mathcal{F},1)+\log N)}^{-2}{\log }^{-2}N\right),$$ (3.18)

and we choose λ = o((Nh)⁻¹), then we have

$$\sqrt{n}({\check{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})⇝N(0,{\sigma }^2{\Sigma }^{-1}),$$

where $\Sigma =\mathbb{E}\left[\mathit{X}{\mathit{X}}^T\right]$ .

Recall that X and Z are not assumed to be independent. Hence, the parametric efficiency bound Σ⁻¹ is not larger than the semiparametric efficiency bound Ω⁻¹.

3.6. Testing for Heterogeneity

The heterogeneity across different sub-populations is a crucial feature of massive data. However, there is still some chance that some sub-populations may share the same underlying distribution. In this section, we consider testing for the heterogeneity among sub-populations. We start from a simple pairwise testing, and then extend it to a more challenging simultaneous testing that can be applied to a large number of sub-populations.

Consider a general class of pairwise heterogeneity testing:

$$H_0:Q({\beta }_0^{\left(j\right)}-{\beta }_0^{\left(k\right)})=0\text{for}j\ne k,$$ (3.19)

where $Q={(Q_1^T,\dots ,Q_q^T)}^T$ is a q × q matrix with q ≥ p. The general formulation (3.19) can test either the whole vector or one fraction of ${\beta }_0^{\left(j\right)}$ is equal to that of ${\beta }_0^{\left(k\right)}$ . A test statistic can be constructed based on either $\widehat{\beta }$ or its improved version $\check{\beta }$ . Let $C_{\alpha }\subset {\mathbb{R}}^q$ be a confidence region satisfying $\mathbb{P}(\mathit{b}\in C_{\alpha })=1-\alpha$ for any b ~ N(0, I_q). Specifically, we have the following α-level Wald tests:

$$\begin{array}{cc}\hfill {\Psi }_1=& I\{Q({\widehat{\beta }}^{\left(j\right)}-{\widehat{\beta }}^{\left(k\right)})\notin \sqrt{2∕n}\sigma {\left(Q{\Omega }^{-1}{Q}^T\right)}^{1∕2}{C}_{\alpha }\},\hfill \\ \hfill {\Psi }_2=& I\{Q({\check{\beta }}^{\left(j\right)}-{\check{\beta }}^{\left(k\right)})\notin \sqrt{2∕n}\sigma {\left(Q{\Sigma }^{-1}{Q}^T\right)}^{1∕2}{C}_{\alpha }\}.\hfill \end{array}$$

The consistency of the above tests are guaranteed by Theorem 3.6 below. In addition, we note that the power of the latter test is larger than the former; see the analysis below Theorem 3.6. The price we need to pay for this larger power is to require a lower bound on s.

Theorem 3.6

Suppose that the conditions in Theorem 3.4 are satisfied. Under the null hypothesis specified in (3.19), we have

$$\sqrt{n}Q({\widehat{\beta }}^{\left(j\right)}-{\widehat{\beta }}^{\left(k\right)})⇝N(0,2{\sigma }^{2}Q{\Omega }^{-1}{Q}^T).$$

Moreover, under the conditions in Theorem 3.5, we have

$$\sqrt{n}Q({\check{\beta }}^{\left(j\right)}-{\check{\beta }}^{\left(k\right)})⇝N(0,2{\sigma }^{2}Q{\Sigma }^{-1}{Q}^T),$$

where $\Sigma =\mathbb{E}\left[\mathit{X}{\mathit{X}}^T\right]$ .

The larger power of Ψ₂ is due to the smaller asymptotic variance of ${\check{\beta }}^{\left(j\right)}$ , and can be deduced from the following power function. For simplicity, we consider $H_0:{\beta }_{01}^{\left(j\right)}-{\beta }_{01}^{\left(k\right)}=0$ , i.e., Q = (1, 0, 0 ..., 0). In this case, we have ${\Psi }_1=I\{\mid {\widehat{\beta }}_1^{\left(j\right)}-{\widehat{\beta }}_1^{\left(k\right)}\mid >\sqrt{2}\sigma {\left[{\Omega }^{-1}\right]}_{11}^{1∕2}{z}_{\alpha ∕2}∕\sqrt{n}\}$ , and ${\Psi }_2=I\{\mid {\check{\beta }}_1^{\left(j\right)}-{\check{\beta }}_1^{\left(k\right)}\mid >\sqrt{2}\sigma {\left[{\Sigma }^{-1}\right]}_{11}^{1∕2}{z}_{\alpha ∕2}∕\sqrt{n}\}$ . The (asymptotic) power function under the alternative that ${\beta }_{01}^{\left(j\right)}-{\beta }_{01}^{\left(k\right)}={\beta }^{\ast }$ for some non-zero β* is

$$\text{Power}\left({\beta }^{\ast }\right)=1-\mathbb{P}\left(W\in \left[-\frac{{\beta }^{\ast }\sqrt{n}}{{\sigma }^{\ast }}\pm z_{\alpha ∕2}\right]\right),$$

where W ~ N(0, 1) and σ* is $\sqrt{2}\sigma {\left[{\Omega }^{-1}\right]}_{11}^{1∕2}$ for Ψ₁ and $\sqrt{2}\sigma {\left[{\Sigma }^{-1}\right]}_{11}^{1∕2}$ for Ψ₂. Hence, a smaller σ* gives rise to a larger power, and Ψ₂ is more powerful than Ψ₁. Please see Section 6 for empirical support for this power comparison.

We next consider a simultaneous testing that is applied to a large number of sub-populations:

$$H_0:{\beta }^{\left(j\right)}={\tilde{\beta }}^{\left(j\right)}\text{for all}j\in \mathcal{G},$$ (3.20)

where $\mathcal{G}\subset \{1,2,\dots ,s\}$ , versus the alternative:

$$H_1:{\beta }^{\left(j\right)}\ne {\tilde{\beta }}^{\left(j\right)}\text{for some}j\in \mathcal{G}.$$ (3.21)

The above ${\widehat{\beta }}^{\left(j\right)}$ 's are pre-specified for each $j\in \mathcal{G}$ . If all ${\tilde{\beta }}^{\left(j\right)}$ 's are the same, then it becomes a type of heterogeneity test for the group of sub-populations indexed by $\mathcal{G}$ . Here we allow $\mid \mathcal{G}\mid$ to be as large as s, and thus it can increase with n. Let ${\widehat{\Sigma }}^{\left(j\right)}$ be the sample covariance matrix of X for the j-th sub-population, i.e., $n^{-1}{\sum }_{i\in L_j}{\mathit{X}}_i{\mathit{X}}_i^T$ . Define the test statistic

$$T_{\mathcal{G}}≔\underset{j\in \mathcal{G},1\le k\le p}{\max }\sqrt{n}({\check{\beta }}_k^{\left(j\right)}-{\tilde{\beta }}_k^{\left(j\right)}).$$

We approximate the distribution of the above test statistic using multiplier bootstrap. Define the following quantity:

$$W_{\mathcal{G}}≔\underset{j\in \mathcal{G},1\le k\le p}{\max }\frac{1}{\sqrt{n}}\sum _{i\in L_j}{\left({\widehat{\Sigma }}^{\left(j\right)}\right)}_k^{-1}{\mathit{X}}_i{e}_i,$$

where e_i's are i.i.d. N(0, σ2) independent of the data and ${\left({\widehat{\Sigma }}^{\left(j\right)}\right)}_k^{-1}$ is the k-th row of ${\left({\widehat{\Sigma }}^{\left(j\right)}\right)}^{-1}$ . Let $c_{\mathcal{G}}\left(\alpha \right)=\inf \{t\in \mathbb{R}:\mathbb{P}(W_{\mathcal{G}}\le t\mid \mathbb{X})\ge 1-\alpha \}$ . We employ the recent Gaussian approximation and multiplier bootstrap theory (Chernozhukov et al., 2013) to obtain the following theorem.

Theorem 3.7

Suppose Assumptions 3.1 and 3.2 hold. In addition, suppose (3.17) and (3.18) in Theorem 3.5 hold. For any $\mathcal{G}\subset \{1,2,\dots ,s\}$ with $\mid \mathcal{G}\mid =d$ , if (i) $s\gtrsim h^{-2}\log \left(pd\right){\log }^{4}N$ , (ii) ${\left(\log \left(pdn\right)\right)}^7∕n\le C_1{n}^{-c_1}$ for some constants c₁, C₁ > 0, and (iii) $p^2\log \left(pd\right)∕\sqrt{n}=o\left(1\right)$ , then under H₀ and choosing λ = o((Nh)⁻¹), we have

$$\underset{\alpha \in (0,1)}{\sup }\mid \mathbb{P}\left(T_{\mathcal{G}}>c_{\mathcal{G}}\left(\alpha \right)\right)-\alpha \mid =o\left(1\right).$$

Remark 3.2

We can perform heterogeneity testing even without specifying ${\tilde{\beta }}^{\left(j\right)}$ 's. This can be done by simply reformulating the null hypothesis as follows (for simplicity we set $\mathcal{G}=\left[s\right]$ ): H₀ : α^(j) = 0 for j ∈ [s – 1], where α^(j) = β^(j) – β^(j+1) for j = 1,...,s – 1. The test statistic is $T_{\mathcal{G}}^{\prime }={\max }_{1\le j\le s-1}{\max }_{1\le k\le p}{\alpha }_k^{\left(j\right)}$ . The bootstrap quantity is defined as

$$W_{\mathcal{G}}^{\prime }≔\underset{1\le j\le s-1,1\le k\le p}{\max }\frac{1}{\sqrt{n}}\sum _{i\in L_j}{\left({\widehat{\Sigma }}^{\left(j\right)}\right)}_k^{-1}{\mathit{X}}_i{e}_i-\frac{1}{\sqrt{n}}\sum _{i\in L_{j+1}}{\left({\widehat{\Sigma }}^{(j+1)}\right)}_k^{-1}{\mathit{X}}_i{e}_i.$$

The proof is similar to that of Theorem 3.7 and is omitted.

4. Examples

In this section, we consider three specific classes of RKHS with different smoothness, characterized by the decaying rate of the eigenvalues: finite rank, exponential decay and polynomial decay. In particular, we give explicit upper bounds for s under which the combined estimate enjoys the oracle property, and also explicit lower bounds for obtaining efficiency boosting studied in Section 3.5. Interestingly, we find that the upper bound for s increases for RKHS with faster decaying eigenvalues. Hence, our aggregation procedure favors smoother regression functions in the sense that more sub-populations are allowed to be included in the observations. The choice of λ is also explicitly characterized in terms of the entire sample size and the decaying rate of eigenvalues. In all three examples, the undersmoothing is implicitly assumed for removing the nonparametric estimation bias. Our bounds on s and λ here are not the most general ones. Rather, we present the bounds that have less complicated forms but are still sufficient to deliver theoretical insights.

4.1. Example I: Finite Rank Kernel

The RKHS with finite rank kernels includes linear functions, polynomial functions, and, more generally, functional classes with finite dictionaries. In this case, the effective dimension is simply proportional to the rank r. Hence, $h\asymp r^{-1}$ . Combining this fact with Theorem 3.4, we get the following corollary for finite rank kernels:

Corollary 4.1

Suppose Assumption 3.1 – 3.3 hold and s → ∞. For any $z_0\in \mathcal{Z}$ , if λ = o(N^−1/2), log(λ⁻¹) = o(N²log⁻¹²N) and $s=o\left(\frac{N}{\sqrt{\log {\lambda }^{-1}}{\log }^{6}N}\right)$ , then

$$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{N}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Sigma }_{22}^{\ast }\hfill \end{array}\right)\right),$$

where ${\Sigma }_{22}^{\ast }={\sum }_{\ell =1}^r{\varphi }_{\ell }{\left(z_0\right)}^2+{\gamma }_{z_0}^T{\Omega }^{-1}{\gamma }_{z_0}$ and ${\gamma }_{z_0}={\sum }_{\ell =1}^r\langle \mathit{B},{\varphi }_{\ell }\rangle {}_{L_2\left({\mathbb{P}}_Z\right)}{\varphi }_{\ell }\left(z_0\right)$ .

From the above Corollary, we can easily tell that the upper bound for s can be as large as o(N log⁻⁷ N) by choosing a sufficiently large λ. Hence, s can be chosen nearly as large as N. As for the lower bound of s for boosting the efficiency, we have $s\gtrsim r^2{\log }^{4}N$ by plugging $h\asymp r^{-1}$ into (3.16). This lower bound is clearly smaller than the upper bound. Hence, the efficiency boosting is feasible.

Corollary 4.2 below specifies conditions and s and λ under which f̄ achieves the nonparametric minimaxity.

Corollary 4.2

Suppose that Assumption 3.1 - 3.3 hold. When λ = r/N and s = o(N log⁻⁵ N), we have

$$\mathbb{E}\left[{\Vert \stackrel{‒}{f}-f_0\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\right]\le Cr∕N,$$

for some constant C.

4.2. Example II: Exponential Decay Kernel

We next consider the RKHS for which the kernel has exponentially decaying eigenvalues, i.e., ${\mu }_{\ell }=\exp (-\alpha {\ell }^p)$ for some α > 0. In this case, we have $h\asymp {\left(\log {\lambda }^{-1}\right)}^{-1∕p}$ by explicit calculations.

Corollary 4.3

Suppose Assumption 3.1 – 3.3 hold, and for any $z_0\in \mathcal{Z},f_0\in \mathcal{H}$ satisfies ${\sum }_{\ell =1}^{\infty }\mid {\varphi }_{\ell }\left(z_0\right){\langle f_0,{\varphi }_{\ell }\rangle }_{\mathcal{H}}\mid <\infty$ . If $\lambda =o(N^{-1∕2}{\log }^{1∕\left(2p\right)}N\wedge n^{-1∕2})$ , $\log \left({\lambda }^{-1}\right)=o\left(N^{p∕(p+4)}{\log }^{-6p∕(p+4)}N\right)$ and $s=o\left(\frac{N}{{\log }^{6}N{\log }^{(p+4)∕p}{\lambda }^{-1}}\right)$ , then

$$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right)\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{z_0}^2\hfill \end{array}\right)\right),$$

where ${\sigma }_{z_0}^2={\lim }_{N\to \infty }h{\sum }_{\ell =1}^{\infty }\frac{{\varphi }_{\ell }^2\left(z_0\right)}{{(1+\lambda ∕{\mu }_{\ell })}^2}$ .

Corollary 4.3 implies the shrinking rate of the confidence interval for f₀(z₀) as (Nh)^−1/2. This motivates us to choose λ (equivalently h) as large as possible. Plugging such a λ into the upper bound of s yields $s=o\left(N{\log }^{-(7p+4)∕p}N\right)$ . For example, when p = 1(p = 2), the upper bound is $s=o\left(N{\log }^{-11}N\right)(s=o\left(N{\log }^{-9}N\right))$ . Note that this upper bound for s only differs from that for the finite rank kernel up to some logrithmic term. This is mainly because RKHS with exponentially decaying eigenvalues has an effective dimension (log N)^1/p (for the above λ). Again, by (3.16) we get the lower bound of $s\gtrsim {\left(\log {\lambda }^{-1}\right)}^{2∕p}{\log }^2$ When $\lambda \asymp N^{-1∕2}{\log }^{1∕\left(2p\right)}N\wedge n^{-1∕2}$ , it is approximately $s\gtrsim {\log }^{(4p+2)∕p}N$ .

As a concrete example, we consider the Gaussian kernel K(z₁, z₂) = exp (–|z₁ – z₂|²/2). The eigenfunctions are given in (2.1), and the eigenvalues are exponentially decaying, as ${\mu }_{\ell }={\eta }^{2\ell +1}$ , where η = √5–1)/2. According to Krasikov (2004), we can get that

$$c_{\varphi }=\underset{\ell \in \mathbb{N}}{\sup }{\Vert {\varphi }_{\ell }\Vert }_{\sup }\le \frac{2e^{15∕8}{(\sqrt{5}∕4)}^{1∕2}}{3\sqrt{2\pi }{2}^{1∕6}}\le 1.336.$$

Thus, Assumption 3.2 is satisfied. We next give an upper bound of ${\sigma }_{z_0}^2$ in Corollary 4.3 as follows:

$${\sigma }_{z_0}^2\le \underset{N\to \infty }{\lim }{\sigma }^2{c}_{\varphi }^{2}h\sum _{\ell =0}^{\infty }{(1+\lambda \eta \exp (-2\left(\log \eta \right)\ell ))}^{-2}=c_{\varphi }^2\cdot 2{\sigma }^2\log (1∕\eta )\le 1.7178{\sigma }^2,$$

where equality follows from Lemma C.1 in Appendix C with the case t = 2. Hence, a (conservative) 100(1–α)% confidence interval for f₀(z₀) is given by f̄(z₀) ± 1.3106σz_α/2/√Nh.

Corollary 4.4

Suppose that Assumption 3.1 – 3.3 hold. By choosing λ = log^1/p N/N and s = o(N log^–(5p+3)/p N), we have

$$\mathbb{E}\left[{\Vert \stackrel{‒}{f}-f_0\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\right]\le C{\left(\log N\right)}^{1∕p}∕N.$$

We know that the above rate is minimax optimal according to Zhang et al. (2013). Note that the upper bound for s required here is similar as that for obtaining the joint limiting distribution in Corollary 4.3.

4.3. Example III: Polynomial Decay Kernel

We now consider the RKHS for which the kernel has polynomially decaying eigenvalues, i.e., ${\mu }_{\ell }=c{\ell }^{-2\nu }$ for some ν > 1/2. Hence, we can explicitly calculate that h = λ^1/(2ν). The resulting penalized estimate is called as “partial smoothing spline” in the statistics literature; see Gu (2013); Wang (2011).

Corollary 4.5

Suppose Assumption 3.1 – 3.3 hold, and ${\sum }_{\ell =1}^{\infty }\mid {\varphi }_{\ell }\left(z_0\right){\langle f_0,{\varphi }_{\ell }\rangle }_{\mathcal{H}}\mid <\infty$ for any $z_0\in \mathcal{Z}$ and $f_0\in \mathcal{H}$ . For any $\nu >1+\sqrt{3}∕2\approx 1.866,\text{if}\lambda \asymp N^{-d}$ for some $\frac{2\nu }{4\nu +1}<d<\frac{4{\nu }^2}{10\nu -1},\lambda =o\left(n^{-1∕2}\right)$ and $s=o\left({\lambda }^{\frac{10\nu -1}{4{\nu }^2}}N{\log }^{-6}N\right)$ , then

$$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{z_0}^2\hfill \end{array}\right)\right).$$

where ${\sigma }_{z_0}^2={\lim }_{N\to \infty }h{\sum }_{\ell =1}^{\infty }\frac{{\varphi }_{\ell }^2\left(z_0\right)}{{(1+\lambda ∕{\mu }_{\ell })}^2}$ .

Similarly, we choose $\lambda \asymp N^{-\frac{2\nu }{4\nu +1}}\wedge n^{-1∕2}$ to get the fastest shrinking rate of the confidence interval. Plugging the above λ into the upper bound for s, we get

$$s=o\left(N^{\frac{8{\nu }^2-8\nu +1}{2\nu (4\nu +1)}}{\log }^{-6}N\wedge N{\left(\log N\right)}^{-\frac{48{\nu }^2}{8{\nu }^2+10\nu +1}}\right).$$

When N is large, the above bound reduces to $s=o\left(N^{\frac{8{\nu }^2-8\nu +1}{2\nu (4\nu +1)}}{\log }^{-6}N\right)$ . We notice that the upper bound for s increases as ν increases, indicating that the aggregation procedure favors smoother functions. As an example, for the case that ν = 2, we have the upper bound for s = o(N^17/36 log⁻⁶ N) ≈ o(N^0.47 log⁻⁶ N). Again, we obtain the lower bound $s\gtrsim {\lambda }^{-1∕\nu }{\log }^{4}N$ by plugging $h\asymp {\lambda }^{\frac{1}{2\nu }}$ into (3.16). When $\lambda \asymp N^{-\frac{2\nu }{4\nu +2}}$ , we get $s\gtrsim N^{\frac{1}{4\nu +1}}{\log }^{2}N$ . For ν = 2, this is approximately $s\gtrsim N^{0.22}{\log }^{4}N$ .

As a concrete example, we consider the periodic Sobolev space $H_0^{\nu }[0,1]$ with the following eigenfunctions:

$${\varphi }_{\ell }\left(x\right)=\{\begin{array}{cc}\hfill 1,\hfill & \ell =0,\hfill \\ \hfill \sqrt{2}\cos \left(\ell \pi x\right),\hfill & \ell =2k\text{for}k=1,2,\dots ,\hfill \\ \hfill \sqrt{2}\sin \left((\ell +1)\pi x\right),\hfill & \ell =2k-1\text{for}k=1,2,\dots ,\hfill \end{array}\phantom{\}}$$ (4.1)

and eigenvalues

$${\mu }_{\ell }=\{\begin{array}{cc}\hfill \infty ,\hfill & \ell =0,\hfill \\ \hfill {\left(\ell \pi \right)}^{-2\nu },\hfill & \ell =2k\text{for}k=1,2,\dots ,\hfill \\ \hfill {\left((\ell +1)\pi \right)}^{-2\nu },\hfill & \ell =2k=1\text{for}k=1,2,\dots ,\hfill \end{array}\phantom{\}}$$ (4.2)

Hence, Assumption 3.2 trivially holds. Under the above eigensystem, the following lemma gives an explicit expression of ${\sigma }_{z_0}^2$ .

Lemma 4.1

Under the eigen-system defined by (4.1) and (4.2), we can explicitly calculate:

$${\sigma }_{z_0}^2=\underset{N\to \infty }{\lim }h\sum _{\ell =1}^{\infty }\frac{{\varphi }_{\ell }^2\left(z_0\right)}{{(1+\lambda ∕{\mu }_{\ell })}^2}={\int }_0^{\infty }\frac{1}{{(1+x^{2\nu })}^2}dx=\frac{\pi }{2\nu \sin (\pi ∕\left(2\nu \right))}.$$

Therefore, by Corollary 4.5, we have that when $\lambda \asymp N^{-\frac{2\nu }{4\nu +1}}$ and $s=o\left(N^{\frac{8{\nu }^2-8\nu +1}{2\nu (4\nu +1)}}{\log }^{-6}N\right)$ ,

$$\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,{\sigma }^2\left(\begin{array}{cc}\hfill {\Omega }^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{z_0}^2\hfill \end{array}\right)\right).$$ (4.3)

where ${\sigma }_{z_0}^2$ is given in Lemma 4.1. When $\nu =2,\lambda \asymp N^{-4∕9}$ and the upper bound for s = o(N^17/36 log⁻⁶ N).

Corollary 4.6

Suppose that Assumption 3.1 - 3.3 hold. If we choose $\lambda =N^{-\frac{2\nu }{2\nu +1}}$ , and $s=o\left(N^{\frac{4{\nu }^2-4\nu +1}{4{\nu }^2+2\nu }}{\log }^{-4}N\right)$ , the combined estimator achieves optimal rate of convergence, i.e.,

$$\mathbb{E}\left[{\Vert \stackrel{‒}{f}-f_0\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\right]\le C{N}^{-\frac{2\nu }{2\nu +1}}.$$ (4.4)

The above rate is known to be minimax optimal for the class of functions in consideration (Stone, 1985).

5. Application to Homogeneous Data: Divide-and-Conquer Approach

In this section, we apply the divide-and-conquer approach, which is commonly used to deal with massive homogeneous data, to some sub-populations that have huge sample sizes. A general goal of this section is to explore the most computationally efficient way to split the sample in those sub-populations while preserving the best possible statistical inference. Specifically, we want to derive the largest possible number of splits under which the averaged estimators for both components enjoy the same statistical performances as the “oracle” estimator that is computed based on the entire sample. Without loss of generality, we assume the entire sample to be homogeneous by setting all ${\beta }_0^{\left(j\right)}$ 's to be equal throughout this section.

The divide-and-conquer method randomly splits the massive data into s mutually exclusive subsamples. For simplicity, we assume all the subsamples share the same sample size, denoted as n. Hence, N = n × s. With a bit abuse of notation, we define the divide-and-conquer estimators as ${\widehat{\beta }}^{\left(j\right)}$ and ${\widehat{f}}^{\left(j\right)}$ when they are based on the j-th subsample. Thus, the averaged estimator is defined as

$$\stackrel{‒}{\beta }=(1∕s)\sum _{j=1}^s{\widehat{\beta }}^{\left(j\right)}\text{and}\stackrel{‒}{f}(\cdot )=(1∕s)\sum _{j=1}^s{\widehat{f}}^{\left(j\right)}(\cdot ).$$

Comparing to the oracle estimator, the aggregation procedure reduces the computational complexity in terms of the entire sample size N to the sub-sample size N/s. In the case of kernel ridge regression, the complexity is O(N³), while our aggregation procedure (run in one single machine) reduces it to O(N³/s²). Propositions 5.1 and 5.2 below state conditions under which the divide-and-conquer estimators maintain the same statistical properties as oracle estimate, i.e., so-called oracle property.

Our first contribution is a non-asymptotic upper bound for MSE(f̄).

Proposition 5.1

Suppose that the conditions in Theorem 3.1 hold. We have that the divide and conquer estimator f̄ satisfies

$$\mathrm{MSE}\left(\stackrel{‒}{f}\right)\le C_1{\sigma }^2{\left(Nh\right)}^{-1}+2{\Vert f_0\Vert }_{\mathcal{H}}^2\lambda +C_2{\lambda }^2+s^{-1}a(n,s,h,\lambda ,\omega ),$$ (5.1)

where a(n, s, h, λ, ω), C₁ and C₂ are constants defined in Theorem 3.1.

Our second contribution is on the joint asymptotic distribution under the same conditions for (s, λ) required in the heterogeneous data setting.

Proposition 5.2

Suppose that the conditions in Theorem 3.4 hold. If we choose λ = o(N^−1/2), then

$$\left(\begin{array}{c}\hfill \sqrt{N}(\stackrel{‒}{\beta }-{\beta }_0)\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0\left(z_0\right)-W_{\lambda }{f}_0\left(z_0\right))\hfill \end{array}\right)⇝N\left(0,\left(\begin{array}{cc}\hfill {\sigma }^2{\Omega }^{-2}\hfill & \hfill {\Sigma }_{12}^{\ast }\hfill \\ \hfill {\Sigma }_{21}^{\ast }\hfill & \hfill {\Sigma }_{22}^{\ast }\hfill \end{array}\right)\right),$$

where ${\Sigma }_{12}^{\ast }={\Sigma }_{21}^{\ast T}={\sigma }^2{\Omega }^{-1}{\gamma }_{z_0}$ and ${\Sigma }_{22}^{\ast }={\sigma }^2({\sigma }_{z_0}^2+{\gamma }_{z_0}^T{\Omega }^{-1}{\gamma }_{z_0})$ . Moreover, if h → 0, then γ_z0 = 0. In this case, ${\Sigma }_{12}^{\ast }={\Sigma }_{21}^{\ast T}=0$ and ${\Sigma }_{22}^{\ast }={\sigma }^2{\sigma }_{z_0}^2$ .

The conclusion of Proposition 5.2 holds no matter s is fixed or diverges (once the condition for s in Theorem 3.4 are satisfied).

In view of Propositions 5.1 and 5.2, we note that the above upper bound and joint asymptotic distribution are exactly the same as those for the oracle estimate, i.e., s = 1.

6. Numercial Experiment

In this section, we empirically examine the impact of the number of sub-populations on the statistical inference built on $({\widehat{\beta }}^{\left(j\right)},\stackrel{‒}{f})$ . As will be seen, the simulation results strongly support our general theory.

Specifically, we consider the partial smoothing spline models in Section 4.3. In the simulation setup, we let ε ~ N(0,1), p = 1 and ν = 2 (cubic spline). Moreover Z ~ Uniform (−1, 1) and X = (W + Z)/2, where W ~ Unfiform(−1,1), such that X and Z are dependent. It is easy to show that Ω = E[(X – E[X|Z])²)] = 1/12 and Σ = E[X²] = 1/6. To design that heterogeneous data setting, we let ${\beta }_0^{\left(j\right)}=j$ for j = 1,2,...,s on the j-th subpopulation. The nonparametric function f₀(z), which is common across all subpopulations, is assumed to be 0.6b_30,17(z) + 0.4b_3,11, where b_α1,α2 is the density function for Beta(α₁, α₂).

We start from the 95% predictive interval (at (x₀, z₀)) implied by the joint asymptotic distribution (4.3):

$$\left[{\widehat{Y}}^{\left(j\right)}\pm 1.96\sigma \sqrt{x_0^T{\Omega }^{-1}{x}_0∕n+{\sigma }_{z_0}^2∕\left(Nh\right)+1}\right],$$

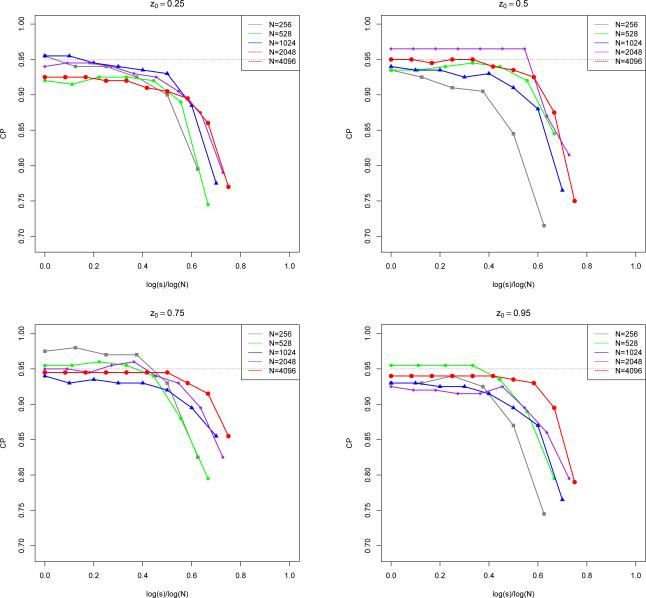
where ${\widehat{Y}}^{\left(j\right)}-x_0^T{\widehat{\beta }}^{\left(j\right)}+\stackrel{‒}{f}\left(z_0\right)$ is the predicted response. The unknown error variance σ is estimated by ${\left({\widehat{\sigma }}^{\left(j\right)}\right)}^2=n^{-1}{\sum }_{i\in L_j}{(Y_i-X_i^T{\widehat{\beta }}^{\left(j\right)}-{\widehat{f}}^{\left(j\right)}\left(Z_i\right))}^2∕(n-Tr\left(A\left(\lambda \right)\right))$ , where A(λ) denotes the smoothing matrix, followed by an aggregation ${\stackrel{‒}{\sigma }}^2=1∕s{\sum }_{j=1}^s{\left({\widehat{\sigma }}^{\left(j\right)}\right)}^2$ . In the simulations, we fix x₀ = 0.5 and choose z₀ = 0.25, 0.5, 0.75 and 0.95. The coverage probability is calculated based on 200 repetitions. As for N and s, we set N = 256, 528, 1024, 2048, 4096, and choose s = 2⁰, 2¹,...,2^t–3 when N = 2^t. The simulation results are summarized in Figure 1. We notice an interesting phase transition from Figure 1: when s ≤ s* where s* ≈ N^0.45, the coverage probability is approximately 95%; when s ≥ s*, the coverage probability drastically decreaes. This empirical observation is strongly supported by our theory developed in Section 4.3 where s* ≈ N^0.42 log⁻⁶N for ν = 2.

Fig 1.

Coverage probability of 95% predictive interval with different choices of s and N

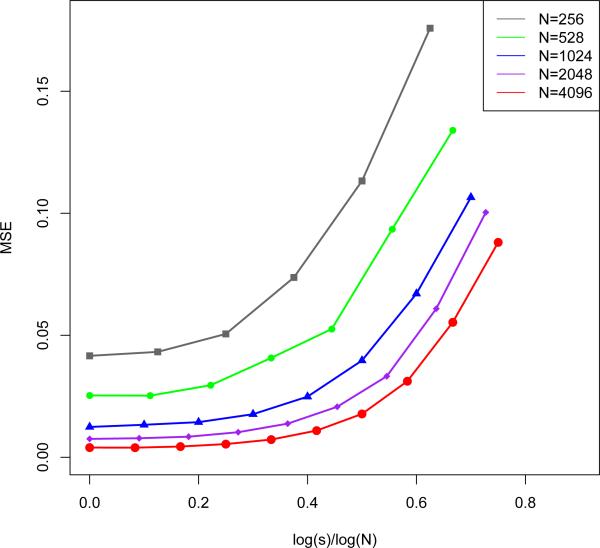
We next compute the mean-squared errors of f̄ under different choices of N and s in Figure 2. It is demonstrated that the increasing trends of MSE as s increases are very similar for different N. More importantly, all the MSE curves suddenly blow up when s ≈ N^0.4. This is also close to our theoretical result that the transition point is around N^0.45 log⁻⁶ N.

Fig 2.

Mean-square errors of f̄ under different choices of N and s

We next empirically verify the efficiency boosting theory developed in Section 3.5. Based on ${\widehat{\beta }}^{\left(j\right)}$ and ${\check{\beta }}^{\left(j\right)}$ , we construct the following two types of 95% confidence intervals for ${\beta }_0^{\left(j\right)}$ .

$$\begin{array}{cc}\hfill {\mathrm{CI}}_1=& \left[{\widehat{\beta }}^{\left(j\right)}\pm 1.96{\Omega }^{-1∕2}{n}^{-1.2}\stackrel{‒}{\sigma }\right],\hfill \\ \hfill {\mathrm{CI}}_2=& \left[{\check{\beta }}^{\left(j\right)}\pm 1.96{\Sigma }^{-1∕2}{n}^{-1.2}\stackrel{‒}{\sigma }\right].\hfill \end{array}$$

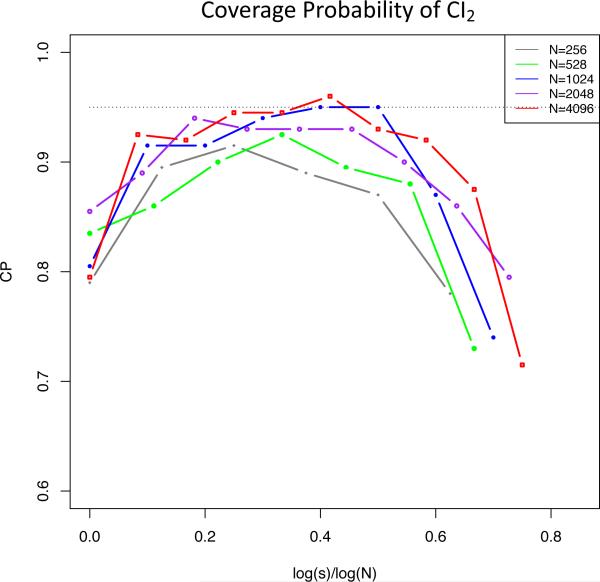
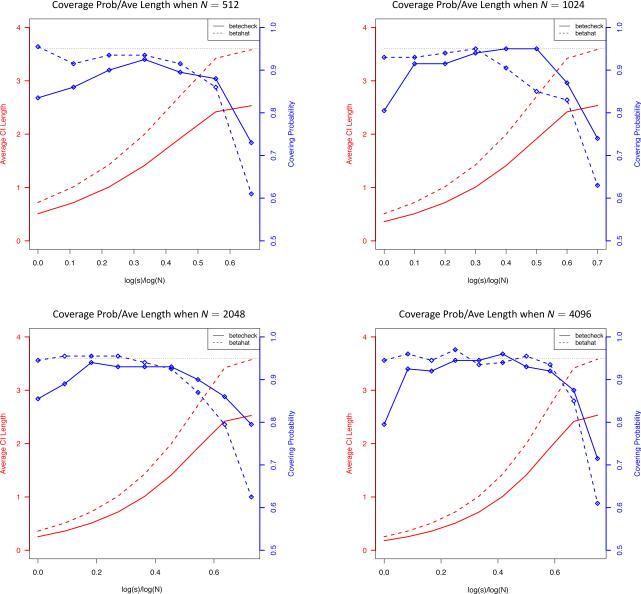
Obviously, CI₂ is shorter than CI₁. However, Theorem 3.5 shows that CI₂ is valid only when s satisfies both a upper bound and a lower bound. This theoretical condition is empirically verified in Figure 3 which exhibits the validity range of CI₂ in terms of s. In Figure 4, we further compare CI₂ and CI₁ in terms of their coverage probabilities and lengths. This figure shows that when s is in a proper range, the coverage probabilities of CI₁ and CI₂ are similar, while CI₂ is significantly shorter.

Fig 3.

Coverage probability of 95% confidence interval based on $\check{\beta }$

Fig 4.

Covergae probabilities and average lengths of 95% confidence intervals constructed based on $\widehat{\beta }$ and $\check{\beta }$ . In the above figures, dashed lines represent CI₁, which is constructed based on $\check{\beta }$ , and solid lines represent CI₂, which is constructed based on $\widehat{\beta }$ .

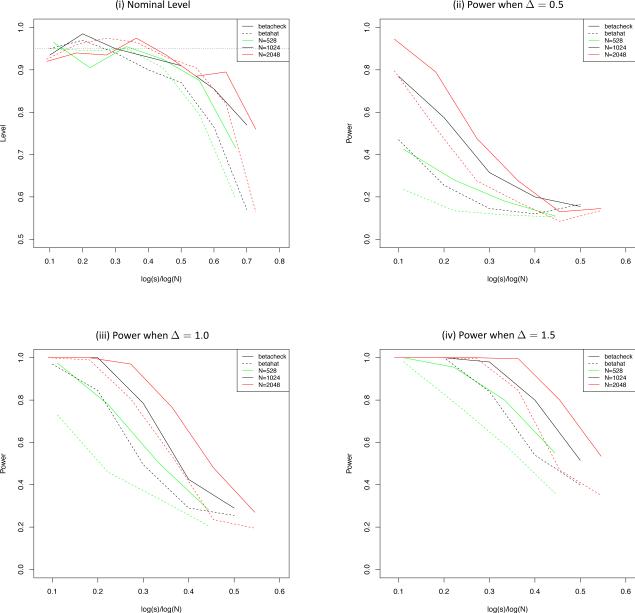
Lastly, we consider the heterogeneity testing. In Figure 5, we compare tests Ψ₁ and Ψ₂ under different choices of N and s ≥ 2. Specifically, Figure 5 (i) compares the nominal levels, while Figure 5 (ii) - (iv) compare the powers under various alternative hypotheses $H_1:{\beta }_0^{\left(j\right)}-{\beta }_0^{\left(k\right)}=\Delta$ , where Δ = 0.5, 1, 1.5. It is clearly seen that both tests are consistent, and their powers increase as Δ or N increases. In addition, we observe that Ψ₂ has uniformly larger powers than Ψ₁.

Fig 5.

(i) Nominal level of heterogeneity tests Ψ₁ and Ψ₂; (ii) - (iv) Power of heterogeneity tests Ψ₁ and Ψ₂ when Δ= 0.5, 1.0, 1.5. In the above figures, dashed lines represent Ψ₁, which is constructed based on $\check{\beta }$ , and solid lines represent Ψ₂, which is constructed based on $\widehat{\beta }$ .

7. Proof of Main Results

In this section, we present main proofs of Theorem 3.1, 3.3 and 3.4 in the main text.

7.1. Proof of Theorem 3.1

Proof

We start from analyzing the minimization problem (3.2) on each sub-population. Recall m = (β,f) and U = (X, Z). The objective function can be rewritten as

$$\begin{array}{cc}\hfill \frac{1}{n}\sum _{i\in L_j}{(Y_i-{\mathit{X}}_i^T\beta -f\left(Z_i\right))}^2+\lambda {\Vert f\Vert }_{\mathcal{H}}^2=& \frac{1}{n}\sum _{i\in L_j}{(Y_i-m\left(U_i\right))}^2+{\langle P_{\lambda }m,m\rangle }_{\mathcal{A}}\hfill \\ \hfill =& \frac{1}{n}\sum _{i\in L_j}{(Y_i-{\langle R{U}_i,m\rangle }_{\mathcal{A}})}^2+{\langle P_{\lambda }m,m\rangle }_{\mathcal{A}}\hfill \end{array}$$

The first order optimality condition (w.r.t. Fréchet derivative) gives

$$\frac{1}{n}\sum _{i\in L_j}{R}_{U_i}({\widehat{m}}^{\left(j\right)}\left(U_i\right)-Y_i)+P_{\lambda }{\widehat{m}}^{\left(j\right)}=0,$$

where ${\widehat{m}}^{\left(j\right)}=({\widehat{\beta }}^{\left(j\right)},{\widehat{f}}^{\left(j\right)})$ . This implies that

$$-\frac{1}{n}\sum _{i\in L_j}{R}_{U_i}{\epsilon }_i+\frac{1}{n}\sum _{i\in L_j}{R}_{U_i}({\widehat{m}}^{\left(j\right)}\left(U_i\right)-m_0^{\left(j\right)}\left(U_i\right))+P_{\lambda }{\widehat{m}}^{\left(j\right)}=0,$$

where $m_0^{\left(j\right)}=({\beta }_0^{\left(j\right)},f_0)$ . Define $\Delta m^{\left(j\right)}≔{\widehat{m}}^{\left(j\right)}-m_0^{\left(j\right)}$ . Adding ${\mathbb{E}}_U\left[R_U\Delta m^{\left(j\right)}\left(U\right)\right]$ on both sides of the above equation, we have

$${\mathbb{E}}_U\left[R_U\Delta m^{\left(j\right)}\left(U\right)\right]+P_{\lambda }\Delta m^{\left(j\right)}=\frac{1}{n}\sum _{i\in L_j}{R}_{U_i}{\epsilon }_i-P_{\lambda }{m}_0^{\left(j\right)}-\frac{1}{n}\sum _{i\in L_j}(R_{U_i}\Delta m^{\left(j\right)}\left(U_i\right)-{\mathbb{E}}_U\left[R_U\Delta m^{\left(j\right)}\left(U\right)\right]).$$ (7.1)

The L.H.S. of (7.1) can be rewritten as

$$\begin{array}{cc}\hfill {\mathbb{E}}_U\left[R_U\Delta m^{\left(j\right)}\left(U\right)\right]+P_{\lambda }\Delta m^{\left(j\right)}=& {\mathbb{E}}_U\left[R_U{\langle R_U,\Delta m^{\left(j\right)}\rangle }_{\mathcal{A}}\right]+P_{\lambda }\Delta m^{\left(j\right)}\hfill \\ \hfill =& ({\mathbb{E}}_U[R_U\otimes R_U]+P_{\lambda })\Delta m^{\left(j\right)}\hfill \\ \hfill =& \Delta m^{\left(j\right)},\hfill \end{array}$$

where the last equality follows from proposition 2.2. Then (7.1) becomes

$${\widehat{m}}^{\left(j\right)}-m_0^{\left(j\right)}=\frac{1}{n}\sum _{i\in L_j}{R}_{U_i}{\epsilon }_i-P_{\lambda }{m}_0^{\left(j\right)}-\frac{1}{n}\sum _{i\in L_j}\left(R_{U_i}\Delta m^{\left(j\right)}\left(U_i\right)-{\mathbb{E}}_U\left[R_U\Delta m^{\left(j\right)}\left(U\right)\right]\right).$$ (7.2)

We will show that the first term in the R.H.S. of (7.2) weakly converges to a normal distribution, the second term contributes to the estimation bias, and that the last term is an asymptotically ignorable remainder term. We denote the last term as $Re{m}^{\left(j\right)}≔\frac{1}{n}{\sum }_{i\in L_j}(R_{U_i}\Delta m^{\left(j\right)}\left(U_i\right)-{\mathbb{E}}_U\left[R_U\Delta m^{\left(j\right)}\left(U\right)\right])$ . Recall that R_u = (L_u, N_u) and $P_{\lambda }{m}_0^{\left(j\right)}=(L_{\lambda }{f}_0,N_{\lambda }{f}_0)$ . Thus the above remainder term decomposes into two components:

$$\begin{array}{cc}\hfill Re{m}_{\beta }^{\left(j\right)}≔& \frac{1}{n}\sum _{i\in L_j}\left(L_{U_i}\Delta m^{\left(j\right)}\left(U_i\right)-{\mathbb{E}}_U\left[L_U\Delta m^{\left(j\right)}\left(U\right)\right]\right)\hfill \\ \hfill Re{m}_f^{\left(j\right)}:=& \frac{1}{n}\sum _{i\in L_j}\left(N{U}_i\Delta m^{\left(j\right)}\left(U_i\right)-{\mathbb{E}}_U\left[N_U\Delta m^{\left(j\right)}\left(U\right)\right]\right).\hfill \end{array}$$

Similarly, (7.2) can be rewritten into the following two equations:

$${\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)}=\frac{1}{n}\sum _{i\in L_j}{L}_{U_i}{\epsilon }_i-L_{\lambda }{f}_0-Re{m}_{\beta }^{\left(j\right)},$$ (7.3)

and

$${\widehat{f}}^{\left(j\right)}-f_0=\frac{1}{n}\sum _{i\in L_j}{N}_{U_i}{\epsilon }_i-N_{\lambda }{f}_0-Re{m}_f^{\left(j\right)},$$ (7.4)

for all j = 1,...,s. Taking average of (7.4) for all j over s, and by definition of f̄, we have

$$\stackrel{‒}{f}-f_0=\frac{1}{N}\sum _{i=1}^N{N}_{U_i}{\epsilon }_i-N_{\lambda }{f}_0-\frac{1}{s}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)},$$ (7.5)

where we used $1∕N{\sum }_{i=1}^N{N}_{U_i}{\epsilon }_i=1∕s{\sum }_{j=1}^{s}1∕n{\sum }_{i\in L_j}{N}_{U_i}{\epsilon }_i$ . By (7.5), it follows that

$$\mathbb{E}\left[{\Vert \stackrel{‒}{f}-f_0\Vert }_{\mathcal{C}}^2\right]\le 3\mathbb{E}\left[{\Vert \frac{1}{N}\sum _{i=1}^N{N}_{U_i}{\epsilon }_i\Vert }_{\mathcal{C}}^2\right]+3\Vert N_{\lambda }{f}_0\Vert {}_{\mathcal{C}}^2+3\mathbb{E}\left[{\Vert \frac{1}{s}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}^2\right].$$ (7.6)

By Lemma A.5 and the fact that each N_Uiε_i is i.i.d., it follows that

$$\mathbb{E}\left[{\Vert \frac{1}{N}\sum _{i=1}^N{N}_{U_i}{\epsilon }_i\Vert }_{\mathcal{C}}^2\right]=\frac{1}{N}\mathbb{E}\left[{\Vert N_U\epsilon \Vert }_{\mathcal{C}}^2\right]\le C_1{\sigma }^2\frac{1}{Nh},$$ (7.7)

and

$${\Vert N_{\lambda }{f}_0\Vert }_{\mathcal{C}}^2\le 2{\Vert f_0\Vert }_{\mathcal{H}}^2\lambda +C_2{\lambda }^2,$$ (7.8)

where C₁ and C₂ are constants specified in Lemma A.5.

As for the third term in (7.6), we have by independence across sub-populations that

$$\mathbb{E}\left[{\Vert \frac{1}{s}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}^2\right]=\frac{1}{s^2}\sum _{j=1}^s\mathbb{E}\left[{\Vert Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}^2\right].$$ (7.9)

Therefore it suffices to bound $\mathbb{E}\left[{\Vert Re{m}_f^{\left(j\right)}\Vert }_c^2\right]$ . We have the following lemma that controls this term:

Lemma 7.1

Suppose Assumptions 3.1, 3.2 and Condition (3.6) hold. We have for all j = 1,...,s

$$\mathbb{E}\left[{\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}^2\right]\le a(n,s,h,\lambda ,\omega ),$$

for sufficiently large n. Moreover, the inequality also holds for $\mathbb{E}\left[{\Vert Re{m}_{\beta }^{\left(j\right)}\Vert }_2^2\right]$ and $\mathbb{E}\left[{\Vert Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}^2\right]$

Combining (7.6) - (7.9) and Lemma 7.1, and by the fact that ${\Vert \stackrel{‒}{f}-f_0\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\le {\Vert \stackrel{‒}{f}-f_0\Vert }_{\mathcal{C}}^2$ , we complete the proof of Theorem 3.1.

7.2. Proof of Theorem 3.3

Proof

Recall that $m_0^{\left(j\right)\ast }=({\beta }_0^{\left(j\right)\ast },f_0^{\ast })=(id-P_{\lambda })m_0^{\left(j\right)}$ where $m_0^{\left(j\right)}=({\beta }_0^{\left(j\right)},f_0)$ . This implies that ${\beta }_0^{\left(j\right)\ast }={\beta }_0^{\left(j\right)}-L_{\lambda }{f}_0$ and (7.5), for arbitrary x and z₀,

$$\begin{array}{cc}\hfill ({\mathit{x}}^T,1)\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)\ast })\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0^{\ast }\left(z_0\right))\hfill \end{array}\right)=& \sqrt{n}{\mathit{x}}^T({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)\ast })+\sqrt{Nh}({\stackrel{‒}{f}}_{N,\lambda }\left(z_0\right)-f_0^{\ast }\left(z_0\right))\hfill \\ \hfill =& \underset{\left(I\right)}{\underbrace{\frac{1}{\sqrt{n}}\sum _{i\in L_j}{\mathit{x}}^T{L}_{U_i}{\epsilon }_i+\frac{1}{\sqrt{N}}\sum _{i=1}^N{h}^{1∕2}{N}_{U_i}\left(z_0\right){\epsilon }_i}}+\underset{\left(II\right)}{\underbrace{\sqrt{n}{\mathit{x}}^{T}Re{m}_{\beta }^{\left(j\right)}+\sqrt{Nh}{s}^{-1}}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\left(z_0\right)}.\hfill \end{array}$$

In what follows, we will show that the main term (I) is asymptotically normal and the remainder term (II) is of order o_P(1). Given that x is arbitrary, we apply Wold device to conclude the proof of joint asymptotic normality.

Asymptotic normality of (I)

We present that result for showing asymptotic normality of (I) in the following lemma and defer its proof to supplemental material.

Lemma 7.2.

Suppose that as $N\to \infty ,h{\Vert {\tilde{K}}_{z_0}\Vert }_{L_2\left({\mathbb{P}}_Z\right)}^2\to {\sigma }_{z_0}^2$ , $h^{1∕2}\left(W_{\lambda }\mathit{A}\right)\left(z_0\right)\to a_{z_0}\in {\mathbb{R}}^p$ and $h^{1∕2}\mathit{A}\left(z_0\right)\to -{\gamma }_{z_0}\in {\mathbb{R}}^p$ . We have

• (i)
  if s → ∞, then

  $$\left(I\right)⇝N(0,{\sigma }^2({\mathit{x}}^T{\Omega }^{-1}\mathit{x}+{\Sigma }_{22})).$$ (7.10)
• (ii) if s is fixed, then

  $$\left(I\right)⇝N(0,{\sigma }^2({\mathit{x}}^T{\Omega }^{-1}\mathit{x}+{\Sigma }_{22}+2s^{-1∕2}{\mathit{x}}^T{\Sigma }_{12})).$$ (7.11)

Control of the remainder term (II)

We now turn to bound the remainder term (II). We need the following lemma:

Lemma 7.3

Suppose Assumption 3.1, 3.2 and Condition (3.6) hold. We have the following two sets of results that control the remainder terms:

• (i)
  For all j = 1,...,s

  $${\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}=o_P\left(b_{n,s}\right).$$

  where $b_{n,s}=C{h}^{-1}{n}^{-1∕2}{r}_{n,s}(\omega (\mathcal{F},1)+\log N)$ and $r_{n,s}={\left(\log N\right)}^2{\left(nh\right)}^{-1∕2}+{\lambda }^{1∕2}$ . Also, ${\Vert Re{m}_{\beta }^{\left(j\right)}\Vert }_2=o_P\left(b_{n,s}\right)$ and ${\Vert Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}=o_P\left(b_{n,s}\right)$ .
• (ii)
  Moreover, we have

  $$\begin{array}{cc}\hfill {\Vert \frac{1}{s}\sum _{j=1}^{s}Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}=& o_P\left(s{w}^{-1∕2}{b}_{n,s}\log N\right)\hfill \\ \hfill {\Vert \frac{1}{s}\sum _{j=1}^{s}Re{m}_{\beta }^{\left(j\right)}\Vert }_2=& o_P\left(s^{-1∕2}{b}_{n,s}\log N\right)\hfill \\ \hfill {\Vert \frac{1}{s}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}=& o_P\left(s^{-1∕2}{b}_{n,s}\log N\right).\hfill \end{array}$$

By Lemma 7.3, we have

$$\sqrt{n}\mid {\mathit{x}}^{T}Re{m}_{\beta }^{\left(j\right)}\mid \le \sqrt{n}{\Vert \mathit{x}\Vert }_2{\Vert Re{m}_{\beta }^{\left(j\right)}\Vert }_2=o_P\left(n^{1∕2}{b}_{n,s}\right)=o_p\left(\sqrt{N}{s}^{-1∕2}{b}_{n.s}\right),$$ (7.12)

where we used the boundedness of x. Also,

$$\begin{array}{cc}\hfill \sqrt{Nh}\mid s^{-1}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\left(z_0\right)\mid & \le \sqrt{Nh}{\Vert {\tilde{K}}_{z_0}\Vert }_{\mathcal{C}}{\Vert s^{-1}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}\hfill \\ \hfill & \lesssim \sqrt{N}{\Vert s^{-1}\sum _{j=1}^{s}Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}\hfill \\ \hfill & =o_P\left(\sqrt{N}{s}^{-1∕2}{b}_{n,s}\log N\right),\hfill \end{array}$$ (7.13)

where the second inequality follows from Lemma A.4. Therefore by (7.12) and (7.13), we have

$$\left(II\right)=o_P\left(\sqrt{N}{s}^{-1∕2}{b}_{n,s}\log N\right).$$ (7.14)

Now by definition of b_n,s and condition (3.7), we have (II) = o_P (1). Combining (7.10) and (7.14), it follows that if s → ∞, then

$$({\mathit{x}}^T,1)\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)\ast })\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0^{\ast }\left(z_0\right))\hfill \end{array}\right)⇝N(0,{\sigma }^2({\mathit{x}}^T{\Omega }^{-1}\mathit{x}+{\Sigma }_{22})).$$

Combining (7.11) and (7.14), it follows that if s is fixed, then

$$({\mathit{x}}^T,1)\left(\begin{array}{c}\hfill \sqrt{n}({\widehat{\beta }}^{\left(j\right)}-{\beta }_0^{\left(j\right)\ast })\hfill \\ \hfill \sqrt{Nh}(\stackrel{‒}{f}\left(z_0\right)-f_0^{\ast }\left(z_0\right))\hfill \end{array}\right)⇝N(0,{\sigma }^2({\mathit{x}}^T{\Omega }^{-1}\mathit{x}+{\Sigma }_{22}+2s^{-1∕2}{\mathit{x}}^T{\Sigma }_{12})).$$

By the arbitrariness of x, we reach the conclusion of the theorem using Wold device.

7.3. Proof of Lemma 7.3: Controlling the Remainder Term

Proof

(i) We first derive the bound of ${\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}$ . Recall

$$Re{m}^{\left(j\right)}=\frac{1}{n}\sum _{i\in L_j}\Delta m^{\left(j\right)}\left(U_i\right)R_{U_i}-{\mathbb{E}}_U\left[\Delta m^{\left(j\right)}\left(U\right)R_U\right].$$

Let $Z_n\left(m\right)-c_r^{-1}{h}^{1∕2}{n}^{-1∕2}{\sum }_{i\in L_j}\{m\left(U_i\right)R_{U_i}-\mathbb{E}\left[m\left(U\right)R_U\right]\}$ , where c_r is the constant specified in Lemma A.4. Note that Z_n(m) is implicitly related to j but we omit the superscript of (j). We have $Re{m}^{\left(j\right)}=c_r^{-1}\sqrt{nh}{Z}_n\left(\Delta m^{\left(j\right)}\right)$ . We apply Lemma F.1 to obtain an exponential inequality for ${\sup }_{m\in \mathcal{F}}{\Vert Z_n\left(m\right)\Vert }_{\mathcal{A}}$ . The first step is to show that Z_n(m) is a sub-Gaussian process by Lemma G.1. Let $g(U_i,m)=c_r^{-1}\sqrt{nh}(m\left(U_i\right)R_{U_i}-\mathbb{E}\left[m\left(U\right)R_U\right])$ . Now for any m₁ and m₂,

$$\begin{gathered} {\Vert g(U_i,m_1)-g(U_i,m_2)\Vert }_{\mathcal{A}}=c_r^{-1}\sqrt{nh}\left\{{\Vert (m_1\left(U_i\right)-m_2\left(U_i\right))R_{U_i}\Vert }_{\mathcal{A}} \\ +{\Vert 𝔼\left[(m_1\left(U\right)-m_2\left(U\right))R_U\right]\Vert }_{\mathcal{A}}\right\} \\ \le 2\sqrt{n}{\Vert m_1-m_2\Vert }_{\sup }, \end{gathered}$$

where we used the fact that ${\Vert R_u\Vert }_{\mathcal{A}}\le c_r{h}^{-1∕2}$ by Lemma A.4. Note that $Z_n\left(m\right)=\frac{1}{n}{\sum }_{i\in L_j}g(U_i,m)$ . Therefore by Lemma G.1, we have for any t > 0,

$$\begin{array}{cc}\hfill \mathbb{P}\left({\Vert Z_n\left(m_1\right)-Z_n\left(m_2\right)\Vert }_{\mathcal{A}}\ge t\right)& =\mathbb{P}\left({\Vert \frac{1}{n}\sum _{i=1}^n\{g(U_i,m_1)-g(U_i,m_2)\}\Vert }_{\mathcal{A}}\ge t\right)\hfill \\ \hfill & \le 2\exp \left(-\frac{t^2}{8{\Vert m_1-m_2\Vert }_{\sup }^2}\right)\hfill \end{array}$$ (7.15)

Then by Lemma F.1, we have

$$\mathbb{P}\left(\underset{m\in \mathcal{F}}{\sup }{\Vert Z_n\left(m\right)\Vert }_{\mathcal{A}}\ge C\omega (\mathcal{F},\mathrm{diam}\left(\mathcal{F}\right))+x\right)\le C\exp \left(\frac{-x^2}{C\mathrm{diam}{\left(\mathcal{F}\right)}^2}\right),$$ (7.16)

where $\mathrm{diam}\left(\mathcal{F}\right)={\sup }_{m_1,m_2\in \mathcal{F}}{\Vert m_1-m_2\Vert }_{\sup }$ .

Define d_n,s = c_rr_n,sh^−1/2 and $\tilde{m}=d_{n,s}^{-1}\Delta m^{\left(j\right)}∕2$ . Again we do not specify its relationship with j. Define the event $\mathcal{E}=\{{\Vert \Delta m^{\left(j\right)}\Vert }_{\mathcal{A}}\le r_{n,s}\}$ . On the event $\mathcal{E}$ , we have

$${\Vert \tilde{m}\Vert }_{\sup }\le c_r{h}^{-1∕2}{\left(2d_{n,s}\right)}^{-1}{\Vert \Delta m^{\left(j\right)}\Vert }_{\mathcal{A}}\le 1∕2,$$

where we used the fact that ${\Vert \tilde{m}\Vert }_{\sup }\le c_r{h}^{-1∕2}{\Vert \tilde{m}\Vert }_{\mathcal{A}}$ by Lemma A.4. This implies $\mid {\mathit{x}}^T\tilde{\beta }+\tilde{f}\left(z\right)\mid \le 1∕2$ for any (x, z). Letting x = 0, one gets ${\Vert \tilde{f}\Vert }_{\sup }\le 1∕2$ , which further implies $\mid {\mathit{x}}^T\tilde{\beta }\mid \le 1$ for all x by triangular inequality. Moreover, on the even $\mathcal{E}$ we have

$${\Vert \tilde{f}\Vert }_{\mathcal{H}}\le {\lambda }^{-1∕2}{\Vert \tilde{m}\Vert }_{\mathcal{A}}\le {\lambda }^{-1∕2}∕\left(2d_{n,s}\right){\Vert \Delta m^{\left(j\right)}\Vert }_{\mathcal{A}}\le c_r^{-1}{h}^{1∕2}{\lambda }^{-1∕2}$$

by the definition of ${\Vert \cdot \Vert }_{\mathcal{A}}$ . Hence, we have shown that $\mathcal{E}\subset \{\tilde{m}\in \mathcal{F}\}$ . Combining this fact with (7.16), and noting that $\mathrm{diam}\left(\mathcal{F}\right)=1$ , we have

$$\mathbb{P}\left(\{{\Vert Z_n\left(\tilde{m}\right)\Vert }_{\mathcal{A}}\ge C\omega (\mathcal{F},1)+x\}\cap \mathcal{E}\right)\le C\exp (-x^2∕C),$$ (7.17)

By the definition of m̃, and the relationship $Re{m}^{\left(j\right)}=c_r^{-1}\sqrt{nh}{Z}_n\left(\Delta m^{\left(j\right)}\right)$ , we calculate that $Z_n\left(\tilde{m}\right)=(1∕2)h^{1∕2}{n}^{1∕2}{d}_{n,s}^{-1}Re{m}^{\left(j\right)}=(1∕2)c_r^{-1}h{n}^{1∕2}{r}_{n,s}^{-1}Re{m}^{\left(j\right)}$ . Plugging the above form of Z_n(m̃) into (7.17) and letting x = log N in (7.17), we have

$$\mathbb{P}\left(\{{\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}\ge b_{n,s}\}\cap \mathcal{E}\right)\le C\exp (-{\log }^{2}N∕C),$$ (7.18)

where we used the definition that $b_{n,s}=C{h}^{-1}{n}^{-1∕2}{r}_{n,s}(\omega (\mathcal{F},1)+\log N)$ . Therefore we have

$$\begin{array}{cc}\hfill \mathbb{P}\left({\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}\ge b_{n,s}\right)& \le \mathbb{P}\left(\{{\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}\ge b_{n,s}\}\cap \mathcal{E}\right)+\mathbb{P}\left({\mathcal{E}}^c\right)\hfill \\ \hfill & \le C\exp (-{\log }^{2}N∕C)+\mathbb{P}\left({\mathcal{E}}^c\right).\hfill \end{array}$$ (7.19)

We have the following lemma that controls $\mathbb{P}\left({\mathcal{E}}^c\right)$ .

Lemma 7.4

If Assumption 3.1, 3.2 and Condition (3.6) are satisfied, then there exist a constant c such that

$$\mathbb{P}\left({\mathcal{E}}^c\right)=\mathbb{P}\left({\Vert \Delta m^{\left(j\right)}\Vert }_{\mathcal{A}}\ge r_{n,s}\right)\lesssim n\exp (-c{\log }^{2}N).$$

for all j = 1,...,s.

By Lemma 7.4 and (7.19) we have

$$\mathbb{P}\left({\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}\ge b_{n,s}\right)\lesssim n\exp (-c{\log }^{2}N).$$ (7.20)

(ii) We will use an Azuma-type inequality in Hilbert space to control the averaging remainder term $s^{-1}{\sum }_{j=1}^{s}Re{m}^{\left(j\right)}$ , as all Rem^(j) are independent and have zero mean. Define the event ${\mathcal{A}}_j=\{{\Vert Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}\le b_{n,s}\}$ . By Lemma G.1, we have

$$\mathbb{P}\left(\left\{{\cap }_j{\mathcal{A}}_j\right\}\cap \left\{{\Vert s^{-1}\sum _{j=1}^{s}Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}>s^{-1∕2}{b}_{n,s}\log N\right\}\right)\le 2\exp (-{\log }^{2}N∕2).$$ (7.21)

Moreover, by (7.20),

$$\mathbb{P}\left({\mathcal{A}}_j^c\right)\lesssim n\exp (-c{\log }^{2}N).$$ (7.22)

Hence it follows that

$$\mathbb{P}\left({\Vert s^{-1}\sum _{j=1}^{s}Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}>s^{1∕2}{b}_{n,s}\log N\right)\le \mathbb{P}\left(\left\{{\cap }_{j=1}^s{\mathcal{A}}_j\right\}\cap \left\{{\Vert s^{-1}\sum _{j=1}^{s}Re{m}^{\left(j\right)}\Vert }_{\mathcal{A}}>s^{-1}{b}_{n,s}\log N\right\}\right)+\mathbb{P}\left({\cup }_j{\mathcal{A}}_j^c\right)$$

as N → ∞, where the last inequality follows from (7.21), (7.22) and union bound. This finishes the proof.

We can apply similar arguments as above to bound ${\Vert Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}$ and ${\Vert 1∕s{\sum }_{j=1}^{s}Re{m}_f^{\left(j\right)}\Vert }_{\mathcal{C}}$ , by changing $\omega (\mathcal{F},1)$ to $\omega ({\mathcal{F}}_2,1)$ , which is dominated by $\omega (\mathcal{F},1)$ . The bounds of $\nabla {\Vert Re{m}_{\beta }^{\left(j\right)}\Vert }_2$ and ${\Vert 1∕s{\sum }_{j=1}^{s}Re{m}_{\beta }^{\left(j\right)}\Vert }_2$ then follow from triangular inequality.

7.4. Proof of Theorem 3.4

Proof

In view of Theorem 3.4, we first prove

$$\left(\begin{array}{c}\hfill \sqrt{n}({\beta }_0^{\left(j\right)\ast }-{\beta }_0^{\left(j\right)})\hfill \\ \hfill \sqrt{Nh}(f_0^{\ast }\left(z_0\right)-f_0\left(z_0\right)-W_{\lambda }{f}_0\left(z_0\right))\hfill \end{array}\right)\to 0$$ (7.23)

for both (i) and (ii). By Proposition 2.3, we have

$$\left(\begin{array}{c}\hfill {\beta }_0^{\left(j\right)\ast }-{\beta }_0^{\left(j\right)}\hfill \\ \hfill f_0^{\ast }\left(z_0\right)-f_0\left(z_0\right)\hfill \end{array}\right)=\left(\begin{array}{c}\hfill L_{\lambda }{f}_0\hfill \\ \hfill W_{\lambda }{f}_0\left(z_0\right)+\mathit{A}{\left(z_0\right)}^T{L}_{\lambda }{f}_0\hfill \end{array}\right).$$ (7.24)

By Lemma A.5, it follows that under Assumption 3.3, ${\Vert L_{\lambda }{f}_0\Vert }_2\lesssim \lambda$ . Now we turn to $f_0^{\ast }\left(z_0\right)-f_0\left(z_0\right)$ . Observe that

$$\mathit{A}\left(z\right)={\langle \mathit{A},{\tilde{K}}_z\rangle }_{\mathcal{C}}={\langle \mathit{B},{\tilde{K}}_z\rangle }_{L_2\left({\mathbb{P}}_Z\right)}=\sum _{\ell =1}^{\infty }\frac{{\langle \mathit{B},{\varphi }_{\ell }\rangle }_{L_2\left({\mathbb{P}}_Z\right)}}{1+\lambda ∕{\mu }_{\ell }}{\varphi }_{\ell }\left(z\right),$$ (7.25)

Applying Cauchy-Schwarz, we obtain

$$\begin{array}{cc}\hfill A_k{\left(z_0\right)}^2& \le \left(\sum _{\ell =1}^{\infty }\frac{{\langle {\mathit{B}}_k,{\varphi }_{\ell }\rangle }_{L_2\left({\mathbb{P}}_Z\right)}^2}{{\mu }_{\ell }}{\varphi }_{\ell }^2\left(z_0\right)\right)\left(\sum _{\ell =1}^{\infty }\frac{{\mu }_{\ell }}{{(1+\lambda ∕{\mu }_{\ell })}^2}\right)\hfill \\ \hfill & \le c_{\varphi }^2{\Vert B_k\Vert }_{\mathcal{H}}^2\mathrm{Tr}\left(K\right),\hfill \end{array}$$

where the last inequality follows from the uniform boundedness of ${\varphi }_{\ell }$ . Hence we have that A_k(z₀) is uniformly bounded, which implies

$$\mathit{A}{\left(z_0\right)}^T{L}_{\lambda }{f}_0\le {\Vert \mathit{A}\left(z_0\right)\Vert }_2{\Vert L_{\lambda }{f}_0\Vert }_2\lesssim \lambda .$$

Therefore, if we choose $\lambda =o({\left(Nh\right)}^{-1∕2}\wedge n^{-1∕2})$ , then we get (7.23), which eliminates the estimation bias for ${\beta }_0^{\left(j\right)}$ .

Now we consider the asymptotic variance for cases (i) and (ii). It suffices to show that ${\alpha }_{z_0}={\lim }_{N\to \infty }{h}^{1∕2}{W}_{\lambda }\mathit{A}\left(z_0\right)$ . By Lemma A.2 and (7.25), we have

$$\begin{array}{cc}\hfill W_{\lambda }{A}_k\left(z_0\right)=& \sum _{\ell =1}^{\infty }\frac{{\langle B_k,{\varphi }_{\ell }\rangle }_{L_2\left({\mathbb{P}}_Z\right)}}{1+\lambda ∕{\mu }_{\ell }}\frac{\lambda }{\lambda +{\mu }_{\ell }}{\varphi }_{\ell }\left(z_0\right)\hfill \\ \hfill & \le \left(\sum _{\ell =1}^{\infty }\frac{{\langle B_k,{\varphi }_{\ell }\rangle }_{L_2\left({\mathbb{P}}_Z\right)}^2}{{\mu }_{\ell }}{\varphi }_{\ell }^2\left(z_0\right)\right)\left(\sum _{\ell =1}^{\infty }\frac{{\mu }_{\ell }}{{(1+\lambda ∕{\mu }_{\ell })}^2}\right)\hfill \\ \hfill & \le c_{\varphi }^2{\Vert B_k\Vert }_{\mathcal{H}}^2\mathrm{Tr}\left(K\right).\hfill \end{array}$$

Hence by dominated conference theorem, as λ → 0 we have $W_{\lambda }{A}_k\left(z_0\right)\to 0$ . As h = O(1), it follows that ${\alpha }_{z_0}={\lim }_{N\to \infty }{h}^{1∕2}{W}_{\lambda }\mathit{A}\left(z_0\right)=0$ .

When h → 0, we have ${\gamma }_{z_0}=-{\lim }_{N\to \infty }{h}^{1∕2}\mathit{A}\left(z_0\right)=0$ , as A_k(z₀) is uniformly bounded. Hence ${\Sigma }_{12}^{\ast }={\Sigma }_{21}^{\ast }=0$ and ${\Sigma }_{22}^{\ast }={\sigma }^2{\sigma }_{z_0}^2$ .