Computational Biomechanics of Human Red Blood Cells in Hematological Disorders

Abstract

We review recent advances in multiscale modeling of the biomechanical characteristics of red blood cells (RBCs) in hematological diseases, and their relevance to the structure and dynamics of defective RBCs. We highlight examples of successful simulations of blood disorders including malaria and other hereditary disorders, such as sickle-cell anemia, spherocytosis, and elliptocytosis.

1. Introduction

Blood comprises primarily blood cells suspended in plasma, which constitutes ∼55% of total blood volume. Plasma contains mostly water and other substances including proteins, glucose, and vital minerals such as sodium and potassium. Blood cells are mainly composed of red blood cells (RBCs), white blood cells and platelets. Together, these three types of blood cells add up to a total 45% of the volume of whole blood.

Human RBCs, compared with other cells in the human body, are particularly simple in their structure. A normal RBC is a nucleus-free cell; it adopts a distinctive biconcave shape of ∼8.0 μm in diameter and ∼2.0 μm in thickness (Fig. 1(a)) [1,2]. The membrane of an RBC consists of two components: a lipid bilayer and an attached spectrin-based skeleton (cytoskeleton). These two components are connected by transmembrane proteins such as band-3 and glycophorin C (Fig. 1(b)). The lipid bilayer is considered to be nearly viscous and area preserving, while the spectrin-based network is largely responsible for the elastic properties of the RBCs [3]. The thickness of the composite bilayer-spectrin membrane is around 10 nm [4,5]; hence, the RBC membrane can be treated as a two-dimensional viscoelastic material embedded in a three-dimensional space.

Fig. 1.

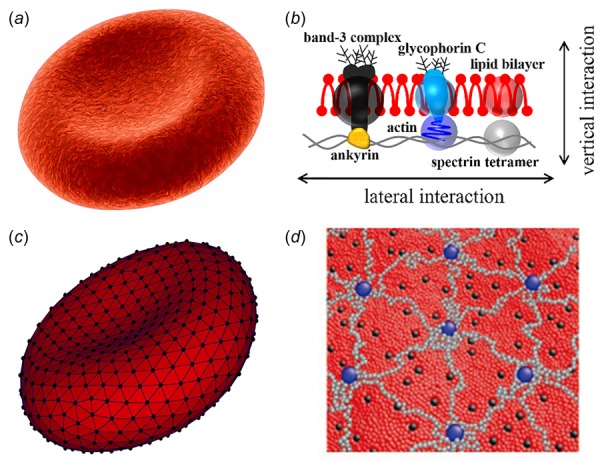
(a and b) Schematic representation of a healthy human RBC (a) and its complex membrane structure (b). The cell membrane is made of a lipid bilayer reinforced on its inner face by a flexible two-dimensional spectrin network. (c and d) Schematic view of the particle-based whole-cell model (c) and composite membrane model (d). For the whole-cell model (c), the lipid bilayer and cytoskeleton are rendered in dark gray and black triangular networks. For the coarse-grained composite membrane model (d), the dark gray, black, and light gray particles represent clusters of lipid molecules, actin junctions, and spectrin filaments of cytoskeleton, respectively; the black particles signify band-3 complexes.

The human RBCs circulate the body delivering oxygen from lungs to tissues during their normal lifespan of 120 days. The deformability of the RBCs, or the ability of the RBCs to deform their shape under applied stress, plays an important role in the main function of the RBCs. Advances in experimental techniques have allowed accurate measurements of RBC deformability [6–19]. These available experimental methods can be divided into two categories: techniques that measure the deformability of a large number of RBCs at the same time and single-cell techniques. The former experimental methods, e.g., blood viscometer [6,7], ektacytometry [8], filtration [9], and flow chambers [10], measure properties averaged over all RBCs in a blood sample, and they do not take into account the heterogeneity or size differences within the RBC population. Single-cell techniques, including atomic force microscopy (AFM) [11,20], diffraction phase microscopy [12], magnetic twisting cytometry [13,14], micropipette aspiration [15], optical tweezers [16,17], and ultrasound-based techniques [18,19], can measure the biomechanical properties of RBC membranes, such as shear modulus (μ₀) and bending modulus (k_c) of RBCs. For example, AFM measurements found that the Young's modulus of normal RBCs is in the range of 1 kPa [21]. RBCs from patients with sickle-cell anemia (SCA) are stiffer than normal RBCs with a broadly distributed Young's modulus ranging from approximately 3 kPa to 50 kPa depending on oxygenation conditions and probably on the severity of the disease [22]. Micropipette aspiration subjects the RBC directly to mechanical deformation and yields μ₀ in the range of 4–12 μN/m [15,23]. Techniques based on diffraction phase microscopy, magnetic twisting cytometry, and optical tweezers have also reported consistent values of μ₀ [14,16,17,24]. The bending modulus of RBCs, which is determined by chemical compositions of the lipid bilayer, has been measured by micropipette aspiration and several other techniques. The measured values of k_c lies between 1.0 × 10^–19 J and 7.0 × 10^–19 J [24–26]. These experimental measurements reveal that RBCs have remarkable deformability, and hence they can bend and flow smoothly without any damage when passing through narrow capillaries. However, this general feature of RBCs may be significantly altered under various pathophysiological conditions. For example, membrane stiffening of RBCs induced by parasitic infectious diseases like malaria [27,28] and certain hereditary hematological disorders like SCA [29,30] can result in vaso-occlusion and blood flow impairment. RBC deformability has also been demonstrated to be impaired in hereditary spherocytosis (HS) [31] and hereditary elliptocytosis (HE) [32], diabetes mellitus (DM) [33,34], and a variety of other diseases. For example, mechanical weakness or fragility of RBCs in HS and HE can lead to vesiculation and membrane loss [35], or even cause the extravascular hemolysis [36]. Also, impaired deformability of RBC due to DM induces insulin-dependent platelet aggregation. The RBC deformability is an important determinant of blood viscosity, hence blood flow resistance in the microcirculation. In addition, it is also known that deformed RBCs can release adenosine triphosphate (ATP) regulating the blood flow [37–39]. Thus, RBCs and their biomechanical properties are of physiological and pathological importance.

During erythrocyte maturation, RBCs expel the nucleus, all organells, and ribosomal ribonucleic acid and what remains is a hemoglobin solution encapsulated by the plasma membrane. We note, however, that several biochemical processes common in several types of nucleated cells are still active in RBCs [40–42]. A common problem in hematological disorders is the defective membrane skeleton and the corresponding changes in the structure and viscoelastic properties of individual RBCs. For example, in malaria, RBCs infected with Plasmodium falciparum (Pf-RBCs) become progressively less deformable and more spherical during the intraerythrocytic cycle [28,43]. In SCA, the detachment of the lipid bilayer from the spectrin network owing to the polymerization of sickle hemoglobin (HbS) causes “budding off” of the lipid bilayer, which in turn results in reduced cell deformability [30]. In addition, HS is usually caused by the defects in anchoring proteins involved in vertical interactions between lipid bilayer and spectrin network, whereas HE is a result of defects in spectrin filaments related to lateral interactions in the spectrin network [44]. Protein mutations associated with membrane defects subsequently lead to aberrant cell shape and impaired deformability. Thus, studying the biomechanical properties of RBCs and their related dynamic behavior in vitro can contribute greatly to the understanding of the pathophysiology and development of new treatments for such diseases.

Along with the aforementioned experimental studies, recent advances in computational modeling and simulation enable investigation of a broad range of biomechanical and rheological problems associated with RBCs. This is a very active area of research, see recent review [45–51]. Several computational approaches, including continuum-based fluid-structure interaction models [52–56] and particle-based numerical models [57–65], have been developed recently and applied to RBC simulations at different length scales. Traditionally, continuum-based RBC models have been used for studying blood dynamics on macroscopic length and time scales. In the recent years, particle-based RBC models are increasingly popular as a promising tool for multiscale modeling of blood flow. In general, the mechanical properties of the modeled RBC membrane are determined by the experimentally established RBC macroscopic properties such as shear and bending moduli. The RBC models are validated against the available experiments that examine RBC mechanics, rheology, and dynamics. For example, the linear and nonlinear elastic deformations of modeled RBCs are compared with RBC deformation in stretching experiments by optical-tweezers [17], and the dynamics of modeled RBCs in shear flow are validated against RBC shearing experiments [66–69] and theoretical predictions [70]. It has been demonstrated that these RBC models capture the known biomechanical properties of RBCs. Moreover, computational RBC modeling also provides predictions of properties beyond available experimental measurements, and is related to the strength of RBC aggregation and its effect on blood viscosity [71] and to the quantification of molecular-level mechanical forces involved in bilayer–cytoskeletal dissociation [65]. Current experimental studies alone have not been able to determine the molecular details, accurate numerical modeling, combined with diverse experimental measurements, could also be used to provide valuable information such as the discovery of new mechanism responsible for the stiffening of malaria-infected RBCs [72].

In this article, we review the applications of these computational approaches on the modeling of biomechanical properties and dynamic behavior of RBCs in hematological diseases with focus on the most recent contributions.

2. Computational Models for Simulations of Human RBCs

Continuum-based RBC models treat the RBC membrane and fluids as homogeneous materials, using boundary integral method (BIM) [54,55,73,74], immersed boundary method (IBM) [52,53,75,76], and fictitious domain method (FDM) [77,78]. Therefore, the continuum-based RBC models allow the study of blood flow on macroscopic length and time scales. For example, microcirculatory blood flow normally falls in the Stokes flow regime where the effect of inertia is negligible, hence making BIM a good candidate for modeling RBC suspensions under flow [79]. The BIM exploits the fact that the governing equations of fluid dynamics are linear, which can often be recast into an integral equation to study the evolution of the interface. For instance, for equiviscous encapsulated and suspending fluids

$${\mathbf{v}}^{\text{mm}}={\mathbf{v}}^{\infty }-\frac{1}{8\pi {\eta }^{\text{ex}}}{\int }_A\left(\mathbf{G}·{\tau }^{\text{mm}}\right)dA\hspace{0.17em}$$ (1)

where v^∞ is the applied fluid flow, and ${\tau }^{\text{mm}}={\tau }^{\kappa }+{\tau }^{\mu }+{\tau }^{\gamma },\hspace{0.17em}\mathbf{G}$ is Green's function for the Stokes equations. Several extensions of IBM have also been developed, depending on the choice of fluid or structure [53,75,80,81]. For example, the front-tracking, immersed boundary method (FT-IBM) in Refs. [53] and [75] used a finite element triangulation to represent the RBC membrane and a projection splitting scheme to solve the Navier–Stokes equation. In addition, Lattice-Boltzmann (LB) method has emerged as a promising tool for modeling complex fluid flow such as RBC suspensions [80,81,82,83]. A coupled finite element–lattice Boltzmann (FE-LB) method, which combined a linear FE analysis for RBC deformation with the LB method for the fluid phase, has been developed for blood flow [84]. The FE-LB method could not resolve the large deformation of RBCs in small capillaries. To overcome these issues, the LB method is coupled with a coarse-grained spectrin-link RBC model [85,86].

Although the continuum-based RBC models provide an accurate description of RBC deformation at the whole cell level, it does not provide a detailed picture of the changes of local subcellular structures and specific molecules during cell deformation. Therefore, they are not able to describe phenomena at the mesoscopic and microscopic scales, such as membrane thermal fluctuations, which affect RBC biomechanics. Particle-based RBC models, on the other hand, can resolve cellular and subcellular scales, using coarse-grained molecular dynamics (CGMD) [72,87,88], dissipative particle dynamics (DPD) [62–65], smoothed dissipative particle dynamics (SDPD) [89], smoothed particle hydrodynamics (SPH) [90,91], and multiparticle collision dynamics (MPCD) [59,92]. Therefore, the particle-based RBC models are more suitable to study the dynamics and rheology of RBCs and of microcirculatory blood flow in disease. Several particle-based RBC models, including coarse-grained whole-cell models (Fig. 1(c)) [62–65,90,91] and molecular-detailed composite membrane models (Fig. 1(d)) [72,87,88], have been developed and employed to quantify the biomechanical properties and dynamic behavior of RBCs in health and disease [91,93–97].

Generally, the molecular-detailed composite membrane models, which account separately for the lipid bilayer and cytoskeleton and also include explicit transmembrane proteins, are able to capture the molecular structures of the RBC membrane in both normal and defective states. The molecular-detailed membrane models have been successfully applied to study some issues associated with RBC membrane defects, such as the diffusion of transmembrane proteins in the defective RBC membrane [98]. However, at present, they are computationally very expensive for large-scale applications such as modeling whole blood involving a large number of RBCs. On the other hand, coarse-grained whole-cell model provides the opportunity to significantly reduce the computational complexity. For example, a three-dimensional multiscale RBC (MS-RBC) model has been developed and successfully applied to RBC simulations at different length scales [62,63]. In the MS-RBC model, the RBC membrane is modeled as a two-dimensional triangulated network of viscoelastic springs, which includes elastic, bending, and viscous properties. Specifically, the elastic potential of the RBC membrane is represented by

$$V_s=\sum _{j\in 1\dots N_s}\left[\frac{k_{B}T{l}_m(3x_j^2-2x_j^3)}{4p(1-x_j)}+\frac{k_p}{(n-1)l_j^{n-1}}\right]$$ (2)

where l_j and l_m are the length and maximum extension of spring j, p is the persistence length of the RBC membrane network, k_p is the spring constant, and k_BT is the energy unit. The bending resistance of the RBC membrane is modeled by

$$V_b=\sum _{j\in 1\dots N_s}{k}_b[1-\text{cos}({\theta }_j-{\theta }_0)]$$ (3)

where θ_j and θ₀ are the instantaneous and spontaneous angles between two adjacent triangles (having a common edge j), and k_b is the bending constant. In addition, the conservation constraints on the RBC area and volume are imposed to mimic the area incompressibility of lipid bilayer and the volume incompressibility of intracellular fluid

$$V_{a+v}=\sum _{j\in 1\dots N_t}\frac{k_d{(A_j-A_0)}^2}{2A_0}+\frac{k_a{(A-A_0^{\text{tot}})}^2}{2A_0^{\text{tot}}}+\frac{k_v{(V-V_0^{\text{tot}})}^2}{2V_0^{\text{tot}}}$$ (4)

where k_d, k_a, and k_v are the local area, global area, and volume constraint coefficients, respectively. The terms $A_0^{\text{tot}}$ and $V_0^{\text{tot}}$ are the total area and volume of RBC, and N_t is the number of triangles in the RBC membrane network. Being constructed from a CGMD approach, the MS-RBC model can naturally include membrane thermal fluctuations. Such formulations are compatible with coarse-grained mechanics descriptions of the RBC membrane with the advantage of including the viscosity of the RBC membrane without additional cost. Thus, the particle-based whole-cell models can resolve subcellular and cellular scales.

3. Morphological Change in Diseased RBCs

A healthy human RBC has a biconcave shape as the high surface-to-volume ratio of cell membrane facilitates transport of oxygen through cell membrane and also contributes to the remarkable deformability of RBCs. Thus, the RBCs can change their shape easily under the influence of mechanical forces in blood flow. It was recognized early on that the RBCs take the shape that minimizes their membrane-bending energies under the prescribed area and enclosed volume. The cost for bending is described by several continuum models based on the Helfrich energy: the spontaneous curvature model (SCM) [99,100], the bilayer coupling model (BCM) [100,101], and the area-difference-elasticity (ADE) model [102,103]. These theoretical models have been applied to predict the energy-minimizing RBC shapes such as discocytic and stomatocytic morphologies. In addition, several computational particle-based models have been employed to explain the variety of existing shapes. For example, Li et al. illustrated the shape transformation of membrane vesicles by using the DPD approach [47,104]. Numerous complex vesicle shapes, including RBC-like ones, were revealed when the reduced area difference between the outer and inner leaflets of the bilayer membrane was appropriately adjusted (Fig. 2(a)).

Fig. 2.

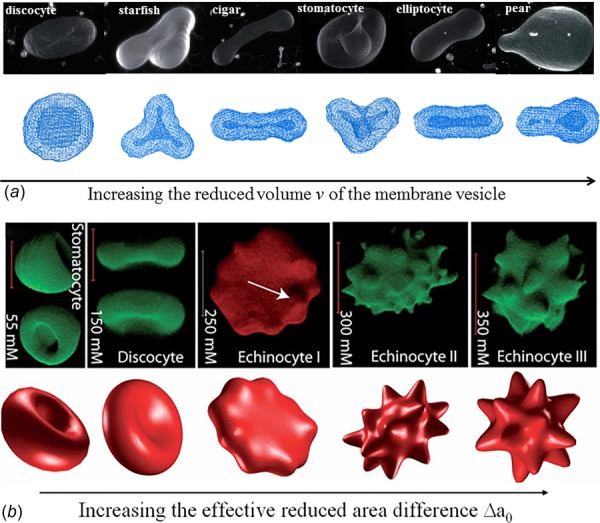
Shape transformation pathways of membrane vesicles (a) and RBCs (b) obtained from experimental investigations (upper) and model predictions (lower). Reproduced from Refs. [47,105].

Under pathological conditions, a variety of morphological alterations in RBCs are observed [106–108]. For example, spherocytes, observed in HS, are caused by defects in ankyrin, protein 4.2 or band-3 proteins, which tether the cytoskeleton to the lipid bilayer [32,109,110]. A common feature of HS RBC is loss of membrane surface area and resultant change in cell shape from discocytes to spherocytes [110]. In HE [31,111,112] and hereditary pyropoikilocytosis (HPP), a severe case of HE [113,114], the protein defects occur at membrane cytoskeletal proteins such as α-spectrin, β-spectrin, and protein 4.1, and thus interrupt the self-association of spectrin α/β heterodimers, leading to the formation of elliptocytes and poikilocytes. Echinocytes are characterized by small, evenly spaced thorny projections [115,116], also referred as burr cells. Formation of echinocytes is often reversible and can be induced by altering the cell's environment, such as pH of the medium, the metabolic state, and adding chemical substances. Similar to echinocytes, acanthocytes are also characterized by spicules on the cell membrane, but they are irregular in size, shape, and distribution [117,118]. The formation of acanthocytes is attributed to abnormal lipid composition with altered lipid distribution between the inner and outer leaflets of the bilayer membrane.

Defects in the band-3 protein may also cause formation of stomatocytes, which are characterized by the “coffee beans” or “cup”-shaped RBCs [119,120]. The function of band-3 protein is to mediate the exchange of chloride with bicarbonate across membranes. Defective band-3 results in cation leakage, leading to increased membrane permeability to sodium and potassium. As a result, intracellular water and RBC volume increase. RBCs transform from biconcave shape to cup shape due to the decreased surface-to-volume ratio. Schistocytes are fragments of RBCs, which exhibit various shapes, such as triangular shape (triangulocytes), or horn-like projections (keratocytes), or helmet shape [121,122]. Schistocytes are produced when RBCs are trapped by fibrin strands during blood clotting. When the RBCs are exposed to nonphysiological conditions, like in the case of circulating through artificial organs or devices, they might be affected resulting in deteriorations at various degrees, ranging from slight morphological alterations to the rupture of their membrane resulting in hemolysis. Finally, sickle-shaped RBCs [29,123,124], which result from the polymerization of HbS inside the RBCs, are not flexible and can stick to vessel walls, causing a blockage that slows or stops the flow of blood. An overview of the morphological abnormalities of RBCs in these blood disorders is available elsewhere [30,44,125].

Although numerous experimental studies have been performed to identify the protein defects causing different blood disorders, the biomechanical mechanisms on how the defective proteins alter cell morphology in the diseased RBCs is still not well understood due to the limitation on the length and time scales of experiments. Therefore, several numerical studies have been conducted to explain the cell morphological changes and the associated vesicle formation [126]. As a key component of the RBC membrane, the cytoskeletal network is associated with the lipid bilayer from the cytoplasmic side, and endows the RBC with shear elasticity. It is revealed that the membrane elasticity is necessary to account for shapes of real RBCs, especially those with highly curved features such as echinocytes. As a result, RBCs are more often modeled as membrane vesicles associated with the cytoskeleton, by introducing the effect of elastic energy of the cytoskeleton into the ADE model. For example, Lim et al. proposed a coupled model, by combining the bending and elastic energies, to simulate the stomatocyte-discocyte-echinocyte transformations of RBC [127]. Khairy and Howard studied the variety of echinocytic shapes in terms of the resting shape of the cytoskeleton [105]. They found that a prolate ellipsoid resting shape can result in a large variety of echinocyte Shapes (Fig. 2(b), upper right three pictures). The ADE model with involvement of effect of cytoskeleton is capable of describing the cell shape transition, but it is hard to validate due to the challenge of measuring the area difference between two leaflets in experiment. In addition, the interactions between the lipid and cytoskeleton, which can yield critical insights into the etiology of HS and HE, are not explicitly accounted for in the model.

As an alternative choice, mesoscale particle-based methods have been employed to study the morphological changes in defective RBC membrane. For example, Spangler et al. developed a mesoscale implicit-solvent model to investigate the kinetics of protrusion (blebbing) on RBC surfaces [128]. Their simulations show that membrane blebbing can result from a localized disruption (Figs. 3(a)–3(c)) or a uniform contraction of the cytoskeleton (Figs. 3(d)–3(f)). More importantly, they proved that the disruption of the cytoskeleton can alter the cell morphology, which favors the mechanism that the cytoskeleton controls the RBC shape [129]. Li and Lykotrafitis applied the two-component composite model to simulate the buckling and vesiculation of the RBC membrane [130]. Besides simulating the sequence of membrane blebbing (Figs. 3(g)–3(h)), they observed vesiculation when the RBC membrane underwent large compression (Fig. 3(i)). Since this RBC model used one layer of coarse-grained particles, spontaneous curvature is introduced into the model to simulate local ADE. They found that large spontaneous curvature leads to the formation of nanovesicles with a size of ∼25 nm independently of the cytoskeleton corral structure. They also found that lateral cytoskeletal compression in the RBC without spontaneous curvature can produce vesicles of the size of ∼100 nm which may explain the mechanism by which normal RBCs shed membrane during circulation and during storage [131] and measures of stored red blood cell quality [132]. In addition, they showed that lateral cytoskeleton compression can facilitate the formation of vesicles of ∼60 nm in areas of the RBC membrane with intermediate level of spontaneous curvature. This result is consistent with experimental findings that vesicles are preferentially shed from the tip of spicules in echinocytes [133]. Overall, the underlying mechanisms for morphological change of diseased RBCs can be patient-specific and is more likely to result from the combined effect of spontaneous curvature induced by the area difference between two leaflets and the cytoskeleton-induced compression. For example, increased intracellular calcium or depleted ATP not only promote asymmetry of leaflets but also activate proteolytic enzymes like calpain, which breaks down the tethering points between the cytoskeleton and the lipid bilayer [134].

Fig. 3.

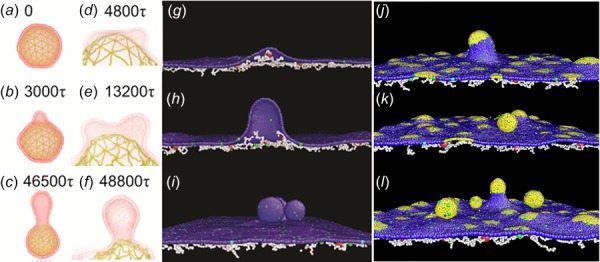
(a–c) Snapshot of a vesicle undergoing blebbing as a result of a localized ablation of the RBC cytoskeleton. (d–f) Sequences of coalescence of two blebs on vesicle during a uniform contraction of RBC cytoskeleton (Reproduced from Ref. [128]). CGMD modeling of one-component (g–i) and two-component (j–l) RBC membrane under uniform compression at compression ratio of (g) 2%, (h) 5%, and (i) 15%. Gray color highlights the lipid bilayer component with spontaneous curvature. The compression ratio is defined as the ratio of the decrease in the horizontally projected area due to compression, to the projected area of the membrane at equilibrium (Reproduced with permission from Li and Lykotrafitis [130]. Copyright 2015 by American Physical Society.

Particle-based RBC models have also been applied to study RBC morphology in SCA. For example, by using the MS-RBC model, Lei and Karniadakis quantified the morphology of SCA RBCs [135]. In their simulations, the irregular-shaped RBCs are obtained by exerting surface tension at outer rim of the RBC membrane. Starting from the normal biconcave shape, the RBC undergoes a dramatic shape transformation to granular, elongated, and crescent shapes.

4. Biomechanical Properties of Diseased RBCs

In humans, normal RBCs are remarkably flexible and deformable. The extreme deformability allows them to squeeze through narrow capillaries as small as 3 μm in diameter without any damage. However, in many hematological disorders such as malaria and SCA, the spectrin network and lipid bilayer of diseased RBCs may be significantly altered, leading to impaired functionality including loss of deformability. Numerical simulations have been successfully exploited in numerous hematological studies, due to its precise predictions on biomechanics and dynamics of RBCs [93,95,136]. Below we highlight some of the researches on biomechanical and dynamic properties of diseased RBCs.

4.1. Malaria-Infected RBCs.

Malaria is one of the most prevalent human infections worldwide. In malaria, RBCs are hosts of Plasmodium parasites which change the cell biomechanical properties. Progression through the parasite development from ring to trophozoite then to schizont stages leads to Pf-RBCs loss of their deformability with a relative membrane stiffening more than ten-fold in comparison to healthy ones. Moreover, at the final stage (schizont) of the parasite development, the Pf-RBCs often show near-spherical shapes due to the formation of intracellular parasitophorous vacuoles, which further impaires cell deformability. These changes can greatly affect the dynamic and rheological properties of Pf-RBCs, alter blood flow and may even cause occlusions of small capillaries.

Quantifying cell deformability for various stages of Pf-RBCs is significant. Recent efforts have been directed toward this end. For example, at molecular level, a two-component composite model of the RBC membrane has been successfully applied to study the stiffening effects of developed nanoscale knobs and remodeling of the spectrin network of Pf-RBCs [72]. The simulations show that the deposition of nanoscale knobs, rather than spectrin network remodeling, is the primary cause of the dramatically increased stiffness of the Pf-RBC membranes. The simulation results further reveal that the knobs stiffen the RBC membrane in a unique manner by simultaneously harnessing composite strengthening, strain hardening, and knob density-dependent vertical coupling effects.

At the cellular level, different particle-based RBC models have been used to characterize the biomechanical properties of Pf-RBCs [137–141]. For example, MS-RBC models have been used to simulate healthy RBCs and Pf-RBCs [65,138]. The simulations show that the membrane fluctuation predictions depend on the cell geometry, the experimental or simulation conditions (e.g., adhesion strength, metabolic activity), and the membrane properties (e.g., shear modulus, bending rigidity) [138]. Moreover, the bilayer-cytoskeletal elastic interaction coefficient plays a key role in the thermal fluctuations experiments [65]. Thus, determining the RBC membrane fluctuations provides a diagnostic capability to assess the health or pathological state of the whole RBC.

Different particle-based RBC models have also been employed to investigate the dynamic behavior of Pf-RBCs under flow. For example, Imai et al. employed a numerical model to simulate the altered hemodynamics of Pf-RBCs [137,140]. They examined the deformation of RBCs in shear flow and found that the membrane stiffening of Pf-RBCs can lead to microvascular occlusion. Bow et al. employed a MS-RBC model to study the biomechanical properties of Pf-RBCs [142]. They investigated a progressive stiffening of Pf-RBCs with parasite growth (Fig. 4). Wu and Feng used SPH to simulate Pf-RBCs flowing in a converging microfluidic channel [91]. They demonstrated that Pf-RBCs gradually lost their deformability as malaria infection progressed. Ye et al. simulated the flow dynamics of Pf-RBCs in shear flow [143]. They found that malaria parasites can perturb blood flow, causing Pf-RBCs move toward blood vessel wall and adhere to the subendothelium surface.

Fig. 4.

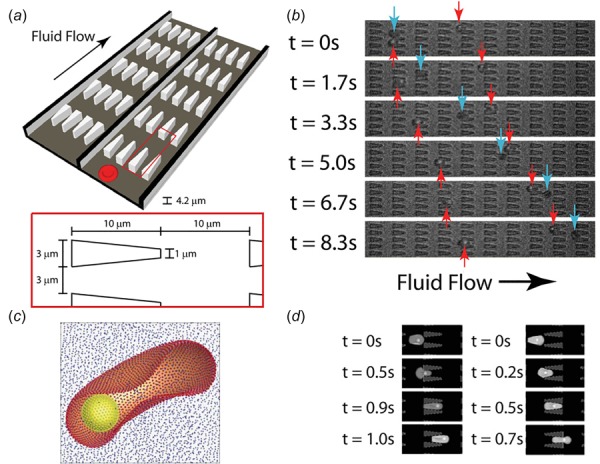
(a) Illustration of the flow cytometer device. (b) Experimental images of ring-stage infected (dark gray arrows) and uninfected (light gray arrows) RBCs in the channels. (c) The computational RBC model consists of 5000 particles connected with links. The parasite is modeled as a rigid sphere inside the cell. (d) DPD simulation images of Pf-RBCs traveling in channels of converging (left) and diverging (right) pore geometries. (Reproduced with permission from Bow et al. [142]. Copyright 2011 by Royal Society of Chemistry).

RBCs infected by the Plasmodium falciparum parasite lose their membrane deformability and exhibit enhanced cytoadherence to vascular endothelium and to other healthy and infected RBCs. To this end, Fedosov and coworkers employed a MS-RBC model to investigate the adhesive dynamics of Pf-RBCs [93,144]. Their simulation results revealed several types of cell dynamics such as firm adhesion and intermittent slipping. They also probed the effect of solid parasite inside the Pf-RBCs and found that the presence of a rigid body inside the RBC induces higher variances in cell motion and pronounces flipping of the Pf-RBC as it tethers to the surface.

Most blood test analyses in medical laboratories are often performed on cell-free samples, requiring the separation of RBCs from the whole blood. It has been shown that several microfluidic techniques can successfully separate plasma from blood cells which can then be fractionate into different cell types [145]. The blood-plasma separation depends on cell deformability. The malaria-infected RBCs lose their deformability and this, in turn, affects the blood flow. The motion of RBC flow in bifurcating microfluidic channel was simulated using a low-dimensional RBC (LD-RBC) model [94]. The separation efficiency of Pf-RBCs was found to be lower than that of healthy RBCs.

4.2. Sickle-Cell Anemia.

SCA is a genetic blood disorder exhibiting heterogeneous cell morphology and abnormal rheology under hypoxic conditions [146,147]. The underlying molecular cause of this altered blood rheology is the intracelluar HbS polymerization and RBC sickling due to a single point mutation in hemoglobin [29].

HbS nucleation followed by polymerization and RBC sickling significantly contributes to vasoocclusion which is the hallmark of SCA. Numerical models may provide useful insights into the mechanisms of HbS fiber nucleation and growth. To this end, the polymerization of HbS has been modeled with a double nucleation mechanism [148,149]. According to this mechanism, homogeneous nucleation of HbS polymer fibers is followed by fiber growth and branching by secondary nucleation of new fibers on top of existing ones. For insight into the nature of the HbS polymer fiber formation, in a recent study, Lu et al. developed a coarse-grained patchy particle model of HbS and simulated the growth of HbS polymer fiber by assuming a pre-existing nucleus [150] (Fig. 5). They demonstrated that the formation process of HbS polymer fiber occurs through monomer addition, but does not follow a layer-by-layer growth mode. In addition, they found that the molecular chirality is the critical determinant of the mechanical and structural properties of HbS polymer fiber. Dynamic self-assembly of coarse-grained HbS models was also simulated with DPD in Ref. [151]. Chain chirality was confirmed to be the main driver for the formation of HbS fibers. Different coarse-grained HbS polymer fiber models have also been introduced to simulate the biomechanical properties of HbS fibers, demonstrating the decisive role of fiber frustration and compression [152,153].

Fig. 5.

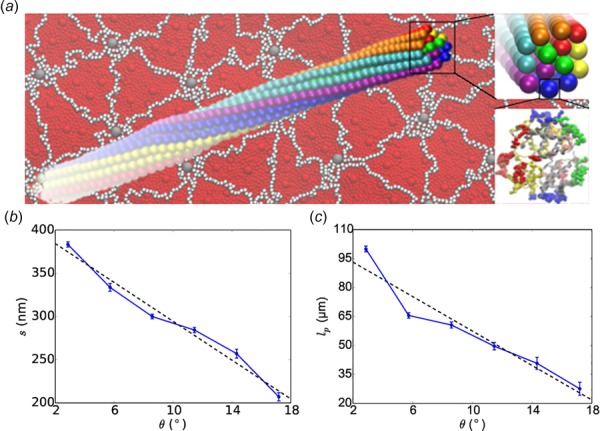
The twisted structure of HbS fiber (a) and its pitch length s (b) and persistence length l_p (c) properties obtained from CGMD simulations. (Reproduced with permission from Lu et al. [150]. Copyright 2016 by Elsevier).

The HbS fibers are quite stiff, so they distort the RBC morphology and in conjunction with RBC dehydration alter their mechanical and rheological properties [29,154,155]. In combination with several associated processes, sickling of RBCs leads to vaso-occlusion and related organ and systemic damage. Some simulation attempts have been made to understand the dynamic behavior of blood flow in SCA. For example, Dupin et al. studied sickle blood flow through an aperture of diameter less than the size of a single cell [156]. Lei and Karniadakis examined the adhesive dynamics of single sickle RBCs of different density groups [95]. They found that the sickle RBCs with a different cell rigidity and morphologies exhibit substantially different adhesive dynamics as shown in Fig. 6. A deformable sickle RBC (Cell I) exhibits firm adhesion to the lower plate with a large contact area. For a rigid sickle RBC (Cell II), however, it shows weaker adhesivity than Cell I. Although it also exhibits transient adhesion to the lower plate initially, it undergoes a periodic flip movement along the flow direction and eventually detaches from the surface after two to three flips. Accordingly, the contact area achieves minimum values at those times. Different from Cells I and II, an irreversibly sickled RBC (Cell III), it does not show any adhesion to the plate; instead, it directly detaches from the lower plate and moves freely without adhesive bonds established thereafter. They also applied adhesion dynamics to the effect of SCA and found that blood flow exhibits a transition from steady flow to partial/full occluded state. Their simulation results showed that the adhesion interaction between sickle RBCs and vessel walls plays a profound effect on the hemodynamics of sickle RBCs. They also addressed the conditions of sickle cell shape, adhesiveness, and elasticity that can cause the occlusion of a small blood vessel [95].

Fig. 6.

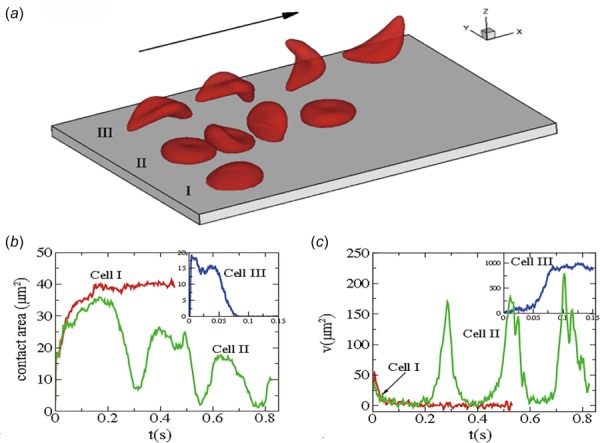
Sickle cells in shear flow: (a) Successive snapshots of SS-RBCs in shear flow. Labels I, II, and III correspond to a deformable SS2 cell, rigid SS3 cell, and ISC, respectively. The arrow indicates the flow direction; (b-c) Instantaneous contact area and velocity for sickle RBC in shear flow conditions. (Reproduced from Ref. [95]).

4.3. Defective RBCs in Hereditary Spherocytosis and Elliptocytosis.

A particle-based two-component RBC membrane model has been recently developed and applied to probe the biomechanical properties of the defective RBC membrane in HS and HE [87,88]. For defective RBCs in HS and HE, the interactions between the cytoskeleton and lipid bilayer could be significantly weakened due to the protein abnormalities. Chang et al. have recently employed CGMD on a small RBC patch to estimate the average bilayer-cytoskeleton interaction strength [157]. Their simulation results show that the interaction strength for HS RBCs and HE RBCs is decreased at least by one order of magnitude than that for healthy RBCs.

HS and HE RBCs exhibit increased vesiculation compared to normal RBCs [134]. Simulations have shown that while at normal RBC membrane connectivity favors the formation of vesicles with size similar to the size of the spectrin corals, in HS RBCs the vesicle size is more diverse extended from 90 nm diameter to approximately 500 nm while these vesicles are enriched in band-3 protein [130]. The hallmark of HE is the loss of elasticity of the RBC membrane because of defects in the membrane skeleton which make HE RBCs more prone to fragmentation and probably to membrane loss. Simulations performed in the HE RBC membrane show that the defects in the horizontal connectivity of the membrane skeleton increase membrane deformability and can induce formation of large vesicles that may contain cytoskeleton fragments [130].

In addition to altering the morphology and deformability of RBCs, protein defects affect diffusion of membrane proteins in the lipid bilayer. In HS and HE, defects in the proteins that tether the cytoskeleton to the lipid bilayer or in the proteins constituting the cytoskeleton enhance the lateral diffusion motion of band-3 proteins. In the RBC membrane, approximately one third of the band-3 proteins bind to the cytoskeleton and they are considered to be immobile band-3. The rest of the band-3 proteins are not connected to the cytoskeleton and thus are referred as mobile band-3 proteins. Although mobile band-3 proteins do not directly bind to the cytoskeleton, their lateral diffusion motion in the membrane is hindered by the presence of cytoskeleton. In the short time range (∼10 ms), the motions of the mobile band-3 proteins are constrained within the compartments formed by the spectrin network underneath the membrane. In the long time range, the band-3 proteins occasionally hop from one compartment to a neighboring compartment. Previous experimental measurements showed that the diffusion of the mobile band-3 proteins strongly depends on the integrity of the cytoskeleton [158, 159]. Hence, disruptions of the vertical interactions or horizontal interactions in the RBC membrane in HS or HE RBC can largely influence the lateral diffusive motion of band-3 protein.

Experimental studies show the steric hindrance effect of the cytoskeleton on the lateral diffusion of the band-3 proteins. In addition, any changes in the cytoskeleton structure or in the linkages between the cytoskeleton and the lipid bilayer influence the lateral diffusion of band-3 proteins [160–163]. Analytical models and numerical models have been developed to study band-3 diffusion, but mainly focusing on the mechanism of the band-3 hop diffusion [164–169]. While significant work has been carried out on band-3 diffusion in the normal RBC membrane, the effect of membrane defects on band-3 diffusion has attracted comparably limited attention. Saxton applied a Monte Carlo simulation to study dependence of the band-3 diffusion coefficients on the cytoskeleton connectivity [165]. In this work, the measured band-3 diffusion coefficient drops significantly as the cytoskeleton connectivity increased, which is in agreement with multiple experimental measurements. However, this Monte Carlo simulation did not take into consideration the effects of the spectrin filaments and lipid bilayer fluctuations. Auth and Gov proposed an analytical model, where the effect of the spectrin filaments is simulated by static pressure field [170]. This model was capable of showing the band-3 diffusion in the normal RBC membrane and in the membrane with ankyrin protein defects, but did not simulate the cases where protein defects occurred in the cytoskeleton. Li et al. simulated the band-3 diffusion in the RBC membrane with protein defects via CGMD RBC membrane model and quantitatively measured the dependence of band-3 diffusion coefficients on the percentage of protein defects [98]. They showed that the effect of the horizontal connectivity of the membrane skeleton on band-3 diffusion is more significant than the effect of vertical connectivity in agreement with experimental measurements in HS and HE RBCs [158]. The measurements of band-3 diffusion show that when vertical connectivity C_V.C. is decreased from 100% to 0%, the measured band-3 diffusion coefficients are increased by 20 times (Fig. 7a), whereas the band-3 diffusion coefficients are boosted by 50–100 times with significantly reduced C_H.C. (≤50%) (Fig. 7(b)).

Fig. 7.

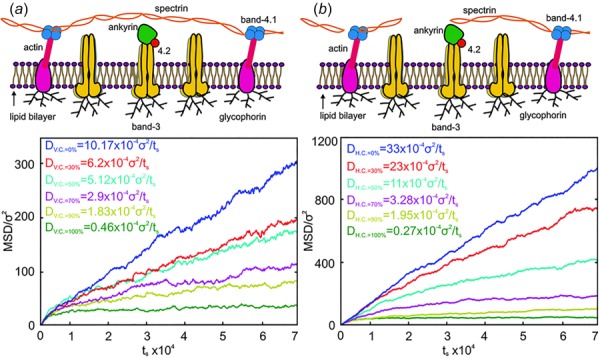
MSDs of band-3 particles against time and corresponding diffusion coefficients of the mobile band-3 in the membrane with various vertical (a) and horizontal (b) connectivities. (Reproduced from Ref. [98].).

An important problem is the type of band-3 diffusion in HS and HE erythrocytes. Hindering of band-3 motion by the RBC membrane skeleton results to subdiffusion. One type of subdiffusion is anomalous diffusion where the mean square displacement (MSD) is proportional to a fractional power of time (MSD ∼ t^α), where α is the anomalous diffusion exponent [171]. It can be generated by an infinite hierarchy of binding sites or by barriers that partially hinder diffusion. For cells where hierarchies are finite, diffusion can be transient anomalous at short times and normal at long times [172]. For the RBC membrane, however, band-3 diffusion can appear as artificial transient anomalous diffusion. At very short time scales for which the cytoskeleton does not affect band-3 motion, band-3 diffusion is Brownian. At very long time scales, band-3 diffusion is also Brownian but with a much smaller diffusion coefficient. Diffusion at intermediate times can be considered as transient anomalous as it transitions between Brownian motions at the two time scales but it is not clear if it is true or spurious anomalous diffusion. It has been shown that a simple equation which approximates an exact analytical solution for confined diffusion by a semi-permeable barrier can describe band-3 diffusion [173,174]. Li et al. recently demonstrated that band-3 subdiffusion in HE RBCs with low membrane skeleton connectivity can be approximated as anomalous subdiffusion where the diffusion exponent depends on the connectivity. In HE RBCs with high cytoskeletal connectivity band-3 diffusion can be described as confined not-anomalous subdiffusion [98].

4.4. Diabetes Mellitus.

Diabetes mellitus resulting from either insufficient insulin production (type 1 DM) or insulin resistance (type 2 DM) is characterized by metabolic abnormalities of the hyperglycemia. Several studies have observed the impaired deformability of RBC in diabetic patients, which is believed to be relevant to the microvascular complications such as retinopathy and nephropathy [175–177]. Since the deformability of the RBC is determined by its geometry, the viscosity of the intracellular fluid, and the viscoelastic properties of membrane, changes in these elements could bring significant influences on the mechanical and rheological properties of RBC [178].

A number of studies on the impaired deformability of diabetic RBC have been reported [179–182]. For example, Agrawal et al. found that the size of the quiescent RBC in type 2 DM is larger than the size of the normal RBC because of possible metabolic disturbances [176]. By using a dual optical tweezers method, the inverse relationship between the cell size and the erythrocyte deformability has been quantified. Recently, ultrastructural analysis of RBCs by scanning electron microscopy (SEM) showed an elongated shape of diabetic RBC with a smooth surface [183]. The roughness measurements of the cell surface by atomic force microscopy (AFM) indicated structural alterations not only in the cytoskeletal matrix but also in the lipid bilayer and surface membrane proteins [183]. As suggested by Mcmillan et al. [33], a decrease in the RBC deformability could be attributed to the elevation of the nonenzymatic glycation of hemoglobin associated with the increased intracellular viscosity. In addition, the glycation of membrane proteins leading to oxidation of spectrin might also be responsible for the reduced cell deformability [34]. On the other hand, increased evidences have shown a key role in advanced glycation end-products (AGEs), formed by the protein glycation and glycoxidation reactions at hyperglycemia, in the pathogenesis of diabetic complications [184,185].

It is worth noting that attenuated activity of Na⁺-K⁺-ATPase activity in erythrocytes, usually observed in type 1 diabetic patients, might also contribute to the decrease of erythrocyte deformability [186]. Kunt et al. discovered a beneficial impact of pro-insulin C-peptide on ameliorating the impaired deformability of RBC in type 1 DM, which is mediated by the restoration of Na⁺-K⁺-ATPase activity [187].

In comparison to the exclusively hematological disorders, e.g., malaria and SCA, studies on the biomechanical properties of RBC in DM are not as many. In a recent paper, the Lattice Boltzmann (LB)-based methods have been employed to investigate the effect of some human diseases such as diabetes on the RBC sedimentation rate [188]. Their simulations show that the deformation and rotation of a diabetic RBC are less than that of a healthy cell and RBC tends to settle near the centerline of the tube. The mechanism underlying the influences of impaired RBC deformability on diabetic complications remains unclear. Extensive experiments and also computational simulations are certainly required for better understanding the characteristics of RBC biomechanics in diabetic microangiopathy.

5. Summary and Outlook

Computational simulations have been playing an increasingly important role in enhancing our understanding of the dynamics and rheology of RBC suspensions, in particular in diseases such as malaria, SCA, and DM. In this article, an overview on the current progress in modeling of biomechanics of defective RBCs was given.

The current computational models of RBCs offer unique tools for the qualitative and quantitative description of dynamic and biomechanical properties of healthy and pathological RBCs and of blood flow in small arteries. Continuum models allow the study of blood flow on macroscopic length and time scales; however, they currently do not model critical biophysical processes such as detailed whole-cell investigations of a wide variety of biophysical problems involving the RBCs, including bilayer loss in HS and bilayer–cytoskeleton uncoupling in SCA. On the other hand, particle-based methods can resolve cellular and subcellular scales, yet they are computationally very expensive to scale up to large domains. For example, there are about 5 × 10⁶ RBCs per microliter of human blood, which would require more than a billion particles to be resolved accurately. A challenge in computational modeling of blood flow which encompasses all scales would be to develop a hybrid model that integrates both approaches, balancing biophysical fidelity with computational efficiency. Recent efforts have been directed toward this approach, e.g., using continuum-based plasma and particle-based RBCs.

Another challenge would be to develop a more reliable method and an overall modeling framework to extract dynamic and rheological properties of RBCs. For example, changes in the biomechanical properties of the RBC membrane, including bending rigidity and shear modulus, in certain diseases can be evaluated by modeling a small piece of cell membrane with detailed composite models; however, the detailed composite models of RBC membrane with explicit descriptions of lipid bilayer, cytoskeleton, and transmembrane proteins are extremely limited by their excessive computational cost. Particle-based whole-cell models have been applied to investigate RBC response and dynamics in blood flow, but the lack of molecular details in these whole-cell models may limit their predictive capacity in identifying the key factors that cause reorganization of the RBC membrane. An effective way to address this problem is to incorporate only the necessary molecular information from experimental observations and measurements as well as molecular-detailed composite membrane model into a more coarse-grained whole-cell model. First, one can employ a particle-based composite membrane model on a small RBC patch to compute the shear modulus, bending stiffness, and network parameters. Subsequently, by passing the aforementioned parameters as input to a whole-cell model, one can predict the altered biomechanical properties of RBCs associated with their pathophysiological states. Such simulations would potentially answer questions concerning the coupling of biochemistry and mechanics, for example, shear-induced ATP release [37] and the biomechanics of RBCs in pathological conditions [28], e.g., the structural link between sickle hemoglobin polymerization and altered biomechanics of RBCs in SCA [30].

In addition, in laboratory investigation of blood disorders, most tests have been performed on groups of cells under the assumption that all cells with a particular type are identical. However, recent evidence from single-cell analysis reveals that individual cells from the same population may differ significantly in cell size, mechanical properties, and protein expression levels. These variations can have important consequences for the health and function of the entire cell population [189]. For example, individual patients with SCA particularly show high levels of phenotypic heterogeneity in cell morphology [123], cell deformability [190], and cell adhesion [191,192]. These heterogeneity-related issues in SCA pose a serious challenge for disease management. For these reasons, there is a compelling need to develop predictive patient- or disease-specific models that can be differentiated into various cell types, cell shapes, and cell rigidity. Recent efforts have been directed toward this approach. For example, by using an MS-RBC model with parameters derived from patient-specific data, Li et al. described a computational simulation framework for assessing how the blood of a specific patient would respond to treatment for SCA [193]. Nevertheless, the heterogeneous nature of RBCs in SCA and other disorders results in special challenges for developing predictive models. For example, experimental evidence shows that heterogeneity of RBC is dynamic and versatile [194], i.e., the repetitive sickling of an individual RBC does not result in the same pattern of deformation. Therefore, it remains a challenge to examine the time-dependent morphological and mechanical properties of RBCs in experiments and incorporate this information into predictive models. To make model predictions more reliable, it would require further mesoscopic validation and reliability testing of these models against experimental and clinical studies. Such simulations from these predictive models for specific patients would potentially be used to identify new biomarkers of a certain disease and tailor treatment to the individual patient.