Chromosomal dynamics predicted by an elastic network model explains genome-wide accessibility and long-range couplings

Abstract

Understanding the three-dimensional (3D) architecture of chromatin and its relation to gene expression and regulation is fundamental to understanding how the genome functions. Advances in Hi-C technology now permit us to study 3D genome organization, but we still lack an understanding of the structural dynamics of chromosomes. The dynamic couplings between regions separated by large genomic distances (>50 Mb) have yet to be characterized. We adapted a well-established protein-modeling framework, the Gaussian Network Model (GNM), to model chromatin dynamics using Hi-C data. We show that the GNM can identify spatial couplings at multiple scales: it can quantify the correlated fluctuations in the positions of gene loci, find large genomic compartments and smaller topologically-associating domains (TADs) that undergo en bloc movements, and identify dynamically coupled distal regions along the chromosomes. We show that the predictions of the GNM correlate well with genome-wide experimental measurements. We use the GNM to identify novel cross-correlated distal domains (CCDDs) representing pairs of regions distinguished by their long-range dynamic coupling and show that CCDDs are associated with increased gene co-expression. Together, these results show that GNM provides a mathematically well-founded unified framework for modeling chromatin dynamics and assessing the structural basis of genome-wide observations.

INTRODUCTION

The spatial arrangement of chromosomes within the nucleus plays a crucial role in gene regulation, cell replication and mutations (1–5). Recent experimental methods such as Hi-C (6) derived from chromosome conformation capture (3C) (7) have made it possible to characterize the physical contacts between gene loci on a genome-wide scale. These studies revealed hierarchical levels of organization, from large (so called ‘A’ and ‘B’) compartments corresponding to active and inactive chromatin respectively (6), to smaller compact regions called topologically associating domains (TADs) (8). Hi-C-measured spatial relationships have been related to chromosomal alterations in cancer (9) and TADs have been pointed out to contain clusters of genes that are co-regulated (10). Interactions between sequentially (but not necessarily spatially) distant genes along the DNA 1-dimensional (1D) structure, termed long-range interactions, have been implicated in gene regulation —for example, distal expression quantitative trait loci (eQTLs) tend to be much closer in 3D space (11) to their target genes than expected by chance.

Several computational methods have contributed to these and other characterizations of chromosomal architecture (8,12–18). However, chromosome structure is dynamic and complex, and its exact nature and influence on gene expression and regulation remain unclear. The scale, complexity, and noise inherent in the available data make it challenging to determine exact spatial relationships and underlying chromatin architecture, and its structure-based dynamics. In particular, long-range spatial interactions have proven difficult to characterize with Hi-C data, and most computational analyses attempt to identify a static chromosomal architecture despite its known dynamic nature. There have also been efforts to mathematically characterize the dynamics of the genome separate from its structure, particularly through describing the emergence of cell types during development as bifurcations from a stable equilibrium (19).

Chromatin structure is often described in terms of TADs, whose identification is a 1D problem: it involves searching for sequentially contiguous groups of highly interconnected loci along the diagonal of the Hi-C matrix of intra-chromosomal contacts. Spatial couplings between sequentially distant genomic regions, on the other hand, represent a new dimension to search and the identification of such long-range couplings is a more challenging problem. Several methods have sought to identify long-range interactions from 3C-based data (13,20–23), but the scale of these interactions is still small compared to that of the full chromosome. Most methods detect interactions within 1–2 Mbp, or up to 10 Mbp (24), so extending the span of predicted long-range couplings to the order of tens of millions of base pairs may yield further insights into regulatory actions. Such long-range correlations may originate from physical proximity in space, or other indirect effects similar to those in allosteric structures. Assessment of such long-range correlations is important for gaining a better understanding of the physical basis of gene expression and regulation.

We adopt here the Gaussian Network Model (GNM), a highly robust and widely tested framework developed for modeling the intrinsic dynamics of biomolecular systems (25–27), and we adapt it to the topology-based modeling of chromosomal dynamics. Chromosomal dynamics refers to the coupled spatial movements of loci under equilibrium conditions, as uniquely defined by the topology of an elastic network representative of the chromosome architecture. The only input GNM requires is a map of 3D contacts. Here, this information is provided by Hi-C data, which gives contact frequencies between genomic loci. The Hi-C matrix is used for constructing the Kirchhoff (or Laplacian) matrix 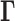which uniquely defines the equilibrium dynamics of the network nodes (genomic loci) as well as their spatial cross-correlations. Notably, the use of Laplacian-based graph segmentation has been recently shown to help identify topological domains from Hi-C data (28,29). Our approach differs in the method of construction of the network topology embodied in 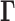, the inclusion of the complete spectrum of motions, and the application to a broad range of observables. We show, and verify upon comparison with an array of experimental data and genome-wide statistical analyses, that the GNM provides a robust description of accessibility to the nuclear environment as well as co-expression patterns between gene-loci pairs separated by tens of megabases. The analysis is mathematically rigorous, efficient, and extensible, and may serve as an excellent framework for drawing inferences from Hi-C and other advanced genome-wide studies toward establishing the structural and dynamic bases of regulation.

MATERIALS AND METHODS

Extension of the Gaussian network model to modeling chromatin dynamics

The GNM has proven to be a powerful tool for efficiently predicting the equilibrium dynamics of almost all proteins and their complexes/assemblies which can be accessed in the Protein Data Bank (PDB) (30), and has been incorporated into widely used molecular simulation tools such as CHARMM (31). It is particularly adept at predicting topology-dependent dynamics and identifying long-range correlations—the type of modeling that has been a challenge in chromatin 3D modeling studies. Hi-C matrices, in which each entry represents the frequency of contacts between pairs of genomic loci, can be interpreted as chromosomal contact maps similar to those between residues adopted in the GNM representation of proteins.

There are several differences between the Hi-C and GNM 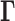matrices. The first is the size: human chromosomes range from ∼50 to 250 million base pairs. When binned at 5 kb resolution, this leads to 10 000–50 000 bins per chromosome. GNM provides a scalable framework, where the collective dynamics of supramolecular systems represented by 10⁴–10⁵ nodes (such as the ribosome or viruses) can be efficiently characterized. GNM may therefore be readily used for analyzing intrachromosomal contact maps at high resolution. The second is the precision of the data. Experimental methods for resolving biomolecular structures such as X-ray crystallography, NMR, and even cryo-electron microscopy yield structural data at a much higher resolution than current genome-wide studies. The Hi-C method is population-based (derived from hundreds of thousands to millions of cells) and noisy. Hi-C matrices furthermore contain unmapped regions (see Supplementary Data). However, the GNM results are usually robust to variations in the precision/resolution of the data on a local scale, and require information on only the overall contact topology rather than detailed spatial coordinates, which supports the utility of Hi-C data and applicability of the GNM. Third, the chromatin is likely to be less ‘structured’ than the structures at the molecular level, and it is likely to sample an ensemble of conformations that may be cell- or context-dependent. Single-cell Hi-C experiments have indicated cell–cell variability in chromosome structure on a global scale, though the domain organization at the megabase scale is largely conserved (32). Therefore, structure-based dynamic features may be assessed at best at a probabilistic level. With these approximations in mind, we now proceed to the extension of GNM to characterize chromosomal dynamics (see Figure 1).

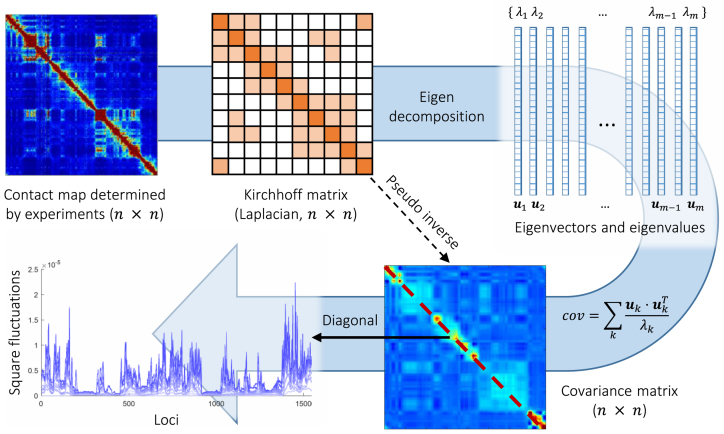
Figure 1.

Schematic description of GNM methodology applied to Hi-C data. The inter-loci contact data represented by the Hi-C map (upper left, for 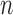genomic bins (loci)) is used to construct the GNM Kirchhoff matrix, 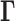(top, middle). Eigenvalue decomposition of 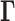yields a series of eigenmodes which are used for computing the covariance matrix (lower, right), the diagonal elements of which reflect the mobility profile of the loci (bottom, left), and the off-diagonal elements provide information on locus-locus spatial cross-correlations. 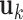, 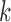th eigenvector; 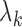, 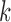th eigenvalue; 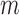, number of nonzero modes, starting from the lowest-frequency mode, included in the GNM analysis (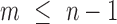). In the present application to the chromosomes, 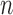varies in the range 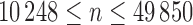, the lower and upper limits corresponding respectively to chromosomes 22 and 1.

The GNM describes the structure as a network of beads/nodes connected by elastic springs. The network topology is defined by the Kirchhoff matrix 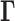, whose elements are

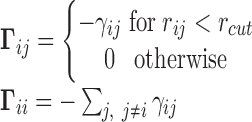(1)

Here, 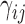represents the strength or stiffness of interaction between beads i and j (or the force constant associated with the spring that connects them), 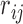is their separation in the 3D structure, and 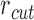is the distance limit for making contacts (or for being connected by a spring). In the application to proteins, the beads represent the individual amino acids (n of them), their positions are identified with those of the α-carbons, and a uniform force-constant 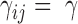is adopted for all pairs (1 ≤ i, j ≤ n), with a cutoff distance of r_cut ∼ 7 Å. In the extension to human chromosomes, we redefine the network nodes and springs such that beads represent genomic loci consistent with the resolution of the Hi-C data. We set 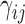equal to 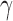z_ij where z_ij is the Hi-C contact counts reported for the pair of genomic bins (15) i and j after normalization by vanilla coverage (VC) method (13), and 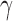is taken as unity. The element 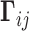is thus taken to be directly proportional to the actual number of physical contacts between the loci i and j, which permits us to directly incorporate the strength of interactions in the network model. The parameter 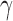uniformly scales all elements, physically representing the strength (or spring constant) of individual contacts. A recent study normalized the diagonal elements of the Laplacian matrix (constructed using Hi-C contact counts, similarly to 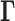) after construction (28,29), but we choose not to, because it removes the information on packing density of nodes, renders the calculation of square fluctuations meaningless, and disables the comparison with chromatin accessibility.

The cross-correlation between the spatial displacements of loci i and j is obtained from the pseudoinverse of 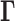, as

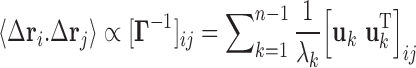(2)

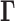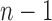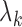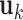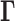where the summation is performed over all modes of motion intrinsically accessible to the network, obtained by eigenvalue decomposition of . The respective frequencies and shapes of these modes are given by the non-zero eigenvalues () and corresponding eigenvectors () of , and 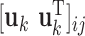designates the ijth element of the matrix enclosed in square brackets. The eigenvector 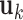is an n-dimensional vector representing the normalized displacements of the n loci along the kth mode axis, and 1/λ_k rescales the amplitude of the motion along this mode. Lower frequency modes (smaller 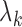) make higher contributions to observed fluctuations and correlations; they usually embody large substructures, if not the entire structure, hence their designation as global modes. In contrast, high frequency modes are highly localized, and often filtered out to better visualize cooperative events represented by global modes. See Supplementary Data for more details on the GNM analysis.

Cross-correlations are organized in the 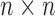covariance matrix, C (and displayed by an 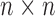map). The ith diagonal element of C, 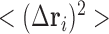, is the predicted mean-square fluctuation (MSF) in the positions of the ith loci under physiological conditions; and 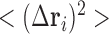plotted as a function of locus index i is called the mobility profile. The MSFs are inversely proportional to the elastic spring constant 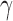. While their absolute values uniformly depend on this parameter, their relative magnitudes do not; the MSF profiles thus provide a measure of the relative size of motions of the different gene loci (irrespective of 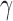), exclusively defined by the particular loci-loci contact topology. They represent ensemble averages over all accessible motions to a given locus.

Data

Our Hi-C data came from the large, high-resolution Hi-C dataset (GEO accession: GSE63525), pre-processed using vanilla coverage (VC) normalization (13). The methods section in Supplementary Data provides a comparative analysis of different normalization schema. We used Hi-C data at 5 kb resolution unless otherwise noted. DNase-seq data were collected as part of the ENCODE project (ENCFF000SKV for GM12878 cells, ENCFF740JVK for IMR90 cells) (33). The ATAC-seq measurements (34) were also obtained for GM12878 and IMR90 cells (GEO accessions GSM1155959 and GSM1418975, respectively). For both of these experimental datasets, bed-formatted peak files were downloaded from the study authors and the data was binned to the same resolution as the Hi-C data by adding all peak values within each bin. The binned data were then smoothed using moving average with a window size of 200 kb. The long-range interactions from ChIA-PET were from ENCODE (ENCFF002EMO) (35). We used a two-sample t-test assuming unequal variances to quantify the difference between the covariance distributions of ChIA-PET and background interactions.

GNM domain identification

GNM domain boundaries for a given mode k are identified by plotting the elements of 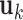as a function of loci index, and identifying the crossover region (also referred to as hinge regions), from positive to negative direction of motion (or vice versa), along the mode axis. The eigenvectors are often noisy, so we first smoothed them with local regression using weighted linear least squares and a first-degree polynomial model. The smoothing window was chosen to be the smallest value that minimizes the number of domains of length one, where a domain of length one is defined as a domain that begins and ends in the same bin. In general, the size of the domains decreases with increasing mode number. The domains resulting from the superposition of multiple modes were delimited by the union of hinge sites. As a quantitative measure of agreement between GNM-predicted domains, TADs, and compartments, the variation of information (VI) metric was used as described in the Supplementary Data.

Co-expression calculation

In order to calculate co-expression values for genes in this cell type, we downloaded every publicly available RNA-seq experiment on GM12878 cells from the Sequence Read Archive (36), which gave 212 data sets. These raw read data were quantified using Salmon (37), resulting in 212 transcripts per kilobase million (TPM) values for every gene. Quantification was performed with and without bias correction, with qualitatively similar results. Co-expression was then measured as the Pearson correlation of the two vectors of TPM values for a given gene pair.

RESULTS

Loci dynamics correlate well with experimental measures of chromatin accessibility

We first evaluated the mobility profiles of the chromosomes for GM12878 cells from a human lympho-blastoid cell line with relatively normal karyotype. Figure 2 illustrates the MSFs obtained with the GNM (blue curves) for the loci on three chromosomes (1, 15 and 17, in respective panels A, B and C). Results for all other chromosomes are presented in Supplementary Figure S1.

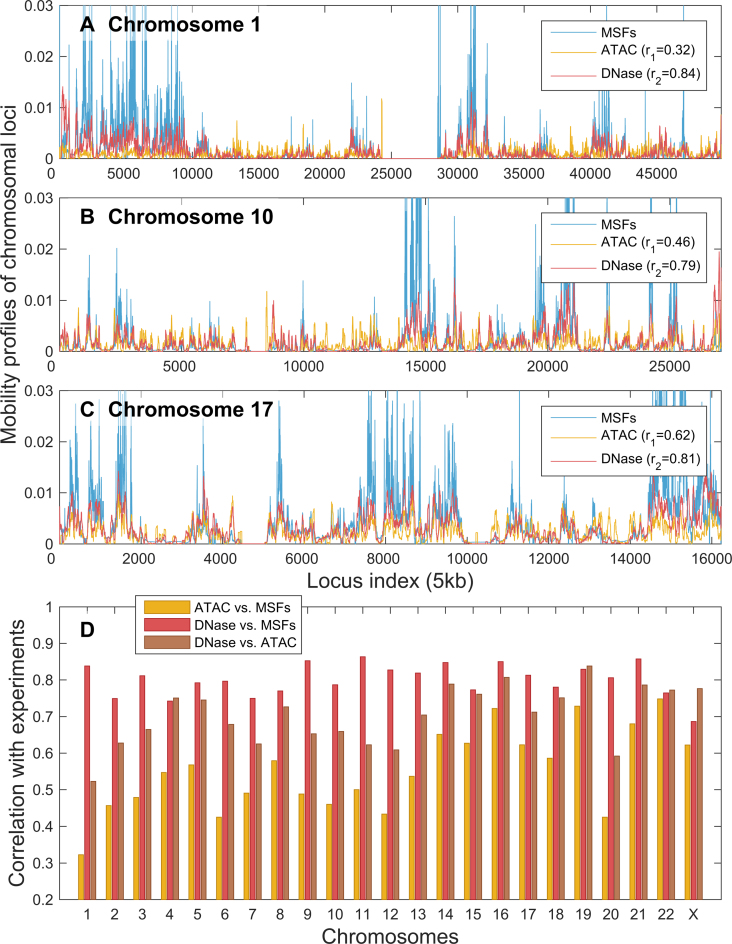
Figure 2.

GNM-predicted mobilities of chromosomal loci in GM12878 show good agreement with data from chromatin accessibility experiments. (A–C) Mobility profiles (MSFs of loci) obtained from GNM analysis of the equilibrium dynamics of chromosomes 1, 17 and X, respectively, shown in blue, are compared to the DNA accessibilities probed by ATAC-seq (yellow) and DNA-seq (red) experiments. GNM results are based on 500 slowest modes. r₁ is the Spearman correlations between GNM predictions and DNase-seq experiments; and r₂ is that between GNM and ATAC-seq. (D) Spearman correlations between theory and experiments for all chromosomes (red and yellow bars, as labeled). The Spearman correlation between the computed MSFs and experimental ATAC-seq data averaged over all chromosomes is 0.55 ± 0.11, and that between MSFs and DNase-seq data is 0.80 ± 0.04. For comparison, we also display the Spearman correlation between the two sets of experimental data (brown bars); the average in this case is 0.70 ± 0.08.

GNM application to H/D exchange data has shown that the MSFs of network nodes can be directly related to the accessibility of the corresponding sites: exposed sites enjoy higher mobility, and those buried have suppressed mobilities. The entropic cost of exposure to the environment for a given site can be shown to be inversely proportional to its MSFs based on simple thermodynamic arguments applied to macromolecules subject to Gaussian fluctuations (such as those represented by the GNM) (38). We examined whether GNM-predicted mobility profiles were also consistent with data from chromatin accessibility experiments. We compared our predictions with two measures of chromatin accessibility, DNase-seq (39) and ATAC-seq (34), shown respectively by the yellow and red curves in Figure 2A–C.

Figure 2 shows that the MSFs of chromosomal loci, predicted by the GNM, are in very good agreement with the accessibility of loci as measured by DNase-seq. The corresponding Spearman correlations for the three chromosomes illustrated in panels A–C vary in the range 0.78–0.85 (see inset), and the computations for all 23 chromosomes (panel D, yellow bars) yield an average Spearman correlation of 0.800 (standard deviation of 0.044). The average Spearman correlation between GNM MSFs and ATAC-seq data is somewhat lower: 0.552 ± 0.112. Interestingly, the average Spearman correlation between the two sets of experimental data was 0.741 ± 0.089, suggesting that the accuracy of computational predictions is comparable to that of experiments, and that the DNase-seq provides data more consistent with computational predictions. ATAC-seq maps not only the open chromatin, but also transcription factors and nucleosome occupancy (40), which may help explain the observed difference.

We performed the same analysis on the available data for a different cell type, IMR90, and found even better agreement with experiments (Supplementary Figure S2). The Spearman correlation between the computed MSFs and experimental ATAC-seq data averaged over all chromosomes was 0.63 ± 0.08 IMR90 cells, and that between MSFs and DNase-seq data was 0.82 ± 0.03. Consistently, the two sets of experiments also exhibit a higher correlation (0.81 ± 0.06) in this case.

GNM results are robust to changes in the resolution of Hi-C data and can be efficiently reproduced with a representative subset of global modes

These results for two different types of cell lines show that the mobility profiles predicted by the GNM for the 23 chromosomes accurately capture the accessibility of gene loci. The agreement with experimental data lends support to the applicability and utility of the GNM for making predictions on chromatin dynamics.

The current results were obtained by using subsets of 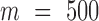GNM modes for each chromosome, which essentially yield the same profiles and the same level of agreement with experiments as those obtained with all modes (see Supplementary Figure S3). The use of a subset of modes at the low frequency end of the spectrum improves the efficiency of computations, without compromising the accuracy of the results. Computations repeated for different levels of resolution (from 5 to 50 kb per bin) also showed that the results are insensitive to the level of coarse-graining (Supplementary Figure S4), which further supports the robustness of GNM results.

We note that all results are obtained by adopting the VC normalization for Hi-C data. Computations repeated with two alternative normalization schema, square-root VC (13) and Knight-Ruiz (41) normalization, showed a significant decrease in the level of agreement with experimental data regardless of the number of modes included in the GNM computations (Supplementary Figures S5 and S6), and the underperformance of these schema became particularly pronounced in the case of high resolution data (Supplementary Figures S6 and S7), in support of the VC normalization adopted here.

Domains identified by GNM at different granularities correlate with known structural features

Compartments, first identified by Lieberman-Aiden et al. (6), are multi-megabase-sized regions in the genome that correspond to known genomic features such as gene presence, levels of gene expression, chromatin accessibility, and histone markers. Hi-C experiments have revealed two broad classes of compartments: ‘A’ compartments generally associated with active chromatin, containing more genes, fewer repressive histone markers, and more highly expressed genes; and ‘B’ compartments, for less accessible DNA, sparser genes, and higher occurrence of repressive histone marks. TADs (8) are finer resolution groupings of chromatin distinguished by denser self-interactions and associated with characteristic patterns of histone markers and CTCF binding sites near their boundaries. The multiscale nature of GNM spectral analysis allows hierarchical levels of organization to be identified computationally, and it is of interest to examine to what extent these two levels can be detected.

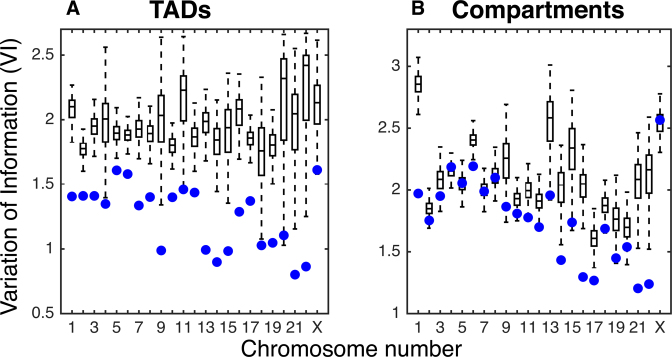
As presented above, the GNM low frequency modes reflect the global dynamics of the 3D structure, and increasingly more localized motions are represented by higher frequency modes. We identified domains from subsets of GNM modes that group regions of similar dynamics (see Methods). In order to verify whether these dynamical domains correspond to TADs at various resolutions, we used the TAD-finder Armatus (14), varying its ‘γ’ parameter that controls resolution. We refer to this latter parameter as the Armatus γ, to distinguish it from the force constant in the GNM. We measure the agreement between GNM domains and TADs using the variation of information (VI) distance, which computes the agreement between two partitions, and where a lower value indicates greater agreement (42). For more information on the VI metric, see the Methods section of Supplementary Data. For each choice k of number of modes, the Armatus γ_k that minimizes the VI distance between the GNM domains and the Armatus domains was selected. This resulted in a mean VI value for optimal parameters of 1.251, significantly lower than the VI distance of 1.946 obtained when the GNM domains were randomly re-ordered along the chromosome and compared back to the original TADs (empirical p-value < 0.01 for all chromosomes). Figure 3A shows the comparison for each chromosome between the VI value for the optimally matched TAD boundaries with the GNM domains and the distribution of VI values from the randomly shuffled domains. As the number of included GNM modes is increased, γ_k monotonically increases as well, showing that the number of GNM modes is a good proxy for the scale of chromatin structures sought (Supplementary Figure S8).

Figure 3.

Comparison of GNM domains with TADs and Compartments in GM12878. Variation of information (VI) measures for comparing GNM domains with (A) TADs and (B) compartments (lower VI indicates greater agreement). Box plots show the distribution of VI values obtained by randomly shuffling GNM domains and comparing to original TAD and compartment boundaries. Blue dots represent the VI value of the true GNM domains with TADs and compartments, respectively.

Furthermore, GNM predicts large-scale global motions using a relatively low number of modes, so we compared these to larger-scale compartments. We found that the first 5–20 non-zero modes correspond fairly well to compartments. For each chromosome, we selected the number of modes that produced the smallest VI distance between Lieberman–Aiden compartments and GNM domains. This yielded a mean optimal VI distance of 1.771 (using an average of 13 modes). This is significantly lower than the mean optimal VI distance of 2.088 when the locations of Lieberman–Aiden compartments are randomly shuffled along the chromosome, though the difference is only statistically significant for 16 of the 23 chromosomes, with p-value equal to 0.05. The comparisons of GNM domains with compartments for each chromosome in GM12878 cells can be seen in Figure 3B. The same calculations were performed on IMR90 cells, with qualitatively similar results. For the comparisons with randomly shuffled domains on IMR90 cells, only 1 chromosome for TADs and 3 for compartments were statistically insignificant (see Supplementary Figure S9). Supplementary Figure S10 shows an example of the GNM domains found using the number of modes that minimizes the VI with compartments or TADs. The ability of GNM to recapitulate both TADs and compartments—two organizational levels of wildly different scales—shows the flexibility and generality of the GNM approach. We note that a TAD-finding method using only the second eigenpair (Fiedler value/vector) of the Laplacian has also been developed (28) and tested on 100 kb resolution data. By including more eigenvectors, we are able to identify TADs closer to Armatus on all chromosomes (as measured by lower VI) at 5 kb and for 18/23 chromosomes at 100 kb resolution (see Supplementary Figure S11A and C). Though the Fiedler vector-based method identifies compartments better at low resolution, that method performs poorly at finer resolution, while GNM remains robust to resolution changes. We are also able to identify compartment sets with lower VI on all chromosomes at 5 kb (Supplementary Figure S11B and D). Further corroborating the benefit of using multiple modes, it has been shown in early studies that spectral clustering by using more eigenvectors can outperform partitioning methods which only use one eigenvector (43,44).

Loci pairs separated by similar 1D distance exhibit differential levels of dynamic coupling, consistent with ChIA-PET data

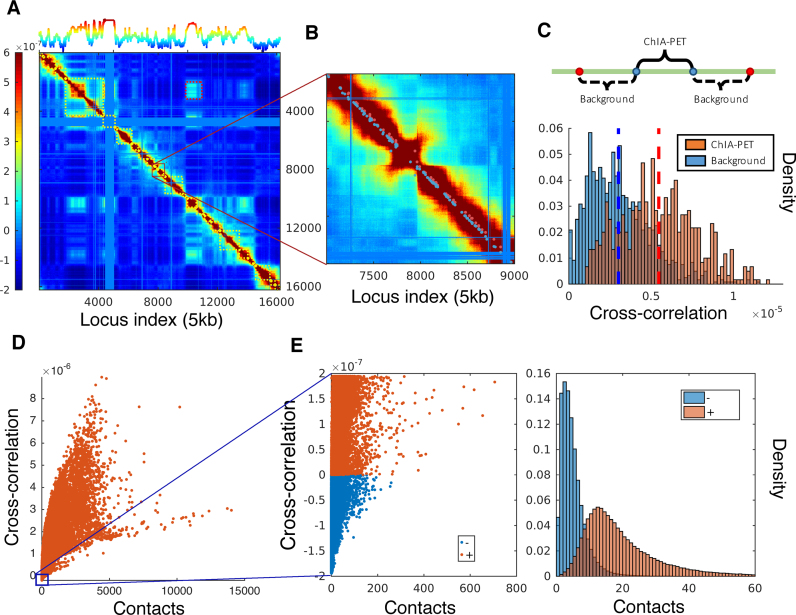
Figure 4 displays the covariance map generated for the coupled movements of the loci on chromosome 17 (of GM12878 cells), based on Hi-C data at 5 kb resolution. Panel A displays the cross-correlations (see Equation 2) between all loci-pairs as a heat map. Diagonal elements are the MSFs (presented in Figure 2C). The curve along the upper abscissa in Figure 4A shows the average cross-correlation of each locus with respect to all others; the peaks indicate the regions tightly coupled to all others, probably occupying central positions in the 3D architecture. Results for other chromosomes are presented in Supplementary Figure S12. The covariance map is highly robust and insensitive to the resolution of the Hi-C data. The results in Figure 4A were obtained using all the m = 15 218 nonzero modes corresponding to 5 kb resolution representation of chromosome 17. Calculations repeated with lower resolution data (50 kb) and fewer modes (500 modes) yielded covariance maps that maintained the same features (Supplementary Figure S13).

Figure 4.

Covariance map computed for chromosome 17 and comparison with ChIA-PET data and contacts from Hi-C experiments in GM12878. (A) Covariance matrix computed for chromosome 17, color-coded by the strength and type of cross-correlation between loci pairs ranged from 5th to 95th percentile of all cross-correlation values (see the color bar on the left). The curve on the upper abscissa shows the average overall off-diagonal elements in each column, which provides a metric of the coupling of individual loci to all others. The blocks along the diagonal indicate loci clusters of different sizes that form strongly coupled clusters. The red dashed boxes indicate the pairs of regions exhibiting weak correlations despite genomic distances of several megabases. The blue bands correspond to the centromere, where there are no mapped interactions. (B) Close-up view of a region along the diagonal. Red dots near the diagonal indicate pairs (separated by ∼100 kb) identified by ChIA-PET to interact with each other; nearby blue points are control/background pairs. (C) Stronger cross-correlations of ChIA-PET pairs compared to the background pairs. (D) Dependence of cross-correlations on the number of contacts observed in Hi-C experiments. A broad distribution is observed, indicating the effect of the overall network topology (beyond local contacts) on the observed cross-correlations. (E) Loci pairs exhibiting anti-correlated (same direction, opposite sense) movements usually have fewer contacts, compared to those exhibiting correlated (same direction, same sense) pairs of the same strength.

Owing to their genomic sequence proximity, the entries near the main diagonal of the covariance map tend to show relatively high covariance values (colored yellow-to-brown; Figure 4A). Note that even the close vicinity of the diagonals (e.g. loci intervals of ≥200) represents (at 5 kb resolution) genomic loci separated by >1 Mb. The covariance map clearly shows that there are strong couplings between loci separated by a few megabases. We show an example of such regions in Figure 4B. While the loci pairs located in the dark red band along the diagonal appear all to exhibit strong couplings, a closer examination reveals differential levels of cross-correlations that are in good agreement with the data from Chromatin Interaction Analysis by Paired-End Tag Sequencing (ChIA-PET) experiments (45). The ‘long-range’ interactions identified by ChIA-PET (35) are indicated in panel B by red dots (close to the diagonal). These are interacting loci separated by several hundreds of kb. We selected background pairs separated by the same 1D distance, on both sides of the ChIA-PET pair, and compared the cross-correlations predicted for the two sets along each chromosome (Figure 4C). The background pairs (blue bars) show weaker GNM cross-correlations compared to the ChIA-PET pairs (red bars) although they are separated by the same genomic distance along the chromosome.

Similar statistical analysis repeated for all 23 chromosomes showed that the cross-correlations of ChIA-PET pairs were greater than those of background pairs of the same genomic distance on every chromosome, with all P-values less than 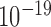(two-sided t-test).

Cross-correlations between loci motions are global properties that result from the overall chromosomal network topology

In general, loci-loci cross-correlations become weaker with increasing distance along the chromosome, and some pairs show anticorrelations (i.e. move in opposite directions; see scale bar in Figure 4A). Yet, we can distinguish distal regions that exhibit notable cross-correlations in the spatial movements (off-diagonal lighter-colored blocks). The levels of cross-correlations do not necessarily need to scale with the interaction strengths between the correlated loci (or number of contacts detected by Hi-C). On the contrary, a broad range of cross-correlations is observed for a given number of contacts, indicating that the observed correlations are global properties defined by the entire network topology and reflect the collective behavior of the entire structure. Figure 4D displays the computed cross-correlations as a function the number of contacts, showing that some pairs of loci display much stronger correlations revealed by the GNM than others that make more Hi-C contacts. Figure 4E shows that the anticorrelated pairs of loci (blue) usually have fewer contacts than those (red) exhibiting positive cross-correlations of the same strength.

Distal regions that are predicted to be strongly correlated in their spatial dynamics exhibit higher co-expression

The GNM covariance map further shows correlations between farther apart (>10 Mb) regions. In contrast to the main diagonal, the majority of the off-diagonal space typically shows significantly weaker correlations. Regions in this space with higher than expected covariance values represent dynamically linked windows along the chromosome, which may represent long-range interactions. We call these pairs of windows cross-correlated distal domains (CCDDs). To identify CCDDs, we set a threshold for each covariance matrix equal to the absolute value of the minimum covariance. Treating the remaining adjacent pairs as edges in a graph, we then locate connected components beyond the widest section of the main diagonal and above the threshold that contain more than one bin pair, and find the maximal-area rectangle contained within each connected region of high covariance values (see Supplementary Figure S14). These CCDDs are therefore pairs of regions distant along the chromosome, composed each of highly interconnected loci, which also exhibit relatively high cross-correlations compared to other regions of similar genomic separation. Previous methods for identifying long-range chromatin interactions (13,20,21,45) have focused on locating individual points of interaction within 1–2 Mb apart, while CCDDs tend to be on the order of tens of Mb apart and supported by groups of interacting loci.

The covariance matrix results from the overall coupling of the complete network of loci upon inversion of the connectivity/Kirchhoff matrix for the entire chromosomes. As such, it permits to capture, or better discriminate, the long-range correlations resulting from the complex topology of loci-loci contacts, as opposed to the raw data on local loci-loci contacts described by Hi-C maps. The covariance data also permit the identification of an appropriate threshold value for defining the significant CCDDs, consistent with the cooperative couplings within the entire structure, including distal correlations. There is no correspondingly clear threshold value for raw Hi-C data, which makes identifying these regions difficult without covariance matrices.

Highly distant gene pairs within CCDDs show greater co-expression values than gene pairs outside these regions (p-value < 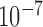using the background defined below). For each CCDD, we identified the genes contained within the region and measured the co-expression of each gene pair from distant chromosomal segments. The background gene pairs were gathered from outside the CCDDs but with similar genomic separation as the CCDD gene pairs. We computed gene expression correlations from 212 experiments (see Methods and Supplementary Table S1).

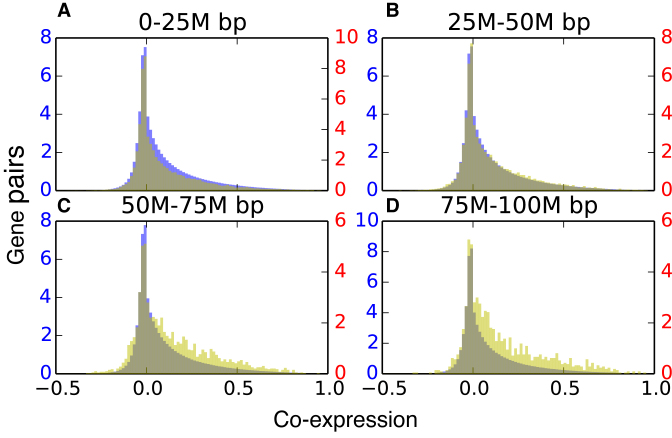
As seen in Figure 5, the CCDDs containing specifically gene pairs that are between 50 and 100 Mb apart are much more highly co-expressed than background gene pairs at the same genomic distance (P-value < 10⁻¹⁹, see Methods for details). This indicates that the dynamic coupling of these genes, as revealed by GNM, may often be biologically important. CCDDs at smaller genomic distance (<50 Mb) exhibit similar co-expression distributions to the background gene pairs, likely due to the effect of shorter genomic distances including more co-regulated genes within the background. Beyond distances of 100 Mb, there are not sufficient gene pairs within CCDDs to draw any meaningful conclusions. Dynamically coupled regions that are very distant sequentially but biologically linked through gene expression are therefore identifiable using the GNM covariance matrix.

Figure 5.

Co-expression is significantly enriched in distant CCDDs. In each histogram, the yellow distribution represents gene pairs from CCDDs and the blue distribution represents background gene pairs. All are showing the normalized number of gene pairs with a particular Pearson expression correlation for gene pairs within a distance of (A) 0–25 million base pairs, (B) 25–50 million base pairs, (C) 50–75 million base pairs and (D) 75–100 million base pairs. The more distant pairs (50–100 million base pairs apart) within the CCDDs show enriched expression correlations as compared to the background pairs. There were not enough gene pairs within CCDDs more than 100M base pairs apart to draw significant conclusions.

DISCUSSION

This work represents the first analysis of chromosome dynamics using an elastic network model, GNM, which has found wide applications in molecular structural biology. Though other models (28,29) have examined genome structure through graph theoretical methods, the inclusion of the complete spectrum of motions in the analysis provides a more realistic picture of chromosomal dynamics in accord with a wealth of experimental data. The approach brings three key advantages. First, this is a mathematically rigorous approach, based on first physical principles, with intuitive interpretations and well-established theoretical and physical underpinnings. Second, it enables us to evaluate, compare and consolidate a broad range of biologically significant genome-wide properties with the help of a unified model. These include the evaluation of loci MSFs at 5 kb resolution, the discrimination of short-range regulatory interactions among close-neighboring loci, and the identification of TADs and compartments. These respective predictions were shown to satisfactorily compare with data from chromatin accessibility (DNase-seq and ATAC-seq) and ChIA-PET experiments, and predictions from previous computational methods. The agreement with experiments not only validates the applicability of the GNM, but also provides a new set of independent data, which consolidate those from experiments, especially when the experimental data themselves exhibit some differences (see Figure 2D and Supplementary Figure S2D). The application to two different cell types also showed that GNM data comply with cell-cell variability. This unifying framework further led to the discovery of biologically significant, dynamically coupled regions, termed CCDDs. No existing method has located spatially coupled co-expressed regions of the genome which are so distant (over 50 Mb apart) along the chromosomes, and this information cannot be found from gene expression or other experimental data alone.

Due to the fact that the Hi-C experiment is known to suffer several systematic biases, we chose Vanilla Coverage normalization to eliminate such biases based on the correlation with chromatin accessibility (see Normalization in Supplementary Data) (13,46), and we assessed the impact of one type of simplest bias, GC content, on our results. In order to verify that the agreement with experimental data was not simply due to obvious covariates, we measured the correlation between GC content and both DNase-seq and ATAC-seq. On all chromosomes, the MSFs from GNM exhibited higher correlation with both experimental data sets than GC content. The correlation between GC content and accessibility data averaged to 0.606 and 0.278 for DNase-seq and ATAC-seq, respectively, compared to 0.800 and 0.552 achieved by the GNM-predicted MSFs (Supplementary Figure S15). In the case of structural component identification (TADs and Compartments), GNM clearly locates boundaries of multiple resolutions of structural domains beyond the influence of GC content. GC content shows no significant change in behavior around TAD or compartment boundaries as compared to its behavior at the center of these structures (see Supplementary Figure S16), demonstrating that this feature of GNM has no dependence on GC content bias. Finally, co-expression enrichment of CCDDs was maintained after bias-corrected RNA-seq quantification (Supplementary Figure S17), again supporting the significance of the GNM-predicted distal correlations. Future efforts may focus on deploying methods that can remove bias factors from both Hi-C and accessibility data, in order to fully separate the capabilities of GNM from simple covariates.

In general, the evaluation of dynamic features using structure-based models becomes prohibitively expensive with increasing size of the structure, hence the development of coarse-grained models and methods for exploring supramolecular systems dynamics. The chromatin size is well beyond the range that can be tackled efficiently by structure-based methods and realistic force fields. The applicability of the GNM to modeling chromatin dynamics lies in its ability to solve for the collective fluctuations and cross-correlations based on network contact topology, exclusively. No knowledge of structural coordinates is needed, nor do we predict structural models—a task that has been undertaken successfully by recent studies (17,18,47–55). We characterize the collective dynamics encoded by the overall chromosomal contact topology, driven by entropy, consistent with the ensemble-based properties of the genome structure. MSFs predicted by the GNM represent ensemble averages over thermal fluctuations (or spectrum of modes; see Supplementary Methods), and reflect population-averaged behavior examined in the Hi-C experiments, hence their applicability to population-average based experiments such as ATAC-seq and DNase-seq.

The method is extremely efficient. For example, GNM averages a real computing time of 1.5 h per chromosome at 5 kb resolution using 10 CPUs, and no multiple runs are needed, since a unique analytical solution is obtained for each system. The computing time is further shortened when lower resolution data are used: all GNM computations are performed within 1 min for every chromosome at the resolution of 50 kb. The efficiency of the computations permits a systematic study of different types of cell lines as well as the extension of the methodology to the entire set of interchromosomal contacts, rather than individual chromosomes.

Future GNM analyses of chromatin dynamics could focus on the nature of the long-range couplings, analysis of their biological significance, or the meaning of genomic regions that exhibit high covariances. GNM also predicts a measure of overall coupling of each genomic locus to others (see the curve along the upper abscissa in Figure 4A), the significance of which requires further investigation. The GNM was shown to capture several biological properties of chromosomes, but further insights on cooperative events, including the interchromosomal (trans) interactions is within reach by focusing on the softest (lowest frequency) modes of motion predicted by the GNM. Finally, advances in 3D embeddings of Hi-C data may open the way to adopting the Anisotropic Network Model (ANM) (56–58) for efficient modeling and visualization of the whole chromatin dynamics.

The present study is performed on GM12878 and IMR90 cells, but the GNM can be readily used for analyzing different cell types provided that Hi-C data are available, and the comparative analysis of the fluctuation spectrum and CCDDs can reveal the differences across cell types. Our preliminary analysis of the equilibrium fluctuations of chromosome 17 for four other cell types (K562, KBM7, HUVEC and NHEK) indeed showed similarities between the MSFs of gene loci as well as their cross-correlations, although some notable differences were also seen, e.g. the mobility profile for the epidermal cell line, NHEK, exhibited distinctive patterns at selected regions. Further work is needed to understand the biological significance of the observed heterogeneities in the genome-wide fluctuation spectrum of the different types of cells. Examination of structural variabilities across orthologous proteins and their mutants revealed close similarities between evolutionary changes in structure and the intrinsic dynamics of proteins (59). Conversely, ANM-predicted global dynamics conforms to the principal changes in structure across different forms of the same protein (60,61), and thus explains the structural adaptability of the protein to different functional states (62). It would be of interest to explore whether cell-cell variabilities as well differences in disease vs normal states could equally be rationalized in the light of chromatin dynamics as more data become accessible on cell-specific 3D genome organization.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health (NIH) [P41-GM103712, R01-GM099738 and U54-HG008540 to I.B., R01-HG007104 to C.K.]; Gordon and Betty Moore Foundation's Data-Driven Discovery Initiative [GBMF5445 to C.K.]; National Science Foundation (NSF) [CCF-1256087, CCF-1319998 to C.K.]; Alfred P. Sloan Research Fellow (to C.K.). Funding for open access charge: P41-GM103712.

Conflict of interest statement. None declared.