Abstract
Using precomputed near neighbor or proximal distribution functions (pDFs) that approximate solvent density about atoms in a chemically bonded context one can estimate the solvation structures around complex solutes and the corresponding solute–solvent energetics. In this contribution, we extend this technique to calculate the solvation free energies (ΔG) of a variety of solutes. In particular we use pDFs computed for small peptide molecules to estimate ΔG for larger peptide systems. We separately compute the non polar (ΔGvdW) and electrostatic (ΔGelec) components of the underlying potential model. Here we show how the former can be estimated by thermodynamic integration using pDF-reconstructed solute–solvent interaction energy. The electrostatic component can be approximated with Linear Response theory as half of the electrostatic solute–solvent interaction energy. We test the method by calculating the solvation free energies of butane, propanol, polyalanine, and polyglycine and by comparing with traditional free energy simulations. Results indicate that the pDF-reconstruction algorithm approximately reproduces ΔGvdW calculated by benchmark free energy simulations to within ~ kcal/mol accuracy. The use of transferable pDFs for each solute atom allows for a rapid estimation of ΔG for arbitrary molecular systems.
INTRODUCTION
The accurate calculation of solvation free energies is critical to computational drug design and structure optimization as well as understanding important biophysical processes like aggregation and protein folding. Two central issues in computational free energy calculations include ensuring sufficient sampling of phase space and the accuracy of the force field used to model molecular interactions. The sampling issue remains a bottleneck in applications of free energy approaches to ever more complex systems; that is, in order to investigate thermodynamic behavior of a system, sampling of a representative number of configurations within the given ensemble is required, which often requires expensive simulations.1–3Force fields continue advancing in accuracy often at the expense of added complexity.4–6
Due to the transferable nature of atomic level force fields for a given chemical context, molecular mechanics force fields provide an extensible architecture to study the thermodynamic properties of a wide range of solutes.7 Free energies of solvation (ΔG) depend on the solute–solvent potential,8 and the distribution of solvent around a solute. Here, we seek a set of transferable functions to approximate solvent density distributions which will allow for rapid estimation of ΔG and its differences due to chemical processes in solution.
In assessing free energy differences it is common to consider a thermodynamic cycle for a given reaction process. For example, the relative change in free energy associated with the change or mutation of molecule A to B is given by the difference in solvation free energy (ΔΔG) of the two molecules.9–14 In computational free energy methods, the solvation process in which a solute is transferred from the gas phase to the aqueous phase is often decomposed into two stages or contributions. First an uncharged, solute cavity is created in the solution and the free energy required to insert this cavity is defined as ΔGvdW. This cavity is then gradually charged and the change in free energy associated with this process is defined as ΔGelec.15 This process, though nonphysical, does allow us to calculate each component of the potential function with explicit simulations16 or individual functional theories with less computational costs.17,18 While ΔG is a state function and path independent, the components ΔGelec and ΔGvdW are well-known to be defined only by a process and therefore path-dependent.19
Many approximate techniques have been developed to rapidly estimate ΔG. ΔGelec is often estimated using dielectric continuum theory based techniques,15,20 such as the generalized Born model,21,22 Poisson–Boltzmann equation,23,24 or Linear Response theory (LRT).25–27 The nonpolar cavity contribution, ΔGvdW, has been approximated as a linear function of the solvent accessible surface area (SASA).28–30 However, the correlation between ΔGvdW calculated by SASA and explicit solvent models using rigorous thermodynamic integration or free energy perturbation is far from exact for organic molecules, especially at the level of small nonpolar molecules.16,31–33 Further decomposition of ΔGvdW into the solute–solvent repulsive and attractive interactions has been proposed with an additional estimator accounting for solvent accessible volume.18 The use of implicit solvation models to estimate ΔGvdW remains a challenge due to nonadditive, multibody correlations with neighboring atoms,33–35 and the complex geometry of the solute–solvent interface.36–39 An approach that yields estimates of solvation free energies rapidly but retains the accuracy associated with explicit solvent models would be highly desirable. Methods relying on precomputed quantities from explicit simulations of small solutes to estimate ΔGvdW of large solutes are therefore being developed. For example, the Semi-Explicit Assembly (SEA) approach40–42 precomputes the modified nonbonded van der Waals interactions between a series of nonpolar solute spheres and water, then assembles the total interactions based on the given configurations of large solutes.
Here, using precomputed near neighbor or proximal distribution functions (pDFs) of solvation about atoms in chemically bonded (small molecule) context we estimate the solvation structures around larger and more complex solutes. We then use these approximately transferable distributions to calculate ΔG. pDFs approximate solute–solvent pair correlation functions at the near neighbor level to describe the local solvent structure around a solute.43–47 They have been shown to be a near universal and transferable descriptor between different globular proteins.48 That is, pDFs constructed for small molecules can be used to predict the solvent structures around complex biological macromolecules that are composed of chemically similar components.49–51 Average solute–solvent interaction energies, and subsequently solvation free energies, can then be calculated from these reconstructed solvent structures.
Electrostatic interaction energies estimated using pDFs in combination with LRT have been shown to approximate ΔGelec well for a variety of solutes compared to simulation.52–54 We have recently shown that van der Waals solute–solvent interaction energies can be approximated with good accuracy using precomputed pDFs, but requires a finer spatial resolution than what is used to estimate the more smoothly varying electrostatic interactions.55 Here, we extend the pDF-approach to calculate ΔGvdW of a variety of solutes and assess the accuracy of this approach by a comparison with the more expensive explicit solvent thermodynamic integration.
Below we review the generation of pDFs from small solutes and how they can be used to reconstruct the distribution of solvent density around an arbitrary solute to estimate average solute–solvent interaction energies. Then we show how to calculate ΔGvdW by constructing a set of pDFs as a function of a coupling parameter that gradually scales the van der Waals interactions between a small solute and solvent (i.e., we define a pathway along which to calculate ΔGvdW). To benchmark this approach, we calculate ΔGvdW of butane, and propanol and compare with more rigorous estimates obtained from alternative approaches. We then generate transferable pDFs from monomers of alanine and glycine and use those to calculate ΔGvdW for various triglycine and deca-alanine systems. We study the effects of flexibility, or disorder, on ΔGvdW by comparing ΔGvdW of a fixed, extended conformation of triglycine to that obtained for a large ensemble of triglycine conformers generated from a molecular dynamics (MD) simulation. For completeness, we include linear response estimates of ΔGelec and thus construct an approximate total solvation free energy.
THEORY
In this section, we briefly review nearest neighbor proximal distribution functions (pDFs) and how they are used to reconstruct solute–solvent density distributions and subsequently estimate solute–solvent energetics. Then we discuss how the pDF formalism can be modified to estimate ΔGvdW using a thermodynamic integration scheme.
Distribution Functions and Solute–Solvent Energetics
Proximal distribution functions (pDFs, or g⊥(r)) are average density distributions calculated from solvent molecules to their nearest solute atom.43,56,57 The solvent probability distribution most nearly perpendicular to the kth solute atom can be written as
| (1) |
where represents the position vector from the ith solute atom to the jth solvent atom at time t, m is the number of solute atoms and n is the total number of solvent molecules in the system. returns the distance between a particular solvent atom and the nearest solute atom k, i.e., k is the assigned solute atom with the closest distance to the jth solvent atom. In this way, the solvent space is effectively divided into Voronoi polyhedra58 and the resulting distribution functions are defined essentially perpendicularly to the exposed surface of the respective solute atoms52 (illustrated in Supporting Information). is the volume element around the jth solvent molecule, which is defined by all vectors, where . A graphical illustration for this process can be found in the Supporting Information. In practice, a pDF can be computed from a MD simulation mapped to a three-dimensional grid where each individual grid point along with its corresponding time-averaged solvent density is assigned to the closest solute atom for calculations. The detailed theory and computational procedure can be found elsewhere.43,45
A variety of solute atom sets or groupings can be used to define the pDFs. For example, at one extreme one could take each atom of a molecule as having a unique g⊥(r). Alternatively, pDFs can be constructed for each force field atom type or, using an even coarser grouping, by chemical identity or similarity.49 In general, we refer to a particular grouping or atom set by χ and refer to a particular pDF defined by this grouping with χk. Previous work shows that the pDFs classified using force field atom types for proteins and nucleic acids yields nearly universal functions which are thus transferable to chemically similar solute molecules.45,48,50
We can reconstruct the solvation density around a given solute configuration with a three-dimensional grid and assign solvent density to the grid point (x, y, z) with the precomputed :
| (2) |
where is the minimum distance between the grid point and all solute atoms i, χk is the assigned atom set type of the closest solute atom and (x, y, z) denotes the center of the grid volume. In this framework, the solvent density at grid point (x, y, z) is therefore
| (3) |
where ρ is the bulk solvent number density. In our pDF calculations (both pDF-collections and solvent density reconstructions), we used 0.2 and 0.01 Å as the reconstruction grid space resolution and g⊥(r) collection resolution, respectively. The selection of g⊥(r) resolution is more important in the van der Waals reconstruction process and a resolution of 0.01 Å is suggested based on previous work.55
Any solute atom may exclude solvent from any grid point when there is overlap or volume exclusion. In solvent density reconstruction, a grid point is assigned zero solvent density if any . As an example we consider a grid point density assignment near a hydrogen covalently bonded to a heavy atom whose van der Waals radius effectively eclipses that of the hydrogen’s. While the hydrogen atom is the nearest grid point and , the pDF of the bonded heavy atom (i.e., next nearest neighbor) could dictate that solvent should be excluded at the grid point with the given distance, r′. This becomes increasingly important at small distances when using a soft-core van der Waals potential as is common in free energy calculations (addressed in next section, Supporting Information, and ref 55).
We use a two step process to ensure that grid points are assigned the appropriate solvent density during reconstruction. First we eliminate grid points at distances in which the pDFs of heavy atoms in the set χ predict essentially zero solvent occupation (referred to as the cavity rule). Conceptually, solvent space is divided into Vornoi polyhedra with heavy atoms at this step. Then, we exclude or zero out any grid points in a similar manner using of the remaining atoms (referred to as the exclusion rule). The whole reconstruction process including the cavity and exclusion rules can therefore be formulated as
| (4) |
Here mH is the number of solute heavy atoms, and m is the number of all solute atoms. The cavity factor is defined as
| (5) |
and notice that i loops over solute heavy atoms only. Similarly, the exclusion factor is written as
| (6) |
where j loops over the remaining atoms in the set χ.
Once the solvent density is reconstructed around the solute, the average solute–solvent interaction energy can then be written as
| (7) |
where is the solute–solvent interaction energy for solute atom i, Δv is the unit volume which depends on the spatial resolution and the outer sum is taken over all grid points. Depending on the potential energy function, U may be decomposed into the sum of electrostatic and van der Waals interaction energies. The average electrostatic and van der Waals solute–solvent interaction energies can then be calculated using eq 7.
We have previously shown that the solute–solvent electrostatic interaction energy and electrostatic solvation free energy can be reasonably approximated from the pDF-reconstructed solvent density. Here, we extend the pDF approach to estimate the change in free energy (ΔGvdW) upon inserting uncharged solutes in solution using a soft-core van der Waals potential and a thermodynamic integration scheme.
Thermodynamic Integration with Soft-Core Potentials
To calculate the solvation free energy of cavity formation (ΔGvdW) we use a thermodynamic integration (TI) approach. We construct a pathway between the initial gas phase and final solvated state by means of a coupling parameter, λ, which varies between 0 and 1 such that when λ = 0 the interaction energy (Uij) between solute atom i and solvent atom j is zero and when λ = 1, , or the typical van der Waals potential energy function. To avoid singularities and numerical instabilities at the λ = 0 end-point, a soft-core potential is commonly used to scale along the pathway:59,60
| (8) |
where rij is the distance between solute and solvent atoms, ϵ is the van der Waals well depth, and σ is the contact distance. δ is a radius-shifting coefficient of λ and here is taken to be 5.0 throughout the simulations and pDF-reconstructions. Trivially at λ = 1 this is the usual Lennard-Jones form. We note that the effective σij is reduced as λ decreases, which leads to water residing at closer distances to the solute atoms.
The total solute–solvent van der Waals interaction energy (UvdW) is the sum of over all solute–solvent atom pairs. The van der Waals solvation free energy is calculated as the integral of the average derivative of UvdW with respect to λ:
| (9) |
One can approximately calculate ΔGvdW using numerical integration methods with the ensemble averages of ∂UvdW/∂λ at various values of λ. The derivative of UvdW with respect to λ is readily obtained from the analytical expression:
| (10) |
In our pDF approach, we first construct for the atom type set of a small representative chemical group (e.g., an alkane or peptide substituent) from MD simulations performed at regularly spaced values of λ. For each λ, we obtain unique . Then using these precomputed pDFs, we reconstruct the average, λ-dependent solvent density distributions on a 3D grid around a given solute configuration (e.g., a long alkane or polypeptide) for each λ value. We directly estimate ⟨∂UvdW/∂λ⟩λ using a form like eq 7 but with Uij replaced with . Finally, numerically integrating ⟨∂UvdW/∂λ⟩λ along λ yields ΔGvdW. Note that the λ-dependent pDFs only need to be constructed once but may be used to predict ΔGvdW of more complex solutes that are composed of similar atom type sets for which the pDFs were generated.
METHODS
Simulation
The solutes butane, propanol, ala1, ala10, gly1, gly3 were chosen for this study. Molecular dynamics simulations were performed with NAMD 2.9 and 2.1061,62 with the CHARMM36 force field parameters63 to generate the pDFs and calculate free energy benchmarks. pDFs were generated for butane and propanol as a control to compare with more rigorous free energy calculations. The pDFs generated for ala1 and gly1 were used in the analysis of longer peptides. Each solute was solvated with TIP3P water64 in a volume with at least 10 Å from each boundary to the solute atoms. Peptides were capped with neutral acetyl (ACE) and N-methyl amide (NME) chemical groups. The initial conformations of decaalanines and triglycine peptides are from previous studies33,52,55,65 and presented in the Supporting Information. Three-dimensional periodic boundary conditions were applied. A rigid water geometry is enforced using SHAKE.66 Particle Mesh Ewald (PME)67 was used to treat electrostatic interactions using a grid of 1.0 Å resolution. The Lennard-Jones (L-J) interactions were gradually switched off over the range 10 Å to 11 Å. The temperature was fixed at 300 K via a Langevin thermostat with damping coefficient of 5 ps−1. A time step of 2.0 fs was used to integrate the equations of motion.
The pDFs for this free energy study were generated in 11 windows with a λ-spacing of 0.1 between 0 and 1. Solvent reconstruction and calculation of ΔGvdW were performed with these λ values. In general, it is necessary to sample more extensively at certain λ-windows depending on the chosen soft-core potential function (near end points in our case) to accurately depict the repulsive van der Waals forces when inserting the solute into the system.11 More detail on the analysis can be found in the Results Section below. In this article we show how to use pDFs to reproduce ⟨∂UvdW/∂λ⟩ at all λ-windows with our pDF-reconstruction algorithm, which is subsequently integrated to estimate ΔGvdW.
Throughout the simulations, the solute molecules were rigid except as noted below for gly3. The pDF sampling simulations were initially equilibrated in the NVT ensemble for 1 ns. The simulations were then switched to NPT at 1 atm pressure, with the first 1 ns excluded as equilibration. The pDFs and ⟨∂UvdW/∂λ⟩ were calculated from production simulations that ranged between 4 and 10 ns at each λ. Trajectory snapshots were saved every 0.2 ps for analyses. The convergence of ⟨∂UvdW/∂λ⟩ at each λ window is discussed in the Supporting Information. For each λ window, the uncertainty of ⟨∂UvdW/∂λ⟩ is estimated as the block standard error.68 The final uncertainty of ΔGvdW is calculated by the propagation of errors across all λ.
In addition to the fixed solute conformations, we also examined ΔGvdW of gly3 without positional constraints (i.e., allowed to be completely flexible during simulations). The simulation parameters and λ-windows are identical to those of simulations with gly3 fixed in an extended conformation. We used 10000 solute configurations from a typical 50 ns MD simulation (λ = 1) of flexible gly3 for calculating ΔGvdW from pDF-reconstructions.
In the following sections, we also provide estimates of ΔGelec based on LRT. That is, ΔGelec can be approximated as half of the solute–solvent electrostatic interaction energy instead of integrating the average derivative of Uelec with respect to a coupling parameter that gradually scales solute–solvent electrostatic interactions. Thus, a set of simulations with charged solutes is employed to achieve full electrostatic solute–solvent interactions. In our previous work, we have reported the averaged solute–solvent electrostatic interaction energies for configurations of butane, propanol, and ala10,55 along with the corresponding pDFs used for solvent density reconstruction. In this contribution, with a goal of calculating total solvation free energy, we further include estimates of ΔGelec for fixed ala1, gly1, and flexible gly3 from free energy simulations to compare with pDF-reconstructions. The simulation details are the same as the above free energy simulations except for having charges on solute atoms and the total sampling time for each system is 100 ns with a 2 ps save frequency.
RESULTS AND DISCUSSIONS
Butane and Propanol
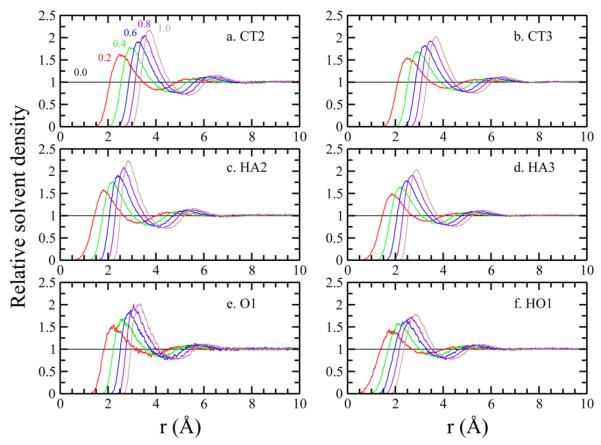
We compare the ⟨∂UvdW/∂λ⟩ of a single butane/propanol molecule obtained from TI simulations and pDF-reconstruction using the same solute configuration and same number of λ points. In general, the more extensive the set of atom types we include, the higher the accuracy in solvent structure and solute–solvent energetics we can expect during the reconstructions,51,55 especially for the nonpolar contributions. Here, we consider all six force field atom types (i.e., the set χ) for butane and propanol: methylene carbon (CT2), methyl carbon (CT3), methylene hydrogen (HA2), methyl hydrogen (HA3), the hydroxyl oxygen (O1), and the bonded polar hydrogen (HO1). The pDFs of each atom type with respect to water oxygen atom (OT) at selected λ windows are shown in Figure 1. The pDFs of each atom type with water hydrogen atoms (HT) are included in the Supporting Information.
Figure 1.
pDF of the butane/propanol atoms to water oxygen atoms at different λ. Numbers above each pDF indicate the corresponding λ of this atom type.
Ideally, the pDFs at λ = 0 should be 1 (i.e., bulk solvent density) at all interatomic distances. Therefore, we set the pDFs at λ = 0 to 1 for all distances. Essentially, all atom types are uncharged and considered as pure covalently bonded L-J spheres, and thus show similar behaviors; as λ increases, the position of the peaks are shifted to larger distances with stronger magnitudes in the first peak.
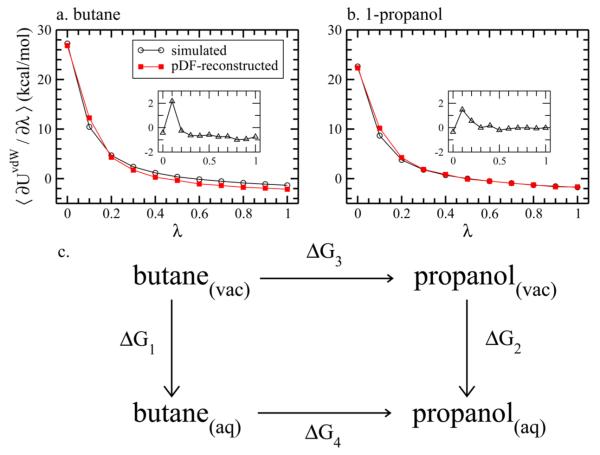
The simulated and pDF-reconstructed estimates ⟨∂UvdW/∂λ⟩ for each λ are presented in Figure 2. Differences between ⟨∂UvdW/∂λ⟩ calculated by TI simulations and pDF reconstruction at each λ are shown in the insets. Overall ⟨∂UvdW/∂λ⟩ calculated by pDF reconstruction for both solutes are consistent with the simulations with deviations for most windows less than 1 kcal/mol. The largest deviation (~2 kcal/mol) of ⟨∂UvdW/∂λ⟩ between both methods occurs at λ = 0.1. The deviations are diluted upon integration when computing ΔGvdW. ΔGvdW calculated for both solutes and methods are listed in Table 1. Differences in simulated and pDF-reconstructed ΔGvdW for butane and propanol are −0.33 and 0.18 kcal/mol, respectively. The uncertainty for each λ window is estimated using block standard errors,68 and the final uncertainty of ΔGvdW is computed using error propagation. We include the estimated ΔGelec for butane and propanol from TI simulations and pDF-reconstructions in Table 1. These values are obtained as half of solute-water electrostatic interaction energies based on standard LRT48,52 and are adapted from our previous work.55 Essentially all free energy components are in good accord with those obtained from TI simulations.
Figure 2.
Simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩ at each λ window for (a) butane (b) propanol. The inset of each panel shows the difference between the simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩. Panel (c) illustrates the thermodynamic cycle of mutating a methyl group of a butane into hydroxyl group to form a propanol.
Table 1.
Comparison of Solvation Free Energies of Butane and Propanol Using Thermodynamic Integration with Simulations and pDF-Reconstructionsa
| Δ G | simulated T.I. | pDF T.I. |
|---|---|---|
| butane | ||
| Δ G vdW | 2.67 (0.14) | 2.34 |
| Δ G elec | −0.13 (0.01) | −0.14 |
| Δ G total | 2.54 (0.14) | 2.20 |
| propanol | ||
| Δ G vdW | 1.88 (0.28) | 2.06 |
| Δ G elec | −6.84 (0.03) | −6.42 |
| Δ G total | −4.96 (0.28) | −4.36 |
ΔGvdW is obtained using eq 9. ΔGelec is approximated as half of electrostatic solute–solvent interaction energy using LRT and is adapted from ref 55. Uncertainties obtained as the block standard errors68 are denoted in parentheses. Uncertainties for ΔGvdW and ΔGtotal are calculated using error propagation. The units are all in kcal/mol.
To demonstrate the utility of using this pDF approach to estimate solvation free energies, we consider a free energy cycle of mutating the methyl group in butane to a hydroxyl group to form propanol (illustrated in Figure 2). Since free energy is a state function, ΔΔG = ΔG4 – ΔG3 = ΔG2 – ΔG1. ΔG3 and ΔG4 are the free energies of mutating butane to propanol in vacuum and solution, respectively, and their difference can be calculated by the difference in solvation free energies of butane and propanol. Using the values reported in Table 1, we obtain the pDF-reconstructed ΔΔG = −6.56 kcal/mol, which is within 1 kcal/mol of the simulated ΔΔG = −7.50 kcal/mol.
Deca-alanine
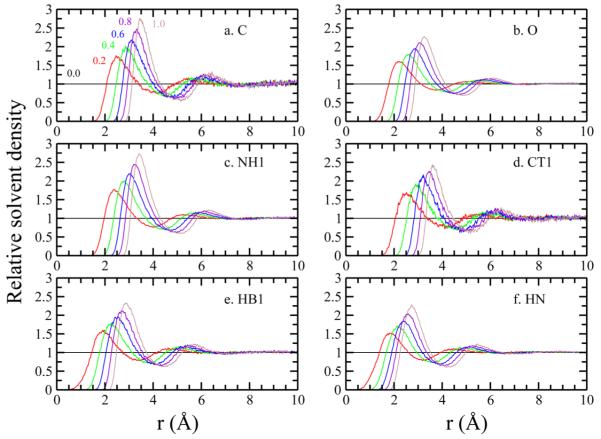
We next estimate ΔGvdW from precomputed pDFs for a deca-peptide. pDFs were constructed from a single alanine monomer (ala1) and used to compute ΔGvdW of four different conformers of deca-alanine, ala10 (referred to as d, d1, d2, d3 in Supporting Information). The set of atoms chosen for pDF generation and solvent density reconstruction include {CT3, C, O, NH1, CT1, HA3, HN, HB1}, where C and O represent the carbon and oxygen atoms of the carbonyl group, NH1 is the peptide nitrogen, HN is the polar hydrogen bonded to the nitrogen, CT1 is the backbone carbon, and HB1 is the backbone hydrogen. We use the pDFs for CT3 and HA3 from our analysis of butane and propanol (Figure 1). The pDFs for the rest of the atom types at several values of λ are presented in Figure 3.
Figure 3.
pDF of alanine/glycine atoms to water oxygen atoms at different λ. Numbers above each pDF indicate the corresponding λ.
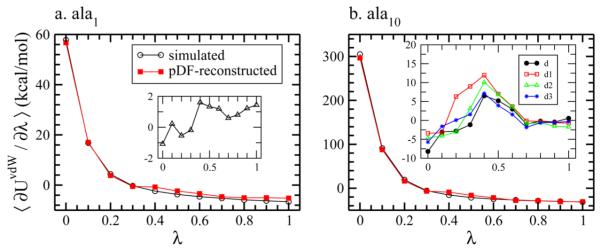
We start with comparing the simulated and pDF-reconstructed estimates of ⟨∂UvdW/∂λ⟩ for ala1, as shown in Figure 4a, using the same solute configuration. From the inset we observe that the deviations of ⟨∂UvdW/∂λ⟩ between both methods are slightly larger than those observed for butane and propanol for all λ windows, but still within 2 kcal/mol. The simulated and the pDF-reconstructed ΔGvdW and ΔGelec are listed in Table 2. The difference in ΔGvdW between simulation and pDF-reconstruction is 0.60 kcal/mol, while the difference in ΔGelec is −0.51 kcal/mol. These differences cancel and yield a pDF reconstructed ΔG within the uncertainty of ΔG obtained by TI simulations. We note ΔGelec is generally the dominating term in ΔG. Estimated uncertainties of ΔGelec are smaller than the uncertainties of ΔGvdW in most of our studies.
Figure 4.
Simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩ at each λ window for (a) ala1 (b) ala10 (the configuration referred to as d in Supporting Information). The inset of each panel shows the difference between the simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩.
Table 2.
Comparison of Solvation Free Energies of Single Alanine and Different Conformers of Deca-alanines Using Thermodynamic Integration with Simulations and pDF-Reconstructionsa
| Δ G | simulated T.I. | pDF T.I. |
|---|---|---|
| ala1 | ||
| Δ G vdW | 1.08 (0.36) | 1.78 |
| Δ G elec | −20.21 (0.02) | −20.72 |
| Δ G total | −19.13 (0.36) | −18.94 |
| d | ||
| Δ G vdW | 5.75 (1.77) | 5.92 |
| Δ G elec | −78.19 (0.08) | −74.26 |
| Δ G total | −72.44 (1.77) | −68.34 |
| d1 | ||
| Δ G vdW | 5.83 (2.20) | 8.70 |
| Δ G elec | −67.75 (0.08) | −60.70 |
| Δ G total | −61.92 (2.20) | −52.00 |
| d2 | ||
| Δ G vdW | 5.42 (1.81) | 6.27 |
| Δ G elec | −89.97 (0.10) | −89.00 |
| Δ G total | −84.55 (1.81) | −82.73 |
| d3 | ||
| Δ G vdW | 5.72 (1.69) | 5.67 |
| Δ G elec | −86.88 (0.08) | −85.86 |
| Δ G total | −81.16 (1.69) | −80.19 |
We use the pDFs calculated from ala1 to estimate the ΔGvdW of ala10. The results of simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩ at each λ for conformer d are shown in Figure 4b. The results for the other three conformers are similar and included in the Supporting Information. The inset shows the deviations of ⟨∂UvdW/∂λ⟩ between simulations and pDF-reconstructions at each λ for all four conformers. While the deviations are large (10–15 kcal/mol/window) and increase with system size, they are suppressed upon integration when calculating ΔGvdw in a manner similar to what we observed for butane and propanol. The pDF reconstructed estimates of ΔGvdW of all ala10 conformers are consistent with those obtained from TI simulations (Table 2). The differences between simulated and reconstructed ΔGvdW for the different conformers in order are 0.17, 2.88, 0.84, and −0.05 kcal/mol. Differences of ΔGelec between methods (adapted from our previous work55) are larger than those observed for ΔGvdW. Owing to the extremely twisted configuration of conformer d1, we find the largest deviation between simulation and reconstruction for both ΔGvdW and ΔGelec. We note that Poisson–Boltzmann calculations fared worse in reproducing the ΔGelec of d1.52 This highly twisted conformation is a low probability structure with peculiar internal interatomic correlations. Thus, we consider this conformer to be a most challenging case for this theory based on pairwise near neighbor solvent correlations for the estimation of ΔG.
Flexible and Fixed Triglycine
Finally, we extend our approach to the calculation of ΔGvdW for a large, diverse ensemble of gly3 conformations and assess the effects of flexibility, or disorder, on these calculations by comparing to a single fixed/extended conformation of gly3. We chose to calculate the pDFs from a single fixed glycine (gly1) to evaluate the ΔGvdW of fixed and flexible triglycines (gly3). The configuration of fixed gly3 is in the Supporting Information. The atom set used to generate the pDFs used here include {CT3, C, O, NH1, CT2, HA3, HN, HB2}. pDFs for these atom types have been presented in the previous sections except for HB2, which represents the aliphatic backbone hydrogen atoms bonded to the CT2 atoms. Results of simulated and pDF-reconstructed ΔGvdW and ΔGelec for fixed gly1 are presented in Table 3. Differences of both components between methods are 0.06 kcal/mol. We next use these precomputed pDFs to estimate ΔGvdW of fixed and flexible gly3.
Table 3.
Comparison of Solvation Free Energies of Glycine and Tri-glycine Using Thermodynamic Integration with Simulations, pDF-Reconstructions, and Benchmark Free Energy Perturbation Calculationsa
| Δ G | simulated TI | pDF TI | FEPb |
|---|---|---|---|
| gly1 | |||
| Δ G vdW | 0.39 (0.34) | 0.45 | |
| Δ G elec | −16.31 (0.12) | −16.25 | |
| Δ G total | −15.92 (0.36) | −15.80 | |
| gly3, flexible | |||
| −0.41 (0.32) | −0.33 | −0.03 (0.05) | |
| −28.75 | −24.01 (0.50) | ||
| −29.08 | −24.04 (0.50) | ||
| gly3, fixed | |||
| −1.29 (0.38) | −1.10 | −0.84 (0.04) | |
| −25.62 (0.12) | −24.13 | −22.08 (0.03) | |
| −26.91 (0.40) | −25.23 | −22.16 (0.05) | |
ΔGvdW is obtained using eq 9. For fixed configurations, ΔGelec are approximated as half of electrostatic solute–solvent interaction energies using LRT. An average is taken over configurations for flexible solutes. The units are all in kcal/mol.
Free energy perturbation results are adapted from ref 65.
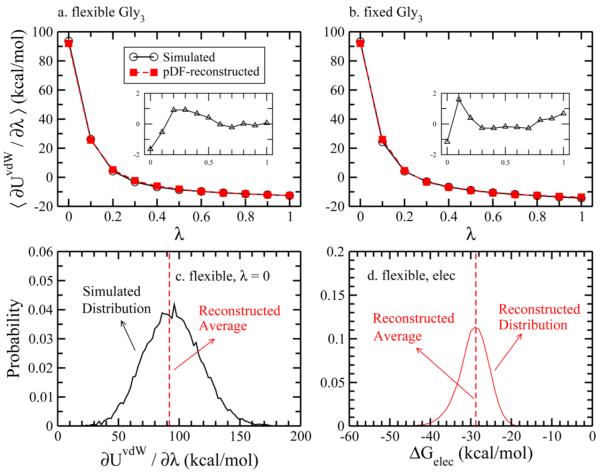
Consider the ΔGvdW term. The comparisons of simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩, along with the deviations (in the insets) at each λ for flexible and fixed gly3 are presented in Figure 5a,b. The deviations are all within 2 kcal/mol. The values of ΔGvdW are listed in Table 3. To estimate ΔGvdW of flexible gly3, we extracted 10000 solute configurations from a molecular dynamics simulation and, for each one, calculated ⟨∂UvdW/∂λ⟩ at all λ values. The ⟨∂UvdW/∂λ⟩ values are then configurationally averaged. We show the distribution over all conformations of ⟨∂UvdW/∂λ⟩ at λ = 0 from simulation in Figure 5c. This shows the deviation among the solute configurations. We expect the distribution of ⟨∂UvdW/∂λ⟩ to be different depending on the force field used given that we have previously shown that CHARMM36 and Amber ff12SB generate different ensembles of structures.69 It would be an interesting comparison to test the distributions of ΔGvdW using different force fields as they can display different distributions of solute configurations and flexibility.
Figure 5.
Simulated and pDF-reconstructed ⟨∂UvdW/∂λ⟩ at each λ window for (a) flexible gly3 and (b) fixed gly3. The inset of each panel shows the difference between the simulated and pDF-reconstruced ⟨∂UvdW/∂λ⟩. Panel (c) shows the distribution of ⟨∂UvdW/∂λ⟩ for flexible gly3 at λ = 0. The average of pDF-reconstructed ⟨∂UvdW/∂λ⟩ corresponds closely with the average of the simulated ⟨∂UvdW/∂λ⟩. Panel (d) shows the distribution of pDF-reconstructed ΔGelec using the solute configurations from flexible gly3 simulations, with the red dashed line representing the ensemble average.
The differences between simulated and pDF-reconstructed ΔGvdW for flexible and fixed gly3 are within 0.2 kcal/mol. In addition to the 11 λ windows used for thermodynamic integration, we include the results using the free energy perturbation (FEP) method with 50 equally spaced λ windows between 0 and 1 from recently published work.65 Due to the nature of the soft-core potential used in this contribution, the integrand is changing more rapidly (as shown in all ⟨∂UvdW/∂λ⟩ figures) at small λ. This is a likely source of error in the ΔGvdW reported here. The comparison of using different numbers of λ windows for calculating the ΔGvdW of the same solute can be found in Supporting Information. We observe that calculated from the current free energy simulations, pDF-reconstructions, and FEP are 0.88, 0.77, and 0.81, respectively. The fact that the ΔGvdW for flexible gly3 is less favorable (or more repulsive) than the fixed gly3 is not surprising. With solute flexibility, gly3 can form configurations that prevent water from accessing parts of the solute, consequently increasing ΔGvdW. The striking part is that all three methods eventually lead to a consistent ΔΔGvdW, which is not trivial. More extensive tests of our approximate ΔΔGvdW are certainly warranted.
To complete the estimation of the total solvation free energy, results for ΔGelec are presented in Table 3. Here we do not include the ΔGelec of flexible gly3 calculated by TI simulations since the noise of ΔGelec computed from the ensemble of solute and solvent configurations instead of from only the ensemble of solute configurations (like in continuum models or the current concept using pDF-reconstruction) is much larger.70–72 For the fixed gly3, the differences of ΔGelec between these three methods are within 4 kcal/mol. For flexible gly3, the difference of ΔGelec between pDF-reconstruction and FEP increases slightly and is within 5 kcal/mol considering a 0.5 kcal/mol uncertainty for FEP reported ΔGelec. Figure 5 d shows the distribution of pDF-reconstructed ΔGelec using 10000 solute configurations generated from simulation. This distribution has a standard deviation of 7.42 and is larger than the distribution from pDF-reconstructed ΔGvdW. calculated from pDF-reconstruction and FEP are 4.62 and 1.93 kcal/mol, respectively.
DISCUSSION AND CONCLUSION
In this contribution, we used precomputed solvent density distributions at multiple alchemical windows with free energy methods to estimate the van der Waals and electrostatic solvation free energies for a variety of solutes. By computing solute–solvent pDFs from small molecules, we can reconstruct the solvent densities around arbitrary solutes with similar chemical composition and, subsequently, estimate solvation free energies without performing lengthy simulations. Using this framework, we have shown that ΔGvdW can be reproduced to within useful accuracy. In the future, we will extend our work to the calculation of solvation free energies of complex macromolecules.
The examples of calculating ΔΔG encourage applications to different biological systems. Combinations of solvation free energies with appropriate free energy cycles may allow rapid estimations for molecular associations,10 alanine scanning,73 and the predictions of pKa values of proteins and amino acid side chains.74
Supplementary Material
ACKNOWLEDGMENTS
We gratefully acknowledge the Robert A. Welch Foundation (H-0037), the National Science Foundation (CHE-1152876), and the National Institutes of Health (GM-037657) for partial support of this work. We thank the scientific computing staff at the Sealy Center for Structural Biology and Molecular Biophysics for computing support.
Footnotes
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.6b09528.
Graphical illustration of calculating pDFs, test of cavity and exclusion factors for pDF-reconstructions, fixed solute configurations, convergence of ⟨∂UvdW/∂λ⟩, pDFs for solute atoms with water hydrogen atoms, pDF-reconstructed ⟨∂UvdW/∂λ⟩ for all four conformers of deca-alanine, comparison of using different amount of λ windows for calculating ΔGvdW of polyalanines (PDF)
ORCID
B. Montgomery Pettitt: 0000-0003-4902-3046
Notes
The authors declare no competing financial interest.
REFERENCES
- (1).Mazor M, Pettitt BM. Convergence of the Chemical Potential in Aqueous Simulations. Mol. Simul. 1991;6:1–4. [Google Scholar]
- (2).Mitchell MJ, McCammon JA. Free Energy Difference Calculations by Thermodynamic Integration: Difficulties in Obtaining a Precise Value. J. Comput. Chem. 1991;12:271–275. [Google Scholar]
- (3).Chipot C, Pohorille A. Free Energy Calculations: Theory and Applications in Chemistry and Biology. Springer; Berlin, Germany: 2007. [Google Scholar]
- (4).Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015;11:3696–3713. doi: 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Lemkul JA, Huang J, Roux B, MacKerell AD., Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016;116:4983–5013. doi: 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Robertson MJ, Tirado-Rives J, Jorgensen WL. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015;11:3499–3509. doi: 10.1021/acs.jctc.5b00356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Jorgensen W. Transferable Intermolecular Potential Functions for Water, Alcohols, and Ethers. Application to Liquid Water. J. Am. Chem. Soc. 1981;103:335–340. [Google Scholar]
- (8).Yu HA, Karplus M. A Thermodynamic Analysis of Solvation. J. Chem. Phys. 1988;89:2366–2379. [Google Scholar]
- (9).Tembre B, McCammon J. Ligand-Receptor Interactions. Comput. Chem. 1984;8:281–283. [Google Scholar]
- (10).Kollman P. Free Energy Calculations: Applications to Chemical and Biochemical Phenomena. Chem. Rev. 1993;93:2395–2417. [Google Scholar]
- (11).Jorgensen WL, Ravimohan C. Monte Carlo Simulation of Differences in Free Energies of Hydration. J. Chem. Phys. 1985;83:3050–3054. [Google Scholar]
- (12).Caldwell JW, Agard DA, Kollman PA. Free Energy Calculations on Binding and Catalysis by Alpha-Lytic Protease: the Role of Substrate Size in the P1 Pocket. Proteins: Struct., Funct., Genet. 1991;10:140–148. doi: 10.1002/prot.340100207. [DOI] [PubMed] [Google Scholar]
- (13).Prevost M, Wodak SJ, Tidor B, Karplus M. Contribution of the Hydrophobic Effect to Protein Stability: Analysis Based on Simulations of the Ile96-Ala Mutation in Barnase. Proc. Natl. Acad. Sci. U. S. A. 1991;88:10880–10884. doi: 10.1073/pnas.88.23.10880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Dang LX, Merz KM, Jr., Kollman PA. Free Energy Calculations on Protein Stability: Thr-157—-Val-157 Mutation of T4 Lysozyme. J. Am. Chem. Soc. 1989;111:8505–8508. [Google Scholar]
- (15).Cramer CJ, Truhlar DG. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- (16).Mobley DL, Bayly CI, Cooper MD, Shirts MR, Dill KA. Small Molecule Hydration Free Energies in Explicit Solvent: An Extensive Test of Fixed-Charge Atomistic Simulations. J. Chem. Theory Comput. 2009;5:350–358. doi: 10.1021/ct800409d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Simonson T, Roux B. Concepts and Protocols for Electrostatic Free Energies. Mol. Simul. 2016;42:1090–1101. [Google Scholar]
- (18).Levy RM, Zhang LY, Gallicchio E, Felts AK. On the Nonpolar Hydration Free Energy of Proteins: Surface Area and Continuum Solvent Models for the Solute-Solvent Interaction Energy. J. Am. Chem. Soc. 2003;125:9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- (19).Smith PE, van Gunsteren WF. When Are Free Energy Components Meaningful? J. Phys. Chem. 1994;98:13735–13740. [Google Scholar]
- (20).Schaefer M, van Vlijmen HWT, Karplus M. Electrostatic Contributions to Molecular Free Energies in Solution. Adv. Protein Chem. 1998;51:1–58. doi: 10.1016/s0065-3233(08)60650-6. [DOI] [PubMed] [Google Scholar]
- (21).Roux B, Yu HA, Karplus M. Molecular Basis for the Born Model of Solvation. J. Phys. Chem. 1990;94:4683–4688. [Google Scholar]
- (22).Bashford D, Case DA. Generalized Born Models of Macromolecular Solvation Effects. Annu. Rev. Phys. Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- (23).Netz RR, Orland H. Beyond Poisson-Boltzmann: Fluctuation Effects and Correlation Functions. Eur. Phys. J. E: Soft Matter Biol. Phys. 2000;1:203–214. [Google Scholar]
- (24).Grochowski P, Trylska J. Continuum Molecular Electrostatics, Salt Effects, and Counterion Binding - A Review of the Poisson-Boltzmann Theory and Its Modifications. Biopolymers. 2008;89:93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- (25).Hansen JP, McDonald IR. Theory of Simple Liquids. Academic Press; San Diego, CA: 1976. [Google Scholar]
- (26).Chandler D. Introduction to Modern Statistical Mechanics. Oxford University Press; New York, NY: 1987. [Google Scholar]
- (27).Aqvist J, Luzhkov VB, Brandsdal BO. Ligand Binding Affinities from MD Simulations. Acc. Chem. Res. 2002;35:358–365. doi: 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- (28).Sharp KA, Nicholls A, Fine RF, Honig B. Reconciling the Magnitude of the Microscopic and Macroscopic Hydrophobic Effects. Science. 1991;252:106–109. doi: 10.1126/science.2011744. [DOI] [PubMed] [Google Scholar]
- (29).Cramer CJ, Truhlar DG. An SCF Solvation Model for the Hydrophobic Effect and Absolute Free Energies of Aqueous Solvation. Science. 1992;256:213–217. doi: 10.1126/science.256.5054.213. [DOI] [PubMed] [Google Scholar]
- (30).Raschke TM, Tsai J, Levitt M. Quantification of the Hydrophobic Interaction by Simulations of the Aggregation of Small Hydrophobic Solutes in Water. Proc. Natl. Acad. Sci. U. S. A. 2001;98:5965–5969. doi: 10.1073/pnas.111158498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Gallicchio E, Kubo MM, Levy RM. Enthalpy-Entropy and Cavity Decomposition of Alkane Hydration Free Energies: Numerical Results and Implications for Theories of Hydrophobic Solvation. J. Phys. Chem. B. 2000;104:6271–6285. [Google Scholar]
- (32).Tan C, Tan YH, Luo R. Implicit Nonpolar Solvent Models. J. Phys. Chem. B. 2007;111:12263–12274. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- (33).Harris RC, Pettitt BM. Effects of Geometry and Chemistry on Hydrophobic Solvation. Proc. Natl. Acad. Sci. U. S. A. 2014;111:14681–14686. doi: 10.1073/pnas.1406080111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Czaplewski C, Ripoll DR, Liwo A, Rodziewicz-Motowidlo S, Wawak J, Scheraga HA. Can Cooperativity in Hydrophobic Association be Reproduced Correctly by Implicit Solvation Models? Int. J. Quantum Chem. 2002;88:41–45. [Google Scholar]
- (35).Shimizu S, Chan HS. Anti-Cooperativity and Cooperativity in Hydrophobic Interactions: Three-Body Free Energy Landscapes and Comparison with Implicit-Solvent Potential Functions for Proteins. Proteins: Struct., Funct., Genet. 2002;48:15–30. doi: 10.1002/prot.10108. [DOI] [PubMed] [Google Scholar]
- (36).Jamadagni SN, Godawat S, Garde S. Hydrophobicity of Proteins and Interfaces: Insights from Density Fluctuations. Annu. Rev. Chem. Biomol. Eng. 2011;2:147–171. doi: 10.1146/annurev-chembioeng-061010-114156. [DOI] [PubMed] [Google Scholar]
- (37).Patel AJ, Varilly P, Jamadagni SN, Acharya H, Garde S, Chandler D. Extended Surfaces Modulate Hydrophobic Interactions of Neighboring Solutes. Proc. Natl. Acad. Sci. U. S. A. 2011;108:17678–17683. doi: 10.1073/pnas.1110703108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Cui D, Ou S, Patel S. Free Energetics of Rigid Body Association of Ubiquitin Binding Domains: A Biochemical Model for Binding Mediated by Hydrophobic Interaction. Proteins: Struct., Funct., Genet. 2014;82:1453–1468. doi: 10.1002/prot.24513. [DOI] [PubMed] [Google Scholar]
- (39).Giovambattista N, Debenedetti P, Rossky P. Hydration Behavior under Confinement by Nanoscale Surfaces with Patterned Hydrophobicity and Hydrophilicity. J. Phys. Chem. C. 2007;111:1323–1332. [Google Scholar]
- (40).Fennell CJ, Kehoe C, Dill KA. Oil/Water Transfer Is Partly Driven by Molecular Shape, Not Just Size. J. Am. Chem. Soc. 2010;132:234–240. doi: 10.1021/ja906399e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Fennell CJ, Kehoe CW, Dill KA. Modeling Aqueous Solvation with Semi-Explicit Assembly. Proc. Natl. Acad. Sci. U. S. A. 2011;108:3234–3239. doi: 10.1073/pnas.1017130108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Li L, Fennell CJ, Dill KA. Field-SEA: A Model for Computing the Solvation Free Energies of Nonpolar, Polar, and Charged Solutes in Water. J. Phys. Chem. B. 2014;118:6431–6437. doi: 10.1021/jp4115139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Mezei M, Beveridge DL. Structural Chemistry of Biomolecular Hydration via Computer Simulation: The Proximity Criterion. Methods Enzymol. 1986;127:21–47. doi: 10.1016/0076-6879(86)27005-6. [DOI] [PubMed] [Google Scholar]
- (44).Subramanian PS, Ravishanker G, Beveridge DL. Theoretical Considerations on the ’Spine of Hydration’ in the Minor Groove of d(CGCGAATTCGCG).d(GCGCTTAAGCGC): Monte Carlo Computer Simulation. Proc. Natl. Acad. Sci. U. S. A. 1988;85:1836–1840. doi: 10.1073/pnas.85.6.1836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Lounnas V, Pettitt BM, Phillips G., Jr. A Global Model of the Protein-Solvent Interface. Biophys. J. 1994;66:601–614. doi: 10.1016/s0006-3495(94)80835-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Phillips GN, Jr., Pettitt BM. Structure and Dynamics of the Water around Myoglobin. Protein Sci. 1995;4:149–158. doi: 10.1002/pro.5560040202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Burling FT, Weis WI, Flaherty KM, Brünger AT. Direct Observation of Protein Solvation and Discrete Disorder with Experimental Crystallographic Phases. Science. 1996;271:72–77. doi: 10.1126/science.271.5245.72. [DOI] [PubMed] [Google Scholar]
- (48).Lin B, Pettitt BM. Note: On the Universality of Proximal Radial Distribution Functions of Proteins. J. Chem. Phys. 2011;134:106101. doi: 10.1063/1.3565035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Rudnicki WR, Pettitt BM. Modeling the DNA-Solvent Interface. Biopolymers. 1997;41:107–119. doi: 10.1002/(SICI)1097-0282(199701)41:1<107::AID-BIP10>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- (50).Makarov VA, Andrews BK, Pettitt BM. Reconstructing the Protein-Water Interface. Biopolymers. 1998;45:469–478. doi: 10.1002/(SICI)1097-0282(199806)45:7<469::AID-BIP1>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- (51).Nguyen BL, Pettitt BM. Effects of Acids, Bases, and Heteroatoms on Proximal Radial Distribution Functions for Proteins. J. Chem. Theory Comput. 2015;11:1399–1409. doi: 10.1021/ct501116v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Lin B, Wong KY, Hu C, Kokubo H, Pettitt BM. Fast Calculations of Electrostatic Solvation Free Energy from Reconstructed Solvent Density using Proximal Radial Distribution Functions. J. Phys. Chem. Lett. 2011;2:1626–1632. doi: 10.1021/jz200609v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Lin B, Pettitt BM. Electrostatic Solvation Free Energy of Amino Acid Side Chain Analogs: Implications for the Validity of Electrostatic Linear Response in Water. J. Comput. Chem. 2011;32:878–885. doi: 10.1002/jcc.21668. [DOI] [PubMed] [Google Scholar]
- (54).Virtanen JJ, Makowski L, Sosnick TR, Freed KF. Modeling the Hydration Layer around Proteins: Applications to Small-and Wide-Angle X-Ray Scattering. Biophys. J. 2011;101:2061–2069. doi: 10.1016/j.bpj.2011.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Ou SC, Pettitt BM. Solute-Solvent Energetics Based on Proximal Distribution Functions. J. Phys. Chem. B. 2016;120:8230–8237. doi: 10.1021/acs.jpcb.6b01898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Ben-Naim A. Water and Aqueous Solutions. Plenum Press; New York, NY: 1992. [Google Scholar]
- (57).Mehrotra PK, Beveridge DL. Structural Analysis of Molecular Solutions Based on Quasi-Component Distribution Functions. Application to [H2CO]aq at 25.Degree.C. J. Am. Chem. Soc. 1980;102:4287–4294. [Google Scholar]
- (58).Gerstein M, Tsai J, Levitt M. The Volume of Atoms on the Protein Surface: Calculated from Simulation, using Voronoi Polyhedra. J. Mol. Biol. 1995;249:955–966. doi: 10.1006/jmbi.1995.0351. [DOI] [PubMed] [Google Scholar]
- (59).Beutler TC, Mark AE, van Schaik RC, Gerber PR, van Gunsteren WF. Avoiding Singularities and Numerical Instabilities in Free Energy Calculations Based on Molecular Simulations. Chem. Phys. Lett. 1994;222:529–539. [Google Scholar]
- (60).Zacharias M, Straatsma TP, McCammon JA. Separation-Shifted Scaling, A New Scaling Method for Lennard-Jones Interactions in Thermodynamic Integration. J. Chem. Phys. 1994;100:9025. [Google Scholar]
- (61).Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Kale L, Skeel R, Bhandarkar M, Brunner R, Gursoy A, Krawetz N, Phillips J, Shinozaki A, Varadarajan K, Schulten K. NAMD2: Greater Scalability for Parallel Molecular Dynamics. J. Comput. Phys. 1999;151:283–312. [Google Scholar]
- (63).Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, Mackerell AD, CHARMM General Force Field (CGenFF) A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2009;31:671–690. doi: 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- (65).Drake JA, Harris RC, Pettitt BM. Solvation Thermodynamics of Oligoglycine with Respect to Chain Length and Flexibility. Biophys. J. 2016;111:756–767. doi: 10.1016/j.bpj.2016.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- (67).Darden T, York D, Pedersen L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- (68).Grossfield A, Zuckerman DM. Quantifying Uncertainty and Sampling Quality in Biomolecular Simulations. Annu. Rep. Comput. Chem. 2009;5:23–48. doi: 10.1016/S1574-1400(09)00502-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Drake JA, Pettitt BM. Force Field-Dependent Solution Properties of Glycine Oligomers. J. Comput. Chem. 2015;36:1275–1285. doi: 10.1002/jcc.23934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Morreale A, de la Cruz X, Meyer T, Gelpí JL, Luque FJ, Orozco M. Linear Response Theory: An Alternative to PB and GB Methods for the Analysis of Molecular Dynamics Trajectories? Proteins: Struct., Funct., Genet. 2004;57:458–467. doi: 10.1002/prot.20169. [DOI] [PubMed] [Google Scholar]
- (71).Carlson HA, Jorgensen WL. An Extended Linear Response Method for Determining Free Energies of Hydration. J. Phys. Chem. 1995;99:10667–10673. [Google Scholar]
- (72).Carlson HA, Nguyen TB, Orozco M, Jorgensen WL. Accuracy of Free Energies of Hydration for Organic Molecules from 6-31g*-Derived Partial Charges. J. Comput. Chem. 1993;14:1240–1249. [Google Scholar]
- (73).Pomès R, Willson RC, McCammon JA. Free Energy Simulations of the HyHEL-10/HEL Antibody-Antigen Complex. Protein Eng., Des. Sel. 1995;8:663–675. doi: 10.1093/protein/8.7.663. [DOI] [PubMed] [Google Scholar]
- (74).Li G, Cui Q. pKa Calculations with QM/MM Free Energy Perturbations. J. Phys. Chem. B. 2003;107:14521–14528. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.