Modeling Tumor Clonal Evolution for Drug Combinations Design

Abstract

Cancer is a clonal evolutionary process. This presents challenges for effective therapeutic intervention, given the constant selective pressure towards drug resistance. Mathematical modeling from population genetics, evolutionary dynamics, and engineering perspectives are being increasingly employed to study tumor progression, intratumoral heterogeneity, drug resistance, and rational drug scheduling and combinations design. In this review, we discuss promising opportunities these inter-disciplinary approaches hold for advances in cancer biology and treatment. We propose that quantitative modeling perspectives can complement emerging experimental technologies to facilitate enhanced understanding of disease progression and improved capabilities for therapeutic drug regimen designs.

Quantitative Approach to Study Tumor Evolution and Therapeutic Response

Recent data from tumor sequencing has increased attention on the broad relevance of intratumoral heterogeneity in cancer patients and their treatment. In light of these studies, the tumor biology field now more than ever regards cancer as an ongoing evolutionary process. As such, a systematic and comprehensive understanding of this malignancy and its dynamics will require capitalizing on quantitative methods from population genetics, evolution, and engineering. A number of excellent reviews on tumor heterogeneity^1–4, drug resistance^5–8, drug combinations design^9–12 are available, so we aim here to integrate germane quantitative approaches, with a focus on recent developments and applications to understanding and predicting therapeutic effects. Whenever possible, we will refer readers to relevant existing reviews, but will also provide brief historical context, and most importantly will offer introduction to foundational mathematical frameworks.

Tumor Clonal Evolution and Intratumoral Heterogeneity

The notion of cancer as a clonal evolutionary process dates to seminal work in 1976 by Nowell¹³. A key consequence of tumor clonal evolution is intratumoral heterogeneity – as the founder clone develops successive alterations with fitness advantages subject to selection forces (e.g., tumor progression, metastasis, and drug resistance). Heterogeneity in tumor cells across different regions was indeed observed by pathologists as early as the 1800s, based on cell morphology and other cytological characteristics¹⁴. Cytogeneticists have since used chromosome G-banding, spectral karyotyping, and florescence in situ hybridization to further show distinct subpopulations with copy number variations and chromosomal rearrangements¹⁴. More recently, with the advent of high throughput technologies (e.g., SNP arrays, comparative genomic hybridization microarrays) and next-generation sequencing (NGS), the field has begun to realize at much greater resolution the complexity of tumor heterogeneity and clonal dynamics.

Clonal evolution may be conceptualized as progressing via accumulation of what many term ‘driver’ and ‘passenger’ mutations. From an evolutionary perspective, drivers can be considered as genetic (or epigenetic) alterations that offer significant relative fitness advantage, while passengers are mutations appearing to present only weak or neutral influences. Numerous computational techniques have been developed to test for positive selection and identification of such ‘drivers’¹⁵. Drivers and passengers can also be context dependent, and complicated by potential epistatic interactions¹⁶ as well as passengers exposing additional cancer vulnerabilities¹⁷. Over time, evolutionary processes – genetic drift and Darwinian selection – play a critical role in the progression and fixation (i.e., establishment) of subclones with these various alterations. Specifically, if the supply rate of driver mutations is slower than the time it takes for the established subclone to selectively sweep through the population, a classical linear model of clonal evolution^3,18 is followed. In contrast, however, tumor clonal architectures are often observed experimentally to be the consequence of a complex branched clonal process³, as originally described by Nowell. Here, multiple subclones may present and compete via clonal interference prior to fixation. Such branched clonal evolutionary processes have been observed in many tumor types, including leukemias^19–21, renal-cell carcinoma²², pancreatic cancer^23,24, amongst others. Recently a ‘big bang’ model of tumor evolution was observed in an analysis of 349 glands from 15 colorectal tumors – where a majority of alterations transpire early during transformation, resulting in tumor growth via concomitant single expansion of multiple mixed subclones without selective sweeps and with minimal selection pressures²⁵. It should be emphasized, moreover, that heterogeneity is not restricted to genetic alterations, as epigenetic heterogeneities have also been reported²⁶. In addition, for particular tumor types such as chronic myeloid leukemia (CML), the population structure can be hierarchical with the overall tumor population supplied by a small number of cancer stem cells²⁷.

Intratumoral heterogeneity may have functional roles beyond mere indication of tumor history. Studies in breast cancer xenograft models with component or combined mixed heterogeneous tumor populations suggest the importance of heterogeneity in tumor maintenance²⁸. Drug treatment also can impose tremendous selective pressure on reshaping the clonal architecture, as will be discussed later in this review.

Quantitative Approaches to Modeling Clonal Evolution

Mathematical modeling of tumor development and metastasis has been the subject of comprehensive reviews periodically over the past decade^6,29. Building on these, here we will introduce vital fundamental tools from population genetics³⁰ and evolutionary dynamics³¹ as applied to cancer and then move to emphasize a view of clonal evolution based on fitness landscapes and focus on relation to therapy. Mathematical studies of cancer began as early as the 1950s, from works by Nordling³², Armitage and Doll^33,34, Fisher³⁵, and Knudson³⁶ on the age-incidence of cancer and the multistage theory of carcinogenesis. Since then, a large number of models have been based on well-mixed populations with the assumption of no cell-cell interaction. These models provide a tractable system to study cancer dynamics and serve as the foundation for additional model complexity. Several important evolutionary forces (i.e., genetic drift, selection, and mutation) underlie much of our observed tumor dynamics and are of differential importance under specific parameter regions (e.g., population size). In particular, selection is largely a deterministic process. Here, the same outcome will generally be achieved given the same initial conditions. On the other hand, in a stochastic process, the same initial condition can yield different outputs (as described by probability distributions) – a feature that is important in modeling processes such as genetic drift.

Stochastic models

Several tools from stochastic modeling have been utilized to analyze tumor evolution. These include Markov models, where a system’s future state depends only on the current state of the system (i.e., the Markov property)³⁷. Specifically, a Markov chain consists of a series of probabilistic variables, satisfying the Markov property, with the transition between states described by the transition matrix of rate constants for movement of the variables between different values. A Markov chain is considered as a time-homogeneous process if the transition matrix stays the same after each step; otherwise the process is time-nonhomogeneous. A Markov process can be further classified based on it being cast as discrete or continuous with respect to time, and on the ‘space’ of the system’s state being characterized by variables either discrete or continuous in nature. We provide a brief overview below of the Markov models that have been used, which can be broadly considered within two categories: finite constant and finite fluctuating population size models.

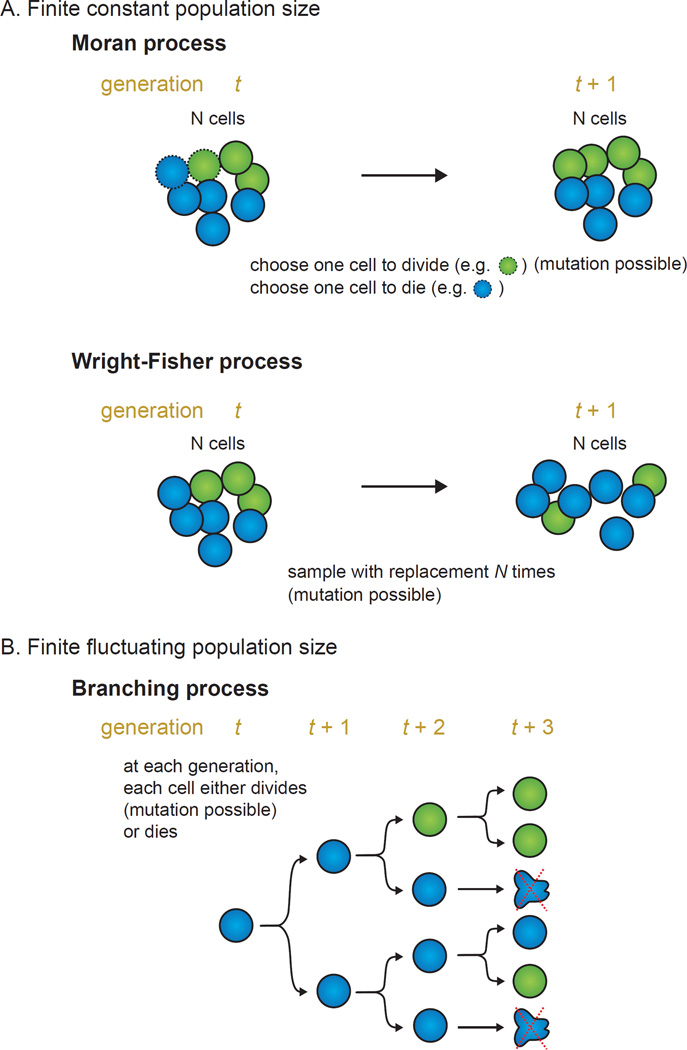
Assuming, on one hand, a constant population size, the Moran process and Fisher-Wright process have been classical and standard models in population genetics to study genetic drift (and hence changes in allele frequency over time in a population, with possible incorporation of selection and/or mutation) (Box 1A). Moran process models have been used in a number of studies on tumor initiation and progression^38–40, in understanding the incidence rates (and their dependence on fitness distributions), rates of allele inactivation/activation, and stochastic tunneling. The Wright-Fisher process has also been used in the study of tumor progression^41,42, clonal interference⁴³, and intratumoral heterogeneity⁴⁴. Both Moran and Fisher-Wright processes converge to same results under large population size and rescaling^30,45. Fisher-Wright models are more often used given its computational efficiency in simulations.

Box 1. Stochastic models of finite constant and fluctuating population size.

Panel A. Finite constant population size.

A Moran process is a discrete-time Markov chain (specifically a birth/death process)³¹ with overlapping generations. We suppose a total fixed population size N and two cell types (A and B) and corresponding fitness f_A and f_B. At each generation (time step), a random cell is selected to replicate with probability proportional to its fitness, and another cell uniformly selected to die. As such, this constitutes a birth/death pair event with constant overall population size and two absorbing states (i = 0 or i = N). Under neutral drift (where f_A = f_B), the fixation probability of cell type A with i cells is given by,

$$x_i=\frac{i}{N}$$

Under selection with relative fitness r (i.e. suppose cell type B has fitness of 1 and cell type A has fitness of r), the fixation probability of cell type A with i cells is given by,

$$x_i=\frac{1-1/r^i}{1-1/r^N}$$

With a large population (N ≫ 1) and advantageous mutation for A (r > 1), the fixation probability a single new cell type A is x = 1 − 1/r. This means large population size does not guarantee fixation. Mutation can also be incorporated, such that with a mutation rate u, the rate of evolution from a shift of the entire population being A to B is given by

$$R=Nu{x}_1$$

Under neutral drift, the equation simplifies to R = u, meaning that the rate of neutral evolution is simply the mutation rate.

In a Wright-Fisher process, the entire population is sampled at each generation (instead of just a single birth/death pair event), and as such assumes non-overlapping generations. To stay with the two-cell type example above, a Wright-Fisher process here involves given a total fixed population size N, we sample with replacement from the current population pool to derive the population composition at the next generation. Thus, the probability of cell type A with j cells in the current generation to contain i cells at the next generation simply follows the binomial distribution,

$$\mathrm{P}(N_j\to N_i)~\text{Bin}(i;N,\frac{j}{N})=\left(\begin{array}{c}\hfill N\hfill \\ \hfill i\hfill \end{array}\right){\left(\frac{j}{N}\right)}^i{\left(\frac{N-j}{N}\right)}^{N-i}$$

The association between the two processes is apparent, as one generation in the Wright-Fisher process corresponds to N generations in the Moran process. In the limit of large population size and with rescaling, both models lead to similar results (e.g. fixation probabilities)^30,45. Other evolutionary forces such as selection and mutation can also be incorporated, and with multi-type subpopulations, in which case a multinomial distribution would be used. Although Moran model has more benefits with regards to exact analyses, Wright-Fisher process is much more computationally efficient, particularly for large population sizes. It is also of note that Wright-Fisher process and Moran process have been used with modifications for an exponential growing tumor population size^41,123.

Panel B. Finite fluctuating population size.

With a finite fluctuating population size, branching process¹²⁴ has been widely used for the study of tumor evolution and dynamics with exponential growth. The basic premise is that each cell in a population independently gives rise to a random number of offspring accordingly to a probability distribution at some later time. The simplest branching process is that of a single-type discrete-time Bienaymé-Galton-Watson process, which can be defined as,

$$X_{n+1}=\sum _{j=1}^{X_n}{\xi }_j^{(n)}$$

where X_n refers to the population size at the nth generation and each ${\xi }_j^{(n)}$ is an independently and identically distributed random variable describing the offspring distribution for the jth cell at the nth generation. Probability generating functions are the primary tool used in the analysis of these processes.

Several special cases exist. If Galton-Watson process follows a Poisson offspring distribution conditioned at a constant population size, we can obtain the Wright-Fisher process as described above¹²⁴. If each cell divides (into two offspring) or dies with a specific birth or death rate, then this branching process is a nonhomogeneous continuous-time birth/death process. Note that birth/death processes are a special case of continuous-time Markov chains. In general, continuous-time Markov chains can be simulated with the Gillespie algorithm (or with modified methods such as tau-leaping for computational efficiency).

On the other hand, assuming a fluctuating population size, the branching process (Box 1B) has been very widely used in the study of tumor heterogeneity and initiation/progression^{6,46–50,16,51}. For example, Bozic et al.⁴⁶ studied the accumulation of driver and passenger mutations and the timing of these events in relation to epidemiologic and clinical observations. Parameterization to experimental data suggests that the selective advantage conferred by somatic mutations is very small. This model was later extended with consideration to epistasis¹⁶. Studies by birth/death models were also applied to studying the role of moderate deleterious passenger mutations on tumors and their effects in potentially alternating cancer progression and therapeutic response^52,53. These mathematical models have also becoming increasingly used in studying effects of drug treatment (as further discussed in a later section).

An alternative to analyze stochastic processes that can be more tractable is with approximation using diffusion models (Box 2). The diffusion approximations are helpful in determining fixation probabilities and mean fixation times⁴⁵. Recently, Tomasetti et al. used the diffusion approximation to the Moran process to estimate the expected number of passenger mutations, and their studies suggest that a substantial number of somatic mutations in tumors may have occurred prior to tumor initiation⁵⁴.

Box 2. Stochastic models (diffusion approximation).

Fokker-Planck (Kolmogorov forward) equation models the time evolution of a probability distribution density φ(p, t) for allele frequency p and time t of a Markov process as

$$\frac{\partial }{\partial t}\phi (p,t)=-\frac{\partial }{\partial p}M(p)\phi (p,t)+\frac{1}{2}\frac{{\partial }^2}{\partial p^2}V(p)\phi (p,t)$$

where M(p) and V(p) represents the mean and variance of the Markov process, and models directional (e.g. selection) and non-directional (e.g. genetic drift) processes, respectively.

Deterministic models

At sufficiently large population size, the population can be usefully modeled using deterministic models with difference or differential equations, especially if the goal is to also study average population behaviors. In addition, models used in evolutionary game dynamics have also been developed to describe selection and mutation of infinitely large populations (Box 3). Page and Nowak have provided a review on the relation among these different deterministic evolutionary dynamics models (e.g., quasi-species equation, replicator-mutator equation, replicator equation, Lotka-Volterra equation, Price equation, etc.)⁵⁵. Deterministic models⁵⁶ and hybrid of deterministic/stochastic models⁵⁷ have been used in the study of CML dynamics under treatment. In the hybrid deterministic/stochastic model⁵⁷, the deterministic model was used to model the wild-type cancer stem cells and branching process for the mutant cancer stem cells. The results were identical to a full stochastic model, yet usage of the deterministic models provide mathematical simplifications and more tractable investigations of different growth models. A wide range of differential equation based models has also been used for the study of drug scheduling (discussed later). Lastly, the quasi-species equation was used in the study of genetic instability during tumor progression⁵⁸.

Box 3. Deterministic models (evolutionary dynamics).

In evolutionary game dynamics, the quasispecies equation (formulated by Eigen and Schuster for the study of molecular evolution) have been used to describe selection and mutation of an infinitely large population³¹. Given x_i as the frequency of genotype i with fitness f_i and a mutation matrix Q, we can describe the derivative of x_i as,

$${ẋ}_{\iota }={\sum }_j{x}_j{f}_j{Q}_{ji}-\varphi (x)x_i$$

where ϕ(x) is average population fitness and defined as,

$$\varphi (x)={\sum }_j{x}_j{f}_j$$

The quasispecies equation is a special case of the replicator-mutator equation, which also accounts for frequency-dependent selection (where each fitness value f_i depends on the frequency of other cells in the population).

Fitness Landscapes

The mathematical models discussed thus far lack connection of genotype to phenotype, and of either or both to parameters characterizing ‘fitness’ of the population under a given environment (e.g., drug treatment condition). This can be accomplished via description of a fitness landscape (also known as adaptive landscape)^59,60 – a mapping of multidimensional genotype (and/or phenotype) space to its corresponding fitness. An idealized realization of this space may be seen in three dimensions (Fig 1A), with the xy plane representing the genotype space and the z-axis representing fitness. Fitness landscape was originally proposed by Wright in a seminal 1932 paper⁶¹ on ‘shifting balance’ theory. Later advances on understanding evolutionary adaptation followed (reviewed elsewhere⁶⁰) with emphasis on a molecular basis of inheritance, first by Smith’s analysis of protein space⁶². Subsequently, Gillespie tried to investigate specifically the distribution of fitness values by proposing that these parameters are likely to be drawn from the extreme tail of the distribution, such that extreme value theory (EVT) can be applied to study the tails of distribution independent of knowing the distribution itself⁶³.

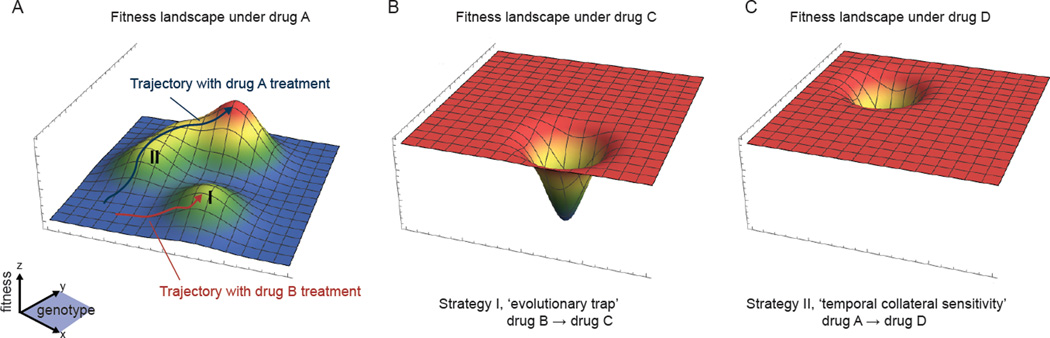
Figure 1. Fitness landscapes and transversion upon drug treatments.

(A) An illustration of a fitness landscape in 3-D space, with the x and y plane representing genotype space and the z axis representing fitness. The white asterisk indicates a possible initial genotype of the tumor population. The fitness landscape with the corresponding peaks and valleys is one possible realization of the fitness under drug A. Upon selection with drug A, the likely evolutionary trajectory is shown in blue. Alternatively, upon selection with drug B, the population can transverse the fitness landscape with a different trajectory and terminal state (shown in red). These drug selection perturbations open opportunities for rational design of subsequent treatment strategies (e.g. I vs II). (B) In strategy I (‘evolutionary trap’)⁷⁵, drug B can be used to drive the tumor toward a specific state such that the resulting tumor genotype state will be vulnerable to another drug C. The corresponding fitness landscape under drug C is shown. (C) In strategy II (‘temporal collateral sensitivity’)⁸⁰, by understanding the propensity and trajectories of tumor evolution under the canonical drug A selection, there may exists vulnerabilities at intermediate stages of clonal evolution we can exploit. Based on the fitness landscape shown for same genotype space under drug D, we see that we can switch to drug D when the tumor is evolving (under drug A) at a particular intermediate state for maximized kill.

Several approaches exist for modeling fitness landscapes⁵⁹, broadly falling into three categories: random field, sequence-structure, and phenotype-fitness models (Box 4). Aside from these mathematical models of fitness landscapes, there has been an increasing number of empirical landscapes derived based on evolutionary or systematic combinatorial experiments (reviewed elsewhere^59,64). Recent developments using CRISPR/Cas9 have enabled saturation editing and analyses at the endogenous locus⁶⁵, specifically applying this to genomic regions of BRCA1 and DBR1 and measured the functional impact/fitness of different alterations. It is conceivable that this technology will enable the detailed investigation in a native context the mapping between genotype and fitness. This is particularly of interest in cancer as in some cases, the resistance mechanisms are established via on-target point mutations that directly affect the binding affinity of the small molecule drug. This includes resistance-conferring mutations in the kinase domain of BCR-ABL1 in chronic myeloid leukemia/Ph+ acute lymphoblastic leukemia, ALK in non-small-cell lung cancer, or cKIT in gastrointestinal stromal tumor⁸. Saturation analyses would be important to empirically determine fitness of different genotypes as well as any epistatic interactions, and to thus get a general understanding on the topology of cancer fitness landscapes.

Traversing on the fitness landscape

Topology of landscapes is of particular importance as it provides information regarding evolutionary trajectories, predictability, or rate of adaptation. In particular, rugged landscapes (bearing multiple peaks and valleys) can occur as a result of sign epistasis, whereby the effects of a specific allele depend contextually on the genetic background at the other loci. This would cause certain paths along the fitness landscape to become inaccessible. Pathway inaccessibility in a rugged landscape can constrain evolutionary trajectories and consequently increases repeatability and predictability. Experimental evidence based on mutagenesis and fitness measurements (viz. drug resistance) suggest microbial evolution may be constrained with a large number of inaccessible mutational trajectories^66,67. Additionally, several experimental studies also showed convergent and parallel evolution when the populations (E. coli and S. cerevisiae) were independently evolved^68–70. Evolutionary predictability and convergent evolution is of particular relevance as to our understanding of whether tumor clonal evolution has defined trajectories and potential forward predictions on how tumor responds to treatment. We have similarly observed convergent resistance paths in particular cancer types, with resistance mechanisms to targeted therapies being limited to on-target point mutations in kinase domains (e.g. BCR-ABL1, ALK, cKIT, EGFR, etc.) or activation of compensatory/downstream pathways (e.g. IGF1R, PDGFR, FGFR, MET, KRAS, etc.)⁸. Nevertheless, stochastic processes can still present challenges in predictability even within these limited set of genotypes.

For analysis of evolutionary predictability, several parameters must be considered^59,71: mutation rate, strength of selection, and population size. With a small population size, this is under a so-called strong-selection-weak-mutation (SSWM) regime, a condition considered and studied by Gillespie in his work on EVT and mutational landscapes. SSWM assumes the mutation supply rate is sufficiently low and selection is high. This leads to stochastic process playing a dominant role in driving evolution, and thus a challenge in predictability. With increasing population size, the population is likely to be more heterogeneous, and SSWM dynamics transitions to a ‘greedy’ adaptation dynamics, where different subclones compete and bias the selection of the fitter clones; correspondingly, predictability of system outcome is enhanced. At sufficiently large population sizes, clones possessing multiple mutations may be present, allowing passage along trajectories not previously accessible (i.e., enables valley crossing via ‘tunnels’ through intermediate states). This then generates greater stochasticity and accordingly decreased predictability⁷¹. Thus, predictability does not strictly scale linearly with population size, but can vary under distinct population size regimes. Furthermore, a trade-off exists between the rate of adaptation and eventual fitness level achieved. Here small population sizes can reach higher fitness (as stochasticity allows exploration of more diverse areas in a rugged landscape), whereas larger population sizes can remain trapped at the local fitness peak^72–74.

The concept of ‘evolutionary trap’ (Fig 1B) has been studied in microbial systems (e.g., S. cerevisiae, C. albicans) whereby karyotypically heterogeneous populations were driven by a first drug to a region of the fitness landscape with reduced diversity, followed by maximized kill using a second drug⁷⁵. Specific regions of the fitness landscape with distinct vulnerability under different conditions have been also recently exploited using a concept of ‘temporal collateral sensitivity’ in cancer (Fig 1C). Collateral sensitivity is a form of synthetic lethality, again studied frequently in bacterial evolution, for which due to evolutionary constraints and trade-offs, populations becoming resistant to one drug can be sensitized to other classes of drugs^76–79. The difference between Panel C and Panel B in Figure 1 is with respect to chronology; Panel B represents fixation of a subpopulation to a final state (that also happens to be resistant to drug A in this case) that is sensitive to drug C, whereas Panel C represents treatment with drug D during a transient period as a subpopulation is starting to develop resistance to drug A but before establishment of the final emergent clone.

New work has begun to introduce this notion of temporal collateral sensitivity (Fig 1C) to understanding tumor evolution and drug responses, and especially to elucidating more effective sequential combination treatments. In a series of drug selection and small molecule screening experiments using murine Ph+ acute lymphoblastic leukemia cells, the authors have shown that an intermediate stage during clonal evolution toward resistance to classical BCR-ABL1 inhibitors can be hyper-sensitized to non-classical BCR-ABL1 inhibitors⁸⁰. This finding demonstrates potential opportunities on the utility of diverse small molecules for targeting distinct stages of clonal evolution as tumor transverse along a fitness landscape toward resistance. Nevertheless, broad applicability of these phenomenon in cancer remains to be seen. As such, it would be critical in also using different random fields models of fitness landscapes to gain insight on how topology can affect the predictability and success/failure of drug combinations on resistance trajectories.

It should be noted that although the general assumption is that of a static landscape, actual evolution may also involve an ever-changing fitness landscape that varies with clonal evolution^81,82. The advent of next-generation sequencing has increased capabilities for high-resolution tracking of clonal evolution. In one study, high-resolution barcoding libraries (~500,000 barcodes) and sequencing enabled lineage tracing of S. cerevisiae evolution and evaluation of the dynamics of mutations and corresponding fitness⁸³. In another evolution study using yeast, fluorophore-labeled competition assays combined with sequencing and mathematical modeling based on branching process models also explored the role of polyploidy on evolutionary adaptation⁸⁴. Most importantly, these methods are translatable to cancer in its high-resolution tracking of tumor subclonal dynamics and their relative fitness, for a better understanding of the complexity of cancer fitness landscapes and how populations evolve in response to distinct selective pressures. Here it is also important to consider the physiological relevance of in vitro models and patient derived xenograft models and with respect to their context specific selective pressures.

Effects of drug treatment on clonal evolution

In parallel with the rising utility of NGS in studying intratumoral heterogeneity and tumor progression, analyses of matched biopsies of patients prior and post drug treatment have also revealed extensive clonal dynamics. The mechanisms by which resistance/relapse occurs can be via (i) de novo mutations (e.g. genotoxic chemotherapy that induces mutagenesis), (ii) selection of pre-existing resistant subclone with higher fitness, or (iii) tumor reduction and competitive release (whereby significant tumor reduction leads to a regime of small population size, followed by the outgrowth of a different subclone)¹. Experimental and clinical evidence has been extensive and reviewed elsewhere¹. Of central importance is the determination of pre-existing subpopulations that ultimately expand to dominance at relapse^85,86 and thus reshape the underlying tumor population architecture. Polyclonal drug resistance can be particularly challenging as tumors with multiple resistance mechanisms can co-evolve independently^87,88, complicating effective drug combinations design. Here, we will elaborate on the quantitative approaches taken (using many tools we have discussed in earlier sections) to interrogate the effects of therapeutic intervention through an evolutionary lens.

Empirical drug combinations design

Much of the early clinical work on empirical combination chemotherapy design was initiated by Frei and Freireich in the early 1950s. These studies have led to some of the common drug regimens in existence even to this day. With the advent of targeted therapy (and now advances in immuno-oncology), we have a greater arsenal of drugs to attempt to rationally combine. Moreover, we can design drug combinations not only based on non-overlapping toxicity, but also on mechanism of actions and resistance^9,10. We will further emphasize this trend in light of other converging conceptual advances and methodologies discussed in our concluding remarks.

Stochastic and deterministic models

Early quantitative work on resistance was initiated by Luria and Delbrück in their classic phage resistance studies⁸⁹ in 1943. The work demonstrated the use of fluctuation analysis to confirm the emergence of resistance via Darwinian selection and expansion of a pre-existing bacterial subpopulation, rather than via induction. Assuming deterministic exponential growth for both wild-type and mutant populations and probabilistic mutation, they derived a distribution (now known as the Luria-Delbrück distribution⁹⁰) describing the number of resistant colonies. Tumor growth kinetics under therapy was studied soon after using murine L1210 leukemia cells, by Law (for antimetabolite resistance via selection and also showed superiority of drug combinations over single drug treatment)^91,92 and by Skipper (for the Skipper-Schabel-Wilcox model on exponential tumor growth and log-kill tumor regression)⁹³. Norton and Simon^94,95 subsequently observed in the 1970s that some tumors follow Gompertz growth, which they modeled using differential equations to predict the superiority of dose dense drug combination schedule (e.g. drugs need to be given with as little ‘off’ intervals as possible between cycles). This result arises from the treatment typically having higher dose density along with integrated drug effects. Accordingly, dose intensification would prevent rapid leukemia cell regrowth under Gompertz growth kinetics. In the 1980s, Goldie and Coldman^96–98 applied stochastic mathematical models (of growth dynamics and incorporated mutation) to predict that the most efficacious regimen is an alternating drug combination schedule that is given as early as possible to minimize chances of resistance. The concept of dose intensity has also been explored using an empirically-derived equation to calculate a summation dose-intensity (SDI) of drug combinations, proposed by Hryniuk^99,100.

Many of the mathematical models have since been extended and the issue of drug scheduling has been studied extensively (reviewed elsewhere^5–7,101). In recent studies, a linear quadratic model was used to derive optimal radiotherapy scheduling for glioblastoma treatment, with demonstrated improved survival on mice¹⁰². The concept of ‘adaptive therapy’ was also recently proposed based on mathematical modeling to show potential efficacy in a modulated drug scheduling that controls a stable tumor burden, allowing a sensitive tumor subpopulation to suppress the outgrowth of the resistant subpopulation^103,104. The differential fitness differences between resistant and sensitive subpopulations have been studied in other tumor models that provide rationales for drug holiday schedules. Here, if the resistant subpopulation has relative lower fitness in the absence of drug, this suggests that intermittent drug dosing will enable the alternating rise and fall of the wild-type and resistant subpopulations, thus delaying resistance onset. This idea has been analyzed using stochastic birth/death process modeling with experimental validation in a non-small cell lung cancer (NSCLC) model in vitro and in vivo¹⁰⁵. This was also corroborated in a recent experimental study in BRAF(V600E) melanoma models, where due to a fitness defect of the resistant subpopulation in the absence of drug, an intermittent dosing schedule was shown to be effective¹⁰⁶.

In addition to drug scheduling, mathematical models have also been used in determining (and quantifying) the existence of resistant subpopulations prior to treatment. Due to the limit of detection of NGS technologies (at 0.1–1% due to its error rate)¹⁰⁷ and other technical issues in the sequencing/computational analyses pipeline (e.g. sequencing coverage, depth, or limitations in aligners/mutation callers), detection of rare minor subpopulation is oftentimes a challenge. Although sophisticated barcoding methods have been developed with significant lower error rates¹⁰⁸, these have yet to be widely adopted and implemented. However, several studies utilized mathematical modeling parameterized based on experimentally derived tumor dynamics data to indicate and estimate the minor subpopulation. Diaz et al. employed a branching process model to conclude the existence of rare KRAS-mutant cells prior to initiation of monotherapy with panitumumab in patients with colorectal cancer, based on observed clinical kinetics of resistance from circulating tumor DNA (ctDNA). This was similarly used in estimating the number of pre-existing BCR-ABL1 resistant mutants in vitro^80,109. Other studies have similarly begun to address these questions in regards to pre-existence and risk of relapse^{110– 114}.

Optimal control theory and combinatorial optimization

Besides the stochastic and deterministic models described earlier, complementary quantitative approaches from engineering disciplines have been applied to drug combinations and drug scheduling since the 1970s. Specifically, with dynamical systems modeled using deterministic differential equations, we can apply many concepts from optimal control theory in engineering to study the stability and control of cancer – with the goal of maximizing tumor kill and minimizing drug toxicity. Bahrami and Kim¹¹⁵ first reported applications of optimal control theory to minimize tumor growth (and used an example with vincristine against murine AKR leukemia). Swan and Vincent¹¹⁶ subsequently studied optimal control of chemotherapy in human IgG multiple myeloma. Since then, numerous studies have appeared^117,118 (with many based on the control model formulated by Martin¹¹⁹) and have been solved analytically, using numerical methods (e.g. via formulation as a linear or nonlinear programming problem) or other heuristics methods (e.g. genetic algorithms, particle swarm optimization, simulated annealing, etc).

While the majority of the mathematical optimization contributions have centered on drug scheduling, analogous efforts have also been made to study the choice of drug combinations. These include theoretical analysis using integer programming to determine the minimal set of drugs that maximizes the coverage of molecular target variants based on drug-target binding affinity properties¹²⁰. Recently, combinatorial and multi-objective optimization has also been applied to study how to design drug combinations in the context of intratumoral heterogeneity^121,122. The results (with in vitro and in vivo validation in a Burkitt’s lymphoma model) show that consideration of heterogeneity can at times lead to non-intuitive optimal drug combinations. These approaches could be combined with different fitness landscape topologies in understanding how to best rationally design drug combinations with desirable trajectories and outcomes.

Concluding remarks

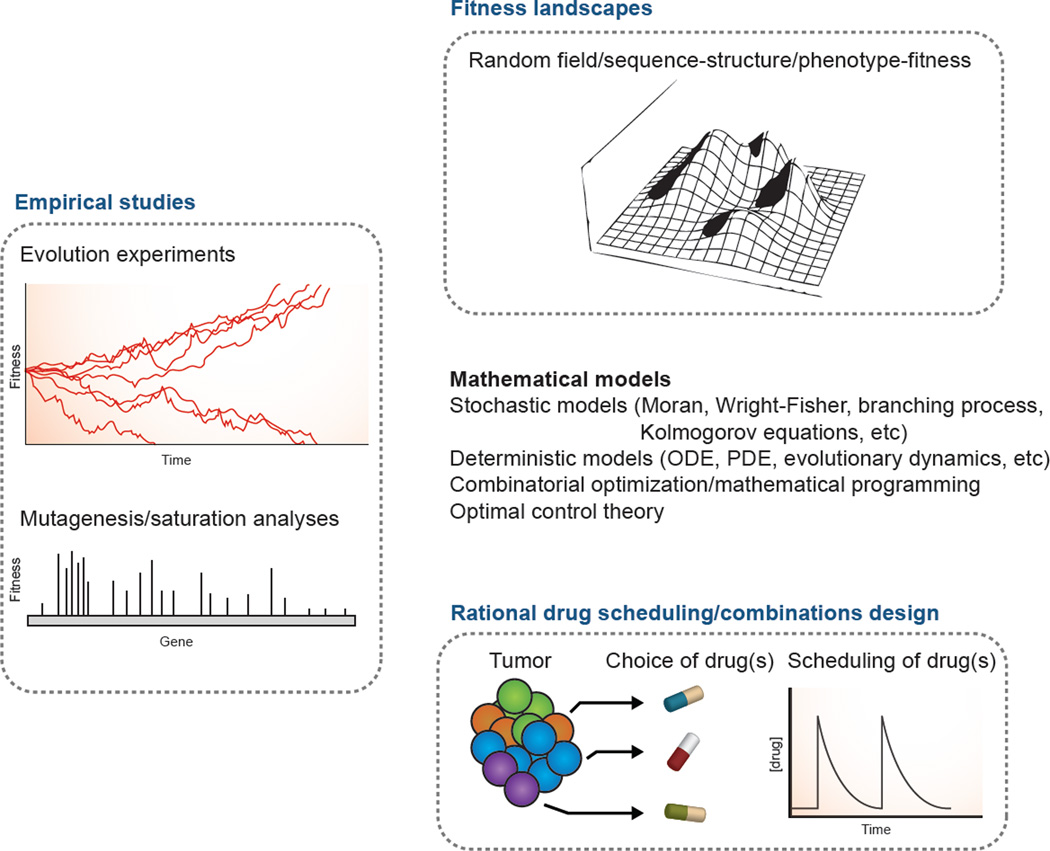
With our increased focus on viewing cancer through the evolutionary lens, we necessarily have to equip ourselves with the quantitative tools from population genetics, evolutionary dynamics, and engineering to understand how cancer evolves and respond to treatment. Here, we have presented an overview of the quantitative approaches (Fig 2) that are becoming increasingly used in cancer research. Coupled with the enabling technology of high-throughput next-generation sequencing, several themes are starting to emerge that address the critical questions of: 1) how can we predict evolutionary trajectories of tumor progression? and 2) how do we tackle drug resistance? (see Outstanding Questions for more detailed questions).

Figure 2. Outlook of using enabling technologies and quantitative approaches to study cancer.

Cancer is currently viewed as an evolutionary process. This necessitates the design of empirical studies to specifically address cancer evolution as we have done in population genetics studies – including evolution experiments with high-resolution lineage tracing and mutagenesis/saturation analyses to systemically understand the fitness of specific alterations. Fitness landscapes provide one way to gain insight into how genotype or phenotype are mapped to fitness under different conditions. This information will be invaluable for the effective and rational design of optimal drug scheduling and drug combinations. Critical to these studies are the use of quantitative approaches rooted in population genetics, evolutionary biology, and engineering.

Outstanding questions.

• How rugged is the underlying fitness landscape for cancer?

• Related to the above question, how constrained are the clonal evolutionary trajectories in tumor progression and development of drug resistance? Answers to the question will provide insight into how repeatable/predictable are tumor evolutionary processes.

• How do we best rationally schedule drug regimens to account for tumor evolutionary dynamics and fitness tradeoffs of diverse subclones to maximize long-term survival?

• How can we best exploit vulnerabilities during tumor progression and known likely trajectories for forward prediction and drug regimen design?

• Can we capitalize on repurposing of existing chemotherapeutics and targeted therapies into our drug combinations design?

First, the advent of NGS will enable a much greater resolution of lineage tracking and at finer time scales in studying tumor clonal evolution. Although population genetic studies have benefited from evolution experiments and sequencing of lower organisms in yeast and bacteria, the utility of NGS specifically to study tumor evolutionary dynamics in vitro and in vivo at the desired level of resolution in regards to lineage complexity and time has been lacking. NGS efforts on studying patient biopsies have thus far provided greater understanding of the tumor clonal complexity and architecture. However, experiments need to be designed that capitalize on the availability of high complexity barcoding libraries and finer time resolution to specifically address questions on tumor evolutionary dynamics. These include the dynamics and distribution of beneficial, passenger, and deleterious mutations that arise (and go on to fixation or extinction) and their associated fitness effects. Mathematical modeling from population genetics is critical in parameterizing experimentally observed dynamics and in estimating parameters such as mutation rate, selection coefficients, time to fixation, and regimes of dominance between genetic drift vs selection. Additionally, an understanding of the clonal trajectories will also enable us to visualize (based on parameterized fitness landscape models and/or conceptually) the underlying fitness landscape (static or dynamic) as the tumor evolves over time. This will directly address our questions in regards to how rugged such landscapes are and how constrained are tumor evolutionary trajectories. As we have discussed in this review, knowledge of the fitness terrain would have direct implications on our understanding of repeatability and predictability of the tumor clonal evolutionary process. This is particularly important in regimes where stochastic process play a role and thus knowledge of the drivers and clonal distribution would be inefficient for perfect predictability and utility of mathematical models can inform probabilistically the different trajectories and outcomes.

Viewing and understanding cancer through the evolutionary perspective also provides fresh opportunities for rational therapeutic intervention. As a particular fitness landscape can consist of peaks and valleys (and can be viewed as source and sinks in a vector field), this begs the question of whether we can control (or drive) the tumor toward particular desirable states. As we have discussed that some experimental models have started to address these questions, classical engineering approaches in control theory are one such approach to address the controllability of a given system. Alternatively, aside from control, our insight into the natural trajectories of tumor clonal evolution may reveal distinct stages along this path – beyond our current focus on terminal states – that are vulnerable for therapeutic intervention. These perturbations will no doubt have effects on the subsequent trajectories of tumor evolution. As such, exploring these trajectories using stochastic/deterministic mathematical models will be critical to explore these outcome scenarios. Furthermore, the search space for the choice and scheduling of drug to be utilized for these interventions are vast (including perhaps repurposing of drugs against non-classical targets), and optimization methodologies will facilitate the discovery of optimal solution (or solution sets) given a particular outcome scenario we desire. Taken together, we believe these new waves of enabling technologies and methodologies will be an important part of our toolset to advance our understanding in cancer research.

Trends.

• Cancer is largely viewed as a clonal evolution process, and this view has implications on our understanding of tumor progression and occurrence of relapse.

• Mathematical models from population genetics, evolutionary dynamics, and engineering are increasingly used to study tumor dynamics during progression and in response to treatment.

• Enabling technologies including next-generation sequencing are providing opportunities for high-resolution lineage tracing in clonal evolution experiments.

• Mathematical models, combinatorial optimization, and engineering approaches are increasingly used to complement experiments for rational design of drug combinations and drug scheduling.

Box 4. Fitness landscapes (random fields model).

Random field models^59,64 are utilized to generate theoretical fitness landscapes with different size of loci and epistatic interactions, to study how these terms affect the topology and accessibility of paths of fitness landscapes. Comparison of these fitness landscapes to empirical data can thus provide inference to the likely fitness landscapes under investigation. The random fields models include the Kauffman’s NK model¹²⁵, which for a system with N total number of loci and K number of interactions between loci, the fitness for particular genotype x is defined as,

$$f(\mathit{x})=\sum _{i=1}^N{f}_i(x_i,x_1^i,\dots ,x_K^i)$$

where f_i is a fitness function (also known as fitness contribution) and defined as an independent and identically distributed random variable. The choice of the K interaction partners can be chosen at random uniformly. By tuning the N and K parameter values, one can achieve fitness landscapes with different ruggedness. When K = K − 1, the genotypes become uncorrelated and is known as the House of Cards (HoC) model¹²⁶. When K= 0, the landscape is additive and non-epistatic and is known as Mount Fuji model. The Rough Mount Fuji (RMF) model¹²⁷ is an additive landscape with added noise. Sequence-structure models¹²⁸ describe explicit mapping of sequence or structure (e.g. RNA, DNA, protein) to predicted fitness metrics (e.g. stability, affinity, etc). Lastly, phenotype-fitness models include heuristic phenotype-based landscapes loosely based on Fisher’s geometric model⁶⁰.

Glossary

Selection

a process that drives changes in allele frequency based on their relative fitness in the population.

Mutation

a process that generates new genetic variations in a population.

Genetic drift

a process that describes the random sampling of an allele in a population, as a result of random birth and death events.

Deterministic process

a deterministic process will always yield the same result given the same initial condition.

Stochastic process

as opposed to a deterministic process, a stochastic process captures intrinsic randomness of event occurrence and will yield different results given the same initial condition.

Fitness landscape

a way to visualize the mapping of genotype/phenotype to fitness.

Ruggedness

a measure of the complexity of fitness landscapes. A highly rugged landscape corresponds to many peaks and valleys, and affects the trajectory and predictability of the evolving population.

Epistasis

genetic interaction where the effect of one genetic alteration depends on the presence of one or more other alterations (genetic background).

Sign epistasis

a classification of epistasis where the genetic interaction affects the sign of the effect, i.e. the genetic alteration can be either beneficial or deleterious depending on the genetic background.

Stochastic tunneling

a phenomenon of fitness valley crossing, whereby two alterations arise without the appearance of an intermediate state (at the connecting peak between the two valleys).

Exponential growth

a growth model where the growth rate of the cells is proportional to population size.

Gompertz growth

a growth model where the growth rate slows (and eventually plateau) at larger population size. Gompertz growth are used for modeling tumors growing in confined space with limited nutrients, where ultimate depletion of nutrients will eventually slow tumor growth.

Control theory

studies the behavior of dynamical systems (e.g. electronics, mechanics, tumor population) in response to varying inputs, with the goal of developing ways to control the system and desired output responses.

Mathematical optimization

methods in selecting a set of input values (e.g. set of drugs) to maximize/minimize an objective (e.g. tumor killing) while satisfying defined constraints (e.g. non-overlapping toxicity). Additional constraints on the input value types (e.g. as real numbers or integers) and objective function (e.g. as linear or nonlinear) further subdivide methods into linear, integer, quadratic programming (amongst many others).

Multiobjective optimization

methods of finding solutions that maximize/minimize multiple objectives while satisfying defined constraints. In multi-objective optimization, because of multiple competing objectives, the solution is a solution set (or Pareto optimal set) instead of a single optimal solution