Enzyme Efficiency but Not Thermostability Drives Cefotaxime Resistance Evolution in TEM-1 β-Lactamase

Abstract

A leading intellectual challenge in evolutionary genetics is to identify the specific phenotypes that drive adaptation. Enzymes offer a particularly promising opportunity to pursue this question, because many enzymes’ contributions to organismal fitness depend on a comparatively small number of experimentally accessible properties. Moreover, on first principles the demands of enzyme thermostability stand in opposition to the demands of catalytic activity. This observation, coupled with the fact that enzymes are only marginally thermostable, motivates the widely held hypothesis that mutations conferring functional improvement require compensatory mutations to restore thermostability. Here, we explicitly test this hypothesis for the first time, using four missense mutations in TEM-1 β-lactamase that jointly increase cefotaxime Minimum Inhibitory Concentration (MIC) ∼1500-fold. First, we report enzymatic efficiency (k_cat/K_M) and thermostability (T_m, and thence ΔG of folding) for all combinations of these mutations. Next, we fit a quantitative model that predicts MIC as a function of k_cat/K_M and ΔG. While k_cat/K_M explains ∼54% of the variance in cefotaxime MIC (∼92% after log transformation), ΔG does not improve explanatory power of the model. We also find that cefotaxime MIC rises more slowly in k_cat/K_M than predicted. Several explanations for these discrepancies are suggested. Finally, we demonstrate substantial sign epistasis in MIC and k_cat/K_M, and antagonistic pleiotropy between phenotypes, in spite of near numerical additivity in the system. Thus constraints on selectively accessible trajectories, as well as limitations in our ability to explain such constraints in terms of underlying mechanisms are observed in a comparatively “well-behaved” system.

Introduction

To first approximation, proteins evolve by the sequential substitution of individual missense mutations (Maynard Smith 1970), motivating interest in the underlying biochemical and biophysical determinants of such events (Dean and Thornton 2007; Harms and Thornton 2013). For example the mechanistic basis of adaptation has been explored in enzymes [Lunzer et al. (2005) in isopropyl malate dehydrogenase; Couñago et al. (2006, 2008), Tomatis et al. (2008), and Peña et al. (2010) in adenylate kinase; Walkiewicz et al. (2012) in a tetracycline-degrading enzyme; Meini et al. (2015) in metallo-β-lactamase; Bershtein et al. (2015) and Rodrigues et al. (2016) in dihydrofolate reductase], cellular receptors [Bridgham et al. (2009) in corticoid receptors; Rosenblum et al. (2010) in Mc1r; Baldwin et al. (2014) in sweet taste receptors], hemoglobin (Tufts et al. 2015), two-component signaling pathways (Capra et al. 2012), and fluorescent proteins (Field and Matz 2010).

Enzymes in particular are faced with an intrinsic tension between thermostability and catalytic activity. As reviewed by Beadle and Shoichet (2002), thermostability requires a tightly packed core of hydrophobic residues surrounded by a shell of exposed hydrophilic residues, together with interior hydrogen bonding and pairing of opposite charges. On the other hand, catalytic activity depends on exposed hydrophobic residues, sequestration of charge groups from solvent water, clustering of like charges, and unfilled hydrogen bond partners. Consistent with this view, it is now well established that the removal of catalytic residues usually stabilizes an enzyme (Zhi et al. 1991; Meiering et al. 1992; Shoichet et al. 1995), while mutations endowing an enzyme with novel function are generally destabilizing (Tokuriki et al. 2008). Mutations such as these, which simultaneously affect two or more phenotypes (e.g., activity and thermostability) are said to act pleiotropically. Moreover, most enzymes are only marginally thermostable (DePristo et al. 2005; Zeldovich et al. 2007; Tokuriki and Tawfik 2009). Together, these observations motivate the widespread hypothesis that enzyme adaptation should require both functionally beneficial but thermodynamically destabilizing mutations, and compensatory stabilizing mutations (Orencia et al. 2001; Wang et al. 2002; DePristo et al. 2005; Tokuriki and Tawfik 2009).

Here, we explicitly test this hypothesis for the first time, using cefotaxime resistance evolution in TEM-1 β-lactamase. β-lactamases are enzymes that hydrolyze otherwise toxic β-lactam antibiotics such as penicillin and its cognates (Walsh 2003). β-lactamases in E. coli and other gram-negative bacteria have long served as a model system for the quantitative, mechanistic dissection of mutational effects on fitness (Zimmermann and Rosselet 1977; Nikaido and Normark 1987; Raquet et al. 1994; Blazquez et al. 1995; Raquet et al. 1995; Wang et al. 2002; Bloom et al. 2005; Bershtein et al. 2006; Singh and Dominy 2012; Jacquier et al. 2013; Firnberg et al. 2014; Dellus-Gur et al. 2015; Stiffler et al. 2015). The utility of β-lactamases in this work follows from their comparatively simple biological function (Frère et al. 1999). β-lactam antibiotics diffuse from the environment into the cell’s periplasm, where they bind to and inactivate penicillin-binding proteins (PBPs), enzymes critical for bacterial cell wall maintenance. β-lactamase enzymes in turn are solely responsible for the hydrolysis of β-lactams, thereby allowing cells to survive in an otherwise lethal environment.

Specifically, by assuming that periplasmic β-lactam concentration is at equilibrium between diffusion and hydrolysis, Nikaido and Normark (1987) modeled the minimum inhibitory concentration (MIC) of antibiotic that blocks cell growth as

$$\mathrm{M}\mathrm{I}\mathrm{C}={\left[S\right]}_{\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{l}}+\frac{{\left[S\right]}_{\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{l}}·k_{\mathrm{c}\mathrm{a}\mathrm{t}}·{\left[E\right]}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}}{P·A·\left(K_{\mathrm{M}}+{\left[S\right]}_{\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{l}}\right)},$$

where [S]_lethal is the periplasmic β-lactam concentration that lethally inhibits the cell’s PBPs in the absence of any β-lactamase, k_cat and K_M are the β-lactamase’s turnover rate and Michaelis constant, respectively, [E]_active is the periplasmic concentration of catalytically active enzyme, and P and A are the cell’s periplasmic permeability coefficient and surface area, respectively. Next, if [S]_lethal≪MIC (i.e., that the enzyme confers substantial protection from the β-lactam)

$$\mathrm{M}\mathrm{I}\mathrm{C}\mathrm{}\approx Z\cdot \frac{k_{\mathrm{c}\mathrm{a}\mathrm{t}}\cdot {\left[E\right]}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}}{K_{\mathrm{M}}+{\left[S\right]}_{\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{l}}},$$ (1a)

where Z = $\frac{{\left[S\right]}_{lethal}}{P·A}$ is independent of β-lactamase allele. Further assuming K_M ≫ [S]_lethal (i.e., that the β-lactamase is not saturated by substrate), we find

$$\mathrm{M}\mathrm{I}\mathrm{C}\mathrm{}\approx Z\cdot \frac{k_{\mathrm{c}\mathrm{a}\mathrm{t}}\cdot {\left[E\right]}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}}{K_{\mathrm{M}}}.$$ (1b)

Additionally, the principled consideration of two-state folding of the β-lactamase (Bloom et al. 2004; Tokuriki and Tawfik 2009; Wylie and Shakhnovich 2011; Jacquier et al. 2013) suggests

$${\left[\mathrm{E}\right]}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}\mathrm{}=\frac{{\left[E\right]}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{1+{\mathrm{e}}^{\raisebox{1ex}{$\mathrm{\Delta }G$}\!\left/ \!\raisebox{-1ex}{$R·T$}\right.}},$$ (2)

where [E]_total is the total cellular enzyme concentration, ΔG is the Gibbs free energy of native-form folding, R is the gas constant and T is the temperature in degrees Kelvin. Finally, substituting Equation (2) into Equations (1b) yields

$$\mathrm{M}\mathrm{I}\mathrm{C}\mathrm{}\approx Z\mathrm{\text{'}}\cdot \frac{k_{\mathrm{c}\mathrm{a}\mathrm{t}}}{K_{\mathrm{M}}}·\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$\mathrm{\Delta }G$}\!\left/ \!\raisebox{-1ex}{$R·T$}\right.}},$$ (3)

where Z’ = [E]_total⋅Z is again independent of β-lactamase allele.

In order to quantitatively test the mechanistic underpinnings of MIC suggested by Equation (3), we here report k_cat/K_M and ΔG values for all 16 combinations of four missense mutations previously shown to increase the MIC of TEM-1 by more than three log-orders against the β-lactam cefotaxime (Hall 2002; Weinreich et al. 2006; Knies et al. in prep.). A second, more abstract motivation for this work stems from our earlier finding that while the phenotypic landscape of TEM-1 for cefotaxime MIC is single-peaked, most mutational trajectories to the highest resistance allele are selectively inaccessible (Weinreich et al. 2006). This is necessarily the consequence of the fact that at least some of these mutations are only conditionally beneficial (called sign epistasis, Weinreich et al. 2005). The hypothesis that catalytically beneficial mutations commonly require compensatory, stabilizing mutations immediately suggests a mechanism for widespread sign epistasis (Camps et al. 2007; Weinreich 2010; Weinreich and Knies 2013), and so we were keen to test its relevance in this system.

Results

In order to understand the mechanistic basis of increased cefotaxime resistance achieved during the evolution of TEM-1 β-lactamase (Stemmer 1994; Hall 2002), and more abstractly the source and generality of sign epistasis previously described in this system (Weinreich et al. 2006), we have now characterized the catalytic activity and thermostability of all 4²=16 combinations of the four missense mutations involved. [The fifth mutation examined in Weinreich et al. (2006) lies 52 nucleotides upstream of the start codon and thus is unlikely to affect activity or thermostability.] Table 1 presents in vitro catalytic efficiencies for all 16 enzyme variants (k_cat/K_M, and where possible, independent measures of k_cat and K_M, all at 25 °C) against cefotaxime. Table 1 also presents melting temperature, van’t Hoff enthalpy (T_m and ΔH, respectively) and thence thermodynamic stabilities (ΔG computed at 25 °C; see “Methods”), for each enzyme variant. MIC values (also measured at 25° C) for the 16 g4205 alleles (see “Methods”) from Knies et al. (in prep) are presented in table 2. Minimum and maximum values for all seven phenotypes are highlighted in underlined in tables 1 and 2.

Table 1.

Biochemical and Biophysical Phenotypes for TEM-1 β-Lactamase Alleles (Minimum and Maximum Values Shown in Underlined).

Mutationa,b				Kinetics against Cefotaxime				Biophysical phenotypesg
A42G	E104K	M182T	G238S	kcat/KMc (M−1 s−1 @ 25 °C)	Nonlinear estimatesd			Tm (° C)	ΔH (kcal/mol° C)	ΔG (kcal/mol @ 25° C)
					ne	kcat (s−1)	KM (M−1)
–	–	–	–	(1.5 ± 0.170) × 102	1	1.7 × 10−1 ± n.d.f	7.5 × 10−4 ± n.d.f	56.42 ± 0.20	–78. ± 5.1	–7.5 ± 0.483
–	–	–	+	(2.2 ± 0.221) × 104	9	(1.43 ± 0.00498) ×101	(7. ± 1.51) ×10−4	53.0 ± 0.26	–62. ± 5.2	–5.3 ± 0.42
–	–	+	–	(1.2 ± 0.270) × 102	0	n.d.f	n.d.f	62.4 ± 0.08	(–1.0 ± 0.011) × 102	–11. ± 0.11
–	–	+	+	(3.6 ± 0.517)× 104	7	(1.7 ± 0.357) × 101	(4. ± 0.988) × 10−4	59.7 ± 0.08	(–7. ± 1.0) × 102	–7. ± 1.1
–	+	–	–	(6. ± 1.05) × 102	3	3.9 ± 0.18	(5. ± 2.9) × 10−3	56.3 ± 0.24	–75. ± 6.6	–7.1 ± 0.62
–	+	–	+	(2.0 ± 0.133) ×104	9	9.21 ± 7.43 × 10−3	(4.6 ± 0.376) × 10−4	53.1 ± 0.33	–51. ± 3.7	–4.4 ± 0.29
–	+	+	–	(5.4 ± 0.420) × 102	7	2.04 ± 5.08 × 10−2	(3.5 ± 0.882) × 10−3	61.7 ± 0.54	(–8. ± 1.7) × 101	–9. ± 2.0
–	+	+	+	(5.5 ± 0.146) × 105	10	(8.19 ± 0.00149) × 101	(1.51 ± 0.0508) × 10−4	59.2 ± 0.16	–89. ± 7.9	–9.3 ± 0.81
+	–	–	–	(2.0 ± 0.498) × 102	1	2.5 × 10−1 ± n.d.f	1.1 × 10−3 ± n.d.f	57.2 ± 0.11	(–1.1 ± 0.68) × 102	–11. ± 0.68
+	–	–	+	(2.3 ± 0.204) ×105	10	(2.13 ± 0.00125) × 101	(1.1 ± 0.213) × 10−4	55.0 ± 0.40	–51. ± 2.2	–4.7 ± 0.24
+	–	+	–	(4.5 ± 0.301) × 102	4	1.2 ± 2.6 × 10−2	(2.5 ± 0.57) × 10−3	64.3 ± 0.38	(–1.7 ± 0.34) × 102	–21. ± 4.1
+	–	+	+	(2.9 ± 0.231) × 104	8	9.42 ± 7.25 × 10−3	(3.1 ± 0.296) × 10−4	61.4 ± 0.14	(–1.1 ± 0.89) × 102	–12. ± 0.92
+	+	–	–	(2.2 ± 0.313) × 103	10	7.6 ± 1.86 × 10−1	(3.1 ± 0.581) × 10−3	57.6 ± 0.22	–80. ± 5.3	–7.8 ± 0.48
+	+	–	+	(2.2 ± 0.222) × 105	7	(2.61 ± 0.00429) × 101	(1.1 ± 0.241) × 10−4	53.8 ± 0.09	–61. ± 3.1	–5.3 ± 0.27
+	+	+	–	(1.23 ± 0.0596) × 103	3	6.5 ± 1.2 × 10−1	(5. ± 1.9) × 10−3	63.2 ± 0.27	(–1.0 ± 0.87) × 102	–11.8 ± 0.92
+	+	+	+	(2.9 ± 0.565) × 105	9	(2.08 ± 0.000877) × 101	(8. ± 1.16) × 10−5	60.7 ± 0.24	–89. ± 6.1	–9.5 ± 0.71

^aNumbering as in Ambler et al. (1991). One-letter amino acid abbreviations used here: A = alanine; G = glycine; E = glutamic acid; K = lysine; M = methionine; T = threonine and S = serine.

^bClinical designations shown in table 2.

^cMean ± s.e.m. across n = 10 replicates. For each replicate, the best fitting model (linear or nonlinear) was chosen by AIC_c score, and for each allele mean and standard error of k_cat/K_M across best-model-fit estimates are reported.

^dMean ± s.e.m. across those replicates in which non-linear model had better AIC_c score.

^eNumber of replicates in which non-linear model had better AIC_c score.

^fToo few replicates to allow estimation of this quantity.

^gMean ± s.e.m. across n = 9 replicates for TEM-1 and n = 3 for all other alleles.

Table 2.

Minimum Inhibitory Concentration (MIC) for TEM-1 β-Lactamase Alleles^a Against Cefotaxime (Minimum and Maximum Values Shown in Underlined).

Mutationb
A42G	E104K	M182T	G238S	Clinical Designationc	MICd (µg/mL)
–	–	–	–	TEM-1	5.7
–	–	–	+	TEM-19	2.6 × 102
–	–	+	–	TEM-135	8.0
–	–	+	+	TEM-20	2.6 × 102
–	+	–	–	TEM-17	11.
–	+	–	+	TEM-15	2.0 × 103
–	+	+	–	TEM-106	11.
–	+	+	+	TEM-52	4.1 × 103
+	–	–	–	None	5.7
+	–	–	+	None	7.2 × 102
+	–	+	–	None	4.0
+	–	+	+	None	7.2 × 102
+	+	–	–	None	32.
+	+	–	+	None	2.9 × 102
+	+	+	–	None	23.
+	+	+	+	None	8.2 × 103

^aData from Knies et al. (in prep).

^bNumbering as in Ambler et al. (1991). One-letter amino acid abbreviations used here: A = alanine; G = glycine; E = glutamic acid; K = lysine; M = methionine; T = threonine and S = serine.

^cFrom Jacoby and Bush (2005).

^dThree replicate measures gave identical results.

Statistical Significance of Mutational Effects on Phenotype

The 16 TEM-1 enzyme variants examined define 4⋅16/2 = 32 pairs of mutationally adjacent alleles and $\left(\begin{array}{c}16\\ 2\end{array}\right)$ = 120 pairs without regard to mutational adjacency. No variance estimates for our independent k_cat and K_M measurements were possible for the – – – –, – – + – or + – – – variants (table 1; + and – represent the presence or absence of each mutation in N-to-C order). This leaves only 22 mutationally adjacent and 78 total pairwise comparisons for which significant differences in those phenotypes can be assessed. The numbers of these pairwise differences that are statistically significant after Bonferroni correction (Holm 1979) for each phenotype examined are presented in table 3.

Table 3.

Fraction of Statistically Significant Mutational Effects on Phenotype^a.

Phenotype	Mutationally Adjacent			All Comparisons
	P < 0.05	P < 0.01	P < 0.001	P < 0.05	P < 0.01	P < 0.001
kcat/KMb	23/32	19/32	15/32	104/120	83/120	71/120
kcatc	20/22	20/22	20/22	70/78	67/78	67/78
KMc	6/22	6/22	3/22	13/78	8/78	3/78
Tmb	16/32	10/32	8/32	80/120	62/120	50/120
ΔGb	5/32	5/32	0/32	26/120	14/120	3/120

^aAfter sequential Bonferroni correction (Holm 1979).

^bFour mutations define 4 × 2⁴/2 = 32 mutationally adjacent pairs of TEM-1 variants and $\left(\begin{array}{c}{2}^4\\ 2\end{array}\right)$ = 120 pairs of variants without regard to mutational adjacency.

^cNo independent variance estimates were possible for three TEM-1 variants (table 1), reducing the number of mutationally adjacent comparisons to 22 and to 78 without regard to mutational adjacency.

All differences in cefotaxime MIC assessed at 25 °C between mutationally adjacent β-lactamase alleles are statistically significant at P < 0.05 after sequential Bonferroni correction (Knies et al., in prep.).

Modeling MIC as a Function of Biophysics and Biochemistry

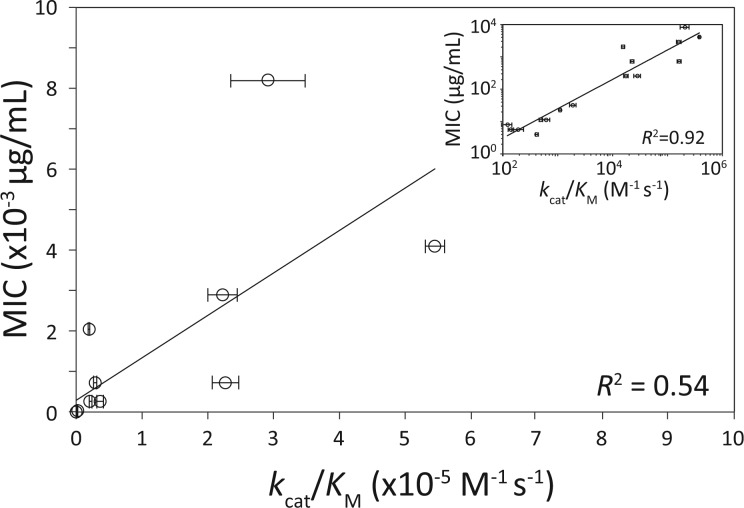
We first regressed observed MIC values at 25 °C (table 2) against those predicted by Equation 3 using data from table 1. This linear regression exhibited an R² of 0.54. However the regression of MIC against k_cat/K_M alone has exactly the same explanatory power (fig. 1). This can be understood by observing first that ΔG has a sharply sigmoidal influence on [E]_active in Equation (2). For example, at 25 °C, ∼99% of all molecules with a thermostability of −2.7 kcal/mol are predicted to be in their native, folded form. And empirically, ΔG for all 16 TEM-1 variants (table 1) are significantly more negative than −2.7 kcal/mol by a one-tailed t-test (P < 0.05 after Bonferroni correction). In other words, at physiological temperatures, our in vitro thermodynamic stability measures imply that all TEM-1 variants are essentially 100% folded.

Fig. 1.

Correlation between MIC and k_cat/K_M. Error bars in k_cat/K_M represent standard error across n = 10 replicates. No variance was observed across n = 3 MIC assays. MIC results are from g4205 alleles (see “Methods”; qualitatively similar results observed for MIC data from 4205a alleles). Best-fit linear regression MIC = .0105 × (k_cat/K_M) + 288.42. Inset: same data on log-log plot. Best-fit power-law regression: MIC = 0.0553 × (k_cat/K_M)^0.8713.

Note that β-lactamase kinetic results (table 1) were normalized by µg of total soluble protein (see “Methods”). However, this finding—that all 16 TEM-1 variants are essentially fully folded at 25 °C—implies that these data can also be regarded as having been normalized by µg of active protein, as assumed by Equation (1).

Additivity and Interaction in Mutational Effects

Traditionally, genetics has examined individual mutational effects on phenotype together with epistatic interactions between pairs of mutations. However in principle any subset of k mutations can exhibit epistasis (Weinreich et al. 2013). The Walsh transformation (see “Methods”) decomposes a data set containing phenotypes for all 2^L combinations of L mutations into the orthogonal contributions to phenotype due to each subset of mutations of size 1 to L. These contributions are called Walsh coefficients, and the order 1 ≤ k ≤ L of each Walsh coefficient is the size of the corresponding subset of mutations. Thus first-order coefficients (k = 1) capture the average effect of each mutation in isolation and are analogous to selection coefficients, second-order coefficients (k = 2) capture the average interaction between each pair of mutations and are analogous to traditional pairwise effects, and so on (Weinreich et al. 2013).

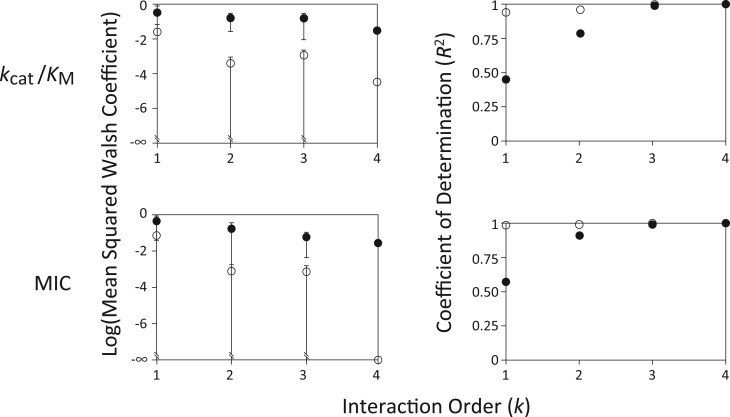
Because thermostability does not influence MIC, we only report the mean squared Walsh coefficient as a function of interaction order k for k_cat/K_M and MIC (fig. 2, left). We note first that for the raw k_cat/K_M and MIC data, mean interaction terms (those of order k > 1) are comparable to mean effects of individual mutations (order k = 1). In other words, substantial epistasis is observed in these data. Interestingly after log-transformation, mean interactions terms are ∼100× smaller than mean individual mutational effects in these two datasets (fig. 2, left: compare open and filled symbols). This finding implies near additivity in mutational effect on log-transformed data, a point to which we return in the “Discussion” section. Mean epistatic terms for T_m are ∼100× smaller than mean effects of individual mutations both before and after log-transformation (data not shown). In other words, we observe almost no epistasis in T_m.

Fig. 2.

Epistasis in k_cat/K_M and MIC. Given the phenotype for each of the 2^L combinations of L mutations, epistatic interactions associated with all subsets of 0 ≤ k ≤ L mutations can be computed as Walsh coefficients (see “Methods”). Interactions among subsets of k mutations are described as k^th-order. (Left) Mean squared Walsh coefficients (± standard deviation across $\left(\begin{array}{c}L\\ k\end{array}\right)$ values; those that extend to the x-axis overlap 0) as a function of order. For each phenotype, Walsh coefficients were normalized to the mean value across all alleles to allow comparisons across phenotypes. First and second order terms are analogous to classical selection coefficients and classical pairwise epistatic terms, respectively (see “Methods”). Filled symbols: raw phenotypic data; open symbols: log-transformed data. (Right) The coefficient of determination (R²) between observed phenotypes and those predicted by successive models incorporating only the lowest order k = 1, 2, … L terms. Filled symbols: raw phenotypic data; open symbols: log-transformed data.

Figure 2, right presents another way of visualizing epistatic contributions to these phenotypes. Here, we report the coefficient of determination (R²) between observed phenotypes and those predicted by successive models incorporating only the lowest k = 1, 2, … L interaction terms. Consistent with results presented in figure 2, left, we observe that the additive model (k = 1, accounting only for the effects of mutations in isolation) does a poor job of explaining raw values of k_cat/K_M or MIC (R²<0.60). On the other hand, the additive model already does a very good job (R²>0.94) of predicting observed phenotypes for log-transformed values of k_cat/K_M and MIC. In both cases, R² increases as additional interaction terms are added to the model, and is numerically equal to 1 when all terms are included (as it must; Weinreich et al. 2013).

Sign Epistasis and Selective Constraints on k_cat/K_M and MIC

Sign epistasis is necessary (though not sufficient) for multiple maxima on any landscape, and always constrains natural selection by reducing the number of selectively accessible trajectories to high-fitness alleles [Weinreich et al. 2005; though see Palmer et al. (2015) for a more nuanced perspective]. Cases of sign epistasis for k_cat/K_M and MIC are enumerated in table 4. The density of sign epistasis (Methods) for k_cat/K_M is 11/32 = 34%; this figure drops slightly to 7/32 = 22% for MIC. Moreover, our k_cat/K_M data (table 1) define a catalytic landscape with two peaks (– + + + and + – – +). Only three of the eight mutational trajectories from TEM-1 to the first of these are selectively accessible (i.e., exhibit a monotonic increase in k_cat/K_M), although both trajectories to the second are. The MIC data exhibit a single maximum at (+ + + +), but only nine of the 24 mutational trajectories from TEM-1 are selectively accessible. These results are strongly reminiscent of earlier work in this system (Weinreich et al. 2006).

Table 4.

Sign of Mutational Effect on k_cat/K_M and MIC against Cefotaxime, and Antagonistic Pleiotropy between These Two Phenotypes.

TEM-1 Genetic Background				Mutational Effect on kcat/KM				Mutational Effect on MICa				Antagonistic Pleiotropyb
A42G	E104K	M182T	G238S	A42G	E104K	M182T	G238S	A42G	E104K	M182T	G238S	A42G	E104K	M182T	G238S
–	–	–	–	↑c	↑	↓c	↑	0	↑	↑	↑	No	No	Yes	No
–	–	–	+	↑	↓c	↑c		↑	↑	0		No	Yes	No
–	–	+	–	↑	↑		↑	↓	↑		↑	Yes	No		No
–	–	+	+	↓c	↑			↑	↑			Yes	No
–	+	–	–	↑		↓c	↑	↑		↓	↑	No		No	No
–	+	–	+	↑		↑		↑		↑		No		No
–	+	+	–	↑			↑	↑			↑	No			No
–	+	+	+	↓				↑				Yes
+	–	–	–		↑	↑	↑		↑	↓	↑		No	Yes	No
+	–	–	+		↓c	↓			↑	↓			Yes	No
+	–	+	–		↑		↑		↑		↑		No		No
+	–	+	+		↑				↑				No
+	+	–	–			↓c	↑			↓	↑			No	No
+	+	–	+			↑c				↑				Yes
+	+	+	–				↑				↑				No
+	+	+	+
Sumsd				5	6	2	8	6	8	3	8	3	2	3	0

^aAll differences in MIC are statistically different at P < 0.05 after sequential Bonferroni correction (Knies et al, in prep.).

^bCases in which the sign of mutational effect is significantly (P < 0.05 after Bonferroni correction) positive on only one of k_cat/K_M and MIC.

^cNo significant effect at P < 0.05 after sequential Bonferroni correction.

^dFor mutational effects, the number of cases in which mean mutational effect is significantly beneficial (P < 0.05 after Bonferroni correction). For antagonistic pleiotropy, the number of cases in which sign of mutational effect is significantly positive (P < 0.05 after Bonferroni correction) on only one of k_cat/K_M and MIC.

Antagonistic Pleiotropy is Necessarily Responsible for Gross Discrepancies between MIC and k_cat/K_M Landscapes

The first objective of this study was to quantitatively dissect mutational effects on MIC in terms of their underlying mechanistic components. However, a second motivation was to identify the mechanistic underpinnings of the selective constraint on cefotaxime resistance evolution induced by sign epistasis (Weinreich et al. 2006). We thus wondered, to what extent does sign epistasis in k_cat/K_M explain sign epistasis in MIC? [Trivially there are discrepancies, as we have just seen that the maxima for these phenotypes occur for different alleles (Weinreich et al. 2005).]

The answer necessarily lies in the incidence of antagonistic pleiotropy (AP) between phenotypes. Given our interest in adaptation, we follow Remold (2012) and restrict our definition of AP to those cases in which mutations significantly improve only one of the two phenotypes. Such cases represent particularly noteworthy failures of the approach captured by Equation (3), and are also enumerated in table 4. Mutations significantly affect k_cat/K_M and MIC in opposite directions in 8/32 = 25% of the mutationally adjacent comparisons, and these cases of AP are distributed over three of the four mutations examined.

Discussion

Natural selection acts simultaneously on variation in diverse phenotypes that together determine an organism’s fitness. Thus dissecting mutational effects on these components of fitness is a central question in evolutionary genetics. In general this suite of phenotypes will span tremendous biological complexity, ranging from development and morphology to biochemistry and physiology to ecology. Proteins offer a much simplified model system in which to decompose fitness into its constituent components, because the relevant underlying phenotypes are often easily identified and assessed (Dean and Thornton 2007; Harms and Thornton 2013). As outlined above, enzymes in particular need to be both catalytically active and thermostable, and individual mutations commonly act pleiotropically (i.e., simultaneously) on both phenotypes. These facts motivate the widespread hypothesis that enzyme adaptation requires a succession of mutations that improve activity at the expense of thermostability, compensated for by mutations that restore thermostability (Wang et al. 2002; DePristo et al. 2005; Tokuriki and Tawfik 2009). Here we explicitly tested this hypothesis in TEM-1 β-lactamase. In addition to our interest in understanding the mechanistic determinants of antibiotic resistance evolution, we hoped to test a second hypothesis. Namely, we wondered whether the need for compensatory stabilizing mutations might provide a generically important mechanistic explanation for sign epistasis in enzymes (Camps et al. 2007; Weinreich 2010; Weinreich and Knies 2013).

Enzymatic Efficiency but Not Thermostability Drives Cefotaxime Resistance Evolution in TEM-1 β-Lactamase

Perhaps our most surprising result is thus our first: that cefotaxime resistance evolution in TEM-1 is entirely unaffected by differences in melting temperature (T_m) and thus thermodynamic stability (ΔG) among enzyme variants (fig. 1). On the contrary, melting temperature estimates for all 16 TEM-1 variants examined (table 1) are significantly (P < 0.05 after Bonferroni correction) above 52 °C, i.e., greater than 15 °C above physiological temperatures. Seen another way, all enzyme variants examined here appear to be fully stable [Equation (2)], a finding corroborated computationally with FoldX (Van Durme et al. 2011) and PoPMuSic (Dehouck et al. 2011) (data not shown). We acknowledge that our empirical in vitro estimates for both ΔG and T_m imply modestly (<10%) more thermostability than those made by others for subsets of these alleles (Wang et al. 2002; Kather et al. 2008; Dellus-Gur et al. 2013). However, these small differences are unable to reconcile the discrepancy between theory and data. Indeed, we observe no positive rank correlation between MIC and either ΔG or T_m values (Spearman rank correlation coefficient ρ = 0.18, P = 0.25 and ρ = −0.30, P = 0.90 by one-tailed tests, respectively). This limits the possibility of a systematic bias between our in vitro stability assays and in vivo conditions.

This result is particularly noteworthy inasmuch as work in TEM-1 largely motivated the hypothesis that functionally beneficial mutations need to be compensated by stabilizing mutations (Orencia et al. 2001; see Fig. 6 in Wang et al. 2002). Importantly, our results do not contradict several closely related empirical principles about enzyme evolution, many also derived from work in TEM-1. First, there remains little doubt that deleterious mutations often act by reducing thermostability (Bloom et al. 2005; Bershtein et al. 2008; Jacquier et al. 2013; Firnberg et al. 2014). Relatedly, our findings do not undermine the idea that genetically increasing an enzyme’s thermostability increases its robustness to deleterious mutations (Bloom et al. 2005; Bershtein et al. 2006; Besenmatter et al. 2007). Similarly, our results cast no doubt that thermostabilizing mutations are often beneficial on genetically destabilized alleles (Huang and Palzkill 1997; Sideraki et al. 2001; Hecky and Müller 2005; Kather et al. 2008; Brown et al. 2010), or when environmental temperature increases (Couñago et al. 2006; Couñago et al. 2008). In short, functional enzymes require adequate thermostability.

Rather, while catalytic residues per se substantially reduce any enzyme’s thermostability (Zhi et al. 1991; Meiering et al. 1992; Shoichet et al. 1995), we find that the more modest stability consequences of the adaptive mutations examined here do not have appreciable physiological consequences. Indeed our conclusion that the 16 TEM-1 alleles examined are essentially fully folded echoes observations from several other systems. Recently, Thomas et al. (2010) considered five mutations in AmpC (another β-lactamase) that increase catalytic activity against cefotaxime between 100- and 200-fold. Those mutations were found to reduce stability by up to ∼4.0 kcal/mol. However, as in the case of our TEM-1 results, the AmpC wild type has substantial thermostability (−14.0 kcal/mol; Beadle et al. 1999), implying again that none of these mutations are capable of perturbing the physiological concentration of native-form folded enzyme [Equation (2)]. Similarly in CTX-M (yet another β-lactamase), three catalytically beneficial mutations were found to reduce T_m, but not below 47 °C (Chen et al. 2005; Patel et al. 2015), i.e., not below 10 °C above physiological temperatures. And, working in bacterial DHFR (the target of antifolates, another class of antimicrobial compound), Rodrigues et al. (2016) found that many beneficial alleles were destabilized, but in only one case did T_m drop below 48 °C. Moreover, our finding that TEM-1 thermostability is uncorrelated with MIC recapitulate results in three meta-analyses. Two found almost no correlation (positive or negative) between functional importance and ΔΔG among beneficial mutations (Sánchez et al. 2006; Tokuriki et al. 2008) and a third found no clear pattern between effect on substrate affinity and ΔΔG (Teilum et al. 2011).

Of course some functionally beneficial mutations do have physiologically significant pleiotropic effects on thermostability. For example, the temperature sensitivity of a clorobiocin-resistance mutation in the GyrB subunit of the DNA gyrase enzyme in E. coli is mediated by thermostability (Blance et al. 2000). More recently, Gong et al. (2013) demonstrated that five missense mutations (out of 39) that differentiate H3N2 influenza nucleoproteins separated by 39 years of evolution reduce T_m to below 41.5 °C, with concomitant reductions in activity and viral growth. [In this case, each of these mutations was shown to have been compensated for by stabilizing mutations (Gong et al. 2013).] And increasing an allele’s thermostability often increases the number of beneficial mutations in protein directed evolution experiments (Bershtein et al. 2006; Bloom et al. 2006; Fasan et al. 2007).

However, cefotaxime resistance evolution in TEM-1 appears to be unaffected by pleiotropic effects on enzyme thermostability, and in this respect TEM-1 is far from unique. This finding calls for a critical evaluation of the widespread hypothesis that the thermodynamically destabilizing effects of functionally beneficial mutations are a central aspect of enzyme evolution.

Other Phenotypes that May Underlie Enzyme Evolution

If the mutational effects on enzymatic efficiency and thermostability modeled in Equation (3) are unable to fully explain the evolution of increased cefotaxime resistance in TEM-1, what other phenotypes might be involved? The first possibility is that mutational effects on thermostability are mediated by a mechanism other than that represented by Equation (2). Recently, elegant experimental work in a metallo-β-lactamases has highlighted the role of loop destabilization as the enzyme evolves to more effectively bind and hydrolyze a novel substrate (Tomatis et al. 2008; González et al. 2016b). Conversely, Couñago et al. (2008) have documented the importance of loop stabilization in cofactor binding during the evolution of thermotolerance by adenylate kinase. And, Bershtein et al. (2012) find that destabilizing mutations facilitate increased soluble oligomerization during the course of antifolate resistance evolution in the bacterial enzyme DHFR. More abstractly, several authors have noted that thermostability isn’t necessarily a global property of an enzyme (Chen et al. 2005; Singh and Dominy 2012; Dellus-Gur et al. 2013); thus the mutational influence of ΔG may not be mediated entirely by the effect captured by Equation (2).

Another (non-exclusive) possibility is that mutations mediate their effect on MIC via their influence on enzyme aggregation and degradation rates (DePristo et al. 2005). For example, again using TEM-1 β-lactamase, Sideraki et al. (2001) demonstrate that the L76N mutation causes roughly half the enzyme’s periplasmic fraction to become insoluble while also rendering the remaining fraction anomalously susceptible to proteolysis. However, adding M182T to the L76N mutant increases periplasmic concentration while reducing proteolysis-susceptibility, both to near wild-type levels. Importantly, the deleterious effects of L76N (and their compensation by M182T) are mediated not by native form thermostability, but rather by misfolding, leading to aggregation and proteolysis (Sideraki et al. 2001). Similarly, González et al. (2016a, 2016b) demonstrate that lipidation and the resulting membrane anchoring of the New Delhi metallo-β-lactamase allele increases its thermostability and thus protects this enzyme from degradation.

More broadly, this line of thinking draws attention to the role of kinetic stability, i.e., an enzyme’s propensity for misfolding (Baker and Agard 1994). The connection from misfolding, denaturation and aggregation to proteolysis (Sideraki et al. 2001; DePristo et al. 2005) suggest the possibility that kinetic stability may be an important component of enzyme function in the crowded and complex intracellular milieu in which they operate [see Peña et al. (2010) for a quantitative treatment of this phenomenon in adenylate kinase; Sanchez-Ruiz 2010; Meini et al. 2015]. Critically for our purposes, mutational influence on kinetic and thermodynamic stability need not be correlated (Vanhove et al. 1997; Sanchez-Ruiz 2010). Thus the poor correlation between thermostability and MIC observed here does not necessarily undermine the hypothesis that mutational effects on kinetic stability may be an important component of TEM-1 evolution.

A third (again, non-exclusive) explanation for the poor predictive value of Equation (3) is that substantial differences exist between in vitro thermostability values and the corresponding in vivo values underlying MIC assays. For example, Meini et al. (2015) recently found that thermostability of metallo-β-lactamase in crude periplasmic extracts explains a great deal more of the observed variance in MIC than do in vitro CD measurements of the sort employed here. In that study, thermostability measured in periplasmic extracts were up to 10 °C lower than (and again importantly for our purposes, uncorrelated with) in vitro measurements.

Those authors hypothesize that interactions with other periplasmic components may be responsible for these effects. (See also González et al. 2016a) The same explanation has been offered for a more modest (∼1 kcal/mol) reduction in in vivo thermostability compared with in vitro measurements reported for a bacterial cellular retinoic acid binding protein (Ignatova et al. 2007). And, recently, Sarkar et al. (2013) demonstrated comparable differences in thermostability of chymotrypsin inhibitor 2 when cytosolic extracts were used in favor of a dilute buffer such as that used here. [Though no substantial differences between in vivo and in vitro thermostability assays were observed for the λ repressor protein (Ghaemmaghami and Oas 2001).] Indeed, E. coli cells are ∼30 to 40% macromolecules by weight (Zimmerman and Trach 1991), and a considerable theoretical and experimental literature exists on the entropic and enthalpic consequences of this fact for protein folding [e.g., see recent reviews by Zhou et al. (2008), Elcock (2010), Christiansen et al. (2013), Luby-Phelps (2013), Kuznetsova et al. (2014)].

Overall then, we conclude that several additional experimentally accessible phenotypes might plausibly contribute to mutational effects on cefotaxime MIC in TEM-1, including local stability and kinetic stability. Importantly for our purposes, these phenotypes are often uncorrelated with in vitro ΔG values, meaning that our negative results do not undermine the explanatory potential for these alternative candidates. We also note that differences between in vitro and in vivo conditions may complicate interpretation of assays such as those employed here.

MIC Increases More Slowly than Linearly in k_cat/K_M

A second noteworthy result of ours is that our data are much more closely modeled by a power relationship whose exponent is less than unity (fig. 1 inset). As noted, a linear dependence of MIC on k_cat/K_M is expected from first principles [Equation (1b)], and this expectation has also received empirical support from work with deleterious mutations in TEM-1 β-lactamase (Cantu and Palzkill 1998; Firnberg et al. 2014) as well as in the wild-type kanamycin acetyltransferase enzyme from E. coli against a panel of aminoglycosides (Radika and Northrop 1984). What accounts for the discrepancy between our data and previous theory and experiments?

We note first that the data in figure 1 inset can be divided into two groups of eight alleles, those with serine and glycine residues at residue 238. These correspond to alleles with catalytic activity above and below ∼10⁴ M⁻¹ s⁻¹, and resistance above and below ∼10² µg/mL. (The eight G238 alleles are indistinguishable in the main panel of fig. 1.) G238S has long been recognized to sharply increase cefotaxime MIC [reviewed in Salverda et al. (2010)]. Interestingly, the linear regression of MIC against k_cat/K_M among just the eight G238 alleles has a steeper slope (0.0135 vs. 0.0105) and a much better fit (R²=0.93 vs. 0.54) than seen among all 16 alleles in figure 1.

Taken together these observations imply that MIC saturates for large values of k_cat/K_M. One possible explanation for this saturation lies in the assumption underlying Equation (1b), that substrate is limiting relative to the Michaelis constant. In fact, Equation (1b) overestimates the true Michaelis–Menten reaction rate by a factor 1 + [S]_lethal/K_M [compare with Equations (1a) and (1b)]. For those alleles for which we were able to independently estimate K_M, this quantity is just ∼1.01 for G238 alleles but ∼1.14 for 238S alleles [K_M estimates from table 1; [S]_lethal taken as equal to the MIC of cells lacking β-lactamase (Zimmermann and Rosselet 1977), reported to be 11.3 µg/mL at 25 °C (Knies et al, in prep.) or 2.4 × 10⁻⁵ M]. Adjusting the predicted MIC values by this factor (i.e., using Equation (1a) instead (1b) while holding [E]_active constant) raises the exponent on the power relationship between catalytic velocity and antibiotic resistance across all 16 alleles examined from 0.87 to 0.92 (i.e., closer to 1, the linear expectation).

Another possible explanation for the observed saturation is that some of our best β-lactamase alleles may approach the diffusion limit, as previously observed for TEM-1 in other bacterial species (Hardy and Kirsch 1984; Christensen et al. 1990; Bulychev and Mobashery 1999). Classically (Albery and Knowles 1976), this condition requires k_cat/K_M values on the order of 10⁸–10⁹ M⁻¹ s⁻¹. However, it has also long been appreciated that viscosity resulting from macromolecular crowding within bacterial cells can reduce this threshold by two log-orders (Benner 1989). Moreover, enzymatic velocity is attenuated in a continuous fashion as k_cat/K_M approaches the relevant physical diffusion-limitation rate (Brouwer and Kirsch 1982; Hardy and Kirsch 1984; Bulychev and Mobashery 1999). As the mean k_cat/K_M among 238S alleles is 2.78 × 10⁵ M⁻¹ s⁻¹ (though only 1.11 × 10³ M⁻¹ s⁻¹ for G238 alleles; table 1), it seems reasonable to suppose that in vivo diffusion may further contribute to the fact that for large values of k_cat/K_M, observed MIC values are lower than predicted.

Admittedly, more recent work has raised two caveats to this line of reasoning. First, for many enzymes k_cat/K_M exhibits a non-linear response to increasing concentration of crowding agent (e.g., see recent reviews by Zhou et al. 2008; Luby-Phelps 2013; Kuznetsova et al. 2014). Moreover, as noted above, Sarkar et al. (2013) find that using inert, synthetic polymers rather than cellular extracts to simulate intracellular crowding can substantially affect thermostability estimates. To the best of our knowledge, the role of crowding on enzyme kinetics has only been explored with inert, synthetic polymers (Luby-Phelps 2013; Kuznetsova et al. 2014), raising the possibility of still greater complexity in this response.

Overall then, we conclude that while the consideration of TEM-1 β-lactamase’s behavior in isolation motivates predictions of a linear response in MIC to variation in the k_cat/K_M [Equation (1b)], the complexity of the cellular milieu in which the enzyme operates suggests the opportunity for more sophisticated models. However, addressing these considerations is well beyond the scope of the present study.

The Mechanistic Determinants of Sign Epistasis in MIC Remain Obscure

Beyond our interest in the mapping from biochemistry and biophysics to cefotaxime resistance in TEM-1 β-lactamase, we also sought the mechanistic basis of the sign epistasis previously described in this system (Weinreich et al. 2006). Specifically, sign epistasis emerges generically from the hypothesis that beneficial mutations commonly require compensatory, stabilizing mutations (Camps et al. 2007; Weinreich 2010; Weinreich and Knies 2013). However, our finding that cefotaxime resistance is unaffected by mutational effects on thermostability is fatal to that explanation. Others (Martin et al. 2007; Rokyta et al. 2011) have observed that stabilizing selection on a single underlying phenotype can also give rise to sign epistasis. However, in the case of TEM-1 β-lactamase, there is little evidence to support the notion that MIC is maximized for any intermediate value of k_cat/K_M (fig. 1).

Instead, we find considerable sign epistasis already present in k_cat/K_M (table 4), pushing the mechanism more deeply into the molecular biology of the enzyme. Moreover, we observe substantial antagonistic pleiotropy between k_cat/K_M and MIC: natural selection favors only one but not the other of the two phenotypes in roughly 25% of the cases examined here (table 4). In other words, the sign epistasis in k_cat/K_M itself is not sufficient to explain much of the sign epistasis observed in MIC. Importantly, neither of these observations are artifacts of poor experimental resolution (table 3).

Sign Epistasis and Antagonistic Pleiotropy are “Brittle” Biological Properties

Sign epistasis is a statement about phenotypic rank ordering, and thus survives log transformation of the data. Consequently the sign epistasis in cefotaxime MIC observed in table 4 and previously (Weinreich et al. 2006) already resides in the less than 10% of variance in log-transformed phenotype left unexplained by a purely additive model (fig. 2). While sign epistasis is synonymous with the frustration (in the physicist’s sense) imposed on natural selection by the fitness landscape, it thus can already emerge on comparatively “well-behaved” (nearly non-epistatic) fitness landscapes.

To confirm the generality of this observation, we examined several other suitable datasets (Weinreich et al. 2013). For each, we computed the density of sign epistasis and R² of the non-epistatic model of mutational effect (supplementary table S1, Supplementary Material online, which in each case conservatively reports the larger of the two R² values computed for the raw and log-transformed data). As one might expect, the explanatory power of an additive model is negatively correlated with the density of sign epistasis. On the other hand, the seven independent datasets in which a non-epistatic model is most successful (shown in bold in supplementary table S1, Supplementary Material online, all with R² greater than 0.80) exhibit a mean density of sign epistasis (see “Methods”) of 11%. In other words, appreciable sign epistasis does not require dramatic deviations from mutational additivity.

Similarly, antagonistic pleiotropy (AP) frustrates (in the quotidian sense) our attempts to understand the mechanistic basis of sign epistasis. As above, AP is also a statement about discrepancies between rank orders, and therefore also survives log transformation. Thus the 25% density of AP reported in table 4 already resides in the ∼8% of variance in phenotype left unexplained by the power relationship in the inset of figure 1. This in no way undermines the evolutionary importance of AP, which again captures real complexities that genetics can impose on natural selection. Rather, we note that at least in TEM-1 β-lactamase, rank order discrepancies between phenotypes reflect comparatively small (though significant, table 3) numeric differences. We are unaware of any other datasets in which to test the generality of this observation.

Summary

Two empirical findings in this study are particularly noteworthy. First, contrary to widely held expectations, in vitro measurement of the thermodynamic effects of beneficial mutations are uncorrelated with cefotaxime resistance in TEM-1 β-lactamase. We suggest that mutational effects on localized thermostability, as well as kinetic stability may instead make important contributions to antibiotic resistance evolution. Moreover, we emphasize the possibility that components of the cellular milieu, lost during purification, may substantially influence in vivo protein stability. Second, MIC appears to saturate as TEM-1 variants achieve increasingly good catalytic kinetics. The saturation of MIC may also reflect important differences between in vitro assays and in vivo conditions. Both these empirical findings are likely to be echoed in other mechanistic studies of enzyme evolution. Finally and of particular interest for theoreticians, we observe that because both sign epistasis and antagonistic pleiotropy reflect discrepancies in phenotypic rank order, they can emerge from comparatively small quantitative differences in phenotype. Consequently, sign epistasis (both necessary and sufficient for constraint on the number of selectively accessible trajectories to high-fitness genotypes, Weinreich et al. 2005) can already be observed in systems exhibiting comparatively modest deviations from mutational additivity (supplementary table S1, Supplementary Material online). And, antagonistic pleiotropy (representing discrepancies in identity of the favored allele for two phenotypes) is shown here for the first time to be widespread in a system in which one phenotype [log(k_cat/K_M)] explains 92% of the variance in another [log(MIC)].

Materials and Methods

Cloning

Weinreich et al. (2006) employed 32 β-lactamase alleles defined by five point mutations. Because one of those five mutations (g4205, numbering as in Watson 1988) is upstream of the gene’s start codon, that study only employed 16 distinct protein-coding alleles. These protein-coding alleles, on an arabinose-inducible over-expression and purification vector (pBAD Directional TOPO expression kit, Invitrogen, Carlsbad, CA), were kindly provided by Kyle Brown and Mark DePristo. The pBAD vector provides a 28 residue C-terminal linker including a 6xHis tag to facilitate protein binding on a nickel-affinity column. Each construct was transformed into E. coli strain DH5α (Life Technologies, Grand Island, NY).

Enzyme Purification

β-Lactamase purification was performed as follows. Cells grown overnight at 37 °C were diluted 100-fold in Terrific Broth and grown at 37 °C to an OD₆₀₀=0.6. At this point, the medium was supplemented with 0.02% arabinose and cells were grown overnight at 18 °C, pelleted, and periplasmic extract was obtained by osmotic shock in 30 mL ice-cold 5 mM MgSO₄. This extract was sequentially incubated with two 1 mL volumes of equilibrated nickel beads (Qiagen, Valencia, CA) at 4 °C for 60 min, after which combined bound bead volumes were incubated in 30 mL wash buffer (50 mM sodium phosphate pH 6.0, 300 mM NaCl, 10% glycerol) supplemented with 20 mM imidazole. Next, beads were packed in disposable columns (Bio-Rad, Herculese, CA) and washed with five column volumes of wash buffer again supplemented with 20 mM imidazole. Finally, bound β-lactamase was eluted with 5 column-volumes wash buffer supplemented with 100 mM imidazole. Quantity, purity, and activity were confirmed respectively by Bradford assay, SDS-PAGE gel and catalytic activity against ampicillin (λ = 235 nm). In our hands this yielded 2–20 mg purified β-lactamase per mL of overnight culture, which was then dialyzed into 200 mM potassium phosphate buffer pH 7.0, combined with an equal volume of glycerol, and stored at −80 °C.

Enzyme Kinetics

The in vitro catalytic activity against cefotaxime (Sigma-Aldrich, St. Louis, MO) for each of the 16 alleles of β-lactamase was measured by n = 10 replicate measurements at 25 °C. Absorbance was measured at 260 nm for each enzyme at each substrate concentration for 200 s on a Biotek Synergy HT spectrophotometer (Winooski, VT) using Corning UV-transparent 96-well flat bottom microtiter plates (Corning, NY). Eight different concentrations of substrate (0, 25, 50, 100, 200, 400, 600, and 800 µM) were prepared in 100 mM sodium phosphate buffer. (Optimal enzyme concentrations of each allele were determined empirically by screening over the range 10³–10⁵ pg/µL of soluble protein.)

For each allele, Michaelis-Menten kinetic parameters k_cat and K_M were estimated by fitting nonlinear [Equation (1a)] and linear [Equation (1b)] models to each replicate velocity measurement as a function of substrate concentration. For each replicate, the best fitting Michaelis Menten model (linear or nonlinear) was chosen by small sample AIC (AIC_c, Burnham and Anderson 2002) and for each allele, the mean and standard error of k_cat/K_M across best-model-fit estimates were recorded. Additionally, mean and standard error of individual k_cat and K_M values were recorded across those replicates for which the nonlinear model had the better (lower) AIC_c score.

We follow Xiao et al. (2015) in assuming that the presence of a histidine affinity tag on the TEM-1 β-lactamase does not substantially influence catalytic kinetic data, although we are unaware of any systematic examinations of this hypothesis.

Enzyme Native-Form Thermodynamic Stability

Native-form thermodynamic stability was determined for each allele by circular dichroism (CD) on a Jasco J-815 CD (Easton, MD). Briefly, purified enzyme was dialyzed into 200 mM potassium phosphate pH 7.0 supplemented with 4% glycerol and diluted to 1 mM, which we found maximized signal to noise ratio. After equilibrating each enzyme at room temperature for 10 min, circular dichroism at 223 nm was characterized by raising sample temperature 5 °C/min from 25 to 70 °C. We then determined melting temperature (T_m) and van’t Hoff enthalpy (ΔH) by fitting data to a two-state transition melting curve in PSIPLOT (Pearl River, NY). Because β-lactamase CD profiles are reversible (not shown), Gibbs free energy (ΔG) of unfolding was calculated from the van’t Hoff enthalpy at 25 °C as ΔG = ΔH(1 – T/T_m) (see Equation 5 in Greenfield 2006, where T = 298.15°K and ΔC_p = 0). In total, three experimental replicate measures for each of one biological replicate was performed for each allele.

Cefotaxime MIC Assays

MIC assays for all 32 β-lactamase constructs previously described (Weinreich et al. 2006), were performed at 25 °C by the broth microdilution method (NCCLS 2004; Weinreich et al. 2006). Briefly, starting from single colonies, cells were grown to stationary phase (OD₆₀₀>1.8, ∼1 × 10⁹ cfu/mL) with shaking at 25 °C in cation-adjusted Mueller Hinton Broth (MHB) or Luria Broth (LB; both Becton Dickenson, Franklin Lakes, NJ). Experimental strains (but not control strains, NCCLS 2004) were grown in media supplemented with 50 μg/mL of ampicillin to maintain the plasmid. Cultures were next supplemented with glycerol (15% v/v), divided into enough aliquots to perform all assays, and frozen at −80 F.

39 √2-fold dilutions of cefotaxime (Sigma-Aldrich, St. Louis, MO) in 0.1M phosphate buffer were prepared from a single 81.9 mg/mL stock, and stored in single-use aliquots at −80°F to guarantee long-term stability (Nickolai et al. 1985).

Finally, each √2-fold antibiotic dilution (further diluted 1:10 in MHB after thawing) and cells (diluted 1:1000 in MHB after thawing) were combined (1:1 v/v; total volume 200 µl) in sterile 96-well flat-bottom polystyrene plates (VWR, West Chester, PA). These were sealed with sealing film (Thermo-Fisher Scientific, Waltham, MA) and incubated at 25 °C. OD₆₀₀ was assayed 96 times at 30 min intervals, each after shaking for 30 s, on an Envision 2013 Multilabel Plate Reader (Perkin-Elmer, Waltham, MA). MIC was recorded as the minimum antibiotic concentration that displayed no change in OD₆₀₀ after 48 h. One allele (– + + + +; mutations enumerated in 5′-to-3′ order as in Weinreich et al. 2006) exhibited growth even at this highest cefotaxime concentration (4096 µg/mL). Consequently, we prepared two additional √2-fold dilutions (8.19 and 5.79 mg/mL) to identify its MIC.

All MIC assays were performed in triplicate.

Our protocol differs from the CLSI/NCCLS standard in three respects. First, √2-fold dilutions were employed (Weinreich et al. 2006) to increase resolution of the assay. Second, cells went through a single freeze-thaw cycle before the assay was performed. This work was part of a larger study (Knies et al., in prep) to spectrophotometrically measure full growth kinetics of these same 32 alleles at six temperatures between 20 °C and 41 °C. Because this larger experiment couldn’t be performed on a single day, we introduced a single freeze-thaw cycle in order to avoid variability across replicate liquid culture growth within strains. Third, test cultures were incubated for 48 h rather than 24 h because the no-antibiotic positive control cultures took 48 h to reach stationary phase at 25 °C. Importantly, all positive control MIC assay results (NCCLS 2004) were as expected.

MIC data were then subdivided into two sets of 16 alleles each: those with and without the non-coding g4205a mutation. This allows direct comparisons between biochemical and biophysical phenotypes (naturally assessed for just 16 protein-coding alleles) and MIC in two genetic backgrounds (designated g4205 and 4205a). Because analyses based on these two sets of alleles were largely indistinguishable, and for simplicity we only report results based on MIC values from the g4205 genetic background. On both backgrounds, these four missense mutations increase cefotaxime MIC ∼1500-fold.

Characterizing Epistasis with the Walsh Transformation

Epistasis describes non-linear interaction(s) among mutations in determining phenotype (Phillips 1998, 2008). More colloquially, epistasis represents our surprise at the phenotype conferred by some set of mutations given the phenotypes observed for subsets of those same mutations (Weinreich et al. 2013). Interest has traditionally focused on epistasis between pairs of mutations. However given L mutations, interactions may in principle exist among any of the 2^L possible subsets of these. An interaction involving k > 1 mutations is said to be k^th order; among L mutations there are thus $\left(\begin{array}{c}L\\ k\end{array}\right)$ interactions of order k.

A dataset containing phenotypic data for all combinations of L mutations is called combinatorially complete (Weinreich et al. 2013). The Walsh transformation (Goldberg 1989) converts a vector containing a combinatorially complete phenotypic dataset into a new vector containing orthogonal, independent components corresponding to the phenotypic contributions of each of the 2^L subsets of these mutations. First order terms represent the contribution to phenotype of each mutation in isolation and terms of order k > 1 represent epistatic interactions. [This new vector is easily computed, e.g., with the hadamard() function in MATLAB, MathWorks, Natick, MA. See Box 1 in Weinreich et al. (2013) for further details.] The Walsh transformation is numerically equivalent to computing each main effect and interaction term in a fully factorial ANOVA design (Reeves and Wright 1995; Li et al. 2006) and also to the discrete Fourier decomposition of a function defined on a hypercube (Pumir and Shraiman 2011; Neidhart et al. 2013). The interested reader is directed to Poelwijk et al. (2016) for two other schemes to compute higher-order epistatic effects.

When the phenotype in question is fitness, first order Walsh coefficients are proportional to classical selection coefficients and second order Walsh coefficients are proportional to classical pairwise epistasis coefficients (Weinreich et al. 2013). Consequently, Weinreich et al. (2013) proposed using this framework to allow computation of epistatic coefficients of all order. And regardless the phenotype, perfect additivity among mutations is equivalent to all second- and higher-order Walsh coefficients (i.e., all epistatic terms) being equal to zero.

To summarize the magnitude of epistasis underlying each phenotype examined, we report the mean squared values (± standard deviation) of the $\left(\begin{array}{c}L\\ k\end{array}\right)$ Walsh coefficients at each interaction order. Values are squared because individual Walsh coefficients can be positive or negative. Values were also normalized by the grand average of each phenotype, in order to allow comparison across phenotypes. Additionally, we report the coefficient of determination (R²) between observed phenotypes and those predicted by successive models incorporating only the lowest order k = 1, 2, … L terms. To do this, we took advantage of the fact that the Walsh transform of a vector of Walsh coefficients recovers the initial phenotypic vector (Weinreich et al. 2013). Thus, for each vector of Walsh coefficients computed from our data, we set the appropriate higher-order terms to zero, computed a new vector of phenotypes, and computed R² between the new vector and the original data. (This approach is formally equivalent to computing the explanatory power of additive terms in an analysis of variance.)

The Density of Sign Epistasis and Antagonistic Pleiotropy

Sign epistasis means a mutation fails to influence some phenotype in the same direction on all genetic backgrounds examined. Of particular interest for evolutionary genetics are cases of mutations that are beneficial on only some genetic backgrounds. We define the density of sign epistasis at a locus as the fraction of genetic backgrounds on which that mutation fails to be significantly beneficial. For example, table 4 illustrates that the A42G mutation significantly increases k_cat/K_M on five backgrounds but not on the other three examined. On the assumption that increasing catalytic efficiency is beneficial, the density of sign epistasis for this phenotype ascribed to A42G is thus 3/8 = 37.5%. In contrast the density of sign epistasis for k_cat/K_M is 0% at G238S. Finally, the density of sign epistasis for a phenotype across a dataset is defined as the average mean density of sign epistasis among all mutations in the dataset.

Antagonistic pleiotropy (AP) means that a mutation affects two phenotypes in opposite directions. Given our interest in adaptation, we follow Remold (2012) and restrict our definition of AP to those cases in which mutations are significantly beneficial for only one of the two phenotypes. We define the density of antagonistic pleiotropy in a dataset as the fraction of genetic backgrounds on which that a mutation exhibits antagonistic pleiotropy.

Statistics

Statistical significance of differences in phenotypes (k_cat/K_M, k_cat, K_M, T_m, and ΔG) between β-lactamase alleles was calculated by Welch’s or Student’s t-test (Sokal and Rohlf 1995). Significance values were corrected for multiple tests using the Holm–Bonferroni method (Holm 1979). Significance in rank correlations were computed with the Spearman rank correlation ρ (Sokal and Rohlf 1995) and statistical significance was assessed by purpose-built MATLAB permutation test over 10⁶ realizations.

ΔΔG Computation

ΔΔG values of all protein-coding alleles were computed relative to the 1BTL PDB crystal structure of TEM-1 (Jelsch et al. 1993) using two public domain software packages. The graphical user interface version of FoldX (Van Durme et al. 2011, downloaded May 31, 2015) was run from inside YASARA (Krieger and Vriend 2014, downloaded May 31, 2015) using standard parameter values (3 runs at 298°K in pH 7.0 with ionic strength 5 × 100 and Van der Waal design 2). Queries were also performed with the web-based interface for PoPMuSiC 2.1 (Dehouck et al. 2011, last accessed May 31, 2015) in manual mode.

Supplementary Material

Supplementary data is available at Molecular Biology and Evolution online.