Nonreciprocal charge transport in noncentrosymmetric superconductors

Giant nonreciprocal transport effect in noncentrosymmetric superconductors is studied both theoretically and experimentally.

Abstract

Lack of spatial inversion symmetry in crystals offers a rich variety of physical phenomena, such as ferroelectricity and nonlinear optical effects (for example, second harmonic generation). One such phenomenon is magnetochiral anisotropy, where the electrical resistance depends on the current direction under the external magnetic field. We demonstrate both experimentally and theoretically that this magnetochiral anisotropy is markedly enhanced by orders of magnitude once the materials enter into a superconducting state. To exemplify this enhancement, we study the magnetotransport properties of the two-dimensional noncentrosymmetric superconducting state induced by gating of MoS₂. These results indicate that electrons feel the noncentrosymmetric crystal potential much coherently and sensitively over the correlation length when they form Cooper pairs, and show open a new route to enhance the nonreciprocal response toward novel functionalities, including superconducting diodes.

INTRODUCTION

Rectification is a fundamental nonreciprocal effect or phenomenon, where the current-voltage (I-V) characteristics of right and left directions are distinct. As naturally expected, it requires systems without inversion symmetry, for example, p-n junction. In p-n junctions, the width of the depletion layer changes differently as a function of voltage between right and left directions. In contrast with these junction systems, in bulk crystals without interfaces, the crystal momentum k is a good quantum number, and the situation is much less trivial. The lack of inversion symmetry manifests itself as the spin splitting of bands when the relativistic spin-orbit interaction is present. However, time-reversal symmetry relates the energy dispersion at k and −k with the spin direction reversed. Therefore, the nonreciprocal current responses usually appear when both inversion and time-reversal symmetries are broken. In the case of dc transport in metals with broken inversion symmetry, the nonreciprocal nature necessarily appears in nonlinear responses, such as the current proportional to the square of the electric field E under the external magnetic field B, as expressed by the current-dependent resistivity R

$$\mathit{R}={\mathit{R}}_0(1+\mathrm{\gamma }\mathit{B}\mathit{I})$$ (1)

where I = |I| is the current and γ is the coefficient representing the strength of this effect called magnetochiral anisotropy (MCA) (1–6). The magnitude of γ is usually small in metals typically of the order of ~10⁻³ to 10⁻² T⁻¹ A⁻¹. The reason is that the spin-orbit interaction and magnetic energy are much smaller than the Fermi energy ε_F and hence are weak perturbations (see Fig. 1A).

Fig. 1. Schematic illustration of nonreciprocal transport in noncentrosymmetric bulk crystals.

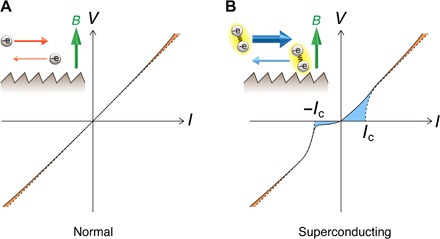
(A) I-V curve in the normal state of a noncentrosymmetric crystal, whose nonreciprocal current is usually small. (The dashed line is the linear I-V relation.) Inset: Electron motion in the asymmetric potential, which represents the lack of inversion symmetry. (B) I-V curve in the resistive superconducting state, whose nonreciprocal current is much larger than that of the normal state below the critical current (I_c), whereas it remains unchanged at larger I. Inset: Enhanced nonreciprocity due to the coherence of Cooper pairs.

When the superconductivity sets in, a new energy scale enters, that is, the transition temperature T_c or the superconducting gap Δ, which are much smaller than ε_F. Therefore, it is possible that the effects of spin-orbit interaction and magnetic field are enhanced in the superconducting state. It is known that the noncentrosymmetric superconductors have several unique features, including the mixed singlet and triplet pairings and the associated large upper critical field beyond the Pauli limit, super spin current, and supercurrent induced by the Zeeman field (7–9). These superconducting properties have been intensively studied thus far, but the nature of the superconducting fluctuation (10–15) in the resistive state has not been well explored, especially under a magnetic field.

Here, we report the MCA in the resistive superconducting fluctuation in noncentrosymmetric superconductors. In particular, with the example of electric field–induced superconductivity in MoS₂, the signal of the MCA in the superconducting state was found to be markedly enhanced compared to that in the normal state (see Fig. 1, A and B). This experimental result is consistent with the theoretical prediction, which suggests that intrinsic properties of noncentrosymmetric systems can be accessed by the coherence of Cooper pairs.

RESULTS

MoS₂ is an archetypal layered semiconducting transition metal dichalcogenides (TMDs), which have been attracting significant attentions as two-dimensional (2D) materials for various functionalities (16–18). MoS₂ is composed of the stacked layers with weak van der Waals interaction. In the monolayer, one Mo atom is sandwiched by two S atoms, forming a 2D network with D_3h symmetry (Fig. 2A). Reflecting this threefold symmetry, the semiconducting TMDs have trigonal warping in the Fermi surfaces (19). In the isolated monolayer, in-plane inversion symmetry is broken, causing out-of-plane spin polarization together with effective Zeeman fields, which results in spin splitting at the K points (20, 21). Because of the sign difference in the effective Zeeman fields at the K and −K valleys, the spin polarization is oppositely locked depending on the valley. However, in this state, only spatial inversion symmetry is broken, and time-reversal symmetry still holds. Time-reversal symmetry is broken by the application of an external magnetic field. A schematic structure of the conduction band bottom under an external out-of-plane magnetic field is illustrated in Fig. 2B. Recently, MoS₂ was reported to show superconductivity by electrostatic doping in an electric double-layer transistor (EDLT) configuration (22).

Fig. 2. Crystal and band structures of 2H-MoS₂ and experimental setup.

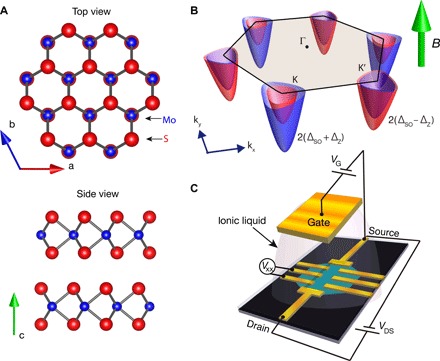
(A) Top and side views of a 2H-MoS₂ 2D crystal. In monolayers, spatial inversion symmetry is broken because the Mo and S sites are not equivalent, but the inversion symmetry is restored in 2H-type multilayers. (B) Schematic band structure of the conduction bottom of 2D MoS₂. The magnetic field is applied perpendicular to the plane. Owing to the combination of the spin-orbit interaction and Zeeman effect, the band asymmetry appears between the K and K′ = −K points. Their spin splittings are 2(Δ_SO + Δ_Z) and 2(Δ_SO − Δ_Z), respectively. (C) Schematic image of a MoS₂-EDLT. V_xx is a four-probe longitudinal voltage of the channel. Here, the channel direction was parallel to the zigzag edge (29).

The EDLT forms an electrochemical interface, in which a high-density 2D electron system is created without introducing extrinsic disorder. Furthermore, because superconductivity occurs in chemically undoped crystals, highly crystalline 2D superconductors can be realized, (23, 24), showing quantum metallic states in the low temperature (25). In addition, a signature of the noncentrosymmetric superconductor was observed by an enhanced in-plane upper critical fields owing to the spin-valley locking (26–28). Thus, the gate-induced superconductivity in MoS₂ is an ideal platform for investigating the properties intrinsic to the crystal structure, such as broken spatial inversion symmetry.

We prepared an EDLT structure with a 20-nm-thick 2H-MoS₂ thin flake with N,N-diethyl-N-(2-methoxyethyl)-N-methylammonium bis(trifluoromethylsulphonyl) imide (DEME-TFSI) as a gate medium (Fig. 2C). The electrodes (Cr/Au, 5 nm/90 nm) in a Hall bar configuration were covered with SiO₂ thin film for each electrode to define the channel shape (see Materials and Methods). Following the recent literature (29), the device was fabricated so that the source-drain current (I_DS) flow was parallel to the zigzag edge. Figure 3A shows the temperature dependence of sheet resistance R_sheet of the MoS₂-EDLT at a gate voltage V_G of 5.0 V and a sheet carrier density n_2D of 1.2 × 10¹⁴ cm⁻². Superconducting transition was observed at the critical temperature of 8.8 K, as defined at the midpoint of the transition with R_sheet being 50% of the normal state. We identify this temperature as the mean-field transition temperature T_c, whereas that determined by the zero resistance is regarded as the Kosterlitz-Thouless (KT) transition temperature T_KT (25). Here, note that the sample we measured was a MoS₂ multilayer flake with the 2H polytype, in which the two adjacent layers are rotated by π with respect to each other, therefore making the whole structure centrosymmetric in contrast to the noncentrosymmetric monolayer (Fig. 2A). However, once the gate voltage is applied, the electric field breaks the out-of-plane inversion symmetry, making the neighboring monolayers inequivalent. At the same time, the conduction band minimum shifts to the ±K points, where interlayer coupling is very weak, and thus electrons are quite localized within each layer. Consequently, the in-plane inversion asymmetry in each monolayer reappears. Therefore, the gate-induced conducting and superconducting states are effectively regarded as a monolayer (30). Note that the point group symmetry is reduced down to C_3v in the presence of the strong electric field.

Fig. 3. Magnetochiral anisotropy in ion-gated MoS₂.

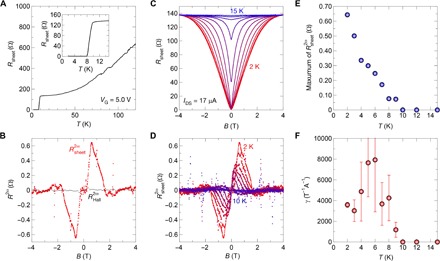
(A) Temperature (T) dependence of sheet resistance R_sheet of a MoS₂-EDLT at a gate voltage V_G of 5.0 V. Inset: A close-up of the resistive transition. The T_c is 8.8 K as defined at the midpoint of the transition with sheet resistance R_sheet being 50% of the normal state. (B) Antisymmetrized sheet $({\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }},\text{red})$ and Hall $({\mathit{R}}_{\text{Hall}}^{2\mathrm{\omega }},\text{black})$ second harmonic magnetoresistance at 2 K. Compared to the signals of ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$, the value of ${\mathit{R}}_{\text{Hall}}^{2\mathrm{\omega }}$ is much smaller. (C) Magnetoresistance at 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, and 15K at I_DS of 17 μA. (D) Antisymmetrized second harmonic sheet magnetoresistance ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ at 2 to 10 K. (E) Maximum of the ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ as a function of temperature. (F) Temperature dependence of γ at the I_DS of 17 μA. The γ suddenly increases up to ~1200 T⁻¹ A⁻¹ around the superconducting transition. Error bars are estimated by the uncertainty of the R_sheet because of the broad peak of the ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}\dot{}$

To extract the intrinsic MCA in a 2H-MoS₂–EDLT, we measured both the first (R^ω) and second harmonic signals (R^2ω) of the longitudinal and transverse magnetoresistance in the out-of-plane magnetic field geometry by the application of the ac excitation bias voltage with the constant frequency of 13 Hz. Figure 3B shows the antisymmetric component of R^2ω for the longitudinal and transverse magnetoresistance (${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ and ${\mathit{R}}_{\text{Hall}}^{2\mathrm{\omega }}$) at 2 K at a I_DS of 17 μA. Once the magnetic field is switched on, ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ first increases, then peaks around 0.5 T, and finally decreases. On the other hand, ${\mathit{R}}_{\text{Hall}}^{2\mathrm{\omega }}$ was extremely small compared with ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$, being consistent with the expected selection rule, as expressed in Eq. 4. Figure 3 (C and D) shows R_sheet and ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$, respectively, as a function of the magnetic field between 2 and 15 K. The ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ signal was significantly enhanced in the superconducting state with decreasing temperature. In the normal state above 10 K, ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ was too small to be detected by the lock-in amplifier. The maximum value of ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ increased with decreasing temperature, reaching 0.65 ohms at 2 K, which corresponds to 0.46% of the normal state resistance (Fig. 3E). In Fig. 3F, we plotted the γ value (see Eq. 1), which is calculated as γ = $\frac{2{\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}}{{\mathit{R}}_{\text{sheet}}\mathit{B}{\mathit{I}}_{\text{DS}}}$, as a function of temperature. Here, the values of ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ were taken from the maximum point of the ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ (Fig. 3D) for each temperature, and γ was calculated by the corresponding values of B and R_sheet. In the normal state above the transition temperature, the γ value shows almost zero, whereas it suddenly increases up to ~1200 T⁻¹ A⁻¹ at the mean-field transition temperature T_c = 8.8 K. In the superconducting state, all the γ values are order of 10³ T⁻¹ A⁻¹, and the maximum value is nearly 8000 T⁻¹ A⁻¹, both of which are approximately five orders of magnitude larger than those of conventional materials (1–3). These results provide unambiguous evidence that the MCA signals are significantly enhanced in the superconducting phase at the same current.

Now, we describe the theoretical analysis of MCA near and above T_c for MoS₂ under an out-of-plane magnetic field. 2D MoS₂ is well described by the Hamiltonian given by (31, 32)

$${\mathit{H}}_{\mathit{k}\mathrm{\sigma }\mathrm{\tau }}=\frac{{\mathit{ħ}}^2{\mathbf{k}}^2}{2\mathit{m}}+{\mathrm{\tau }}_{\mathit{z}}\mathrm{\lambda }{\mathit{k}}_{\mathit{x}}({\mathit{k}}_{\mathit{x}}^2-3{\mathit{k}}_{\mathit{y}}^2)-{\mathrm{\Delta }}_{\mathrm{Z}}{\mathrm{\sigma }}_{\mathit{z}}-{\mathrm{\Delta }}_{\text{SO}}{\mathrm{\sigma }}_{\mathit{z}}{\mathrm{\tau }}_{\mathit{z}}$$ (2)

around the K and −K points. Here, λ is the parameter of the trigonal warping (21), Δ_Z and Δ_SO are the spin splittings due to the Zeeman effect and the spin-orbit interaction, respectively, and σ_z = ±1 (or ↑, ↓) and τ_z = ±1 (or +, −) represent the spin and valley degrees of freedom, respectively. For simplicity, we neglected the Rashba spin-orbit interaction because of the electric field in the EDLT device because the Rashba term does not contribute to the nonreciprocal response (see Supplementary Materials).

We first derive the Ginzburg-Landau (GL) free energy as (see Materials and Methods)

$$\mathit{F}={\displaystyle \int }\mathit{d}\mathit{r}\mathrm{\Psi }*[\mathit{a}+\frac{{\mathit{p}}^2}{4\mathit{m}}+\frac{\mathrm{\Lambda }\mathit{B}}{{\mathit{ħ}}^3}({\mathit{p}}_{\mathit{x}}^3-3{\mathit{p}}_{\mathit{x}}{\mathit{p}}_{\mathit{y}}^2\left)\right]\mathrm{\Psi }+\frac{\mathit{b}}{2}{\displaystyle \int }\mathit{d}\mathit{r}{|\mathrm{\Psi }(\mathit{r})|}^4$$ (3)

where p = −iħ∇, $\mathrm{\Lambda }=\frac{93\mathrm{\zeta }(5)}{28\mathrm{\zeta }(3)}\frac{\mathit{g}{\mathrm{\mu }}_{\mathrm{B}}{\mathrm{\Delta }}_{\text{SO}}\mathrm{\lambda }}{{(\mathrm{\pi }{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}})}^2}$, g is the g-factor, and μ_B is the Bohr magneton. a and b are the conventional coefficients in the GL theory. In 2D superconductors in the type II limit, there are two characteristic temperatures. One is the mean-field transition temperature T_c, which indicates the crossover temperature around which the amplitude of the order parameter develops, whereas the phase fluctuation remains because of the unbound vortices and antivortices. At the KT temperature T_KT < T_c, these vortices and antivortices form bound pairs, and, hence, the phase rigidity appears. Here, we theoretically discuss the Gaussian fluctuation region T_c ≲ T. Following the analysis of Schmid (33), using the time-dependent GL equation, we obtain the excess current because of the superconducting fluctuation (10, 11), which is called paraconductivity, as

$$\mathit{j}=\frac{{\mathit{e}}^2}{16\mathit{ħ}}{\mathrm{ϵ}}^{-1}\mathit{E}-\frac{\mathrm{\pi }{\mathit{e}}^3\mathit{m}\mathrm{\Lambda }\mathit{B}}{64{\mathit{ħ}}^3{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}}}{\mathrm{ϵ}}^{-2}\mathit{F}(\mathit{E})$$ (4)

where $\mathrm{ϵ}=\frac{\mathit{T}-{\mathit{T}}_{\mathrm{c}}}{{\mathit{T}}_{\mathrm{c}}}$ and $\mathit{F}(\mathit{E})=({\mathit{E}}_{\mathit{x}}^2-{\mathit{E}}_{\mathit{y}}^2,-2{\mathit{E}}_{\mathit{x}}{\mathit{E}}_{\mathit{y}})$, which satisfies the transformation rule of the C_3v point group. We have finite nonreciprocal current, which develops around the critical region.

On the other hand, the normal phase does not carry the nonreciprocal current in this model because the contributions from the two pairs of the bands cancel out in the lowest order (see Materials and Methods). Hence, neglecting the nonreciprocal current in the normal state, one can define the linear and nonlinear transport coefficients as j = (σ₁ + σ_n)E + σ₂ F(E), where σ₁ and σ₂ are the contributions from superconducting fluctuation, and σ_n is the normal conductivity. Around the critical region, the fluctuation conductivity gets larger than the normal conductivity, and the γ value is approximately

$$\mathrm{\gamma }=\frac{{\mathrm{\sigma }}_2}{{\mathrm{\sigma }}_1^2\mathit{W}\mathit{B}}=\frac{4\mathrm{\pi }\mathit{m}\mathrm{\Lambda }}{\mathit{e}\mathit{W}\mathit{ħ}{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}}}$$ (5)

where W is the channel width. We will estimate the amplitude of the γ value and show below that it is markedly enhanced in the superconducting state.

Although the normal state does not carry nonreciprocal current in this model, one can estimate its typical order of magnitude using the current from only one of the band pairs. Thus, the ratio of the γ values in the normal region (γ_N) and the resistive superconducting region (γ_S) is

$$\frac{{\mathrm{\gamma }}_{\mathrm{S}}}{{\mathrm{\gamma }}_{\mathrm{N}}}~{\left(\frac{{\mathrm{\epsilon }}_{\mathrm{F}}}{{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}}}\right)}^3$$ (6)

which is quite large. We emphasize that this anomalous enhancement of the γ parameter should be a universal feature in noncentrosymmetric superconductors because it derives from the energy scale difference between the Fermi energy and the superconducting gap.

In the resistive state at low temperature T ≲ T_c, which is continued smoothly to the normal state, the amplitude develops, whereas the phase fluctuation remains, and, hence, the nonlinear interaction term in Eq. 3 becomes relevant. The dynamics of vortices under the current flow and its nonreciprocal nature becomes relevant in this case, which is left for future investigations.

DISCUSSION

Here, we estimate the physical quantities of the clean MoS₂. According to ab initio calculations, 2mλ/ħ² = −0.49 Å and Δ_SO ≈ 7.5 meV around the Fermi energy (26, 31, 32). We take the experimental parameters W ≅ 3 μm, ${\mathrm{\sigma }}_{\mathrm{n}}^{-1}=140 \text{ohms}$, and T_c = 8.8 K. The MCA is reflected in the physical quantity γ = (σ₂/WB)/(σ₁ + σ_n)². The γ value is largely enhanced by the superconducting fluctuation and reaches γ ≈ 250 T⁻¹ A⁻¹, which should be compared with γ ≈ 1200 T⁻¹ A⁻¹ that is experimentally observed at T_c = 8.8 K (Fig. 3F). Although there is a discrepancy of a factor of ~5, the rapid increase in γ is captured by theoretical calculation.

In conclusion, we have demonstrated that the MCA in the gate-induced superconductivity in MoS₂ is enhanced by five orders of magnitude compared with the normal state. It is ascribed to the difference of the characteristic energy scale between the Fermi energy (~1 eV) and the superconducting gap (~1 meV). Our argument is quite general, and we believe that the anomalous enhancement of the γ value occurs in any noncentrosymmetric superconductors, although we have shown explicitly so for MoS₂.

MATERIALS AND METHODS

Device fabrication

Bulk 2H-polytype MoS₂ single crystals were cleaved into thin flakes with dozens of nanometers in thickness using the Scotch tape method, and then flakes were transferred onto a Si/SiO₂ substrate. Au (90 nm)/Cr (5 nm) electrodes were patterned onto an isolated thin flake in a Hall bar configuration, and a side-gate electrode was patterned onto the substrate. We covered the device with the polymethylmethacrylate (used as the resist for electron beam lithography), except for the channel surface, to avoid chemical intercalation from the edge of the flake and define the channel. We used DEME-TFSI as a gate medium.

Transport measurements

The resistance measurements (including both the first and second harmonic measurements) of a MoS₂-EDLT under zero and finite magnetic fields were made with the four-point probe 2D MoS₂ is well described by the Hamiltonian method in a Quantum Design Physical Property Measurement System combined with two ac lock-in amplifiers (Stanford Research Systems Model SR830 DSP and Signal Recovery Model 5210). We confirmed that the phase of the first and second harmonic signals in the ac resistance measurements kept showing around 0° and 90°, respectively, which indicates the validity of our ac measurements. The gate voltage was supplied by a Keithley 2400 SourceMeter. We applied gate voltages to the device at 240 K, just above the glass transition temperature of DEME-TFSI, under high vacuum (less than 10⁻⁴ torr), and then lowered temperatures. The magnetoresistance measurements were performed under a helium atmosphere (5 to 10 torr).

Definition of γ

We note the relations derived from the definition of γ in Eq. 1. The current density is described as j = σ₁E + σ₂E², where we considered only one direction. If we solve in terms of E, then we obtain

$$\mathit{E}=\frac{-{\mathrm{\sigma }}_1\pm \sqrt{{\mathrm{\sigma }}_1^2+4{\mathrm{\sigma }}_2\mathit{j}}}{2{\mathrm{\sigma }}_2}\approx \frac{1}{{\mathrm{\sigma }}_1}\mathit{j}+\frac{{\mathrm{\sigma }}_2}{{\mathrm{\sigma }}_1^3}{\mathit{j}}^2$$ (7)

Here, we chose the plus sign to satisfy the linear order relation.

With the sample width W and length L, we had the current I = Wj and the voltage drop V = −EL. Then, we obtained

$$\mathit{V}=-\frac{\mathit{L}}{{\mathrm{\sigma }}_1\mathit{W}}\mathit{I}-\frac{{\mathrm{\sigma }}_2\mathit{L}}{{\mathrm{\sigma }}_1^3{\mathit{W}}^2}{\mathit{I}}^2$$ (8)

With the ac I = I_DScos ωt, the first and second harmonic signals are

$$\begin{array}{c}{\mathit{R}}^{\mathrm{\omega }}={\mathit{R}}_{\text{sheet}}=\mathit{R}\\ {\mathit{R}}^{2\mathrm{\omega }}=\frac{\mathit{R}\mathrm{\gamma }\mathit{B}{\mathit{I}}_{\text{DS}}}{2}\end{array}$$ (9)

Therefore, γ can be calculated as

$$\mathrm{\gamma }=\frac{2{\mathit{R}}^{2\mathrm{\omega }}}{{\mathit{R}}^{\mathrm{\omega }}\mathit{B}{\mathit{I}}_{\text{DS}}}$$ (10)

Calculation of paraconductivity by time-dependent GL equation

We reviewed how to calculate the paraconductivity due to the superconducting fluctuation following Schmid (33). The GL free energy quadratic in the order parameter reads

$$\mathit{F}={\displaystyle \int }\mathit{d}\mathit{r}\mathrm{\Psi }*(\mathit{r})\mathrm{\eta }(\mathit{r})\mathrm{\Psi }(\mathit{r})={\displaystyle \sum _{\mathit{q}}}{\mathrm{\eta }}_{\mathit{q}}{|{\mathrm{\Psi }}_{\mathit{q}}|}^2$$ (11)

where we assumed the uniform system and expressed the free energy in the momentum space, and η_q will be given as Eq. 30. The expectation value of the excess current density was evaluated by calculating the time dependence of Ψ explicitly on the basis of the time-dependent GL equation with a stochastic force, namely

$$\mathit{ħ}\mathrm{\Gamma }{\partial }_{\mathit{t}}\mathrm{\Psi }(\mathit{r},\mathit{t})=-\mathrm{\eta }(\mathit{r},\mathit{t})\mathrm{\Psi }(\mathit{r},\mathit{t})+\mathit{f}(\mathit{r},\mathit{t})$$ (12)

where Γ is the damping coefficient for Ψ, and f is the uncorrelated random force satisfying

$$<\mathit{f}*(\mathit{r},\mathit{t})\mathit{f}({\mathit{r}}^{\prime },{\mathit{t}}^{\prime })>=2\mathit{ħ}\mathrm{\Gamma }{\mathit{k}}_{\mathrm{B}}\mathit{T}\mathrm{\delta }(\mathit{r}-{\mathit{r}}^{\prime })\mathrm{\delta }(\mathit{t}-{\mathit{t}}^{\prime })$$ (13)

or

$$<{\mathit{f}*}_{\mathit{q}}(\mathit{t}){\mathit{f}}_{{\mathit{q}}^{\prime }}({\mathit{t}}^{\prime })>=2\mathit{ħ}\mathrm{\Gamma }{\mathit{k}}_{\mathrm{B}}\mathit{T}{\mathrm{\delta }}_{\mathit{q},{\mathit{q}}^{\prime }}\mathrm{\delta }(\mathit{t}-{\mathit{t}}^{\prime })$$ (14)

One can check that the stochastic force reproduces the appropriate value 〈|Ψ_q|²〉 = k_BT/η_q. Next, we calculated the time evolution of Ψ_q(t), and then the expectation value of the current density. The formal solution of Eq. 12 is given by

$${\mathrm{\Psi }}_{\mathit{q}}(\mathit{t})=\frac{1}{\mathit{ħ}\mathrm{\Gamma }}{\displaystyle {\int }_{-\infty }^{\mathit{t}}}\mathit{d}{\mathit{t}}^{\prime }{\mathit{f}}_{\mathit{q}}({\mathit{t}}^{\prime })\text{exp}[-\frac{1}{\mathit{ħ}\mathrm{\Gamma }}{\displaystyle {\int }_{{\mathit{t}}^{\prime }}^{\mathit{t}}}\mathit{d}{\mathit{t}}^{\prime \prime }{\mathrm{\eta }}_{\mathit{q}}({\mathit{t}}^{\prime \prime })]$$ (15)

where we assumed Ψ_q(−∞) = 0. Therefore, the expectation value of the order parameter is

$$\langle {|{\mathrm{\Psi }}_{\mathit{q}}(\mathit{t})|}^2\rangle =\frac{2{\mathit{k}}_{\mathrm{B}}\mathit{T}}{\mathit{ħ}\mathrm{\Gamma }}{\displaystyle {\int }_{-\infty }^{\mathit{t}}}\mathit{d}{\mathit{t}}^{\prime } \text{exp}[-\frac{2}{\mathit{ħ}\mathrm{\Gamma }}{\displaystyle {\int }_{{\mathit{t}}^{\prime }}^{\mathit{t}}}\mathit{d}{\mathit{t}}^{\prime \prime }{\mathrm{\eta }}_{\mathit{q}}({\mathit{t}}^{\prime \prime })]$$ (16)

On the other hand, the current density is expressed as

$$\widehat{\mathit{j}}=-\frac{\mathit{c}\mathrm{\delta }\mathit{F}}{\mathit{V}\mathrm{\delta }\mathit{A}}=\frac{1}{\mathit{V}}{\displaystyle \sum _{\mathit{q}}}(-\frac{\mathit{c}\partial {\mathrm{\eta }}_{\mathit{q}}}{\partial \mathit{A}}){|{\mathrm{\Psi }}_{\mathit{q}}|}^2=\frac{1}{\mathit{V}}{\displaystyle \sum _{\mathit{q}}}{\widehat{\mathit{j}}}_{\mathit{q}}{|{\mathrm{\Psi }}_{\mathit{q}}|}^2$$ (17)

whose expectation value leads to

$$\mathit{j}(\mathit{t})=\frac{2{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}}}{\mathit{V}\mathit{ħ}\mathrm{\Gamma }}{\displaystyle \sum _{\mathit{q}}}{\displaystyle {\int }_{-\infty }^{\mathit{t}}}\mathit{d}{\mathit{t}}^{\prime }{\widehat{\mathit{j}}}_{\mathit{q}}({\mathit{t}}^{\prime })\text{exp}[-\frac{1}{\mathit{ħ}\mathrm{\Gamma }}{\displaystyle {\int }_{{\mathit{t}}^{\prime }}^{\mathit{t}}}\mathit{d}{\mathit{t}}^{\prime \prime }{\mathrm{\eta }}_{\mathit{q}}({\mathit{t}}^{\prime \prime })]$$ (18)

where we set the vector potential A = −cEt for the static and uniform electric field E.

Microscopic derivation of the GL theory for superconducting TMDs

We derived the GL theory for the TMDs and showed that the nonreciprocal current emerges because of the third-order term in the momentum. The Hamiltonian is

$${\mathit{H}}_{\mathit{k}\mathrm{\sigma }\mathrm{\tau }}={\mathrm{\epsilon }}_{\mathit{k}\mathrm{\tau }}-\mathrm{\mu }-{\mathrm{\sigma }\mathrm{\Delta }}_{\mathrm{Z}}-{\mathrm{\sigma }\mathrm{\tau }\mathrm{\Delta }}_{\text{SO}}$$ (19)

$${\mathrm{\epsilon }}_{\mathit{k}\mathrm{\tau }}=\frac{{\mathit{ħ}}^2{\mathit{k}}^2}{2\mathit{m}}+\mathrm{\tau }\mathrm{\lambda }{\mathit{k}}_{\mathit{x}}({\mathit{k}}_{\mathit{x}}^2-3{\mathit{k}}_{\mathit{y}}^2)\equiv {\mathrm{\epsilon }}_{\mathit{k}}^0+\mathrm{\tau }\mathrm{\lambda }{\mathit{f}}_{\mathit{k}}$$ (20)

If we assume a contact-attractive interaction, then s-wave singlet pairing occurs between the (↑, +) and (↓, −) pair and between the (↑, −) and (↓, +) pair. The free energy for the order parameter Δ is calculated as

$$\mathit{F}={\displaystyle \sum _{\mathit{q}}}[\frac{1}{\mathit{g}}+\frac{\mathit{T}}{\mathit{V}}{\displaystyle \sum _{\mathit{k},\mathrm{\tau }=\pm }}{\mathit{G}}_{\mathit{k}+\mathit{q}/2,\uparrow ,\mathrm{\tau }}^{\mathit{e}}{\mathit{G}}_{\mathit{k}-\mathit{q}/2,\downarrow ,-\mathrm{\tau }}^{\mathit{h}}]{|{\mathrm{\Delta }}_{\mathit{q}}|}^2$$ (21)

where g is the strength of the attractive interaction, and

$${\mathit{G}}_{\mathit{k}\mathrm{\sigma }\mathrm{\tau }}^{\mathit{e}}=\frac{1}{\mathit{i}{\mathrm{\omega }}_{\mathit{n}}-{\mathit{H}}_{\mathit{k}\mathrm{\sigma }\mathrm{\tau }}}=\frac{1}{\mathit{i}{\mathrm{\omega }}_{\mathit{n}}-{\mathrm{\epsilon }}_{\mathit{k}\mathrm{\tau }}+\mathrm{\mu }+{\mathrm{\sigma }\mathrm{\Delta }}_{\mathit{Z}}+{\mathrm{\sigma }\mathrm{\tau }\mathrm{\Delta }}_{\text{SO}}}$$ (22)

$${\mathit{G}}_{\mathit{k}\mathrm{\sigma }\mathrm{\tau }}^{\mathit{h}}=\frac{1}{\mathit{i}{\mathrm{\omega }}_{\mathit{n}}+{\mathit{H}*}_{-\mathit{k}\mathrm{\sigma }\mathrm{\tau }}}=\frac{1}{\mathit{i}{\mathrm{\omega }}_{\mathit{n}}+{\mathrm{\epsilon }}_{\mathit{k}\mathrm{\tau }}-\mathrm{\mu }-{\mathrm{\sigma }\mathrm{\Delta }}_{\mathit{Z}}-{\mathrm{\sigma }\mathrm{\tau }\mathrm{\Delta }}_{\text{SO}}}$$ (23)

are the electron and hole Green’s functions with the Matsubara frequency ω_n = (2n + 1)πk_BT. We also define the Green’s functions without the trigonal warping term as ${\mathit{g}}_{\mathit{k}}^{\mathit{e}}$ and ${\mathit{g}}_{\mathit{k}}^{\mathit{h}}$.

We expanded Eq. 21 up to the third order of q and the first order of λ and Δ_Z. We can perform the calculation with the aid of the point group symmetry of the crystal. The character table for the point group C_3v is shown in Table 1. Here, the column, linear, quadratic, and cubic functions are the basis functions and R_z is the pseudovector along the z direction. Because ${\mathit{G}}_{\mathit{k}}^{\mathit{e}}$ and ${\mathit{G}}_{\mathit{k}}^{\mathit{h}}$ transform as the trivial representation, the other parts, which transform as the A₂ or E representations, vanished in the k integral. Moreover, the result has to transform as the trivial representation in the q space.

Table 1. Character table for the point group C_3v.

C3v	E	2C3	3σv	Linear	Quadratic	Cubic
A1	+1	+1	+1	z	x2 + y2, z2	z3, x(x2 − 3y2), z(x2 + y2)
A2	+1	+1	−1	Rz	—	y(3x2 − y2)
E	+2	−1	0	(x, y), (Rx, Ry)	(x2 − y2, xy), (xz, yz)	(xz2, yz2), (xyz, z(x2 − y2)), (x(x2 + y2), y(x2 + y2))

We first expanded Eq. 21 with respect to q. The zeroth-order term in q is 2νϵ, where ν is the density of states for one band. For the higher-order terms, we considered the first term in Eq. 21, that is, στ = 1 pair first. If we omit the spin and valley indices, then we have

$${\mathit{G}}_{\mathit{k}+\mathit{q}}^{\mathit{e}}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}={\mathit{G}}_{\mathit{k}}^{\mathit{h}}[1+\mathit{q}\cdot {\nabla }_{\mathit{k}}+\frac{1}{2}{(\mathit{q}\cdot {\nabla }_{\mathit{k}})}^2+\frac{1}{6}{(\mathit{q}\cdot {\nabla }_{\mathit{k}})}^3]{\mathit{G}}_{\mathit{k}}^{\mathit{e}}$$ (24)

where ∇_k is the derivative of the wave number. The first-order term is

$$\frac{\mathit{T}}{\mathit{V}}{\displaystyle \sum _{\mathit{k}}}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}\mathit{q}\cdot {\nabla }_{\mathit{k}}{\mathit{G}}_{\mathit{k}}^{\mathit{e}}=\frac{\mathit{T}}{\mathit{V}}{\displaystyle \sum _{\mathit{k}}}{\mathit{q}}_{\mathit{i}}\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{i}}}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^2=0$$ (25)

The second-order term is

$$\begin{array}{c}\frac{\mathit{T}}{\mathit{V}}{\displaystyle \sum _{\mathit{k}}}\frac{1}{2}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}{(\mathit{q}\cdot {\nabla }_{\mathit{k}})}^2{\mathit{G}}_{\mathit{k}}^{\mathit{e}}=-\frac{\mathit{T}}{2\mathit{V}}{\displaystyle \sum _{\mathit{k}}}\mathit{q}\cdot {\nabla }_{\mathit{k}}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}\mathit{q}\cdot {\nabla }_{\mathit{k}}{\mathit{G}}_{\mathit{k}}^{\mathit{e}}\\ =\frac{\mathit{T}}{2\mathit{V}}{\displaystyle \sum _{\mathit{k}}}{\mathit{q}}_{\mathit{i}}{\mathit{q}}_{\mathit{j}}\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{i}}}\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{j}}}{({\mathit{G}}_{\mathit{k}}^{\mathit{h}})}^2{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^2\\ =\frac{\mathit{T}}{\mathit{V}}{\mathrm{\epsilon }}_{\mathit{q}}^0{\displaystyle \sum _{\mathit{k}}}({\mathrm{\epsilon }}_{\mathit{k}}^0+3\mathrm{\lambda }{\mathit{f}}_{\mathit{k}}){({\mathit{G}}_{\mathit{k}}^{\mathit{h}})}^2{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^2\\ =\frac{\mathit{T}}{\mathit{V}}{\mathrm{\epsilon }}_{\mathit{q}}^0{\displaystyle \sum _{\mathit{k}}}{\mathrm{\epsilon }}_{\mathit{k}}^0{({\mathit{g}}_{\mathit{k}}^{\mathit{e}})}^2{({\mathit{g}}_{\mathit{k}}^{\mathit{h}})}^2\\ =\frac{\mathrm{\pi }\mathrm{\nu }\mathit{T}}{2}{\mathrm{\epsilon }}_{\mathit{q}}^0{\displaystyle \sum _{\mathit{n}}}\frac{\mathrm{\mu }+{\mathrm{\Delta }}_{\text{SO}}}{{|{\mathrm{\omega }}_{\mathit{n}}|}^3}\\ =\frac{7\mathrm{\zeta }(3)}{16}\frac{{\mathit{ħ}}^2\mathrm{\nu }(\mathrm{\mu }+{\mathrm{\Delta }}_{\text{SO}})}{\mathit{m}{(\mathrm{\pi }\mathit{T})}^2}{\mathit{q}}^2\end{array}$$ (26)

The third-order term is

$$\begin{array}{c}\frac{\mathit{T}}{\mathit{V}}{\displaystyle \sum _{\mathit{k}}}\frac{1}{6}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}{(\mathit{q}\cdot {\nabla }_{\mathit{k}})}^3{\mathit{G}}_{\mathit{k}}^{\mathit{e}}\\ =\frac{\mathit{T}}{\mathit{V}}{\displaystyle \sum _{\mathit{k}}}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}{\mathit{q}}_{\mathit{i}}{\mathit{q}}_{\mathit{j}}{\mathit{q}}_{\mathit{k}}[\frac{1}{6}\frac{{\partial }^3{\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{i}}\partial {\mathit{k}}_{\mathit{j}}\partial {\mathit{k}}_{\mathit{k}}}{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^2+\frac{{\partial }^2{\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{i}}\partial {\mathit{k}}_{\mathit{j}}}\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{k}}}{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^3+\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{i}}}\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{j}}}\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\partial {\mathit{k}}_{\mathit{k}}}{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^4]\\ =\frac{\mathit{T}}{\mathit{V}}{\mathit{f}}_{\mathit{q}}{\displaystyle \sum _{\mathit{k}}}{\mathit{G}}_{\mathit{k}}^{\mathit{h}}{({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^2[\mathrm{\lambda }+6{\mathrm{\lambda }\mathrm{\epsilon }}_{\mathit{k}}^0{\mathit{G}}_{\mathit{k}}^{\mathit{e}}+(\frac{{\hslash }^6}{4{\mathit{m}}^3}{\mathit{f}}_{\mathit{k}}+9\mathrm{\lambda }{({\mathrm{\epsilon }}_{\mathit{k}}^0)}^2\left){({\mathit{G}}_{\mathit{k}}^{\mathit{e}})}^2\right]\\ =\frac{\mathit{T}}{\mathit{V}}\mathrm{\lambda }{\mathit{f}}_{\mathit{q}}{\displaystyle \sum _{\mathit{k}}}{\mathit{g}}_{\mathit{k}}^{\mathit{h}}{({\mathit{g}}_{\mathit{k}}^{\mathit{e}})}^2[1+6{\mathrm{\epsilon }}_{\mathit{k}}^0{\mathit{g}}_{\mathit{k}}^{\mathit{e}}+9{({\mathrm{\epsilon }}_{\mathit{k}}^0)}^2{({\mathit{g}}_{\mathit{k}}^{\mathit{e}})}^2+{({\mathrm{\epsilon }}_{\mathit{k}}^0)}^3{({\mathit{g}}_{\mathit{k}}^{\mathit{e}})}^2(4{\mathit{g}}_{\mathit{k}}^{\mathit{e}}-{\mathit{g}}_{\mathit{k}}^{\mathit{h}})]\\ =\mathrm{\pi }\mathit{T}{\mathrm{\lambda }\mathrm{\Delta }}_{\mathrm{Z}}\mathrm{\nu }{\mathit{f}}_{\mathit{q}}{\displaystyle \sum _{\mathit{n}}}(\frac{1}{2{|{\mathrm{\omega }}_{\mathit{n}}|}^3}+\frac{3{(\mathrm{\mu }+{\mathrm{\Delta }}_{\text{SO}})}^2}{{|{\mathrm{\omega }}_{\mathit{n}}|}^5})\\ =\mathrm{\pi }\mathit{T}{\mathrm{\lambda }\mathrm{\Delta }}_{\mathrm{Z}}\mathrm{\nu }{\mathit{f}}_{\mathit{q}}[\frac{7\mathrm{\zeta }(3)}{8}\frac{1}{{(\mathrm{\pi }\mathit{T})}^3}+\frac{93\mathrm{\zeta }(5)}{16}\frac{{(\mathrm{\mu }+{\mathrm{\Delta }}_{\text{SO}})}^2}{{(\mathrm{\pi }\mathit{T})}^5}]\\ \approx \frac{93\mathrm{\zeta }(5)}{16}\frac{\mathrm{\nu }{(\mathrm{\mu }+{\mathrm{\Delta }}_{\text{SO}})}^2{\mathrm{\Delta }}_{\mathit{Z}}\mathrm{\lambda }}{{(\mathrm{\pi }\mathit{T})}^4}{\mathit{f}}_{\mathit{q}}\end{array}$$ (27)

Finally, by adding the two contributions in Eq. 21 and defining the wave function ${\mathrm{\Psi }}_{\mathit{q}}=\sqrt{\frac{7\mathrm{\zeta }(3)\mathit{n}}{2{(\mathrm{\pi }{\mathit{T}}_{\mathrm{c}})}^2}}{\mathrm{\Delta }}_{\mathit{q}}$ with the electron number n, we obtained the GL free energy as

$$\mathit{F}={\displaystyle \sum _{\mathit{q}}}[\mathit{a}+\frac{{\mathit{ħ}}^2{\mathit{q}}^2}{4\mathit{m}}+\mathrm{\Lambda }\mathit{B}{\mathit{q}}_{\mathit{x}}({\mathit{q}}_{\mathit{x}}^2-3{\mathit{q}}_{\mathit{y}}^2\left)\right]{|{\mathrm{\Psi }}_{\mathit{q}}|}^2+\frac{\mathit{b}}{2}{|{\mathrm{\Psi }}_{\mathit{q}}|}^4$$ (28)

where

$$\mathrm{\Lambda }=\frac{93\mathrm{\zeta }(5)\mathit{g}{\mathrm{\mu }}_{\mathrm{B}}{\mathrm{\Delta }}_{\text{SO}}\mathrm{\lambda }}{28\mathrm{\zeta }(3){(\mathrm{\pi }{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}})}^2}$$ (29)

a = 4(πk_BT_c)²ϵ/7ζ(3)ε_F and b = a/8nϵ are the conventional coefficients in the GL theory.

Then, if we neglect the interaction term for T_c ≲ T, then we have

$${\mathrm{\eta }}_{\mathit{q}}(\mathit{t})=\mathit{a}+\frac{{\mathit{ħ}}^2}{4\mathit{m}}{(\mathit{q}-\frac{2\mathit{e}}{\mathit{ħ}}\mathit{E}\mathit{t})}^2+\mathrm{\Lambda }\mathit{B}({\mathit{q}}_{\mathit{x}}-\frac{2\mathit{e}}{\mathit{ħ}}{\mathit{E}}_{\mathit{x}}\mathit{t})\times [{({\mathit{q}}_{\mathit{x}}-\frac{2\mathit{e}}{\mathit{ħ}}{\mathit{E}}_{\mathit{x}}\mathit{t})}^2-3{({\mathit{q}}_{\mathit{y}}-\frac{2\mathit{e}}{\mathit{ħ}}{\mathit{E}}_{\mathit{y}}\mathit{t})}^2]$$ (30)

$${\mathit{j}}_{\mathit{q}}(\mathit{t})=-\frac{\mathit{e}\mathit{ħ}}{\mathit{m}}(\mathit{q}-\frac{2\mathit{e}}{\mathit{ħ}}\mathit{E}\mathit{t})-\frac{6\mathit{e}\mathrm{\Lambda }\mathit{B}}{\mathit{ħ}}\mathit{F}(\mathit{q}-\frac{2\mathit{e}}{\mathit{ħ}}\mathit{E}\mathit{t})$$ (31)

where we introduced $\mathit{F}(\mathit{E})=({\mathit{E}}_{\mathit{x}}^2-{\mathit{E}}_{\mathit{y}}^2,-2{\mathit{E}}_{\mathit{x}}{\mathit{E}}_{\mathit{y}})$. Note that the model is valid only in a small momentum region. By applying Eq. 18 and expanding the excess current with respect to both of λ and E, we obtained

$$\mathit{j}=\frac{{\mathit{e}}^2}{16\mathit{ħ}}{\mathrm{ϵ}}^{-1}\mathit{E}-\frac{\mathrm{\pi }{\mathit{e}}^3\mathit{m}\mathrm{\Lambda }\mathit{B}}{64{\mathit{ħ}}^3{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{c}}}{\mathrm{ϵ}}^{-2}\mathit{F}(\mathit{E})$$ (32)

which is Eq. 4.

Normal state transport

We calculated the normal state conductivity on the basis of the Boltzmann theory with the relaxation time approximation. The Boltzmann equation is

$${\partial }_{\mathit{t}}\mathit{f}+\stackrel{.}{\mathit{r}}\cdot {\partial }_{\mathit{r}}\mathit{f}+\stackrel{.}{\mathit{k}}\cdot {\partial }_{\mathit{k}}\mathit{f}=-\frac{\mathit{f}-{\mathit{f}}^0}{\mathrm{\tau }}$$ (33)

where τ is the relaxation time and f and f⁰ are the nonequilibrium and equilibrium distribution functions, respectively. For the uniform and stationary system, we have

$$\stackrel{.}{\mathit{k}}\cdot {\partial }_{\mathit{k}}\mathit{f}=-\frac{\mathit{f}-{\mathit{f}}^0}{\mathrm{\tau }}$$ (34)

The equation of motion of the wave packet is

$$\mathit{ħ}\stackrel{.}{\mathit{k}}=-\mathit{e}\mathit{E}$$ (35)

where we ignored the magnetic field and Berry curvature contributions. By solving the equation iteratively, we obtained

$$\mathit{f}\approx {\mathit{f}}^0+\frac{\mathrm{\tau }\mathit{e}}{\mathit{ħ}}\mathit{E}\cdot {\partial }_{\mathit{k}}({\mathit{f}}^0+\frac{\mathrm{\tau }\mathit{e}}{\mathit{ħ}}\mathit{E}\cdot {\partial }_{\mathit{k}}{\mathit{f}}^0)$$ (36)

Then, the current density was calculated as

$$\mathit{j}=-\mathit{e}{\displaystyle \int }\frac{\mathit{d}\mathit{k}}{{(2\mathrm{\pi })}^2}{\mathit{v}}_{\mathit{k}}{\mathit{f}}_{\mathit{k}}$$ (37)

where ${\mathbf{v}}_{\mathit{k}}=\frac{\partial {\mathrm{\epsilon }}_{\mathit{k}}}{\mathit{ħ}\partial \mathit{k}}$ is the group velocity. The (↑,+) band contribution is

$$\mathit{j}=\frac{\mathrm{\tau }{\mathit{e}}^2\mathit{n}}{\mathit{m}}\mathit{E}-\frac{6{\mathrm{\lambda }\mathrm{\tau }}^2{\mathit{e}}^3\mathit{n}}{{\mathit{ħ}}^3}\mathit{F}(\mathit{E})$$ (38)

The contribution from the (↑,+) and (↓,−) bands is

$$\mathit{j}=\frac{2\mathrm{\tau }{\mathit{e}}^2\mathit{n}}{\mathit{m}}\mathit{E}-\frac{12{\mathrm{\lambda }\mathrm{\tau }}^2{\mathit{e}}^3{\mathrm{\Delta }}_{\mathit{Z}}\mathrm{\nu }}{{\mathit{ħ}}^3}\mathit{F}(\mathit{E})$$ (39)

Then, the total current density from all the four bands is

$$\mathit{j}=\frac{4\mathrm{\tau }{\mathit{e}}^2\mathit{n}}{\mathit{m}}\mathit{E}$$ (40)

which shows that the system has no nonreciprocal response in the lowest order of q.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1602390/DC1

Effect of the Rashba term