Global detection approach for clustered microcalcifications in mammograms using a deep learning network

Abstract.

In computerized detection of clustered microcalcifications (MCs) from mammograms, the traditional approach is to apply a pattern detector to locate the presence of individual MCs, which are subsequently grouped into clusters. Such an approach is often susceptible to the occurrence of false positives (FPs) caused by local image patterns that resemble MCs. We investigate the feasibility of a direct detection approach to determining whether an image region contains clustered MCs or not. Toward this goal, we develop a deep convolutional neural network (CNN) as the classifier model to which the input consists of a large image window ($1{\mathrm{cm}}^2$ in size). The multiple layers in the CNN classifier are trained to automatically extract image features relevant to MCs at different spatial scales. In the experiments, we demonstrated this approach on a dataset consisting of both screen-film mammograms and full-field digital mammograms. We evaluated the detection performance both on classifying image regions of clustered MCs using a receiver operating characteristic (ROC) analysis and on detecting clustered MCs from full mammograms by a free-response receiver operating characteristic analysis. For comparison, we also considered a recently developed MC detector with FP suppression. In classifying image regions of clustered MCs, the CNN classifier achieved 0.971 in the area under the ROC curve, compared to 0.944 for the MC detector. In detecting clustered MCs from full mammograms, at 90% sensitivity, the CNN classifier obtained an FP rate of 0.69 clusters/image, compared to 1.17 clusters/image by the MC detector. These results indicate that using global image features can be more effective in discriminating clustered MCs from FPs caused by various sources, such as linear structures, thereby providing a more accurate detection of clustered MCs on mammograms.

1. Introduction

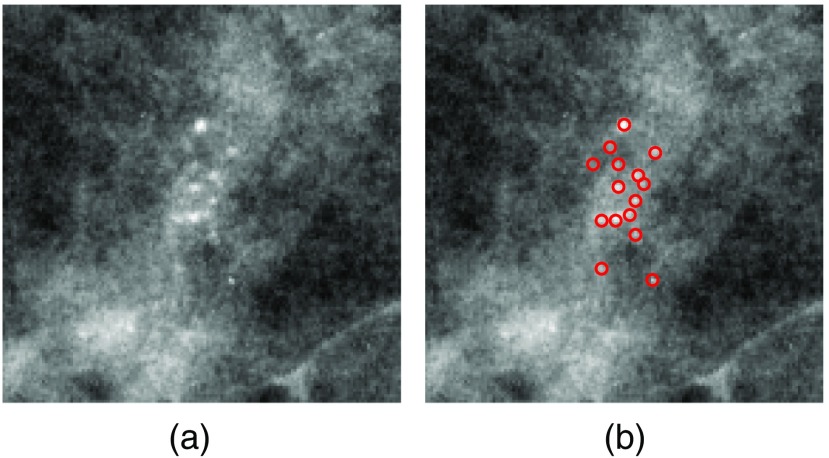
Breast cancer is currently the most frequently diagnosed nonskin cancer in women. It is estimated that about 252,710 new breast cancer cases will occur among women in the United States in 2017.¹ Mammography is currently an effective screening tool for diagnosis of breast cancer, which can detect about 80% to 90% of breast cancer cases in women without symptoms.¹ One important early sign of breast cancer in mammograms is the appearance of clustered microcalcifications (MCs), which are found in 30% to 50% of mammographically diagnosed cancer cases.² MCs are tiny calcium deposits that appear as bright spots in mammograms [Fig. 1(a)]. Clustered MCs can be found in both benign and malignant cases. Compared to benign MCs, malignant MCs tend to be more irregular in shape and exhibit a wider range of variability within a cluster.³

Fig. 1.

(a) An example ROI with clustered MCs ($140\times 140\text{pixels}$ and $0.1\mathrm{mm}/\text{pixel}$) and (b) locations of individual MCs marked by red circles.

Despite their frequent appearance, accurate detection of clustered MCs can be a challenging task due to the subtlety of MCs.² As shown in Fig. 1, the MCs in a cluster may vary greatly in terms of their shape, size, and image contrast. In the literature, there have been great efforts in development of computerized methods for the automatic detection of clustered MCs in mammograms (e.g., Refs. ^4–10). While such methods are successful in achieving high sensitivity, an often-cited problem is the frequent occurrence of false positives (FPs). There are many factors that can contribute to the occurrence of FPs, including MC-like noise patterns, linear structures, inhomogeneity in tissue background, imaging artifacts, etc.¹⁰ In screening mammography, the purpose of a computerized system is to identify suspicious regions in a mammogram for further consideration. Thus, it is critical to keep the FPs low while maintaining a high true-positive (TP) rate.

Traditionally, detection of clustered MCs is performed in two typical steps. In the first step, an MC detector (i.e., pattern classifier) is applied to locate the candidates of individual MCs in a mammogram image; in the second step, the detected MCs are grouped into clusters according to a set of clustering criteria. Based on the fact that MCs are limited in extent (typically 0.1 to 1 mm in diameter), almost all the existing MC detectors are designed to exploit the local image characteristics at a detection location. For example, Oliver et al.⁸ extracted features by using a filter bank to obtain a description of the local morphology of an MC; Salfity et al.⁵ used a difference-of-Gaussians (DoG) filter wherein the filter consisted of two kernels of limited width parameters. El-Naqa et al.⁷ adopted a local image window centered at a location under consideration.

While it is natural and computationally efficient for an MC detector to utilize local image features, it also makes the detector susceptible to FPs associated with local image patterns that resemble MCs. For example, when examined locally, a segment of a linear structure can resemble an MC due to its high image contrast and shape.¹⁰ Because of this, in the literature there exist many studies on how to suppress FPs in detecting MCs by also utilizing global image features in the context of a detection location. For example, noise equalization techniques were developed for reducing the noise variability in a mammogram;^11,12 background removal methods were used to suppress the inhomogeneity in tissue background;¹³ there were also detection algorithms studied for linear and curve-like structures (attributed to vessels, ducts, fibrous tissue, skinfolds, edges, and other anatomical features);^9,10,14,15 and features derived from linear structures were used to reduce FPs in MC detection.^9,15,16 Recently, we developed a context-sensitive MC detector for FP reduction in which the detection classification function was adapted according to the presence or absence of linear structures.¹⁰

In this study, we investigate the feasibility of applying a direct detection approach for clustered MCs in a mammogram. Instead of first detecting the presence of individual MCs, we aim to employ a pattern classifier to determine in one step whether a given mammogram region contains clustered MCs or not. With this approach, the input to the classifier is no longer limited to the local image features at a detection location; instead, it consists of a more global image pattern that includes not only the potential individual MCs when they are present but also their surrounding context. This can avoid some of the pitfalls associated with a localized MC detector. For example, while a segment of a linear structure may resemble an MC, when examined on a larger scale, the image pattern of a linear structure can be easily differentiated from that of clustered MCs (as to be seen later in the results).

Specifically, we formulate the detection of clustered MC in a mammogram as a two-class classification problem as follows: for a mammogram region under consideration, we apply a pattern classifier to determine whether the image region contains clustered MCs (“cluster” class) or not (“noncluster” class). By definition, a cluster of MCs has at least three individual MCs contained within a $1{\mathrm{cm}}^2$ area in a mammogram.¹⁷ However, without knowing either the number or the locations of individual MCs in a mammogram region, it is difficult to design and extract a set of features to directly characterize their presence within the region. Note that the individual MCs are far smaller in size than a $1{\mathrm{cm}}^2$ area (a typical MC is only about 0.3 mm in diameter). To deal with this issue, we consider a deep convolutional neural network (CNN) as the classifier model. By exploiting the learning capabilities of a deep CNN architecture in multiscale spatial processing and feature extraction, we aim to investigate whether it can effectively detect the presence of clustered MCs in a large input image region.

In recent years, deep CNN has increasingly been applied in many pattern classification applications, ranging from digit recognition,¹⁸ object detection,¹⁹ to image classification.^20–22 It was demonstrated that the features automatically extracted by CNN could outperform manually designed features in image classification problems.^23,24 Deep CNN has been also applied in many medical imaging applications. For example, in Ref. 25, a max-pooling CNN was studied for mitosis detection in breast cancer histology images; in Ref. 26, a CNN was used to refine candidate lesions in sclerotic spine metastases detection in CT images; in Ref. 27, a multiscale CNN was developed for lung nodule detection in CT images; and, in Ref. 28, a 12-layer CNN was applied for cardiovascular disease detection from mammograms. Most recently, Mordang et al.²⁹ applied two CNNs for MC detection in multivendor mammography, in which a shallower CNN was trained to remove easy samples and a deeper CNN was used for the survived samples; Samala et al.³⁰ used a deep CNN to reduce FPs in MC detection in digital breast tomosynthesis. Both of these detectors were focused on the detection of individual MCs. To the best of our knowledge, no work has been reported on direct detection of clustered MCs from a mammogram region.

The rest of the article is organized as follows. The formulation of a CNN classifier for clustered MC detection is described in Sec. 2. The experiments for evaluating the performance of the proposed CNN detector are described in Sec. 3, and the evaluation results are presented in Sec. 4. Finally, conclusions are given in Sec. 5.

2. CNN Formulation for Microcalcification Cluster Detection

2.1. Overview

In this study, we formulate the detection of clustered MCs as a two-class classification problem, wherein a CNN classifier is applied to determine whether a given mammogram region contains clustered MCs (“cluster” class) or not (“noncluster” class). For this purpose, the input image region to the classifier is chosen to be sufficiently large (e.g., $1{\mathrm{cm}}^2$ in area) in order for it to cover the presence of multiple MCs. Instead of deriving descriptive image features, we directly input the image region under consideration to the classifier and exploit the feature learning capabilities of the CNN through supervised learning. One major advantage of deep CNN is that it can automatically learn lower-level to higher-level features in the input data through its multiple convolutional layers.³¹ The specific CNN structure used in this study is given in detail below.

2.2. Deep CNN Architecture

By design, a deep CNN is typically comprised of a cascade of multiple convolutional layers, followed by one or more fully connected layers (FC) as in a standard feedforward neural network. In this study, we consider a network architecture based on the popular AlexNet²⁰ and VGG network.³² We illustrate this architecture in Fig. 2 with a seven-layer network that consists of five convolutional layers (Conv) and two FC layers. These seven layers are known as learning layers, of which the associated parameters are determined from training. In addition, each of the first three convolutional layers is followed by a max-pooling (pooling) layer and a local response normalization layer (LRN), and the last convolutional layer is followed by a max-pooling layer. These different types of layers are briefly described below.

Fig. 2.

Architecture of deep CNN considered in this study. It includes five convolutional (Conv) layers and two fully connected layers.

As shown in Fig. 2, the convolutional layers are used to extract the features in the input image at varying spatial scales. Within each convolutional layer, a set of convolutional filters is used to operate on the input, from which the output is fed into the subsequent layer. The output of each filter is called a feature map. For example, the first layer has 32 filters, yielding 32 feature maps. More specifically, for a given layer, let ${\mathbf{x}}_k$ denote the $k$’th input feature map, and ${\mathbf{h}}_j^k$ denote its corresponding convolutional filter for output feature map $j$. Then, the output can be represented as

$${\mathbf{y}}_j=f(\sum _{k=1}^K{\mathbf{x}}_k*{\mathbf{h}}_j^k+b),$$ (1)

where * denotes the convolution operation, $K$ is the number of input maps, $b$ is a bias constant, and $f(·)$ is an activation function, which is a nonlinear transformation from the input to the output.

In this study, we use the standard rectifier function, called rectified linear unit (ReLU), for the activation function $f(·)$. Such a function is known to achieve faster training in deep CNN than the traditional sigmoid-type activation functions.²⁰ For each convolutional layer, the filters ${\mathbf{h}}_j^k$ are $3\times 3$ in size and are determined during the training phase. The rationale is that these filters are trained to automatically capture the spatial features in the input image relevant to the classification task at hand. Indeed, as to be demonstrated later in the results (Sec. 4.4), the response at the different layers reflects the image features of clustered MCs at scale levels in the input image.

Since it is impossible to determine beforehand the adequate network structure to use for our MC cluster detection problem, in this study we apply a validation procedure by varying the number of convolutional layers (as described below in Sec. 2.5).

In the network, the max-pooling layers are used to subsample the feature map by a factor of two at given layers. The rationale is to enable these Conv layers to extract image features at increasingly higher levels (i.e., scales). For each max-pooling layer, the maximal value of a $3\times 3$ window centered at every other location (i.e., with stride 2) of the feature map is obtained. This is indicated by $3\times 3s2$ in Fig. 2.

As shown in Fig. 2, the output at each max-pooling layer is further normalized by a so-called LRN. This is to achieve the effect of lateral inhibition where the activation of an excited neuron suppresses its neighbors. It is also used to suppress the potentially unbound activation output by an ReLU.²⁰ Specifically, let ${\mathbf{x}}_i(m,n)$ be the value of feature map $i$ at location $(m,n)$. Then, the LRN output is given by

$${\mathbf{y}}_i(m,n)={\mathbf{x}}_i(m,n)/{[1+\frac{\alpha }{n}\sum _{j=\max (1,i-q/2)}^{\min (K,i+q/2)}{\mathbf{x}}_j{(m,n)}^2]}^{\beta },$$ (2)

where $q$ is the number of adjacent feature maps at the same spatial location, and $K$ is the number of input feature maps. In this study, the parameters are set to be $q=5$, $\alpha ={10}^{-4}$, and $\beta =0.75$ according to the optimal parameters obtained in Ref. 20.

Finally, the two fully FCs in Fig. 2 play the same role as in a standard feedforward neural network.²⁰ Note that these two layers have 128 and 2 neurons, respectively. In the final output layer, a softmax activation function is used,²¹ of which the output can be interpreted as the probability of an input belonging to a particular class. As with the rest of the network, the parameters of the softmax function are also determined from training.

2.3. Classifier Input Image Pattern

As input to the CNN classifier, we choose a square image window of $M\times M$ pixels from a mammogram. Conceptually, this image window should be sufficiently large in extent so that it can effectively enclose the multiple MCs that may exist within a cluster. However, too large an input window can unduly increase both the computational complexity and the number of parameters to be determined in the CNN classifier. Considering that clustered MCs are typically distributed locally in a mammogram and that they are well within an $1{\mathrm{cm}}^2$ area in extent, we choose the image window to be $95\times 95$ (for spatial resolution $0.1\mathrm{mm}/\text{pixel}$), as shown in Fig. 2.

In Fig. 3, we show examples of several extracted image windows containing clustered MCs. These examples show different numbers of MCs and different spatial extent patterns of MCs. For comparison, several examples of image windows without any MCs are also shown. For better visualization of the MCs, the tissue background is suppressed in these images.

Fig. 3.

Examples of input image windows for both (a) “cluster” and (b) “noncluster” classes.

2.4. Generation of Training Samples

The effective training of the CNN classifier requires a large number of training samples. For this purpose, we make use of a large set of mammogram images of which all contain clustered MCs (Sec. 3.1). To maximize the yield of training samples, we extract multiple image windows for the “cluster” class from each mammogram image as follows: (1) select randomly $P$ locations from the region of clustered MCs within the mammogram; (2) at each of these $P$ locations, extract a $95\times 95$ window centered at the location such that it contains at least three MCs. This is based on the fact that by definition, an MC cluster in a mammogram has at least three MCs. Similarly, we extract a number of $2P$ image windows (without any MCs) for the “noncluster” class from the rest of the mammogram region.

Since the MC clusters can vary greatly both in area and in the number of MCs among different mammograms, we adjust the number of extracted samples accordingly in proportion to the area of an MC cluster. Specifically, let $A$ denote the area (measured by the number of pixels) of an MC cluster. Then, we set $P$ for each cluster as follows:

$$P=\{\begin{array}{cc}15& A<150\\ 150& A>1500\\ [0.1*A]& \text{otherwise}\end{array},$$ (3)

where $[·]$ is the nearest integer function. That is, the number of training samples from each MC cluster varies from 15 to 150 depending on the size of the cluster. With this strategy, there were $P=49.6$ samples on average extracted for the “cluster” class from each mammogram image.

To further enlarge the training set, we apply a data augmentation procedure in order to improve the CNN training.^20,33 Specifically, we apply the following operations to augment the extracted image samples in the training set: (1) flipping the image from left to right, (2) flipping the image up-down, and (3) rotating the image by 90 deg, 180 deg, and 270 deg, respectively. Note that these operations do not alter the spatial resolution of the samples, which is important in detection of MCs in a mammogram. In the end, the number of training samples is increased by five times after data augmentation. In the experiments, we found that such data augmentation could further improve the classification accuracy.

2.5. Model Training and Selection

To optimize the classifier model for our MC cluster detection problem, we vary the number of convolutional layers in the architecture shown in Fig. 2. For this purpose, we employ a validation set of “cluster” and “noncluster” samples (Sec. 3.1), which is independent of the training set. In our experiments, we started with a five-layer CNN (three Conv layers) and gradually increased the number of Conv layers until the best validation error was found. This was based on the observation that the number of layers tends to have a larger impact on performance than other parameters (such as the number of filters and filter size) in the design of deep architectures.³⁴ The different network structures considered in the experiments are summarized in Table 1; for brevity, the input layer and two FC layers shared by all the structures are omitted. As explained in Sec. 2.2, the convolutional layers in a network structure are trained to extract features from the input while the pooling layers are used to enable feature extraction at increasingly higher levels. For optimization, we varied the combinations of Conv and pooling layers in the four networks (as specified in Table 1). Specifically, in the five-layer, the spatial size of the feature maps was reduced successively from $95\times 95$ to $11\times 11$ with the use of three pooling layers (as shown in Fig. 2). For the other three architectures, the size of the feature maps was further reduced to $5\times 5$ with one additional pooling layer. Furthermore, as the number of layers increased in these three architectures, additional convolutional layers were introduced to further refine the feature maps. For each classifier structure model, the validation error, which is the fraction of samples in the validation set that are misclassified by the classifier, was computed at every 1000 iterations until the maximum number of iterations (20,000) was reached. In the end, the model with the smallest validation error was selected as the classifier model.

Table 1.

CNN structures used in classifier model optimization. For each structure, the presence of a layer is marked by ✓.

	# filters	Five-layer	Six-layer	Seven-layer	Eight-layer
Conv	32	✓	✓	✓	✓
Pooling	—	✓	✓	✓	✓
LRN	—	✓	✓	✓	✓
Conv	64	✓	✓	✓	✓
Pooling	—	✓	✓	✓	✓
LRN	—	✓	✓	✓	✓
Conv	128	✓	✓	✓	✓
Conv	128				✓
Pooling	—		✓	✓	✓
LRN	—		✓	✓	✓
Conv	256		✓	✓	✓
Conv	128			✓	✓
Pooling	—	✓	✓	✓	✓

For a given network structure, the associated various parameters are determined during the training phase. This is accomplished by minimizing the binomial logistic loss on the set of training samples, or equivalently, the cross-entropy between the model output and the actual labels of training samples.³⁵ In this study, we implemented our classifier models using the Caffe package developed by the Berkeley vision and learning center.³⁶ For model training, the stochastic gradient descent method was used³⁷ with a batch size of 256, a learning rate of 0.01, momentum of 0.9, and weight decay of 0.0005.²⁰ Moreover, to overcome the potential overfitting by the CNN model, a stochastic dropout technique³⁸ was applied to the first fully FC during training. This dropout procedure is a regularization technique in which the different neural units and their connections are randomly dropped from the network with a certain probability (0.5 was used in our experiments).

3. Experiments

3.1. Mammogram Dataset

In this study, we demonstrate the proposed approach using both screen-film mammogram (SFM) images and full-field digital mammogram (FFDM) images. We make use of 521 SFM images from 297 cases (151 benign/146 cancer) and 188 FFDM images (in for-processing format) from 95 cases (52 benign/43 cancer). All of the mammogram images were collected by the Department of Radiology at the University of Chicago. They were consecutive cases collected over different time periods and were all sent for biopsy due to the subtlety of their MC lesions. Each mammogram image has at least one cluster of MCs that was histologically proven. The SFM images were acquired using a Lumiscan film digitizer (Lumisys; Sunnyvale, California). The FFDM images were acquired using a Senographe 2000D FFDM system (General Electric Medical Systems; Milwaukee, Wisconsin). The FFDM images were preprocessed with logarithmic transformation³⁹ in this study. All the images were of $0.1\mathrm{mm}/\text{pixel}$ in spatial resolution. The MCs in each mammogram were manually identified by a group of experienced radiologists.

In the experiments, the mammogram images were randomly partitioned into three subsets, one with 167 cases (300 images: 91 FFDM and 209 SFM) for training, one with 67 cases (117 images: 43 FFDM and 74 SFM) for validation, and one with 158 cases (292 images: 54 FFDM and 238 SFM) for testing. It is noted that most of the cases have multiple views (mediolateral oblique view, cranio-caudal view, or views from both breasts). To avoid any potential bias, the different views from one case were assigned together to either the training, validation, or testing subset exclusively. For each mammogram image, the region of clustered MCs was formed by a morphological dilation from the locations of marked individual MCs. The structuring element used was a circular disk with a radius of 25 pixels. This region was used as ground truth for training sample extraction and detection performance evaluation.

Prior to MC detection, a background subtraction step was first applied to the mammogram image under consideration in order to suppress the inhomogeneity in the tissue background. For each location, the background was estimated as the average intensity of a circular region with a diameter of 7 pixels centered at the location.¹¹ Afterward, the resulting image was normalized to have zero mean and unit standard deviation.

In the experiments, we conducted two separate studies to evaluate the performance of the proposed CNN classifier. In the first study, we evaluated the accuracy of the classifier in differentiating MC “cluster” regions from “noncluster” regions using a portion of the test subset. In the second study, we evaluated the accuracy of the classifier in detection of MC clusters regions from mammograms. The details of these studies are described below.

3.2. Study 1: Classification Accuracy on MC Cluster Samples

In this study, we evaluated the accuracy of the trained CNN classifier on a set of “cluster” regions extracted from test mammogram images. For this purpose, we allocated 125 images from the test set of mammograms and applied the sample extraction procedure as in Sec. 2.4. This resulted in a total of 5134 “cluster” samples and 10,268 “noncluster” samples. No data augmentation was applied to these samples during testing.

To assess the classification accuracy on the test samples, we conducted a receiver operating characteristic (ROC) analysis. An ROC curve is a plot of the true-positive (TP) rate versus the false-positive (FP) rate as the decision threshold is varied in continuum over its operating range. To summarize the classification performance, the area under the ROC curve (AUC) was used. A larger AUC corresponds to better performance by the classifier.

For comparison, we also demonstrated the classification performance on the same set of test samples by an MC detector (unified SVM classifier) reported recently in Ref. 10. This detector was developed to suppress FPs caused by linear structures and MC-like noise patterns, and was demonstrated to yield improved performance over several detectors.¹⁰ In our experiments, this detector was first applied to detect the presence of individual MCs in each test sample region. The region was treated as “cluster” if there were three or more detections; otherwise, it was treated as “noncluster.” This was to be consistent with the clustering criterion. Afterward, the classification result was compared against of the truth of each image sample.

For statistical comparison of the two methods in ROC, a bootstrapping procedure⁴⁰ was applied on the set of test image samples. A total of 20,000 bootstrap samples were used.

3.3. Study 2: Detection of MC Clusters on Mammograms

We also demonstrated the performance of the CNN classifier in detection of MC clusters from mammograms. For this purpose, we used 167 images (113 SFM and 54 FFDM) from the remaining 84 cases in the test set. For a mammogram image, the CNN classifier was applied to each pixel location to detect the presence of an MC cluster or not. Symmetric padding was used near tissue boundaries where the input image windows enclosed pixels outside the breast tissue.

To evaluate the MC cluster detection performance, we conducted a free-response receiver operating characteristic (FROC) analysis. An FROC curve is a plot of the TP rate of detected MC clusters versus the average number FPs per image with the decision threshold varied continuously over its operating range.

In the FROC analysis, a detected region was considered as a TP cluster according to the following criterion:¹⁷ (1) it includes at least two true MCs and (2) its center of gravity is within 1 cm of that of a known true MC cluster region. Likewise, a detected region is considered as an FP cluster provided that (1) it contains no true MCs or (2) the distance between its center of gravity and that of any known cluster region is larger than 1 cm.

For comparison, we also tested the detection performance on the same set of test mammograms by the unified SVM classifier in Ref. 10. For the FROC analysis, the detected MCs in a mammogram were first grouped into cluster regions by dilation with a circular element of 25 pixels in radius. Those regions with fewer than three detections were discarded. Afterward, each detected region was determined to be TP or FP with the same criteria as above.

To reduce the effect of case variation, we applied a bootstrapping procedure on the set of test mammograms for obtaining the FROC.⁴¹ A total of 20,000 bootstrap samples were used, based on which the partial area under the FROC curve ($p\mathrm{AUC}$) was obtained. This bootstrapping procedure was also used to perform statistical comparison of the performance by the two detection methods.⁴¹ To speed up the FROC analysis, in the experiments we first applied a prescouting step as in Ref. 10 during which up to four most suspicious regions of $5\mathrm{cm}\times 5\mathrm{cm}$ in size were identified in each mammogram image for further consideration.

4. Results

4.1. Model Training and Selection

For model selection, in Table 2, we show the classification error achieved by the trained network on the image samples in the validation subset. For each network structure (from five-layer to eight-layer), the optimal classification error and the corresponding number of iterations are given in the first two rows in Table 2, respectively. In addition, the mean and standard deviation (std) of the classification error achieved by the network with different number of iterations are given in the third and fourth rows in Table 2, respectively. These values were calculated from the classification error of the trained network after 4000 iterations with an increment of 1000.

Table 2.

Classification errors achieved by different architectures on the validation set.

Network	Five-layer	Six-layer	Seven-layer	Eight-layer
Optimal error	0.0637	0.0594	0.0578	0.0587
Number of iterations	7000	8000	8000	9000
Mean error	0.0675	0.0649	0.0634	0.0649
Standard deviation	0.0032	0.0045	0.0037	0.0051

It can be seen from Table 2 that the seven-layer CNN achieved the best classification error of 0.0578 with 8000 iterations of training. Moreover, it is noted that the seven-layer CNN achieved the lowest mean error of 0.0634, along with the second lowest std of 0.0037. Based on these results, the seven-layer CNN was chosen as the best structure for subsequent evaluation in detection of MC clusters.

4.2. Test 1: Classification Accuracy on MC Cluster Samples

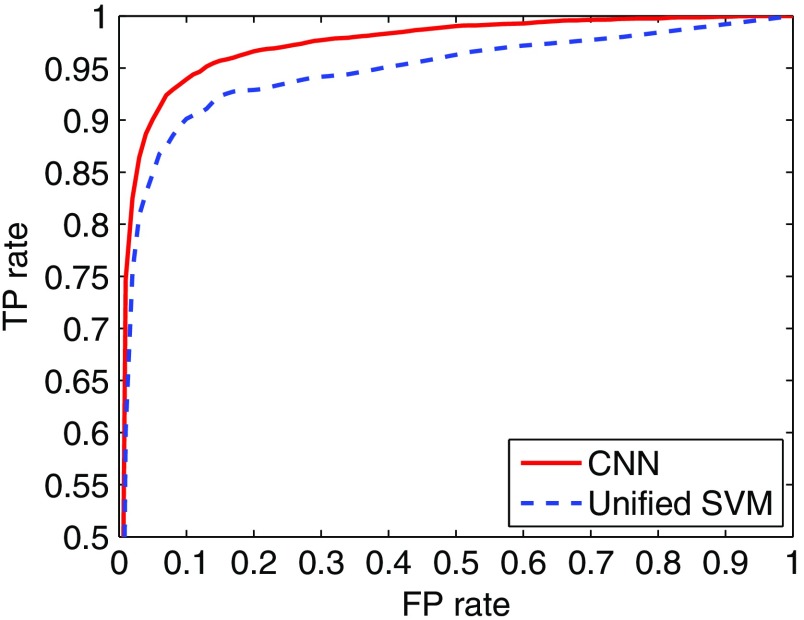
In Fig. 4 we show the ROC curve obtained by the seven-layer CNN classifier on the test set of cluster and noncluster samples. For comparison, the ROC curve obtained by the unified SVM detector is also shown in Fig. 4. As can be seen, the ROC curve is notably higher (hence better classification performance) for the CNN classifier. Indeed, its AUC value is 0.971, compared to 0.944 for the unified SVM. A statistical comparison between the two yields a $p\text{-}\text{value}<{10}^{-4}$ and a 95% confidence interval (C. I.) of [0.0233, 0.0308] on the AUC difference. In particular, with TP rate at 95%, the CNN classifier achieved an FP rate of 12.71%, compared to 39.08% for the unified SVM. The results indicate that the CNN classifier could significantly reduce the FP rate in classifying image regions of MC clusters.

Fig. 4.

ROC curves obtained by the CNN classifier and the unified SVM detector.

4.3. Test 2: Detection of MC Clusters on Mammograms

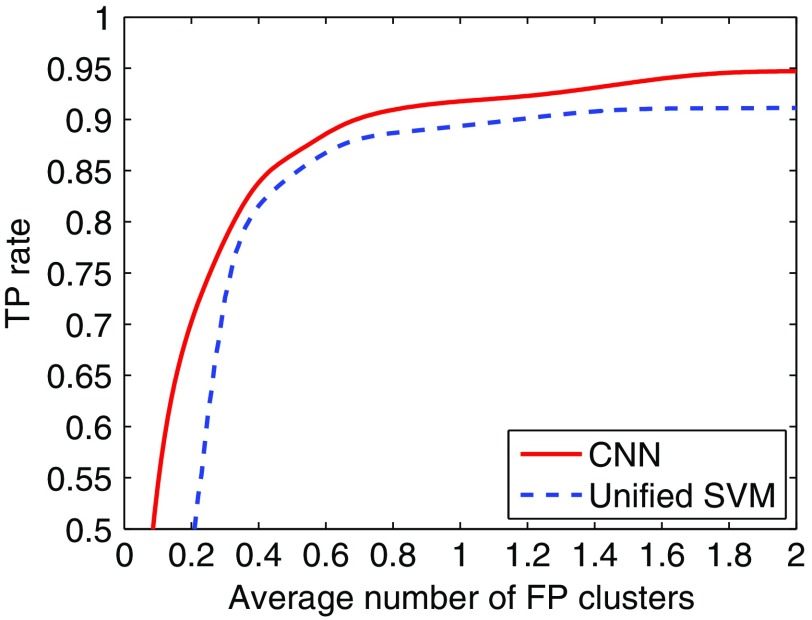
In Fig. 5, we show the FROC curve obtained by the CNN classifier in detection of MC clusters in mammograms. For comparison, the FROC curve obtained with the unified SVM detector is also shown. As can be seen, the FROC curve is higher for the CNN classifier. A statistical comparison between the two yields a difference of 0.0981 in $p\mathrm{AUC}$ ($p\text{-}\text{value}=0.0082$) for FP rate over the range of [0, 2] clusters/image (95% C. I. of [0.0170, 0.1792] in $p\mathrm{AUC}$ difference). In particular, with TPF at 90%, the CNN classifier achieved an FP rate of 0.69 clusters/image, compared to 1.17 by the unified SVM (a reduction of 41.03%). Moreover, with FP rate at 0.5 clusters/image the CNN classifier achieved a sensitivity of 86.55%, compared to 84.58% for the unified SVM.

Fig. 5.

FROC curves obtained by the CNN classifier and the unified SVM detector.

In the experiments, the unified SVM detector was implemented in MATLAB^® and it took 1.96 s per mammogram on average (Intel Core i7-3770 CPU, 3.40 GHz, 16 GB memory). The CNN detector was implemented using the Caffe package and it took 45.24 s per mammogram on average (GPU of GeForce GTX TITAN X with 12 GB memory). Both detectors were applied to the mammogram images after the prescouting step (Sec. 3.3).

4.4. Visual Interpretation of Feature Maps

The results both on classification of cluster image samples and on detection of MC clusters in mammograms above demonstrate that the CNN classifier is more effective in rejection of FPs. To illustrate how the CNN classifier achieved this through its multiple layers of feature extraction, below we examine the response on several representative image samples with and without clustered MCs. Specifically, in Fig. 6(a), we show an image sample ($95\times 95$ pixels in size) of clusters MCs; in Figs. 6(b)–6(f), we show the corresponding response at the five Conv layers, where the two feature maps with the highest energy in response within each layer are shown. As can be seen, the individual MCs generated high response in Figs. 6(b) and 6(c), which appears to match the local image features of MCs. Furthermore, the multiple MCs also led to high response in Figs. 6(e) and 6(f), although the locations of individual MCs seem to have been somewhat suppressed. The predicted probability is 0.9996 by the CNN classifier for this sample to be an MC cluster, indicating a high confidence for the cluster class.

Fig. 6.

(a) An input image sample of clustered MCs; (b)–(f) feature maps obtained from the first to the fifth Conv layers, respectively. For each layer, the two feature maps with the highest energy in response are shown.

For comparison, in Fig. 7(a), we show a noncluster image sample that has no MCs. As in Fig. 6 above, the two feature maps with the highest response are shown for each of the five Conv layers in Figs. 7(b)–7(f). These feature maps are shown in the same range as their counterparts in Fig. 6. As can be seen, these feature maps show that the response is much lower for the input image in Fig. 7(a), indicating that there is no relevant MC features. Indeed, the predicted probability by the CNN classifier is 0.0087 for this sample to be an MC cluster, indicating a high confidence for the noncluster class.

Fig. 7.

(a) An input image sample without any MCs; (b)–(f) feature maps obtained from the first to the fifth Conv layers, respectively. For each layer, the two feature maps with the highest energy in response are shown.

Finally, in Fig. 8(a), we show a noncluster image sample with the presence of linear structures, which are a known cause of FPs in MC detections.^9,10 The corresponding two feature maps with the highest response are shown for each of the five layers in Figs. 8(b)–8(f). As can be seen, the linear structures generated some noticeable response in the lower layer maps in Figs. 8(b) and 8(c). However, they are effectively suppressed in the higher layer maps in Figs. 8(d)–8(f). Indeed, the predicted probability by the CNN classifier for this sample to be an MC cluster is only 0.0034, indicating a high confidence for the noncluster class.

Fig. 8.

(a) An input image sample with linear structures present; (b)–(f) feature maps obtained from the first to the fifth Conv layers, respectively. For each layer, the two feature maps with the highest energy in response are shown.

The above examples illustrate that the first two Conv layers in the network mainly respond to low-level image patterns, such as edges of MCs and linear structures. However, the later Conv layers in the network have the capability to discriminate MCs from other non-MC features such as linear structures. The latter is believed to have contributed to the reduction of FPs in classification of cluster versus noncluster samples.

4.5. Discussions

In this work, we developed a deep learning approach for directly identifying whether a given image region contains multiple MCs or not. Such an approach allows the MC signals to be processed on a scale much larger than the size of individual MCs by the classifier. When applied to a mammogram, the CNN classifier is designed to detect the presence of suspicious regions of clustered MCs for further consideration. Our evaluation results demonstrate that it could effectively reduce the level of FPs in detection of clustered MCs.

However, unlike traditional MC detectors that are aimed for detecting individual MCs, the CNN classifier does not localize the individual MCs in a detected region. Nevertheless, if there is a need in applications for individual MCs to be further analyzed, for example, in computerized analysis of a detected MC lesion being malignant or benign,⁴² one may apply an existing MC detector (e.g., DoG detector⁵ or SVM detector⁷) to further localize the individual MCs in a detected region by the CNN classifier. It would be interesting to investigate the accuracy of the resulting individual MCs with such an approach in the future. It would be also interesting to incorporate the location of individual MCs in the training of a deep CNN classifier for locating the individual MCs in a cluster.

Noted that the FROC curve for MC detection can be sensitive to a number of factors, including the detection criteria used¹⁷ and the distribution of cases in the test set, so one has to be cautious when comparing the FROC results reported from different sources. However, the relative performance by the different methods with respect to a common set of criteria and test cases tends to be consistent.⁷ In this study, we compared the performance of CNN (a cluster-based detector) and the unified SVM (an MC-based detector). The comparison between them may not be completely equivalent because of the use of the clustering and dilation of the MC detections in the unified SVM.

Finally, all of the cases used in this study contain MC clusters. It might be desirable to also include a number of normal cases with no MC clusters. However, the spatial extent of an MC cluster in a mammogram is typically well localized to a small area ($<1{\mathrm{cm}}^2$); the overwhelming majority of the area in a mammogram does not have any MCs and thus can be viewed as a substitute for normal mammograms. Therefore, the reported FPs per image in the FROC analysis would likely change little when normal cases are included.

5. Conclusion

In this study, we investigated the feasibility of a direct detection approach for clustered MCs in mammograms. That is, for a given mammogram region, we aimed to determine whether it contains clustered MCs or not. We formulated this task as a two-class classification problem and developed a deep CNN classifier to discriminate between “cluster” and “noncluster” classes. We demonstrated this approach with both SFM and FFDM images in this study, which included 521 SFM images and 188 FFDM images. We evaluated the performance of the proposed method both on classification of image regions of clustered MCs and on detection of clustered MCs on mammograms. The results demonstrate that the proposed approach can improve the detection performance significantly, both in classifying image regions of clustered MCs and in detecting clustered MCs on mammograms. In the future, it would be interesting to further investigate how this approach can be adapted for locating the individual MCs in a detected image region.

Biographies

Juan Wang is a research scientist at Delta Micro Technology Inc., Laguna Hills, California, USA. She received her BS and MS degrees in electrical engineering from the University of Electronic Science and Technology of China, in 2007 and 2010, respectively, and her PhD in electrical engineering from the Illinois Institute of Technology in 2015. This work was done when she was at Illinois Institute of Technology. Her research interests are in medical imaging, machine learning, and deep learning.

Robert M. Nishikawa is currently a professor and director of the Clinical Translational Medical Physics Lab in the Department of Radiology at the University of Pittsburgh. He has over 200 publications in breast imaging. He is a fellow of the American Association of Physicists in Medicine, the Society of Breast Imaging, the College of American Institute for Medical and Biological Engineering. His research interests are in computer-aided diagnosis, breast imaging, image quality assessment, and evaluation of medical technologies.

Yongyi Yang is a Harris Perlstein professor at the Department of Electrical and Computer Engineering, Illinois Institute of Technology. His research interests are in medical imaging, machine learning, pattern recognition, and biomedical applications. He has authored or coauthored over 250 peer-reviewed publications in these areas. His recent research activities are mostly in computerized techniques for breast cancer detection and diagnosis, and in image reconstruction methods for cardiac diagnostic imaging.

Disclosures

The authors have no competing interests to declare.