Unraveling the disease consequences and mechanisms of modular structure in animal social networks

Significance

Modular organization in animal social networks is hypothesized to alleviate the cost of disease burden in group-living species. However, our analysis of empirical social networks of 43 animal species along with theoretical networks demonstrates that infectious disease spread is largely unaffected by the underlying modular organization, except when social networks are extremely subdivided. We show that high fragmentation and high subgroup cohesion, which are both associated with high modularity in social networks, induce structural delay and trapping of infections that spread through these networks, reducing disease burden. We validate our results using real animal social networks and recommend the use of appropriate null network models when data-limited estimates of epidemic consequences are necessary.

Abstract

Disease risk is a potential cost of group living. Although modular organization is thought to reduce this cost in animal societies, empirical evidence toward this hypothesis has been conflicting. We analyzed empirical social networks from 43 animal species to motivate our study of the epidemiological consequences of modular structure in animal societies. From these empirical studies, we identified the features of interaction patterns associated with network modularity and developed a theoretical network model to investigate when and how subdivisions in social networks influence disease dynamics. Contrary to prior work, we found that disease risk is largely unaffected by modular structure, although social networks beyond a modular threshold experience smaller disease burden and longer disease duration. Our results illustrate that the lowering of disease burden in highly modular social networks is driven by two mechanisms of modular organization: network fragmentation and subgroup cohesion. Highly fragmented social networks with cohesive subgroups are able to structurally trap infections within a few subgroups and also cause a structural delay to the spread of disease outbreaks. Finally, we show that network models incorporating modular structure are necessary only when prior knowledge suggests that interactions within the population are highly subdivided. Otherwise, null networks based on basic knowledge about group size and local contact heterogeneity may be sufficient when data-limited estimates of epidemic consequences are necessary. Overall, our work does not support the hypothesis that modular structure universally mitigates the disease impact of group living.

Social behavior is ubiquitous in vertebrates and arthropods. An evolutionary product of sociality in animal populations is group living. Group-living societies benefit from improved success in intergroup competition, protection from predation, mating opportunities, cooperative care of young, foraging success, and group defense. Conversely, group living is also associated with the costs of elevated disease burden due to a higher frequency of contact between hosts (1). Recently, it has been suggested that modular subdivisions in social interactions alleviate the association between group size and disease burden (2, 3).

Modular organization emerges in animal groups when subsets of conspecifics consistently interact with each other more often than they do with other individuals in the group, forming subgroups. Such modular structure is widespread across social networks in wildlife species, including relatively solitary species (4, 5), and can emerge from a combination of social behavior, demography, environmental, and landscape factors. However, theoretical investigations of the impact of modularity on spreading processes have produced mixed results in the past. Although some studies have suggested that modular subdivisions reduce transmission by creating structural bottlenecks (6–8), a few have found modular structure to increase outbreak size due to higher connectivity within subgroups (9, 10). This discrepancy in past research implies the need to consider realistic ranges of modularity (because not all animal social networks exhibit the high levels of modular subdivision typically investigated in past studies) and the need to mechanistically understand how modular structure in social networks affects the dynamics of disease spread.

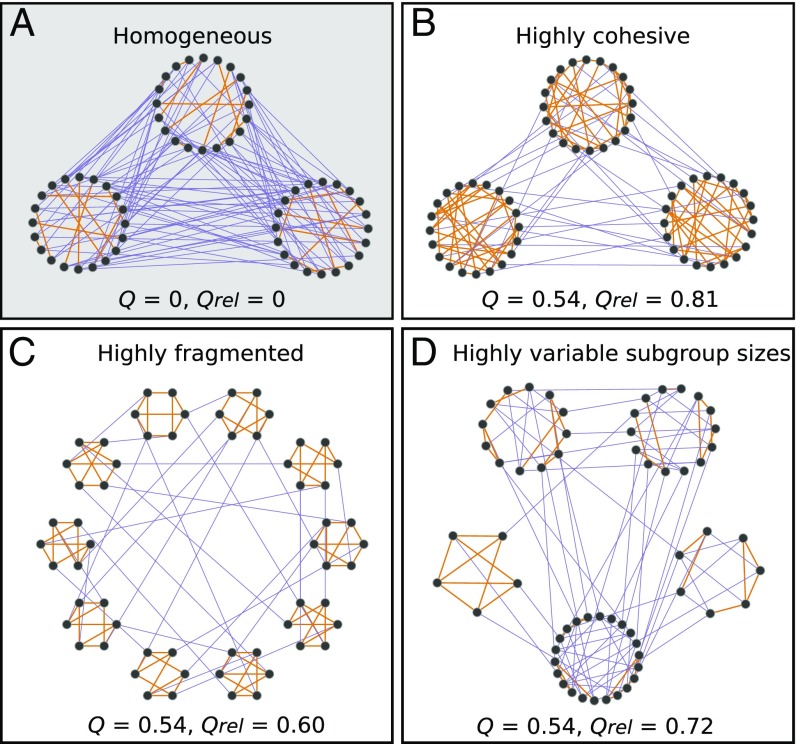
Thus, we propose an empirically driven investigation of the structural features of interaction patterns that are associated with modular subdivisions in animal groups, including the ones that change the degree of network fragmentation (i.e., the number of subgroups), promote subgroup cohesion (i.e., individual preferences to interact with subgroup members), and drive variation in subgroup size (Fig. 1).

Fig. 1.

Schematic representation of a homogeneous social network with no modular subdivision (A) and highly modular social networks with high cohesion within subgroups (B), high network fragmentation (C), and high subgroup size variation (D). Each network has 60 nodes. Orange edges indicate interactions within a subgroup, and purple edges are between-subgroup interactions. $Q$ is Newman modularity (11) and $Q_{rel}$ is relative modularity.

We have three objectives: (i) identify features of animal interaction patterns that increase the strength of modular organization in their social networks; (ii) explore the conditions under which modular organization influences the dynamics of disease spread and explain the mechanisms behind observed effects; and (iii) investigate whether knowledge of modular organization in animal social networks is necessary (and sufficient) to build accurate contact network models of disease spread. Overall, our study provides mechanistic insights on the context in which modular structure influences infectious disease spread in animal populations. We further suggest the use of appropriate null models when data-limited estimates of epidemic consequences in animal groups are necessary.

Results and Discussion

Modular Organization and Disease in Animal Social Networks.

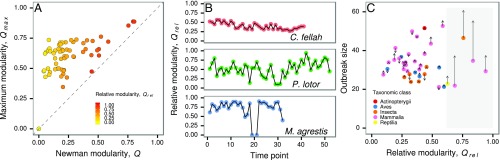
We obtained published (and publicly available) social networks for 69 groups across 43 animal species where edges can serve as realistic routes of infection spread. Newman modularity, $Q$, is a commonly used measure to estimate the strength of subdivision in networks (11). When $Q=0$, the density of interactions within subgroups is equivalent to the density of interactions between subgroups. Higher values of Newman modularity indicate stronger subdivisions of social networks. However, using Newman modularity to compare modular subdivision across networks is problematic because the measure is inherently correlated to the size and number of links in the network (12). This is because, in principle, we expect the maximum modularity $Q_{max}$ of all networks to be equal to one. However, for smaller networks, $Q_{max}$ tends to be a much smaller value (Fig. 2A). We therefore estimated relative modularity (obtained by normalizing $Q$ by $Q_{max}$) to facilitate comparison of modular subdivision strength across different animal groups. Animal social networks in our database ranged from homogeneous ($Q_{rel}$ = 0) to highly subdivided structure (Fig. 2A). Animal interactions are dynamic in nature, and therefore social networks of the same set of individuals can also fluctuate between being relatively homogeneous to highly modular over time (Fig. 2B).

Fig. 2.

Animal social networks with modular subdivisions. (A) Values of Newman modularity, $Q$, and maximum possible modularity given the network configuration, $Q_{max}$, across all animal groups in the database. Point color represents the relative modularity estimated as the ratio of $Q$ over $Q_{max}$. The dashed line represents $Q$ = $Q_{max}$ and the maximum value of $Q_{rel}=1$. (B) Relative modularity values of dynamic interactions in ants (Camponotus fellah), raccoons (Procyon lotor), and field voles (Microtus agrestis), where time points represent consecutive days, weeks, and trapping sessions, respectively. (C) Comparisons between real (filled points) and their homogeneous null networks (tips of arrows) with respect to the percentage of infected individuals (outbreak size) due to an outbreak with basic reproduction number, $R_0=1.2$. Point color corresponds to the taxonomic class of the animal group. Social networks with nonsignificant modular subdivision (as indicated by t test analysis) have been excluded in C. The generated homogeneous null networks preserve only the local heterogeneity of contacts among individuals; the arrows therefore indicate the change in direction and magnitude of outbreak size under the scenario in which all higher-order structural complexities (including modular subdivisions) are removed from animal social networks. The shaded area represents the region where empirical networks tend to experience reduced outbreak size (at $Q_{rel}>0.6$; SI Appendix, Fig. S2). The networks that experienced lower disease burden included social networks of raccoons (P. lotor), elephant seals (Mirounga angustirostris), ants (Camponotus pennsylvanicus), bottlenose dolphins (Tursiops truncatus), and Australian sleepy lizards (Tiliqua rugosa). In A and C, we used a randomly selected network snapshot for groups with temporal interaction data.

To gain intuition about how modular organization in animal social networks influences epidemiological outcomes, we first generated homogeneous null networks for each empirical animal social network in our database. In homogeneous null networks, higher-order organization in social networks (such as modular structure, clustering coefficient, cliquishness, and degree homophily) are randomized, weakening relative modularity (SI Appendix, Fig. S1), but individual contact heterogeneity (degree distribution) of the empirical network is preserved. We next performed susceptible–infected–recovered (SIR) disease simulations of a moderately transmissible infectious disease (basic reproduction number, $R_0=1.2$) through these empirical networks and their homogeneous null network counterparts. Based on previous work suggesting a protective effect of modular structure on disease risk (3, 6), we expected a lower disease burden (measured as the proportion of population infected) in empirical networks than in homogeneous null networks. Reduced disease burden, however, was apparent only in social networks with $Q_{rel}>0.6$ for moderately spreading infectious disease (Fig. 2C and SI Appendix, Fig. S2). Additionally, none of the empirical networks demonstrated a major reduction in disease burden for a highly transmissible infectious disease ($R_0=4.8$, SI Appendix, Fig. S3). This implies that the protective effect of modular subdivisions is realized only at high values of relative modularity, but the presence of a threshold depends on pathogen transmissibility (SI Appendix, Fig. S3).

Determinants of Modular Organization in Animal Social Networks.

Fig. 2C suggests that the epidemiological consequences of modular structure are context-dependent, depending on the strength of relative modularity, and only above a certain threshold. Additionally, the extent of outbreak size reduction above the modularity threshold was fairly inconsistent across networks. This could be due to varying features of interaction patterns driving modular subdivision in animal social networks. We therefore first turned our attention to some of these network features, including the number of individuals present in the social network (network size); (log of the) number of subgroups in the social network (network fragmentation); preferential association with own subgroup (subgroup cohesion, measured as the proportion of total contacts that occur within subgroups); variation in subgroup cohesion across the network; average and variation in subgroup sizes; average and variation in number of individual contacts (degree); and variation in contacts among subgroups (subgroup degree variation). For groups that had multiple temporal snapshots of a social network, we randomly selected one snapshot network for the analysis to avoid intragroup correlation in network metrics (and we analyze these temporal networks separately below).

The mixed-effects beta-regression model identified three network features driving modular organization in animal social networks: subgroup cohesion, network fragmentation, and subgroup size variation (Table 1). Of the three factors, subgroup cohesiveness and network fragmentation had strong positive effects on modular organization. Cohesiveness can be a direct result of strong social bonds due to similar nutrient requirements [e.g., in spotted hyenas (13)], time spent foraging together, or matrilineal descent [e.g., in African elephants (14)]. High network fragmentation, conversely, can be caused by constraints on resource density, resource distribution, or high intragroup competition [e.g., in brown spider monkeys (15)]. In contrast to network fragmentation and subgroup cohesion, we found variation in subgroup sizes to have a weak negative effect on network modularity. Fluid subgroup sizes are common in many social species (e.g., in spotted hyenas, elks, chimpanzees, bottlenose dolphins, and African lions) and can be brought about by changes in resource availability, intragroup aggression, demographic factors (such as sex ratio), dominance hierarchy, and female reproductive state (13, 15, 16).

Table 1.

Multivariable analysis on determinants of modular organization ($Q_{rel}$) across groups of different species

Explanatory variable	Effect size	95% confidence intervals
Intercept	−0.42	−0.59 to −0.25
Network size	−0.07	−0.17 to 0.03
Network fragmentation*	0.66	0.51 to 0.82
Subgroup cohesion*	1.14	1.03 to 1.25
Subgroup cohesion variation	−0.03	−0.14 to 0.08
Subgroup size average	—	—
Subgroup size variation*	−0.13	−0.26 to −0.01
Individual degree average	—	—
Individual degree variation	0.07	0.04 to 0.18
Subgroup degree variation	0.01	−0.08 to 0.10
Random effects	Variance estimate (${\sigma }^{\mathrm{2}}$)
Taxonomic order	0.066
Sociality	$<$0.001

Asterisks and bold text indicate significance. Explanatory variables with VIF > 5 were dropped from the model, and therefore their effect sizes were not estimated.

Thus, far, we have considered only a single snapshot of interactions for each animal group in our database for consistent comparison across species with unequal sampling efforts. However, dynamic interactions between group members in fission–fusion species, species with nomadic individuals, or species with seasonally driven social interactions can change the level of network modularity over time (Fig. 2B). We therefore repeated the analysis by considering dynamic interactions for a few animal groups for which such data are available. Consistent with our previous analysis of aggregated interactions, we found that animals groups become increasingly modular with higher subgroup cohesion or network fragmentation (SI Appendix, Table S1). In addition, variation in subgroup size and variation in contacts among subgroups had a weak negative correlation on relative modularity within animal groups.

The Impact of Modularity on Dynamics of Disease Spread.

We have shown that network fragmentation and cohesion within subgroups are associated with modular structure in animal social networks. Do the two factors also determine the disease consequences of modular subdivisions in animal social networks? To answer this question, we used synthetic modular networks generated using our model proposed in ref. 17. The model generates networks with a tunable strength of modularity, while keeping other higher-order network features (such as degree homophily, clustering coefficient, and path length) close to the configuration realized in homogeneous networks (17). Because several structural features of networks can influence disease spread, this approach is appropriate to isolate the epidemiological consequences of modular organization in social networks. Performing SIR disease simulations on synthetic modular networks, we found that the magnitude of outbreak size experienced by low modular networks ($Q_{rel}<0.6$) was similar to that of homogeneous networks ($Q_{rel}=0$). Outbreak size was reduced only in extremely modular networks for moderately transmissible pathogens (Fig. 3 A and B). We corroborated our finding that highly (but not low) modular networks inhibit global parasite transmission by using empirical data to investigate the spread of protozoan parasites Babesia in the social networks of field voles (18) (SI Appendix, Fig. S11). In addition, we found no empirical evidence of structural trapping of a gastrointestinal parasitic infection in the low modular social network of brown spider monkeys (19) (SI Appendix, Fig. S12).

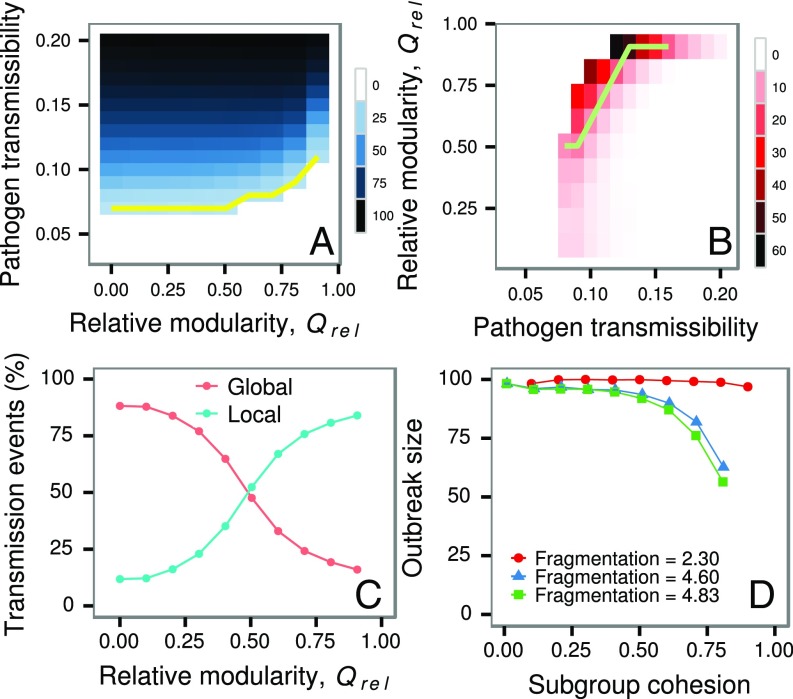
Fig. 3.

Overall disease implications of modular subdivisions in synthetic modular networks. (A) Average outbreak size, measured as the percentage of infected individuals, over increasing subdivided social networks and pathogen transmissibility. Outbreak size values have been normalized to the maximum observed outbreak. The solid line indicates epidemic threshold—namely, the threshold value of pathogen contagiousness below which there is no risk of a large outbreak ($>$10% outbreak size; Materials and Methods). (B) Epidemic robustness of networks with increasing value of relative modularity, measured as the percentage reduction in outbreak size compared with outbreak size experienced by homogeneous ($Q_{rel}=0$) networks. The solid line indicates the modularity threshold, where networks experience at least a 10% reduction in outbreak size. (C) Infection transmission events, expressed as the percentage of total outbreak size, within subgroups (local) and between subgroups (global); pathogen transmissibility = 0.18. (D) Disease implications of modular subdivisions as a function of subgroup cohesion and network fragmentation (measured as the log-number of subgroups present in the network).

We next quantified the robustness of modular social networks toward disease spread in two ways. First, we estimated the minimum level of pathogen contagiousness below which there is no risk of a large outbreak (epidemic threshold; solid line in Fig. 3A). We found networks with $Q_{rel}>0.6$ to have a higher epidemic threshold compared with homogeneous and low modular networks, implying that highly modular networks alleviate the risk of large disease outbreaks for low contagious pathogens. Second, for pathogen transmissibility beyond the epidemic threshold, we calculated the minimum level of relative modularity in which networks experience at least a 10% reduction in outbreak size compared with homogeneous ($Q_{rel}=0$) networks (modularity threshold; solid line in Fig. 3B). We found that networks with $Q_{rel}\ge 0.5$ mitigated disease spread for moderately contagious (transmissibility = 0.08–0.16) but not highly contagious pathogens (transmissibility > 0.16). Highly modular networks ($Q_{rel}>$0.8) had a striking impact on disease transmission—outbreak sizes of moderately transmissible pathogens were reduced up to 58% compared with homogeneous networks. Such highly modular networks, although rare, do occur in some host interaction networks. In our database, three animal species demonstrated $Q_{rel}$ values of >0.8—raccoons (P. lotor), field voles (M. agrestis), and northern elephant seals (M. angustirostris).

The question then is why do not all levels of modularity reduce disease burden in animal social networks? The relationship between disease burden and modularity depends on the tradeoff between local disease transmission within subgroups and global disease spread (Fig. 3C). Compared with homogeneous networks (with $Q_{rel}=0$), modular networks experience higher local transmission due to a high density of contacts within subgroups; conversely, low intersubgroup contacts in these networks reduce global disease transmission (Fig. 3C). This tradeoff balances the overall disease spread, and thus modular structure, under most conditions, does not lower disease burden. The conditions under which modularity does reduce disease burden of social networks is largely determined by the two factors underlying network modularity—network fragmentation and subgroup cohesion (Table 1). Synthetic networks that possess both high subgroup cohesion and high network fragmentation experience lower outbreak size compared with homogeneous and low modular social networks (Fig. 3C and SI Appendix, Fig. S6). In addition, high variation in subgroup sizes along with high subgroup cohesion and fragmentation further reduce outbreak size and increase outbreak duration in social networks (SI Appendix, Fig. S7). Disease consequences in real animal social networks, however, tend to be driven by subgroup cohesion because they typically exhibit a much lower range of fragmentation and subgroup size variation compared with subgroup cohesion (SI Appendix, Figs. S4 and S5).

Mechanisms That Drive the Impact of High Modular Structure on Disease Spread: Structural Delay and Trapping.

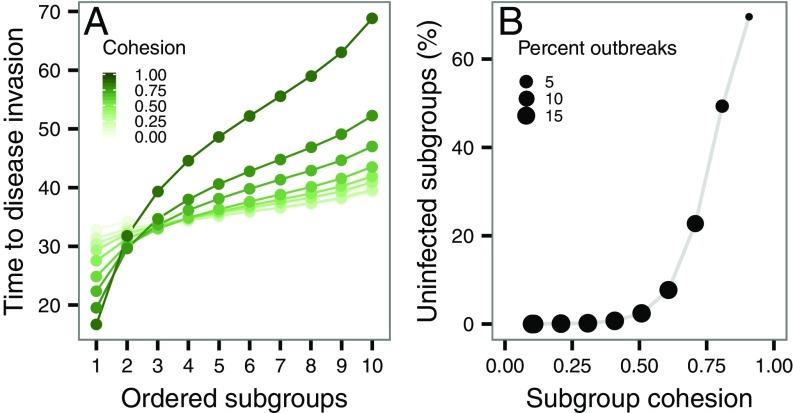
We next examined the mechanisms by which highly fragmented social networks with cohesive subgroups experience reduced disease burden. The presence of only a few interactions between highly cohesive subgroups increased the amount of time it took for an infection to spread from one subgroup to another (the structural delay effect; Fig. 4A), causing longer disease outbreaks. When networks were fragmented into highly cohesive subgroups, the structural delay imposed by cohesion caused infection to be localized to a small proportion of subgroups before dying out (Fig. 4B). Popularly known as structural trapping (20), this effect also reduces the overall likelihood of a major outbreak by a novel infection in modular social networks. The structural trapping effect (albeit weak) has been observed in a field study of pneumonia transmission in highly subdivided networks of bighorn lambs (SI Appendix, Fig. S13) (21) and others (SI Appendix, Table S2). We also found empirical evidence of structural delay in the spread of mycoplasma in the low-modular network, but highly cohesive subgroups, of house finches described in ref. 22 (SI Appendix, Fig. S14). A high probability of extinction associated with the structural trapping effect has been reported in theoretical studies of disease spread in spatially structured metapopulation models (7, 8). We note that the magnitude of structural trapping and delay depends on the contagiousness of the infection—moderately transmissible pathogens spread slowly through populations and are therefore able to perceive modular structures present in networks. For rapidly spreading pathogens, highly fragmented and cohesive networks do not contain, but delay, the spread of disease to other subgroups, creating only a structural delay effect.

Fig. 4.

Mechanisms behind the effect of modular organization on disease spread of a moderately transmissible pathogen (= 0.1). (A) Structural delay effect in a moderately fragmented network (fragmentation = 2.30): We considered the time to disease invasion for a subgroup as the number of time steps it takes for at least 2$\%$ of individuals to acquire infection. Subgroups at the x axis are sorted according to the increasing disease invasion time. (B) Structural trapping effect in a highly fragmented network (fragmentation = 4.83): High fragmentation and subgroup cohesion localize infection to a small proportion of subgroups in the social network. Structural trapping also increases the likelihood of stochastic extinction of disease outbreaks.

Is Knowledge of Modular Structure Necessary (and Sufficient) to Predict Disease Outcomes?

Our investigations of disease consequences on synthetic networks suggest that only modular subdivision beyond a certain threshold can reduce disease burden of moderately transmissible pathogens. Other topological features of the network—and, in particular, heterogeneity in host contact (23)—are, however, bound to confound the effect of modularity on infectious disease spread. Our work thus far assumes high variation in contacts among individuals (24), although factors including sociality (25) and nonpersistent space use (26) are known to reduce variation in individual contact rate. Does individual contact heterogeneity then affect the way modular organization influences disease spread? We found that for social networks with low contact heterogeneity, high modularity brings about a greater reduction in disease burden compared with networks with high contact heterogeneity (SI Appendix, Fig. S8). These results imply that the local contact patterns should also be considered when estimating the reduction of disease burden in extremely subdivided social networks.

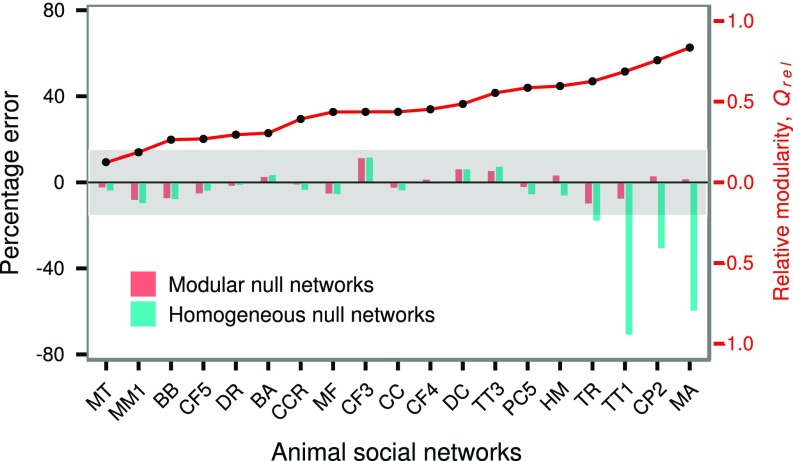
Although modular subdivision is a common feature observed in many animal groups, it is often correlated with other higher-order network structures, such as clustering coefficient and degree homophily (27). In empirical networks, it is therefore important to ask whether modular organization has any epidemiological consequence above and beyond these network properties, after accounting for contact heterogeneity. To answer this question, we performed disease simulations through 19 animal social networks in our database and their modular null networks. Modular null networks preserve the modularity level and degree distribution of their empirical network counterparts, but randomize all other network structure. We expected a high error rate in outbreak size prediction from modular null networks if other structural features mask the effect of modular subdivisions. We also compared the performance of modular null networks with that of homogeneous null networks, where all network structure, except degree distribution, was randomized (similar to the networks used in Fig. 2C). We found low (but not zero) percentage error in outbreak size predictions from modular null networks (Fig. 5 and SI Appendix, Fig. S9). Homogeneous null networks, however, performed equally well in predicting disease outcome for most animal social networks, except when relative modularity of empirical networks was high ($Q_{rel}$ > 0.6). We note that this $Q_{rel}$ value is similar to the threshold identified above (Fig. 2C and SI Appendix, Fig. S2). For moderately transmissible infections, animal social networks experience low outbreak size at this level of modular structure due to the structural trapping effect. Homogeneous null networks do not preserve the modular structure of the empirical networks and, therefore, overestimate the true disease burden. In contrast to moderately spreading infectious diseases, slowly ($R_0$ < 1) and rapidly spreading infections are unaffected by higher-order complexities of the networks, and therefore outbreak size estimates of homogeneous and modular null networks are similar across all levels of relative modularity (SI Appendix, Fig. S10). To empirically confirm the results of our disease simulations, we compared the performance of modular and homogenous null networks to predict outbreak size of two Salmonella enterica strains in the Australian sleepy lizards, T. rugosa, using data described in ref. 28 (SI Appendix, Fig. S15). Congruent to the theoretical predictions, homogeneous and modular networks produced identical and accurate outbreak size predictions for the low-transmissibility strain. For the moderately transmissible strain, conversely, modular null networks performed better in estimating the true disease burden.

Fig. 5.

Percentage error in outbreak size predictions using modular and homogeneous null networks for 19 animal social networks due to an outbreak with $R_0=1.2$. Percentage error is calculated as $(S_{emp}-S_{null})/S_{emp}\times 100$, where S = outbreak size, $emp$ = empirical network, and $null$ are modular or homogeneous null networks of the empirical network. The social networks are ordered according to the increasing value of relative modularity (red solid curve, secondary y axis). The shaded region indicates the range of percentage error values <$15\%$. BA, Brachyteles arachnoides; BB, Bison bison; CC, Cercopithecus campbelli; CCR, Crocuta crocuta; CF, C. fellah; CP, C. pennsylvanicus; DC, dairy cattle; DR, Desmodus rotundus; HM, Haemorhous mexicanus; MA, M. angustirostris; MF, Macaca fuscata; MM, Macaca mulatta; MT, Macaca tonkeana; PC, Papio cynocephalus; TR, T. rugosa; TT, T. truncates. Numbers denote separate groups of the same species.

Conclusions

While modular social organization has been postulated to alleviate the disease burden of group-living species, past evidence supporting this hypothesis has been equivocal. More importantly, the features of interaction patterns that cause animal social networks to be subdivided have not been identified before. In this study, we resolved the ambiguity of past research on disease consequences of network modularity in three ways. First, we introduced a normalized version of Newman modularity called relative modularity ($Q_{rel}$) to allow comparison across networks of different sizes and identified two distinct mechanisms that can lead to modular structure. Second, we systematically studied the epidemiological consequences of modular organization by using a model (17) that allows for the mechanistic generation of synthetic modular networks and null networks (of empirical animal social networks), while minimizing the presence of higher-order network properties. Third, we combined published social networks across 43 animal species with this theoretical network model and biologically realistic disease simulation to derive insights into disease consequences of mechanisms of modular organization in animal societies.

It has been hypothesized that subgroups in animal social networks reduce the disease costs of group living (2, 3). Contrary to this hypothesis, our study shows that disease burden is largely unaffected by modular subdivisions in animal groups, except when social networks are extremely fragmented and have high cohesion within subgroups. High subgroup cohesion and fragmentation in networks structurally trap moderately transmissible infections to a few subgroups and therefore reduce the overall disease burden. We note that, although overall disease burden is unaffected at most levels of modularity, the design of control strategy will vary for different levels of network modularity. An effective intervention should aim to minimize global spread of infection for low network modularity, but reduce local transmission at high network modularity. Because our analysis is based on a systematic investigation of contagion spread in synthetic modular networks, the results of this study are potentially applicable across a wide range of systems, including spreading processes at higher ecological scales (SI Appendix, Table S2), infectious disease spread in human interaction networks and transportation networks, and perturbation spread in metabolic and ecological networks, as well as spread of information through communication networks.

Because this study involved meta-analysis of social networks across a broad range of taxonomic groups, we made a number of simplifying assumptions that should be considered before extending the results to a specific system. First, we filtered the weights assigned to social interactions between individuals to construct unweighted networks. This was because the impact of weights (whether they represent frequency, duration, or intensity of contact) on transmission potential is generally unclear and usually context-dependent. We advise leveraging transmission studies in captive populations or historical disease spread data, where available, to identify the appropriate weighting criterion of contact networks. Second, we assume that the aggregated static networks and temporal “snapshots” of dynamic networks in our database coincide with the temporal scale relevant to infection spread in our disease simulations. Consideration of the relevant time interval of animal interactions relative to the transmission mode and infectious period of the pathogen, however, is crucial to developing accurate network models of disease spread (7, 29). Because many animal interactions can be infrequent or intermittent, particularly between subgroups, aggregating interactions over a small time window may ignore these fleeting contacts and overestimate the modularity of social networks. Conversely, pooling interactions over large time windows may amplify the role of temporary contact, and, consequently, the social subgroups might appear more connected. In addition, chronic infections with a long infectious period will be relatively unaffected by high network modularity if the time scale of network fluctuations is shorter than the average infectious period. Acute infections with short infectious periods, however, will be highly sensitive to the state of network modularity at the time of disease outbreaks.

This study suggests the presence of a high modularity threshold, above which social networks experience reduced outbreak size. However, we caution against the use of a single modularity threshold that is applicable to all systems. Multiple behavioral, ecological, and epidemiological factors—including pathogen infectiousness (Fig. 3B), infectious period, local contact heterogeneity, seasonality of contacts, and transmission, coupled with recruitment of susceptible through births—can influence the $Q_{rel}$ threshold and the extent to which network fragmentation and subgroup cohesiveness structurally trap and delay infection spread. Therefore, to assess the disease implications of modular structure observed in specific social groups, we recommend the use of null networks, as presented in this study. Comparison of disease consequences on empirical network data with those on a hierarchy of null networks clarifies whether modular structure is important. If natural history and limited observations suggest a species’ network will be highly modular, then models that incorporate modularity should be used; otherwise, homogeneous null models (based on basic knowledge about network size and local heterogeneity) may be sufficient when data-limited estimates of epidemic consequences are necessary.

Materials and Methods

Extended methods are provided in SI Appendix, SI Text.

Measuring Modularity.

We used modularity ($Q$) proposed by Newman (11) to measure the strength of modular organization in networks. Modularity can be defined as $Q={\sum }_{k=1}^K[\frac{L_k^w}{L}-{\left(\frac{L_k}{L}\right)}^2])$, where $L_k$ is the total number of edges in a subgroup $k$, of which $L_k^w$ are the edges within the subgroup, and $L$ is the number of total edges in the network. Community structure, or the number and composition of subgroups, for each animal social network was estimated by using the Louvain method (30). The highest possible modularity in a network ($Q_{max}$) is achieved when all individuals in a subgroup $k$ only interact with each other and no edges are present between subgroups (i.e., subgroups are disjointed). In other words, $Qmax$ of a network is when $L_k^w$ = $L_k$, and can be written as $Q_{max}={\sum }_{k=1}^K\frac{L_k}{L}\left(1-\frac{L_k}{L}\right)$. We measured the relative modularity of networks as $Q_{rel}=\frac{Q}{Q_{max}}$.

Mechanisms of Modular Organization.

To examine the relative contribution of factors such as network size, network fragmentation, average subgroup size, etc., toward network modularity, we ran a mixed-effects beta regression model using the glmmADMB package (Version 0.8.3.3) in R (Version 3.2.3). We treated the species nested within the taxonomic order of the animal group as a random effect in the model to account for any correlations in network metrics. However, the variance accounted for by the nesting of species was negligible (${\sigma }^2\approx 0$), and we therefore considered only taxonomic order as the random effect in the analysis. We also accounted for differences between the social organization of different species by defining three broad levels of sociality—relative solitary, social, and fission-fusion—and included sociality as a random effect in the model.

Generation of Synthetic Modular and Null Networks.

We used the network generator described in ref. 17 to generate networks of a specified modularity and degree sequence, while keeping other network properties close to homogeneous null networks. For Figs. 3 and 4, we generated synthetic modular networks with 10,000 nodes, with an exponential degree distribution with a mean degree of 10. Two types of null networks were generated for each animal social network. Modular null networks were created by randomizing within- and between-subgroup connections. The modular null networks therefore had identical modular configuration and degree sequence as empirical networks, but were random with respect to other higher-order network properties. We generated homogeneous null networks by performing simultaneous edge swaps over within- and between-subgroup connections, which preserves the local contact heterogeneity, but randomizes all higher-order features of the network, including network modularity.

Disease Simulations.

We performed Monte Carlo simulations of a discrete-time SIR model of disease spread. Because we were interested only in major outbreaks, we considered only those simulations in our calculations where at least 10% of the population acquired infection. Transmission occurred according to a pathogen transmissibility, defined as the probability of transmission from an infected to susceptible host during the period when the infected host is infectious. The recovery probability was assumed to be constant across hosts.